Prediction of marl reservoir distribution based on facies-constrained reflectivity inversion method

Accurate characterization of carbonate reservoirs remains a significant challenge due to complex facies variations and the substantial effects of wave propagation. We propose a facies-constrained reflectivity inversion strategy. The method establishes a relationship between logging data and seismic waveforms, applies clustering analysis using the Self-Organizing Map (SOM) technique, and utilizes the clustering results to constrain the construction of an initial model with realistic lateral variations. Based on this initial model, a Bayesian-based reflectivity inversion is performed, incorporating a modified Cauchy prior distribution to enhance inversion accuracy and stability. The reflectivity method offers a one-dimensional analytical solution to the wave equation, tacking thin layer thicknesses and wave propagation effects into consideration, thereby significantly alleviating inversion problems encountered in marl reservoirs. Compared to traditional inversion methods based on the Zoeppritz equation, the facies-constrained reflectivity inversion delivers higher accuracy and resolution. The application of this technique to identify marl reservoirs in the Lei₃² sub-member of the Sichuan Basin has yielded promising results, effectively delineating favorable reservoir areas of approximately 210 km² and offering strong support for future exploration and development.

1 Introduction

Carbonate reservoirs are one of the most important types of reservoirs worldwide (Yang et al., 2020; Dai et al., 2021; Zhu et al., 2021; Li et al., 2022; Meng et al., 2022; Sarhan, 2024). In the Sichuan Basin of China, the second sub-member of the third member of Leikoupo Formation (Lei₃² sub-member) of Middle Triassic hosts high-quality carbonate hydrocarbon source rocks (Yang et al., 2022; Wang et al., 2023; Zhang et al., 2024). Additionally, the dense anhydrite layers above and below the Lei₃² sub-member provide excellent preservation conditions (Jiang et al., 2021; Su et al., 2021; Zhang et al., 2023; Sarhan, 2024). This geological setting can form evaporite seals and integrated source-reservoir unconventional oil and gas accumulations.

Recent testing across multiple wells has revealed significant potential for industrial oil and gas production within the marl reservoir of Lei₃² sub-member (Xin et al., 2013; Tian et al., 2021; Xin et al., 2022; Wang et al., 2023; Xin et al., 2024; Zhang et al., 2024). However, predicting and studying the marl reservoirs present several challenges. Firstly, the marl reservoirs are primarily located at the top of the sub-member, but their small impedance differences with the overlying salt rocks make them hard to distinguish using traditional inversion methods (Zhang et al., 2024; Yang et al., 2022). Secondly, extensive gypsum layers within the Lei₃² sub-member are interbedded with the marl (Zhang et al., 2023a; Zhang et al., 2023b; Yang et al., 2022), causing significant seismic wave propagation effects. Thirdly, the marl reservoirs are relatively thin, and with seismic data’s primary frequency at around 20 Hz, accurately characterizing these thin reservoirs is challenging. Finally, the lateral variation and unclear distribution pattern of marl reservoirs, coupled with a limited number of wells for analysis, result in low inversion accuracy and ambiguous results. These challenges present severe obstacles to the detailed characterization of marl reservoirs, and the lack of prior research on predicting marl reservoirs hampers future exploration strategies. Therefore, an effective geophysical method is urgently needed to achieve precise characterization of the marl reservoirs in Lei₃² sub-member.

The quantitative reservoir characterization often relies on seismic inversion (Bosch et al., 2010; Grana and Della, 2010), but traditional methods are mostly based on the Zoeppritz equation or its approximations (Aki and Richard, 1980; Gidlow et al., 1992; Fatii et al., 1994; Shuey, 2012; Zhou et al., 2020; Zhou et al., 2021; Song et al., 2023). Traditional methods can directly predict the elastic parameters for high-quality seismic data under simple geological conditions (Babasafari et al., 2021). But these methods include certain constraints, such as assuming that the received seismic data consists of primary reflections, thereby neglecting wave propagation effects (such as geometric spreading, attenuation, transmission loss, etc.) and the influence of reservoir thickness. Additionally, the approximations assume small variations in elastic parameters and incident waves are projected at small angles (Mallick, 2007; Mallick and Adhikari, 2015). Inversion using these methods can lead to inaccuracies, which restricts their effectiveness in accurately predicting thin carbonate reservoirs.

The elastic wave equation inversion may be the most suitable method for predicting elastic parameters of the thin carbonate reservoirs (Liu et al., 2022), but it faces challenges with computational efficiency and stability. The reflectivity method (RM) is a vectorized recursive computational approach for full-wavefield simulation under the assumption of a one-dimensional layered Earth model. It factors in reservoir thickness and wave propagation effects, providing a significantly higher computational efficiency (Zhao et al., 1994; Ma et al., 2004). Therefore, RM effectively addresses the challenges posed by wave propagation effects and thin reservoirs in marl reservoir analysis. The most widely utilized RM is the recursive matrix algorithm introduced by Kennett (1983). Subsequent developments and applications in RM methods are largely rooted in or evolved from this theory, leading to its designation as KRM (Kennett RM) (Fuchs and Müller, 1971; Kennett, 1983; Muller, 1985; Zhang and Yin, 2004; Fryer, 2007; Yin et al., 2006). However, these methods incur substantial computational overheads due to their nested calculation approach, which complicates derivative computations. In order to streamline this process, a vectorized RM for computing recursive matrices was proposed (Phinney et al., 1987). This vectorized approach has since been refined to address problems associated with derivative calculations (Chen et al., 2020). The RM study in this paper builds upon this modified vectorized technique for inversion research. Additionally, sparse solutions can be achieved through Bayesian inversion methodologies that utilize appropriately chosen long-tailed prior probability distributions (Misra and Sacchi, 2008; Alemie and Sacchi, 2011). A modified Cauchy distribution (Sacchi, 1997; Alemie and Sacchi, 2010; Theune et al., 2010) is incorporated within a Bayesian framework to preserve weak reflection signals and enhance the overall accuracy and stability of predictions (Sen and Roy, 2003; Liu et al., 2016).

To tackle the challenges of rapid lateral variations in marl reservoirs and limited well data, which hinder the establishment of accurate initial models and consequently reduce inversion accuracy, we propose a seismic facies-constrained reflectivity inversion strategy. This strategy hinges on analyzing logging data and correlating them with seismic waveforms. Subsequently, cluster analysis is applied to these waveforms to identify seismic facies, which serve as constraints for constructing the initial model. This model, incorporating reasonable lateral variations, is essential for subsequent inversion studies. The clustering analysis here is performed using Self-Organizing Maps (SOM) technique (Kohonen, 1990; De Matos et al., 2007; Liang, 2024; Owusu et al., 2024), which is an unsupervised learning neural network consisting of a two-dimensional grid, where each grid cell is called a neuron. Each neuron on the grid has a weight vector that represents its position in data space. The learning process involves two stages: competition and cooperation. In the competition stage, input samples are matched to determine the optimal winning neuron. In the cooperation stage, the winning neuron and its neighboring neurons adjust their weight vectors based on the input data, making them closer to the winning sample. This process allows SOM to map high-dimensional input data onto a two-dimensional grid while preserving its topological structure and forming clustering results.

In brief, we propose a seismic facies-constrained reflectivity inversion strategy based on Bayesian framework to enhance the accuracy of thin marl reservoir inversion. The paper begins with an overview of the regional geology, detailing the lithology, physical properties, and characteristics of the reservoir. It then introduces the facies-constrained reflectivity inversion theory. Utilizing this technique, we achieved high-precision characterization of the thin marl reservoirs in Lei₃² sub-member. This approach enabled the determination of thickness distributions for upper salt formations and the marl reservoirs. The method’s feasibility and effectiveness were confirmed through verification against actual well data and geological understanding.

2 Methods

The facies-constrained inversion is a strategy for constructing initial models in seismic inversion based on constraints of seismic facies. Traditional inversion methods analyze seismic data trace by trace, primarily focusing on vertical amplitude changes. In contrast, facies-constrained inversion utilizes lateral waveform variations to characterize spatial heterogeneity of reservoirs, closely related to depositional environments (Gu et al., 2016; Zhang et al., 2018; Zhang et al., 2018; Ting et al., 2023). The method integrates sedimentary facies and logging data, utilizing SOM technique for waveform clustering analysis. The clustering results are then used as constraints for constructing an initial model that reflects spatial variations of reservoirs and incorporates facies information. Based on the initial model, high-precision inversion of marl reservoirs using the reflectivity method is achieved within a Bayesian framework. See Figure 1 for the detailed workflow.

Figure 1

Figure 1. The workflow of the facies-constrained reflectivity inversion method.

2.1 Establishment of facies-constrained initial model

The facies-constrained inversion method integrates geological information into waveform attributes during the inversion process, enhancing the accuracy of the inversion results in representing actual sedimentary patterns (Zhang et al., 2021). The essence behind this method is to analyze well log data, integrate sedimentary facies and geological information to classify well log facies. These classifications then serve as a basis for distinguishing among various seismic waveforms. Cluster analysis is performed around these seismic waveforms to obtain seismic facies results, and finally, the clustered seismic facies are used as constraints to establish the initial inversion model.

In this study, the initial phase of the constrained modeling technique involves filtering out low-frequency and high-frequency components from the well log data to better match the seismic bandwidth. Next, the characteristic waveforms of the area are clustered. Guided by the principle that well logs belonging to the same seismic facies exhibit comparable features with seismic waveforms, we retrieve M-trace waveform data that exhibits a high degree of similarity to the waveforms adjacent to each well. This process allows us to construct a waveform sample library tailored to the target layer of the study area. Following this, we utilize the wavelet transform to map the well logging data into the wavelet domain for a comprehensive multiscale analysis. By extracting similar structures from each sample, we construct the initial inversion model. Elaborate on the construction of the waveform sample set, within the same study stratum, using Markov chain Monte Carlo random network to perform unbiased estimation on these M-trace waveforms. The specific expression is given by Equation 1:

$\mathit{P}\left({\mathit{u}}_{\mathbf{0}}\right)={\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}{\mathit{\beta }}_{\mathit{i}}\mathit{P}\left({\mathit{u}}_{\mathit{i}}\right)(1)$

Where $N$ is the number of optimal waveforms selected from the sample library. $P\left(u_0\right)$ is the attribute value of the unknown point in the target layer of the study area. $P\left(u_i\right)$ is the attribute value of the waveform in the sample library. ${\beta }_i$ is the weighting coefficient of the ith representative waveform sample point with respect to the other unknown sample points, serving as a coefficient upon distance. After establishing the initial model, we can implement the reflectivity inversion method based on the Bayesian framework.

In addition, cluster analysis is performed using the Self-Organizing Map (SOM) method, which is a competitive neural network widely used for clustering and dimensionality reduction. The fundamental principles and steps involved in this process are outlined below.

(1) Initialization: Initialize the neural network with each neuron possessing a weight vector that matches the dimensionality of the input data. These weight vectors are typically initialized to small random values.

(2) Selecting the winning neuron: For each input sample, calculate its distance from the weight vectors of each neuron. Choose the neuron with the smallest distance, known as the winning neuron. This process ensures that the winning neuron exhibits the strongest response to the input data, making it the best match for the current input within the network.

(3) Updating neighboring neurons: Update the weight vectors of the winning neuron and its neighboring neurons to move their weight vectors towards the direction of the input sample. This process ensures that neighboring neurons in the input space move closer to each other as well. The magnitude of the update depends on the topological distance and the learning rate between the neurons and the winning neuron.

(4) Adjusting the learning rate and neighborhood radius: As training progresses, decrease the learning rate and the neighborhood radius to gradually stabilize the model.

(5) Iterative repetition: Repeat steps (2) and (3) to continuously adjust the weights of neurons, gradually forming clusters. Typically, multiple iterations are required to train the network to ensure adequate topological mapping and cluster formation.

After SOM learning is complete, each neuron represents a cluster center. Similar input data samples are mapped to nearby neurons, forming clusters that represent the clustering results of the data.

2.2 The reflectivity inversion method

As mentioned above, the reflectivity method can achieve full-wave field simulation of elastic wave equations, factoring in both the wave propagation effect and layer thickness. Assuming there are $\mathrm{N}$ layers of horizontally layered media underground, the total reflectivity coefficient $R\left(p,\omega \right)$ can be calculated through a six-element vector $\mathrm{\Gamma }$ (Equation 2) in the domain of frequency and slowness (Phinney et al., 1987; Chen et al., 2020):

${\mathit{\Gamma }}_{\mathit{n}}={\left[\begin{array}{cccccc}\mathit{\delta }& -{\mathit{R}}_{\mathit{S}\mathit{P}}\mathit{\delta }& -{\mathit{R}}_{\mathit{S}\mathit{S}}\mathit{\delta }& {\mathit{R}}_{\mathit{P}\mathit{P}}\mathit{\delta }& {\mathit{R}}_{\mathit{P}\mathit{S}}\mathit{\delta }& \left|\mathit{R}\right|\end{array}\mathit{\delta }\right]}^{\mathit{T}}(2)$

Among them, ${\mathrm{\Gamma }}_{\mathrm{n}}$ represents the overall reflection response below the $n$-th layer interface of the medium, the element $R$ represents the reflection coefficient, the first subscript of $R$ is the type of incident wave, and the second subscript is the type of reflected wave. $\delta$ is the scaling factor, usually taken as a constant of 1. $\left|R\right|$ is a determinant of the reflection coefficient and has no clear physical meaning.

Based on the elastic half-space below the base of the medium, the total response ${\mathrm{\Gamma }}_{\mathrm{N}}$ under layer N (Equation 3) can be formulated as:

${\mathit{\Gamma }}_{\mathit{N}}={\left[\begin{array}{cccccc}\mathbf{1}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\end{array}\right]}^{\mathit{T}}(3)$

Then we can use a recursive method (Equation 4) like this:

$\begin{array}{l}{\mathrm{\Gamma }}_n={\mathbf{W}}_n{\mathrm{\Gamma }}_{n+1}\\ {\mathbf{W}}_n={\mathbf{P}}_n^{+}{\mathbf{O}}_n{\mathbf{P}}_n^{-}\end{array}(4)$

Where ${\mathbf{Q}}_n$ is wave propagator matrix for layer $n$, ${\mathbf{O}}_n$ is layer crossing matrix, ${\mathbf{P}}_n^{+}$, ${\mathbf{P}}_n^{-}$ is downward and upward interface crossing matrix respectively.

Starting from the response at the bottom interface of the medium, the overall response below the top interface can be calculated through Equation 5:

${\mathrm{\Gamma }}_0={\mathbf{W}}_0{\mathbf{W}}_1\cdots {\mathbf{W}}_{N-1}{\mathrm{\Gamma }}_N(5)$

The total reflectivity in the frequency-wavenumber domain can be computed for PP waves (Equation 6):

${\mathbf{R}}_{PP}\left(\omega ,p\right)={\mathrm{\Gamma }}_0\left(4\right)/{\mathrm{\Gamma }}_0\left(1\right)(6)$

By integrating its slowness and frequency, and then convolving the seismic wavelet, the seismic records in the spatiotemporal domain can be calculated through Equation 7 (Mallick and Frazer, 1987):

$\mathrm{\Omega }\left(t,x\right)=1/2\pi {\int }_{-\infty }^{\infty }\chi \left(\omega \right)e^{iwt}d\omega {\int }_{-\infty }^{\infty }{\omega }^{2}p\mathbf{R}\left(\omega ,p\right){\mathrm{\Upsilon }}_0\left(wpx\right)dp(7)$

Where $\chi \left(\omega \right)$ is the seismic wavelets in the frequency domain, ${\mathrm{\Upsilon }}_0\left(wpx\right)$ is the Bessel function. However, the integration of slowness requires sufficient sampling to mitigate the phenomenon of spatial aliasing. Practical experience has demonstrated that the time needed for integration increases exponentially with the number of samples. To minimize time loss, we directly integrate over frequencies and resample slowness to obtain synthetic seismic data in the time-angle domain as shown in Equation 8:

$\begin{array}{l}{p}_n={\sin \theta /\alpha }_n\\ \mathbf{R}\left(\theta ,t\right)=1/2\pi {\int }_{-\infty }^{\infty }\mathbf{R}\left(\theta ,\omega \right)e^{iwt}d\omega \end{array}(8)$

The aforementioned content presents the forward modelling theory of reflectivity method. To better identify marl reservoirs, the reflectivity method is introduced into the Bayesian inversion framework. Based on the prior distribution and likelihood function, the posterior probability distribution can be computed. By calculating the derivative of the posterior probability distribution function with respect to the model parameters and setting it equal to zero, the maximum a posteriori (MAP) solution can be calculated. Therefore, the problem is transformed into solving the objective function (Equation 9):

$\mathrm{\Psi }\left(\mathbf{m}\right)=1/2{\sigma }_d^2{\left(\mathbf{d}-\mathbf{G}\left(\mathbf{m}\right)\right)}^T\left(\mathbf{d}-\mathbf{G}\left(\mathbf{m}\right)\right)+\mathrm{ƛ}\left(\mathbf{m}\right)(9)$

Where $\mathbf{m}$ represents the parameter to be inverted (including the velocity of compressional and shear waves, and density), $\mathbf{d}$ is the observed seismic data, $\mathbf{G}$ is the reflectivity forward operator, and $\mathbf{G}\left(\mathbf{m}\right)$ represents the regularization term. ${\sigma }_d^2$ is the noise variance.

The Gaussian distribution is one of the most common prior distributions and is widely used in pre-stack reservoir inversion. However, its smooth solutions tend to suppress high values, leading to reflection coefficient estimates that are lower than the true values, thereby reducing the resolution of the inversion. In contrast, the Cauchy distribution is designed to achieve sparse solutions, which allows for better recovery of high values in model parameters during the inversion process, enhancing resolution (Alemie and Sacchi, 2010). However, the Cauchy distribution is not a convex function, which means that it cannot guarantee convergence to the optimal solution during the iterative solving process. Therefore, we use the modified Cauchy distribution to conduct inversion research, which can effectively balance the enhancement of signal-to-noise ratio at strong reflection boundaries while providing appropriate protection for weak signals (Yin et al., 2013). Thus, $\mathrm{ƛ}\left(\mathbf{m}\right)$ can be expressed as Equation 10:

$\mathrm{ƛ}\left(\mathbf{m}\right)={\displaystyle \sum _{i=1}^N}\frac{{\left(\mathbf{m}-\mathbf{\mu }\right)}^T{\mathbf{\xi }}^i\left(\mathbf{m}-\mathbf{\mu }\right)}{1+{\left(\mathbf{m}-\mathbf{\mu }\right)}^T{\mathbf{\xi }}^i\left(\mathbf{m}-\mathbf{\mu }\right)}(10)$

Where $\mathbf{\mu }$ represents the mean, ${\mathbf{\xi }}_i={\left({\mathbf{D}}^i\right)}^T{\mathbf{\Sigma }}^{-1}{\mathbf{D}}^i$, $\mathbf{\Sigma }$ is the covariance matrix, and ${\mathbf{D}}^i$ is the sorting matrix.

Considering the nonlinearity of the forward operator $\mathbf{G}\left(\mathbf{m}\right)$, the objective function can be solved through the Gauss-Newton iteration method (Liu et al., 2016; Chen et al., 2020). The iteration formula is expressed as:

${\mathbf{m}}^{r+1}={\mathbf{m}}^r-\kappa \mathbf{P}\left({\mathbf{m}}^r\right)\mathbf{H}{\left({\mathbf{m}}^r\right)}^{-1}(11)$

where $\kappa$ represents the inversion iteration step size, while $\mathbf{P}$ and $\mathbf{H}$ denote the first and second-order partial derivatives of $\mathrm{\Psi }\left(\mathbf{m}\right)$ with respect to the model parameters, respectively. $\mathbf{P}$ and $\mathbf{H}$ can be expresses as:

$\begin{array}{l}\mathbf{P}\left(\mathbf{m}\right)=\frac{\mathrm{\partial }\mathrm{\Psi }\left(\mathbf{m}\right)}{\mathrm{\partial }\mathbf{m}}={\left(\frac{\mathrm{\partial }\mathbf{G}\left(\mathbf{m}\right)}{\mathrm{\partial }\mathbf{m}}\right)}^T\left(\mathbf{G}\left(\mathbf{m}\right)-\mathbf{d}\right)+{\sigma }_d^2\lambda \left(\mathbf{m}-\mathbf{\mu }\right)\\ \mathbf{H}\left(\mathbf{m}\right)=\frac{{\mathrm{\partial }}^2\mathrm{\Psi }\left(\mathbf{m}\right)}{{\mathrm{\partial }}^2\mathbf{m}}\approx {\left(\frac{\mathrm{\partial }\mathbf{G}\left(\mathbf{m}\right)}{\mathrm{\partial }\mathbf{m}}\right)}^T\frac{\mathrm{\partial }\mathbf{G}\left(\mathbf{m}\right)}{\mathrm{\partial }\mathbf{m}}+{\sigma }_d^2\lambda \end{array}(12)$

where $\lambda$ is the regularization factor.

Setting the initial model constrained by seismic facies as ${\mathbf{m}}_0$, the reflection coefficient $\mathbf{R}$ can be calculated based on the aforementioned reflectivity method forward theory. Subsequently, by convolving the reflection coefficient with the seismic wavelet, the synthetic seismic record $\mathbf{G}\left(\mathbf{m}\right)$ can be obtained. The derivative of $\mathbf{G}\left(\mathbf{m}\right)$ with respect to the model parameters ${\mathbf{m}}_0$ is then computed. Iterative calculations are performed using Equation 12 by substituting $\mathbf{G}\left(\mathbf{m}\right)$ and the calculated derivatives, and the model parameters are updated according to Equation 11 until reaching the maximum iteration count.

3 Case study

3.1 Geological setting

During the Middle Triassic period, the Indosinian Orogeny instigated a collective uplift of the carbonate platform. This geological event resulted in the formation of the ancient Luzhou-Kaijiang uplift in the eastern region of the basin, while the western section eventually evolved into the present-day western Sichuan Basin (Zhang and Yin, 2006; Ma et al., 2010; Li et al., 2012), as illustrated in Figure 2. Our study area, Block X, is situated in Sichuan Basin of southwestern China, covering an area of approximately 420 square kilometers. There is only one well in the study area: the CT1 well, which was drilled in 2023. Currently, the exploration of the marl reservoir is in its initial stage.

Figure 2

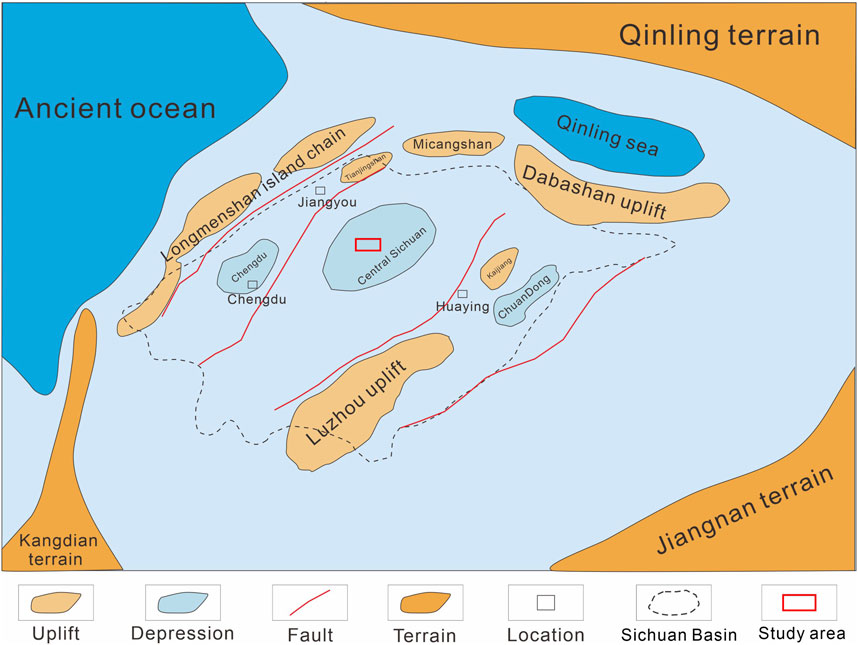
Figure 2. Paleogeographic background of the Middle Triassic Leikoupo Formation sedimentary period in the Upper Yangtze region.

This ancient geographical pattern affected the depositional environment during the formation period of Leikoupo layers. Influenced by the Indosinian Orogeny, the Lei₃² sub-member is characterized by lagoon deposits. Characterized by relatively weak hydrodynamic conditions and high salinity levels, the lagoon was controlled by sea-level fluctuations, leading to the deposition of alternating layers of gypsum, salt rock, and argillaceous limestone (Li et al., 2012; Tan et al., 2014). Multiple sets of organic-rich argillaceous limestones and calcareous mudstones were also deposited during this period. Moving outward from this gypsum salt rock lagoonal center, there is a gradual transition to gypsum-bearing argillaceous limestone lagoon and then argillaceous limestone lagoon. Notably, the thickness of these deposits peaks in the central regions and tapers off towards the edges. The uplifted area in the east underwent significant erosion (Figure 3B). Surrounding the lagoon, there are successive deposits of argillaceous limestone and calcareous mudstone. Closer to the gypsum salt rock lagoonal center, the development of gypsum and salt rocks was more pronounced. Conversely, as the distance increases, the content of gypsum and salt rocks gradually decreased, and the proportion of argillaceous limestone and calcareous mudstone in the strata increased accordingly (Figure 3A).

Figure 3

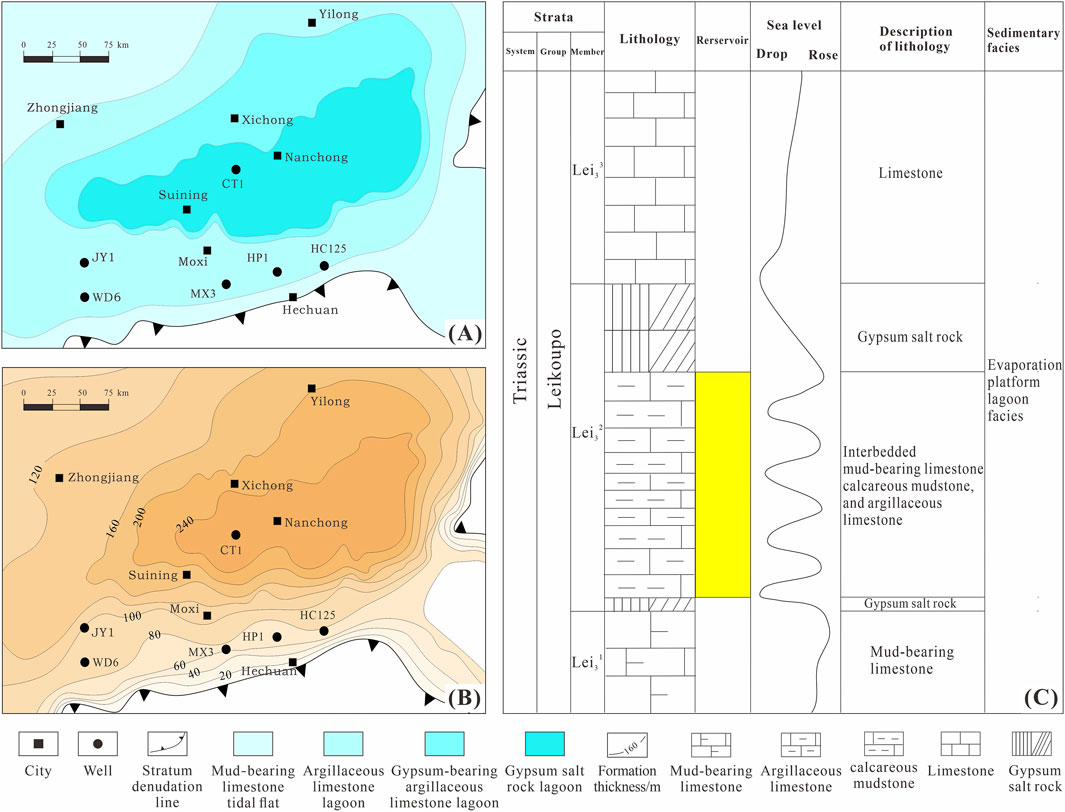
Figure 3. (A) Sedimentary facies of the Lei₃² sub-member (B) Residual formation thickness of the Lei₃² sub-member (C) Stratigraphic columns of the Lei₃² sub-member in central Sichuan Basin.

The strata of the Leikoupo Formation mainly consist of interbedded limestone and gypsum deposits. The top is in unconformable contact with the continental clastic rocks of the Upper Triassic Xujiahe Formation, while its underlying strata conformably contact the Jialingjiang Formation of the Lower Triassic. According to electrical properties, lithology, and sedimentary cycles, the Leikoupo Formation can be subdivided into four sections, Lei-1, Lei-2, Lei-3, and Lei-4. The Lei-3 member can be further refined into three sub-members, namely, Lei₃¹, Lei₃², and Lei₃³, arranged sequentially from bottom to top. In the Central Sichuan Basin, the Lei₃¹ sub-member predominantly features argillaceous limestone as its lithology. Similarly, the Lei₃³ sub-member is also primarily composed of argillaceous limestone. The Lei₃² sub-member, on the other hand, exhibits an interbedding of gypsum and argillaceous limestone, with hallow burial depth. This combination of features makes the Lei₃² sub-member a prime area for exploration within the central Sichuan region (Figure 3C).

3.2 Reservoir conditions

The Lei₃² sub-member can be further divided into two sections based on lithological variations. The upper section is predominantly characterized by salt rocks, whereas the lower section is mainly comprised of argillaceous limestones and calcareous mudstones (Xin et al., 2022). Integrating core observation, SEM and other laboratory techniques, the reservoir lithology is mainly argillaceous limestone and calcareous mudstone beneath the salt rock at the top of Lei₃² sub-member. The reservoir space is dominated by inorganic micro-nanopores, organic micro-nanopores and microfractures. Structural cracks are relatively developed, including early low angle cracks and late high angle cracks, with some of the cracks filled with calcite (Figure 4). The minerals that produce mineral related pores mainly include clay minerals, dolomite, calcite, and pyrite, while organic matter pores are mainly developed in organic matter. Under the scanning electron microscope, it is evident that organic matter pores and pores related to clay, as well as micro-fractures, are well developed. In contrast, the pure limestone areas exhibit an abnormally dense structure.

Figure 4

Figure 4. The reservoir characteristic in the Lei₃² sub-member of Central Sichuan Basin. (A) Well CT1, 3496 m, core of mudstone limestone. (B) Well CT1, 3550 m, cracks and dissolved pores that expand along cracks. (C) Well CT1, 3496 m, cracks and dissolved pores that expand along cracks. (D) Well CT1, 3495 m, core of gray mudstone. (E) Well HP1, 2648 m, gray mudstone, micro fractures and small amount of nanopores developed within the organic matter. (F) Well CT1, 3565.81 m, mudstone limestone, the mud crystal calcite developed intergranular pores.

Based on actual physical property measurements conducted on core samples, the reservoir porosity ranges from 2.00% to 8.51%, averaging at 2.7%, while the reservoir permeability spans from 0.00076 to 1.68 mD, with an average of 0.19 mD. Overall, the marl reservoir of Lei₃² sub-member is characterized as a low-porosity, low-permeability unconventional reservoir. Besides, the reservoir properties are jointly controlled by clay content, gypsum content and the presence of fractures. There exists a certain positive correlation between permeability and porosity (Figure 5A). Specifically, the content of clay minerals is the main factor affecting the reservoir porosity, with a positive correlation existing between porosity and clay mineral content, as illustrated in Figure 5B. With the increase of clay mineral content, the intergranular pores and contraction joints related to clay minerals will also increase, leading to an increase in porosity. Moreover, dissolved pores and caves developed along fractures in gypsum containing mudstone limestone have better physical properties compared to non-gypsum containing mudstone reservoirs. Fractures play a significant role in enhancing the permeability of the reservoir, potentially increasing it by several orders of magnitude when fractures are well-developed.

Figure 5

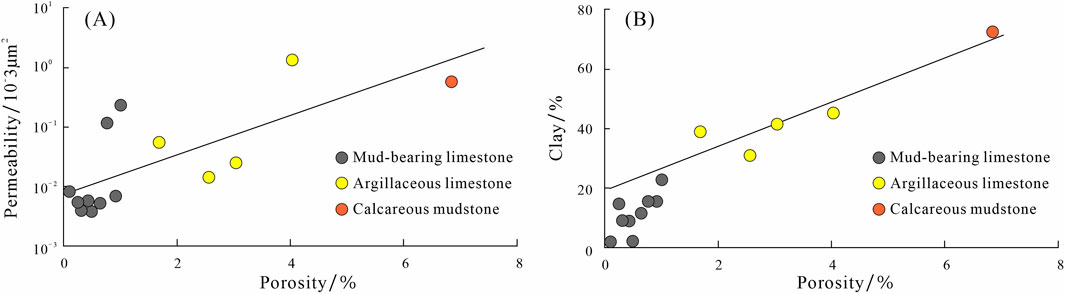
Figure 5. Relationship between NMR porosity and permeability (A) and clay content (B) in the Lei₃² sub-member.

3.3 Rock physics analysis

The targeted reservoir is the marl of Lei₃² sub-member, which lies beneath a substantial layer of gypsum salt rock. This gypsum salt layer poses challenges for the inversion of the underlying target reservoir. This study employs the proposed method to conduct quantitative reservoir prediction in this region. Initially, rock physics analysis is performed to identify sensitive parameters that differentiate between salt rock and marl reservoir. Figure 6A shows a scatter plot of P-wave velocity against density, illustrating the range of parameter values for different reservoir types. Here, the yellow, red, and blue dots represent reservoirs, poor reservoirs and dry layers, respectively. The classification of these reservoir types is grounded in well log interpretation. Significantly, there is considerable overlap in P-wave velocity between the reservoir and the dry layer, posing a challenge for conventional inversion techniques. For deeper analysis, the intersection of P-wave velocity and density is still conducted, but this time it is differentiated by lithology rather than reservoir type, as shown in Figure 6B. We can observe that there is a noticeable density variation between salt rock and marl, with the dry layer of low P-wave velocity corresponding to salt rock. Typically, salt rocks exhibit densities below 2.5 g/cm³, whereas marls generally surpass this threshold. Upon excluding the influence of salt rock, it is evident that the reservoir is distinguished by low P-wave velocity and medium-low density. Consequently, P-wave velocity proves to be a reliable parameter for differentiating between the reservoir, poor reservoir, and dry layer.

Figure 6

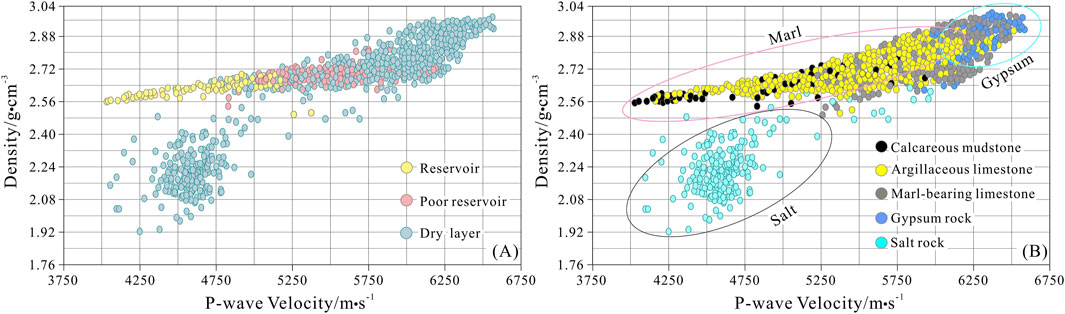
Figure 6. Scatter diagram of the relationship between P-wave velocity and density of different reservoirs (A) and lithology (B).

3.4 Waveform clustering analysis

As previously mentioned, leveraging sedimentary and logging facies, we establish correlations between seismic waveforms and logging facies. We utilize SOM waveform clustering to analyze distinctive waveform characteristics and derive clustering outcomes. Subsequently, these results are utilized to impose constraints on the development of the initial phase model.

Figure 7 displays the logging facies division for well CT1 within the study area, which is categorized into three types: gypsum salt rock lagoon, argillaceous limestone lagoon and mud-bearing limestone lagoon. The gypsum salt rock lagoon deposits are primarily characterized by grey and white gypsum and salt rock sediments. The argillaceous limestone lagoon deposits are mainly composed of dark grey and grey-black argillaceous limestone and calcareous mudstone sediments. The mud-bearing limestone lagoon deposits are primarily composed of grey mud-bearing limestone sediments. Notably, the top of the Lei₃² sub-member consists of a gypsum salt rock lagoon facies, while the middle and lower parts are characterized by argillaceous limestone lagoon and mud-bearing limestone lagoon.

Figure 7

Figure 7. Comprehensive stratigraphic column of Lei₃² sub-member of well CT1.

Figure 8B is the waveform clustering analysis results cross the well CT1, namely, the identified seismic facies. As we can see, the identified seismic facies exhibit a close alignment with the logging facies, demonstrating a high degree of discrimination and exceptional resolution. In addition, we also noticed a robust correlation between the clustering results and the seismic wave group characteristics shown in Figure 8A. This correspondence underscores the effectiveness of the clustering method and its capacity to capture lateral variations accurately. Following this, these clustering results are utilized to constrain the establishment of the initial model that faithfully capture lateral variations in line with sedimentary patterns. These models serve as the foundational basis for Bayesian-based reflectivity inversion studies.

Figure 8

Figure 8. Seismic profile (A) and seismic facies classification profile (B) cross the well CT1.

3.5 Inversion of salt rocks

According to the aforementioned petrophysical analysis results, salt rock is distinguished by its low density, which sets it apart from other rock types. Therefore, we initially employed the Bayesian reflectivity method within a facies-constrained model to conduct pre-stack inversion, aiming to obtain density profiles for identifying salt rock. Notably, the salt rock of Lei₃² sub-member is primarily concentrated at the top, with a substantial thickness exceeding 20 m. Figures 9A–C represent the raw seismic profile, the inverted density profile derived from the facies-constrained reflectivity method, and the inverted density profile based on the traditional Zoeppritz equation, respectively. The warm colour at the top of Lei₃² sub-member signify low density, corresponding to the presence of salt rock. The blue curve adjacent to the well is the actual density curve from well logging.

Figure 9

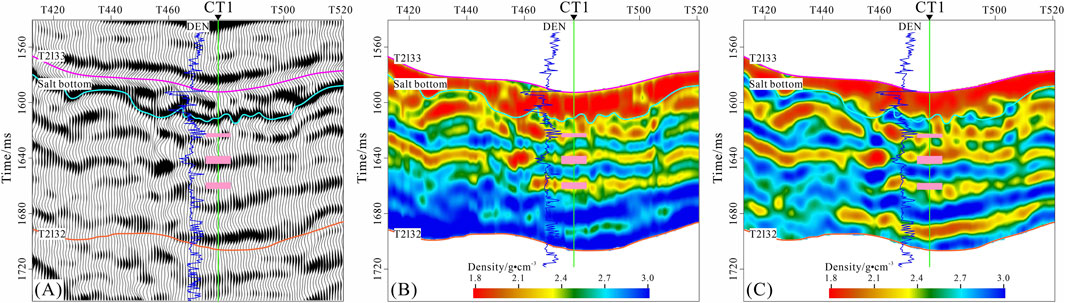
Figure 9. Seismic profile (A); inverted density profile based on the facies-constrained reflectivity method (B) and on traditional Zoeppritz equation (C). The purple squares in the figure represent the reservoirs.

Clearly, the top of the salt rock exhibits a low-density signature, closely following the curve adjacent to the well. However, tracking the base of the salt rock, marked by the peak reflection, proves challenging due to significant lateral variations in thickness observed in seismic profiles. Traditional inversion results using the Zoeppritz equation (Figure 9C) show relatively lower accuracy and resolution, thereby complicating the precise identification of the base of salt rock. In contrast, the density profiles from the recommended inversion method (Figure 9B) allow for easy comparison and accurate tracking of the bottom boundary of the salt rock. The salt bottom horizon traced aligns more consistently with the strong peak reflection observed in the seismic data. By establishing a framework model based on this tracked boundary and the Lei₃² sub-member bottom, we can confine the vertical range for subsequent reservoir inversion, thereby effectively eliminating the influence of the salt rock.

3.6 Inversion of marl reservoirs

After removing the influence of salt rock, we use the facies-constrained reflectivity inversion technique to compute the P-wave velocity profile, thereby achieving effective identification of marl reservoirs. Figure 10B depicts the inverted profile, where the pink curve adjacent to the well is the actual P-wave velocity curve. It is evident that the marl reservoirs are associated with lower P-wave velocity, and the inversion results align closely with the P-wave velocity curve derived from real drilling. Specifically, the three sets of reservoirs in Well CT1 are corresponding to three distinct zones of low P-wave velocity, showcasing robust lateral continuity of the reservoir. Furthermore, the inversion result indicates a significantly higher resolution using this recommended method. This alignment demonstrates the credibility of the facies-constrained reflectivity inversion method in predicting marl reservoir. To provide additional insights into the inversion performance, Figure 10C displays the P-wave velocity profile obtained from the traditional Zoeppritz equation for comparison. The conventional method is influenced by the weak peaks at the bottom of the Lei₃² sub-member, resulting in the inversion of a set of low-impedance reservoirs at the bottom. This discrepancy between the inverted reservoir and actual drilling results underscores the limitations of traditional methods in identifying marl reservoirs.

Figure 10

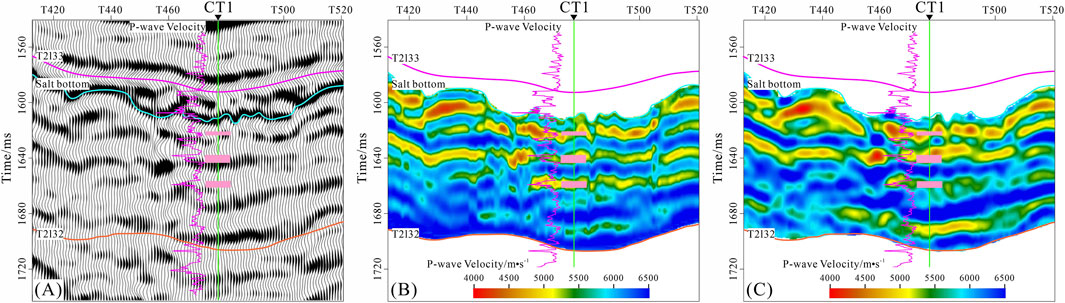
Figure 10. Seismic profile (A); inverted P-wave velocity profile based on the facies-constrained reflectivity method (B) and on traditional Zoeppritz equation (C). The purple squares in the figure represent the reservoirs.

The velocity threshold for marl reservoirs, as determined by rock physics analysis, has been established at 5,500 m/s. Utilizing this threshold, we can delineate a criterion for the inverted P-wave velocity data, where values falling below this threshold signify the presence of target reservoirs, thereby facilitating the prediction of reservoir thickness. The predicted thickness of the marl reservoir in Lei₃² sub-member of Well CT1 is 59 m, and the well log interpretation indicates a reservoir thickness of 55 m. The minimal discrepancy between these values is deemed acceptable, and the primary source of error can be attributed to differences in resolution between well logging and seismic reservoir prediction techniques.

To further demonstrate the accuracy of the inversion results, the inversion results based on the facies-constrained reflectivity method at the location of Well CT1 were extracted separately. Figure 11 are the comparisons between the actual velocity curves (a), density curves (b) from well CT1 and the inverted curves. It can be observed that both the P-wave velocity and density derived from the inversion match well with the actual well data. Notably, the inversion of P-wave velocity is more accurate and can even capture areas of significant variation, while the density inversion results maintain the same trend as the real data. This further indicates that the proposed method is quite suitable for the inversion of marl reservoir data.

Figure 11

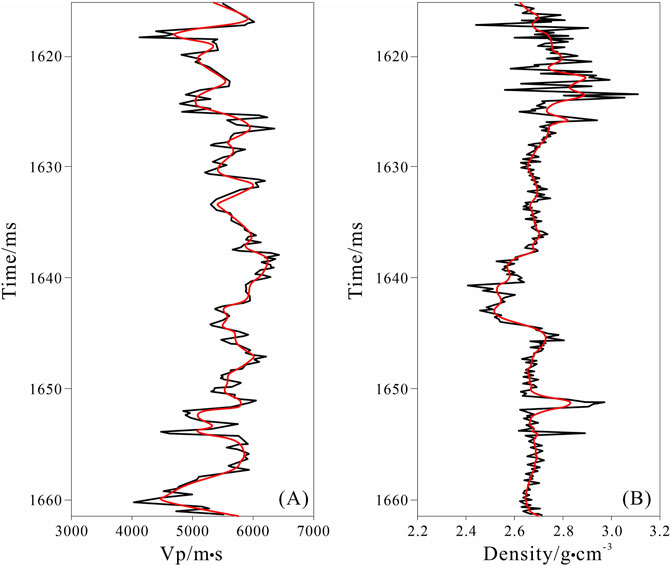
Figure 11. The comparisons between the actual velocity curves (A), density curves (B) from well CT1 and the inverted curves. The black curves represent the actual well logging data, while the red curves represent the inverted data derived from the well location based on the facies-constrained reflectivity method.

3.7 Reservoir planar distribution

By incorporating rock physics analysis, we have determined that the density threshold for salt rock is 2.5 g/cm³, and the P-wave velocity threshold for marl reservoirs is 5,500 m/s. Based on the inverted density and P-wave velocity using the facies-constrained reflectivity method, and by setting these thresholds, we can effectively map out the planar distribution of both salt rocks and marl reservoirs.

Figures 12A, B represent the salt rock thickness map of the Lei₃² sub-member based on the facies-constrained reflectivity method and on traditional Zoeppritz equation, respectively. The thickness of salt rock is predominantly influenced by fault-related folding and squeezing deformation. In regions experiencing intense squeezing deformation, the salt rock thickness tends to be larger. The thicker salt rock zones are mainly concentrated in the central section of the study area, which is enclosed by northeast-trending, east-west-trending, and northwest-trending faults. The study area is situated in the transitional facies zone, transitioning from gypsum salt lagoon to muddy lagoon. The overall predicted thickness of the salt rock is moderate, ranging between 40 and 70 m. When compared to the inversion results obtained using the traditional Zoeppritz equation, the salt rock thickness based on the facies-constrained reflectivity method is in good agreement with the regional depositional facies, and exhibits a superior planar resolution. This higher resolution allows for a more detailed representation of geological structures or features.

Figure 12

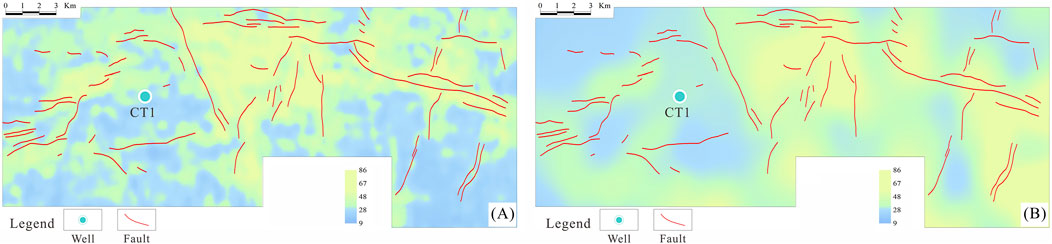
Figure 12. Salt thickness map of the Lei₃² sub-member based on the facies-constrained reflectivity method (A) and on traditional Zoeppritz equation (B). The red lines in the map represent faults.

Figures 13A, B illustrate the predicted marl reservoir thickness, derived from the facies-constrained reflectivity method and the traditional Zoeppritz equation, respectively. Compared to the reservoir distribution from the inversion method utilizing the traditional Zoeppritz equation, the planar distribution of marl reservoir thickness, characterized by facies-constrained reflectivity inversion method, exhibits notable variability. This distribution demonstrates a lesser correlation with major faults and is primarily influenced by sedimentary facies. Generally, the marl reservoirs are well-developed, with thickness varying between 20 and 60 m. With a reservoir thickness threshold set at 30 m, the favourable reservoir development area in the study area covers an extent of 210 km², which can be identified as a prospective zone for future exploration of the marl reservoirs. The implementation of techniques such as horizontal wells around the favourable area can effectively achieve the economies of scale in the development of these marl reservoirs.

Figure 13

Figure 13. Marl reservoir thickness map of the Lei₃² sub-member based on the facies-constrained reflectivity method (A) and on traditional Zoeppritz equation (B).

4 Conclusions and discussion

In this study, we introduce a reflectivity inversion method for marl reservoirs, utilizing seismic facies constraints. Given the pronounced lateral variations in marl reservoirs, a seismic facies-constrained initial model construction method is proposed to enhance the identification of these reservoirs, which overcomes the shortcomings of conventional initial model construction that did not consider lateral features. Furthermore, in light of the complex geological conditions, thin reservoir layers, and significant wave propagation effects characteristic of marl reservoirs, we introduce a Bayesian inversion method based on reflectivity, along with a modified Cauchy distribution to better handle weak reflections from marl reservoirs. Compared to traditional inversion methods based on the Zoeppritz equation, this method is better suited for predicting marl reservoirs. Practical applications in the Sichuan Basin demonstrate the effectiveness and advantages of this method, highlighting its promising potential for marl reservoir prediction.

The reflectivity method presented in this paper is used to obtain a one-dimensional analytical solution of the wave equation. However, this method is based on the assumption of a one-dimensional layered medium. It is applicable in regions with relatively simple geological structures. In contrast, when dealing with complex geological formations where the subsurface media do not conform to a simple one-dimensional layered structure, it becomes necessary to use depth migration or reverse-time migration techniques to correctly position the strata, thereby making the data more representative of a one-dimensional layered medium.

The reflectivity inversion method studied here originally focused on single-trace inversion, neglecting the lateral correlation of subsurface media. However, the phase-controlled inversion strategy carefully considers the spatial heterogeneity of the subsurface media and reservoirs during modelling, addressing this limitation. Additionally, in constraining the initial model, we utilized SOM technique for waveform clustering analysis. SOM is an unsupervised learning method that is sensitive to parameters such as learning rate and neighborhood function, and its clustering results can be significantly influenced by the network topology, potentially affecting the outcomes. Therefore, supervised or semi-supervised clustering methods, such as Gaussian Mixture Models (GMM), Support Vector Machines (SVM), and K-Nearest Neighbors (KNN), may serve as new avenues for comparison or improvement of clustering results.

Data availability statement

The datasets presented in this article are not readily available because the data that support the findings of this study are available from CNPC, but restrictions apply to the availability of these data, which were used under license for the current study, and so are not publicly available. Requests to access the datasets should be directed to Hao Zhang, MTMyNjE5ODk2ODNAMTYzLmNvbQ==.

Author contributions

HZ: Conceptualization, Methodology, Writing–original draft, Writing–review and editing, Formal Analysis. LC: Conceptualization, Methodology, Writing–original draft, Writing–review and editing. HZ: Formal Analysis, Resources, Visualization, Writing–original draft. YX: Formal Analysis, Writing–original draft, Investigation. YW: Data curation, Writing–original draft, Validation. XS: Writing–original draft, Project administration.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This paper is supported by the Scientific Research and Technology Development Project of CNPC (2023ZZ16YJ01, 2023YQX10101).

Conflict of interest

HaZ, YX, YW, and XS were employed by Petrochina Hangzhou Research Institute of Geology. HuZ was employed by PetroChina Southwest Oil and Gasfield Company.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aki, K., and Richards, P. G. (1980). Quantitative seismology: theory and methods. San Francisco: WH Freeman Pr.

Google Scholar

Alemie, W., and Sacchi, M. (2010). High-resolution three-term AVO inversion via a Trivariate Cauchy probability distribution. 81st Ann. Intern. Mtg., Soc. Expl. Geophys., Expand. Abstr. 420, 424.

Google Scholar

Alemie, W. M., and Sacchi, M. D. (2011). High-resolution three-term AVO inversion by means of a trivariate Cauchy probability distribution. Geophysics 76 (3), R43–R55. doi:10.1190/1.3554627

CrossRef Full Text | Google Scholar

Babasafari, A. A., Rezaei, S., Salim, A. M. A., Kazemeini, S. H., and Ghosh, D. P. (2021). Petrophysical seismic inversion based on lithofacies classification to enhance reservoir properties estimation: a machine learning approach. J. Petrol Explor Prod. Technol. 11, 673–684. doi:10.1007/s13202-020-01013-0

CrossRef Full Text | Google Scholar

Bosch, M., Mukerji, T., and González, E. F. (2010). Seismic inversion for reservoir properties combining statistical rock physics and geostatistics: a review. Geophysics. 75 (5), 75A165–75A176. doi:10.1190/1.3478209

CrossRef Full Text | Google Scholar

Chen, L., Li, J. Y., Chen, X. H., Liu, H. X., and Zhou, L. (2020). Prestack AVO inversion based on the vectorised reflectivity method with blockiness constraint. Explor. Geophys. 51 (5), 535–548. doi:10.1080/08123985.2020.1801082

CrossRef Full Text | Google Scholar

Dai, J. X., Ni, Y. Y., Liu, Q. Y., Wu, X. Q., Gong, D. Y., Hong, F., et al. (2021). Sichuan super gas basin in southwest China. Petroleum Explor. Dev. 48 (06), 1251–1259. doi:10.1016/s1876-3804(21)60284-7

CrossRef Full Text | Google Scholar

De Matos, M. C., Osorio, P. L., and Johann, P. R. (2007). Unsupervised seismic facies analysis using wavelet transform and self-organizing maps. Geophysics 72 (1), P9–P21. doi:10.1190/1.2392789

CrossRef Full Text | Google Scholar

Fatti, J. L., Smith, G. C., Vail, P. J., Strauss, P. J., and Levitt, P. R. (1994). Detection of gas in sandstone reservoirs using AVO analysis: a 3-D seismic case history using the Geostack technique. Geophysics 59 (9), 1362–1376. doi:10.1190/1.1443695

CrossRef Full Text | Google Scholar

Fryer, G. J. (2007). A slowness approach to the reflectivity method of seismogram synthesis. Geophys. J. Int. 63 (3), 747–758. doi:10.1111/j.1365-246x.1980.tb02649.x

CrossRef Full Text | Google Scholar

Fuchs, K., and Müller, G. (1971). Computation of synthetic seismograms with the reflectivity method and comparison with observations. Geophys. J. R. Astronomical Soc. 23 (4), 417–433. doi:10.1111/j.1365-246x.1971.tb01834.x

CrossRef Full Text | Google Scholar

Gidlow, P. M., Smith, G. C., and Vail, P. (1992). “Hydrocarbon detection using fluid factor traces, a case study: how useful is AVO analysis,” in Joint SEG/EAEG summer research workshop, 78–89.

Google Scholar

Grana, D., and Della, R. E. (2010). Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion. Geophysics 75 (3), O21–O37. doi:10.1190/1.3386676

CrossRef Full Text | Google Scholar

Gu, W., Xu, M., and Wang, D. H. (2016). Waveform indication inversion technique in thin reservoir prediction. Application—taking the thin-layer sandstone gas reservoir in the B area of Junggar Basin as an example. Nat. Gas. Geosci. 27 (11), 2064–2069. doi:10.11764/j.issn.1672-1926.2016.11.2064

CrossRef Full Text | Google Scholar

Jiang, Q. C., Wang, Z. C., Su, W., Huang, S. P., Zeng, F. Y., Feng, Z., et al. (2021). Accumulation conditions and favorable exploration orientation of unconventional natural gas in the marl source rock of the first member of the Middle Permian Maokou Formation, Sichuan Basin. China Pet. Explor. 26 (6), 82–97. doi:10.3969/j.issn.1672-7703.2021.06.006

CrossRef Full Text | Google Scholar

Kennett, B. (1983). Seismic wave propagation in stratified media. Cambridge University Press, 158–192.

Google Scholar

Kohonen, T. (1990). The self-organizing map. Proc. IEEE 78 (9), 1464–1480. doi:10.1109/5.58325

CrossRef Full Text | Google Scholar

Li, G. H., Yuan, B. G., Zhu, H., Yang, G., and Dai, X. (2022). Genesis of super-rich gas in the Sichuan Basin. Nat. Gas. Ind. 42 (5), 1–10. doi:10.3787/j.issn.1000-0976.2022.05.001

CrossRef Full Text | Google Scholar

Li, L., Tan, X. C., Zhou, S. Y., and Zou, C. (2012). Sequence lithofacies paleography of Leikoupo Formation, Sichuan Basin. J. Southwest Petroleum Univ. Sci. and Technol. Ed. 34 (4), 13–22. doi:10.3863/j.issn.1674-5086.2012.04.002

CrossRef Full Text | Google Scholar

Li, L., Tan, X. C., Zou, C., Ding, X., Yang, G., and Ying, D. L. (2012). Origin of the gypsum-salt in the Leikoupo Formation and migration evolution of the gypsum-salt pot in the Sichuan Basin, and their structural significance. Acta Geol. Sin. 86 (02), 316–324. doi:10.3969/j.issn.0001-5717.2012.02.010

CrossRef Full Text | Google Scholar

Liang, R. (2024). Comprehensive review on seismic facies identification. Int. J. Comput. Sci. Inf. Technol. 3 (2), 416–420. doi:10.62051/ijcsit.v3n2.46

CrossRef Full Text | Google Scholar

Liu, H. X., Li, J. Y., Chen, X. H., Hou, B., and Chen, L. (2016). Amplitude variation with offset inversion using the reflectivity method. Geophysics 81, R185–R195. doi:10.1190/geo2015-0332.1

CrossRef Full Text | Google Scholar

Liu, W., Hu, Z., Yong, X., Peng, G., Xu, Z., and Han, L. (2022). Wave equation numerical simulation and RTM with mixed staggered-grid finite-difference schemes. Front. Earth Sci. 10, 873541. doi:10.3389/feart.2022.873541

CrossRef Full Text | Google Scholar

Ma, Y., Loures, L., and Margrave, G. F. (2004). Seismic modeling with the reflectivity method. CREWES Res. Rep. 15, 1–7.

Google Scholar

Ma, Y. S., Cai, X. Y., Zhao, P. R., Luo, Y., and Zhang, X. F. (2010). Distribution characteristics and exploration direction of large and medium-sized gas fields in Sichuan Basin. Acta Pet. Sin. 31 (3), 347–354. doi:10.7623/syxb201003001

CrossRef Full Text | Google Scholar

Mallick, S. (2007). Amplitude-variation-with-offset, elastic-impedence, and wave-equation synthetics — a modeling study. Geophysics 72 (1), C1–C7. doi:10.1190/1.2387108

CrossRef Full Text | Google Scholar

Mallick, S., and Adhikari, S. (2015). Amplitude-variation-with-offset and prestack-waveform inversion: a direct comparison using a real data example from the Rock Springs Uplift, Wyoming, USA. Geophysics. 80 (2), B45–B59. doi:10.1190/geo2014-0233.1

CrossRef Full Text | Google Scholar

Mallick, S., and Frazer, L. N. (1987). Practical aspects of reflectivity modeling. Geophysics 52 (10), 1355–1364. doi:10.1190/1.1442248

CrossRef Full Text | Google Scholar

Meng, Q., Ding, W., Diao, X., Han, P., Wang, H., and Xiao, Z. (2022). Fracture identification of deep dolomite reservoir based on R/S-fFD analysis: a case study of the cambrian sinian reservoirs in the sandaoqiao gas field, northern tarim basin. Front. Earth Sci. 10, 918683. doi:10.3389/feart.2022.918683

CrossRef Full Text | Google Scholar

Misra, S., and Sacchi, M. D. (2008). Global optimization with model-space preconditioning: application to AVO inversion. Geophysics 73 (5), R71–R82. doi:10.1190/1.2958008

CrossRef Full Text | Google Scholar

Muller, G. (1985). The reflectivity method-a tutorial. J. Geophys. 58, 153–174.

Google Scholar

Owusu, B. A., Boateng, C. D., Asare, V. D. S., Danuor, S. K., Adenutsi, C. D., and Quaye, J. A. (2024). Seismic facies analysis using machine learning techniques: a review and case study. Earth Sci. Inf. 17, 3899–3924. doi:10.1007/s12145-024-01395-3

CrossRef Full Text | Google Scholar

Phinney, R. A., Odom, R. I., and Fryer, G. J. (1987). Rapid generation of synthetic seismograms in layered media by vectorization of the algorithm. Bull. Seismol. Soc. Am. 77 (6), 2218–2226. doi:10.1016/0040-1951(87)90023-0

CrossRef Full Text | Google Scholar

Sacchi, M. D. (1997). Reweighting strategies in seismic deconvolution. Geophys. J. Int. 129 (3), 651–656. doi:10.1111/j.1365-246x.1997.tb04500.x

CrossRef Full Text | Google Scholar

Sarhan, M. A. (2024). Editorial: advanced techniques and applications for characterizing the hydrocarbon potential in carbonate reservoirs. Front. Earth Sci. 12, 1385645. doi:10.3389/feart.2024.1385645

CrossRef Full Text | Google Scholar

Sen, M. K., and Roy, I. G. (2003). Computation of differential seismograms and iteration adaptive regularization in prestack waveform inversion. Geophysics 68 (6), 2026–2039. doi:10.1190/1.1635056

CrossRef Full Text | Google Scholar

Shuey, R. T. (2012). A simplification of the Zoeppritz equations. Geophysics 50 (50), 609–614. doi:10.1190/1.1441936

CrossRef Full Text | Google Scholar

Song, B., Li, X. Y., Ding, P., Chen, S., and Cai, J. (2023). Direct pre-stack inversion of elastic modulus using the exact Zoeppritz equation and the application in shale reservoir. Front. Earth Sci. 11, 1107068. doi:10.3389/feart.2023.1107068

CrossRef Full Text | Google Scholar

Tan, X. C., Li, L., Liu, H., Cao, J., Wu, X. Q., Zhou, S. Y., et al. (2014). Mega-shoaling in carbonate platform of the middle triassic Leikoupo Formation, Sichuan Basin, southwest China. Sci. China Earth Sci. 57, 465–479. doi:10.1007/s11430-013-4667-5

CrossRef Full Text | Google Scholar

Theune, U., Jensås, I. Ø., and Eidsvik, J. (2010). Analysis of prior models for a blocky inversion of seismic AVA data. Geophysics 75 (3), C25–C35. doi:10.1190/1.3427538

CrossRef Full Text | Google Scholar

Tian, H., Wang, G. W., Duan, S. F., Xin, Y. G., and Zhang, H. (2021). Reservoir characteristics and exploration target of the middle triassic Leikoupo Formation in Sichuan Basin. China Pet. Explor. 26 (5), 60–73. doi:10.3969/j.issn.1672-7703.2021.05.006

CrossRef Full Text | Google Scholar

Ting, C., Wang, Y. J., Li, K. H., Cai, H. P., Yu, G., and Hu, G. G. (2023). A prestack seismic inversion method constrained by facies-controlled sedimentary structural features. Geophysics 88, R209–R223. doi:10.1190/geo2022-0301.1

CrossRef Full Text | Google Scholar

Wang, Z. C., Xin, Y. G., Xie, W. R., Wen, L., Zhang, H., Xie, Z. Y., et al. (2023). Petroleum geology of marl in triassic Leikoupo Formation and discovery significance of well Chongtan1 in central Sichuan Basin, SW China. Petroleum Explor. Dev. 50 (5), 1092–1104. doi:10.1016/s1876-3804(23)60451-3

CrossRef Full Text | Google Scholar

Xin, Y. G., Li, W. Z., Zhang, H., Tian, H., Fu, X. D., and Xie, Z. Y. (2024). Mechanisms by which an evaporated lagoon sedimentation system controls source–reservoir preservation in Lei₃² sub-member unconventional oil and gas. Energies 17 (4), 964. doi:10.3390/en17040964

CrossRef Full Text | Google Scholar

Xin, Y. G., Wen, L., Zhang, H., Tian, H., Wang, X., Sun, H. F., et al. (2022). Study on reservoir characteristics and exploration field of the middle triassic Leikoupo Formation in Sichuan Basin. China Pet. Explor. 27 (4), 91–102. doi:10.3969/j.issn.1672-7703.2022.04.007

CrossRef Full Text | Google Scholar

Xin, Y. G., Zheng, X. P., Zhou, J. G., Ni, C., Gu, M. F., Gong, Q. S., et al. (2013). Reservoir characteristics and distribution in lei-33 member of Leikoupo Formation, middle triassic, central and western Sichuan Basin. Nat. Gas. Ind. 33 (3), 1–5. doi:10.3787/j.issn.1000-0976.2013.03.002

CrossRef Full Text | Google Scholar

Yang, G., Zhu, H., Huang, D., Li, G. H., Yuan, B. G., and Ying, D. L. (2020). Characteristics and exploration potential of the super gas-rich Sichuan Basin. Nat. Gas Explor. Dev. 43 (3), 1–7. doi:10.12055/gaskk.issn.1673-3177.2020.03.001

CrossRef Full Text | Google Scholar

Yang, Y., Xie, J. R., Zhang, J. Y., Wen, L., Zhao, L. Z., Zhang, H., et al. (2022). Characteristics and exploration potential of unconventional middle triassic Lei₃² reservoirs in the central Sichuan Basin. Nat. Gas. Ind. 42 (12), 12–22. doi:10.3787/j.issn.1000-0976.2022.12.002

CrossRef Full Text | Google Scholar

Yin, X. Y., Zhang, S. X., and Zhang, F. (2013). Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification. Chinses J. Geophys. 56 (7), 2378–2390. doi:10.6038/cjg20130724

CrossRef Full Text | Google Scholar

Yin, X. Y., Zhao, J., Zhang, F. C., Sun, C. Y., and Luo, H. Z. (2006). Method of generating prestack synthetic seismograms of spherical wave. J. China Univ. Petroleum 30 (1), 26–32. doi:10.3321/j.issn:1000-5870.2006.01.006

CrossRef Full Text | Google Scholar

Zhang, B. J., Sun, H. F., Luo, Q., Zeng, H. C., Xu, L., Li, L., et al. (2023). Geochemical characteristics and hydrocarbon origin of Leikoupo Formation platform lagoon facies shale in central Sichuan Basin. Nat. Gas. Ind. 43 (6), 15–29. doi:10.3787/j.issn.1000-0976.2023.06.002

CrossRef Full Text | Google Scholar

Zhang, F. C., and Yin, X. Y. (2004). Wave equation forward modeling of prestack seismogram in a stratified half space. J. China Univ. Petroleum 28 (3), 25–29. doi:10.3321/j.issn:1000-5870.2004.03.008

CrossRef Full Text | Google Scholar

Zhang, H., Xin, Y. G., Ma, H. L., Sun, H. F., Zhu, X. J., Xie, C., et al. (2024). Study on the fine prediction of a marlstone reservoir in the Lei₃² sub-member in Chongxi area, central Sichuan. J. Chengdu Univ. Technol. Sci. &Technology Ed. 52 (2), 247–257. doi:10.3969/j.issn.1671-9727.2024.02.05

CrossRef Full Text | Google Scholar

Zhang, J. Y., Xin, Y. G., Zhang, H., Tian, H., Zhu, X. J., and Chen, W. (2023a). A new unconventional gas reservoir type: source-reservoir integrated carbonate gas reservoir from evaporated lagoon facies in Lei₃² sub-member in Central Sichuan Basin. Nat. Gas. Geosci. 34 (1), 23–34. doi:10.11764/j.issn.1672-1926.2022.10.012

CrossRef Full Text | Google Scholar

Zhang, J. Y., Xin, Y. G., Zhang, H., Tian, H., Chen, W., and Zhu, X. J. (2023b). Self-sourced unconventional tight marlstone reservoir potential from evaporative lagoon of Triassic Leikoupo Formation in the central Sichuan Basin. Energies 16 (13), 5086. doi:10.3390/en16135086

CrossRef Full Text | Google Scholar

Zhang, R. Y., Deng, X. J., Wang, X. L., Tan, R. B., Luo, J., Guo, Y. C., et al. (2021). “Phase-controlled inversion under high-resolution pseudo-impedance curve,” in International field exploration and development conference 2019. doi:10.11648/J.AJMA.20210901.12

CrossRef Full Text | Google Scholar

Zhang, S. C., and Zhu, G. Y. (2006). Characteristics and exploration potential of Marine gas rich integration reservoirs in Sichuan Basin. Acta Pet. Sin. 27 (5), 1–8. doi:10.3321/j.issn:0253-2697.2006.05.001

CrossRef Full Text | Google Scholar

Zhang, X., Zhang, B. J., Liang, H., Xu, M., Zhang, D. J., and Zeng, Y. (2018). The application of pre-stack inversion based on seismic waveform indicator to the prediction of compact and thin oil-bearing sand layer. Geophys. Geochem. Explor. 42 (3), 545–554. doi:10.11720/wtyht.2018.1050

CrossRef Full Text | Google Scholar

Zhao, H., Ursin, B., and Amundsen, L. (1994). Frequency-wavenumber elastic inversion of marine seismic data. Geophysics 11 (1), 1868–1881. doi:10.1190/1.1443574

CrossRef Full Text | Google Scholar

Zhou, L., Liao, J. P., Li, J. Y., Chen, X. H., Yang, T. C., and Andrew, H. (2020). Bayesian time-lapse difference inversion based on the exact zoeppritz equations with blockiness constraint. J. Environ. Eng. Geophys. 25 (1), 89–100. doi:10.2113/JEEG19-045

CrossRef Full Text | Google Scholar

Zhou, L., Liu, X. Y., Li, J. Y., and Liao, J. P. (2021). Robust AVO inversion for the fluid factor and shear modulus. Geophysics 86 (4), R471–R483. doi:10.1190/geo2020-0234.1

CrossRef Full Text | Google Scholar

Zhu, G., Milkov, A. V., Li, J., Xue, N., Chen, Y., Hu, J., et al. (2021). Deepest oil in asia: characteristics of petroleum system in the tarim basin, China. J. Pet. Sci. Eng. 199, 108246. doi:10.1016/j.petrol.2020.108246

CrossRef Full Text | Google Scholar