Polarization multiplexing multichannel high-Q terahertz sensing system

Terahertz functional devices with high-Q factor play an important role in spectral sensing, security imaging, and wireless communication. The reported terahertz devices based on the electromagnetic induction transparency (EIT) effect cannot meet the needs of high-Q in practical applications due to the low-Q factor. Therefore, to increase the Q-factor of resonance, researchers introduced the concept of bound state in the continuum (BIC). In the quasi-BIC state, the metasurface can be excited by the incident wave and provide resonance with a high-Q factor because the condition that the resonant state of the BIC state is orthogonal is not satisfied. The split ring resonator (SRR) is one of the most representative artificial microstructures in the metasurface field, and it shows great potential in BIC. In this paper, based on the classical single-SRR array structure, we combine the large and small SRR and change the resonance mode of the inner and outer SRR by changing the outer radius of the inner SRR. The metasurface based on parameter-tuned BIC verified that the continuous modulation of parameters in a system could make a pair of resonant states strongly coupled, and the coherent cancellation of the resonant states will cause the linewidth of one of the resonant states to disappear, thus forming BIC. Compared with the single-SRR array metasurface based on symmetry-protected BIC, the dual-SRR array metasurface designed in this paper has multiple accidental BICs and realizes multichannel multiplexing of X-polarization and Y-polarization. It provides a brilliant platform for high-sensitivity optical sensor array, low threshold laser and efficient optical harmonic generation.

1 Introduction

Artificial microstructures can capture photons at a sub-wavelength scale, thus generating high-density local electromagnetic energy, which has been widely used in optical field control, Lan et al. (2021) Zang et al. (2019). Artificial microstructures can also realize complex wavefront modulation, including modulation of light amplitude, phase, dispersion, and polarization Al-Naib and Withayachumnankul (2017), Zhu et al. (2022), Zang et al. (2021), Zang et al. (2020). Among them, metallic structures based on plasmon response can enhance the electric or magnetic field at the surface or gap of the structure Ren et al. (2018), Ren et al. (2019). The intrinsic ohmic loss and Q-factor of metal structures are generally low, and the radiation loss will reduce the Q-factor, thereby reducing the efficiency of light-matter interaction Ren et al. (2021). For the application of terahertz technology in spectral sensing, security imaging, and wireless communication, terahertz functional devices with high-Q factor play an essential role Jansen et al. (2011), Singh et al. (2014). The high-Q factor is an essential performance index in nonlinear research based on solid field terahertz technology, which means better monochromaticity, maximum dispersion of slow light, and more vital terahertz matter interactionMittleman (2017), Ren et al. (2020), Wang et al. (2021). However, the reported Q-factor of terahertz devices based on EIT effect is normally lower than 10, which can not meet the needs of practical applications for high-Q factor Xu et al. (2016). The concept of the bound state in the continuum (BIC) provides help to break this bottleneck.

BIC is located in the radiation continuum region in the energy spectrum and is orthogonal to the radiation continuum, also called the implanted eigenstate Bogdanov et al. (2019a), Wang L. et al. (2022). Theoretically, BIC has an infinite 8Q-factor but cannot be excited by the incident wave Doeleman et al. (2018), Lee et al. (2020). However, near the parameter space of BIC, quasi-BIC can be excited by the incident wave because it does not meet the orthogonality condition of the deep state Azzam et al. (2018). At this time, the Q-factor of the resonant state is considerably improved, which is of great significance to the development of devices Wang X. et al. (2022). In 1985, Friedrich and Wintgen could make a pair of resonance states firmly coupled by continuously modulating the parameters in a system Friedrich and Wintgen (1985). Coherent cancellation of the resonance states will cause the linewidth of one of the resonance states to disappear, thus forming BIC Bogdanov et al. (2019b). This mechanism is also called the Friedrich-Wintgen condition, which provides a simple and effective method for researchers to find high-Q factor resonance states in various wave systems Hsu et al. (2013), Kang et al. (2021). In the momentum space of a two-dimensional photonic crystal, the mass factor of the guided mode resonance state diverges not only at the origin but also at the non-high symmetry point. The BIC at the non-high symmetrical point is called the accidental BIC, and the accidental BIC can be formed by tuning the system parameters Hsu et al. (2016a), Meng et al. (2022). BIC based on Friedrich-Wintgen condition (FW-BIC) is an accidental BIC with parameter modulation. In principle, BIC, introduced by Friedrich-Wintgen’s parametric modulation method, is easier to realize than predicted in quantum-damping potential wells Lu et al. (2021). In the artificial microstructure photonic system, researchers only need to continuously modulate some parameters, such as wave vector and structure parameters, to achieve coherent cancellation of modes under stable coupling conditions and then achieve BIC Han et al. (2021); Sadreev (2021). When the two resonators are distant apart, the BIC generated by parameter tuning can be interpreted as the Fabry-Perot BIC (FP-BIC). Two resonances are coupled to one radiation channel, and each resonance acts as a perfect reflector near the resonance frequency, so the two can trap waves in between when the round-trip phase shift is an integer multiple of 2π, resulting in FP-BIC.Hsu et al. (2016b).

Various BIC-based optical metasurfaces with ultra high-Q factor have been realized by the extremely high degree of freedom of design and the advantages of plane integration of the metasurface in recent years Wang et al. (2021), Xu et al. (2016), Rybin et al. (2017). Split ring resonator (SRR), as the earliest and most representative artificial microstructure in the metasurface, has the advantages of solid resonance, clear principle, and easy processing. However, the application of SRR in BIC has yet to be thoroughly studied. Using classical metal SRR to realize BIC in the terahertz band is expected to realize high-Q THz functional devices with precise mechanisms and convenient application. Previous studies have found symmetry-protected BIC in metal SSRs in terahertz and optical bands Ren et al. (2021), Niu et al. (2021), Cong and Singh (2019). If only the symmetry-protected BIC of the SRR structure is used to realize BIC, the design idea is limited, and it is not easy to further improve the Q-factor of the device.

So in this paper, based on the classical metal single-SRR array, we embed a small split ring resonator into a large split ring resonator to form a polarization multiplexing multi-channel metasurface. The designed polarization multiplexing metasurface can transmit two independent data information simultaneously through two mutually orthogonal X and Y polarization states of light in the same wavelength channel to double the total system capacity and spectrum utilization. This will greatly improve the performance of the sensing system. We conduct numerical simulation research on the metasurface by using electromagnetic simulation software. The resonance mode of the inner SRR and the outer SRR switch by changing the outer radius of the inner SRR. We verified that there are multiple BIC states on the metal metasurface, and obtained the high-Q resonances formed by BIC leakage. In addition, we discussed eigenmodes of symmetry-protected BIC by simulating a single-SRR array. Compared with the single-SRR array based on symmetry-protected BIC, the dual-SRR array metasurface designed in this paper based on FW-BIC and FP-BIC has more sharp resonance and additional BIC points, providing a massive platform for high-sensitivity array optical sensing, low threshold laser, and efficient optical harmonic generation. The more the outer radius of the inner circle deviates from the BIC state, the more pronounced is the resonant response, which makes the transmittance spectrum of the metasurface capable of sensing beyond the spacing.

2 Materials and methods

To realize the metasurface based on parameter-tuned BIC, we designed a model element consisting of two coupled split ring resonators, and the whole metasurface extends to infinity along the translational symmetry. Our structure can resonate under the normal incidence terahertz wave with the polarization direction of both X and Y and produce different results in the range of 0.2–1.6 THz as shown in Figure 1. The metamaterial structure consists of an aluminum device and a PI substrate. The period of the metasurface is p = 200 um, and additional parameters are shown in Figure 1B. The substrate is polyimide with a dielectric constant of 3.5, negative tangent angle of 0.037, and thickness of 20 um. Aluminum devices are coplanar and composed of internal and external SRRs. The thickness of aluminum is 200 nm, and the conductivity is 3.74E7 S/m. We have fixed these parameters throughout the paper, and the only exception is the outer radius of the inner ring. We performed the simulation using the finite element method (FEM) of COMSOL Multiphysics 6.1, Inc. (2020). The change of the outer radius of the inner ring (R2) will alter the resonance mode of the inner and outer SRRs, thus switching the state between quasi-BIC and BIC. Since SRRs do not introduce symmetrical breakage elements, the physical mechanism behind them contrasts sharply to the metasurface based on the symmetry-protected BIC proposed previously.

FIGURE 1

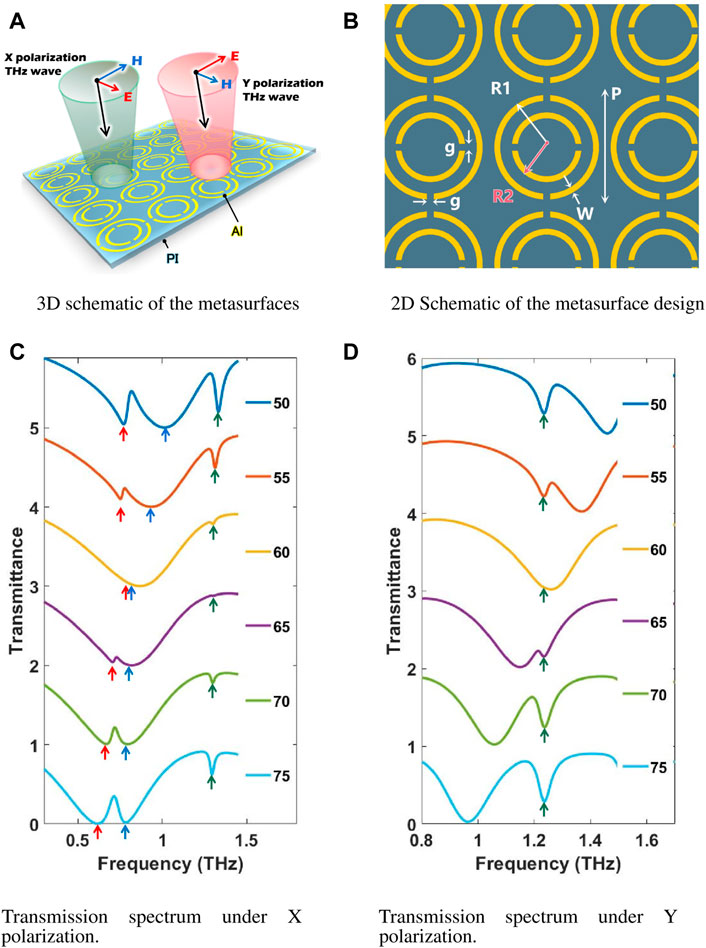
FIGURE 1. Model design and transmission spectrum measurement. (A) 3D sketch map of the metasurface. (B) Plan sketch of design metasurface. The design dimensions are p = 200 um, R1 = 90 um, W = 10 um, g = 12 um, and R2 changes. (C) Amplitude transmission spectra of the elementary surfaces with different R2 under X polarization. (D) Amplitude transmission spectra of metasurfaces with different R2 under Y polarization. The red arrow and the blue arrow mark the two different eigenfrequency corresponding to FW-BIC, and the green arrow mark the two same eigenfrequency corresponding to FP-BIC.

To better explain the FW-BIC principle, we describe the two-mode system coupled by two ports using a time-coupled mode theoretical model:

$\frac{\mathrm{d}}{\mathrm{d}t}\left[\begin{array}{c}\hfill r_1\hfill \\ \hfill r_2\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill d_{11}\hfill & \hfill d_{12}\hfill \\ \hfill d_{21}\hfill & \hfill d_{22}\hfill \end{array}\right]\left[\begin{array}{c}\hfill p_{1+}\hfill \\ \hfill p_{2+}\hfill \end{array}\right]+j\left[\begin{array}{cc}\hfill {\omega }_1+j{\tau }_1\hfill & \hfill d+j{\tau }_{12}\hfill \\ \hfill d+j{\tau }_{21}\hfill & \hfill {\omega }_2+j{\tau }_2\hfill \end{array}\right]\left[\begin{array}{c}\hfill r_1\hfill \\ \hfill r_2\hfill \end{array}\right]$

As given by the formula, the coupling coefficient between mode i and port j is expressed by d_ij (i, j ∈ 1, 2); the input amplitudes of ports one and two are p₁₊ and p₂₊; ω₁ and ω₂, τ₁ and τ₂ indicate the resonant frequency and attenuation rate of the two modes, respectively; d is the direct coupling rate between the two modes; τ₁₂ and τ₂₁ are the coupling coefficients generated by damping, and finally, the resonance amplitude of the mode supported by the system could be expressed by r₁ and r₂. Due to the symmetry of the system, τ₁₂ = τ₂₁ = $\sqrt{{\tau }_1{\tau }_2}$.

The Hamiltonian of the system can be calculated as:

$H=\left[\begin{array}{cc}\hfill j{\omega }_1-{\tau }_1\hfill & \hfill jd-{\tau }_{12}\hfill \\ \hfill jd-{\tau }_{21}\hfill & \hfill j{\omega }_2-{\tau }_2\hfill \end{array}\right]$

By calculating the eigenvalues of H, we obtain the resonant frequencies of the mixed mode as follows:

$f_{\pm }=\frac{\pm \sqrt{{\left[j\left({\omega }_1-{\omega }_2\right)-\left({\tau }_1-{\tau }_2\right)\right]}^2+4{\left(jd-\sqrt{{\tau }_1{\tau }_2}\right)}^2}-\left({\tau }_1+{\tau }_2\right)}{2}+j\frac{\left({\omega }_1+{\omega }_2\right)}{2}$

The first term in the formula is the real part of the eigenmode, and the second term is the imaginary part of the eigenmode.The real and imaginary parts represent the resonance frequency and decay rate of the mixed eigenmodes, respectively. f₊ and f₋ denote the two resonant modes. Once the two modes couple to each other, the resonant frequencies of the two resonant modes correspond to transmission valleys and the coupling between the two modes forms a transmission peak. When the Friedrich-Wintgen condition $(\delta \omega \sqrt{{\tau }_1{\tau }_2}=n({\tau }_1-{\tau }_2))$ is satisfied, the real number of f₊ is offset to 0 and becomes a pure imaginary number, meaning that this eigenmode becomes a BIC with zero radiative loss. If the Friedrichs-Wintgen condition is not satisfied, calculating the ratio of the central frequency of the transmission valley (f₀) to the full width of the half peak of the transmission spectrum (HWFM) can obtain the Q-factor of the transmission valley (Q = f₀/HWFM). Similarly, we can obtain two eigenvalues of Hamiltonian of FP-BIC is f_± = ω₀ ± d − jτ(1 ± e^jψ). Hsu et al. (2016b) Obviously, when ψ is an integer multiple of π, one of the two eigenmodes becomes a FP-BIC with a purely real eigen-frequency, while the other eigenmode becomes more lossy with twice the original decay rate.

3 Resluts

With an X-polarized incident wave, when the outer radius of the inner SRR (R2) is 50 um, transmission valleys corresponding to quasi-BIC appear at 0.74 THz and 1.25 THz, as shown in Figure 1C. The current distribution shows that the first transmission minimum marked by the red arrow is LC mode, the second marked by the blue arrow is dipole mode, and the third marked by the green arrow is LC mode. The transmission valley at 0.76 THz results from coupling LC mode marked by the red arrow and dipole mode marked by the blue arrow. Since the LC and dipole modes are coupled through resonant and leaky channels, the quasi-BIC die has the Fano line shape predicted by theoretical calculations. As R2 increases, the dipole mode shifts to a lower frequency, close to the frequency of the first LC resonance. The transmission valley 1.23 THz is the result of coupling between two adjacent dual-SRR units. With the increase of R2, it gradually reaches an integral multiple of ψ being π, and the eigenmode becomes a BIC mode with pure real eigenfrequency. The corresponding eigenfrequency is marked with green arrows. The decrease of frequency detuning leads to the decrease of transmission valley value and the increase of Q-factor. For the outer radius of the inner SRR of 60 um, the FW-BIC at 0.76 THz can be identified by the vanishing of the Fano transmission valley. For an inner ring radius of 65 um, the FP-BIC at 1.23 THz can be identified by the vanishing of the Fano transmission valley. When the BIC condition is broken by additionally increasing the radius of the inner ring, a transmission valley appears again.

With a Y-polarized incident wave, the quasi-BIC Fano valley also appears when R2 is 50 um, as shown in Figure 1D. The transmission valley 1.23 THz is the result of coupling between two adjacent dual-SRR units. With the increase of R2, it gradually reaches an integral multiple of ψ being π, and the eigenmode becomes a BIC mode with pure real eigenfrequency. The corresponding eigenfrequency is marked with green arrows. The quasi-BIC valley also appears when R2 is 50 um, as shown in Figure 1D. The decrease of frequency detuning leads to the decrease of transmission valley value and the increase of Q factor. For an outer radius of 60 um from the inner SRR, the FP-BIC can be identified by the vanishing of the Fano transmission valley. When the BIC condition is broken by additionally increasing the radius of the inner ring, a transmission valley appears again.

It is worth noting that, unlike the symmetry-protected BIC, the current quasi-BIC in the structure is mirror symmetric and is not compromised by changing the size of the inner ring radius. In our structure, the resonant frequency of the dipole mode can be tuned by changing the radius of the inner ring (R2). However, changing the outer radius of the inner SRR does not change the resonance frequency of the LC mode, which is considerably different from the symmetry-protected BIC case. With such a platform, we can control the frequency detuning between the two modes near the ideal BIC.

4 Discussion

For a more intuitive comparison with the symmetry-protected BIC, we simulate the transmission spectrum, surface current, and magnetic field of a single asymmetric SRR array. Figures 2A,B and show the transmission spectrum of a single-SRR array with X- and Y polarized incident wave when the asymmetry parameter is increased. It can be seen that a symmetry-protected BIC state is observed at about 0.38 THz for both X- and Y-polarized modes. The single channel regulated by the symmetry-protected BIC has the same frequency in the X and Y polarization modes. For a single-SRR array metasurface with an asymmetry parameter of 20 um, the Q-factor is 19.3 for X-polarization and 22 for Y-polarization, which is higher than the general Q-factor of EIT devices.The simulated surface current and magnetic field distribution clearly show the BIC-related mode in Figures 2C,D and show that the quasi-BIC of the annular symmetric protection is a standard four dipole. When the symmetry is broken, the opposite direction currents of the two arms of the resonator are responsible for the quasi-BIC phenomenon. Although the BIC is excited by two different polarization waves, they arise from the same mechanism.

FIGURE 2

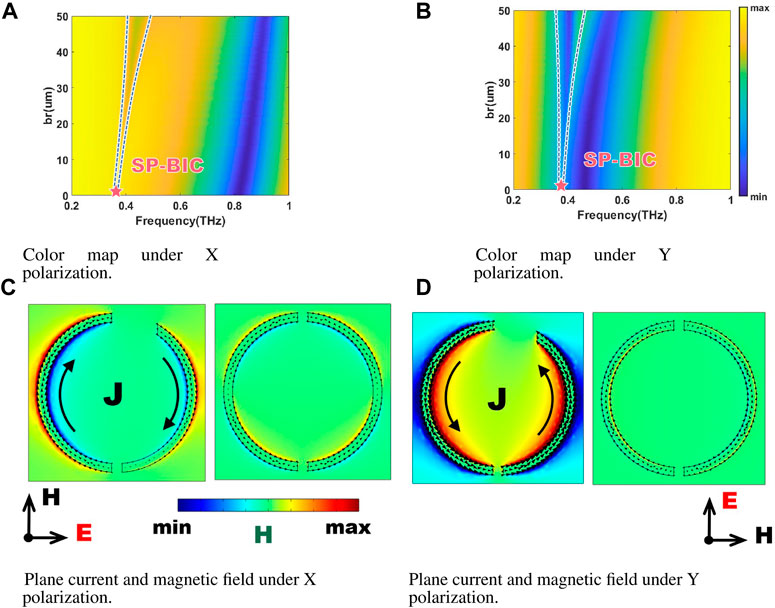
FIGURE 2. The figure shows the symmetry-protected BIC (SP-BIC) excited by a single-SRR array. (A) A color map of the simulated transmission spectrum of BIC is drawn by scanning the symmetrical broken gap from 0 um to 50 um with an X-polarized incident wave. (B) A color map of the simulated transmission spectrum of BIC is drawn by scanning the symmetrical broken gap from 0 um to 50 um with a Y-polarized incident wave. (C) The X-O-Y plane current and Z-direction magnetic field intensity correspond to quasi-BIC and BIC modes under X polarization. (D) The X-O-Y plane current and Z-direction magnetic field intensity correspond to quasi-BIC and BIC modes under Y polarization.

Based on the above traditional SRR array, we propose a dual-SRR array metasurface, which uses the interaction of two quadrupoles to obtain resonances with higher Q-factors. In Figure 3A, two significant BIC features are observed at about 0.74 THz and R2 = 57 um, 1.25 THz and R2 = 61 um under X-polarized wave, labeled BIC1 and BIC2, respectively. A BIC labeled BIC3 can also be observed at 1.18 THz and R2 = 63 um under Y-polarized wave in Figure 3B. We marked the positions of the three BICs with red stars. When R2 parameter is 50 um, the Q-factor of quasi-BIC1 under X-polarized wave, quasi-BIC2 and quasi-BIC3 under Y-polarized wave are 9.2, 31.2, and 33.5 respectively. Compared with the BIC in Figure 2, the phenomenon of these three BICs is more obvious, and the Q-factor of quasi-BIC2 and quasi-BIC3 is higher than that of symmetry-protected quasi-BIC.

FIGURE 3

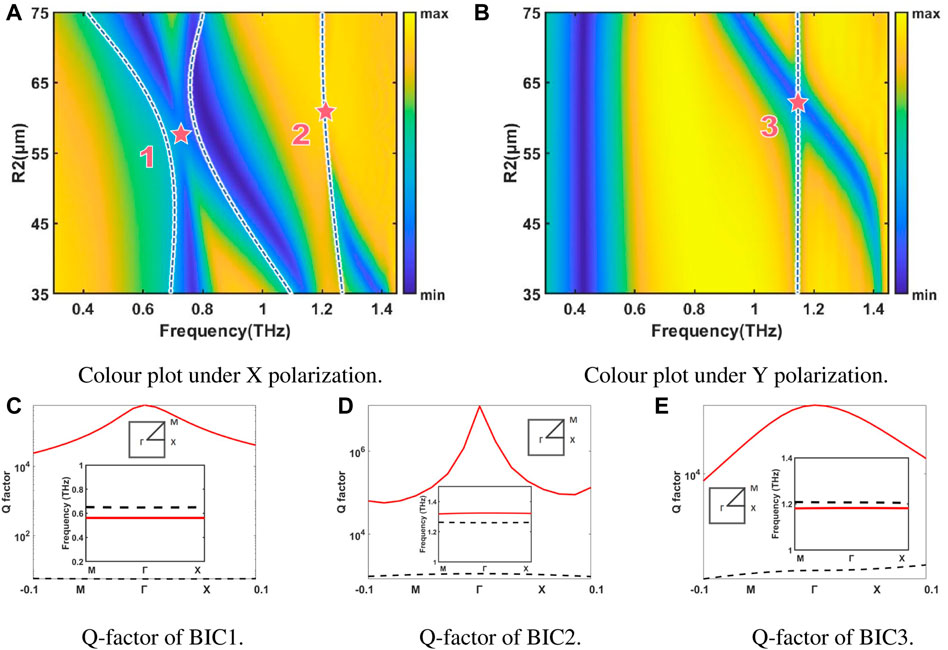
FIGURE 3. The numerical study of quasi-BIC caused by inter and outer double-ring resonance is shown. (A) Under the X-polarized incident wave, by scanning the inner ring radius from 35 um to 75 um, a color map of the simulated transmission spectrum of parameter-tuned BIC is drawn. (B) Under the Y-polarized incident wave, by scanning the inner ring radius from 35 um to 75 um, a color map of the simulated transmission spectrum of parameter-tuned BIC is drawn. (C) Corresponding to the first BIC’s Q-factor and energy band structure (illustration). (D) Corresponding to the second BIC’s Q-factor and energy band structure (illustration). (E) Corresponding to the third BIC’s Q-factor and energy band structure (illustration). Reduction of metal loss, the imaginary part of dielectric constant ϵ reduced to 10e-6. The quasi-BIC we studied appears in the first Brillouin zone Γ point, with an extremely high-Q factor.

For an ideal BIC, the theoretical Q-factor should go to infinity when the imaginary part of the permittivity is set to 0. However, the intrinsic loss of metals leads to a finite Q-factor. In such a lossy BIC, the loss mechanism comes from the ohmic losses in the metal and the dielectric losses in the substrate, while the energy leakage from the metasurface to the ports is zero. We simplified the imaginary part of the dielectric constant to 10E-6, and the loss factor of the substrate to 0 to calculate the Q-factor close to the lossless metal (the first Brillouin zone of the square lattice is plotted at the upper left of Figure 3). Figures 3C–E shows the Q-factor calculated by this method around 0.74 THz, 1.25 THz, and 1.16 THz (the insert figure shows the possible eigenmodes near the eigenfrequency), indicating that the Q-factor calculated by quasi-BIC is located at the symmetric point Γ.

In the BIC state, the energy transfer of electromagnetic waves is mainly in the z-axis direction, and the magnetic field is limited to the X-O-Y plane. However, in the case of quasi-BIC, due to energy leakage, part of the magnetic field will be generated outside the X-O-Y plane. Therefore, by monitoring the magnetic field component in the z-axis direction, it is easy to verify the energy leakage in the case of quasi-BIC. We monitored the z-direction magnetic field intensity and the corresponding current distribution of the transmission valleys with R2 = 50 um, 60 um, and 70 um at 0.74 THz, 1.25 THz, and 1.16 THz, respectively, as shown in Figure 4. Under the ideal BIC state, the magnetic field in the z-axis direction should be 0. The magnetic field in the z-axis direction excited under the state close to BIC corresponding to R2 = 60 um is tiny, indicating that the energy leakage is small. In comparison, R2 = 50 um and R2 = 70 um correspond to the strong magnetic field in the Z direction around the SRRs in a quasi-BIC state. It can be seen that the magnetic field in the quasi-BIC state is more substantial than that in the BIC state, indicating that there is apparent magnetic field leakage. This further verified our conjecture that the high-Q transmission peak is excited by quasi-BIC phenomena.

FIGURE 4

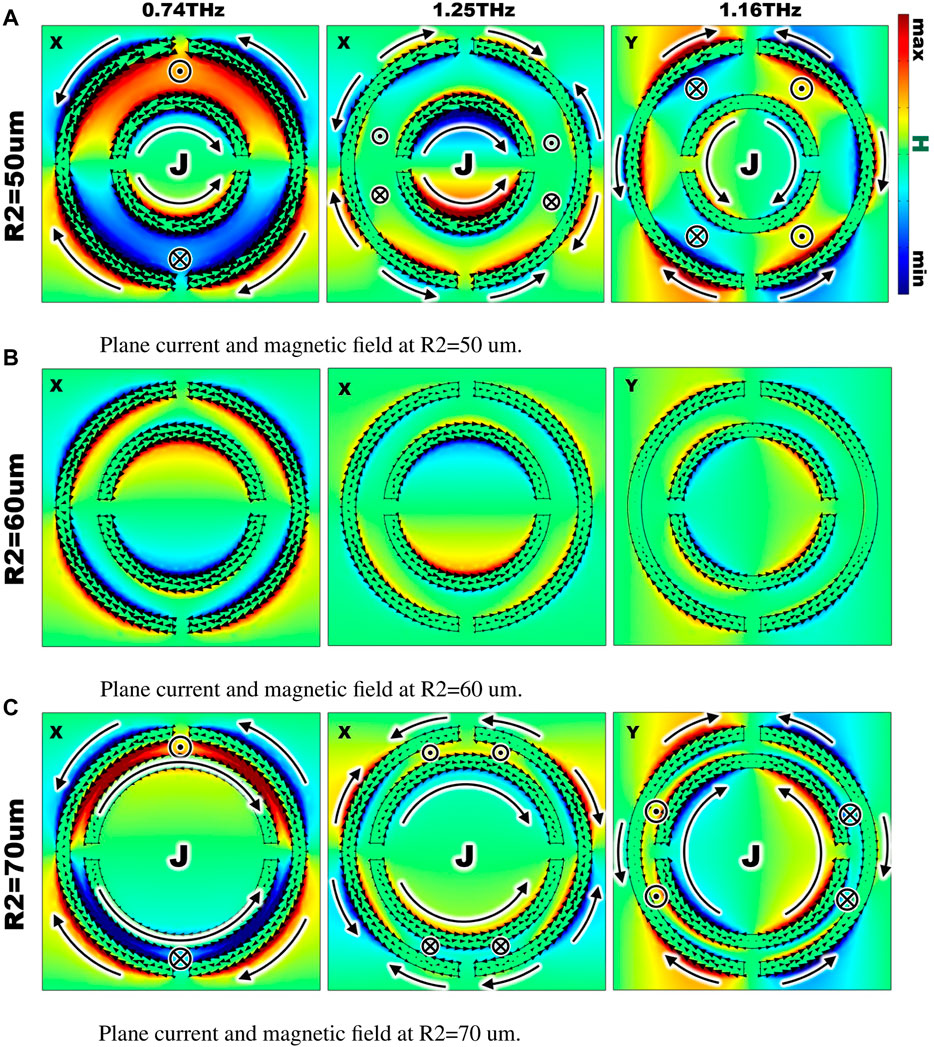
FIGURE 4. (A) Corresponding to the quasi-BIC mode with smaller R2, the X-O-Y plane current and Z direction magnetic field intensity under different frequencies and modes. (B) Corresponding to the BIC mode with R2 close to the X-O-Y plane current and Z direction magnetic field intensity under different frequencies and modes. (C) The current in the X-O-Y plane and magnetic field intensity in the Z direction corresponds to quasi-BIC mode with larger R2 at different frequencies and modes. The dashed line indicates the position of the BIC eigenfrequency.

According to the surface current analysis, the dual-SRR array has two kinds of resonant modes: the LC mode with opposite current direction and the dipole mode with the same current direction. By monitoring the frequencies corresponding to the transmission valleys, it can be found that when the quasi-BIC switches to the BIC, the LC mode entirely disappears and the dipole mode remains. At 0.74 THz, 1.25 THz, and 1.16 THz, the surface currents are distributed in opposite flow directions along the double metal SRRs of the cell, and both generate anti-homogeneous magnetic dipoles when R2 is 50 um. Fano resonances have been reported to be excited by a set of antiparallel magnetic dipoles. The magnetic dipoles are weakly coupled to free space and appear as high-Q resonances. It can be verified that in the case of nested double SRRs, three independent BICs can be generated by the interaction of two quadrupoles.

In this paper, we propose a double SRRs nested model, which uses the interaction of two quadrupoles to obtain a higher Q-factor. The high-Q resonance due to the BIC leakage can be obtained by switching the resonant modes of the inter-SRR and the outer SRR by varying the inter-SRR radius. We verified that all three high-Q transmission peaks are excited by BIC-like phenomena by simulating magnetic field leakage in the Z-direction and surface currents. That is, the interaction of two quadrupoles can give rise to three parameter-tuned BICs. Compared with the single ring based on symmetry-protected BIC, the dual-SRR array metasurface based on accidental BIC designed in this paper has more sharp resonance and more BIC points, which can realize the function of polarization multiplexing multi-channel and can provide a huge platform for highly sensitive array optical sensing and efficient optical harmonic generation.In addition, the higher the outer radius of the inner circle deviates from the BIC state, the more pronounced is the resonant response, which makes the transmittance spectrum of the metasurface capable of sensing beyond the spacing.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

XYW, XMW, and QR contributed to conception and design of the study. HC, JX, and YL performed the statistical analysis. XMW wrote the first draft of the manuscript. XX, ZL, JWY, and WS wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was financially sponsored by the National Natural Science Foundation of China (12104339), Open Fund of State Key Laboratory of Millimeter Wave, Southeast University (K202216) and China Postdoctoral Science Foundation funded project (258023).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Naib, I., and Withayachumnankul, W. (2017). Recent progress in terahertz metasurfaces. J. Infrared, Millim. Terahertz Waves 38, 1067–1084. doi:10.1007/s10762-017-0381-2

CrossRef Full Text | Google Scholar

Azzam, S. I., Shalaev, V. M., Boltasseva, A., and Kildishev, A. V. (2018). Formation of bound states in the continuum in hybrid plasmonic-photonic systems. Phys. Rev. Lett. 121, 253901. doi:10.1103/PhysRevLett.121.253901

PubMed Abstract | CrossRef Full Text | Google Scholar

Bogdanov, A. A., Koshelev, K. L., Kapitanova, P. V., Rybin, M. V., Gladyshev, S. A., Sadrieva, Z. F., et al. (2019a). Bound states in the continuum and Fano resonances in the strong mode coupling regime. Adv. Photonics 1, 016001. doi:10.1117/1.AP.1.1.016001

CrossRef Full Text | Google Scholar

Bogdanov, A. A., Koshelev, K. L., Kapitanova, P. V., Rybin, M. V., Gladyshev, S. A., Sadrieva, Z. F., et al. (2019b). Bound states in the continuum and fano resonances in the strong mode coupling regime. Adv. Photonics 1, 016001. doi:10.1117/1.ap.1.1.016001

CrossRef Full Text | Google Scholar

Cong, L., and Singh, R. (2019). Symmetry-protected dual bound states in the continuum in metamaterials. Adv. Opt. Mater. 7, 1900383. doi:10.1002/adom.201900383

CrossRef Full Text | Google Scholar

Doeleman, H. M., Monticone, F., den Hollander, W., Alù, A., and Koenderink, A. F. (2018). Experimental observation of a polarization vortex at an optical bound state in the continuum. Nat. Photonics 12, 397–401. doi:10.1038/s41566-018-0177-5

CrossRef Full Text | Google Scholar

Friedrich, H., and Wintgen, D. (1985). Interfering resonances and bound states in the continuum. Phys. Rev. A 32, 3231–3242. doi:10.1103/PhysRevA.32.3231

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, S., Pitchappa, P., Wang, W., Srivastava, Y. K., Rybin, M. V., and Singh, R. (2021). Extended bound states in the continuum with symmetry-broken terahertz dielectric metasurfaces. Adv. Opt. Mater. 9, 2002001. doi:10.1002/adom.202002001

CrossRef Full Text | Google Scholar

Hsu, C. W., Zhen, B., Lee, J., Chua, S.-L., Johnson, S. G., Joannopoulos, J. D., et al. (2013). Observation of trapped light within the radiation continuum. Nature 7, 188. Frontiers in Optics 2013 Postdeadline (Optica Publishing Group). doi:10.1364/FIO.2013.FW6B.7

PubMed Abstract | CrossRef Full Text | Google Scholar

Hsu, C. W., Zhen, B., Stone, A. D., Joannopoulos, J. D., and Soljačić, M. (2016b). Bound states in the continuum. Nat. Rev. Mater. 1, 4–8. doi:10.1038/natrevmats.2016.48

CrossRef Full Text | Google Scholar

Hsu, C. W., Zhen, B., Stone, A., Joannopoulos, J., and Soljačić, M. (2016a). Bound states in the continuum. Nat. Rev. Mater. 1, 16048. doi:10.1038/natrevmats.2016.48

CrossRef Full Text | Google Scholar

Inc, C. (2020). COMSOL Multiphysics® v. 6.1. Stockholm, Sweden: COMSOL AB. Available at: www.comsol.com.

Google Scholar

Jansen, C., Al-Naib, I. A., Born, N., and Koch, M. (2011). Terahertz metasurfaces with high q-factors. Appl. Phys. Lett. 98, 051109. doi:10.1063/1.3553193

CrossRef Full Text | Google Scholar

Kang, M., Zhang, S., Xiao, M., and Xu, H. (2021). Merging bound states in the continuum at off-high symmetry points. Phys. Rev. Lett. 126, 117402. doi:10.1103/PhysRevLett.126.117402

PubMed Abstract | CrossRef Full Text | Google Scholar

Lan, Z., You, J. W., Ren, Q., Sha, W. E. I., and Panoiu, N. C. (2021). Second-harmonic generation via double topological valley-hall kink modes in all-dielectric photonic crystals. Phys. Rev. A 103, L041502. doi:10.1103/PhysRevA.103.L041502

CrossRef Full Text | Google Scholar

Lee, S.-G., Kim, S.-H., and Kee, C.-S. (2020). Bound states in the continuum (bic) accompanied by avoided crossings in leaky-mode photonic lattices. Nanophotonics 9, 4373–4380. doi:10.1515/nanoph-2020-0346

CrossRef Full Text | Google Scholar

Lu, C., Wang, C., Xiao, M., Zhang, Z. Q., and Chan, C. T. (2021). Topological rainbow concentrator based on synthetic dimension. Phys. Rev. Lett. 126, 113902. doi:10.1103/PhysRevLett.126.113902

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, B., Wang, J., Zhou, C., and Huang, L. (2022). Bound states in the continuum supported by silicon oligomer metasurfaces. Opt. Lett. 47, 1549–1552. doi:10.1364/OL.453076

PubMed Abstract | CrossRef Full Text | Google Scholar

Mittleman, D. M. (2017). Perspective: Terahertz science and technology. J. Appl. Phys. 122, 230901. doi:10.1063/1.5007683

CrossRef Full Text | Google Scholar

Niu, J., Zhai, Y., Han, Q., Liu, J., and Yang, B. (2021). Resonance-trapped bound states in the continuum in metallic thz metasurfaces. Opt. Lett. 46, 162–165. doi:10.1364/OL.410791

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, Q., Feng, F., Yao, X., Xu, Q., Xin, M., Lan, Z., et al. (2021). Multiplexing-oriented plasmon-mos2 hybrid metasurfaces driven by nonlinear quasi bound states in the continuum. Opt. Express 29, 5384–5396. doi:10.1364/OE.414730

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, Q., You, J., and Panoiu, N. (2019). Large enhancement of the effective second-order nonlinearity in graphene metasurfaces. Phys. Rev. B 99, 205404. doi:10.1103/physrevb.99.205404

CrossRef Full Text | Google Scholar

Ren, Q., You, J. W., and Panoiu, N.-C. (2020). Comparison between the linear and nonlinear homogenization of graphene and silicon metasurfaces. IEEE Access 8, 175753–175764. doi:10.1109/ACCESS.2020.3026313

CrossRef Full Text | Google Scholar

Ren, Q., You, J. W., and Panoiu, N. C. (2018). Giant enhancement of the effective Raman susceptibility in metasurfaces made of silicon photonic crystal nanocavities. Opt. Express 26, 30383–30392. doi:10.1364/OE.26.030383

PubMed Abstract | CrossRef Full Text | Google Scholar

Rybin, M. V., Koshelev, K. L., Sadrieva, Z. F., Samusev, K. B., Bogdanov, A. A., Limonov, M. F., et al. (2017). High-q supercavity modes in subwavelength dielectric resonators. Phys. Rev. Lett. 119, 243901. doi:10.1103/PhysRevLett.119.243901

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadreev, A. F. (2021). Interference traps waves in an open system: Bound states in the continuum. Rep. Prog. Phys. 84, 055901. doi:10.1088/1361-6633/abefb9

CrossRef Full Text | Google Scholar

Singh, R., Cao, W., Al-Naib, I., Cong, L., Withayachumnankul, W., and Zhang, W. (2014). Ultrasensitive terahertz sensing with high-q fano resonances in metasurfaces. Appl. Phys. Lett. 105, 171101. doi:10.1063/1.4895595

CrossRef Full Text | Google Scholar

Wang, L., Zhao, Z., Du, M., Qin, H., Ako, R. T., and Sriram, S. (2022a). Tuning symmetry-protected quasi bound state in the continuum using terahertz meta-atoms of rotational and reflectional symmetry. Opt. Express 30, 23631–23639. doi:10.1364/OE.454739

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Xin, J., Ren, Q., Cai, H., Han, J., Tian, C., et al. (2022b). Plasmon hybridization induced by quasi bound state in the continuum of graphene metasurfaces oriented for high-accuracy polarization-insensitive two-dimensional sensors. Chin. Opt. Lett. 20, 042201. doi:10.3788/col202220.042201

CrossRef Full Text | Google Scholar

Wang, Y., Han, Z., Du, Y., and Qin, J. (2021). Ultrasensitive terahertz sensing with high-q toroidal dipole resonance governed by bound states in the continuum in all-dielectric metasurface. Nanophotonics 10, 1295–1307. doi:10.1515/nanoph-2020-0582

CrossRef Full Text | Google Scholar

Xu, N., Singh, R., and Zhang, W. (2016). High-q lattice mode matched structural resonances in terahertz metasurfaces. Appl. Phys. Lett. 109, 021108. doi:10.1063/1.4958730

CrossRef Full Text | Google Scholar

Zang, X., Balakin, A. V., Shkurinov, A. P., Zhu, Y., and Zhuang, S. (2021). “Metasurfaces for phase/polarization manipulation and imaging,” in 2021 46th International Conference on Infrared, Millimeter and Terahertz Waves (IRMMW-THz, Chengdu, 29 August 2021 (IEEE).1–1

PubMed Abstract | CrossRef Full Text | Google Scholar

Zang, X., Ding, H., Intaravanne, Y., Chen, L., Peng, Y., Xie, J., et al. (2019). A multi-foci metalens with polarization-rotated focal points. Laser & Photonics Rev. 13, 1900182. doi:10.1002/lpor.201900182

CrossRef Full Text | Google Scholar

Zang, X., Xu, W., Gu, M., Yao, B., Chen, L., Peng, Y., et al. (2020). Polarization-insensitive metalens with extended focal depth and longitudinal high-tolerance imaging. Adv. Opt. Mater. 8, 1901342. doi:10.1002/adom.201901342

CrossRef Full Text | Google Scholar

Zhu, Y., Lu, B., Fan, Z., Yue, F., Zang, X., Balakin, A. V., et al. (2022). Geometric metasurface for polarization synthesis and multidimensional multiplexing of terahertz converged vortices. Photonics Res. 10, 1517–1532. doi:10.1364/prj.455459

CrossRef Full Text | Google Scholar