Temperature-controlled optical switch metasurface with large local field enhancement based on FW-BIC

Introduction: Many researchers have explored the bound states in the continuum (BIC_s) as a particular bound wave state which can be used to achieve a very high Q-factor. High-Q factor devices, typically based on the bound states in the continuum (BIC_s), are well used in the fields of hypersensitive biochemical sensors, non-linear effects enhancement, plasmon lasers, and hi-performance filtering. However, symmetrical-protected BIC is difficult to achieve experimentally high-Q factor because it strongly depends on the geometry and can be destroyed by any slight disturbance in the potential well.

Methods: Therefore, we proposed a parameter-adjusted Friedrich-Wintergen BIC based on the analysis model of time-coupled model theory, where the target system parameters can be tuned to achieve high-Q excitation.

Results: Moreover, considering the tunability and flexibility of the components in various practical applications, we integrate active materials into metasurface arrays with the help of external stimuli to achieve modulation of high-Q resonances. Our results demonstrate that an optical resonator based on FW-BIC can modulate the BIC state by changing the intermediate gap.

Discussion: The BIC state and the high-Q factor Fano resonance can be dynamically tuned by adding temperature-sensitive VO₂ material.

1 Introduction

With the bound states lying inside the continuum spectrum and coexisting with extended waves, bound state in the continuum (BIC) was initially proposed in quantum mechanics and widely used in diverse scientific fields as a particular bound state located in the radiation region (Lu et al., 2021b; Bogdanov et al., 2019; Hsu et al., 2016). The bound states lie inside the continuum spectrum and coexist with extended waves (Wang et al., 2022a; Kang et al., 2022). Bound states in the continuums (BICs) differ from conventional wave-binding mechanisms because they are perfectly bound by the system without any radiation. BIC mode can be achieved in two methods (Huang et al., 2021). One is to construct a symmetry-protected BIC, wherein the capture mode with a certain symmetry is embedded into an apparent-symmetric continuum, preventing the capture mode from leaking (Cong and Singh, 2019). Because even the smallest disturbance may destroy the potential well, this kind of BIC may be difficult to obtain experimentally (Sadreev, 2021). Another is to create a Friedrich-Wintergen BIC (FW-BIC), where the target system parameters are tuned to achieve high-Q excitation via continuous cancellation (Zhao et al., 2020; Friedrich and Wintgen, 1985).

Textcolorred with a broad application in highly sensitive refractive sensors (Meng et al., 2022; Bogdanov et al., 2019; Chen et al., 2022), electric field enhancement (Ren et al., 2018; electromagnetic induced transparency (Azzam et al., 2018) and non-linear effects enhancement (Mittleman, 2017; Lu et al., 2021a; Fang et al., 2018) as well as a significant demand in photonic systems. High-Q resonators greatly enhance the interaction between light and matter, reduce the radiation loss of devices. Be capable of capturing the energy in the resonator in the BIC mode with little leakage into the continuum, an extremely high-Q factor could be achieved in the BIC (Lee et al., 2020). Due to the infinite lifetime and the absence of leakage in an ideal BIC, external excitations cannot couple to the BIC, and the ideal BIC is unobservable in the electromagnetic spectrum (Doeleman et al., 2018). However, by introducing structural perturbations in the metasurfaces supporting the BIC, the high-Q resonance mode induced by the two low-Q mode couplings identifies the emergence of a quasi-BIC in the far-field response (Ren et al., 2021).

When considering the diverse practical applications of the optical medium’s components in optical switching, optical sensors, and hyperactivity spetroscopy, their tunability and flexibility are noteworthy (Ren et al., 2019; Han et al., 2021; Fang et al., 2021). It can be observed that passively adjusting the geometrical parameters of the resonance structure allows for a finite extent of tuning of the resonance frequency, modulation depth, and linewidth of the Fano resonance. The results have initially demonstrated that accurate active control of the Fano resonance can be achieved at additional levels in bringing active materials into the meta surface arrays, such as semiconductors, graphene (Xiao et al., 2018; Ren et al., 2020; Lan et al., 2021; Wang et al., 2022a), and VO₂ (Yang et al., 2022). VO₂, as an active material, has temperature-sensitive insulator-metal transition (IMT) characteristics, and its conductivity can rapidly increase by 4-5 orders of magnitude under external thermal excitation (Fan et al., 2013; Zhu et al., 2012; Mandal et al., 2011; Liu et al., 2012; Zhao et al., 2018).

In this paper, we propose a split-ring resonator based on Friedrich-Wintergen BIC (FW-BIC). We tune the high-Q factor Fano resonance of the split-ring resonator by adding temperature sensitive vanadium dioxide material (VO₂). High-Q factor Fano resonances coupled with significant near-field enhancement in optical cavities are essential for a wide range of applications in filtering and sensing, lasers, and non-linear effects enhancement. A metasurface array with an integrated active material enables active control of the components, which is beneficial for various practical applications such as optical switches, optical sensors, and transitivity spectroscopy. The proposed metasurface provides a platform for trapping and manipulating electromagnetic waves provided by free-space radiation. The employed theoretical model can be generalized to help design quasi-BIC in other frequency regions.

2 Materials and methods

To experimentally realize the FW-BIC response of the coupled resonance, we designed a device consisting of a split-ring resonator. The period P of the metasurface is 200 µm, and the other parameters are shown in Figure 1. The metamaterial structure consists of an aluminum device and a silicon substrate. The aluminum thickness is 1 µm, and electrical conductivity is 3.74 × 10⁷S/m. The silicon substrate is 20 µm thick, ϵ = 11.7, and 100 µm thick glass below. Our structure is resonant at a terahertz frequency, with both an inductor-capacitance (LC) mode and a dipole mode. In our structure, the resonance frequency of the LC mode can be tuned by changing the intermediate gap (g₂) to produce the FW-BIC state with little effect on the resonance frequency of the dipole mode. The two-sided gap can affect the resonance frequency of the dipole mode. The function of regulating the BIC position or quasi-BIC to BIC conversion is achieved by adding sensitive materials at different sites, such as temperature-sensitive vanadium oxides. With such a plateau, we can control the frequency detuning between the two modes near the ideal BIC. We performed simulations using the finite element method (FEM) with COMSOL Inc (2020) to obtain the response.

FIGURE 1

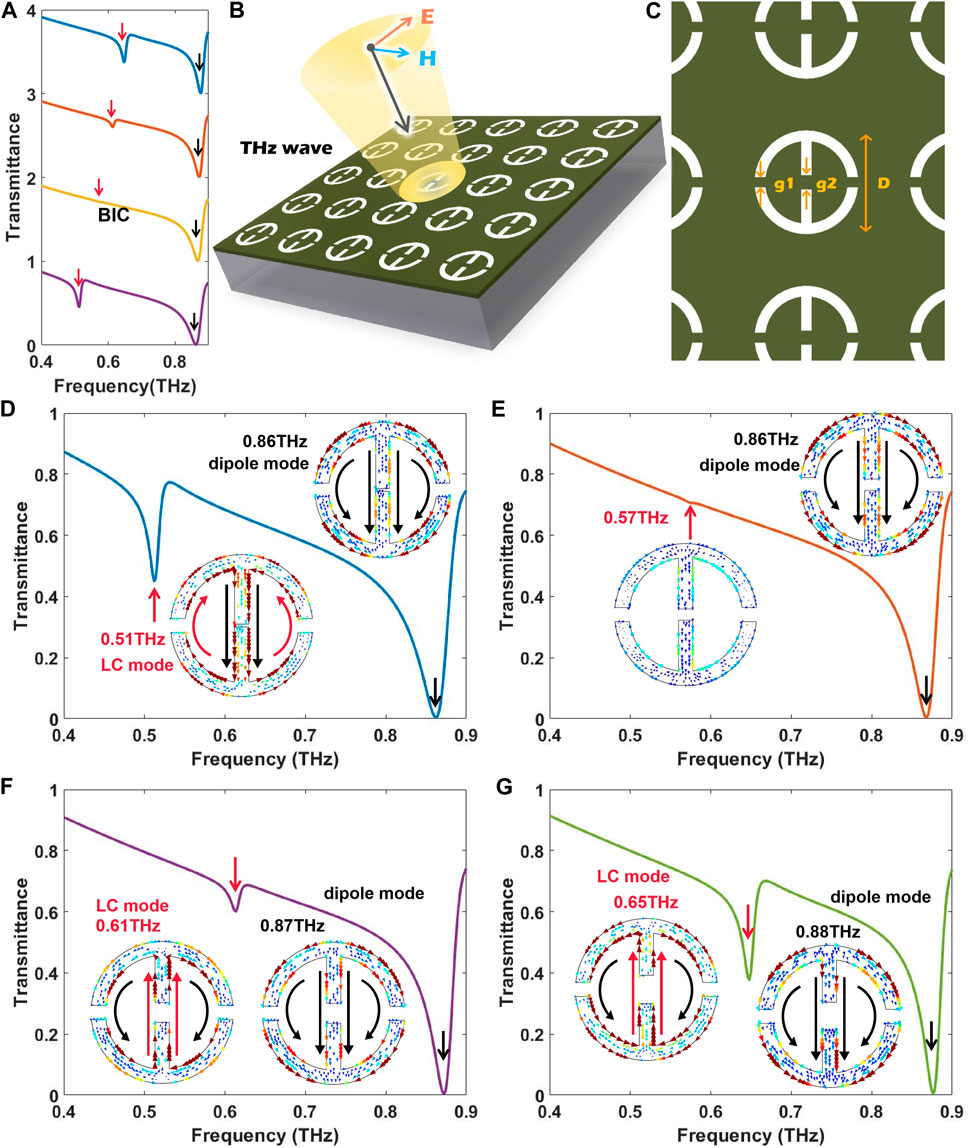
FIGURE 1. Illustration of the generation of BIC via coupled resonant modes, model design and measurement of transmission spectra. (A) The transmission coefficient for different frequency settings. The Q-factor is infinite in the BIC mode. (The red arrows label ω₁ and the black arrows label ω₂.). (B) 3D schematic diagram of the metasurfaces. (C) Schematic of the metasurface design. The design dimensions are as follows: period p = 100 µm, the ring outer diameter D = 120 µm, width W = 10 µm, double seam width g₁ = 10 µm, control the shift of g₂. (D) The amplitude transmission spectrum of the metasurface at g₂ = 2 µm under the Y polarization and the current distribution corresponding to the transmission valley. (E) The amplitude transmission spectrum of the metasurface of g₂ = 8 µm, and the current distribution corresponds to the transmission valley. (F) The amplitude transmission spectrum of the metasurface of g₂ = 14 µm, and the current distribution corresponds to the transmission valley. (G) The amplitude transmission spectrum of the metasurface at g₂ = 20 µm and the current distribution correspond to the transmission valley.

Here, a two-mode system coupled by two ports is described using a time-coupled mode theory model to better explain the principle of Friedrich-Wintergen (Zhao et al., 2019; Suh et al., 2004):

$\frac{\mathrm{d}}{\mathrm{d}t}\left[\begin{array}{c}\hfill r_1\hfill \\ \hfill r_2\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill d_{11}\hfill & \hfill d_{12}\hfill \\ \hfill d_{21}\hfill & \hfill d_{22}\hfill \end{array}\right]\left[\begin{array}{c}\hfill p_{1+}\hfill \\ \hfill p_{2+}\hfill \end{array}\right]+j\left[\begin{array}{cc}\hfill {\omega }_1+j{\tau }_1\hfill & \hfill d+j{\tau }_{12}\hfill \\ \hfill d+j{\tau }_{21}\hfill & \hfill {\omega }_2+j{\tau }_2\hfill \end{array}\right]\left[\begin{array}{c}\hfill r_1\hfill \\ \hfill r_2\hfill \end{array}\right]$

As given by the formula, the coupling coefficient between mode i and port j is expressed by d_ij (i, j ∈ 1, 2); the input amplitudes of ports 1 and 2 are p₁₊ and p₂₊; ω₁ and ω₂, τ₁ and τ₂ indicate the resonant frequency and attenuation rate of the two modes, respectively; d is the direct coupling rate between the two modes; τ₁₂ and τ₂₁ are the coupling coefficients generated by damping, and finally, the resonance amplitude of the mode supported by the system could be expressed by r₁ and r₂. Due to the symmetry of the system, τ₁₂ = τ₂₁ = $\sqrt{{\tau }_1{\tau }_2}$.

In this system, the output wave that excites the resonant mode is represented as follows:

$\left[\begin{array}{c}\hfill p_{1-}\hfill \\ \hfill p_{2-}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill r\hfill & \hfill t\hfill \\ \hfill t\hfill & \hfill r\hfill \end{array}\right]\left[\begin{array}{c}\hfill p_{1+}\hfill \\ \hfill p_{2+}\hfill \end{array}\right]+\left[\begin{array}{cc}\hfill c_{11}\hfill & \hfill c_{12}\hfill \\ \hfill c_{21}\hfill & \hfill c_{22}\hfill \end{array}\right]\left[\begin{array}{c}\hfill r_1\hfill \\ \hfill r_2\hfill \end{array}\right]$

where p₁₋ and p₂₋ are the outgoing wave amplitudes at ports 1 and 2; r and t are the direct reflection and transmission coefficient between the ports in the absence of the resonant modes; c_ij is the coupling coefficient between the port j and the mode i; r₁ and r₂ are the resonance amplitude of modes supported by the system.

Under the above framework, the transmission coefficients of uncoupled single mode and coupling mode can be calculated. The transmission valley in the transmission occurs at the resonant frequencies (ω₁ and ω₂) for each individual mode. The transmission spectrum is represented by a Fano response with two transmission valleys and a peak. Once the two modes are coupled to each other, the resonant frequencies of the two resonance modes correspond to the transmission valleys, and the coupling between the two modes forms a transmission peak. ω₁ + jτ₁ and ω₂ + jτ₂ demonstrate two complex eigenvalues exhibited by the coupled resonator, where the imaginary and real parts are the resonant frequency and attenuation rate of the hybrid eigenmode, respectively. Q = ω/(2τ) is expressed as a quality factor for the eigenmode. The peak transmission coefficient corresponds to one eigenmode with a high-Q factor, while the other eigenmode suppressed by the high attenuation rate has a Q value less than 1. The Fano resonance may shift with the frequency detuning between the resonant modes (δω = ω₁ − ω₂) as shown in Figure 1. One of the eigenmodes is promoted to the BIC state, and the eigenvalue radiation becomes a pure imaginary number due to a loss of zero when the Friedrich-Wintgen condition $(\delta \omega \sqrt{{\tau }_1{\tau }_2}=n({\tau }_1-{\tau }_2))$ is satisfied.

3 Results

As shown in Figure 1, when the two-sided gap g₁ is 10 µm unchanged, the peak of quasi-BIC appears when the intermediate gap g₂ size is 2 µm. The current distribution indicates that 0.51 THz corresponds to the LC mode and 0.86 THz corresponds to the dipole mode. The transport peak at 0.55 THz results from the coupling of the LC and dipole mode and act as a quasi-BIC mode. It has been reported that the Fano resonances can be excited by a set of antiparallel magnetic dipoles that are weakly coupled to the free space and emerge as high-Q resonances. Since the LC mode and the dipole mode are coupled to each other through resonant and leaky channels, the quasi-BIC mode has been theoretically and computationally predicted to have Fano line shapes. As the gap g₂ increases, the LC mode moves towards a higher frequency, closing to the dipole resonance frequency. A decrease in the frequency detuning leads to a decrease in the transmission peak and an increase in the Q-factor. When the gap size is 14 µm, the BIC can be identified by the vanishing of the Fano transmission peak. As for the FW-BIC, on the one hand, the surface current is weak, suggesting that it is barely coupled to free-space radiation and is entirely confined by bound states in the absence of leaky channels.

On the other hand, the faint in-phase collective current on the upper and lower arms of the resonator with the same incident THz wave direction comes from the dipole resonance of the symmetric structure. When the BIC condition is broken by increasing the gap size of g₂, the transmission peak appears again. At this time, the surface current is considerably excited, and the current direction on the resonator surface is rearranged, indicating that the bound state is coupled with the incident radiation, thus generating quasi-BIC resonance. Note that unlike symmetry-protected BIC, quasi-BIC of FW-BIC in this structure is realized by changing the gap size without destroying the symmetry.

Recently, a few studies have tentatively demonstrated that Fano resonances enable precise active control at an additional level if specific active materials are integrated into metasurface arrays, such as semiconductors, graphene, and vanadium dioxide. As an active material, VO₂ has temperature-sensitive insulator-metal transition (IMT) characteristics. Its conductivity can be rapidly increased by 4-5 orders of magnitude under external thermal excitation, and it is only one order of magnitude lower than gold. VO₂ can be expressed as a material with dielectric ϵ_r = 9 in the terahertz band, and its conductivity can shift from 10S/m to 100000S/m with the increase of temperature.

Since the gap on both sides can affect the resonance frequency of the dipole mode, in order to realize the function of regulating the BIC position, we designed the Al-VO₂ hybrid metasurface, as shown in Figure 2. Interactions between electrons, orbitals, and crystal structures can cause abrupt changes in the electromagnetic and thermal properties of VO₂ near the phase transition temperature. During the phase transition, VO₂ dramatically changes the properties of electromagnetic waves at all wavelengths, especially in the terahertz band. At temperatures lower than the phase transition temperature, VO₂ is in the insulating phase, and the band gap of VO₂ is 6eV, which allows THz wave to fully penetrate the equivalent transparent state. At temperatures higher than the phase transition temperature, VO₂ is a metallic phase and its Fermi level coincides with the 3D band of the V atom, such that the band gap of VO₂ becomes 0. At this point, VO₂ can approximately replace the metal, which leads to a reduction of the equivalent gap width and thus affects the position of the FW-BIC. As can be seen from the simulation results, for the designed Al-VO₂ hybrid metasurface, we can easily shift the frequency corresponding to the BIC from 0.64 THz to 0.69 THz by using external thermal excitation to shift the temperature.

FIGURE 2

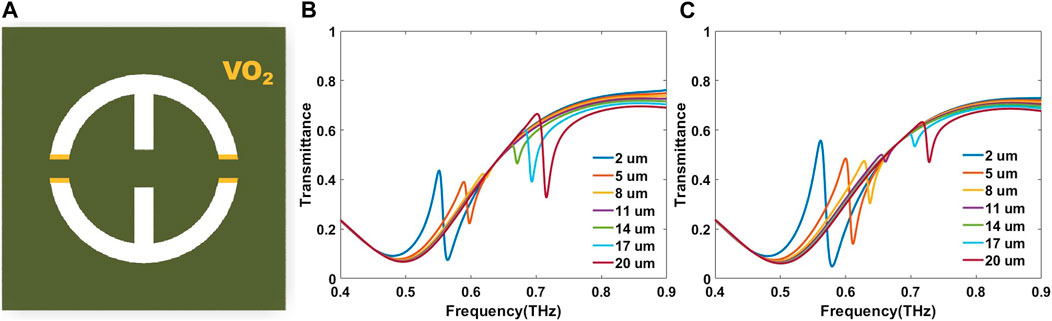
FIGURE 2. (A) Schematic diagram of the Al − VO₂ metasurface. The metal design dimensions are as follows: period p = 100 µm, the ring outer diameter D = 120 µm, width W = 10 µm, double seam width g₁ = 15 µm, control the change of g₂. Vanadium oxide filling both sides seam width to 10 µm. (B) The low-temperature regime and the amplitude transmission spectrum of the metasurfaces of different g₂. (C) High-temperature state, the amplitude transmission spectrum of the metasurfaces of different g₂.

4 Discussion

Based on the above analysis of the time-domain coupled model, for an ideal FW-BIC, the decay rate of this mode (τ) should be close to 0, and hence the theoretical Q-factor (Q = ω/(2τ)) should be approximately infinite. For the lossy BIC in the experiment, although the energy leakage from the element surface to the port is 0, the ohmic loss in the metal and the dielectric loss in the substrate will still lead to a large decal rate, thus leading to a finite Q-factor. Therefore, we used COMSOL to reduce the imaginary part of the ϵ to 10^–5 to calculate the Q-factor of BIC with a near-loss-free metal (the first Brillouin zone of the square lattice is plotted on the top left in Figure 3). Figure 3 shows the Q factors of eigenmodes close to 0.56 THz calculated by this method. Figure 3 shows the Q factors of eigenmodes close to 0.56 THz calculated by this method, and the Q factor of BIC rises rapidly to a maximum value at the point of Γ. The insertion diagram below shows the possible eigenmodes near 0.56 THz in the M-Γ direction.

FIGURE 3

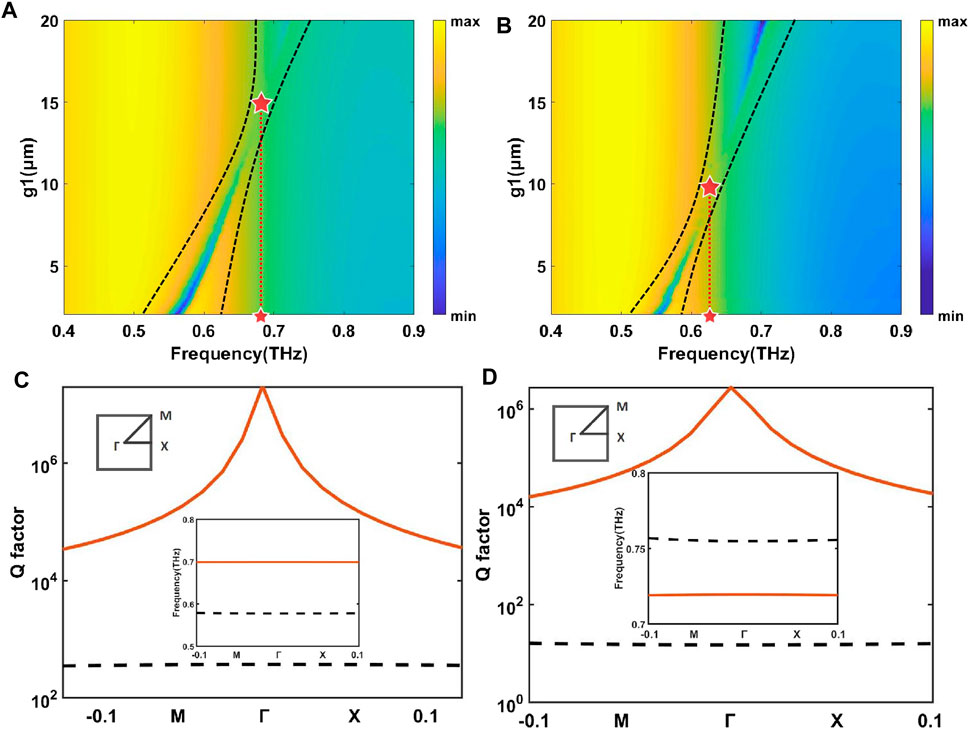
FIGURE 3. (A) The colour plot of the simulated transmission spectra of the BIC at low temperatures by scanning g₂ from 2 µm to 20 µm. (B) The colour plot of the simulated transmission spectra of the BIC at the high-temperature state by sweeping g₂ from 2 µm–20 µm. (C) The Q factor and band structure correspond to the low-temperature BIC (inset) state. (D) The Q factor and band structure correspond to the high-temperature BIC (inset) state. The metal loss is reduced, and the imaginary part ϵ of the dielectric constant is reduced to 10⁻⁵S/m. The quasi-BIC we study appears at the Γ point in the first red Brillouin zone with an extremely high Q factor.

In the BIC state, the energy transfer of electromagnetic waves is mainly in the z-axis direction, so that the magnetic field is confined in the x-o-y plane. However, in the case of a quasi-BIC, a part of the magnetic field arises out of the x-o-y plane due to energy leakage. Therefore, the energy leakage in the case of a quasi-BIC can be easily verified by monitoring the magnetic field component in the z-axis direction. We monitored the z-directional magnetic field strength of the metal split-ring resonator pair at the Fano resonance, as shown in Figure 4. Split-ring resonator has nearly no Z-direction magnetic field in the BIC state, indicating no energy leakage in the split-ring resonator and an extremely strong Z-direction magnetic field around the split-ring resonator in the quasi-BIC state. It can be seen that the magnetic field in the quasi-BIC state is enhanced more than that in the BIC state, indicating a significant magnetic field leakage.

FIGURE 4

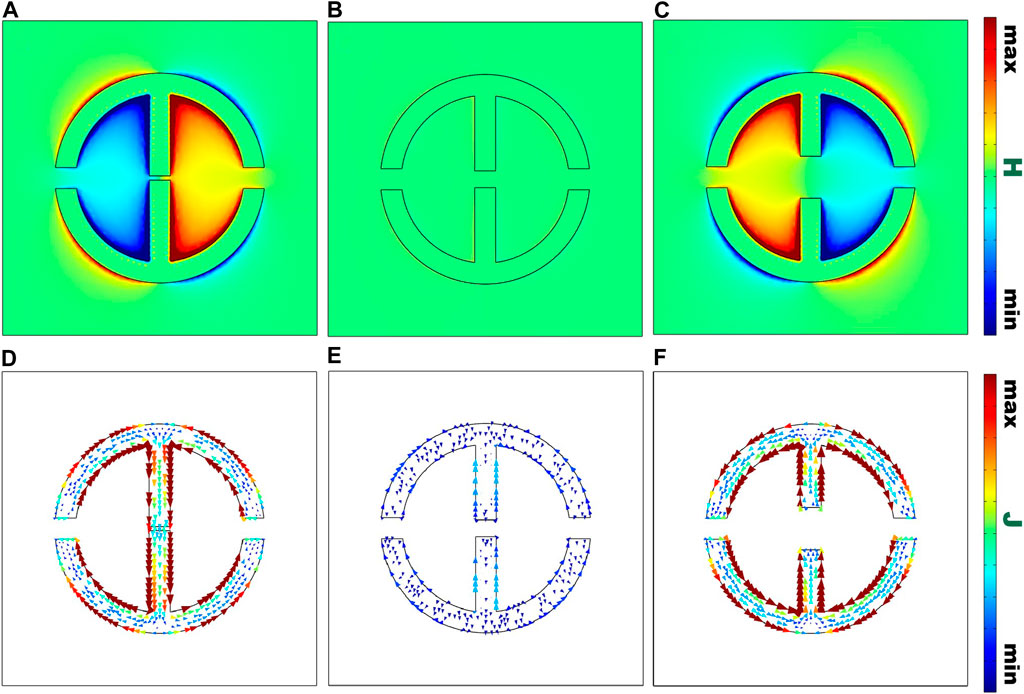
FIGURE 4. (A) Z direction magnetic field strength corresponds to the quasi-BIC mode of g₂ = 2 µm. (B) Z direction magnetic field strength corresponds to the BIC mode of g₂ = 8 µm. (C) The Z-direction magnetic field strength corresponds to the quasi-BIC mode of g₂ = 20 µm. (D) The x-o-y plane current corresponds to the quasi-BIC mode of g₂ = 2 µm. (E) The x-o-y plane current corresponds to the BIC mode of g₂ = 8 µm. (F) The x-o-y plane current corresponds to the quasi-BIC mode of g₂ = 20 µm.

By varying the intermediate gap (g₂), we can tune the resonant frequency of the LC mode to switch between the BIC state and the quasi-BIC state, which slightly affects the resonant frequency of the dipole mode. Therefore, in order to achieve adjustable BIC resonance and active switch of Fano resonance, we embed VO₂ in the middle gap to present the dielectric state and mental state at different temperatures as well as realize the control by employing external thermal excitation.

The conductivity of VO₂ can be expressed by the effective medium theory (EMT) formula: (Lu et al., 2021a).

$\left(1-g\right){\sigma }_{\mathit{eff}}^2+\left[g{\sigma }_i+g{\sigma }_m-{\sigma }_i+f_v\left({\sigma }_i-{\sigma }_m\right)\right]{\sigma }_{\mathit{eff}}-g{\sigma }_i{\sigma }_m=0$

where g is the shape-related parameter controlling the seepage threshold. σ_i, σ_m and σ_eff is the conductivity of insulating phase, metal phase and effective frequency, respectively, f_v is the volume fraction of the metal domain. Wherein, the volume fraction of metal phase f_v can be expressed as: (Ma et al., 2020).

$f_v=f_{\mathit{max}}\left(1-\frac{1}{1+e^{\frac{T-T_0}{\mathrm{\Delta }T}}}\right)$

where f_max = 0.95 is the maximum volume fraction of metal composition at the highest temperature in vanadium dioxide, T is the regulated VO₂ temperature, T₀ is the phase transition temperature, the heating point and cooling point are 68 °C and 64 °C respectively, ΔT = 2 °C is the transition width. From the above equations, it is clear that tuning the temperature can alter the volume fraction of the metallic phase and thus the conductivity of VO₂. As the temperature increases from room temperature to above the phase transition temperature, the VO₂ embedded in the intermediate gap will gradually decrease the equivalent intermediate gap width. The transmission peak at 0.63 THz is the result of coupling between the LC and dipole mode. As the equivalent gap approaches the gap corresponding to the BIC mode, the frequency detuning $(\left|\delta \omega \right|)$ almost satisfies the Friedrich-Wintgen condition $(\delta \omega \sqrt{{\tau }_1{\tau }_2}=n({\tau }_1-{\tau }_2))$, which will reduce the transmission peak.

The metasurfaces supporting quasi-BIC modes can provide significant local field enhancement due to high Q resonances. The electric field is confined to the gap region for metal split-ring resonator, leading to a substantial electric field enhancement. The simulation results in Figure 5 show that when g₂ = 2 µm, the quasi-BIC mode achieves a maximum electric field enhancement of 163 at the resonant frequency of the coupled mode compared to the BIC mode when g₂ = 9 µm. For a metasurface with BIC modes, the electric field enhancement disappears because the incident wave does not couple to the coupled modes of the metasurface. For the Al-VO₂ hybrid metasurface in Figure 5, as the temperature increases, the equivalent intermediate gap decreases and the electric field enhancement gradually increases. It is shown that the closer the quasi-BIC state is to the BIC state, the higher the quality factor and the lower the electric field enhancement rate.

FIGURE 5

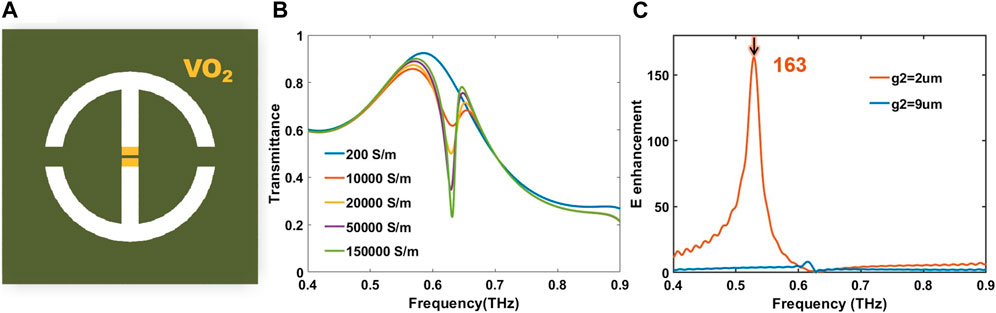
FIGURE 5. (A)Schematic diagram of the VO₂ − Al metasurface. The metal design dimensions are as follows: period p = 100 µm, the ring outer diameter D = 120 µm, width W = 10 µm, both side seam width g₁ = 10 µm, g₂ = 8 µm. After vanadium oxide filling, the intermediate seam width changes to 2 µm. (B)The amplitude transmission spectrum of the metasurfaces at the corresponding conductivity to different temperatures. High-temperature state, the amplitude transmission spectrum of the metasurfaces of different g₂. (C)Simulated field enhancement of the metasurface center. Electric field enhancement to quasi-BIC responses distant from the BIC point (red) and close to the BIC point (blue). Field enhancement away from the BIC point (red) can reach 163.

In this paper, we propose a split-ring resonator based on the Friedrich-Wintergen BIC. By changing the parameters and using magnetic field leakage to confirm the split-ring resonator’s BIC mode, we are able to generate high-Q resonances. Additionally, we tune the frequency positions of the temperature-sensitive vanadium dioxide material at various points in the BIC and high-Q factor Fano resonance switches. The metasurface supporting the quasi-BIC mode has been shown to be capable of generating a local electric field increase of 163 approximately, which is critical for a variety of applications in filtering, sensing, and enhancing non-linear effects. Metasurface arrays integrated with novel active materials enable active control of components as a function of optical switches. It provides a platform for capturing and manipulating electromagnetic waves via free-space radiation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

XYW, XMW, and QR contributed to conception and design of the study. HC, JX, and YL performed the statistical analysis. XMW wrote the first draft of the manuscript. XX, ZL, JY, and WS wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was financially sponsored by National Natural Science Foundation of China (12104339), Open Fund of State Key Laboratory of Millimeter Wave, Southeast University (K202216) and China Postdoctoral Science Foundation funded project (258023).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Azzam, S. I., Shalaev, V. M., Boltasseva, A., and Kildishev, A. V. (2018). Formation of bound states in the continuum in hybrid plasmonic-photonic systems. Phys. Rev. Lett. 121, 253901. doi:10.1103/PhysRevLett.121.253901

PubMed Abstract | CrossRef Full Text | Google Scholar

Bogdanov, A. A., Koshelev, K. L., Kapitanova, P. V., Rybin, M. V., Gladyshev, S. A., Sadrieva, Z. F., et al. (2019). Bound states in the continuum and Fano resonances in the strong mode coupling regime. Adv. Photonics 1, 016001. doi:10.1117/1.AP.1.1.016001

CrossRef Full Text | Google Scholar

Chen, S., Ren, Q., Zhang, K., Wei, E., Hao, T., Xu, H., et al. (2022). A highly sensitive and flexible photonic crystal oxygen sensor. Sensors Actuators B Chem. 355, 131326. doi:10.1016/j.snb.2021.131326

CrossRef Full Text | Google Scholar

COMSOL Inc (2020). Simulate real-world designs, devices, and processes with multiphysics software. Stockholm, Sweden: COMSOL Inc. https://www.comsol.com/

Google Scholar

Cong, L., and Singh, R. (2019). Symmetry-protected dual bound states in the continuum in metamaterials. Adv. Opt. Mater. 7, 1900383. doi:10.1002/adom.201900383

CrossRef Full Text | Google Scholar

Doeleman, H. M., Monticone, F., den Hollander, W., Alù, A., and Koenderink, A. F. (2018). Experimental observation of a polarization vortex at an optical bound state in the continuum. Nat. Photonics 12, 397–401. doi:10.1038/s41566-018-0177-5

CrossRef Full Text | Google Scholar

Fan, F., Gu, W. H., Chen, S., Wang, X. H., and Chang, S. J. (2013). State conversion based on terahertz plasmonics with vanadium dioxide coating controlled by optical pumping. Opt. Lett. 38, 1582–1584. doi:10.1364/ol.38.001582

PubMed Abstract | CrossRef Full Text | Google Scholar

Fang, M., Huang, Z., Wei, E., and Soukoulis, C. M. (2021). Modelling of the fluctuation and coherent dynamics in active metamaterial devices. IEEE Trans. Nanotechnol. 20, 543–551. doi:10.1109/tnano.2021.3092059

CrossRef Full Text | Google Scholar

Fang, M., Niu, K., Huang, Z., Wei, E., Wu, X., Koschny, T., et al. (2018). Investigation of broadband terahertz generation from metasurface. Opt. Express 26, 14241–14250. doi:10.1364/oe.26.014241

PubMed Abstract | CrossRef Full Text | Google Scholar

Friedrich, H., and Wintgen, D. (1985). Interfering resonances and bound states in the continuum. Phys. Rev. A 32, 3231–3242. doi:10.1103/PhysRevA.32.3231

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, S., Pitchappa, P., Wang, W., Srivastava, Y. K., Rybin, M. V., and Singh, R. (2021). Extended bound states in the continuum with symmetry-broken terahertz dielectric metasurfaces. Adv. Opt. Mater. 9, 2002001. doi:10.1002/adom.202002001

CrossRef Full Text | Google Scholar

Hsu, C. W., Zhen, B., Stone, A., Joannopoulos, J., and Soljačić, M. (2016). Bound states in the continuum. Nat. Rev. Mater. 1, 16048. doi:10.1038/natrevmats.2016.48

CrossRef Full Text | Google Scholar

Huang, L., Chiang, Y. K., Huang, S., Shen, C., Deng, F., Cheng, Y., et al. (2021). Sound trapping in an open resonator. Nat. Commun. 12, 4819–4827. doi:10.1038/s41467-021-25130-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Kang, M., Zhang, Z., Wu, T., Zhang, X., Xu, Q., Krasnok, A., et al. (2022). Coherent full polarization control based on bound states in the continuum. Nat. Commun. 13, 4536. doi:10.1038/s41467-022-31726-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Lan, Z., You, J. W., Ren, Q., Sha, W. E. I., and Panoiu, N. C. (2021). Second-harmonic generation via double topological valley-hall kink modes in all-dielectric photonic crystals. Phys. Rev. A 103, L041502. doi:10.1103/PhysRevA.103.L041502

CrossRef Full Text | Google Scholar

Lee, S. G., Kim, S. H., and Kee, C. S. (2020). Bound states in the continuum (bic) accompanied by avoided crossings in leaky-mode photonic lattices. Nanophotonics 9, 4373–4380. doi:10.1515/nanoph-2020-0346

CrossRef Full Text | Google Scholar

Liu, M., Hwang, H. Y., Tao, H., Strikwerda, A. C., Fan, K., Keiser, G. R., et al. (2012). Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 487, 345–348. doi:10.1038/nature11231

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, C., Lu, Q., Gao, M., and Lin, Y. (2021a). Dynamic manipulation of thz waves enabled by phase-transition vo2 thin film. Nanomaterials 11, 114. doi:10.3390/nano11010114

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, C., Wang, C., Xiao, M., Zhang, Z. Q., and Chan, C. T. (2021b). Topological rainbow concentrator based on synthetic dimension. Phys. Rev. Lett. 126, 113902. doi:10.1103/PhysRevLett.126.113902

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, Y., Feng, X., Wang, Q., Zhang, X., Fang, M., Sha, W. E., et al. (2021c). Integrated terahertz generator-manipulators using epsilon-near-zero-hybrid nonlinear metasurfaces. Nano Lett. 21, 7699–7707. doi:10.1021/acs.nanolett.1c02372

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, J., Wang, Z. H., Liu, H., Fan, Y. X., and Tao, Z. Y. (2020). Active switching of extremely high-q fano resonances using vanadium oxide-implanted terahertz metamaterials. Appl. Sci. 10, 330. doi:10.3390/app10010330

CrossRef Full Text | Google Scholar

Mandal, P., Speck, A., Ko, C., and Ramanathan, S. (2011). Terahertz spectroscopy studies on epitaxial vanadium dioxide thin films across the metal-insulator transition. Opt. Lett. 36, 1927–1929. doi:10.1364/ol.36.001927

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, B., Wang, J., Zhou, C., and Huang, L. (2022). Bound states in the continuum supported by silicon oligomer metasurfaces. Opt. Lett. 47, 1549–1552. doi:10.1364/OL.453076

PubMed Abstract | CrossRef Full Text | Google Scholar

Mittleman, D. M. (2017). Perspective: Terahertz science and technology. J. Appl. Phys. 122, 230901. doi:10.1063/1.5007683

CrossRef Full Text | Google Scholar

Ren, Q., Feng, F., Yao, X., Xu, Q., Xin, M., Lan, Z., et al. (2021). Multiplexing-oriented plasmon-mos2 hybrid metasurfaces driven by nonlinear quasi bound states in the continuum. Opt. Express 29, 5384–5396. doi:10.1364/OE.414730

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, Q., You, J., and Panoiu, N. (2019). Large enhancement of the effective second-order nonlinearity in graphene metasurfaces. Phys. Rev. B 99, 205404. doi:10.1103/physrevb.99.205404

CrossRef Full Text | Google Scholar

Ren, Q., You, J. W., and Panoiu, N. C. (2020). Comparison between the linear and nonlinear homogenization of graphene and silicon metasurfaces. IEEE Access 8, 175753–175764. doi:10.1109/ACCESS.2020.3026313

CrossRef Full Text | Google Scholar

Ren, Q., You, J. W., and Panoiu, N. C. (2018). Giant enhancement of the effective Raman susceptibility in metasurfaces made of silicon photonic crystal nanocavities. Opt. Express 26, 30383–30392. doi:10.1364/OE.26.030383

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadreev, A. F. (2021). Interference traps waves in an open system: Bound states in the continuum. Rep. Prog. Phys. 84, 055901. doi:10.1088/1361-6633/abefb9

CrossRef Full Text | Google Scholar

Suh, W., Wang, Z., and Fan, S. (2004). Temporal coupled-mode theory and the presence of non-orthogonal modes in lossless multimode cavities. IEEE J. Quantum Electron. 40, 1511–1518. doi:10.1109/jqe.2004.834773

CrossRef Full Text | Google Scholar

Wang, L., Zhao, Z., Du, M., Qin, H., Ako, R. T., and Sriram, S. (2022a). Tuning symmetry-protected quasi bound state in the continuum using terahertz meta-atoms of rotational and reflectional symmetry. Opt. Express 30, 23631–23639. doi:10.1364/OE.454739

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Xin, J., Ren, Q., Cai, H., Han, J., Tian, C., et al. (2022b). Plasmon hybridization induced by quasi bound state in the continuum of graphene metasurfaces oriented for high-accuracy polarization-insensitive two-dimensional sensors. Chin. Opt. Lett. 20, 042201. doi:10.3788/col202220.042201

CrossRef Full Text | Google Scholar

Xiao, S., Wang, T., Liu, T., Yan, X., Li, Z., and Xu, C. (2018). Active modulation of electromagnetically induced transparency analogue in terahertz hybrid metal-graphene metamaterials. Carbon 126, 271–278. doi:10.1016/j.carbon.2017.10.035

CrossRef Full Text | Google Scholar

Yang, D., Wang, W., Lv, E., Wang, H., Liu, B., Hou, Y., et al. (2022). Programmable vo2 metasurface for terahertz wave beam steering. iScience 25, 104824. doi:10.1016/j.isci.2022.104824

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, X., Chen, C., Kaj, K., Hammock, I., Huang, Y., Averitt, R. D., et al. (2020). Terahertz investigation of bound states in the continuum of metallic metasurfaces. Optica 7, 1548–1554. doi:10.1364/OPTICA.404754

CrossRef Full Text | Google Scholar

Zhao, X., Zhang, J., Fan, K., Duan, G., Schalch, J., Keiser, G. R., et al. (2019). Real-time tunable phase response and group delay in broadside coupled split-ring resonators. Phys. Rev. B 99, V. doi:10.1103/physrevb.99.245111

CrossRef Full Text | Google Scholar

Zhao, Y., Huang, Q., Cai, H., Lin, X., and Lu, Y. (2018). A broadband and switchable vo2-based perfect absorber at the thz frequency. Opt. Commun. 426, 443–449. doi:10.1016/j.optcom.2018.05.085

CrossRef Full Text | Google Scholar

Zhu, Y., Zhao, Y., Holtz, M., Fan, Z., and Bernussi, A. A. (2012). Effect of substrate orientation on terahertz optical transmission through vo 2 thin films and application to functional antireflection coatings. JOSA B 29, 2373–2378.

CrossRef Full Text | Google Scholar