- Department of Teacher Education, Turtle Mountain College, Belcourt, ND, United States
This article introduces the CRISP (Culturally Relevant, Imbued, and Sustaining Pedagogy) framework in the context of a three-course sequence, “Indigenous Math I, II, and III,” taught at Turtle Mountain College. These three courses seek to revitalize mathematical ways of knowing embedded within the Turtle Mountain language(s) and culture(s). The Indigenous Math framework and Indigenous Math Education framework guide these three courses, as well as the Secondary Math Education bachelor’s degree program that spurred development of these courses. Discussing the relationship (i.e., connections, similarities, differences) between Western math and Indigenous math is central to these courses. The CRISP framework extends this discussion by describing four significant components of revitalizing and teaching Indigenous math. Multiple Indigenous math examples are shared as evidence for the value of the CRISP framework.
1 Introduction
1.1 Author introduction
Halito. Sv hohchifo yvt Danny Luecke. Fargo, North Dakota, USA, amiti li (Choctaw language). Greetings. My name is Danny Luecke. I grew up in Fargo, North Dakota. Boozhoo. Danny Luecke indizhinikaaz. Fargo indoonjii (Ojibwe language). Tawnchii, Danny Luecke dishinakashoon. Oshhiichii Fargo (Michif language). I am a math and math education faculty at Turtle Mountain College (TMC), a tribally controlled college/university (TCU). TMC is chartered by Turtle Mountain Band of Chippewa, an American Indian tribe recognized by the United States government. My role has been to develop, and now instruct, the bachelor’s degree program in Secondary Math Education. I am enrolled in, meaning a dual citizen of the USA and the Choctaw Nation of Oklahoma. Further, as part of my introduction, it is important to acknowledge that I am often perceived as a “white guy” which allows me to experience societal norms that benefit me and my family. Lastly, my learning of Indigenous knowledges and research began in books (Archibald, 2008; Kovach, 2009; Wilson, 2008) and has slowly become more experiential, relational, and spiritual.
1.2 Study context
Culturally connected math curriculum is a broad topic with diverse definitions, terms, and applications. The CRISP (culturally relevant, imbued, and sustaining pedagogy) framework for culturally connected math curriculum attempts to describe four significant components of this broad topic. They are grade level, depth of detail, depth of culture, and the relevant to sustaining spectrum. From my experience instructing a three-course sequence “Indigenous Math I, II, and III” at Turtle Mountain College, the need for a framework to articulate characteristic differences in culturally connected STEM content and pedagogy emerged. Thus, through these Indigenous Math courses, the CRISP framework was developed, implemented, and refined.
1.3 Author’s approach
This article will first lay out the context of Indigenous Math at TMC, and then describe the CRISP framework and apply it to multiple examples of culturally connected math curricula from both the literature and my experience. In doing so, I attempt to write in first person storywork following guidance from Indigenous research paradigm scholars (Archibald, 2008; Wilson, 2008; Kovach, 2009; Windchief and San Pedro, 2019). Kovach (2009) writes that she “… knew from a Nêhiýaw point of view that knowledge and story are inseparable, and that interpretative knowing is highly valued, that story is purposeful… [thus] Story as methodology is decolonizing research” (pp. 98, 103). Further, Windchief and San Pedro (2019) expand on Archibald’s Indigenous storywork (Archibald, 2008). They state:
Storywork practice is very different from Western commonsense notions of ‘universal stories,’ with presumed universal listeners and omniscient narrators who are never actually universal. In these stories, ‘universal’ means unmarked; perspectives that are often masculinist, conquering, and Eurocentric are normalized as gender-neutral, timeless, and placeless. By contrast, storywork makes transparent the listener and the teller” (Windchief and San Pedro, 2019, p. x).
Along with influencing my writing style, the notion of universal stories as unmarked and Eurocentric is very similar to math and math education where universal often means unmarked Western perspectives of math mythologized and proclaimed as culture-free and culturally neutral (Aikenhead, 2017; Bishop, 1990; Ernest, 2021; Kawagley, 1997; Medina et al., 2024; Stevens, 2021).
The Indigenous Math classes at TMC are in part an attempt to mark the unmarked Western perspectives of Western math and make clear some of the similarities and distinctions between Western Math and Indigenous Math. Further, this article, and the CRISP framework, is only one approach in clarifying how culture influences our understanding and application of math and math education. There are many others that I learn from and/or use in my class (Cajete, 1999; Kawagley, 1997; Sanders, 2011; Stevens, 2021).
Lastly as part of my introduction I want to make clear that I do not own any of this knowledge or framework. Within an Indigenous research paradigm, knowledge is a web of relationships amongst all of the cosmos. There is no place to own a relationship (Meyer, 2014; Wilson, 2008). Rather, I am accountable to all my relations. In this article, I am sharing some of the relationships I have formed with culturally connected math curriculum and education. Readers will make unique connections with the writing based on their own web of relationships. We each are accountable to all our relations (Archibald, 2008; Cajete, 1994; Kovach, 2009; Meyer, 2014; Wilson, 2008).
2 Indigenous math courses and frameworks at TMC
2.1 Indigenous math education framework
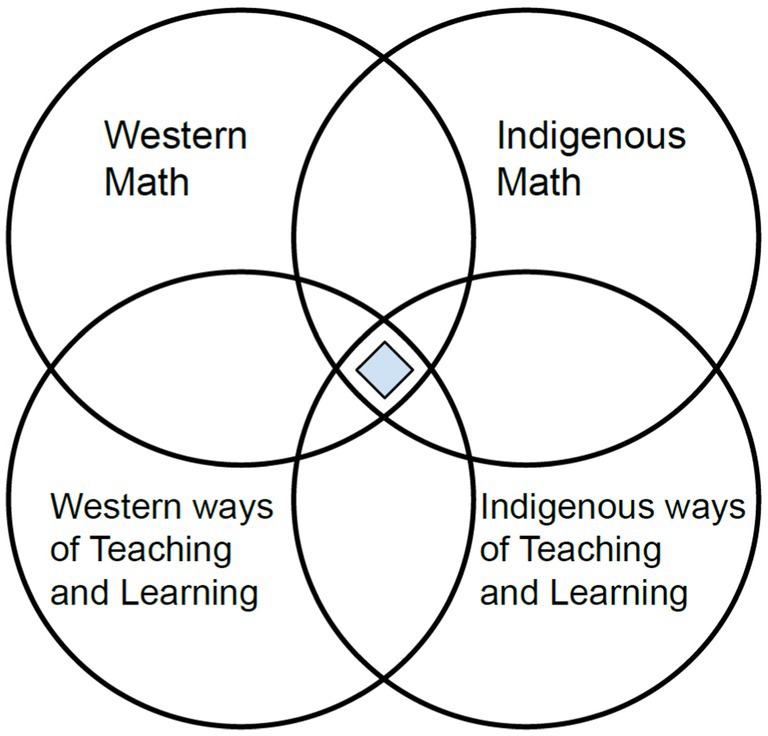
Turtle Mountain College was chartered by Turtle Mountain Band of Chippewa in 1972. In the American education system, TMC is recognized as a TCU (tribally controlled college/university). I was hired in 2021 to join the established Teacher Education Department and develop a new bachelor’s degree program in Secondary Math Education. The program now follows the Indigenous Math Education framework (Figure 1), which seeks to bring balance and harmony between the four circles of Western Math and Indigenous Math as well as Western Education and Indigenous Ways of Teaching and Learning. Notice the balance between Western and Indigenous as well as math content and pedagogy (Luecke, 2023).
Each of the four circles are distinct and can stand on their own. Further, each circle is self-justifying, meaning that it does not need justification nor validation from another circle. Specifically, Indigenous Math does not need to be validated or verified by Western Math to be considered legitimate. Third, each circle is equivalent in size showing equivalent value. This is the desired and ideal scenario but not our current reality. The incessant pressure of colonial thinking and constructs trains us to overvalue Western Math and devalue Indigenous Math (Aikenhead, 2017; Bishop, 1990; Cajete, 1999; Ernest, 2021; Stevens, 2021).
Lastly, the four circles are all interconnected. Despite the little black lines showing rigid boundaries between the intersection areas and exclusive areas, these four topics are interconnected, interdependent, and always shifting in relationship with each other (Cajete, 1994; Wiseman and Lunney Borden, 2018; Luecke, 2023). Indigenous science education scholar Dr. Gregory Cajete (Santa Clara Pueblo) describes the interconnection between Western science and Indigenous science with two hand motions that apply to Western and Indigenous math as well. First, he holds his two hands in fists pushing against each other and explains that some people view Western science and Indigenous science in constant conflict, a dualistic competition. Secondly, he holds his two hands in the same place but with all his fingers intertwined together. With hands folded together with interlocking fingers he describes the integration and interconnectedness of Western science and Indigenous science (Cajete, 2021). These two hand motions also describe Indigenous math as overlapping and intertwined with Western math.
The Indigenous Math Education framework builds upon wisdom from local elders as well as the Dakota/Lakota Math Connections project (Luecke and Sanders, 2023). This framework guides the bachelor’s degree program in Secondary Math Education at TMC, and demonstrates the need for a three-course sequence called ‘Indigenous Math I, II, and III.’
2.2 Indigenous math I, II, and III
The Indigenous Math three-course sequence (labeled MATH 172, 272, and 372 respectively) seeks to revitalize the mathematical ways of knowing embedded within the Turtle Mountain language(s), culture(s), and place so they can once again be widely known and normalized within the community. A major component of the Indigenous Math courses is discussing the relationship (connections, similarities, differences) between Western math and Indigenous math. Students in these courses are most familiar with Western math (often viewed as the ‘universal’ math) through schooling in a Western education system. This is easily demonstrated by a math class that is separated from the sciences, language, history, and art. A value of Western math is removing relationships, that is separating all context from the content. This value of Western math leads to the most common question from math students, “When will I ever use this?” The framework described in this article helps demonstrate that removing relationships is a Western math value and not an Indigenous math value. Thus, throughout the three courses, guiding students toward an experience of Indigenous math first and then a description of Indigenous math is critical (Hogue, 2014).
Indigenous Math I has no pre-requisites in math or Indigenous language courses as a way to eliminate barriers for students to take the course and potentially encourage them to take more Indigenous math courses. Indigenous Math II is typically taught in the spring following the fall semester of Indigenous Math I. Lastly, Indigenous Math III is primarily open to students in the bachelor’s degree program for Secondary Math Education. All three courses attempt to fully follow Indigenous ways of teaching and learning, especially so in authentic and self-determining grading policies.
On the first day of Indigenous Math I, students are introduced to the term mathematizing, the activity of thinking, doing, living, and being in a mathematical way (Aikenhead, 2018; Stevens, 2021). This initial introduction to Indigenous math builds upon Indigenous language and ways of thinking. Indigenous mathematizing is verb-oriented and not isolated from relationships or context. In contrast to Western math that focuses primarily on content and thinking, Indigenous mathematizing connects with place, language, culture, spirituality, and other school subjects. Western math, focusing on content, is exemplified by learning inside, on paper, at a desk and often alone. Whereas Indigenous mathematizing comes from a relational worldview and often takes place outside and in the community through specific activities. Western math assumes itself to be culturally neutral, value free, universal, decontextualized, pure, and objective (Aikenhead, 2017, 2018; Bishop, 1990; Cajete, 1999; Ernest, 2021; Kawagley, 1997; Medina et al., 2024; Stevens, 2021). Further, Western math emphasizes the mythology that the adjective “Western” is irrelevant and unnecessary because it indeed is universal and contains all mathematical knowledge (Luecke, 2023).
A closer look at language gives further evidence. Indigenous languages tend to be more verb-focused and action-based in contrast to English which is more noun-focused and definition-based (Lunney Borden, 2011, 2012). These deep themes of a language influence Indigenous math to be more verb-focused and action-based and Western math toward being more noun-focused and definition-based. Certainly upper-level Western mathematics is still advancing the understanding of mathematical objects and their relationships through research. However, most people experience Western math as a static body of knowledge to memorize and reproduce throughout their K-12 education. Substantial connections to other school subjects, place, culture, spirituality, etc. are not valued as much in Western math (Cajete, 1999; Luecke, 2023).
A few Ojibwe words help highlight the verb-oriented nature of the Ojibwe language and thus Ojibwe math. The same can be said for the D/Lakota language and thus D/Lakota math. Taken together, these two examples show Indigenous math as both language-specific and place-based. First, look at the Ojibwe word agindaasowinan, which is one way to say “math” in Ojibwe. The root is the verb agindaaso which means “s/he counts.” The suffix -win changes the verb to mean the activity of counting. Lastly, the suffix –an means the activity is plural, or done in community. Thus the verb-based term agindaasowinan is not a direct 1–1 translation with mathematics. The 1–1 translation breaks between the more noun-focused perspective of math content and the verb/action-based perspective of mathematical activity in community (Luecke, 2023). Similar can be said for the Dakota/Lakota word wówiyawa, which is one way to say “math” in D/Lakota. Again, the root word is iyawa which is the verb ‘to count’ and the prefix wó- changes the verb to mean the activity of counting. When translating these twos word from Ojibwe and Dakota/Lakota, respectively, back into English it may not simply mean the noun ‘math’ but rather ‘mathematizing’ or ‘the activity of doing math.’ To give further evidence, I share two examples of numbers themselves acting like verbs through typical verb conjugation patterns in Ojibwe and D/Lakota, respectively. In Ojibwe, the sentence “Niizhinoon” conjugates the number two/niizh as an inanimate, intransitive verb (Ojibwe People’s Dictionary) to mean “there are two of those things.” In Lakota, a sentence my daughter might say is, “Waníyetu matópa,” meaning I am 4 years old. Again, the number four/tópa is conjugated with a standard verb prefix ma-. Thus, from these language examples we can see both math and numbers themselves as verbs/action-focused in contrast to English and Western math.
Be wary of conflating the current math reforms emphasizing math practices of doing math and engaging in mathematical thinking with verb-focused Indigenous mathematizing. Current math reforms are moving in the direction of Indigenous mathematizing but still fall way short. Actively participating in Western math processes (rather than memorizing procedures or formulas) is a positive step but the math knowledge is still stuck in the noun/object-focused language and worldview of Western math. As a metaphor, current math reforms of doing math are like writing the word ‘verb’ on a piece of paper in contrast to Indigenous mathematizing of physically doing said ‘verb.’ Despite the increased focus on real-life applications through current math reforms (which I view as a step in the right direction), real-life application problems continue to demonstrate that Western math has the foundation of separation/isolation from context and action such that an emphasis on real-life applications even needs to be made!
In contrast, a recent example from D/Lakota first language speakers demonstrates the foundation of Indigenous mathematizing as not only verb-focused but context/relationship-focused. Indigenous mathematizing does not separate from context/relationship to then later have an application to real-life. So, during a Summer 2024 math and language workshop of D/Lakota first language speakers at Sitting Bull College in North Dakota, an image of 100 stick people – 33 gray and 67 black - was displayed on the screen. The first language speakers described the picture in the D/Lakota language saying, “Opáwiŋğekiya etáŋhaŋ wikčémna yámni sáŋm yámni ȟótapi,” which translated roughly means “thirty-three out of one hundred are gray.” However, when I asked the group of first language speakers about removing ‘are gray’ to just have 33/100 as a fraction on a vocabulary list, they shared that the D/Lakota vocabulary was no longer appropriate when removed from the context. Thirty-three out of one hundred as spoken in D/Lakota, “opáwiŋğekiya etáŋhaŋ wikčémna yámni sáŋm yámni,” has no context and no relationship. Western math saying 33/100 emphasizes removing relationships, taking out context, and abstraction. However, the D/Lakota speakers felt that removing the context to only say the fraction did not fit the language. This shows a distinction between the Western math value of removing relationships (even with current reforms moving toward real-life applications) and the D/Lakota Math (and Indigenous math more broadly) value of emphasizing context and relationship.
In my ‘Indigenous Math I’ class, after students are introduced to the term Indigenous mathematizing, I encourage them to re-name this course for themselves as the mathematizing of their identity and ancestors. Alternative names might include Agindaasowinan Bezhig (1), Niizh (2), Niswi (3), Ojibwe Mathematizing, Michif Mathematizing, D/Lakota Mathematizing, Wówiyawa Wáŋči (1), etc. All these alternative names used in place of “Indigenous Math” demonstrate the more language-specific and place-based nature of Indigenous math. These courses encourage specificity of community, language, and place. Each student is encouraged to personalize the course learning outcomes to their own language, culture, and identity. This practice aligns with the definition of Indigenous from the book Indigenous Statistics (Walter and Andersen, 2013) to mean both modern and place specific (Luecke, 2023).
2.3 Indigenous math framework
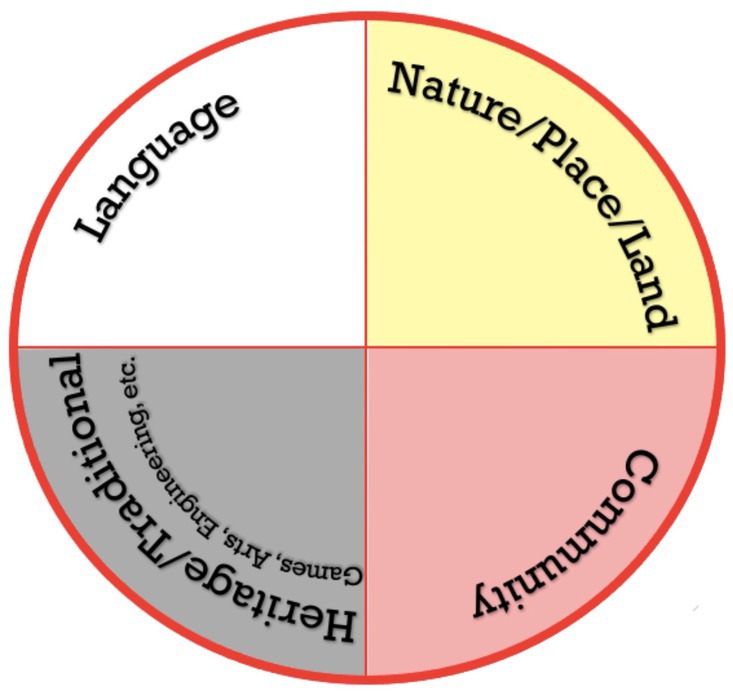
The Indigenous Math I, II, and III courses are guided by the Indigenous Math Framework. However, this framework (Figure 2) is certainly not the only way nor the superior way to think about Indigenous math (Aikenhead, 2017; Cajete, 1999). Rather, it is simply our approach at TMC in the Indigenous math courses to describe some of the components and nuances of Indigenous math/mathematizing.
The framework has four components - nature/place/land, community, heritage/tradition (including games, arts, engineering, etc.), and language. Each component is place-based and language specific. The math, mathematizing, mathematical thinking, and mathematical activity embedded within these four components makes up the core of the Indigenous Math I, II, and III curriculum. Spirituality and identity are intertwined throughout and demonstrated by viewing the four components as part of the mashkiki detibise (medicine wheel) teachings (Luecke, 2023).
The development of the three courses and two frameworks (Indigenous Math and Indigenous Math Education) has been highly influenced by the Dakota/Lakota Math Connections project (Luecke et al., 2022; Luecke, in press; Luecke, 2023) and fluent elders in the Turtle Mountain community (Luecke, 2023). The Dakota/Lakota Math Connections project built upon Sanders (2011) work on math education toward tribal self-determination in Lakota country. Sanders used Bishop’s (1991) six universal math activities - counting, designing, locating, measuring, playing, and explaining - to describe Lakota math. The Dakota/Lakota Math Connections project continued this work (Luecke and Sanders, 2023). Further guidance came from two fluent speakers in the Turtle Mountain community who shared Ojibwe math vocabulary and so much more. Their insight shaped the foundational beliefs and pedagogy for these courses. They shared examples of cultural activities that had mathematical connections, the need for experiential/hands-on learning, and the need for Indigenous math to be connected to the community and the land (Cajete, 1999; Luecke, 2023).
To explain the Indigenous Math framework, I begin in the East with the nature/place/land component. Land is our first and greatest teacher, for “embedded in our places [is] where land, learning, identity, and education intersect” (Styres, 2018, p. 24). Indigenous math is based in Indigenous ways of thinking, knowing, and being of the land. The term Indigenous comes from Latin and means “born of the land” or “springs from the land” (Wilson, 2008, p. 88). Indigenous peoples have a place-based sense of identity that emphasizes that we come from “Mother Earth” (Cajete, 1994; Wilson, 2008). Similarly, Indigenous mathematizing is from nature/place/land. In English, nature, place, and land each have their own nuances, but altogether they convey math/mathematizing is from Mother Earth. Math is universal in the sense that math comes from the universe and from nature. However, in contrast to Western views of math as being culturally neutral, nature teaches us that mathematizing, like the land, is unique to each place (Luecke, 2023). For example, many Indigenous peoples observed patterns of the stars, sun, and moon to determine the timing of solstices and equinoxes which guided ceremonies. The timing of the solstice is determined by the earth’s movement around the sun, and thus can be described as universal. However, each Indigenous community connects with this reality through their own place and relationships.
Imagine the sunrise at your home. The sun rises on the eastern horizon each morning, at different times, moving throughout the year left and right (north and south) along the horizon. When the sun moves left/north on the horizon, the days get longer. As the sunrise location moves left/north each day, the movement along the horizon appears to slow down its pace until it stops, changes directions, and returns to the right/south. This stopping/turning point of the sunrise location on the horizon marks the summer solstice. This annual cycle/pattern was seemingly well known by most Indigenous peoples and described uniquely in each place, community, language.
In Western math, we describe this movement as a sine wave. The x-axis represents time and the y-axis represents a specific place on the horizon. Many Indigenous nations were able to observe the patterns of the sun, moon and stars with even greater detail than just the summer solstice. Spiritual ceremonies, at sunrise and at the solstices, and often architectural structures, were built in alignment with the patterns observed and movements above. Chichen Itza, Chaco Canyon, and the Big Horn Medicine Wheel are a few famous examples, but there are many more. Following these examples, the Indigenous math courses at TMC seek to include local stories and knowledge of place (Luecke, 2023).
Indigenous math is not only from nature but also from and for the community. While Indigenous math values mathematizing that is valuable for the local community, Western math, and math education, values isolation and purity from other subjects, as demonstrated by teaching math class separate from science class. However, some examples such as applied math, mathematical modeling, and interdisciplinary education are attempting not to value the isolation/purity of math as much.
The community aspect of the Indigenous Math framework also aligns with Indigenous ways of learning. The students in the Indigenous math courses are reminded regularly that their learning is not solely for themselves as individuals. Rather, their learning is also for their family, community, ancestors, Mother Earth, and future generations (Cajete, 1994; First Nations Education Steering Committee, 2007). To highlight the community component of Indigenous math, the final project of all three courses is a free, public, community presentation. Students spend the semester focusing on a topic. Often, but not exclusively, in Indigenous Math I students record star observations, identifying Ojibwe constellations, and learning the stories of these constellations as they move through the sky each night and season. Each student’s presentation highlights their personal observations and experiences as well as their understanding of Indigenous mathematizing aligned with their identities. All students, faculty, and staff from the college are invited, as well as family, friends, tribal leaders, and community members. Teachers and faculty from multiple Indigenous communities have also joined virtually (Luecke, 2023).
An example of community math from the Indigenous Math I course is the Shell Valley aquifer which provides water for the Turtle Mountain reservation and surrounding area. Math is both from nature and a powerful language to describe nature. Describing aspects of the aquifer through mathematical modeling connects math with science, geology, water rights, politics, spirituality, and community needs. Using math/mathematizing to better understand the aquifer is both useful and valuable to the Turtle Mountain community.
Traditional/heritage activities also embed Indigenous mathematizing. For example, traditional games such as hand games, moccasin game, and plum stone game all embed pattern recognition, strategy development within a set of rules, score-keeping, community building, inter-generational relationships, song, and medicine. The Indigenous Math II course holds multiple college-wide and community events to learn and play these games. After experiencing these games, students are encouraged to describe the Western math connections and Indigenous mathematizing within the game experience. Further, traditional art, engineering, and architecture embed Indigenous mathematizing. This mathematizing is not necessarily written down but rather embodied through experiential activities. These activities are passed down generationally through community experiences and stories that intertwine spirituality. Traditional structures such as a wigwam or a tipi have mathematizing and Western math connections describing their physical capabilities, and are loaded with spiritual meaning through the physical aspects of the tipi as well as through stories. A modern example is the center of TMC’s main building where a large medicine wheel is engraved into the floor. Above that a large tipi structure engraved with the Seven Teachings makes the highest point of the building, while the whole building is in the shape of an eagle silhouette (Luecke, 2023).
In the preface of Dr. Kamuela Yong’s open source textbook, Trigonometry Through Wayfinding and Navigation Across the Pacific, Yong (2024) shares, “In Hawai‘i, people performed complex calculations of trigonometric angles, algebraic wind speed, and geometrical star houses for centuries, yet there was no word for “mathematician” or “scientist” (p. ix). These traditional activities were not described as math/mathematizing, yet mathematical thinking is certainly embedded within them. The people were mathematizing (doing the math) in contrast to separating the math from its context to be later applied to real-life. Altogether, traditional art, games, engineering, and architecture make the third component of the Indigenous math framework while being intertwined with the other three components.
The last component of the framework is language. Indigenous languages embed mathematical thinking within the number system, quantifying vocabulary, time-describing vocabulary, and a form of abstraction within the grammatical structures. Both the Ojibwe and D/Lakota number system embed place-value and exponential thinking through their word structures. Additionally, as shared before, they both use numbers as verbs that can be conjugated in contrast to English and Western math that strictly views numbers as adjectives/nouns (Luecke, 2023). Further, the Ojibwe vocabulary about time (as relational and connected to the land) is distinct from English and Western views of time, standardized and abstracted, for example the length of a second, minute, or hour. The same can be said for measuring. In sum, language is intertwined with culture, identity, and worldview.
Altogether, the Indigenous language of each student guides and describes their understanding of Indigenous mathematizing toward verb-oriented, embodied, and valuing relationships over isolation or separation (Luecke, 2023). However, Indigenizing math is about more than translating a Western math textbook into an Indigenous language so that students can learn Western math concepts taught in their Indigenous language. Distinct mathematical thinking is already embedded within the language(s). For example, záptaŋ is the D/Lakota word for five but multiple conjugations/variations of this word exist. The phrase “divided into five equal parts” can be described with one Lakota word, záptaŋkiya, which includes the suffix -kiya. Further, the notion of “in groups of five” can be described with one Lakota word, záptaŋptaŋ. In linguistics this is referred to as reduplication. These two examples demonstrate that there is a richness already embedded within the D/Lakota language (and Indigenous languages more broadly) that could easily be missed, ignored, and devalued if our focus is solely on translating Western math ideas and symbols into Indigenous language(s).
The Indigenous Math courses are new to TMC as they have only been taught for 2 years. Many students enter these courses uncertain what to expect. One student shared that both learning math and learning language can be very intimidating on their own. So, a course that tries to put math and language together seemed out of line. However, the “putting together” of language, identity, nature, mathematical thinking, and community (past, present, and future generations) is exactly what the Indigenous math courses at TMC are about. Making connections and relationships between math and language, Indigenous and Western, content and pedagogy is the focus of Indigenous mathematizing and the three-course sequence (Cajete, 1999; Kawagley, 1997; Luecke, 2023) at TMC.
3 The CRISP (culturally relevant, imbued, and sustaining pedagogy) framework for culturally connected math curriculum
3.1 The need for a CRISP framework
Culturally connected math curriculum is a broad topic with diverse and evolving terms, definitions, and variations (Abdulrahim and Orosco, 2020; Aguirre and del Rosario Zavala, 2013; Aikenhead, 2017, 2018; American Indian Science and Engineering Society, 2020; Bishop, 1991; Boyer, 2011; Cajete, 1999; Closs, 1986; D’Ambrosio, 2000; Furuto, 2013; Garcia-Olp et al., 2019; Gutiérrez, 2012, 2017, 2018; Gutstein, 2016; Kana‘iaupuni et al., 2017; Kisker et al., 2012; Ladson-Billings, 1995, 2014; Lipka and Adams, 2004; Medina et al., 2024; McCarty and Lee, 2014; Meyer and Aikenhead, 2021a, 2021b; Nicol et al., 2019; Paris, 2012; Paris and Alim, 2014; Rosa et al., 2016; Ruef et al., 2020; Walter and Andersen, 2013; Webb et al., 2017). The CRISP framework for culturally connected math curriculum attempts to describe four components of this broad topic for class discussions about Indigenous math and Indigenous math revitalization. The CRISP framework has been developed, implemented, and refined via four distinct semesters of Indigenous Math I, II, and III at TMC.
Again, following the epistemology of relationships forming reality and knowledge as presented by Indigenous research paradigm scholars (Archibald, 2008; Kovach, 2009; Wilson, 2008), I am not proposing the CRISP framework is the only approach or superior way to discuss culturally connected math curriculum. Rather, the framework as presented here offers one approach to describing culturally connected curriculum that we use in the Indigenous Math courses at TMC. For TMC, the CRISP framework has given the students and me clear and common terminology when discussing many diverse examples of culturally connected math curricula. Depending on your (as the reader) web of relations, the CRISP framework could extend to impact Indigenous pedagogy in general, Indigenous knowledge in STEM education, and Indigenizing curriculum in all STEM disciplines preschool through university-level.
Throughout the three courses, students are exposed to a variety of approaches to and examples of Indigenous math/mathematizing. Specifically, in course two and three, students are guided to describe and evaluate varying strategies for revitalizing Indigenous math, since revitalizing Indigenous math/mathematizing is one of the main goals of the three-course sequence. From my experience of classroom discussions with the students about Indigenous math and varying ways to revitalize Indigenous math, the need for a specific framework articulating differences in culturally connected STEM content and pedagogy emerged. In the first semester(s), class discussions lacked consistent vocabulary to describe different aspects of math connections with Indigenous language and culture.
The framework was initially conceived while reading culturally relevant/responsive/sustaining curriculum literature (Cajete, 1999; Kawagley, 1997; Ladson-Billings, 1995, 2014; McCarty and Lee, 2014; Nicol et al., 2019; Paris, 2012; Paris and Alim, 2014). This literature has multiple types of cultural connections and applications of culturally connected math pedagogy and curriculum (Aguirre and del Rosario Zavala, 2013; Aikenhead, 2017, 2018; American Indian Science and Engineering Society, 2020; Boyer, 2011; Cajete, 1999; Garcia-Olp et al., 2019; Gutstein, 2016; Gutiérrez, 2012, 2017, 2018; Kana‘iaupuni et al., 2017; Kisker et al., 2012; Lipka and Adams, 2004; Meyer and Aikenhead, 2021a, 2021b; Nicol et al., 2019; Ruef et al., 2020; Walter and Andersen, 2013; Webb et al., 2017). While reviewing this literature, I reviewed an article by Aguirre and del Rosario Zavala (2013) who developed a lesson analysis tool for culturally responsive mathematics teaching, which situates itself within both culturally responsive pedagogy and pedagogical content knowledge. Their goal was developing culturally responsive math teachers and their analysis tool offered guiding questions to teachers for shifting their math lessons toward being more culturally responsive to a growing culturally and linguistically diverse student population.
The CRISP framework offers more in-depth classroom discussions for articulating different types of connections between Indigenous math and Western math (Figure 1). Further, the CRISP framework has given us deeper insight into how we at TMC and others are revitalizing Indigenous math. The CRISP framework, along with the previous two frameworks - Indigenous Math and Indigenous Math Education, help move students toward greater clarity before the community presentations on Indigenous Math at the end of the semester. It also allows students to think critically through the aspects of their presentation as an example of culturally connected math curriculum.
3.2 The CRISP framework
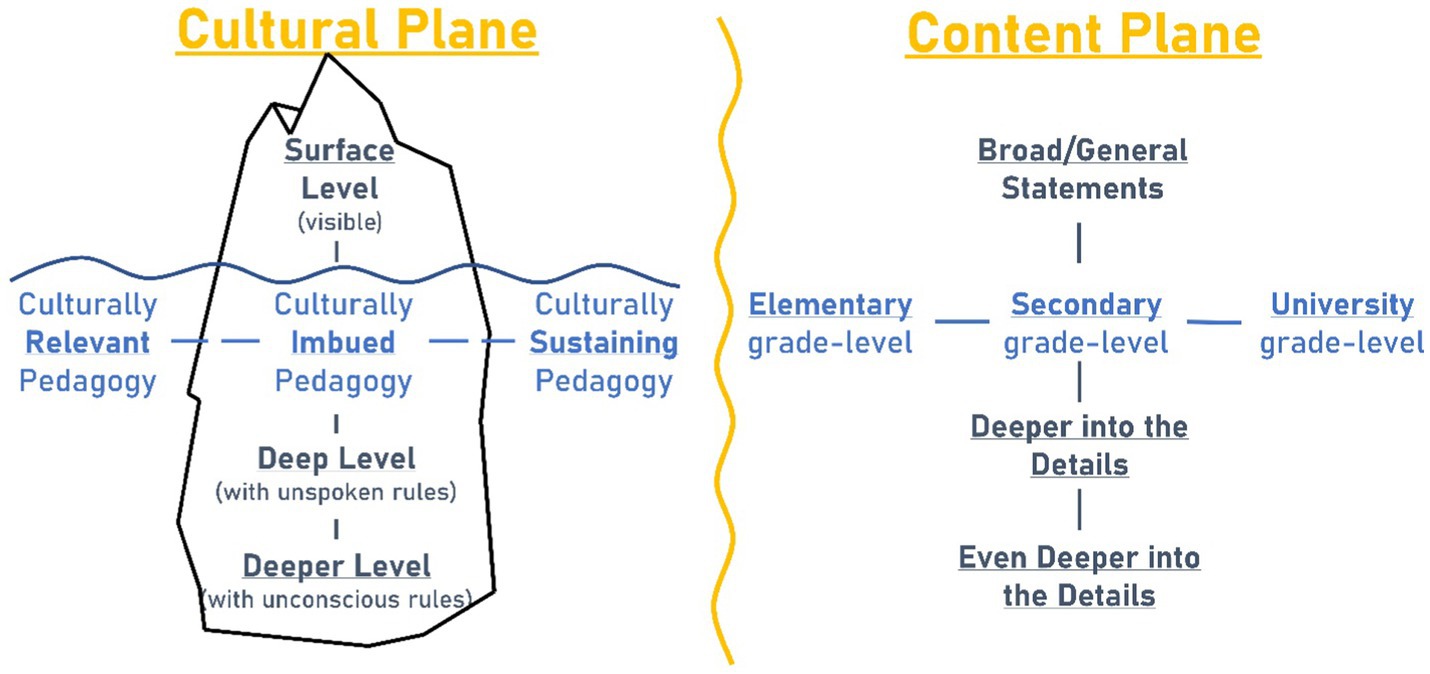
The CRISP framework for culturally connected math curriculum (Figure 3) attempts to describe four significant components of this broad topic for the Indigenous Math courses at TMC. The four components are grade level, depth of detail, depth of culture, and the relevant to sustaining spectrum. All four components are considered when evaluating, discussing, and/or developing culturally connected math curriculum. For example, as both formative and summative assessments, students are asked to compare and contrast different approaches to revitalizing Indigenous math using the CRISP framework’s four components and how these components interact with each other. The framework allows potential users to determine how the framework connects with their web of relationships and if the framework may also prove beneficial in their context (Archibald, 2008; Kovach, 2009; Wilson, 2008). The four components are visually displayed in two planes. The cultural plane has two axes and the content plane has two axes.
The four components/dimensions are visually displayed with two 2D representations. Because it is difficult for our brains to visualize four dimensions, the CRISP framework makes use of a practice in quantum mechanics to represent four dimensions with two two-dimensional scales. However, unlike a precise notion of distance in the metric and vector spaces used in quantum mechanics, the distances in the CRISP framework are not uniform in either plane. Rather distance is more like a Likert scale showing a general location.
3.2.1 The cultural plane
The two axes of the cultural plane are the CRISP spectrum and the cultural iceberg (Hall, 1973). The well-known cultural iceberg has three levels - surface level, deep level with unspoken rules, and deeper level with unconscious rules - making up the vertical axis. The horizontal axis is made up of the CRISP spectrum ranging from culturally relevant curriculum and pedagogy to culturally sustaining curriculum and pedagogy.
3.2.1.1 Imbued culture within mathematics
The cultural plane centers around the belief that all math and STEM content and learning happen within culture. Culture is inescapable in all that we observe and experience. More specifically, all math curricula is imbued with culture (Cajete, 1999). It cannot be culturally neutral or culture-free. The only question is which culture. Imbued is the “I” of CRISP, which is at the center of the framework. The vertical component iceberg in the cultural plane attempts to further describe the culture that math and math education is embedded within. The cultural iceberg has three levels. The surface level is the visible/material culture which is readily visible through food, dress, art, etc. The surface level does not emphasize (or even acknowledge) that there is so much more below the surface supporting the material culture. Some people prefer a cultural tree instead of an iceberg to emphasize that the leaves (most visible at surface level) are only there because of the supportive limbs, trunk, and roots beneath them.
The deeper levels are a little murkier. Depending on what type of culture you are talking about, such as school culture, family culture, co-worker culture, ethnic/ancestral culture, community culture, etc., these deeper levels beneath the surface could mean different things. Further, different people will likely have different perceptions of how deep a particular idea may be in that particular culture. The CRISP framework does not view the cultural iceberg (or tree) as the final authority on culture. Rather, the iceberg (or tree) helps to demonstrate that there is so much more beneath the surface than simply the visible material culture. The tipi can be used an example, viewing the tipi as a right circular cone in order to teach the area of a circle (πr2) or volume of a cone ( πr2) or cutting the cone in half to teach Pythagorean theorem is surface level. These are all surface level connections because the cultural connection is made solely on the visible shape of the tipi. No connection is made to a deeper (or more authentic) cultural meaning of the tipi. Here, we see that using surface level culture with no supporting, deeper culture, for the purposes of Western math can be offensive (Abtahi, 2022).
In contrast, going deeper into culturally connected math might include sharing a local story about a tornado on our campus in the early 2000s that ripped oak trees from the ground but the tipi stayed in place. Or sharing my experience of once being in a tipi with a center fire burning, but because nobody there at that moment was confident in how to use the tipi flaps (and thus air convection) correctly, the smoke did not leave through the top. Going deeper could include the spiritual significance of the tipi symbol in art designs as the confluence between the land and the spirit world above. Going deeper could include talking about the three or four initial poles needed to set up the tipi and the spiritual/cultural meaning of them, as well as the meaning of the top circular web shape when all the poles are tied together. The tipi is still part of the visible/material culture but going deeper in the cultural iceberg shows the supporting culture beneath, valuing the culture as legitimate in itself.
To further articulate how knowledge, (math) education, and learning (math) are imbued with culture, let us look at Grande’s (Quechua) description of the five key beliefs of Western knowledge from her book Red Pedagogy (2015). She articulates some of the Western cultural assumptions that are mythologized as universal truth and reality imbued within Western culture and education. Grande’s (2015) description of the first key belief of Western knowledge is the “belief in progress as change and change as progress” (p. 69). She elaborates that Western culture believes that humanity is improving, and change is positive. Western beliefs of time follow from this, moving forward in a linear manner. Improvements are measured through material gain and often in a set time frame to measure improved efficiency. This happens both individually and collectively as more education, more income, more status, etc.
Grande (2015) shares the second belief of Western knowledge is the “belief in the effective separateness of faith and reason” (p. 69). This belief leads to the notion of objectivity, that knowledge is an object/thing and someone distinct from the knowledge can be an expert on the topic. Further, this view of knowledge holds that intellectual knowledge (aka book knowledge) is the superior form of knowing. Positivism and empiricism in research come from this belief as well. Establishing distance as an appropriate separation from the research/knowledge demonstrates objectivity. Lastly, this belief of effective separation leads to the notion that the mind is superior and has authority over one’s spirit, life, and body (Grande, 2015).
Third, “belief in the essential quality of the universe and of ‘reality’ as impersonal, secular, material, mechanistic, and relativistic” (p. 69). An impersonal view of reality, nature, and the universe is describing a universe that is not alive, and certainly not a family member to be in a personal relationship with. Further, this impersonal universe is made of matter, that is physical substance as an object that can be broken down and analyzed at the successively smaller levels to determine cause and effect, properties and laws, and all other mechanisms (Grande, 2015).
According to Grande (2015), the fourth belief of Western knowledge is the “subscription to ontological individualism” (p. 69). Rene Descartes’ famous philosophical line - “I think, therefore I am” - epitomizes this belief of an individualistic reality. Through this belief, the individual person is the base unit of society and to be productive in society that individual must be autonomous with no perceived dependence on anyone or anything else. Emotionally and financially, the individual is meant to be sufficient on their own. Further, the individual is both the source and owner of knowledge. In the area of research methodologies, Smith agrees as she writes, “the most fundamental belief of all [Western research paradigms is] that individual researchers have an inherent right to knowledge and truth” (Smith, 2021, p. 173).
Lastly, the fifth belief of Western knowledge is the “belief in human beings as separate from and superior to the rest of nature” (Grande, 2015, p. 69). This is fairly self-explanatory and can easily be seen in views of land and natural resources. This belief promotes the idea that land is to be owned as property. Natural resources are to be used to exhaustion for the benefit of people even if it is to the detriment of another part of nature.
When I first read these five key beliefs of Western knowledge, I was shocked to see how much I agreed with these beliefs, yet I was unable to articulate these cultural beliefs until I read Grande’s words. These beliefs and assumptions of reality were unconscious to me until learning from Grande. Her words spoke powerfully to my heart and mind.
Grande summarizes by referring to these five beliefs as “the deep structures of colonialist consciousness” (Grande, 2015, p. 69) and expands on the five implications these beliefs have for education. First is “Independence. Children are expected to be self-reliant. Appropriate, on-task behavior is measured by the degree to which students behave as if they were in solitude, even though they are not” (Grande, 2015, pp. 70–71). Second is “Achievement…Success and individual worth are measured by abstract and impersonal standards of excellence” (Grande, 2015, p. 71) such as scoring seven out of 10, or performing at the level of a C student. Third is “Humanism” (Grande, 2015, p. 71), described as encouraging students to believe they are the master of their own destinies who have complete control over all situations. Further, humanism boasts the belief that through human effort, technology, and science all of nature can be understood and predicted. This implicitly, and often explicitly, rejects any form of spirituality in individual cognition and worldviews. Fourth is “Detachment from sources of local and personal knowledge” (Grande, 2015, p. 71) such as family, communal, and spiritual knowledge, implying that ‘book’ knowledge is the more valuable and worthwhile knowledge. Last is “Detachment from nature” (Grande, 2015, p. 71), implying that ‘real’ learning occurs indoors. Even when the subject matter is earth, animals, or plants, a majority of the learning is done sitting in rows of desks inside a building. Through these five implications of the colonizing consciousness within education, Western knowledge beliefs are reproduced by leading students “to develop as progressive, competitive, rational, material, consumeristic, and anthropocentric individuals” (Grande, 2015, p. 71).
My first experience reading these five key beliefs of Western knowledge and five implications impacted my spirit, heart, and mind. Claiming a culturally-neutral education system erroneously continues to keep Western culture as the mythologized superior. Sadly, many Indigenous scholars confirm that colonial education is still the dominant form of our education system in the United States (Brayboy et al., 2015; Cajete, 1994; Deloria and Wildcat, 2001; McCarty and Lee, 2014; Smith et al., 2018). Not only is this the dominating perspective in education at-large, but also in math (Aikenhead, 2017, 2018; Bishop, 1990; Cajete, 1999; Ernest, 2021; Kawagley, 1997; Stevens, 2021).
Grande’s description of five key beliefs of Western knowledge and five implications of education relates to the perception of Western math as an impersonal/universal view of reality, where math is a chunk of information to know. Western math values removing relationships, detaching itself from nature and self. I believe this is one of the main reasons for the most common question in a Western math class, “When am I ever going to use this?” This happens, in part, because math content has been taught in isolation from context. Relationships have been removed.
Western math can be beautiful and very powerful; however, not recognizing nor acknowledging one’s Western assumptions paves the way to view Western math as the sole/universal way to think mathematically and/or do math. Bishop (1990) describes Western math forcing Western assumptions on all people as “the secret weapon of cultural imperialism” (p. 51). Another example that is less extreme is making assumptions when writing mathematical proofs. It is not wrong to make assumptions; however, making unstated assumptions is both incorrect and problematic. Thus, the first component of the CRISP framework, and the vertical axis of the cultural plane, is stating that all knowledge and learning are imbued with culture. Specifically, all math knowledge and learning are culturally based. Within this assumption that all math (and math education) are imbued with cultural practices and beliefs, that is all education is responsive to some culture(s), the cultural iceberg attempts to distinguish different types of cultural connections with math as the vertical component of the cultural plane.
3.2.1.2 Spectrum of culturally relevant to culturally sustaining pedagogy
The horizontal axis of the cultural plane is the CRISP spectrum between culturally relevant and culturally sustaining pedagogy. The spectrum between relevant and sustaining highlights the end goal of learning. Is the end mathematical goal more focused on learning Western math through the relevancy and richness of Indigenous culture and language? Or is the end mathematical goal to sustain/learn/revitalize Indigenous culture and language through experiencing and articulating Indigenous mathematizing? The answers to these questions found within examples of culturally connected math curriculum can help articulate the difference between culturally relevant pedagogy and culturally sustaining pedagogy.
The term culturally relevant pedagogy was coined by Ladson-Billings (1995) as an avenue to value the cultural identity of students within instruction (Ladson-Billings, 2014). Specifically in math, culturally relevant pedagogy has been shown to strengthen students’ cultural identity and increase math exam scores (Kisker et al., 2012; Lipka and Adams, 2004; Lipka et al., 2007). Within Gutierrez’s math equity framework (2009), culturally relevant pedagogy aligns with strategically “playing the game” by working within the current system to pursue positive change. When crossed with the cultural iceberg, the vertical component of the cultural plane, a large spectrum of types of culturally relevant pedagogy exist.
With the tipi example, we see that surface level culturally relevant pedagogy is at its worst in using the tipi as a cross-section to teach Pythagorean theorem. However, deeper level culturally relevant pedagogy may teach about the strength of the tipi against high winds by modeling fluid dynamics or demonstrate the ingenuity of the tipi design with flaps and the center fire through basic physics and heat transfer equations. Further, the deeper level culturally relevant pedagogy makes connections between Western math, engineering, thermodynamics, spirituality, place, community, language, history, self, and the ancestors. These connections could be general or described explicitly.
Culturally sustaining pedagogy (Paris, 2012; Paris and Alim, 2014) goes beyond valuing cultural identity in teaching Western math to valuing an Indigenous community’s culture and language expressed through Indigenous mathematizing. This can often mean doing the cultural activity instead of talking about it in the classroom. By doing the cultural activity, students can learn through hands-on experience and sustain that cultural activity into the next generation. Within Gutierrez’s math equity framework (2009), culturally sustaining pedagogy aligns with “changing the game.” This means that Math class will no longer be able to stay inside the school building separated from science, history, and art class. McCarty and Lee (2014) describe these pedagogies within the context of Indigenous education sovereignty. They coin the term revitalizing pedagogy of place-based and community-specific cultural knowledge.
Again, using the tipi example, culturally sustaining pedagogy could look like a local knowledge keeper guiding students in setting up the tipi while sharing the cultural teachings and stories that go along with it. The students could learn how to make the center fire and set the flaps according to the wind direction. They would be embodying Indigenous mathematical knowledge (that is mathematizing) in how to recognize the patterns and relationships of thermodynamics to keep the smoke rising out of the center hole on top. The students could then articulate and describe the relationships and patterns they experienced (Hogue, 2014). The Indigenous Math courses seeking to follow Indigenous ways of teaching and learning attempt to employ this “experience then describe” pedagogy in every module.
3.2.2 The content plane
The two axes of the content plane are grade level (elementary, secondary, and university) and a depth of detail spectrum. Recall there are four dimensions displayed in two planes. The horizontal dimension of the content plane describes the grade level giving a general idea of what age level this culturally connected math example is designed for. Sometimes this takes on the notion of Western math grade-level standards, but it does not have to. In class discussions, it’s often simpler to play the game, make the strategic concession, and let Western math grade level dictate the broad level of elementary, secondary, and university. However, asking students to envision changing the game of math education (Gutiérrez, 2009) and determining what Indigenous mathematizing could be appropriate at different age levels could prove valuable as well. For example, if the topic relates to addition of small integers or counting the number of tipi poles, then that likely fits into elementary. Whereas in the tipi example, if the connection to Western math focuses on modeling fluid dynamics of strong winds and/or hot air rising then that is university level.
The vertical component of the content plane is depth of detail and is the final component of the CRISP framework to be discussed. Depth of detail/knowledge describes how detailed the connection is. Throughout each semester of each course, I have reminded students to go deeper into the details. Similarly to the cultural iceberg there are three levels from broad/general statements to deeper into the details. As a particular example gets deeper into the details, it becomes more evident where that example lands on the relevant to sustaining spectrum. A broad/general statement such as, “Indigenous people have been doing math for millennia,” is a true statement and a great overview. However, going deeper into the details allows for evidence and substance to support the broad statement, similar to the deeper layers of the cultural iceberg supporting the material culture. In different contexts and for varying reasons, one may choose different levels of going deep into the details. For example, a student may say, “We, the Plains Ojibwe people, were great engineers because we made the Red River Cart.” As an instructor, I would applaud the connection they have made at the broad/general level. Then, I would encourage the undergraduate students to go deeper into the details. For a deeper into the details engineering connection, a student might say something like, “According to local knowledge keeper Jerome (2012) and his book Hands On A Legacy, the Red River Cart has outward dished wheels at an angle of about 9% (Figure 4) so it can handle the heavy load of buffalo meat across bumpy roads/paths through the prairie. The axles were typically made of oak since oak is the strongest wood in the region and readily available to make spare axles. When the heavy load bowed the axles slightly, the bottom portion of the wheels were pushed out for greater stability.” Even deeper into the details could be modeling or building an experiment to test different dished wheel angles over a variety of terrains. This might take a whole semester or it could even be a graduate level research project depending on the level of sophistication. This experimental simulation would go deeper into the details of culturally relevant pedagogy. Going deeper into the details of culturally sustaining pedagogy could be making a full-size Red River Cart with community partners and a transdisciplinary course with math and many more subjects.

Figure 4. Red River cart images. (A) Red River Cart showing the dished wheel. (B) Red River Cart at center of TMC main building.
The content plane and the cultural plane make up the four dimensions of the CRISP framework for culturally connected math/STEM curriculum. Different examples of culturally connected math curricula can land in any of the four dimensions. Multiple factors influence the perceived placement of a particular example. Including the specific content, the specific pedagogy enacted, how the knowledge was developed, and how it is presented.
4 Examples of the CRISP framework in practice
Throughout the Indigenous math three-course sequence, many examples of culturally connected math curriculum are discussed via different aspects of the CRISP framework. This section will focus on a variety of examples from the literature as well as from my experiences in researching Indigenous math. The goal is not to judge or critique the work of others as this does not fit with an epistemology based in relationships and accountability to all my relations. To do so would be like saying I know another’s web of relationships more than they do (Wilson, 2008). Instead, the CRISP framework allows students to discuss and review varying aspects of culturally connected math curriculum and come to their own decision. The following examples help demonstrate the value and validity of the CRISP framework in practice.
4.1 Handgames example
Handgames is a traditional game of many Indigenous peoples of North America. As stated earlier, “handgames embeds pattern recognition, strategy development within a set of rules, score-keeping, community building, inter-generational relationships, song, and medicine.” To begin, I will review this description of handgames through the CRISP framework. Then, I will provide two more descriptions of handgames and review them through the CRISP framework.
This first description of handgames is still broad/general even though it does give some details. Broad/general statements like this example can sometimes make the other components of the CRISP framework difficult to assess because there is not enough information. Grade level - elementary, secondary, or university - is difficult to assess. The iceberg cultural level of depth is below the surface, but still not too deep. The relevant to sustaining spectrum is also difficult to assess with so few details.
Handgames can further be described as haŋpápečhuŋpi in Lakota and oninji-odaminong in Ojibwe. This is a community game played at pow wows and at stand-alone tournaments. Each year at the American Indian Higher Education Consortium student conference, TCUs from across the country compete against each other in handgames. The Teacher Education Department and Secondary Math Education program at TMC have also initiated and financially supported multiple youth and adult handgames tournaments throughout the Turtle Mountain community. Even though this is not in the classroom, the Indigenous Math students participate as well as help organize these tournaments. This is an example of culturally sustaining pedagogy through creating more opportunities to experience Indigenous mathematizing by experiencing the skill-needed and thrill of handgames.
An avid handgames player shared with me that every player has a pattern for guessing and hiding the bones. Some players hide or guess based on the hiding or guessing pattern of their opponent and others hide or guess based on their past patterns. The experienced player further shared that when she hides or guesses against another player a little file pops into her mind of their most recent guesses or hides and what pattern they have followed. She then makes her strategic decision based upon this information. Although the term guess is used in handgames it is not a guessing game but rather a game of strategy. Similar to card games like poker, in handgames it is not solely the random deal of cards that determines the winner but the skill of a player in reading people, not being distracted, memorizing, and intuitively recognizing and applying patterns in real time is what gives the stronger players the greater chance of winning (Luecke, 2023).
This explanation of handgames goes much deeper into the details, the vertical component of the content plane. Further, it specifies that both youth and adults can play, learn the game, and build strategy, which is Indigenous mathematizing. This description is helping to sustain the game in the community and has the Indigenous math students participating, a form of sustaining pedagogy. Lastly, this description is beyond the surface level of the game.
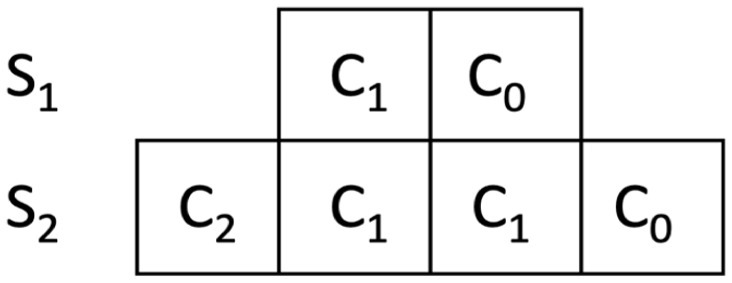
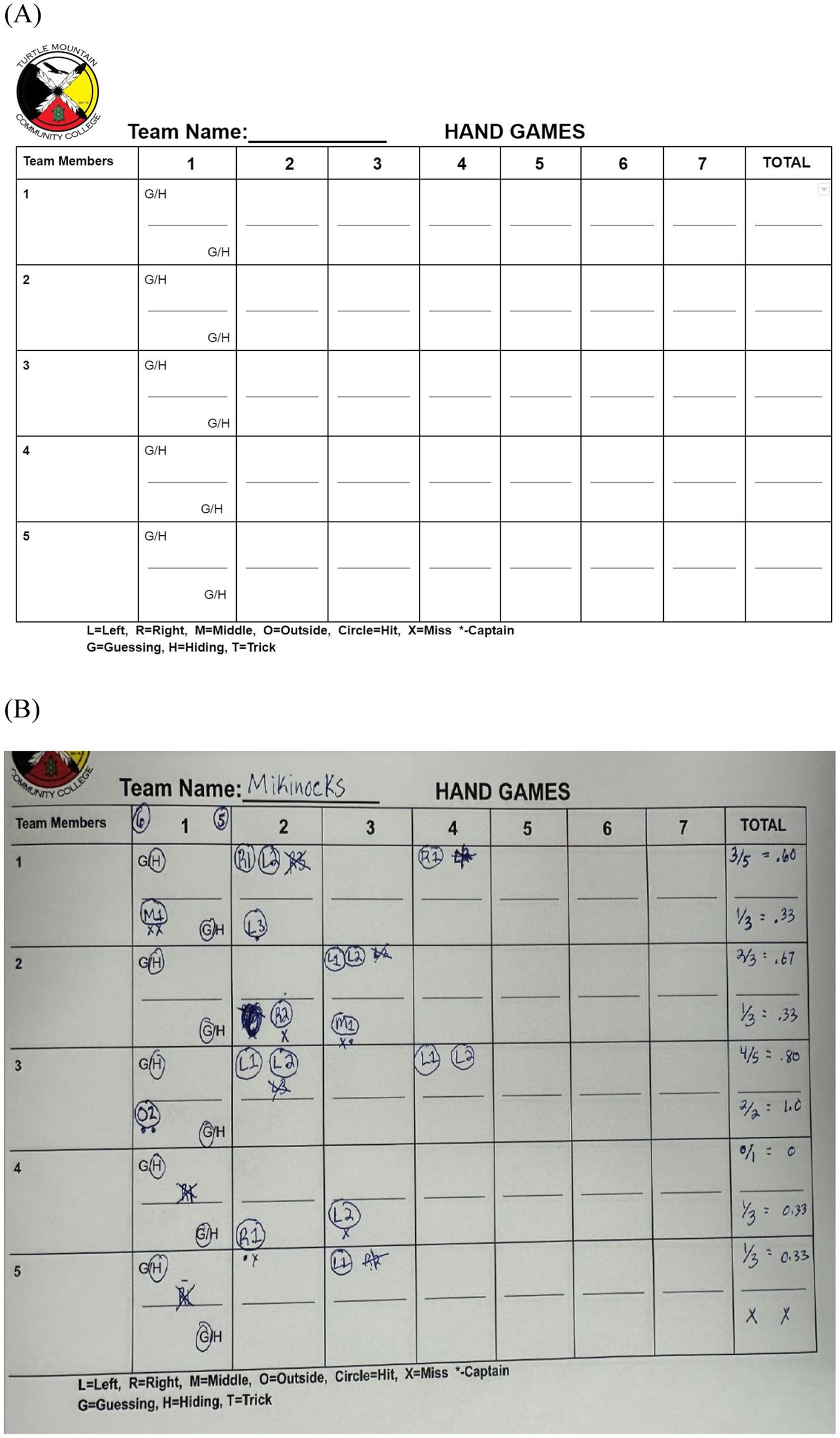
Another way to discuss handgames is through Western math connections. However, these connections are not needed to validate Indigenous mathematizing within the game. Rather, this exemplifies intertwining Western math and Indigenous math by adding more into the web of relationships connecting handgames with probability and statistics taught at the secondary level. Below is sample space for a single guess in handgames. In Figure 5, P(C2|S2) describes the conditional probability of correctly guessing both sets of bones given both sets are in play and is equal to ¼ (Luecke, in press).
As shown in Figure 6, a student in Indigenous Math III developed a scorecard somewhat similar to a baseball batting average or basketball field goal percentage. Each player’s hiding and guessing are tracked allowing simple statistics to be determined. What is the point-scoring hiding percentage of player 3? The sample above (see Figure 6) shows it is 80%, which is the best on the team and very valuable information to the captain who is picking the guessers and hiders for each round. Additionally, one could ask what is the theoretical probability that the hiding team wins all 11 sticks before the guessing team even has a chance to hide?
This explanation of handgames goes deep into the details, the vertical component of the content plane. Also, in the content plane, this explanation discusses the secondary level math of statistics and probability. In the cultural plane horizontal component of the culturally relevant to sustaining spectrum, these statistics and probability are relevant to the community culture. You need to know the rules of the game but you do not necessarily need to play, and thus mathematize, to learn the Western math connections of statistics and probability. On the cultural iceberg, without experiencing the songs and sounds, the stress of picking a hand signal, and community building aspects of handgames, this description is not the deepest level of the cultural iceberg. This description is not surface level either because it is describing real strategies that players implemented.
4.2 Logarithms, perception of sound intensity, and drums example
The previous example of Handgames begins with a cultural activity. The final description makes culturally relevant connections with Western math terminology in statistics and probability to describe the activity. Now, example 2 moves in the other direction beginning with logarithms, a Western math concept, and moves into a cultural connection. Moving this direction can easily lend itself to only culturally relevant pedagogy and perhaps even worse in appropriation of cultural knowledge for the purposes of teaching the “more valuable” Western math. It can potentially cause students to have a negative feeling like this process is sprinkling or adding on surface-level culture to get to more important Western math standards (Abtahi, 2022). Alternatively, diving into the details of the cultural connection could potentially lead to a deeper cultural connection and more culturally sustaining pedagogy, depending on how it is presented.
This example began with a student in Indigenous Math III asking about logarithms. She asked, “What cultural connection can be made with a worksheet on logarithms in the secondary math classroom?” One approach to answering this question followed from the Indigenous Math framework (Figure 2) and specifically the nature/place/land component that the framework begins with, recognizing that math is both from nature and a powerful way to describe nature. Together, the students and I went to ChatGPT and asked, “What are nature-based examples for logarithms?” ChatGPT 3.5 (April 2024) responded with, “Nature provides numerous examples of logarithmic relationships. Here are a few: Sound intensity, Earthquakes, pH Scale, Astronomy, Population Growth,” and a sentence or two about each. We discussed which of these nature-based examples we could use to articulate a clear connection to our community culture. One of the main examples that arose was the difference in perception of sound intensity and how your body feels when you hear a big drum versus when you hear a hand drum. The decibel scale and sound perception is based on logarithms.
A culturally relevant connection could be made by starting the logarithm worksheet with a sentence or two describing how logarithms are the mathematical basis for the decibel scale and how we feel the difference between the two drums. Then the instructor could move into the logarithm worksheet. Note that a logarithm worksheet completed inside a building, seated at individual desks, is Western math and favors Western ways of teaching and learning. With no further connection to the big drum and hand drum, this could feel like a “sprinkling” or “add-on” of surface level culture. However, if the worksheet focuses on applying the decibel scale in the context of hearing different drum songs, I think this would be closer to the culturally relevant curriculum that has been shown to strengthen cultural identity and improve math exam scores (Lipka and Adams, 2004; Kisker et al., 2012; Lipka et al., 2007).
However, to move this further toward culturally sustaining pedagogy, a worksheet cannot be the sole experience for the student. Perhaps a local drum keeper comes into class to discuss drum etiquette or there is a transdisciplinary unit with science, history, language, culture, and art in which there is time to make a hand drum. Indigenous mathematizing takes place in making the drum and many Western math connections could be made in addition to describing perceived sound intensity through the decibel scale. Going even deeper into the details of Western math connections, you could look at tone/pitch of the hand drums modeling it through frequency of sound waves. You could also look at different wood types, skins, drumsticks, etc. and their impact on frequency. Notice here that culturally relevant Western math learning and culturally sustaining Indigenous mathematizing are not mutually exclusive. They can both happen together.
Further, a connection can be made to Gutierrez’s equity framework (2009, 2012, 2017, 2018) on “playing the game” by adding a culturally relevant connection to a logarithm worksheet or “changing the game” by restructuring the entire math class into transdisciplinary units based on the hand drum. Both of these approaches may be the best fit in different environments. Overall, the CRISP framework is not designed to determine the value of different culturally connected math curricula. Rather, reviewing these examples through the lens of the four dimensions of the CRISP framework enhances critical conversations on approaches to revitalizing Indigenous math. The Indigenous Math courses seek these critical conversations regularly.
4.3 Ethnomathematics curriculum textbook example
The Ethnomathematics Curriculum Textbook (Furuto, 2013) has 10 examples of ethnomathematics lessons developed by the Ethnomathematics Summer Institute (Furuto, 2013). Each of the 10 examples can be placed in different spots on the CRISP framework. The 10 examples are specifically broken up into three sections - elementary, secondary, and university level - aligning with the horizontal axis of the content plane. In general, the 10 examples on the content plane go deeper into the details beyond broad/general statements. For example, chapter 7 is on vectors and voyaging. Recently, an entire trigonometry textbook has been developed based on wayfinding (Yong, 2024). From my perspective the ethnomathematics textbook (Furuto, 2013) lands in the middle of the going deeper in the details scale.
On the cultural plane, each lesson plan of the Ethnomathematics Curriculum Textbook has the component titled “Goal of Lesson Plan” and gives insight into the culturally relevant to culturally sustaining pedagogy (CRISP) spectrum. The contributors to the ethnomathematics textbook (Furuto, 2013) certainly agree that math learning is imbued with culture and they are prioritizing experiential learning, going deeper than surface level cultural connections. Yong’s (2024) book, Trigonometry Through Wayfinding and Navigation Across the Pacific, is a great example of culturally relevant curriculum deeper on the cultural iceberg. The literature shows this approach is likely to increase exam scores and strengthen cultural identity (Kisker et al., 2012; Lipka and Adams, 2004; Lipka et al., 2007). Addressing these ideas in a textbook is an example of culturally relevant pedagogy and having students go do these activities in practice in the wayfinding community is culturally sustaining pedagogy. Again, note how “playing the game/system” vs. “changing the game/system” of math education aligns with culturally relevant and sustaining pedagogy. Both are valuable depending on the context/scenario.
4.4 Place value, polynomials and series connected to the D/Lakota number system example
Throughout this article there are multiple examples of how Indigenous languages guide our understanding of Indigenous mathematizing. One of the Ojibwe words for math, agindaasowinan, is verb-oriented, emphasizing the doing/experiencing of math and not just the thinking of content of math. Examples in both Ojibwe and D/Lakota showed numbers acting as verbs and not just static quantities as the English language teaches. Further, the conjugation of the D/Lakota word for five, záptaŋ, into záptaŋkiya and záptaŋptaŋ, show higher order mathematical thinking embedded within the language that is unique to each Indigenous language, yet collectively distinct from how English represents math, and numbers specifically, as static and noun-based. These are all examples deeper in the cultural iceberg, the vertical component of the cultural plane, emphasizing the “I” of CRISP, because they are describing unspoken and perhaps unconscious guidelines that come from the language(s).
The example below, of connecting place value, polynomials and series within the D/Lakota number system, is not as deep on the cultural iceberg. Further, it demonstrates how the D/Lakota number system can be a culturally relevant teaching tool for polynomials and series within school-based mathematics. The D/Lakota number system has a clear structure/pattern for expressing large numbers. The example below demonstrates how the number four hundred two thousand sixteen (402,016) is expressed in the D/Lakota language Figure 7.
The pattern/structure has many similarities to base-ten place value, polynomials (i.e., x2 + 4x - 11) and series/partial sums (i.e., ). Notice the use of the word sáŋm to separate terms with an additive structure. In place value, terms are separated only by place, but the extended form of the number 402,016 = 4⋅105 + 2⋅103 + 1⋅101 + 6⋅100 has terms separated by addition similar to polynomials and series/partial sums. Further, notice how kȟoktá is used twice using term-based expression, which is distinct to how English expresses large numbers using thousand only once in a grouping-based expression of large numbers. Grouping-based expression decreases the number of syllables in pronunciation but hides the underlying structure that term-based expression highlights. Further, notice the assumption of multiplication within the terms for expressing large D/Lakota numbers, within polynomials and series/partial sums (Luecke, 2023). Additionally, the term-based expression of large numbers could be a teaching tool for multiplication of numbers, polynomials, and series as seen in Figure 8.

Figure 8. Multiplication of numbers, polynomials, and series following term-based expression. (A) Multiplication of three-digit numbers following termbased expression. (B) Multiplication of polynomials following term-based expression. (C) Multiplication of series following term-based expression.
In conclusion, this example at the elementary, secondary, and university level goes deep into the details of a culturally relevant content and teaching approach. The CRISP framework allows us to describe how the language component of the Indigenous Math framework can include both culturally relevant and culturally sustaining curriculum and pedagogy.
4.5 D/Lakota math connections project: tahokmu and flute making
The D/Lakota Math Connections project held two workshops on D/Lakota Math in the summer of 2023 and 2024 on tahokmu, a traditional cultural composition strategy, and on making the traditional Indigenous flute. Elder and knowledge keeper Bryan Akipa (Sisseton Wahpeton Oyate) instructed both workshops. He shared that tahokmu is seen in the composition of petroglyphs as well as in the late Dakota painter Oscar Howe, whom he learned tahokmu from. Tahokmu is a composition strategy that implements abstract thought imagery through lines and intuitive esthetic points. Patterns, structure, and observation are all involved. Tahokmu does not need to be justified by Western math to be legitimate. The composition strategy is a form of mathematical thinking and example of D/Lakota Math.
Similarly, making the traditional Indigenous flute does not need to be connected with Western math to demonstrate the mathematizing of carving, shaping, and precisely tuning the flute. The traditional Indigenous flute does not follow the twelve-tone equal temperament of nearly all modern Western music. The traditional Indigenous flute has its own distinct tuning/temperament that has been passed down for generations. Traditional Indigenous flute makers did not call themselves mathematicians but rather through applying the proportional reasoning to fine tune a flute they were mathematizing.
These two examples are broad/general statements. They are more detailed than that statement, “We as Indigenous people have always been engineers, scientists, and mathematicians” but still they are only generalizing the depth of detail that can be articulated. Both examples are culturally sustaining because community members experienced the cultural activity of painting within a traditional composition strategy and making a traditional Indigenous cedar flute. The end goal was not teaching Western math curriculum but rather experiencing and advancing the cultural activity (and the mathematizing within it). To me both of these written descriptions on the cultural iceberg are below the surface level but the community members/workshop participants experienced an even deeper level on the cultural iceberg through the relationships built among ourselves via hands-on intergenerational learning. The workshops did not take place within the US education system but rather outside of the US system. Further, these mathematizing experiences do not line up with US grade-level math standards.
4.6 Many more examples to explore
There are many more examples of culturally connected math curriculum and pedagogy in the literature that have impacted my understanding of the topic and my development/instruction of the Indigenous Math courses (Beatty and Clyne, 2024; Lunney Borden et al., 2019; Cajete, 1999; Closs, 1986; Eglash et al., 2006; Garcia-Olp et al., 2019; Kawagley, 1997; Kisker et al., 2012; Lipka and Adams, 2004; Meyer and Aikenhead, 2021a, 2021b; Nicol et al., 2019; Ruef et al., 2020; Stevens, 2021; Walter and Andersen, 2013; Webb et al., 2017).
This article shares many examples of Indigenous mathematizing from both the literature and my experience with the Dakota/Lakota Math Connections project and teaching the three-course Indigenous math sequence at Turtle Mountain College. The goal is not to categorize or determine the value of different approaches to Indigenous math curriculum but rather strengthen connections with the varying approaches. As an academic storyteller attempting to live out Indigenous storywork through this research and article, “my main obligation is to make as many connections or relationships available as possible and to respect the reader’s ability to take in what they are ready to receive or what their current relationships allow” (Wilson, 2008, p.133). Each reader will connect with different aspects of this work based on their own web of relations. Since I cannot know the entirety of another’s web of relationships, it becomes inappropriate to tell the readers what lessons or connections they were supposed to make (Archibald, 2008; Kovach, 2009; Wilson, 2008).
“[This article] is not intended to impose conclusions on other people or to be a manual of techniques for their research. This would narrow their thinking. I hope that an Indigenous research paradigm [and this article] provides a foundation for which to work but not a ceiling or walls to enclose or encage others… what is presented in this book [article] is only one version… the very nature of our epistemology is that it will be different in other contexts.” (Wilson, 2008, p. 136).
Further, as an academic storyteller, I see multiple shortcomings and limitations of my work. I am not from the communities I work with. I am a beginner in my language learning. I am relatively new to both research and ceremony (Wilson, 2008). I have a long way to go in embodying my Choctaw identity as a person and a scholar. Further, due to the boarding school era and the continued impacts of ongoing colonial education, the Indigenous languages of these places are not currently the medium of education. Hopefully, my overall work and this specific article are a small step back toward Indigenous languages as the medium of communication in these communities.
One notable limitation of the CRISP framework is that it focuses on content (i.e., knowledge and curriculum) instead of relationship and process. This emphasis on content can easily overlook the extremely significant aspects of how the curriculum was developed (the process) and who participated in that process (relationships). This is a major limitation of the framework. Further, the focus on content/curriculum can undermine the importance of relationships in all communication. “Communication for Native people then, as asserted here, is not the mere exchange of facts or messages. For Native people, communication involved primarily relationship building” (Long Feather, 2007, p.51).
Further, all three frameworks (Indigenous math framework, Indigenous math education framework, and the CRISP framework for Indigenous math) are not based in a physical metaphor but rather a not-so-concrete theoretical visual. Metaphors are a common teaching tool within Indigenous communities and allow readers/listeners to more easily draw their own conclusions and to make a personal connection (Archibald, 2008; Harris, 2002; Kovach, 2009; Wilson, 2008). Specifically, the theoretical and not-so-concrete visuals lead to more academic and philosophical discussions about Indigenous math. This can limit some knowledge keepers and first language speakers who are doing the Indigenous mathematizing from engaging as much in the dialog. They may have so much more to share if these frameworks were metaphors and not visual abstractions. Further, these visual abstractions emphasize knowledge through written text instead of a metaphor that emphasizes knowledge through story, relationship, humor, personal interpretation, and spiritual connection (Archibald, 2008; Kovach, 2009; Wilson, 2008).
Lastly, another notable limitation is the environment that the Indigenous Math courses are within. Colonial education is still the dominant form of education in the United States (Brayboy et al., 2015; Cajete, 1994; Deloria and Wildcat, 2001; McCarty and Lee, 2014; Smith et al., 2018). This is not solely in education at large but specifically in math as well (Aikenhead, 2017, 2018; Bishop, 1990; Cajete, 1999; Ernest, 2021; Kawagley, 1997; Stevens, 2021). Many students entering the Indigenous math courses have been conditioned to view Western math as culturally neutral, universal, and the only way to do/think mathematically. The incessant pressure of the Western beliefs of knowledge throughout the United States education system leads to overvaluing Western math and ignoring Indigenous mathematizing (Aikenhead, 2017; Bishop, 1990; Cajete, 1999; Ernest, 2021; Grande, 2015; Stevens, 2021).
5 Conclusion
There is no single or superior way to frame culturally connected math curriculum. Each approach is unique to its context and place. The CRISP framework used in the Indigenous Math courses at TMC is simply one approach. The CRISP framework focuses on four components including depth of detail; grade level; cultural iceberg, the center “I” of CRISP showing all math education is imbued with culture(s) as well as the iceberg emphasizing the level of depth/authenticity; and lastly, the culturally relevant to sustaining spectrum, which looks at the end goal. The four components make up the 2D content and cultural planes, respectively. The CRISP framework was developed, refined, and implemented within the three-course Indigenous Math sequence at TMC. The CRISP framework builds from and works with the Indigenous Math framework as well as the Indigenous Math Education framework.
The CRISP framework is not designed to determine the value of varying types of culturally connected math curricula and pedagogy. It is not meant to categorize but rather build relationships with varying approaches to Indigenous math. For the Indigenous Math courses at TMC, this framework has proven valuable in allowing me, as the instructor, to guide students through the vast types of culturally connected math curricula (content and pedagogy) highlighting four components of grade level, depth of detail, depth of culture, and the relevant to sustaining spectrum. Perhaps the framework may prove valuable beyond our context. The CRISP framework could potentially impact Indigenous pedagogical approaches and strategies, Indigenous knowledge redefining STEM education, and the development of culturally connected STEM curricula in all disciplines preschool through university-level.
The CRISP framework highlights how much more work in developing culturally connected math curricula can be done, specifically going deeper into the details of broad statements/examples. Further, the framework can offer guidance in developing Indigenous math curriculum resources. The framework allows us to be more explicit about the type of cultural connection being made and shared. Personally, much more work can be done with language as well as articulating the mathematizing and Western math connections to flute tuning in the particular traditional Indigenous scale and the tahokmu composition strategy. Further, another area with lots of potential is the use of finger weaving to make sashes in connection with group theory of abstract algebra. Along with these examples of future work, the CRISP framework will continue to be used in the Indigenous Math courses here at TMC.
My hope is that the CRISP framework, as well as the Indigenous Math framework and Indigenous Math Education framework, will allow my students and others to think more critically about culturally connected math curriculum in our community and more broadly other Indigenous communities. The ultimate goal of the Indigenous Math three-course sequence is to revitalize the mathematical ways of knowing embedded within the Turtle Mountain language(s), culture(s), and place so they can once again be widely known and normalized within the community. I believe that the CRISP framework is one step toward this goal in helping to articulate and value specific examples of Indigenous mathematizing.
Author’s note
Danny Luecke is the developer/instructor for the Secondary Math Education bachelor’s degree program at Turtle Mountain College. He completed his doctoral degree through North Dakota State University with a research focus on Dakota/Lakota Math Connections at Sitting Bull College. He was born in Fargo, North Dakota and lived there a majority of his life. He is an enrolled member of the Choctaw Nation of Oklahoma and has ancestry from multiple European nations. He believes he is honoring all of his ancestors through his life and work with the Standing Rock and Turtle Mountain communities.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Author contributions
DL: Writing – original draft, Writing – review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Funding to publish open access from NSF (Grant number 1855385) Turtle Mountain STEM Infusion Project. NSF Program: Tribal Colleges and Universities Program.
Acknowledgments
Chi-miigwech (huge thank you) to all the students who have taken any of the Indigenous math courses at TMC. Your input has been invaluable through your engagement in the courses. You all have been so generous to me. Further I thank my colleagues in the Teacher Education Department (and all of TMC) for being supportive of these new courses. This article builds upon a previous paper published in the Tribal College Journal (Luecke, 2023). Lastly, I thank Dr. Susan Faircloth (Coharie) for her contributions in editing.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdulrahim, N. A., and Orosco, M. J. (2020). Culturally responsive mathematics teaching: a research synthesis. Urban Rev. 52, 1–25. doi: 10.1007/s11256-019-00509-2
Abtahi, Y. (2022). What if I was harmful? Reflecting on the ethical tensions associated with teaching the dominant mathematics. Educ. Stud. Math. 110, 149–165. doi: 10.1007/s10649-021-10117-1
Aguirre, J. M., and del Rosario Zavala, M. (2013). Making culturally responsive mathematics teaching explicit: a lesson analysis tool. Pedagogies 8, 163–190. doi: 10.1080/1554480X.2013.768518
Aikenhead, G. S. (2017). Enhancing school mathematics culturally: a path of reconciliation. Can. J. Sci. Math. Technol. Educ. 17, 73–140. doi: 10.1080/14926156.2017.1308043
Aikenhead, G. (2018). “Indigenous perspectives in school mathematics: from intellect to wisdom” in Teaching and learning secondary school mathematics: Canadian perspectives in an international context. ed. E. J. Chernoff (Springer), 39–49.
American Indian Science and Engineering Society. (2020). Literature review: STEM education for native American students. 1–16. Available at: https://www.aises.org/sites/default/files/AISES-Literature-Review.pdf
Archibald, J. (2008). Indigenous storywork: Educating the heart, mind, body, and spirit. Vancouver, BC, Canada: UBC Press.
Beatty, R., and Clyne, C. (2024). “Relationships and reciprocity in mathematics education” in Unsettling education: Decolonizing and indigenizing the land. Eds. A.-L. King, K. O’Reilly, and P. J. Lewis (Toronto, ON, Canada: Canadian Scholars), 214–237.
Bishop, A. J. (1990). Western mathematics: the secret weapon of cultural imperialism. Race Class 32, 51–65. doi: 10.1177/030639689003200204
Bishop, A. J. (1991). Mathematical enculturation: A cultural perspective on mathematics education. Norwell, MA: Kluwer Academic Publishers.
Boyer, P. (2011). Ancient wisdom, modern science: The integration of native knowledge at tribally controlled colleges and universities. Pablo, MT: Salish Kootenai College Press and Lincoln, NE: University of Nebraska Press.
Brayboy, B. M. J., Faircloth, S. C., Lee, T. S., Maaka, M. J., and Richardson, T. A. (2015). Sovereignty and education: an overview of the unique nature of indigenous education. J. Amer. Indian Educ. 54, 1–9. doi: 10.1353/jaie.2015.a835529
Cajete, G. (1994). Look to the mountain: An ecology of indigenous education. (1st Edn.) Edn. Durango, CO: Kivaki Press https://eric.ed.gov/?id=ED375993.
Cajete, G. A. (1999). Igniting the sparkle: An indigenous science education model. Durango, CO: Kivaki Press.
Cajete, G. A. (2021). Creating culturally-responsive indigenous science education curriculum. Waasamoogikinwaa’amaading: Post-pandemic online and distance learning at tribal colleges. Cass Lake, MN: Leach Lake Tribal College.
D’Ambrosio, U. (2000). “A historiographical proposal for non-western mathematics” in Mathematics across cultures. ed. H. Selin (Springer Netherlands), 79–92.
Deloria, V., and Wildcat, D. (2001). Power and place: Indian education in America, vol. 2. Golden, CO: Fulcrum Publishing.
EGLASH, R., BENNETT, A., O'DONNELL, C., JENNINGS, S., and CINTORINO, M. (2006). Culturally situated design tools: Ethnocomputing from field site to classroom. Am. Anthropol. 108, 347–362. doi: 10.1525/aa.2006.108.2.347
Ernest, P. (2021). The ethics of mathematical practice: rejection, realisation and responsibility. Phil. Math. Educ. J. 33, 1–38. doi: 10.1007/978-3-030-19071-2_9-1
First Nations Education Steering Committee. (2007). First peoples principles of learning. West Vancouver, BC, Canada. Available at: https://www.fnesc.ca/first-peoples-principles-of-learning/
Furuto, L. (2013). Ethnomathematics curriculum textbook: Symbolic reasoning and quantitative literacy. Honolulu: University of Hawai′i SEED Office and the National Science Foundation. p. 84.
Garcia-Olp, M., Nelson, C., and Saiz, L. R. (2019). Conceptualizing a mathematics curriculum: indigenous knowledge has always been mathematics education. Educ. Stud. 55, 689–706. doi: 10.1080/00131946.2019.1680374
Grande, S. (2015). Red pedagogy: Native American social and political thought. 2nd Edn. Lanham, Maryland, US: Rowman & Littlefield.
Gutiérrez, R. (2009). Framing equity: helping students “play the game” and “change the game. Teach. Excell. Equity Math. 1, 4–8.
Gutiérrez, R. (2012). “Context matters: how should we conceptualize equity in mathematics education?” in Equity in discourse for mathematics education: Theories, practices, and policies. eds. B. Herbel-Eisenmann, J. Choppin, D. Wagner, and D. Pimm (Dordrecht, Netherlands: Springer Netherlands), 17–33.
Gutiérrez, R. (2017). Living mathematx: Towards a vision for the future. North American chapter of the International Group for the Psychology of mathematics education.
Gutiérrez, R. (2018). “Introduction: the need to rehumanize mathematics” in Rehumanizing mathematics for black, indigenous, and Latinx students. eds. I. Goffney, R. Gutiérrez, and M. Boston. Annual Perspectives in Mathematics Education; Vol. 2018 (United States: National Council of Teachers of Mathematics).
Gutstein, E. R. (2016). “Our issues, our people—math as our weapon”: critical mathematics in a Chicago neighborhood high school. J. Res. Math. Educ. 47, 454–504. doi: 10.5951/jresematheduc.47.5.0454
Harris, H. (2002). Coyote Goes to school: the paradox of indigenous higher education. Can. J. Native Educ. 26, 187–196. doi: 10.14288/cjne.v26i2.195930
Hogue, M. M. (2014). Let’s do it first and talk about it later: rethinking post-secondary science teaching for aboriginal learners. Education 19, 137–151. doi: 10.37119/ojs2014.v19i3.154
Jerome, D. F. (2012). Hands on a legacy: A pictorial journey honoring the ancestors—A gift for the future. Belcourt, ND, USA: Turtle Mountain Band of Chippewa. p. 126.
Kana‘iaupuni, S. M., Ledward, B., and Malone, N. (2017). Mohala i ka wai. Am. Educ. Res. J. 54, 311S–339S. doi: 10.3102/0002831216664779
Kawagley, A. O. (1997). Yupiaq mathematics: pattern and form in space and place. Sharing Our Pathways 2, 1–4.
Kisker, E. E., Lipka, J., Adams, B. L., Rickard, A., Andrew-Ihrke, D., Yanez, E. E., et al. (2012). The potential of a culturally based supplemental mathematics curriculum to improve the mathematics performance of Alaska native and other students. J. Res. Math. Educ. 43, 75–113. doi: 10.5951/jresematheduc.43.1.0075
Kovach, M. (2009). Indigenous methodologies: Characteristics, conversations, and contexts. Toronto, Ontario, Canada: University of Toronto Press.
Ladson-Billings, G. (1995). Toward a theory of culturally relevant pedagogy. Am. Educ. Res. J. 32, 465–491. doi: 10.3102/00028312032003465
Ladson-Billings, G. (2014). Culturally relevant pedagogy 2.0: a.k.a. the remix. Harv. Educ. Rev. 84, 74–84. doi: 10.17763/haer.84.1.p2rj131485484751
Lipka, J., and Adams, B. (2004). Culturally based math education as a way to improve Alaska native students’ math performance. ACCLAIM (Appalachian Collaborative Center for Learning, Assessment, and Instruction in Mathematics) Research Institute. Ohio University, Athens, Ohio: University of Louisville. p. 1–52.
Lipka, J., Sharp, N., Adams, B., and Sharp, F. (2007). Creating a third space for authentic biculturalism: examples from math in a cultural context. J. Amer. Ind. Educ. 46, 94–115.
Long Feather, C. (2007). A Lakota/Nakota/Dakota model of oratory. Communication Department, University of North Dakota, Grand Forks, ND, USA. p. 240. Available at: https://commons.und.edu/theses/731
Luecke, D. (2023). Balance and harmony: Ojibwe math at Turtle Mountain community college. Tribal College J. 35, 28–33.
Luecke, D. (in press). Dakota/Lakota math connections: results from developing a community-based math resource. Tribal College Univ. Res. J. 8. doi: 10.3389/feduc.2023.1151376
Luecke, D., and Sanders, D. (2023). Dakota/Lakota math connections: an epistemological framework for teaching and learning mathematics with indigenous communities and students. Front. Educ. 8, 1–20. doi: 10.3389/feduc.2023.1151376
Luecke, D., Carlow, S., Mattes, J., Christensen, W., and Mackey, H. (2022). Circulating conversations methodology: Co-connecting knowledge to develop research questions at sitting bull college. Philosophy of Mathematics Education Journal. United Kingdom: University of Exeter.
Lunney Borden, L. (2011). The ‘verbification’of mathematics: using the grammatical structures of Mi’kmaq to support student learning. For Learn. Math. 31, 8–13.
Lunney Borden, L. (2012). What’s the word for…? Is there a word for…? How understanding Mi’kmaw language can help support Mi’kmaw learners in mathematics. Math. Educ. Res. J. 25, 5–22. doi: 10.1007/s13394-012-0042-7
Lunney Borden, L., Wagner, D., and Johnson, N. (2019). Show me your math: Mi’kmaw community members explore mathematics. Living culturally responsive mathematics education with/in indigenous communities. Eds. C. Nicol, J. A. Q’um Q’um Xiiem, F. Glanfield, and A. J. Sandy Dawson (pp. 91–112). Brill. Available at: https://brill.com/downloadpdf/book/edcoll/9789004415768/BP000005.pdf
McCarty, T. L., and Lee, T. S. (2014). Critical culturally sustaining/revitalizing pedagogy and indigenous education sovereignty. Harv. Educ. Rev. 84, 101–124. doi: 10.17763/haer.84.1.q83746nl5pj34216
Medina, M. A., Gerofsky, S., and Nicol, C. (2024). “Weaving indigenous mathematics: bringing indigenous ways and stories into conversation with ethnomathematics” in Ethnomathematics and mathematics education: International perspectives in times of local and global change. eds. C. Nicol, G. Knijnik, A. Peng, M. Cherinda, and A. Bose (Cham, Switzerland: Springer Nature Switzerland), 77–100.
Meyer, M. A. (2014). “Holographic epistemology: native common sense” in Encyclopedia of global archaeology. ed. C. Smith (New York: Springer), 3435–3443.
Meyer, S., and Aikenhead, G. (2021a). Indigenous culture-based school mathematics in action: part I: professional development for creating teaching materials. Math. Enthusiast 18, 100–118. doi: 10.54870/1551-3440.1516
Meyer, S., and Aikenhead, G. (2021b). Indigenous culture-based school mathematics in action: part II: the study’s results: what support do teachers need? Mathemat. Enthusiast 18, 119–138. doi: 10.54870/1551-3440.1517
Nicol, C., Glanfield, F., and Dawsom, A. J. S. (2019). Living culturally responsive mathematics education with/in indigenous communities. Leiden, Netherlands: Brill.
Paris, D. (2012). Culturally sustaining pedagogy. Educ. Res. 41, 93–97. doi: 10.3102/0013189X12441244
Paris, D., and Alim, H. S. (2014). What are we seeking to sustain through culturally sustaining pedagogy? A loving critique forward. Harv. Educ. Rev. 84, 85–100. doi: 10.17763/haer.84.1.982l873k2ht16m77
Rosa, M., D’Ambrosio, U., Orey, D. C., Shirley, L., Alangui, W. V., Palhares, P., et al. (2016). Current and future perspectives on ethnomathematics as a program : Springer.
Ruef, J. L., Jacob, M. M., Walker, G. K., and Beavert, V. R. (2020). Why indigenous languages matter for mathematics education: a case study of Ichishkíin. Educ. Stud. Math. 104, 313–332. doi: 10.1007/s10649-020-09957-0
Sanders, D. (2011). Mathematical views within a Lakota community: towards a mathematics for tribal self-determination. (dissertation). Boulder, CO, United States: University of Colorado Boulder. p. 423.
Smith, L. T. (2021). Decolonizing methodologies: Research and indigenous peoples. 3rd Edn. New York, NY, USA: Zed Books Ltd.
Smith, L. T., Tuck, E., and Yang, K. W. (Eds.) (2018). Indigenous and decolonizing studies in education: Mapping the long view. London, UK: Routledge. p. 292.
Stevens, P. J. (2021). A woodcutter’s story: perceptions and uses of mathematics on the San Carlos apache reservation. Anthropol. Educ. Q. 52, 430–450. doi: 10.1111/aeq.12399
Styres, S. (2018). “Literacies of land” in Indigenous and decolonizing studies in education: Mapping the long view. eds. L. T. Smith, E. Tuck, and K. W. Yang (London, UK: Routledge), 24–37.
Walter, M., and Andersen, C. (2013). Indigenous statistics: A quantitative research methodology. London, UK: Routledge. p. 160.
Webb, D., Groseth, B., and Coggins, P. (2017). Incorporating culture into the post-secondary mathematics classroom. In the mathematics education for the future project. Proceedings of the 14th international conference: challenges in mathematics education for the next decade. Balatonfüred Hungary, 347–352.
Wilson, S. (2008). Research is ceremony: Indigenous research methods. Winnipeg, MB, Canada: Fernwood Publishing. p. 144.
Windchief, S., and San Pedro, T. (2019). Applying Indigenous research methods: Storying with peoples and communities. London, UK: Routledge. p. 194.
Wiseman, D., and Lunney Borden, L. (2018). Echoed rememberings: Considering mathematics and science as reconciliation. In: Transdisciplinarity in mathematics education: Blurring disciplinary boundaries. Eds. L. Jao and N. Radakovic (Springer International Publishing) pp. 175–192.
Yong, K. (2024). Trigonometry through wayfinding and navigation across the Pacific. University of Hawai’i – West O’ahu. Available at: https://www.kamuelayong.com/trigonometry/meta_frontmatter.html (Accessed May 07, 2024).
Keywords: indigenous math, Ojibwe, Dakota/Lakota, tribal college and university, culturally relevant, culturally sustaining, curriculum, ethnomathematics
Citation: Luecke D (2025) A culturally relevant, imbued, and sustaining pedagogy framework for culturally connected math curriculum. Front. Educ. 9:1502449. doi: 10.3389/feduc.2024.1502449
Edited by:
Zahid Pranjol, University of Sussex, United KingdomReviewed by:
Niroj Dahal, Kathmandu University, NepalTej Dalvi, University of Massachusetts Boston, United States
Copyright © 2025 Luecke. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Danny Luecke, ZGx1ZWNrZUB0bS5lZHU=
 Danny Luecke
Danny Luecke