- Institut für Mechanik, Technische Universität Berlin, Berlin, Germany
Based on the example of wear of polymers, which exhibit a power-law time variation of the wear loss under constant loading conditions, a fractional time-derivative wear equation has been introduced. The wear contact problem with a fixed contact zone is solved using the known method of separation of spatial and time variables. It is shown that during the wear process, the contact pressure approaches a uniform distribution over the contact area, which is termed as a quasi-steady-state solution, since the mean volumetric wear rate does not tend to become constant. It is of interest that the contact pressure variation displays a decaying oscillatory nature in the case of severe wear, when the mean volumetric wear rate increases with time.
1 Introduction
Wear is a tribological phenomenon that accompanies contact interaction of solids with interfacial sliding between their surfaces and manifests itself primarily in gradual loss of material due to the subsurface damage accumulation and surface degradation (Zmitrowicz, 2006). In wear material testing, the wear loss is usually measured in terms of the volume of lost material, V, which yields the wear depth, w, by relating to the area of contact, A, as
Eq. 1 tentatively assumes that the wear loss is the same at each point of the contact zone, and this condition is characteristic of the steady-state wear process (Dundurs and Comninou, 1980; Páczelt and Mróz, 2007).
Usually, sliding wear tests are performed under constant normal loading conditions, which are characterized by either contact load, P, or mean contact pressure,
In the cases of mild or moderate wear, after some initial running-in (Wright and Kukureka, 2001; Khonsari et al., 2021) or wearing-in (Blau, 2005) period of time, the condition of steady state
In the steady-state wear process, the linear wear rate, defined as the time derivative
where t1 and t2 are any two different moments of time taken during the steady-state period.
In many cases, the wear equation can be written in the following form (Kragelsky, 1965):
Here, v is the sliding velocity, and kw is the wear coefficient. In view of Eqs 1, 2, Eq. 4 can be represented as
which is known as Archard’s equation (Meng and Ludema, 1995), though similar wear equations were introduced earlier by Reye (1860), Khrushchov and Babichev (1941), and Holm (1946). The wear coefficient kw is determined during the steady-state conditions by using Eqs 3, 5.
A generalization of the wear Eq. 4, which was suggested by Rhee (1970) for polymer-bonded friction materials, takes the form
where Kw is the wear factor, and α, β, γ are parameters. However, while Eq. 6 has been successfully used to predict the wear resistance of polymer composite materials designed for extreme environmental conditions (Gardos, 1982; Sedakova and Kozyrev, 2021), there is a problem with applying the wear Eq. 6 for solving the wear contact problems with the spatial-temporal variation of the contact pressures (Grzelczyk and Awrejcewicz, 2015; Ciavarella et al., 2020).
In recent years, there has been a growing interest in modeling severe wear (Nguyen et al., 2018; Popov and Pohrt, 2018; Li et al., 2020). In a broad sense, severe wear is defined as a form of wear characterized by a rapid increase in the amount and size of wear particles (Blau, 1992). In many situations, the regime of severe wear can be characterized by the absence of any steady-state regime under constant conditions. This is so, for example, in wear of polymers (Viswanath and Bellow, 1995), when under constant normal load and sliding speed (see Figure 1), the wear volume loss V varies proportionally to some power of time, that is tα, and therefore, the wear rate
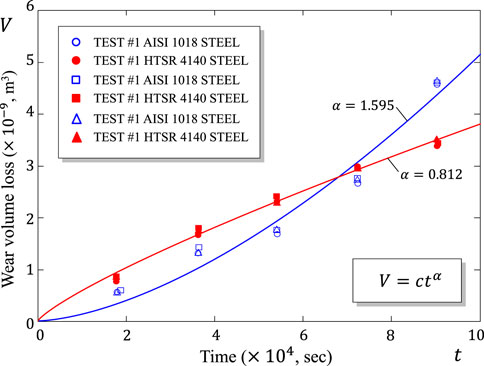
FIGURE 1. Volume loss vs. time on linear coordinates with best fit power-law lines for Delrin against two counterparts (based on the experimental data taken obtained by Viswanath and Bellow (1995)).
It is clear that in experiments like that, whose results are shown in Figure 1, Eq. 3 is not applicable. Instead we can consider the ratio V(t)/t that defines the mean volumetric wear rate. The two cases α = 0.812 and α = 1.595 differ by the decreasing/increasing trend of this quantity. The wear process with increasing in time mean volumetric wear rate (that is when α > 1) will be termed as severe wear in a narrow sense. At the same time, the case α < 1 may called mild wear, as the wear rate decreases towards zero during the wear process.
Further, when comparing the Archard Eq. 4 with the Rhee Eq. 6, we see that for polymers the Archard wear coefficient kw, which is evaluated as the ratio V/Pvt, is found to depend on time, that is
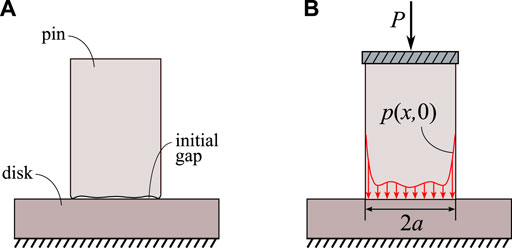
However, a natural concern arises about the effect of the wearing-in period, when the initial contact pressure evolves due to the contact geometry adaptation (Argatov I and Chai, 2020). In a pin-on-disk sliding wear tests, when a wearable pin is put on an abrasive disk, there exists a small initial gap between the surfaces brought into contact (see Figure 2A), which influences the initial contact pressure, p(x, t) at t = 0, in the loaded state (see Figure 2B).
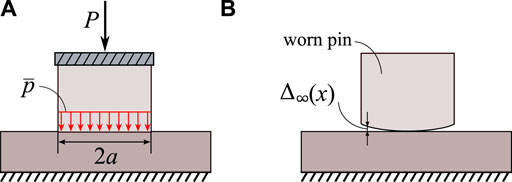
During the wear process, because of the contact geometry adaptation, the contact pressure p(x, t) evolves in time and approaches a steady-state pattern of uniform distribution over the contact zone (see Figure 3A). The corresponding steady-state shape of the pin surface facing the disk is characterized by the limiting gap function, Δ∞(x), which does not depend on the initial gap (see Figure 3B).
When the theoretical modeling framework of the contact geometry adaptation (Figures 2, 3) is applied to the case of super-Archard wear, the main problem to solve in this way is a generalization of the experimentally observed non-stationary relation between
In recent years, the apparatus of fractional differentiation has been used in mechanics, in particular, to generalize models of diffusion (Mainardi, 1996), rough contact (Argatov, 2003), and viscoelasticity (Su et al., 2021). In the present study, we use the classical Riemann–Liouville derivative. It should be noted that a number of different approaches exist to introduce a more general notion of the derivative (Ortigueira and Machado, 2015). In particular, a so-called fractal fractional derivative (Chen et al., 2010; He, 2011) does not involve the integral convolution and represents a local operator. However, whereas fractals have emerged as a useful mathematical tool in tribological research (Ling, 1990; Borodich and Onishchenko, 1993; Borodich, 1999), the present study pioneers the use of concept of the fractional derivative in modeling wear processes.
Since the theory of wear contact problem is well established (Aleksandrov and Kovalenko, 1980; Kovalenko, 1985), we adopt the approach suggested in the constructive review (Argatov I and Chai Y. S, 2020) and take a general point of view on the description of the pin/disk contact interaction, which is applicable both in the three- and two-dimensional settings. To illustrate the contact pressure evolution, we consider a two-dimensional wear contact problem (Galin, 1976), for which a detailed analysis has been available in the literature (Aleksandrov et al., 1978; Argatov and Fadin, 2011). It is anticipated that with certain modifications the fractional time-derivative approach developed below can be applied to model other temporary-spatial severe damage processes like mechanochemical corrosion (Sedova and Pronina, 2022), wear/scratch damage (Dasari et al., 2009), and wear of metamaterials (Garland et al., 2020).
The rest of the paper is organized as follows. In Section 2, we introduce a fractional time-derivative (FTD) wear equation as a straightforward generalization of the Archard wear equation by replacing the time derivative in the definition of the linear wear rate with appropriate fractional derivative. The FTD wear equation when applied under constant load conditions predicts a power-law time variation for the volumetric wear similar to the Rhee wear equation. This observation explains the main goal of the present study and that is to generalize the Rhee wear equation to the case of non-constant (spatial-temporal) variations of the contact pressure. It is hypothesized that the FTD wear equation provides such a generalization. The main body of the paper is devoted to the analysis of implications drawn from the solution of the model wear contact problem formulated in Section 3. In particular, the existence of a quasi-steady state is identified in Section 4 and, using the method of variables separation (Section 5), the evaluation of the contact pressure towards the quasi-steady state is considered in detail in Section 6. A particularly novel aspect—oscillatory nature—of the contact pressure variations is discussed in Section 7. The spatial-temporal variation of the worn profile is presented in Section 8. Finally, in Section 9, we discuss the obtained results and further generalizations and formulate the conclusions.
2 Fractional Time-Derivative Wear Equation
In its basic version due to Archard (1953), the wear equation linearly relates the wear rate at a point with coordinate x and at time t to the contact pressure as
with some constant κ, which is related to the wear coefficient, kw, as κ = kwv, where v is the speed of relative sliding at the contact interface.
Under the assumption that the worn material is absent at the initial moment t = 0 , that is w(x, 0) = 0, Eq. 7 is equivalent to the relation
The integral form Eq. 8 of the wear Eq. 7 is used in formulating the wear contact problems (Galin, 1976; Argatov and Tato, 2012), as the wear depth w(x, t) directly describes the evolution of the contact geometry in the direction normal to the contact interface.
Let us replace the differentiation with respect to time on the left-hand side of Eq. 7 with a more general notion of the derivative. In particular, we make use of the fractional Riemann–Liouville derivative of order α, which will be denoted by
which contains two parameters, namely, κ and α.
In the framework of fractional calculus, from Eq. 9, it follows that
where Γ(x) is the gamma function.
The right-hand side of Eq. 10 contains the Riemann–Liouville integral of order α which is consistent with the inversion of the respective fractional derivative appearing in Eq. 9.
It is to emphasize that by taking α = 1 in Eq. 10, in view of the normalization condition Γ(1) = 1, we recover the integral form Eq. 8 of the non-fractional Archard wear equation. Therefore, it makes sense to assume that 0 < α < 2, since Eq. 9 generalizes Archard’s Eq. 7, which exactly corresponds to the basic case α = 1.
Remark 1. Observe that in the case of steady state, when
and thus, the mean linear wear rate (evaluated from the very onset of the wear process) will be non-constant
In view of Eq. 1, from Eq. 11, it follows that
3 Wear Contact Problem Formulation
Following Komogortsev (1985) and Argatov and Fadin (2011), we consider a wear contact problem for an elastic solid (pin) in contact with a rigid base (disk) with a fixed zone of contact, x ∈ ω, under a constant normal load, P. In this case, the resultant of the contact pressure p(x, t) satisfies the equilibrium equation
The wear contact problem can be reduced to the following governing integral equation in the domain x ∈ ω, t ≥ 0, which involves two unknowns, namely, the contact pressure p(x, t) and the contact displacement δ0(t):
Here, K(x, ξ) is a given surface-influence function (with x and ξ being the points of observation and integration), Δ0(x) is a known function of initial gap between the contacting surfaces, and w(x, t) is the wear depth which is related to the contact pressure p(x, t) by Eq. 10. It is to note that the gap function is usually subject to the centering condition Δ0(0) = 0.
We recall that the surface-influence function K(x, ξ) is defined as the normal component of the corresponding vector Green’s function restricted to the surface of the elastic solid, and thus, the equilibrium equations inside the elastic solid (Shillor et al., 2004) are naturally satisfied by the construction of the function K(x, ξ). The reduction of the wear contact problem to the corresponding governing integral equation is well known (Argatov I and Chai Y. S, 2020) and allows applying the boundary element method (Sfantos and Aliabadi, 2006) for the direct evaluation of the contact pressures.
4 Uniform Contact Pressure as a Quasi-Steady State
By integrating Eq. 10 over the contact interval and taking into account the equilibrium Eq. 13, we derive the following the relations for the volumetric wear loss:
Thus, making use of Eq. 15 and following the previously introduced method (Komogortsev, 1985), we can reduce the governing integral Eq. 14 to the equation
where x ∈ ω and t > 0. Moreover, A denotes the measure of the contact area defined as
and we have introduced the notation
The form of Eq. 16 is preferable in wear contact problems (Komogortsev, 1985), as the effect of the initial contact configuration, which is associated with the gap function Δ0(x), is now incorporated into the initial contact pressure density p(x, 0).
Now, let us introduce the notation for the mean contact pressure and the point-wise deviation of the contact pressure from its mean value
Thus, in view of (Eqs 15, 19), Eq. 16 can be rewritten in the form
where x ∈ ω and t > 0, and we have introduced the notation
We note that in regard to the kernel of the integral Eq. 16, the third term on the right-hand side of Eq. 21 has been introduced for symmetrization (Argatov and Chai, 2019). This is convenient but does not affect the result because of the zero-mean property
which follows from the definition (19)2 of the function q(x, t) and the equation of equilibrium Eq. 13.
To this end, the behavior of the residual function q(x, t) as time progresses is shown to be described by Eq. 20. By analogy with the wear contact problems based on the Archard wear equation, it can be anticipated that the deviation of the contact pressure from its mean value diminishes with time. In the case under consideration, we also find that q(x, t) → 0 as t → ∞, and hence the mean contact pressure
5 Non-Dimensionalization and Separation of Variables
For the sake of simplicity, we assume that the pin material is isotropic and can be characterized by Young’s modulus, E, and Poisson’s ratio, ν. In contact mechanics, an important role is played by the reduced elastic modulus E* = E/(1 − ν2). Also, let a denote a characteristic size of the contact domain ω, which can be taken to be equal to the half-diameter of ω.
Following Komogortsev (1985), we take advantage of the fact that Eq. 20, in view of Eq. 10, is in a separable form (the kernel function K2(x, ξ) does not depend on the time variable t) that makes it possible to construct its solution in the form
where ϕn(x) is the nth eigenfunction of the integral operator with the kernel K2(x, ξ) given by Eq. 21, i.e.,
We note that the non-dimensionalising factor E*/a has been introduced on the left-hand side of Eq. 24 to ensure that the eigenvalues λ1, λ2, … are dimensionless. It is pertinent to note here that, in view of Eqs 21, 22, the eigenfunctions possess the zero-mean property
Without loss of generality, we assume that the solutions of the eigenvalue problem Eq. 24 are normalized as
Thus, taking into account relations (19)2 and Eq. 23, we can represent the contact pressure in the form
where
By setting t = 0, from Eq. 27, it follows that
where p(x, 0) solves the integral equation of initial contact, which is obtained from Eq. 14 by setting t = 0, whereas, in view of Eq. 26, the coefficients of the infinite sum are given by
In the next section, we consider the evolution of the functions bn(t), which satisfy the initial conditions (29). The corresponding equation is simply obtained by substituting the expansion (Eq. 23) into Eq. 20 and utilizing Eq. 24.
6 Evolution of the Contact Pressure Towards the Quasi-Steady State
In view of Eq. 24, the series solution Eq. 23 satisfies Eq. 20, if and only if
Equation 30 is classified as Abel’s integral equation of the second kind (see, e.g., (Gorenflo and Mainardi, 1997; Gorenflo et al., 2014)), and its solution bn(t) is given in the form
in terms of the single-parameter Mittag-Leffler function of order α, defined as
where Γ(x) is the gamma function.
It is also convenient to consider the Mittag-Leffler type function
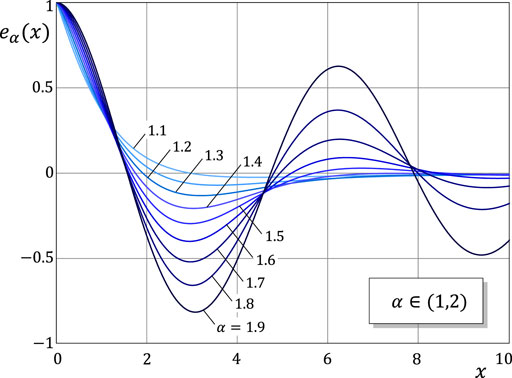
which for α ∈ (0, 1) is known (Mainardi, 2020) to be completely monotone on the positive real semi-axis. The variation of the function eα(x) for different values of the parameter α ∈ (1, 2) in shown in Figure 4.
Moreover, let us introduce a characteristic time of the wearing-in process
So, in view of Eqs 33, 34, Eq. 31 can be represented as
and thus, using Eqs 27, 35, we find that
To characterize the evolution of the contact pressure p(x, t) as the time variable t tends to infinity, we consider the following asymptotic formula for eα(x), α ∈ (0, 2), α ≠ 1, is known for sufficiently large values of the argument (Mainardi, 2020):
Thus, in view of Eqs 36, 37, the contact pressure approaches the uniform distribution
Remark 2. It should be noted that the asymptotic Eq. 37 reflects the decaying behavior of the Mittag-Leffler function Eα(x) on the negative real axis as x → −∞. This formula can be used to analyze the asymptotics of the contact pressure (Eq. 36), provided all eigenvalues λn are positive. To prove that this is the fact, we consider the elastic energy,
Thus, since the elastic energy
7 Oscillatory Nature of the Contact Pressure Variation in Super-archard Wear
Equation 37 provides information about the limiting evolution of the contact pressure p(x, t) as the time variable t tends to infinity. During the wearing-in period, the evolution of p(x, t) strongly depends on the variation of the Mittag-Leffler type function eα(x), which changes its behavior from completely monotonic for α ∈ (0, 1) to decaying oscillatory for α ∈ (1, 2) (see Figure 4).
To illustrate the contact pressure variation during the wearing-in period, we consider the example of two-dimensional contact for an elastic layer and a wearable indenter, which establishes a fixed contact interval x ∈ ( − a, a) of a relatively small half-width, a, compared to the layer thickness. The corresponding wear contact problem in the case of the Archard type wear equation was studied by Aleksandrov et al. (1978), using the Galerkin method for evaluating the eigenfunctions. We refer to the paper by Argatov and Fadin (2011) for more details.
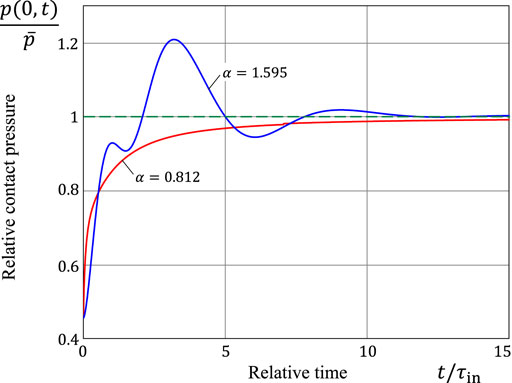
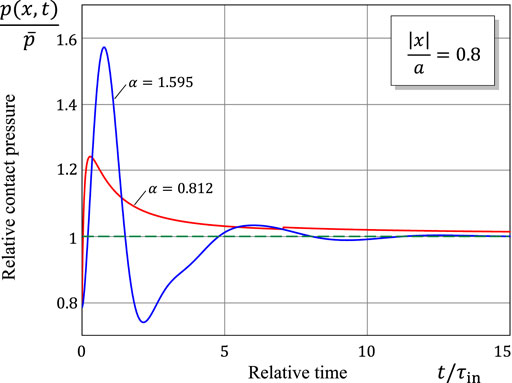
Figure 5 shows the time-variation of the relative contact pressure
In the example of contact geometry under consideration, which is taken to be almost flat (with a small initial gap between the contacting surfaces), the initial contact pressure shows a strong stress concentration in a periphery region of contact (see curves τ = 0 in Figures 6, 7). That is why, in the initial period of time, the wear rate
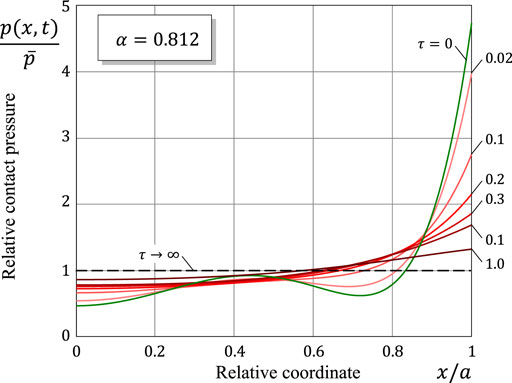
FIGURE 6. Space-variation of the contact pressure for different values of the relative time variable τ = t/τin in the sub-Archard wear case.
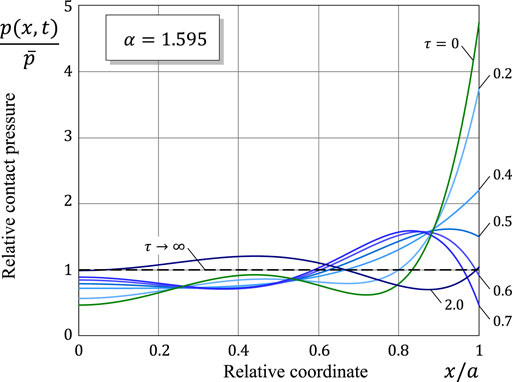
FIGURE 7. Space-variation of the contact pressure for different values of the relative time variable τ = t/τin in the super-Archard wear case.
The discrete-time progression of the spatial variation of the contact pressure is shown in Figures 6, 7 in the cases of sub-Archard and super-Archard wear, respectively. Observe that a drastic reduction in the contact stress concentration occurs during the initial time interval of duration comparable with the characteristic time τin. From the comparison of Figures 6, 7, it can be concluded that the wearing-in period in super-Archard wear lasts much longer than in the case of sub-Archard wear.
8 Evolution of the Worn Profile
Due to the wear process, the contact geometry gradually changes, while the contact pressure approaches a uniform distribution of the applied load over the contact area. The initial contact geometry is characterized by the initial gap function Δ0(x), which is subject to the centering condition Δ0(0) = 0. The current gap function, Δ(x, t), is defined as follows (Argatov I. I and Chai Y. S, 2020):
When the contact pressure density p(x, t) is given by the eigenfunction expansion method in the form Eq. 36, in view of Eqs 18, 24, we will have
where we have used the zero-mean property (Eq. 22) of the eigenfunctions ϕn(x), n = 1, 2, …, and the symmetry property of the surface influence function, that is K(x, ξ) = K(ξ, x).
Since bn(t) → 0 as t → ∞, the limiting gap function is defined only by the first term on the right-hand side of Eq. 40, and thus, we obtain
So, from Eqs 39–41, it follows that
The evolution of the relative gap function is illustrated in Figures 9, 10. It is of interest to observe a non-monotonic progression of the worn profile Δ(x, t) towards the limiting shape Δ∞(x) in the case of super-Archard wear.
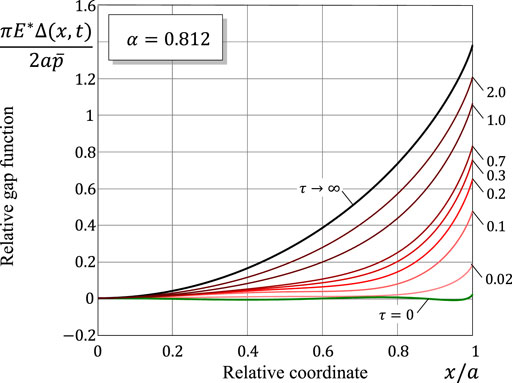
FIGURE 9. Space-variation of the gap function for different values of the relative time variable τ = t/τin in the sub-Archard wear case.
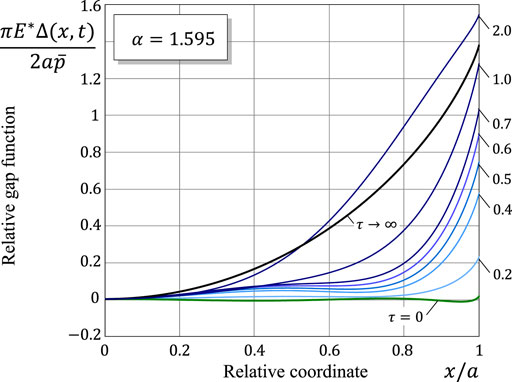
FIGURE 10. Space-variation of the gap function for different values of the relative time variable τ = t/τin in the super-Archard wear case.
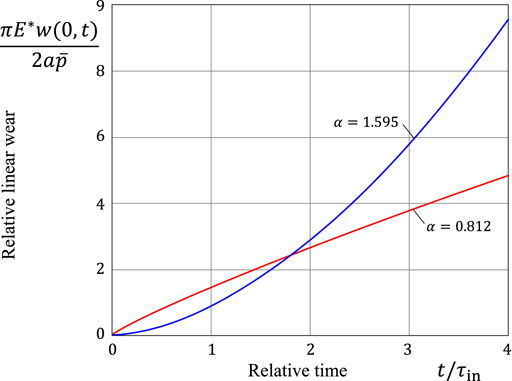
Figure 11 presents the evolution of wear depth w(0, t), which corresponds to the evolution of the contact pressure at the center of the contact zone shown in Figure 5. It is to note that, in view of Eq. 34, the wear equation transforms as
where
Interpretation of the evolution of the relative gap function shown in Figures 9, 10 will be simplified if we consider the evolution of the pin shape described by the function D(x, t) = Δ0(x) + w(x, t) (see Figures 12, 13). It is of interest to observe that in the case of super-Archard wear, the evolution of the worn profile is also found to be slightly oscillatory (see Figures 10, 13), as it could be predicted based on Eq. 39, which defines the current gap function, and the oscillatory evolution of the contact pressure. It should be emphasized that, though the worn profile progresses non-monotonically in time, this does not mean that locally (in spatial sense) there could exist profile growth, because the fractional wear Eq. 9 predicts a positive wear depth w(x, t) for any positive contact pressure history p(x, τ), τ ∈ (0, t).
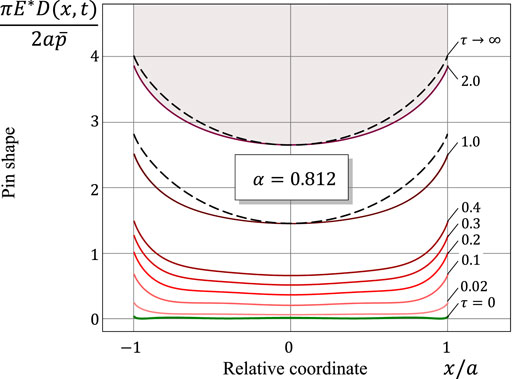
FIGURE 12. Pin shape at different values of the relative time variable τ = t/τin in the sub-Archard wear case. The dashed lines correspond to the limiting profile.
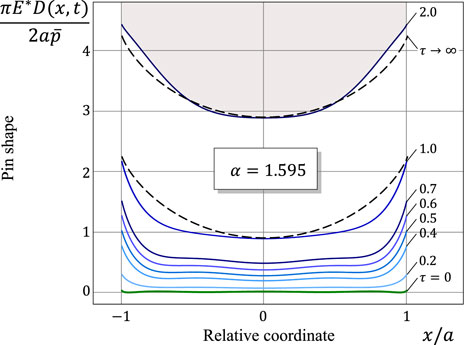
FIGURE 13. Pin shape at different values of the relative time variable τ = t/τin in the super-Archard wear case. The dashed lines correspond to the limiting profile.
In the case of sub-Archard wear, when 0 < α < 1, the duration of wearing-in process, when the contact pressure approaches the mean value
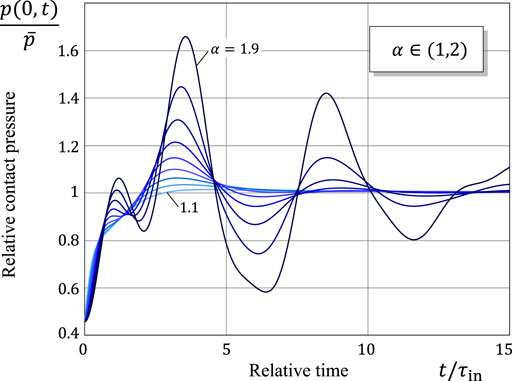
FIGURE 14. Time-variation of the contact pressure at the center of the contact zone for different values of the parameter α ranging from 0.1 to 0.9 with an increment of 0.1.
9 Discussion and Conclusion
First of all, we note that the example of two-dimensional contact has been used for illustrative purposes. A more realistic information about the eigenvalues λn, which depend on the global geometry of the wearable pin, can be obtained by means of finite element simulations (Liu et al., 2014).
We would like to emphasize that the numerical results presented in Figures 5–13 were obtained based on the exact solution of the model two-dimensional wear contact problem for an elastic layer (Aleksandrov et al., 1978) with a controllable error determined by the approximate evaluation of the eigenvalues λn. In the analysis of real pin-on-disk experiments, the application of FEM-based numerical methods is required (Liu et al., 2014). However, the oscillating nature of the contact pressure variation observed in Figure 5 is caused by the properties of solutions (see Figure 4) of Abel’s integral Eq. 30, which will remain the same in the three-dimensional contact problems. To be more precise, the contact geometry affects the eigenvalue problem Eq. 24, which depends on the surface-influence function (see Eq. 21), whereas the evolution Eq. 30 is fully determined by the adopted fractional time-derivative (FTD) model for wear. This means that while FEM simulations cannot serve for the model verification, spatial-temporal variation of the contact geometry and the contact pressures, if observed experimentally, would support the introduced FDT wear equation. At the same time, though verification experimental studies fall outside the scope of this theoretical work, the simple analytical model presented above will definitely aid in planning such experiments.
Based on the presented analysis, it becomes clear that the temporary evolution of wear process, which is governed by the fractional time-derivative model (10), is determined by the properties of the Mittag-Leffler type function eα(x), which, in turn, strongly depend on the value of the index α. In particular, for α ∈ (1, 2), the number of zeros, n(α), of the function eα(x), x ∈ (0, ∞), which determines the number of oscillations, exponentially increases as α approaches 2 (see Figure 15).
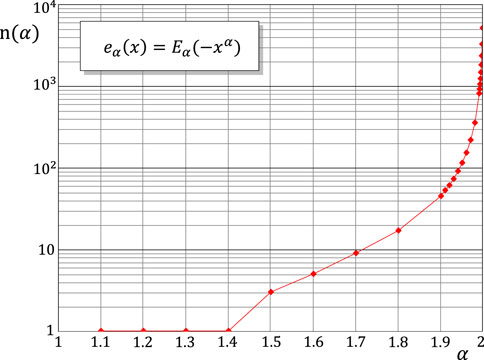
FIGURE 15. Number of real zeros of the Mittag-Leffler type function eα(x) based on the numerical results from presented by Hanneken et al. (2007).
Observe that the FTD wear Eq. 9 is linear, and under the constant load condition (Eq. 13) it implies the following relation between the contact load and the worn volume (see Eq. 12):
Here, k = κ/αΓ(α) is a constant coefficient. It is to emphasize again that Eq. 43 is in complete agreement with the Rhee Eq. 6, which in this special case (γ = 1) takes the form
Thus, by comparing Eqs 43, 44, we can write that k = Kwvβ, and therefore, we obtain κ = αΓ(α)Kwvβ. In other words, under the condition of constant sliding velocity, the wear coefficient κ in the FTD wear Eq. 9 may be regarded to be parametrically dependent on the sliding velocity v. The effect of surface roughness of the hard counterpart (disk), along which a wearable solid (pin) slides, is incorporated in the value of the coefficient κ as well.
It is of practical interest to have a closer look at the quality of power-law approximations of the experimental data for the volumetric wear loss under constant load (Viswanath and Bellow, 1995), which are presented in Figure 1. In particular, it is instructive to consider the variation of the absolute error as shown in Figure 16, from where it is seen that in the case of super-Archard wear (α > 1), the experimental data exhibits pronounced deviations from the power-law curve. This fact implies that the fractional wear rate
by introducing an additional fitting constant γ.
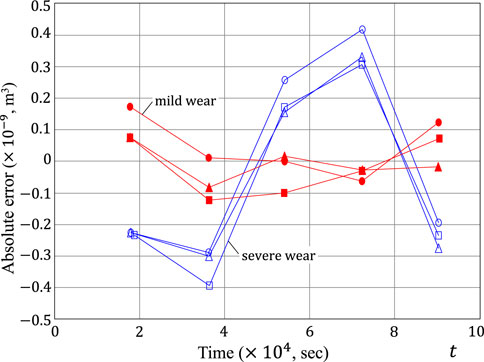
FIGURE 16. Difference between the power-law predictions and the experimental data (Viswanath and Bellow, 1995) shown in Figure 1 (the same legend applies).
Correspondingly, in light of Eq. 45, Eq. 10 can be generalized as follows:
As a consequence of the nonlinear wear Eq. 46, the volumetric wear loss V(t) will no longer be predicted by the power-law Eq. 15. Indeed, by integrating Eq. 46, we arrive at the equation
where the inner integral over the contact domain will no longer be constant under a constant load, but may become oscillatory during the wear process.
It is to note that the nonlinearity in the fractional wear Eqs 45–47 has been introduced in the spirit of the Archard–Kragelsky model for the linear wear rate (Kragelsky, 1965), and thus, they can be applied under the assumption of constant speed of relative sliding at the contact interface with the wear coefficient κ being nonlinearly dependent on the sliding speed.
It should be emphasized that though the simple example of two-dimensional wear contact problem has been employed in the analysis above, the main findings about the decaying oscillatory nature of the approach to the quasi-steady state will hold true for the corresponding three-dimensional contact configurations, since this feature is rooted in the fractional time description of the wear process.
Observe (Soldatenkov, 2010) that the wear Eq. 10 is merely a special case of the more general type
where K1(t) and K2(t) are known functions. In particular, Eq. 48 with K1(t) ≡ 1 and K2(t) = (κ/Γ(α))tα−1 simply coincides with Eq. 10. On the other side, it is of interest to observe that Eq. 48 with K1(t) = (κ/Γ(α))tα−1 and K2(t) ≡ 1 in the case of constant loading also leads to Eq. 11. Moreover, it can be shown that Eq. 9 with
Thus, there are possible different ways of generalizing the Rhee wear Eq. 6 to the case of non-constant (spatial-temporal) variations of the contact pressure, which have the same power-law time behavior in the steady state. While the present study gives no physical motivation for the fractional wear model (9), the hypotheses and implications formulated above can be verified experimentally without much difficulty. Also, a separate study is required to identify key differences and similarities between the wear equations discussed in the previous paragraph.
The systematic analysis of the physical variables that influence the wear process of polymers (Viswanath and Bellow, 1995) is showing an intensive effect of temperature and thus deserves a comment that the thermo-elasticity framework (Yevtushenko and Pyryev, 1999) should be applied for modeling contact deformations once the temperature exceeds a certain threshold.
To conclude, the fractional time-derivative wear rate is introduced to describe a power-law time-growth of the volumetric wear loss under constant loading conditions, which is encountered in wear testing of polymers. The newly introduced fractional time-derivative wear equation allows to extend the experimentally observed dependence to the case of a variable contact pressure. The cases of sub-Archard and super-Archard wear are distinguished based on the value of the time exponent α ∈ (0, 2), which describes decreasing (α < 1, “mild” wear) or increasing (α > 1, “severe” wear) variation of the mean wear rate.
A striking implication of the developed wear contact model is the prediction of a decaying oscillatory behavior for the contact pressure variation in time during the wearing-in period, when it approaches a uniform distribution over the contact area. The main theoretical finding of the paper is supported by the analysis of the power-law approximations for the volumetric wear loss obtained under constant applied loads. The developed fractional time-derivative approach can be applied to modeling other temporary-spatial damage processes that maintain a power-law growth of the accumulated damage under constant loading conditions.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer EW declared a shared affiliation with the author IV to the handling editor at the time of review.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The financial support from the Ba-Yu Scholar program of Chongqing City (China) is gratefully acknowledged. The author would like to thank Dr. Dmitry Ponomarev (TU Wien) for useful discussions. Also, the author expresses his gratitude to the Referees for their insightful and constructive comments on this study. We acknowledge support by the German Research Foundation and the Open Access Publication Fund of TU Berlin.
References
Aleksandrov, V. M., and Kovalenko, E. V. (1980). Plane Contact Problems of the Theory of Elasticity for Nonclassical Regions in the Presence of Wear. J. Appl. Mech. Tech. Phys. 21, 421–427.
Aleksandrov, V. M., Galin, L. A., and Piriev, N. P. (1978). A Plane Contact Problem for an Elastic Layer of Considerable Thickness in the Presence of Wear. Mech. Sol. 4, 60–67.
Archard, J. F. (1953). Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 24, 981–988. doi:10.1063/1.1721448
Argatov, I. I., and Chai, Y. S. (2019). Effective Wear Coefficient and Wearing-In Period for a Functionally Graded Wear-Resisting Punch. Acta Mech. 230, 2295–2307. doi:10.1007/s00707-019-2366-9
Argatov, I. I., and Fadin, Y. A. (2011). A Macro-Scale Approximation for the Running-In Period. Tribol Lett. 42, 311–317. doi:10.1007/s11249-011-9775-9
Argatov, I., and Tato, W. (2012). Asymptotic Modeling of Reciprocating Sliding Wear - Comparison with Finite-Element Simulations. Eur. J. Mech. - A/Solids 34, 1–11. doi:10.1016/j.euromechsol.2011.11.008
Argatov, I., and Chai, Y. S. (2020). Contact Geometry Adaptation in Fretting Wear: A Constructive Review. Front. Mech. Eng. 6, 51. doi:10.3389/fmech.2020.00051
Argatov, I. I., and Chai, Y. S. (2020). Wear Contact Problem with Friction: Steady-State Regime and Wearing-In Period. Int. J. Sol. Structures 193-194, 213–221. doi:10.1016/j.ijsolstr.2020.02.019
Argatov, I. I. (2003). Theory of Unsaturated Elastic Contact of Rough Surfaces. J. Friction Wear 24, 22–29.
P. J. Blau (Editor) (1992). ASM Handbook, Volume 18–Friction, Lubrication, and Wear Technology (Russell Township: ASM International).
Blau, P. J. (2005). On the Nature of Running-In. Tribology Int. 38, 1007–1012. doi:10.1016/j.triboint.2005.07.020
Borodich, F. M., and Onishchenko, D. A. (1993). Fractal Roughness in Contact and Friction Problems (The Simplest Models). J. Friction Wear 14, 14.
Borodich, F. M. (1999). Fractals and Fractal Scaling in Fracture Mechanics. Int. J. Fracture 95, 239–259. doi:10.1007/978-94-011-4659-3_13
Chen, W., Zhang, X.-D., and Korošak, D. (2010). Investigation on Fractional and Fractal Derivative Relaxation- Oscillation Models. Int. J. Nonlinear Sci. Numer. Simulation 11, 3–10. doi:10.1515/ijnsns.2010.11.1.3
Ciavarella, M., Papangelo, A., and Barber, J. R. (2020). Effect of Wear on the Evolution of Contact Pressure at a Bimaterial Sliding Interface. Tribology Lett. 68, 1–7. doi:10.1007/s11249-020-1269-1
Dasari, A., Yu, Z.-Z., and Mai, Y.-W. (2009). Fundamental Aspects and Recent Progress on Wear/scratch Damage in Polymer Nanocomposites. Mater. Sci. Eng. R: Rep. 63, 31–80. doi:10.1016/j.mser.2008.10.001
Dundurs, J., and Comninou, M. (1980). Shape of a Worn Slider. Wear 62, 419–424. doi:10.1016/0043-1648(80)90183-0
Galin, L. A. (1976). Contact Problems of the Theory of Elasticity in the Presence of Wear. J. Appl. Maths. Mech. 40, 931–936. doi:10.1016/0021-8928(76)90132-5
Gardos, M. N. (1982). Self-lubricating Composites for Extreme Environment Applications. Tribology Int. 15, 273–283. doi:10.1016/0301-679x(82)90084-6
Garland, A. P., Adstedt, K. M., Casias, Z. J., White, B. C., Mook, W. M., Kaehr, B., et al. (2020). Coulombic Friction in Metamaterials to Dissipate Mechanical Energy. Extreme Mech. Lett. 40, 100847. doi:10.1016/j.eml.2020.100847
Gorenflo, R., and Mainardi, F. (1997). “Fractional Calculus: Integral and Differential Equations of Fractional Order,” in Fractals and Fractional Calculus in Continuum Mechanics. Editors A. Carpinteri, and F. Mainardi (Wien and New York: Springer-Verlag), 223–276. 276. doi:10.1007/978-3-7091-2664-6_5
Gorenflo, R., Kilbas, A. A., Mainardi, F., and Rogosin, S. V. (2014). Mittag-Leffler Functions, Related Topics and Applications. Berlin, Heidelberg: Springer.
Grzelczyk, D., and Awrejcewicz, J. (2015). Wear Processes in a Mechanical Friction Clutch: Theoretical, Numerical, and Experimental Studies. Math. Probl. Eng. 2015, 1–25. doi:10.1155/2015/725685
Hanneken, J. W., Vaught, D. M., and Achar, B. N. N. (2007). “Enumeration of the Real Zeros of the Mittag-Leffler Function Eα(z), 1 < α < 2,” in Advances in Fractional Calculus. Editors J. Sabatier, O. P. Agrawal, and J. A. Tenreiro Machado (Dordrecht: Springer), 15–26. doi:10.1007/978-1-4020-6042-7_2
Khonsari, M. M., Ghatrehsamani, S., and Akbarzadeh, S. (2021). On the Running-In Nature of Metallic Tribo-Components: A Review. Wear 474-475, 203871. doi:10.1016/j.wear.2021.203871
Khrushchov, M. M., and Babichev, M. A. (1941). “Wear Test of Pure Metals and Antifriction Alloys during Friction on an Abrasive Surface [in Russian],” in Friction and Wear in Machines (Moscow–Leningrad: Publishing House of the Academy of Sciences of the USSR), 1, 89–98.
Komogortsev, V. F. (1985). Contact between a Moving Stamp and an Elastic Half-Plane when There Is Wear. J. Appl. Maths. Mech. 49, 243–246. doi:10.1016/0021-8928(85)90110-8
Kovalenko, E. V. (1985). Study of the Axisymmetric Contact Problem of the Wear of a Pair Consisting of an Annular Stamp and a Rough Half-Space. J. Appl. Maths. Mech. 49, 641–647. doi:10.1016/0021-8928(85)90085-1
Li, W., Zhang, L., Chen, X., Wu, C., Cui, Z., and Niu, C. (2020). Fuzzy Modelling of Surface Scratching in Contact Sliding. IOP Conf. Ser. Mater. Sci. Eng. 967, 012022. IOP Publishing. doi:10.1088/1757-899x/967/1/012022
Ling, F. F. (1990). Fractals, Engineering Surfaces and Tribology. Wear 136, 141–156. doi:10.1016/0043-1648(90)90077-n
Liu, Y., Hoon Jang, Y., and Barber, J. R. (2014). Finite Element Implementation of an Eigenfunction Solution for the Contact Pressure Variation Due to Wear. Wear 309, 134–138. doi:10.1016/j.wear.2013.11.004
Mainardi, F. (1996). Fractional Relaxation-Oscillation and Fractional Diffusion-Wave Phenomena. Chaos, Solitons & Fractals 7, 1461–1477. doi:10.1016/0960-0779(95)00125-5
Mainardi, F. (2020). Why the Mittag-Leffler Function Can Be Considered the Queen Function of the Fractional Calculus? Entropy 22, 1359. doi:10.3390/e22121359
Meng, H. C., and Ludema, K. C. (1995). Wear Models and Predictive Equations: Their Form and Content. Wear 181-183, 443–457. doi:10.1016/0043-1648(95)90158-2
Nguyen, V. H., Zheng, D., Schmerwitz, F., and Wriggers, P. (2018). An Advanced Abrasion Model for Tire Wear. Wear 396-397, 75–85. doi:10.1016/j.wear.2017.11.009
Ortigueira, M. D., and Tenreiro Machado, J. A. (2015). What Is a Fractional Derivative? J. Comput. Phys. 293, 4–13. doi:10.1016/j.jcp.2014.07.019
Páczelt, I., and Mróz, Z. (2007). Optimal Shapes of Contact Interfaces Due to Sliding Wear in the Steady Relative Motion. Int. J. Sol. Structures 44, 895–925. doi:10.1016/j.ijsolstr.2006.05.027
Popov, V. L., and Pohrt, R. (2018). Adhesive Wear and Particle Emission: Numerical Approach Based on Asperity-free Formulation of Rabinowicz Criterion. Friction 6, 260–273. doi:10.1007/s40544-018-0236-4
Rhee, S. K. (1970). Wear Equation for Polymers Sliding against Metal Surfaces. Wear 16, 431–445. doi:10.1016/0043-1648(70)90170-5
Sedakova, E. B., and Kozyrev, Y. P. (2021). Estimation of the Tribotechnical Efficiency of Polytetrafluoroethylene Filling. J. Mach. Manuf. Reliab. 50, 236–242. doi:10.3103/s1052618821030146
Sedova, O., and Pronina, Y. (2022). The Thermoelasticity Problem for Pressure Vessels with Protective Coatings, Operating under Conditions of Mechanochemical Corrosion. Int. J. Eng. Sci. 170, 103589. doi:10.1016/j.ijengsci.2021.103589
Sfantos, G. K., and Aliabadi, M. H. (2006). Wear Simulation Using an Incremental Sliding Boundary Element Method. Wear 260, 1119–1128. doi:10.1016/j.wear.2005.07.020
Shillor, M., Sofonea, M., and Telega, J. J. (2004). Models and Analysis of Quasistatic Contact: Variational Methods. Berlin: Springer.
Soldatenkov, I. A. (2010). Wear-contact Problem with Applications to Engineering Calculation of Wear. Moscow: Fizmatkniga. [in Russian].
Su, X., Yao, D., and Xu, W. (2021). Processing of Viscoelastic Data via a Generalized Fractional Model. Int. J. Eng. Sci. 161, 103465. doi:10.1016/j.ijengsci.2021.103465
Viswanath, N., and Bellow, D. G. (1995). Development of an Equation for the Wear of Polymers. Wear 181-183, 42–49. doi:10.1016/0043-1648(94)07055-5
Wright, N. A., and Kukureka, S. N. (2001). Wear Testing and Measurement Techniques for Polymer Composite Gears. Wear 251, 1567–1578. doi:10.1016/s0043-1648(01)00793-1
Yevtushenko, A. A., and Pyr'yev, Y. A. (1999). The Applicability of a Hereditary Model of Wear with an Exponential Kernel in the One-Dimensional Contact Problem Taking Frictional Heat Generation into Account. J. Appl. Maths. Mech. 63, 795–801. doi:10.1016/s0021-8928(99)00100-8
Keywords: severe wear, fractional time derivative, wearing-in, quasi-steady state, wear equation
Citation: Argatov I (2022) A Fractional Time-Derivative Model for Severe Wear: Hypothesis and Implications. Front. Mech. Eng 8:905026. doi: 10.3389/fmech.2022.905026
Received: 26 March 2022; Accepted: 08 April 2022;
Published: 27 April 2022.
Edited by:
Yu Tian, Tsinghua University, ChinaReviewed by:
Emanuel Willert, Technical University of Berlin, GermanyFeodor M Borodich, Cardiff University, United Kingdom
Copyright © 2022 Argatov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ivan Argatov, ivan.argatov@campus.tu-berlin.de
 Ivan Argatov
Ivan Argatov