Atomic Force Microscopy of Polymer Brushes: Insights into Controversies

Atomic force microscopes (AFM) and nanoindenters have been used for decades to evaluate mechanical properties of thin films at the nanoscale. It is argued that the elastic solutions to the indentation problem, which are most often associated with the names of Galin or Sneddon, may be used for extracting elastic contact modulus of bulk samples and continual films, while their application to contact between an AFM probe and a polymer brush is a priori questionable. This is because the character of compression of a polymer brush is drastically different from the response of an elastic half-space to indentation. In the present paper, a number of controversial issues related to the interpretation of the AFM data obtained for polymer brushes tested with a rigid probe are studied. In particular, a correct relation has been established between the constitutive equation for a single polymer brush in compression with a bare rigid surface and the constitutive equation for two identical polymer brushes in compression under the assumption of lack of interpenetration of compressed brushes. It is shown that the so-called apparent elastic modulus of a polymer brush introduced based on the Hertzian force-displacement relation depends on the indenter radius and, thus, may not serve as a characteristic of polymer brush. Also, the Derjaguin’s approximation-based method of identifying the point of initial contact is given in opposition to controversial methods, which are broadly based on the Hertzian contact mechanics.

1 Introduction

In recent years, polymer brushes, i.e., end-grafted polymer layers (Milner, 1991), have found wide use in engineering, including lubrication (Espinosa-Marzal et al., 2013; Yu et al., 2016), antibiofouling (Yang and Zhou, 2017), sensing and wetting control (Ritsema van Eck et al., 2022). The discovery of the so-called stimulus-responsive polymer brushes (Luzinov et al., 2004; Chen et al., 2010), which can exhibit controllable and reversible changes in conformation and structure due to certain external stimuli, has brought great opportunities for a range of applications (Benetti et al., 2009; Orski et al., 2011). In particular, motivated by the development of intelligent nanofibrillar interfaces and inspired by the gecko’s adhesive switching (Gorb, 2008; Zhang et al., 2021), chemically responsive polymer brushes were utilized to alter the interfacial contact with the aim of in situ reversible friction switching (Ma et al., 2015).

The mechanical testing of polymer brushes and other physically adsorbed ultrathin polymer layers can be conveniently assessed using atomic force microscopy (AFM) (Butt et al., 1999; Mendez et al., 2009), though the analysis of the AFM data still poses certain challenges. It is known (Halperin and Zhulina, 2010) that the interpretation of force versus distance curves obtained for polymer brushes via AFM strongly depends on the geometry of the AFM probe. Similar indentation problems for linearly elastic layers has been addressed in a number of publications (Dimitriadis et al., 2002; Yang, 2003; Argatov, 2011), and the marked distinction between the cases of relatively thick (Aleksandrov and Vorovich, 1960; Hayes et al., 1972; Argatov et al., 2013) and thin (Aleksandrov, 1969; Jaffar, 1989; Barber, 1990; Chadwick, 2002; Argatov et al., 2016; Borodich et al., 2019) elastic layers has been formally enshrined based on the ratio ɛ = a/L of the contact radius a and the layer thickness L. In particular, it was first rigorously established by Aleksandrov and Vorovich (1960) that the compression deformation of a thin compressible (with the material Poisson’s ratio not very close to 0.5) elastic layer is asymptotically equivalent to that of a linear Winkler–Fuss elastic foundation, which in part mimics the deformation of polymer brushes, which are composed of individually deforming polymer chains. However, the application of the mentioned above elastic solutions for polymer brushes is limited by the fact that their deformations in compression testing lie outside the linear elastic range.

When realizing the fact that polymer brushes predominantly operate under large compressive deformations, it becomes convenient to make use of spherical indenters of relatively large radius (in comparison with the brush layer thickness), e.g., colloidal probes (Butt et al., 2005), instead of standard pyramidal indenters. In such a way, the interpretation of the AFM force versus distance curves can be based on the approximation developed by Derjaguin (1934), which (in application to polymer brushes) utilizes the so-called planar force law (Halperin and Zhulina, 2010). And though this approach is per se known, there are still some points to clarify about the evaluation of the Derjaguin approximation for indenters of arbitrary shapes.

Further, in recent years, the AFM has emerged as a powerful technique for testing of biointerfaces (Huber et al., 2005; Boyd et al., 2021). In the absence of theoretical predictive expressions (constitutive models) for describing the compressive deformations of biofilms, a simple exponential decaying approximation (Israelachvili, 1992) is widely used to determine the biofilm thickness. However, while the mentioned exponential approximation was introduced for the Alexander–de Gennes (AdG) model (Alexander, 1977; de Gennes, 1987), its relation to other compression constitutive models was not discussed before. It should be made clear that the present study cannot serve as an introduction to the mathematical equations of the AFM indentation procedures, as our focus is on certain ambiguities or controversies still surrounding the interpretation of the AFM data on the indentation of polymer brushes. We refer to the review by Butt et al. (2005) and the references therein for an overview of the AFM technique and basics of its interpretation and applications.

Another controversial aspect regarding the interpretation of the AFM data for polymer brushes concerns the application of the solution developed by Sneddon (1965) for evaluating the so-called equivalent (Tranchida et al., 2011) or apparent (Kutnyanszky and Vancso, 2012) elastic modulus and determining the contact point (Parra et al., 2007; Melzak et al., 2010). Without dwelling on mathematical details, it is only to be noted that the general solution of the elastic contact problem, which is often associated with the name of Sneddon, assumes the elastic half-space approximation for a tested sample (see, e.g., Borodich (2014); Argatov and Mishuris (2018); Popov et al. (2019)), which is in direct contradiction to both the geometry and mechanics of polymer brushes.

1.1 Preliminaries for Non-Mathematically Inclined Researchers

Polymer brushes can be formed by polymer chains with one end bonded to a substrate surface, provided the grafting density is high enough to make the chains aligned in the direction perpendicular to the surface (Milner, 1991). Thus, the polymer layer thickness, L, is the only macro-geometrical parameter of a polymer brush. In many cases, the substrate can be assumed to be absolutely rigid, and it is called a wall.

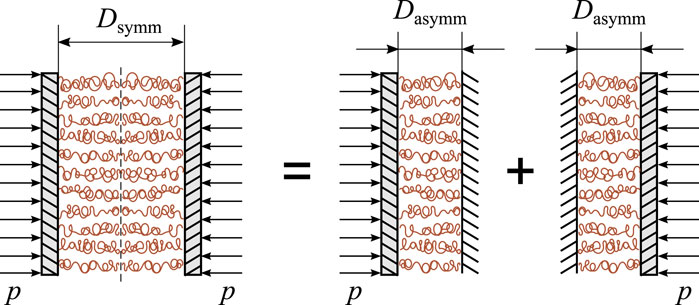
When two polymer brushes are brought in contact under a compressive load, the wall separation distance, D, becomes a primary dimensional variable that controls the level of compressive deformation induced in the polymer layers, whereas the compressive pressure, p, (load per apparent area of contact) is the main loading parameter. The relation between p and D will be called a constitutive equation.

The following exponential approximation (Israelachvili, 1992)) is a popular simple form of the constitutive equation for compression of two identical brushes:

$p=\frac{100}{s^3}{k}_{\text{B}}T\exp \left(-\pi \frac{D}{L}\right).(1)$

Here, k_B is Boltzmann’s constant, T is the temperature, and s is the average distance between grafted polymer chains. It should be noted that while formula (1) was suggested as an approximation for the Alexander–de Gennes (AdG) model (Alexander, 1977; de Gennes, 1987), it still remains unclear whether an exponential-type approximation has a more or less universal character.

When the constitutive equation is experimentally determined from the compression of two identical brushes, the question arises how to derive from it the constitutive equation for a single polymer brush in contact with a bare rigid wall. This question is considered herein under the assumption of non-penetration between the compressed polymer brushes (O’Shea et al., 1993).

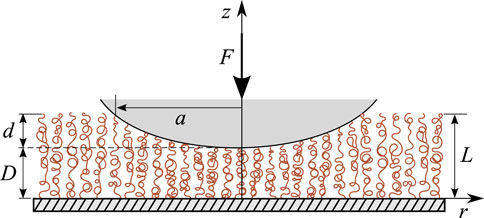
Atomic Force Microscopy (AFM) provides a convenient way of evaluating the deformation response of soft matter to indentation at the nanoscale (Butt et al., 2005). In regard to polymer brushes, the use of a spherical colloidal probe of relatively large diameter (compared to the brush thickness), which is attached to the AFM cantilever, was proposed as a special AFM probe instead of conventional AFM indenter of pyramidal shape. The main difficulty in extracting the constitutive equation for a polymer brush from the AFM data is that the contact pressure, p, exerted by the probe on the upper surface of a polymer brush layer is not uniform and the contact radius, a, is also unknown and should be determined as a part of the solution of the corresponding indentation problem. What is directly measured in the AFM indentation (via bending of the AFM cantilever) is the contact force, F, which is the total compression load, i.e.,

$F=2\pi \underset{0}{\overset{a}{\int }}p\left(r\right)r\mathrm{d}r.(2)$

The equilibrium Eq. 2 applies for an arbitrary axisymmetric indenter that produces an axisymmetric (depending on the polar radius r with respect to the point of initial contact) pattern of the contact pressure distribution over a circular area of contact, whose radius is denoted by a.

In principle, a part of a polymer brush of a given apparent area consists of a finite number of polymer chains, which interact with the surface of an AFM probe in a discrete fashion, and thus, formula (2) employs a continuum approximation for the contact interaction between the AFM probe and a tested polymer brush, which is widely adopted thanks to its simplicity.

On the other hand, the discrete structure of a polymer brush prompts the development of mechanistic models of the Winkler–Fuss type that represent a polymer brush as a set of springs (Villanueva et al., 2014). From a continuum viewpoint, the main underlying assumption of such an approach is that the contact pressure p at a given point inside the contact region is determined only by the local compression, that is by the distance from the AFM probe’s surface to the wall, to which the tested polymer brush is attached. In the literature on indentation of polymer brushes (Halperin and Zhulina, 2010), the corresponding solution to the indentation problem is called the Derjaguin approximation, though originally it was introduced by Derjaguin (1934) for the analysis of attractive forces acting between two surfaces.

Usually, the solution of the indentation problem is thought of as a closed-form relation between the contact force F and the indenter displacement, which will be denoted by d (see below, Figure 5). At the point of initial contact, we have d = 0, and the wall separation distance, D, of the AFM probe’s apex that just touches the upper surface of a tested polymer brush is equal to the brush thickness L in the initial (undeformed) state. In the loaded state, we have the simple relation d = L − D between the indenter (probe) displacement d and the wall separation distance of the indenter D, which is measured at the indenter’s apex.

The specificity of the AFM technique poses a difficulty in detecting the initial contact point, because the indenter displacement d cannot be monitored directly, and the inception of the cantilever deflection due to the resistance to indentation becomes a primary prerequisite for the identification of the point of initial contact. It is of interest to note that there is a collision between the need to know the form of constitutive equation (at least for the range of small deformations) for solving the problem of detecting the initial contact and an a priori lack of such model for a (generally novel) polymer brush under testing. This collision is apparently a reason that the elastic solutions to the indentation problem, which are most often associated with the names of Galin (2008) and Sneddon (1965), as well as the simple force-displacement relation from the Hertzian theory are applied for polymer brushes in direct violation of the underlying assumptions of the Hertzian contact mechanics. It should be also emphasized that exponential approximations like 1) are not applicable for the purpose of the accurate identification of the initial contact point, because formula (1) predicts that the contact pressure remains positive for D = 2L, whereas it should vanish for two brushes in the initial (unloaded) contact.

The rest of the paper is organized as follows. In Section 2, we introduce a general form of the constitutive relation for polymer brushes in compression, which is suggested by the classical Alexander–de Gennes model and the constitutive models of nonlinear elasticity operating with the concept of stretch ratio. The superiority of the introduced approach is illustrated in Section 2.1 on the example of the so-called hybrid mechanistic compression model (Villanueva et al., 2014) by rewriting its equations in a very simple form. The main result of this section is a correct relation between the constitutive equations in the cases of a single polymer brush in compression with a bare rigid surface and two identical polymer brushes in compression under the assumption of lack of interpenetration of compressed brushes. In Section 3, we consider the exponential approximation introduced by Israelachvili (1992) for the AdG model, which can be applied for estimating the brush layer thickness. A controversial issue arises when the exponential approximation is used outside the range of validity of the AdG model. Here we consider two methods of evaluating the parameters of the exponential approximation for an arbitrary constitutive function. In Section 4, we outline Derjaguin’s approximation for the contact force produced by an AFM indenter pressed onto a polymer brush and represent it in terms of the indenter area function. Section 5, Section 6 are devoted to controversies about the identification of the point of initial contact and the apparent elastic modulus by using the methods, which are broadly based on the Hertzian contact mechanics. Finally, in Section 7, we outline a discussion of the presented results and formulate our conclusions.

2 Constitutive Equation

To fix our ideas, we consider the Alexander–de Gennes (AdG) model (Alexander, 1977; de Gennes, 1987) which predicts the following repulsive pressure between two neutral polymer brushes pressed against each other:

$p_{\text{AdG,\hspace{0.17em}symm}}\left(D\right)=\frac{k_{\text{B}}T}{s^3}\left[{\left(\frac{2L}{D}\right)}^{9/4}-{\left(\frac{D}{2L}\right)}^{3/4}\right]\mathrm{f}\mathrm{o}\mathrm{r}D<2L.(3)$

Here, p is the compressive pressure, k_B is Boltzmann’s constant, T is the absolute temperature, L is the equilibrium thickness of a single polymer brush, s is the average distance between adjacent grafting points, and D denotes the wall surface separation (see Figure 1). Observe (O’Shea et al., 1993) that the first term in brackets in Eq. 3 represents the osmotic repulsion due to increasing polymer concentration as the wall surfaces, onto which the polymer brushes are grafted, are pressed together (when the distance D decreases), whereas the second (negative) term accounts for the decrease in elastic energy of the polymer chains as they are compressed.

FIGURE 1

FIGURE 1. Schematic of compression of two polymer brushes.

Equation 3 relates the pressure p the wall separation distance D in the case of compression of two identical polymer brushes (see the left part of Figure 1). It is of genuine interest to derive from Eq. 3 the constitutive relation that describes the compression of a single polymer brush by a flat rigid surface (see the right part of Figure 1). Under the assumption of lack of interpenetration of compressed brushes, Eq. 3 was reduced by O’Shea et al. (1993) to the following equation in the case of contact interaction of one polymer brush with a bare, nonadsorbing rigid surface:

$p_{\text{AdG,\hspace{0.17em}asymm}}\left(D\right)=\frac{k_{\text{B}}T}{2s^3}\left[{\left(\frac{L}{D}\right)}^{9/4}-{\left(\frac{D}{L}\right)}^{3/4}\right]\mathrm{f}\mathrm{o}\mathrm{r}D<L.(4)$

It is to note that, while in Eq. 3 the variable D denotes the distance between the two wall surfaces, onto which two identical polymer brushes are grafted, in Eq. 4 the same variable D denotes the distance between one wall surface and a bare rigid surface. As it is seen from the notation, Eq. 4 is supposed to correspond to the AdG model as well.

As it was formulated by Block and Helm (2008), the constitutive equation for the asymmetric case Eq. 4 is obtained from the constitutive equation for the symmetric case Eq. 3 by replacing 2L by L and dividing the prefactor by 2.

It is our intention to show that the passage from Eq. 3, Eq. 4 is in error. To be more precise, the factor 2 in the denominator of the prefactor in Eq. 4, which is indicated in red color, is erroneous. Indeed, let us start with the asymmetric case and represent the constitutive equation for compression deformation of a single polymer brush in contact with a rigid plane in a general form as

$p=p_{1}f\left(\lambda \right),(5)$

where we have introduced the notation

$\lambda =\frac{D}{L},(6)$

and f(λ) is a dimensionless constitutive function.

Now, let us consider the relation inverse to Eq. 5, that is

$\lambda =f^{-1}\left(\frac{p}{p_1}\right),(7)$

where p is the applied compressive pressure, and f⁻¹ denotes the inverse function of f(λ).

In view of Eq. 6, Eq. 7 can be rewritten in the form

$D_{\text{asymm}}=L{f}^{-1}\left(\frac{p}{p_1}\right),(8)$

which relates the wall separation distance D_asymm to the applied pressure p in the case of a single polymer brush.

Now, let us consider the symmetric case (Figure 1). Under the assumption of non-penetration for the brush/brush contact, the distance between the two walls, D_symm, equals the sum of the two brush thicknesses under compression, which acan be evaluated according to Eq. 8, so that

$D_{\text{symm}}=2D_{\text{asymm}}.(9)$

It is to emphasize that Eq. 9 holds true for two identical brushes in contact.

Thus, from Eq. 8, Eq. 9, it follows that

$D_{\text{symm}}=2L{f}^{-1}\left(\frac{p}{p_1}\right),(10)$

By inverting Eq. 10, we arrive at the relation

$p=p_{1}f\left(\frac{D_{\text{symm}}}{2L}\right),(11)$

or, which is the same, as

$p_{\text{symm}}\left(D\right)=p_{1}f\left(\frac{D}{2L}\right)\mathrm{f}\mathrm{o}\mathrm{r}D<2L.(12)$

At the same time, the constitutive equation in the asymmetric case, in view of Eq. 5, Eq. 6, can be represented as

$p_{\text{asymm}}\left(D\right)=p_{1}f\left(\frac{D}{L}\right)\mathrm{f}\mathrm{o}\mathrm{r}D<L.(13)$

It is to point out that Eq. 12, Eq. 13 possess exactly the same prefactor p₁, and this fact contradicts the rule formulated above for deriving Eq. 4 from Eq. 3.

Observe that from Eq. 6, Eq. 9, we find that

$\lambda =\frac{D_{\text{asymm}}}{L}=\frac{D_{\text{symm}}}{2L}.(14)$

The dimensionless parameter λ has a mechanical meaning of the stretch ratio. In view of the assumption made above that both distances D_asymm and D_symm were evaluated for the same compressive pressure p, Eq. 14 state that the compressive deformation realized in the symmetric and asymmetric cases (for a single brush or two identical brushes) will be the same for the same applied loading.

Thus, the constitutive relation in the form of Eq. 5 applies in both cases, provided the stretch ratio λ is defined as the ratio of the total compression thickness (D_asymm or D_symm) to the total equilibrium thickness (L or 2L) of polymer layer (one brush or two brushes), which is under compression. It is to emphasize that we assume that the self-interaction of polymer chains in each brush would be the same in the cases of one compressed brush and two identical compressed brushes, provided that there is no interpenetration of the polymer brushes as they are brought together.

Remark 2.1. It should be emphasized (Milner, 1991) that strictly speaking the constitutive Eq. 3 should be written in the form $p_{\text{AdG,\hspace{0.17em}symm}}\sim (k_{\text{B}}T/s^3)\left({\lambda }^{-9/4}-{\lambda }^{3/4}\right)$, where a tilde, ∼, denotes the omission of a dimensionless constant of order unity. The same applies to the scaling equations similar to Eq. 18.

2.1 Hybrid Mechanistic Compression Model

As an example of the constitutive equation for compression of polymer brush systems, we consider the so-called hybrid mechanistic compression model developed by Villanueva et al. (2014). Under the assumption that each chain in a polymer brush is identical and contributes independently to its mechanical response to indentation, the total force produced by an indenter will be given by

$F_{\text{tot}}=-\sum _{i=1}^{N_{\text{c}}}{k}_i\mathrm{\Delta }{z}_i,(15)$

where k_i is the stiffness of the ith chain, Δz_i is its indentation, and N_c is the total number of compressed chains.

Let us apply Eq. 15 to the case of uniform compression, when

$\mathrm{\Delta }{z}_i=-\left(L-D\right),(16)$

where L is the equilibrium thickness of the polymer brush, and D is the wall separation distance. It is to emphasize that, according to the adopted rule of signs (Villanueva et al., 2014), the chain indentation Δz_i is taken to be the negative of the change in brush thickness (see Eq. 16).

By the definition, the corresponding contact pressure can be evaluated as

$p=\frac{F_{\text{tot}}}{A_{\text{tot}}},(17)$

where A_tot is the total apparent area of contact.

In many situations, it may be assumed that

$A_{\text{tot}}=N_{\text{c}}{s}^2,(18)$

where s is the average distance between grafted chains, so that the grafting (adsorption) density, N_c/A_tot, equals 1/s².

From Eqs. 15–18, it follows that

$p=\frac{k_i}{s^2}\left(L-D\right),(19)$

where k_i denotes the chain stiffness, which may depend on the level of compression.

According to the model developed by Villanueva et al. (2014), we have

$k_i=\frac{\pi }{4}K\left(2s{\left(\frac{s}{R_{\text{F}}}\right)}^{5/3}-\frac{\mathrm{\Delta }{z}_i}{{\left(\frac{R_{\text{F}}}{s}\right)}^{10/3}+{\left(\frac{R_{\text{F}}}{s}\right)}^{5/3}\frac{\mathrm{\Delta }{z}_i}{s}}\right).(20)$

Here, K is the bulk modulus of the polymer material, R_F = n^3/5l is the Flory radius, l is the length of a single monomer, and n is the number of monomers in the polymer chain.

In the polymer brush regime (s < R_F), the brush thickness can be estimated as L = nl^5/3s^−2/3 (Alexander, 1977), so that

$\frac{R_{\text{F}}}{s}={\left(\frac{L}{s}\right)}^{3/5}.(21)$

Thus, the substitution of (20) into Eq. 19, in view of Eq. 16, Eq. 21, yields the very simple result

$p=\frac{\pi }{4}K\left(\frac{L}{D}-\frac{D}{L}\right).(22)$

Finally, with the notation introduced above for the stretch ratio (see Eq. 6), the constitutive equation of the Villanueva–Huang–Sirbuly (VHS) model 22) can be represented in the form

$p=p_1\left(\frac{1}{\lambda }-\lambda \right),(23)$

where p₁ = (π/4)K is the prefactor.

Thus, the example of the VHS model is clearly indicative of the usefulness of operating with the stretch ratio while formulating the constitutive equation (compare our Eq. 23 with Eqs. 19,20, which are equivalent provided that Eq. 21 holds).

2.2 Examples of Constitutive Equations

In view of (3), the Alexander–de Gennes (AdG) theory (Alexander, 1977; de Gennes, 1987) predicts that

$f_{\text{AdG}}\left(\lambda \right)={\lambda }^{-9/4}-{\lambda }^{3/4}.(24)$

Further, in the framework of the Milner–Witten–Cates (MWC) theory (Milner et al., 1988), which accounts for a paraboloidal density profile of polymer chain units, we have

$f_{\text{MWC}}\left(\lambda \right)={\lambda }^{-2}-2\lambda +{\lambda }^4={\left({\lambda }^{-1}-{\lambda }^2\right)}^2.(25)$

In the non-entropic model developed by Drozdov (Drozdov, 2005) for an ensemble of non-interacting chains grafted on a rigid plane, the constitutive function can be written as

$f_{\text{D}}\left(\lambda \right)=\left({\lambda }^{-2}-1\right)-\left(1+\frac{1}{\sqrt{2}}\right)\left({\lambda }^2-1\right).(26)$

Finally, according to Eq. 23, the Villanueva–Huang–Sirbuly (VHS) model implies that

$f_{\text{VHS}}\left(\lambda \right)=\frac{1}{\lambda }-\lambda .(27)$

Figure 2 shows the relative constitutive curves for the models outlined above. We would like to emphasize that the normalizations of the functions f_AdG(λ), f_MWC(λ), f_D(λ), and f_VHS(λ) are arbitrary.

FIGURE 2

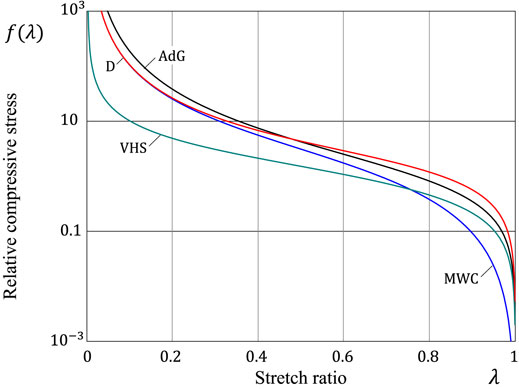
FIGURE 2. Examples of constitutive equations: AdG (Alexander, 1977; de Gennes, 1987) — Eq. 24; MWC (Milner et al., 1988) — Eq. 25; D (Drozdov, 2005) — Eq. 26; VHS (Villanueva et al., 2014) — Eq. 27.

Let us observe common features in the constitutive functions (24)–(27). First of all, the compressive pressures are always positive and vanish in the equilibrium (unloaded state), when λ = 1, so that we have

$f\left(\lambda \right)>0,\lambda \in \left(\mathrm{0,1}\right),(28)$

and

$f\left(1\right)=0.(29)$

Second, all constitutive Eq. 24–27 show that

$f^{\prime }\left(\lambda \right)<0,\lambda \in \left(\mathrm{0,1}\right).(30)$

In other words, the compression response of a polymer brush is monotonic.

However, we have f′(1) = 0 for the MWC model, which predicts much softer response of a polymer brush at small levels of compression than other models considered above.

3 Exponential Approximation

Let us return to the symmetric AdG model (3). It was observed (Israelachvili, 1992; Butt et al., 1999) that for D/2L in the range 0.2–0.9, the functional dependence p_{AdG, symm}(D) is roughly exponential, that is

$p_{\text{AdG,\hspace{0.17em}symm}}\left(D\right)\approx \frac{100}{s^3}{k}_{\text{B}}T\exp \left(-2\pi \frac{D}{2L}\right).(31)$

In the general case, when the constitutive relation is given by Eq. 5, it makes sense to consider the analogous approximation

$\frac{p}{p_1}\approx \mathrm{\Lambda }\exp \left(-b\lambda \right),(32)$

where Λ and b are constant parameters determined by fitting the approximation Eq. 32 to the function f(λ) in some interval λ ∈ (λ₁, λ₂), where 0 < λ₁ < λ₂ < 1.

By using a least square optimization approach, we arrive at the problem

$\underset{{\lambda }_1}{\overset{{\lambda }_2}{\int }}{\left[\ln \left(f\left(\lambda \right)\right)-\ln \mathrm{\Lambda }+b\lambda \right]}^2\mathrm{d}\lambda \to \min ,$

from where it follows that

$b=\frac{6\left({\lambda }_2+{\lambda }_1\right)}{{\left({\lambda }_2-{\lambda }_1\right)}^2}\left(F_1-\frac{2F_2}{{\lambda }_2+{\lambda }_1}\right),(33)$

$\ln \mathrm{\Lambda }=\frac{4\left({\lambda }_2^2+{\lambda }_2{\lambda }_1+{\lambda }_1^2\right)}{{\left({\lambda }_2-{\lambda }_1\right)}^2}{F}_1-\frac{6\left({\lambda }_2+{\lambda }_1\right)}{{\left({\lambda }_2-{\lambda }_1\right)}^2}{F}_2,(34)$

where we have introduced the notation

$F_1=\frac{1}{{\lambda }_2-{\lambda }_1}\underset{{\lambda }_1}{\overset{{\lambda }_2}{\int }}\ln \left(f\left(\lambda \right)\right)\mathrm{d}\lambda ,F_2=\frac{1}{{\lambda }_2-{\lambda }_1}\underset{{\lambda }_1}{\overset{{\lambda }_2}{\int }}\ln \left(f\left(\lambda \right)\right)\lambda \mathrm{d}\lambda .(35)$

Another approach for evaluating the parameters of the exponential approximation Eq. 32 can be based on the approximation

$\frac{1}{f\left(\lambda \right)}\frac{\mathrm{d}f}{\mathrm{d}\lambda }\left(\lambda \right)\approx -b,(36)$

which follows from the approximate relation (32).

Thus, in view of (36), the parameter b can be evaluated as

$b=-\frac{f^{\prime }\left({\lambda }_{\ast }\right)}{f\left({\lambda }_{\ast }\right)},(37)$

where f′(λ) is the derivative of the function f(λ), and λ_* is some middle point inside the interval (λ₁, λ₂). We note that, in light of Eq. 28, Eq. 30, the right hand side of Eq. 37 is positive.

Moreover, we put

$\mathrm{\Lambda }=f\left({\lambda }_{\ast }\right)\exp \left(b{\lambda }_{\ast }\right),(38)$

where b is given by formula (37).

Figure 3 illustrates how the right-hand side of Eq. 37 varies for the constitutive models Eqs. 24–27. It is of interest to observe that each of the curves shows the existence of a local minimum, with which the point λ = λ_* can be associated. We note that the horizontal dashed line corresponds to the exponential approximation Eq. 31. From Figure 3, it is readily seen that the dimensionless parameter b in the general exponential approximation Eq. 32 varies in a rather wide range (roughly speaking, between π and 2π). It is clear that the value of the ratio f′(λ)/f(λ) is independent of the normalization of the function f(λ).

FIGURE 3

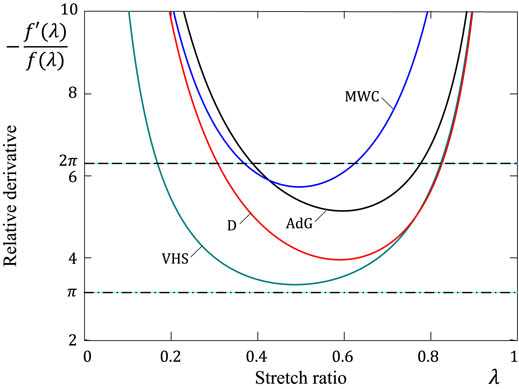
FIGURE 3. Variation of the right-hand side of Eq. 37 for the constitutive models presented in Figure 2.

Figure 4 illustrates the application of the formulas presented above for the Alexander–de Gennes model. We note that Line 3 is a tangent line at the point of concave/convex deflection. The small difference between Lines 1 and 2 is explained by two factors: rounding errors in formula (31) and the fact that it was obtained by direct fitting the AdG curve, whereas Line 2 fits the semilog plot of the AdG curve.

FIGURE 4

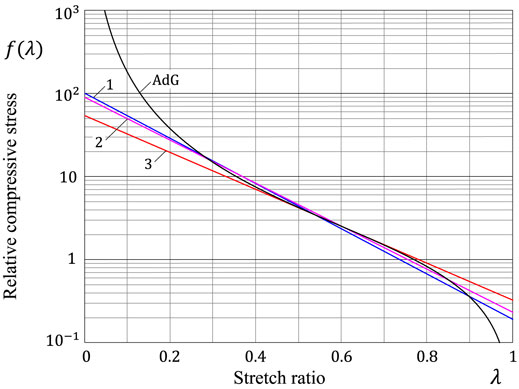
FIGURE 4. The AdG constitutive function and its exponential approximates: Line 1 represents formula (31), Lines 2 and 3 are obtained using Eqs. 33, 34 and Eqs. 37, 38, respectively.

Remark 3.1. We recall that the engineering normal strain, ɛ, is defined as the ratio (D − L)/L, so that λ = 1 + ɛ. Therefore, the range of small engineering deformations corresponds to the values of the stretch ratio close to 1. The constitutive relation for small deformations reckons on Taylor’s series of the function f(1 + ɛ) for small values of the variable ɛ. In view of Eq. 29, this expansion starts with the term f′(1)ɛ. At the same time, the value of f′1) depends on the normalization of the function f(λ) via the choice of the prefactor p₁ in Eq. 5. That is why to compare the model predictions in the range of small deformations, we consider the quantity f′(1)/f(0.5), which is independent of the normalization adopted for the constitutive function via the choice of the prefactor p₁ in Eq. 5. That. It can be easily verified that the following relations hold (up to three digits after the decimal point):

$\frac{f_{\text{AdG}}^{\prime }\left(1\right)}{f_{\text{AdG}}\left(0.5\right)}=-0.721,\frac{f_{\text{VHS}}^{\prime }\left(1\right)}{f_{\text{VHS}}\left(0.5\right)}=-1.333,\frac{f_{\text{D}}^{\prime }\left(1\right)}{f_{\text{D}}\left(0.5\right)}=-1.256.$

It is also to note that p > 0, λ < 1, and ɛ < 0 in compression, while p < 0, λ > 1, and ɛ > 0 in stretching. Hence, the MWC model is not applicable for describing the deformation of a polymer brush under stretching in adhesive contact with a bare, adsorbing rigid surface.

4 Derjaguin’s Approximation

In this section, we are looking at the problem of evaluating the contact force that is produced by inserting an AFM probe into a polymer brush. To simplify our discussion, we first, following Butt et al. (1999), take advantage of the exponential approximation Eq. 32 that formally extends the constitutive relation to the entire interval λ ∈ (0, + ∞).

Moreover, we consider the special case of a paraboloidal indenter, when the indenter surface equation in cylindrical coordinates (Figure 5) can be represented as

$z=D+\frac{r^2}{2R},(39)$

where r is the polar radius, z is the normal coordinate, D is the wall separation distance of the indenter apex. We note that the paraboloidal approximation (39) is widely used in the Hertzian contact mechanics for describing spherical surfaces in local contact (Johnson, 1987), while being applicable for the indentation depths much smaller than the contact radius.

FIGURE 5

FIGURE 5. Schematic of indentation of a polymer brush.

By accounting for the rotational symmetry, the total contact force, F, can be evaluated from the contact pressure p as follows (Butt et al., 1999):

$F\approx 2\pi \underset{0}{\overset{\infty }{\int }}pr\mathrm{d}r=2\pi \underset{D}{\overset{\infty }{\int }}pr\frac{\mathrm{d}r}{\mathrm{d}z}\mathrm{d}z.(40)$

According to Eq. 39, we obtain R dz = r dr, whereas, in view of (32), we have p ≈ p₁Λ exp(−bz/L), where L is the brush thickness. In such a case, formula (40) implies that

$F\approx 2\pi p_{1}RL\frac{\mathrm{\Lambda }}{b}\exp \left(-b\frac{D}{L}\right).(41)$

Formula (41) represents (in a general form) the corresponding result first derived by Butt et al. (1999) for the special exponential approximation (31). When the exponential approximation (32) is used, the upper limit of the integration in the above formula can be extended to infinity, and, therefore, formula (40) overestimates the contact force.

Observe that by getting rid of the exponential approximation, the second relation (40) can be rewritten in the form

$F=\underset{D}{\overset{L}{\int }}p\left(z\right)A^{\prime }\left(z\right)\mathrm{d}z,(42)$

where A′(z) is the derivative of the cross-sectional area A = πr². We note that the Derjaguin approximation in a form similar to (42) was presented by Halperin and Zhulina (2010). It can be shown that in applications to polymer brushes, the Derjaguin approximation (42) holds also for non-axisymmetric indenters.

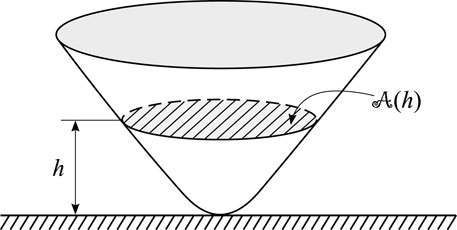
In nanoindentation, the shape of real pyramidal indenters is characterized by the indenter area function, $\mathcal{A}(h)$, where h is the distance from the indenter apex measured inside the indenter along its axis (Figure 6). In other words, by setting h = z − D, the following relation will take place:

$A\left(z\right)=\mathcal{A}\left(z-D\right).(43)$

FIGURE 6

FIGURE 6. Definition of the indenter area function.

Thus, in view of (43), we transform formula (42) as follows:

$F=\underset{D}{\overset{L}{\int }}p\left(z\right){\mathcal{A}}^{\prime }\left(z-D\right)\mathrm{d}z.(44)$

Here, ${\mathcal{A}}^{\prime }(h)$ is the derivative of the function $\mathcal{A}(h)$.

Apparently, the Derjaguin approximation in the form (44) represents a new result.

We note that for a paraboloidal indenter, $\mathcal{A}(h)=2\pi Rh$ and ${\mathcal{A}}^{\prime }(h)\equiv 2\pi R$, so that formula (44) reduces to the solutions previously presented elsewhere (Taunton et al., 1990).

4.1 Derjaguin’s Approximation for a Monomial Indenter

Following Galin (1946) and Borodich (2014), we consider an axisymmetric indenter whose surface in the displaced (loaded) state is given by

$z=D+B{r}^{\beta }.(45)$

We note that for β = 2 and B = 1/(2R), Eq. 45 reduces to Eq. 39, which corresponds to a paraboloidal indenter.

For a monomial indenter, the indenter area function is given by

$\mathcal{A}\left(h\right)=\pi {\left(\frac{h}{B}\right)}^{2/\beta },(46)$

so that

${\mathcal{A}}^{\prime }\left(h\right)=\frac{2\pi }{\beta B}{\left(\frac{h}{B}\right)}^{\left(2-\beta \right)/\beta }.(47)$

In view of Eqs. 5, 44, 47, the Derjaguin approximation for a monomial indenter takes the form

$F=\frac{2\pi p_1}{\beta }{\left(\frac{L}{B}\right)}^{2/\beta }\underset{D/L}{\overset{1}{\int }}f\left(\lambda \right){\left(\lambda -\frac{D}{L}\right)}^{\left(2-\beta \right)/\beta }\mathrm{d}\lambda .(48)$

It is to note that the indenter shape parameter B has the following physical dimension: [B] = L^1−β, where L denotes the dimension of length, and thus, the dimension of (L/B)^2/β does not depend on the value of the parameter β and coincides with the dimension of area.

5 Identification of the Contact Point

The AFM measurements are used to identify the constitutive relation (5) from the AFM indentation data (Butt et al., 2005), based on the assumed force-distance curve (44). However, the problem is that the wall separation distance D, that is the distance between the AFM tip (or, more precisely, the apex point of the indenter contact surface) and the rigid base (wall), to which the tested polymer brush is attached, cannot be directly measured in nanoindentation testing.

To proceed, we introduce the indentation depth (see Figure 5)

$d=L-D.(49)$

We note that in many cases the brush thickness L may not be known in advance and must be evaluated from the force-displacement curve.

Let ${\mathcal{Z}}_{\text{p}}$ and ${\mathcal{Z}}_{\text{c}}$ denote the hight position of the piezoelectric translator and the deflection of the cantilever to which the AFM probe is attached. The cantilever deflection is assumed to be positive for the compressive contact force, so that

$F=k_{\text{c}}{\mathcal{Z}}_{\text{c}},(50)$

where k_c is the cantilever stiffness.

Following Butt et al. (2005), we count ${\mathcal{Z}}_{\text{p}}$ positive if it is retracted away from the tested sample and introduce the distance, $\mathcal{D}$, as the sum of the cantilever deflection ${\mathcal{Z}}_{\text{c}}$ and the piezo position ${\mathcal{Z}}_{\text{p}}$, that is

$\mathcal{D}={\mathcal{Z}}_{\text{p}}+{\mathcal{Z}}_{\text{c}}.(51)$

In the absence of surface (attractive) forces, the force-distance curve (F vs. $\mathcal{D}$) is divided into the following two parts. In the non-contact part of the force-distance curve, F = 0 and, therefore, in view of (50), we have ${\mathcal{Z}}_{\text{c}}=0$ and $\mathcal{D}={\mathcal{Z}}_{\text{p}}$. In the contact part, when the AFM probe indents the tested sample, the following relation holds (Butt et al., 2005):

$\mathcal{D}-{\mathcal{D}}_0=-d,(52)$

where ${\mathcal{D}}_0$ denotes the contact point.

Thus, in the non-contact part we have

$F=0\mathrm{f}\mathrm{o}\mathrm{r}\mathcal{D}\ge {\mathcal{D}}_0.(53)$

In the contact part, in view of Eqs. 44, 49, 52, we obtain

$F=\underset{L+\mathcal{D}-{\mathcal{D}}_0}{\overset{L}{\int }}p\left(z\right){\mathcal{A}}^{\prime }\left(z-L-\mathcal{D}+{\mathcal{D}}_0\right)\mathrm{d}z\mathrm{f}\mathrm{o}\mathrm{r}\mathcal{D}\le {\mathcal{D}}_0.(54)$

Now, let $\mathcal{F}(d)$ denote the force-indentation curve (F vs. d) for a given pair (polymer brush/AFM tip). In view of Eqs. 44, 49, we have

$\mathcal{F}\left(d\right)=\underset{L-d}{\overset{L}{\int }}p\left(z\right){\mathcal{A}}^{\prime }\left(z-L+d\right)\mathrm{d}z.(55)$

Then, using the notation introduced above, the force-distance curve (F vs. $\mathcal{D}$), which is given by Eqs. 53, 54, can be represented as follows:

$F=\left\{\begin{array}{c}0,\mathcal{D}\ge {\mathcal{D}}_0,\hfill \\ \mathcal{F}\left({\mathcal{D}}_0-\mathcal{D}\right),\mathcal{D}\le {\mathcal{D}}_0.\hfill \end{array}\right.(56)$

Thus, the fitting of the experimental force-distance curve (F vs. $\mathcal{D}$) with formulas (55) and 56, using the appropriate constitutive relation for the tested polymer brush, provides not only the parameters of the constitutive model but also the contact point ${\mathcal{D}}_0$.

5.1 Force-Indentation Law for a Monomial Indenter

The problem of identification of the contact point requires the knowledge of the function $\mathcal{F}(d)$ for relatively small indentations (to be more precise, for small values of the ratio d/L or, which is the same, for values of the stretch ratio λ close to unit). That is why, it is of practical interest to derive from Eq. 55 the corresponding approximate relation. With this aim, we consider the Taylor expansion

$f\left(\lambda \right)=f\left(1\right)+f^{\prime }\left(1\right)\left(\lambda -1\right)+\frac{f^{\prime \prime }\left(1\right)}{2!}{\left(\lambda -1\right)}^2+\cdots$

In view of Eqs. 29, 30, we put

$f\left(\lambda \right)\simeq f_1{\left(1-\lambda \right)}^{\nu },\lambda \nearrow 1,(57)$

where f₁ and ν are constant parameters, and λ approaches 1 from the left.

As it was shown in Section 2.2, we have ν = 2 for the MWC model and ν = 1 for the other constitutive models considered above, including the AdG model. So, in what follows, we may assume that 1 ≤ ν ≤ 2.

Let us also introduce the compressive engineering strain as

$\epsilon =\frac{d}{L}.(58)$

Now, by taking into account Eqs. 49, 58, it can be verified that the substitution of (57) into Eq. 48 yields.

$F=\frac{2\pi }{\beta }{\left(\frac{L}{B}\right)}^{2/\beta }{p}_1{f}_1\underset{0}{\overset{\epsilon }{\int }}{\xi }^{\nu }{\left(\epsilon -\xi \right)}^{\left(2-\beta \right)/\beta }\mathrm{d}\xi ,$

so that

$F\simeq F_1{\left(\frac{d}{L}\right)}^{\alpha },(59)$

where we have introduced the notation

$\alpha =1+\nu +\frac{2-\beta }{\beta },(60)$

$F_1=\frac{2\pi }{\beta }{\left(\frac{L}{B}\right)}^{2/\beta }{p}_1{f}_1\mathrm{B}\left(1+\nu ,\frac{2}{\beta }\right),(61)$

and B(x, y) is the beta function.

We note that, in view of (61), the prefactor in Eq. 59 scales as F₁ ∼ p₁L² with a dimensionless proportionality constant depending on both the indenter shape and the constitutive law.

Observe that Eq. 59 is the force-displacement relation of the power-law type, which in the mechanics of elastic contact is encountered for indenters of self-similar form (Borodich, 1993).

It is well known (Johnson, 1987) that the case α = 3/2 corresponds to the Hertzian force-displacement relation for a paraboloidal indenter, when β = 2. It is to note that Eq. 59 with α = 3/2 is sometimes (predominantly in applied experimental studies) referred to as the Sneddon equation (Tranchida et al., 2006). Figure 7 shows the results of fitting the experimental data obtained by Tranchida et al. (2011) using a spherical AFM tip. It is readily seen that Eq. 59 with α = 2, which corresponds to the combination β = 2 (paraboloidal indenter) and ν = 1 (e.g., AdG model), provides a better fit than the Hertzian equation (α = 3/2). Furthermore, it is readily imaginable that if the value of ν is allowed to be varied in the closed interval [1, 2], the quality of the fit of the red solid curve in Figure 7 can be substantially improved.

FIGURE 7

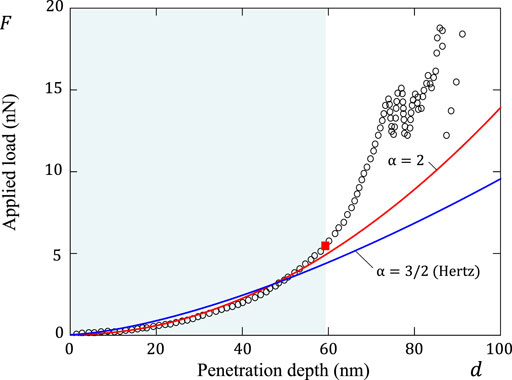
FIGURE 7. Fitting the AFM indentation data (Tranchida et al., 2011) for poly(diethylene glycol methylether methacrylate) (PDEGMA) brush (dry thickness 40 nm) acquired in buffer: Solid blue line, α =3/2, and solid red line, α =2. A red square symbol indicates the end of the fitting range.

It should be noted that a three times smaller fitting range was used by Tranchida et al. (2011). However, it is clear that the larger the fitting range, the more robust is fitting itself, and therefore, the more effective will be the determination of of the contact point.

Observe that, when the indenter shape exponent β varies from 1 to infinity, the indenter shape changes from the conical shape to that of a flat-ended cylindrical indenter (see, e.g., Argatov and Mishuris (2018)). At the same time, the exponent parameter α in Eq. 59 decreases from 2 + ν to ν, and therefore, α varies in the range from 1 to 4, provided ν ∈ [1, 2].

Thus, depending on the compression constitutive model for a tested sample, the force-indentation Eq. 59, in view of (58), represents a power law of the form F = F₁ɛ^α with an exponent α ranging from 1 to 4, depending on the indenter shape. In particular, as it was shown by Borodich et al. (2003), the shape of real pyramidal indenters used for nanoindentation (that is the local shape near the indenter apex at the nanoscale) can be approximated by a monomial indenter with β = 1.7532, so that we will have α = 2.141 for the AdG model and α = 3.141 for the MWC model. It is important to note that the tip bluntness depends on its working position (Baqain et al., 2022).

5.2 Data Analysis of Force-Indentation Curves

When assuming the power law 59) for the initial response of a polymer brush to indentation, the indentation-force relation, which is inverse to Eq. 59, can be represented as

$d=L{\left(\frac{F}{F_1}\right)}^{1/\alpha }.(62)$

In view of Eqs. 51, 52, we have

${\mathcal{D}}_0-{\mathcal{Z}}_{\text{p}}={\mathcal{Z}}_{\text{c}}+d,(63)$

where ${\mathcal{Z}}_{\text{p}}$ and ${\mathcal{Z}}_{\text{c}}$ are directly measured during AFM indentation testing.

Thus, from Eqs. 50, 62, 63, it follows that

${\mathcal{D}}_0-{\mathcal{Z}}_{\text{p}}={\mathcal{Z}}_{\text{c}}+L{\left(\frac{k_{\text{c}}}{F_1}\right)}^{1/\alpha }{\mathcal{Z}}_{\text{c}}^{1/\alpha }.(64)$

It is to note that the zero cantilever deflection (in the absence of the contact load) is assumed to be zero, so that the contact force F equals zero for ${\mathcal{Z}}_{\text{c}}=0$.

Up to notation and choice of positive direction for the hight position of the piezoelectric translator, Eq. 64 coincides with the resulting equation derived by Parra et al. (2007) for the relation between the cantilever deflection and the sample relative distance.

6 Apparent Elastic Modulus

When applying a power law like (59), that is

$F\sim d^{\alpha },(65)$

for polymer brushes, one can argue that it may not matter where it comes from, if this power law approximation fits AFM data, at least for a certain level of initial indentation. However, such argumentation is not so innocent, when it concerns determining the so-called apparent (or equivalent) elastic modulus of a polymer brush (Tranchida et al., 2011; Kutnyanszky and Vancso, 2012).

Let us first recall the Hertzian force-displacement relation

$F=\frac{4E}{3\left(1-{\nu }^2\right)}\sqrt{R}{d}^{3/2},(66)$

where E and ν are Young’s modulus and Poisson’s ratio of a tested bulk elastic material, R is the radius of spherical indenter. To be more precise, Eq. 66 follows from the axisymmetric theory of local contact between three-dimensional elastic solids developed by Hertz (1882), if one of the contacting solids is assumed to be absolutely rigid (it is called indenter) and another one is assumed to be modeled as an elastic half-space (without any characteristic size).

It was first established by Love (1939) that the force-displacement relation for a conical indenter pressed against an elastic half-space has the power-law form (65) with α = 2. We note that for a conical indenter, the area function is given by $\mathcal{A}(h)=\pi h^2{\tan }^2\mathrm{\Theta }$, where Θ is the half-apex angle of the cone. As it follows from the solution derived by Love (1939), the dependence of the contact force F on the elastic constants in the case of a conical indenter is the same as that in the Hertzian Eq. 66.

In the spacial case of a monomial indenter, when the indenter area function has the form of Eq. 46 with β = 2n, and n is a natural number, the solution to the contact problem was published by Shtaerman (1939). In the general case of a monomial indenter (when β is a real number not less than unit), the solution was obtained by Galin (1946), from where it follows that

$F\sim \frac{E}{\left(1-{\nu }^2\right)}{B}^{-1/\beta }{d}^{\left(\beta +1\right)/\beta },(67)$

where B and β are parameters of the indenter area function (46).

Now, returning to the question of determining the so-called apparent elastic modulus of a polymer brush (Tranchida et al., 2011; Kutnyanszky and Vancso, 2012) using a spherical (strictly speaking, paraboloidal) indenter and the Hertzian formula (66), that is

$E_{\text{apparent}}\sim \frac{F}{\sqrt{R}{d}^{3/2}},(68)$

we would like to emphasize that this approach is erroneous not only owing to the fact that a linear elasticity theory-based model is not appropriate for polymer brushes. The main problem with this approach is that it leads to erroneous results, because the apparent modulus E_apparent obtained in this way will depend on the indenter radius.

However, similar to the concept of elastic modulus, as a characteristic of material, the apparent elastic modulus should serve as a characteristic of polymer brush itself. This means that the apparent modulus may depend on the brush thickness but should be independent of the indenter radius, otherwise it does not make any sense to introduce such a quantity for comparative studies.

On the other hand, as it is seen from our model (see Eqs. 59–61, which is specified for a paraboloidal indenter (β = 2 and B = 1/(2R)), we have that

$F\sim RL{p}_1{\left(\frac{d}{L}\right)}^{1+\nu }.(69)$

By comparing formula (69) with (66), we conclude that even in the hypothetical case ν = 1/2, when the right-hand side of (69) formally depends on the indentation depth as d^3/2, formula (68) introduces a quantity which strongly depends on the indenter radius, and therefore, the apparent elastic modulus E_apparent introduced based on the Hertzian model (using formula (68) and the method of least-squares fitting to the initial curve of the force-indentation curve) may not serve as a reliable characteristic of a polymer brush, to say nothing of the evident fact that formula (68) does not take any account of the brush thickness.

7 Discussion and Conclusions

As it is shown above, the interpretation of the AFM data requires specifying the AFM tip geometry at the nanoscale, because the brush layer thickness is often limited to several tens of nanometers (Tranchida et al., 2011). Since in the regime of Derjaguin’s approximation, polymer brushes resist to compression like the Winkler–Fuss non-linear elastic layer, the indenter area function is shown to be ideally suitable for characterizing the tip geometry.

Also, we advocate for using the notion of the stretch ratio, λ, to characterize compressive deformation of a polymer brush. In this way, the constitutive equation for compression of two identical brushes, p_symm = p₁f(λ), under the condition of non-penetration is naturally related to the constitutive equation for compression of one brush, p_asymm = p₁f(λ), provided the stretch ratio is defined by the formulas λ = D/2L (for two brushes) and λ = D/L (for one brush), respectively. It should be emphasized that the prefactor p₁ is the same in both cases, otherwise, it would contradict Newton’s third law.

It is shown that the general exponential approximation (32) can be introduced for any constitutive model, satisfying the necessary conditions (28)–(30), which are fulfilled by each of the models considered above. Because the dimensionless parameter b is found to vary between π and 2π for these models, it can be expected that, generally speaking, the application of the specific exponential approximation (31) provides a rather coarse estimate for the brush thickness, unless the constitutive AdG model is known to be accurate the tested brush.

Moreover, we have shown that the initial response of a polymer brush to indentation is well approximated by a power law (59) with the exponent parameter α ranging from 1 to 4 depending on both the constitutive model and the indenter geometry. This fact explains why the application of Galin’s solution (67), which predicts a power-law-like force-displacement relation, may not fail in the identification of the contact point. However, the application of the Galin–Sneddon general solution, which by its very nature is based on the Hertzian contact mechanics, for evaluating an elastic modulus of a polymer brush is not justified at all.

It was shown that the introduction of the apparent elastic modulus of a polymer brush based on the Hertzian formula (68) does not withstand scrutiny. However, the question still remains: how to characterize polymer brushes with a single dimensional parameter? When the constitutive equation for a polymer brush is presented in the form (5) (with a dimensionless function f(λ) of a dimensionless argument λ), it becomes clear that the prefactor p₁ is the only dimensional parameter (with the dimension of Young’s modulus), whose value, however, depends on the normalization of the function f(λ). In particular, one can fix that f(0.5) = 1. Then, the compression pressure measured for the wall separation distance equal to the half of the thickness of the polymer brush layer (i.e., D = L/2 so that D/L = 0.5) will exactly produce the value of p₁. However, this approach may be inconvenient when the brush layer thickness is not known in advance.

Further, by analogy with (68) but using formula (69), the characteristic elastic modulus can be introduced as

$E_{\text{charact}}\sim \frac{F}{RL}{\left(\frac{L}{d}\right)}^{\alpha },(70)$

where the exponent α is determined by fitting the power-law approximation (69) to the AFM indentation data in a certain initial range of indentation depths. Nevertheless, an effective application of formula (70) also requires knowledge of the polymer brush thickness L.

Yet another way to characterize the deformation properties of polymer brushes under normal compression can be based on the application of the exponential approximation (32) for fitting the experimental data. As it was shown above, the parameter b does not depend on the normalization of the constitutive function f(λ) (see, e.g., relation (36)). Hence, formula (32) can be rewritten in the form

$p=100E_{\text{charact}}\exp \left(-b\lambda \right),(71)$

where the exponential prefactor has units of pressure. It is to note that the value of the characteristic elastic modulus E_charact introduced in such a way will somewhat depend on the method of fitting the exponential approximation (71) to the experimental data (see the discussion at the end of Section 3), and therefore, the fitting method should be clearly specified. At the same time, the value the polymer brush thickness is not required, when applying formula (71) for introducing the characteristic elastic modulus.

To conclude, the Derjaguin approximation assumes that a polymer brush resists to compressive deformation produced by an AFM probe as the Winkler–Fuss non-linear elastic layer (each end-grafted polymer chain contributes independently to the total mechanical response). As such, neither the Hertzian contact mechanics nor Sneddon’s theoretical framework, which are based on the approximation of a tested sample by a linearly elastic half-space, can serve as appropriate mathematical models for correct interpreting the AFM-based testing of polymer brushes.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

IA and FMB. worked on theory derivation and drafted the manuscript. XJ contributed to the discussion and interpretation of the results. FMB and XJ edited the paper. All authors discussed the results, reviewed the manuscript, and approved the final version.

Funding

This work is supported by the National Science Foundation of China (Grant Nos: 11932004 and 51875059). XJ would like to acknowledge the support from Chongqing City Science and Technology Program (Grant No: cstc2020jcyj-msxmX0850). IA is grateful to the financial support from the Ba-Yu Scholar program of Chongqing City (China). We acknowledge support by the German Research Foundation and the Open Access Publication Fund of TU Berlin.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aleksandrov, V. M. (1969). Asymptotic Solution of the Contact Problem for a Thin Elastic Layer. J. Appl. Math. Mech. 33, 49–63. doi:10.1016/0021-8928(69)90113-0

CrossRef Full Text | Google Scholar

Aleksandrov, V. M., and Vorovich, I. I. (1960). The action of a die on an elastic layer of finite thickness. J. Appl. Math. Mech. 24, 462–476. doi:10.1016/0021-8928(60)90049-6

CrossRef Full Text | Google Scholar

Alexander, S. (1977). Adsorption of Chain Molecules with a Polar Head a Scaling Description. J. Phys. Fr. 38, 983–987. doi:10.1051/jphys:01977003808098300

CrossRef Full Text | Google Scholar

Argatov, I., Daniels, A. U., Mishuris, G., Ronken, S., and Wirz, D. (2013). Accounting for the Thickness Effect in Dynamic Spherical Indentation of a Viscoelastic Layer: Application to Non-destructive Testing of Articular Cartilage. Eur. J. Mech. - A/Solids 37, 304–317. doi:10.1016/j.euromechsol.2012.07.004

CrossRef Full Text | Google Scholar

Argatov, I. I. (2011). Depth-sensing Indentation of a Transversely Isotropic Elastic Layer: Second-Order Asymptotic Models for Canonical Indenters. Int. J. Solids Struct. 48, 3444–3452. doi:10.1016/j.ijsolstr.2011.08.011

CrossRef Full Text | Google Scholar

Argatov, I. I., Mishuris, G. S., and Popov, V. L. (2016). Asymptotic Modelling of the JKR Adhesion Contact for a Thin Elastic Layer. Q. J. Mech. Appl. Math. 69, 161–179. doi:10.1093/qjmam/hbw002

CrossRef Full Text | Google Scholar

Argatov, I., and Mishuris, G. (2018). Indentation Testing of Biological Materials. Cham: Springer.

Google Scholar

Baqain, S., Borodich, F. M., and Brousseau, E. (2022). “Characterisation of an AFM Tip Bluntness Using Indentation of Soft Materials,” in Contact Problems for Soft, Biological and Bioinspired Materials. Editors F. M. Borodich, and X. Jin (Switzerland: Springer Nature), Vol. 15, 221–242. doi:10.1007/978-3-030-85175-0_11

CrossRef Full Text | Google Scholar

Barber, J. R. (1990). Contact Problems for the Thin Elastic Layer. Int. J. Mech. Sci. 32, 129–132. doi:10.1016/0020-7403(90)90112-v

CrossRef Full Text | Google Scholar

Benetti, E., Navarro, M., Zapotoczny, S., and Vancso, G. J. (2009). “Stimuli-responsive Polymer Brushes,” in Surface Design: Applications in Bioscience and Nanotechnology (Hoboken, NJ, USA: John Wiley & Sons), 125–144. chap. 2.2. doi:10.1002/9783527628599.ch6

CrossRef Full Text | Google Scholar

Block, S., and Helm, C. A. (2008). Conformation of Poly(styrene Sulfonate) Layers Physisorbed from High Salt Solution Studied by Force Measurements on Two Different Length Scales. J. Phys. Chem. B 112, 9318–9327. doi:10.1021/jp8020672

PubMed Abstract | CrossRef Full Text | Google Scholar

Borodich, F. M., Galanov, B. A., Perepelkin, N. V., and Prikazchikov, D. A. (2019). Adhesive Contact Problems for a Thin Elastic Layer: Asymptotic Analysis and the JKR Theory. Math. Mech. Solids 24, 1405–1424. doi:10.1177/1081286518797378

CrossRef Full Text | Google Scholar

Borodich, F. M., Keer, L. M., and Korach, C. S. (2003). Analytical Study of Fundamental Nanoindentation Test Relations for Indenters of Non-ideal Shapes. Nanotechnology 14, 803–808. doi:10.1088/0957-4484/14/7/319

CrossRef Full Text | Google Scholar

Borodich, F. M. (1993). The Hertz Frictional Contact between Nonlinear Elastic Anisotropic Bodies (The Similarity Approach). Int. J. Solids Struct. 30, 1513–1526. doi:10.1016/0020-7683(93)90075-i

CrossRef Full Text | Google Scholar

Borodich, F. M. (2014). The Hertz-type and Adhesive Contact Problems for Depth-Sensing Indentation. Adv. Appl. Mech. 47, 225–366. doi:10.1016/b978-0-12-800130-1.00003-5

CrossRef Full Text | Google Scholar

Boyd, H., Gonzalez-Martinez, J. F., Welbourn, R. J. L., Gutfreund, P., Klechikov, A., Robertsson, C., et al. (2021). A Comparison between the Structures of Reconstituted Salivary Pellicles and Oral Mucin (MUC5B) Films. J. Colloid Interface Sci. 584, 660–668. doi:10.1016/j.jcis.2020.10.124

PubMed Abstract | CrossRef Full Text | Google Scholar

Butt, H.-J., Cappella, B., and Kappl, M. (2005). Force Measurements with the Atomic Force Microscope: Technique, Interpretation and Applications. Surf. Sci. Rep. 59, 1–152. doi:10.1016/j.surfrep.2005.08.003

CrossRef Full Text | Google Scholar

Butt, H.-J., Kappl, M., Mueller, H., Raiteri, R., Meyer, W., and Rühe, J. (1999). Steric Forces Measured with the Atomic Force Microscope at Various Temperatures. Langmuir 15, 2559–2565. doi:10.1021/la981503+

CrossRef Full Text | Google Scholar

Chadwick, R. S. (2002). Axisymmetric Indentation of a Thin Incompressible Elastic Layer. SIAM J. Appl. Math. 62, 1520–1530. doi:10.1137/s0036139901388222

CrossRef Full Text | Google Scholar

Chen, T., Ferris, R., Zhang, J., Ducker, R., and Zauscher, S. (2010). Stimulus-responsive Polymer Brushes on Surfaces: Transduction Mechanisms and Applications. Prog. Polym. Sci. 35, 94–112. doi:10.1016/j.progpolymsci.2009.11.004

CrossRef Full Text | Google Scholar

de Gennes, P. G. (1987). Polymers at an Interface; a Simplified View. Adv. Colloid Interface Sci. 27, 189–209. doi:10.1016/0001-8686(87)85003-0

CrossRef Full Text | Google Scholar

Derjaguin, B. (1934). Untersuchungen über die Reibung und Adhäsion, IV. Kolloid-Zeitschrift 69, 155–164. doi:10.1007/bf01433225

CrossRef Full Text | Google Scholar

Dimitriadis, E. K., Horkay, F., Maresca, J., Kachar, B., and Chadwick, R. S. (2002). Determination of Elastic Moduli of Thin Layers of Soft Material Using the Atomic Force Microscope. Biophysical J. 82, 2798–2810. doi:10.1016/s0006-3495(02)75620-8

CrossRef Full Text | Google Scholar

Drozdov, A. D. (2005). Non-entropic Theory of Rubber Elasticity: Flexible Chains Grafted on a Rigid Surface. Int. J. Eng. Sci. 43, 1121–1137. doi:10.1016/j.ijengsci.2005.03.010

CrossRef Full Text | Google Scholar

Espinosa-Marzal, R. M., Bielecki, R. M., and Spencer, N. D. (2013). Understanding the Role of Viscous Solvent Confinement in the Tribological Behavior of Polymer Brushes: a Bioinspired Approach. Soft Matter 9, 10572–10585. doi:10.1039/c3sm51415c

CrossRef Full Text | Google Scholar

Galin, L. A. (2008). Contact Problems: The Legacy of L.A. Galin. Dordrecht: Springer.

Google Scholar

Galin, L. A. (1946). Spatial Contact Problems of the Theory of Elasticity for Punches of Circular Shape in Planar Projection [in Russian]. J. Appl. Math. Mech. (PMM) 10, 425–448.

Google Scholar

Gorb, S. N. (2008). Biological Attachment Devices: Exploring Nature's Diversity for Biomimetics. Phil. Trans. R. Soc. A 366, 1557–1574. doi:10.1098/rsta.2007.2172

PubMed Abstract | CrossRef Full Text | Google Scholar

Halperin, A., and Zhulina, E. B. (2010). Atomic Force Microscopy of Polymer Brushes: Colloidal versus Sharp Tips. Langmuir 26, 8933–8940. doi:10.1021/la9047374

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayes, W. C., Keer, L. M., Herrmann, G., and Mockros, L. F. (1972). A Mathematical Analysis for Indentation Tests of Articular Cartilage. J. Biomechanics 5, 541–551. doi:10.1016/0021-9290(72)90010-3

CrossRef Full Text | Google Scholar

Hertz, H. (1882). Ueber die Berührung fester elastischer Körper. J. für die reine und angewandte Math. 92, 156–171. doi:10.1515/9783112342404-004

CrossRef Full Text | Google Scholar

Huber, G., Gorb, S. N., Spolenak, R., and Arzt, E. (2005). Resolving the Nanoscale Adhesion of Individual Gecko Spatulae by Atomic Force Microscopy. Biol. Lett. 1, 2–4. doi:10.1098/rsbl.2004.0254

PubMed Abstract | CrossRef Full Text | Google Scholar

Israelachvili, J. N. (1992). Intermolecular and Surface Forces. New York: Academic Press.

Google Scholar

Jaffar, M. J. (1989). Asymptotic Behaviour of Thin Elastic Layers Bonded and Unbonded to a Rigid Foundation. Int. J. Mech. Sci. 31, 229–235. doi:10.1016/0020-7403(89)90113-6

CrossRef Full Text | Google Scholar

Johnson, K. L. (1987). Contact Mechanics. Cambridge: Cambridge University Press.

Google Scholar

Kutnyanszky, E., and Vancso, G. J. (2012). Nanomechanical Properties of Polymer Brushes by Colloidal AFM Probes. Eur. Polym. J. 48, 8–15. doi:10.1016/j.eurpolymj.2011.09.008

CrossRef Full Text | Google Scholar

Love, A. E. H. (1939). Boussinesq's Problem for a Rigid Cone. Q. J. Math. os-10, 161–175. doi:10.1093/qmath/os-10.1.161

CrossRef Full Text | Google Scholar

Luzinov, I., Minko, S., and Tsukruk, V. V. (2004). Adaptive and Responsive Surfaces through Controlled Reorganization of Interfacial Polymer Layers. Prog. Polym. Sci. 29, 635–698. doi:10.1016/j.progpolymsci.2004.03.001

CrossRef Full Text | Google Scholar

Ma, S., Wang, D., Liang, Y., Sun, B., Gorb, S. N., and Zhou, F. (2015). Gecko-inspired but Chemically Switched Friction and Adhesion on Nanofibrillar Surfaces. Small 11, 1131–1137. doi:10.1002/smll.201402484

PubMed Abstract | CrossRef Full Text | Google Scholar

Melzak, K. A., Moreno-Flores, S., Yu, K., Kizhakkedathu, J., and Toca-Herrera, J. L. (2010). Rationalized Approach to the Determination of Contact Point in Force-Distance Curves: Application to Polymer Brushes in Salt Solutions and in Water. Microsc. Res. Tech. 73, 959–964. doi:10.1002/jemt.20851

PubMed Abstract | CrossRef Full Text | Google Scholar

Mendez, S., Andrzejewski, B. P., Canavan, H. E., Keller, D. J., McCoy, J. D., Lopez, G. P., et al. (2009). Understanding the Force-Vs-Distance Profiles of Terminally Attached Poly(N-Isopropyl Acrylamide) Thin Films. Langmuir 25, 10624–10632. doi:10.1021/la9002687

PubMed Abstract | CrossRef Full Text | Google Scholar

Milner, S. T. (1991). Polymer Brushes. Science 251, 905–914. doi:10.1126/science.251.4996.905

PubMed Abstract | CrossRef Full Text | Google Scholar

Milner, S. T., Witten, T. A., and Cates, M. E. (1988). Theory of the Grafted Polymer Brush. Macromolecules 21, 2610–2619. doi:10.1021/ma00186a051

CrossRef Full Text | Google Scholar

Orski, S. V., Fries, K. H., Sontag, S. K., and Locklin, J. (2011). Fabrication of Nanostructures Using Polymer Brushes. J. Mat. Chem. 21, 14135–14149. doi:10.1039/c1jm11039j

CrossRef Full Text | Google Scholar

O’Shea, S. J., Welland, M. E., and Rayment, T. (1993). An Atomic Force Microscope Study of Grafted Polymers on Mica. Langmuir 9, 1826–1835.

Google Scholar

Parra, A., Casero, E., Lorenzo, E., Pariente, F., and Vázquez, L. (2007). Nanomechanical Properties of Globular Proteins: Lactate Oxidase. Langmuir 23, 2747–2754. doi:10.1021/la062864p

PubMed Abstract | CrossRef Full Text | Google Scholar

Popov, V. L., Heß, M., and Willert, E. (2019). Handbook of Contact Mechanics: Exact Solutions of Axisymmetric Contact Problems. Berlin: Springer Nature.

Google Scholar

Ritsema van Eck, G. C., Chiappisi, L., and de Beer, S. (2022). Fundamentals and Applications of Polymer Brushes in Air. ACS Appl. Polym. Mat. 4, 3062–3087. doi:10.1021/acsapm.1c01615

CrossRef Full Text | Google Scholar

Shtaerman, I. Y. (1939). On the Hertz Theory of Local Deformations Resulting from the Pressure of Elastic Solids [in Russian]. Dokl. Akad. Nauk. SSSR 25, 360–362.

Google Scholar

Sneddon, I. N. (1965). The Relation between Load and Penetration in the Axisymmetric Boussinesq Problem for a Punch of Arbitrary Profile. Int. J. Eng. Sci. 3, 47–57. doi:10.1016/0020-7225(65)90019-4

CrossRef Full Text | Google Scholar

Taunton, H. J., Toprakcioglu, C., Fetters, L. J., and Klein, J. (1990). Interactions between Surfaces Bearing End-Adsorbed Chains in a Good Solvent. Macromolecules 23, 571–580. doi:10.1021/ma00204a033

CrossRef Full Text | Google Scholar

Tranchida, D., Piccarolo, S., and Soliman, M. (2006). Nanoscale Mechanical Characterization of Polymers by AFM Nanoindentations: Critical Approach to the Elastic Characterization. Macromolecules 39, 4547–4556. doi:10.1021/ma052727j

CrossRef Full Text | Google Scholar

Tranchida, D., Sperotto, E., Staedler, T., Jiang, X., and Schönherr, H. (2011). Nanomechanical Properties of Oligo(ethylene Glycol Methacrylate) Polymer Brush-Based Biointerfaces. Adv. Eng. Mat. 13, B369–B376. doi:10.1002/adem.201080129

CrossRef Full Text | Google Scholar

Villanueva, J., Huang, Q., and Sirbuly, D. J. (2014). Identification and Design of Novel Polymer-Based Mechanical Transducers: A Nano-Structural Model for Thin Film Indentation. J. Appl. Phys. 116, 104307. doi:10.1063/1.4895338

CrossRef Full Text | Google Scholar

Yang, F. (2003). Thickness Effect on the Indentation of an Elastic Layer. Mater. Sci. Eng. A 358, 226–232. doi:10.1016/s0921-5093(03)00289-2

CrossRef Full Text | Google Scholar

Yang, W., and Zhou, F. (2017). Polymer Brushes for Antibiofouling and Lubrication. Biosurface Biotribology 3, 97–114. doi:10.1016/j.bsbt.2017.10.001

CrossRef Full Text | Google Scholar

Yu, Y., Cirelli, M., Kieviet, B. D., Kooij, E. S., Vancso, G. J., and de Beer, S. (2016). Tunable Friction by Employment of Co-non-solvency of PNIPAM Brushes. Polymer 102, 372–378. doi:10.1016/j.polymer.2016.08.029

CrossRef Full Text | Google Scholar

Zhang, Y., Ma, S., Li, B., Yu, B., Lee, H., Cai, M., et al. (2021). Gecko's Feet-Inspired Self-Peeling Switchable Dry/Wet Adhesive. Chem. Mat. 33, 2785–2795. doi:10.1021/acs.chemmater.0c04576

CrossRef Full Text | Google Scholar