- State Grid Electric Power Research Institute, (NARI Group) Co., Ltd., Nanjing, China
As the complexity of microgrid systems, the randomness of load disturbances, and the data dimensionality increase, traditional load frequency control methods for microgrids are no longer capable of handling such highly complex and nonlinear control systems. This can result in this can result in significant frequency fluctuations and oscillations, potentially leading to blackouts in microgrids. To address the random power disturbances introduced by a large amount of renewable energy, this paper proposes a Learning-Driven Load Frequency Control (LD-LFC) method. Additionally, a Graph Convolution Neural Networks -Proximal Policy Optimization (GCNN -PPO) algorithm is introduced, which enhances the random power disturbances introduced by a large amount of renewable energy. Algorithm is introduced, which enhances the perception ability of the reinforcement learning agent regarding grid state data by embedding a graph convolutional network. The effectiveness of this approach is validated through simulations on the isolated microgrid Load Frequency Control (LFC) model of China Southern Grid (CSG).
1 Introduction
Alternative energy growth has substantially increased with introducing the nation’s first-class energy structure and the world’s first-class power generation systems online. As a result of this change, renewable energy sources like solar, wind, lakes, and gas have been promoted (Li et al., 2022). These tools are necessary to apply less energy and reduce carbon emissions. Cases of renewable energy systems include large, well-known apartments, more minor local features, and specific ones. Distributed technology is widely accepted among these because of its lower maintenance costs, cost-effectiveness, and economic gains. This group includes all kinds of strength besides clean energy, climate, infrared, biomass, river, and hydrogen-based strength (Zhou et al., 2023). Nearby island’s power systems are often used to solve power issues, especially in mountains and land. These thermal systems have benefits but often need help maintaining a steady frequency due to their low strength and outcome. When there is much energy over frequency, these issues only worsen. Today, the importance of Load frequency control (LFC) is paramount to smart grids, and it is being thoroughly investigated (Chen, 2023; Li and Cheng, 2023; Hassan et al., 2022).
Using in LFC microgrid systems is challenging because the data is complex, people use energy differently at different times, and the weather changes significantly. Conventional methods often have issues due to construction limitations and need help to employ thorough answers as data expands. Model-driven approaches may also lead to false prediction when the condition is confusing, lowering the possibilities’ value. Standard algorithms are less effective and accurate because of aspects with useless features. Modern transistors require more than just regular model-based approaches to achieve the best possible weight frequency control (LFC) because of their difficulty and restricted nature (Su et al., 2021).
Due to the expansion of linked renewables and the swings in the energy industry, power systems spanning many regions have become more complex. These methods require new ideas for challenging behaviours, changing circumstances, miscommunications, and speech delays. New energy tools have been developed, such as cerebral group control, predicted energy, and excellent control (Huang and Lv, 2023). High-dimensional variables with redundant and irrelevant features further diminish the efficiency and accuracy of standard algorithms. The nonlinear and constraint-laden nature of these systems complicates problem-solving efforts, making traditional model-based methods inadequate for achieving optimal LFC in modern microgrids (Zhang et al., 2021).
The growth of interconnected microgrids and the evolution of power markets have led to the development of more extensive and complex multi-regional power systems. These systems require innovative strategies to address nonlinearity, time-varying behaviors, uncertainties, and communication delays. Consequently, advanced control strategies, such as neural network-based control, robust control, and predictive control, have emerged.
For instance, Wang et al. (2022) demonstrated how neural systems can improve connected products in credible websites in denial-of-service damage. Similarly, Xu et al. (2017) examined the administration of gas-cell and device-mix energy storage systems. They sought to increase the fat frequency energy using distinctive machine types known as the Hammerstein neurological network. Practical tools were developed simultaneously to limit the risks and restrictions of products in a range of fields. These ideas were tested using different computer simulation techniques and Lyapunov’s concept of devotion.
Several researchers have successfully solved complex software issues using recently developed LFC techniques. Kazemy et al. (2020) suggested using extensive neurological systems to solve power system issues among the population. Kumar et al. (2021) created a system that uses brain sites to quickly adapt power options to changing business issues.
Based on proper column variations, suitable H∞ control methods have been proven to have challenges and problems and maintain balance within prescribed parameters. For instance, Li and individuals. They developed LFC activities that increased phone frequency and improved strength performance. As validated designs demonstrate, these cutting-edge techniques are essential to sustaining power network security. Zhang H. et al. (2019) developed event-triggered LFC schemes that optimize communication bandwidth utilization while preserving control performance. These techniques, validated through simulations, highlight the importance of novel strategies for maintaining grid stability. This adaptive event-triggered scheme, which utilizes Lyapunov stability theory and linear matrix inequalities, reduces transmission frequency while preserving control performance. Wang et al. (2021) suggested a strong, event-based H-LFC strategy to enhance its endurance against violence and show its rewards using real-world examples.
Using the Extended State Observer (ESO) method, Active Disturbance Rejection Control (ADRC) addresses all unresolved problems that might affect the system’s output. This enables a particular message perspective. Zhang et al. (2022) developed a new control method known as Estimated Flatness-based ADRC (EF-ADRC) for power system’s automatic load frequency control (LFC). In contrast to the traditional step-by-step method, this approach uses stage outputs to determine the system’s state, allowing it to follow desired pathways properly. In both single-area and multi-area practices, this technique was effective. Ma and others correctly address charm and limitations thanks to improved techniques and forecasting models. Ma et al. (2016) suggested a connection plan that would improve cooperation and control over a number of remote locations while also considering the effects that events offer. The system demonstrated greater freedom and power in calculations than North products.
System variants in interior design power (IMC) are used to create products that respond immediately. Jia et al. (2020) proposed IMC and design reduction for complex systems to control weight frequency power LFC issues, facilitating quick and precise communications.
Traditional methods need help keeping microgrid fat frequency energy because of changing routines, shifts in energy usage, and the uncertainty of renewable energy sources. Standard methods are impacted and become more complicated as a result of the widespread use of solar and wind energy. On the other hand, flexible system control mechanisms are provided by RL algorithms. They often engage with their environment, alter how they act, and improve their abilities to respond in more specific ways.
Yan and Xu (2020) demonstrated a teamwork-based approach to managing weight LFC across linked sites by working with various brokers. This method combines distributed management with extensive understanding to increase resilience. Thanks to creating a novel online resource that self-improves without using specific forms. Yin et al. (2019) developed an adaptive online RL method that minimizes reliance on precise models, enhancing adaptability to system dynamics, particularly for wind power. Wei et al. (2020) applied a DQN-based RL approach for multi-area LFC, leveraging deep neural networks to independently adjust generation in response to frequency shifts. Zhang X. et al. (2019) presented a model-free DRL approach that effectively managed LFC without precise modeling. Zhao and Lu (2021) deployed policy-gradient DRL to manage frequency stability in grids with high renewable shares, demonstrating superior speed and accuracy compared to traditional methods. Nian and Sun (2021) applied the Deep Deterministic Policy Gradient (DDPG) algorithm to LFC, effectively managing power system fluctuations with a robust adaptive control strategy. Nguyen and Huang (2020) proposed a cooperative LFC framework with multi-agent DRL, suitable for maintaining stability across interconnected regions. García and Torres (2022) enhanced scalability and efficiency by structuring a hierarchical DRL approach, improving frequency regulation in large-scale systems. Li and Zhou (2024) developed a DRL-based LFC with fault tolerance to withstand cyber-physical disruptions, emphasizing security in interconnected digital power systems.
In the intricate domain of microgrid load frequency control, modern approaches demand both technical and economic resilience, underscoring the importance of Graph Convolutional Networks combined with Proximal Policy Optimization (GCNN-PPO) for robust performance. To address these challenges, a novel Learning-Driven Load Frequency Control (LD-LFC) method is proposed, designed to stabilize frequency amid renewable energy integration, enhance grid efficiency, and reduce operational costs.
The GCNN-PPO algorithm speeds up the decision-making operation in the electricity system. Using graph convolutional networks and proximal policy optimization (PPO) increases the learning agent’s capacity to quickly comprehend and interpret grid state information. Using GCNs, you can better comprehend connections and social dynamics. Because of this, the assistant training director has a wiser, wiser, and more accurate decision on mass frequency management options. This novel idea is helpful in a complex, spread-out energy grid. Knowing how many pieces of society connect and depend on one another is crucial for everything to run smoothly and effectively.
Simulations of LD-LFC and GCNN-PPO on the China Southern Grid microgrid model illustrated frequency stability enhancements under load and renewable variability, showing promise in renewable-dominant systems. Key contributions of this work are the LD-LFC’s dynamic adaptation to renewable-induced disturbances and the GCNN-PPO algorithm’s advanced handling of grid-state data, reinforcing stability in complex power networks.
The innovative points of this article are as follows.
1) Introduction of the Learning-Driven Load Frequency Control (LD-LFC) technique, which uses a variety of renewable energy sources, including wind and solar, to quickly react to unanticipated power changes. The LD-LFC approach reduces running costs by maintaining the frequency of the microgrid. This method uses solid files, considerably improving its ability to handle power more efficiently and effectively than traditional methods.
2) This engine simplifies the understanding and use of grid-state information by connecting Graph Convolutional Networks (GGNs) with a support learning tool. Because it comprehends the organization and composition of the game, the confirmation learning programme makes better, faster choices. This new technique improves power system’s ability to handle complex and scattered work.
The manuscript systematically guides the reader through its research, starting with an explanation of the microgrid’s architecture (Section 2), followed by the introduction of a novel frequency control method (Section 3), empirical case study analysis (Section 4), and concluding with a synthesis of key findings and their implications for microgrid management (Section 5).
2 Islanded microgrids
2.1 LD-LFC model for islanded microgrids
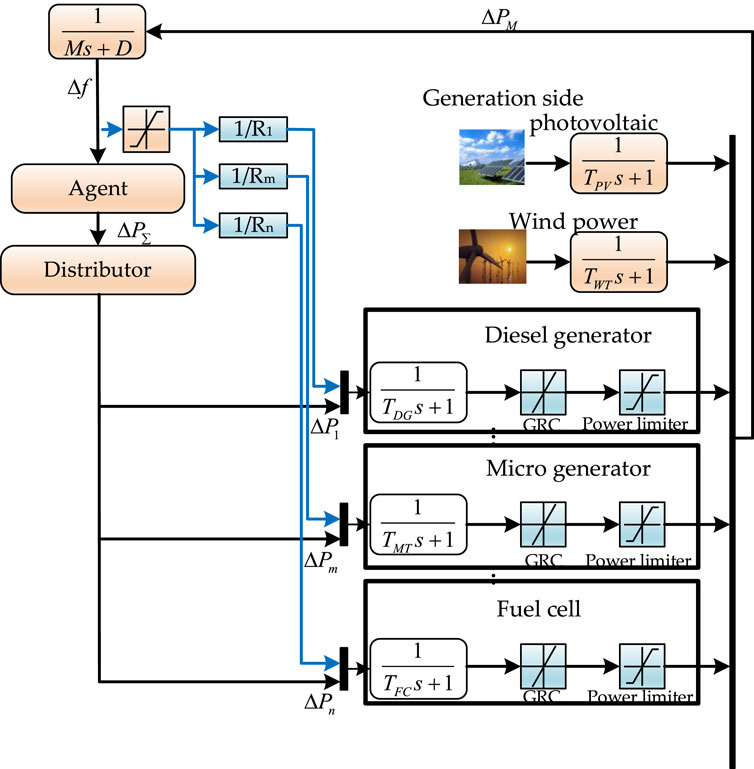
An innovative LFC model is introduced, building on the framework outlined in reference (Chen). This model is meticulously designed to reflect the intricate characteristics of modern microgrids, incorporating diverse distributed energy resources such as fuel cells, wind turbines, and diesel engines. Figure 1 provides a comprehensive visual representation, detailing the advanced transfer function and systematic modeling approach. It also illustrates the complete LFC control model, seamlessly integrating all the mentioned energy-generating units. The detailed schematic in Figure 1 (Yin et al., 2019) captures the dynamic interactions and responses of these units within the LFC framework, offering profound insights into its performance and operational intricacies. This schematic not only highlights the energy generation capabilities of the system but also unpacks the complexities of its operational dynamics, making it an essential reference for understanding the LFC model’s functionality.
2.2 Unit modeling
2.2.1 Micro gas turbine load frequency control modeling
A micro gas turbine is a compact thermal generator noted for its high reliability and safety, along with efficient energy conversion, low emissions, and eco-friendly qualities. It is extensively utilized within microgrids, making it the primary unit selected for analysis in this study. The dynamic characteristic functions of the turbine’s fuel system and turbine rotor system are detailed as Equations 1, 2:
where
2.2.2 Load frequency control model for energy storage systems
Research indicates that Battery Energy Storage Systems (BESS) outperform other storage types, such as flywheel, superconducting electromagnetic, and capacitor storage systems. Reference (Huang and Lv, 2023) analyzed a BESS model for grid frequency regulation, presenting a simulation model with a suitable structure that meets both primary and secondary frequency regulation needs. Consequently, the BESS model in this paper adopts this battery storage simulation framework.
where
2.2.3 Electric vehicle load frequency control model
Electric Vehicles (EVs) offer advantages such as rapid response, flexible dispatch, and combined source-storage capabilities, enabling services like peak shaving, valley filling, and auxiliary frequency and voltage regulation through Vehicle-to-Grid (V2G) technology. Reference (Zhang et al., 2021) examined frequency control in power systems with large-scale wind integration using a V2G model, demonstrating that V2G effectively mitigates wind power fluctuations, enhancing system frequency control and operational efficiency. The mathematical model of EV participation in primary frequency regulation is discussed in (Xu et al., 2017) as Equation 5:
Due to the battery characteristics, frequent charging and discharging operations of EV are not favorable to the health of the battery, so a dead zone module is added to the model so that EV does not participate in the frequency regulation task when the system frequency fluctuates in a small range.
When the frequency deviation
When the frequency deviation
When the frequency deviation
where
2.3 Wind power modeling
Wind power generation is primarily influenced by wind speed, noted for its intermittent and fluctuating nature. At present, the Weibull distribution is commonly applied to model wind speed, with its probability density function represented as Equations 9, 10:
where
When wind speed falls between the cut-in and cut-out thresholds, the wind turbine’s output power varies with wind speed as follows:
where,
2.4 Objective functions and constraints
The LD-LFC plan is a perfect strategy for enhancing some goals in managing power systems, concentrating on keeping the right frequency and saving cash. This method lowers production costs while maintaining the desired frequency. It strikes a balance between cost-effectiveness and operating stability. This method maintains the desired frequency while lowering the program’s overall costs. It strikes a balance between being reliable and affordable. The LD-LFC structure carefully considers the laws governing power tools, the weather, health rules, and technical needs. The possibilities it suggests are both excellent and beneficial in this regard. Because of its integrated approach, the LD-LFC approach is helpful and appropriate for the changing needs of modern electric program management. Because of this mixture approach, the LD-LFC tool is significant and relevant to the evolving needs of modern electric system administration. The objectives and constraints are shown below as Equations 11, 12.
where ΔPorder-∑ is the total command, ΔPimax and ΔPimin are the limits of the ith unit, ΔPiin is the command of the ith unit.
3 GCNN -PPO algorithm based LD-LFC
3.1 Reinforcement learning and graph neural networks
Reinforcement learning is a data-driven approach that addresses the problem of controlling dynamic systems. Reinforcement learning intelligences capture the dynamic properties of the desired problem by continuously interacting with the simulation environment, and then learn appropriate strategies guided by reward values based on historical experience. The whole process is usually modelled as an MDP. It use a quintuple
The state action value function
The state-value function in Equation 14 is usually expressed as Equation 15.
Graph Neural Networks (GNNs) are a special class of neural networks that can capture the relationships between different nodes from graphically structured data. The core idea of GNNs is to utilize a message passing mechanism to aggregate the features of neighboring nodes. Most of the current GNNs models can be viewed as a method for learning “substitution invariant functions,” whose inputs are a feature matrix X and a connection matrix A. X describes the features of each node
where
3.2 Markov decision process
In this section, the LD-LFC model of the power grid is described as an MDP model where the state space, action space, reward function and state transfer process are as follows.
3.2.1 Action space
The configuration of the action space is illustrated below as Equation 17.
where
3.2.2 State space
The corresponding state space representation is shown below as Equation 18.
where
3.2.3 Reward function
The microgrid management approach’s vehicle design considers the total electricity produced and the president’s frequency variation. This two-part view highlights the vehicle’s dedication to improving process stability and cost-effectiveness. The election job can demonstrate the controller’s performance in achieving these goals. For some actions taken to promote the development of the best power structure, rewards are offered as part of the reward program. By maintaining precise control over energy production, this energy reduces inefficient or insufficient function. The owner is motivated to use energy sources best by imposing these restrictions. The award work examines the device’s ability to reduce expenses while keeping frequency versions at a minimum and considering charges for its actions. The target maintains program stability and funds because of this conduct. The agent may create cost-effective and cost-effective ideas using this study tool as Equations 19, 20.
The proposed control strategy is designed to mitigate frequency fluctuations and reduce power production costs simultaneously. To fulfill these objectives, the reward function r incorporates a penalty mechanism A that discourages inefficient actions and fosters the development of optimal policies. This equilibrium between reward and penalty directs the agent to concentrate on enhancing both system efficiency and cost-effectiveness, thereby guiding it toward the most effective operational strategies.
3.2.4 State transfer process
At each time step t, the agent observes the current state
3.3 Proximal policy optimization algorithm based on GCNNs
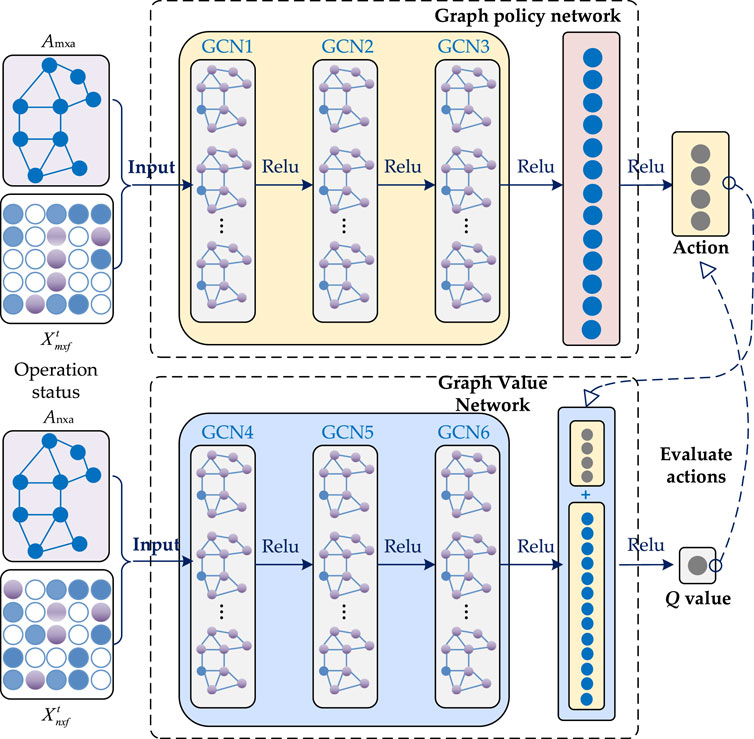
Currently reinforcement learning methods can be categorized into three groups: value-based methods, policy-based methods and algorithms based on the AC framework. In this thesis, we use the proximal policy optimization (PPO) algorithm designed based on the AC framework (Li and Zhou, 2024), which has the advantage of high stability of stochastic policies. The GCNN-PPO algorithm proposed in this thesis adds a graph convolutional layer in front of the Multi-Layer Perception (MLP) neural network, which improves the ability of the PPO intelligences to perceive graph data. Figure 2 illustrates the structure of the Actor network and Critic network in the GCN-PPO algorithm. The Actor network architecture we use consists of two graph convolutional layers and three MLP layers, each of which is accompanied by a ReLU activation function and uses a summation pooling function to aggregate the output of the graph convolutional layers over neighboring nodes and then passes it to the MLP layer to output a policy. The architecture of the Critic network defining the value function is more or less the same as the Actor network, the main difference is that a global summation pooling function is added behind its graph convolutional layer, which enables the value function to aggregate the information from all the nodes in the graph to compute an estimate for the whole network.
The PPO algorithm is an improvement on the trust domain policy optimization. The TRPO algorithm uses the Kullback-Leibler (KL) scatter-constrained policy network to make its updated policy close to the old one, and its optimization objective and constraints are shown in Equations 21, 22.
where
where clip ( ) is a truncation function to control the change of old and new policies within
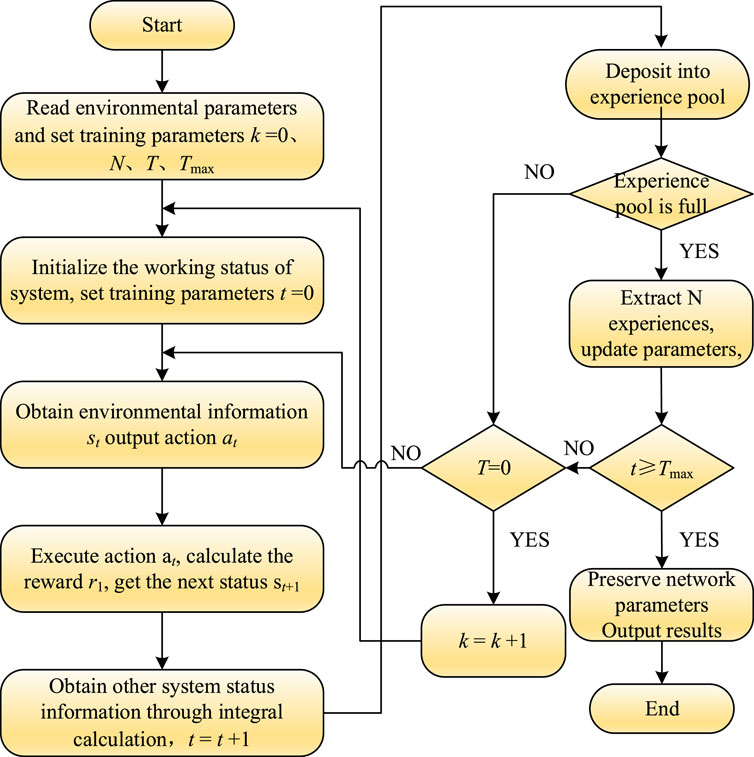
3.4 LFC solving process based on GCNN-PPO algorithm
The Actor network is a policy function that maps the state
At the beginning of training, the parameters θ and θold for the Actor network and
where
where
4 Case studies
In the field of advanced power system control methods, this study performs an extensive evaluation of a novel approach using comprehensive simulation exercises for an isolated urban microgrid. The research rigorously assesses the effectiveness of the LD-LFC developed using the Graph Convolutional Neural Networks - Proximal Policy Optimization (GCNN-PPO) algorithm. The research rigorously assesses the effectiveness of the LD-LFC developed using the Graph Convolutional Neural Networks - Proximal Policy Optimization (GCNN-PPO) algorithm. Established control algorithms, including Proximal policy optimization (PPO) algorithm-based LD-LFC (Nian and Sun, 2021), Proximal policy optimization (PPO) algorithm-based LD-LFC (Nguyen and Huang, 2020), Soft actor critic (SAC) algorithm-based LD-LFC (García and Torres, 2022), Trust Region Policy Optimization-based LD-LFC (Li and Zhou, 2024), Twin Delayed Deep Deterministic Policy Gradient algorithm-based LD-LFC, Deep Deterministic Policy Gradient (DDPG) algorithm-based LD-LFC, Takagi Sugeno (TS) fuzzy PI controller. Distributed Distribal Deterministic Policy Gradients (D4PG) (Yan and Xu, 2020), Asynchronous Actor-Critic Agents (A3C) (Yin et al., 2019), Twin Delayed Deep Deterministic Policy Gradient (TD3) (Zhao and Lu, 2021), Deep Deterministic Policy Gradient (DDPG), Double Deep Q-Network (DDQN) (Zhang H. et al., 2019), Deep Q-Network (DQN) (Nian and Sun, 2021), Distributed Model Predictive Control (DMPC) (Chen), Model Predictive Control (MPC) (Su et al., 2021), Fuzzy Fractional Order Proportional Integral (Fuzzy-FOPI) (Zhang et al., 2021), Fuzzy Proportional Integral (Fuzzy-PI) (Zhang H. et al., 2019), and Particle Swarm Optimization Proportional Integral (PSO-PI) (Zhang et al., 2022) for LFC purposes.
4.1 Case 1: step disturbance
The LFC model is tested under various disturbance scenarios, including wind, photovoltaic energy, and irregular load changes. A 7,200-s (2-h) simulation period is set to capture both transient and steady-state responses, as well as the impact of the LFC on the environment.
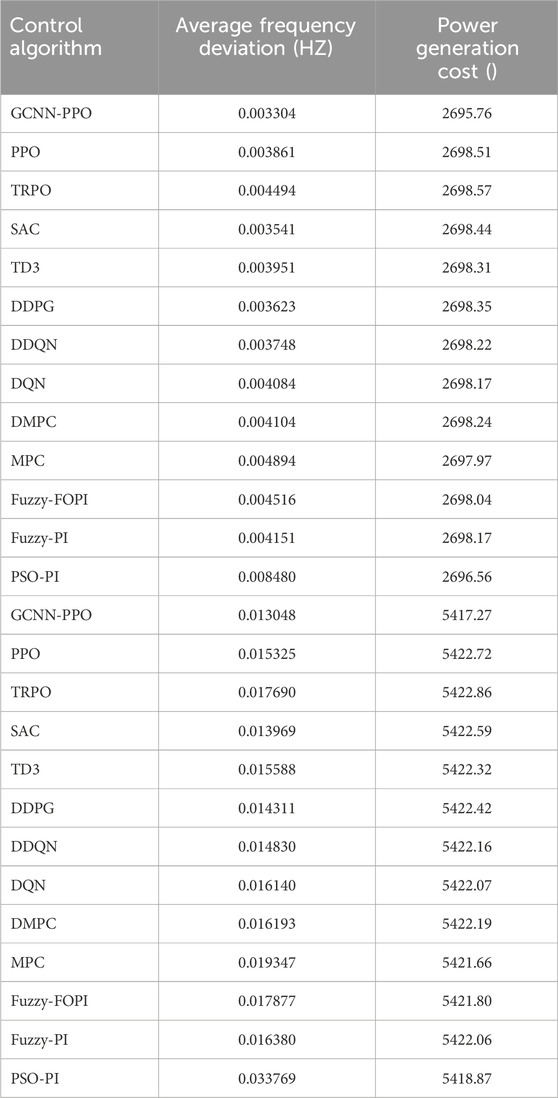
Table 1 demonstrates the effectiveness of the GCNN-PPO approach, showing significant reductions in frequency deviation (19.5%–83.1%) and generation costs (0.0018%–0.098%). These results highlight the method’s ability to enhance both efficiency and cost control in power generation. Figure 4 further illustrates the early-stage use of the method. Illustrates the early-stage use of a prioritized replay mechanism, which strengthens system resilience and facilitates quicker learning, enabling GCNN-PPO consistently outperforms other methods by minimizing average frequency deviation and reducing generation unit overload. GCNN-PPO consistently outperforms other methods by minimizing average frequency deviation and reducing generation unit overshoot, showcasing superior stability and robustness in managing power system fluctuations. Contrast, the DDPG method falls short in developing an optimal LFC strategy due to its reliance on a basic replay system, lacking the sophistication of Although DDPG reduces frequency deviation, its control becomes erratic under disturbances, reflecting its insufficient robustness strategies. Although DDPG reduces frequency deviation, its control becomes erratic under disturbances, reflecting its insufficient robustness strategies. GCNN-PPO, however, integrates cost reduction into its control design, effectively lowering operational expenses and ensuring more consistent and stable generation costs. Fuzzy logic-based algorithms also struggle to balance frequency deviation and cost optimization in microgrids, especially during varied disturbances. Optimization in microgrids, often resulting in inconsistent frequency regulation, particularly under specific disturbances, as seen in the second In conclusion, GCNN-PPO sets a new benchmark with its reliable performance across different disturbances, delivering the In conclusion, GCNN-PPO sets a new benchmark with its reliable performance across different disturbances, delivering the fastest frequency response and minimal overshoot, leading to the lowest average frequency deviation and optimized generation costs. Establishes GCNN-PPO as a top choice for power generation optimization.
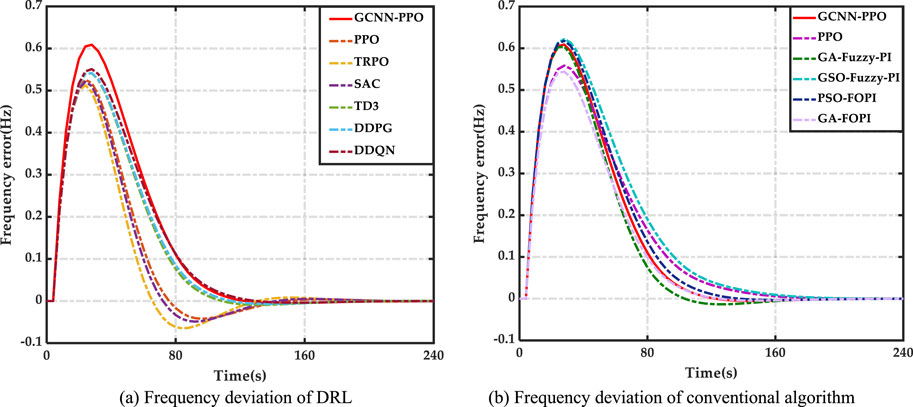
Figure 4. Results in Case 1 (A) Frequency deviation of DRL (B) Frequency deviation of conventional algorithm.
4.2 Case 2: step disturbance and renewable disturbance
To simulate the unpredictability of EVs, wind turbines, and PV systems, these elements are modeled as random load disturbances, ensuring the system’s frequency regulation remains intact.
The table presents a comprehensive comparison of control algorithms, highlighting their impact on generation costs—defined as the total regulatory expenses for all generators over a 24-h period. The SGCNN-PPO algorithm achieves frequency deviations that are 1.36–1.99 times lower than those of other methods, reducing generation costs by 0.0513%–0.0655%. Similarly, the GCNN-PPO algorithm demonstrates superior performance, attaining frequency deviations 1.61 to 1.71 times lower than other approaches and decreasing generation costs by 0.0422%–0.0633%, according to distribution network data.
This efficiency underscores GCNN-PPO’s ability to balance cost reduction with operational effectiveness. Its strengths in economic performance, adaptability, and optimization provide a distinct advantage. This sets the website apart from other practices because it automatically adjusts its options in response to changing circumstances. Numerous changes, including rapid shifts, effortless waves, and random ups and downs, have demonstrated its robust and flexible ability.
Test results demonstrate that GCNN-PPO is adaptable, simple to learn, and powerful. This reduces mysterious issues and improves strength transmission network monitoring. Its inventive approach and careful use make it a good choice for treating complex problems daily. In conclusion, GCNN-PPO increases flexibility and development while lowering electricity and production costs. Its ability to handle various issues demonstrates how it strengthens and facilitates active, complex present system.
5 Conclusion
This paper introduces a new LD-LFC approach that simplifies frequency handling. Additionally, it improves management performance and reduces savings. The basis of this approach is the GCNN-PPO algorithm, which improves and evaluates pack frequency control. As it adjusts to method changes, the GCNN- PPO page learns more quickly and quickly, helping to increase overall outcomes by concentrating on essential learning experiences.
The LD-LFC approach and GCNN-PPO site were used to properly test the island microgrid model from China’s South Grid. This creative strategy outperforms earlier variants. Boosts frequency, improves accuracy and prevents interpretation when needed. Also, this method had the most reasonable average difference in frequency, which can keep the software firm when conditions change. The LD-LFC view improved performance while reducing production costs, demonstrating its performance and benefits.
Perhaps most notably, the LD-LFC method managed to reduce generation costs while achieving these performance improvements, showcasing its potential for both operational efficiency and cost-effectiveness.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
WG: Methodology, Writing–original draft, Writing–review and editing. HD: Writing–original draft, Writing–review and editing. TH: Writing–original draft, Writing–review and editing. SL: Writing–original draft, Writing–review and editing. CL: Writing–original draft, Writing–review and editing, Formal Analysis, Funding acquisition. XH: Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by Science and Technology Project under Grant No. 5400-202357828A-4-1-KJ.
Conflict of interest
Authors WG, HD, TH, SL, CL and XH were employed by (NARI Group) Co., Ltd.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Chen, J. (2023). “Deep reinforcement learning-based data-driven load frequency control for microgrid,” in 2023 8th Asia Conference on Power and Electrical Engineering, 14–16 April, 2023 (ACPEE), 1717–1721.
García, L., and Torres, A. (2022). Hierarchical deep reinforcement learning for load frequency control in large-scale power systems. Energy 237, 121554.
Hassan, S., Anwari, M., and Milyani, A. (2022). Robust load frequency control of hybrid solar power systems using optimization techniques. Front. Energy Res. 10, 902776. doi:10.3389/fenrg.2022.902776
Huang, T., and Lv, X. (2023). Load frequency control of power system based on improved AFSA-PSO event-triggering scheme. Front. Energy Res. 11, 1235467. doi:10.3389/fenrg.2023.1235467
Jia, Y., Meng, K., Wu, K., Sun, C., and Dong, Z. Y. (2020). Optimal load frequency control for networked power systems based on distributed economic MPC. IEEE Trans. Syst. Man, Cybern. Syst. 51 (4), 2123–2133. doi:10.1109/tsmc.2020.3019444
Kazemy, A., Lam, J., and Zhang, X. M. (2020). Event-triggered output feedback synchronization of master-slave neural networks under deception attacks. IEEE Trans. Neural Netw. Learn. Syst. 33 (3), 952–961. doi:10.1109/tnnls.2020.3030638
Kumar, A., Singh, S. P., Singh, B., Alotaibi, M. A., and Nassar, M. E. (2021). Novel neural network-based load frequency control scheme: a case study of restructured power system. IEEE Access 9, 162231–162242. doi:10.1109/access.2021.3133360
Li, J., and Cheng, Y. (2023). Deep meta-reinforcement learning based data-driven active fault tolerance load frequency control for islanded microgrids considering internet of things. IEEE Internet Things J., 1.
Li, J., Yu, T., and Zhang, X. (2022). Coordinated load frequency control of multi-area integrated energy system using multi-agent deep reinforcement learning. Appl. Energy 306, 117900. doi:10.1016/j.apenergy.2021.117900
Li, J., and Zhou, T. (2024). Efficient replay deep meta reinforcement learning for active fault-tolerant control of solid oxide fuel cell systems considering multivariable coordination. IEEE Trans. Transp. Electrification, 1. doi:10.1109/TTE.2024.3470240
Ma, M., Zhang, C., Liu, X., and Chen, H. (2016). Distributed model predictive load frequency control of the multi-area power system after deregulation. IEEE Trans. Industrial Electron. 64 (6), 5129–5139. doi:10.1109/tie.2016.2613923
Nguyen, K., and Huang, S. (2020). Multi-agent deep reinforcement learning for cooperative load frequency control. Int. J. Electr. Power and Energy Syst. 120, 106030.
Nian, F., and Sun, C. (2021). Adaptive load frequency control using deep deterministic policy gradient. Appl. Energy 289, 116731.
Su, K., Li, Y., Chen, J., and Duan, W. (2021). Optimization and H∞ performance analysis for load frequency control of power systems with time-varying delays. Front. Energy Res. 9, 762480. doi:10.3389/fenrg.2021.762480
Wang, D., Chen, F., Meng, B., Hu, X., and Wang, J. (2021). Event-based secure H-infinity load frequency control for delayed power systems subject to deception attacks. Appl. Math. Comput. 394, 125788. doi:10.1016/j.amc.2020.125788
Wang, X., Ding, D., Ge, X., and Dong, H. (2022). Neural-network-based control with dynamic event-triggered mechanisms under DoS attacks and applications in load frequency control. IEEE Trans. Circuits Syst. I Regul. Pap. 69 (12), 5312–5324. doi:10.1109/tcsi.2022.3206370
Wei, Y., Liu, C., and Zhong, J. (2020). A deep reinforcement learning-based control approach for load frequency control in multi-area power systems. Electr. Power Syst. Res. 189, 106746.
Xu, D., Liu, J., Yan, X. G., and Yan, W. (2017). A novel adaptive neural network constrained control for a multi-area interconnected power system with hybrid energy storage. IEEE Trans. Industrial Electron. 65 (8), 6625–6634. doi:10.1109/tie.2017.2767544
Yan, Z., and Xu, Y. (2020). A multi-agent deep reinforcement learning method for cooperative load frequency control of a multi-area power system. IEEE Trans. Power Syst. 35 (6), 4599–4608. doi:10.1109/tpwrs.2020.2999890
Yin, L., Yu, T., Yang, B., and Zhang, X. (2019). Adaptive deep dynamic programming for integrated frequency control of multi-area multi-microgrid systems. Neurocomputing 344, 49–60. doi:10.1016/j.neucom.2018.06.092
Zhang, B., Li, J., Tan, W., Sira-Ramírez, H., and Gao, Z. (2022). Estimated flatness-based active disturbance rejection control for load frequency control of power systems. Electr. Power Components Syst. 50, 1250–1262. doi:10.1080/15325008.2022.2153286
Zhang, H., Liu, J., and Xu, S. (2019a). H-infinity load frequency control of networked power systems via an event-triggered scheme. IEEE Trans. Industrial Electron. 67 (8), 7104–7113. doi:10.1109/tie.2019.2939994
Zhang, X., Xu, Y., and Zhao, J. (2019b). Model-free load frequency control based on deep reinforcement learning. IEEE Trans. Power Syst. 34 (6), 5162–5165.
Zhang, Y., Lu, J., Jiang, X., Shen, S., and Wang, X. (2021). A study on heat transfer load in large space buildings with stratified air-conditioning systems based on building energy modeling: model validation and load analysis. Sci. Prog. 104 (3), 00368504211036133. doi:10.1177/00368504211036133
Zhao, Y., and Lu, X. (2021). Deep reinforcement learning for frequency regulation in renewable-dominant power grids. IEEE Access 9, 23820–23830.
Keywords: load frequency control, graph convolution neural networks, isolated microgrid, multi-objective optimization, proximal policy optimization
Citation: Guo W, Du H, Han T, Li S, Lu C and Huang X (2024) Learning-driven load frequency control for islanded microgrid using graph networks-based deep reinforcement learning. Front. Energy Res. 12:1517861. doi: 10.3389/fenrg.2024.1517861
Received: 27 October 2024; Accepted: 28 November 2024;
Published: 23 December 2024.
Edited by:
Haifeng Qiu, Nanyang Technological University, SingaporeReviewed by:
Linfei Yin, Guangxi University, ChinaZhijian Hu, Nanyang Technological University, Singapore
Yixuan Chen, The University of Hong Kong, Hong Kong SAR, China
Copyright © 2024 Guo, Du, Han, Li, Lu and Huang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wangyong Guo, wangyongguo@gdcsg.com
 Wangyong Guo
Wangyong Guo