Deep reinforcement learning for adaptive frequency control of island microgrid considering control performance and economy

To achieve frequency stability and economic efficiency in isolated microgrids, grid operators face a trade-off between multiple performance indicators. This paper introduces a data-driven adaptive load frequency control (DD-ALFC) approach, where the load frequency controller is modeled as an agent that can balance different objectives autonomously. The paper also proposes a priority replay soft actor critic (PR-SAC) algorithm to implement the DD-ALFC method. The PR-SAC algorithm enhances the policy randomness by using entropy regularization and maximization, and improves the learning adaptability and generalization by using priority experience replay. The proposed DD-ALFC method based on the PR-SAC algorithm can achieve higher adaptability and robustness in complex microgrid environments with multiple performance indicators, and improve both the frequency control and the economic efficiency. The paper validates the effectiveness of the proposed method in the Zhuzhou Island microgrid.

1 Introduction

Traditional islanded energy systems mainly rely on diesel generators, wind turbines (WT), photovoltaic (PV) and energy storage facilities to provide power supply. Diesel generators, as representatives of traditional energy sources, have the advantages of stability and robustness, but they also have the disadvantages of high operating cost, slow response, and serious environmental pollution. Therefore, their share of power generation is gradually decreasing. Wind turbines and photovoltaic, as representatives of distributed renewable energy sources, have the advantages of safety, flexibility and low pollution, but they are also highly dependent on external factors such as weather, temperature and light, resulting in strong fluctuations and time-varying characteristics. This may cause power shortage or surplus, leading to system imbalance and frequency instability. To address the energy balance problem between the demand side and the supply side of the islanded energy system, improve the operational reliability of the system, and ensure the quality of energy, the hybrid energy system that combines diesel generators and distributed renewable energy sources has become the mainstream of future development. Therefore, it is of great significance to develop advanced energy storage systems (ESS) and corresponding energy management systems (EMS), to achieve the coordinated control of traditional energy and distributed renewable energy, and ultimately realize the optimal control of energy. When the microgrid is disconnected from the main grid, it enters the islanded operation mode, in which the microgrid needs to independently establish the voltage and frequency reference, and maintain the power balance and frequency stability within the system. This requires the secondary frequency control of the microgrid, that is, based on the primary frequency control, the microgrid central controller or distributed controller coordinates the distributed power generation and energy storage devices within the system to control the frequency, so that the frequency of the microgrid is restored to the rated value, and the economic operation of the microgrid is achieved.

Load frequency control (LFC) of microgrids is a challenging problem that has been addressed by various control methods, from the classical Proportional Integral Derivative (PID) control to advanced control theories. PID control is a traditional control policy that was widely adopted in the early studies of LFC (Xi et al., 2022; Li and Zhou, 2023a; Li and Zhou, 2023b). However, PID control has some limitations, such as the continuous change of parameters and some constraints in the power system, which affect the control performance and the dynamic index of the system (Li et al., 2023a; Li et al., 2023b). A method that combines integral compensation and state feedback was applied to the LFC system in (Xi et al., 2020). With the development of various agent optimization algorithms, the traditional control algorithm was improved by integrating agent control method with classical control method to enhance the control effect of LFC. For example, Cavin and Calovic et al. (Cavin et al., 1971; Calovic, 1972) applied the optimal control method based on the traditional PID control and proposed the controller parameter design of agent optimization algorithm. Wang et al. (2018) proposed a design method based on model predictive control, which can improve the frequency response of the system when the load changes. More advanced control strategies were also applied in the LFC system with the development of control method. For the study of adaptive control, Xie et al. (2023) designed a decentralized adaptive control method to ensure that the frequency fluctuation of each region converges to an acceptable range and the deviation range is maintained in a very small range. Deng et al. (2022) proposed a virtual inertia and virtual damping parameters adaptive control policy, which can better track the frequency changes and set the action threshold of adaptive control. In the study of sliding mode variable structure control, Chen et al. (2018) designed the control policy of modular multilevel converter under unbalanced grid voltage according to the principle of sliding mode variable structure control. Dong et al. (2019) also considered the system parameter uncertainty, energy storage system and traditional unit control channel delay problem, reduced the capacity configuration of the energy storage system, and proposed a sliding mode LFC controller and energy storage coordination control policy for the LFC model containing wind storage. In terms of predictive control, Elmouatamid et al. (2021) proposed a Generalized Predictive Control (GPC) policy for energy management in Micro-Grid (MG) systems. Qian et al. (2016) proposed a robust distributed predictive control algorithm based on linear matrix inequality with adjustable parameters, considering both generators change rate constraints and valve position constraints, and transforming the solution of a set of convex optimization problems into a linear matrix inequality solution. In the robust control, Toghani Holari et al. (2021) considered Input Output Feedback Linearization (IOFL) and Sliding Mode Control (SMC) under load variations and parameter uncertainties for AC-DC hybrid microgrid systems. Su et al. (2021) proposed a structural singular value based design methodology for robust decentralized automatic power generation controllers for deregulated multi-area power systems.

Traditional methods for load frequency control (LFC) of islanded microgrids also face some challenges, which include the following aspects:

(1) It is challenging to improve the frequency control performance of microgrids. Due to the low inertia of the microgrid and the large fluctuations of the load and renewable energy, the frequency of the microgrid is prone to large deviations, which affect the frequency quality and stability of the microgrid. Therefore, microgrids need effective frequency control strategies to suppress frequency deviations, restore the frequency to the rated value, and ensure the normal operation of microgrids. However, the existing frequency control methods, such as constant power control, constant frequency control, constant virtual inertia control, sliding mode control, fuzzy control, neural network control, etc., have certain limitations and drawbacks, such as fixed control parameters, unsatisfactory control effect, complex control logic, and non-robust control system.

(2) It is challenging to consider the multi-objective synthesis of microgrids. Since frequency control and optimal operation of microgrids are two interrelated problems and involve multiple performance indicators, such as frequency deviation, operating cost, renewable energy utilization, etc., microgrids need to consider these performance indicators comprehensively to achieve multi-objective optimization of microgrids. Therefore, microgrids need effective multi-objective optimization methods to balance the performance indicators of microgrids and achieve comprehensive optimization of microgrids. However, existing multi-objective optimization methods, such as weighted sum method, ideal point method, fuzzy set method, hierarchical analysis method, and multi-objective evolutionary algorithm, have certain limitations and drawbacks, such as subjective selection of weights, difficulty in determining the ideal point, difficulty in constructing fuzzy sets, complexity of hierarchical analysis, and slow convergence of multi-objective evolutionary algorithm.

Artificial intelligence algorithms have emerged as a promising technique for LFC of islanded microgrids with a high penetration of renewable energy sources. Many AI methods have been proposed to address the challenges of LFC, especially the reinforcement learning method, which can significantly improve the CPS performance. Zhang et al. (2021) applied Q-learning to solve the LFC problem and demonstrated its robustness. Zhang et al. (2023) proposed Q methods with a “relaxation” policy, which effectively dealt with the large time lag of thermal power units, and reduced the frequent regulation and inversion issues caused by improper LFC control strategies. Yin et al. (Linfei et al., 2017) combined the “human emotion” function with Q-learning to form an emotion reinforcement Learning, and modified the Q-learning parameters of “learning rate, reward function, and action selection” by simulating the nonlinear emotion function of humans in complex situations, which greatly enhanced the index. Yu et al. (Li et al., 2023c) proposed an agent controller that uses double deep Q-learning to operate energy storage elements in islanded microgrids. This controller minimizes the power loss in the grid even under the influence of intermittent energy sources. However, the controller is designed for steady state operation and hence transient stability is not considered. In another study, Li et al. (2022) proposed a dual deep Q-network (DDQN) controller for a microgrid energy storage system that reduces the power used from the main grid to maximize the profit. An agent microgrid power management approach to minimize the exchanged power with the main grid was proposed in (Mahboob Ul Hassan et al., 2022), where a fitted Q algorithm was used. However, the authors did not consider the transient behavior of the microgrid during disturbances. The above methods have low robustness and performance and cannot meet the requirements of islanded microgrids. Reinforcement learning methods can learn the optimal control policy by interacting with the environment, but they require the analysis of the Mercuriality of the problem, the construction of a Markov decision process, and the design of a reasonable reward function. The optimal control variables can be obtained by building an optimization model, but it requires the analysis of the constraints of the problem and the choice of a suitable solution algorithm. However, these methods have low adaptability and robustness, and are prone to the curse of dimensionality, which makes it impossible to obtain an LFC policy that can consider a wide range of metrics in a complex islanded microgrid environment.

This paper tackles the challenges of balancing multiple performance indicators for isolated microgrids, such as frequency stability and economic efficiency, which are often conflicting objectives. The paper proposes a data-driven Adaptive Load Frequency Control (DD-ALFC) method that uses deep reinforcement learning to design an agent that can make independent decisions and optimize multiple indicators. The paper also introduces a Priority Replay Soft Actor Critic (PR-SAC) algorithm that enhances the policy randomness and adaptability of the agent by using entropy regularization and prioritized experience replay. The paper demonstrates the effectiveness of the proposed method and algorithm in improving the frequency control performance and economy of a complex microgrid environment, using the Zhuzhou Island microgrid as a case study.

The main contributions and innovations of this paper are as follows:

(1) Improved deep reinforcement learning method: We propose a Priority Replay Soft Actor Critic (PR-SAC) algorithm to solve the frequency control and optimal operation problems of microgrids. PR-SAC uses entropy regularization and maximization of entropy objective to make the policy more randomly distributed, and employs the priority experience replay policy to enhance the adaptability and generalization of the algorithm. This enables the data-driven adaptive load frequency control (DD-ALFC) based on this algorithm to consider multiple performance indicators in complex microgrid environments and to improve the frequency control and economic performance.

(2) Data-driven adaptive load frequency control: We develop a DD-ALFC to evaluate the effectiveness of frequency control and optimal operation of microgrids by considering multiple performance indicators. We consider not only the frequency deviation of the microgrid, but also the operating cost of the microgrid as the objective function of the multi-objective optimization of the microgrid to achieve a comprehensive optimization of the microgrid. We design a suitable reward function to balance these performance indicators so that the frequency control and optimal operation of the microgrid can simultaneously satisfy frequency stability, economy and environmental benefits.

The structure of this paper is as follows: Section 2 introduces the problem statement and the mathematical formulation of the proposed approach. Section 3 describes the design and implementation details of the proposed method. Section 4 presents the simulation model and the analysis of the results. Section 5 concludes the paper and discusses the future work directions.

2 Model of DD-ALFC

2.1 Island microgrid model

The grid-connected inverter interface allows distributed photovoltaic (PV), wind power (WP) and energy storage (ES) units to connect to the microgrid. The distributed generation (DG) unit can track a given reference power quickly by controlling the grid-tie inverter. A first-order model is adopted to represent the grid-connected inverter model in the LFC model (Deng et al., 2022). The previous section introduces the load frequency control model of conventional thermal power units, the simplified equivalent model of renewable energy units with certain frequency regulation capability, and the simplified equivalent model of battery energy storage. Based on these models, this paper constructs a single-area load-frequency control microgrid model, which consists of two wind turbines, two photovoltaic units, an energy storage system and a diesel engine. Figure 1 shows the load frequency control model.

Figure 1

Figure 1. DD-ALFC structure.

Figure 2

Figure 2. Learning processes and programs.

This paper presents an islanded microgrid system with various distributed energy sources, such as photovoltaic (PV), wind turbine (WT), microturbine (MT), diesel generator (DG), and fuel cell (FC). A benefit and penalty function is proposed to optimize the microgrid operation, considering both the economic cost and the control cost. The smart body uses a DD-ALFC controller to generate the total regulation commands, which are then distributed to each unit by the PROP command distributor. The structure of the DD-ALFC controller is described in detail.

2.1.1 Micro gas turbines

Various fuels, such as natural gas, biogas, biomass gas, diesel, etc., can be utilized by micro gas turbines, which have the benefits of high efficiency, reliability, environmental protection and flexibility. These turbines can serve as the core power equipment in various fields, such as distributed energy, mobile emergency power generation, new energy utilization, transportation, etc. Details as Eqs 1, 2.

$C_{\text{MT},\text{OM}}={\displaystyle \sum _{t=1}^T}{k}_{\text{MT},\text{OM}}{P}_{\text{MT}}\left(t\right)(1)$

$C_{\text{MT},\text{fuel}}=C_{\text{MT}}\Delta t\frac{1}{LHV}{\displaystyle \sum _{t=1}^T}\frac{P_{\text{MT}}\left(t\right)}{{\eta }_{\text{MT}}}(2)$

where C_MT is the maintenance cost of the power consumption, k_MT,OM is the maintenance coefficient, the value of C_MT,fuel is the unit price of MT fuel gas, LHV is the low calorific value of natural gas, and P_MT is the operating efficiency of MT.

2.1.2 Diesel generators

Sag control is a technique that enables diesel generators to achieve stable frequency and voltage output. By using sag control, each unit can adjust its power output according to the voltage sag, without requiring communication or coordination with other units. This enhances the reliability and flexibility of the distributed generation system. Details as Eqs 3, 4.

$C_{\text{DG},\text{OM}}={\displaystyle \sum _{t=1}^T}{k}_{\text{DG},\text{OM}}{P}_{\text{DG}}\left(t\right)(3)$

$C_{\text{DG},\text{fuel}}=\alpha +\beta {\displaystyle \sum _{t=1}^T}{P}_{\text{DG}}\left(t\right)+\gamma {\displaystyle \sum _{t=1}^T}{P}_{\text{DG}}^2\left(t\right)(4)$

where C_DG,OM is the cost of the DG, k_DG,OM is the DG maintenance factor; P_DG is the fuel cost of the DG, and α, β, and γ are the fuel cost coefficients.

2.1.3 Fuel cell modeling

A possible way to provide secondary frequency regulation for the grid is to employ fuel cells, which can adjust their output power according to the grid frequency deviation and the area control error signal. This way, the system can restore the frequency and power balance by using fuel cells as flexible resources. Details as Eqs 5, 6.

$C_{\text{FC},\text{OM}}={\displaystyle \sum _{t=1}^T}{k}_{\text{FC},\text{OM}}{P}_{\text{FC}}\left(t\right)(5)$

$C_{\text{FC},\text{fuel}}=C_{\text{FC}}\Delta t\frac{1}{LHV}{\displaystyle \sum _{t=1}^T}\frac{P_{\text{FC}}\left(t\right)}{{\eta }_{\text{FC}}}(6)$

where C_FC,OM is the cost of the FC, k_FC,OM is the maintenance factor of the FC, P_FC (t) is the output power of the FC at time period t; C_FC,fuel is the fuel cost of the FC, C_FC is the unit price of gas for the FC and η_FC is the operating efficiency of the FC.

2.2 Objective functions and constraints

This paper presents an optimization method for the scheduling of an islanded microgrid that operates under system constraints, economic cost and frequency control objectives. A penalty function is introduced to enable the multi-objective optimization of the microgrid. The paper considers the cost and frequency regulation performance of three types of distributed generators: micro gas turbine, diesel generator and fuel cell: Details as Eqs 7, 8.

$\min {\displaystyle \sum _{t=1}^T}\left|\Delta f\right|+{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{i=1}^n}\left({\alpha }_i\Delta P_{\mathrm{G}i}^2+{\beta }_i\Delta P_{\mathrm{G}i}+{\gamma }_i\right)(7)$

$\left\{\begin{array}{l}{\displaystyle \sum _{i=1}^n}\Delta P_i^{\text{in}}=\Delta P_{\text{order}-\sum }\\ \Delta P_{\text{order}-\sum }*\Delta P_i^{\text{in}}\ge 0\\ \Delta P_i^{\min }\le \Delta P_i^{\text{in}}\le \Delta P_i^{\max }\\ \left|\Delta P_{\mathrm{G}i}\left(t\right)-\Delta P_{\mathrm{G}i}\left(t+1\right)\right|\le \Delta P_i^{\text{rate}}\end{array}\right.(8)$

where ΔP_order-∑ is the total generation power command, ΔP_i^max and ΔP_i^min are the upper and lower limits of the generation units respectively, ΔP_i^rate is the creep rate of the unit, and ΔP_iⁱⁿ is the generation power command input to the ith unit.

3 MDP model and PER-SAC algorithm for DD-ALFC

3.1 MDP model for the proposed method

Reinforcement learning is a framework for decision-making, where an agent interacts with an environment by observing its state, performing actions, and receiving rewards. The agent aims to learn a policy that maps states to actions in order to maximize the expected return over time. However, reinforcement learning algorithms often suffer from instability during training, which affects their performance (Su et al., 2021).

3.1.1 The concept of MDP in the DD-ALFC

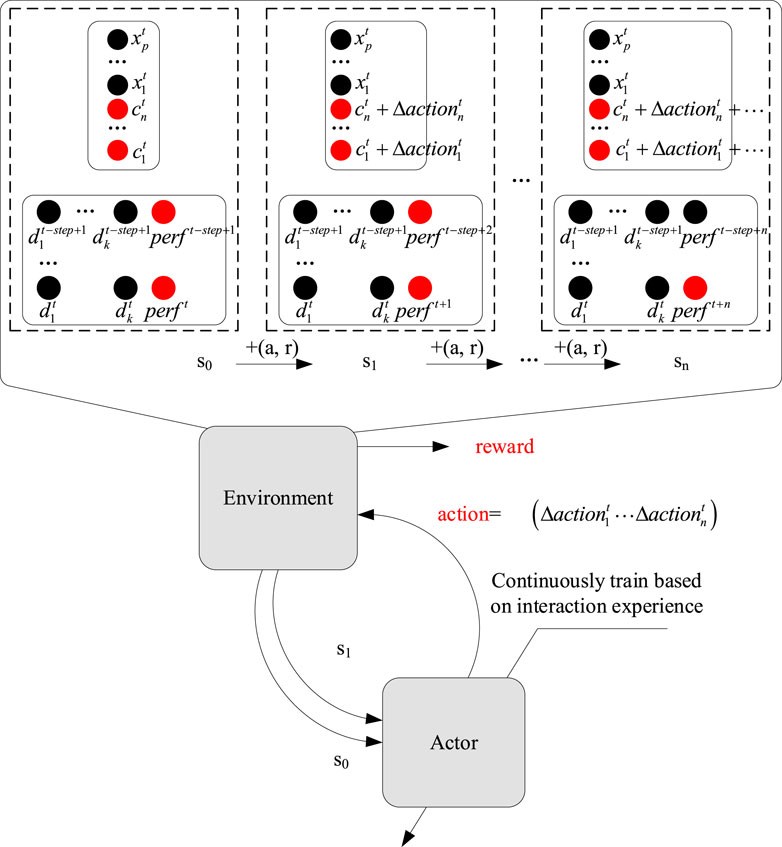
Reinforcement learning is a learning paradigm that enables agents to acquire optimal behaviors through trial-and-error interactions with stochastic environments. The theoretical foundation of reinforcement learning is the Markov Decision Process (MDP), a mathematical framework that captures the essential features of sequential decision making under uncertainty. Figure 1 illustrates the basic elements of an MDP. At each discrete time step, the agent perceives the current state s_t of the environment, selects an action at according to its strategy, and receives a scalar reward r_t+1 as a feedback, The environment then transitions to a new state s_t+1, and the process continues. The agent’s behavior is determined by one or more of the following components: policy, value function, and model. These components are defined as follows.

3.1.1.1 Policy

An agent’s behavior in different states is described by a probability distribution, which is called a policy. A policy fully determines the agent’s behavior, meaning that it assigns probabilities to all possible actions that the agent can take in each state. The policy is invariant in the same state, but the action probabilities may vary. The agent’s objective is to find the optimal policy that maximizes the expected reward over time. The policy is denoted by π (a|s), and Eq. 9 defines all the possible behaviors and probabilities of the agent in each state.

$\pi \left(a\mid s\right)=P\left(A_t=a\mid S_t=s\right)(9)$

where P is the probability of choosing action A_t to be a at time t.

3.1.1.2 Value functions

The performance of an agent in each state, or the degree of merit of a given behavior in a given state, is captured by the value function. The merit is measured by the expected future reward, which depends on the policy followed by the agent. All value functions are estimated with respect to a given policy. The reward G_t is the discounted sum of all future rewards starting from time t, as defined by the following equation. Details as Eq. 10.

$G_t=R_{t+1}+\gamma R_{t+2}+\dots ={\displaystyle \sum _{k=0}^{\infty }}{\gamma }^k{R}_{t+k+1}(10)$

The discount factor γ embodies the proportion of the value of future rewards in the current moment, and the value of the reward R obtained at k+1 moment is γ^kR at t. When γ is 0, the agent only pays attention to the immediate rewards in front of it, and does not consider the long-term benefits in the future. When γ is 1, the agent will fully consider the future rewards and regard the long-term benefits as important.

3.1.1.3 Models

An agent can use a model to represent the environment internally, which can facilitate its decision-making and planning processes in its interaction with the environment. Two problems need to be addressed by the environment model: one is the state transition probability P_ssʹ^a, which characterizes the dynamic properties of the environment and is used to predict the probability distribution of the next state sʹ after taking a behavior a in state s; the other is the prediction of the possible instantaneous rewards R_s^a. R_s^a characterizes the rewards obtained after taking a behavior a in state s. The formula is described as follows. Details as Eqs 11, 12.

$P_{s{s}^{\prime }}^a=P\left(S_{t+1}=s^{\prime }\mid S_t=s,A_t=a\right)(11)$

$R_s^a=E\left[R_{t+1}\mid S_t=s,A_t=a\right](12)$

where S_t denotes the state at moment t, A_t denotes the action at moment t; P_ssʹ^a denotes the state transfer probability, and R_s^a denotes the reward. The following is the MDP modeling of the agent.

3.1.2 The MDP model in the DD-ALFC

3.1.2.1 Action space

The ith unit (agent) functions as the output of the command of the ith unit, which makes the exploration range to be reduced in order to obtain. The action is shown as follows. Details as Eq. 13.

$a_i=\Delta P_{\text{order}-i}(13)$

where a_i is the action of the ith agent and ΔP_order-i is the regulation command of the ith agent (unit).

3.1.2.2 State space

The state of the agent is shown below. Details as Eq. 14.

$s_j=\left[\Delta f\left(k\right){\int }_0^t\Delta fdt\Delta P_{\text{order}-i}\left(k-1\right)\right](14)$

where ${\mathrm{s}}_{\mathrm{i}}$ is the state of the ith agent, Δf is the frequency deviation, and $\Delta {\mathrm{P}}_{\text{order}-\mathrm{i}}\left(\mathrm{k}\right)$ is the regulation command.

3.1.2.3 Reward function

According to Eq. 7, the reward function of the agent is shown as follows. Details as Eq. 15.

$r_i\left(k\right)=-\left[{\mu }_1\left|\Delta f\left(k\right)\right|-{\mu }_2{C}_{\mathrm{\Sigma }}^{\mathrm{p}}\right]+P_T(15)$

where ${\mathrm{r}}_i$ is the reward function of agent i, and μ₁ and μ₂ are the weight coefficients. Details as Eq. 16.

Among them

$P_T=\left\{\begin{array}{l}-5\left|\Delta f\left(k\right)\right|\ge 1KW\\ 0\left|\Delta f\left(k\right)\right|<1KW\end{array}\right.(16)$

Deterministic policies based on deep reinforcement learning algorithms have the advantage of selecting a unique action for each state. However, this also limits the exploration of the environment in the initial stage of training, when the agents have limited knowledge. Therefore, deterministic policies can only improve gradually, resulting in low learning efficiency. To address this issue, the agents should explore more randomly and adaptively in the early stage of learning, so that they can find a policy that maximizes the Q value under insufficient information. As the learning progresses, the agents should reduce the randomness and focus on the best policy according to the current information. Moreover, the exploration degree of the agents in deterministic policies is usually controlled by human intervention, which may not match the agent’s state and lead to high reward variance. This can misguide the agents to choose suboptimal policies and lower the learning efficiency. Hence, this section aims to find a DRL algorithm that can adjust the exploration degree autonomously based on the agent’s state, and select the most suitable exploration for the environment, thus reducing the reward variance and improving the learning efficiency. In summary, this section proposes a randomized DRL algorithm based on the PR-SAC algorithm, which enables the agents to explore more randomly and adaptively. The algorithm overcomes the main challenges of model-free DRL algorithms, such as poor convergence, difficulty in choosing the optimal policy, and high sampling complexity.

PR-SAC is an off-policy, actor-critic reinforcement learning algorithm that follows the maximum entropy principle. It uses a stochastic policy function that resembles deterministic deep reinforcement learning algorithms with a replay buffer storage scheme. Unlike other reinforcement learning algorithms, PR-SAC encourages exploration and exploitation of policies that maximize the expected return. By introducing an entropy term, the policy can be as random as possible, effectively balancing exploration and exploitation. This prevents the policy from getting stuck in a local optimum and allows it to explore multiple feasible solutions for a given task. This also improves the robustness of the algorithm to disturbances. The Q-function of the critic, which evaluates the quality of the actions, is modeled as follows: Details as Eq. 17.

$Q^{\mu }\left(s,a\right)=-{\displaystyle \sum _{t=1}^T}\left[\Delta t\left[{\left(B_i\Delta f\right)}^2+{\displaystyle \sum _{i=1}^n}\left(C_{total}\right)\right]\right](17)$

The policy improvement phase aims to maximize the soft Q values while maintaining the similarity between the soft Q values and the policy distribution. Hence, the new policy is obtained by minimizing the KL divergence between the policy distribution and the soft Q values. A novel approach to enhance the Actor-Critic framework is PR-SAC, which incorporates entropy into the reward function. The agent receives a reward at each step that is proportional to the entropy of the policy at the current time step, as shown in the following equation. Details as Eq. 18.

${\pi }^{*}={\mathrm{argmax}}_{\pi }{\displaystyle \sum _t}{\mathbf{E}}_{\left(s,a\right)-{\rho }_z}\left[r\left(s_t,a_t\right)+\alpha H\left(\pi \left(\cdot \mid s_t\right)\right)\right](18)$

where ρ_s denotes the distribution of state-action pairs obtained from the interaction between the agent and the environment under the control of the policy π; α denotes the entropy coefficient, which is used to adjust the degree of emphasis on the picking value. The policy π controls the agent’s interaction with the environment, resulting in a distribution of state-action pairs ρ_s. The entropy coefficient α adjusts the trade-off between the value and the entropy of the policy. The objective of maximizing the entropy-regularized value encourages the agent to explore more diverse strategies without neglecting the low-reward ones.

Entropy is introduced in both the state action value function and the state value function, called the flexible action value function Q_seft^π and the flexible state value function V_seff^π, with the following expressions. Details as Eqs 19, 20.

$Q_{seft}^{\pi }\left(s_t,a_t\right)\stackrel{\Delta }{=}r\left(s_t,a_t\right)+\gamma {\mathbf{E}}_{s_{s+1}-{\rho }_z}\left[V\left(s_{t+1}\right)\right](19)$

$V_{\text{seft}}^{\pi }\left(s_t\right)=\underset{s_t,a_t-{\rho }_z}{\mathbf{E}}\left[Q\left(s_t,a_t\right)-\alpha \log \pi \left(a_t\mid s_t\right)\right](20)$

Similarly, the actor network parameter policy gradient is computed as. Details as Eq. 21.

${\widehat{\nabla }}_{\varphi }{J}_{\pi }\left(\varphi \right)={\nabla }_{\varphi }\alpha \log \left({\pi }_{\varphi }\right)+\left({\nabla }_{a_{\theta }}\alpha \log \left({\pi }_{\varphi }\right)-{\nabla }_{a_i}{Q}_{\theta }\left(s_t,a_t\right)\right){\nabla }_{\varphi }{f}_{\varphi }(21)$

where f_φ denotes the parameterization policy for neural network transformation.

The target value in the Double-Critic network is prone to error propagation, which affects the accuracy of the action value function and leads to suboptimal solutions in Q-learning. A related challenge in reinforcement learning is policy selection, which aims to balance exploration and exploitation by retaining good policies and exploring new ones. Therefore, minimizing error propagation and achieving exploration-exploitation trade-off in double-critic networks are important problems in deep reinforcement learning. Kullback-Leibler (KL) divergence measures the similarity between two distributions, with lower values indicating higher similarity. For a random variable in the set χ, the KL divergence of two continuous probability distributions p and q is defined as follows. Details as Eq. 22.

$D_{\text{KL}}\left(p\Vert q\right)={\int }_{z}p\left(x\right)\log \left(\frac{p\left(x\right)}{q\left(x\right)}\right)dx(22)$

where p(x) and q(x) are distributed as p and q and probability density functions.

The PR-SAC algorithm alternates between two phases: policy evaluation and policy improvement. In each phase, the five neural networks that constitute the PR-SAC algorithm are updated with different objectives: Details as Eqs 23, 24.

$q_{\pi }^{\text{soft}}\left(s_t,a_t\right)=r_t+\gamma {\mathbb{E}}_{s_{t+1}-p}\left[v_{\pi }^{\text{soft}}\left(s_{t+1}\right)\right](23)$

$v_{\pi }^{\text{soff}}\left(s_t\right)={\mathbb{E}}_{a_t-\pi }\left[q_{\pi }^{\text{soft}}\left(s_t,a_t\right)-\lambda \log \left(\pi \left(a_t\mid s_t\right)\right)\right](24)$

where p denotes the state transfer probability function under the randomized policy π. π(a_t|s_t) denotes the stochastic policy π under which the agent makes the action a_t in state s_t.

3.2 Mixed priority experience replay

PR- SAC algorithms employ experience replay and random sampling of transitions to update parameters. This approach is inefficient for sparse reward scenarios, where only a few samples can provide meaningful learning signals for the agent, while most samples have small and indistinguishable rewards. Moreover, the algorithm samples transitions uniformly at random from the replay buffer, which can introduce strong temporal correlations among adjacent data and different contributions of data to the gradient learning, thus reducing the learning efficiency and even causing overfitting.

This paper proposes a method to calculate the sampling probability of samples based on the discretization of sample mixing priority. The method aims to address the problems of greedy sampling of high-error samples and poor guidance of the evaluation network in prioritized experience replay. The paper argues that high-error samples are not conducive to the optimization of the policy network, and that low-error samples should be sampled more frequently to train the evaluation network and the policy network. The paper also suggests that the dispersion of sample priority can be used to improve the diversity of training samples and to balance the sampling probability of high-error and low-error samples. The paper claims that the proposed method can reduce the uncertainty of the evaluation network and enhance the optimization ability of the policy network. The weight coefficients are as follows: Details as Eqs 25, 26.

$z_i={\left(u_i-\lambda \right)}^2+\omega (25)$

$p_i=\frac{z_i^{\zeta }}{{\displaystyle \sum _k}{z}_k^{\zeta }}(26)$

where z_i denotes the dispersion of the first i sample, λ denotes the mean of the mixed prioritization of all the samples in the experience pool, and ω denotes a small positive constant to ensure that the prioritization of each sample in the experience pool is not 0. p_i denotes the probability of sampling the first i sample, and ζ denotes the conditioning factor of the prioritization. When ζ=0, the prioritized experience replay is degraded to random uniform sampling; when 0<ζ<1, partial-priority sampling is used; when ζ=1, full-priority sampling is used. In this paper, full-priority sampling is used to calculate the sample sampling probability. The specific learning process is shown as follows:

4 Experiment and case studies

A DD-ALFC based on the PR-SAC algorithm is proposed and applied to the DD-ALFC model of the CSG microgrid (Li and Cheng, 2023). The parameters are taken from (Xi et al., 2022) and represent actual data. The CSG microgrid is an off-grid smart microgrid system in Sanya Zhuzhou Island, which uses wind power and photovoltaic power as the main energy sources and energy storage batteries and diesel generators as auxiliary energy sources. The main parameters of the CSG microgrid are as follows: wind power generation system: two 50 KW wind turbines, with an annual power generation capacity of about 200,000 kwh; photovoltaic power generation system: two sets of 130 kW photovoltaic power generation systems, with annual power generation of about 300,000 kwh; energy storage system: 2 sets of 300 kw/650 kwh lithium iron phosphate energy storage system, 1 set of 150 kw/20.6f super capacitor; diesel generator: one 150 KW diesel generator with an annual fuel consumption of about 11000L. The smart microgrid controller is used in the microgrid control system to realize the coordinated control of wind, light, storage and diesel, optimize power distribution and improve system efficiency. The aim of the CSG microgrid is to solve the problem of power supply on the island, utilize the local abundant wind and solar energy resources, realize the diversification and cleaning of energy, reduce the dependence on diesel power generation, reduce carbon emissions, and protect the island ecological environment. The proposed method is compared with DD-ALFC based on DRL algorithms such as soft actor critic (SAC) (Deng et al., 2022), trust region policy optimization (TRPO) (Xiao et al., 2023a), twin delayed deep deterministic policy gradient algorithm (TD3) (Chen et al., 2018), Deep deterministic policy gradient (DDPG) (Calovic, 1972), Double deep Q-learning (DDQN) (Zhang et al., 2021) and LFC based on algorithms such as Model predictive control (MPC) (Li and Zhou, 2023a), particle swarm optimization fuzzy proportional integral differential algorithm (PSO- Fuzzy-PI) (Harnefors et al., 2022), Genetic algorithm optimized fuzzy proportional integral differential algorithm (GA-Fuzzy-PI) (Calovic, 1972), glowworm swarm optimization fuzzy proportional integral differential algorithm (GSO-Fuzzy-PI) (Xie et al., 2023), particle swarm optimization fractional order proportional integral (PSO-FOPI), genetic algorithm optimized fractional order proportional integral (GA-FOPI).

4.1 Case 1: randomized disturbances

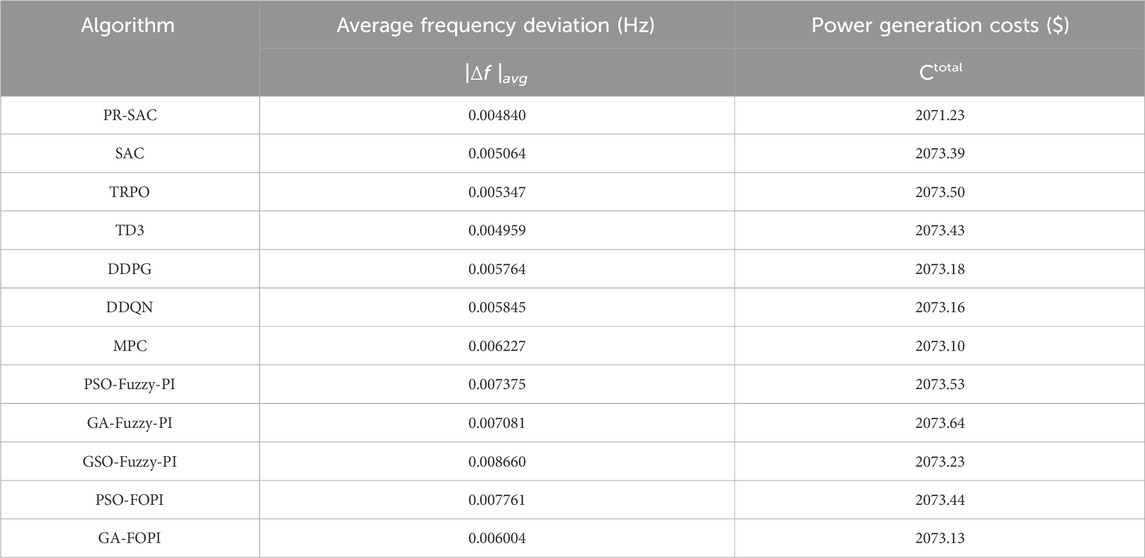
A step disturbance is applied to the system and the algorithm is tested for its robustness. The comparison of the algorithm with other methods is shown in Figures 3A, B and Table 1.

Figure 3

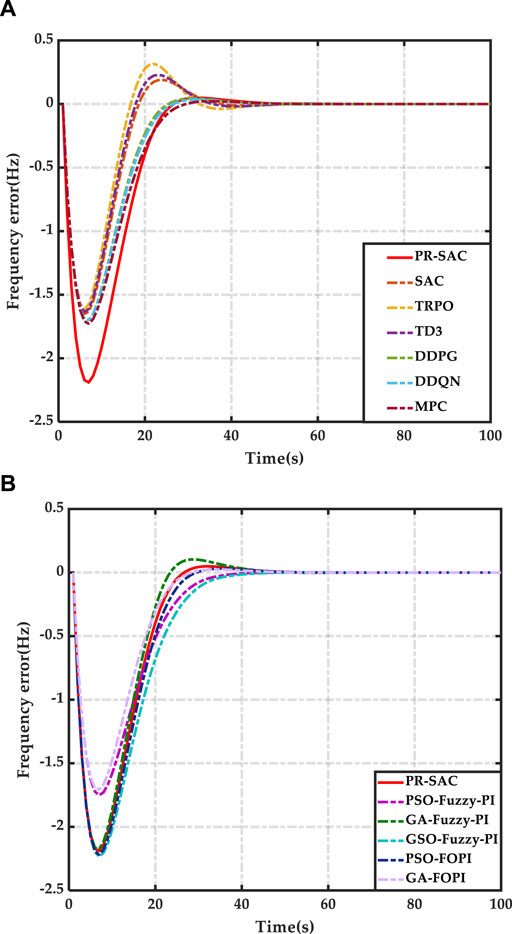
Figure 3. Results of case 1. (A) Frequency error of advanced control. (B) Frequency error of conventional control.

Table 1

Table 1. Statistical results for Case 1.

Table 1 shows the comparison between pr-sac algorithm and other algorithms in terms of frequency deviation and power generation cost. The frequency deviation of pr-sac algorithm is significantly lower than that of other algorithms, which is reduced by 2.45%–78.92%, and the generation cost of PR-SAC algorithm is also reduced by 0.09%–0.117%. Figures 3A, B shows the frequency response and diesel generator output power of the microgrid under different control modes. The simulation results show that pr-sac has the best control performance among the four intelligent algorithms, followed by SAC. This is because both pr-sac and sac adopt maximum entropy exploration, which can adjust the learning rate adaptively. By sharing experience and dynamically updating the function table, the relative weights of each region can be obtained, so that each control region can adjust the control strategy appropriately and improve the flexibility of control. The advantage of pr-sac is that it does not need average strategy estimation, but directly makes decisions based on dynamic joint trajectory and historical state action pairs. At the same time, it has strong adaptability to learners’ real-time learning rate, so it can obtain better LFC coordination control.

PR-SAC shows strong adaptability and better control performance under different conditions of the system, which fully proves the effectiveness and scalability of the proposed algorithm. Reinforcement learning has strong competitiveness among many methods because of its simplicity and universality of parameter setting. However, the application of reinforcement learning method also faces new challenges. Firstly, when dealing with large-scale tasks, it is difficult to reasonably define an optimal common exploration goal for multiple single agent reinforcement learning; Secondly, each agent needs to record the actions of other agents (resulting in poor stability) in order to interact with other agents to get joint actions. This poor stability also makes the convergence speed of many methods slow. In this context, multi-agent reinforcement learning technology with group characteristics has been rapidly developed and widely used. Reinforcement learning focuses on how to use agent exploration technology to solve dynamic tasks in real time in dynamic planning and time sequence difference methods. The pr-sac based on reinforcement learning proposed in this paper is innovative and efficient due to its more accurate independent self-optimization ability.

4.2 Case 2: renewable energy disturbances

This paper presents an intelligent distribution network model that incorporates various new energy sources, such as electric vehicles, wind power, hydropower, gas turbines, fuel cells, photovoltaic and biomass energy, to examine the regulation performance of PR-SAC in a highly stochastic environment. In this model, new energy sources such as electric vehicles, wind power and photovoltaic are considered as random load disturbances and do not participate in the system frequency control. The input signal of the wind turbine is determined by the random wind simulated by the band-limited white noise, which results in the wind power output. The active power output of the photovoltaic unit is determined by simulating the diurnal variation of solar irradiance. The relevant parameters of each unit are given in (Li and Zhou, 2023b).

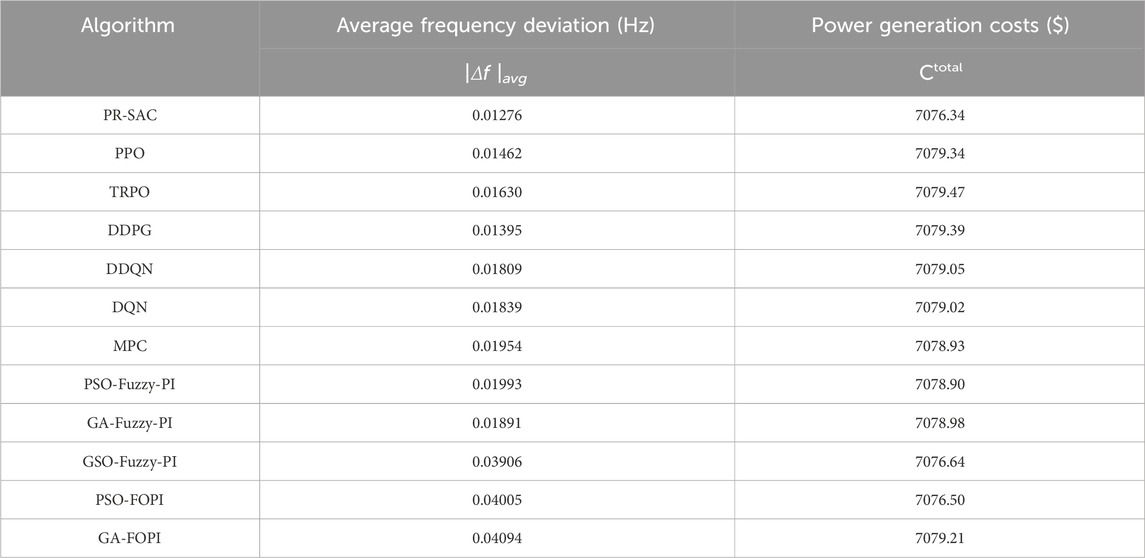
The long-term control effect of PR-SAC under strong random load disturbance was evaluated by using 24-hour random white noise as the test signal. The output curve of PR-SAC was able to track the change of random disturbance quickly and accurately, as shown in Figure 4. The statistical data of the simulation experiment were also analyzed and presented in Table 2. The generation cost was defined as the sum of the total regulation costs of all generating units within 24 h. The distribution network data indicated that the frequency deviation of other algorithms was 1.09–3.20 times higher than that of pr-sac algorithm, while the generation cost of PR-SAC algorithm was reduced by 0.0005%–0.017%. Moreover, PR-SAC had higher economy, stronger adaptive ability and better coordinated optimization control performance than other intelligent algorithms.

Figure 4

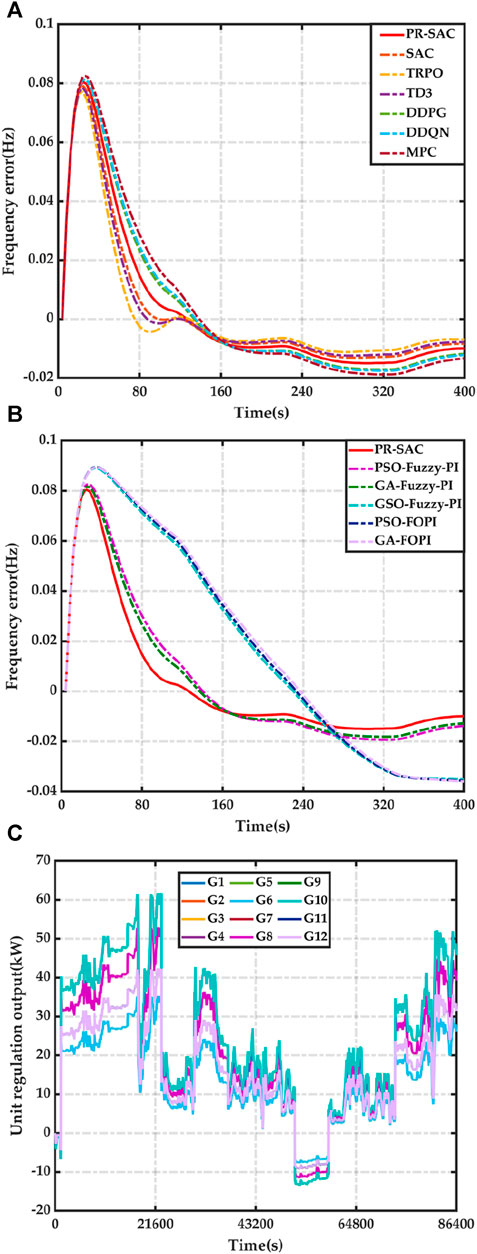
Figure 4. Results of case 2. (A) Frequency error of advanced control. (B) Frequency error of conventional control. (C) Unit regulation of output.

Table 2

Table 2. Statistical results for Case 2.

The convergence characteristics and learning efficiency of pr-sac were also verified by introducing various interference signals such as step wave, square wave and random wave. The results demonstrated that pr-sac had excellent adaptability in random environment. It could not only resist random disturbance, but also improve the dynamic control performance in interconnected power grid environment. Figure 4A illustrated the balance response relationship between the output power of various units and the load demand within 24 h. It was observed that the total power of the units could well track the load change. Under the control of the total power command, the coordinated and optimized operation of multiple energy sources was achieved in each unit period. Among them, new energy units had the advantages of fast start-up and stop, fast climbing, and large adjustment range compared with diesel units. As shown in Figure 4B, new energy units were the most important frequency modulation unit in the system and undertook most of the output tasks to cope with the load fluctuation of the power grid.

5 Conclusion

In summary, the main contributions of this work are given as follows.

This work presents a data-driven Adaptive Load Frequency Control (DD-ALFC) for isolated microgrids, which aims to balance multiple performance indicators, such as frequency stability and economic efficiency. These indicators are often conflicting, requiring grid operators to make trade-offs. The DD-ALFC treats the Load Frequency Control (LFC) controller as an agent that can make independent decisions based on the data.

To implement the DD-ALFC, a Priority replay Soft Actor Critic (PR-SAC) algorithm is proposed. The PR-SAC algorithm uses entropy regularization and maximization to achieve a more random policy distribution, and employs a priority experience replay mechanism to enhance the adaptability and generalization of the algorithm. The PR-SAC based DD-ALFC can achieve higher adaptivity and robustness in complex microgrid environments with multiple performance indicators, and improve both the frequency control and the economic performance. The proposed method is validated in the Zhuzhou Island microgrid.

Future work: The PR-SAC algorithm proposed in this article is still difficult to apply in practice due to its low generalization. Future work aims to improve the generalization of the algorithm to make it more practical.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

WaD: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft. XH: Writing–original draft, Writing–review and editing. YZ: Writing–original draft, Writing–review and editing. LW: Writing–original draft, Writing–review and editing. WeD: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the China Southern Grid Technology Project (Grant. GDKJXM20210178) and the National Natural Science Foundation of China (52177085).

Acknowledgments

The authors gratefully acknowledge the support of the China Southern Grid Technology Project and National Natural Science Foundation of China.

Conflict of interest

Authors WaD, YZ, and LW were employed by Electric Power Research Institute of Guangdong Power Grid Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1361869/full#supplementary-material

References

Calovic, M. (1972). Linear regulator design for a load and frequency control. IEEE Trans. Power Appar. Syst. PAS- 91 (6), 2271–2285. doi:10.1109/TPAS.1972.293383

CrossRef Full Text | Google Scholar

Cavin, R. K., Budge, M. C., and Rasmussen, P. (1971). An optimal linear systems approach to load-frequency control. IEEE Trans. Power Appar. Syst. PAS- 90 (6), 2472–2482. doi:10.1109/TPAS.1971.292858

CrossRef Full Text | Google Scholar

Chen, M.-R., Zeng, G.-Q., and Xie, X.-Q. (2018). Population extremal optimization-based extended distributed model predictive load frequency control of multi-area interconnected power systems. J. Frankl. Inst. 355 (17), 8266–8295. doi:10.1016/j.jfranklin.2018.08.020

CrossRef Full Text | Google Scholar

Deng, W., Zhong, J., Huang, M., Zhang, J., and Zhang, Z. (2022). Adaptive control strategy with threshold of virtual inertia and virtual damping for virtual synchronous generator. J. Phys. Conf. Ser. 2203 (1), 012039. doi:10.1088/1742-6596/2203/1/012039

CrossRef Full Text | Google Scholar

Dong, Y., Liang, S., and Wang, H. (2019). Robust stability and H_<i>∞</i> control for nonlinear discrete-time switched systems with interval time-varying delay. Math. Methods Appl. Sci. 42 (6), 1999–2015. doi:10.1002/mma.5493

CrossRef Full Text | Google Scholar

Elmouatamid, A., Ouladsine, R., Bakhouya, M., El Kamoun, N., and Zine-Dine, K. (2021). A predictive control strategy for energy management in micro-grid systems. Electronics 10 (14), 1666. doi:10.3390/electronics10141666

CrossRef Full Text | Google Scholar

Harnefors, L., Schweizer, M., Kukkola, J., Routimo, M., Hinkkanen, M., and Wang, X. (2022). Generic PLL-based grid-forming control. IEEE Trans. Power Electron. 37 (2), 1201–1204. doi:10.1109/TPEL.2021.3106045

CrossRef Full Text | Google Scholar

Li, J., and Cheng, Y. (2023). Deep meta-reinforcement learning based data-driven active fault tolerance load frequency control for islanded microgrids considering internet of things. IEEE Internet Things J. 2023, 1. doi:10.1109/JIOT.2023.3325482

CrossRef Full Text | Google Scholar

Li, J., Cui, H., and Jiang, W. (2023b). Distributed deep reinforcement learning-based gas supply system coordination management method for solid oxide fuel cell. Eng. Appl. Artif. Intell. 120, 120105818. doi:10.1016/j.engappai.2023.105818

CrossRef Full Text | Google Scholar

Li, J., Cui, H., Jiang, W., and Yu, H. (2023c). Optimal dual-model controller of solid oxide fuel cell output voltage using imitation distributed deep reinforcement learning. Int. J. Hydrog. Energy 48 (37), 14053–14067. doi:10.1016/j.ijhydene.2022.12.194

CrossRef Full Text | Google Scholar

Li, J., Yu, T., and Zhang, X. (2022). Coordinated load frequency control of multi-area integrated energy system using multi-agent deep reinforcement learning. Appl. Energy 306, 306117900. doi:10.1016/j.apenergy.2021.117900

CrossRef Full Text | Google Scholar

Li, J., and Zhou, T. (2023a). Active fault-tolerant coordination energy management for a proton exchange membrane fuel cell using curriculum-based multiagent deep meta-reinforcement learning. Renew. Sust. Energy Rev. 185, 185113581. doi:10.1016/j.rser.2023.113581

CrossRef Full Text | Google Scholar

Li, J., and Zhou, T. (2023b). Evolutionary multi-agent deep meta reinforcement learning method for swarm intelligence energy management of isolated multi-area microgrid with internet of things. IEEE Internet Things J. 10 (14), 12923–12937. doi:10.1109/JIOT.2023.3253693

CrossRef Full Text | Google Scholar

Li, J., Zhou, T., and Cui, H. (2023a). Brain-inspired deep meta-reinforcement learning for active coordinated fault-tolerant load frequency control of multi-area grids. IEEE Trans. Autom. Sci. Eng. 1-13, 1–13. doi:10.1109/TASE.2023.3263005

CrossRef Full Text | Google Scholar

Linfei, Y., Tao, Y. U., Zhou, L., Huang, L., Zhang, X., and Zheng, B. (2017). Artificial emotional reinforcement learning for automatic generation control of large-scale interconnected power grids. IET Gener. Transm. Distrib. 11 (9), 2305–2313. doi:10.1049/iet-gtd.2016.1734

CrossRef Full Text | Google Scholar

Mahboob Ul Hassan, S., Ramli, M. a. M., and Milyani, A. H. (2022). Robust load frequency control of hybrid solar power systems using optimization techniques. Front. Energy Res. 10. doi:10.3389/fenrg.2022.902776

CrossRef Full Text | Google Scholar

Qian, D., Tong, S., Liu, H., and Liu, X. (2016). Load frequency control by neural-network-based integral sliding mode for nonlinear power systems with wind turbines. Neurocomputing 173, 173875–173885. doi:10.1016/j.neucom.2015.08.043

CrossRef Full Text | Google Scholar

Su, K., Li, Y., Chen, J., and Duan, W. (2021). Optimization and H∞ performance analysis for load frequency control of power systems with time-varying delays. Front. Energy Res. 9. doi:10.3389/fenrg.2021.762480

CrossRef Full Text | Google Scholar

Toghani Holari, Y., Taher, S. A., and Mehrasa, M. (2021). Power management using robust control strategy in hybrid microgrid for both grid-connected and islanding modes. J. Energy. Storage 39, 39102600. doi:10.1016/j.est.2021.102600

CrossRef Full Text | Google Scholar

Wang, H., Yang, J., Chen, Z., Ge, W., Ma, Y., Xing, Z., et al. (2018). Model predictive control of PMSG-based wind turbines for frequency regulation in an isolated grid. IEEE Trans. Ind. Appl. 54 (4), 3077–3089. doi:10.1109/TIA.2018.2817619

CrossRef Full Text | Google Scholar

Xi, L., Li, H., Zhu, J., Li, Y., and Wang, S. (2022). A novel automatic generation control method based on the large-scale electric vehicles and wind power integration into the grid. IEEE Trans. Neural. Netw. Learn. Syst. 2023, 1–11. doi:10.1109/TNNLS.2022.3194247

CrossRef Full Text | Google Scholar

Xi, L., Yu, L., Xu, Y., Wang, S., and Chen, X. (2020). A novel multi-agent DDQN-AD method-based distributed strategy for automatic generation control of integrated energy systems. IEEE Trans. Sustain. Energy 11 (4), 2417–2426. doi:10.1109/TSTE.2019.2958361

CrossRef Full Text | Google Scholar

Xiao, H., Gan, H., Yang, P., Li, L., Li, D., Hao, Q., et al. (2023b). Robust submodule fault management in modular multilevel converters with nearest level modulation for uninterrupted power transmission. IEEE Trans. Power Deliv. 2023, 1–16. doi:10.1109/TPWRD.2023.3343693

CrossRef Full Text | Google Scholar

Xiao, H., He, H., Zhang, L., and Liu, T. (2023a). Adaptive grid-synchronization based grid-forming control for voltage source converters. IEEE Trans. Power Syst. 2023, 1–4. doi:10.1109/TPWRS.2023.3338967

CrossRef Full Text | Google Scholar

Xie, L., Wu, J., Li, Y., Sun, Q., and Xi, L. (2023). Automatic generation control strategy for integrated energy system based on ubiquitous power internet of things. IEEE Internet Things J. 10 (9), 7645–7654. doi:10.1109/JIOT.2022.3209792

CrossRef Full Text | Google Scholar

Zhang, L., Harnefors, L., and Nee, H. P. (2010). Power-synchronization control of grid-connected voltage-source converters. IEEE Trans. Power Syst. 25 (2), 809–820. doi:10.1109/TPWRS.2009.2032231

CrossRef Full Text | Google Scholar

Zhang, X., Li, C., Xu, B., Pan, Z., and Yu, T. (2023). Dropout deep neural network assisted transfer learning for Bi-objective pareto AGC dispatch. IEEE Trans. Power Syst. 38 (2), 1432–1444. doi:10.1109/TPWRS.2022.3179372

CrossRef Full Text | Google Scholar

Zhang, X., Yu, T., Yang, B., and Jiang, L. (2021). A random forest-assisted fast distributed auction-based algorithm for hierarchical coordinated power control in a large-scale PV power plant. IEEE Trans. Sustain. Energy 12 (4), 2471–2481. doi:10.1109/TSTE.2021.3101520

CrossRef Full Text | Google Scholar

Glossary