Multiphysics modeling and validation of a microwave applicator with a three-stub tuner for the continuous flow pasteurization of fruit juices with low reflection

Microwave heating technology offers several advantages for the continuous flow pasteurization of fluid foods compared to conventional heat exchangers. These advantages include rapid and volumetric heating, high energy efficiency allowing for using electricity from sustainable sources, and reduced sensory and quality loss. In fruit products, where the low pH inhibits the growth of harmful microorganisms, the primary thermal targets for pasteurization are heat-resistant enzymes such as peroxidase, polyphenol oxidase, and pectin methylesterase. The microwave applicator can quickly heat the product stream to the enzyme inactivation temperature, followed by a holding period to achieve the desired level of enzyme inactivation. The modeling and simulation of the microwave applicator is particularly challenging because it requires the coupling of three physical phenomena: propagation of electromagnetic radiation, fluid flow, and heat generation and heat transfer. Temperature-dependent changes in the product’s dielectric properties affect radiation penetration, thereby influencing heat generation. In this study, a multiphysics model was developed in COMSOL v.5.3 to numerically simulate the heating of orange juice (OJ), mango puree (MP), and mango juice (MJ; flow rate: 0.2–1.2 L/min; outlet temperature: 70–100°C) in the cavity of a pilot-scale microwave-assisted pasteurizer. The dielectric properties of the products were measured, and the model was validated against experimental results. The microwave cavity, an octagonal prism with a vertical applicator tube, is linked to a 6-kW microwave generator operating at 2.45 GHz. The model includes the waveguide and a three-stub tuner, an element seldom integrated into similar models. Simulation results provide insights into the distribution of the electric field in the domain, temperature profiles in the product, and losses of incident power due to reflection. Using the principles of electromagnetism and the Monte Carlo method, the stub heights in the tuner were optimized to minimize power reflection, quantified by the scattering parameter (S11). Seventeen processing conditions, varying in product types, temperatures, and flow rates, were simulated and compared with experimental data. The model demonstrated an overall prediction error of 1.6 ± 1.3°C for the outlet temperature of orange juice, while errors for mango purée and mango juice ranged between 1.8 and 5.5°C. The validated model serves as a valuable tool for the analyzing, designing and optimizing the microwave applicators. As an example, it was used to evaluate the influence of the cavity cross-section shape and tube positioning on power reflection and heating uniformity.

1 Introduction

Microwave heating technology can be used for a wide range of applications in the industry, such as pyrolysis processes (Ge et al., 2021; Li et al., 2022), transesterification processes (Nayak et al., 2019), and the thermal processing of liquid foods (Koutchma, 2023; Oishi et al., 2022; Karatas et al., 2022). Compared to conventional heating processes, the advantages of microwave heating include volumetric heating, the use of electric energy that can be supplied from renewable sources, high energy efficiency, and faster heating (Fellows, 2017; Kumar et al., 2008; Salazar-González et al., 2012). However, microwave heating can be non-homogeneous, creating cold or hot spots that are difficult to predict and detect, which leads to non-uniform heating (Chandrasekaran et al., 2013). The literature presents numerous studies on the continuous flow microwave heating of liquid foods, including orange juice (OJ), liquid egg, beer, apple juice, milk, peanut butter, tomato pulp, and coconut water (Yang et al., 2023; Amaro et al., 2024; Siguemoto et al., 2018; Karatas et al., 2022; Coskun et al., 2022; Teleken et al., 2022; Oishi et al., 2023).

The ability of materials to absorb and dissipate microwave energy is governed by their dielectric properties, which significantly vary with temperature. These properties influence the heating rate and uniformity of liquid in a continuous flow microwave heating system (Singh and Heldman, 2008; Chang et al., 2022). Furthermore, the design of microwave systems directly impacts heating and temperature distribution. Microwave systems consist of three main parts: (1) a microwave generator (either a magnetron or solid state); (2) a waveguide to propagate the wave to the cavity; and (3) an applicator cavity (Topcam and Erdogdu, 2021; Chang et al., 2022).

The cavity geometry and design largely influence the distribution of the electromagnetic field and temperature within the product (Topcam and Erdogdu, 2021). Recent studies investigate the impact of tube and cavity geometries on temperature uniformity in continuous flow microwave processing units. Cylindrical and elliptical prismatic cavities are commonly used for continuous flow microwave heating applications (Coskun et al., 2022; Muley and Boldor, 2012; Topcam and Erdogdu, 2021; Tuta and Palazoğlu, 2017; Nde et al., 2021; Salvi et al., 2011). These geometries allow for the microwave energy to be focused on a specific region, thereby influencing energy efficiency and heating uniformity (Chang et al., 2022).

Although recent studies achieving more uniform heating profiles for low-viscosity foods, ensuring uniform heating of high-viscosity foods remains a challenge (Kumar et al., 2008; Topcam and Erdogdu, 2021; Yang et al., 2023). One approach to improve the heating of high-viscosity foods involves increasing fluid mixing (Chang et al., 2022). Static mixers, which induce chaotic mixing and improve heat transfer coefficients, represent a potential solution (Valdés et al., 2022; Baro et al., 2025). However, the complex geometry of static mixers complicates cleaning, potentially increasing contamination risks and limiting their practical application (Campañone et al., 2023).

The position, geometry, and location of the tubes significantly affect the efficiency of continuous-flow microwave heating. Topcam and Erdogdu (2021) reported that using more than two tubes changes the electric field distribution. Another strategy to improve heating is using helical tubes instead of straight ones, as they promote fluid mixing and secondary flow while increasing the residence time in the cavity (Ruthven, 1971; Tuta and Palazoğlu, 2017; Coskun et al., 2022).

Numerical modeling and simulation serve as valuable tools for gaining process insights in both practical and idealized contexts (Datta and Sablani, 2006). A multiphysics model is essential for investigating microwave heating, as it integrates electromagnetic fields, heat transfer, and fluid flow physics. Predicting the electric field distribution within a cavity is complex. COMSOL Multiphysics, which utilizes the finite element numerical method, has been used for modeling and simulating continuous flow microwave heating (Salvi et al., 2011; Vencels et al., 2019; Topcam and Erdogdu, 2021; Chang et al., 2022; Oishi et al., 2023; Baro et al., 2025). While COMSOL is well-suited for electromagnetic simulations, it may occasionally face convergence challenges with non-isothermal fluid flow in complex tube configurations (Vencels et al., 2019).

The objectives of this study were to (1) develop a multiphysics numerical model of the microwave heater in a pasteurization unit to simulate electric field distribution, heat transfer, and laminar flow; (2) incorporate the geometry of a three-stub tuner into the model for tuning optimization; (3) validate the model using experimental data from the thermal processing of orange juice, mango puree (MP), and mango juice (MJ); and (4) use the model to study the effect of the cavity’s geometric parameters on electric field distribution and heating uniformity, thereby aiming to improve power absorption.

2 Materials and methods

2.1 Experimental runs

The experimental runs for microwave-assisted thermal processing of OJ were conducted in collaboration with Amaro et al. (2024), while those for MP and MJ were carried out in collaboration with Cavalcante et al. (2023). The food products were processed in the pilot-scale microwave-assisted pasteurizer, Lab25-UHT/HTST EMVH (MicroThermics, United States), which consists of two counter-flow helical coil heat exchangers (for conventional heating and cooling), a continuous flow microwave heater, and a holding tube, as shown in Supplementary Figure S1. The food product is pumped to the pasteurization unit using a positive displacement pump (eccentric screw). The product passes through the pre-heater before entering the microwave heating section. The conventional heater was used to preheat the food product to a temperature of 40°C for OJ and MP and 45°C for MJ prior to microwave heating, as the microwave power was inadequate to reach the required processing temperature under certain conditions.

The temperature set point for the microwave heater (temperature transmitter TT3 in Supplementary Figure S1) was chosen to ensure that the temperature at the end of the holding tube reaches the desired processing temperature. After microwave heating, the product flows through the holding tube and is eventually cooled in a cooler. Both the pre-heater and the cooler are spiral tube heat exchangers supported by an 18-kW hot-water circuit and a 3.5-kW cold-water circuit, respectively. The magnetron power level is adjusted by the controller based on the temperature set point for temperature transmitter TT3, as shown in Supplementary Figure S1. The equipment is designed to pasteurize liquid food products using either conventional heating or the microwave applicator (in this case, the conventional heater can be used as a pre-heating step). The microwave heater consists of an octagonal cavity connected to a water-cooled magnetron operating at 2,450 MHz and a 6-kW microwave generator. The applicator tube is made of alumina, a ceramic material that is transparent to microwaves. In this study, the model and simulation focused solely on the microwave heater. Modeling and simulation of the entire process were conducted by Siguemoto et al. (2018) and Russo and Gut (2022); however, they employed a highly simplified model for the microwave heater.

The processing conditions for microwave pasteurization of OJ, MP, and MJ are shown in Table 1. Room temperature, as well as the inlet and outlet temperatures of the microwave heater (temperature transmitters TT2 and TT3, respectively), and flow rates were monitored for a 2-min period following the achievement of steady-state conditions. The pilot-scale pasteurizer is equipped with temperature and flow transmitters that record experimental values every 10 s.

Table 1

Table 1. Processing conditions for the microwave pasteurization of OJ, MP, and MJ.

2.2 Numerical modeling

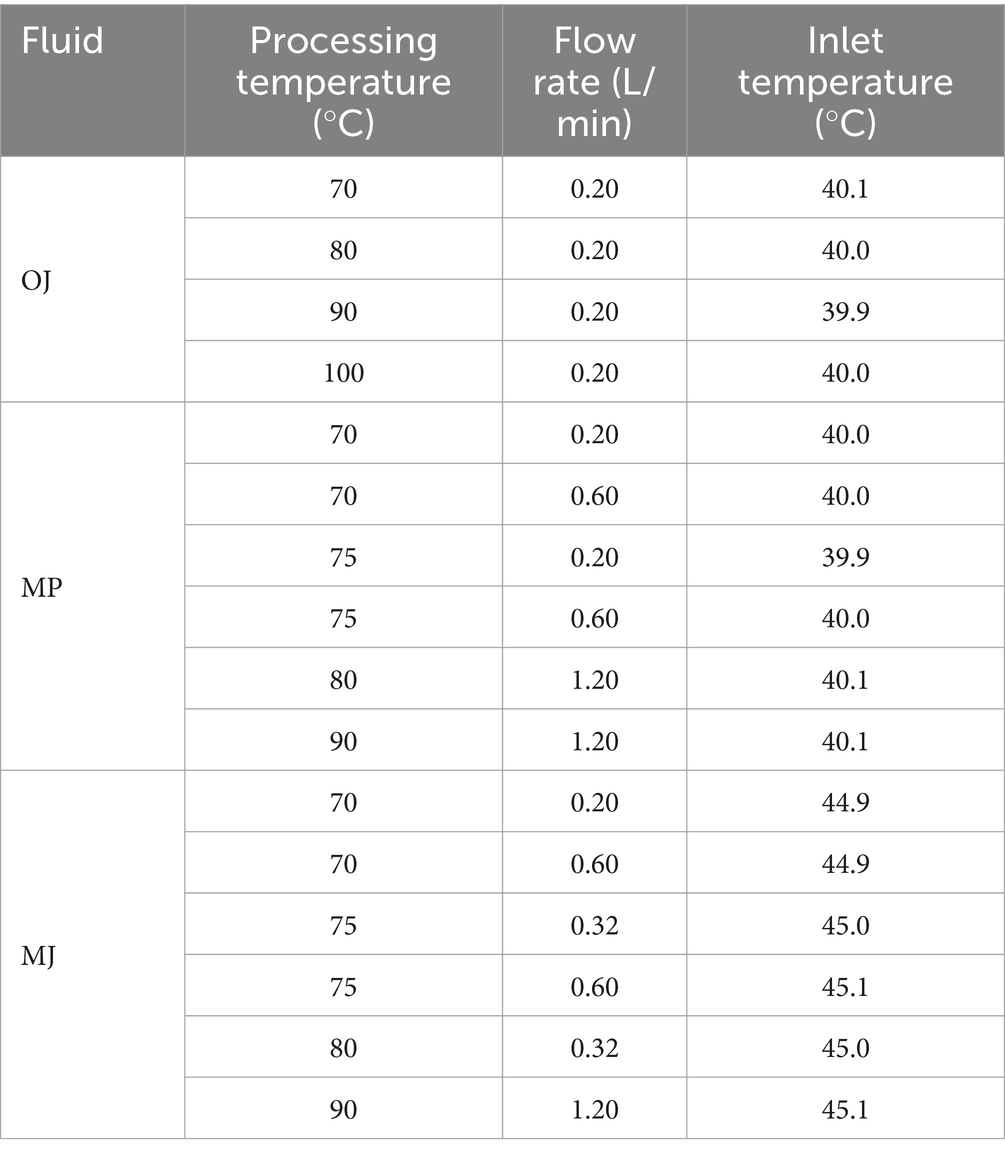
The numerical model was developed using COMSOL Multiphysics 5.3 for the microwave heater of the pilot-scale pasteurization unit. The 3D model is presented in Figure 1, which includes the cavity, waveguide, applicator tube, food product, metal inlet and outlet tubes, and tuning stubs. The applicator tube is made of alumina and has an internal diameter of 6.65 mm, an external diameter of 12.5 mm, and a length of 32.7 cm (Industrial Microwave Systems, United States). The metal tubes outside the cavity share the same diameters as the applicator tube, with bottom and top lengths of 5.0 cm and 9.5 cm, respectively. The metal tubes, stubs, and internal walls of the cavity and waveguide were modeled as aluminum, while the inside of the cavity was modeled as air. Four cross-sections were chosen to aid in visualizing the heating of the food product along the tube, as shown in Figure 1: A1 is at the entrance of the cavity; A2 is in the midpoint of the cavity height; A3 is at the end of the cavity; and A4 is where the thermocouple is located.

Figure 1

Figure 1. Tridimensional model of the microwave heater and fluid cross-sections A1, A2, A3, and A4.

The numerical model integrates three distinct areas of physics: electromagnetism, heat transfer, and fluid flow. The thermophysical and dielectric properties of OJ, MP, and MJ are shown in Supplementary Table S1.

The heights of the three stubs in the tuner can be adjusted to minimize reflection loss in the cavity. To determine the optimal individual stub heights, the S11 parameter was minimized using Monte Carlo optimization, considering only the electromagnetic field physics. The optimization goal was to minimize reflection loss and, consequently, maximize microwave energy absorption.

With the optimized stub heights, the multiphysics model was simulated. The “Frequency-Stationary” study was employed to solve the electromagnetic field, heat transfer, and fluid flow equations. Initially, the electromagnetic waves module was solved in the frequency domain, providing the electric field intensity, which was then coupled with the heat transfer and laminar flow modules. Subsequently, the temperature-dependent dielectric properties were updated, and the electromagnetic model was recalculated in the frequency domain. This iterative process continued until convergence was achieved across all three physics. The laminar flow module was used for the food product, while the heat transfer model accounted for the food product, the applicator tube, and the inlet/outlet metal tubes.

The model was validated by comparing the mixing cup temperature ($T_m$) of the food product at the outlet using Equation 1 (cross-section A4 in Figure 1) with the corresponding experimental measurements:

$\begin{array}{ll}{T}_m=\frac{1}{v_m}\underset{0}{\overset{A}{{\displaystyle \int }}}{v}_{z}TdA\text{,}& (1)\end{array}$

where $v_m$ is the bulk velocity (m/s), $v_z$ is the velocity along the cross-section (m/s), and $A$ is the cross-section area.

2.3 Mesh size

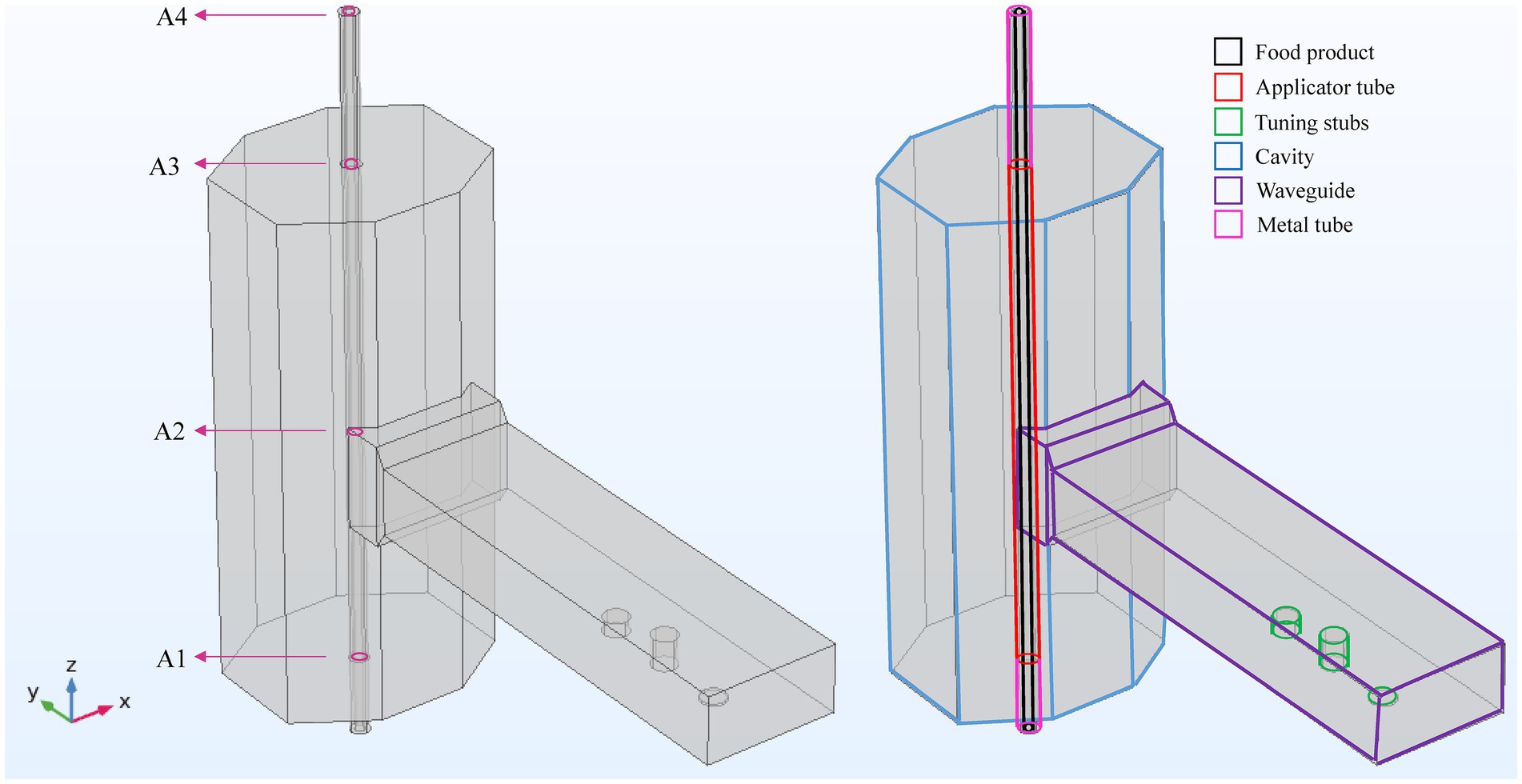
The mesh consists of free tetrahedral elements for the air domain (including cavity, waveguide, and tuners) following the Nyquist criterion $S_{\text{max}}$ in Equation 2 (Mirabito et al., 2005). However, a finer mesh was necessary for the food product, applicator tube, and metal tubes. The “free quad” generator was used to create a surface at the tube inlet, which was then swept along the tubes and food product domains. Additionally, boundary layers were added to the surfaces of the tube and product to enhance accuracy in resolving thermal gradients. The final mesh configuration is shown in Figure 2.

$\begin{array}{ll}{S}_{\text{max}}<\left[\frac{\lambda }{2}=\frac{c}{2f\sqrt{{\epsilon }^{\prime }{\mu }^{\prime }}}\right]& (2)\end{array}$

In Equation 2, $\lambda$ is the free space wavelength (m), $f$ is the field frequency (2.450 GHz), $c$ is the speed of the light in a vacuum (2.998 $\times$ 10⁸ m/s), ${\epsilon }^{\prime }$ is the dielectric constant (−), and ${\mu }^{\prime }$ is the relative permeability (−).

Figure 2

Figure 2. Free tetrahedral mesh (A) and “free quad” mesh with boundary layers (B).

A mesh study was conducted to reduce the size of the mesh elements of the food and tube domains until the average product temperature at the outlet and the return loss factor did not change. The final mesh consisted of 890,542 elements, with an average simulation time of 8 h and 49 min. All simulations were performed on a workstation computer equipped with 128 GB of RAM and a 20-core Intel 2.2 GHz processor. After the optimization of the stub heights, the mesh size varied between 830,062 and 845,591 elements for the original and alternative cavity geometries (described further in the “Study of the influence of cavity geometry and tube position” section). This variation, however, did not affect the overall solution, as the relevant physics coupling occurs exclusively within the tube and fluid regions, where the mesh remained unchanged despite alterations to the cavity geometry and stubs heights.

2.4 Governing equations

Numerical modeling of continuous flow microwave heating under steady-state operation requires coupling of electromagnetism, heat transfer, and fluid flow physics. The electric field distribution in the microwave heater was determined using Maxwell’s equation using Equation 3 (Datta and Anantheswaran, 2001):

$\begin{array}{ll}\nabla \times \left(\frac{1}{{\mu }^{\prime }}\nabla \times E\right)-{k_0}^2\left(\left({\epsilon }^{\prime }-i{\epsilon }^{"}\right)-\frac{i\sigma }{\omega {\epsilon }_0}E\right)=0& (3)\end{array}$

where $E$ is the electric field intensity vector (V/m), ${\epsilon }_0$ is the free space permittivity (8.854 $\times$ 10⁻¹² F/m), $k_0$ is the free space wave number (rad/m), $\sigma$ is the electrical conductivity of the product (S/m), and ${\epsilon }^{″}$ is the relative dielectric loss (−).

Temperature distribution within the food product was calculated using Equation 4 (Bird et al., 2002):

$\begin{array}{ll}\rho C_{p}v\cdot \nabla T+\nabla \cdot \left(-k\nabla T\right)=Q_{vd}+Q_p+Q& (4)\end{array}$

where $\rho$ is the density (kg/m³), $C_p$ is the specific heat (J/kg K), $T$ is the temperature (K), $k$ is the thermal conductivity (W/m K), $v$ is the velocity vector (m/s), $Q_{vd}$ (=0 in this model) is the work done by pressure changes (W/m³), $Q_p$ (=0 in this model) is the viscous dissipation in the fluid (W/m³), and $Q$ is the volumetric heat source generation due to incident microwave energy (W/m³).

The volumetric heat source generation due to the incident microwave energy can be calculated using Equation 5, which incorporates the electric field intensity and the dielectric properties of the food product:

$\begin{array}{ll}Q=\frac{1}{2}Re\left(i\omega B\cdot H\right)+\frac{1}{2}Re\left(J\cdot E\right)& (5)\end{array}$

where $\omega$ is the angular wave frequency ($2\pi f$, rad/s), $Re$ indicates the real part of the complex variables, $B$ is the magnetic flux density (T), $H$ is the magnetic field (A/m), and $J$ is the current density (A/m²).

Velocity profiles of the food product were obtained by solving the vector equation representing the conservation of momentum (Equation 6) and the continuity equation (Equation 7) (Bird et al., 2002).

$\begin{array}{ll}\rho \left(v\cdot \nabla \right)v=\nabla \cdot \left(-\mathit{PI}+K\right)+F& (6)\end{array}$

$\begin{array}{ll}\nabla \cdot \left(\rho v\right)=0& (7)\end{array}$

where $P$ is pressure (N/m²), $\mu$ is the dynamic viscosity (Pa s), $I$ is the identity matrix, $F$ is the volume force vector (N/m³), and $K$ is the viscous stress tensor (Pa).

2.5 Boundary conditions and initial values

The boundary conditions for the “Electromagnetic Waves, Frequency Domain” module were defined as follows: (1) The perfect electric conductor boundary condition ($n\times \overrightarrow{E}=0$) was applied to all metal surfaces of the microwave cavity; (2) for the input microwave power boundary condition, the transverse electric mode TE₁₀ was used at the rectangular port; (3) the scattering boundary condition was applied at the inlet and outlet of the food product cross sections (A1 and A3 in Figure 1). The value of the supplied power was calculated based on the $S11$ parameter (obtained from the solution of the electromagnetic model and the absorbed energy values derived from experimental runs (Amaro et al., 2024; Cavalcante et al., 2023).

The boundary conditions for the “Heat Transfer” module were defined as follows: (1) Heat loss at the outer surface of the applicator tube and metal tubes was considered due to natural convection and (2) the inlet product temperature was defined and set equal to the experimental temperature obtained from the experimental runs.

For the “Laminar Flow” module, the boundary conditions were set as follows: (1) no-slip condition for the food product in contact with the tube walls; (2) the average inlet velocity set equal to the experimental values; and (3) the outlet pressure was set as 4.5 bar, based on pressure measurements recorded during the experimental runs.

A visual representation of all boundary conditions for the “Electromagnetic Waves, Frequency Domain,” “Heat Transfer,” and “Laminar Flow” modules is shown in Supplementary Figures S2–S4, respectively.

2.6 Study of the influence of cavity geometry and tube position

After the validation of the model described in the “Numerical modeling” section with experimental data, the multiphysics model was used to study the effect of modifications to the geometry and dimensions of the cavity, as well as to the position of the applicator tube. These changes aimed to enhance the absorption of microwave energy by the food product. For this study, the food considered was OJ, and the processing conditions were 100°C at 0.20 L/min (Amaro et al., 2024). Three geometries were studied by varying the shape of the cavity cross-section, as shown in Figure 3: (1) an irregular octagonal prism cavity (OC), based on the original design; (2) a cylindrical cavity (CC); and (3) an elliptical cavity (EC). The latter two were based on other examples found in the literature (Nde et al., 2021; Topcam and Erdogdu, 2021; Salvi et al., 2011).

Figure 3

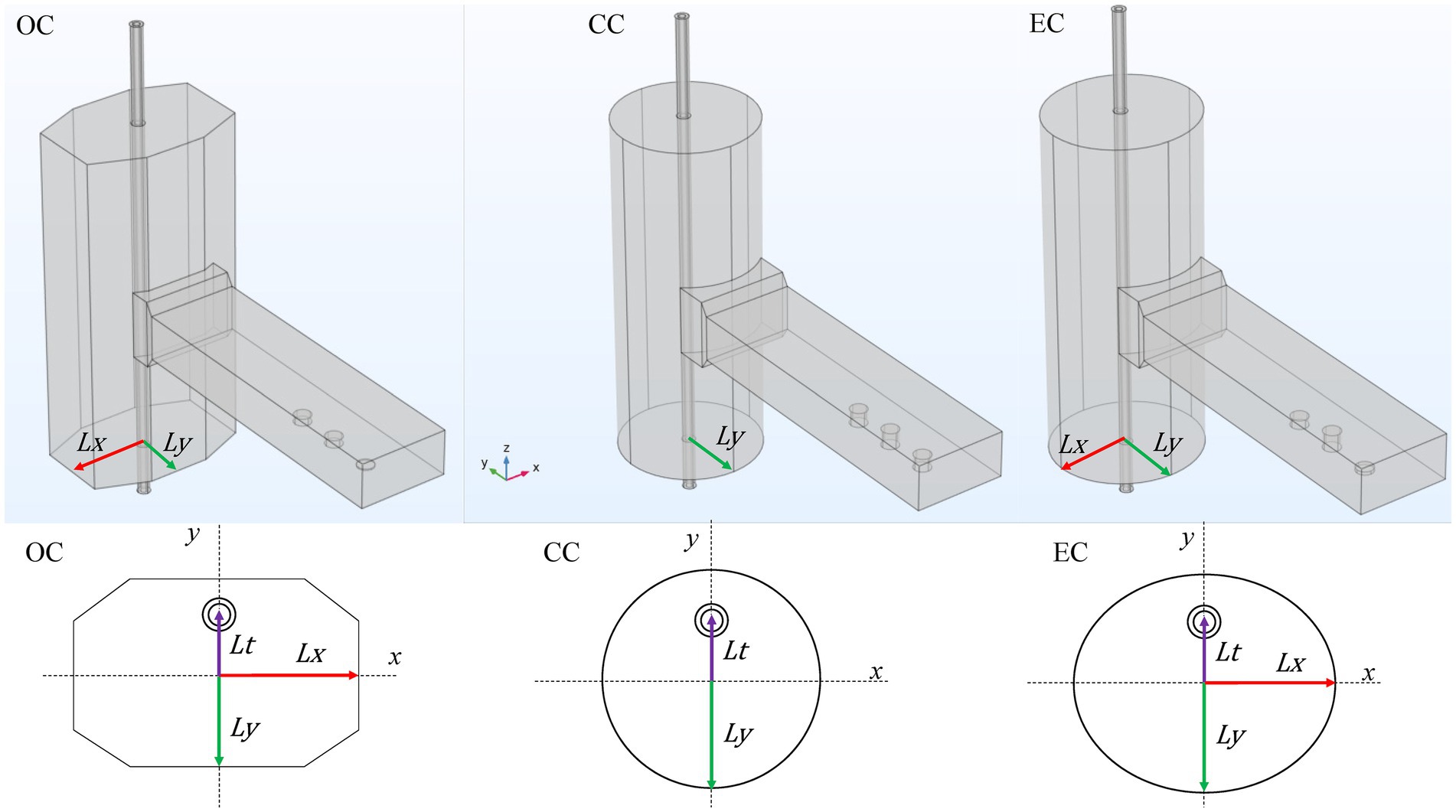
Figure 3. Octagonal prism (OC), cylindrical (CC), and elliptical (EC) cavities proposed and parameters $Lx$, $Ly\text{,}$ and $Lt$.

To determine the best geometry and dimensions of the cavity, the $S11$ parameter was minimized. The initial condition was the original design of the cavity. The dimensions chosen for the study were $Lx$, $Ly\text{,}$ and $Lt\text{,}$ as shown in Figure 3. $Lx$ and $Ly$ are the distance from the geometric center of the cavity to the walls in the $x$ and $y$ directions, respectively. $Lt$ is the distance of the geometric center of the tube from the geometric center of the cavity in the $y$ direction, as shown in Figure 3. Optimization was conducted in three steps. First, $Ly$ values were swept to minimize reflection loss ($S11$ parameter). Afterward, different values of $Lx$ were swept with the same objective, and finally, the tube position ($Lt$) was optimized for $S11$. For the CC, $Ly$ was set equal to $Lx$. The sweep ranges of $Ly$, $Lx\text{,}$ and $Lt$ are shown in Supplementary Table S2. The swept pace for $Ly$, $Lx\text{,}$ and $Lt$ was 1 mm. After optimizing $Lx$, $Ly\text{,}$ and $Lt$ for each cavity geometry, the model was simulated to obtain the outlet temperature of the OJ and the radial temperature profiles along the applicator tube.

3 Results and discussion

3.1 Model simulation and validation

With the mesh defined in the “Mesh size” section, the model was first used to optimize the heights of the tuning stubs using the electromagnetic radiofrequency module. The minimized values of the $S11$ parameter were − 30.4, −36.2, and − 23.9 dB for OJ, MP, and MJ, respectively, which corresponds to a reflection of less than 0.5%. The heights of the three-stub tuner are shown in Figure 4. The optimization of the stub heights considered only the electromagnetic physics, while the dielectric properties were calculated based on the inlet temperature of the product. However, when flow and heat transfer are taken into account in the multiphysics model, the dielectric properties become non-uniform. In these simulations, the $S11$ parameter increased to −17.2, −8.14, and − 6.87 dB for OJ, MP, and MJ, respectively, raising the microwave power reflection, particularly for MJ, which rises to 20.6%, as shown in Table 2. The temperature difference between the experimental and predicted values at cross-section A4 is also shown in Table 2 (the experimental and predicted temperatures exceed the desired processing temperatures to account for heat losses in the holding tube). OJ simulations showed temperature discrepancies between predicted and experimental data of less than 2°C across all process conditions, while MJ and MP temperature predictions showed differences ranging from 1.8 to 5.5°C.

Figure 4

Figure 4. Stub heights in the waveguide for the microwave heating of OJ, MP, and MJ.

Table 2

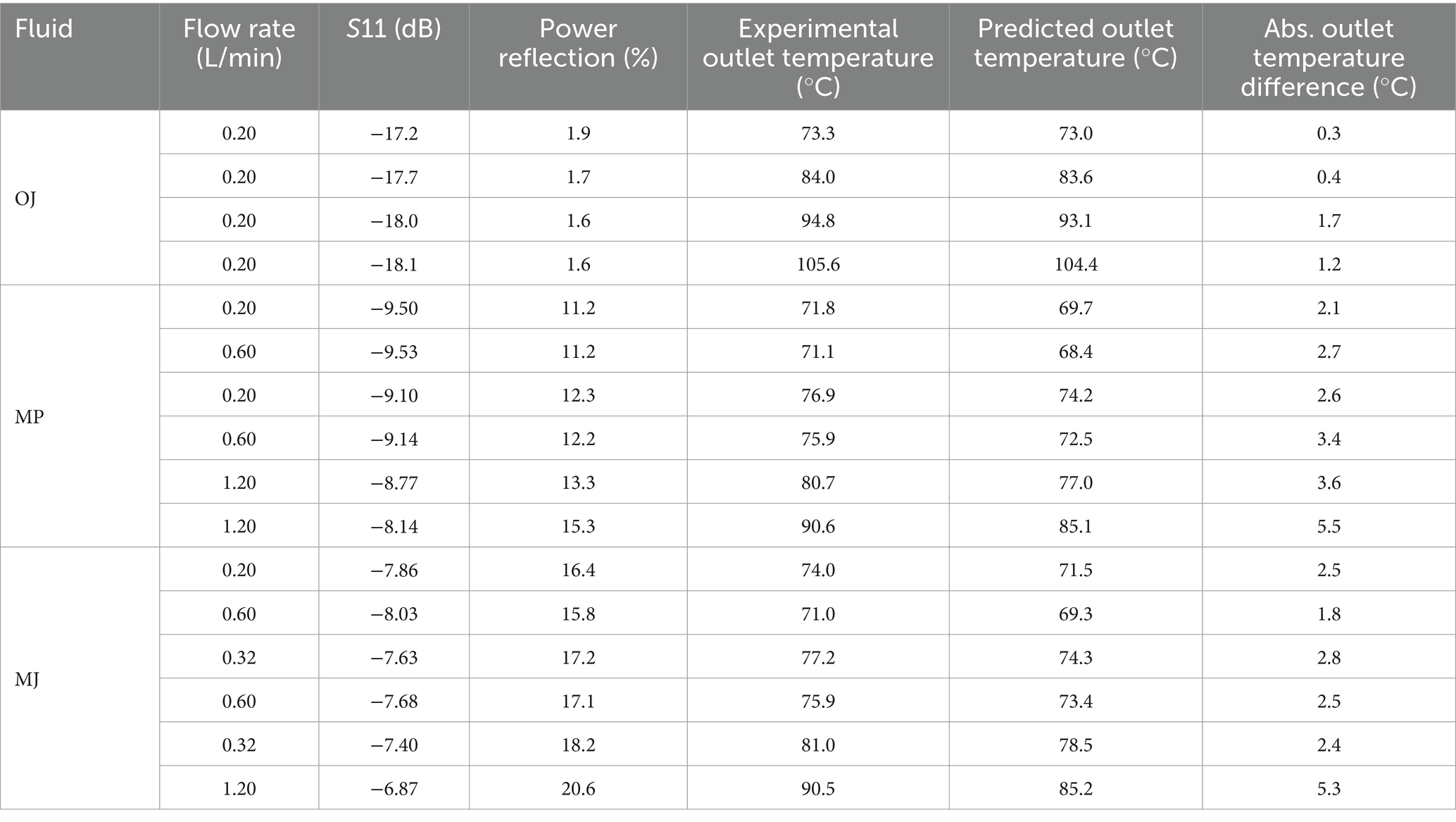
Table 2. The $S11$ parameter, power reflection, and temperature difference between experimental and predicted temperatures at the outlet.

The predicted temperature was lower than the experimental temperature for all processing conditions, which could be related to the scattering boundary condition in the model.

The intensity of electric fields (in V/m) along the tube for heating three food products at 70°C and 0.20 L/min is shown in Figure 5. Three areas with the highest electric field intensity are observed at cross-sections A1, A2, and A3 (Figure 1). The greatest electric field intensity occurs in the middle of the cavity near the waveguide (cross-section A2), as expected. The electric fields at cross-section A2 for OJ, MJ, and MP are shown in Figure 6. For MJ and MP, the electric field at cross-section A2 is slightly shifted from the center of the tube, moving closer to the entrance of the waveguide. In contrast, for OJ, the electric field at cross-section A2 is centered, aligning with the region where particles of the food product exhibit the highest velocity, which is important for achieving heating homogeneity.

Figure 5

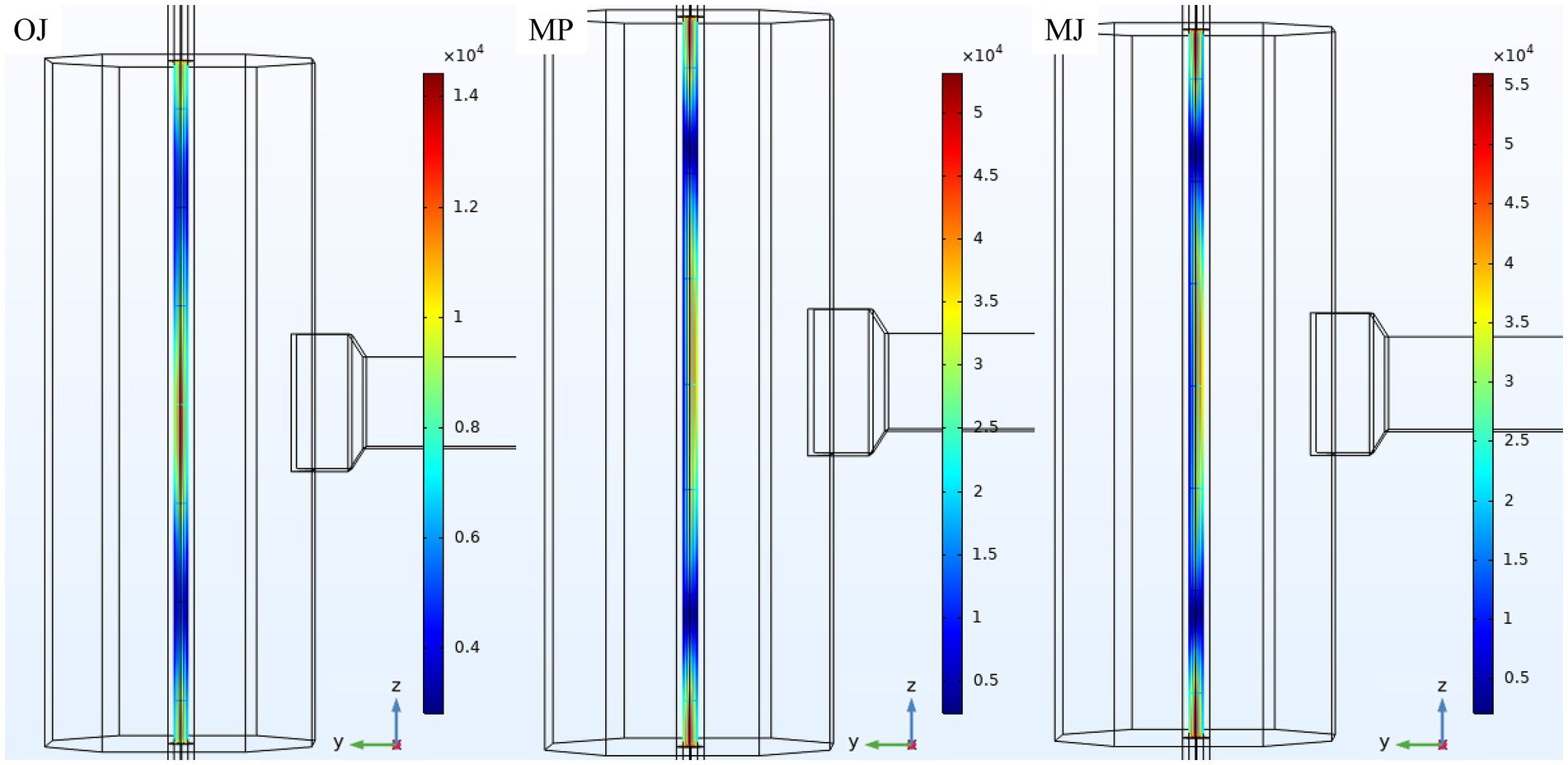
Figure 5. Electric field intensity distribution (in V/m) along the tube for the heating of OJ, MP, and MJ at a processing temperature of 70°C and a flow rate of 0.20 L/min.

Figure 6

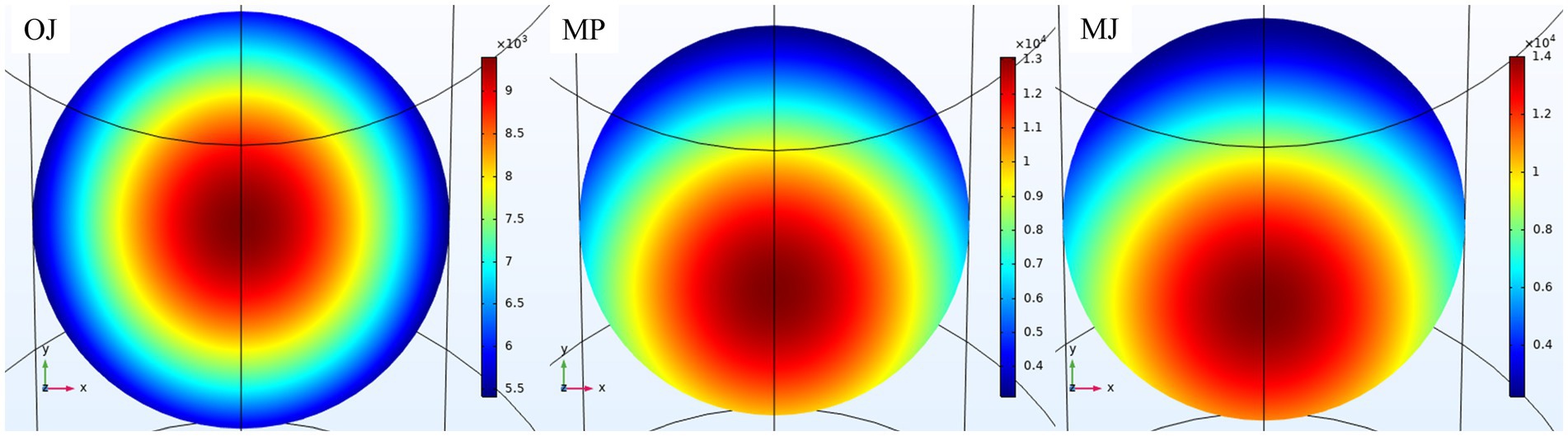
Figure 6. Electric field distribution intensity (in V/m) at cross-section A2 for the heating of OJ, MP and MJ at a processing temperature of 70°C and a flow rate of 0.20 L/min.

The radial temperature profile (in °C) at cross -sections A1, A2, A3, and A4 for the processing of OJ at 70°C and 0.20 L/min is shown in Figure 7. Different processing temperatures did not exhibit variations in the temperature profile patterns at the same flow rate. The radial temperature profile of OJ was symmetric, with higher temperatures at the edges and cooler temperatures in the center, along with a slightly higher temperature hot spot near the tube wall closer to the waveguide (section A3). Despite the intense electric field at the center of the tube, as shown in Figure 6, the product velocity at the center of the tube is much higher than near the walls; consequently, the temperature is lower at the center.

Figure 7

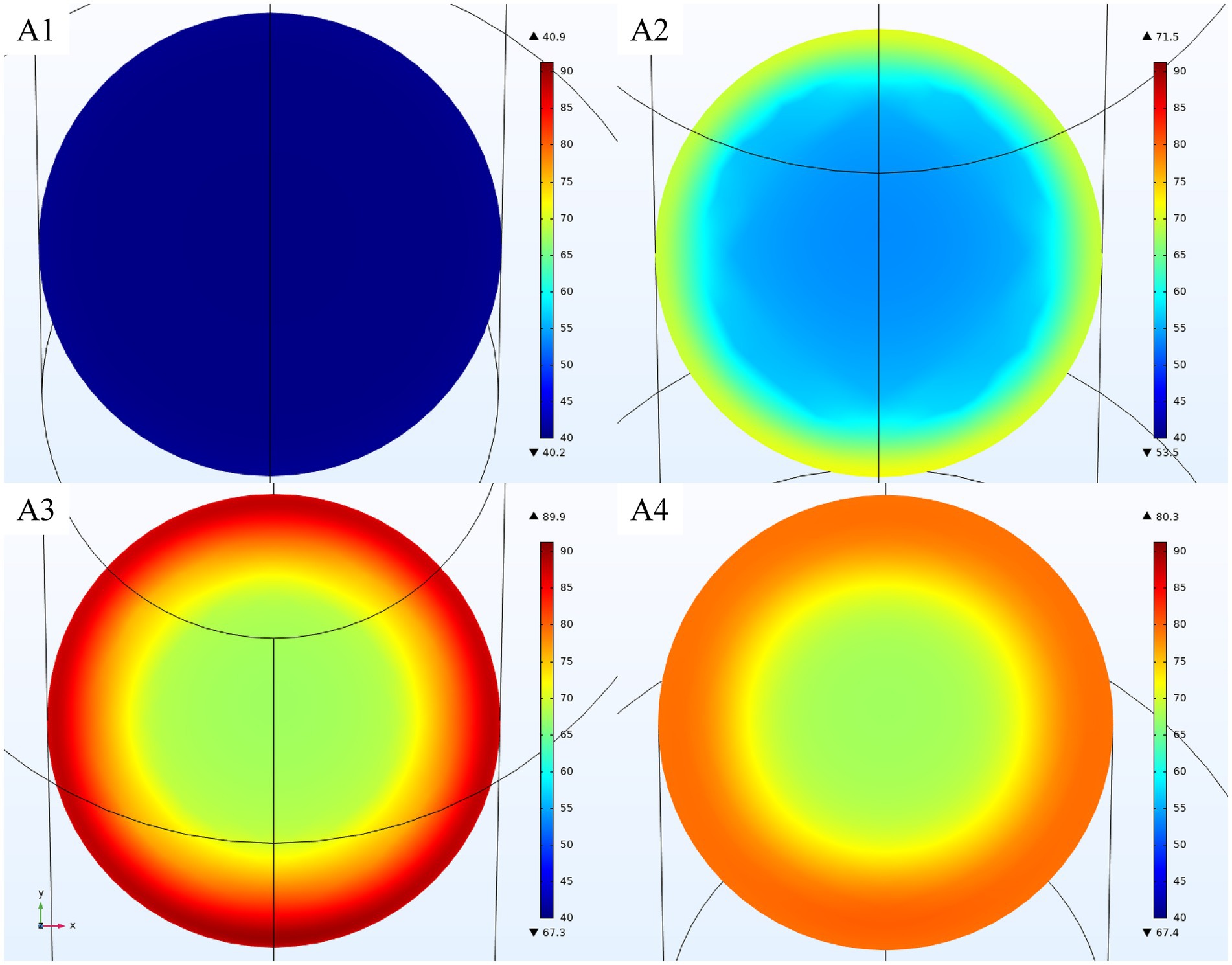
Figure 7. Radial temperature profiles (in °C) of OJ at a processing temperature of 70°C and a flow rate of 0.20 L/min at cross-sections A1, A2, A3, and A4.

Figure 8 shows the radial temperature profiles of MP at a processing temperature of 70°C and a flow rate of 0.20 L/min, while Figure 9 shows the temperature profiles for MJ under the same processing conditions. The radial temperature profiles for MP and MJ did not exhibit noticeable differences at identical flow rates, which is consistent with the results from OJ modeling. Both MP and MJ temperature profiles showed a hot spot near the wall adjacent to the waveguide, corresponding to the electric fields shown in Figure 6.

Figure 8

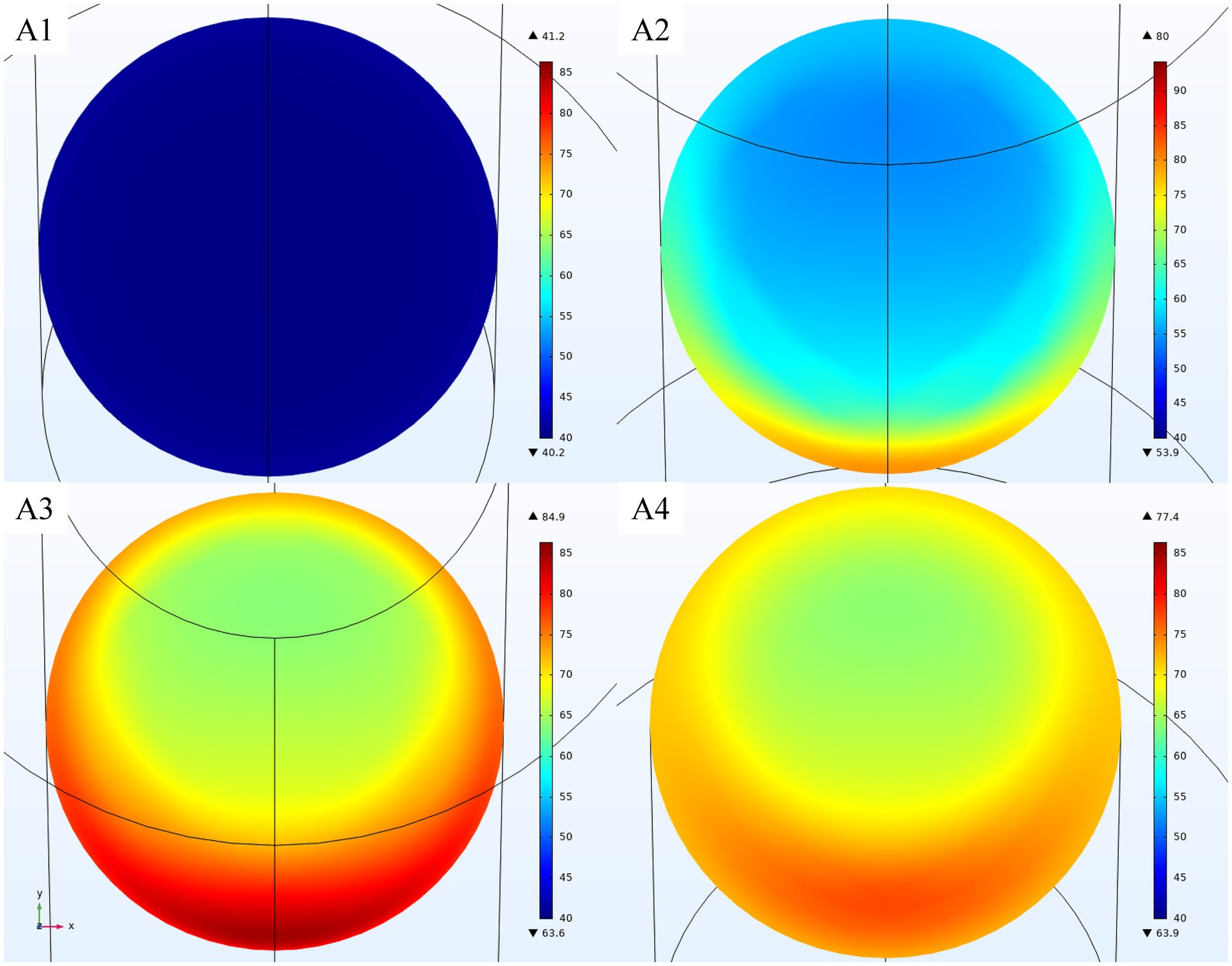
Figure 8. Radial temperature profiles (in °C) of MP for at a processing temperature of 70°C processing temperature and a flow rate of 0.20 L/min at cross-sections A1, A2, A3, and A4.

Figure 9

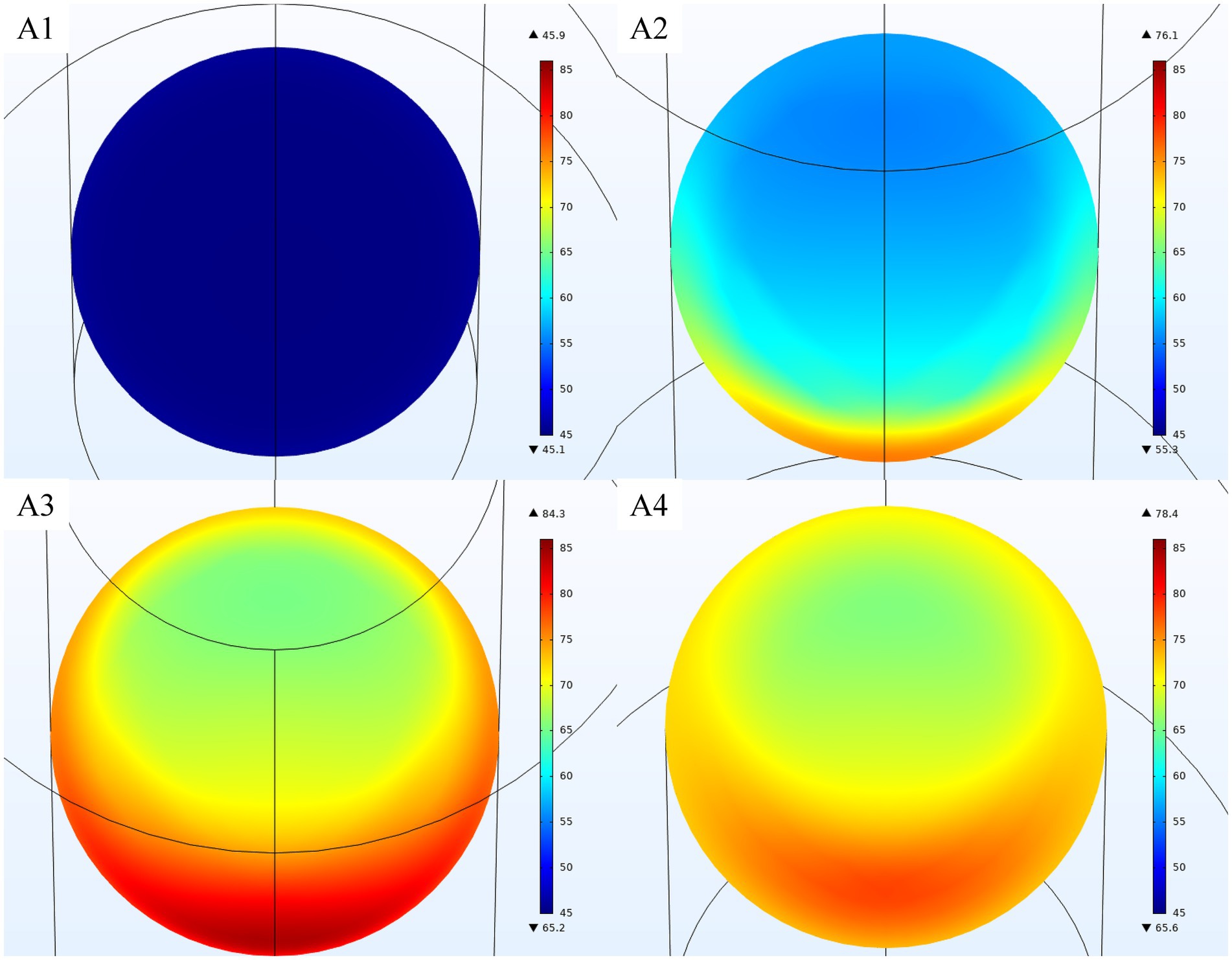
Figure 9. Radial temperature profiles (in °C) of MJ for at a processing temperature of 70°C processing temperature and a flow rate of 0.20 L/min at cross-sections A1, A2, A3, and A4.

The radial profiles for the processing of MP and MJ at a higher flow rate (0.60 L/min) are shown in Supplementary Figures S5, S6, respectively. When comparing the radial profiles at 0.20 L/min and 0.60 L/min, it can be noted that a higher flow rate resulted in a greater temperature amplitude (the difference between the highest and lowest temperatures) at the outlet cross-section A4. These results show less homogenous heating at higher flow rates. The increased temperature amplitude can be attributed to the shorter residence time in the applicator tube (4.8 s at 0.20 L/min and 1.6 s at 0.60 L/min) and the fact that microwave energy is primarily absorbed near one side of the wall for the mango products. The temperature amplitude decreased by at least 6.3°C from the radial temperature profiles at A3 (the end of microwave heating) to those at A4 (where the thermocouple is located) in less than 2 s at the lowest flow rate due to heat diffusion.

The outlet temperature profile was mainly non-uniform across all process conditions and products, which can pose a food safety issue (cold spots). Recent studies in the literature explore various methods to improve heating uniformity, such as using helical tubes (Dewangan and Kumar, 2020; Zhang et al., 2021; Yang et al., 2023; Zafar et al., 2024) or curved tubes (Topcam and Erdogdu, 2021), modifying the curvature pitch (Zhang et al., 2021), changing the applicator tube diameter (Teleken et al., 2022), and adjusting the entrance position of the applicator tube (Topcam and Erdogdu, 2021). Most of these studies suggest that promoting radial mixing in laminar flow is crucial.

To maximize the absorbed microwave energy, three distinct geometries for the microwave cavity and modifications to the inlet position of the applicator tube were proposed.

3.2 Study of the influence of cavity geometry and tube position

To maximize microwave power absorption, three distinct geometries for the microwave cavity (OC, CC, and EC) were analyzed and optimized, as described in the “Study of the influence of cavity geometry and tube position” section, considering the heating of OJ. The multiphysics model used was the same as the one validated with experimental data in the previous section.

The optimized dimensions $Lx$, $Ly\text{,}$ and $Lt$ for each cavity configuration are shown in Table 3. Among the evaluated geometries, the original octagonal cavity (OC) had the lowest $S11$ parameter, indicating the highest microwave energy absorption. In contrast, the cylindrical cavity (CC) and elliptical cavity (EC) showed similar values of the minimized $S11$ parameter. The highest power reflection was at 0.59% for the EC, suggesting a slightly lower energy absorption efficiency than the OC. Additionally, displacing the applicator tube from the center did not improve the $S11$ parameter for the OC. However, for the EC and CC, positioning the applicator tube slightly away from the waveguide (positive value of $Lt$) decreased the value of the $S11$ parameter.

Table 3

Table 3. Optimized cavity dimensions and applicator tube position for minimization of the $S11$ parameter.

After the values of $Lx$, $Ly\text{,}$ and $Lt$ were determined, the heights of each individual stub were further optimized to minimize the $S11$ parameter using the electromagnetic wave module. These optimized values are also shown in Table 3. The heights of the 3-stub positions are shown in Supplementary Figure S7. The power reflection for all three optimized cavities was below 0.5%, indicating minimal power reflection.

Electric fields along the fluid for OC, CC, and EC cavities are shown in Figure 10. For all cavities, the electric field intensity had a circular symmetry, but it is not aligned with the center of the tube; instead, it is displaced away from the waveguide. Overall, the electromagnetic field is more evenly distributed along the length of the tube in the three cavities (Figure 10) compared to the original cavity (Figure 5).

Figure 10

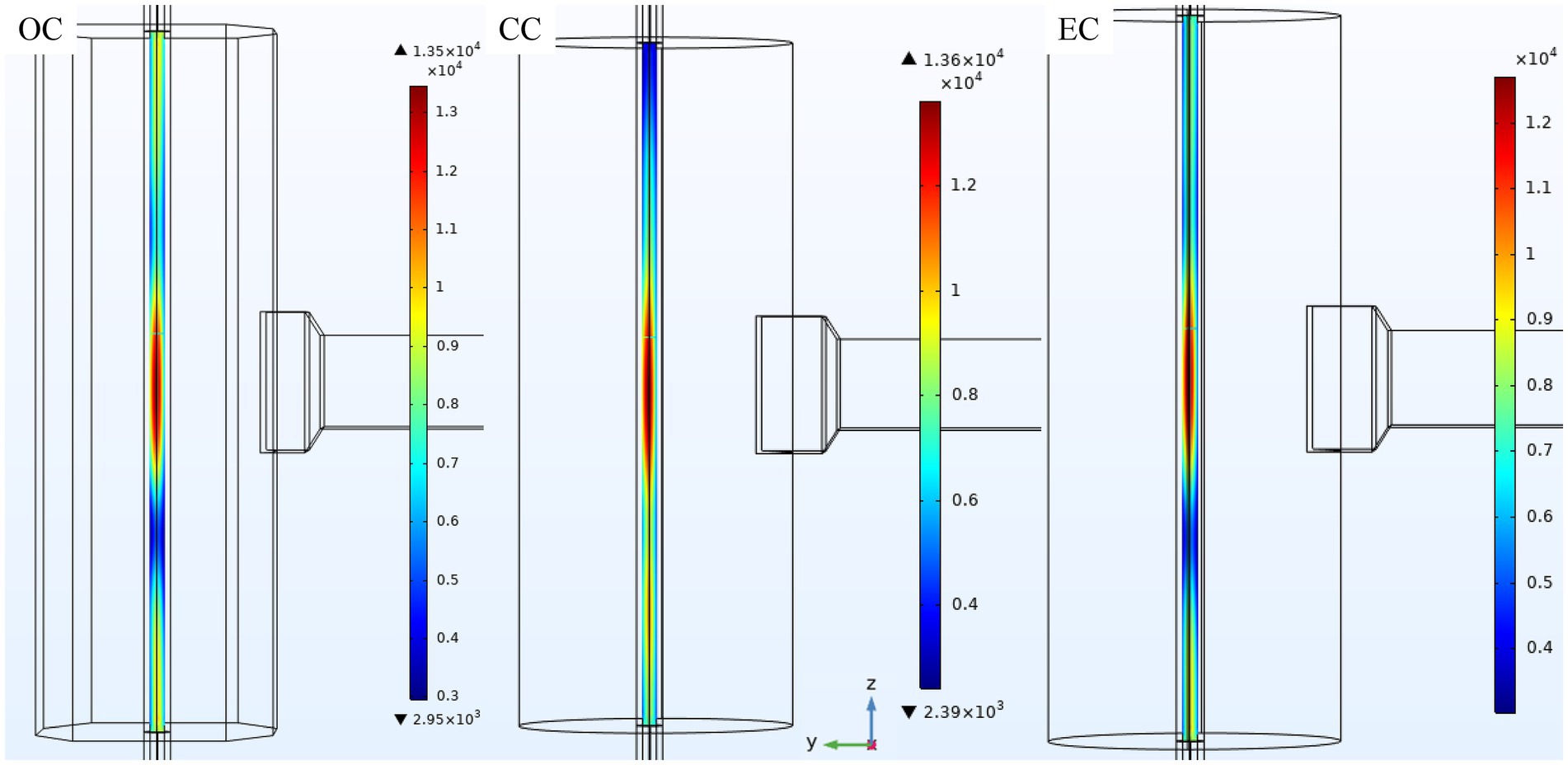
Figure 10. Electric field intensity distribution (in V/m) along the food fluids for the OC, CC, and EC cavities.

The electric field intensity in the product at cross-section A2 for the OC, CC, and EC are shown in Figure 11. For the three studied geometries, the electric field was more intense near the center of the tube but shifted in the $y$ direction, away from the waveguide.

Figure 11

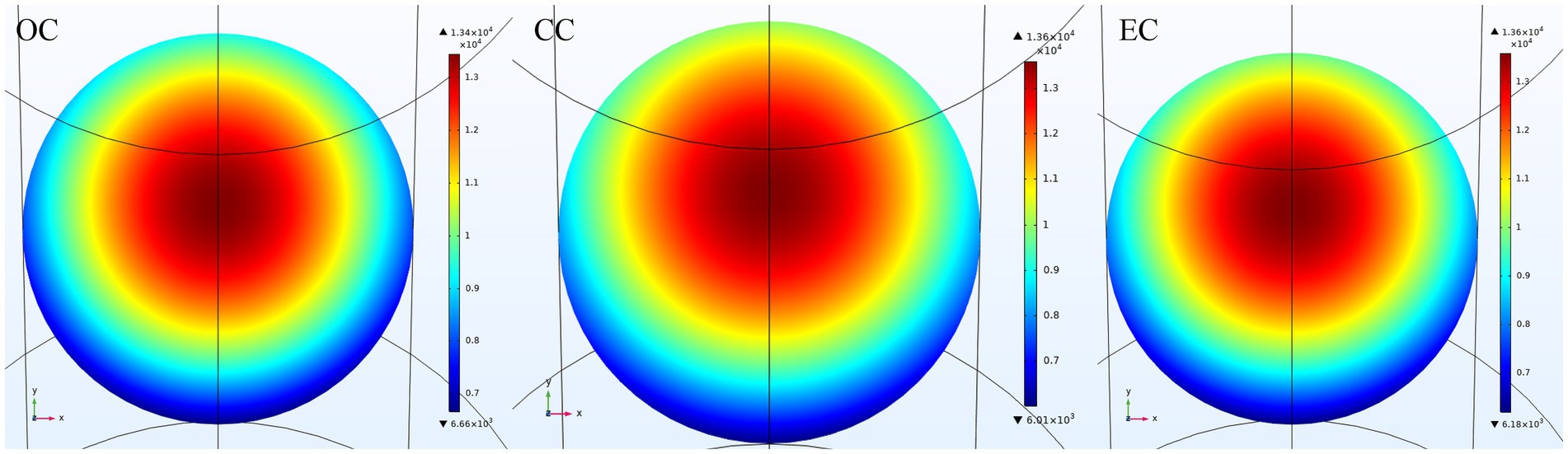
Figure 11. Distribution of electric field intensity (in V/m) at the cross-section A2 for the OC, CC, and EC cavities.

After optimizing the cavity dimensions and stub heights, the multiphysics model was run to predict the radial temperature profiles of the food product along the tube. The multiphysics model utilized input parameters corresponding to the processing of OJ at 100°C and 0.20 L/min.

The predicted mixing cup temperature at cross-section A4 (cavity outlet) and the S11 parameter are shown in Table 4. When comparing results from Tables 2 (OJ, 0.20 L/min, 100°C) and 4, the optimized cavities promote an increase in the predicted outlet temperature of 2–3°C.

Table 4

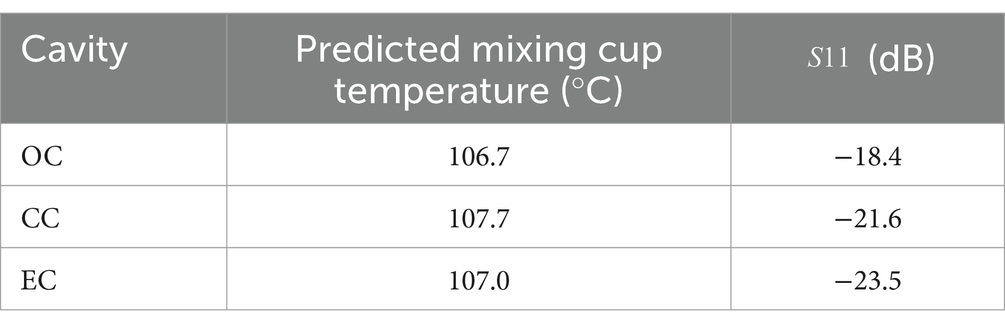
Table 4. Predicted mixing cup temperature of OJ at outlet and the $S11$ parameter of the cavity for all cavities with optimized dimensions and tuning.

The OC showed the largest difference in the $S11$ parameter when the model considered only the electromagnetic wave module (Table 3) and when heat transfer and fluid flow were coupled (Table 4), showing the importance of considering temperature-dependent dielectric properties. The CC had the highest predicted mixing cup temperature of the three cavities; however, the differences between the predicted mixing cup temperatures of all cavities were lower than or equal to 1.0°C.

The radial temperature profiles of the product in the OC, CC, and EC are shown in Supplementary Figures S8–S10, respectively. All cavities exhibited a hot spot in the tube near the wall opposite the waveguide, consistent with the electric field intensity shown in Figure 11.

While the OC had the lowest outlet temperature and the highest $S11$ parameter (Table 4), it exhibited a lower temperature amplitude at section A4 (25.6°C) compared to CC (44.9°C) and EC (38.3°C). This finding suggests that the OC achieved a more homogenous radial temperature profile than the CC and the EC.

Although the OC exhibited a lower temperature amplitude than the other proposed cavities and the original cavity under the same processing conditions, it still resulted in a non-homogenous heating profile. To address this issue, one approach would be to use a curved or helical applicator tube. Such designs promote radial mixing effects due to centrifugal forces and secondary flow, improving temperature uniformity (Kumar et al., 2021; Yang et al., 2023; Zafar et al., 2024).

Another strategy is to use sanitary static mixers at the cavity outlet or between two associated cavities (Coronel and Sandeep, 2003; Kumar et al., 2008).

4 Conclusion

In this study, a multiphysics numerical model was proposed to simulate the continuous flow microwave heating of a food product in a pilot-scale pasteurization unit. The model included electromagnetism, laminar flow, and heat transfer physics. The heights of three stubs were optimized through Monte Carlo optimization, using only the electromagnetic field physics, to minimize reflection loss in the cavity. The numerical model was validated with experimental data obtained from the thermal processing of orange juice, mango puree, and mango juice. While the differences between experimental and predicted temperatures for orange juice were 1.7°C or lower, those for mango juice and mango puree reached up to 5.5°C. However, most differences between experimental and predicted temperatures were less than 3.0°C, which represents a temperature difference of 3.6% or lower.

With the validated model, the three dimensions of the cavity geometry and the position of the applicator tube were optimized to minimize power reflection and thereby maximize microwave power absorption. The octagonal prism cavity exhibited a lower temperature amplitude (the difference between the maximum and minimum values in a given cross-sectional plane) at the outlet, suggesting a more homogenous radial temperature profile, even though the outlet temperature was 1.0°C lower than that of the cylindrical cavity. While the optimized octagonal prism cavity demonstrated a lower temperature amplitude than the original design, the temperature amplitude remained at 25.6°C, indicating non-homogeneous heating.

This study’s numerical model showed the influence of cavity geometry and the position of the applicator tube on microwave energy absorption by the food fluid and the uniformity of heating. Future research should explore alternative tube configurations, such as curved or helical tubes, that encourage radial mixing in the laminar regime to further enhance heating uniformity.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

GR: Conceptualization, Formal analysis, Investigation, Methodology, Resources, Writing – original draft. JG: Conceptualization, Funding acquisition, Resources, Supervision, Writing – review & editing. DB: Conceptualization, Funding acquisition, Project administration, Resources, Software, Supervision, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was financed by CAPES (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – grants 88887.469353/2019-00 and 88887.832637/2023-00) and in part by FAPESP (Fundação de Amparo à Pesquisa do Estado de São Paulo – grants 2013/07914-8 and 2023/13161-4) and CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico – grant 316388/2021-1). Co-author Boldor acknowledges the partial support from USDA NIFA Hatch Program (Project #LAB94672). Published with the approval of the Director of the Louisiana Agricultural Experiment Station as manuscript # 2025- 232-39869.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsufs.2025.1560122/full#supplementary-material

References

Amaro, K. C., Russo, G., Lu, D., Gut, J. A. W., and Tadini, C. C. (2024). Food and bioproducts processing modeling and experimental validation of the time-temperature profile, pectin methylesterase inactivation, and ascorbic acid degradation during the continuous flow microwave-assisted pasteurization of orange juice. Food Bioprod. Process. 144, 191–202. doi: 10.1016/j.fbp.2024.01.015

Crossref Full Text | Google Scholar

Baro, R. K., Kotecha, P., and Anandalakshmi, R. (2025). Optimization of continuous-flow microwave processing with static mixers for enhanced heating uniformity. Food Bioprod. Process. 149, 401–414. doi: 10.1016/j.fbp.2024.12.010

Crossref Full Text | Google Scholar

Bird, R. B., Stewart, W. E., and Lightfoot, E. N. (2002). Transport phenomena. 2nd Edn. John Wiley & Sons: Nova York.

Google Scholar

Campañone, L. A., Chaparro, J. R., Mascheroni, R. H., Lespinard, A. R., Mercatante, M. M., Goñi, S. M., et al. (2023). “6 - Microwave heating equipment for the food industry,” in ed. S. M. Jafari. Emerging Thermal Processes in the Food Industry. Woodhead Publishing (Unit Operations and Processing Equipment in the Food Industry), 119–163. doi: 10.1016/B978-0-12-822107-5.00013-1

Crossref Full Text | Google Scholar

Cavalcante, T. A. B. B., Tadini, C. C., and Gut, J. A. W. (2023). “Microwave-assisted pasteurization of mango pulp and nectar: thermo-physical, electrical and dielectric properties and inactivation kinetics of pectin methylesterase” in 14th International Congress on Engineering and Food, 2023 (Nantes). ICEF14 Proceedings

Google Scholar

Chandrasekaran, S., Ramanathan, S., and Basak, T. (2013). Microwave food processing-a review. Food Res. Int. 52, 243–261. doi: 10.1016/j.foodres.2013.02.033

Crossref Full Text | Google Scholar

Chang, X., Zhang, L., Xu, Q., Zheng, Z., Wang, R., and Li, Z. (2022). Continuous flow microwave heating and sterilization for liquid food. Int. J. Food Eng. 18, 717–735. doi: 10.1515/ijfe-2022-0130

Crossref Full Text | Google Scholar

Coronel, P., and Sandeep, K. P. (2003). “Flow Dynamics and Heat Transfer in Helical Heat Exchangers”, in Transport phenomena in food processing, 374–395. doi: 10.1201/9781420006261

Crossref Full Text | Google Scholar

Coskun, E., Ozturk, S., Topcam, H., Karatas, O., Li, R., Wang, S., et al. (2022). Continuous flow microwave processing of peanut butter: a (hypothetical) computational process design study with experimental validation. Innov. Food Sci. Emerg. Technol. 82:103184. doi: 10.1016/j.ifset.2022.103184

Crossref Full Text | Google Scholar

Datta, A. K., and Anantheswaran, R. C. (2001). Handbook of microwave Technology for Food Application. New York: Marcel Dekker.

Google Scholar

Datta, A. K., and Sablani, S. S. (2006). ‘Mathematical modeling techniques in food and bioprocesses: An overview’ in handbook of food and bioprocess modelling techniques. Bocca Raton, FL: CRC Press.

Google Scholar

Dewangan, S. K., and Kumar, D. K. (2020). Numerical modeling of fluid flow and heat transfer through helical tube. Int. J. Heat. Technol. 38, 541–552. doi: 10.18280/ijht.380232

Crossref Full Text | Google Scholar

Fellows, P. J. (editor) (2017). 1 - Properties of food and principles of processing’, in Food Processing Technology. Fourth Edition. (Woodhead Publishing Series in Food Science, Technology and Nutrition), 3–200. doi: 10.1016/B978-0-08-100522-4.00001-8

Crossref Full Text | Google Scholar

Ge, S., Nai, P., Yek, Y., Wang, Y., Xia, C., Adibah, W., et al. (2021). Progress in microwave pyrolysis conversion of agricultural waste to value-added biofuels: a batch to continuous approach. Renew. Sust. Energ. Rev. 135:110148. doi: 10.1016/j.rser.2020.110148

Crossref Full Text | Google Scholar

Karatas, O., Topcam, H., Altin, O., and Erdogdu, F. (2022). Computational study for microwave pasteurization of beer and hypothetical continuous flow system design. Innov. Food Sci. Emerg. Technol. 75:102878. doi: 10.1016/j.ifset.2021.102878

Crossref Full Text | Google Scholar

Koutchma, T. (2023). “Chapter 4 - Microwave heating and quality of food,” in Microwave and Radio Frequency Heating in Food and Beverages, 81–111. doi: 10.1016/B978-0-12-818715-9.00008-X

Crossref Full Text | Google Scholar

Kumar, P., Coronel, P., Truong, V. D., Simunovic, J., and Swartzel, K. R. (2008). Overcoming issues associated with the scale-up of a continuous flow microwave system for aseptic processing of vegetable purees. Food Res. Int. 41, 454–461. doi: 10.1016/j.foodres.2007.11.004

Crossref Full Text | Google Scholar

Kumar, G., Kumar, A., Ansari, N. A., and Zunaid, M. (2021). Comparative numerical study of flow characteristics in shell & helical coil heat exchangers with hybrid models. Mater. Today 46, 10831–10836. doi: 10.1016/j.matpr.2021.01.775

Crossref Full Text | Google Scholar

Li, H., Xu, J., Mbugua, S., Wang, J., Li, C., Zhu, X., et al. (2022). Food waste pyrolysis by traditional heating and microwave heating: a review. Fuel 324:124574. doi: 10.1016/j.fuel.2022.124574

Crossref Full Text | Google Scholar

Mirabito, C., Narayanan, A., Pérez, D., and Stone, B. (2005) FEMLAB model of a coupled electromagnetic-thermal boundary value problem. Research Experience: Worcester Polytechnic Institute, MA.

Google Scholar

Muley, P. D., and Boldor, D. (2012). “Multiphysics Numerical Modeling of the Continuous Flow Microwave-Assisted Transesterification Process,” Journal of Microwave Power and Electromagnetic Energy, 46, 141–164. doi: 10.1080/08327823.2012.11689832

Crossref Full Text | Google Scholar

Nayak, S. N., Prakash, C., and Nayak, M. G. (2019). A review on microwave-assisted transesteri fi cation processes using various catalytic and non-catalytic systems. Renew. Energy 143, 1366–1387. doi: 10.1016/j.renene.2019.05.056

Crossref Full Text | Google Scholar

Nde, D. B., Muley, P. D., Sabliov, C. M., Nokes, S. E., and Boldor, D. (2021). Microwave assisted pyrolysis of Kraft lignin in single mode high-Q resonant cavities: degradation kinetics, product chemical composition, and numerical modeling. Energy Convers. Manag. 230:113754. doi: 10.1016/j.enconman.2020.113754

Crossref Full Text | Google Scholar

Oishi, T. K., Cassares, M., Pouzada, E. V. S., and Gut, J. A. W. (2023). Multiphysics modeling of polyphenol oxidase and peroxidase inactivation in continuous - flow microwave thermal processing of coconut water. Braz. J. Chem. Eng. 41, 1035–1046. doi: 10.1007/s43153-023-00391-2

Crossref Full Text | Google Scholar

Oishi, T. K., Pouzada, E. V. S., and Gut, J. A. W. (2022). Experimental validation of a multiphysics model for the microwave-assisted pasteurization of apple juice. Digit. Chem. Eng. 5:100053. doi: 10.1016/j.dche.2022.100053

Crossref Full Text | Google Scholar

Russo, G., and Gut, J. A. W. (2022). Study of heat transfer coefficients and temperature distribution in a continuous flow pasteurizer with helical tubes using model fluids in laminar flow. Int. J. Food Eng. 18, 559–570. doi: 10.1515/ijfe-2021-0340

Crossref Full Text | Google Scholar

Ruthven, D. M. (1971). The residence time distribution for ideal laminar flow in helical tube. Chem. Eng. Sci. 26, 1113–1121. doi: 10.1016/0009-2509(71)80025-8

Crossref Full Text | Google Scholar

Salazar-González, C., Martín-González, M. F. S., Lópes-Malo, A., and Sosa-Morales, M. E. (2012). Recent studies related to microwave processing of fluid foods. Food Bioprocess Technol. 5, 31–46. doi: 10.1007/s11947-011-0639-y

Crossref Full Text | Google Scholar

Salvi, D., Boldor, D., Aita, G. M., and Sabliov, C. M. (2011). COMSOL Multiphysics model for continuous flow microwave heating of liquids. J. Food Eng. 104, 422–429. doi: 10.1016/j.jfoodeng.2011.01.005

Crossref Full Text | Google Scholar

Siguemoto, É. S., Funcia, E. D. S., Pires, M. N., and Gut, J. A. W. (2018). Modeling of time-temperature history and enzymatic inactivation of cloudy apple juice in continuous flow microwave assisted pasteurization. Food Bioprod. Process. 111, 45–53. doi: 10.1016/j.fbp.2018.06.004

Crossref Full Text | Google Scholar

Singh, R. P., and Heldman, D. R. (2008). “Heat transfer in food processing” in Introduction to food engineering. 4th ed (London: Academic Press), 247–402.

Google Scholar

Teleken, J. T., Dutra, A. C., Laurindo, J. B., and Carciofi, B. A. M. (2022). Numerical modeling of heating tomato pulp in continuous flow microwave-assisted thermal processing: estimation of quality parameters. J. Food Process Eng. 46, 1–15. doi: 10.1111/jfpe.14216

Crossref Full Text | Google Scholar

Topcam, H., and Erdogdu, F. (2021). Food and bioproducts processing designing system cavity geometry and optimizing process variables for continuous flow microwave processing. Food Bioprod. Process. 127, 295–308. doi: 10.1016/j.fbp.2021.03.006

Crossref Full Text | Google Scholar

Tuta, S., and Palazoğlu, T. K. (2017). Finite element modeling of continuous-flow microwave heating of fluid foods and experimental validation. J. Food Eng. 192, 79–92. doi: 10.1016/j.jfoodeng.2016.08.003

Crossref Full Text | Google Scholar

Valdés, J. P., Kahouadji, L., and Matar, O. K. (2022). Current advances in liquid–liquid mixing in static mixers: a review. Chem. Eng. Res. Des. 177, 694–731. doi: 10.1016/j.cherd.2021.11.016

Crossref Full Text | Google Scholar

Vencels, J., Birjukovs, M., Kataja, J., and Råback, P. (2019). Microwave heating of water in a rectangular waveguide: validating EOF-library against COMSOL multiphysics and existing numerical studies. Case Stud. Therm. Eng. 15:100530. doi: 10.1016/j.csite.2019.100530

Crossref Full Text | Google Scholar

Yang, H., Sun, M., Yan, B., Zhang, N., Zhao, J., and Zhang, H. (2023). Continuous flow microwave processing of liquid whole egg: pasteurization and functional characteristics evaluation. Innov. Food Sci. Emerg. Technol. 90:103495. doi: 10.1016/j.ifset.2023.103495

Crossref Full Text | Google Scholar

Zafar, S., Saleem, Q. S. H. S., and Bayazit, M. K. (2024). Numerical investigation of heat transfer and temperature distribution in a microwave-heated Heli-flow reactor and experimental validation. Chem. Eng. J. 488:150914. doi: 10.1016/j.cej.2024.150914

Crossref Full Text | Google Scholar

Zhang, Y., Yang, H., Yan, B., Zhu, H., Gao, W., and Zhao, J. (2021). Continuous flow microwave system with helical tubes for liquid food heating. J. Food Eng. 294:110409. doi: 10.1016/j.jfoodeng.2020.110409

Crossref Full Text | Google Scholar