Does cooperative intervention affect pricing decisions in the agricultural supply chain?

In global agricultural markets, farmers often face profit squeezes due to low bargaining power, which affects the sustainability of agriculture and the livelihoods of farmers. Cooperative intervention is seen as a key solution to improve bargaining power and optimize profit distribution in the agricultural supply chain. In this study, a two-stage dynamic game model is adopted to focus on bargaining power and compare the effects of linear pricing versus a double charging system under cooperative intervention. It is found that the cooperative is better when it has full bargaining power or when it faces downstream sellers with comparable bargaining power, and the dual-charging system is more favorable. When cooperatives bargain with sellers, the degree of differentiation of agricultural products affects the cooperatives’ profitability and cooperatives tend to maintain the two-part tariff when the bargaining power is less than a threshold condition containing the degree of differentiation of agricultural products; when discounts exceed the threshold, cooperatives shift to linear pricing to safeguard their profitability. Numerical analysis validates the theory and reveals the changing pattern of cooperative profits under market forces. This study not only provides theoretical support for the study of supply chain pricing strategies under the condition of considering the bargaining power of producers (farmers) but also provides management insights for the stability and sustainable development of agricultural supply chains. Its novel dynamic game framework is cross-culturally applicable to help farmers’ cooperatives cope with the challenge of profit distribution in a global context and emphasizes the importance of differentiation strategies to enhance bargaining power and promote fairness and efficiency in global agricultural supply chains.

1 Introduction

In view of the combined effects of population growth, accelerated industrialization, and environmental pollution, land resources suitable for agricultural production are decreasing worldwide (Panwar et al., 2011). This trend not only exacerbates the scarcity of land resources but also profoundly affects the production costs and price stability of agricultural products, especially the strong linkage between the prices of agricultural products and the price of fuel (Vochozka et al., 2020). With the progress of industrialization, fuel has become an important input factor in agricultural production. Its price fluctuations directly affect the costs of fertilizers, pesticides, agricultural equipment, agricultural transportation, and other aspects of agriculture, which in turn creates a chain reaction impacting the market price of agricultural products. In this context, improving the rational allocation of the agricultural supply chain has become particularly important, as it is not only directly related to the enhancement of national resilience, economic and social security, and the promotion of sustainable growth but also how to effectively respond to the challenges posed by fuel price volatility. The urgency of this challenge is further emphasized by projections from the Food and Agriculture Organization of the United Nations (FAO), which state that the total world population is expected to increase to 9.73 billion by 2050 (Ronaghi et al., 2021) and that such a large population base means that the demand for agricultural products will continue to climb, while on the supply side, diminishing land resources are intertwined with fluctuating fuel prices, which makes the contradiction between supply and demand more prominent. It is this complex supply–demand relationship and market environment that has led farmers to become increasingly concerned about the dual risks of stagnant sales and price volatility of the agricultural products they grow. Specifically, the volatility of agricultural markets, rapid changes in consumer preferences, and the instability of international trade patterns can all be external factors contributing to stagnation. Declining land resources further limit the ability of farmers to naturally offset market volatility by scaling up production. In the face of this challenge, recent research trends remind us of the importance of production efficiency (Maroušek et al., 2023). By adopting advanced agricultural technologies, optimizing the cropping structure, and improving management efficiency, the allocation of agricultural supply chains can be effectively improved, thus alleviating to a certain extent the pressure brought by factors such as the scarcity of land resources. In addition, the intervention of cooperatives can also enhance the bargaining power of farmers, help them fight for more favorable pricing power in the market, and ensure the reasonable realization of the value of agricultural products. In China, for example, according to the 2023 edition of CCAD’s New Agricultural Management Mainstay Farmer Specialized Cooperatives Database, the rapid development of cooperatives has significantly improved the economic situation of farmers, but this phenomenon is not an isolated one, but a microcosm of the global cooperative movement. Therefore, the cooperative intervention model will undoubtedly optimize the profit distribution of agricultural products in the supply chain, bring more economic benefits to farmers, and thus promote the stable and sustainable development of global agriculture.

Cooperation is crucial for enhancing farmers’ capabilities, especially those in communities with low socio-economic status (Dania et al., 2018). Cooperatives are economic organizations voluntarily formed and democratically managed by farmers. They can replace individual farmers with low bargaining power and take on agricultural production and management activities (Ganesh Kumar et al., 2017; Wu et al., 2022). Chao et al. (2021) and Xu et al. (2022) point out that cooperatives can improve farmers’ bargaining power through economies of scale, improving agricultural product quality (Zhong et al., 2023) and brand awareness, and eliminating price uncertainty (An et al., 2015; Ranjan, 2017), thereby becoming an important link in the agricultural supply chain. Simultaneously, cooperatives can integrate information on agricultural products produced by farmers and arrange planting activities with lower costs and more detailed planning (Zhong et al., 2023). Ways to improve individual farmers’ bargaining power mainly include using e-commerce platforms (Feng, 2024) and joining cooperatives (Niu et al., 2016; Ranjan, 2017). Specifically, globally, some farmers are gradually transitioning away from traditional agricultural production activities and toward new types of agricultural enterprises, with cooperatives at their core. This trend highlights the key role of the cooperative model in the optimization and performance improvement of global agricultural supply chains. As important drivers of agricultural modernization, cooperatives not only promote the efficient integration and utilization of resources but also significantly enhance the bargaining power and risk resistance of farmers in the marketplace, laying a solid foundation for the sustainable development of agricultural production.

To date, numerous studies have been conducted on the optimization and upgrading of supply chains from various perspectives and industries. Some scholars have investigated the enhancement and optimization of agricultural product supply chains through organizational management or information management (Yan et al., 2016; Kumar et al., 2020), digitalization or blockchain technology (Alonso et al., 2020; De Giovanni, 2020; Rana et al., 2021; Song et al., 2022; Wu et al., 2023; Hamidoğlu et al., 2024), and pricing decisions (Golmohammadi and Hassini, 2019; He et al., 2024; Jiang et al., 2024). However, research investigating pricing decisions in agricultural product supply chains remains limited. De and Singh (2023) examined how channel leadership strategies in fresh agricultural product supply chains can foster resilient agricultural supply chains post-COVID-19, thereby reducing price losses for suppliers and retailers. Yan et al. (2021) focused on the optimal pricing and coordination of agricultural product supply chains based on two-stage pricing, wholesale prices, and option contracts in the context of fresh agricultural products. Perlman et al. (2022) constructed a dual-channel supply chain to explore agricultural product pricing decisions and profit distribution issues within the supply chain. Wang et al. (2024) considered pricing and channel selection strategies for agricultural products in dual-channel supply chain systems encompassing online direct sales and distribution, also examining whether producers utilize blockchain technology. However, most of the aforementioned studies fail to consider bargaining power and primarily focus on pricing decisions for perishable or cold-chain agricultural products. Agricultural product supply chains worldwide typically feature numerous distribution links, significant price differences between upstream and downstream players, and uneven profit distribution. In addition, agricultural products directly impact farmers’ incomes and the high-quality development of agriculture. As cooperatives serve as an essential form to enhance farmers’ bargaining power and welfare, examining agricultural product pricing decisions under the intervention of cooperatives is of significant importance for farmers’ welfare and agricultural supply chain coordination.

This study discusses agricultural product supply chain pricing decisions under the intervention of cooperatives, considering the current development status of the “farmer + cooperative” model. It proposes a pricing model for agricultural product supply chains based on bargaining power to explain the theoretical rationale for the cooperative intervention model. The marginal contributions of this study are as follows: (1) exploring agricultural product pricing decisions under the intervention of cooperatives; (2) discussing profit distribution issues in agricultural product supply chains under the intervention of cooperatives; and (3) providing theoretical support for the intervention of cooperative models and referential suggestions for pricing decisions in agricultural product supply chains.

2 Basic model

In this study, we assume that the upstream supplier of agricultural products in the supply chain is a cooperative that can organize farmers to produce agricultural products, and downstream are two sellers (called Seller 1 and Seller 2, respectively), which will buy agricultural products and sell them to consumers. They compete in decentralized markets, one of which is chosen for the study. The marginal cost of production of the cooperative is c. For simplicity in the later calculations, it is normalized to zero here, and there are no fixed costs.

We assume that Supplier 1 is a branded supplier and Supplier 2 is non-branded and that the agricultural products sold by Supplier 1 and Supplier 2 differ in terms of marketing techniques, shopping environment, or service. Therefore, they are differentiated products that are imperfect substitutes from the consumer’s point of view.

Suppose the simplified squared utility function is taken as the consumer’s utility function:

$\begin{array}{ll}u\left(q_1,q_2\right)=q_1+q_2-\frac{1}{2}\left({q^2}_1+{q^2}_2+2\alpha q_1{q}_2\right)+X& (1)\end{array}$

where $q_1$ and $q_2$ are the quantities of agricultural products purchased by consumers from Seller 1 and Seller 2, respectively, and they denote the utility obtained by consumers from consuming other agricultural products. The parameter $\alpha \in \left(0,1\right)$ measures the degree of differentiation of agricultural products. When $\alpha \to 0$ , Seller 1 and Seller 2 sell differentiated agricultural products in the eyes of consumers; when $\alpha \to 1$ , sellers sell a single agricultural product; and when $0<\alpha <1$ , there is imperfect substitution between sellers, which corresponds to differentiated products that are imperfect substitutes for sellers’ agricultural products in the eyes of consumers. In addition, $\alpha$ can also be understood in terms of the degree of differentiation among sellers, with smaller values of $\alpha$ indicating greater differentiation among sellers and less intense competition; conversely, larger values of α indicate less differentiation and more intense competition among sellers.

For analytical convenience, assume that all of the sellers’ costs of goods sold are the same and normalized to 0, so that the sellers have only the cost of what they spend on purchasing the produce.

The seller’s inverse demand function can be derived from the consumer’s utility function:

$\begin{array}{ll}{s}_i=1-q_i-\alpha q_j& (2)\end{array}$

where $i,j=1,2$ and $i\ne j$ , $s_i$ is the selling price of Vendor $i$ ; and $q_i$ is the quantity sold by Vendor $i$ . The following figure shows the involvement of cooperatives and the choice of pricing methods for agricultural products (Figure 1).

Figure 1

Figure 1. Sequence of events.

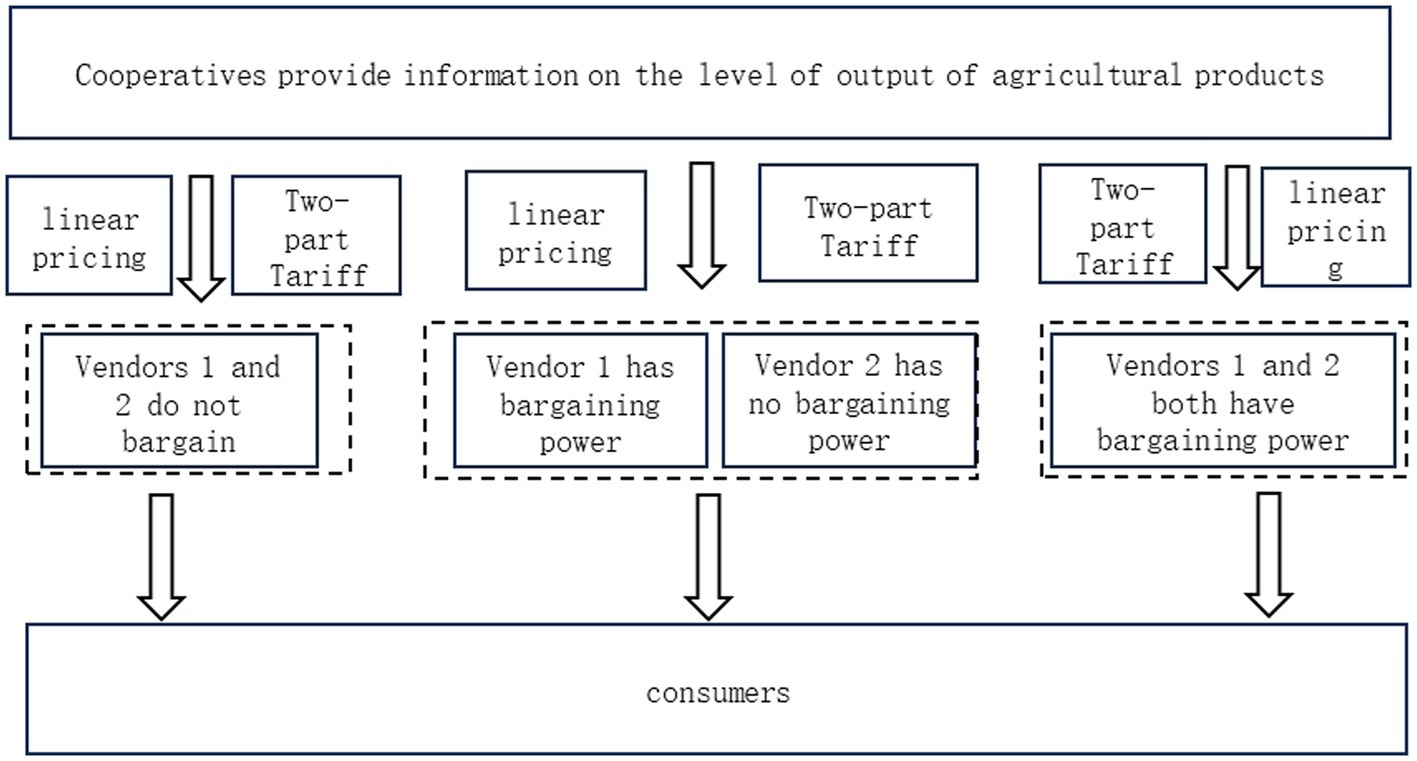
3 Cooperatives–seller relationship under non-negotiated pricing

In this section, we assume that neither Seller 1 nor Seller 2 has bargaining power or negotiates with the cooperative but directly accepts the price proposed by the cooperative. However, for consumers, there are differences and competition between sellers, and we assume that there is Cournot quantity competition between these sellers.

3.1 Linear pricing model

In cases where the seller has no bargaining power or does not bargain, the game between the cooperative and the seller is divided into two stages. In the first stage, the cooperative sets a price for produce ${p_i}^L$ (where $i=1,2$ ) to the sellers, who purchase produce at this price; in the second stage, there is a Cournot quantity competition between sellers.

Using backward induction, we can find that in the second stage, the seller’s profit is

$\begin{array}{ll}{{\pi }_i}^L=\left({s_i}^L-{p_i}^L\right){q_i}^L& (3)\end{array}$

Then, the first-order condition for maximizing the seller’s profit is

$\begin{array}{ll}\raisebox{1ex}{$\partial {{\pi }_i}^L$}\!\left/ \!\raisebox{-1ex}{$\partial {q_i}^L$}\right.=\raisebox{1ex}{$\partial {s_i}^L{q_i}^L$}\!\left/ \!\raisebox{-1ex}{$\partial {q_i}^L$}\right.+1-{q_i}^L-\alpha {q_j}^L-{p_i}^L=0& (4)\end{array}$

Substituting equation (2), we can solve for

$\begin{array}{ll}{q_i}^L=\frac{2-\alpha +\alpha {p_j}^L-2{p_i}^L}{4-{\alpha }^2}& (5)\end{array}$

Profits from cooperatives:

$\begin{array}{ll}{{\pi }_F}^L={\displaystyle \sum }_{i=1,2}{p_i}^L{q_i}^L& (6)\end{array}$

Substituting equation (5) into equation (6), the original price of agricultural products at equilibrium can be found through the first-order condition of maximizing the seller’s profit ${p_1}^L={p_2}^L=\frac{1}{2}$ , and the price and sales volume of agricultural products sold at equilibrium are ${s_1}^L={s_2}^L=\frac{3+\alpha }{2\left(\alpha +2\right)}$ and ${q_1}^L={q_2}^L=\frac{1}{2\left(\alpha +2\right)}$ , respectively. At this point, the profit of the cooperative is

$\begin{array}{ll}{{\pi }_F}^L=\frac{1}{2\left(\alpha +2\right)}& (7)\end{array}$

3.2 Two-part fee system

The two-part fee system is where the cooperative charges a total fee to the seller, which is composed of a fixed compensation fee and a variable fee proportional to the quantity sold. The game is played as follows: First, the cooperative sets a pricing contract ( ${p_i}^{TP}$ , ${F_i}^{TP}$ ) based on its own information about the produce, where ${p_i}^{TP}$ is the price at which seller $i$ buys the produce, and ${F_i}^{TP}$is the fixed compensation fee that seller $i$ pays to the cooperative. Then, in the second stage, sellers compete for quantity in the downstream market.

The cooperative needs to maximize its profit by making an optimal pricing contract subject to the participation constraints of the vendors, that is,

$\begin{array}{ll}\underset{\left({{\omega }_i}^{TP},{F_i}^{TP}\right)}{max}{{\pi }_F}^{TP}={\displaystyle \sum }_{i=1,2}\left({p_i}^{TP}{q_i}^{TP}+{F_i}^{TP}\right)& (8)\end{array}$

$\begin{array}{ll}s.t.\left({s_i}^{TP}-{p_i}^{TP}\right){q_i}^{TP}+{F_i}^{TP}\ge 0.& (9)\end{array}$

Vendor’s decision is

$\begin{array}{ll}\underset{{q_i}^{TP}}{max}{{\pi }_i}^{TP}=\left({s_i}^{TP}-{p_i}^{TP}\right){q_i}^{TP}-{F_i}^{TP}& (10)\end{array}$

Similar to the solution process of linear pricing, it can be found that in equilibrium, the seller purchases the produce at the original price of ${p_1}^{TP}={p_2}^{TP}=\frac{\alpha }{2\left(\alpha +1\right)}$ , pays a fixed fee of ${F_1}^{TP}={F_2}^{TP}=\frac{1}{4{\left(\alpha +1\right)}^2}$ , and sells the produce at the price and sales volume of ${s_1}^{TP}={s_2}^{TP}=\frac{1}{2}$ and ${q_1}^{TP}={q_2}^{TP}=\frac{1}{2\left(\alpha +2\right)}$ , respectively, in equilibrium. At this point, the cooperative’s profit is

$\begin{array}{ll}{{\pi }_F}^{TP}=\frac{1}{2\left(\alpha +1\right)}& (11)\end{array}$

Equations (7) and (11) clearly reveal that cooperatives are able to achieve higher profits when adopting a two-part pricing strategy as opposed to linear pricing. Given the differentiated nature of the agricultural products sold by cooperatives, which gives them a certain degree of seller power in the market, if they insist on linear pricing, it is difficult to avoid the phenomenon of “incomplete pass-through,” that is, cost increases cannot be fully passed on to consumers through higher selling prices, which may weaken the profitability of the supply chain of agricultural products and adversely affect the profitability of cooperatives. This may weaken the profitability of the agricultural supply chain and adversely affect the profitability objectives of cooperatives.

In this context, the advantages of the two-part fee are particularly prominent. It not only allows cooperatives to reduce price externalities by adjusting the base selling price of agricultural products, that is, to reduce the problem of incomplete price transmission due to fierce competition among sellers but also effectively compensates for the loss of cooperative profits due to the reduction of selling price by charging a fixed compensation fee. It is worth noting that there is a negative correlation between changes in α and cooperative profits, which further emphasizes the importance of fine-tuning pricing strategies.

In today’s globalization, as consumer demand for high-quality, organic, and specialty agricultural products continues to climb, cooperatives have unprecedented development opportunities. By integrating internal resources and planting expertise, and focusing on the cultivation and production of specialty agricultural products, cooperatives are not only able to meet the diversified demands of the market but also significantly increase the added value of their products, which will bring more lucrative returns and profits to the cooperatives.

In addition, to better serve international consumers, cooperatives need to consider the issue of currency convertibility in their pricing strategy, ensuring that only currencies that are generally accepted by international audiences and freely convertible are used in communicating pricing information, thereby eliminating the uncertainty caused by exchange rate fluctuations, enhancing the transparency and acceptability of pricing information, further expanding the international market, and enhancing the global competitiveness of cooperatives.

4 Cooperative profitability under negotiated pricing

Included in this section are variations and explorations of the cooperative’s profits when it bargains with sellers (i.e., negotiated pricing). One is where only Seller 1 (the brand seller) has bargaining power, and the other is where both Seller 1 and Seller 2 have bargaining power. All other assumptions being equal, a negotiation between the cooperative and the seller on the original price of the produce can result in a discount $\beta$ and $\beta \in \left(0,1\right)$ , with the smaller $\beta$ , the greater the bargaining power of the seller and the greater the discount obtained by the seller, and vice versa.

4.1 Profit analysis of single-seller negotiations

4.1.1 Linear pricing

When Seller 1 engages in linear pricing with the cooperative, there is a two-stage game between them. The game proceeds as follows: In the first stage, the cooperative sets an original price based on information about the agricultural products produced by the farmers, and since vendor 1 has bargaining power, they negotiate an assumed discount $\beta$ . Vendor 2 does not have bargaining power, so it either accepts the cooperative’s original price or withdraws from the market if it wants to purchase agricultural products, and it is assumed that all vendors accept the cooperative’s price. In the second stage, there is volume competition between sellers. Sellers will make decisions based on the quantity of produce to be purchased to maximize their profits, so that the ${{\pi }_i}^L$ profits of Seller 1 and Seller 2 are, respectively, as follows:

$\begin{array}{ll}{{\pi }_1}^L=\left({s_1}^L-\beta {p_1}^L\right){q_1}^L& (12)\end{array}$

$\begin{array}{ll}{{\pi }_2}^L=\left({s_2}^L-{p_2}^L\right){q_2}^L& (13)\end{array}$

Pass the first-order condition for profit maximization:

$\begin{array}{ll}\raisebox{1ex}{$\partial {{\pi }_1}^L$}\!\left/ \!\raisebox{-1ex}{$\partial {q_1}^L$}\right.=\raisebox{1ex}{$\partial {s_1}^L{q_1}^L$}\!\left/ \!\raisebox{-1ex}{$\partial {q_1}^L$}\right.+1-{q_1}^L-\alpha {q_2}^L-\beta {p_1}^L=0& (14)\end{array}$

$\begin{array}{ll}\raisebox{1ex}{$\partial {{\pi }_2}^L$}\!\left/ \!\raisebox{-1ex}{$\partial {q_2}^L$}\right.=\raisebox{1ex}{$\partial {s_2}^L{q_2}^L$}\!\left/ \!\raisebox{-1ex}{$\partial {q_2}^L$}\right.+1-{q_2}^L-\alpha {q_1}^L-{p_2}^L=0& (15)\end{array}$

Substitute Eq. (2) to obtain the equilibrium solutions for ${s_1}^L$ , ${s_2}^L$ , ${q_1}^L$ , and ${q_2}^L$ :

$\begin{array}{ll}{q_1}^L=\frac{\alpha -2-p^L\left(\alpha -2\beta \right)}{{\alpha }^2-4}& (16)\end{array}$

$\begin{array}{ll}{q_2}^L=\frac{\alpha -2+p^L\left(2-\alpha \beta \right)}{{\alpha }^2-4}& (17)\end{array}$

$\begin{array}{ll}{s_1}^L=\frac{\alpha -2-p^L\left[\beta \left({\alpha }^2-2\right)-\alpha \right]}{{\alpha }^2-4}& (18)\end{array}$

$\begin{array}{ll}{s_2}^L=\frac{\alpha -2-p^L\left({\alpha }^2-2-\alpha \beta \right)}{{\alpha }^2-4}& (19)\end{array}$

In the first stage, the original price of the produce set by the cooperative will maximize its profit, that is,

$\begin{array}{ll}\underset{\left(p^L\right)}{max}{{\pi }_C}^L=\beta p^L{q_1}^L+p^L{q_2}^L& (20)\end{array}$

The original price of the produce at equilibrium can be obtained by solving the first-order condition for profit maximization:

$\begin{array}{ll}{p}^L=\frac{\left(1+\beta \right)\left(2-\alpha \right)}{4\left(1-\alpha \beta +{\beta }^2\right)}& (21)\end{array}$

Substituting (16), (17), and (21) into (20) yields the profit of the cooperative in equilibrium as

$\begin{array}{ll}{{\pi }_C}^L=\frac{1}{2\left(\alpha +2\right)}-\frac{{\left(1-\beta \right)}^2}{8\left(1+{\beta }^2-\alpha \beta \right)}& (22)\end{array}$

4.1.2 Two-part fee system

When the cooperative sets the total fee charged to the seller by integrating information on the output of the produce, it is set as a fixed compensation fee plus a variable fee proportional to the quantity sold. When the two-part fee system is implemented, the game process is as follows: First, the cooperative sets a pricing contract( ${p_i}^{TP}$ , ${F_i}^{TP}$ ), where ${p_i}^{TP}$ is the original price per unit of the produce purchased by the seller $i$ , and ${F_i}^{TP}$is the fixed compensation fee paid by the seller $i$ to the cooperative. Since Vendor 1 has bargaining power, the cooperative will give it a discount $\beta$ , so the price relationship between vendors for purchasing agricultural products is ${p_1}^{TP}=\beta {p_2}^{TP}$ . At this point, the pricing contract of Seller 1 is $\left(\beta {p_1}^{TP},{F_1}^{TP}\right)$ and the pricing contract of Seller 2 is $\left({p_2}^{TP},{F_2}^{TP}\right)$ . In the second stage, sellers compete for quantity in the consumer market.

This game is sought from the second stage. The sellers maximize their profits by deciding the quantity of their respective agricultural products to be purchased, and the profits of Seller 1 and Seller 2 are, respectively, as follows:

$\begin{array}{ll}{{\pi }_1}^{TP}=\left({s_1}^{TP}-\beta {p_1}^{TP}\right){q_1}^{TP}-{F_1}^{TP}& (23)\end{array}$

$\begin{array}{ll}{{\pi }_2}^{TP}=\left({s_2}^{TP}-p^{TP}\right){q_2}^{TP}-{F_2}^{TP}& (24)\end{array}$

The equilibrium solutions of ${p_1}^{TP}$ , ${p_2}^{TP}$ , ${q_1}^{TP}$ , and ${q_2}^{TP}$ can be obtained through the first-order conditions for profit maximization, which are of the same form as equations (16)–(19).

In the first stage, the cooperative’s contract for agricultural products $\left(p^{TP},{F_1}^{TP},{F_2}^{TP}\right)$ maximizes its profit, that is,

$\begin{array}{ll}\underset{\left({p_i}^{TP},{F_1}^{TP},{F_2}^{TP}\right)}{max}{{\pi }_C}^{TP}=\beta p^{TP}{q_1}^{TP}+{F_1}^{TP}+p^{TP}{q_2}^{TP}+{F_2}^{TP}& (25)\end{array}$

$\begin{array}{ll}s.t.\left({s_1}^{TP}-\beta p^{TP}\right){q_1}^{TP}-{F_1}^{TP}\ge \left(1-\beta \right)p^{TP}{q_1}^{TP}& (26)\end{array}$

$\begin{array}{ll}\left(1-\beta \right)p^{TP}{q_1}^{TP}\ge 0& (27)\end{array}$

$\begin{array}{ll}\left({s_2}^{TP}-p^{TP}\right){q_2}^{TP}-{F_2}^{TP}\ge 0& (28)\end{array}$

where equations (26) and (27) are participation constraints for Seller 1 and Seller 2, respectively. Since Seller 1 has bargaining power and can obtain a price through negotiation with the cooperative $\beta$ , relative to Seller 2 who has no bargaining power, Seller 1 can obtain savings in the cost of purchased agricultural products $\left(1-\beta \right)p^{TP}{q_1}^{TP}$ ; however, if Seller 1 does not have bargaining power, the cooperative makes a contract that prevents it from obtaining a profit, and so compared to the no-power case, it needs to be ensured that the bargaining power of Vendor 1 will not make less profit than the saving cost of the produce it purchases, that is, equation (26) holds. In addition, it is necessary to ensure that the profit $\left(1-\beta \right)p^{TP}{q_1}^{TP}$ earned by Seller 1 is non-negative, that is, equation (27) holds. For Seller 2, who has no bargaining power, they can exist in the market as long as their profit is non-negative, that is, equation (28) holds.

The Kuhn–Tucker condition can be used to find the original price of the produce:

$\begin{array}{ll}{P}^{TP}=\frac{{\left(2-\alpha \right)}^2\left(\alpha \beta +\beta -1\right)}{A}& (29)\end{array}$

and $A=\left(12-5{\alpha }^2\right){\beta }^2+\left(3{\alpha }^3+2{\alpha }^2-4\alpha -8\right)\beta -{\alpha }^3-3{\alpha }^2+4\alpha +4$ . The selling price and quantity of agricultural products at equilibrium are

$\begin{array}{ll}{s_1}^{TP}=\frac{\left({\alpha }^3-3{\alpha }^2-3\alpha +8\right){\beta }^2+\left({\alpha }^2+3\alpha -6\right)\beta -{\alpha }^2+2}{A}& (30)\end{array}$

$\begin{array}{ll}{s_2}^{TP}=\frac{\left(6-{\alpha }^2-2\alpha \right){\beta }^2+\left({\alpha }^3-\alpha -2\right)\beta -2{\alpha }^2+3\alpha }{A}& (31)\end{array}$

$\begin{array}{ll}{q_1}^{TF}=\frac{\left(4-3\alpha \right){\beta }^2-\left({\alpha }^3-2{\alpha }^2+\alpha +2\right)\beta -{\alpha }^3+3{\alpha }^2-2\alpha -2}{A}& (32)\end{array}$

$\begin{array}{ll}{q_2}^{TF}=\frac{\left(2-\alpha \right)\left[\left(3+\alpha \right){\beta }^2-\left(3\alpha +3\right)\beta +2+\alpha \right]}{A}& (33)\end{array}$

The profit made by the cooperative in equilibrium is

$\begin{array}{ll}{{\pi }_C}^{TP}=\frac{\left({\alpha }^2-6\alpha +7\right){\beta }^2+2\beta \left(2\alpha -3\right)-2\alpha +3}{A}& (34)\end{array}$

The profit gained by the powerful Seller 1 is

$\begin{array}{ll}{{\pi }_1}^{TP}=\frac{B\left(1-\beta \right){\left(2-\alpha \right)}^2\left(\alpha \beta +\beta -1\right)}{A^2}& (35)\end{array}$

and $B=\left(4-3\alpha \right){\beta }^2+\left(2{\alpha }^2-\alpha -2\right)\beta -{\alpha }^2+2$ , the profit obtained by Seller 2 is 0.

It can be shown $A,B,C>0$ (see Supplementary Table S1 for proof) that to ensure that the seller’s profit is constantly greater than 0 and equation (40) holds, it is necessary to have

$\begin{array}{ll}\alpha \beta +\beta -1\ge 0& (36)\end{array}$

$\begin{array}{ll}0\le \beta \le \frac{1}{\left(\alpha +1\right)}& (37)\end{array}$

Proposition 1: In the case of a single seller bargaining with a cooperative, for a given degree of differentiation in agricultural products, the cooperative’s implementation of a two-part fee system is effective only if $0\le \beta \le \frac{1}{\left(\alpha +1\right)}$ .The previous analysis leads to the conclusion that when the cooperative has full bargaining power or when either the seller or the downstream seller bargains, the two-part fee system maximizes its profit, that is, it eliminates the seller’s price externality and avoids the phenomenon of incomplete price transmission to obtain the full profit in the supply chain of agricultural products. But when Seller 1 has bargaining power, for a given degree of differentiation of agricultural products, the two-part fee contract is effective only if the bargaining power is within the constraint ( $0\le \beta \le \frac{1}{\left(\alpha +1\right)}$ ). The profit earned by the cooperative in equilibrium can be simplified as follows: ${{\pi }_C}^{TP}={s_1}^{TP}{q_1}^{TP}+{s_2}^{TP}{q_2}^{TP}+\left(1-\beta \right){p_1}^{TP}{q_1}^{TP}$ , where ${s_1}^{TP}{q_1}^{TP}+{s_2}^{TP}{q_2}^{TP}$ is the total profit of the entire supply chain of agricultural products, and $\left(1-\beta \right)p^{TP}{q_1}^{TP}$ is the profit earned by Seller 1 through negotiation. If the original price $p^{TP}$ of the produce remains constant, $\beta$ _, the smaller the bargaining power of Vendor 1, the larger the profit Vendor 1 makes, and the smaller the profit to the farmer. Since $p^{TP}$ is determined by the cooperative based on the information of the agricultural products produced by the farmers, as the bargaining power of Seller 1 increases, to reduce the profit $\left(1-\beta \right)p^{TP}{q_1}^{TP}$ obtained by Seller 1 through negotiation, the cooperative also chooses to reduce the original price of the agricultural products to slow down its growth rate. When the bargaining power of Seller 1 is too large, the cooperative will also consider lowering the original price below the marginal cost, but the lower original price of the produce can be compensated by increasing the fixed compensation fee in the two-part fee pricing contract. Given the assumed constraints in this study, the two-part fee pricing ensures that competition in the market is effective only if the bargaining power is in the range of $0\le \beta \le \frac{1}{\left(\alpha +1\right)}$ .

4.2 Profit comparison for multi-vendor negotiations

4.2.1 Linear pricing

When the seller has the ability to bargain with the cooperative (denoted by subscript D), the game between the two parties is divided into two stages. The game proceeds in the same way as when Seller 1 engages in linear pricing with the cooperative, except that in this section both sellers bargain with the cooperative. To maximize profit, the seller makes a decision based on the quantity of produce to be purchased, and the seller’s profit is

$\begin{array}{ll}{{\pi }_{\mathit{iD}}}^L=\left({s_i}^L-\beta {p_i}^L\right){q_i}^L& (38)\end{array}$

Pass the first-order condition for profit maximization:

$\begin{array}{ll}\raisebox{1ex}{$\partial {{\pi }_{\mathit{iD}}}^L$}\!\left/ \!\raisebox{-1ex}{$\partial {q_i}^L$}\right.=\raisebox{1ex}{$\partial {s_i}^L{q_i}^L$}\!\left/ \!\raisebox{-1ex}{$\partial {q_i}^L$}\right.+1-{q_i}^L-\alpha {q_j}^L-\beta {p_i}^L=0& (39)\end{array}$

Substituting equation (2), we can solve for:

$\begin{array}{ll}{q_D}^L=\frac{2-2\beta {p_i}^L-\alpha \left(1+{p_j}^L\right)}{4-{\alpha }^2}& (40)\end{array}$

The profits of the cooperative are.

$\begin{array}{ll}{{\pi }_{CD}}^L={\displaystyle \sum }_{i=1,2}\beta {p_i}^L{q_i}^L& (41)\end{array}$

Substituting equation (38) into equation (39), through the first-order condition for maximizing the seller’s profit, the original price of the agricultural product at equilibrium is ${p_1}^L={p_2}^L=\frac{1}{2\beta }$ , and the selling price and sales volume at equilibrium are ${s_1}^L={s_2}^L=\frac{3\beta -2{\alpha }^2\beta -\alpha -1}{\beta \left(4-{\alpha }^2\right)}$ and ${q_1}^L={q_2}^L=\frac{\beta -\alpha \beta +1}{\beta \left(4-{\alpha }^2\right)}$ .

Substituting the above equation into (41), we can find the profit earned by the cooperative at equilibrium as

$\begin{array}{ll}{{\pi }_{CD}}^L=\frac{\beta -\alpha \beta +1}{{\beta }^2\left(4-{\alpha }^2\right)}& (42)\end{array}$

From equation (22), the profit earned by the cooperative when Seller 1 has bargaining power consists of two parts. Comparing equations (7) and (22), it can be seen that the former part is the profit gained through linear pricing when the seller does not bargain, and the profit gained by the cooperative decreases when Seller 1 has bargaining power, and the reduced part may be gained in the form of excess profit by Seller 1 who has bargaining power.

4.2.2 Two-part fee system

When both Seller 1 and Seller 2 have bargaining power, the game proceeds in the same way as when Seller 1 engages in two-part toll pricing with the cooperative, except that both sellers participate in the cooperative bargaining.

The cooperative needs to develop an optimal two-part fee contract that satisfies the seller’s participation constraints to make a profit:

$\begin{array}{ll}\underset{\left({p_i}^{TP},{F_{1D}}^{TP},{F_{2D}}^{TP}\right)}{max}{{\pi }_{CD}}^{TP}={\displaystyle \sum }_{i=1,2}\beta {p_{\mathit{iD}}}^{TP}{q_{\mathit{iD}}}^{TP}+{F_{\mathit{iD}}}^{TP}& (43)\end{array}$

$\begin{array}{ll}s.t.\left({s_{\mathit{iD}}}^{TP}-\beta {p_{\mathit{iD}}}^{TP}\right){q_{\mathit{iD}}}^{TP}-{F_{\mathit{iD}}}^{TP}\ge 0& (44)\end{array}$

Vendors maximize their respective profits by determining the quantity of produce to purchase:

$\begin{array}{ll}{{\pi }_{\mathit{iD}}}^{TP}=\left({s_{\mathit{iD}}}^{TP}-\beta {p_{\mathit{iD}}}^{TP}\right){q_{\mathit{iD}}}^{TP}-{F_{\mathit{iD}}}^{TP}& (45)\end{array}$

The first-order condition for profit maximization gives that the original price and fixed cost of the produce in equilibrium are ${p_{1D}}^{TP}={p_{2D}}^{TP}=\frac{\alpha }{2\beta \left(1+\alpha \right)}$ and ${F_{1D}}^{TP}={F_{2D}}^{TP}=\frac{C}{4{\beta }^2{\left(\alpha +1\right)}^2{\left(4-{\alpha }^2\right)}^2}$ , and the selling price and sales volume in equilibrium are ${s_{1D}}^{TP}={s_{2D}}^{TP}=\frac{\left(8\beta -2\alpha \beta -\alpha +2\right)}{2\beta \left(4-{\alpha }^2\right)}$ and ${q_{1D}}^{TP}={q_{2D}}^{TP}=\frac{4\beta +2\alpha \beta -2{\alpha }^2\beta +\alpha -2}{2\beta \left(\alpha +1\right)\left(4-{\alpha }^2\right)}$ , respectively. Where $\begin{array}{l}C={\alpha }^2\left(4{\alpha }^2-3\alpha -1\right)+2\beta \left(12\beta -5\right)-4\\ +\alpha \beta \left[36\beta +7-\alpha \left(2\beta +13\right)-{\alpha }^2\left(\beta +10\right)+{\alpha }^3\left(2\beta +5\right)\right]\end{array}$ . At this point, the profit of the cooperative is

$\begin{array}{ll}{\pi }_{CD}TP=\frac{4\alpha \beta +2{\alpha }^2\beta -2{\alpha }^3\beta +{\alpha }^2-2\alpha }{2\beta {\left(\alpha +1\right)}^2\left(4-{\alpha }^2\right)}+F& (46)\end{array}$

Proposition 2: The two-part fee system is superior to linear fees when both sellers have bargaining power.

Proof: By comparing the profits made by the cooperative under the two pricing forms, we can obtain the conclusion of Proposition 2. See Supplementary Table S1 for the detailed proof procedure.

5 Simulation analysis

Due to the complexity of the results of the cooperative’s profit, the next step is to use MATLAB R2023a to carry out numerical simulations and draw two-dimensional surface diagrams. From the previous section, it can be seen that the profit gained by the cooperative will change with the change of α. Setting β as a constant can more intuitively reflect the effect of the change of α on the profit gained by the cooperative. This not only proves the conclusion of the previous section but also provides partial support for cooperatives to organize the production of agricultural products.

5.1 Full bargaining power of cooperatives

Figure 2A clearly depicts a two-dimensional graphical representation of the profit accrued by a cooperative endowed with full bargaining power, employing a linear pricing strategy. In contrast, Figure 2B presents an analogous two-dimensional plot, illustrating the profit achieved by the same cooperative when it opts for a two-part tariff pricing scheme. In both figures, the horizontal axis signifies the level of differentiation among agricultural products, while the vertical axis quantifies the cooperative’s profit.

Figure 2

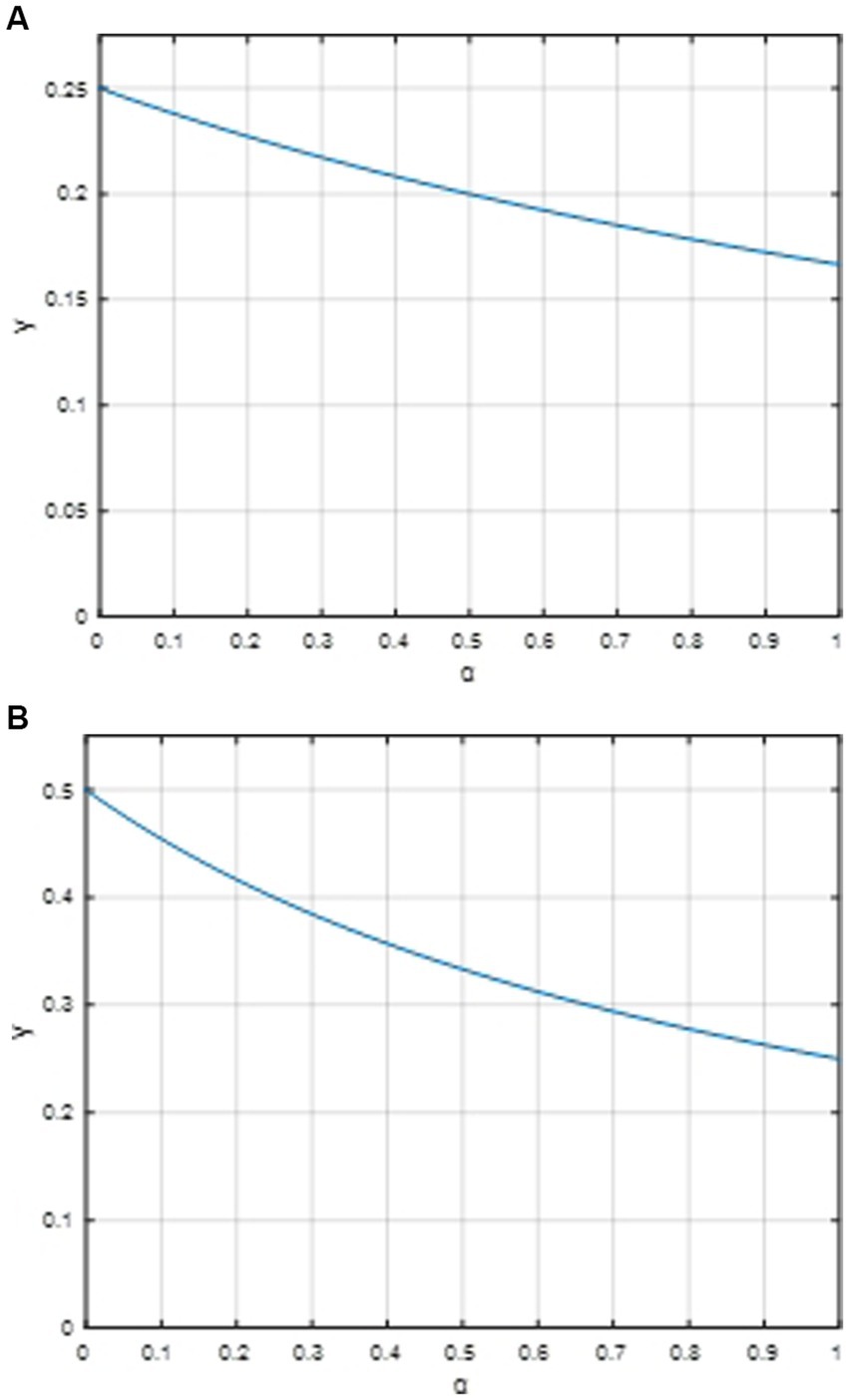
Figure 2. Two-dimensional plot of changes in profits earned when cooperatives have full bargaining power. (A) A two-dimensional graph of the profit earned by a cooperative with full bargaining power that chooses linear pricing. (B) A two-dimensional graph of the profit earned by a cooperative with full bargaining power that chooses a dual fee system.

The comparison reveals that, under identical conditions, adopting a two-part tariff system surpasses linear pricing in terms of profitability, echoing the conclusion drawn earlier. Notably, within the context of both pricing methodologies, there exists an inverse relationship with a hypothetical value of 0 (which, for clarity, may represent a threshold or an optimal state of differentiation/pricing efficiency). As this hypothetical value approaches 0, the cooperative’s profit margins expand significantly.

This finding underscores a strategic opportunity for cooperatives to orchestrate farmers’ efforts toward cultivating differentiated agricultural products—those imbued with “local characteristics”—and leveraging their unique regional resources to further distinguish their production. By doing so, cooperatives can maximize their profits, demonstrating the superiority of the two-part tariff model over linear pricing in harnessing the power of differentiation to enhance economic returns.

5.2 Bargaining process between sellers and cooperatives

Figures 3A,B show two-dimensional plots of the profit earned by the cooperative when Seller 1 has bargaining power and the profit earned by the cooperative when both sellers have bargaining power under linear pricing, respectively.

Figure 3

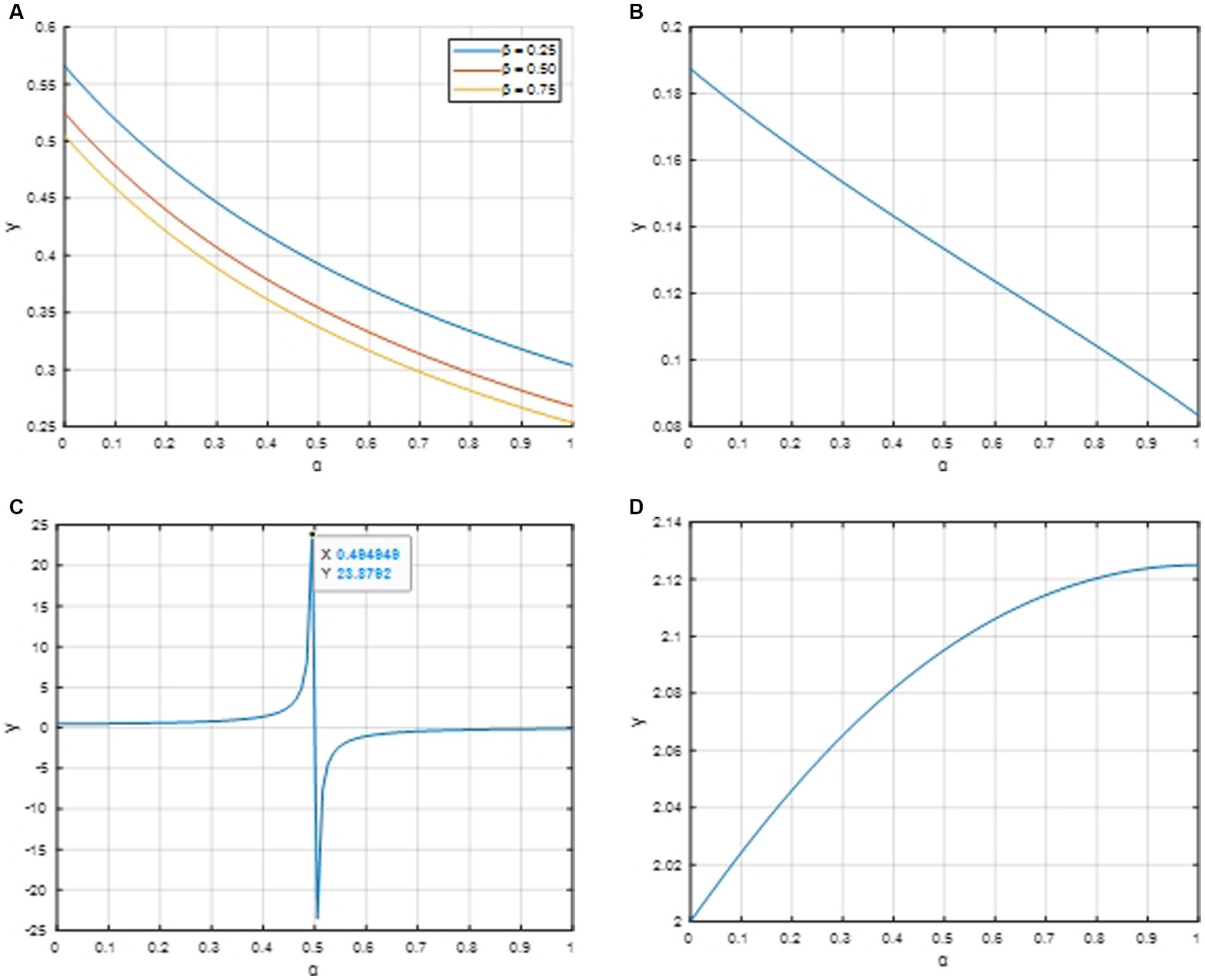
Figure 3. Two-dimensional plot of changes in profits earned by cooperatives under linear pricing and a two-part fee system. (A) The profit earned by the cooperative under linear pricing when seller 1 has bargaining power. (B) The profit earned by the cooperative when both sellers have bargaining power under linear pricing. (C) The profit earned by the cooperative when seller 1 has bargaining power under the dual fee system. (D) The profit earned by the cooperative when both sellers have bargaining power under the dual fee system.

Figures 3C,D exhibit two-dimensional visualizations of the cooperative’s profit dynamics under a two-part tariff system, specifically addressing scenarios where Seller 1 possesses bargaining power and where both sellers share bargaining power. Conversely, Figures 3A,B demonstrate that as a hypothetical value (representative of a threshold or optimization point) approaches 0, the cooperative’s profits escalate significantly under linear pricing. This indicates that, within a linear pricing framework, cooperatives can maximize their earnings by organizing farmers to cultivate differentiated agricultural products, strategically targeting consumer segments, and enhancing product quality attributes such as taste and nutritional value.

However, Figures 3C,D reveal a contrasting strategy under the two-part tariff system: Cooperatives should foster the production of homogeneous agricultural products to optimize profitability through process efficiency, cost reduction, quality enhancement, and bolstering consumer loyalty and positive word of mouth. Notably, Figure 3C underscores that the proposed two-part tariff system’s viability is contingent upon bargaining power remaining within a specified range. As α nears 0.5, the scope for implementing pricing constraints narrows, revealing an optimal profit window exclusive to this range. Beyond this range, linear pricing emerges as the more reliable option, ensuring cooperative profitability even in the face of constraint breaches.

Furthermore, Figures 3C,D reaffirm that cooperatives prefer the two-part tariff over linear pricing, recognizing that while linear pricing fosters profit distribution improvements within the agricultural supply chain through differentiated production, the two-part tariff model incentivizes and organizes farmers toward profit maximization through agricultural production, emphasizing a strategic shift based on the pricing model chosen.

6 Discussion and managerial implication

In the context of different bargaining power of sellers, how to choose the optimal pricing strategy for agricultural products is an important decision-making problem faced by cooperatives. Based on the profound analysis of bargaining power, this paper constructs a vertical market structure model covering upstream monopoly suppliers and downstream duopoly sellers to explore the optimal pricing path for cooperatives.

The core finding of the study differs from previous conventional knowledge by pointing out that linear pricing is not a universally optimal solution for cooperatives. Specifically, when there is no bargaining space between cooperatives and sellers, the two-part tariff pricing strategy is preferred because of its unique advantages and helps cooperatives maximize profits. However, when cooperatives bargain with sellers, the situation becomes more complex: If a single seller has bargaining power, the price discount β needs to be maintained within a certain range, and cooperatives will choose to continue to use the two-part tariff pricing; once the discount exceeds a certain range, cooperatives need to flexibly shift to linear pricing to protect their profits. More significantly, when all sellers bargain with the cooperative, the two-part tariff pricing strategy shows an overwhelming advantage over linear pricing.

Through the simulation analysis, we further draw practical guidance lessons and conclusions: Cooperatives should lead farmers to shift to differentiated agricultural production to optimize supply chain profit distribution when they have stronger bargaining power. When dealing with downstream sellers, if linear pricing is adopted, the cooperative should incentivize farmers to cultivate differentiated products with unique market advantages; if two-part tariff pricing is implemented, it is appropriate to advocate farmers to produce homogeneous agricultural products to maximize profits through economies of scale and production process optimization.

These findings not only reflect the original contribution of this study, which enriches the theoretical treasury of agricultural economics and supply chain management but also reveal the key role of cooperatives in optimizing the agricultural value chain. Its generalizable value lies in the fact that the logic of pricing strategies revealed in this study is widely applicable to all types of cooperatives and their upstream and downstream relationship management, opening up new paths for the sustainable development of the agricultural industry. At the level of industry practice, this study provides a valuable guide for cooperatives to adjust their strategies. When cooperatives have strong bargaining power, they should actively promote the production of differentiated agricultural products to optimize the profit distribution structure of the supply chain; and when negotiating pricing with downstream sellers, cooperatives should flexibly adjust their production strategies according to the different pricing models (linear or two-part tariffs) adopted.

In delving into the impact of cooperative intervention on pricing decisions in the agricultural supply chain, we cannot help but extend our perspective to the broader business and technology arena. Modern computational methods, with their superior predictive power, not only map the path to commercial success for complex technologies but also reveal the potential for data-based insights into future trends in the traditional area of agricultural pricing. Energy pricing, as a core element of the cost structure, is not only economically important but also politically crucial and cannot be ignored. In addition, the rapid development of artificial intelligence technology is significantly enhancing our ability to solve multi-factor intertwined techno-economic problems, providing unprecedented intelligent support for the optimization of agricultural pricing strategies.

Notably, the prevalence of the bargaining phenomenon transcends the boundaries of the agricultural industry chain, with diversified industries such as coal and power, pharmaceuticals, steel, and automobiles demonstrating the significant impact of buyer bargaining power.

Based on the above analysis, the findings of this study provide the following insights for cooperatives and policymakers:

1. Cooperatives should demonstrate a high degree of market sensitivity and flexibility and tailor their pricing strategies to the specific needs and characteristics of diversified distributors such as large supermarkets and small wholesalers. At the same time, they should actively guide farmers to adjust their planting structure according to the market dynamics. Whether pursuing large-scale homogenized production of agricultural products or differentiated planting, the aim is to optimize the profit distribution structure of the supply chain of agricultural products and promote the synergistic development of the upstream and downstream of the industrial chain.

2. Local governments should play a leading role in increasing support for the development of cooperatives. By attracting and cultivating diversified talents such as migrant workers, veterans, and university graduates, they can inject fresh blood and vitality into cooperatives. At the same time, they should improve the management mechanism of cooperatives, implement the strategy of introducing cooperative enterprises, and enhance the overall competitiveness of cooperatives. At the financial and policy levels, we provide cooperatives with the necessary financial support and investment in agricultural infrastructure construction, strengthen the enforcement of relevant regulations, and ensure that agricultural products meet safety and quality standards at every stage from production to consumption, so as to lay a solid foundation for the sustainable development of cooperatives.

However, this model also has its limitations. In the real world, it is often difficult for cooperatives to obtain complete information about seller behavior and strategies, which may lead them to make decisions based on incomplete information. In addition, the model assumes that participants are rational and will make decisions based on maximizing their own interests. However, in reality, the behavior of cooperatives may be influenced by emotions, biases, and moral perceptions, which may deviate from the rationality assumption.

Meanwhile, the current analytical framework focuses on the direct transactional relationships between traditional merchants, hypermarkets, and integrated platforms but neglects an emerging phenomenon—namely, platform models that exhibit bilateral network externalities, such as online grocery delivery platforms like Instacart. Such platforms not only connect consumers to retailers but also greatly facilitate supply–demand matching and value creation in the market through their unique network effects. As a result, our existing analysis may fail to adequately capture the importance of network externalities in this platform economy. To take a more comprehensive look at this phenomenon, future research should focus on taking network externalities into account in order to explore in greater depth how it affects market structure, transaction efficiency, and the behavioral strategies of various participants.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JH: Writing – review & editing. ZS: Writing – original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was funded by the Key Project of Social Science Planning Fund of Liaoning Province “Research on Marketing Channels and Development Countermeasures of Agricultural Products in Liaoning Province under the Background of Digital Economy” (L23AJY007).

Acknowledgments

ZS would like to express heartfelt thanks to his supervisors, Han and Meng, whose patient guidance and valuable suggestions constantly encouraged the author to complete this work. ZS would also like to thank the editors and reviewers of Frontiers in Sustainable Food Systems for their valuable comments. In addition, he would like to thank his parents, whose care and support encouraged him to continue his journey. Finally, a thank you to the authors of the published articles who gave ZS the inspiration to write this thesis.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpsyg.2024.1175591/full#supplementary-material

References

Alonso, R. S., Sittón-Candanedo, I., García, Ó., Prieto, J., and Rodríguez-González, S. (2020). An intelligent edge-IoT platform for monitoring livestock and crops in a dairy farming scenario. Ad Hoc Netw. 98:102047. doi: 10.1016/j.adhoc.2019.102047

Crossref Full Text | Google Scholar

An, J., Cho, S. H., and Tang, C. S. (2015). Aggregating smallholder farmers in emerging economies. Prod. Oper. Manag. 24, 1414–1429. doi: 10.1111/poms.12372

Crossref Full Text | Google Scholar

Chao, P. E. N. G., Biao, M. A., and Zhang, C. (2021). Poverty alleviation through e-commerce: village involvement and demonstration policies in rural China. J. Integr. Agric. 20, 998–1011. doi: 10.1016/S2095-3119(20)63422-0

Crossref Full Text | Google Scholar

Dania, W. A. P., Xing, K., and Amer, Y. (2018). Collaboration behavioural factors for sustainable agri-food supply chains: a systematic review. J. Clean. Prod. 186, 851–864. doi: 10.1016/j.jclepro.2018.03.148

Crossref Full Text | Google Scholar

De Giovanni, P. (2020). Blockchain and smart contracts in supply chain management: a game theoretic model. Int. J. Prod. Econ. 228:107855. doi: 10.1016/j.ijpe.2020.107855

Crossref Full Text | Google Scholar

De, A., and Singh, S. P. (2023). A resilient pricing and service quality level decision for fresh Agri-product supply chain in post-COVID-19 era. Int. J. Logistics Manag. 34, 1101–1140. doi: 10.1108/IJLM-02-2021-0117

Crossref Full Text | Google Scholar

Feng, X. (2024). Control, exploitation and exclusion: experiences of small farmer e-tailers in agricultural e-commerce in China. J. Agrar. Chang. 24:e12567. doi: 10.1111/joac.12567

Crossref Full Text | Google Scholar

Ganesh Kumar, C., Murugaiyan, P., and Madanmohan, G. (2017). Agri-food supply chain management: literature review. Intell. Inf. Manag. 9, 68–96. doi: 10.4236/iim.2017.92004

Crossref Full Text | Google Scholar

Golmohammadi, A., and Hassini, E. (2019). Capacity, pricing and production under supply and demand uncertainties with an application in agriculture. Eur. J. Oper. Res. 275, 1037–1049. doi: 10.1016/j.ejor.2018.12.027

Crossref Full Text | Google Scholar

Hamidoğlu, A., Gül, Ö. M., and Kadry, S. N. (2024). A game-theoretical approach for the adoption of government-supported blockchain application in the IoT-enabled agricultural supply chain. Internet Things 26:101163. doi: 10.1016/j.iot.2024.101163

Crossref Full Text | Google Scholar

He, Y., Chen, L., and Xu, Q. (2024). Optimal pricing decisions for a global fresh product supply chain in the blockchain technology era. Int J Log Res Appl 27, 649–666. doi: 10.1080/13675567.2021.1981275

Crossref Full Text | Google Scholar

Jiang, J., Jiang, S., Xu, G., and Li, J. (2024). Research on pricing strategy and profit-distribution mechanism of green and low-carbon agricultural products’ traceability supply chain. Sustain. For. 16:2087. doi: 10.3390/su16052087

Crossref Full Text | Google Scholar

Kumar, A., Singh, R. K., and Modgil, S. (2020). Exploring the relationship between ICT, SCM practices and organizational performance in Agri-food supply chain. BIJ 27, 1003–1041. doi: 10.1108/BIJ-11-2019-0500

Crossref Full Text | Google Scholar

Maroušek, J., Minofar, B., Maroušková, A., Strunecký, O., and Gavurová, B. (2023). Environmental and economic advantages of production and application of digestate biochar. Environment. Technol. Innov. 30:103109. doi: 10.1016/j.eti.2023.103109

Crossref Full Text | Google Scholar

Niu, B., Jin, D., and Pu, X. (2016). Coordination of channel members’ efforts and utilities in contract farming operations. Eur. J. Oper. Res. 255, 869–883. doi: 10.1016/j.ejor.2016.05.064

Crossref Full Text | Google Scholar

Panwar, N. L., Kaushik, S. C., and Kothari, S. (2011). Solar greenhouse an option for renewable and sustainable farming. Renew. Sust. Energ. Rev. 15, 3934–3945. doi: 10.1016/j.rser.2011.07.030

Crossref Full Text | Google Scholar

Perlman, Y., Ozinci, Y., and Westrich, S. (2022). Pricing decisions in a dual supply chain of organic and conventional agricultural products. Ann. Oper. Res. 314, 601–616. doi: 10.1007/s10479-019-03169-3

Crossref Full Text | Google Scholar

Rana, S. K., Kim, H. C., Pani, S. K., Rana, S. K., Joo, M. I., Rana, A. K., et al. (2021). Blockchain-based model to improve the performance of the next-generation digital supply chain. Sustain. For. 13:10008. doi: 10.3390/su131810008

Crossref Full Text | Google Scholar

Ranjan, R. (2017). Challenges to farm produce marketing: a model of bargaining between farmers and middlemen under risk. J. Agric. Resour. Econ. 42, 386–405.

Google Scholar

Ronaghi, N., Shade, D., Moon, H. J., Najmi, S., Cleveland, J. W., Walton, K. S., et al. (2021). Modulation and tuning of UiO-66 for Lewis acid catalyzed carbohydrate conversion: Conversion of unprotected aldose sugars to polyhydroxyalkyl and C-glycosyl furans. ACS Sustain. Chem. Eng. 9, 11581–11595.

Google Scholar

Song, L., Luo, Y., Chang, Z., Jin, C., and Nicolas, M. (2022). Blockchain adoption in agricultural supply chain for better sustainability: a game theory perspective. Sustain. For. 14:1470. doi: 10.3390/su14031470

Crossref Full Text | Google Scholar

Vochozka, M., Rowland, Z., Suler, P., and Marousek, J. (2020). The influence of the international price of oil on the value of the EUR/USD exchange rate. J. Competitiv. 12, 167–190. doi: 10.7441/joc.2020.02.10

Crossref Full Text | Google Scholar

Wang, D., Tian, X., and Guo, M. (2024). Pricing decision and channel selection of fresh agricultural products dual-channel supply chain based on blockchain. PLoS One 19:e0297484. doi: 10.1371/journal.pone.0297484

PubMed Abstract | Crossref Full Text | Google Scholar

Wu, X. Y., Fan, Z. P., and Cao, B. B. (2023). An analysis of strategies for adopting blockchain technology in the fresh product supply chain. Int. J. Prod. Res. 61, 3717–3734. doi: 10.1080/00207543.2021.1894497

Crossref Full Text | Google Scholar

Wu, T. Q., Yang, D. L., and Ma, J. (2022). Influencing factors of new agricultural management subjects in the metropolitan area to the response of farmland mortgage loan-taking Shan District of Shanghai as an example. 116–122.

Google Scholar

Xu, N., Xu, C., Jin, Y., and Yu, Z. (2022). Research on the operating mechanism of E-commerce poverty alleviation in agricultural cooperatives: an actor network theory perspective. Front. Psychol. 13:847902. doi: 10.3389/fpsyg.2022.847902

PubMed Abstract | Crossref Full Text | Google Scholar

Yan, B., Liu, G., Wu, X., and Wu, J. (2021). Decision-making on the supply chain of fresh agricultural products with two-period price and option contract. Asia-Pacific J. Operat. Res. 38:2050038. doi: 10.1142/S0217595920500384

Crossref Full Text | Google Scholar

Yan, B., Yan, C., Ke, C., and Tan, X. (2016). Information sharing in supply chain of agricultural products based on the internet of things. Ind. Manag. Data Syst. 116, 1397–1416. doi: 10.1108/IMDS-12-2015-0512

Crossref Full Text | Google Scholar

Zhong, Z., Jiang, W., and Li, Y. (2023). Bridging the gap between smallholders and modern agriculture: full insight into China's agricultural cooperatives. J. Rural. Stud. 101:103037. doi: 10.1016/j.jrurstud.2023.103037

Crossref Full Text | Google Scholar