Stochastic evolutionary game analysis of food cooperation among countries along the Belt and Road from the perspective of food security

Introduction: In recent years, the combination of the public health crisis and the climate crisis has greatly weakened the resilience of food systems. The Belt and Road food cooperation will make outstanding contributions to consolidate food security and reduce global poverty in countries along the Belt and Road.

Methods: This paper constructs a three-party stochastic evolutionary game model from the perspective of food security, distinguishes the difference between large and small countries by calculating the cereal self-sufficiency rate, which studies the cooperation strategy with the Belt and Road cereal large countries, cereal small countries and regulatory committees as the object. In addition, we introduce the Gaussian white noise characteristics to characterize the stochastic disturbance of the game system. Then we combine the mathematical derivation of the stochastic evolutionary game analysis with the simulation method, examine the effect of the stochastic disturbance factors on the cooperation, and find out the factors that affect the cooperation. And finally verifies the model and proves the reasonableness and practicability of the model.

Results: The stochastic evolutionary game model analyzes the interaction of stochastic disturbance and influencing factors from a dynamic perspective, and the stability of evolution is related to the strength of Gaussian white noise. The level of effort of large cereal countries and the incentives of regulatory committees can have a positive impact, but high income in small cereal countries can lead to instability in the strategic choices of other players.

Discussion: Taking the countries along the Belt and Road as the research object, Gaussian white noise is introduced to describe the stochastic external environment, discriminate the stability of the game system through stochastic differential equations, and analyze the influencing factors of the dynamic behavioral strategies of the parties in combination with simulation methods. To improve the capacity of national food security governance and help improve the resilience of the world food system.

1. Introduction

The Belt and Road Initiative includes a major initiative to build the Silk Road Economic Belt and to build the twenty first Century Maritime Silk Road. China's goal is to connect the economically developed countries of East Asia and Europe along the two ancient Silk Roads, creating a platform for economic cooperation on the Eurasian continent with the widest extension and largest scale. As of June 2023, China had signed more than 200 cooperation documents on the construction of the Belt and Road with 152 countries and 32 international organizations (Qi, 2023). These include countries in Africa, Europe, East Asia, Central Asia, South-East Asia, the Pacific, North Africa, Latin America, and the Caribbean. The beauty of China's Belt and Road Initiative is that it creates a diverse and interconnected network. It is a network of transportation routes and new trade hubs connecting Central Europe, an economic system covering the entire Eurasian region. This cooperation belt unites the greatest consensus of the countries along the route that aspire to develop and meets the most urgent will of the countries and regions along the route for economic upgrading. With the deepening of the Belt and Road (B&R) construction, policy integration, financial connectivity, infrastructure interconnection, and cultural communication among the participating parties have created important conditions for promoting the countries along the route to give full play to their comparative advantages in agriculture, promoting the free flow of agricultural production factors in the region and establishing good interaction relationship in agricultural trade. All countries along the B&R hope to promote sustained and stable economic and social development by strengthening international cooperation in agriculture and cooperation in agriculture and food security has become the pillar of the Belt and Road (Ministry of Agriculture, 2017). According to the Food and Agriculture Organization of the United Nations, India, Russia, and Ukraine are the most important core nodes of food trade among the Belt and Road countries, and the scale of food trade has long been at the forefront of the countries along the route (Chen and Zhang, 2022). Russia and Ukraine account for one-third of global food exports, and approximately 50 countries and regions depend on Russia and Ukraine for more than 30% of their wheat supplies (Ben Hassen and El Bilali, 2022). The conflict between Russia and Ukraine has forced the closure of food export routes between the two countries, soaring prices for some agricultural products, and global food supply shortages, with food security problems particularly acute in the Middle East and Africa (Xu et al., 2021a). The La Niña phenomenon, which began in the second half of 2020 (Antonio et al., 2021), has caused extreme drought conditions in the core major corn and soybean-producing regions located in North and South America that have been uncommon for many years, driving up international food prices (FAO, 2022). Border closures and logistical restrictions taken by countries to control the new crown epidemic have also affected agricultural production and food supply chain stability, pushing up international food prices to some extent (Devereux et al., 2020; O'Hara and Toussaint, 2021). To solve the food crisis, many governments have formulated various policies including restricting food exports and actively seeking food cooperation (Zhao, 2019; Béné, 2022; Clapp, 2023). However, the B&R food cooperation system involves multiple parties, and the existence of conflicting interests makes it difficult to implement cooperation effectively. In particular, there is a high degree of complexity in the behavior of participants in the B&R food cooperation system due to a range of uncertainties in the external environment (Foster and Young, 1990; Xu, 2010). In view of this, this article considers the impact of external stochastic perturbations on the evolution of the game system, constructs a three-party stochastic evolutionary game model of a large cereal country, a small cereal country, and a regulatory committee, and systematically studies the strategic choices of game players under uncertain environments and their influence on the stochastic evolutionary process.

Zhou and Tong (2022b) studied the agricultural trade competitiveness of China and countries along the Belt and Road and its influencing factors by using MS, RSCA index, and other methods. The results show that there are large differences between China and the regions and countries along the Belt and Road because financial resources are not integrated into competitiveness. Wang (2019) analyzed the trade pattern of China–ASEAN agricultural products in terms of total trade volume and product structure based on trade data from 2013 to 2017 and found that China-ASEAN agricultural trade is actually facing a slowdown in the growth of trade scale and trade volume. Chen and Zhang (2022) studied the structural characteristics and spatial and temporal dynamics of cereal trade networks of countries along the Belt and Road through network analysis, which helps to optimize the structure of grain trade networks. Zhou and Tong (2022a) analyzes the influencing factors of spatial network structure in terms of planar structure and concludes that agricultural trade in countries along the Belt and Road is highly concentrated in regions and types with high trade intensity. Ya and Pei (2022) conducts an empirical analysis of factors affecting China–Africa agricultural trade based on an extended gravity model and proposes agricultural technology upgrading to accelerate bilateral trade. Zheng and Zhuang (2021) analyzed the factors influencing the construction of agricultural cooperative zones in countries along the “Belt and Road” based on the Logit model, which can provide a reference for the spatial layout of overseas agricultural cooperative zones. Based on OFDI and the new economic geography theory, Tian and Liu (2022) discusses the factors that influence investment in the food industry in countries along the Belt and Road and the impact of investment on bilateral economic distance. However, few scholars have studied food cooperation among Belt and Road countries from the perspective of the food crisis, and many studies have neglected the impact of game interactions among Belt and Road cooperating countries on participants' decisions. In reality, the uncertain external environment is an important factor that cannot be ignored by Belt and Road countries participating in food cooperation.

To fill these research gaps, in this article, we establish a three-party stochastic evolutionary game model of food cooperation in B&R countries based on bounded rationality theory, which determines the payment matrix and the replication dynamic equation. In addition, the model we established considers the influence of random factor interference and introduces Gaussian white noise in the formula. Then, the numerical approximation can be solved by Taylor expansion. The evolution trajectory of food cooperation is described by numerical simulation of the B&R countries from three aspects: stability, rate of change, and convergence speed. This article is innovative in the following aspects:

(1) The majority of current research on the B&R is concentrated on economic, water, and ecological security and energy and lacks competing studies from the perspective of food security. The impact of the food crisis on global food security is significant. In this article, we propose to develop a three-way stochastic game model for large cereal countries, small cereal countries, and regulatory committees from the perspective of food security combined with the game characteristics of Belt and Road countries.

(2) Traditional evolutionary games can only analyze the strategy choice in a deterministic scenario and cannot describe realistic stochastic disturbances. The stochastic disturbance was introduced into the evolutionary game model of grain cooperation, which made up for the shortcomings of the existing literature in model construction and improved the reliability of the research on cooperation strategy selection of countries along the Belt and Road.

(3) The tripartite evolution trajectory of the game is described from three aspects: stability, variability, and convergence rate, and the strategy stability, strategy choice interaction, and dynamic decision-making of the parties are studied. Through comparative analysis of the evolution of cooperation paths under tripartite random disturbance, some instructive cooperation suggestions are obtained.

This article is structured as follows: Section 2 reviews the relevant studies. Section 3 describes the problems, proposes the assumptions, describes the building of a basic model, and utilization of the tripartite stochastic evolutionary game model, and the presence and stability of equilibrium solutions are investigated. Section 4 evaluates the results of the coefficients in the model that influence the food cooperation strategy with the numerical simulations. In Section 5, model verification is carried out. The discussion is in Section 6.

2. Literature review

2.1. Belt and Road food cooperation

Food and agriculture cooperation is a key but neglected aspect of BRI. Yao finds that investment in agriculture remains surprisingly low for most countries (Yao et al., 2020). Agricultural trade along the B&R has both direct and indirect positive effects on food security in cooperative countries. These positive impacts are evident when agricultural trade is conducted in the B&R countries. Gunasekera et al. (2015) concluded that B&R countries can strengthen food security by attracting more foreign direct investment (FDI) in agriculture, especially those that increase local agricultural productivity. Many studies have been conducted to evaluate China and certain countries along the B&R agriculture trade (Wang, 2019; Tian and Liu, 2022), or to analyze the structure, spatial, and temporal characteristics and use existing methods to identify factors that affect the agricultural trade among nations along the B&R (Zheng and Zhuang, 2021; Chen and Zhang, 2022; Ya and Pei, 2022; Zhou and Tong, 2022a,b). These studies do not consider the food cooperation of the B&R countries from the perspective of the food crisis. Tortajada and Zhang (2021) point out that agriculture and food security cooperation along the Belt and Road has become an effective solution for food security in countries along the route. However, with the overlapping of various natural and man-made disasters and the spreading of food crises, more comprehensive planning is needed on how to play the leading role of the Belt and Road in solving the global food security problem and reshaping the food security governance of the Belt and Road.

2.2. Stochastic evolutionary game of the Belt and Road

Evolutionary game theory became a recognized subject of research thanks to Smith and Price (1973), who were the first to develop the ideas of evolutionary games and evolutionary stability techniques (Smith, 1974). A replicator equation defined by Taylor and Jonker for a single species plays an important role in game dynamics (Cressman and Tao, 2014), and the evolutionary game theory has produced yet another groundbreaking development. Evolutionary game theory is a tool to understand the interactions among decision-makers with rational and strategic thinking abilities (Zhang et al., 2020), and some scholars have made many efforts to use evolutionary game theory to study the cooperation of countries along the B&R. In the context of BRI, a dynamic choice of logistics service providers was explored using an evolutionary game model and logistic service integrators in the context of corporate information co-strategy (Li et al., 2020). Based on Li's study, Wang et al. (2022) examined the interaction mechanism between the regulatory committees of upstream and downstream countries and how transboundary ecological compensation can be sustained. Subsequently, Zhao et al. (2022) constructs a dynamic game model with China and the countries along the Belt and Road as players, evaluating the effects of various strategies and increasing the possibility of cooperation between them. Since there is uncertainty in reality, it is difficult to use deterministic evolutionary game models to portray the actual food cooperative situation in B&R countries. Therefore, for analysis and judgment of stochastic evolution's stability, the stochastic disturbance is necessary (Cobb, 1978; Foster and Young, 1990).

3. Materials and methods

3.1. Problem description and parameter setting

As the main source of food for humans, food plays an important role in feeding the population and the majority of agricultural trade takes place in this sector. In this article, we adopt the concept of “cereal” (HS10) as defined by the Convention on the Harmonized System of International Commodity Description and Coding used by Chen and Zhang (2022), which includes wheat and mescaline (HS1001); rye (HS1002); barley (HS1003); oats (HS1004); maize (HS1005); rice (HS1006); grain sorghum (HS1007); and buckwheat, millet, and canary seeds (HS1008), that is, we have chosen a narrow concept of food—“cereal.”

We refer to Brankov et al. (2021), Brankov and Matkovski (2022) formula for calculating the cereal self-sufficiency rate (SSR):

$\begin{array}{ll}SSR=P/D\times 100\%\hfill & (1)\end{array}$

Where SSR is the food self-sufficiency rate, P is the total domestic food production, and D is the total supply.

Combined with the FAO cereal self-sufficiency ratio (SSR) calculation (FAOSTAT, 2021), the D formula can be written as follows:

$\begin{array}{ll}D=P-E+Z+I\hfill & (2)\end{array}$

where E, Z, and I are food exports, inventory changes (decrease or increase), and imports, respectively; P is the quantity of food production, and D is the quantity of food domestic supply.

According to Equations (1) and (2) and combined with the cereal import dependency ratio issued by FAO, the cereal self-sufficiency rates of some major countries along the Belt and Road can be derived as shown in Table 1:

TABLE 1

Table 1. Cereal self-sufficiency rates of some major countries along the Belt and Road.

The cereal self-sufficiency rates of other countries along the Belt and Road can be calculated according to the same method. According to literature references (Qiquan, 2022; Xu and Yang, 2022), an SSR above 95% is a safe level, while <95% indicates an increased risk of cereal supply and demand. Therefore, we define countries with an SSR <95% as small cereal countries and those with an SSR above 95% as large cereal countries, using the security level of cereal self-sufficiency as the criterion.

By transferring or granting certain rights to member states in the development of treaties, regulatory committees can play an active role in cooperation (Schmeier and Shubber, 2018; Wang et al., 2022). Referring to Wang et al. (2022), the functions of the regulatory committee in this article are to ensure compliance by member countries, prevent opportunistic behavior, and supervise cooperative behavior.

Assumption 1. There are three main bodies of the B&R food security cooperation, namely, large cereal countries, small cereal countries, and regulatory committees. The large cereal countries have two strategies namely contractual joint cooperation and non-cooperation denoted by x and 1 − x, respectively; the small cereal countries also have two strategies namely information-sharing cooperation and non-cooperation denoted by y and 1 − y, respectively; and the regulatory committee has two strategies namely supervision and non-supervision denoted by z and 1 − z, respectively. In terms of the strength of cooperation constraints (Lin et al., 2020), cooperation can be categorized into two types: one is contractual joint cooperation, which complies with strict cost-sharing, risk-sharing, and benefit-sharing mechanisms. The second is information-sharing cooperation, where both partners reach a friendly agreement on the project, agree to an alliance, and maintain good information interchange, without a clear sharing agreement and power and responsibility relationship, which is a weaker binding cooperation, such as enterprise alliance. Since there is a large gap between the two cooperating parties, the larger and more technically competent party leads the smaller and less technically competent party to cooperate in an information-sharing manner (Avalos, 2009; Li et al., 2020; Lin et al., 2020).

Assumption 2. There is an information cost for each country in choosing a cooperation strategy, and cooperation costs a certain amount of money while bringing additional benefits to the country. The information cost of the large cereal country is M1 (Li et al., 2020), and the information cost of the small cereal country is M2, M1 > M2.

Assumption 3. Countries differ in experience with government, technological advancements, rules and regulations, and cultural perspectives, and these differences prevent them from acting in concert on food cooperation. When two countries cooperate, the cost of eliminating obstacles to collaboration for a single country is indicated by C (Xu et al., 2021b). The cost of eliminating obstacles to cooperation for a large country is C1 and the cost of eliminating obstacles to cooperation for a small country is C2, C1 > C2 (Li et al., 2020).

Assumption 4. During food cooperation between large and small countries, there are a number of possible risks, including moral hazard and the disclosure of technical secrets, which will lead to increased national operating costs. Using θ to denote the risk coefficient in the food cooperation process, which is usually 0 < θ < 0.5 (Li et al., 2020), the size of the risk coefficient is related to the information cost Mi. These risk costs and speculative gains are positively related to the number of countries cooperating. When one party chooses not to cooperate, the party that chooses not to cooperate will obtain speculative gains, and the speculative gains are S. In addition, the size of speculative gains is also related to Mi. The large and small countries are speculating under the supervision of the regulatory committees, which is defined by P (Li et al., 2020).

Assumption 5. The BRI receives active support from the governments of the countries along the B&R. Increasing infrastructure construction and the development of exchange platforms have helped to accelerate the process of food cooperation. Assuming that the cooperative income is F (Wang et al., 2022), without the supervision of the regulatory committee, the income of the large country is F1 and the income of the small country is F2, F1 > F2.

Assumption 6. To promote food cooperation and exchange, bolster the integration of knowledge about food resources and prod small countries to adopt information sharing, and countries with a large cereal to encourage information sharing, and the extent of efforts by large cereal countries promote cooperation G (Li et al., 2020).

Assumption 7. Food cooperation has spillover effects. Thus, spillover benefits from governance cooperation increase as governance cooperation expands, and the number of cooperating countries is positively correlated with spillover benefits. Bi (i = 1, 2) (Xu et al., 2021a) denotes the spillover benefits obtained from country-to-country cooperation (Tortajada and Zhang, 2021) the benefits for large countries are B1 and for small countries are B2, B1 > B2. It also earns the regulatory committee a good reputation and improves the image of the regulatory committee, and the spillover effect of the regulatory committee is K (FAO, 2023).

Assumption 8. Even if they choose not to engage in food cooperation, this partnership will continue. Therefore, the normal benefit is obtained by completing other cooperative operations Ri (i = 1, 2) (Li et al., 2020). The benefit of the large country is R1, and the benefit of the small country is R2, R1 > R2.

Assumption 9. The revenue at the time of regulatory committee supervision is E and the cost is H. It is set to E > H. If the regulatory commission does not regulate, the payoff is 0 (Wang et al., 2022). World food security policies should contribute to improving food security in food-deficit countries. The incentive behavior of the regulatory committee is L (FAO, 2023).

The presumption is summarized as follows:

(1) Large cereal countries, small cereal countries, and regulatory committees each have limited rationality and try to find the value that maximizes their own interests.

(2) The initial state may not enable participants to adopt an equilibrium strategy. Based on the behavior of other participants, they continuously adjust their optimal strategic choices according to their learning and adaptation to the uncertain environment (Liu et al., 2021a).

(3) According to the evolutionary system, as long as the return on the strategy is higher than the average return, the proportion of adopters will increase. In essence, the likelihood of adoption is higher for more successful strategies. Usually, this principle can be expressed in terms of the replication dynamics equation.

(4) The external environment is complex and uncertain, so participants may not always make rational decisions to maximize profits. That is to say, there are stochastic perturbations in the replication dynamics equation (Liu et al., 2021a; Xu and Yang, 2022).

Based on the aforementioned problem description and presumptions, the tripartite game tree for large cereal countries is shown in Figure 1 and the various parameters of the stochastic evolutionary game model are shown in Table 2.

FIGURE 1

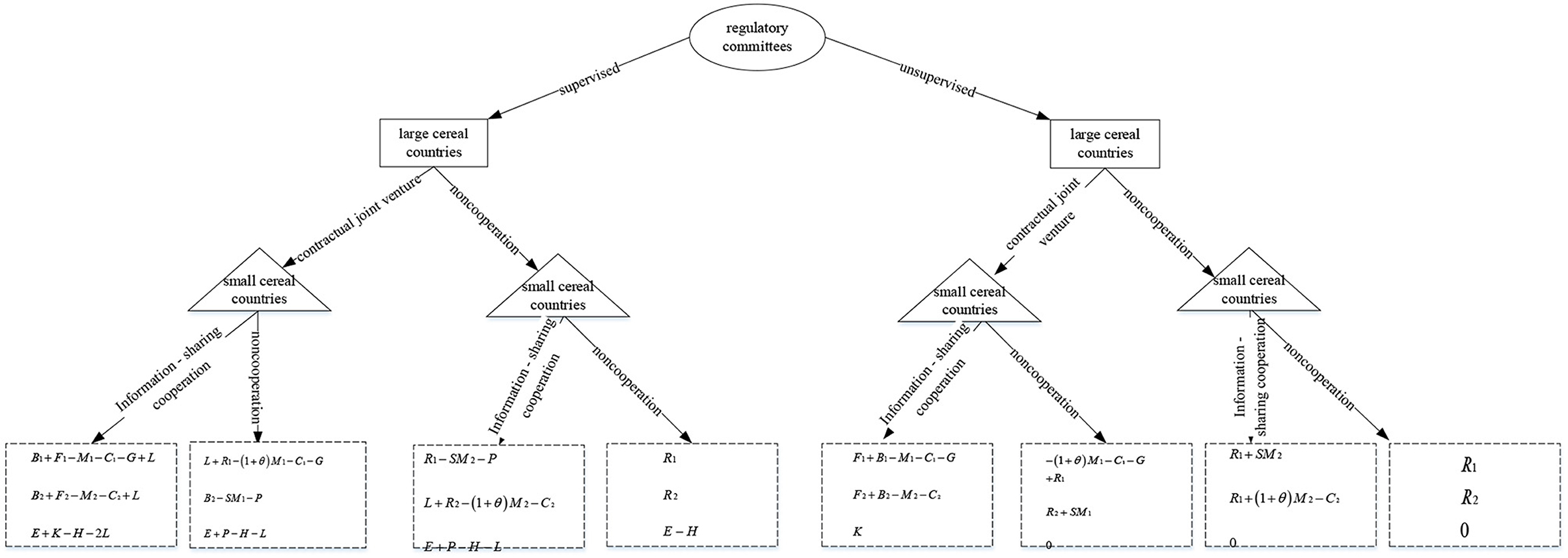
Figure 1. Tripartite game tree among large cereal countries, small cereal countries, and regulatory committees.

TABLE 2

Table 2. Various parameters of the stochastic evolutionary game model.

3.2. Payment matrix and replication dynamic equations

The payment matrices for large cereal countries, small cereal countries, and regulatory committees under different combinations of strategies are shown in Table 3.

TABLE 3

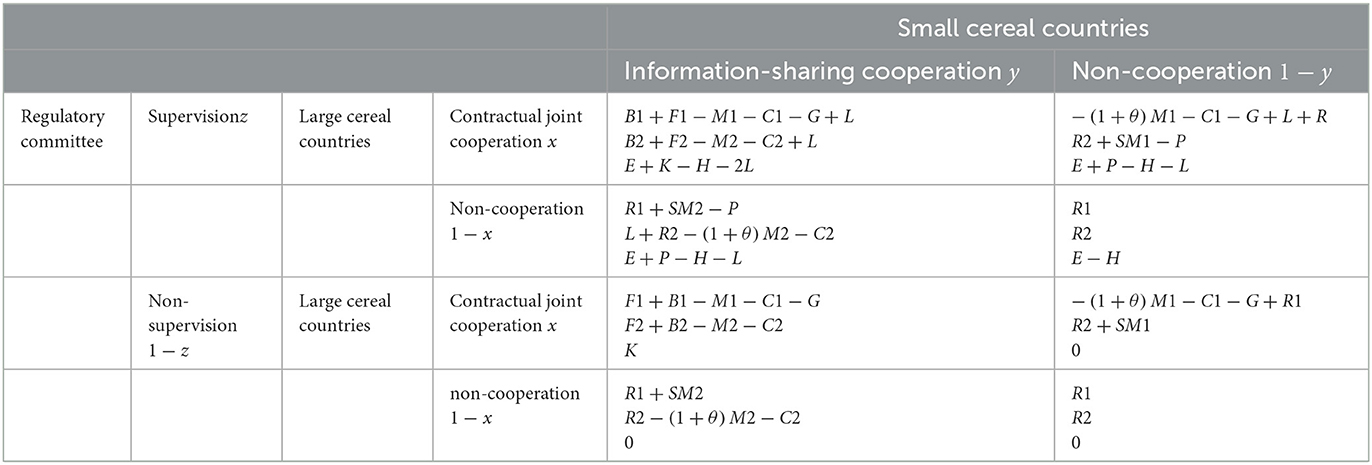
Table 3. Payment matrices for large cereal countries, small cereal countries, and regulatory committees under different combinations of strategies.

Let Vx and V1 − x represent the expected revenues of large cereal countries for contractual joint and non-cooperation, and the average revenues are denoted by $\overline{Vx}$.

$\begin{array}{ll}\begin{array}{c}Vx=yz\left[L+B1+F1-M1-C1-G\right]\hfill \\ +(1-y)z\left[L-(1+\theta )M1-C1-G+R1\right]\hfill \\ +(1-z)y\left[B1+F1-M1-C1-G\right]\hfill \\ +(1-y)(1-z)\left[R1-(1+\theta )M1-C1-G\right]\hfill \\ =zL+(1-y)\left[R1-(1+\theta )M1\right]+y(F1+B1-M1)-C1-G\hfill \end{array}\hfill & (3)\end{array}$

$\begin{array}{ll}\begin{array}{c}V1-x=yz\left[R1+M2S-P\right]\hfill \\ +(1-y)zR1\hfill \\ +y(1-z)\left[R1+M2S\right]\hfill \\ +(1-y)(1-z)R1\hfill \\ \text{=}y(M2S-zP)+R1\hfill \end{array}\hfill & (4)\end{array}$

$\begin{array}{ll}\overline{Vx}=xVx+(1-x)V1-x\hfill & (5)\end{array}$

Then, we can calculate the replicator dynamics equation of large cereal countries adopting contractual joint strategy as Eq. (6):

$\begin{array}{ll}\begin{array}{c}F(x)=\frac{dx}{dt}=x(Vx-\overline{Vx})\hfill \\ =x(1-x)\left[\begin{array}{c}(1-y)\left[R1-(1+\theta )M1\right]+y(F1+B1-M1)\hfill \\ zL-C1-G-y(M2S-zP)-R1\hfill \end{array}\right]\hfill \end{array}\hfill & (6)\end{array}$

Similarly, we can get the expected revenues of small cereal countries for information-sharing cooperation and non-cooperation, denoted by Vy, V1 − y, respectively. And $\overline{Vy}$ represents the average revenues.

Cooperation and the average revenues are denoted by $\overline{Vx}$.

$\begin{array}{ll}\begin{array}{c}Vy=xz\left[B2+F2+L-M2-C2\right]\hfill \\ +(1-x)z\left[-(1+\theta )M2-C2+R2+L\right]\hfill \\ +x(1-z)(B2-M2-C2+F2)\hfill \\ +(1-x)(1-z)\left[R2-(1+\theta )M2-C2\right]\hfill \\ \text{=}zL+x(B2+F2-M2)+(1-x)\left[R2-(1+\theta )M2\right]-C2\hfill \end{array}\hfill & (7)\end{array}$

$\begin{array}{ll}\begin{array}{c}V1-y=xz(R2+M1S-P)\hfill \\ +(1-x)zR2\hfill \\ +x(1-z)(R2+M1S)\hfill \\ +(1-x)(1-z)R2\hfill \\ =x(M1S-zP)+R2\hfill \end{array}\hfill & (8)\end{array}$

$\begin{array}{ll}\overline{Vy}=yVy+(1-y)V1-y\hfill & (9)\end{array}$

Then, we can calculate the replicator dynamics equation of small cereal countries adopting an information-sharing cooperation strategy as Eq. (10):

$\begin{array}{ll}\begin{array}{c}F(y)=\frac{dy}{dt}=y(Vy-\overline{Vy})\hfill \\ =y(1-y)\left[\begin{array}{c}x(B2+F2-M2)+(1-x)\left[R2-(1+\theta )M2\right]\hfill \\ zL-C2-x(M1S-zP)-R2\hfill \end{array}\right]\hfill \end{array}\hfill & (10)\end{array}$

Finally, let Vz and V1 − z represent the expected revenues of regulatory committees for choosing positive supervised and unsupervised, and the average revenues are denoted by $\overline{Vz}$.

$\begin{array}{ll}\begin{array}{c}Vz=xy(E+K-H-2L)\hfill \\ +x(1-y)(E-H+P-L)\hfill \\ +(1-x)y(E-H+P-L)\hfill \\ +(1-x)(1-y)(E-H)\hfill \\ =xy(K-2P)+(x+y)(P-L)+E-H\hfill \end{array}\hfill & (11)\end{array}$

$\begin{array}{ll}V1-z=xyK\hfill & (12)\end{array}$

$\begin{array}{ll}\overline{Vz}=zVz+(1-z)V1-z\hfill & (13)\end{array}$

Then, we can calculate the replicator dynamics equation of regulatory committees adopting positive supervision strategy as Eq. (14):

$\begin{array}{ll}\begin{array}{c}F(z)=\frac{dz}{dt}=z(Vz-\overline{Vz})\hfill \\ =z(1-z)((x+y)(P-L)-2xyP+E-H)\hfill \end{array}\hfill & (14)\end{array}$

3.3. Replicator dynamics analysis

Based on Eqs. (6), (10), and (14), we can get the tripartite dynamic replication equations of the B&R food cooperation:

$\begin{array}{ll}\left\{\begin{array}{c}F(x)=x(1-x)\left[\begin{array}{c}(1-y)\left[R1-(1+\theta )M1\right]+y(F1+B1-M1)\hfill \\ +zL-C1-G-y(M2S-zP)-R1\hfill \end{array}\right]\hfill \\ F(y)=y(1-y)\left[\begin{array}{c}x(B2+F2-M2)+(1-x)\left[R2-(1+\theta )M2\right]\hfill \\ +zL-C2-x(M1S-zP)-R2\hfill \end{array}\right]\hfill \\ F(z)=z(1-z)((x+y)(P-L)-2xyP+E-H)\hfill \end{array}\right\}\hfill & (15)\end{array}$

Let {F(x) = 0F(y) = 0F(z) = 0}, then 8 purely strategic solutions for the B&R food cooperation can be obtained as follows: A1(0, 0, 0), A2(0, 0, 1), A3(0, 1, 0), A4(0, 1, 1), A5(1, 0, 0), A6(1, 0, 1), A7(1, 1, 0), and A8(1, 1, 1). In addition, there are hybrid strategy solutions Q(x^*, y^*, z^*) which satisfy Eq. (16):

$\begin{array}{ll}\left\{\begin{array}{c}F(x^{*})=\left[\begin{array}{c}(1-y^{*})\left[R1-(1+\theta )M1\right]+y^{*}(F1+B1-M1)\hfill \\ +z^{*}L-C1-G-y^{*}(M2S-z^{*}P)-R1\hfill \end{array}\right]\hfill \\ F(y^{*})=\left[\begin{array}{c}{x}^{*}(B2+F2-M2)+(1-x^{*})\left[R2-(1+\theta )M2\right]\hfill \\ +z^{*}L-C2-x^{*}(M1S-z^{*}P)-R2\hfill \end{array}\right]\hfill \\ F(z^{*})=((x^{*}+y^{*})(P-L)-2x^{*}{y}^{*}P+E-H)\hfill \end{array}\right\}\hfill & (16)\end{array}$

Therefore, we can obtain:

$\begin{array}{l}{x}^{*}=\frac{2\left[2b{P}^2+f-(b-M1S)(P-L)P\right](H-E)-(P-L)\left[-(g+h)+\sqrt{{(g+h)}^2-8j\left[2b{P}^2+f-(b-M1S)(P-L)P\right]}\right]}{2\left[2b{P}^2+f-(b-M1S)(P-L)P\right](P-L)-2P\left[-(g+h)+\sqrt{{(g+h)}^2-8j\left[2b{P}^2+f-(b-M1S)(P-L)P\right]}\right]}\hfill \end{array}$

$\begin{array}{l}{y}^{*}=\frac{-(g+h)+\sqrt{{(g+h)}^2-8j\left[2b{P}^2+f-(b-M1S)(P-L)P\right]}}{2\left[2b{P}^2+f-(b-M1S)(P-L)P\right]}\hfill \end{array}$

$\begin{array}{l}{z}^{*}=\frac{d+(c+M2S-F1-B1+M1)\left[-(g+h)+\sqrt{{(g+h)}^2-8j\left[2b{P}^2+f-(b-M1S)(P-L)P\right]}\right]}{2\left[2b{P}^2+f-(b-M1S)(P-L)P\right]L+P\left[-(g+h)+\sqrt{{(g+h)}^2-8j\left[2b{P}^2+f-(b-M1S)(P-L)P\right]}\right]}\hfill \end{array}$

where a = B2 + F2 + M2

$\begin{array}{l}b=R2-\left(1+\theta \right)M2\hfill \\ c=R1-\left(1+\theta \right)M1\hfill \\ d=2\left[2b{P}^2+f-\left(b-M1S\right)\left(P-L\right)P\right]\left(c-C1-R1-G\right)\hfill \\ g=[bP-\left(C2+R2\right)-(a-b+c-M1S+M2S-F1-B1\hfill \\ +M1)L]\left(P-L\right)\hfill \\ j=\left(M1S-a\right)\left(H-E\right)L+\left(C2+R2-c-C1-R1-G\right)\hfill \\ \left(P-L\right)L\hfill \end{array}$

0 < x^* < 1, 0 < y^* < 1and 0 < z^* < 1.

Then, we rewrite the replication factor dynamics equations for the large cereal country, the small cereal country, and the regulatory committee as in Eq. (17):

$\begin{array}{ll}\left\{\begin{array}{c}F(x)=\frac{dx}{dt}=x\left[\begin{array}{c}(1-y)\left[R1-(1+\theta )M1\right]+y(F1+B1-M1)\hfill \\ +zL-C1-G-y(M2S-zP)-R1\hfill \end{array}\right]\hfill \\ F(y)=\frac{dy}{dt}=y\left[\begin{array}{c}x(B2+F2-M2)+(1-x)\left[R2-(1+\theta )M2\right]\hfill \\ +zL-C2-x(M1S-zP)-R2\hfill \end{array}\right]\hfill \\ F(z)=\frac{dz}{dt}=z((x+y)(P-L)-2xyP+E-H)\hfill \end{array}\right\}\hfill & (17)\end{array}$

3.4. Stochastic evolutionary game model

In the process of food cooperation, due to the complex external environment, the subjects will choose different strategies according to their profitability. In particular, there are stochastic perturbations in the replication dynamics equations, which lead to stochastic evolutionary game models. Consequently, in the process of food cooperation, there is an influencing factor of uncertainty in the external environment, and the strategic adjustments made by each player cannot be accurately reflected by a primitive evolutionary game. To overcome this drawback, the tripartite game model should consider random noise. Gaussian white noise is a non-linear normal distribution function that provides a better description of the random nature of the external environment (Jumarie, 2003; Xu and Yang, 2022); therefore, in this article, Gaussian white noise is introduced as a representation of stochastic disturbance in game systems, and the replicated dynamic equation is improved to obtain:

$\begin{array}{ll}\left\{\begin{array}{c}dx(t)=x(t)\left[\begin{array}{c}(1-y)\left[R1-(1+\theta )M1\right]+y(F1+B1-M1)\hfill \\ +zL-C1-G-y(M2S-zP)-R1\hfill \end{array}\right]\hfill \\ dt+\sigma x(t)dw(t)\hfill \\ dy(t)=y(t)\left[\begin{array}{c}x(B2+F2-M2)+(1-x)\left[R2-(1+\theta )M2\right]\hfill \\ +zL-C2-x(M1S-zP)-R2\hfill \end{array}\right]\hfill \\ dt+\sigma y(t)dw(t)\hfill \\ dz(t)=z(t)((x+y)(P-L)-2xyP+E-H)dt+\sigma z(t)dw(t)\hfill \end{array}\right\}\hfill & (18)\end{array}$

In this equation, σ represents the intensity of noise, where dω(t) denotes Gaussian white noise. ω(t) is one-dimensional Brownian motion, and the stochastic process {ω(t)} is an independent increments process, which satisfies ∀t, h > 0, $\Delta \omega (t)=\omega (t+h)-\omega (t)\stackrel{~}{}\mathrm{\text{N}}(0,\sqrt{h})$.ω(t)is the standard one-dimensional Brown motion, an irregular random rise and fall phenomenon, which can well describe the effect of random disturbance factors.

3.5. Analysis of the existence and stability of equilibrium solutions

It is known that Equation (18) is Itô-type stochastic differential formula, therefore, assuming that the initial moment is t = 0, x(0) = 0, y(0) = 0, and z(0) = 0, respectively. Then, we can obtain:

$\begin{array}{ll}\left\{\begin{array}{c}\left[\begin{array}{c}(1-y)\left[R1-(1+\theta )M1\right]+y(F1+B1-M1)\hfill \\ +zL-C1-G-y(M2S-zP)-R1\hfill \end{array}\right]\hfill \\ *0+\sigma x(t)dw(t)=0\hfill \\ \left[\begin{array}{c}x(B2+F2-M2)+(1-x)\left[R2-(1+\theta )M2\right]\hfill \\ +zL-C2-x(M1S-zP)-R2\hfill \end{array}\right]\hfill \\ *0+\sigma y(t)dw(t)=0\hfill \\ ((x+y)(P-L)-2xyP+E-H)*0+\sigma z(t)dw(t)=0\hfill \end{array}\right\}\hfill & (19)\end{array}$

Based on Equation (19), it can be seen that dw(t)|t = 0 = w′(t)dt|t = 0 = 0, and Eq. (18) exists null solutions, which means that the game system will always persist on the state without external interference, that is, the null solution is the equilibrium solution. This ideal state is typically hard to accomplish due to the high level of unpredictability in the actual world, and every member is always subject to varying degrees of random factors. Therefore, considering stochastic disturbances (Foster and Young, 1990), according to the stochastic differential equation stability discriminant theorem, the game system's stability is distinguished (Traulsen et al., 2006):

Given stochastic differential equation (Li et al., 2020):

$\begin{array}{ll}\{\begin{array}{c}dx(t)=f(t,x(t))dt+g(t,x(t))dw(t)\hfill \\ x(t_0)=x_0\hfill \end{array}\hfill & (20)\end{array}$

It is assumed that there is a function V(t, x) for which there exists positive constants σ1, σ2, such that (Liu et al., 2021b):

$\begin{array}{ll}\delta 1{\left|x\right|}^p\le V(t,x)\le \delta 2{\left|x\right|}^p,t>0\hfill & (21)\end{array}$

Next, two specific scenarios about system stability are analyzed:

Scenario 1: If ∀μ > 0, t ≥ 0 is founded, the null solution of Eq. (20) is globally exponentially stable in p-th mean. Then, $E\left|x{(t,x_0)}^p\right|<\frac{\delta 2}{\delta 1}{\left|x_0\right|}^p{e}^{-\mu t}$, t ≥ 0.

Scenario 2: If ∀μ > 0, LV(t, x)≥μV(t, x), t≥0 is founded, then the null solution of Eq. (20) is not exponentially stable in p-th mean, that is, $E\left|x{(t,x_0)}^p\right|\ge \frac{\delta 2}{\delta 1}{\left|x_0\right|}^p{e}^{-\mu t}$, t ≥ 0.

For Equations (18), let V(t, x) = x, V(t, y) = y, V(t, z) = z, x ∈ [0, 1], y ∈ [0, 1], z ∈ [0, 1], δ1 = 1, δ2 = 1, p = 1 and μ = 1, then, let LV(t, x) = f(t, x), LV(t, y) = f(t, y), LV(t, z) = f(t, z). If the null solutions p–th moment exponential of equations (21) is stable, it needs to satisfy:

$\begin{array}{ll}\left\{\begin{array}{c}x\left[\begin{array}{c}(1-y)\left[R1-(1+\theta )M1\right]+y(F1+B1-M1)\hfill \\ +zL-C1-G-y(M2S-zP)-R1\hfill \end{array}\right]\le -x\hfill \\ y\left[\begin{array}{c}x(B2+F2-M2)+(1-x)\left[R2-(1+\theta )M2\right]\hfill \\ +zL-C2-x(M1S-zP)-R2\hfill \end{array}\right]\le -y\hfill \\ z((x+y)(P-L)-2xyP+E-H)\le -z\hfill \end{array}\right\}\hfill & (22)\end{array}$

When the above condition (22) is satisfied, the p-th moment index of equation (18) is stable. This means that over time, the proportion of non-cooperative strategies will exponentially decay to zero. At this point, the only evolutionarily stable strategy is the cooperative strategy.

3.6. Taylor expansion of evolution equation

Since the non-linear Itô stochastic differential equation (18) is non-linear and it is not possible to obtain a numerical solution directly, the stochastic Taylor expansion and the Itô formula are used to solve the numerical approximation to find it. A stochastic differential equation (23) is as follows:

$\begin{array}{ll}dx(t)=f(t,x(t))dt+g(t,x(t))dw(t)\hfill & (23)\end{array}$

In this equation, t ∈ [t₀, T], x(t₀) = x0, x₀ ∈ R, w(t) is the standard winner process (Liu et al., 2021a). Suppose further that, where $h=\frac{T-t}{n}$, tn = t₀ + nh, we can obtain the stochastic Taylor expansion of the above formula is given in Eq. (24):

$\begin{array}{l}x(tn+1)=x(tn)+I_{0}f(x(tn))+I_{1}g(x(tn))+I_{11}{L}^{1}g(x(tn))\hfill \\ +I_{100}{L}^{0}f(x(tn))+R\hfill & (24)\end{array}$

where $L^0=f(x)\frac{\partial }{\partial x}+\frac{1}{2}{g}^2(x)\frac{{\partial }^2}{\partial x^2}$, $L^1=g(x)\frac{\partial }{\partial x}$, I₀ = h, I1 = Δwn, $I_{100}=\frac{1}{2}{h}^2$, $I_{11}=\frac{1}{2}\left[{(\Delta wn)}^2-h\right]$, and R is the remainder of the Taylor expansion.

Then, the above formula can be expressed as Eq. (25):

$\begin{array}{ll}\begin{array}{c}x(tn+1)=x(tn)+hf(x(tn))+\Delta wng(x(tn))\hfill \\ +\frac{1}{2}\left[{(\Delta wn)}^2-h\right]g(x(tn))g^{\prime }(x(tn))\hfill \\ +\frac{1}{2}{h}^2\left[f(x(tn))f^{\prime }(x(tn))+\frac{1}{2}{g}^2(x(tn))f^{″}(x(tn))\right]+R\hfill \end{array}\hfill & (25)\end{array}$

So the Milstein numerical method is used to solve this problem. Taylor expansion for large cereal countries, small cereal countries, and regulatory committees is as follows:

$\begin{array}{ll}\begin{array}{c}x(tn+1)=x(tn)\hfill \\ +h\left[\begin{array}{c}(1-y(tn))\left[R1-(1+\theta )M1\right]+y(tn)(F1+B1-M1)\hfill \\ +z(tn)L-C1-G-y(tn)(M2S-z(tn)P)-R1\hfill \end{array}\right]x(tn)\hfill \\ +\frac{1}{2}\left[{(\Delta wn)}^2-h\right]{\sigma }^{2}x(tn)\hfill \\ +\frac{1}{2}{h}^2{\left[\begin{array}{c}(1-y(tn))\left[R1-(1+\theta )M1\right]+y(tn)(F1+B1-M1)\hfill \\ +z(tn)L-C1-G-y(tn)(M2S-z(tn)P)-R1\hfill \end{array}\right]}^{2}x(tn)\hfill \\ +\Delta wn\sigma x(tn)+R1\hfill \end{array}\hfill & (26)\end{array}$

$\begin{array}{ll}\begin{array}{c}y(tn+1)=y(tn)\hfill \\ +h\left[\begin{array}{c}x(tn)(B2+F2-M2)+(1-x(tn))\left[R2-(1+\theta )M2\right]\hfill \\ +z(tn)L-C2-x(tn)(M1S-z(tn)P)-R2\hfill \end{array}\right]y(tn)\hfill \\ +\frac{1}{2}\left[{(\Delta wn)}^2-h\right]{\sigma }^{2}y(tn)\hfill \\ +\frac{1}{2}{h}^2{\left[\begin{array}{c}x(tn)(B2+F2-M2)+(1-x(tn))\left[R2-(1+\theta )M2\right]\hfill \\ +z(tn)L-C2-x(tn)(M1S-z(tn)P)-R2\hfill \end{array}\right]}^{2}y(tn)\hfill \\ +\Delta wn\sigma y(tn)+R2\hfill \end{array}\hfill & (27)\end{array}$

$\begin{array}{ll}\begin{array}{c}z(tn+1)=z(tn)+h((x(tn)+y(tn))(P-L)-2x(tn)y(tn)P\hfill \\ +E-H)z(tn)\hfill \\ +\frac{1}{2}\left[{(\Delta wn)}^2-h\right]{\sigma }^{2}z(tn)\hfill \\ +\frac{1}{2}{h}^2{((x(tn)+y(tn))(P-L)-2x(tn)y(tn)P+E-H)}^{2}z(tn)\hfill \\ +\Delta wn\sigma z(tn)+R3\hfill \end{array}\hfill & (28)\end{array}$

3.7. Results and analysis of simulation

Since the non-linear Itô differential equation is difficult to solve exactly, our model of the trajectory of the tripartite dynamic evolution is modeled numerically using numerical simulation. This article establishes a stochastic evolutionary game model of the B&R tripartite from the perspective of food security cooperation, analyzes the influence mechanisms of the degree of effort of large cereal countries, the income of small cereal countries, the incentive behavior of the regulatory committee, and Gaussian white noise on the evolutionary path of the tripartite, and further analyzes the evolutionary trajectory in terms of stability, rate of change, and convergence speed. In contrast, the incentive study for the regulatory committee allows large and small cereal countries to exhibit negative behavior in the initial moment, thus setting the initial willingness to x = 0.4 and y = 0.3, while the regulatory committee prefers a positive regulatory strategy at the beginning, which is z = 0.5. In accordance with this, and after consulting a number of experts in B&R agriculture, we borrowed the idea of parameter assignment from Liu et al. (2021b) and Sun and Gu (2022) in the context of the B&R strategy, while considering the interaction between parameters and assigning them to parameters that directly affect the structure and attributes of the model.

3.7.1. Influence of the efforts of large cereal countries on the evolution of the three parties

The degree of effort of large cereal countries is an important part of ensuring food cooperation along the B&R. Therefore, by learning from the ideas of Li et al. (2020) and others on the assignment of parameters, combining with the practice of international economic and trade exchange management, and considering the interplay of parameters, we set the degree of effort G of large cereal countries as 1, 1.5, and 2, respectively, and every subject's evolutionary path under the change in the degree of effort of the large cereal countries was studied and the evolutionary results are shown in Figure 2. From Figure 2A, we can conclude that when G = 1 ~ 1.5, the willingness of large cereal countries to adopt contractual joint cooperation strategies quickly converges to 1. When G = 2, the willingness of large cereal countries to adopt the contractual joint cooperation strategy converges to 1 slower than when G = 1 ~ 1.5 and finally reaches the equilibrium point, suggesting that too high a level of effort reduces the incentive of large cereal countries to cooperate to some extent. In terms of convergence speed and stability, when G = 1 ~ 1.5, a point of equilibrium is reached first, and when G = 1 ~ 2, the strategy tends to be stable. In the meantime, as shown in Figures 2B, C when G = 1 ~ 1.5, the willingness of small cereal countries to be non-cooperative and the willingness of regulatory committees to be non-regulatory converges to 1 and tends to be stable; when G = 2, the willingness of regulatory committees to adopt regulatory strategies converges to 1 rapidly and remains relatively stable, and the willingness of small cereal countries to adopt cooperative information-sharing strategies converges to 1 slowly and eventually reaches the equilibrium point. This is due to the fact that different countries have different concepts, approaches, and expectations of food cooperation, and it is, therefore, crucial to harmonize the interests and responsibilities of the Belt and Road food cooperating countries to ensure the long-term stability of the cooperation and to mitigate the food crisis. In addition, we also discuss the response of small cereal countries and regulatory commissions to the efforts of large cereal countries without external interference (σ = 0). When G = 1 ~ 1.5, the three parties reach the equilibrium point stably and quickly. It can be seen that the three parties are more likely to cooperate at a lower level of effort without external interference, which indicates that the probability of participants choosing cooperation is disturbed by Gaussian white noise; when G = 2, the trajectory is in the X-Z coordinates, where z = 1. Thus, the level of effort by large cereal countries can not only increase the incentive for active regulation by regulatory commissions but also weaken the speculative incentives of small cereal countries.

FIGURE 2

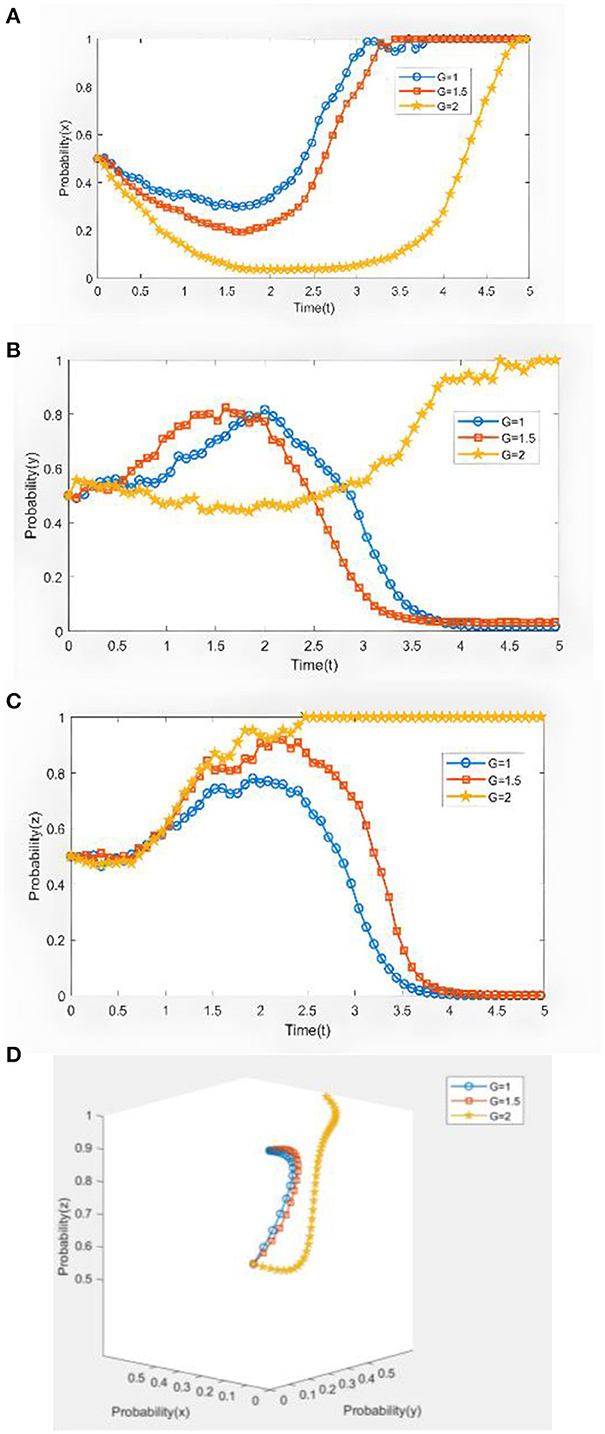
Figure 2. Evolutionary path of tripartite dynamics under different levels of effort in large cereal countries. S = 0.6 θ = 0.28 M1 = 2.6 M2 = 2.2 C1 = 2.2 C2 = 2 B1 = 2.2 B2 = 2 F1 = 9.8 F2 = 7.5E = 6.5H = 2.85. (A) The evolutionary impact of the level of effort of large cereal countries on the evolution of large cereal countries. (B) The evolutionary impact of the level of effort of large cereal countries on the evolution of small cereal countries. (C) The evolutionary impact of the level of effort of large cereal countries on the evolution of regulatory committees. (D) The evolutionary impact of the three parties without external interference.

3.7.2. Impact of small cereal country income on the evolution of the three parties

The income of small cereal countries in cooperation is the most important factor for small cereal countries to cooperate in food or not, therefore, combining with the studies on cooperation among relevant countries (Xu et al., 2021b), constructing stable and long-term cooperation relationship, and setting F2 of cooperation income of small cereal countries as 3.5, 5.5, and 7.5, respectively. Every subject's evolutionary path under the income change in cooperation in small cereal countries is studied, and the evolutionary results are shown in Figure 3. From Figure 3A, we can conclude that when F2 = 3.5 ~ 5.5, the willingness of large cereal countries to adopt a contractual joint cooperation strategy converges slowly and finally converges to 1. When F2 = 7.5, the willingness of large cereal countries to adopt contractual joint cooperation strategies drops to stabilize around 0.4. Meanwhile, as seen in Figure 3B, when F2 = 3.5, the willingness of small cereal countries to prefer information-sharing cooperation converges to approximately 0.7 and tends to stabilize; when F2 = 5.5 ~ 7.5, the willingness of small cereal countries to adopt information-sharing cooperation strategies converges to 1 slowly and eventually reaches the equilibrium point, and F2 = 7.5 converges to 1 faster than F2 = 5.5. This means that reasonable and higher cooperative income enables small cereal countries to reach a balance faster and more stable. As shown in Figure 3C, when F2 = 3.5 ~ 5.5, the regulatory committee's willingness to supervise quickly converges to 1 and tends to be stable; when F2 = 7.5, the willingness of the regulatory committee to adopt regulatory strategies fluctuates at higher levels before quickly converging to 0 and stabilizing. This suggests that appropriate income in small cereal countries can have a positive impact on food cooperation among the B&R countries, reflecting the importance of a reasonable income distribution among large and small cereal countries. As shown in Figure 3D, in the absence of external interference (σ = 0), when F2 = 3.5 ~ 5.5, the equilibrium point is achieved smoothly along the tripartite evolutionary trajectory, which indicates that the probability of participants choosing to cooperate only fluctuates under the interference of Gaussian white noise. When F2 = 7.5, the trajectory is in the X-Y coordinate, where z = 0.

FIGURE 3

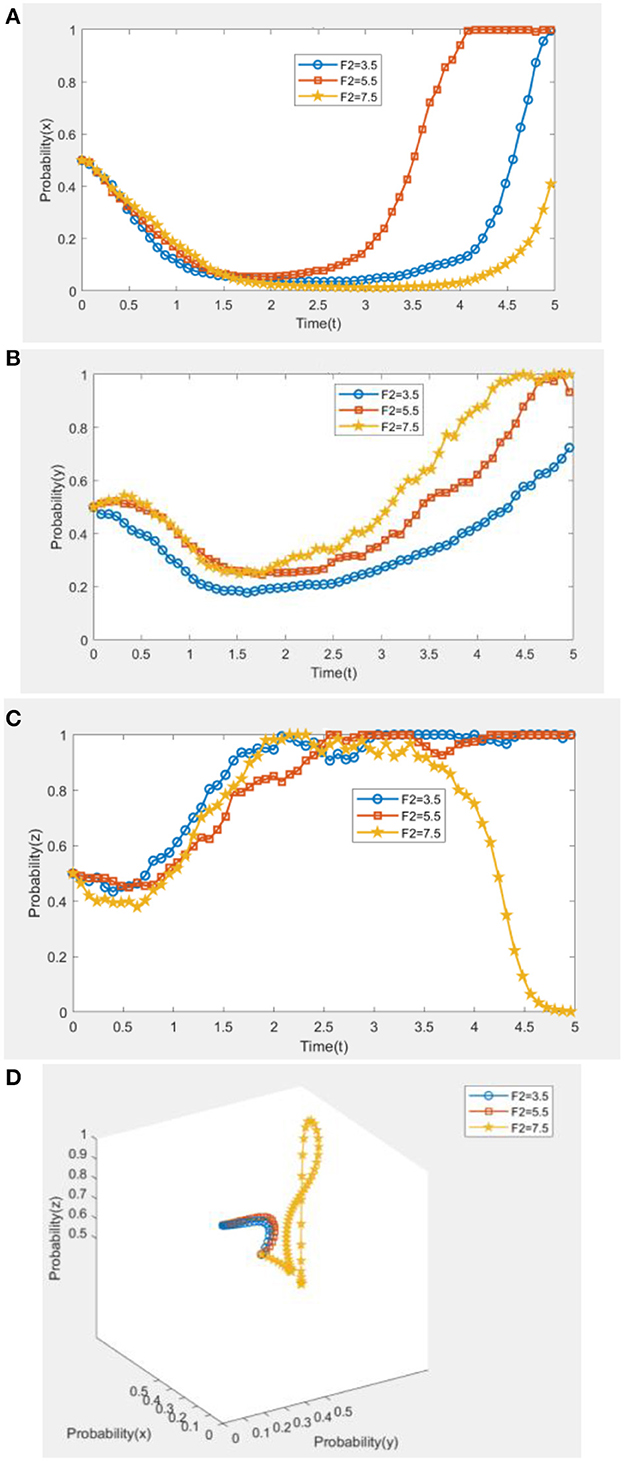
Figure 3. Evolutionary path of tripartite dynamics under different incomes in small cereal countries. S = 0.65 θ = 0.35 M1 = 2.6 M2 = 2.2 C1 = 2.2 C2 = 2 B1 = 3.2 B2 = 3 F1 = 9.8 G = 2 E = 6.5H = 2.85. (A) The influence of income of small cereal countries on the evolution of large cereal countries. (B) The influence of income of small cereal countries on the evolution of small cereal countries. (C) The impact of the income of small cereal countries on the evolution of regulatory commission. (D) The evolutionary impact of the three parties without external interference.

3.7.3. Impact of regulatory committee incentives on the evolution of the three parties

The incentive behavior of the regulatory committee under food cooperation can well reflect the multiple objectives of the regulatory committee to ensure food security policies, help food-deficient countries improve food security, and promote food cooperation. Therefore, referring to the country cooperation study and combining the practice of country cooperation, drawing on Wang et al. (2022) idea of parameter assignment, the incentive behavior of the regulatory committee L was set as 1, 2.5, and 5, respectively. Every subject's evolutionary path under the change of incentive behavior of the regulatory committee is studied, and Figure 4 illustrates the evolution results. From Figures 4A, B, we can conclude that when L = 1 ~ 2.5, the willingness of large cereal countries and small cereal countries to adopt non-cooperative strategies quickly converges to 1 and tends to be stable; when L = 5, the willingness of large cereal countries to adopt a contractual joint cooperation strategy and of small cereal countries to adopt an information-sharing cooperation strategy slowly rises to 1 and reaches the equilibrium point, suggesting that too low incentive behavior of the regulatory committee discourages cooperation by large and small cereal countries to some extent. In the meantime, it can be seen from Figure 4C that L = 1 converges faster than L = 2.5~5, and reaches the equilibrium point first, L = 2.5 shows unstable fluctuations around 1, and the regulatory committees show active regulatory behavior for L = 1~5, and the strategies all tend to stabilize. This is due to the determination and efforts of the regulatory committee to promote the development of the economies of the cooperating countries, and ultimately solve the food crisis. As shown in Figure 4D, in the absence of external interference (σ = 0), when L = 1~2.5, the cooperative triad steadily and quickly reaches the equilibrium point, and this can be seen that when there is no external interference, the three parties are more likely to cooperate at a lower incentive level. In addition, as the incentive behavior increases, the trajectory is on the X-Z coordinate, where x = 0.1, which indicates that the probability of participants choosing to cooperate is disturbed by Gaussian white noise.

FIGURE 4

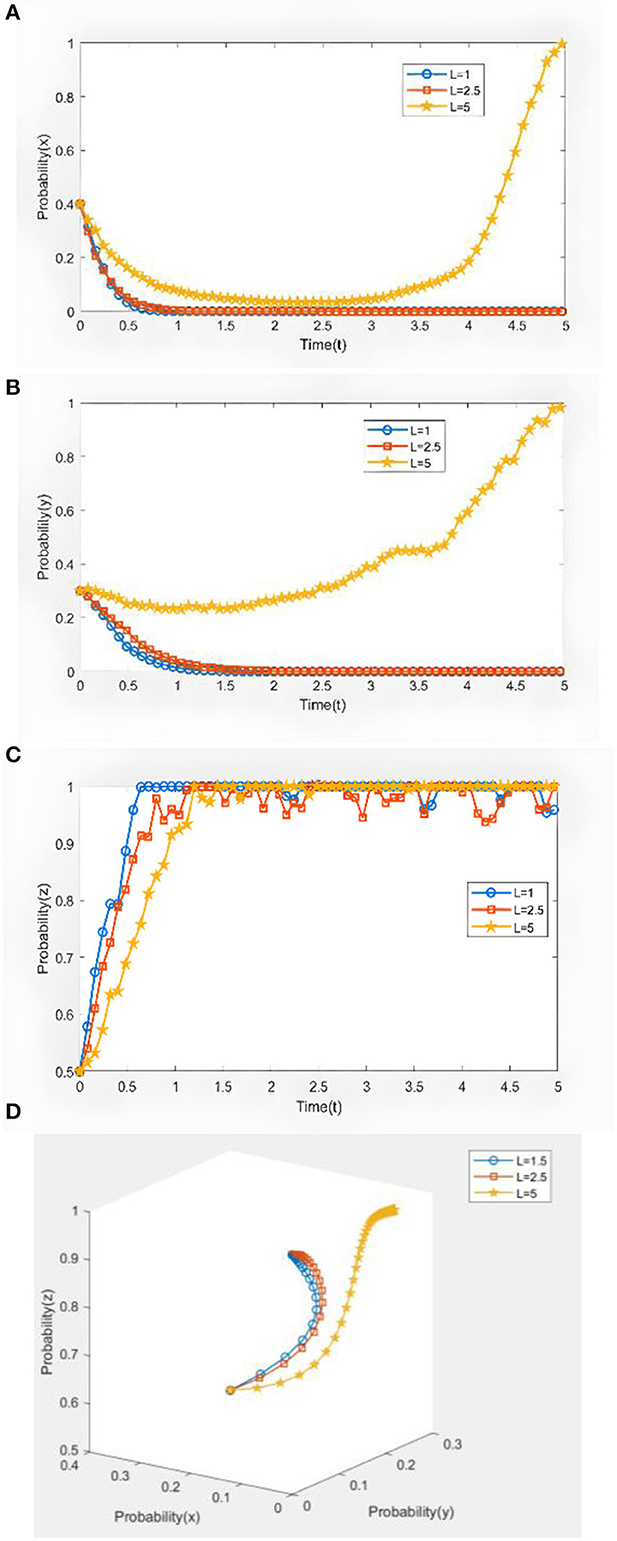
Figure 4. Evolutionary path of tripartite dynamics under different incomes of regulatory committees. When S = 0.65 θ = 0.35 M1 = 2.6 M2 = 2.2 C1 = 2.2 C2 = 2 B1 = 2.6 B2 = 2 F1 = 9.8 F2 = 7.5 G = 2 E = 6.5H = 2.85. (A) The impact of regulatory committee incentives on the evolution of large cereal countries. (B) The impact of regulatory committee incentives on the evolution of small cereal countries. (C) The impact of regulatory committee incentives on the evolution of regulatory committees. (D) The evolutionary impact of the three parties without external interference.

3.7.4. Effect of Gaussian White Noise intensity on the evolution of the three parties

The random interference coefficient can describe the uncertain environment in reality. This article refers to the suggestions for numerical settings in related articles. Therefore, the random interference intensity σ is set to 0, 0.1, and 0.3, respectively. The evolution trend under the change of random interference intensity is studied, and Figure 5 illustrates the evolution results. When there are no stochastic disturbances, that is, the deterministic evolutionary game model, the trajectories of the large cereal country, the small cereal country, and the regulatory committee evolve smoothly toward the set of contractual joint cooperation, information-sharing cooperation, and regulation strategies, with the small cereal country evolving at the fastest rate. With the increase of Gaussian white noise, the three-way evolutionary trajectory shows fluctuation locally, while the overall evolutionary trajectory remains unchanged and all are smooth curves. When σ = 0.3, we can see that the fluctuations in the strategic choices of the three subjects start to increase, with the largest fluctuations in the small cereal countries, which indicates that the strategic choices of the small cereal country are the most unstable and the subjects most likely to be speculative in food cooperation, smaller food countries have increasingly deviated from a balanced strategy, and larger food countries and regulatory committees have better stability; therefore, this anomaly reflects real-life irrationality behavior of participants. Due to the constant presence of random disturbance factors, choosing a strategy is not always optimal, and Gaussian white noise is introduced to some extent in stochastic evolutionary games, which compensates for the shortcomings of the deterministic evolutionary game.

FIGURE 5

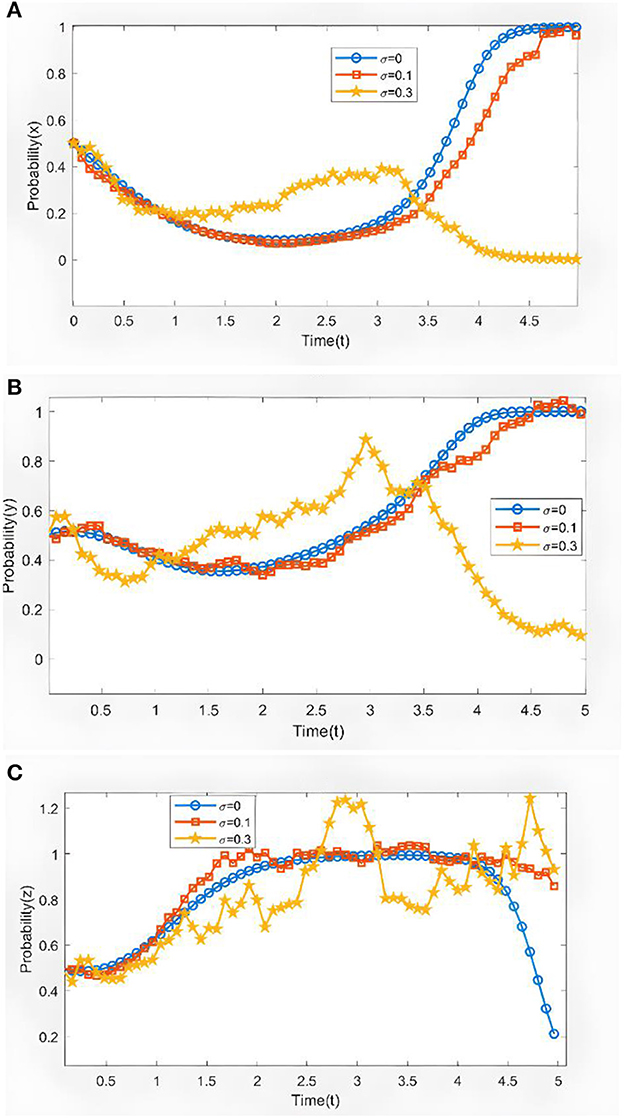
Figure 5. Three-way dynamic evolution paths with different Gaussian white noise. When S = 0.65 θ = 0.28 M1 = 2.6 M2 = 2.2 C1 = 2.2 C2 = 2 B1 = 2.6 B2 = 2 F1 = 9.8 F2 = 7.5 G = 2 E = 6.5 H = 2.85. (A) The influence of Gaussian white noise intensity on the evolution of large cereal countries. (B) The influence of Gaussian white noise intensity on the evolution of small cereal countries. (C) The influence of Gaussian white noise intensity on the evolution of the regulatory committee.

4. Model validation

There are few research literature studies on the Belt and Road food cooperation, and no comparable model of the evolutionary game of food cooperation has been found. We have no way to verify the validity of the model in this article from the perspective of model comparison. This article intends to compare the real situation of grain cooperation along the Belt and Road with the simulation results of the model in this article. If the two fit well, it can indicate the high rationality and validity of this article's model, which in turn can also predict the potential problems and evolutionary trends in Belt and Road food cooperation and make feasible suggestions for future cooperation development.

Abula et al. (2022) found that there is a significant downward trend in agricultural trade between China and Central Asia. The main reason for this is that the supply chains have different capabilities in terms of resource inputs, technology, and management. This article proposes using the level of effort of large cereal countries as a variable, driving the development of partners through the export of infrastructure and technological spillovers, and stimulating an increase in the interests of both sides. The variable we proposed can solve the problem of declining cooperation in Kahaer's study and provide a research direction to promote the B&R Food Silk Road cooperation.

Dithmer and Abdulai (2017) and Chen and Zhang (2022) point out that there is a clear power asymmetry in the actual development of countries due to differences in food supply and demand. Grain-exporting countries occupy a central position by controlling more resources through autonomous participation in trade transactions, while import-dependent countries are in a passive position due to the need to ensure the security of food supply. This article takes the gains of small cereal countries as a research factor to explore the direction of cooperation under the game of interests between the two sides in the cooperation process, and to address the phenomenon of increasing polarization of grain trade networks in Dudek et al. (2021) study.

The United Nations Sustainable Development Goals (SDGs) (Chen et al., 2019; Huan et al., 2021) and the Food and Agriculture Organization (FAO) (Saint Ville et al., 2019) emphasize the need to eradicate hunger and achieve food security. Most regions with abundant arable land resources have poor economic development and insufficient financial support. Other regions that lack arable land resources have relatively sufficient financial support, but arable land resources and financial resources cannot be combined into competitiveness. To address this problem, this article takes the incentive of the regulatory board as a research factor to explore the changes in the cooperative behavior of small and large cereal countries under the incentive of the third-party subject, to adjust and optimize the value of the partner's resources (Zhou and Tong, 2022b) and to develop a greater potential for development.

5. Discussion

Promoting food cooperation among B&R countries is an important way to solve the food crisis, so it is important and relevant to study the complex interactive behaviors exhibited by B&R participants in food cooperation. In this article, the main findings are as follows:

(1) The findings of this article suggest that a higher level of effort adopted by the large cereal countries can facilitate positive tripartite cooperation.

(2) There is “short-sightedness” in the large and small cereal countries and regulatory committees, and the evolutionary game is dynamic, so all three parties in the cooperation are easy to fall into a “locked-in state” with low income. The ways to avoid falling into this state of affairs include increasing the level of effort of the cooperating large cereal countries and regulatory commissions increasing penalties for speculative behavior.

(3) The regulatory committee improves incentive behavior, promotes active cooperation among large and small cereal countries, attracts more B&R countries to participate in food cooperation, improves the international image of the regulatory committee, and wins a good reputation.

(4) Gaussian white noise is introduced and the participants' evolutionary trajectories fluctuate smoothly around a curve. However, the equilibrium strategy can be biased by large Gaussian white noise.

In summary, this article studies a tripartite stochastic evolutionary game model of food cooperation among the B&R countries from the perspective of the food crisis, which enriches the theory of B&R cooperation and gives a basis for application for national governments to better prevent and solve food crisis. To describe the uncertainty in the environment, Gaussian white noise is introduced. This provides a richer background upon which stochastic theory is applied to the field of food cooperation.

To provide a theoretical foundation for food cooperation among the B&R countries, and also to effectively solve the food crisis in practice and build an efficient and stable food cooperation system, this article puts forward some suggestions as follows:

(1) From the simulation, the regulatory commission is quite determined to lock in regulatory strategies, and it is recommended that the regulatory commission increases the incentives and penalties for speculative behavior, which will help establish a system of food cooperation (Lin et al., 2020). For example, by actively seeking funds to establish a Belt and Road Food Cooperation Development Fund and developing and implementing a guarantee mechanism with stability and risk resistance, as a way to improve the compensation mechanism for food dedication in the cooperating countries, thus improving the food scale efficiency and rapid economic development of the Belt and Road food cooperation countries.

(2) Rationalizing the distribution of the benefits of cooperation between large cereal countries and small cereal countries and developing differentiated food trade strategies. The regulatory commission and large cereal countries should increase incentives for small cereal countries, for example, signing large food import orders with enterprises in small cereal countries, abolishing non-tariff measures such as import quotas and licenses for relevant agricultural products, drastically reducing import tariffs for other food varieties, and establishing closer exchange and cooperation relations, which can increase the enthusiasm of small food countries to cooperate and maintain the stability of the global food supply chain and industrial chain.

(3) Large cereal countries have strong advantages in technology, machinery, professional talents, deep processing of food products, and green ecological agriculture construction, relying on the support of modern agricultural production concepts, production technologies, and production machinery in large cereal countries (Zhao et al., 2021), mentoring and training for small cereal countries can increase the type, scale, and output value of agricultural machinery in small cereal countries and improve the coverage and benefits of labor export in large cereal countries (Lei et al., 2022). This will help to increase the willingness of large and small cereal countries to opt for cooperation and lay a solid foundation for the establishment of a mechanism for inter-country food cooperation, which will develop in a healthy, sustainable, and scaled-up direction.

This study also has some limitations. On the one hand, there is a gap between the model and the actual Great Power Game since a process as intricate as the Great Power Game involves both political and economic factors. On the other hand, different subjects fall under the scope of B&R food cooperation, but this article focuses only on the more significant subject level of countries and cannot fully recreate the interactions that take place in reality. Thus, in subsequent studies, more subjects may be considered and incorporated into the model to construct a multi-level model for studying the efficiency of food cooperation among the B&R countries and to provide a deeper understanding of risks.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MQ: conceptualization, methodology, writing—reviewing and editing. XL: formal analysis, methodology, and writing—original draft. SQ: methodology, validation, writing—reviewing and editing. GM: investigation and supervision. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by the Qinhuangdao Social Science Development Research Project, grant number 2022LX024.

Acknowledgments

Thanks are given to my tutor for his guidance on this article, which greatly improved the quality of the article. Thank you for providing this academic platform for me to submit my manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abula, K., Abula, B., Wang, X., and Wang, D. (2022). Performance evaluations and influencing factors of the agricultural product trade supply Chain between China and central Asian countries. Sustainability 14, 15622. doi: 10.3390/su142315622

CrossRef Full Text | Google Scholar

Antonio, C., Ovando, G. G., and Díaz, G. J. (2021). ENSO influence on corn and soybean yields as a base of an early warning system for agriculture in Córdoba, Argentina. Eur. J. Agron. 129, 126340. doi: 10.1016/j.eja.2021.126340

CrossRef Full Text | Google Scholar

Avalos, F. M. (2009). The Two Sided Coin: An Examination of On-line and Off-line Communication in Social Justice Movements. The Claremont Graduate University.

Google Scholar

Ben Hassen, T., and El Bilali, H. (2022). Impacts of the Russia-Ukraine war on global food security: towards more sustainable and resilient food systems? Foods, 11, 2301. doi: 10.3390/foods11152301

PubMed Abstract | CrossRef Full Text | Google Scholar

Béné, C. (2022). Why the Great food transformation may not happen – a deep-dive into our food systems'political economy, controversies and politics of evidence. World Dev., 154, 105881. doi: 10.1016/j.worlddev.2022.105881

CrossRef Full Text | Google Scholar

Brankov, T., and Matkovski, B. (2022). Is a food shortage coming to the western balkans? Foods, 11, 3672. doi: 10.3390/foods11223672

PubMed Abstract | CrossRef Full Text | Google Scholar

Brankov, T., Matkovski, B., Jeremić, M., and Đurić, I. (2021). Food self-sufficiency of the SEE countries; is the region prepared for a future crisis? Sustainability 13, 8747. doi: 10.3390/su13168747

CrossRef Full Text | Google Scholar

Chen, S., Liu, Y., and Su, L. (2019). Sustainable agriculture in the “Belt and Road” region in conjunction with the Sustainable Development Goals. J. Res. Ecol. 10, 649–656. doi: 10.5814/j.issn.1674-764x.2019.06.010

CrossRef Full Text | Google Scholar

Chen, W., and Zhang, H. (2022). Characterizing the structural evolution of cereal trade networks in the belt and road regions: a network analysis approach. Foods 11, 1468. doi: 10.3390/foods11101468

PubMed Abstract | CrossRef Full Text | Google Scholar

Clapp, J. (2023). Concentration and crises: exploring the deep roots of vulnerability in the global industrial food system. The J. Peas. Stu. 50, 1–25. doi: 10.1080/03066150.2022.2129013

CrossRef Full Text | Google Scholar

Cobb, L. (1978). Stochstic catastrophe models and multimodal. Behav. Sci. 23, 360–374. doi: 10.1002/bs.3830230407

PubMed Abstract | CrossRef Full Text | Google Scholar

Cressman, R., and Tao, Y. (2014). The replicator equation and other game dynamics. Proc. Natl. Acad. Sci. U.S.A. 111(Suppl_3), 10810–10817. doi: 10.1073/pnas.1400823111

PubMed Abstract | CrossRef Full Text | Google Scholar

Devereux, S., Béné, C., and Hoddinott, J. (2020). Conceptualising COVID-19's impacts on household food security. Food Secur. 12, 769–772. doi: 10.1007/s12571-020-01085-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Dithmer, J., and Abdulai, A. (2017). Does trade openness contribute to food security? A dynamic panel analysis. Food Policy 69, 218–230. doi: 10.1016/j.foodpol.2017.04.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Dudek, H., Myszkowska-Ryciak, J., and Wojewódzka-Wiewiórska, A. (2021). Profiles of food insecurity: similarities and differences across selected CEE countries. Energies 14, 5070. doi: 10.3390/en14165070

CrossRef Full Text | Google Scholar

FAO (2022). The Importance of Ukraine and the Russian Federation for Global Agricultural Markets and the Risks Associated with the War in Ukraine. Available online at: https://www.fao.org/3/cb9013en/cb9013en.pdf (accessed June 5, 2023).

Google Scholar

FAO (2023). In Focus, FAO Response to Global Food Security Challenges. Available online at: https://www.fao.org/in-focus/en/ (accessed 5 June 2023).

Google Scholar

FAOSTAT (2021). Available online at: https://www.fao.org/faostat/en/ (accessed June 5, 2023).

Google Scholar

Foster, D., and Young, P. (1990). Stochastic evolutionary game dynamics*. Theor. Pop. Biol. 38, 219–232. doi: 10.1016/0040-5809(90)90011-J

CrossRef Full Text | Google Scholar

Gunasekera, D., Cai, Y., and Newth, D. (2015). Effects of foreign direct investment in african agriculture. Agric. Econ. Rev. 7, 167–184. doi: 10.1108/CAER-08-2014-0080

CrossRef Full Text | Google Scholar

Huan, Y., Liang, T., Li, H., and Zhang, C. (2021). A systematic method for assessing progress of achieving sustainable development goals: a case study of 15 countries. Sci. Total Environ. 752, 141875. doi: 10.1016/j.scitotenv.2020.141875

PubMed Abstract | CrossRef Full Text | Google Scholar

Jumarie, G. (2003). Both Gaussian and White Noises. Appl. Mathem. Lett. 16, 1171–1177. doi: 10.1016/S0893-9659(03)90113-3

CrossRef Full Text | Google Scholar

Lei, C., Qi, Q., Fu, Y., and Jiang, L. Q. (2022). Analysis on mechanism of China's grain production development and evolution from 1985 to 2019. IEEE Access 10, 43221–43234. doi: 10.1109/ACCESS.2022.3165189

CrossRef Full Text | Google Scholar

Li, G., Zhang, Q., Bai, Z., and Sabeeh, P. (2020). Research on logistics service supply chain information sharing mechanism in the belt and road initiative. IEEE Access 8, 189684–189701. doi: 10.1109/ACCESS.2020.3031929

CrossRef Full Text | Google Scholar

Lin, F., Longfang, L., and Haibo, K. (2020). Game study on the evolution of cooperation along the 21st century maritime silk road. Sci. Res. Manage. 41, 113–123. doi: 10.19571/j.cnki.1000-2995.2020.11.011

CrossRef Full Text | Google Scholar

Liu, X., Lin, K., and Wang, L. (2021b). Stochastic evolutionary game analysis of e-waste recycling in environmental regulation from the perspective of dual governance system. J. Clean. Prod. 319, 128685. doi: 10.1016/j.jclepro.2021.128685

CrossRef Full Text | Google Scholar

Liu, X., Lin, K., and Wang, L. H. (2021a). Stochastic evolutionary game analysis between special committees and ceo: Incentive and supervision. Dyn. Games Appl. 11, 538–555. doi: 10.1007/s13235-020-00372-x

CrossRef Full Text | Google Scholar

Ministry of Agriculture (2017). National Development and Reform Commission, Ministry of Commerce and Ministry of Foreign Affairs, in: Belt and Road Portal, China's Free Trade Agreements. Available online at: http://www.china.org.cn/business/node_7233287.htm#a9 (accessed June 5, 2023).

Google Scholar

O'Hara, S., and Toussaint, E. C. (2021). Food access in crisis: food security and COVID-19. Ecol. Econ. 180, 106859. doi: 10.1016/j.ecolecon.2020.106859

CrossRef Full Text | Google Scholar

Qi, G. (2023). Chinese Cultural Enterprises “Going to Sea” Intellectual Property Risk Concern and Strategy Formulation Under the Background of “One Belt and One Road” Initiative. Chinese Publishing House, 49–54.

Google Scholar

Qiquan, X. (2022). China's Rrue cereal import scale and self-sufficiency rate. J. South China Agric. Univ. 21, 85–101. doi: 10.7671/j.issn.1672-0202.2022.03.008

CrossRef Full Text | Google Scholar

Saint Ville, A., Po, J. Y. T., Sen, A., Bui, A., and Melgar-Quiñonez, H. (2019). Food security and the food insecurity experience scale (FIES): ensuring progress by 2030. Food Secur. 11, 483–491. doi: 10.1007/s12571-019-00936-9

CrossRef Full Text | Google Scholar

Schmeier, S., and Shubber, Z. (2018). Anchoring water diplomacy – the legal nature of international river basin organizations. J. Hydrol. 567, 114–120. doi: 10.1016/j.jhydrol.2018.09.054

CrossRef Full Text | Google Scholar

Smith, J. M. (1974). The theory of games and the evolution of animal conllkts. J. Theor. Biol. 47, 209–221. doi: 10.1016/0022-5193(74)90110-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, J. M., and Price, G. R. (1973). The logic of animal conflict. Nature 246, 1–5. doi: 10.1038/246015a0

CrossRef Full Text | Google Scholar

Sun, Y., and Gu, Z. (2022). Implementation of construction waste recycling under construction sustainability incentives: a multi-agent stochastic evolutionary game approach. Sustainability 14, 3702. doi: 10.3390/su14063702

CrossRef Full Text | Google Scholar

Tian, J., and Liu, Y. (2022). A study on agricultural investment along the belt and road. Front. Sust. Food Syst. 6, 1036958. doi: 10.3389/fsufs.2022.1036958

CrossRef Full Text | Google Scholar

Tortajada, C., and Zhang, H. (2021). When food meets BRI: China's emerging food silk road. Global Food Secur. 29, 100518. doi: 10.1016/j.gfs.2021.100518

CrossRef Full Text | Google Scholar

Traulsen, A., Pacheco, J. M., and Imhof, L. A. (2006). Stochasticity and Evolutionary Stability. Phys. Rev. Stat. soft Matter Phys. 74, 10. doi: 10.1103/PhysRevE.74.021905

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L. (2019). Analysis of China-ASEAN agricultural trade pattern under “the belt and road”. Adv. Soc. Sci. Educ. Hum. Res. 314, 1–5. doi: 10.2991/icssed-19.2019.13

CrossRef Full Text | Google Scholar

Wang, W., Wu, F., and Yu, H. (2022). Optimal design of the ecological compensation mechanism in transboundary river basins under the belt and road initiative. Sust. Prod. Consump. 32, 173–183. doi: 10.1016/j.spc.2022.04.018

CrossRef Full Text | Google Scholar

Xu, C. (2010). The fundamental institutions of China 's reforms and development1. J. Econ. Lit. 49, 1076–1151. doi: 10.1257/jel.49.4.1076

CrossRef Full Text | Google Scholar

Xu, X., Hou, Y., Zhao, C., Shi, L., and Gong, Y. (2021a). Research on cooperation mechanism of marine plastic waste management based on complex network evolutionary game. Marine Policy 134, 104774. doi: 10.1016/j.marpol.2021.104774

CrossRef Full Text | Google Scholar

Xu, X., and Yang, Y. (2022). Analysis of the dilemma of promoting circular logistics packaging in China: a stochastic evolutionary game-based approach. Int. J. Environ. Res. Public Health 19, 7363. doi: 10.3390/ijerph19127363

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Z., Elomri, A., El Omri, A., Kerbache, L., and Liu, H. (2021b). The compounded effects of COVID-19 pandemic and desert locust outbreak on food security and food supply chain. Sustainability 13, 1063. doi: 10.3390/su13031063

CrossRef Full Text | Google Scholar

Ya, Z., and Pei, K. (2022). Factors influencing agricultural products trade between China and Africa. Sustainability 14, 5589. doi: 10.3390/su14095589

CrossRef Full Text | Google Scholar

Yao, H., Alhussam, M. I., Abu Risha, O., and Memon, B. A. (2020). Analyzing the relationship between agricultural FDI and food security: evidence from belt and road countries. Sustainability 12, 2906. doi: 10.3390/su12072906

CrossRef Full Text | Google Scholar

Zhang, C., Lin, K., and Wang, L. (2020). Incentive and supervisory contract between special committees and CEO based on the evolutionary game model. Mathemat. Probl. Eng. 2020, 1–17. doi: 10.1155/2020/4089634

CrossRef Full Text | Google Scholar

Zhao, L. D., Guo, X., Xue, J., Wang, C., and Sun, W. (2021). Cooperation risk of oil and gas resources between china and the countries along the belt and road. Energy, 227, 120445. doi: 10.1016/j.energy.2021.120445

CrossRef Full Text | Google Scholar

Zhao, Y., Shuai, J., Shi, Y., Lu, Y., and Zhang, Z. (2022). Exploring the co-opetition mechanism of renewable energy trade between China and the “belt and road” countries: a dynamic game approach. Renew. Energ. 191, 998–1008. doi: 10.1016/j.renene.2022.04.022

CrossRef Full Text | Google Scholar

Zhao, Z. (2019). The political economy of the world food crisis: centred on structural, institutional and triggers. Ewha J. Soc. Sci. doi: 10.16935/ejss.35.2019.2.003

CrossRef Full Text | Google Scholar

Zheng, H., and Zhuang, P. (2021). An analysis of the influencing factors in the establishment of the overseas agricultural cooperation zones under the Belt and Road initiative based on Logit model. J. Math. 2021, 9625242. doi: 10.1155/2021/9625242

CrossRef Full Text | Google Scholar

Zhou, L., and Tong, G. (2022a). Structural evolution and sustainability of agricultural trade between China and countries along the “Belt and Road”. Sustainability 14, 9512. doi: 10.3390/su14159512

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, L., and Tong, G. (2022b). Research on the competitiveness and influencing factors of agricultural products trade between China and the countries along the “Belt and Road”. Alexandria Eng. J. 61, 8919–8931. doi: 10.1016/j.aej.2022.02.030

CrossRef Full Text | Google Scholar