Explore article hub
- Emeritus, Center for Functional Magnetic Resonance Imaging, University of California, San Diego, San Diego, CA, United States
A Viewpoint on the Frontiers in Science Lead Article
Breakdown and repair of metabolism in the aging brain
Key points
- Brain function depends on the interplay of neurons, glia, and vascular elements working in a coordinated way as the neurovascular unit; a detailed modeling framework based on current knowledge provides a powerful tool for investigating the working brain and understanding brain aging.
- Building on this framework will be an ongoing effort as new experimental results on the basic mechanisms emerge, modifying both the connections and rates of different processes.
- A thermodynamic perspective offers an important complement to traditional modeling, ensuring a thermodynamically consistent model and potentially explaining the physiological functions involved even when the underlying mechanisms are not known.
Introduction
In their lead article, Shichkova and colleagues report a remarkably detailed model of the metabolic dynamics underlying energy metabolism in the brain (1). By incorporating many metabolic pathways based on a broad range of earlier work, they have designed a useful tool for probing the dynamics of brain energetics. By comparing a young and an aged brain metabolic state, they identified key differences and tested how modifications of specific metabolic components in the aged state could restore the young state. For example, in one case it was sufficient to simply increase the activity of the sodium/potassium ATPase, the transporter of three Na+ ions out of the cell and two K+ ions into the cell coupled with the conversion of one molecule of adenosine triphosphate (ATP) to one molecule of adenosine diphosphate (ADP). This so-called “sodium pump” is thought to be a key player in brain energetics, consuming most of the ATP required for neural function, especially at excitatory synapses (2, 3).
The goal of modeling brain energy metabolism is to incorporate all the features of the neurons, glia, and vascular elements that function as a neurovascular unit. This would provide a framework for integrating a wide range of studies from genetics to neurophysiology to non-invasive functional neuroimaging to novel therapeutics. It is a sweeping goal, and a challenging one because we are still trying to understand key elements of physiology. For example, many metabolic and neural factors affect cerebral blood flow (CBF) (4), but it is not clear how all these potential mechanisms combine to create a smoothly functioning CBF response to neural activity. Expanding the model to include this ongoing work is an important direction for the future. Nevertheless, by including many aspects of brain energetics, the model by Shichkova et al., which is openly available (1), is an important framework on which to build.
The central question in modeling brain energetics is: how do we know the rates of different processes? Shichkova and colleagues used RNA expression data to estimate enzyme concentrations and extrapolate to the associated enzyme kinetics. They acknowledged the caveat that messenger RNA (mRNA) levels do not fully reflect protein levels and activities. In addition, however, there are thermodynamic effects on reaction rates when the processes are not far from equilibrium—as the change in entropy decreases, the process slows down, independent of the details of the enzyme kinetics. These are essentially physiological effects that cannot be predicted from RNA expression alone but instead depend on the dynamically changing concentrations of key ions and metabolites.
This viewpoint article considers the modeling of brain energetics from a thermodynamic perspective, clarifying the basic ideas and describing an important, and somewhat counterintuitive, physiological effect.
Thermodynamic limitations of dynamic modeling in the context of the fluctuation theorem
Thermodynamic reasoning enables us to identify aspects of the dynamics that are independent of the specific mechanisms involved. For example, to model how a cup of hot coffee cools, we could include the thermal conductivity of the coffee and the cup, possible convective motions within the coffee, and even convective air motions due to blowing gently on the surface. However, independent of the exact mechanisms, the thermodynamics alone predicts the endpoint of the cooling process: the temperatures of the coffee and the room will equalize, and the detailed mechanistic modeling must be consistent with this endpoint. Creating a model that conforms to thermodynamic constraints can be challenging if the rates of the different mechanisms are taken from empirical data that are far from equilibrium, and another step may be needed to achieve thermodynamic consistency (5).
Thermodynamic effects on the rate of a process depend on the net entropy change (ΔS) involved, including all the interacting components. An intuitive way to formulate the role of ΔS in dynamics is in terms of the fluctuation theorem, a perspective borrowed from physics (6). Essentially, the fluctuation theorem captures the statistical nature of the second law of thermodynamics by dealing with probabilities for the forward direction of change (P+, the direction for positive ΔS) and the reverse direction of change (P−, negative ΔS) within a given time interval τ. The fluctuation theorem relates these probabilities:
where k is the Boltzmann constant.
The fluctuation theorem provides a way to move beyond equilibrium and treat the nonequilibrium dynamics of biological systems (7). Defining R0 = P+/τ as the forward rate of the process, the net rate R of a process is:
The net rate involves two terms: a kinetic rate constant R0, which depends on the concentrations of the reactants, enzyme activity, membrane permeability, and other parameters usually included in modeling dynamics; and a thermodynamic term, which depends on the net entropy change. When ΔS = 0, the system is in equilibrium, and the net rate of the process is zero. When ΔS is large, the thermodynamic term no longer has a significant effect, and the process is irreversible in a thermodynamic sense with a rate of R0.
In practice, we typically deal with a physiological system interacting with a thermal bath at temperature T. The net entropy change ΔS is expressed as the change in the Gibbs function ΔG, with ΔG = −TΔS (positive ΔS corresponds to negative ΔG). In the usual units, expressed on a per mole basis, the exponent ΔS/k in Equation 2 becomes −ΔG/RT, where RT is ~2.6 kJ/mol at human body temperature. If ΔG = −12 kJ/mol, the thermodynamic effect reduces the rate by only ~1%, and the process is essentially irreversible. The ΔG for a process depends on the ratio Φ of reactant to product concentrations (8):
where Φ0 is the value of Φ at equilibrium. For the sodium gradient, Φ is the ratio of extracellular to intracellular concentrations, and Φ0 depends on the membrane potential.
The brain’s batteries
Figure 1 is a sketch of the brain’s energy metabolism, focusing on the key components that involve an entropy change and a few key mechanisms. For the entropy components, the dependence of Φ on key reactant and product concentrations is indicated for the forward direction of change when entropy increases. Ion fluxes involved in neural activity include calcium ion entry into both the pre-synaptic and post-synaptic neurons and ion currents due to the opening of Na+ and K+ channels (Na+ influx, K+ efflux). The result is that neural activity increases the intracellular Na+ and Ca2+ concentrations and the extracellular K+ concentration. The energetics pathway indicated by the solid black arrows reverses these changes.
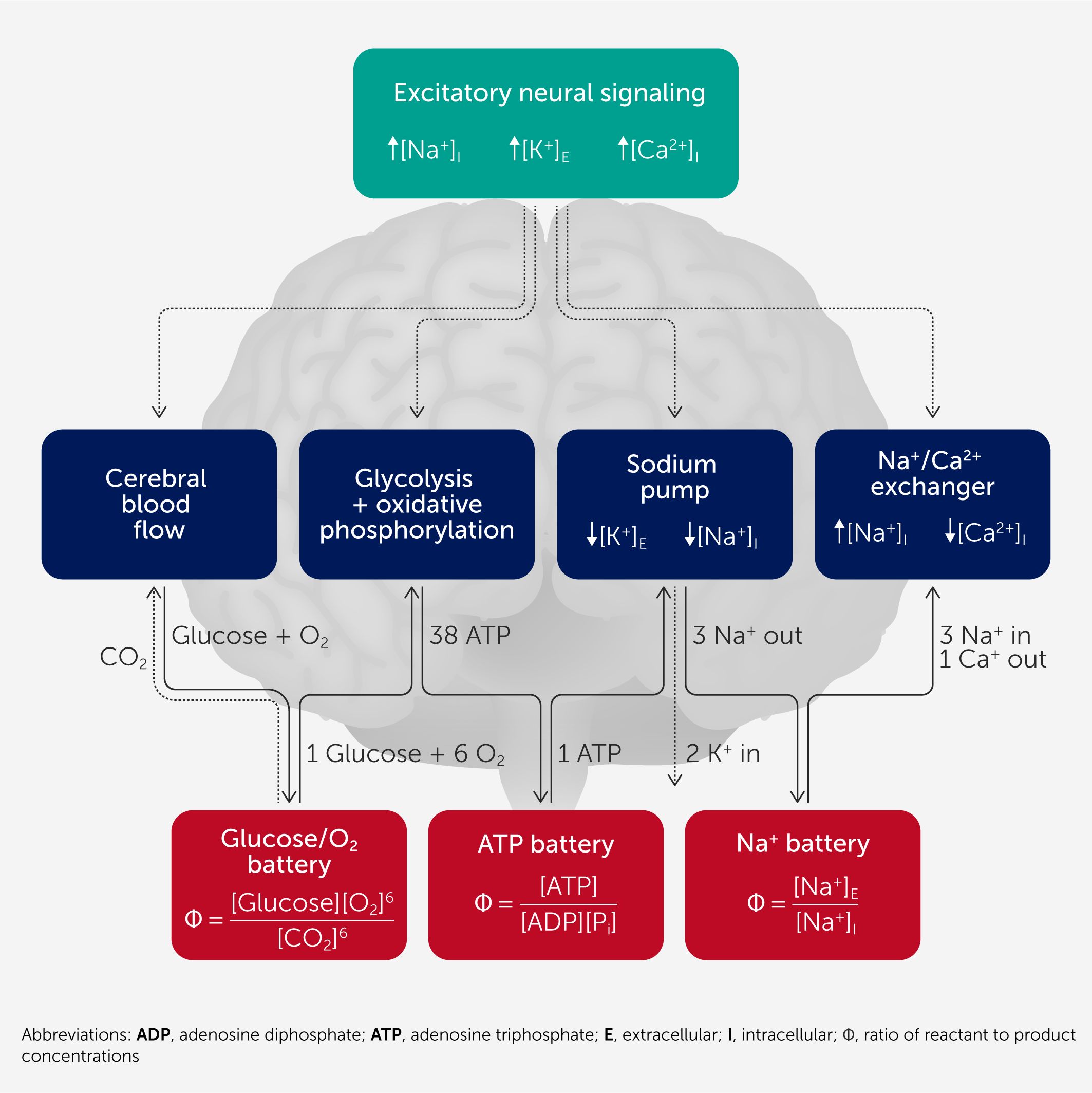
Figure 1. The brain’s batteries. From a thermodynamic perspective, brain energetics can be viewed as a linked sequence of batteries, indicated by the red boxes. The blue boxes indicate mechanisms that connect these batteries to specific processes (such as the sodium pump). The voltage equivalent of the batteries is the net change in the Gibbs function (ΔG) associated with the process, which depends on Φ, the ratio of reactants to products. The rate of each process is potentially limited by Equation 2 when the net ΔG becomes small (see text). The processes are linked through ΔG: e.g., the ΔGNa affects the sodium pump with a positive contribution to net ΔG but affects the Na+-Ca2+ exchanger with a negative ΔG, which acts as a driving battery. The effect of ongoing neural activity in terms of ion movement is indicated in the upper part (green box) and the energetic cost of brain activity is dominated by restoring the ion gradients.
The sodium gradient between the inside and outside of the cell is a focal point of brain energetics. It serves as an amplifier for neural signaling, providing a strong inward sodium current when sodium channels open. The Na+ gradient also acts as a battery to power other thermodynamically uphill processes involving neurotransmitter recycling and ion transport across the cell membrane. For example, Figure 1 includes the sodium/calcium exchanger that couples the transport of three Na+ into the cell, a process with a negative ΔG, to the transport of one Ca2+ out of the cell, with a positive ΔG. The Na+ gradient, in turn, is restored with the sodium pump by coupling the uphill movement of Na+ out of the cell (now positive ΔG) to a stronger battery—the ATP system. The ATP battery is restored by coupling to an even stronger battery, the metabolism of glucose with the production of ATP. We can think of this as a chain of batteries, each charged by the previous battery and in turn charging the next battery, with voltages analogous to the associated ΔG.
Balanced metabolic rates despite failing batteries
In neural activity, the rates of each process indicated by a solid arrow in Figure 1 must be balanced to achieve a steady state, with equal rates of Na+ efflux and influx, and ATP restoration and consumption. If this rate balance is maintained, it is tempting to say that the system is working well. However, this is complicated by another effect related to the thermodynamic perspective taken (7), which depends on downstream effects related to Equation 2. Essentially, voltage degradation in one of the batteries in Figure 1 can cascade—degrading the voltage in the battery being recharged, even though the net rates remain balanced.
For example, the net ΔG for the sodium pump depends on the negative ΔGATP from the ATP-to-ADP conversion and the positive ΔGNa from pumping sodium against its gradient. If the negative ΔGATP degrades (e.g., by reduction of the ATP/ADP ratio), the net ΔG will fall, and if it falls low enough, the sodium pump will slow down according to Equation 2. The sodium gradient will fall, but this will also lower the positive ΔGNa required to pump sodium against its gradient. If ΔGNa falls sufficiently to restore the original net ΔG, despite the reduction of ΔGATP, the rate of the sodium pump can be restored. The somewhat counterintuitive result is that the overall rate of the sodium pump is maintained but at the cost of degrading the ΔGNa available from the sodium gradient. This has a cascading effect on downstream processes that depend on the negative ΔGNa available when a sodium ion moves down its gradient, i.e., when the sodium gradient is used as a battery. For example, for the Na+/Ca2+ exchanger, the net ΔG has been estimated to be about −7 kJ/mol in cardiac myocytes (9), a range in which thermodynamic effects are significant.
Another physiological effect that becomes clearer from a thermodynamic perspective is the observation that increased neural activity produces an increase in CBF that is two to three times greater than the increase in cerebral oxygen metabolism (CMRO2)—the origin of the blood oxygenation level-dependent (BOLD) effect in functional magnetic resonance imaging (fMRI) studies. Because the ΔG associated with oxidative metabolism depends on the O2 concentration in the mitochondria, it is not enough to simply think about the delivery of O2 to the capillary bed: O2 must be delivered while maintaining a sufficient O2 concentration in the tissue to avoid degrading the available ΔG (7, 10). Modeling shows that a large increase in CBF is needed to prevent the partial pressure of O2 in tissue from falling, in good quantitative agreement with studies of brain activation and hypoxia (7). In this way, a thermodynamic perspective explains the physiological function served by a large change in CBF, although the mechanisms that produce this change in CBF are not yet fully understood.
A thermodynamic perspective changes the way we think about energy metabolism. Preserving the metabolic rate is necessary but not sufficient—a healthy brain must also keep its batteries charged. In practice, there is a buffer in the sense that ΔG could be reduced without impairing the next stage. An important research question is to determine how large this buffer is for each of the systems in Figure 1.
In conclusion, the detailed modeling of brain energetics by Shichkova and colleagues (1) is an important advance. As the field progresses, modifying and building upon this framework, a thermodynamic perspective may provide a useful complementary angle for modeling and understanding physiology.
Statements
Author contributions
RB: Conceptualization, Formal Analysis, Writing – original draft, Writing – review & editing, Visualization.
Funding
The author(s) declare that no financial support was received for the research presented in this article.
Conflict of interest
The author declares that the research was conducted in the absence of financial relationships that could be construed as a potential conflict of interest.
The author declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Generative AI statement
The author(s) declare that no generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Shichkova P, Coggan JS, Kanari L, Boci E, Favreau C, Antonel SM, et al. Breakdown and repair of metabolism in the aging brain. Front Sci (2025) 3:1441297. doi: 10.3389/fsci.2025.1441297
2. Attwell D, Laughlin SB. An energy budget for signaling in the grey matter of the brain. J Cereb Blood Flow Metab (2001) 21(10):1133–45. doi: 10.1097/00004647-200110000-00001
3. Yu Y, Herman P, Rothman DL, Agarwal D, Hyder F. Evaluating the gray and white matter energy budgets of human brain function. J Cereb Blood Flow Metab (2018) 38(8):1339–53. doi: 10.1177/0271678X17708691
4. Howarth C, Mishra A, Hall CN. More than just summed neuronal activity: how multiple cell types shape the BOLD response. Philos Trans R Soc Lond B Biol Sci (2021) 376(1815):20190630. doi: 10.1098/rstb.2019.0630
5. Pan M, Gawthrop PJ, Tran K, Cursons J, Crampin EJ. A thermodynamic framework for modelling membrane transporters. J Theor Biol (2019) 481:10–23. doi: 10.1016/j.jtbi.2018.09.034
6. Evans DJ, Searles DJ. The fluctuation theorem. Adv Phys (2002) 51(7):1529–85. doi: 10.1080/00018730210155133
7. Buxton RB. Thermodynamic limitations on brain oxygen metabolism: physiological implications. J Physiol (2024) 602(4):683–712. doi: 10.1113/JP284358
9. Baartscheer A, Schumacher CA, Coronel R, Fiolet JW. The driving force of the Na/Ca-exchanger during metabolic inhibition. Front Physiol (2011) 2:10. doi: 10.3389/fphys.2011.00010
Keywords: brain energetics, cerebral blood flow, sodium/potassium pump, thermodynamic modeling, brain aging
Citation: Buxton RB. Recharging the brain’s batteries: a thermodynamic perspective on modeling brain energetics. Front Sci (2025) 3:1556319. doi: 10.3389/fsci.2025.1556319
Received: 06 January 2025; Accepted: 04 February 2025;
Published: 25 March 2025.
Edited and reviewed by:
Jon Storm-Mathisen, University of Oslo, NorwayCopyright © 2025 Buxton. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Richard B. Buxton, cmJ1eHRvbkBoZWFsdGgudWNzZC5lZHU=
 Richard B. Buxton
Richard B. Buxton