- 1Hubei Key Laboratory of Optical Information and Pattern Recognition, Wuhan Institute of Technology, Wuhan, China
- 2Department of Physics and Mechanical & Electrical Engineering, Hubei University of Education, Wuhan, China
We theoretically investigate the photoelectron momentum distributions of 1s and 2px,y states of hydrogen by twisted attosecond X waves carrying orbital angular momentum based on first-order perturbation theory. The photoionization spectra as a function of photoelectron energy and emission angle are analyzed respectively. The results indicate that there are interference fringes in the energy spectra and more nodes in the angular distributions. These angular nodes are attributed to both orbital structure and the temporal-spatial structure of X waves. We derive an equation that can quantitatively describe the angular nodes in the photoelectron angular distributions. Our results and analyses indicate that the angular distribution is an important observation for the investigation of the information of both orbitals and X waves.
1 Introduction
Advances of extreme ultraviolet (XUV) and soft x-ray pulses have opened up the intriguing opportunity of probing and control of electronic dynamics on the attosecond time scale (1 as = 10–18 s) and Å spatial dimension (1 Å = 10–10 m) [1–8]. The attosecond XUV and soft x-ray pulses can be accessible by high-order harmonic generation (HHG) [9–13] and free-electron lasers (FEL) [14, 15]. Based on the interaction of these shorter pulses with targets, a variety of applications, such as the ultrafast molecular orbital imaging [16–18], measurement of time delays in photoemission [19, 20], and detection of the charge migration in molecules, nanoparticles and materials [21–25], have been promised. In the majority of strong-field processes above, the adopted attosecond XUV and soft x-ray are general plane-wave pulses, which have been quite well understood.
Since the pioneering studies of Beth and Allen et al. [26, 27], one knows that, apart from the pulses with a plane-wave front, beams of light can possess a helical wavefront and carry orbital angular momentum (OAM) as well as their spin angular momentum (SAM). The polarization state of light is associated with its SAM, whereas the spatial distribution of the wave-front is related to the OAM of the light [27, 28]. Light with non-zero OAM is known as twisted or vortex light beams, such as the Bessel and Laguerre–Gaussian (LG) beams. Beyond the Bessel and LG pulses, another twisted beam, the X wave, formed by a superposition of Bessel beams, has also obtained much attention for its localization feature both in the spatial and temporal domain [29, 30]. These twisted light fields provide powerful capabilities for applications in the area of optical sensing and communication, quantum communication, optical tweezers and optical manipulation [31–36]. Until now, there are various ways to generate the twisted light pulses, such as spiral phase plates, axicons, computer-generated holograms and integrated ring resonators [37–41]. Although the OAM of light produced by these ways can be imprinted into waveforms over a large frequency range, it was not possible to generate the coherent light possessing OAM beyond the ultraviolet regime. So, the applications exploiting OAM interactions were limited to macroscopic systems using visible light. Fortunately, recent advances in HHG have broken this photonic limitation, producing the fully coherent attosecond XUV and soft X-ray pulses with designer OAM, which have opened up the possibility of monitoring and manipulating the OAM of light-matter interactions on the atomic scale [42–45].
Understanding photoionization in intense laser fields is of central importance in ultrafast optical sciences. In recent years, the twisted XUV pulses with OAM as a new powerful tool for probing ultrafast electron dynamics have gradually obtained much attention in theoretical and experimental studies on photoionization. For example, the twisted XUV Bessel and LG pulses have been used to theoretically study the above-threshold ionization and dichroism signals of targets [46, 47]. In an experiment [48], the attosecond vortex pulses have been applied to generate and manipulate, through photoionization, attosecond electron beams carrying OAM. Additionally, the energy spectrum of atoms irradiated by the twisted attosecond X wave has also been investigated [49, 50]. In contrast to plane-waves, a twisted X wave is a non-diffracting electromagnetic field in both space and time [30]. Most previous works, related to the attosecond X waves, mainly focused on the energy spectra [49, 50]. And the influence of the structure of orbitals on photoelectron angular distributions (PADs) have also been well studies. However, up to now, the PADs of different orbitals in the twisted attosecond X pulses have rarely been studied and the influence of the structure of X waves on the PADs have rarely been reported.
In this work, the PMDs of hydrogen atoms irradiated by twisted attosecond X waves are investigated based on first-order perturbation theory. Due to the temporal-spatial structure of X waves, interference fringes in the radial and more nodes in the angle direction of PMDs are observed. In order to interpret these phenomena in detail, we study the energy spectra and angular distributions by integrating the PMDs over emission angle and momentum, respectively. We derive a concise equation, which can quantitatively interpret the angular nodes in PADs. They are attributed to the spatial structures of orbitals and X waves. Our results and analyses indicate that the PADs can reveal the information about X waves and orbitals that cannot be revealed in energy spectra. Atomic units (me = qe = ℏ = 1) are used throughout this work unless otherwise stated. The atomic units (a.u.) of time, distance, energy and momentum are τ0 = 24.2 × 10–18 s, a0 = 0.053 × 10–9 m, E0 = 27.2 eV and v0 = 2.18 × 106 m/s.
2 Theoretical model
X waves are localized waves and formed by the superposition of Bessel beams
in which m, Λ and θk are the projection of total angular momentum (PTAM), helicity and opening angle in momentum space. α is the electromagnetic fine structure constant. The cylindrical coordinates r = (r, ϕr, z) are applied. Distinguishing from plane-wave,
where
with the wave vector k = (k⊥, kz) = (κ, ϕk, kz) and the Fourier coefficients
The opening angle is θk = arctan(κ/kz). The polarization vector ɛkΛ describes a circularly polarized plane-wave with helicity Λ = ±1 and depends on the angles θk and ϕk in momentum space,
with the condition k ⋅ɛkΛ = 0. Note that, whether the Bessel pulses are constructed with linearly or circularly polarized pulses, the analyses and conclusions about the influence of X wave structures on PMDs is the same.Pulses applied in experiments of the light-target interactions possess a finite pulse duration TX. Such pulses can be obtained by weighted non-monochromatic superposition of continuous Bessel beams [30]. The superposition with a fixed θk can construct X wave vector potential as
where Δω = 1/TX is the width of the Gaussian spectral distribution and the ω0 is the central frequency.Eq. 3 is the most general form of the twisted states vector potential, which will be employed in the following discussions about the PMDs. For the sake of description of twisted X waves, we write the wave vector
in which
In Eq. 7,
The set-up for the ionization of an atom by an X wave pulse is shown in Figure 1. The atom ionized is localized at position b = (b, ϕb = 0, bz = 0). The XUV pulse propagates along the z-axis with helicity Λ = +1. We assume that the central frequency ω0 = 3 a.u. is large enough and the intensity of the pulse is very weak. The single-photon ionization process can be induced. The pulse duration is TX = 1.9 TL0 with TL0 = 110 a.u. = 2.7 fs. The photoelectron ionized from the atom is collected at the detector with the asymptotic momentum p = (p, ϕp, θp). We shall analyze the PMDs at the px-py plane for θp = π/2. Within first-order perturbation theory [49], the transition amplitude at impact parameter b reads as
where Ψi and Ψf are the initial (bound) and final (continuum) wave functions. For hydrogen atoms, the wave functions can be analytically described. The continuum states are typically described by Volkov wave functions
Substituting Eq. 6 into Eq. 10, we obtain the transition amplitude as a superposition of
where
Here,
in which Ip is the ionization potential of Ψi.
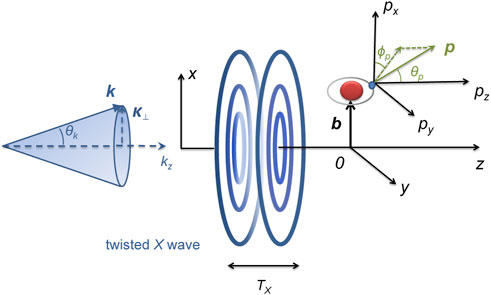
FIGURE 1. Ionization schematic of a hydrogen atom with twisted X wave with pulse duration TX. Left panel: in momentum space, all wave vectors k contributing to Eq. 3 lie on a cone with opening angle θk = arctan(κ/kz) with κ = |k⊥|. kz is parallel with z-axis. Right panel: the pulse propagates along z direction. An atom is localized at the impact parameter b=(b, ϕb = 0, zb = 0) relative to the beam z-axis. Then, x-z plane is determined by the position of the target and the pulse propagation. The photoelectron is observed with asymptotic momentum p=(p, ϕp, θp) at the detector.
3 Results and discussions
We first calculate the PMDs of the hydrogen atom irradiated by the plane-wave pulses, which are the twisted X waves in the limit θk → 0 in Eq. 6. The results are presented in Figure 2. We display the modulus of the plane-wave pulse potential vector as a function of time t and distance r from the beam axis in Figure 2A. One can see that the vector potential is independent of r and exhibits a single maximum in time. For better visualization of the XUV pulse polarization and its temporal properties, we also plot the projection of the potential vector on AX,x−AX,y plane and the real part Re{AX(r0, t)} with r0 = 11350 a.u. in Figures 2B,C. It is shown that the electric field is circularly polarized with helicity Λ = +1. In Figure 2C, only one XUV pulse is exhibited. The time-duration of the pulse is TX. Then, we calculate the PMDs of 1s and 2px,y states of hydrogen atom placed at the impact parameter b = 11350 a.u. from the X wave beam axis. The results are shown in Figures 2D–F respectively. Note that, for a plane-wave pulse, the impact parameter b will not affect the results. In Figure 2D, the PAD of the 1s state is isotropic. For 2px,y states, the PADs present a distinct two-lobed structure in Figures 2E,F. The structures of PADs are attributed to the symmetry of the systems, which have been investigated in previous works [51, 52]. From Figures 2D–F, one can see that there are no interference structures and only one probability peak in the radial direction of PMDs. Besides, according to the energy conservation, the momentum corresponding to the maximum probability of PMDs satisfies
So, for the 1s state with Ip = 1/2 a.u. and 2px,y states with Ip = 1/8 a.u., the momenta mentioned above are |p| = 2.2361 a.u. and |p| = 2.3979 a.u. respectively, which are very agree with the results in Figure 2D–F. Overall, Figure 2 illustrates that, in circular plane-wave pulses, the structures of PADs are only induced by orbitals. In this situation, the temporal-spatial structures of X waves play no role in PMDs at all.
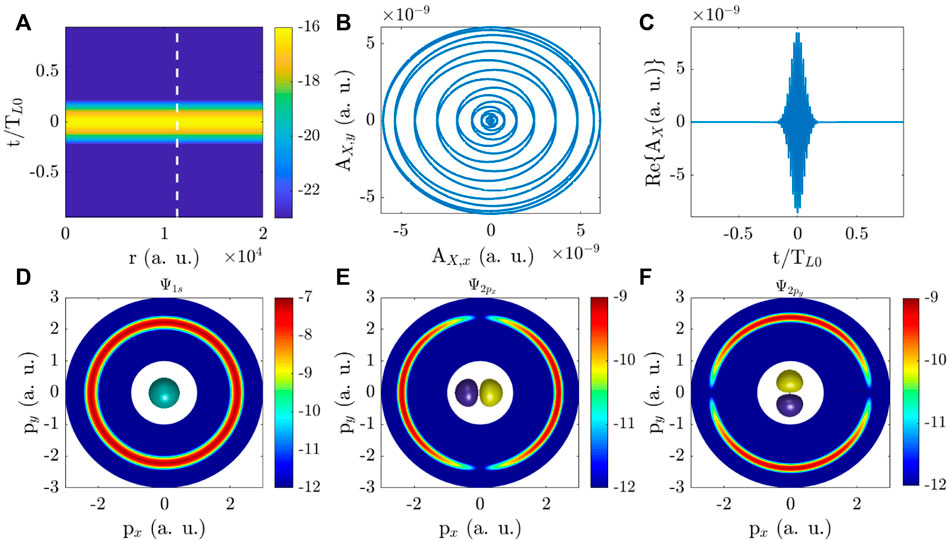
FIGURE 2. PMDs in plane-wave pulses. (A) Modulus of the pulse vector potential as a function of the distance r from the beam axis and time t on a logarithmic scale. r0 = 11350 a.u. is labeled by the white dashed line. (B) The projection of the pulse vector potential on the AX,x-AX,y plane at position r0. (C) Real part of the pulse vector potential Re{AX(r0, t)}. (D–F) PMDs of 1s, 2px and 2py states of a hydrogen atom at b = r0. PMD of 1s state is isotropic and centered at zero momentum. For 2p states, there is a nodal plane in PMDs. The structures of PMDs in plane-wave pulses are contributed only by the orbital. The insets in (D–F) present the 1s, 2px and 2py orbitals of a hydrogen atom. The units of physical quantities in figures are atomic units (a.u).
Then, we study the PMDs in twisted X waves with larger θk. When the opening angle θk of the X pulses increases, the structure of X pulses changes, which will affect the PMDs. In Figures 3A,F, for θk = 5° and 60°, the moduli of X wave vector potential with m = 1 versus distance r and time t are plotted. By comparing with the vector potential in Figure 2A, one can see that the X wave vector potential splits into two pulses in the time domain. At a specific distance r0, the time-delay τ between these two pulses is concerned with the opening angle θk of the X wave. For example, at r0 = 11350 a.u., the time-delays are τ = 0.142 TL0 for θk = 5° in Figure 3A and τ = 1.302 TL0 for θk = 60° in Figure 3E. It is worth noting that, we are mainly concerned with the influence of θk and PTAM on PMDs through adjusting the time-delay rather than the spatial structure in the plane (r, ϕ). Additionally, under the conditions of the laser waves applied in our work, the maximum excursion distance of the electron is much smaller than the spatial size of the fields and the electron does not feel the spatial structure of the X waves. Thus, we can apply the local dipole approximation in the matrix element: ⟨p|eik⋅r|Ψi⟩ ≈ ⟨p|Ψi⟩ in Eq. 14. Then, the X wave pulse interacts with the hydrogen atom placed at the distance b = 11350 a.u. The PMDs of 1s and 2px,y states are presented in Figures 3B–D for θk = 5° and in Figures 3F–H for θk = 60°. From Figures 3B–D, one can see that, rather than a single probability peak of PMDs as shown in Figures 2D–F, two probability peaks appear in the radial direction of PMDs. In Figures 3F–H, there are more probability peaks in the radial direction of PMDs. For a clear visualization, momentum distributions outlined by white lines have been zoomed in. From the results in Figure 3, one can see that the opening angle θk of the twisted X pulses can affect the probability peaks of PMDs. These complex structures in the radial direction of PMDs are attributed to the interference of the ionization processes from the two split pulses, which will be discussed quantitatively below. In addition, the momentum corresponding to the maximum probability of PMDs still almost satisfies Eq. 15. In the angular direction, when θk increases, for 1s state, the isotropic PADs turn to a two-lobed distribution. For 2px,y states, some variations of the PAD also take place. A closer examination of PADs will be discussed in Figure 6.
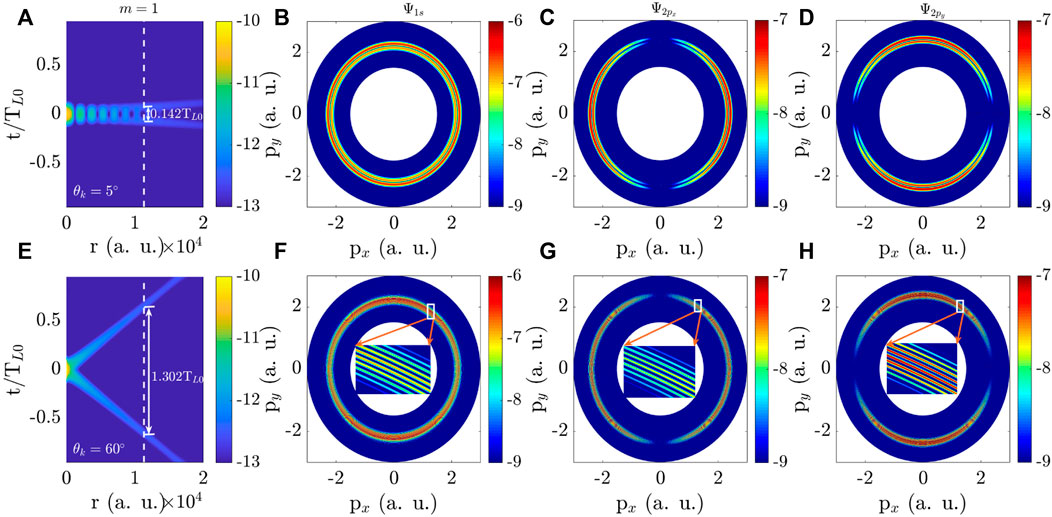
FIGURE 3. PMDs of an atom by the twisted X wave pulse at r = (r, ϕr = 0, z = 0). Moduli of the X wave vector potential as a function of the distance r to beam axis and time t for the PTAM m = 1 and two values of the opening angle (A) θk = 5° and (E) θk = 60° on a logarithmic scale. The time-delay τ between the two split pulses of the X wave at the position r0 = 11350 a.u. labeled by the white dashed line is labeled by the solid line with double arrows. (B–D), (F–H) PMDs of 1 s, 2px and 2py states of a hydrogen atom at the impact parameter b = 11350 a.u. in the X waves for (A) and (E). The insets in (F–H) show the details of PMDs within the area outlined in white. The units of physical quantities in figures are a.u.
We have discussed the dependence of the PMDs on the opening angle θk in Figures 2,3. Next, we investigate the effect of PTAM m on PMDs. The moduli of X wave potential and the PMDs are displayed in Figure 4 for the same beam parameters as those in Figure 3, except for a different value of m = 20. As seen from Figures 4A,E, the structure of X waves changes compared with that in Figure 3. The first maximum of the X wave potential shifts away from the beam axis r = 0 to a larger distance in contrast to the wave with m = 1. Mathematically, this shift arises from the r dependence of the Bessel functions
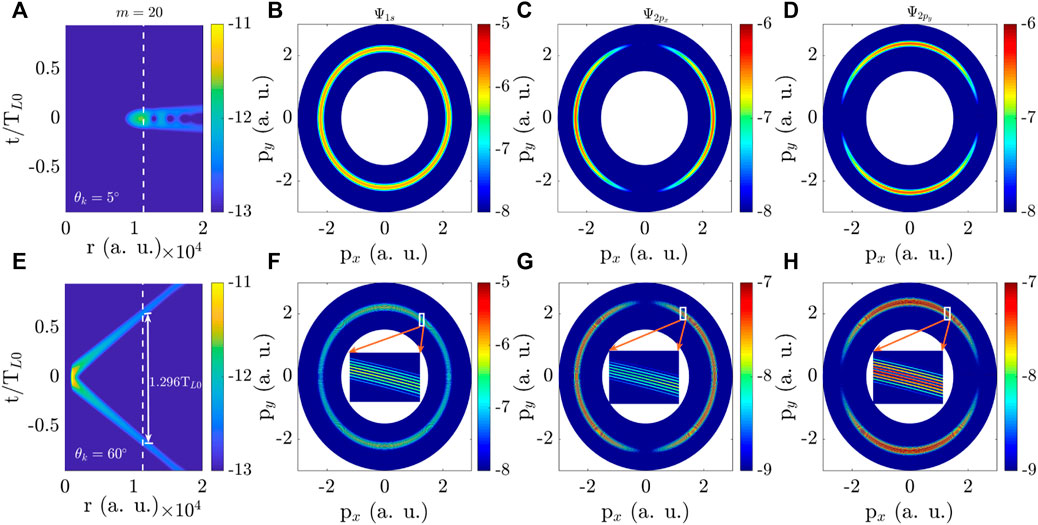
FIGURE 4. Same as Figure 3 but for a different PTAM m = 20 of the X wave. (A–D) θk = 5° and (E–H) θk = 60°.
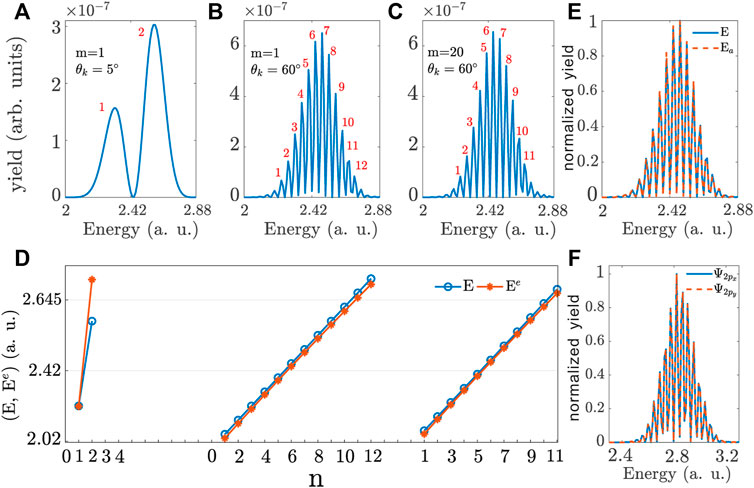
FIGURE 5. The energy spectra of 1s state of a hydrogen atom for ϕp = pz = 0 with the PTAM and opening angle of the X wave (A) m = 1, θk = 5°, (B) m = 1, θk = 60° and (C) m = 20, θk = 60°. The red integers represent the peak numbers of the energy spectra. (D) Comparison of E (blue line) and Ee (red line) corresponding to the peak numbers in (A–C). Ee is the evaluated result according to Eq. 16 and E is the numerical result. The units of photoelectron yield are arbitrary units (arb. units) and the units of energy are a.u. (E) Comparison of the energy spectra of X wave (E labeled by the blue solid line) and double circular plane-wave pulses with the same time-delay τ as that in Figure 3E (Ea labeled by the red dashed line). (F) Comparison of the energy spectra of 2px,y orbitals corresponding to the PMDs in Figures 3G, H. The yield in (E) and (F) is normalized.
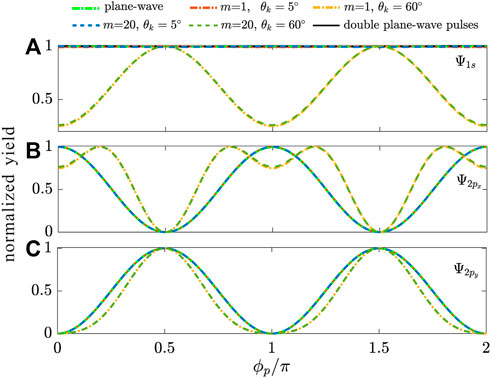
FIGURE 6. Photoelectron angular distributions by integration over the p of electrons emitted from (A) 1 s, (B) 2px and (C) 2py states of a hydrogen atom by plane-wave pulse and twisted X wave with m = 1, 20 and θk = 5°, 60°. The black solid line represents the PAD of double plane-wave pulses with the same time-delay τ as that in Figure 3E. The yield is normalized.
In order to interpret the interference fringes of PMDs in Figures 3,4, we propose a concise theoretical model. Here, we focus on the structure of energy spectra by integrating the PMDs over ϕp with θp = π/2. We define the transition amplitude of the photoelectron from one split pulse of the twisted X wave as
From Eq. 16, one can determine the positions of the interference fringes based on Ee = 2nπ/τ (n is an integer). The numerical interference fringe of energy spectra can be obtained by integrating the PMDs over ϕp with θp = π/2. We take the case of 1s orbital as an example to verify that our theoretical model can precisely describe the interference fringes in the radial direction of PMDs. The energy spectra for Figures 3B,F,4F are plotted in Figures 5A–C. For ease of comparison with the evaluate results, the interference fringes are numbered. For the time-delay τ = 0.142TL0, 1.302TL0 and 1.296TL0 presented in Figures 3B,F,4F respectively, the evaluate energy Ee can be calculated. Then, the comparison between the numerical (labeled by the blue hollow-circle lines) and evaluate (labeled by the red solid-circle lines) results is displayed in Figure 5D. From this figure, one can see that the evaluate results almost coincide with the numerical ones, which indicates that our theoretical model can reproduce the numerical results and quantitative interpret the mechanism of interference fringes. From Eq. 16, we know that the energy spectra are only dependent on the time-delay τ. They are independent of the spatial information of the orbital and X wave pulse. That is to say, the PTAM m and opening angle θk have an influence on the PAM through affecting the time-delay τ rather than the spatial structure of X waves. Besides, the information of orbital and X wave structures cannot be revealed only in these energy spectra. In order to demonstrate this point, we have calculated the photoelectron momentum distributions of 1s orbital in the double plane-wave pulses with the same time-delay τ as that in Figure 3E. The wavefront structure of these pulses is plane and different from the twisted wavefront of X waves. The comparison between the energy spectra of the two cases is presented in Figure 5E. One can see that the energy spectra are the same. Besides, we also compare the energy spectra of 2px,y orbitals for PMDs in Figures 3G, H. The results are plotted in Figure 5F. From this figure, one can see that the energy spectra are the same and orbital structures have no influence on them. Therefore, the discussions above demonstrate that, the interference fringes of PMDs are due to the two ionization events from the two split pulses, which can be interpreted by our theoretical model. Our model can also reproduce the interference fringe positions. Additionally, this model implies that the information of the X wave and orbital structures cannot be revealed in energy spectra.
At last, we discuss in detail the PADs, i.e., the photoionization yield versus azimuthal angle ϕp. We integrate the PMDs in Figures 2–4 over the momentum p:
in which Ψi(p) is the initial wave function in the momentum space. For 2px,y states,
4 Conclusion
In conclusion, we investigated the PMDs of 1s and 2px,y states of hydrogen atoms irradiated by the twisted attosecond X waves carrying OAM using first-order perturbation theory. Different from the plane-wave, the X wave carrying orbital angular momentum can induce more complex structures in PMDs, such as the interference fringes in the radial direction and more nodes in the angle direction of PMDs. In order to interpret these structures in detail, we respectively analyzed the energy spectra and angular distributions. We found that the PADs can reveal the spatial information of orbitals and X waves. A concise equation is derived to quantitatively interpret the PADs. It describes the influence of orbitals and X waves on PADs individually. A comparison of the results in X waves and double time-delayed plane-wave pulses has been carried out to further demonstrate our point, i.e., PAD is an important observation encoding the structure information of X waves. X waves for their non-diffraction and OAM-carrying characteristics can be an ideal candidate in quantum communication and give the possibility to increase the amount of information that can be transferred in an undistorted way through the atmosphere. They can be also applied in other fields like acoustics, electromagnetism and even medicine. When X waves interact with complex molecules or solids, there may be more abundant strong-field phenomena, which are of great significance for stimulating new applications in various fields from quantum information to microscopy.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
XZ conceived the idea, conducted the simulations and wrote the manuscript. The data was analyzed by XZ and XM.
Funding
This work was supported by National Natural Science Foundation of China (NSFC) (Grants Nos. 11904269), the Natural Science Foundation of Hubei Province under Grant Nos. 2021CFB300, 2020CFB362, the Science Research Foundation of Wuhan Institute of Technology (Grant No. 21QD74).
Acknowledgments
We thank Feng Wang, Profs. Xiao-song Zhu and Qing Liao for the helpful discussion.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Paul PM, Toma ES, Breger P, Mullot G, Augé F, Balcou P, et al. Observation of a train of attosecond pulses from high harmonic generation. Science (2001) 292:1689–92. doi:10.1126/science.1059413
2. Krausz F, Ivanov M. Attosecond physics. Rev Mod Phys (2009) 81:163–234. doi:10.1103/RevModPhys.81.163
3. Mairesse Y, de Bohan A, Frasinski LJ, Merdji H, Dinu LC, Monchicourt P, et al. Attosecond synchronization of high-harmonic soft x-rays. Science (2003) 302:1540–3. doi:10.1126/science.1090277
4. Kienberger R, Goulielmakis E, Uiberacker M, Baltuska A, Yakovlev V, Bammer F, et al. Atomic transient recorder. Nature (2004) 427:817–21. doi:10.1038/nature02277
5. Allaria E, Appio R, Badano L, Barletta WA, Bassanese S, Biedron SG, et al. Highly coherent and stable pulses from the fermi seeded free-electron laser in the extreme ultraviolet. Nat Photon (2012) 6:699–704. doi:10.1038/nphoton.2012.233
6. Smirnova O, Mairesse Y, Patchkovskii S, Dudovich N, Villeneuve D, Corkum P, et al. High harmonic interferometry of multi-electron dynamics in molecules. Nature (London) (2009) 460:972–7. doi:10.1038/nature08253
7. Lan P, Ruhmann M, He L, Zhai C, Wang F, Zhu X, et al. Attosecond probing of nuclear dynamics with trajectory-resolved high-harmonic spectroscopy. Phys Rev Lett (2017) 119:033201. doi:10.1103/PhysRevLett.119.033201
8. Shafir D, Soifer H, Bruner BD, Dagan M, Mairesse Y, Patchkovskii S, et al. Resolving the time when an electron exits a tunnelling barrier. Nature (London) (2012) 485:343–6. doi:10.1038/nature11025
9. Sansone G, Benedetti E, Calegari F, Vozzi C, Avaldi L, Flammini R, et al. Isolated single-cycle attosecond pulses. Science (2006) 314:443–6. doi:10.1126/science.1132838
10. Li J, Ren X, Yin Y, Zhao K, Chew A, Cheng Y, et al. 53-attosecond x-ray pulses reach the carbon k-edge. Nat Commun (2017) 8:186. doi:10.1038/s41467-017-00321-0
11. Gaumnitz T, Jain A, Pertot Y, Huppert M, Jordan I, Ardana-Lamas F, et al. Streaking of 43-attosecond soft-x-ray pulses generated by a passively cep-stable mid-infrared driver. Opt Express (2017) 25:27506–27518. doi:10.1364/OE.25.027506
12. Ferré A, Handschin C, Dumergue M, Burgy F, Comby A, Descamps D, et al. A table-top ultrashort light source in the extreme ultraviolet for circular dichroism experiments. Nat Photon (2015) 9:93–8. doi:10.1038/nphoton.2014.314
13. Zhang X, Zhu X, Liu X, Wang F, Qin M, Liao Q, et al. Elliptical isolated attosecond-pulse generation from an atom in a linear laser field. Phys Rev A (2020) 102:033103. doi:10.1103/PhysRevA.102.033103
14. Bostedt C, Boutet S, Fritz DM, Huang Z, Lee HJ, Lemke HT, et al. Linac coherent light source: The first five years. Rev Mod Phys (2016) 88:015007. doi:10.1103/RevModPhys.88.015007
15. Huang S, Ding Y, Feng Y, Hemsing E, Huang Z, Krzywinski J, et al. Generating single-spike hard x-ray pulses with nonlinear bunch compression in free-electron lasers. Phys Rev Lett (2017) 119:154801. doi:10.1103/PhysRevLett.119.154801
16. Villeneuve DM, Hockett P, Mjj V, Niikura H. Coherent imaging of an attosecond electron wave packet. Science (2017) 356:1150–3. doi:10.1126/science.aam8393
17. Peng P, Marceau C, Villeneuve DM. Attosecond imaging of molecules using high harmonic spectroscopy. Phys Rev Lett (2019) 1:144–55. doi:10.1038/s42254-018-0015-1
18. Bian XB, Bandrauk AD. Attosecond time-resolved imaging of molecular structure by photoelectron holography. Phys Rev Lett (2012) 108:263003. doi:10.1103/PhysRevLett.108.263003
19. Schultze M, Fies M, Karpowicz N, Gagnon J, Korbman M, Hofstetter M, et al. Delay in photoemission. Science (2010) 328:1658–62. doi:10.1126/science.1189401
20. Vos J, Cattaneo L, Patchkovskii S, Zimmermann T, Cirelli C, Lucchini M, et al. Orientation-dependent stereo wigner time delay and electron localization in a small molecule. Science (2018) 360:1326–30. doi:10.1126/science.aao4731
21. Ranitovic P, Hogle CW, Rivière P, Palacios A, Tong XM, Toshima N, et al. Attosecond vacuum uv coherent control of molecular dynamics. Proc Natl Acad Sci USA (2014) 111:912–7. doi:10.1073/pnas.1321999111
22. Liao Q, Cao W, Zhang Q, Liu K, Wang F, Lu P, et al. Distinction of electron dispersion in time-resolved photoemission spectroscopy. Phys Rev Lett (2020) 125:043201. doi:10.1103/PhysRevLett.125.043201
23. Ellis JL, Hickstein DD, Xiong W, Dollar F, Palm BB, Keister KE, et al. Materials properties and solvated electron dynamics of isolated nanoparticles and nanodroplets probed with ultrafast extreme ultraviolet beams. J Phys Chem Lett (2016) 7:609–15. doi:10.1021/acs.jpclett.5b02772
24. Ghimire S, DiChiara AD, Sistrunk E, Agostini P, DiMauro LF, Reis DA. Observation of high-order harmonic generation in a bulk crystal. Nat Phys (2011) 7:138–41. doi:10.1038/nphys1847
25. Luu TT, Garg M, Kruchinin SY, Moulet A, Hassan MT, Goulielmakis E. Extreme ultraviolet high-harmonic spectroscopy of solids. Nature (London) (2015) 521:498–502. doi:10.1038/nature14456
26. Beth RA. Mechanical detection and measurement of the angular momentum of light. Phys Rev 50 (1936) 115–25. doi:10.1103/PhysRev.50.115
27. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of laguerre-Gaussian laser modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/PhysRevA.45.8185
28. Molina-Terriza G, Torres JP, Torner L. Twisted photons. Nat Phys (2007) 3:305–10. doi:10.1038/nphys607
29. Saari P, Sonajalg H. Pulsed bessel beams. In: T Smith, editor. International workshop on laser Physics. Bristol, United Kingdom: IOP Publishing Ltd (1997). p. 32–9.
31. Willner AE, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, et al. Optical communications using orbital angular momentum beams. Adv Opt Photon (2015) 7:66–106. doi:10.1364/AOP.7.000066
32. Beaulieu S, Comby A, Descamps D, Fabre B, Garcia GA, Géneaux R, et al. Photoexcitation circular dichroism in chiral molecules. Nat Phys (2018) 14:484–9. doi:10.1038/s41567-017-0038-z
33. Padgett M, Bowman R. Tweezers with a twist. Nat Photon (2011) 5:343–8. doi:10.1038/nphoton.2011.81
34. Marrucci L, Manzo C, Paparo D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys Rev Lett (2006) 96:163905. doi:10.1103/PhysRevLett.96.163905
35. Forbes KA. Raman optical activity using twisted photons. Phys Rev Lett (2019) 122:103201. doi:10.1103/PhysRevLett.122.103201
36. Vicidomini G, Bianchini P, Diaspro A. Sted super-resolved microscopy. Nat Methods (2018) 15:173–82. doi:10.1038/nmeth.4593
37. Beijersbergen MW, Coerwinkel RPC, Kristensen M, Woerdman JP. Helical-wavefront laser beams produced with a spiral phaseplate. Opt Commun (1994) 112:321–7. doi:10.1016/0030-4018(94)90638-6
38. Arlt J, Dholakia K. Generation of high-order bessel beams by use of an axicon. Opt Commun (2000) 177:297–301. doi:10.1016/S0030-4018(00)00572-1
39. Heckenberg NR, McDuff R, Smith CP, White AG. Generation of optical phase singularities by computer-generated holograms. Opt Lett (1992) 17:221–3. doi:10.1364/OL.17.000221
40. Cai X, Wang J, Strain MJ, Johnson-Morris B, Zhu J, Sorel M, et al. Integrated compact optical vortex beam emitters. Science (2012) 338:363–6. doi:10.1126/science.1226528
41. Ninno GD, Wätzel J, Ribič PR, Allaria E, Coreno M, Danailov MB, et al. Photoelectric effect with a twist. Nat Photon (2020) 14:554–8. doi:10.1038/s41566-020-0669-y
42. Dorney KM, Rego L, Brooks NJ, Román JS, Liao CT, Ellis JL, et al. Controlling the polarization and vortex charge of attosecond high-harmonic beams via simultaneous spin-orbit momentum conservation. Nat Photon (2019) 13:123–30. doi:10.1038/s41566-018-0304-3
43. Rego L, Dorney KM, Brooks NJ, Nguyen QL, Liao CT, Román JS, et al. Generation of extreme-ultraviolet beams with time-varying orbital angular momentum. Science (2019) 364:9486. doi:10.1126/science.aaw9486
44. Kong F, Zhang C, Bouchard F, Li Z, Brown GG, Ko DH, et al. Controlling the orbital angular momentum of high harmonic vortices. Nat Commun (2017) 8:14970. doi:10.1038/ncomms14970
45. Gauthier D, Ribic̆ PR, Adhikary G, Camper A, Chappuis C, Cucini R, et al. Tunable orbital angular momentum in high-harmonic generation. Nat Commun (2017) 8:14971. doi:10.1038/ncomms14971
46. Boning B, Paufler W, Fritzsche S. Above-threshold ionization by few-cycle bessel pulses carrying orbital angular momentum. Phys Rev A (2018) 98:023407. doi:10.1103/PhysRevA.98.023407
47. Baghdasaryan B, Boning B, Paufler W, Fritzsche S. Dichroism in two-color above-threshold ionization with twisted xuv beams and intense infrared laser fields. Phys Rev A (2019) 99:023403. doi:10.1103/PhysRevA.99.023403
48. Geneaux R, Camper A, Auguste T, Gobert O, Caillat J, Taieb R, et al. Synthesis and characterization of attosecond light vortices in the extreme ultraviolet. Nat Commun (2016) 7:12583. doi:10.1038/ncomms12583
49. Muller RA, Seipt D, Beerwerth R, Ornigotti M, Szameit A, Fritzsche S, et al. Photoionization of neutral atoms by x waves carrying orbital angular momentum. Phys Rev A (2016) 94:041402. (R). doi:10.1103/PhysRevA.94.041402
50. Boning B, Paufler W, Fritzsche S. Attosecond streaking with twisted x waves and intense infrared pulses. Phys Rev A (2017) 96:043423. doi:10.1103/PhysRevA.96.043423
51. Faisal FHM. Multiple absorption of laser photons by atoms. J Phys B: Mol Opt Phys (1973) 6:L89–92. doi:10.1088/0022-3700/6/4/011
Keywords: twisted attosecond X waves, photoelectron momentum distribution, orbital angular mometnum, photoelectron angular distribution, ultrafast electron dynamics
Citation: Zhang X and Ma X (2023) Photoelectron momentum distributions with twisted attosecond X waves carrying orbital angular momentum. Front. Phys. 10:1103142. doi: 10.3389/fphy.2022.1103142
Received: 20 November 2022; Accepted: 21 December 2022;
Published: 09 January 2023.
Edited by:
Weiren Zhu, Shanghai Jiao Tong University, ChinaReviewed by:
Nobuhiko Yokoshi, Osaka Prefecture University, JapanZhenkun Wu, Henan University, China
Copyright © 2023 Zhang and Ma. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaofan Zhang, xiaofan_z@163.com
 Xiaofan Zhang
Xiaofan Zhang