Evolution of the orbital angular momentum flux density of partially coherent vortex beams in atmospheric turbulence

We investigate the behavior of the orbital angular momentum (OAM) flux density of partially coherent vortex (PCV) beams in atmospheric turbulence. It is shown that for PCV beams with different spatial coherence structures, the OAM flux density distribution exhibits rich variations along the propagation path. Our findings provide insight into the use of the OAM in free-space optical communications when turbulence effects are significant.

Introduction

During the past few decades, the study of vortex structures in optical fields, and more complicated wavefield singularities, has become a stand-alone area of investigation of modern optics, named singular optics [1–3]. Spatially coherent beams carrying optical vortices, called vortex beams, have attracted much interest due to their potential applications in many areas including coronagraph [4], coherence filtering [5], and free-space optical communication [6]. Since Allen et al. found that Laguerre–Gauss beams carry a well-defined OAM as a consequence of their vortex core [7], vortex beams have also found application in optical tweezing [8], optical spanning [9], design of light-driven machines [10], high-resolution microscopy [11], security holograms [12], quantum information transfer [13], and rotation measurements [14].

Partially coherent beams have been shown to benefit a number of applications, such as free-space optical communication [15], particle trapping [16], and atom cooling [17]. It is therefore of great interest to consider vortex structures in partially coherent beams. Unlike spatially coherent beams, however, partially coherent beams do not have a well-defined phase structure and their behavior can only be described using coherence functions. Some years ago, Schouten et al showed that these coherence functions can possess their own phase singularities (and optical vortices) that are closely related to their coherent counterparts [18], and since then, much attention has been given to these so-called coherence singularities or coherence vortices [19–23]. For partially coherent beams carrying vortex structures, which are called PCV beams, when the coherence decreases, coherence singularities are shown to be more robust than phase singularities [24].

Recently, it was found that the OAM of PCV beams exhibits a number of novel characteristics. For example, different types of PCV beams can have different distributions of the OAM flux density in their cross-sections. The OAM flux density can represent a Rankine vortex, a rigid body rotator, a fluid rotator, or even more rich varieties of OAM distributions; these results indicate that PCV beams can provide additional control over OAM than their coherence counterparts [25–28]. More recently, we found that one can manipulate the source coherence to change the OAM flux density of PCV beams on propagation in free space [29], and this effect joins correlation-induced spectral and polarization changes in a family of source coherence influenced propagation phenomena (for the summary see Ch. 4 of Ref. [30]).

However, despite the fact that free-space optical communication is one of the most significant applications of such beams, the propagation characteristics of the OAM flux density of PCV beams in atmospheric turbulence has yet to be studied. In this paper, we study the propagation of the OAM flux density of PCV beams in atmospheric turbulence. We derive analytic formulas showing how atmospheric turbulence affects the OAM flux density on propagation, and illustrate the changes with a number of model partially coherent beams with structured spatial coherence.

Theory

We consider a scalar, statistically stationary random source that is located in a plane perpendicular to the direction of propagation. The second-order statistical properties of the source can be characterized by the cross-spectral density (CSD) function [31],

$W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)={〈U^{*}\left({\mathbf{r}}_1\right)U\left({\mathbf{r}}_2\right)〉}_{\omega },(1)$

where ${〈\cdot \cdot \cdot 〉}_{\omega }$ represents averaging over a spatial-frequency ensemble of the field $U\left(\mathbf{r}\right)$, and the asterisk stands for complex conjugate. Here, r is the two-dimensional position vector in the source plane.

To model a variety of partially coherent vortex beams, we consider isotropic Schell-model sources with a definite topological charge, of the form

$W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)=U_l^{*}\left({\mathbf{r}}_1\right)U_l\left({\mathbf{r}}_2\right){\mu }_0\left(\left|{\mathbf{r}}_1-{\mathbf{r}}_2\right|\right),(2)$

with

$U_l\left(\mathbf{r}\right)=C_l{r}^{\left|l\right|}\exp \left(il\phi \right)\exp \left(-\frac{r^2}{w^2}\right)(3)$

representing the normalized Laguerre–Gauss mode of radial order 0 and azimuthal order l, and

$C_l=\sqrt{\frac{2}{\pi w^2\left|l\right|!}}{\left(\frac{\sqrt{2}}{w}\right)}^{\left|l\right|},(4)$

where $\mathbf{r}=\left(r,\phi \right)$, ${\mu }_0\left(\left|{\mathbf{r}}_1-{\mathbf{r}}_2\right|\right)$ is the source spectral degree of coherence, w is the initial beam width, and l is the topological charge.

The CSD function of the PCV beam after propagating in atmospheric turbulence can be calculated with the extended Collins integral [32].

$W\left({\mathbf{\rho }}_1,{\mathbf{\rho }}_2,z\right)=\frac{1}{{\left(\lambda z\right)}^2}\int \int W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)\exp \left\{-\frac{ik}{2z}\left[{\left({\mathbf{r}}_1-{\mathbf{\rho }}_1\right)}^2-{\left({\mathbf{r}}_2-{\mathbf{\rho }}_2\right)}^2\right]\right\}\langle \exp \left[\psi \left({\mathbf{\rho }}_1,{\mathbf{r}}_1,z,\omega \right)+{\psi }^{*}\left({\mathbf{\rho }}_2,{\mathbf{r}}_2,z,\omega \right)\right]\rangle d^2{r}_1{d}^2{r}_2,(5)$

where ${\mathbf{\rho }}_1$ and ${\mathbf{\rho }}_2$ denote the coordinates of two arbitrary points at the receiver plane, $k=2\pi /\lambda$ is the wave number of light with $\lambda$ being the wavelength. The angle brackets $<>$ represent an average over an ensemble of turbulence states, which can be expressed as [33]

$\begin{array}{l}\langle \exp \left[{\psi }^{*}\left({\mathbf{r}}_{01},{\mathbf{r}}_1,z\right)+\psi \left({\mathbf{r}}_{02},{\mathbf{r}}_2,z\right)\right]\rangle \\ =\exp \left\{-\frac{{\pi }^2{k}^{2}Tz}{3}\left[{\left({\mathbf{r}}_{01}-{\mathbf{r}}_{02}\right)}^2+\left({\mathbf{r}}_{01}-{\mathbf{r}}_{02}\right)\cdot \left({\mathbf{r}}_1-{\mathbf{r}}_2\right)+{\left({\mathbf{r}}_1-{\mathbf{r}}_2\right)}^2\right]\right\},\\ \end{array}(6)$

where

$T={\int }_0^{\infty }{\kappa }^3{\mathrm{\Phi }}_n\left(\kappa \right)d\kappa .(7)$

Here, $T$ is the quantity denoting the effect of turbulence, ${\Phi }_n\left(\kappa \right)$ is the one-dimensional power spectrum of the refractive-index fluctuations of the turbulent medium, and $\kappa$ is the spatial frequency.

If turbulence is governed by non-Kolmogorov statistics and the power spectrum ${\Phi }_n\left(\kappa \right)$ has the van Karman form, in which slope 11/3 is generalized to an arbitrary parameter $\alpha$ [34], i.e.,

${\mathrm{\Phi }}_n\left(\kappa \right)=A\left(\alpha \right){\stackrel{\sim }{C}}_n^2\frac{\exp \left(-{\kappa }^2/{\kappa }_m^2\right)}{{\left({\kappa }^2+{\kappa }_0^2\right)}^{\alpha /2}},0\le \kappa <\infty ,3<\alpha <4,(8)$

with

${\kappa }_0=2\pi /L_0,(9)$

${\kappa }_m=c\left(\alpha \right)/l_0,(10)$

$c\left(\alpha \right)={\left[\frac{2\pi }{3}A\left(\alpha \right)\Gamma \left(5-\frac{\alpha }{2}\right)\right]}^{1/\left(\alpha -5\right)},(11)$

$A\left(\alpha \right)=\frac{1}{4{\pi }^2}\cos \left(\frac{\alpha \pi }{2}\right)\Gamma \left(\alpha -1\right),(12)$

where $L_0$ and $l_0$ are the outer and inner scales of the turbulence, respectively; $\alpha$ is the power law exponent; ${\stackrel{\sim }{C}}_n^2$ is a generalized refractive-index structure parameter with units ${\mathrm{m}}^{3-\alpha }$, and $\Gamma \left(.\right)$ is the gamma function. For the power spectrum in Eq. 7, $T$ can be expressed as

$T=\frac{A\left(\alpha \right)}{2\left(\alpha -2\right)}{\stackrel{\sim }{C}}_n^2\left[\beta {\kappa }_m^{2-\alpha }\exp \left({\kappa }_0^2/{\kappa }_m^2\right)\Gamma \left(2-\alpha /2,{\kappa }_0^2/{\kappa }_m^2\right)-2{\kappa }_0^{4-\alpha }\right],3<\alpha <4,(13)$

where $\beta =2{\kappa }_0^2-2{\kappa }_m^2+\alpha {\kappa }_m^2$, $\Gamma \left(.\right)$ is the incomplete Gamma function. For the case of $\alpha$ = 11/3, the power spectrum ${\Phi }_n\left(\kappa \right)$ reduces to the van Karman spectrum with Kolmogorov statistics, and Eq. 6 can be expressed as

$\begin{array}{l}\langle \exp \left[\psi \left({\mathbf{\rho }}_1,{\mathbf{r}}_1,z,\omega \right)+{\psi }^{*}\left({\mathbf{\rho }}_2,{\mathbf{r}}_2,z,\omega \right)\right]\rangle \\ =\exp \left[-\frac{{\left({\mathbf{\rho }}_1-{\mathbf{\rho }}_2\right)}^2+\left({\mathbf{\rho }}_1-{\mathbf{\rho }}_2\right)·\left({\mathbf{r}}_1-{\mathbf{r}}_2\right)+{\left({\mathbf{r}}_1-{\mathbf{r}}_2\right)}^2}{{\rho }_0^2}\right],\end{array}(14)$

where ${\rho }_0={\left(0.545C_n^2{k}^{2}z\right)}^{-3/5}$ is the coherence length of a spherical wave propagating through the turbulent medium.

In the modeling of a partially coherent vortex beam, we begin with a planar, secondary Gaussian Schell-model vortex (GSMV) source, with a source spectral degree of coherence of the form

${\mu }_0\left(\left|{\mathbf{r}}_1-{\mathbf{r}}_2\right|\right)=\exp \left[-\frac{{\left|{\mathbf{r}}_1-{\mathbf{r}}_2\right|}^2}{{\delta }^2}\right],(15)$

where $\delta$ is the coherence width. Substituting Eqs. 2, 14, 15 into Eq. 5, the cross-spectral density function of the GSMV beam with l = 1 in the plane z can be derived analytically. The result is given by the expression

$\begin{array}{l}W\left({\mathbf{\rho }}_1,{\mathbf{\rho }}_2,z\right)=\frac{{\left|C\right|}^2}{{\left(\lambda z\right)}^2}\frac{{\pi }^2}{4A_2^2{M}^2}\exp \left[-\frac{ik}{2z}\left({\rho }_1^2-{\rho }_2^2\right)-\frac{1}{{\rho }_0^2}{\left({\mathbf{\rho }}_1-{\mathbf{\rho }}_2\right)}^2\right]\times \exp \left\{\frac{1}{4A_2}{\left(\frac{{\mathbf{\rho }}_1-{\mathbf{\rho }}_2}{{\rho }_0^2}-\frac{ik{\mathbf{\rho }}_2}{z}\right)}^2+\frac{1}{4M}{\left[\left(\frac{{\mathbf{\rho }}_1-{\mathbf{\rho }}_2}{{\rho }_0^2}-\frac{ik{\mathbf{\rho }}_1}{z}\right)-\frac{A_3}{2A_2}\left(\frac{{\mathbf{\rho }}_1-{\mathbf{\rho }}_2}{{\rho }_0^2}-\frac{ik{\mathbf{\rho }}_2}{z}\right)\right]}^2\right\}\\ \times \left\{2A_3+\frac{A_3}{2M}{\left[\left(\frac{{\mathbf{\rho }}_1-{\mathbf{\rho }}_2}{{\rho }_0^2}-\frac{ik{\mathbf{\rho }}_1}{z}\right)-\frac{A_3}{2A_2}\left(\frac{{\mathbf{\rho }}_1-{\mathbf{\rho }}_2}{{\rho }_0^2}-\frac{ik{\mathbf{\rho }}_2}{z}\right)\right]}^2+\frac{A_3}{2A_2}{\left(\frac{{\mathbf{\rho }}_1-{\mathbf{\rho }}_2}{{\rho }_0^2}-\frac{ik{\mathbf{\rho }}_2}{z}\right)}^2\right.-\left[\frac{{\left({\mathbf{\rho }}_1-{\mathbf{\rho }}_2\right)}^2}{{\rho }_0^4}-\frac{ik\left({\rho }_1^2-{\rho }_2^2\right)}{{\rho }_0^{2}z}-\frac{k^2{\mathbf{\rho }}_1\cdot {\mathbf{\rho }}_2}{z^2}\right]\left.+\frac{ik}{z^2}\mathbf{k}\cdot \left({\mathbf{\rho }}_1\times {\mathbf{\rho }}_2\right)\right\},\end{array}(16)$

with

$\begin{array}{l}{A}_1=\frac{1}{w^2}+\frac{1}{{\delta }^2}+\frac{1}{{\rho }_0^2}+\frac{ik}{2z},\\ A_2=\frac{1}{w^2}+\frac{1}{{\delta }^2}+\frac{1}{{\rho }_0^2}-\frac{ik}{2z},\\ A_3=\frac{2}{{\rho }_0^2}+\frac{2}{{\delta }^2},\\ M=A_1-\frac{A_3^2}{4A_2}.\end{array}.(17)$

For a paraxial scalar PCV beam, the average OAM flux density can be shown to be related to the CSD function by the expression [25]

$L_d\left(\mathbf{r}\right)=-\frac{{\epsilon }_0}{k}\mathrm{I}\mathrm{m}{\left[\left(y_1{\partial }_{x_2}-x_1{\partial }_{y_2}\right)W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)\right]}_{{\mathbf{r}}_1={\mathbf{r}}_2},(18)$

where ${\epsilon }_0$ is the free-space permittivity, ${\partial }_{x_2}$ and ${\partial }_{y_2}$ represent partial derivatives with respect to $x_2$ and $y_2$, respectively. It is to be noted that the OAM flux density at a point depends not only on the strength of rotation at the point, but also on the local intensity. To better understand the physics of the OAM distribution, we may consider a normalized OAM flux density $l_d$, which represents the average OAM flux density per photon,

$l_d=\frac{\mathit{\hslash }\omega L_d\left(\mathbf{r}\right)}{S\left(\mathbf{r}\right)},(19)$

where $S\left(\mathbf{r}\right)=\frac{k}{{\mu }_0\omega }W\left(\mathbf{r},\mathbf{r}\right)$ is the z-component of the Poynting vector. The total OAM per photon can be given by the ratio of integrated $L_d\left(r\right)$ and $S\left(r\right)$,

$l_t=\frac{\mathit{\hslash }\omega \int L_d\left(\mathbf{r}\right)d^{2}r}{\int S\left(\mathbf{r}\right)d^{2}r}.(20)$

The total OAM $l_t$ is conserved on propagation, while the distribution of OAM flux density may change during propagation. These changes will be a combination of correlation-induced OAM changes and turbulence-induced OAM changes. Substituting Eq. 16 into Eq. 18, one finds that the average OAM flux density of a GSMV beam is given by the expression

$L_d\left(\mathbf{\rho }\right)=\mathrm{I}\mathrm{m}\langle \frac{i{\epsilon }_0{\left|C\right|}^2{\pi }^{2}k{\rho }^2}{4A_2^2{M}^2{\lambda }^2{z}^4}\exp \left\{-\frac{k^2{\rho }^2}{4z^2}\left[\frac{1}{A_2}+\frac{1}{M}\left(1+\frac{A_3^2}{4A_2^2}-\frac{A_3}{A_2}\right)\right]\right\}\rangle .(21)$

With the help of Eqs. 19, 21, we can calculate the distribution of normalized OAM flux density $l_d$ for the GSMV beam propagating in atmospheric turbulence.

To illustrate the possible effects of atmospheric turbulence on the distribution of the OAM flux density of PCV beams with different spatial coherence states, we will involve multi-Gaussian Schell-model vortex (MGSMV) source, for which the source spectral degree of coherence has the form

${\mu }_0\left(\left|{\mathbf{r}}_1-{\mathbf{r}}_2\right|\right)=\frac{1}{C_0}{\displaystyle \sum }_{m=1}^M\frac{{\left(-1\right)}^{m-1}{\left(M\right)}_m}{mm!}\exp \left[-\frac{{\left|{\mathbf{r}}_1-{\mathbf{r}}_2\right|}^2}{{\delta }_m^2}\right],(22)$

where

$C_0={\displaystyle \sum }_{m=1}^M\frac{{\left(-1\right)}^{m-1}{\left(M\right)}_m}{mm!},(23)$

${\left(M\right)}_m=M\left(M-1\right)\cdot \cdot \cdot \left(M-m+1\right).(24)$

Here, $C_0$ is the normalization factor, ${\left(M\right)}_m$ is the Pochhammer symbol (falling factorial) [35], and ${\delta }_m=\sqrt{m}\delta$ are the coherence widths of the constituent Gaussian functions. In the far field, the MGSMV beams with $M>1$ represent flat-topped profiles [36], and the MGSMV beams with $M<1$ represent cusped profiles [37]. For $M=1$, the MGSMV source reduces to the traditional GSMV source in Eq. 15.

We will also consider a source that is the incoherent superposition of GSMV beams with equal and opposite topological charges but different coherence width ${\delta }_n$, for which the CSD function has the form

$W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)={\displaystyle \sum }_{n=+l,-l}{U}_n^{*}\left({\mathbf{r}}_1\right)U_n\left({\mathbf{r}}_2\right)\exp \left[-\frac{{\left|{\mathbf{r}}_1-{\mathbf{r}}_2\right|}^2}{{\delta }_n^2}\right].(25)$

This source has a net zero OAM flux density but will exhibit OAM flux density changes on propagation due to the different correlation widths of the different OAM modes, even in free space [29].

With the help of Eqs. 16, 19, 21, the normalized OAM flux density $l_d$ of MGSMV beams and the incoherent superposition of GSMV beams can be constructed by superposition of the solutions of GSMV beams with different coherence widths $\delta$.

Results

To show the effect of atmospheric turbulence on the evolution of OAM of PCV beams on propagation, we calculate the normalized OAM flux density $l_d$ of GSMV beams, MGSMV beams and the incoherent superposition of GSMV beams, respectively. The distribution of spectral density is also given for comparison.

Figure 1 shows the evolution of the normalized OAM flux density $l_d$ of GSMV beams in atmospheric turbulence, for different propagation distances $z$. We take $w=10\mathrm{m}\mathrm{m}$ and $\lambda =632.8\mathrm{n}\mathrm{m}$ for the remainder of the paper. It can be seen from Figure 1A that over a short propagation distance $z=1\mathrm{k}\mathrm{m}$, the difference between the OAM distribution near the core for $C_n^2=0$ and $C_n^2={10}^{-13}{\mathrm{m}}^{-2/3}$ is small, which is similar with that of the spectral density in Figure 1D, and with the increase of propagation distance the difference becomes larger. However, in the outskirts, even at small propagation distance$z=1\mathrm{k}\mathrm{m}$, the difference between the OAM distribution is obvious, which indicates that the OAM in the outskirts is more affected by atmospheric turbulence than that near the core. This results in an interesting phenomenon that the OAM flux density is larger in atmospheric turbulence than in free space for shorter propagation distances but becomes smaller at longer distances.

FIGURE 1

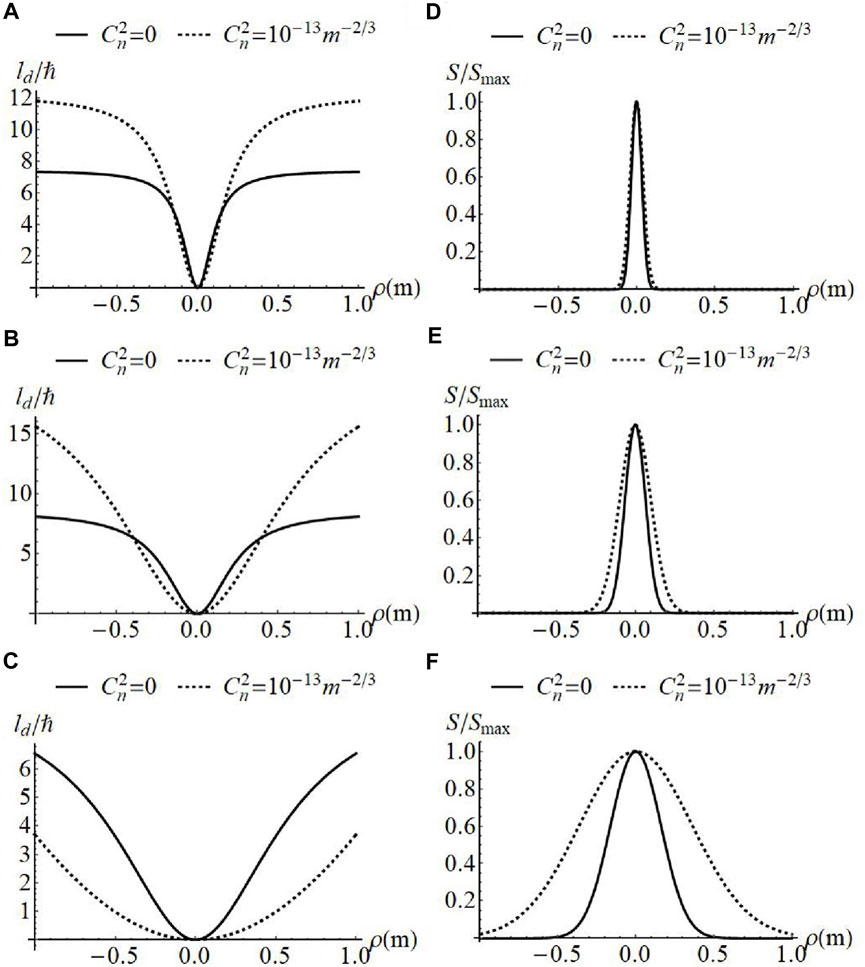
FIGURE 1. Normalized OAM flux density (A–C) and spectral density (D–F) of GSMV beams with w = 10 mm, $\delta =5\text{mm}$, at z = 1 km (A,D), z = 2 km (B,E), and z = 5 km (C,F).

Figures 2, 3 show the evolution of OAM in atmospheric turbulence for $M>1$ and$M<1$, respectively. It can be seen that the distribution of OAM in free space mimics that of the spectral density of the respective beams: the beam ($M=15$) with a flat-topped spectral density results in a flat-bottomed “dead zone” in the OAM, and the beam ($M=1/15$) with a cusped spectral density results in a cusped OAM distribution near the core. As the propagation distance in atmospheric turbulence is increased, the flat-topped spectral density degenerates to a Gaussian profile (see also [38]), while it is interesting to find that the “dead zone” of OAM in the core can be maintained, within which there is no circulation. For the cusped OAM distribution in atmospheric turbulence, with the increase of propagation distance, it disappears as does the cusped spectral density distribution (see also [37]).

FIGURE 2

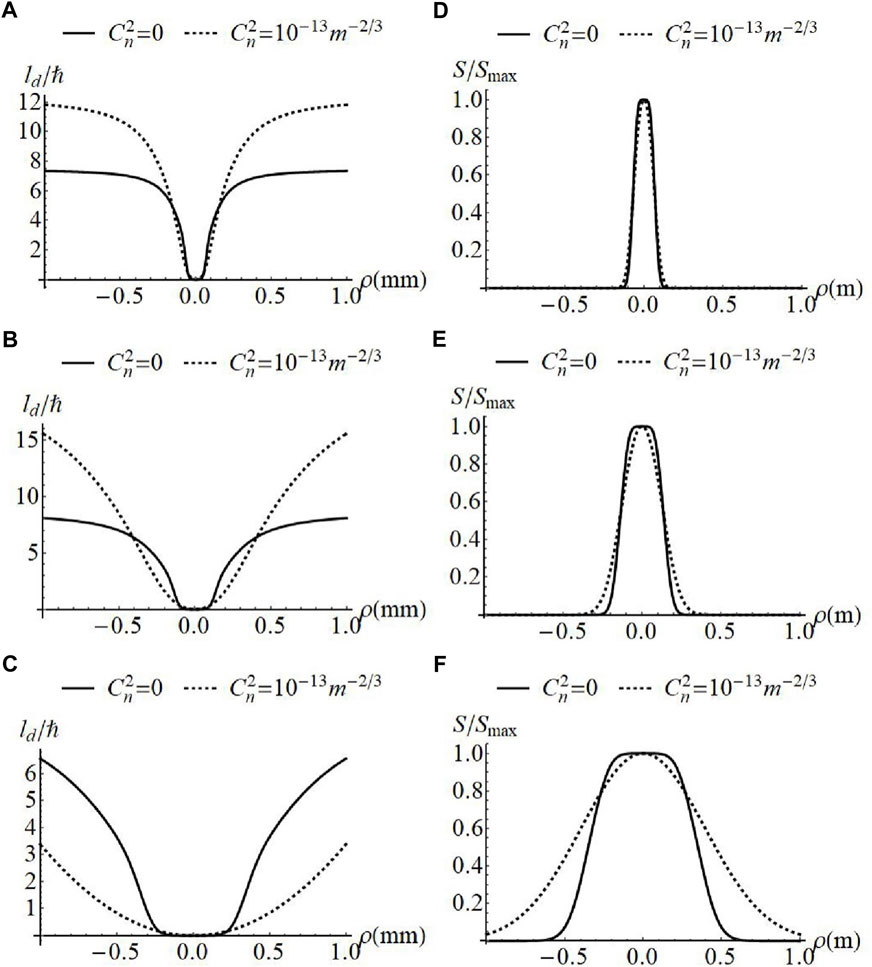
FIGURE 2. Normalized OAM flux density (A–C) and spectral density (D–F) of MGSMV beams with $M=15$, w = 10 mm, $\delta =5\text{mm}$, at z = 1 km (A,D), z = 2 km (B,E), and z = 5 km (C,F).

FIGURE 3

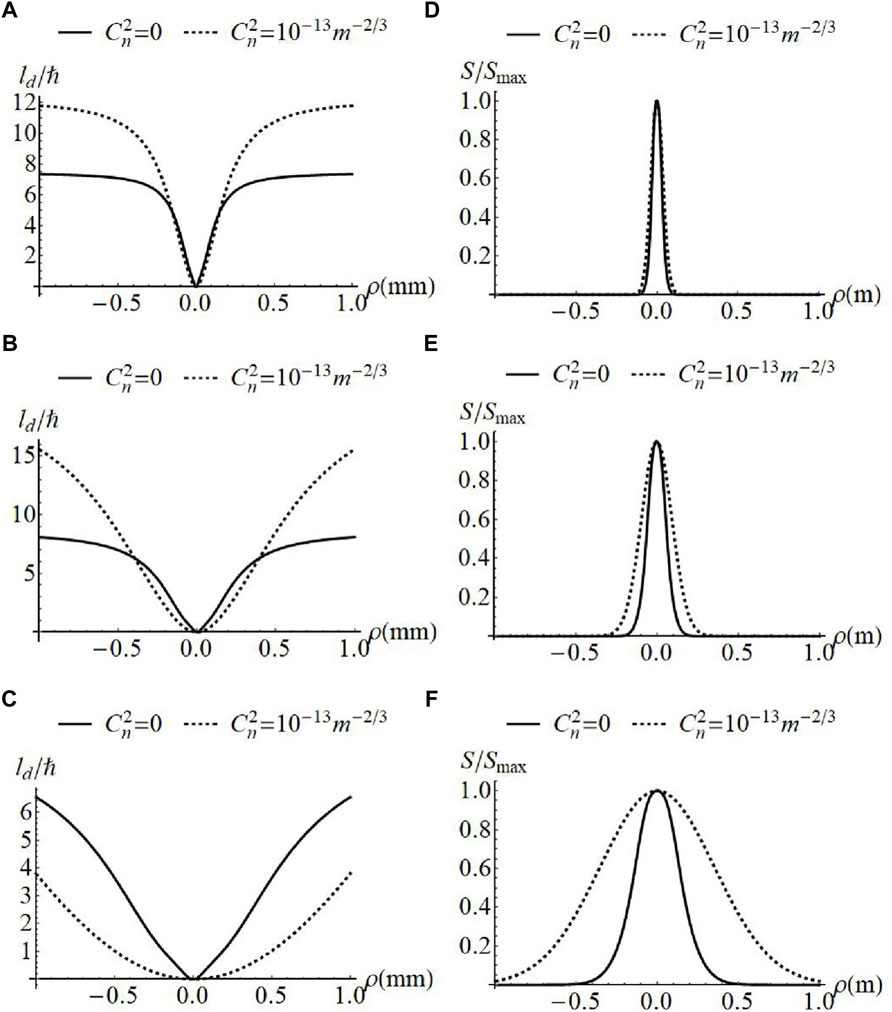
FIGURE 3. Normalized OAM flux density (A–C) and spectral density (D–F) of MGSMV beams with $M=1/15$, w = 10 mm, $\delta =5\text{mm}$, at z = 1 km (A,D), z = 2 km (B,E), and z = 5 km (C,F).

Even more significant variations in the distribution of OAM can be made by the incoherent superposition of GSMV beams with equal and opposite topological charge. We label the positive contribution by the subscript “+” and the negative contribution by the subscript “-”. Figures 4, 5 give the evolution of OAM with the fixed correlation width of the positive vortex beam ${\delta }_{+}=5\text{mm}$, and width ${\delta }_{-}=10\text{mm}$ and ${\delta }_{-}=2.5\text{mm}$ for the negative vortex beam, respectively. Counter-rotating regions of OAM flux density are created due to the different local densities of the modes with different correlation widths, creating, for example, in Figure 4 a beam core with a negative flux density and an outer region with a positive flux density.

FIGURE 4

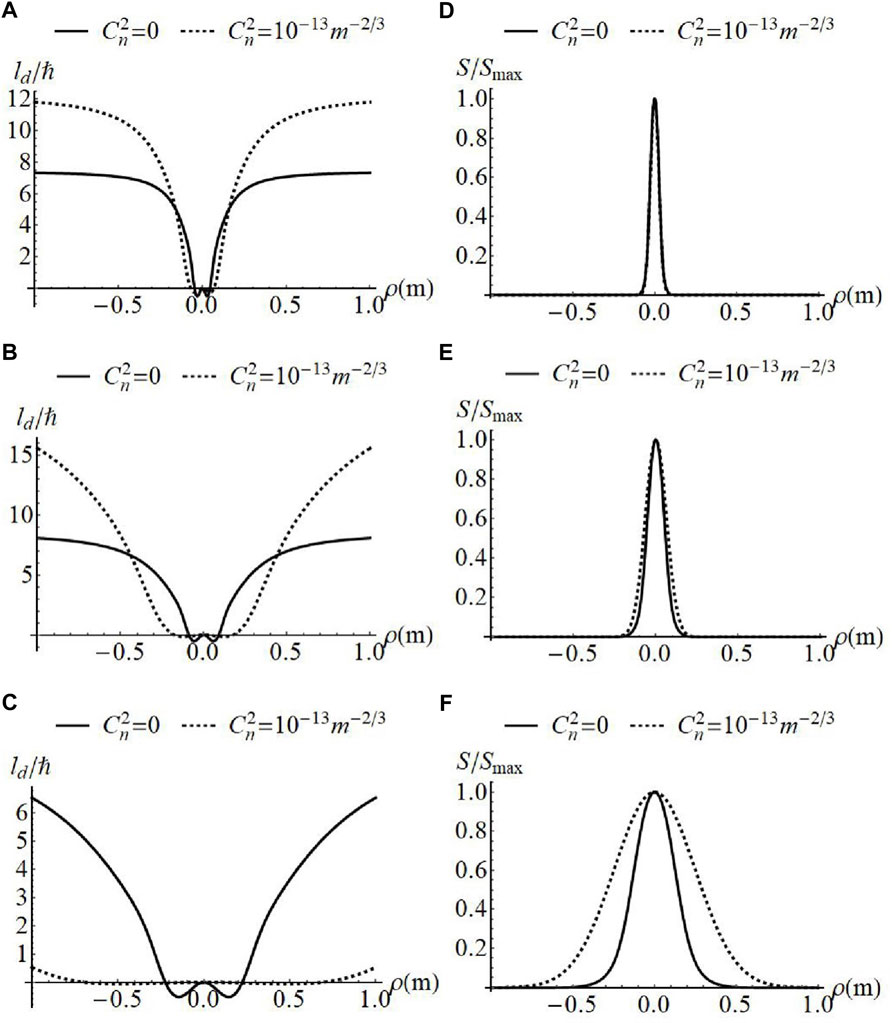
FIGURE 4. Normalized OAM flux density (A–C) and spectral density (D–F) of superposed GSMV beams with w = 10 mm, ${\delta }_{+}=5\text{mm}$, ${\delta }_{-}=10\text{mm}$, at z = 1 km (A,D), z = 2 km (B,E), and z = 5 km (C,F).

FIGURE 5

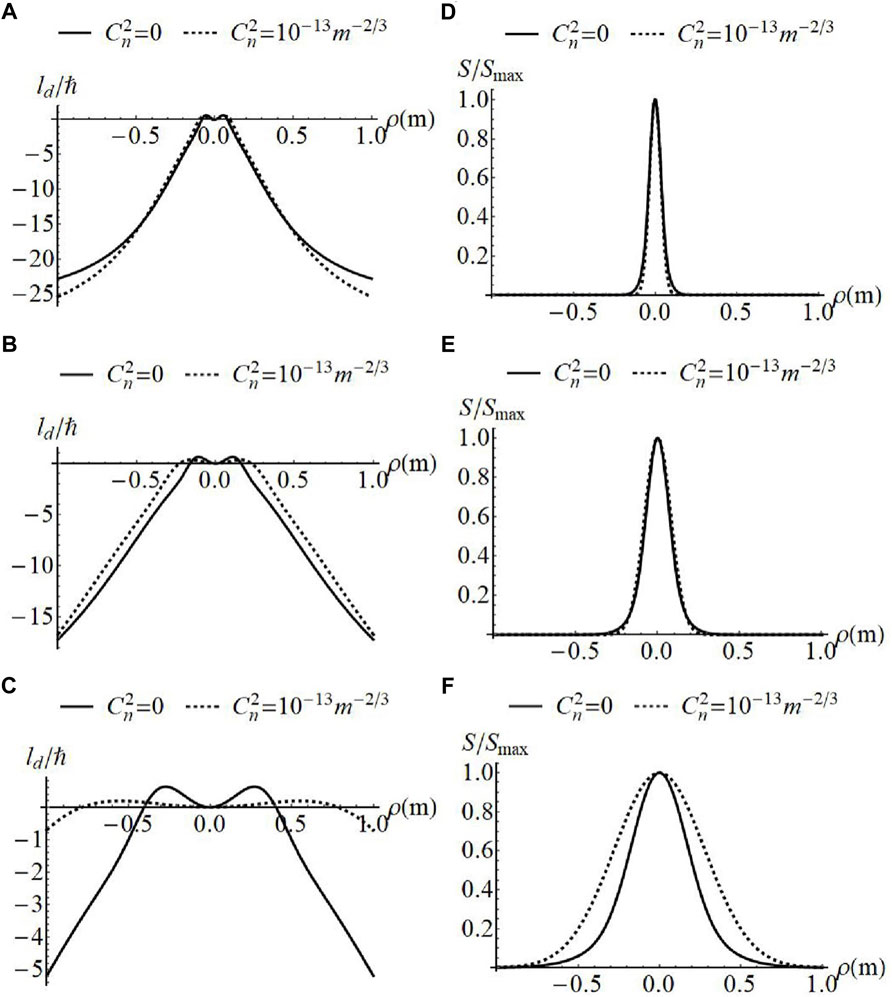
FIGURE 5. Normalized OAM flux density (A–C) and spectral density (D–F) of superposed GSMV beams with w = 10 mm, ${\delta }_{+}=5\text{mm}{\delta }_{-}=2.5\text{mm}$, at z = 1 km (A,D), z = 2 km (B,E), and z = 5 km (C,F).

It can be seen from the figures that this non-trivial counter-rotating structure can be maintained on propagation in atmospheric turbulence, even though the OAM $l_t=0$ and the normalized OAM flux density $l_d=0$ in the source plane. It can also be seen that the distribution of OAM is affected more than the corresponding spectral density.

In comparing Figures 4, 5, it can be seen that the OAM distribution for ${\delta }_{-}=10\text{mm}$ is affected more than that for ${\delta }_{-}=2.5\text{mm}$. This may be explained by the effective turbulence resistance of lower coherence beams: a beam with lower coherence spreads faster, and therefore turbulence-induced beam spreading is less noticeable. For the constituent GSMV beam with larger coherence width and negative topological charge (${\delta }_{-}=10\text{mm}$), the negative part of the counter-rotating OAM distribution becomes a region which is similar to a “dead zone” as the propagation distance in turbulence increases.

Discussion

In summary, we have studied the evolution of the OAM density flux in atmospheric turbulence for PCV beams with different coherence structures, i.e., GSMV beams, MGSMV beams, and the incoherent superposition of GSMV beams. The analytical expression of the average OAM flux density in atmospheric turbulence is derived, with which we illustrate the changes of OAM distribution on propagation. The results show that after propagating in atmospheric turbulence, the OAM distribution of PCV beams exhibits rich behavior. It is found that the OAM distribution in the outskirts is more affected by atmospheric turbulence than that near the core, which results in an interesting phenomenon that the OAM flux density is larger in atmospheric turbulence than that in free space for shorter propagation distances but becomes smaller at longer distances. Especially, for the MGSMV beams with $M>1$, the “dead zone” of OAM in the core can be maintained for long propagation distance. For the incoherent superposition of GSMV beams, the non-trivial counter-rotating structure can be maintained on propagation in atmospheric turbulence, even though the OAM $l_t=0$ and the normalized OAM flux density $l_d=0$ in the source plane. Meanwhile, for the constituent GSMV beam with large coherence width and negative topological charge, with the increase of propagation distance in atmospheric turbulence, the negative part of the counter-rotating OAM distribution becomes a region which is similar as the “dead zone”. Our findings may be useful in the application of free-space OAM communication in the presence of atmospheric turbulence.

We have illustrated the possible OAM changes in air turbulence only for a very small portion of partially coherent beams; an entirely different behavior may be expected for non-Schell model beams, e.g., non-uniformly correlated, twisted beams or radially accelerating random beams. The calculation of the OAM flux is far from trivial even for general Schell-model beams, even in free space [39], and hence, better methods need to be developed for comprehensive analysis of the OAM flux density of beams with arbitrary coherence states, for propagation in both free space and turbulent media.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the study and approved it for publication.

Funding

The authors thank the National Natural Science Foundation of China (12174173, 12004218), the Fujian Provincial Natural Science Foundation of China (2022J02047), and the Shandong Provincial Natural Science Foundation of China (ZR2020QA067). GG was supported by the Air Force Office of Scientific Research (FA9550-21-1-0171) and Office of Naval Research (MURI N00014-20-1-2558). OK was supported by the Cooper Fellowship of the University of Miami.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Soskin MS, Vasnetsov MV. Singular optics. Prog Opt (2001) 42:219–76. doi:10.1016/s0079-6638(01)80018-4

CrossRef Full Text | Google Scholar

2. Dennis MR, O’Holleran K, Padgett MJ. Singular optics: Optical vortices and polarization singularities. Prog Opt (2009) 53:293–363.

CrossRef Full Text | Google Scholar

3. Gbur G. Singular optics. Boca Raton, FL: CRC Press (2017). p. 545.

Google Scholar

4. Lee JH, Foo G, Johnson EG, Swartzlander GA. Experimental verification of an optical vortex coronagraph. Phys Rev Lett (2006) 97:053901. doi:10.1103/physrevlett.97.053901

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Palacios D, Rozas D, Swartzlander GA. Observed scattering into a dark optical vortex core. Phys Rev Lett (2002) 88:103902. doi:10.1103/physrevlett.88.103902

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Gibson G, Courtial J, Padgett MJ, Vasnetsov M, Pas’ko V, Barnett SM, et al. Free-space information transfer using light beams carrying orbital angular momentum. Opt Express (2004) 12:5448–56. doi:10.1364/opex.12.005448

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/physreva.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Grier DG. A revolution in optical manipulation. Nature (2003) 424:810–6. doi:10.1038/nature01935

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Simpson NB, Dholakia K, Allen L, Padgett MJ. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner. Opt Lett (1997) 22:52–4. doi:10.1364/ol.22.000052

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Ladavac K, Grier DG. Microoptomechanical pumps assembled and driven by holographic optical vortex arrays. Opt Express (2004) 12:1144–9. doi:10.1364/opex.12.001144

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Ritsch-Marte M. Orbital angular momentum light in microscopy. Phil Trans R Soc A (2017) 375:20150437. doi:10.1098/rsta.2015.0437

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Ruffato G, Rossi R, Massari M, Mafakheri E, Capaldo P, Romanato F. Design, fabrication and characterization of Computer Generated Holograms for anti-counterfeiting applications using OAM beams as light decoders. Sci Rep (2017) 7:18011. doi:10.1038/s41598-017-18147-7

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Erhard M, Fickler R, Krenn M, Zeilinger A. Twisted photons: New quantum perspectives in high dimensions. Light Sci Appl (2018) 7:17146. doi:10.1038/lsa.2017.146

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang L, Ma J, Xiao M, Zhang Y. Application of optical orbital angular momentum to rotation measurements. Results Opt (2021) 5:100158. doi:10.1016/j.rio.2021.100158

CrossRef Full Text | Google Scholar

15. Ricklin JC, Davidson FM. Atmospheric turbulence effects on a partially coherent Gaussian beam: Implications for free-space laser communication. J Opt Soc Am A (2002) 19:1794–802. doi:10.1364/josaa.19.001794

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Zhao C, Cai Y, Lu X, Eyyuboğlu HT. Radiation force of coherent and partially coherent flat-topped beams on a Rayleigh particle. Opt Express (2009) 17:1753–65. doi:10.1364/oe.17.001753

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Zhang J, Wang Z, Cheng B, Wang Q, Wu B, Shen X, et al. Atom cooling by partially spatially coherent lasers. Phys Rev A (2013) 88:023416. doi:10.1103/physreva.88.023416

CrossRef Full Text | Google Scholar

18. Schouten HF, Gbur G, Visser TD, Wolf E. Phase singularities of the coherence functions in Young’s interference pattern. Opt Lett (2003) 28:968–70. doi:10.1364/ol.28.000968

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Gbur G, Visser TD. Coherence vortices in partially coherent beams. Opt Commun (2003) 222:117–25. doi:10.1016/s0030-4018(03)01606-7

CrossRef Full Text | Google Scholar

20. Gbur G, Visser TD, Wolf E. ‘hidden’ singularities in partially coherent wavefields. J Opt A: Pure Appl Opt (2004) 6:S239–42. doi:10.1088/1464-4258/6/5/017

CrossRef Full Text | Google Scholar

21. Wang W, Takeda M. Coherence current, coherence vortex, and the conservation law of coherence. Phys Rev Lett (2006) 96:223904. doi:10.1103/physrevlett.96.223904

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Raghunathan SB, Schouten HF, Visser TD. Correlation singularities in partially coherent electromagnetic beams. Opt Lett (2012) 37:4179–81. doi:10.1364/ol.37.004179

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Stahl CSD, Gbur G. Complete representation of a correlation singularity in a partially coherent beam. Opt Lett (2014) 39:5985–8. doi:10.1364/ol.39.005985

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Palacios DM, Maleev ID, Marathay AS, Swartzlander GA. Spatial correlation singularity of a vortex field. Phys Rev Lett (2004) 92:143905. doi:10.1103/physrevlett.92.143905

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Kim SM, Gbur G. Angular momentum conservation in partially coherent wave fields. Phys Rev A (2012) 86:043814. doi:10.1103/physreva.86.043814

CrossRef Full Text | Google Scholar

26. Gbur G. Partially coherent vortex beams (Invited). Proc SPIE (2018) 10549:1054903.

Google Scholar

27. Stahl CSD, Gbur G. Partially coherent vortex beams of arbitrary order. J Opt Soc Am A (2017) 34:1793–9. doi:10.1364/josaa.34.001793

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zhang Y, Cai Y, Gbur G. Control of orbital angular momentum with partially coherent vortex beams. Opt Lett (2019) 44:3617–20. doi:10.1364/ol.44.003617

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Zhang Y, Korotkova O, Cai Y, Gbur G. Correlation-induced orbital angular momentum changes. Phys Rev A (2020) 102:063513. doi:10.1103/physreva.102.063513

CrossRef Full Text | Google Scholar

30. Korotkova O. Theoretical statistical optics. London: World Scientific (2021). p. 280.

Google Scholar

31. Wolf E. Introduction to the theory of coherence and polarization of light. New York: Cambridge University Press (2007). p. 222.

Google Scholar

32. Andrews LC, Phillips RL. Laser beam propagation through random media. Bellingham, Washington: SPIE Press (1998). p. 775.

Google Scholar

33. Shirai T, Dogariu A, Wolf E. Mode analysis of spreading of partially coherent beams propagating through atmospheric turbulence. J Opt Soc Am A (2003) 20:1094–102. doi:10.1364/josaa.20.001094

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Shchepakina E, Korotkova O. Second-order statistics of stochastic electromagnetic beams propagating through non-Kolmogorov turbulence. Opt Express (2010) 18:10650–8. doi:10.1364/oe.18.010650

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Korotkova O, Hyde I. Multi-Gaussian random variables for modeling optical phenomena. Opt Express (2021) 29:25771–99. doi:10.1364/oe.432227

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Sahin S, Korotkova O. Light sources generating far fields with tunable flat profiles. Opt Lett (2012) 37:2970–2. doi:10.1364/ol.37.002970

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Wang F, Korotkova O. Circularly symmetric cusped random beams in free space and atmospheric turbulence. Opt Express (2017) 25:5057. doi:10.1364/oe.25.005057

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Korotkova O, Sahin S, Shchepakina E. Multi-Gaussian schell-model beams. J Opt Soc Am A (2012) 29:2159–64. doi:10.1364/josaa.29.002159

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Wang H, Yang Z, Liu L, Chen Y, Wang F, Cai Y. Fast calculation of orbital angular momentum flux density of partially coherent Schell-model beams on propagation. Opt Express (2022) 30:16856–72. doi:10.1364/oe.459089

PubMed Abstract | CrossRef Full Text | Google Scholar