- 1Department of Psychology, Faculty of Psychology and Education, Ludwig Maximilian University of Munich, Munich, Germany
- 2Department of Humanities, Political and Social Sciences, ETH Zurich, Zurich, Switzerland
Introduction: Whereas it is commonly assumed that in learning science, representational competence is a critical prerequisite for the acquisition of conceptual knowledge, comprehensive psychometric investigations of this assumption are rare. We undertake a step in this direction by re-analyzing the data from a recent study that found a substantial correlation between the two constructs in undergraduates in the context of field representations and electromagnetism.
Methods: In this pre-registered contribution, we re-analyzed the data (N = 515 undergraduate students; Mage = 21.81, SDage = 4.04) to examine whether the relation between representational competence and conceptual knowledge, both measured with psychometrically validated test instruments, is similar or varies between four samples from two countries. To this end, we employed correlational analysis and scatter plots. Employing these methods, we examined whether a positive relation between representational competence and conceptual knowledge can be found and is of similar magnitude in all samples. We also employed multiple-group latent profile analysis to examine how the more detailed association between the two constructs varies or is similar across samples.
Results: We found that the relation between the two constructs was positive in all four samples, but was stronger in the samples consisting primarily of engineering and physics students than in environmental sciences and teacher education-students. All latent profiles indicated that high representational competence is a prerequisite for high conceptual knowledge, but not vice versa. We found little relation to learners’ gender and topic-specific learning opportunities in high school.
Discussion: These results indicate that the qualitative findings of a positive relation between representational competence and conceptual knowledge, with no evidence of learners that achieve high conceptual knowledge with low representational competence, generalize across different populations. We derive hypotheses for further moderating factors that can be examined in future research.
1 Introduction
In science education, learners must combine information from multiple external representations such as charts, texts, formulae, or graphs to acquire knowledge (Treagust et al., 2017). The underlying ability to interpret and translate between different representations of scientific concepts, which is referred to as representational competence (Kozma and Russell, 2005), is accordingly commonly portrayed as a critical prerequisite for developing conceptual knowledge in science (Ainsworth, 2008; Corradi et al., 2012). At least three presumed processes link different aspects of representational competence to conceptual knowledge acquisition. First, competence regarding a specific mode of representation (e.g., table, graph, or concrete representation) supports grasping how the different elements of a scientific concept interrelate (e.g., the different parts of a molecule; Stieff et al., 2016). Second, understanding how different representations translate into each other can help grasping the common underlying concept through comparing, contrasting, and self-explaining (Carolan et al., 2008). Third, representational competence supports problem solving, which in turn fosters conceptual understanding (Bowen and Bunce, 1997). Consequently, much research has examined how these two constructs interact during inquiry activities (e.g., Kohl et al., 2007; Nieminen et al., 2013; Scheid et al., 2019).
Recently, more targeted studies have tried to measure representational competence with elaborate psychometric instruments (Klein et al., 2017; Scheid et al., 2018). Klein et al. (2017) developed a two-tier instrument to assess representational competence in Kinematics, and Scheid et al. (2018) an open-answer instrument to assess representational competence in the topic of Ray Optics.
In the present study, we are concerned with the empirical relationship between representational competence and conceptual knowledge and, in particular, with the conditions that might influence the magnitude of this relationship. Although a strong positive relationship has been assumed by many researchers, it has been noted that the quantitative empirical evidence on this relationship is rather sparse and struggles with methodological issues (Chang, 2018; Edelsbrunner et al., 2023a). As Edelsbrunner et al. (2023b) note, instruments that have been used to measure these two constructs and their interrelations often have not been psychometrically validated, or suffer from contextual bias. Specifically, if instruments such as pen-and-paper tests that are assumed to measure the two constructs are both contextualized within the same topic (e.g., electromagnetism; Nieminen et al., 2013; Nitz et al., 2014; Scheid et al., 2019), then the common relation between the two constructs cannot be disentangled from such common topical context.
A recent study by Edelsbrunner et al. (2023b) tried to overcome these issues by using an assessment instrument for representational competence with field representations (such as vector-field plots and field lines) that does not employ an explicit topical context. Using this instrument, the authors investigated the relation between representational competence with fields and conceptual knowledge about electromagnetism in university undergraduates from Germany and Switzerland. Encompassing students from four different universities, the authors found a substantial positive relationship, with a Pearson correlation estimate of r = 0.54, p < 0.001. In addition, the authors found that in a scatter plot, there were almost no students with high conceptual knowledge but low representational competence, whereas there appeared to be more students with high representational competence but low conceptual knowledge. From these results, the authors inferred the hypothesis that representational competence is a necessary yet insufficient prerequisite for developing conceptual knowledge (Edelsbrunner et al., 2023b).
In the present study, we follow up on this hypothesis with an alternative model-based analytical approach. Specifically, whereas a scatter plot is an important and powerful visual tool, it does not prevent getting false impressions about patterns that might be driven by sampling error. Another reason for a model-based re-analysis is that the sample by Edelsbrunner et al. (2023b) encompassed four different student samples from different courses (teacher education, STEM and non-STEM study programs) at three different universities. The authors analyzed the students from all four samples within the same models, potentially hiding important information regarding the generalizability of their findings. The overall pattern might be unreliable if, for example, it is underlain by Simpson’s paradox (e.g., Kievit et al., 2013). This paradox describes situations in which, on the level of a whole population (i.e., the common population underlying all four samples by Edelsbrunner et al., 2023b), a pattern is visible that might actually not exist or even be reversed within the distinct sub-samples forming the larger population. More specific analyses on the level of sub-samples are needed to unravel the generalizability of the findings.
In the context of physics education, such sub-samples might be defined by variables such as gender, topic-specific learning opportunities in the classroom, or individual preferences for specific learning content that can be expected to affect learning in a number of ways. Regarding gender, females seem to perform worse than boys on tests of conceptual knowledge across various physics topics (e.g., Hofer et al., 2018; Madsen et al., 2013; OECD, 2009). Among the manifold explanations provided for this gender effect are missing female role models (e.g., Chen et al., 2020; Mullis et al., 2016) or underlying subject-specific gender differences in motivational-affective variables such as interest and self-concept (e.g., Jansen et al., 2014; Kang et al., 2019; Patall et al., 2018). Although, so far, we do not know much about gender differences in representational competence, female students seem to struggle more with visual graphical representations (e.g., Chan and Wong, 2019; Hegarty and Kriz, 2008; Tam et al., 2019) and different types of mathematical-graphical tasks (e.g., axis tasks; Lowrie and Diezmann, 2011) than male students do. Gender differences in spatial abilities (e.g., Reinhold et al., 2020) might at least in parts explain such findings (see Heo and Toomey, 2020). Concerning the relation between conceptual knowledge and representational competence, Nieminen et al. (2013) reported more problems on the part of female students to infer the same facts from tasks differing in the representational formal.
As regards topic-specific learning opportunities in the classroom, we can expect experiments to be especially effective in promoting understanding of fields and electromagnetism (see de Jong, 2019; National Research Council, 2012; Sandoval et al., 2014; Vilarta Rodriguez et al., 2020). In physics education, student experiments allow learners to observe physical phenomena and explore their dependence on physical quantities. An important tool helping students to acquire the physical concepts underlying observations are external representations. They can help students in acquiring knowledge by visualizing non-visible fundamentals and causes of the observed phenomena (Olympiou et al., 2013). Usually, external representations of physical concepts such as vector fields are presented before or after experimentation. Teachers provide students with explanations and visual-graphical models which represent aspects that cannot be directly observed. Such learning opportunities involving guided experimentation have proven successful in terms of conceptual understanding (Hardy et al., 2006; Van der Graaf et al., 2020). Whether students in the different samples did guided student experiments in the field of electromagnetism, whether they watched the teacher conduct such experiments or whether they did not have this learning opportunity at secondary school at all can hence be expected to influence students’ conceptual knowledge and representational competence as well as their relation.
Finally, sub-samples might be determined by systematic differences in individual preferences for specific learning content as reflected in the choice of a specific study program. There is evidence that interest and prior knowledge are substantially and linearly related (Tobias, 1994). In line with this finding, various studies have documented systematic differences on cognitive variables between students in specific study programs. Comparing (among others) physical sciences, math/computer science, engineering, humanities, and social sciences majors, Lubinski and Benbow (2006), for instance, found considerable differences in terms of mathematical, verbal, and spatial ability, with physical sciences students being the only ones with positive manifestations on all three measures.
The four samples are from two different countries, namely Germany and Switzerland, which have similar track-based educational systems. Country will not be examined as a covariate in the present analysis because there is no reason to expect country-level effects on the relation between and magnitude of students’ conceptual knowledge and representational competence, since they are assumed to depend on learning opportunities varying on the teacher-or school-level as well as on individual experiences and preferences. We do not expect systematic differences between Germany and Switzerland on these variables.
2 The present study
In the present study, we examined the generalizability of the findings by Edelsbrunner et al., 2023b across all four samples from their study. Building on the fact that they published their data set for re-use (the published data set is available from the repository of Malone et al., 2021), we re-analyzed these data. The major reason to use this data set was that the present study and its research questions had been triggered by this study and data. In addition, it is the only study so far that has used psychometrically validated instruments to assess both representational competence and conceptual knowledge that are not embedded within the same context, preventing topical bias (Edelsbrunner et al., 2023b). Whereas this implied that our study and research questions were bound to the variables available within this data set, the data set offered potential for various informative research questions which to the best of our knowledge had not been addressed so far. Based on this data set, we hence addressed the following research questions:
(1) Do we find a positive linear correlation between representational competence and conceptual knowledge in each of the four samples?
To answer this research question, we estimated linear correlations of the relation between the two constructs in all four samples separately. Based on extensive literature emphasizing the importance of representational competence for acquiring conceptual knowledge (e.g., Nitz et al., 2014), we expected a positive linear correlation in all four samples:
H1: A positive linear association between representational competence and conceptual knowledge exists in all four samples.
(2) Do we find comparable linear associations between representational competence and conceptual knowledge in all four samples?
To answer this research question, we compared the four samples with regard to their linear correlation estimates of the relation between the two constructs. This was an exploratory research question aiming at unraveling potential similarities and differences in the magnitude of the association between the two constructs across samples, so we did not have hypotheses regarding this question.
After examining research questions (1) and (2), we produced scatter plots individually within all four samples. These should help us visualize the data patterns underlying the estimated correlations to discuss differences and similarities across samples.
Research questions (3) to (5) were also exploratory, with the aim to generate hypotheses for future research. Here, we applied a method to identify different combinations of conceptual knowledge and representational competence systematically occurring in each of the four samples. These different combinations, for example, high representational competence and low conceptual knowledge, are referred to as latent profiles. The corresponding research questions are as follows:
To what degree do latent profiles of representational competence and conceptual knowledge show similar or different patterns across the four different samples?
(3) To what degree is the pattern of low representational competence but high conceptual knowledge, but not vice versa, visible in all four samples?
(4) Do gender, topic-specific learning opportunities, and individual preferences for specific learning content (as reflected in the choice of study program) explain differences and similarities between the four samples?
(5) To answer research questions (3) to (5), we applied multiple group latent profile analysis (e.g., Morin et al., 2016). In this analysis, latent profiles of representational competence and conceptual knowledge can be extracted and compared across the four samples.
Although this research is predominantly exploratory, a preregistration can be helpful for exploratory research to ensure that researcher degrees of freedom in selecting and presenting analysis and their results are controlled (Dirnagl, 2020; Nosek et al., 2018). In addition, although latent profile analysis is predominantly used as an exploratory tool, there are central decisions such as the process leading to determining the number of latent profiles that are guided by multiple fit criteria and subjective considerations (Edelsbrunner et al., 2023a). In preregistering the approach to determining the number of latent profiles, we can ensure that we keep to a priori criteria that have been agreed upon in peer-review and clearly mark and discuss any deviations thereof.
3 Method
3.1 Sample
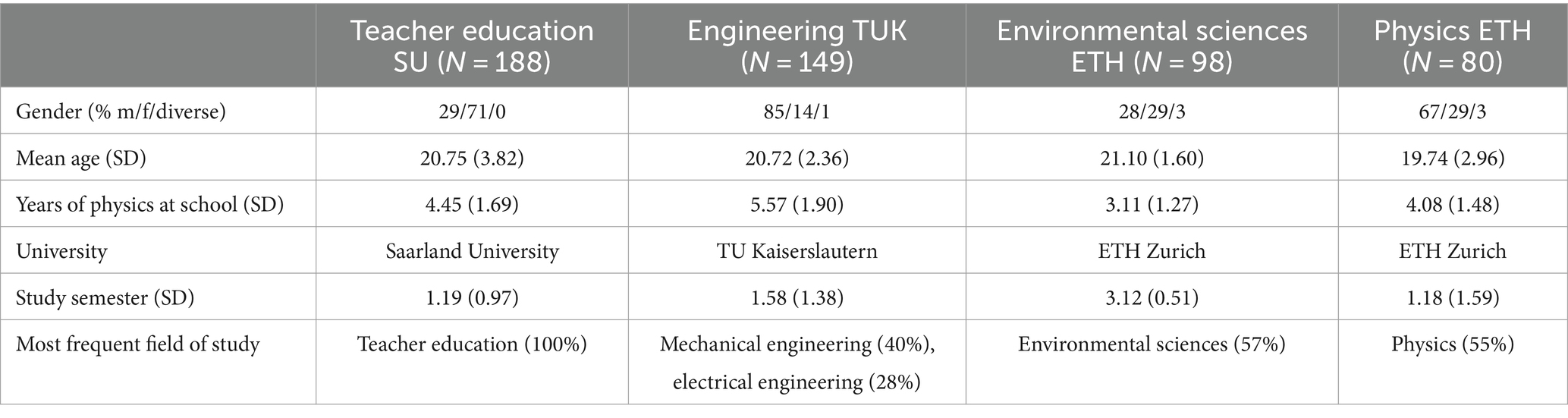
This was a secondary analysis based on the sample by Edelsbrunner et al., 2023b. The theoretical background, research questions, and analytic approach were pre-registered in Edelsbrunner and Hofer (2023). Re-analysis the sample encompassed N = 515 undergraduate students from three different universities in Germany and Switzerland. The main sample characteristics are provided in Table 1. For detailed descriptions of the sampling strategy, see Küchemann et al. (2021).
3.2 Assessment instruments
The authors used a newly developed measure of conceptual knowledge about electromagnetism, encompassing 12 single-choice items, each featuring between five and 10 distractors (internal consistency of ω = 0.92), and another newly developed measure of representational competence with fields that also encompassed 12 items (ω = 0.86). This instrument was utilized to evaluate students’ comprehension of vector-field plots (4 items) and field-line representations (4 items), as well as their ability to translate between the two (4 items). Out of these items, 10 are presented in a single-choice format, offering 4 to 5 answer options, with one correct answer for each. The other two items follow a multiple true-false format and were marked as correct if students selected all appropriate answer options. More detailed psychometric characteristics of the two instruments are provided in Edelsbrunner et al. (2023b), and further details regarding the instrument for representational competence in Küchemann et al. (2021). We used sum scores of items solved from each instrument, which in both cases reach from 0 to 12 points.
As covariates, we used gender, topic-specific learning opportunities, and individual preferences for specific learning content. All variables were assessed in online questionnaires. For gender, participants could indicate female, male, or diverse. We did not include participants with diverse gender in the statistical models, as these were only n = 6 across all four samples, undermining reliable parameter estimation, but we included them in all descriptive analyses for which this was possible.
As an indicator of topic-specific learning opportunities, we administered a question on which participants indicated whether their teachers had used the conductor swing-experiment in their Physics classes, or not. In this experiment, a conducting piece is put within the magnetic field of a magnet. Current is then activated that flows through the conductor, initiating a second electromagnetic field. Through the two magnetic fields’ crossing directions, a Lorentz Force results, causing the conductor piece to swing. The Lorentz Force is a standard topic in German and Swiss Physics education. The conductor swing-experiment, by providing students with a visible phenomenon relating to magnetic fields and the Lorentz force, is supposed to foster students’ conceptual understanding of electromagnetism and fields (Donhauser et al., 2020). We therefore collected information on this question asking participants whether, in high school, their teachers had used the conductor swing-experiment as a demonstration experiment (implemented by the teacher), as a student experiment (implemented by the students themselves), or not at all. In a fourth answer option, the participants could indicate that they could not remember whether this experiment was part of their Physics education. This variable thus has four categorical answer options: Experiment not implemented, implemented as student experiment, implemented as teacher experiment, or cannot remember.
As a final covariate, we considered students’ fields of study. This serves as an indicator of individual preferences for specific learning content. We used two dummy variables to group students into the non-exclusive categories of teacher education student (n = 422) vs. non-teacher education (n = 93), and STEM (n = 305) vs. non-STEM student (n = 210).
4 Results
4.1 Research question 1: do we find a positive linear correlation between representational competence and conceptual knowledge in each of the four samples?
To examine the first research question, whether a positive linear association between representational competence and conceptual knowledge exists within all samples, we estimated bivariate correlations between the sum scores on the two instruments through maximum likelihood-estimation within the Mplus software package version 8.5 (Muthén and Muthén, 2017). We set up a multigroup model in which the variance–covariance matrix is fitted as a structural equation model separately within each sample but parameters can be constrained or freely estimated across the four samples to test for equalities (Hoyle, 2023). We did not test for measurement invariance as this was not of interest to our research questions (Robitzsch and Lüdtke, 2023) and we consider students’ knowledge scores as formative index variables rather than reflective latent variables (Edelsbrunner, 2022; Edelsbrunner et al., 2023a). In order to standardize students’ sum scores for both constructs, we defined single-indicator dummy-latent variables with unit variance and a fixed factor loading of one. By constraining the error variance in students’ scores to 0, all their variance was represented in the respective latent variable standardized with a variance of 1. We estimated the covariance of these two latent variables within each group, which through the standardization represented the correlation estimate between the two constructs (Hoyle, 2023).
To test hypothesis 1 and decide whether correlations were present in all four samples, we inspected bootstrapped 90% confidence intervals based on 10,000 bootstrap draws for the covariance between the two constructs (DiCiccio and Efron, 1996).
If a bootstrapped 90% confidence interval within a sample lies fully above 0, we conclude that a positive correlation between representational competence and conceptual knowledge is present within the respective sample. If the confidence intervals in all four samples are above 0, we interpret this as support of hypothesis 1. If either or all confidence intervals include 0 or are fully below, we interpret this as a lack of evidence for hypothesis 1. The results, which are summarized in Table 2, indicate that positive correlations were present in all four samples, supporting our hypothesis.
4.2 Research question 2: do we find comparable linear associations between representational competence and conceptual knowledge in all four samples?
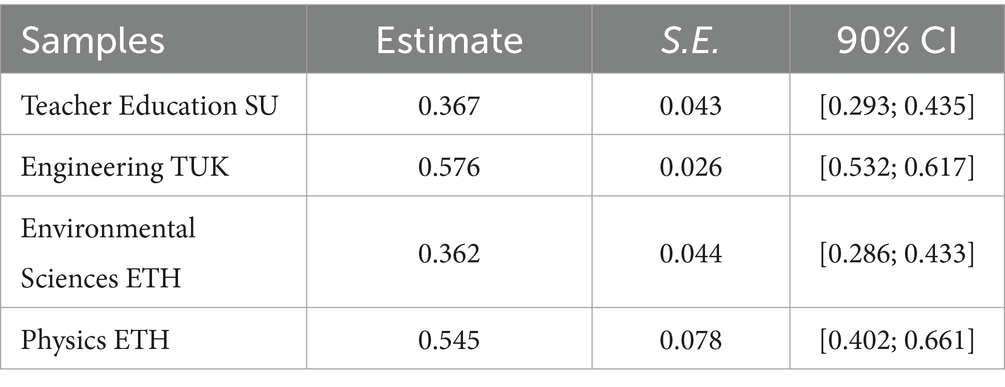
To examine the second research question, whether we find comparable linear associations between representational competence and conceptual knowledge in all four samples, we used parameter constraints to test the covariance parameters between the two constructs for equality between the four samples. We first set all four covariance parameters to equality and compared the fit of this model to that of the model in which the covariance was allowed to vary between all four samples. We used p < 0.10 as a cut-off to decide whether the assumption of parameter equality holds. If the likelihood ratio test was significant at p < 0.10, we inspected which of the samples contributed most to the significant result and freed that sample’s parameter to deviate from the others. This was done until we yielded a model with a non-significant likelihood ratio test and overall good model fit.
As shown in Table 3 the model with one correlation freed, i.e., the correlation estimate for the Engineering TUK sample, resulted in a non-significant likelihood ratio test. However, inspection of the sample-specific statistics suggested testing a third model with the correlation estimates of the Teacher Education SU and the Environmental Sciences ETH samples, on the one hand, and the Engineering TUK and the Physics ETH samples, on the other hand, fixed to the same estimates. This model showed the best model fit and resulted in correlation estimates of r = 0.365 (SE = 0.030) for the first pair and r = 0.572 (SE = 0.028) for the second pair.
After examining research question 2, we produced scatter plots to examine the exact nature of the relation between representational competence and conceptual knowledge within the four samples. This helps interpret similarities and differences in this correlation across samples. In these scatter plots (Figure 1), we see the similarities between the Teacher Education SU and the Environmental Sciences ETH samples, and the Engineering TUK and the Physics ETH samples, with, on average, lower manifestations of conceptual knowledge for the first two samples. The two samples Teacher Education SU and Environmental Sciences ETH both show a quadratic relation that appears to be close to zero up to about seven points of representational competence but is positive thereafter. The two samples Engineering TUK and Physics ETH show just very small quadratic shapes and the linear association in these two samples seems to begin earlier, at about four points of representational competence.
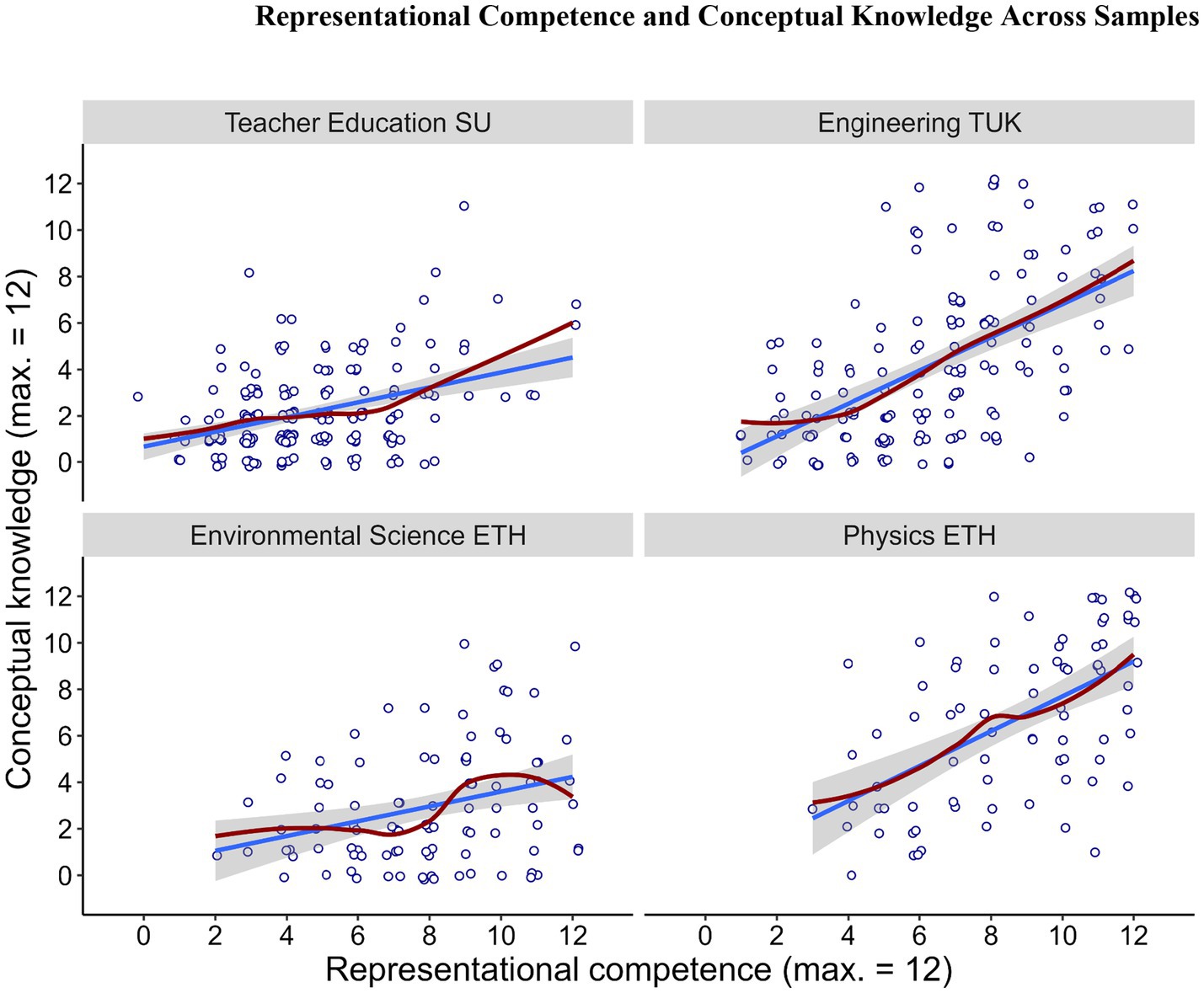
Figure 1. Scatter plots of relation between representational competence and conceptual knowledge in the four samples. Linear lines present regression slopes from a linear model incl. 90% confidence intervals estimated in R (v4.4.1, R Core Team, 2021), non-linear lines best fit from a general additive model.
4.3 Research questions 3–5
To examine research questions 3–5, we conducted (multiple group) latent profile analyses. This statistical method allows capturing patterns such as the one observed by Edelsbrunner et al. (2023b, i.e., low representational competence and high conceptual knowledge) in explicit model parameters. A latent profile analysis allows clustering individuals based on observed patterns of means and variances on one or more variables (Hickendorff et al., 2018). The two clustering variables in our study were students’ mean scores on the representational competence-test and on the conceptual knowledge-test. In the latent profile analyses, systematically different patterns of means and variances across these variables were modelled in a data-driven manner. These patterns were then represented in a latent categorical variable that represents the patterns as different latent profiles. We first determined the number of latent profiles in each sample individually by increasing the number of profiles from 1 to 7 in a step-wise manner. We specified latent profiles differing in means and variances across the two indicator variables. The number of profiles was determined based on the AIC, AIC3, BIC, aBIC, and the VLMR-likelihood ratio test with a significance criterion of p < 0.10 (Edelsbrunner et al., 2023a; Nylund-Gibson and Choi, 2018). The AIC in many cases points to a higher number of profiles than the BIC, with the AIC3 and the aBIC in between (Edelsbrunner et al., 2023a). In these cases or in case the VLMR-test is in disagreement with the other indices, we determined whether the additional profiles shown by the AIC, or by one of the other indices, are informative by relying on our content knowledge (Marsh et al., 2009). More in-depth descriptions of the different steps to determine the number of profiles in latent profile analyses are provided by Ferguson et al. (2020) and Hickendorff et al. (2018).
4.3.1 Research question 3: to what degree do latent profiles of representational competence and conceptual knowledge show similar or different patterns across the four different samples?
As the fit indices depicted in Figure 2 show, across all samples, solutions with four profiles provided the best fit according to the aBIC and the AIC, whereas the BIC and CAIC pointed to the two profiles-solutions and the AIC3 predominantly to the three profiles-solutions. The VLMR indicated two profiles in the Teacher Education SU sample but three profiles in the other samples. Overall, the combined information from these fit indices spoke for three profiles in all of the samples (Figure 3).
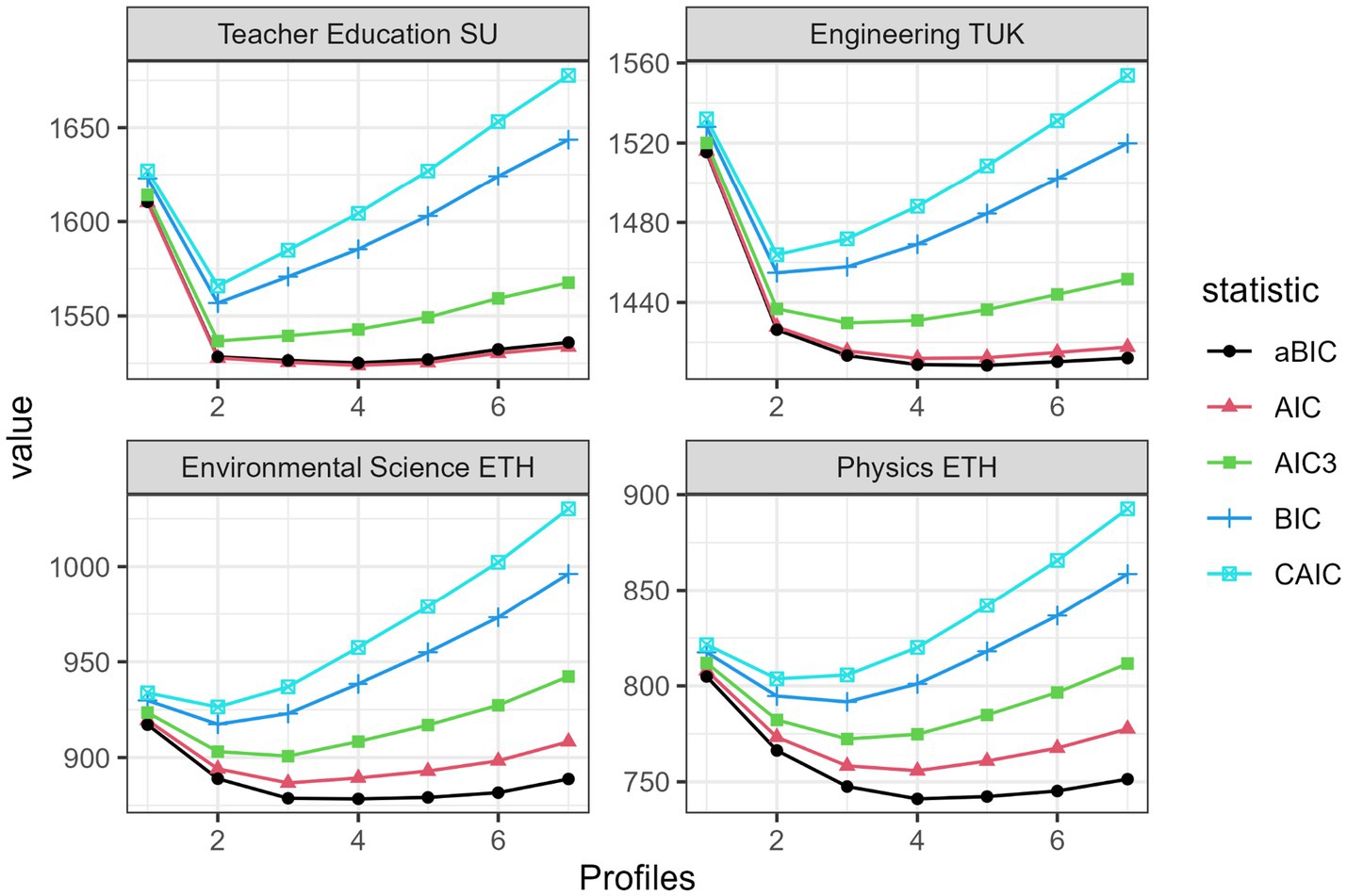
Figure 2. Relative model fit indices for models with different numbers of profiles in the four samples.
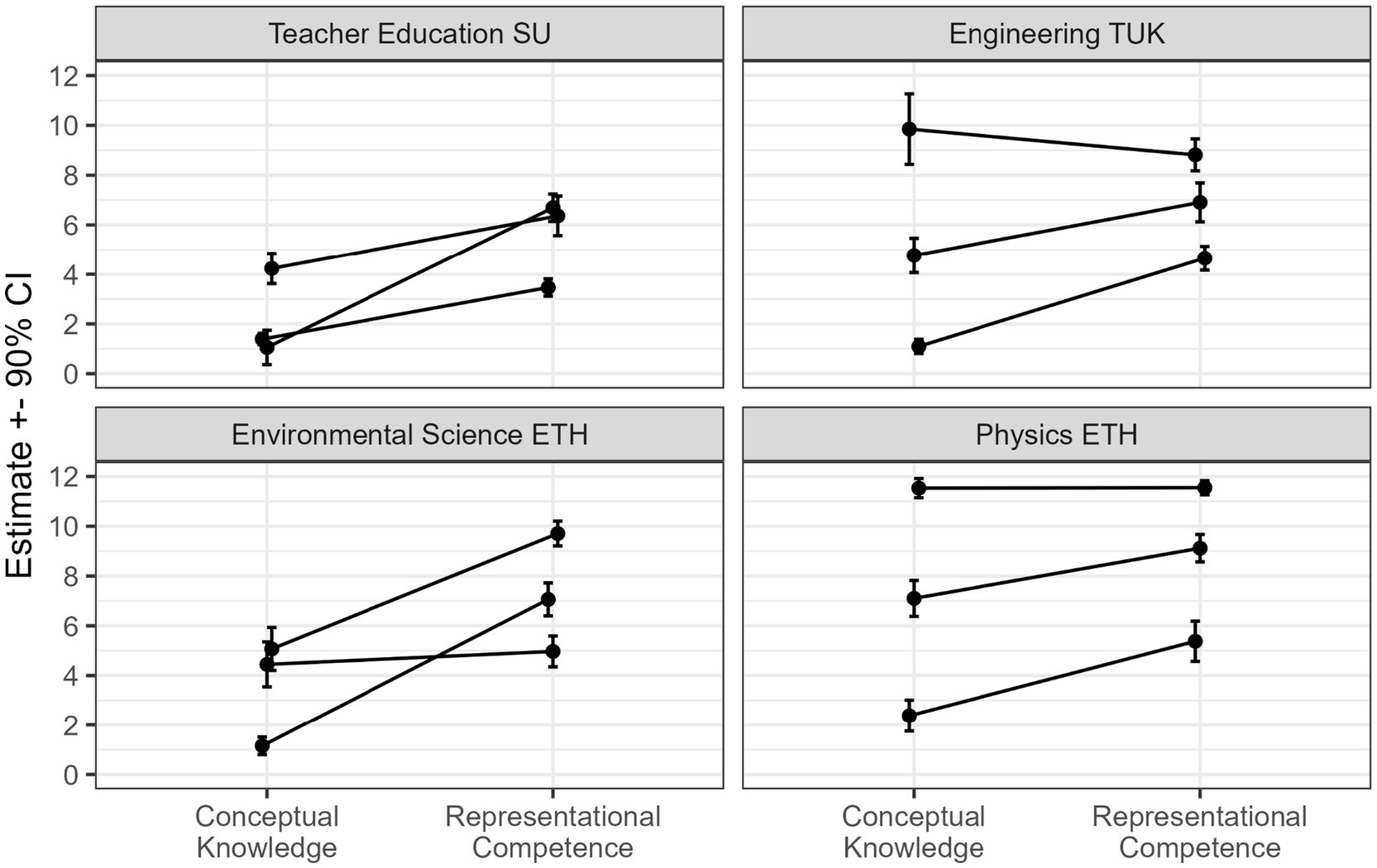
After determining the number of profiles within each sample, we extended the latent profile analyses to a multiple group-model. In the multiple group-extension, profiles can be extracted within each sample individually but within the same model estimation process (Morin et al., 2016). This allows fixing parameters or letting them vary across samples, to test whether one or more parameters (mean-and variance estimates of profiles, or relative profile sizes) differ or are similar across samples. Based on this analytic approach, we examined the comparability and specific patterns of the latent profiles in the four samples. Based on the depiction of all 12 resulting profiles in Figure 4, we inspected which profile parameters appeared similar or different between the samples and then fixed those to equality that we judged to be similar from a theoretical perspective.
Based on the profiles’ estimates and commonalities, we decided to restrict the mean and variance parameters of the following profiles to equality: The parameters of the Teacher Education SU Profile 3 and Environmental Science ETH Profile 3, as well as those of Teacher Education SU Profile 2 and Engineering TUK Profile 1. For all other profiles, at least one of the profile means appeared too far away from all other profiles to be restricted to equality.
After fixing parameters to equality, we tested the respective restriction through a likelihood ratio test (Satorra and Bentler, 2010). This test produced a result of Chi2(8) = 4.06, p = 0.852, indicating that the equality restrictions did not significantly deteriorate model fit and are thus acceptable. After implementing these constraints and re-estimating the model, another two profiles yielded very similar estimates. We also constrained those two profiles to equality, which again yielded a non-significant p-value (p = 0.156). We therefore remained with these restrictions of overall four profiles of which each described the same patterns occurring in two different samples, and another four profiles that could only be found in one of the samples, yielding overall seven different kinds of profiles across the four samples. The resulting profiles, depicted in Figure 5, are the final profiles in the four samples.
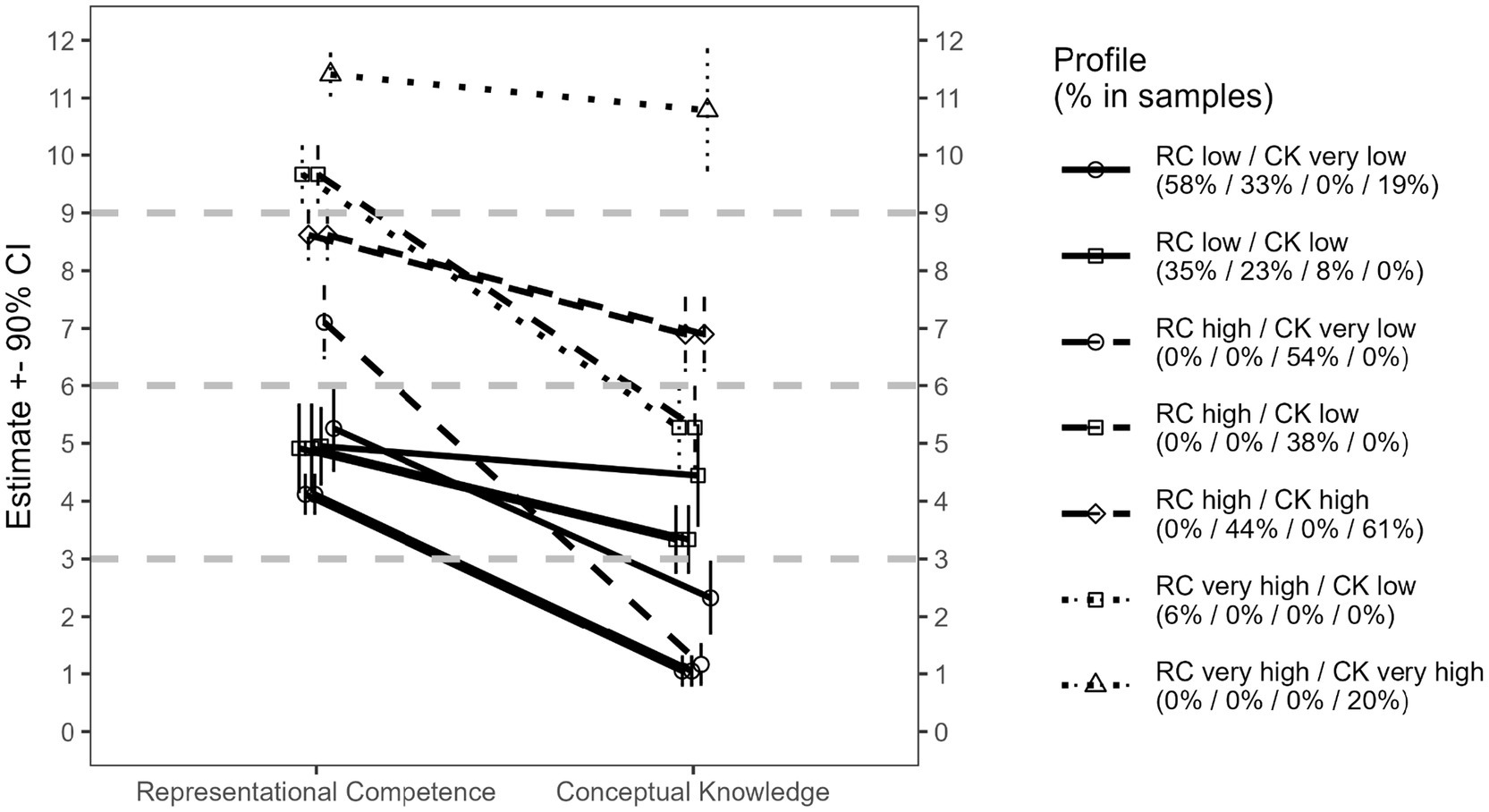
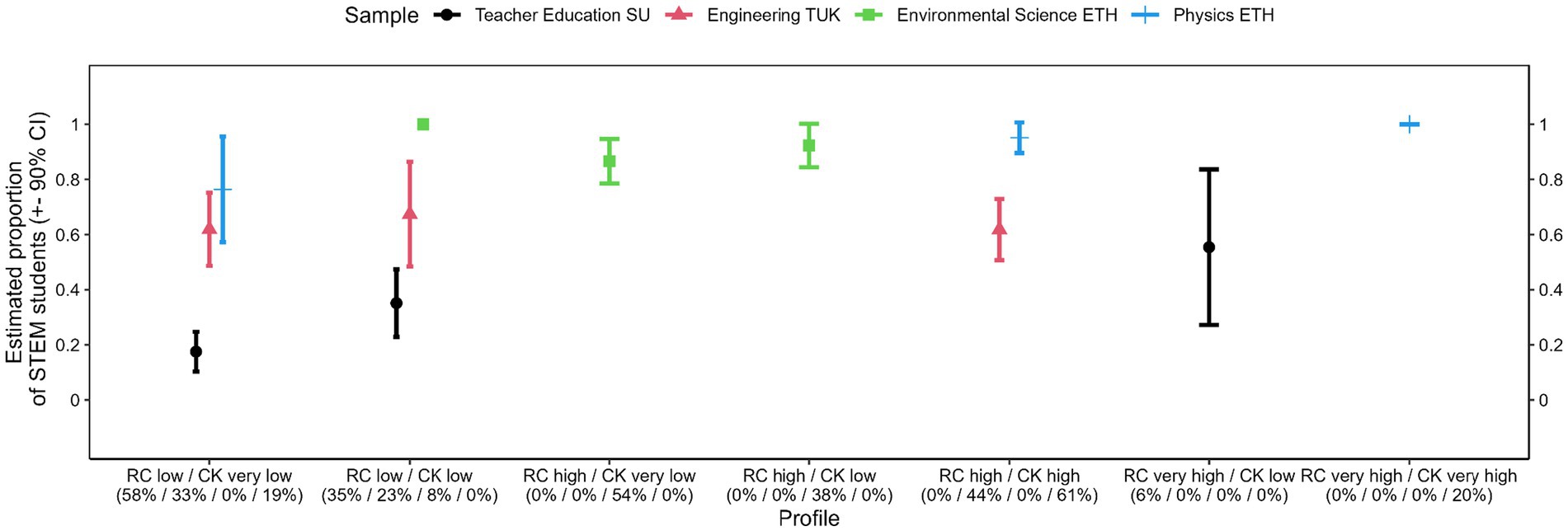
Figure 5. Final profiles in the four samples after equality constraints. Percentages refer to estimated proportions of learners in each profile within each sample, in the order sample 1 = Teacher Education SU, sample 2 = Engineering TUK, sample 3 = Environmental Sciences ETH, sample 4 = Physics ETH. Linetypes indicate level on representational competence according to quantitative category thresholds described in text (solid = low, long-dashed = high, short-dashed = very high), point shapes indicate level on conceptual knowledge (round = very low, quadratic = low, diamond = high, triangle = very high). Error bars indicate 90% confidence intervals.
4.3.2 Research question 4: to what degree is the pattern of low representational competence but high conceptual knowledge, but not vice versa, visible in all four samples?
We next interpreted the resulting profiles to judge to which extent we can find the pattern described in Edelsbrunner et al. (2023b) of students showing high conceptual knowledge only with high representational competence. We abstained from statistical standardization techniques for bringing both variables on the same scale for interpretations (e.g., z-standardization, robust scaling) since the assessment instruments for both constructs have been developed by content experts and didacts. Consequently, we preferred leaving the scores on both variables on their raw scales (i.e., 0–12 items solved) since from an educational perspective, the items cover the central points of understanding according to expert judgments on both instruments. We decided to apply the simple criteria to interpret representational competence-or conceptual knowledge-scores as very low for profile estimates below 3, as low for profile estimates below 6, as high for profile estimates above 6, and as very high for estimates above 9. The resulting profile labels according to these criteria are presented in Figure 5. As visible from Figure 5, all profiles from all samples followed the observation in Edelsbrunner et al. (2023b): There was no profile of learners with very low or low representational competence, but high or very high conceptual knowledge.
4.3.3 Research question 5: do gender, topic-specific learning opportunities, and individual preferences for specific learning content (as reflected in the choice of study program) explain differences and similarities between the four samples?
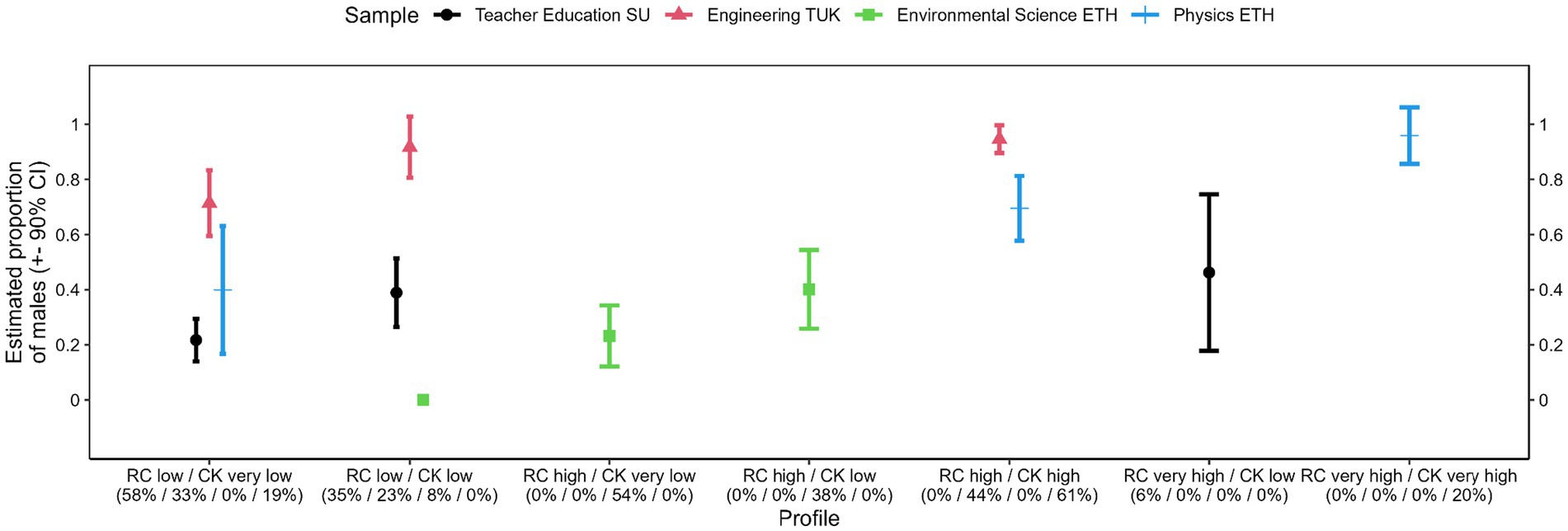
After extracting and comparing the profiles, we added the four covariates to the model via Lanza’s approach (Asparouhov and Muthén, 2014; Lanza et al., 2013) to examine whether the profiles in the four samples relate to different mean values on students’ gender (male = 0, female = 1), topic-specific learning experiences (0 = conductor swing experiment not conducted, 1 = conducted as teacher experiment, 2 = conducted as student experiment, 3 = cannot remember), and individual preferences for specific learning content (two variables; non-teacher = 0, teacher student = 1; non-STEM = 0, STEM = 1). We again relied on p-values <0.10 to draw hypotheses for future research regarding the different profiles’ correlates. Note that this procedure is only available in single-group latent profile analysis. We therefore constrained the latent profile parameters to the estimates from Figure 5 in each of the four samples and conducted four covariate analyses, one for each of the samples. The results from these analyses for the first covariate, the proportion of males in each profile within each sample, are presented in Figure 6.
Whereas none of the comparisons between any two profiles are significant at p < 0.10, there is a pattern in Figure 6 across all samples that the more proficient profiles both in representational competence (profiles ordered according to labels indicating increasing levels on this variable from left to right) and in conceptual knowledge (also ordered from left to right, as secondary variable) contained higher proportions of males.
The results from the second covariate, the differences in the amount of STEM learners across the different profiles, are presented in Figure 7.
Whereas none of the comparisons between two profiles are significant at p < 0.10, there are descriptive patterns in the Teacher Education SU and the Physics ETH samples that students studying a STEM subject are in the more proficient profiles. This pattern is not visible in the Environmental Science ETH and the Engineering TUK samples.
For the last covariate, topic-specific learning opportunities, a clear trend was visible (Figure 8): All profiles scoring very low on conceptual knowledge showed high proportions of learners who had not worked on the conductor swing experiment in school, independently of their level of representational competence (e.g., two right panels in second row). Those with an at least low level of conceptual knowledge indicated much more frequently that they had conducted the conductor swing experiment as a teacher or student experiment.
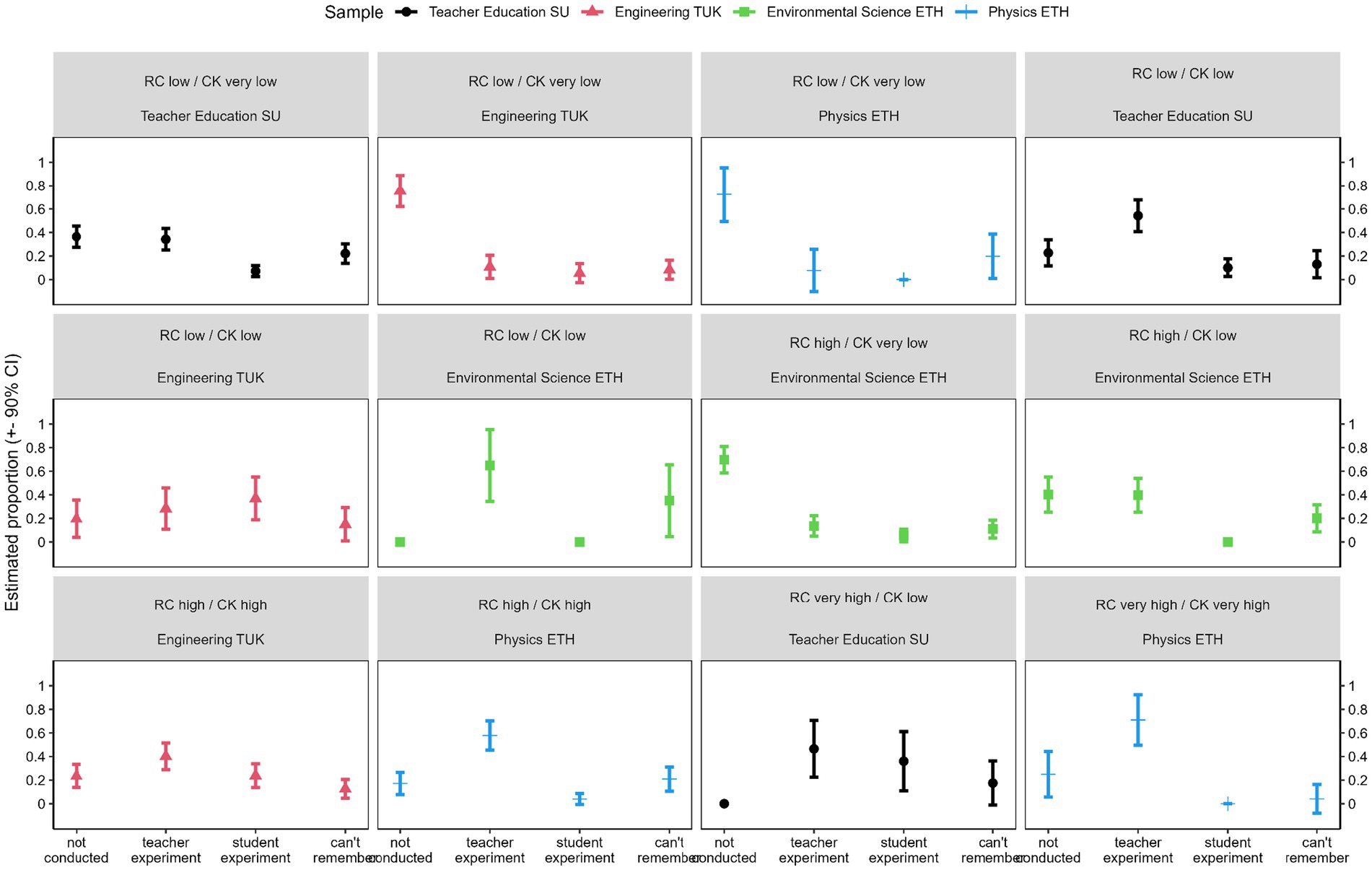
Figure 8. Proportion of learners with different conductor swing-experiences in each of the profiles across the four samples.
5 Discussion
This study confirmed a positive relation between conceptual knowledge and representational competence in all four samples, in line with previous assumptions (Chang, 2018; Edelsbrunner et al., 2023b). By comparing four different samples, we identified a stronger relationship in the samples consisting primarily of engineering and physics students than in environmental sciences and teacher education-students (r = 0.365 compared to r = 0.572). Students in engineering and physics-related samples, on average, show higher representational competence and conceptual knowledge, which are more strongly related (cf. Reinhold et al., 2020). Only up to about four points of representational competence (still considered as low), the two knowledge types seem to be rather unrelated. After that, higher representational competence goes hand in hand with higher conceptual knowledge. In the teacher education and environmental sciences-related samples, the (weaker) positive correlation becomes apparent only with about seven points of representational competence. Accordingly, those students seem to require a rather high level of representational competence as a basis to develop conceptual knowledge. From this finding, we derive the hypothesis for future research that some learners require less representational competence as a basis to develop conceptual knowledge and are better at exploiting their representational competence to develop conceptual knowledge than others.
In line with the overall finding that conceptual knowledge stays at a very low level until a certain threshold level (lower or higher, depending on the sample) of representational competence is reached, all the final latent profiles indicated that high representational competence is a prerequisite for high conceptual knowledge, but not vice versa. This pattern was (moderately) reversed in only one of the 12 independently estimated profiles in the four samples. This profile, with high representational competence and very high conceptual knowledge estimates, detected in the Engineering TUK sample, consisted of more males of which more had undergone the conductor swing experiment as an actual student experiment. As is the case for other intertwined types of knowledge such as conceptual and procedural knowledge in mathematics, bidirectional relations are most likely (e.g., Crooks and Alibali, 2014; Rittle-Johnson, 2017). While representational competence seems to be an important prerequisite for developing conceptual knowledge in the range assessed with the instruments used in this study, at higher levels of proficiency, bidirectional relations and also more interdependent development of the two types of knowledge can be expected. The reversed profile found in the Engineering TUK sample—as well as the almost parallel profile characterized by very high proficiency on both measures in the Physics ETH sample—might be indicative of such effects for high-proficiency sub-groups. By using instruments measuring and differentiating also in higher proficiency ranges, future research could test those assumptions.
While we did find some differences between the Teacher Education SU and the Environmental Sciences ETH samples, on the one hand, and the Engineering TUK and the Physics ETH samples, on the other hand, the investigated covariates gender, topic-specific learning opportunities, and individual preferences for specific learning content (as reflected in the choice of study program) did not help to explain large variation in differences and similarities in the profiles between the samples. The detected patterns, however, were in line with our expectations, suggesting a higher proportion of females in lower-proficiency profiles (Hofer et al., 2018; Madsen et al., 2013; Nieminen et al., 2013), a higher proportion of STEM students in higher-proficiency profiles (Lubinski and Benbow, 2006; Reinhold et al., 2020), and a presumably positive influence of prior own experiences with the swing experiment on higher-proficiency profiles membership (Hardy et al., 2006; Van der Graaf et al., 2020). The effects of specific learning opportunities or training interventions could be examined in controlled experiments in follow-up studies.
The slightly different patterns found across the four samples might indicate self-selection effects as well as effects of differences in the study programs. Study programs help students to develop specific specialized skills, such as spatial skills in the course of an architecture (Berkowitz et al., 2021) or engineering study program (e.g., Uttal et al., 2013; Zorn and Gericke, 2020). In addition to increased spatial skills, representational competence, conceptual knowledge, and the ability to connect the two types of knowledge can be expected to be practiced more extensively in some study programs (especially within STEM fields) than in others. Longitudinal analyses that are fit to capture knowledge development over time as a function of different learning environments can shed more light on underlying processes.
6 Limitations
The cross-sectional nature limits the interpretation of the results of the present study. Other limitations concern the rather small diversity in the samples investigated regarding age and educational level, for instance. Although there was no evidence for country-level effects, we neither considered more than two countries nor several universities within countries, restricting any interpretations on the level of country-specific educational systems. Finally, we are not aware of theories or studies that would allow us to judge the generalizability of the current findings. The generalizability of the findings to other topics in physics and other domains associated with representational competence still needs to be scrutinized. This could, for example, be achieved by assessing representational competence and conceptual knowledge across different topics within domains, as well as across multiple domains, to disentangle the common and specific variation of representational competence, as well as the stability of its relation with conceptual knowledge, across these potential sources of variation.
Despite those limitations, the present study allows to derive some tentative implications for educational practice. We emphasize that this study relies on cross-sectional observational data, making confounding very likely, and the present parameters estimates should not be interpreted to represent causal relations. We relate our findings to prior theories and findings (Nitz et al., 2014; Scheid et al., 2018, 2019) in order to derive practical implications, but longitudinal research with strong designs and well-selected covariates to increase the validity of causal conclusions (Dumas and Edelsbrunner, 2023), as well as experimental designs are required to infer new information regarding causality. We propose as a first step to include strong covariates in future studies based on theoretical models of causal dynamics (Dumas and Edelsbrunner, 2023), considering principles of causal inference that improve the chance that estimated relations are causal (Bailey et al., 2024). As a further step, longitudinal studies observing both constructs repeatedly during schooling or targeted science education activities might provide more valid insight into their mutual developmental dynamics, and in experimental intervention studies, for example representational competence could be trained to examine whether this prepares students for future acquisition of conceptual knowledge (Edelsbrunner et al., 2024). For educators and learners aiming at conceptual knowledge development, a first important step might be to ascertain a certain level of representational competence. As a second step, instead of teaching representational competence and conceptual knowledge in isolation, explicitly pointing at the connections and practicing the interpretation and application of different representations in the context of conceptual learning might be worthwhile. To be able to formulate specific recommendations for different sub-groups based on their characteristics, more research is needed.
To conclude, our results indicate that the qualitative findings of a positive relation between representational competence and conceptual knowledge, with the former as a basis for developing the latter, generalize across different populations with some slight but relevant differences warranting further research.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found at: https://github.com/peter1328/Unraveling.
Ethics statement
Ethical approval was not required for the studies involving humans because the study was conducted in full accordance with the ethical standards for research of the American Psychological Association’s “Ethical Principles of Psychologists and Code of Conduct” (American Psychological Association, 2017). The first author’s Swiss institution as well as German regulations did not require formal ethical approval for studies obtaining anonymized data on adult students within university courses. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
PE: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Software, Visualization, Writing – original draft, Writing – review & editing. SH: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Software, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ainsworth, S. (2008). “The educational value of multiple representations when learning complex scientific concepts” in Visualization: Theory and practice in science education. eds. J. K. Gilbert, M. Reiner, and M. Nakleh (Dordrecht: Springer), 191–208.
American Psychological Association. (2017). Ethical principles of psychologists and code of conduct. APA: Washington DC.
Asparouhov, T., and Muthén, B. (2014). Auxiliary variables in mixture modeling: using the BCH method in Mplus to estimate a distal outcome model and an arbitrary secondary model. Mplus Web Notes 21, 1–22.
Bailey, D. H., Jung, A. J., Beltz, A. M., Eronen, M. I., Gische, C., Hamaker, E. L., et al. (2024). Causal inference on human behaviour. Nat. Hum. Behav. 8, 1448–1459. doi: 10.1038/s41562-024-01939-z
Berkowitz, M., Gerber, A., Thurn, C. M., Emo, B., Hoelscher, C., and Stern, E. (2021). Spatial abilities for architecture: cross sectional and longitudinal assessment with novel and existing spatial ability tests. Front. Psychol. 11:609363. doi: 10.3389/fpsyg.2020.609363
Bowen, C., and Bunce, D. (1997). Testing for conceptual understanding in general chemistry. Chem. Educ. 2, 1–17. doi: 10.1007/s00897970118a
Carolan, J., Prain, V., and Waldrip, B. (2008). Using representations for teaching and learning in science. Teach. Sci. 54, 18–23.
Chan, W. W. L., and Wong, T. T.-Y. (2019). Visuospatial pathways to mathematical achievement. Learn. Instr. 62, 11–19. doi: 10.1016/j.learninstruc.2019.03.001
Chang, H. Y. (2018). Students’ representational competence with drawing technology across two domains of science. Sci. Educ. 102, 1129–1149. doi: 10.1002/sce.21457
Chen, C., Sonnert, G., and Sadler, P. M. (2020). The effect of first high school science teacher's gender and gender matching on students' science identity in college. Sci. Educ. 104, 75–99. doi: 10.1002/sce.21551
Corradi, D., Elen, J., and Clarebout, G. (2012). Understanding and enhancing the use of multiple external representations in chemistry education. J. Sci. Educ. Technol. 21, 780–795. doi: 10.1007/s10956-012-9366-z
Crooks, N. M., and Alibali, M. W. (2014). Defining and measuring conceptual knowledge in mathematics. Dev. Rev. 34, 344–377. doi: 10.1016/j.dr.2014.10.001
de Jong, T. (2019). Moving towards engaged learning in STEM domains; there is no simple answer, but clearly a road ahead. J. Comput. Assist. Learn. 35, 153–167. doi: 10.1111/jcal.12337
DiCiccio, T. J., and Efron, B. (1996). Bootstrap confidence intervals. Stat. Sci. 11, 189–228. doi: 10.1214/ss/1032280214
Dirnagl, U. (2020). Preregistration of exploratory research: learning from the golden age of discovery. PLoS Biol. 18:e3000690. doi: 10.1371/journal.pbio.3000690
Donhauser, A., Küchemann, S., Kuhn, J., Rau, M., Malone, S., Edelsbrunner, P., et al. (2020). Making the invisible visible: visualization of the connection between magnetic field, electric current, and Lorentz force with the help of augmented reality. Phys. Teach. 58, 438–439. doi: 10.1119/10.0001848
Dumas, D., and Edelsbrunner, P. (2023). How to make recommendations for educational practice from correlational data using structural equation models. Educ. Psychol. Rev. 35:48. doi: 10.1007/s10648-023-09770-0
Edelsbrunner, P. A. (2022). A model and its fit lie in the eye of the beholder: long live the sum score. Front. Psychol. 13:986767. doi: 10.3389/fpsyg.2022.986767
Edelsbrunner, P. A., Flaig, M., and Schneider, M. (2023a). A simulation study on latent transition analysis for examining profiles and trajectories in education: recommendations for fit statistic. J. Res. Educ. Effect. 16, 350–375. doi: 10.1080/19345747.2022.2118197
Edelsbrunner, P. A., and Hofer, S. I. (2023). Unraveling the relation between representational competence and conceptual knowledge across four samples from two different countries. Front. Educ. 8:1046492. doi: 10.3389/feduc.2023.1046492
Edelsbrunner, P. A., Lichtenberger, A., Malone, S., Küchemann, S., Stern, E., Brünken, R., et al. (2023b). The relation of representational competence and conceptual knowledge in female and male undergraduates. Int. J. STEM Educ. 10:44. doi: 10.1186/s40594-023-00435-6
Edelsbrunner, P. A., Schumacher, R., Hänger-Surer, B., Schalk, L., and Stern, E. (2024). Preparation for future conceptual learning: content-specific long-term effects of early physics instruction. J. Educ. Psychol. 116, 1479–1499. doi: 10.1037/edu0000887
Ferguson, S. L., Moore, E. W. G., and Hull, D. M. (2020). Finding latent groups in observed data: a primer on latent profile analysis in Mplus for applied researchers. Int. J. Behav. Dev. 44, 458–468. doi: 10.1177/0165025419881721
Hardy, I., Jonen, A., Möller, K., and Stern, E. (2006). Effects of instructional support within constructivist learning environments for elementary school students’ understanding of “floating and sinking”. J. Educ. Psychol. 98, 307–326. doi: 10.1037/0022-0663.98.2.307
Hegarty, M., and Kriz, S. (2008). “Effects of knowledge and spatial ability on learning from animation” in Learning with animation: Research implications for design. eds. R. Lowe and W. Schnotz (New York, NY: Cambridge University Press), 3–29.
Heo, M., and Toomey, N. (2020). Learning with multimedia: the effects of gender, type of multimedia learning resources, and spatial ability. Comput. Educ. 146:103747. doi: 10.1016/j.compedu.2019.103747
Hickendorff, M., Edelsbrunner, P. A., McMullen, J., Schneider, M., and Trezise, K. (2018). Informative tools for characterizing individual differences in learning: latent class, latent profile, and latent transition analysis. Learn. Individ. Differ. 66, 4–15. doi: 10.1016/j.lindif.2017.11.001
Hofer, S. I., Schumacher, R., Rubin, H., and Stern, E. (2018). Enhancing physics learning with cognitively activating instruction: a quasi-experimental classroom intervention study. J. Educ. Psychol. 110, 1175–1191. doi: 10.1037/edu0000266
Hoyle, R. H. (2023). Handbook of structural equation modeling. 2nd Edn. New York, NY: Guilford Press.
Jansen, M., Schroeders, U., and Lüdtke, O. (2014). Academic self-concept in science: multidimensionality, relations to achievement measures, and gender differences. Learn. Individ. Differ. 30, 11–21. doi: 10.1016/j.lindif.2013.12.003
Kang, J., Hense, J., Scheersoi, A., and Keinonen, T. (2019). Gender study on the relationships between science interest and future career perspectives. Int. J. Sci. Educ. 41, 80–101. doi: 10.1080/09500693.2018.1534021
Kievit, R. A., Frankenhuis, W. E., Waldorp, L. J., and Borsboom, D. (2013). Simpson\u0027s paradox in psychological science: a practical guide. Frontiers in psychology, 4, 513. doi: 10.3389/fpsyg.2013.00513
Klein, P., Müller, A., and Kuhn, J. (2017). Assessment of representational competence in kinematics. Phys. Rev. Phys. Educ. Res. 13:010132. doi: 10.1103/PhysRevPhysEducRes.13.010132
Kohl, P. B. (2007). Towards an understanding of how students use representations in physics problem solving (Doctoral dissertation, University of Colorado at Boulder).
Kozma, R., and Russell, J. (2005). Students becoming chemists: Developing Representationl Competence. pp. 121–145.
Küchemann, S., Malone, S., Edelsbrunner, P., Lichtenberger, A., Stern, E., Schumacher, R., et al. (2021). Inventory for the assessment of representational competence of vector fields. Phys. Rev. Phys. Educ. Res. 17:020126. doi: 10.1103/PhysRevPhysEducRes.17.020126
Lanza, S. T., Tan, X., and Bray, B. C. (2013). Latent class analysis with distal outcomes: a flexible model-based approach. Struct. Equ. Model. Multidiscip. J. 20, 1–26. doi: 10.1080/10705511.2013.742377
Lowrie, T., and Diezmann, C. (2011). Solving graphics tasks: gender differences in middleschool students. Learn. Instr. 21, 109–125. doi: 10.1016/j.learninstruc.2009.11.005
Lubinski, D., and Benbow, C. P. (2006). Study of mathematically precocious youth after 35 years: Uncovering antecedents for the development of math-science expertise. Perspectives on psychological science, 1, 316–345. doi: 10.1111/j.1745-6916.2006.00019.x
Madsen, A., McKagan, S. B., and Sayre, E. C. (2013). Gender gap on concept inventories in physics: what is consistent, what is inconsistent, and what factors influence the gap? Phys. Rev. Special Top. Phys. Educ. Res. 9:020121. doi: 10.1103/PhysRevSTPER.9.020121
Malone, S., Küchemann, S., Edelsbrunner, P. A., Lichtenberger, A., Altmeyer, K., Schumacher, R., et al. (2021). CESAR 0 data.
Marsh, H. W., Lüdtke, O., Trautwein, U., and Morin, A. J. S. (2009). Classical latent profile analysis of academic self-concept dimensions: synergy of person-and variable-centered approaches to theoretical models of self-concept. Struct. Equ. Model. Multidiscip. J. 16, 191–225. doi: 10.1080/10705510902751010
Morin, A. J. S., Meyer, J. P., Creusier, J., and Biétry, F. (2016). Multiple-group analysis of similarity in latent profile solutions. Organ. Res. Methods 19, 231–254. doi: 10.1177/1094428115621148
Mullis, I. V. S., Martin, M. O., Foy, P., and Hooper, M. (2016). TIMSS advanced 2015 international results in advanced mathematics and physics. Retrieved from Boston College, TIMSS & PIRLS International Study Center website. Available at: http://timssandpirls.bc.edu/timss2015/international-results/advanced/ (Accessed October 24, 2024).
Muthén, L. K., and Muthén, B. O. (2017). Mplus user’s guide. Eighth Edn. Los Angeles, CA: Muthén & Muthén.
National Research Council. (2012). A framework for K-12 science education: Practices, crosscutting concepts, and core ideas. Washington D.C: National Academy of Sciences.
Nieminen, P., Savinainen, A., and Viiri, J. (2013). Gender differences in learning of the concept of force, representational consistency, and scientific reasoning. Int. J. Sci. Math. Educ. 11, 1137–1156. doi: 10.1007/s10763-012-9363-y
Nitz, S., Ainsworth, S. E., Nerdel, C., and Prechtl, H. (2014). Do student perceptions of teaching predict the development of representational competence and biological knowledge? Learn. Instr. 31, 13–22. doi: 10.1016/j.learninstruc.2013.12.003
Nosek, B. A., Ebersole, C. R., DeHaven, A. C., and Mellor, D. T. (2018). The preregistration revolution. Proc. Natl. Acad. Sci. 115, 2600–2606. doi: 10.1073/pnas.1708274114
Nylund-Gibson, K., and Choi, A. Y. (2018). Ten frequently asked questions about latent class analysis. Trans. Issues Psychol. Sci. 4, 440–461. doi: 10.1037/tps0000176
OECD (2009). Equally prepared for life?: how 15-year-old boys and girls perform in school, PISA. Paris: OECD Publishing.
Olympiou, G., Zacharias, Z., and Dejong, T. (2013). Making the invisible visible: enhancing students’ conceptual understanding by introducing representations of abstract objects in a simulation. Instr. Sci. 41, 575–596. doi: 10.1007/s11251-012-9245-2
Patall, E. A., Steingut, R. R., Freeman, J. L., Pituch, K. A., and Vasquez, A. C. (2018). Gender disparities in students' motivational experiences in high school science classrooms. Sci. Educ. 102, 951–977. doi: 10.1002/sce.21461
R Core Team (2021). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/ (Accessed October 24, 2024).
Reinhold, F., Hofer, S., Berkowitz, M., Strohmaier, A., Scheuerer, S., Loch, F., et al. (2020). The role of spatial verbal numerical and general reasoning abilities in complex word problem solving for young female and male adults. Math. Educ. Res. J. 32, 189–211. doi: 10.1007/s13394-020-00331-0
Rittle-Johnson, B. (2017). Developing mathematics knowledge. Child Dev. Perspect. 11, 184–190. doi: 10.1111/cdep.12229
Robitzsch, A., and Lüdtke, O. (2023). Why full, partial, or approximate measurement invariance are not a prerequisite for meaningful and valid group comparisons. Struct. Equ. Model. Multidiscip. J. 30, 859–870. doi: 10.1080/10705511.2023.2191292
Rodriguez, L. V., van der Veen, J. T., Anjewierden, A., van den Berg, E., and de Jong, T. (2020). Designing inquiry-based learning environments for quantum physics education in secondary schools. Phys. Educ. 55:065026. doi: 10.1088/1361-6552/abb346
Sandoval, W. A., Sodian, B., Koerber, S., and Wong, J. (2014). Developing Children’s early competencies to engage with science. Educ. Psychol. 49, 139–152. doi: 10.1080/00461520.2014.917589
Satorra, A., and Bentler, P. M. (2010). Ensuring positiveness of the scaled difference chi-square test statistic. Psychometrika 75, 243–248. doi: 10.1007/s11336-009-9135-y
Scheid, J., Müller, A., Hettmannsperger, R., and Schnotz, W. (2018). “Representational competence in science education: from theory to assessment” in Towards a framework for representational competence in science education. ed. K. L. Daniel (Cham: Springer). 263–277.
Scheid, J., Müller, A., Hettmannsperger, R., and Schnotz, W. (2019). Improving learners' representational coherence ability with experiment-related representational activity tasks. Phys. Rev. Phys. Educ. Res. 15:010142. doi: 10.1103/PhysRevPhysEducRes.15.010142
Stieff, M., Scopelitis, S., Lira, M., and DeSutter, D. (2016). Improving representational competence with concrete models. Sci. Educ. 100, 344–363. doi: 10.1002/SCE.21203
Tam, Y. P., Wong, T. T. Y., and Chan, W. W. L. (2019). The relation between spatial skills and mathematical abilities: the mediating role of mental number line representation. Contemp. Educ. Psychol. 56, 14–24. doi: 10.1016/j.cedpsych.2018.10.007
Tobias, S. (1994). Interest, prior knowledge, and learning. Rev. Educ. Res. 64, 37–54. doi: 10.3102/00346543064001037
Treagust, D. F., Duit, R., and Fischer, H. E. (2017). Multiple representations in physics education, vol. 10. Cham, Switzerland: Springer International Publishing.
Uttal, D. H., Meadow, N. G., Tipton, E., Hand, L. L., Alden, A. R., Warren, C., et al. (2013). The malleability of spatial skills: a meta-analysis of training studies. Psychol. Bull. 139, 352–402. doi: 10.1037/a0028446
Van der Graaf, J., Segers, E., and De Jong, T. (2020). Fostering integration of informational texts and virtual labs during inquiry-based learning. Contemp. Educ. Psychol. 62:101890. doi: 10.1016/j.cedpsych.2020.101890
Zorn, S., and Gericke, K. (2020). Development of Spatial Abilities in Engineering Education: An Empirical Study of the Influence of Visualisation Media. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. 83976:V008T08A032. American Society of Mechanical Engineers.
Keywords: representational competence, conceptual knowledge, undergraduates, STEM education, latent profile analysis
Citation: Edelsbrunner PA and Hofer SI (2024) Examining and comparing the relation between representational competence and conceptual knowledge across four samples. Front. Educ. 9:1459603. doi: 10.3389/feduc.2024.1459603
Edited by:
Ana Susac, University of Zagreb, CroatiaReviewed by:
Hui Luan, National Taiwan Normal University, TaiwanNicolas Hübner, University of Tübingen, Germany
Copyright © 2024 Edelsbrunner and Hofer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peter Adriaan Edelsbrunner, cGV0ZXIuZWRlbHNicnVubmVyQGxtdS5kZQ==
 Peter Adriaan Edelsbrunner
Peter Adriaan Edelsbrunner Sarah Isabelle Hofer
Sarah Isabelle Hofer