Enhancing performance factor analysis through skill profile and item similarity integration via an attention mechanism of artificial intelligence

Introduction: Frequent formative assessment is essential for accurately evaluating student learning, enhancing engagement, and providing personalized feedback. In STEM education, understanding the relationship between skills that students have internalized (mastered) and those they are developing (emergent) is crucial. Traditional models, including item response and cognitive diagnosis models, primarily focus on emergent skills, often overlooking internalized skills. Moreover, new tools like large language models lack a complete approach for tracking knowledge and capturing complex skill relationships.

Methods: This study incorporates artificial intelligence, specifically attention mechanisms, into educational assessment to evaluate both emergent and internalized skills. We propose a modified version of Performance Factor Analysis (PFA), which assesses student abilities by analyzing past responses and comparing them with peer performance on the same items, using parameters from a sigmoid function. This model leverages attention mechanisms to capture item order-based similarity and decay principles, providing a nuanced view of student skill profiles.

Results: The Modified Performance Factor Analysis model significantly improved discriminative power, accuracy, precision, recall, and F1 scores across various skill areas compared to traditional PFA models.

Discussion: These results indicate that the Modified Performance Factor Analysis model allows for a more accurate and comprehensive evaluation of student performance, effectively identifying both emergent and internalized skills. By integrating AI into assessment, educators gain deeper insights, enabling them to refine teaching strategies and better support students' mastery of both types of skills.

1 Introduction

To successfully progress through school, students need to demonstrate flexibility, motivation, persistence, and the ability to learn, transfer, and apply knowledge (Le et al., 2024). Given the dynamic and constantly evolving nature of student knowledge, assessments must assess current proficiency, as well as provide instructors with information about skill mastery, conceptual profiles, and productive learning trajectories for each student.past skill mastery (Le et al., 2024). In addition, high-quality assessments can enhance student learning (Morphew et al., 2020). Thus assessments function as crucial instruments for measuring student learning and directing their learning progress (Hilbert et al., 2021). Through continuous monitoring of student learning, educators can identify those students facing challenges, assess the effectiveness of their own teaching methods, and cultivate a culture of self-regulated learning amongst the students (Bitzenbauer, 2023; Le et al., 2024).

To accomplish all of these goals, assessments must utilize various models to gather and analyze information about students' overall proficiency, conceptual models, and skill mastery. Item Response Models (IRMs), focus on the correlation between latent traits (usually considered to represent student ability or proficiency) and test item responses, crucial for accurate ability and knowledge assessment in diverse fields. Cognitive Diagnosis Models (CDMs) are widely used methods for estimating student skill mastery through the use of Q-matrices that identify the skills needed to correctly answer each item (Chen et al., 2018; Yuen et al., 2023). The primary focus of CDMs like other IRMs is on individual skill mastery rather than sequential skill mastery, meaning that CDMs assume that skills are not correlated with or build on each other.

Knowledge-tracking models, such as Performance Factor Analysis (PFA), allow for the modeling of the correlation of skills with one another, of skill hierarchies, and of changes in student proficiency over time. Recent advancements in hierarchical and longitudinal CDMs have enhanced the ability for CDMs to model skill hierarchies and track changes in student proficiency over time independently (Chen and Wang, 2023; Lee, 2017). However, even with these recent advances CDMs typically do not account for all these factors simultaneously. In contrast, PFA remains distinct in its adaptability, particularly through the integration of attention mechanisms, which allows for the differentiation of skill importance, the handling of polytomous data, and the identification of emergent skills using data-driven approaches. These features position PFA as a robust framework that addresses multiple challenges simultaneously (Pu et al., 2021).

PFAs are adept at monitoring the attempts of students for each item to predict the probability of correct response for the next attempt (Imambi et al., 2021). PFA considers students' past responses to understand the student's performance in each skill (Pavlik et al., 2009; Mehrabi et al., 2023). Given that PFA models are enhanced by incorporating past responses, the accuracy of PFA-based assessments hinges on understanding the impact of the model parameter estimator, the number of parameters, and the explicitly defined skills. These factors are crucial when the assessed skills exhibit meaningful interrelations. A few existing PFA models attempt to model the influence of question order on student responses by incorporating the impact of closely ordered items, there is a lack of models that account for skill similarity in existing models. PFA models uniquely stand out by enabling the individual consideration of each skill.

Large Language Models (LLMs) represent another alternative avenue for evaluating skill development models. The relevance and quality of the questions that LLMs generate hinge upon the integration of methodologies such as automatic retrieval feedback, text structure modeling, and word transformation fusion. However, these approaches often overlook the linkage between emergent skills and the conceptual models held by students for how the skills relate to each other (i.e., skill internalization) (Bitzenbauer, 2023; Essel et al., 2024). This study aims to identify the effects of skill correlations, both internalized and emergent, on students' responses using an attention mechanism. Knowledge tracking models, such as PFAs, are proficient at monitoring students' attempts on each item to predict the probability of a correct response on subsequent attempts (Imambi et al., 2021). PFAs utilize students' past responses to evaluate their performance across various skills (Pavlik et al., 2009; Mehrabi et al., 2023). In efforts to account for the influence of response order, researchers have explored incorporating attention mechanisms into PFA models to consider skill similarity and internalized skills.

The attention mechanism, integrated within neural networks (NNs), exploits their non-linearity to model complex relationships in students' item responses. This approach, commonly employed in Artificial Intelligence (AI), allows for the consideration of the similarity in student responses. By learning high-order patterns, NNs are capable of capturing the non-linear relationships between skills and response behaviors regardless of data distribution with about more than 1000 sample size depending on their network learning approach, which traditional linear models often fail to identify (Richard and Lippmann, 1991; Bressane et al., 2024; Whalon, 2018; Essel et al., 2024).

The research question of this study investigates whether using attention mechanisms can enhance PFA models' abilities to identify both internalized and emergent skills, and to document the interrelations among emergent skills. As far as the authors are aware, this is the first attempt to integrate attention mechanisms within a PFA model to predict student responses by jointly considering skill similarity and inherent skills. This study introduces and evaluates a modified PFA (MPFA) model that incorporates a comprehensive skill profile, including item-skill relationships and skill relation matrices. The MPFA model described here aims to make innovative contributions to assessments in Science, Technology, Engineering, and Mathematics (STEM) education, particularly within computerized adaptive assessments (e.g., Morphew et al., 2018). Additionally, the study has advanced our understanding of how internalized and emergent skills influence student responses, providing a comprehensive approach to evaluating skill development.

2 Literature review

Understanding students' prior knowledge allows instructors to personalize their instruction, to promote active student engagement, and to improve student learning (Hattie and Timperley, 2007; Fischer et al., 2021). Formative assessments allow instructors to continuously measure student proficiency, gather evidence of student learning, and provide students with personalized feedback and targeted learning activities (Fink, 2023; Effiom, 2021). Contemporary adaptive testing frameworks use response weighting to dynamically adjust item difficulty in real-time, tailoring assessments to individual student's current proficiency (Hamilton, 2021). Adapting assessments to students' current proficiency allows for a more accurate estimate of skill mastery and conceptual understanding. In addition, using models that focus on nearby items and conceptually similar items, allows for more accurate skill mastery estimates (Glas, 2008). This approach supports holistic evaluations of cognitive abilities and allows for cognitive diagnostics and learning trajectory mapping (Mindell et al., 2010; Wormald et al., 2009; Scholl et al., 2021).

2.1 Skill development

2.1.1 Internalized and emergent skills

Constructivist learning theories are among the most commonly used theories to understand student learning within STEM. Constructivism portrays learners as bringing pre-existing knowledge and skills into learning environments, then building (constructing) new conceptual understanding that integrate prior conceptual models with the new experiences. The process of constructing new understandings from prior understandings allows students to develop new skills and learn how to transfer old skills to new problems (Allen, 2022). In this paper, skills are defined as measurable demonstrations of procedures that either solve a problem or get a student closer to solving a problem. We further classify skills as either internalized skills or emergent skills. Internalized skills are the skills a student already has mastered when introduced to a new topic. Emergent skills are the skills are skills that are defined by instructors (either explicitly or implicitly) that are new to students or have not yet been mastered in a given learning context. In education, both types of skills must be assessed since they both play key roles in the problem-solving process (Di et al., 2021), and instructors need to understand both to effectively individualize instruction. When educators assess student responses, they expect students to demonstrate specific skills based on the curriculum, learning objectives, and anticipated outcomes of the instructional process (Pu et al., 2021; Liu et al., 2020). However, student often show different ways of understanding that may not match the learning trajectories instructors expect. Students draw from their unique backgrounds, experiences, and thinking processes to answer assessment questions. We refer to these divergences as internalized skills. This diversity in student understanding highlights the complexity of evaluating student responses and underscores the need for a nuanced approach that considers both instructional alignment and the dynamic nature of student development (Silver et al., 2005; Leikin and Lev, 2007; Boaler, 2022). Conversely, similarities in student responses can indicate that students have adopted discipline-specific epistemological approaches, shared cognitive frameworks, and highlight the emergence of relevant academic skills (Kennedy and McLoughlin, 2023; Li, 2022).

2.1.2 Skill relationships

To assess skill mastery, it is necessary to identify the skills being assessed by each item (Wormald et al., 2009; Scholl et al., 2021). Within STEM, skill relationships are often hierarchical, with skills building off one another, such that later skills have greater complexity than earlier skills (Konidaris et al., 2010; Ghozali et al., 2019; Konidaris et al., 2012). For these types of nested skills, it is also necessary to identify the interrelationships between the skills needed within an educational context (Wormald et al., 2009; Scholl et al., 2021).

2.2 Tools of skill development measurement

Various assessment models incorporate item similarities such as Item Response Theory Models (IRTMs), CDMs, NN models, and knowledge tracking models. These models are commonly used to track the evolving knowledge state of students as they engage in learning activities. Multidimensional IRTs and CDMs don't update characteristics during assessments or consider past responses to the last items of the same assessment (Kingsbury and Houser, 1999). CDMs reveal mastery but lack achievement probabilities. deterministic-input, noisy “and” gate as the most popular CDM and multidimensional IRT need adaptation to use prior knowledge in subsequent assessments (Scholl et al., 2021), with a large student population (Mehrabi et al., 2023). NNs are adept at directly predicting student responses (Wu et al., 2021), however, they are less adept at handling skill development.

The efficacy of question generation by language models has been notably affected through the integration of some principal methodologies: First, establishing a linkage between the defined skill or content underlying the questions (Lin et al., 2024). Secondly, the automatic retrieval feedback mechanisms of reinforcement learning, wherein pertinent data is extracted from extensive document collections and assimilated into the generation process to refine outcomes (Lent et al., 2024). Thirdly, text structure modeling techniques, such as analyzing answer positioning and syntactic dependencies, facilitate the creation of questions that are more contextually pertinent (Schubert et al., 2023). This technique identifies and substitutes inflected word forms with their base forms. It also performs operations like generating interrogative words, replicating words from the source text, and transforming words (Kumah-Crystal et al., 2023). While the assessment in STEM considers two important criteria skills relation and makes the border between the inherent and deterministic skills which one of them can be defined by the teachers and the other one should come from the response similarity of students, we need a method that lets us define or refine parameters to let us add both considerations and at the same time maintain the model simplification for the explanation and application in STEM education (Siddiq and Scherer, 2017). Moreover, literature should refer to its handling for its capabilities to handle the inherent skills in the model. The shortcomings of previous models necessitate the use of a model that can address these limitations.

2.2.1 PFA model

PFA constitutes a methodological approach for evaluating student achievement and the complexity of test items, while also allowing for intercorrelations and hierarchical relationships between skills and overall performance outcomes (Yeung, 2019; Gong et al., 2010). This high-level approach ensures that educators and evaluators can obtain a holistic view of educational achievement supporting targeted interventions and informed decision-making processes in academic settings (Pu et al., 2021; Essel et al., 2024). A few attempts to modify PFA in order to address current shortcomings have recently been undertaken. For example, Mehrabi et al. (2023) addressed the issue of effectively analyzing data from small sample sizes by adopting the Nelder-Mead method as a superior optimization technique specifically suited to small populations.

Mehrabi et al. (2023) also highlighted how incorporating multiple skills per item may compromise model precision, however, they found that such complexity could still be rationalized within the medium or larger datasets by selecting a reasonable optimizer of maximum likelihood estimation.

In another example, Gong et al. (2010) advanced the development of PFA to account for both the difficulty level of individual skills and that of the items themselves. Their findings suggest that a PFA model that incorporates item-level difficulty yields slightly greater accuracy than models primarily focused on skill difficulty parameters. This change addressed the challenge of assessing items that necessitate multiple skills significantly complicates the evaluation process.

Gong et al. (2011) and Gong et al. (2010) introduced a non-parametric and selective decay factor by the experts into the model, designed to adjust the impact of items following their position in the sequence. This modification addressed a major issue of the PFA model, which is the sensitivity to positional effects of items (Pavlik et al., 2009). The adjustment made by Gong et al. (2011) and Gong et al. (2010) allows for a more nuanced interpretation of data, recognizing that the significance of an item's success or failure may diminish over time or as subsequent items are attempted.

2.3 Attention mechanism for item similarities components

Pu et al. (2021) critiqued the traditional emphasis on skill-based modeling for its propensity to detract from the detail of item-level insights. In their investigation, they propose moving toward models that leverage attention mechanisms predicated on item sequencing. This approach sidesteps the conventional skill-item interplay in favor of prediction models based purely on response patterns. NN learns different weights of similarity of various parts of the data, which can be the similarity of item vectors and/or skill vectors (Giusti et al., 2022; Essel et al., 2024). Attention mechanisms acknowledge the complex web of skill similarities and dependencies by defining tailored NN. The potential of NNs to understand complex relationships among variables for different IRMs and knowledge-tracking models provides an opportunity to include skill or response similarity as a parameter in the main model (Niu et al., 2021). For example, Yeung (2019) demonstrates how adding skill profile information while considering students' responses to the IRT model enhances the model's capacity to accurately reflect the dynamics of learning and assessment.

The attention mechanism in NN is a mechanism of AI that allows the network to focus on specific parts of the input data. The vectors in attention mechanisms are defined as keys (k), values (v), and queries (q). The query vector represents the element we are focusing on, the key vector represents the elements we compare against, and the value vector holds the actual data we are interested in. By comparing queries and keys NNs that use attention mechanisms assign attention weights to the values, enabling it to selectively focus on relevant information and thus better capture intricate patterns and relationships in the data (Giusti et al., 2022; Battiloro et al., 2023).

The weights that output from NN models that use attention mechanisms bring high-order non-linearity into the models, which leads to better regularization and smoother learning curves (Battiloro et al., 2023; Pu et al., 2021). This regularization helps models like PFA be more robust to noise, reduces model sensitivity, and uncovers deeper meaning from the data and item relations, improving accuracy (Battiloro et al., 2023; Pu et al., 2021). Within this framework, the literature reveals an unaddressed need for an advanced Performance Factor Analysis (PFA) model capable of segregating items' skill profiles while incorporating the impact of item spacing on the probability of a correct response.

3 Methodology

3.1 PFA model and parameters

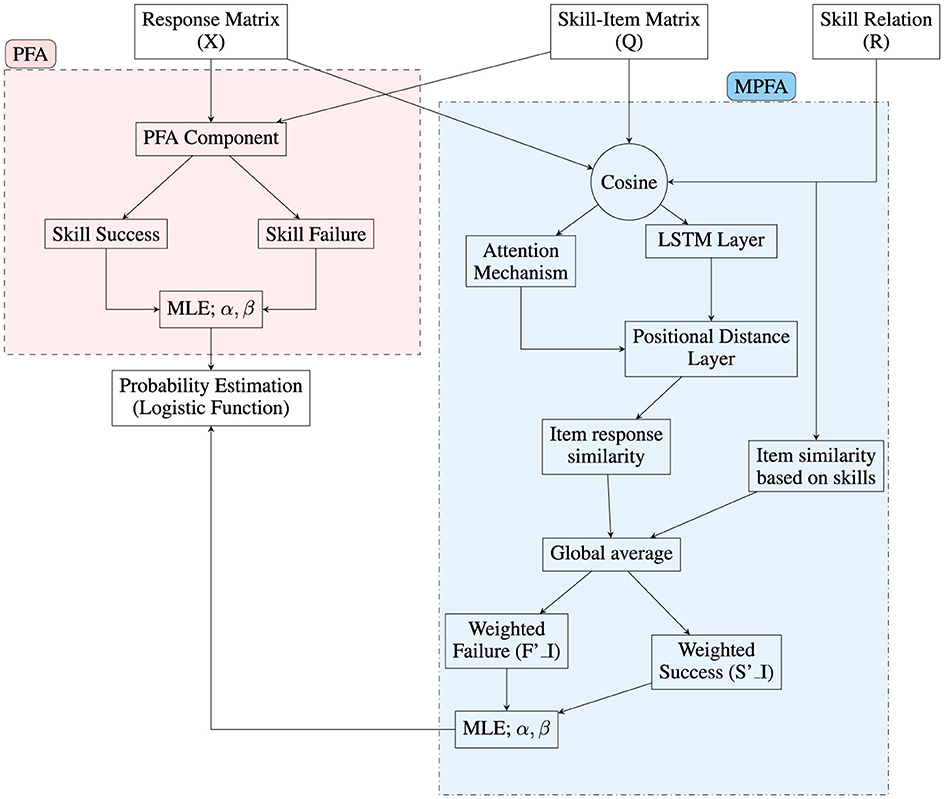
The PFA model assumes that each item response is independent and follows a Bernoulli distribution. Equation 1 indicates the probability of success in one item depending on the student's mastery level for a specific skill or attribute. This approach allows for an effective estimation of both attribute difficulty and the student's ability level as an arrangement of parameters like α_j and ρ_j. In Equation 1, P_a(j) represents the likelihood of proficient performance in skill j, with the sigmoid function denoted by σ(·). The parameter α_j characterizes the bonus arising from successful responses to skill j items across all students. Likewise, ρ_j signifies the penalty incurred from unsuccessful responses across all students. The β_j parameter indicates the difficulty level of skill j based on the aggregated responses of all students to items associated with that skill (Mehrabi et al., 2023). F_ij and S_ij represent the counts of failures or incorrect responses and successes or correct responses, respectively, for student i on items associated with skill j.

$\begin{array}{ll}{P}_a(j)=\sigma ({\alpha }_j·{\text{S}}_{ij}+{\rho }_j·{\text{F}}_{ij})& (1)\end{array}$

To estimate the three model parameters in Equation 1, Maximum Likelihood Estimation (MLE) is commonly used. Mehrabi et al. (2023) indicated that the Neild Mead and Newton optimizer can handle a wide range of populations from small to big population. Instead of MLE, the PFA model considers α_j·S_ij+ρ_j·F_ij as the θ in the sigmoid function and a bias parameter as β which also indicates the difficulty of θ achievement (Yeung, 2019; Mehrabi et al., 2023). WF_ij (Weighted Failure) and WS_ij (Weighted Success) are metrics that aggregate the influence of previous failures and successes, respectively, by weighting each response according to its similarity with the current item.

$\begin{array}{ll}P({\theta }_i)=\frac{1}{exp(-{\theta }_i-{\beta }_i)}& (2)\end{array}$

Pu et al. (2021) implemented an attention mechanism to discern item similarities, integrating additional weights based on item similarities and Positional Encodings as an alternative to Gong et al. (2011)'s decay factor approach. The decay factor, criticized for its lack of a transparent calculation methodology, raises concerns about its efficacy, particularly as it may lead to significant information loss with an increasing number of items. This issue is further exacerbated by the attention mechanism's potential to overlook pertinent information. For instance, in an assessment comprising 30 items, items 4 and 16 might share identical skill profiles. Relying solely on the decay factor or narrowly focusing on the most recent similar items could result in the omission of critical data, thereby compromising the model's ability to accurately predict the response for item 16. The probability of a correct response, P_a(j), is given by the Equation 3. Where σ(·) denotes the sigmoid function, capturing the likelihood of successful performance in skill j by student i, with α and ρ representing parameters that account for the effects of weighted success and failure, respectively.

$\begin{array}{ll}{P}_a(j)=\sigma (\alpha ·W{S}_{ij}+\rho ·W{F}_{ij})& (3)\end{array}$

The weight of similarity between two items replaces the decay factor, focusing on the Weighted Success (WS_ij) and Weighted Fail (WF_ij) for student i on item j (Pavlik et al., 2009). In the proposed methodology, the traditional metrics of success and failure are re-envisioned through the lens of Weighted Success (WS_ij) and Weighted Failure (WF_ij), which ignore the simplistic vision of correct and incorrect responses in favor of a nuanced consideration of item similarities (Equations 4, 5). R_ik is a binary indicator where R_ik = 1 for a correct response and R_ik = 0 for an incorrect response by student i on item k.

$\begin{array}{ll}{\text{WS}}_{ij}={\displaystyle \sum _{k=1}^{j-1}}{R}_{ik}·{\text{W}}_{jk}& (4)\end{array}$

$\begin{array}{ll}{\text{WF}}_{ij}={\displaystyle \sum _{k=1}^{j-1}}(1-R_{ik})·{\text{W}}_{jk}& (5)\end{array}$

This methodology combines both skill similarity and response similarity to refine the analysis by considering the distance of each pair of items. The concern about the response similarity arises from the realization that traditional frameworks, such as the Q-matrix and skill relation defined by educators, may not comprehensively represent the spectrum of skills students utilize when addressing questions (Chiu, 2013; Macdonald and MacLeod, 2018). These frameworks typically link each test item to specific cognitive skills or attributes necessary for a correct response. Particularly in disciplines like Physics and Mathematics, students may draw on a blend of explicitly taught and intuitively applied skills, analyzing similarly patterned responses critically (Chiu, 2013). The skill profile similarity captures the similarity in the items according to the assigned skills that the instructor expects students to apply in answering the item. By adopting a global average across these two dimensions, the model navigates the complexity of student answers (Chiu, 2013). This approach is particularly at mitigating the impact of overlap in responses that, while categorized under a single skill, may share similarities due to students' uniform strategies. Additionally, the integration of an attention mechanism within this framework facilitates the nuanced calculation of Weighted Success (WS_ij) and Weighted Failure (WF_ij), further refining the analysis by adjusting for anomalies in similarity and dissimilarity. The sigmoid function for modified PFA is defined as Equation incorporating the effects of item difficulty:

$\begin{array}{ll}P({\theta }_i)=\frac{1}{exp(-{\theta }_i-{\beta }_i)}& (6)\end{array}$

3.2 Attention mechanism

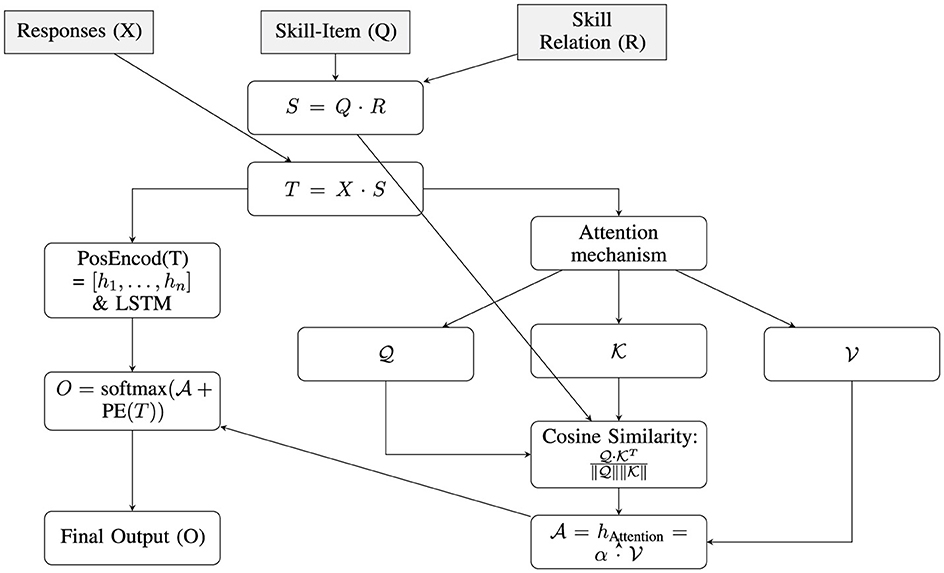
We employ one attention mechanism and one cosine similarity calculation to analyze the interplay of student responses and item skills, thereby enhancing the effectiveness of our evaluations. Each mechanism is designed to address different aspects of the educational data, focusing on student response similarities and skill similarities, respectively (Braun et al., 2018).

In our model, the global average of the attention mechanism is computed by aggregating information from skill and response similarities. The model inherently addresses this imperative by prioritizing content and structural alignment, facilitated through cosine similarity calculations. The global average operation is a pivotal component in the model's architecture, serving as a bridge between the high-dimensional output of the attention mechanism and the subsequent layers of the model. The output of the attention mechanism weight or similarity is denoted as $\mathcal{A}$, which is a function of the input sequence $\mathcal{X}$, and the positional encoding as $\mathcal{P}ℰ(\mathcal{X})$. The combined output O can be represented as:

$\begin{array}{ll}O=\text{softmax}(A+\mathcal{P}ℰ(\mathcal{X}))& (7)\end{array}$

This operation ensures that the attention mechanism's output is modulated by the positional encoding, thereby incorporating positional information into the model's understanding. The global average, denoted as G, is computed as:

$\begin{array}{ll}G=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{O}_i& (8)\end{array}$

where N is the total number of elements in the output O, and O_i is the i-th element of O. The O_i are the similarity weights of the Student Response Similarity Attention Mechanism (Section 3.3) and the Skill Similarity analysis (Section 3.4).

3.3 Student response similarity attention mechanism

For the first attention mechanism, we focus on the similarities among student response vectors to indicate that there are some skills that may not be captured by the emergent skills of teachers. Pu et al. (2021) indicates that the response similarity is an accurate indicator of underlying skills but may find more information about the skills that weren't considered in emergent skills. This mechanism is crucial for identifying patterns in how students respond to various assessment items, which can help in assessing their understanding and predicting future performances (Nguyen et al., 2023; Niu et al., 2021). The proto-feature tensor Z_P, representing student responses, is reshaped into a tensor of size 1 × n×d to maintain the dimensionality n of the data in the attention output h_a:

$\begin{array}{l}{q}^{*}=Z_P·{\theta }_{q^{*}}^T;\\ k=Z_P·{\theta }_k^T;\\ v=Z_P·{\theta }_v^T;& (9)\end{array}$

Here, ${\theta }_{q^{*}}$, θ_k, and θ_v are weight matrices that transform the student response features into query, key, and value representations (Nguyen et al., 2023; Niu et al., 2021). The attention output h_a for the student response similarity is then computed using the “Softmax Attention” mechanism:

$\begin{array}{ll}{h}_a^{S_{\text{Att}}}=\text{softmax}\left[(q^{*}·k^T)/d\right]·v,& (10)\end{array}$

q identifies which student responses to prioritize across items, k encapsulates the comparison criteria among these responses, and v contains the actual student response information. In our student response similarity mechanism, the conventional softmax attention, which typically involves computing the dot product of the query q^* and key k^T vectors, has been adapted to incorporate cosine similarity. This alteration mitigates issues related to the magnitude of feature vectors that can cause instability in the similarity scores and gradient problems during training (Nguyen et al., 2023; Niu et al., 2021). The adjusted attention calculation, now termed “Cosine Attention” for student responses (C_{Att, student}), is represented as:

$\begin{array}{ll}{h}_a^{C_{\text{Att, student}}}=\left[(q^{*}·k^T)\oslash (||q^{*}||||k||)\right]·v,& (11)\end{array}$

Here, the cosine similarity calculation normalizes the dot product by the magnitudes of the query and key vectors, focusing the attention strictly on the directional alignment of the features rather than their lengths. This ensures that the attention scores reflect the true content relevance between student responses, improving the stability and accuracy of the output attention map $\mathcal{A}$ (Nguyen et al., 2023; Niu et al., 2021).

3.4 Skill similarity analysis

The second similarity analysis examines the relationships between items and skills through a structured, matrix-based approach. The primary data components involved are the skill-item matrix (M) and the skill-skill (skill relation) matrix (T). The skill-item matrix, an n×m matrix where n represents the number of items and m represents the number of skills, captures the extent to which each item is associated with each skill. The skill-skill (relation) matrix, an m×k matrix where k = m represents the number of skills, defines the hierarchical dependencies among the skills. The skill-item matrix is first transposed to derive meaningful skill profiles for each item, resulting in a m×n matrix. This transposition ensures proper alignment for matrix multiplication. The transposed skill-item matrix is then multiplied by the skill-skill (skill relation) matrix, yielding a skill profile matrix (S) with dimensions n×k. Each row in this matrix encapsulates the skill profile of a corresponding item, integrating the original skill associations with the hierarchical structure defined in the skill relation.

To assess the similarities between items based on these skill profiles, we employ the dot product similarity measure. This involves calculating the dot product of the S with its transpose (S^T), resulting in an item similarity matrix (τ) of dimensions n×n. Each element τ_ij in this matrix represents the similarity between item i and item j. The dot product operation for two vectors u and v of length k is defined as the sum of the products of their corresponding elements:

$\begin{array}{ll}u·v={\displaystyle \sum _{i=1}^k}{u}_i{v}_i& (12)\end{array}$

Here, u and v represent the skill profile vectors of two items, each containing k elements that quantify the items' associations with each skill in the skill relation. Applied to our matrices, this calculation involves summing the products of corresponding elements in the skill profiles of items i and j:

$\begin{array}{ll}{\tau }_{ij}={\displaystyle \sum _{l=1}^k}{S}_{il}·S_{jl}^T& (13)\end{array}$

This computation (τ) is performed for all pairs of items, resulting in a comprehensive matrix that quantifies the similarities between all items based on their skill profiles.

3.5 Items positional encoding

Despite deep learning architectures leveraging attention mechanisms, these mechanisms alone do not inherently account for the sequence order and item distances. Our model by positional encoding ($\mathcal{P}ℰ(\mathcal{X})$) addresses this gap by incorporating a signal into the data representation, indicating each element's position. $\mathcal{P}ℰ(\mathcal{X})$ enables the model to comprehend how element order affects the output, facilitating the recognition of both immediate and distant element relationships within a sequence (Vaswani et al., 2017; Anderson et al., 2018). In modified PFA, the similarity of two items, or in other words Weighted Success (WS_ij) and Weighted Failure (WF_ij) also depends on the $\mathcal{P}ℰ(\mathcal{X})$.

The attention scores are initially computed using a standard attention formula, involving softmax applied to the dot products of query and key vectors. These scores are then adjusted by learned parameters a and b, reflecting the influence of both response and skill dynamics:

$\begin{array}{ll}{W}_{ij}=\text{Softmax}(A_{ij}+\mathcal{P}ℰ(\mathcal{X}))& (14)\end{array}$

Pu et al. (2021) introduced a positional distance metric to quantify the temporal closeness of a preceding item, expressed as $\mathcal{P}ℰ{(\mathcal{X})}_{i,t+1}=-a(t-i+1)+b$. Here, t−i+1 delineates the positional disparity between the response of item x_i and the subsequent item response x_t+1, while a and b are modifiable parameters. Here, a and b are trainable scalar parameters that are applied as coefficients in a linear transformation to the input data. ${\mathcal{A}}_{ij}$ represents the attention matrix values, while ${\mathcal{W}}_{ij}$ denotes the adjusted attention or weighted attention, taking into account the item position (Pu et al., 2021).

For the attention mechanism analyzing student response similarities, the LSTM is trained on features that include student response vectors and associated probabilities. For the attention mechanism focused on item-skill relationships, the LSTM is trained using a combination of the item-skill association matrix S and student response vectors. The vectors encapsulate student answers or choices, along with probabilities reflecting their likelihood of choosing certain responses based on past performance or question difficulty and enabling the LSTM to learn to associate and weigh various skills to their responses. The coefficients a and b for this mechanism are specifically tuned to enhance the model's ability to dynamically adjust attention based on how students respond to different types of questions over time (Vaswani et al., 2017; Anderson et al., 2018).

3.5.1 Detailed LSTM network architecture and dynamics

The LSTM's architecture leverages backpropagation through time (BPTT) to update its parameters, applying the principles of backpropagation to sequences by propagating errors backward across multiple time steps. This enables LSTM models to capture long-term dependencies and temporal patterns effectively while adjusting weights based on gradient descent (Richard and Lippmann, 1991). The architecture of the LSTM network is intricately designed to manage and process sequences by capturing temporal dependencies. At each timestep t, the LSTM cell updates its internal states based on the current input, previous hidden state, and previous cell state (Nguyen et al., 2023; Sherstinsky, 2020). In our LSTM models, each component is finely tuned to handle specific aspects of educational data, focusing on student responses and item skills. The input gate regulates the influx of new information based on the current input, x_t, which consists of probabilities tied to various student responses in our X2_train dataset. These probabilities inform the model at each timestep, guiding how it should adapt and respond to changing educational scenarios. The forget gate plays a pivotal role in managing memory by determining which parts of the previous cell state, c_t−1, should be retained or forgotten (Nguyen et al., 2023; Sherstinsky, 2020; Lee and Kwon, 2024). This process ensures that only pertinent historical information is preserved, helping the LSTM maintain a focused state that is not cluttered with irrelevant data. The output gate then decides which parts of the updated cell state, c_t, are crucial for forming the hidden state, h_t, which will be used for predictions or passed to subsequent layers. This gate is key in determining how the model interprets and uses the processed information to make informed predictions about student performance or other related metrics. Simultaneously, the cell state receives updates from the cell input, g_t, which incorporates both new information and data retained from the past, providing a balanced approach to state updates (Nguyen et al., 2023; Sherstinsky, 2020). This ensures that the model remains adaptable yet consistent with historical trends. The mathematical formulation for these operations is:

$\begin{array}{l}{i}_t=\sigma (W_{xi}{x}_t+W_{hi}{h}_{t-1}+b_i)\text{ (Input Gate)}\\ f_t=\sigma (W_{xf}{x}_t+W_{hf}{h}_{t-1}+b_f)\text{ (Forget Gate)}\\ o_t=\sigma (W_{xo}{x}_t+W_{ho}{h}_{t-1}+b_o)\text{ (Output Gate)}\\ g_t=\tanh (W_{xc}{x}_t+W_{hc}{h}_{t-1}+b_c)\text{ (Cell Input)}\\ c_t=f_t\odot c_{t-1}+i_t\odot g_t\text{ (Cell State Update)}\\ h_t=o_t\odot \tanh (c_t)\text{ (Hidden State Update)}& (15)\end{array}$

3.5.2 Dynamic positional encoding ($\mathcal{P}ℰ(\mathcal{X})$) derived from LSTM outputs and learning parameters a and b through training

By encoding positional information directly from the LSTM outputs achieved through a transformation function:

$\begin{array}{ll}{\mathcal{PE}}_t=f(h_t;{\theta }_{pe})& (16)\end{array}$

Here, f represents a transformation function parameterized by θ_pe, which is optimized during training. This function transforms the LSTM's output h_t at each timestep t into a $\mathcal{P}ℰ(\mathcal{X})$ that captures not only the absolute position of each data point but also incorporates learned contextual nuances. The training process is meticulously designed to optimize via Adam optimizer both the LSTM architecture and the coefficients a and b which dynamically adjust the attention mechanism's focus (Nguyen et al., 2023; Sherstinsky, 2020). Equation 17 outlines how the LSTM's output h_t is mapped to parameters a and b through a fully connected layer, where W_y represents the weights and b_y the biases.

$\begin{array}{ll}{y}_t=W_y{h}_t+b_y& (17)\end{array}$

3.6 Updating success and failure using attention weights for MPFA

The update process transforms the attention weights into MPFA by utilizing the cumulative similarity weights to appropriately adjust the S and F matrices. We define a cumulative response similarity weight, ${\mathcal{W}}_{\mathrm{\text{cumulative}}}(j)$, which integrates both positional encoded response similarity (Equation 14) and a cumulative skill similarity weights, τ_cumulative(j) (Equation 13). These cumulative similarity weights are shown in following Equations:

$\begin{array}{ll}{\mathcal{W}}_{\text{cumulative}}(j)=\frac{1}{j-1}{\displaystyle \sum _{k=1}^{j-1}}{\mathcal{W}}_{jk}.& (18)\end{array}$

$\begin{array}{ll}{\tau }_{\text{cumulative}}(j)=\frac{1}{j-1}{\displaystyle \sum _{k=1}^{j-1}}{\tau }_{jk}.& (19)\end{array}$

The global average similarity weight for each item, denoted as λ_{global_average}, following Equation 8, is computed as a global average of the cumulative positional encoded response similarity ${\mathcal{W}}_{\mathrm{\text{cumulative}}}$ and the skill similarity τ_jk:

$\begin{array}{ll}{\lambda }_{\text{global\_average}}=\frac{{\mathcal{W}}_{\text{cumulative}}(j)+{\tau }_{\text{cumulative}}(j)}{2}.& (20)\end{array}$

In this manner, the global average reflects a combined influence of empirical response similarity (Equation 14) and skill similarity (Equation 13). This allows the model to account for both item-level and skill-level relationships (Braun et al., 2018). The weighted success WS_ij and weighted failure WF_ij matrices are then updated from Equations 4, 5 using the global average similarity weight λ_{global_average}:

$\begin{array}{ll}{WS}_{ij}={\displaystyle \sum _{k=1}^{j-1}}(R_{ik}·{\lambda }_{\text{global\_average}}),& (21)\end{array}$

$\begin{array}{ll}{WF}_{ij}={\displaystyle \sum _{k=1}^{j-1}}((1-R_{ik})·{\lambda }_{\text{global\_average}}).& (22)\end{array}$

Here, R_ik represents whether the student i responded correctly (R_ik = 1) to item k. These new weights are utilized in the MPFA model (Equation 3). The use of the global average similarity weight λ_{global_average} provides a comprehensive view of how students' skill mastery evolves, influenced by both empirical response data and conceptual skill similarities.

3.7 Settings of study

Our research endeavors to evaluate the modified PFA (MPFA) by employing an attention mechanism computed directly from two main sources: item response similarity to fulfill the inherent skills (discussed in Section 3.3) and skill-based similarity of items to fulfill the emerged skills (outlined in Section 3.4), while also integrating positional encoding (elaborated upon in Section 3.5). Through this approach, we have developed a hard self-attention mechanism (described in Section 3.2) to handle the parameterization of the MPFA. These two components are then combined within the model's global average operation, where the Q-matrix weights and the attention-generated similarity weights are synthesized to create a unified output. This process ensures that both emerging and internalized skills are integrated into the overall skill profile utilized for predictions, enabling the model to adaptively incorporate structured instructional objectives while accounting for the unique prior knowledge that students bring to the learning environment. Subsequently, leveraging actual response data, an item-skill matrix, and a skill relation matrix, we employed the Maximum Likelihood Estimator (MLE) to calibrate PFA and MPFA model (Figure 1).

Figure 1

Figure 1. Process of MPFA and PFA.

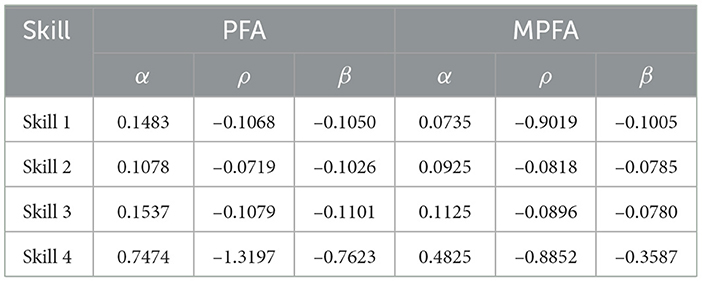
The research methodology is grounded in the analysis of authentic responses from 5,500 students who completed the Force and Motion Conceptual Evaluation (FMCE) physics assessments via the LASSO platform, encompassing data from various schools across the United States (Le et al., 2024). The use of real-world data introduces inherent variability, offering a realistic depiction of student performance and enabling the detection of similarities in response patterns for items with non-similar skills. Such nuanced relationships are often hard to achieve by simulated datasets, which are limited to predefined skill structures and may fail to capture emergent similarities beyond the scope of these defined constructs (Essel et al., 2024; De La Torre, 2009). The FMCE is a linear 47-item physics test tailored for assessing introductory undergraduate mechanics courses (Thornton and Sokoloff, 1998) and is one of the most widely used conceptual inventories used in physics education research to study students' conceptual understanding in physics (e.g., Wells et al., 2020). Each question within the test presents four options from which the respondent can select. Table 1 indicates the distinct skills identified by content experts and evaluated using model fitting measures such as RMSE, accuracy, and F1 as detailed in Le et al. (2024). The four identified skills represent the underlying procedural and conceptual tasks that are common across different content areas. Furthermore, a skill relation, conceptualized by subject matter experts, delineates the hierarchical relationship among these skills; this framework is elucidated in Table 2. While the skill relation is the relation of the skills together defined by the expert. The nexus between individual test items and the identified skills is documented comprehensively in Supplementary Table 1. Responses of 5,500 students to these items are indicated in Supplementary Table 2.

Table 1

Table 1. List of physics FMCE skills.

Table 2

Table 2. Skill relationship matrix.

For positional encoding purposes, the data is split into a training set (70%) and a testing set (30%), ensuring that while the model has ample data to learn from, it is also rigorously tested on unseen data to evaluate its generalizability and robustness configured with 128 units. The choice of cross-entropy as the loss function is particularly apt for classification tasks inherent in analyzing response similarities and skill relationships. The LSTM models were trained on a workstation running Windows 11 Version 10.0.22631, 12th Gen intel(R) core (TM)i7-1255U, 1,700 MHz 10 core(s), equipped with 16 GB of RAM and an SSD for optimal data processing speeds on google collaboratory environment (Manaswi and Manaswi, 2018). The code that runs the LSTM, the attention mechanism, and the skill similarities are described in Supplementary material (Sections 2.1, 2.2, and 2.3) and the LSTM model details are in Section 1.1 of Supplementary material (Figure 2 indicates the process of attention mechanism and positional encoding). The initial test size is set to 0.4. For attention layer purposes, the cosine attention layers are defined by the PyTorch library (Imambi et al., 2021). The model configurations are the same as the LSTM and run on the same code. data configured with 128 units with 20 epochs. The code Script of this layer is indicated in Section 2.1 of Supplementary material. Moreover, the global average and weighted S and F are captured by the following Python script by numpy library (Betancourt et al., 2019) and Pandas (Harrison and Petrou, 2020) indicated in Section 2.2 of Supplementary material.

Figure 2

Figure 2. Process of attention mechanism and positional encoding in MPFA.

4 Results

4.1 Similarity weights between the items of the attention mechanism

4.1.1 Methodology of clustering response similarity

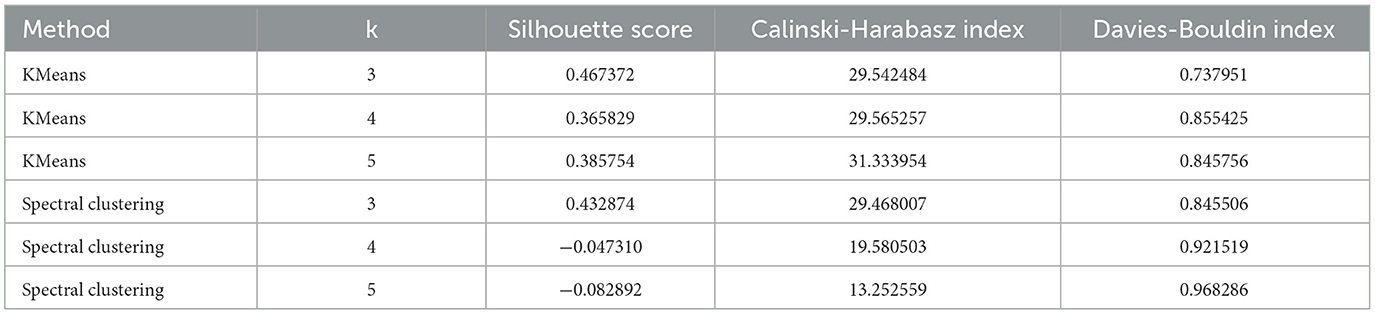
Tonio and Francesca (2016) and Liu et al. (2020), to determine the number of attributes underlying the item for similarity scores, apply the clustering methods like K-mean. Firstly, we convert the similarity matrix into a distance matrix (1-similarity matrix), as clustering algorithms require measures of dissimilarity. Outliers are identified and removed using Z-scores with a threshold of 3, which enhances the robustness of our clustering results. To reduce the dimensionality of the data and facilitate visualization, Principal Component Analysis is applied, focusing on the first two principal components. This step involves finding the principal components that capture the most variance in the data. The original distance data is projected onto these principal components, reducing the data to a 2-dimensional space while preserving the most significant information (Tonio and Francesca, 2016). We employ the K-means algorithm for clustering across a range of cluster numbers (from k = 2 to k = 10). The Sum of Squared Errors (SSE) is plotted against the number of clusters to identify the “elbow point” where the rate of decrease sharply slows, indicating the optimal number of clusters. This method is well-documented for its effectiveness in determining the point at which adding more clusters does not significantly improve the clustering solution (Daffertshofer et al., 2004). Concurrently, the Silhouette Score is calculated for each k to evaluate the quality of the clustering solutions. The Silhouette Score measures how similar an object is to its cluster compared to other clusters, with values ranging from -1 to 1. Higher values indicate better-defined clusters. By plotting the average Silhouette Scores, we can determine the number of clusters that maximize this score, providing a robust method to validate the optimal number of clusters (Daffertshofer et al., 2004). The Calinski-Harabasz Index, which assesses cluster separation and cohesion, and the Davies-Bouldin Index, which evaluates the average similarity ratio of clusters, are also utilized to further confirm the clustering quality. The elbow and Silhouette score and measurement accuracy are indicated in Table 3 and in Figure 3.

Table 3

Table 3. Clustering performance metrics for different methods and cluster sizes.

Figure 3

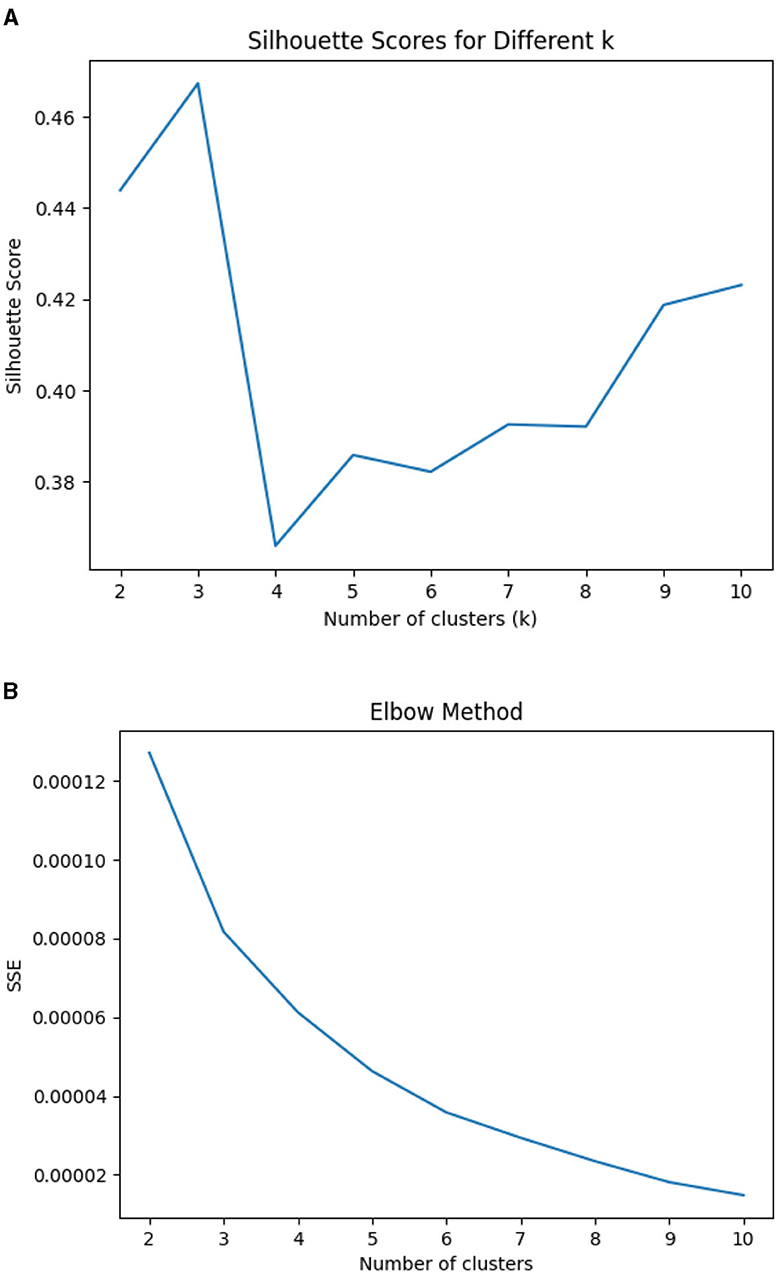
Figure 3. Clustering performance metrics for different methods and cluster sizes by Elbow and Silhouette scores. (A) Silhouette scores for different k in K-mean clustering. (B) Elbow for different k in K-mean clustering.

The Elbow Method plot (Figure 3B) revealed that the most significant decrease in SSE occurred at three clusters, suggesting that this number adequately captures the data's inherent structure without overfitting. This was further supported by the Silhouette Score analysis (Figure 3A), where the highest score was observed with three clusters, indicating well-defined and meaningful clusters. The sharp drop in Silhouette Scores beyond three clusters corroborated the elbow point, affirming that adding more clusters did not significantly improve clustering quality. Comparisons with other clustering methods showed that K-Means with three clusters provided the most coherent clustering. This approach does not indicate the same number of skills that are assigned to the items. Specifically, K-Means achieved a Silhouette Score of 0.467, the highest among the evaluated methods. This method also had a Calinski-Harabasz Index of 29.54 and a Davies-Bouldin Index of 0.74, indicating strong clustering performance. In contrast, Spectral Clustering with three clusters yielded a Silhouette Score of 0.433 and a Calinski-Harabasz Index of 29.47, slightly lower than K-Means. Spectral Clustering with four and five clusters performed poorly, with negative Silhouette Scores and lower Calinski-Harabasz Indices. Based on these metrics, K-Means with three clusters is the optimal choice for the given data, providing the best balance between cluster cohesion and separation.

4.2 Training $\mathcal{P}ℰ(\mathcal{X})$ by LSTM

The ROC curve shows how well a model distinguishes between positive cases (correct predictions) and negative cases (incorrect predictions), and the AUC (Area Under the Curve) quantifies this, with higher values indicating better performance in making this distinction. The LSTM model, focused on analyzing similarities among student response vectors, exhibits a similar trend of performance enhancement but at a slightly slower rate when compared to the first. The receiver operating characteristic (ROC) curves for this model, also resembling a quarter circle, are depicted in Figure 4A. Despite the slower rate of improvement, the model maintains a comparable level of discrimination ability, as evidenced by the shape of its ROC curve.

Figure 4

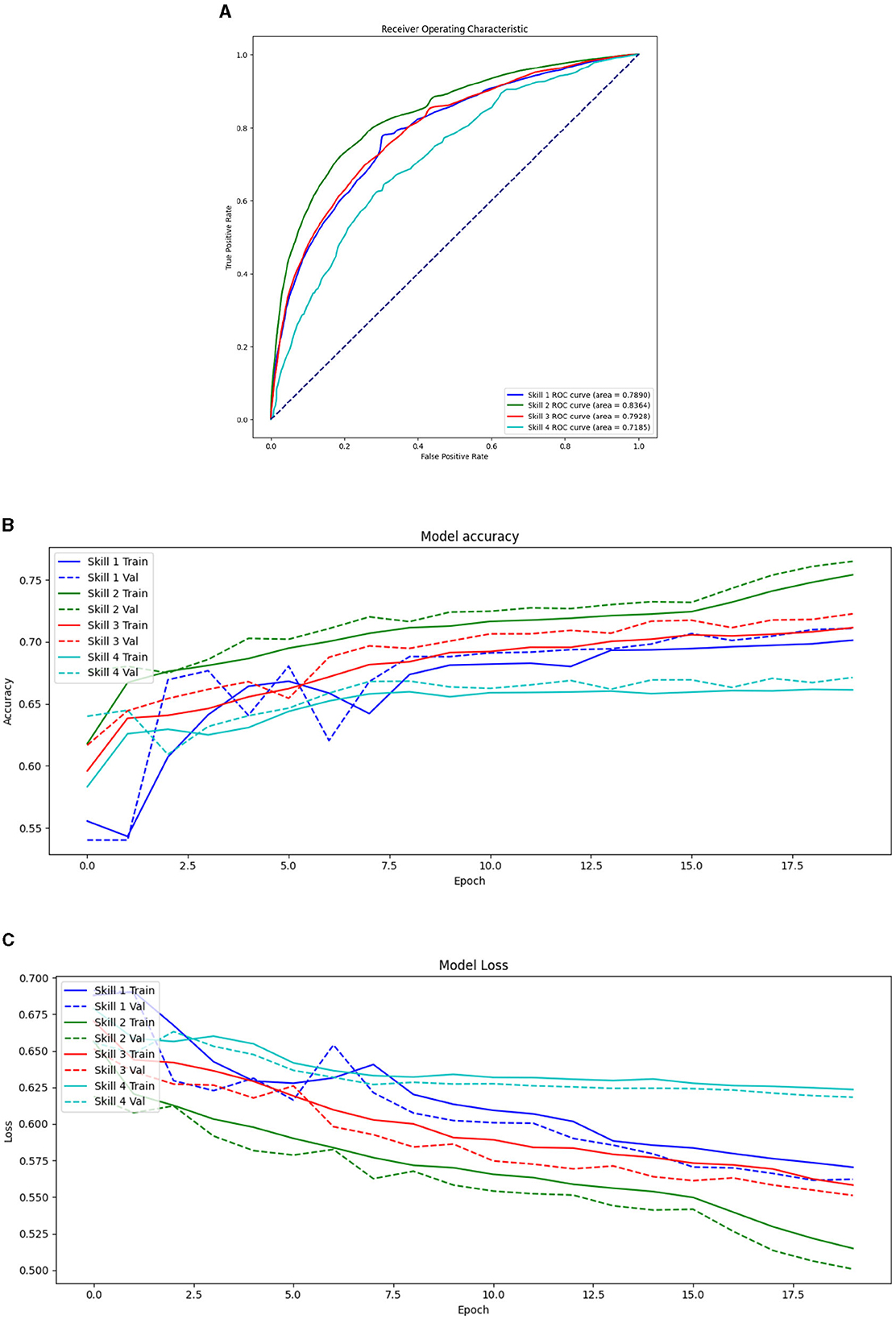
Figure 4. Model fit of the LSTM for skill profile similarities. (A) ROC curve. (B) Loss curve. (C) Accuracy curve.

For Skill 1, the ROC curve shows an area under the curve of 0.7890, indicating reasonably acceptable performance in distinguishing between positive and negative cases. Skill 2 exhibits the highest AUC of 0.8364, demonstrating the model's strong ability to differentiate between classes for this skill. Skill 3, with an AUC of 0.7928, shows performance similar to Skill 1, reflecting a competent but not exceptional discrimination ability. In contrast, Skill 4 has the lowest AUC at 0.7185, suggesting the model has the least effectiveness in distinguishing between classes for this skill (Figure 4A). The loss plots depict the model's performance in minimizing the error for both training and validation datasets. Solid lines represent training loss, while dashed lines indicate validation loss. The training and validation loss for Skill 1 decreases over time, but the gap between them suggests overfitting. Skill 2 shows the lowest training and validation loss, consistent with its high accuracy and AUC, indicating effective learning and generalization. Skill 3 has a moderate loss reduction with a small gap between training and validation loss, reflecting a balanced learning process. The loss for Skill 4 is the highest, with a significant gap between training and validation loss, indicating poor learning and generalization (Figure 4C). The accuracy plots provide insights into how well the model is learning over time for both training and validation datasets. Solid lines denote training accuracy, while dashed lines indicate validation accuracy. The accuracy for Skill 1 shows a steady increase over epochs; however, noticeable fluctuations in validation accuracy could indicate overfitting. Skill 2 shows the highest training and validation accuracy among all skills, suggesting the model learns and generalizes well for this skill. Skill 3 has a moderate accuracy trajectory with less fluctuation in validation accuracy compared to Skill 1, indicating a more stable learning process. Conversely, the accuracy for Skill 4 is consistently the lowest, revealing the model's difficulty in learning patterns for this skill, with fluctuations in validation accuracy further indicating potential overfitting issues. Skill 2 stands out with the best overall performance, evidenced by its highest AUC, accuracy, and lowest loss, indicating effective pattern recognition and generalization capabilities. On the other hand, Skill 4 shows the poorest performance, with the lowest AUC, accuracy, and highest loss, suggesting the model struggles to learn the patterns associated with this skill. Skills 1 and 3 exhibit moderate performance, with Skill 1 showing signs of overfitting, while Skill 3 appears to have a more stable learning process (Figure 4B).

4.3 Model fit comparison

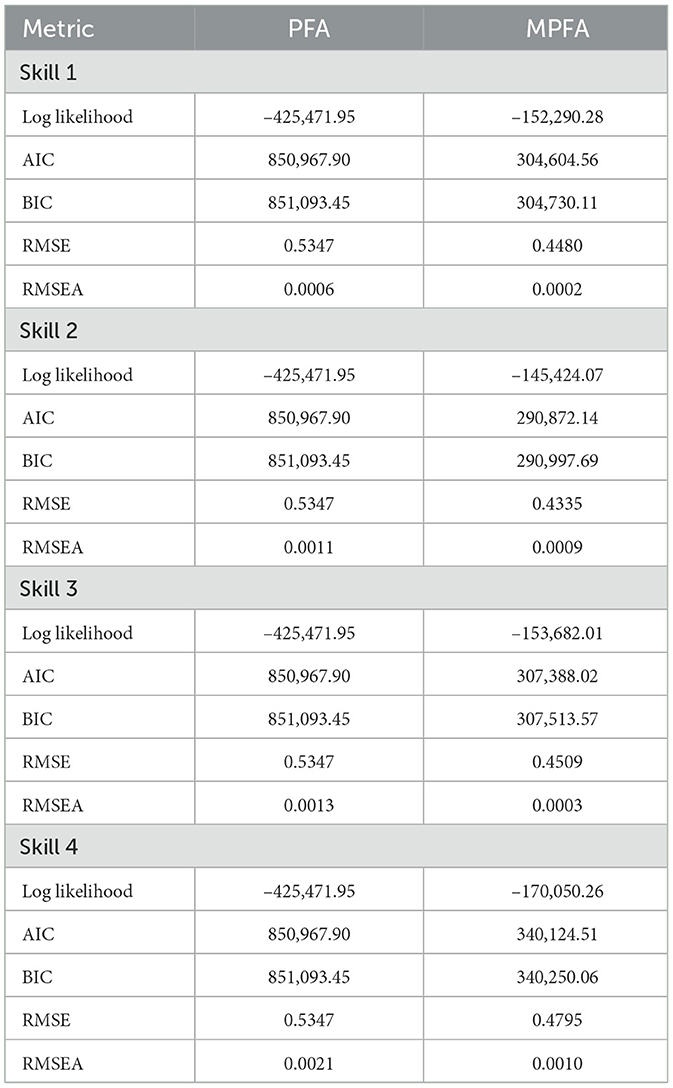
To evaluate the Modified PFA model, it is essential to compare its performance with the traditional PFA model. We start by assessing student responses using the PFA model. The initial parameter values for α, ρ, and β are set to 0.1, -0.1, and -0.1, respectively. Model fit statistics are presented in Table 4, while the estimated parameters for each skill are provided in Table 5. MPFA demonstrates a substantial improvement in log likelihood, suggesting a stronger fit to the data compared to the original PFA. This improvement is significant as it underscores MPFA's enhanced capability in capturing the underlying dynamics of the dataset. The reductions in both the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) further highlight the efficiencies achieved by MPFA (Table 4). The decrease observed in the Root Mean Square Error (RMSE) with MPFA points to a heightened accuracy in predictions. A lower RMSE indicates that the average magnitude of the errors between predicted values and observed values has diminished, reflecting a model that aligns more closely with the practical aspects of the data. The Root Mean Square Error of Approximation (RMSEA) shows only a marginal improvement in MPFA. The slight decrease in RMSEA corroborates the enhanced fit to the data's overall structure, though it does so without significant deviation from the original model's performance (Table 4). MPFA's performance across all evaluated skills suggests it is a more reliable and robust model for educational assessments.

Table 4

Table 4. Comparison of statistical metrics for PFA and MPFA.

Table 5

Table 5. Comparison of PFA and MPFA parameters per skill.

According to the parameter values in Table 5, in Skill 1, 2, and 3 of the PFA model, correct responses moderately enhance skill development mastery (α) while incorrect responses detract significantly from skill development mastery (ρ). MPFA, on the other hand, offers lower (α) values, potentially diminishing the nuanced impact of both correct and incorrect answers. In Skill 4, PFA displays significantly higher coefficients for both positive and negative reinforcement, highlighting the skill's sensitivity to accuracy while MPFA maintains uniform value as other skills. Meanwhile, high AIC and BIC values indicate that Model 1 may be overfitting the data, leading to less generalizable results (Table 4).

4.4 Prediction comparison

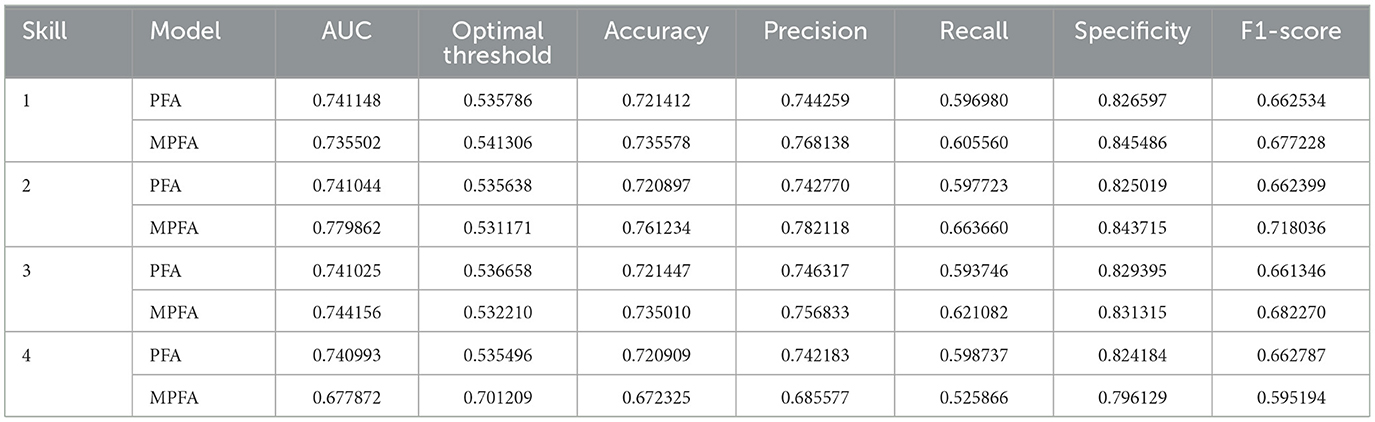
To highlight the model evaluation, metrics such as Prediction Accuracy, Precision, Recall, Specificity, and F1-Score are instrumental in providing a comprehensive assessment (Section 3.3 of Supplementary material). To compare the PFA and MPFA models first, we analyze their prediction ability by a 50% threshold for both models (Zchaluk and Foster, 2009) (Table 6).

Table 6

Table 6. Comparison of metrics between PFA model and MPFA model.

4.4.1 Skill 1

For Skill 1, the MPFA model demonstrates moderate discriminative power, with an AUC indicating its ability to distinguish between positive and negative cases. The optimal threshold shows the probability cutoff that maximizes performance. The model's accuracy reveals it correctly predicts a significant majority of instances. High precision indicates a low rate of false positives, though recall is lower, suggesting some true positives are missed. High specificity highlights strong recognition of negative cases. The F1-Score balances precision and recall, indicating reasonably good performance. The PFA model for Skill 1 shows slightly improved discriminative power with a higher AUC but has marginally lower accuracy, precision, and recall, suggesting a higher false positive rate and reduced ability to identify true positives. Specificity is slightly lower, resulting in a decreased F1-Score and slightly worse overall performance.

4.4.2 Skill 2

For Skill 2, the MPFA model displays better discriminative ability with a higher AUC compared to Skill 1, indicating improved effectiveness at distinguishing between classes. The optimal threshold remains similar, ensuring consistent decision-making. Higher accuracy and precision demonstrate improved predictive performance with fewer false positives, and increased recall shows the model captures more true positives. The F1-Score is higher, reflecting a better balance between precision and recall. In contrast, the PFA model for Skill 2 has a lower AUC than its PFA counterpart, indicating reduced discriminative power. Despite a similar optimal threshold, the MPFA model has lower accuracy, precision, and recall, suggesting a higher false positive rate and reduced effectiveness at identifying true positives. Specificity remains consistent, but the lower F1-Score highlights the need for improvement in balancing precision and recall.

4.4.3 Skill 3

For Skill 3, the MPFA model shows high discriminative power with a strong AUC. The optimal threshold is consistent with previous skills, ensuring uniform decision-making criteria. Accuracy is high, indicating reliable predictions. Precision and recall are balanced, suggesting the model effectively identifies true positives with a low rate of false positives. Specificity is also high, confirming its strong ability to recognize negative cases. The F1-Score reflects excellent overall performance. The PFA model for Skill 3, however, shows a slightly lower AUC compared to the PFA model, indicating reduced discriminative power. Although the optimal threshold is similar, accuracy, precision, and recall are slightly lower, implying a higher false positive rate and a marginally reduced ability to identify true positives. Specificity is consistent, but the lower F1-Score suggests a need for improved balance between precision and recall.

4.4.4 Skill 4

For Skill 4, the MPFA model maintains high discriminative ability with a robust AUC. The optimal threshold is similar to other skills, providing consistent decision-making. High accuracy demonstrates the model's reliable predictions. Precision and recall are well-balanced, indicating effective identification of true positives and a low rate of false positives. Specificity is high, underscoring strong negative case recognition. The F1-Score indicates excellent overall performance. Conversely, the PFA model for Skill 4 exhibits a slightly lower AUC, reflecting reduced discriminative power. Despite a similar optimal threshold, accuracy, precision, and recall are somewhat lower, suggesting a higher false positive rate and diminished capability to identify true positives. Specificity remains high, but the lower F1-Score indicates a need for a better balance between precision and recall.

The MPFA model consistently outperforms the PFA model in terms of discriminative power, accuracy, precision, recall, and F1 scores across all skills. The MPFA model's higher AUC values indicate better discriminative power, while its superior accuracy, precision, recall, and F1 scores reflect its robustness and reliability in educational assessments. The PFA model, although adequate, has lower performance metrics, suggesting it may not be as effective in distinguishing between different skill levels or making accurate predictions. Therefore, the MPFA model is preferred for applications requiring high accuracy and reliable discrimination between skill levels. Future research should focus on enhancing the PFA model to address its current limitations and improve its applicability in educational assessments (Table 6; analysis of key, query, and value vectors explained in Supplementary material).

This study investigates whether integrating attention mechanisms can enhance the modified PFA (MPFA) model's ability to identify both inherent and emergent skills while mapping interrelations among these emergent skills. The MPFA model's evaluation metrics in Table 6 demonstrate that incorporating attention mechanisms indeed strengthens the model's performance over traditional PFA models. The model's improvement in log-likelihood reduced AIC and BIC and lowered RMSE indicate that MPFA provides a more accurate and comprehensive assessment by accounting for the dual influence of internalized skills and emergent skills. This enhanced model not only improves predictive accuracy but also offers a deeper understanding of how students approach and interact with assessment items. By incorporating attention mechanisms, the MPFA model evaluates these positive and negative cases more effectively by dynamically weighting similarities between items based on response patterns and skill relations (Table 6).

4.5 Model implications

4.5.1 Interpretation of the internalized and emergent skills

To interpret and explain the skills, we analyze the positionally encoded response attention weights $\mathcal{W}$, which capture the relationships between student responses across items. This analysis yields a 47 × 47 matrix that quantifies the degree of focus on each item relative to others. Similarly, the skill similarity weights τ are represented by a matrix of the same dimensions, reflecting item relationships based on the underlying skills.

According to attention mechanism methodology, internalized skills refer to abilities that have become automatic or intuitive for students, allowing them to respond consistently to related items, even when the underlying skills that are defined by the Q matrix and skill relation are conceptually unrelated. Our results indicate this phenomenon typically occurs when the response similarity ($\mathcal{W}$) values are high, but the corresponding skill similarity (τ) values are low (see Supplementary material Section for the complete $\mathcal{W}$ and τ tables). Elevated $\mathcal{W}$ values suggest that students exhibit similar response patterns, while low τ values indicate that the skills required for these selected items may differ. For instance, if Items 43 and 47 exhibit a $\mathcal{W}$ value that is 0.31 higher than the average of all $\mathcal{W}$ (0.21: average of all $\mathcal{W}$ matrix) but a τ value that is 1.07 lower than the average of all τ (1.09: average of all τ matrix), this discrepancy suggests that students might be drawing on internalized knowledge as there was minimal distinct emergent skills. This pattern reflects the extent to which some pre or undefined knowledge, allows students to apply them across contexts.

Emergent skills are still in the developmental phase and often require deliberate instructional intervention. They are directly addressed in the Q matrix and in the skill relations matrix. However, MPFA indicated these skills become a main focus of students when both τ and $\mathcal{W}$ values are elevated, signaling that students are actively engaging with and mastering these competencies. For example, Items 36 and 45 exhibits a relatively high $\mathcal{W}$ value of 0.47 and a significantly elevated τ value of 1.28. This alignment suggests that students are consciously applying these skills across different items, indicating they are in the process of solidifying their understanding (Supplementary material Section for the complete $\mathcal{W}$ and τ tables).

4.5.2 Implication for educators

The MPFA model's results provide educators with a nuanced understanding of student performance by identifying both emergent skills—those explicitly taught and aligned with curriculum goals—and inherent skills, which are internalized through students' prior knowledge and unique learning experiences. These inherent skills are inferred from response patterns, capturing the latent knowledge and cognitive frameworks that students apply when interacting with assessment items. By recognizing the dual influence of emergent and inherent skills, the MPFA model allows educators to analyze students' mastery and learning approaches more comprehensively. In other words, previously mastered items can provide information about the probability of each student mastering future items, thereby potentially improving assessment efficiency.

In addition to the potential for improving assessment efficiency, the MPFA model has the potential to measure skill mastery from a student perspective. Student conceptual understanding is often incomplete and fragmented and individual students often solve problems in STEM using different solution strategies (Morphew and Mestre, 2018). As such, existing models that use expert-derived matrices that classify items based on the skills needed to correctly solve a problem may reflect the expert rather than the student's perspective. The MFPA model adjusts expert classification of skills to patterns of student responses, which may be useful for determining and measuring the individual skill mastery patterns from the student's perspective.

The interrelation of inherent skills and emergent skills can also guide curriculum sequencing and instructional strategies. Skills that demonstrate strong interconnections, as indicated by high attention similarity weights, may suggest that inherent cognitive structures contribute to the learning of related skills. For example, if Skill 1 metrics improve as students progress in Skill 3, this may indicate that the inherent skills used in Skill 3 are foundational for Skill 1 mastery. Educators might prioritize the development of these foundational inherent skills earlier in the curriculum, which could enhance students' success in later topics. By leveraging this data-driven insight, educators can strategically adjust instructional pacing and content to align with the learning pathways that are more intuitive for students.

5 Discussion and conclusion

This study presents a modified PFA model (MPFA) that incorporates attention mechanisms into traditional PFA models. The results indicate that the MPFA model can significantly enhance the accuracy of skill mastery. The attention mechanism allows the MPFA model to consider the similarity between items and the inherent skills of students, leading to improved discriminative power, accuracy, precision, recall, and F1 scores across various skills. This enhanced accuracy is critical when dynamically assessing students' internalized and emergent skills in formative assessment.

Notably, the clustering method based on response similarity does not explicitly indicate the same number of attributes underlying the items. By integrating the contextual relevance of internalized skills with the explicit objectives of emergent skills, the MPFA model effectively captures the relationships between skills, allowing for a more comprehensive and nuanced evaluation of student performance. These findings are particularly significant given the necessity of identifying both internalized skills, which students bring from previous instruction and life experiences, and emergent skills, which are explicitly targeted by learning objectives (Colas et al., 2022). The use of the attention mechanism allows the MPFA model to consider both types of skills, thus addressing the limitations of traditional PFA models that typically focus on emergent skills. In addition, by capturing both internalized skills and their interrelations, the MPFA model offers a more holistic evaluation of student performance (Lizardo, 2021).

The integration of attention mechanisms into knowledge-tracking models represents a significant advancement in educational assessments, providing a robust and reliable approach for evaluating the complex interplay of skills in STEM education. This aligns with findings from studies such as Xia et al. (2023) and Liu et al. (2020). This advancement highlights the significant impact of attention mechanisms in improving the accuracy and effectiveness of knowledge-tracking models, making them a valuable tool for educational assessments in STEM education. Traditionally, STEM assessments focus on the application of expert-defined skills and the understanding of content. However, these predefined constructs may show themselves differently due to differing pedagogical approaches or potential biases. Gong et al. (2010) highlights the challenges in demonstrating how relationships between skills alter the model's impact on multi-skill items. Similarly, Pu et al. (2021)'s research underlines that the inter-dependencies among skills influence student responses, revealing a pattern of response similarity. This study further emphasizes the importance of integrating explicit correlations between student skills and potentially unconventional response strategies. Although the skill-related vectors are inherently smaller in number compared to the item-related vectors, they can elucidate why certain items exhibit similar response vectors despite differing in the underlying skills.

The results of this study align with studies like Yuen et al. (2023) and Nouri (2016) that provide evidence that student understanding may not explicitly match the expectations of instructors. As such, instructors would likely benefit from access to assessment tools like the MPFA to assess these mismatches between internalized and emergent skills. Utami et al. (2022) underscore the importance of twenty-first-century learning, highlighting critical thinking, creativity, communication, and collaboration as essential skills for addressing contemporary educational needs. Addressing such a wide variety of learning outcomes necessitates a method to manage the relationship between students' internalized skills and the emergent skills that students are expected to develop in the educational context (Liu et al., 2009). In addition, assessment must be formative and continuous to measure and diagnose effective individualized learning trajectories.

The precision of the MPFA model suggests it can be valuable for effectively allocating educational resources for students who most urgently need them. While the traditional PFA model may be slightly more effective at identifying struggling students, these models also falsely identify more non-struggling students. This trade-off means that instructor resources may not be most efficiently utilized to help those students most in need. The higher specificity of the MPFA model indicates its strength in correctly identifying students who do not require interventions. The MPFA model, with its high precision and specificity, might be preferable when the consequences of false positives are more severe than those of false negatives. The result of this study affirms studies align with Yeung (2019) and Pu et al. (2021) in indicating that the inclusion of an attention mechanism in assessment models preserves the foundational architecture of models and enhances the explainability of the model by directing focus toward particular segments.

This study finds that adding the information of underlying skills or inherent attributes enhances the model's predictive accuracy. A substantial body of literature corroborates considering the underlying attributes of items (De La Torre, 2009) and supports that automated item generation models based on LLMs for assessment should consider defining attention mechanisms about the underlying attributes of items like explicit skills or inherent students' skills according to their background knowledge development (Guinet et al., 2024; Meißner et al., 2024; Säuberli and Clematide, 2024; Lee and Kwon, 2024). While LLMs currently excel in textual analysis, they often falter with non-textual cues and in assessing critical thinking solely through text (Abd El-Haleem et al., 2022). Wilson (2015) adds that socio-emotional aspects of student learning can affect students assessment responses which pose issues for LLMs. This could add to difficulties in using LLMs to accurately distinguish between students who need minimal support and those requiring significant interventions (Abd El-Haleem et al., 2022). Future research should examine how to best integrate the capabilities of LLMs with the assessment advantages of the MPFA model.

6 Future steps

6.1 PFA with fewer parameters

In the evaluation of both the PFA and MPFA models, the metrics most indicative of a need for simplification are Recall, F1-score, and AUC (Section 3.3 in Supplementary material).

The analysis suggests that the complexity inherent in the PFA architecture model that holds the last performance of the student in memory does not uniformly translate into commensurate improvements in overall model performance. Consequently, a simplification of the model's architecture could facilitate a more harmonious balance across all performance metrics. The study proposed an assumption that establishes a relationship between F and S matrices with a specific structure (N = S+F), which facilitates more efficient parameter estimation. The equation:

$\begin{array}{ll}{P}_a(j)=\sigma (({\alpha }_j-{\rho }_j)S_{ij}+({\rho }_j{N}_j-{\beta }_j))& (23)\end{array}$

incorporates this assumption and can be rewritten with two parameters,

$\begin{array}{l}{\alpha }_j-{\rho }_j={{\alpha }^{\prime }}_j\\ {\rho }_j{N}_j-{\beta }_j={{\beta }^{\prime }}_j\end{array}$

which can be employed in different regression and MLE methods. This approach reduces the degrees of freedom in the model, potentially enhancing its efficiency. However, it remains unclear whether reducing the degrees of freedom always guarantees improved model accuracy, necessitating further research to explore the impact of this assumption on model performance.

6.2 Future steps in language model development

Future research should aim to enhance educational assessments by extending the probabilistic modeling approach outlined in this study. This can be achieved by integrating skill-oriented analyzes with natural language processing (NLP) techniques while also accounting for additional variables such as response time and demographic factors. The next step involves developing a pre-trained, transformer-based model that not only predicts student performance but also interprets the underlying skill relationships within textual responses. This model would enable a deeper understanding of how specific skills influence answers, providing educators with insights into skill development paths and interdependencies. By incorporating skill embedding, the model could offer targeted feedback to students, pinpointing not just areas of misunderstanding but also suggesting pathways for skill improvement. Such advancements would mark a shift from binary assessment outcomes toward a more nuanced, skill-centric learning environment, where feedback is personalized, actionable, and geared toward fostering comprehensive skill development. This approach could redefine educational diagnostics, making them more reflective of individual learning processes and more supportive of personalized education strategies.

7 Limitations

The study's results shed light on the performance of students in different skills, and the relationship between these variables. One of the main limitations is that the research group did not have access to a GPU which would help them to reduce the time needed for model evaluation. The complexity of the attention mechanism specifically, dealing with a large number of students and responses, would be greatly assisted by a GPU.

Data availability statement

Datasets are available upon request. Requests to access these datasets should be directed to Jason Morphew, am1vcnBoZXcmI3gwMDA0MDtwdXJkdWUuZWR1.

Author contributions

AM: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Validation, Visualization, Writing – original draft, Writing – review & editing. JM: Funding acquisition, Resources, Supervision, Writing – original draft, Writing – review & editing. BQ: Formal analysis, Investigation, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported in part by the National Science Foundation under Grants DUE-2142317 and RCN 2322015.

Acknowledgments

Special thanks to Sina Nadi, a Ph. D. student in the Mathematics Department of Purdue University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Author disclaimer

Any opinions, findings, and conclusions expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1454319/full#supplementary-material

References

Abd El-Haleem, A. M., Eid, M. M., Elmesalawy, M. M., and Hosny, H. A. H. (2022). A generic ai-based technique for assessing student performance in conducting online virtual and remote controlled laboratories. IEEE Access 10, 128046–128065. doi: 10.1109/ACCESS.2022.3227505

Crossref Full Text | Google Scholar

Allen, A. (2022). An introduction to constructivism: its theoretical roots and impact on contemporary education. J. Learn. Design Leadersh. 1, 1–11.

Google Scholar

Anderson, P., He, X., Buehler, C., Teney, D., Johnson, M., Gould, S., et al. (2018). “Bottom-up and top-down attention for image captioning and visual question answering,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Salt Lake City, UT: IEEE Computer Society), 6077–6086. doi: 10.1109/CVPR.2018.00636

Crossref Full Text | Google Scholar

Battiloro, C., Testa, L., Giusti, L., Sardellitti, S., Di Lorenzo, P., and Barbarossa, S. (2023). Generalized simplicial attention neural networks. arXiv preprint arXiv:2309.02138. doi: 10.1109/TSIPN.2024.3485473

PubMed Abstract | Crossref Full Text | Google Scholar

Betancourt, R., Chen, S., Betancourt, R., and Chen, S. (2019). Pandas library. Python SAS Users 3, 65–109. doi: 10.1007/978-1-4842-5001-3_3

Crossref Full Text | Google Scholar

Bitzenbauer, P. (2023). Chatgpt in physics education: a pilot study on easy-to-implement activities. Contempor. Educ. Technol. 15:ep430. doi: 10.30935/cedtech/13176

Crossref Full Text | Google Scholar

Boaler, J. (2022). Mathematical Mindsets: Unleashing Students' Potential Through Creative Mathematics, Inspiring Messages, and Innovative Teaching, 2nd Edn. Hoboken, NJ: John Wiley & Sons, Inc.

Google Scholar

Braun, S., Neil, D., Anumula, J., Ceolini, E., and Liu, S.-C. (2018). “Multi-channel attention for end-to-end speech recognition,” in Proceedings of Interspeech 2018 (Hyderabad: International Speech Communication Association), 430–434. doi: 10.21437/Interspeech.2018-1301

PubMed Abstract | Crossref Full Text | Google Scholar

Bressane, A., Zwirn, D., Essiptchouk, A., Saraiva, A. C. V., de Campos Carvalho, F. L., Formiga, J. K. S., et al. (2024). Understanding the role of study strategies and learning disabilities on student academic performance to enhance educational approaches: a proposal using artificial intelligence. Comput. Educ. Artif. Intell. 6:100196. doi: 10.1016/j.caeai.2023.100196

Crossref Full Text | Google Scholar

Chen, Y., Culpepper, S. A., Chen, Y., and Douglas, J. (2018). Bayesian estimation of the dina Q matrix. Psychometrika 83, 89–108. doi: 10.1007/s11336-017-9579-4

PubMed Abstract | Crossref Full Text | Google Scholar

Chen Y. and Wang, S.. (2023). Bayesian estimation of attribute hierarchy for cognitive diagnosis models. J. Educ. Behav. Stat. 48, 810–841. doi: 10.3102/10769986231174918

PubMed Abstract | Crossref Full Text | Google Scholar

Chiu, C.-Y. (2013). Statistical refinement of the q-matrix in cognitive diagnosis. Appl. Psychol. Measur. 37, 598–618. doi: 10.1177/0146621613488436

PubMed Abstract | Crossref Full Text | Google Scholar

Colas, C., Karch, T., Moulin-Frier, C., and Oudeyer, P.-Y. (2022). Language and culture internalization for human-like autotelic AI. Nat. Machine Intell. 4, 1068–1076. doi: 10.1038/s42256-022-00591-4

Crossref Full Text | Google Scholar

Daffertshofer, A., Lamoth, C. J., Meijer, O. G., and Beek, P. J. (2004). Pca in studying coordination and variability: a tutorial. Clin. Biomech. 19, 415–428. doi: 10.1016/j.clinbiomech.2004.01.005

PubMed Abstract | Crossref Full Text | Google Scholar

De La Torre, J. (2009). Dina model and parameter estimation: a didactic. J. Educat. Behav. Stat. 34, 115–130. doi: 10.3102/1076998607309474

PubMed Abstract | Crossref Full Text | Google Scholar

Di, C., Zhou, Q., Shen, J., Li, L., Zhou, R., and Lin, J. (2021). Innovation event model for stem education: a constructivism perspective. STEM Educ. 1, 60–74. doi: 10.3934/steme.2021005

Crossref Full Text | Google Scholar

Effiom, A. P. (2021). Test fairness and assessment of differential item functioning of mathematics achievement test for senior secondary students in Cross River State, Nigeria using item response theory. Glob. J. Educat. Res. 20, 55–62. doi: 10.4314/gjedr.v20i1.6

Crossref Full Text | Google Scholar

Essel, H. B., Vlachopoulos, D., Essuman, A. B., and Amankwa, J. O. (2024). Chatgpt effects on cognitive skills of undergraduate students: Receiving instant responses from AI-based conversational large language models (LLMA). Comput. Educ. Artif. Intell. 6:100198. doi: 10.1016/j.caeai.2023.100198

Crossref Full Text | Google Scholar

Fink, M. J. (2023). The importance of formative assessments in AP Physics 1 (Master's thesis). State University of New York, Brockport, NY, United States. Available at: https://soar.suny.edu/handle/20.500.12648/14092

Google Scholar

Fischer, L., Rohm, T., Carstensen, C. H., and Gnambs, T. (2021). Linking of rasch-scaled tests: consequences of limited item pools and model misfit. Front. Psychol. 12:633896. doi: 10.3389/fpsyg.2021.633896

PubMed Abstract | Crossref Full Text | Google Scholar

Ghozali, F. A., Asnawi, R., Khairudin, M., Jati, M. P., and Hoirul, A. (2019). Designing a skill tree model for learning media. Jurnal Pendidikan Teknologi Dan Kejuruan 25, 132–140. doi: 10.21831/jptk.v25i1.20234

PubMed Abstract | Crossref Full Text | Google Scholar

Giusti, L., Battiloro, C., Di Lorenzo, P., Sardellitti, S., and Barbarossa, S. (2022). Simplicial attention neural networks. arXiv preprint arXiv:2203.07485. doi: 10.48550/arXiv.2203.07485

PubMed Abstract | Crossref Full Text | Google Scholar

Glas, C. A. (2008). Item response theory in educational assessment and evaluation. Mesure et évaluation en éducation 31, 19–34. doi: 10.7202/1025005ar

Crossref Full Text | Google Scholar

Gong, Y., Beck, J. E., and Heffernan, N. T. (2010). “Comparing knowledge tracing and performance factor analysis by using multiple model fitting procedures,” in Intelligent Tutoring Systems: 10th International Conference, ITS 2010, Pittsburgh, PA, USA, June 14-18, 2010, Proceedings, Part I 10 (Berlin: Springer), 35–44.

Google Scholar

Gong, Y., Beck, J. E., and Heffernan, N. T. (2011). How to construct more accurate student models: Comparing and optimizing knowledge tracing and performance factor analysis. Int. J. Artif. Intell. Educ. 21, 27–46. doi: 10.3233/JAI-2011-016

Crossref Full Text | Google Scholar

Guinet, G., Omidvar-Tehrani, B., Deoras, A., and Callot, L. (2024). Automated evaluation of retrieval-augmented language models with task-specific exam generation. arXiv preprint arXiv:2405.13622. doi: 10.48550/arXiv.2405.13622

Crossref Full Text | Google Scholar

Hamilton, M. B. (2021). Population Genetics. Hoboken, NJ: John Wiley & Sons.

Google Scholar

Harrison, M., and Petrou, T. (2020). Pandas 1. x Cookbook: Practical Recipes for Scientific Computing, Time Series Analysis, and Exploratory Data Analysis Using Python. Birmingham: Packt Publishing Ltd.

Google Scholar

Hattie, J., and Timperley, H. (2007). The power of feedback. Rev. Educ. Res. 77, 81–112. doi: 10.3102/003465430298487

PubMed Abstract | Crossref Full Text | Google Scholar

Hilbert, S., Coors, S., Kraus, E., Bischl, B., Lindl, A., Frei, M., et al. (2021). Machine learning for the educational sciences. Rev. Educ. 9:e3310. doi: 10.1002/rev3.3310

Crossref Full Text | Google Scholar

Imambi, S., Prakash, K. B., and Kanagachidambaresan, G. (2021). Pytorch. Program. TensorFlow 10, 87–104. doi: 10.1007/978-3-030-57077-4_10

Crossref Full Text | Google Scholar

Kennedy, C., and McLoughlin, A. (2023). Developing the emergent literacy skills of english language learners through dialogic reading: a systematic review. Early Childh. Educ. J. 51, 317–332. doi: 10.1007/s10643-021-01291-1

Crossref Full Text | Google Scholar

Kingsbury, G. G., and Houser, R. L. (1999). Developing computerized adaptive tests for school children. Innov. Comput. Assess 1999, 93–115.

Google Scholar

Konidaris, G., Kuindersma, S., Grupen, R., and Barto, A. (2012). Robot learning from demonstration by constructing skill trees. Int. J. Robot. Res. 31, 360–375. doi: 10.1177/0278364911428653

Crossref Full Text | Google Scholar

Konidaris, G., Kuindersma, S., Grupen, R., and Barto, A. (2021). “Constructing skill trees for reinforcement learning agents from demonstration trajectories,” in Advances in Neural Information Processing Systems (Red Hook, NY), 1162–1170.

Google Scholar

Kumah-Crystal, Y., Mankowitz, S., Embi, P., and Lehmann, C. U. (2023). Chatgpt and the clinical informatics board examination: the end of knowledge-based medical board maintenance? medRxiv 25:23289105. doi: 10.1101/2023.04.25.23289105

PubMed Abstract | Crossref Full Text | Google Scholar

Le, V., Nissen, J. M., Tang, X., Zhang, Y., Mehrabi, A., Morphew, J. W., et al. (2024). Applying cognitive diagnostic models to mechanics concept inventories. arXiv preprint arXiv:2404.00009. doi: 10.48550/arXiv.2404.00009

Crossref Full Text | Google Scholar

Lee, S. J., and Kwon, K. (2024). A systematic review of ai education in K-12 classrooms from 2018 to 2023: topics, strategies, and learning outcomes. Comput. Educ. Artif. Intell. 2024:100211. doi: 10.1016/j.caeai.2024.100211

Crossref Full Text | Google Scholar

Lee, S. Y. (2017). Growth Curve Cognitive Diagnosis Models for Longitudinal Assessment. Berkeley, CA: University of California.

Google Scholar

Leikin, R., and Lev, M. (2007). Multiple solution tasks as a magnifying glass for observation of mathematical creativity. Proc. 31st Int. Conf. Psycholo. Math. Educ. 3, 161–168.

Google Scholar

Lent, H. C., Ortner, V. K., Karmisholt, K. E., Wiegell, S. R., Nissen, C. V., Omland, S. H., et al. (2024). A chat about actinic keratosis: examining capabilities and user experience of chatgpt as a digital health technology in dermato-oncology. JEADV Clin. Pract. 3, 258–265. doi: 10.1002/jvc2.263

Crossref Full Text | Google Scholar

Li, D. (2022). A review of academic literacy research development: from 2002 to 2019. Asian-Pacific J. Sec. For. Lang. Educ. 7:5. doi: 10.1186/s40862-022-00130-z

Crossref Full Text | Google Scholar

Lin, C., Ren, J., He, G., Jiang, Z., Yu, H., and Zhu, X. (2024). Tree-based hard attention with self-motivation for large language models. arXiv preprint arXiv:2402.08874. doi: 10.48550/arXiv.2402.08874

Crossref Full Text | Google Scholar

Liu, D., Dai, H., Zhang, Y., Li, Q., and Zhang, C. (2020). “Deep knowledge tracking based on attention mechanism for student performance prediction,” in 2020 IEEE 2nd International Conference on Computer Science and Educational Informatization (CSEI) (Xinxiang: IEEE), 95–98.

PubMed Abstract | Google Scholar

Liu, X., Zhang, B., Liang, L. L., Fulmer, G., Kim, B., and Yuan, H. (2009). Alignment between the physics content standard and the standardized test: a comparison among the United States-New York State, Singapore, and China-Jiangsu. Sci. Educ. 93, 777–797. doi: 10.1002/sce.20330

Crossref Full Text | Google Scholar

Lizardo, O. (2021). Culture, cognition, and internalization. Sociol. For. 36, 1177–1206. doi: 10.1111/socf.12771

Crossref Full Text | Google Scholar

Macdonald, I., and MacLeod, M. (2018). Design education without borders: how students can engage with a socially conscious pedagogy as global citizens. Int. J. Art Des. Educ. 37, 312–324. doi: 10.1111/jade.12117

Crossref Full Text | Google Scholar

Manaswi, N. K., and Manaswi, N. K. (2018). Understanding and working with Keras. Deep Learn. Appl. Python 2, 31–43. doi: 10.1007/978-1-4842-3516-4_2

Crossref Full Text | Google Scholar

Mehrabi, A., Altintas, O., and Morphew, J. W. (2023). “Optimizing maximum likelihood estimation in performance factor analysis: a comparative study of estimation methods,” in Proceedings of the Mathematics and Statistics. West Lafayette, IN: Springer Nature Switzerland.

Google Scholar

Meißner, N., Speth, S., Kieslinger, J., and Becker, S. (2024). “Evalquiz—LLM-based automated generation of self-assessment quizzes in software engineering education,” in Software Engineering im Unterricht der Hochschulen 2024 (Bonn: Gesellschaft für Informatik e.V.), 53–64.

Google Scholar

Mindell, J. S., Tipping, S., Pickering, K., Hope, S., Roth, M. A., and Erens, B. (2010). The effect of survey method on survey participation: analysis of data from the health survey for england 2006 and the boost survey for London. BMC Med. Res. Methodol. 10, 1–8. doi: 10.1186/1471-2288-10-83

PubMed Abstract | Crossref Full Text | Google Scholar

Morphew, J. W., and Mestre, J. P. (2018). Exploring the connection between problem solving and conceptual understanding in physics. Revista de Enseñanza de la Física. 30, 75–85. doi: 10.55767/2451.6007.v30.n2.22738

Crossref Full Text | Google Scholar

Morphew, J. W., Mestre, J. P., Kang, H. A., Chang, H. H., and Fabry, G. (2018). Using computer adaptive testing to assess physics proficiency and improve exam performance in an introductory physics course. Phys. Rev. Phys. Educ. Res. 14:e020110. doi: 10.1103/PhysRevPhysEducRes.14.020110

Crossref Full Text | Google Scholar

Morphew, J. W., Silva, M., Herman, G., and West, M. (2020). Frequent mastery testing with second-chance exams leads to enhanced student learning in undergraduate engineering. Appl. Cogn. Psychol. 34, 168–181. doi: 10.1002/acp.3605

Crossref Full Text | Google Scholar

Nguyen, H. Q., Nguyen, C. Q., Le, D. D., and Pham, H. H. (2023). Enhancing few-shot image classification with cosine transformer. IEEE Access. 2023:3298299. doi: 10.1109/ACCESS.2023.3298299

Crossref Full Text | Google Scholar

Niu, Z., Zhong, G., and Yu, H. (2021). A review on the attention mechanism of deep learning. Neurocomputing 452, 48–62. doi: 10.1016/j.neucom.2021.03.091

Crossref Full Text | Google Scholar

Nouri, J. (2016). The flipped classroom: for active, effective and increased learning–especially for low achievers. Int. J. Educ. Technol. High. Educ. 13, 1–10. doi: 10.1186/s41239-016-0032-z

Crossref Full Text | Google Scholar

Pavlik, P. I. Jr., Cen, H., and Koedinger, K. R. (2009). “Performance factors analysis-A new alternative to knowledge tracing,” in Proceedings of the International Conference on Artificial Intelligence in Education (Berlin: Springer), 531–538.

Google Scholar

Pu, S., Converse, G., and Huang, Y. (2021). “Deep performance factors analysis for knowledge tracing,” in International Conference on Artificial Intelligence in Education (Berlin: Springer), 331–341.

Google Scholar

Richard, M. D., and Lippmann, R. P. (1991). Neural network classifiers estimate bayesian a posteriori probabilities. Neural Comput. 3, 461–483.

Google Scholar

Säuberli, A., and Clematide, S. (2024). Automatic generation and evaluation of reading comprehension test items with large language models. arXiv preprint arXiv:2404.07720. doi: 10.48550/arXiv.2404.07720

Crossref Full Text | Google Scholar

Scholl, C., Rule, M. E., and Hennig, M. H. (2021). The information theory of developmental pruning: optimizing global network architectures using local synaptic rules. PLoS Comput. Biol. 17:e1009458. doi: 10.1371/journal.pcbi.1009458

PubMed Abstract | Crossref Full Text | Google Scholar

Schubert, M. C., Wick, W., and Venkataramani, V. (2023). Performance of large language models on a neurology board–style examination. J. Am. Med. Assoc. Netw. Open 6:e2346721. doi: 10.1001/jamanetworkopen.2023.46721

PubMed Abstract | Crossref Full Text | Google Scholar

Sherstinsky, A. (2020). Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlin. Phenom. 404:132306. doi: 10.1016/j.physd.2019.132306

Crossref Full Text | Google Scholar

Siddiq, F., and Scherer, R. (2017). Revealing the processes of students' interaction with a novel collaborative problem solving task: an in-depth analysis of think-aloud protocols. Comput. Hum. Behav. 8:7. doi: 10.1016/j.chb.2017.08.007

Crossref Full Text | Google Scholar

Silver, E. A., Ghousseini, H., Gosen, D., Charalambous, C., and Strawhun, B. T. F. (2005). Moving from rhetoric to praxis: issues faced by teachers in having students consider multiple solutions for problems in the mathematics classroom. J. Math. Behav. 24, 287–301. doi: 10.1016/j.jmathb.2005.09.009

Crossref Full Text | Google Scholar

Thornton, R. K., and Sokoloff, D. R. (1998). Assessing student learning of newton's laws: the force and motion conceptual evaluation and the evaluation of active learning laboratory and lecture curricula. Am. J. Phys. 66, 338–352. doi: 10.1119/1.18863

Crossref Full Text | Google Scholar

Tonio, D. B., and Francesca, F. (2016). Clustering dichotomously scored items through functional data analysis. Electr. J. Appl. Stat. Anal. 9, 433–450. doi: 10.1285/i20705948v9n2p433

Crossref Full Text | Google Scholar

Utami, A. W., Dewi, W. S., Liana, M., et al. (2022). Validation result of teaching mechanical waves materials with ICT based material integrated ctl for XI grade students. Pillar Phys. Educ. 15, 92–99. doi: 10.24036/11270171074

Crossref Full Text | Google Scholar

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). Attention is all you need. Adv. Neural Inform. Process. Syst. 30. doi: 10.48550/arXiv.1706.03762

Crossref Full Text | Google Scholar

Wells, J., Henderson, R., Traxler, A., Miller, P., and Stewart, J. (2020). Exploring the structure of misconceptions in the force and motion conceptual evaluation with modified module analysis. Phys. Rev. Phys. Educ. Res. 16:e010121. doi: 10.1103/PhysRevPhysEducRes.16.010121

Crossref Full Text | Google Scholar

Whalon, K. (2018). Enhancing the reading development of learners with autism spectrum disorder. Semin. Speech Lang. 39, 144–157. doi: 10.1055/s-0038-1628366

PubMed Abstract | Crossref Full Text | Google Scholar

Wilson, A. N. (2015). A critique of sociocultural values in PBIS. Behav. Anal. Pract. 8, 92–94. doi: 10.1007/s40617-015-0052-5

PubMed Abstract | Crossref Full Text | Google Scholar

Wormald, B. W., Schoeman, S., Somasunderam, A., and Penn, M. (2009). Assessment drives learning: an unavoidable truth? Anatom. Sci. Educ. 2, 199–204. doi: 10.1002/ase.102

PubMed Abstract | Crossref Full Text | Google Scholar

Wu, M., Davis, R. L., Domingue, B. W., Piech, C., and Goodman, N. (2021). Modeling item response theory with stochastic variational inference. arXiv preprint arXiv:2108.11579. doi: 10.48550/arXiv.2108.11579

Crossref Full Text | Google Scholar

Xia, Z., Dong, N., Wu, J., and Ma, C. (2023). Multi-variate knowledge tracking based on graph neural network in assistments. IEEE Trans. Learn. Technol. 2023:3301011. doi: 10.1109/TLT.2023.3301011

Crossref Full Text | Google Scholar

Yeung, C.-K. (2019). Deep-IRT: make deep learning based knowledge tracing explainable using item response theory. arXiv preprint arXiv:1904.11738. doi: 10.48550/arXiv.1904.11738

Crossref Full Text | Google Scholar

Yuen, S.-Y., Luo, Z., and Wan, S. W.-y. (2023). Challenges and opportunities of implementing differentiated instruction amid the COVID-19 pandemic: insights from a qualitative exploration. Educ. Sci. 13:989. doi: 10.3390/educsci13100989

Crossref Full Text | Google Scholar

Zchaluk, K., and Foster, D. H. (2009). Model-free estimation of the psychometric function. Attent. Percept. Psychophys. 71, 1414–1425. doi: 10.3758/APP.71.6.1414

PubMed Abstract | Crossref Full Text | Google Scholar