- 1CREATE for STEM Institute, Michigan State University, East Lansing, MI, United States
- 2College of Education, University of Wyoming, Laramie, WY, United States
- 3The Concord Consortium, Concord, MA, United States
This paper discusses the potential of two computational modeling approaches in moving students from simple linear causal reasoning to applying more complex aspects of systems thinking (ST) in explanations of scientific phenomena. While linear causal reasoning can help students understand some natural phenomena, it may not be sufficient for understanding more complex issues such as global warming and pandemics, which involve feedback, cyclic patterns, and equilibrium. In contrast, ST has shown promise as an approach for making sense of complex problems. To facilitate ST, computational modeling tools have been developed, but it is not clear to what extent different approaches promote specific aspects of ST and whether scaffolding such thinking should start with supporting students first in linear causal reasoning before moving to more complex causal dimensions. This study compares two computational modeling approaches, static equilibrium and system dynamics modeling, and their potential to engage students in applying ST aspects in their explanations of the evaporative cooling phenomenon. To make such a comparison we analyzed 10th grade chemistry students’ explanations of the phenomenon as they constructed and used both modeling approaches. The findings suggest that using a system dynamics approach prompts more complex reasoning aligning with ST aspects. However, some students remain resistant to the application of ST and continue to favor linear causal explanations with both modeling approaches. This study provides evidence for the potential of using system dynamics models in applying ST. In addition, the results raise questions about whether linear causal reasoning may serve as a scaffold for engaging students in more sophisticated types of reasoning.
1. Introduction
Systems thinking (ST) has gained recognition as a necessary approach for addressing complex problems in various domains (Assaraf and Orion, 2005; Jacobson and Wilensky, 2006; Meadows, 2008). Although much of the research in ST was in disciplines such as biology and Earth science (Yoon et al., 2018), lately there has been a growing awareness and advancement in integrating ST in chemistry education (Flynn et al., 2019; Orgill et al., 2019; York et al., 2019), moving the field forward in an effort to apply ST across disciplines. In recent years, the integration of ST into science education standards has been adopted by a number of countries (National Research Council, 2012; Reynolds et al., 2018; Chiu et al., 2019). According to Meadows (2008), a system is an interconnected set of elements that demonstrates behavior that cannot be understood by examining individual elements in isolation. There have been numerous efforts to operationalize ST and develop frameworks for evaluating its application (Richmond, 1993; Assaraf and Orion, 2005; Hmelo-Silver et al., 2007b).
Despite various approaches in developing students’ understanding of ST, educators continue to face challenges in its application. Many students explain complex phenomena using simple linear cause and effect relationships (Sweeney and Sterman, 2000; Chi, 2005; Chi et al., 2012; Grotzer et al., 2013; Tripto et al., 2013). However, simple linear cause and effect mechanisms cannot account for phenomena that involve equilibrium, feedback, cyclic patterns, and perturbations (Richmond, 1993). Hence, there is a need to facilitate student understanding of non-linear system behaviors to cultivate scientific reasoning and produce scientifically literate citizens (Meadows, 2008; Ke et al., 2021). Despite attempts to engage students in mechanisms that go beyond linear causal thinking, students have shown resistance to adopting an ST approach (Assaraf and Orion, 2005; Chi, 2005; Hmelo-Silver et al., 2007a; Chi et al., 2012).
It has been nearly four decades since scholars began attempting to utilize technology to enhance students’ understanding of ST (Costanza, 1987; Mandinach, 1989; Metcalf et al., 2000). Computational modeling tools have emerged as a promising avenue. There are three main approaches in the field: static equilibrium modeling, system dynamics modeling, and agent-based modeling. Static equilibrium modeling is a computational approach that facilitates the creation of linear and/or branching cause and effect relationships such that changes to one variable are instantly reflected by changes in the values of related linked variables (Bielik et al., 2018). Unlike static equilibrium modeling, system dynamics modeling allows representation of changes in a system over time (Sterman, 2002; Martinez‐Moyano and Richardson, 2013), opening the door for representing dynamic equilibrium and feedback. Agent-based modeling, another time-based modeling system, enables users to explore the actions of individual agents in the system and observe the impact of their interactions on the emergent behavior of the system (Wilensky and Resnick, 1999; Jacobson and Wilensky, 2006). All of the approaches enable users to test and evaluate their models (Bielik et al., 2018). In this paper, we focus on static equilibrium and system dynamics modeling. There are two main reasons to prioritize these two approaches. Firstly, both approaches share similar underlying affordances that enable the setting of causal relationships between variables. Secondly, from a practical standpoint, there is a software tool that we will discuss in detail later, which facilitates seamless switching between these approaches. This feature significantly reduces the learning curve associated with adapting to a new digital environment.
Few studies have compared the effects of various modeling approaches on students’ application of ST (Carolyn and Lee, 2019). In this study, we advance our understanding of how to support students in system modeling by analyzing the effects of static equilibrium and system dynamics modeling on students’ explanations and the mechanisms they use to understand complex phenomena. We also explore to what extent engagement in a simpler modeling approach serves as a scaffold to support students in applying more complex aspects of ST. Our goal is to gain insights into computational tools and scaffolds that can expand students’ ideas from linear to more complex non-linear thinking.
2. Theoretical framework
2.1. Linear causal reasoning
Linear causal reasoning is a fundamental way in which individuals explain the world and make sense of their surroundings from a young age (Driver et al., 1985; Leslie and Keeble, 1987). This method of explanation is commonly used in science to describe mechanisms, such as the direct linear relationships between mass, acceleration, and force in Newton’s third law. Science education often teaches students to reduce complex mechanisms to simple cause and effect relationships, leading to a reductionist approach across disciplines. This has been observed in various areas of study, such as Earth science (Raia, 2005), biology (Gilissen et al., 2019), and chemistry (Tümay, 2016). Additionally, linear causal reasoning often leads to assigning a central agent in a domino-like mechanism (Resnick, 1996; Galea et al., 2010; Kahneman, 2011). While appropriate for understanding topics such as Newton’s third law, this method of explanation is particularly problematic for phenomena with dynamic features such as erosion, evolution, disease spread, and global average temperature rise (Sander et al., 2006).
In this paper, we use the term “linear causal reasoning” as coined by Driver et al. (1985) to refer to thinking about sequential chains of causes and effects. This tendency has further generated more nuanced terminologies. Chi et al. (2012) made a distinction between a direct-causal schema and an emergent-causal schema. Accordingly, the direct causal schema relies on linear, narrative-like cause and effect scripts that when applied in the context of complex and non-sequential processes often result in developing non-canonical understandings. Perkins and Grotzer (2005) suggested evaluating students’ explanations according to dimensions of causality, differentiating between various levels of causal explanations in each of these dimensions. Grotzer et al. (2013) differentiated students’ explanations as event-based or process-based. For example, they noticed that students interpret ecosystems as distinct events with linear cause and effect explanations (event based), instead of a dynamic time-based mechanism (process based), which is more appropriate in that context.
2.2. Systems thinking
Although students need to develop linear causal reasoning, having access to only this type of reasoning restricts the types of problems and phenomena students can explore. Enabling students to familiarize with non-linear reasoning prepares them to be scientifically literate citizens equipped with the intellectual tools to understand and address complex issues and phenomena such as global warming, the spread of diseases, and the impact of invasive species on ecosystems (Liu and Hmelo-Silver, 2009; Yore, 2012).
To support students in developing a more comprehensive understanding of the world, scholars examined the reasoning processes used by experts when facing complex problems (Hmelo-Silver et al., 2007b). This line of inquiry has led to the recognition of a broad range of reasoning skills commonly referred to as ST (Senge and Sterman, 1992; Richmond, 1993; Sterman, 2002; Assaraf and Orion, 2005; Meadows, 2008). Despite the variations in ST approaches, there is a general agreement about the key aspects that support students in solving complex problems and understanding complex phenomena (Sweeney and Sterman, 2000; Hmelo-Silver et al., 2007b; Assaraf et al., 2013). A recent literature review (Shin et al., 2022) summarized ST aspects that are commonly found across various studies on the topic, including framing problems or phenomena in terms of behavior over time (Richmond, 1993; Forrester, 1994), engaging in causal reasoning (Stave and Hopper, 2007; Meadows, 2008), and identifying interconnections and feedback (Richmond, 1993; Sweeney and Sterman, 2000; Haraldsson, 2004; Zuckerman and Resnick, 2005).
Perkins and Grotzer (2005) devised a framework that identifies dimensions of causality and characterizes each dimension’s complexity level. This framework can be used to evaluate the application of systems thinking in student explanations of phenomena. The dimensions are agency, interactive patterns, mechanism, and probability.
• Agency refers to the attribution of the cause given for a phenomenon. The complexity of this causal dimension can range from centralized agents with intentional cause to decentralized agents with non-intentional cause such as self-organizing or emergent systems.
• Interactive patterns describe the complexity of the causal relationship between components in the system. Interactive patterns range from sequential patterns (e.g., A causes B) to simultaneous patterns (e.g., patterns that include feedback and cycles).
• Mechanism refers to the scale or level used to explain a phenomenon. Mechanisms range from an explanation that includes macroscopic entities to an explanation that includes microscopic entities and underlying laws.
• Probability denotes explanations that range from deterministic to random behavior of the components in the system.
Utilizing the more complex levels within each causal dimension is essential to make sense of complex phenomena that are often characterized by steady states, feedback, cyclic patterns, dynamic relationships, and occasional perturbations (Meadows, 2008). In addition, ST has recently been recognized in K-12 science curriculum guides (National Research Council, 2012). The challenge researchers have experienced is devising strategies to support students in applying ST. One of the most promising avenues is in the use of computational models (Sterman, 2002; Gilissen et al., 2019).
2.3. Computational systems modeling
Computational systems modeling offers a valuable tool for students to develop their problem-solving skills and explain complex scientific phenomena (Stratford et al., 1998; Sins et al., 2009; Chandrasekharan and Nersessian, 2015; Shin et al., 2022). Particularly, it provides students the opportunity to explore the interconnected relationships between multiple variables in a system and gain a deeper understanding of the underlying processes that drive a particular phenomenon (Ainsworth, 2008; Linn and Eylon, 2011). Computational models often have simulation features that allow the manipulation of variables in these models. These simulation features provide students with the ability to generate outputs, which they can then compare with data obtained from external sources, such as empirical studies or their own investigations (Lorenz, 2009; Damelin et al., 2017; Hassanibesheli et al., 2020). If the model’s output does not match the external data, students can revise their model or question the validity of the data source. This iterative process of refining the inputs and relationships between variables can help students to improve their models over time (Weintrop et al., 2016; Shin et al., 2022).
Several approaches to computational system modeling exist, each with its own affordances that support learning about complex systems. Because this research focuses on static equilibrium and system dynamics modeling, we will focus on these two approaches.
The first, static equilibrium modeling, provides a computational representation of a system that consists of a set of variables linked by relationships that define how one variable influences another. Any change to an input variable is immediately reflected in new values calculated for each variable in the system (Shin et al., 2022). While enabling users to construct models with cause and effect relationships between system elements, the approach encourages students to go beyond simple linear causal chains and create models with long branching structures and mediating causes (Metcalf et al., 2000; Perkins and Grotzer, 2005); however, static equilibrium modeling does not consider time as a factor.
The second approach, system dynamics modeling, enables the representation of change over time and includes interactions between system components that include stocks and flows (Sweeney and Sterman, 2000; Ossimitz, 2002). Stocks refer to system components that accumulate or deplete over time while flows refer to system components that decrease or increase the amount in the stocks. System dynamic models allow the user to construct nonlinear interactions and structures such as feedback loops and to produce an output that represents change over time (Richmond, 1993, 1994; Forrester, 1994; Sweeney and Sterman, 2000). This approach addresses two major aspects of ST that the static equilibrium modeling approach cannot. The first aspect, feedback present in complex systems (Richmond, 1993, 1994; Forrester, 1994; Sweeney and Sterman, 2000) refers to any action that causes an effect back to the starting point of the action (Haraldsson, 2004). For example, an increase in greenhouse gasses (including methane) causes an increase in global temperatures. Warmer temperatures cause the permafrost in Earth’s Northern regions to thaw. The thawing of the permafrost causes the release of methane, which further adds to the rise in global temperatures. This in turn exacerbates the thawing of the permafrost, which releases more methane to the atmosphere, and so on. The second aspect addresses how a system can change over time. Many phenomena require the consideration of change over time in which a time lag between the cause and effect exists. In some cases, the delay is negligible, as in certain chemical reactions while in others, the time delay is thousands or millions of years, as in evolution or the formation of a canyon (Kali et al., 2003; Assaraf and Orion, 2005; Meadows, 2008).
Researchers have studied students’ use of static equilibrium models constructed to support sensemaking of scientific phenomena (Metcalf et al., 2000; Bielik et al., 2018; Shin et al., 2022), and system dynamics modeling (Eidin et al., 2023), but have not tested the use of both in the same curriculum context. Both static equilibrium and dynamic modeling approaches involve applying aspects of ST. Although using system dynamics has the potential to engage students in additional ST aspects, such as identifying feedback and framing problems in terms of change over time, it does not guarantee that using a system dynamics approach gives rise to different reasoning and growing causal complexity. Despite its potential, constructing system dynamics models remains challenging and it is not clear to what extent their use can benefit students compared to other approaches (Mandinach, 1989; Sweeney and Sterman, 2000; Eidin et al., 2023).
In this work, we investigate the complexity in students’ explanations from an ST perspective as they construct and interpret static equilibrium and system dynamics models. In addition, we examine if static equilibrium models, which engage students in cause and effect reasoning but are considered simpler and more straightforward, could serve as a scaffold for constructing dynamic models that include feedback and thinking in terms of change over time, two of the most challenging aspects of ST.
3. Research question
How do students’ explanations of static equilibrium and system dynamics models reflect aspects of systems thinking as indicated by the presence of various levels of complexity in multiple dimensions of causality?
4. Context
4.1. Curriculum
The present study was part of a six-week project-based learning chemistry unit that incorporated five investigations. The unit was designed to align with the Next Generation Science Standards (NGSS) performance expectations HS-PS1-3, “Plan and conduct an investigation to gather evidence to compare the structure of substances at the bulk scale to infer the strength of electrical forces between particles” and HS-PS3-2, “Develop and use models to illustrate that energy at the macroscopic scale can be accounted for as a combination of energy associated with the motion of particles (objects) and energy associated with the relative positions of particles (objects)” (NGSS Lead States, 2013). The study took place in a school setting, where students participated in two to three lessons per week, each lasting 80 min.
The unit was centered around a driving question: ‘Why do I feel colder when I am wet than when I am dry?’ In an introductory activity, students engaged in a tactile experience by placing droplets of water, ethanol, and acetone on their hands, followed by a group discussion to generate questions and hypotheses using a driving question board (Weizman et al., 2008). To facilitate the process of defining the key components underlying the phenomenon, students worked in small groups of three to four members to develop paper-pencil models, depicting the interrelationships among the variables. This step served as a foundation for a subsequent discussion comparing and contrasting the relative strengths and limitations of paper-pencil versus computational models. Students were introduced to the affordances of computational models, such as their ability to simulate and validate models using real-world data.
After the aforementioned discussion, students were instructed to represent their paper-pencil models as a static-equilibrium model using SageModeler, a free web-based modeling tool to facilitate both static equilibrium and system dynamics modeling (Damelin et al., 2017). Since students had some experience in building static equilibrium models using SageModeler during a previous unit, they were provided with a brief exercise to refresh their memory before constructing models to address the driving question.
Throughout the unit, students took part in various learning experiences, such as conducting hands-on experiments, working with computer simulations, and analyzing real-world data, which they used to iteratively revise their models. Initially, the focus of the unit was on modeling what factors would affect the evaporation rate and “coldness” of an evaporating liquid. These concepts were appropriately modeled using a static equilibrium approach. For example, an increase in intermolecular attractions between the molecules of a liquid would mean a decrease in evaporation rate and a decrease in the “coldness” felt when the liquid evaporated from your skin. Students completed an activity where they used sensors to measure the change in temperature over time, creating a cooling curve for each liquid. This activity led to a plenary discussion on the limitations of static equilibrium models in representing changes over time, as illustrated by the evaporative cooling processes, and created a need for a system dynamics modeling approach.
To support students in constructing dynamic models, they completed an introductory tutorial, which guided them in constructing a simple system dynamics model of their own while learning about the unique features of system dynamics modeling. After that experience, students built a dynamic model to address the driving question while considering the change over time of components in the system.
To validate their system dynamics model, students compared the simulation output from the dynamic models with their experimental results. This process allowed students to test the validity of their models and refine them.
The phenomenon of evaporative cooling presents significant challenges from an ST perspective. Understanding why one feels colder when wet than when dry requires a high level of performance in all dimensions of causality. The transfer of kinetic energy to potential energy, a dynamic process that affects multiple components in a system simultaneously, is a fundamental aspect that must be considered (Chen et al., 2014). In addition, a comprehensive mechanism should address the microscopic and macroscopic entities involved in the process, explaining how interactions between intermolecular forces result in emerging patterns (Ben-Zvi et al., 1986; Dori and Hameiri, 2003; Krist et al., 2019). Moreover, the cooling effect that emerges as a result of the random movement of molecules requires a departure from the use of linear causal reasoning and the attribution of a central causal agent. Research demonstrates that explaining emergent properties at the macroscopic level as a result of interactions at the microscopic level is extremely challenging (Chi, 2005; Tümay, 2016).
The exponentially shaped cooling curve resulting from evaporation cannot be explained by a simple linear cause and effect mechanism. Rather, it involves feedback, which is a prominent ST aspect. The shape of the graph is also a result of the random movement of particles which accounts to an uneven distribution of kinetic energy among the molecules. Molecules with the highest kinetic energy leave the system first, causing the average kinetic energy (and thus temperature) to drop, lowering the evaporation rate. This feedback causes the liquid to evaporate and cool quickly at first, but over time both evaporation rate and cooling slow down as more molecules with the highest energy leave the system. However, explaining such behavior through feedback mechanisms has been documented as particularly challenging for students (Haraldsson, 2004; Tripto et al., 2013). Further details about the unit and the implementation of the evaporative cooling phenomenon using SageModeler can be found in Shin et al. (2022).
Figure 1 shows an example of an appropriate static equilibrium model of the evaporative cooling phenomenon. Figure 2 shows an example of an appropriate system dynamics model of the same phenomenon. The static equilibrium model represents an outcome behavior that accounts for why different liquids have different degrees of “coldness” as they evaporate from the skin at different rates. For example, one can notice in Figure 1 the intermolecular forces variable eventually affects the mass of the liquid evaporated and the final temperature of the liquid. Figure 2 shows a system dynamics model simulation output in which temperature and evaporation rate steeply drop at the beginning and then taper off in an exponential decay trend. This behavior requires the construction of a feedback relationship.
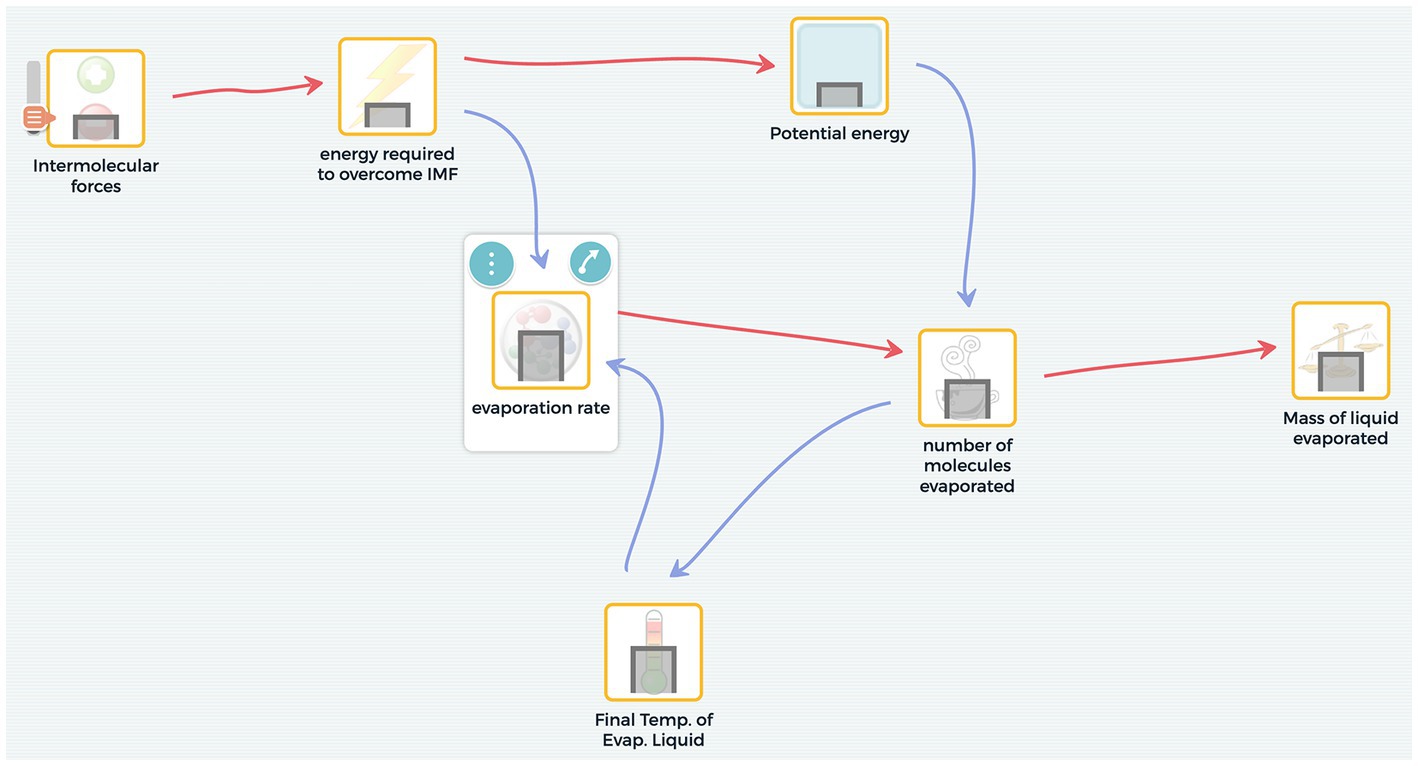
Figure 1. An example of a static equilibrium model constructed by students JU and TR. The nodes represent variables. The red and blue arrows represent a causal relationship between two variables. Red arrows represent a relationship in which an increase in one variable causes an increase in the other. Blue arrows represent a relationship in which an increase in one variable causes a decrease in the other.
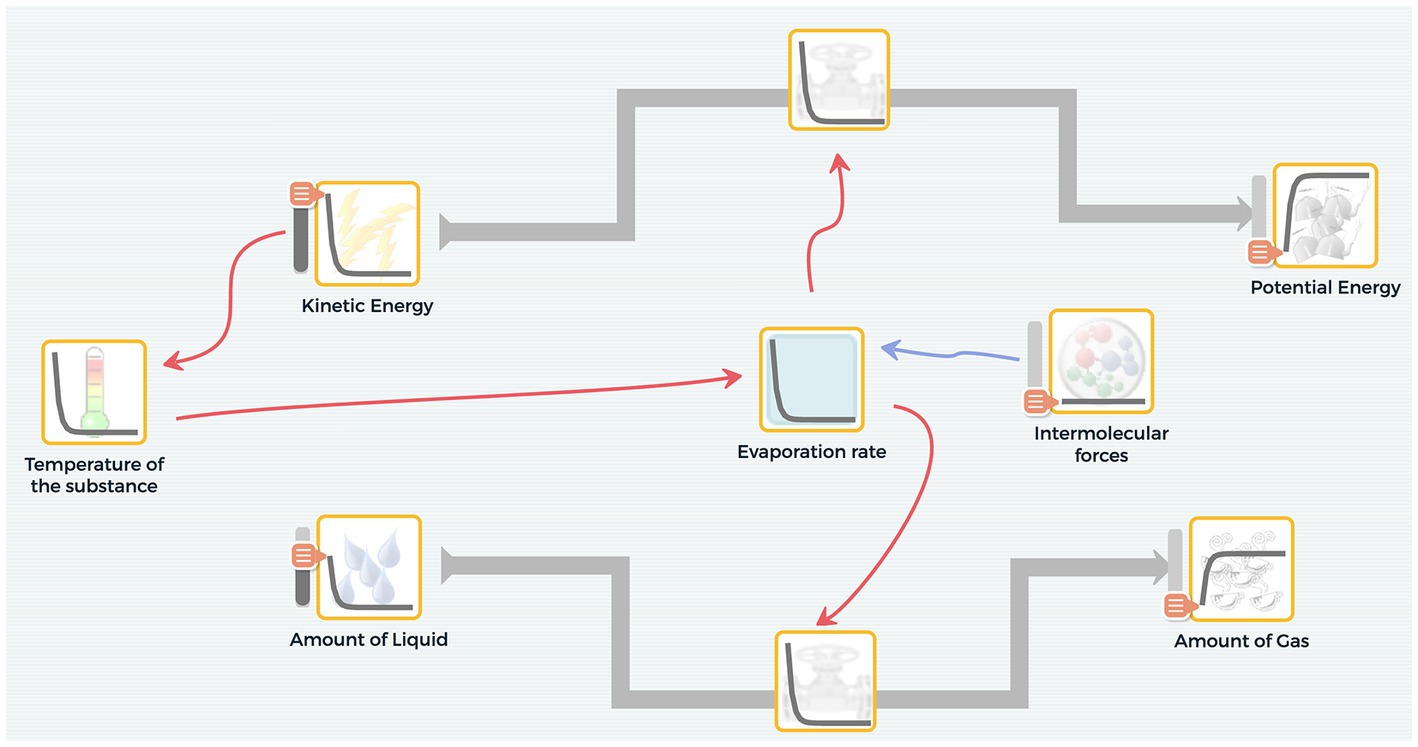
Figure 2. An example of a system dynamics model, which allows learners to set variables that accumulate over time and set the rate of flow between them. The simulation output produces mini-graphs inside the nodes, which represent change over time.
4.2. SageModeler
SageModeler1 is a web-based open-source tool designed to support student learning by facilitating engagement in ST through constructing, evaluating, revising, and using models (Damelin et al., 2017). SageModeler allows students to construct static equilibrium and system dynamics models. The tool has two major modeling affordances: representation of variables and relationships and supporting model validation.
4.2.1. Representation of variables and relationships
SageModeler allows learners to represent components of the system as nodes in a system diagram. The nodes represent variables that are linked together, forming a visible network of cause and effect relationships. For example, consider the evaporative cooling phenomenon. In a static equilibrium model, one can set relationships in which an increase in intermolecular forces causes an increase in the energy required to overcome the intermolecular forces (IMFs) (Figure 1). In a system dynamics model, with one variable representing ‘amount of liquid’ and another representing ‘amount of gas particles,’ the user can set a different type of relationship, called a transfer link, to represent a flow from the liquid state to the gas state (Figure 2). By focusing on an explicit representation of the components and their relationships, SageModeler provides an accessible way for students to create an instantiation of their conception of the system.
To scaffold students in developing system models, SageModeler includes pull-down menus and graphs that students set to describe semi-quantitatively how one variable influence another. This eliminates the need for students to write complex mathematical equations or learn how to code, thus reducing cognitive load (Metcalf et al., 2000). We are not arguing that the use of mathematical equations or programming is not important for 21st century citizens; however, a viable strategy for making computational modeling more accessible is to reduce such barriers. In SageModeler, the relationship setting appears in the form of a sentence, such as, ‘An increase in [variable X] causes [variable Y] to increase by about the same.’ To define the relationship, students choose words with associated graphs. For example, a linear graph is associated with the about the same relationship while an exponential graph is associated with the more and more relationship (Figure 3).
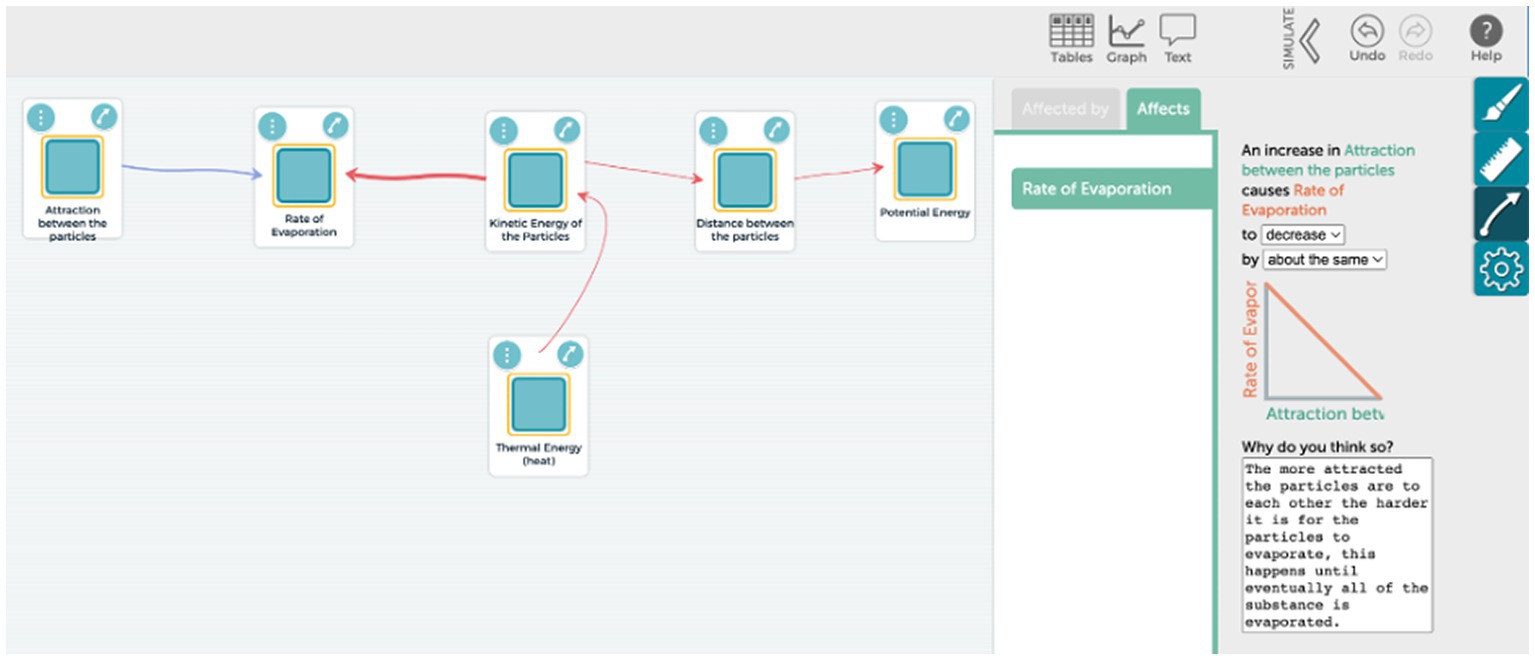
Figure 3. Users can set both the direction (increase or decrease) and the magnitude (about the same, a lot, a little, more and more, less and less) of relationships between variables in SageModeler.
4.2.2. Supporting model validation
SageModeler allows users to simulate their model and test it by comparing their model behavior to real-world data. SageModeler facilitates that comparison by integrating the Common Online Data Analysis Platform (CODAP), which offers graphing and data analysis tools (Finzer and Damelin, 2015) and supports data imported from various sources. Students can import real-world and experimental data or output from other expert models and compare it to data generated from a SageModeler simulation. The software allows users to create graphs from various datasets and make decisions about the validity of their model.
4.3. Participants
Twenty-six 10th grade students from two chemistry classes in a magnet school from a rural–urban fringe district in the Midwestern U.S. participated in this study. Each class consisted of 24 students. The students were selected from the two classes, one taught by Mr. H, a chemistry teacher with 15 years of experience, and the other one taught by Mr. M, a chemistry and environmental science teacher with 6 years of experience. The sample, representative of the two classes, included 12 female and 14 male students, with a mixture of high- and low-achievers. The sample of participants was a convenience sample, based on students’ and their parents’ agreement to participate in human subject research. No data was collected on the students’ socioeconomic background. Among the participants, two identified as Black, one as Asian, and the rest as White. Both teachers had prior experience using SageModeler and teaching both modeling approaches in their classes, although in a different context than the evaporative cooling unit. Mr. H and Mr. M had several meetings with the authors to walk through the activities and experiments in the unit and to discuss strategies for supporting students in constructing models using SageModeler. These meetings, which totaled seven hours, served as a preparatory step before the start of the unit.
5. Methodology
To answer the research question, we utilized two primary sources of data: student interviews and screencasts. The interviews served as the main data source, enabling us to compare the differences in students’ explanations as they used both modeling approaches to explain evaporative cooling. The screencasts enabled a valuable insight into students’ reasoning as they constructed models using each modeling approach. We utilized both the screencasts and interview transcripts to capture student reasoning and application of ST through the analysis of dialog and discussion.
5.1. Interviews
Student interviewees included 11 students, 5 female and 6 male, with each interview lasting 45–60 min. Students were asked to explain the phenomenon as they walked the interviewer through their static equilibrium model and then their system dynamics model. These interviews were semi-structured and included questions such as “Can you walk me through your model?” and “what does your model tell us about the evaporative cooling phenomenon?.” The full interview protocol can be found in the Supplementary material. During the interview students were shown their models on a laptop; their responses to questions and references to their model were recorded. The interviews were fully transcribed. Conducting interviews in which students walk the interviewer through their model has been shown to be an efficient strategy to elicit students’ understanding and reasoning (Schwarz et al., 2009; Eidin et al., 2023; Stephens et al., 2023). We coded and analyzed students’ utterances that followed questions asking them to use their model to explain the evaporative cooling phenomenon.
Interviews were analyzed using the dimensions of causality framework described by Perkins and Grotzer (2005), as it provided a means to assess the complexity of students’ explanations of the evaporative cooling phenomenon and make a fine-grained differentiation between linear causal explanations and more complex types of explanations that address ST aspects. We applied three of the dimensions of the framework (agency, interactive pattern, and mechanism). We established that only two levels of the probability dimension were applicable in the context of the phenomenon, and during the coding and analysis of the interview data, we found that the probability dimension exhibited significant overlap with the levels of the agency dimension. Therefore, we determined that the inclusion of the probability dimension did not yield any additional insights into the evaluation of students’ reasoning, so we decided not to include it in our analysis. Table 1 provides an overview of the different levels of causal dimensions and specific examples of each level in the context of the phenomenon. Table 2 shows which levels of complexity of each causal dimension align with which ST aspects.
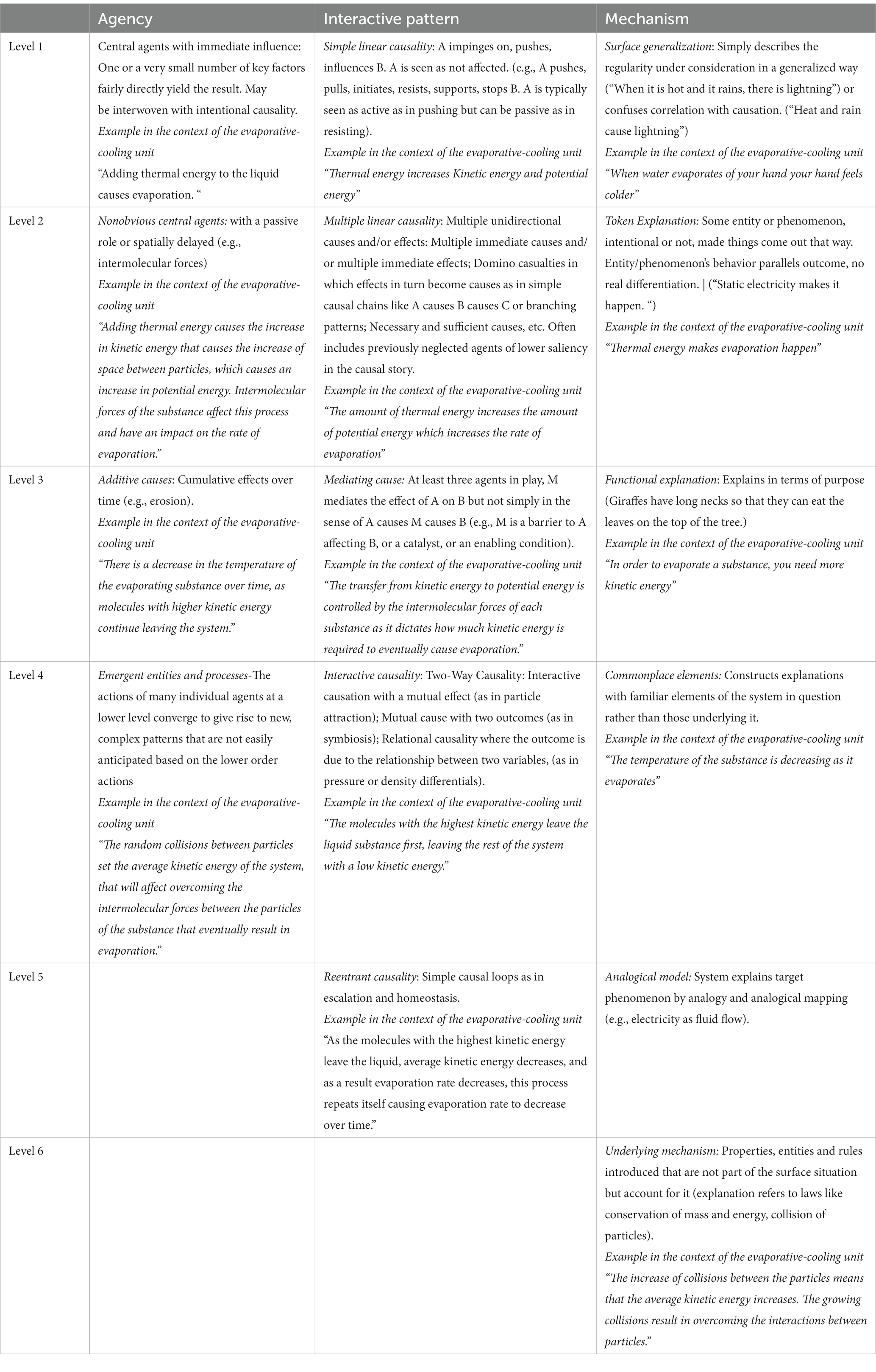
Table 1. Dimensions of causality (Perkins and Grotzer, 2005).
A scientific explanation for evaporative cooling using the causal dimension framework suggests that the agency in the system emerges due to the random collisions of particles. This leads to an uneven distribution of energy, creating a reentrant interactive pattern. In this pattern, particles with the highest kinetic energy overcome intermolecular forces and leave the system, which lowers the average kinetic energy of the remaining particles in the liquid phase. Additionally, as the particles overcome intermolecular forces to evaporate, the increased distance between attracting particles results in an increase in potential energy at the expense of some of the kinetic energy of the particles. This process results in a decreasing temperature and evaporation rate. The explanation also describes a mechanism that accounts for the random collision between particles and the conservation of mass and energy.
Two authors coded the data after two cycles of discussions. The first cycle had a 75% agreement. The second cycle had a 90% agreement. The coders discussed their differences to achieve 100% agreement. Further analysis conducted using Atlas.ti software, focused on differences in the dimensions of causality in students’ explanations of the phenomenon in the static equilibrium and system dynamics models. Each dimension was analyzed separately, allowing for the detection of specific differences in students’ reasoning between the two modeling approaches. Of note, the time allotted during the interviews for students to explain the phenomenon using each type of model was relatively equal for both models.
The following excerpt from student KY offers an example of how we utilized the dimensions of the causality framework when coding the interview transcripts.
“The average kinetic energy is transferring into potential energy. And the spacing of particles and IMF is affecting that transfer. Potential energy is the spacing of particles when you are talking about evaporation. So as the spacing particles increase, so is the potential energy. And then IMF is the opposite of that, because the IMF is the attraction between the particles and it wants to keep the particles together and it does not want them to space out. So, if the IMF is keeping the particles from spacing out, then if that was high, the particles would not be spacing out as much and there would be less potential energy. And then it’s showing that the transfer from kinetic energy to potential energy affects the rate of evaporation.”
To code the excerpt above, we identified various dimensions of causality. It is noteworthy that not all dimensions are necessarily present in each student’s remarks. To determine the level of agency in the student’s explanation, we first identified the variables within the explanation: intermolecular forces, potential energy, kinetic energy, and the rate of evaporation. The student mainly focused on intermolecular forces as a significant variable affecting different variables in the system, albeit not as a central cause that accounts for the evaporative cooling phenomenon. Therefore, we assigned a level 2 to the agency dimension. Moreover, intermolecular forces were also identified as a mediating variable that regulates the transfer from kinetic to potential energy and, accordingly, the rate of evaporation. Consequently, we assigned a level 3 to the interactive pattern dimension. Additionally, since the student addressed the particle level and illustrated the impact of intermolecular forces on the flow of energy within the system, we assigned a level 6 to the mechanism dimension.
5.2. Screencasts
We conducted a screencast analysis of 10 groups engaged in constructing models using SageModeler. The groups were composed of the same individuals who participated in the interviews, along with their modeling partners. The screencasts recorded both the screen and voices of the participants, and varied in length among the different groups, with an average screen time of 120 min per group. The analysis focused on the discussions that transpired between the students, between the students and their teacher, and among students in neighboring groups. Notably, such episodes of discussion were infrequent and heterogeneous across the groups.
The analysis specifically targeted three aspects of ST: cause and effect, change over time, and feedback mechanism (Richmond, 1993; Orgill et al., 2019; Shin et al., 2022). To assess the level of cause and effect, we utilized the interaction pattern causal dimension from Perkins and Grotzer’s (2005) framework. The levels of the interaction pattern provided insight into usage of cause and effect and feedback. To assess thinking in terms of change over time, we utilized the agency dimension with a focus on discussions about processes and aggregative effects. Particular attention was paid to terminology that indicated such thinking and included phrases such as ‘first A happens then B,’ ‘it starts fast, but it slows down,’ and ‘over time as this change and goes down, the other changes and goes up.’ We compared students’ reasoning as reflected at the time they constructed their model and at the time they interpreted their model in the interview. We specifically looked for congruence between the type of reasoning students applied as they constructed the static equilibrium and system dynamics models and the reasoning they applied when they used their model to explain the phenomenon during the interview. For example, we examined correlations between discussions about change over time during the model construction process and the levels of dimensions of causality elicited in students’ explanations during the interviews (Table 3).
6. Results
Student utterances were coded for levels of causal dimensions when providing explanations using their static equilibrium models and compared with those made when using their system dynamics models of evaporative cooling. The differences indicated by the level of causal dimensions revealed three distinct categories of students:
(a) those who demonstrated a consistently low level in dimensions of agency and interactive pattern in both modeling approaches, (b) those who maintained a high level of agency and interactive pattern in both static equilibrium and system dynamics models, and (c) those who showed an increasing level of complexity in dimensions of agency and interactive pattern, starting with a low level in the static equilibrium modeling approach and shifting to a higher level in the system dynamics approach.
To present a detailed differentiation between students’ reasoning while using the two modeling approaches to explain the evaporative cooling phenomenon, we conducted separate analyses for each causal dimension. This fine-grained approach allows us to gain unique insights into students’ application of the ST aspect in each modeling approach. The figure below provide a visualization of the level of the three causal dimensions as elicited from students’ explanations during the interview as well as the number of utterances assigned to each level. The different color of the dots in the figure indicates the category each student fell under; consistently low, consistently high, and increasing in complexity. In the following sections, we discuss the results for each dimension.
6.1. Agency
According to the patterns illustrated in Figure 4, 90% of the students’ utterances who utilized their static equilibrium models to explain the evaporative cooling phenomenon, demonstrated a lower level of complexity in the agency dimension. It was the maximum level achieved for 9 out of 11 students during the interviews, as opposed to when they used system dynamic models. In the system dynamic model, 64% of students’ utterances confined themselves to a lower level.
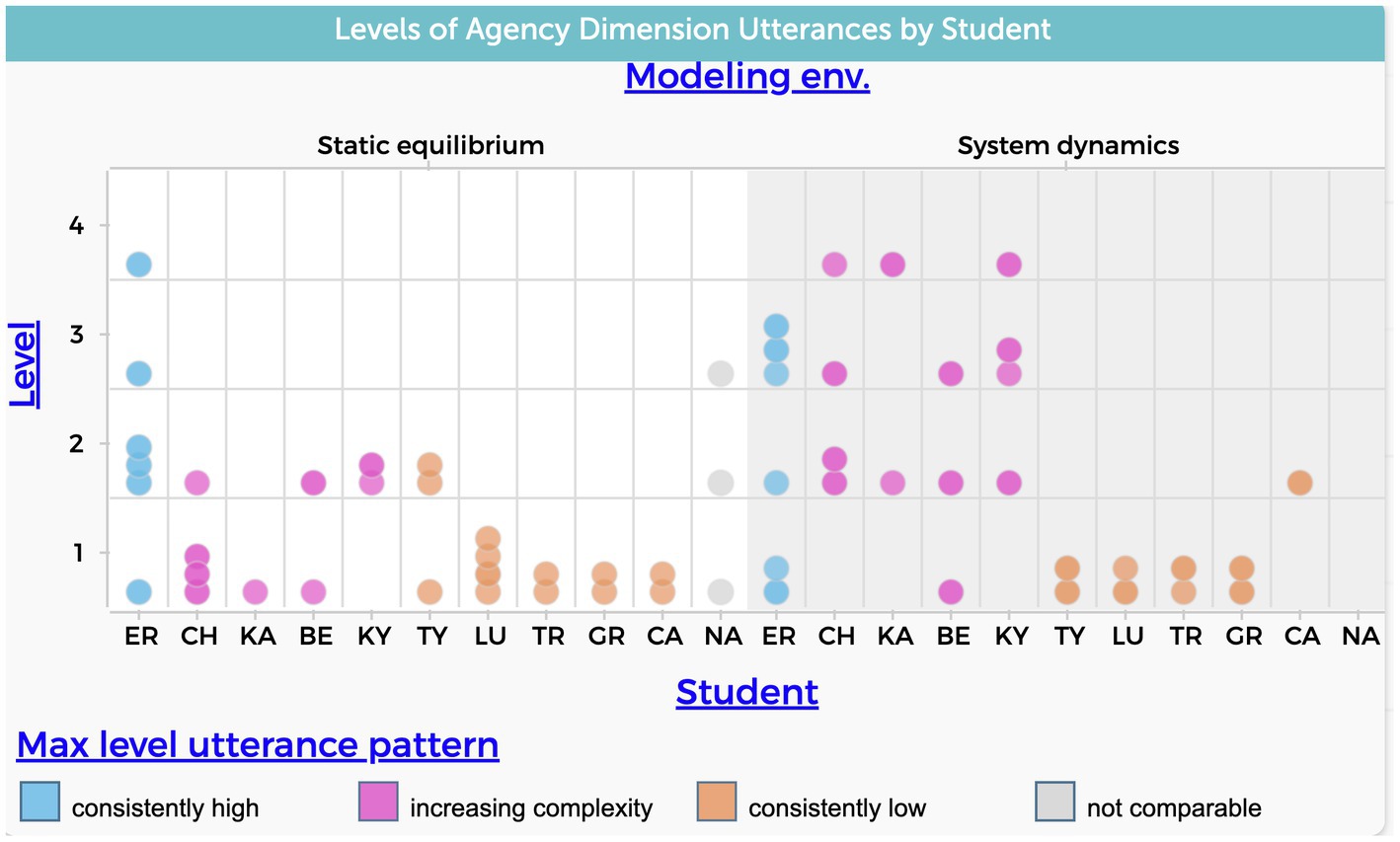
Figure 4. Frequency of students’ utterances that refer to the agency causal dimension. The level variable in the y-axis refers to the four levels of complexity shown in Table 1. Each data point represents a single coded student utterance.
Levels 1 or 2 were used as cutoffs for determining lower levels as they both describe simplistic agency.
Figure 4 shows students falling into three groups as previously mentioned: one student who’s max utterances were high for both modeling approaches (ER), five students who demonstrated a consistent lower level in both modeling approaches (CA, GR, LU, TR, TY), and four students who exhibited an increasing level of complexity when explaining the phenomenon using system dynamics models (BE, CH, KA, KY). The increase in levels refers to explanations that address aggregative effects and emergent behavior which align with these particular aspects of ST.
The data suggests that the use of system dynamics models increases the likelihood of students moving from a view that emphasizes a single prominent factor as the central agent affecting all other variables to a view that recognizes the cumulative effects of multiple factors over time.
Figure 5 shows the total number of utterances within each level of the agency causal dimension. We interpret this graph as indicating that the system dynamics model approach, (1) reduces the tendency to explain the phenomenon with a central component that has an instantaneous effect on the system and (2) encourages explanations with higher levels of complexity that consider accumulation over time and an emergent behavior.
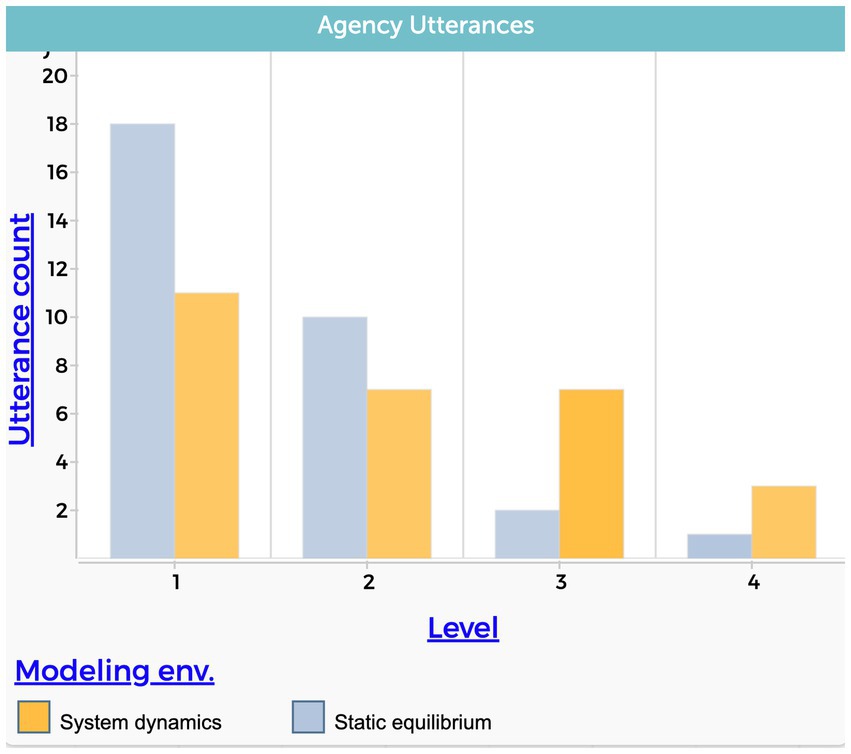
Figure 5. Students’ level of agency causal dimension. Each column represents the total number of utterances in each modeling environment. The level variable stands for the level of complexity, from the lowest value of 1 to the highest value of 4.
Next, we present student quotes to illustrate the different levels of the agency causal dimension as revealed in the context of this research.
6.1.1. Level 1: salient central agent
GR: “I would say the key variable would probably be the temperature because we determined that thermal energy was like the starting point of evaporation. So, then that would be like the main thing.”
In the statement above, GR posits that the addition of thermal energy to the system is the primary variable responsible for initiating the evaporation process and, in turn, induces a cooling effect. In this sense, thermal energy serves as a salient central agent, warranting an evaluation at level 1.
6.1.2. Level 2: non-obvious central agents with long causal chains and branching structures
BE: “So as intermolecular force increases, the time for evaporation also increases. And then you have the amount of the substance. Obviously, the more substance you have, the longer it will take to evaporate. And then you have the kinetic energy. So an increase in kinetic energy of the substance causes the time for evaporation to decrease. Also, we said the same for potential energy. Because potential energy is a measure of energy, when the particles are getting farther apart, that means that they are more likely to evaporate.”
BE’s explanation of her static model is characterized by individual cause and effect relationships and shorter causal chains, rather than a prominent variable that directly influences a specific output. Due to the absence of a salient central agent and a more complex causality relationship considering the influence of different components in the system on each other, this explanation is evaluated at level 2.
6.1.3. Level 3: additive causes, causes with cumulative effect over time
KY: “The average kinetic energy should decrease over time and then the potential energy should increase, which would increase the rate of evaporation.”
KY describes the accumulating change over time for kinetic and potential energy as one type of energy transfers to another. Therefore, this explanation is evaluated at level 3.
6.1.4. Level 4: emergent entities and processes, interaction of system components at a lower level interacting that produces new behavior
CH: “The particles that are being evaporated are taking away the kinetic energy of the surface area by bumping into each other and transferring the kinetic energy. Since they are bumping into water particles, they are just transferring kinetic energy. It’s not like there if I put water on the table, it’s not like the table’s gonna evaporate with the water. It’s just that the table is going to get cold. Like your hand got colder.”
CH explains that the random collisions between particles eventually lead to an uneven distribution of kinetic energy that leads to the evaporative cooling phenomenon. Considering how random behavior of components in the system lead to an emergent behavior at the macroscopic level warrants this explanation at level 4.
6.2. Interactive pattern
According to the patterns illustrated in Figure 6, 73% of the students’ utterances who utilized their static equilibrium models to explain the evaporative cooling phenomenon, demonstrated a lower level of complexity in the interactive pattern dimension. It was the maximum level achieved for 6 out of 11 students during the interviews, as opposed to when they used system dynamic models. In the system dynamic model, 48% of students’ utterances were evaluated as lower level.
Levels 1 or 2 were used as cutoffs for determining lower levels as they both describe simple linear causal patterns.
Figure 6 shows students falling into three groups as previously mentioned: 4 students who’s max utterances were high for both modeling approaches (ER,CH,CA, KY), 4 students who demonstrated a consistent lower level in both modeling approaches (GR, LU, TR, TY), and 2 students who exhibited an increasing level of complexity when explaining the phenomenon using system dynamics models (BE, KA). The increase in levels refers to explanations that demonstrate more complex causal patterns like those that address mediating variables and feedback, which align with aspects of ST. Of note, the same students who demonstrated low level in the interactive pattern dimension also demonstrated a low level in the agency dimension.
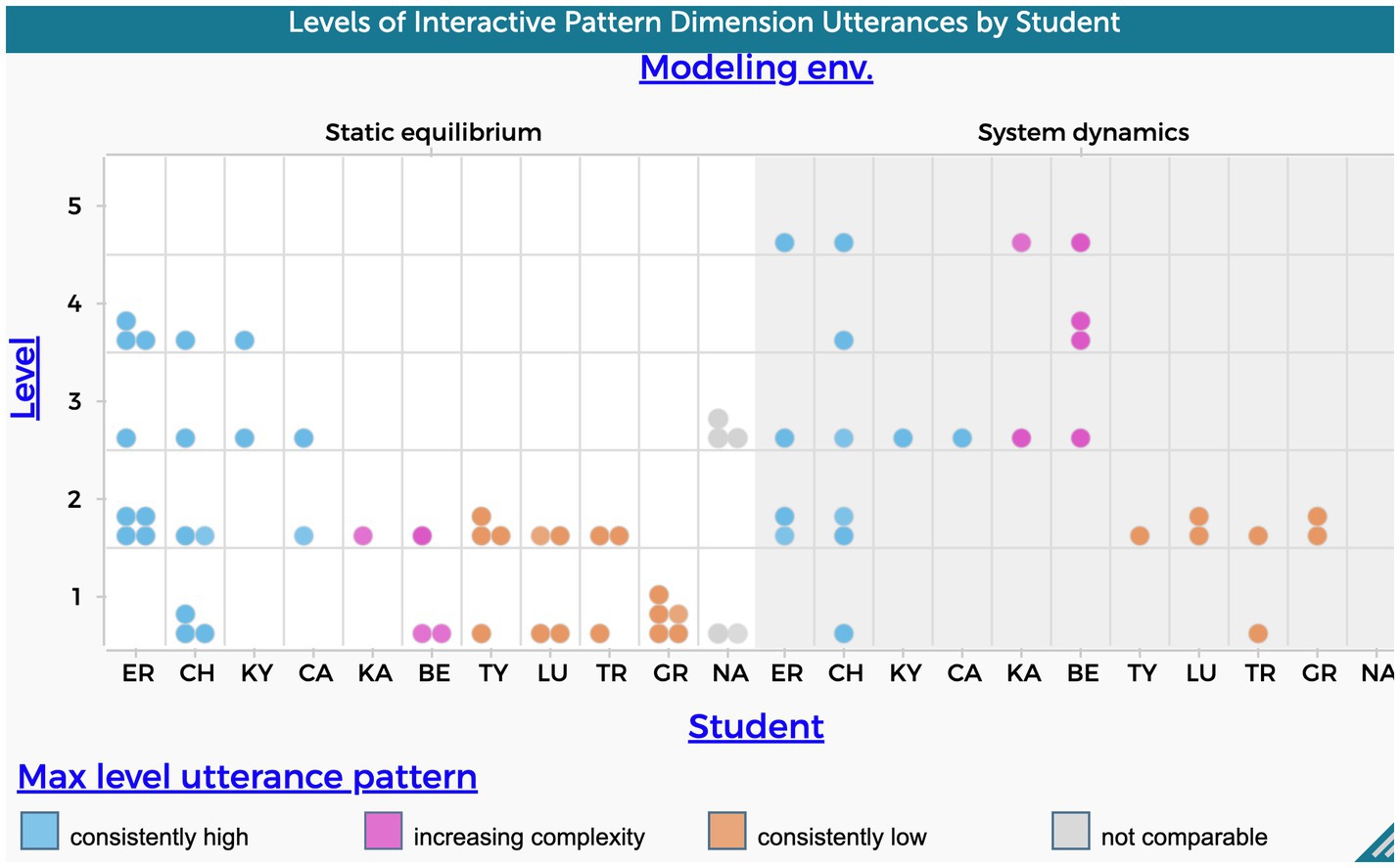
Figure 6. Frequency of students’ utterances that refer to interactive pattern causal dimension. The level variable in the y-axis refers to the five levels of complexity shown in Table 1.
Five students exhibited a relatively high level of interactive patterns while using static equilibrium to explain the phenomenon (CA, CH, ER, KY, NA). A causal explanation that included a mediating variable characterized those explanations. Notably, the use of a system dynamics approach appeared to have a significant impact on the inclusion of feedback (Level 5) of four students’ explanations.
Figure 7 shows the total number of utterances within each level of the interactive patterns causal dimension. It strengthens the notion that the system dynamics modeling approach is more conducive to addressing feedback mechanisms in students’ explanations. In addition, the data presented reveals a reduction in the frequency of simple cause and effect utterances (Level 1) in the system dynamic context. It is interesting to note that many students included feedback as part of their explanations even if their system dynamics model did not include a feedback loop as part of the model’s structure.
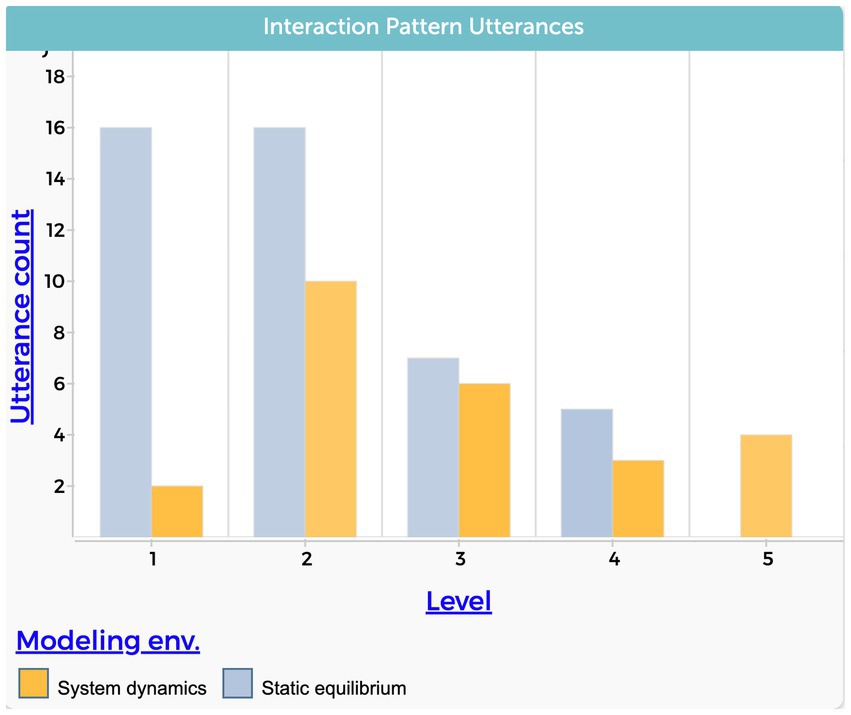
Figure 7. Students’ level of interactive pattern causal dimension. The level variable stands for the level of complexity, from the lowest value of 1 to the highest value of 5.
Next, we present student quotes to illustrate the different levels of the interactive pattern causal dimension as revealed in the context of this research.
6.2.1. Level 1: simple linear causality, A affects B
TY: “So as the strength of the intermolecular forces increases, the amount of liquid particles also increases. And the amount of gas particles decreases because the stronger the intermolecular forces are in the liquid, the harder it is for the particles to get away.”
TY provides a simple linear relationship in which variable A increases variable B and A decreases variable C, in which B and C are the amount of substance in liquid and gas phase, respectively. Given the explanation’s simple linear cause and effect pattern, it was evaluated at level.
6.2.2. Level 2: multiple linear causality, A affects B affects C, may also include a branching pattern
TR: “What our model is saying is that the more thermal energy in particles that you have, the more kinetic energy the particles have. And then when they move around more, they’ll bounce around more, causing molecular forces to get weaker and increase the chances of breaking and then these breaking increases the amount of potential energy.”
This student describes a pattern where A leads to B and then to C. TR characterizes intermolecular forces as extrinsic rather than intrinsic properties of a substance and explains that they become weaker due to particle collisions instead of being overcome by them. However, this simplified representation of a dynamic process does not accurately align with the scientific consensus and may result from the difficulty of representing a complex concept within a static equilibrium model. The rather detailed causal chain warranted a level 2 evaluation.
6.2.3. Level 3: mediating cause, M mediates the effect of A on B
KY: “Right. So like I said earlier, the average kinetic energy is transferring into potential energy, and the spacing of particles and intermolecular forces is affecting that transfer…. So if the intermolecular forces is keeping the particles from spacing out, then if that was high, the particles would not be spacing out as much and there would be less potential energy. And then it’s showing that the transfer from kinetic energy to potential energy is the rate of evaporation, which is affected by intermolecular forces.”
KY refers to intermolecular forces as the mediating factor that controls the transfer from one type of energy to another. The ability to create a transfer link and set a relationship that mediates this transfer in the shape of a valve (Figure 3) supported students in including a mediating cause to their explanations. This explanation was coded at level 3.
6.2.4. Level 4: interactive causality, two-way causality
BE: “So, as the particles gain kinetic energy, the higher energy particles are evaporating, and as they are evaporating, they are taking the kinetic energy with them, and that’s decreasing the temperature of the water on your hands. So, when you have water on your hands, it makes you feel colder because that puddle of water is actually losing heat.”
BE describes how the evaporation affects the temperature of the liquid remaining and how this in turn affects the evaporation. This description of interdependency warranted a level 4 evaluation.
6.2.5. Level 5: reentrant causality, simple causal loops
ER: “So as the temperature goes down, the rate of evaporation is going to go down as well because it’s going to have less high kinetic energy because the average kinetic energy is going down. Well, we are going to have some particles with high, some with low kinetic energy, but if the average going down as the molecules with high kinetic energy leave the system, that means you are losing higher kinetic energy molecules and you are not replacing them with anything. So it just keeps going down slower [temperature].”
In this example, ER addresses the relationship between the distribution of kinetic energy within the particles of a substance and the rate at which its temperature decreases over time. Addressing the gradual change in the rate of evaporation (“keeps going down slower”) distinguishes ER’s explanation from BE’s. ER describes a feedback mechanism where the leaving of particles with high kinetic energy from the system results in a decrease in the average kinetic energy within the system. This, in turn, leads to a reduction in evaporation and a slower decrease in temperature, thus causing a further slowdown in the rate of temperature drop over time.
6.3. Mechanism
The findings presented in Figure 8 reveal that most students reached the highest level in which they mention an underlying mechanism to explain the phenomenon in both modeling approaches. Yet a deeper examination of the explanations shows a difference between the static equilibrium and system dynamics context. In the static equilibrium approach, students explain the evaporative cooling phenomenon by referring to the particle level and describing interactions between molecules. In the system dynamics model approach, in addition to addressing the particle level, students also address underlying laws like the conservation of mass and energy. For example, in the context of static equilibrium modeling, NA says, “Um, I think that because as the number of collisions increases, it increases the ability for the fastest particles to leave the system. So, as more collisions occur, more of those particles are going to be having that high speed, giving them the potential to leave the system in the form of vapor.”
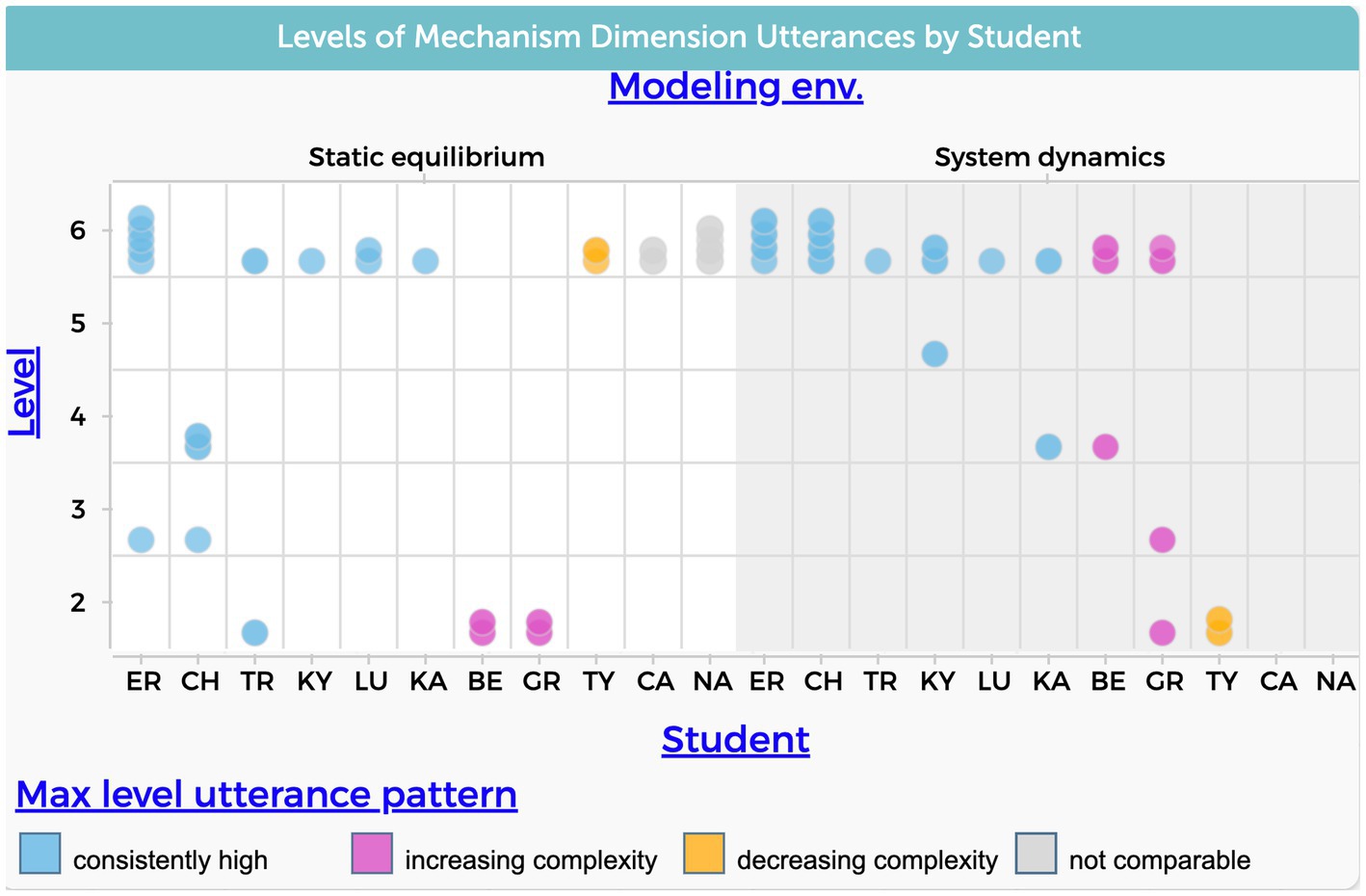
Figure 8. Frequency of students’ utterances that refer to mechanism causal dimension. The level variable in the y-axis refers to the six levels of complexity shown in Table 1.
In the context of system dynamics modeling, CH says, “Well, I believe kinetic energy does transfer into potential energy when it phase changes because energy cannot be created or destroyed, so when gas changes into a liquid and then into a solid, the energy has to be stored somewhere, and it cannot be stored as kinetic, so then it has to be stored as potential.”
Besides those differences the patterns demonstrated in Figure 9 indicate no significant difference in the level of complexity with regards to the mechanism causal dimension between static equilibrium and system dynamics modeling approaches. Therefore, we do not provide examples of quotations for lower levels regarding the mechanism causal dimension as they were rare and insignificant.
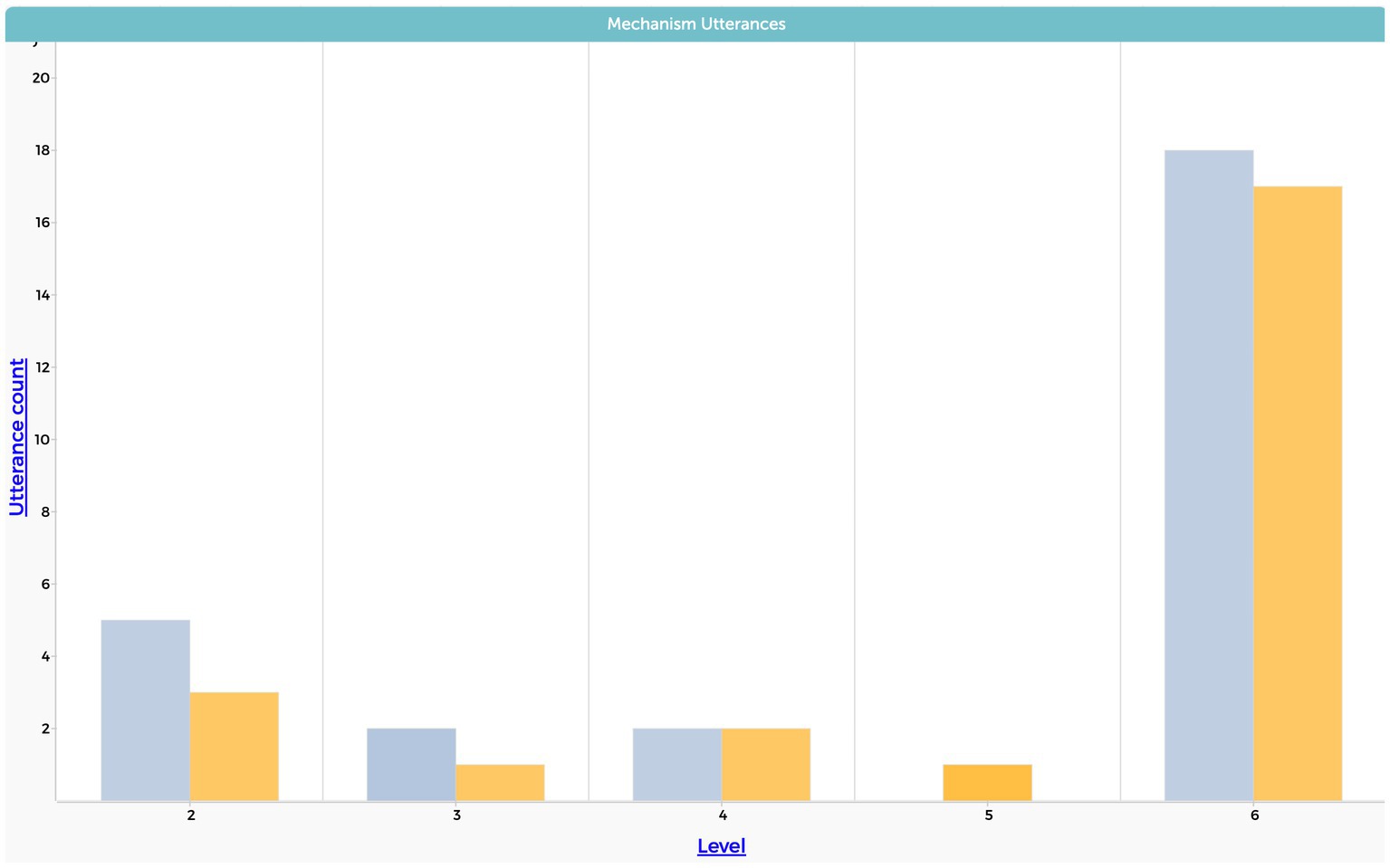
Figure 9. Students’ level of mechanism causal dimension. The y-axis represents the frequency of the total utterances from the interviews.
To summarize the findings so far, we outline three salient patterns in the students’ explanations pertaining to the agency and interactive pattern dimensions as they use the model they constructed in each of the modeling approaches to explain the evaporative cooling phenomenon. Additionally, we observed patterns in students’ utterances within each dimension, with more complex levels of explanations being prevalent as students used their system dynamics model to explain the phenomenon.
6.4. Transitioning from static equilibrium to system dynamics modeling
The interviews solicited descriptions of the students’ experiences during the transition from static equilibrium to dynamic modeling. Six of the 11 students reported a positive experience, stating that the shift from one approach to the other enabled them to better convey their understanding of the underlying processes. Following is a representative comment from a student.
KY: “I think the whole time we were doing the static model, it was hard because we all wanted to explain it dynamically and we had to refine it to a static model where it wasn’t changing over time. But then with the dynamic model, we got to show how it changed over time and explain the situation (the phenomenon). It makes more sense to look at a dynamic model because it’s easier to look at a situation from this starting point and then this is the ending point. You can say like, you start with kinetic energy and then it transfers into potential energy. So, I feel like it’s easier to understand a situation looking at a dynamic model and it was easier in some ways to put our ideas into it, so it helped [the transition from static equilibrium to system dynamic modeling].”
The quote shows how student KY perceived the transition as supporting her in expressing her understanding of the phenomenon better in the dynamic model. She also describes a sense of frustration with the static equilibrium’s limitations. Additionally, three students mentioned that the affordances of system dynamics modeling supported their understanding of the phenomenon. Below is a representative quote from student ER.
ER: “But actually seeing the effect of intermolecular forces on the evaporation rate was a really big connector for me because I did not understand how it changes through time because at first, I thought the rate of evaporation was constant the entire way through the process.”
The data analysis uncovered two recurring themes in the responses of students who reported positive attitudes about the transition. First, these students displayed a greater degree of sophistication in the agency and interactive patterns causal dimensions as evidenced by their interview responses. Second, the screencasts of these students showed that they included time-related variables, such as ‘time,’ ‘time for evaporation,’ and ‘process of phase change,’ while constructing their static equilibrium models. In many instances, the inclusion or exclusion of these variables was accompanied by discussions regarding limitations in accurately representing the evaporative cooling phenomenon, such as the phase change from liquid to gas or the transfer of kinetic energy to potential energy. A summary of these findings can be found in Table 4.
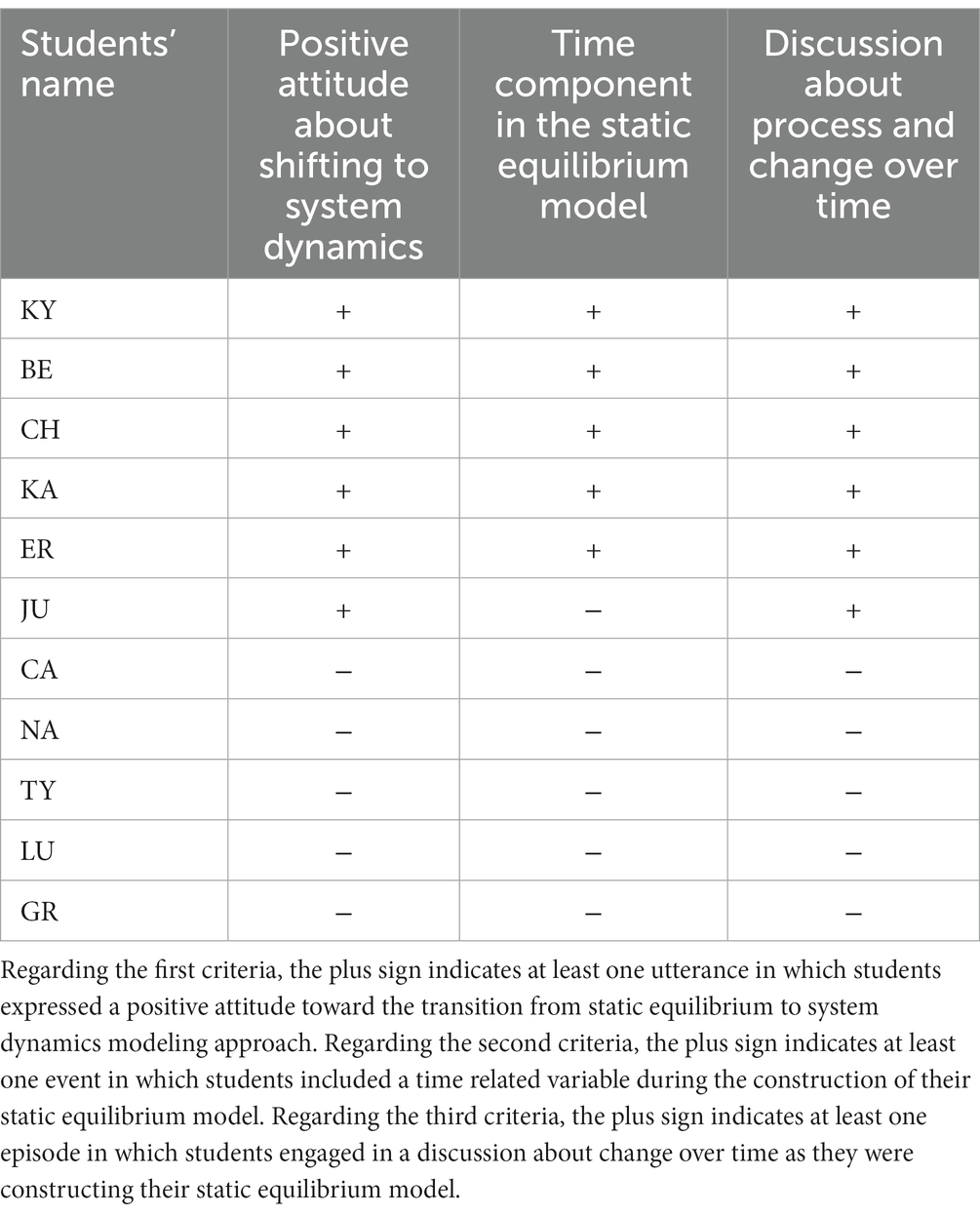
Table 4. The table summarizes three criteria: (1) students’ positive attitudes about shifting to system dynamic modeling as elicited in the interviews, (2) students’ inclusion of a ‘time’ component during the construction of their static equilibrium models, (3) students’ engagement in a discussion which addressed process or change over time during the construction of their static equilibrium models.
For example, KY and her partner integrated in their static equilibrium model variables they named ‘time’ and ‘phase change.’ When Mr. M approached them and asked about those variables, KY answered, ‘We tried to represent the phase change.’ When BE was asked by her peers about their static equilibrium model and the variable they named ‘time for evaporation,’ BE answered, ‘We tried to represent the process of evaporation and the time it takes the substance to evaporate.’
At some point, Mr. M noticed that some students tried to represent a process in their static equilibrium models, so he addressed the whole class, noting, “With the tool given to us, we cannot model a process. We can only model position. If you got things that are procedural, you may want to remove them. You cannot set up a relationship like A becomes B.”
On the other hand, the students who did not perceive that the transition to a different modeling approach supported their understanding of the phenomenon showed a tendency to think of the phenomenon in a linear cause and effect fashion, as evidenced in their interviews and screencasts. CH and NA are a representative example of a group for whom the transfer to dynamic modeling was not sufficient to shift to a more complex explanation and model. The discussion during the construction of their static equilibrium model mostly concerned specific single relationships, even as the teacher was trying to get them to ‘zoom out’ and consider the overall interaction between the system’s components. As they were working on their dynamic model, the pair continued to define linear causal chain relationships and interpreted the dynamic components (i.e., stocks and flow) in the system as cause and effect relationships.
While analyzing students’ dialog and discussion in the screencasts that recorded the construction and revision of their models, we noticed how the limitations of static equilibrium modeling in representing simultaneous events created a confusion about setting relationships between variables. The following quote in which CA, NA, and ER have a discussion is a representative example for such a confusion (While working as a pair, CA and NA talk with ER, who is from a different group).
ER: So you start off with your temperature affecting potential energy, but temperature does not directly affect potential energy.
NA: Yeah, it does.
ER: That’s, well, I mean, temperature affects how far apart the particles are, which affects potential energy.
NA: No, because potential energy affects the spread of particles.
ER: Well, I mean, yes. So, temperature, how does it affect potential energy?
NA: I mean, looking at this yesterday when we put all that heat in it measured the potential energy increasing because of the temperature, it could be related to…
ER: I’m pretty sure that it does not affect the potential energy like it. I’m pretty sure temperature affects the spread of particles.
CA: Yeah eventually.
ER: I am pretty sure the spread of particles is affected by, no, potential energy is affected by the spread of particles.
An analysis of this dialog from a causal dimension perspective reveals a rather low level with both the agency and interactive pattern dimensions. With regard to the agency dimension students perceive temperature as a salient agent serving as a precursor impacting the other variables in the system, hence aligning with a lower level of the agency causal dimension. Examining the interactive pattern causal dimension, it is apparent that students employ a linear causal mechanism to explain the increase in potential energy. The assumption of a single variable driving the behavior of the system with a simplistic linear reasoning impedes students’ ability to consider simultaneous changes. Specifically, they overlook a simultaneous perspective in which kinetic energy converts to potential energy as it overcomes intermolecular forces. This dialog excerpt is an exemplar of how linear causal tendencies can constrain explanations of complex, feedback-oriented phenomena. It suggests that static equilibrium modeling may not be effective in breaking these patterns of thinking.
7. Discussion
Modeling is an essential practice within scientific disciplines, which is crucial to engage students from a young age (Gobert and Buckley, 2000; Matthews, 2007; Schwarz et al., 2009; Louca and Zacharia, 2012). However, modeling tools, particularly those with different computational modeling approaches, have distinct affordances that can support various learning objectives. Therefore, it is imperative to examine to what extent these affordances facilitate students’ application of higher levels of causal complexity and ST to make sense of a phenomenon.
The present study addresses this need by comparing students’ explanations of a phenomenon as they constructed and used two computational modeling approaches to comprehend evaporative cooling. Specifically, this study investigates the extent to which the static equilibrium and system dynamics modeling approaches support explanations that surpass simple linear causal reasoning and apply ST aspects, such as thinking in terms of change over time and identifying feedback. We specifically used the dimensions of causality framework to assess the application of ST in students explanations, as higher levels of dimension of causality align with ST aspects, and the identification of these allowed to assess the application of ST.
Based on our findings, the utilization of both static equilibrium and system dynamics models evoked variations in the rationales provided by students regarding the causal dimensions of agency and interactive pattern as they used the two modeling approaches. Notably, our investigation demonstrated that more complex levels of those dimensions were found in students’ responses when employing system dynamics models compared to static equilibrium models. We do not believe that those results are due to students’ gaining more experience in SageModeler as they progressed throughout the unit, as those students had prior experience with constructing static equilibrium models before the implementation of the unit. If anything, they were lacking more experience with system dynamics models.
Though the discrepancy in the level of explanations and the application of ST between the two modeling approaches does not seem surprising as static equilibrium modeling is not designed to support change over time, one must keep in mind that at the time students were interviewed they had already completed the unit, which included activities that aimed to support them in explaining the evaporative cooling phenomenon in terms of change over time. Also, no additional information was provided to them except the models they constructed during the unit. Hence, we did not expect such a divergence in students’ explanations as our assumption was that the experience from the unit would have caused an overlay of the static equilibrium model explanations with higher level utterances. In that sense the findings are intriguing, because they show that each modeling approach prompts certain types of explanation and reasoning, with the use of system dynamics modeling more likely prompting explanations that address ST aspects. These findings align with prior empirical studies that have established the utility of system dynamics models in fostering reasoning that accounts for temporal transformations (Eidin et al., 2023).
The findings suggest that when utilizing either modeling approach, students interchangeably apply high and low levels of causality to explain phenomena. These results align with the cognitive theory proposed by Chi et al. (2012), which posits two competing causal schemas: direct and non-direct. The former is characterized by a linear narrative script while the latter is characterized by non-linear causal patterns. Notably, Chi (2005) and Chi et al. (2012) demonstrated that students can provide explanations based on both linear directionality and self-organization simultaneously. This theoretical framework corresponds with the work of other cognitive scientists who argue that two types of cognitive processing—one that is more intuitive and the other that is more logical—exist (Anderson, 1996; Kahneman, 2011). Our results corroborate these findings in cognition by demonstrating the presence of reductionist reasoning, which is based on a salient agent and simple linear causal chain, as well as a more complex reasoning that is based on thinking in terms of change over time and feedback. Based on these findings, we argue that a system dynamics approach has the potential to encourage a more complex causal schema of the phenomenon, which the static equilibrium model was unable to support.
The present study reveals that students who incorporated high level dimensions of causality into their explanations, and hence applied ST aspects while utilizing the system dynamics model, engaged in deliberations about change over time while constructing static equilibrium models. Conversely, students who did not incorporate such high levels did not engage in such deliberations. We suggest that the dynamic nature of the phenomenon and the requirement to represent it in a static equilibrium environment may lead to a cognitive dissonance for some students, as a static representation in which variables have an instantaneous effect on one another did not align with the consideration of the system’s change over time. As such, shifting to a system dynamics approach may have reduced that dissonance. However, the factors that prompted such deliberations and the cognitive dissonance that some students experienced are unclear. One possibility is that the extensive time spent working on the static equilibrium models reinforced pre-existing tendencies to think in simple linear causal patterns, perpetuating a linear narrative schema.
This study demonstrates that the use of system dynamics models facilitated some students’ ability to incorporate high levels of agency, such as including cumulative effects over time and addressing emergent behavior in their explanations. Such reasoning, based on the order that emerges from chaos and the random behavior of system components, is not intuitive and often conflicts with prevalent human reasoning across disciplines, which emphasizes salient components that instantaneously affect system behavior (Assaraf and Orion, 2005; Hmelo-Silver et al., 2007b; Chi et al., 2012). Our contribution to the field lies in providing evidence that system dynamics models can prompt students to consider both emergent behavior and change over time, thereby serving as a promising tool for engaging students in these aspects of system thinking.
We also found that both modeling approaches had the potential to elicit high level explanations with regards to the interactive pattern dimension with a high frequency of explanations of multiple linear causality. These results align with previous research that has demonstrated the ability of static equilibrium models to support and encourage multiple linear causality in students’ explanations (Bielik et al., 2018; Shin et al., 2022). Our findings expand upon this previous work by demonstrating the affordances of system dynamics modeling in supporting students in considering a feedback mechanism. Users can represent feedback structures using both modeling approaches, and despite the fact that none of the students included a feedback structure in their static equilibrium or system dynamics models, their dynamic models prompted an explanation based on a feedback mechanism. The results lead us to conjecture that the model’s output that represents change over time elicits more sophisticated causal mechanisms. This claim is based on research that argues that thinking in terms of change over time and accounting for a feedback mechanism are inextricably linked, as the feedback requires the consideration of time delays (Richmond, 1993; Haraldsson, 2004). We acknowledge that the limited amount of evidence collected does not support a substantive generalization; however, the evidence and findings do point to the potential of system dynamics models in considering feedback as an explanatory mechanism of the evaporative cooling phenomenon. In that sense, this work advances the field in supporting students in applying feedback mechanisms, a challenge that has been well documented (Haraldsson, 2004; Hmelo-Silver et al., 2007b; Martinez‐Moyano and Richardson, 2013; Tripto et al., 2013).
Our findings also show no notable differences between the two modeling approaches regarding the mechanism causal dimension. This observation can be attributed to the design of the unit, which effectively integrated macroscopic and microscopic levels (Dori and Hameiri, 2003) and used various simulations that illustrate the behavior of particles. Additionally, the simulations allowed the students to explore abstract concepts such as kinetic energy, potential energy, and intermolecular forces, supporting students in understanding the underlying components that explain the system’s behavior.
Our work also contributes to the field of chemistry education, as it addresses some of the questions posed by York et al. (2019) about the potential implications for integrating ST into chemistry education. For example, by analyzing students’ level of the agency causal dimension in their explanation, we reveal that though the use of thermal energy as an external cause of the evaporative cooling phenomenon is prevalent, such misunderstanding can be mitigated by the use of a system dynamics modeling approach. An implication for chemistry education suggests that the use of system dynamics models can support students in focusing on the system’s variables and distinguish those from external components students may use to make their explanation of the phenomenon more complex than necessary. Furthermore, we show that students’ adopting thinking in terms of change over time, which has also been recognized as a significant component in integrating ST into chemistry education (Flynn et al., 2019; Orgill et al., 2019; York et al., 2019), is pivotal to understanding a phenomenon in which rate is integral. Therefore, we suggest that chemistry educators should be aware of the importance of thinking in terms of change over time, especially when exploring phenomena and concepts that relate to rate, such as chemical kinetics and equilibrium. Using system dynamics models could be a promising approach to meet those goals. Our work suggests that a promising avenue in supporting students in understanding such phenomena and concepts is to engage students in tasks that promote thinking in terms over time, and refrain from encouraging a reductionist approach based on simple cause and effect relationships that might hinder further progress.
7.1. Research limitations
We acknowledge that the sample size of students in this study is small, and, therefore, caution must be exercised when generalizing the findings to a broader population of students. The population of students was also unique as the research was conducted in a magnet school serving students who excel in science from 16 surrounding districts. Furthermore, we acknowledge that the order in which students were asked to use each modeling approach, starting with a static equilibrium and then moving to a system dynamics model, might have an impact on the results. It might be that starting with a system dynamics modeling approach would impact students’ ST in a manner that would render no discernable difference in their explanations when subsequently using their static equilibrium models. Additionally, this study was conducted within the context of the evaporative cooling phenomenon, which involves understanding the emergence of phenomena from microscopic-level interactions among entities. It is possible that different phenomena involving interactions between macroscopic entities, such as those related to ecosystems or geology, may have yielded greater opportunities for the application of ST aspects in both modeling approaches. While the teachers played a crucial role in facilitating students’ understanding, this study did not focus specifically on the teachers’ supporting strategies due to the limited scope of the research. Moreover, both teachers deviated from the curriculum, particularly by the time the students constructed their dynamic model. A greater adherence to the curriculum may have resulted in a higher proportion of students demonstrating complex ST aspects.
7.2. Conclusion
Our study provides evidence of both modeling approaches supporting students in ST, though to different extents. We showed that system dynamics modeling promotes more complex aspects of ST compared to static equilibrium modeling. Our findings demonstrate that system dynamics modeling can support students in shifting from a reductionist, centralized view, in which a major variable dominates the system’s behavior or a simple linear cause and effect relationship accounts for the whole system’s behavior to a more comprehensive perspective that considers the dynamic changes of variables over time and the emergence of patterns from interaction between system’s components. Our contribution lies in elaborating on the potential of using system dynamics models to enhance ST learning and in raising new questions about the use of tools that support cause and effect reasoning as scaffolding for applying ST aspects. We also show evidence that engaging students in linear causal relationships in a context of which a phenomenon is experienced as evolving over time may hinder further application of ST aspects. Given that forming causal relationships is fundamental to science education, our findings open an avenue to further investigation regarding the necessity of striking a balance in which linear causal thinking does not hinder the application of ST aspects.
Moreover, further research is needed to explore the potential of system dynamics modeling in different contexts, including those that exclusively involve macroscopic entities as well as those that involve both macroscopic and microscopic entities. Finally, more research is necessary to better understand whether scaffolding students’ development of complex reasoning skills can facilitate their future adoption of ST practices.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving human participants were reviewed and approved by Michigan State University IRB approval. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This study was supported by National Science Foundation under Grant Nos. DRL-1842035 and DRL-1842037.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1173792/full#supplementary-material
Footnotes
References
Ainsworth, S. (2008). “The educational value of multiple-representations when learning complex scientific concepts” in Visualization: theory and practice in science education (Berlin: Springer), 191–208.
Anderson, J. R. (1996). ACT: A simple theory of complex cognition. Am. Psychol. 51:355. doi: 10.1037/0003-066X.51.4.355
Assaraf, O. B.-Z., Dodick, J., and Tripto, J. (2013). High school students’ understanding of the human body system. Res. Sci. Educ. 43, 33–56. doi: 10.1007/s11165-011-9245-2
Assaraf, O. B. Z., and Orion, N. (2005). Development of system thinking skills in the context of Earth system education. J. Res. Sci. Teach. 42, 518–560. doi: 10.1002/tea.20061
Ben-Zvi, R., Eylon, B.-S., and Silberstein, J. (1986). Is an atom of copper malleable? Journal of Chemical Education, 63, 64.
Bielik, T., Damelin, D., and Krajcik, J. S. (2018). Why Do Fishermen Need Forests? Developing a Project-Based Learning Unit with an Engaging Driving Question. Science Scope, 41, 64–72.
Carolyn, S., and Lee, H.-S. (2019). Agent-Based and Systems Dynamics Modeling of Complex System Behavior. NARST: Baltimore, MD.
Chandrasekharan, S., and Nersessian, N. J. (2015). Building cognition: The construction of computational representations for scientific discovery. Cogn. Sci. 39, 1727–1763. doi: 10.1111/cogs.12203
Chen, R. F., Eisenkraft, A., Fortus, D., Krajcik, J. S., Neumann, K., Nordine, J., et al. (2014). Teaching and learning of energy in K-12 education. Berlin: Springer.
Chi, M. T. (2005). Commonsense conceptions of emergent processes: Why some misconceptions are robust. J. Learn. Sci. 14, 161–199. doi: 10.1207/s15327809jls1402_1
Chi, M. T., Roscoe, R. D., Slotta, J. D., Roy, M., and Chase, C. C. (2012). Misconceived causal explanations for emergent processes. Cogn. Sci. 36, 1–61. doi: 10.1111/j.1551-6709.2011.01207.x
Chiu, M.-H., Mamlok-Naman, R., and Apotheker, J. (2019). Identifying systems thinking components in the school science curricular standards of four countries. J. Chem. Educ. 96, 2814–2824. doi: 10.1021/acs.jchemed.9b00298
Costanza, R. (1987). Simulation modeling on the Macintosh using STELLA. Bioscience 37, 129–132. doi: 10.2307/1310367
Damelin, D., Krajcik, J., McIntyre, C., and Bielik, T. (2017). Students making systems models: An accessible approach. Sci. Scope 40, 78–82. doi: 10.2505/4/ss17_040_05_78
Dori, Y. J., and Hameiri, M. (2003). Multidimensional analysis system for quantitative chemistry problems: Symbol, macro, micro, and process aspects. Journal of Research in Science Teaching: The Official Journal of the National Association for Research in Science Teaching, 40, 278–302.
Driver, R., Guesne, E., and Tiberghien, A. (1985). Some features of children’s ideas and their implications for teaching. Children’s Ideas in Science. 193–201.
Eidin, E., Bielik, T., Touitou, I., Bowers, J., Damelin, D., Mcintyre, C., et al. (2023). Thinking in terms of change over time: Opportunities and challenges of using system dynamics models. Journal of Science Education and Technology.
Flynn, A. B., Orgill, M., Ho, F. M., York, S., Matlin, S. A., Constable, D. J., et al. (2019). Future directions for systems thinking in chemistry education: Putting the pieces together. J. Chem. Educ. 96, 3000–3005. doi: 10.1021/acs.jchemed.9b00637
Forrester, J. W. (1994). System dynamics, systems thinking, and soft OR. Syst. Dyn. Rev. 10, 245–256. doi: 10.1002/sdr.4260100211
Galea, S., Riddle, M., and Kaplan, G. A. (2010). Causal thinking and complex system approaches in epidemiology. Int. J. Epidemiol. 39, 97–106. doi: 10.1093/ije/dyp296
Gilissen, M. G., Knippels, M.-C. P., Verhoeff, R. P., and van Joolingen, W. R. (2019). Teachers’ and educators’ perspectives on systems thinking and its implementation in Dutch biology education. J. Biol. Educ. 54, 1–12. doi: 10.1080/00219266.2019.1609564
Gobert, J. D., and Buckley, B. C. (2000). Introduction to model-based teaching and learning in science education. Int. J. Sci. Educ. 22, 891–894. doi: 10.1080/095006900416839
Grotzer, T. A., Kamarainen, A. M., Tutwiler, M. S., Metcalf, S., and Dede, C. (2013). Learning to reason about ecosystems dynamics over time: The challenges of an event-based causal focus. Bioscience 63, 288–296. doi: 10.1525/bio.2013.63.4.9
Haraldsson, H. V. (2004). Introduction to system thinking and causal loop diagrams. Department of chemical engineering, Lund University Lund: Lund.
Hassanibesheli, F., Boers, N., and Kurths, J. (2020). Reconstructing complex system dynamics from time series: A method comparison. New J. Phys. 22:073053. doi: 10.1088/1367-2630/ab9ce5
Hmelo-Silver, C. E., Duncan, R. G., and Chinn, C. A. (2007a). Scaffolding and achievement in problem-based and inquiry learning: A response to Kirschner, Sweller, and Clark (2006). Educ. Psychol. 42, 99–107. doi: 10.1080/00461520701263368
Hmelo-Silver, C. E., Marathe, S., and Liu, L. (2007b). Fish swim, rocks sit, and lungs breathe: expert-novice understanding of complex systems. J. Learn. Sci. 16, 307–331. doi: 10.1080/10508400701413401
Jacobson, M. J., and Wilensky, U. (2006). Complex systems in education: Scientific and educational importance and implications for the learning sciences. J. Learn. Sci. 15, 11–34. doi: 10.1207/s15327809jls1501_4
Kali, Y., Orion, N., and Eylon, B. S. (2003). Effect of knowledge integration activities on students' perception of the Earth's crust as a cyclic system. J. Res. Sci. Teach. 40, 545–565. doi: 10.1002/tea.10096
Ke, L., Sadler, T. D., Zangori, L., and Friedrichsen, P. J. (2021). Developing and using multiple models to promote scientific literacy in the context of socio-scientific issues. Sci. Educ. 30, 589–607. doi: 10.1007/s11191-021-00206-1
Krist, C., Schwarz, C. V., and Reiser, B. J. (2019). Identifying essential epistemic heuristics for guiding mechanistic reasoning in science learning. J. Learn. Sci. 28, 160–205.
Leslie, A. M., and Keeble, S. (1987). Do six-month-old infants perceive causality? Cognition 25, 265–288. doi: 10.1016/S0010-0277(87)80006-9
Linn, M. C., and Eylon, B.-S. (2011). Science learning and instruction: Taking advantage of technology to promote knowledge integration. Routledge.
Liu, L., and Hmelo-Silver, C. E. (2009). Promoting complex systems learning through the use of conceptual representations in hypermedia. J. Res. Sci. Teach. 46, 1023–1040. doi: 10.1002/tea.20297
Lorenz, T. (2009). “Abductive fallacies with agent-based modeling and system dynamics” in Epistemological Aspects of Computer Simulation in the Social Sciences: Second International Workshop, EPOS 2006, Brescia, Italy, October 5–6, 2006, Revised Selected and Invited Papers (Berlin Heidelberg: Springer), 141–152.
Louca, L. T., and Zacharia, Z. C. (2012). Modeling-based learning in science education: cognitive, metacognitive, social, material and epistemological contributions. Educational Review, 64, 471–492.
Mandinach, E. B. (1989). Model-building and the use of computer simulation of dynamic systems. J. Educ. Comput. Res. 5, 221–243. doi: 10.2190/7W4F-XY0H-L6FH-39R8
Martinez‐Moyano, I. J., and Richardson, G. P. (2013). Best practices in system dynamics modeling. Syst. Dyn. Rev. 29, 102–123. doi: 10.1002/sdr.1495
Matthews, M. R. (2007). Models in science and in science education: an introduction. Sci. Educ. 16, 647–652. doi: 10.1007/s11191-007-9089-3
Metcalf, S. J., Krajcik, J., and Soloway, E. (2000). Model-It: A design retrospective. Innov. Sci. Math. Educ., 77–115.
National Research Council. (2012). A framework for K-12 science education: Practices, crosscutting concepts, and core ideas. Washington, DC: National Academies Press.
NGSS Lead States. (2013). Next generation science standards: For states, by states. The National Academies Press Washington, DC.
Orgill, M., York, S., and MacKellar, J. (2019). Introduction to systems thinking for the chemistry education community. J. Chem. Educ. 96, 2720–2729. doi: 10.1021/acs.jchemed.9b00169
Ossimitz, G. (2002). Stock-flow-thinking and reading stock-flow-related graphs: An empirical investigation in dynamic thinking abilities. Proceedings of the 2002 international system dynamics conference.
Perkins, D. N., and Grotzer, T. A. (2005). Dimensions of causal understanding: the role of complex causal models in students’ understanding of science. Stud. Sci. Educ. 41, 117–165. doi: 10.1080/03057260508560216
Raia, F. (2005). Students' understanding of complex dynamic systems. J. Geosci. Educ. 53, 297–308. doi: 10.5408/1089-9995-53.3.297
Resnick, M. (1996). Beyond the centralized mindset. J. Learn. Sci. 5, 1–22. doi: 10.1207/s15327809jls0501_1
Reynolds, M., Blackmore, C., Ison, R., Shah, R., and Wedlock, E. (2018). Handbook of sustainability science and research. Berlin: Springer.
Richmond, B. (1993). Systems thinking: Critical thinking skills for the 1990s and beyond. Syst. Dyn. Rev. 9, 113–133. doi: 10.1002/sdr.4260090203
Richmond, B. (1994). Systems thinking/system dynamics: Let’s just get on with it. Syst. Dyn. Rev. 10, 135–157.
Sander, E., Jelemenská, P. A., and Kattmann, U. (2006). Towards a better understanding of ecology. J. Biol. Educ. 40, 119–123. doi: 10.1080/00219266.2006.9656028
Schwarz, C. V., Reiser, B. J., Davis, E. A., Kenyon, L., Achér, A., Fortus, D., et al. (2009). Developing a learning progression for scientific modeling: Making scientific modeling accessible and meaningful for learners. J. Res. Sci. Teach. 46, 632–654. doi: 10.1002/tea.20311
Senge, P. M., and Sterman, J. D. (1992). Systems thinking and organizational learning: acting locally and thinking globally in the organization of the future. Eur. J. Oper. Res. 59, 137–150. doi: 10.1016/0377-2217(92)90011-W
Shin, N., Bowers, J., Roderick, S., McIntyre, C., Stephens, A. L., Eidin, E., et al. (2022). A framework for supporting systems thinking and computational thinking through constructing models. Instr. Sci. 50, 933–960. doi: 10.1007/s11251-022-09590-9
Sins, P. H. M., Savelsbergh, E. R., van Joolingen, W. R., and van Hout-Wolters, B. H. A. M. (2009). The relation between students’ epistemological understanding of computer models and their cognitive processing on a modeling task. Int. J. Sci. Educ. 31, 1205–1229. doi: 10.1080/09500690802192181
Stave, K., and Hopper, M. (2007). What constitutes systems thinking? A proposed taxonomy. 25th international conference of the system dynamics Society.
Stephens, A. L., Roderick, S., Shin, N., and Damelin, D. (2023). Students do not always mean what we think they mean: a questioning strategy to elicit the reasoning behind unexpected causal patterns in student system models. Int. J. Sci. Math. Educ. 21, 1591–1614. doi: 10.1007/s10763-022-10308-z
Sterman, J. (2002). All models are wrong: reflections on becoming a systems scientist. System Dynamics Review: The Journal of the System Dynamics Society. 18, 501–531.
Stratford, S. J., Krajcik, J., and Soloway, E. (1998). Secondary students’ dynamic modeling processes: analyzing, reasoning about, synthesizing, and testing models of stream ecosystems. J. Sci. Educ. Technol. 7, 215–234. doi: 10.1023/A:1021840407112
Sweeney, L. B., and Sterman, J. D. (2000). Bathtub dynamics: Initial results of a systems thinking inventory. Syst. Dyn. Rev. 16, 249–286. doi: 10.1002/sdr.198
Tripto, J., Assaraf, O. B.-Z., and Amit, M. (2013). Mapping what they know: Concept maps as an effective tool for assessing students’ systems thinking. Am. J. Operat. Res. 3, 245–258. doi: 10.4236/ajor.2013.31A022
Tümay, H. (2016). Emergence, learning difficulties, and misconceptions in chemistry undergraduate students’ conceptualizations of acid strength. Sci. Educ. 25, 21–46. doi: 10.1007/s11191-015-9799-x
Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., et al. (2016). Defining computational thinking for mathematics and science classrooms. J. Sci. Educ. Technol. 25, 127–147. doi: 10.1007/s10956-015-9581-5
Wilensky, U., and Resnick, M. (1999). Thinking in levels: a dynamic systems approach to making sense of the world. J. Sci. Educ. Technol. 8, 3–19. doi: 10.1023/A:1009421303064
Yoon, S. A., Goh, S.-E., and Park, M. (2018). Teaching and learning about complex systems in K–12 science education: A review of empirical studies 1995–2015. Rev. Educ. Res. 88, 285–325. doi: 10.3102/0034654317746090
Yore, L. D. (2012). “Science literacy for all: More than a slogan, logo, or rally flag!” in Issues and challenges in science education research (Berlin: Springer), 5–23.
York, S., Lavi, R., Dori, Y. J., and Orgill, M. (2019). Applications of systems thinking in STEM education. J. Chem. Educ. 96, 2742–2751. doi: 10.1021/acs.jchemed.9b00261
Keywords: systems thinking, computational system modeling, system dynamics, linear causal reasoning, static equilibrium models
Citation: Eidin E, Bowers J, Damelin D and Krajcik J (2023) The effect of using different computational system modeling approaches on applying systems thinking. Front. Educ. 8:1173792. doi: 10.3389/feduc.2023.1173792
Edited by:
Moritz Krell, University of Kiel, GermanyReviewed by:
Rieke Ammoneit, University of Kiel, GermanyDirk Krüger, Freie Universität Berlin, Germany
MaryKay Orgill, University of Nevada, Las Vegas, United States
Copyright © 2023 Eidin, Bowers, Damelin and Krajcik. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Emil Eidin, eidinema@msu.edu
 Emil Eidin
Emil Eidin