The Effectiveness of Experiential Learning in Teaching Arithmetic and Geometry in Sixth Grade

Many educators and policymakers worldwide have noticed the burgeoning field of experiential learning in the twenty-first century. Learning theory and practice together is beneficial to education in general, and mathematics education in particular, because it enables students to realize their full potential for knowledge and skill, and it connects the two aspects of knowledge. A focus on the cross-cutting and critical role of experience activities within the framework was emphasized in Vietnam’s general education program in mathematics, released in 2018 and included views on the content and methods of teaching and learning mathematics in the country. Experiential learning in mathematics was studied to see if this method could positively help students participate, increase their motivation and interest in learning, and impact their math outcomes. A series of pedagogical experiments with 29 sixth-grade students on arithmetic and geometric topics was conducted to confirm the research goals. Students were required to develop solutions to real-world problems related to their studying subjects. The experimental and control classes are subjected to a pre-test and a post-test design. Mixed methods, including qualitative and quantitative analysis, are handled by the statistical data processing software (SPSS) program and the results of observations and surveys of learners’ opinions. The results were found that experiential learning activities positively influenced math learning attitudes and student achievement progress in the classroom.

Introduction

The educational trend of the twenty-first century is student-centered, experiential, technology-based, and question-based learning and empathic and understanding (Habib et al., 2021). According to Vietnam’s General Education Curriculum for 2018, the math program focuses on application, linking to practice or educational activities. It is not just about implementing math learning topics and projects; it is also about organizing math learning games, clubs, forums, seminars and contests, and other practical and experiential activities in mathematics education that reflect this. In these activities, learners should be allowed to put their knowledge into practice through creative means (Ministry of Education and Training, 2018). Thus, students can learn and be creative while exploring and putting their knowledge into practice in real-world contexts through experiential teaching activities (Ministry of Education and Training, 2018). Experiential learning is essential (McCarty et al., 2018). Many mathematical concepts have been studied and taught experientially by students at the high school and university levels, including the equation of a circle (Tong et al., 2020), function continuity and angle between two planes (Davidovitch et al., 2014), mathematics with statistics (Venkatraman et al., 2019), arithmetic (Mayoral-Rodríguez et al., 2018), some advanced algebraic topics (Wynn, 2018), as well as mathematics and science (Roberts et al., 2016). Also, according to Pambudi’s (2022) research, elementary students’ motivation and achievement in geometry can be attributed to outdoor learning methods. For mathematics education in Vietnam and worldwide, research on mathematical experiential activities should be promoted to allow students to experience positive emotions, exploit their personal experiences, and mobilize their knowledge and skills to perform assigned tasks or solve real-world problems. As a result, learners transform their experiences into new knowledge, understanding, and skills, thereby promoting their creative potential and adaptability to the future life, environment, and career.

Literature Review

The Concept of Experiential Learning

Experiential learning has been studied by many educators in a wide range of fields, including Kolb (1984), is “…the process by which knowledge is created through the transformation of personal experience” [Kolb (1984), as cited in Mutmainah et al. (2019), Cotič et al. (2020)]. According to Dewey (1938), the experience can be divided into two types: the entire experience and the universal experience. An experience is simply a collection of random activities or events someone has joined. In contrast, universal experience results from a methodical, self-reflective survey that considers prior knowledge and future predictions [Dewey, 1938; as cited in Breunig (2017)]. Davidovitch et al. (2014) agree that experiential learning can be divided into personal experiences in life and events and educational programs. The second group’s interpretation necessitates thorough preparation and a lengthy process to conclude (Davidovitch et al., 2014). As such, experiential learning is a form of active learning in which students are actively involved in learning through direct participation, supported by experience, analysis, and reflection (Mutmainah et al., 2019; Habib et al., 2021). Furthermore, the author Voukelatou (2019) claims that students are the driving force behind the learning process and that the effectiveness of learning is influenced by the student’s “learning style” and “thinking”. While participating in various activities, students are encouraged to think critically and creatively, investigate, inquire, and make decisions, according to Mutmainah et al. (2019). Their participation in learning opportunities for students directly results in the development of the necessary skills and knowledge that will support them in succeeding in their future studies [Atherton, 2009; cited in Chesimet et al. (2016)], a concentration on maximizing students’ potential (Tong et al., 2020; Mc Pherson-Geyser et al., 2020). The Design–Instruction–Assessment–Learning model has been remixed by Heinrich and Green (2020) to promote high-quality experiences for both learners and instructors.

Characteristics of Experiential Learning

Students are more likely to persevere in an active learning role if exposed to an authentic experience [Dewey (1938), cited in Behrendt and Franklin (2014), Cotič et al. (2020)]. An experiential learning framework can be successful if each student is directly involved in the experience by carrying out tasks, as Venkatraman et al. (2019) stated. Ultimately, each student must respond rationally to any feedback they receive by transforming their analytical skills experience into higher-order thinking strategies.

According to Kolb and Kolb (2017), experiential learning is characterized by a unique dynamic between educators, students, and the content they are studying. Hence, teachers and students can gain firsthand knowledge of the subject. It is transmitted to them, but they are also responsible for creating it themselves. From there, all subjects can directly participate in the subject experience when using this method, which is similar to previous methods in that they can do so. Depending on the experience’s design and implementation, a wide range of viewpoints on the subject will be expressed.

According to Voukelatou (2019), experiential learning is based on students’ thoughts, feelings, and openness during the educational process. Student-teacher collaboration is also important in teaching and learning because it allows teachers to better engage with and understand the material. Among the ways, question-and-answer, discussion, role play, case study and model interviews, educational tours, brainstorming, confrontation, expert interviews and exercises, group work, art education, and debate are all examples of experiential teaching techniques that can help students participate actively, interact and communicate more effectively (Voukelatou, 2019; Canino et al., 2021). According to Vietnam’s General Mathematics Education Program issued in 2018, it is possible to engage a wide range of students in hands-on math activities by implementing topics and projects focused on the practical application of mathematics; organizing math learning games, math clubs, forums, seminars, and competitions (Ministry of Education and Training, 2018). In their study, the term “mathematical debate” was coined by Davidovitch et al. (2014). For that reason, this is an exercise where students work in groups to solve high-level problems and present their solutions to the class and other groups of students. The most important part of emulation is learning about and critiquing the various options available to members.

Thus, experiential and project-based learning (PBL) are closely related. Moreover, cooperative and collaborative learning are also closely related (Burrell et al., 2017; Scogin et al., 2017; Cline et al., 2020). According to author Larmer (2015), project-based learning is defined as experiential activities linked to oriented and open-ended problems and questions, real-world application of content and skills, and student-centered learning. Students create productions, presentations, or performances that address issues underlying questions. Additionally, cooperative learning is one of the ways to organize group work to improve learning effectiveness and student achievement by organizing how students interact and participate in achieving goals together [Zaitou (2003), as cited in Hossain and Ariffin (2018), Algani and Alhaija (2021)]. Because of these features, these methods of instruction can help foster an environment where experiential learning can have fruitful results. Also, it is believed that the flipped classroom approach, which is based on the experiential learning theoretical perspective, has gained preliminary validation in the system course environment (Chen, 2021).

The Cycle of Experiential Learning

There is no denying that many educational institutions have examined hands-on experience in teaching. In addition, the research of authors Kolb (2014), Breunig (2017), Hsu (2019), Cotič et al. (2020), Lamya et al. (2020), and Mc Pherson-Geyser et al. (2020) in general education and other fields mentioned the application of this model. According to Kolb (1984), the four stages of experiential learning are individual experience, reflective observation, abstract conceptualization, and active experimentation (Muro and Terry, 2007; Cotič et al., 2020). Chesimet et al. (2016) provide the following explanation of the model described above: Starting with a specific experience (e.g., a traumatic event), students then reflect on their experiences from a variety of perspectives (observation). Students build theories or models (conceptualization) from their reflections in order to conduct experiments and act on their findings (experimentation) (Chesimet et al., 2016). Learning through and from experience is described by Kolb (2014) as a process of (1) engaging in individual experiences, (2) observing and reflecting, (3) forming knowledge and testing concepts in new situations, (4) applying and testing concepts (Kolb, 2014). There is also a five-step experiential learning process put forth by that comprises of the following steps: setting up an experiential situation; sharing it with others; putting it into practice; generalizing it; and finally, applying it. Student skill development and knowledge application are encouraged through active, experiential learning, as proposed by this model (Davidovitch et al., 2014).

Benefits of Experiential Learning

It has long been known about the positive effects of experiential learning on educational outcomes, particularly in the field of mathematics education (Avelino et al., 2017; Mutmainah et al., 2019). The quality and effectiveness of learning can be improved by experiential learning (Weinbern et al., 2011; Mayoral-Rodríguez et al., 2018; Wynn, 2018) motivating learning (Venkatraman et al., 2019).

Furthermore, Venkatraman et al. (2019) show that experiential learning positively impacts students’ mathematical creativity. The study of Chesimet et al. (2016) found that the experiential learning method is more effective than traditional teaching and learning methods in enhancing students’ mathematical creativity. As a result, students who engage in experiential learning can better express their creativity in mathematics and develop their critical thinking skills. To help students improve their problem-solving skills, researchers suggest incorporating hands-on activities into the classroom. A study by Mwei (2017) and Manfreda and Hodnik (2021) found that providing students with the opportunity to resolve real-life problems impacted their mathematical problem-solving abilities. It has been found that experiential activities in mathematics help improve students’ knowledge and understanding of math and active learning activities that reduce the burden on the curriculum. Especially, students who complete tasks requiring a thorough understanding of the lesson and openness to confronting unfamiliar problems benefit from this (Davidovitch et al., 2014). Mayoral-Rodríguez et al. (2018) found that experiential learning can teach mathematics.

The use of experiential learning in the classroom has numerous advantages for educators. Teachers must consider whether their teaching methods are in harmony with the skills they want to teach their students or if they need to change them (Wang, 2006). Consequently, according to Pittaway and Cope (2007), teachers are encouraged to abandon a traditional approach in favor of one that emphasizes hands-on learning opportunities through experiential learning. When teachers and schools engage in experiential activities, they are more likely to create effective educational programs, foster an educational and cultural climate for students, and create a positive learning environment (Tong et al., 2020). Besides, using liminality as a lens to examine experiential learning activities provides a new perspective on their impact on individuals, institutions and society (Amigó and Lloyd, 2021).

Drawbacks of Experiential Learning

Despite extensive research into experiential learning and its educational benefits, its application in the classroom remains limited and subject to a set of rules and guidelines. As Kolb and Kolb (2017) found when researching experiential learning in higher education, some challenges can be traced back to similar issues in the educational system. Secondary school students are learning math through hands-on activities. According to the authors, experiential learning should cover all four modes of the learning cycle and apply to all learning situations in class and real-life situations. As a result, the disparity between theoretical courses and hands-on activities hurts both types of learning. Students’ actions in learning projects are not integrated with the conceptual reflections and analyses in the classroom. Experiential learning programs are considered ancillary and only prepare students for low-level professional development in the fixed-duration system.

On the other hand, the teacher focuses on teaching higher-level knowledge (Kolb and Kolb, 2017). According to authors, Cranton (2011) and Tong et al. (2020) found obstacles to implementing experiential learning in the classroom due to time constraints, class structure, and the number of students. Besides, learning content, textbooks, student participation requirements, and grades are all factors that contribute to the difficulties that students face in the classroom. Another factor is that educators and students come from various cultural backgrounds (Giroux, 2015). Another concern Darling-Hammond (2016) expressed was a lack of compatibility between learning content and pedagogy of experiential learning in the traditional teaching program.

Evaluation of Experiential Learning

In an educational setting, learning, and assessment are inextricably linked; therefore, it is critical to determine whether learning serves as the foundation for assessment or vice versa students, according to educators, are concerned about the purpose of assessments, whether or not students assess what they learn, and whether or not course experiences should be taken into account when developing assessments. When evaluating students’ performance, this includes considering fairness and the public interest. On the other hand, research shows that evaluating students’ knowledge and skills must be in harmony with the aspects above (Venkatraman et al., 2019). For the author, this assessment offers a chance to integrate information that students have been taught about cognition, attitude, and psychology. The author mentions cognitive aspects like knowing, comprehending, putting into practice, and synthesizing and evaluating [Payne, 1997; as cited in Venkatraman et al. (2019)].

While students are engaged in active classroom learning activities, practical assessments can be made. There are various ways to conduct student evaluations, from informal to more formal ones. First, teachers must determine which skills will be tested to develop an appropriate assessment strategy (Venkatraman et al., 2019).

A self-assessment tool called the Kolb Educator Role Profile (KERP) was developed by Kolb and Kolb (2017) to help teachers evaluate their teaching methods from the perspective of the experiential learning cycle. For teachers, there are four roles: facilitator, expert, standard-setter and coach, according to the KERP model. Using this model, teachers can better understand the available types of instruction, the responsibilities of teachers and students, and how to make the best possible decisions in specific circumstances.

Theoretical Framework

The Process of Teaching Based on Experiential Learning

According to the findings, a five-stage process for designing and organizing experiential mathematics education is proposed. These steps are illustrated in Figure 1.

FIGURE 1

Figure 1. The process for designing and organizing experiential mathematics education.

Stage 1: Decide on a subject matter of study. Students’ characteristics, basic conditions, and educational objectives are used to determine the characteristics of mathematics in the general education curriculum in mathematics. Teachers in each school work together to identify and develop educational themes.

Stage 2: Aim to organize the experience. The teacher chooses experiential teaching organizations by the learning topic and classroom conditions. The teaching process can be made more efficient by combining different organizational forms. There must be a clear connection between the objectives, content, organizational structure, and activities. Determine the objectives and implementation methods for each task to ensure the project’s success.

Stage 3: Preparation is a key when it comes to academic success. The instructor will gather all necessary supplies and equipment for the hands-on learning session during this step. Basic knowledge is taught and put into practice through hands-on activities.

Stage 4: Experiential activities should be organized. New knowledge will be clarified based on the comprehension of related knowledge; students work with teachers to practice and gain experience. Students learn in school by applying, honing existing skills, and acquiring new knowledge and skills due to new experiences.

Stage 5: Verify and assess the outcomes. Making appropriate assessment tools and criteria for students’ abilities and overall experience outcomes helps teachers understand the level of achievement in each student’s abilities and overall experience outcomes. Teachers can use various assessment methods at this stage to determine whether or not the lesson has been completed successfully.

Experience-based learning processes have been studied by Kolb (1984) and educators on the application of experiential learning in mathematic, all of which have resulted in the proposal of organizational processes. There are six distinct steps of organizing experiential activities in mathematics instruction for students’ experiential learning.

Step 1: Describe what the experience is all about. The teacher gives a brief description of the experience before beginning the lesson by naming it and introducing it.

Step 2: Set up a plan for the time here. Instructors experiment with students, guiding them and asking for their feedback on their performance. It is common practice for students to work in groups to practice what they have learned in their own lives. The teacher will monitor each student’s participation and progress throughout the class, assisting as needed.

Step 3: Feedback, discussion, and evaluation are all encouraged. The teacher does the organization of students to present practice results. The teacher arranges for groups to meet and exchange ideas about working and accomplishing their goals. The teacher organizes students to analyze the data and draw conclusions about their findings.

Step 4: Plan out the ideas. Teachers allow students to draw from their own experiences in the classroom and then sum up their findings with a final statement. The instructor notes the discussion and then calls time on the class.

Step 5: Apply. The teacher helps students put what they have learned into practice in other settings. After the experiment, the teacher helps students identify any behavioral changes they may have made and provides additional opportunities to apply or discuss what they have learned with others.

Step 6: Summarize. The teacher’s responsibility is to provide feedback and assign homework based on the lesson’s content.

Arithmetic and Geometric Topics in the Vietnamese Mathematics Curriculum and Textbooks

Teaching through outdoor activities consists of two main directions in the Math curriculum in Vietnam. The first direction concerns experience to form new knowledge. It is the process by which students directly work with learning objects, observe, analyze, predict, and connect existing knowledge to discover and form new mathematical knowledge. Indeed, that knowledge can be a new concept, a new formula or a theorem, a way of proving under the direction and organization of the teacher. The other direction is practical activities and math experiences for students, such as: Conducting math learning topics and projects, especially topics and projects on applying mathematics in real life; organizing math games, math clubs, forums, seminars, competitions on math; publishing a wall newspaper (or internal magazine) on mathematics; exchanges with gifted students in math, exhibition (Lykke et al., 2021), creative dance (Payne and Costas, 2021), simulation decision-making games (Kuczera, 2021), folk stories (Menon, 2021), and school field trips (Behrendt and Franklin, 2014). These activities will help students apply accumulated knowledge, knowledge, skills, and attitudes; help students initially identify their capacity and forte to orient and choose a career; create some basic competencies for future workers and responsible citizens. Also, learning topics create opportunities for students to recognize their talents and interests, develop interest and confidence in learning mathematics, develop mathematical competence, and explore mathematics-related problems throughout life. Some activities oriented by the program to organize experiences for students are as follows:

(1) Get familiar with savings deposits and bank loans; calculate loss, profit, and outstanding balance; practice calculating interest rates in savings deposits and loans.

(2) The invoice should make payment, or the change should be calculated when making a purchase. Practice keeping track of the income and expenses, and keep invoices on hand if needed.

(3) Apply statistical knowledge to read and understand Grade 6 History and Geography tables.

(4) Collect and represent data from a few real-life situations; for example, collect local temperatures at a certain time in a week to make comments about time changes of local weather for the week.

(5) Put symmetry into practice: folding paper to create shapes with symmetry axis or center of symmetry; collecting shapes in nature that have a center of symmetry or have an axis of symmetry; searching for videos of centered, axial symmetry in the natural world.

(6) Apply the concept of three straight points into practice, such as planting trees in a straight line and placing objects in a straight line.

(7) Apply formulas for calculating area and volume in practice. Measure and calculate the surface area, calculate the volume of objects related to the learned shapes.

Life and nature are reflected in the arithmetic and geometric sequences taught in the 6th-grade math program. When teaching these topics, the learning method can be put into practice. Aside from that, the Vietnam Mathematics General Education Program (2018) emphasizes several requirements for the organization of practical activities and experiences in the teaching of the topic of arithmetic and geometric sequences, which include: Mathematical concepts such as arithmetic and geometry are emphasized heavily in the new 6th grade Math curriculum, and they are covered in numerous periods throughout the school year. Hence, students become more open to the world of numbers, sets, calculations, and problems that they encounter in their daily lives when they study arithmetic in high school. To overcome these problems, they begin to reason, analyze, compare, and synthesize to find solutions to problems and situations they find themselves in. Meanwhile, geometry study progresses, with particular attention paid to the edges and corners of visual and metrological geometry. Using activities such as collage, drawing, and experimenting can help students apply what they have learned about ants in a natural and non-coercive manner outside of the classroom.

According to the General Education Program in Mathematics 2018, the content of calculations with natural numbers includes the requirement to deal with real-world problems that arise as a result of performing the calculations in question (for example, calculating the shopping money, calculating the number of goods purchased from the amount already available). For this reason, students must have the opportunity to apply their learning in real-world situations. As a starting point, students should become familiar with spending and finance, think about balancing needs and wants, gain a more in-depth understanding of the value of money and labor, and learn how to manage their money effectively and appropriately organize their lives.

One of the objectives of visual geometry in the General Education program of mathematics in grade 6 about rectangles, rhombuses, parallelograms, and the isosceles trapezoid is to cope with some real-world problems associated with calculating the perimeter and area of the special shapes mentioned above in the previous paragraph. Because of this, the content of knowledge about perimeter and area is extremely appropriate for students to experience and contribute to developing students’ capacity. Although students need to understand the construction of formulas, they must also calculate the perimeter and area of special shapes. Therefore, the educators want to design and organize a knowledge-forming experiment that will involve developing formulas to calculate the area of geometrical objects. Because of this, the researchers propose that experiential learning be applied to the topic of arithmetic and geometric topics to improve teaching quality, spark student interest in learning, and support students in creating a more positive attitude toward mathematics. Vietnamese math curricula and textbooks strongly emphasize experiential math activities because they are regarded as innovative teaching methods associated with socio-constructivist teaching methods. Because of this, it requires teachers to have digital competences (Pozo-Sánchez et al., 2020a).

Evaluation of Students’ Activities in Experiential Learning

Students may be asked to grade their performance on the criteria in Table 1.

TABLE 1

Table 1. Criteria for students to self-assess.

Teachers evaluate students based on the criteria and levels of assessment in Table 2.

TABLE 2

Table 2. Criteria for teachers to evaluate students.

The Study’s Purpose, as Well as the Research Questions That Will Be Addressed

Ultimately, this research aimed to determine the effectiveness and feasibility of incorporating experiential learning methods into the teaching of arithmetic and geometric topics in sixth grade. The following are the questions that the research will address:

1. When students read the 6th-grade textbook, how do they learn about arithmetic and geometric topics?

2. Can experiential learning help students learn more effectively and achieve better results?

3. When students are instructed through experiential learning, how has their participation, motivation, and attitude toward mathematics changed?

Materials and Methods

Participants

The research team provided training in experiential learning to 30 volunteers, all of whom worked as substitute teachers in their spare time. A teacher was selected because she demonstrated proficiency in implementing the fundamental principles of the experiential learning model while instructing the experimental class of 29 students. In addition, the first names of the students in the experimental groups were coded with the letters S01–S29. According to tradition, a teacher who had not been trained used a conventional model to instruct a class of 27 students who served as the control group. Parents of students were notified in advance of their children’s participation in the experiment, and they were allowed to express their concerns. In this study, the students enrolled are 6th graders at a Duc Tri secondary school in Ho Chi Minh City in Vietnam (from September 29, 2021, to October 29, 2021). Especially, school districts in the city had closed their doors, and students had to attend online classes because of the Covid-19 pandemic, which significantly impacted educational activities at the time of the research.

Data Collection and Analysis

The research looks at classes formed by the school rather than regrouping random samples, so it uses a quasi-experimental approach. The quasi-experiment was conducted similarly to the studies on Sumirattana et al. (2017), Yuberti et al. (2019), and Chusni et al. (2022) to examine how the collected data might differ from testing a hypothesis. The data collection process is shown in Table 3.

TABLE 3

Table 3. Quasi-experimental study design.

The data was gathered using the first year’s average scores (rather than the pre-test results), the post-test results, and responses from a survey of students. After completing the post-test, an evaluation was made of how much the students had learned about problem-solving abilities. The test instrument contained three items related to the arithmetic and geometric topics covered during this study. The pre-test contains three items based on real-world problems in construction and grocery shopping that require students to apply their newly acquired arithmetic and geometry knowledge to complete. The questions on conceptual comprehension were adapted from previous state-level trial examinations to meet the needs of the researchers who used them. According to Anderson Taxonomy, the test question items were also created. Also devised by researchers, the test’s scoring method was given a rubric by the team. The instrument and rubric were reviewed and scored by three mathematics teachers with over 10 years of classroom experience and two mathematics lecturers who were subject experts on arithmetic and geometry to determine their facial and content validity. The study by Yuberti et al. (2019) provided data that was confirmed to be extremely reliable.

The data was analyzed quantitatively with statistical data processing software (SPSS) 22 software and qualitatively with a qualitative analysis tool. Experiential learning-based treatment was effective by conducting qualitative assessments before and after each intervention. According to the paired t-test method, it was hypothesized that the average score of students in the experimental class would differ from the average score of students in the control class. The qualitative assessment results were used to analyze students’ worksheets, which evaluated students’ abilities to identify problems and resolve them in a real-world context.

Experimental Design

Based on the learning outcomes of the experimental and control classes, the researcher team and teacher collaborated to develop lesson plans that covered the arithmetic and geometric topics in the context of the experiential learning model application and its applications. Three distinct periods are proposed for the experimental lesson plan, which are as follows: the new lesson period, the practice-and-consolidation period, and the test period. Finally, students completed a post-test and a survey about their overall experience with the program. To evaluate the effectiveness of the pedagogical experiment, both quantitative and qualitative data were collected.

About Quantitative Analysis

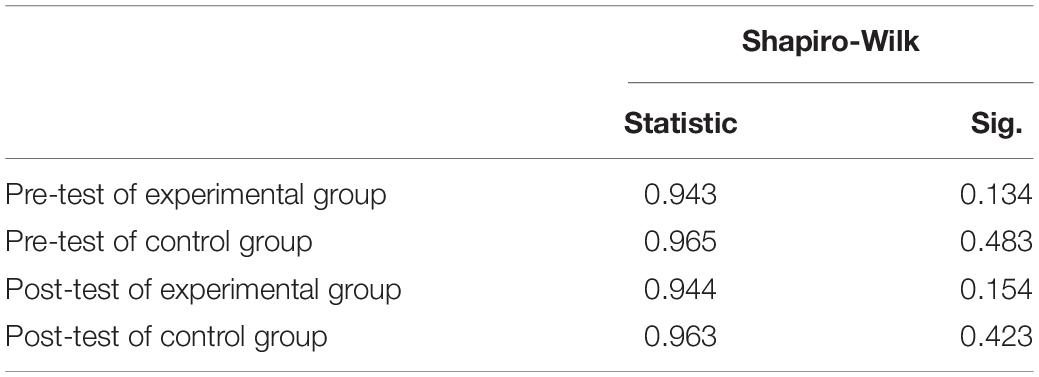
Table 4 shows the tests using Shapiro-Wilk distributions to see if the scores before and after the classes were normally distributed. It can be concluded from the data processing results obtained using the SPSS 20 software that the two data scores have Sig values greater than 0.05, indicating that the two test scores obtained before and after the experiment are normally distributed.

TABLE 4

Table 4. Shapiro-Wilk test normally distributed pre-test and post-test.

Before the experiment, the t-test independent of the experimental class and the control class was used to determine level equivalence between the experimental class and the control class and the difference in mean score value between the experimental class and the control class after the experiment (2-tail). The formula developed by Cohen et al. (2005) is used to determine the extent to which the experimental class influences the mean score difference between the experimental class and the control class between two groups. The magnitude of the impact is indicated by the level of influence (ES), which is a percentage.

In order to assess attitudes, the student survey statements include a total of six items on a Likert scale with five levels, as follows: The following are the possible responses: strongly disagree, disagree, neutral, agree, strongly agree. A set of questionnaires to survey students after the experiment about their attitudes toward experiential lessons in the experimental class was developed based on a 5-level Likert scale and SPSS results. Correspondingly, the researchers concluded that the scale meets the requirements of internal reliability with a suitable variable-total correlation coefficient (not less than 0.3). The Cronbach’s alpha coefficient of the post-test questionnaire is greater than 0.7; specifically, this coefficient equals 0.871. With a variable-total correlation coefficient that is appropriate, the researchers also concluded that the scale meets the requirements for external reliability (not less than 0.3). Additionally, students in the experimental class were asked to answer the additional question “Do you have a different opinion about the class?” to express their opinions about the lessons taught. Besides, the criteria in Tables 1, 2 were used to clarify the student worksheets further.

Results

Pre-test Results

As previously described in the data collection and analysis section, a pre-test was administered to both the experimental and control classes to ensure that the two classes were on the same level of performance. These are the pre-test results that have been statistically processed and presented in Tables 5, 6.

TABLE 5

Table 5. Descriptive statistics of pre-test scores.

TABLE 6

Table 6. Independent t-test of pre-test results.

Table 5 shows that the mean of the experimental and control classes were 6.83 and 6.85, respectively, with no statistically significant differences between them. To test for variance differences between the experimental and control groups, the Levene test in Table 6 yielded Sig values of 0.601 > 0.05. The independent t-test revealed that the difference between the mean scores of the two classes was statistically insignificant (Sig = 0.957 > 0.05). As a result, the experimental and control classes’ mathematical learning levels can be related well.

Post-test Results

Table 7 shows that the experimental and control classes had mean values of 7.66 and 6.26, respectively, indicating a statistically significant difference between the two groups. The Levene test in Table 8 shows Sig = 0.501 > 0.05, indicating no variance difference between the two groups. The results of the independent t-test reveal the significance of the result. Because the difference in mean score between the two classes was statistically significant (two-tailed), the difference in mean score between the two classes was 0.005. So the null hypothesis was rejected, and the alternative hypothesis was accepted as the conclusion. Notably, the experimental students appear to have outperformed the control students in overall academic achievement, based on the two classes’ average scores. The mean standard deviation has been calculated as 0.74 based on the data. It is between 0.50 and 0.79 on Cohen’s scale, indicating a moderate effect size. In conclusion, experiential learning has a moderate impact on students and helps them learn more efficiently.

TABLE 7

Table 7. Descriptive statistics of post-test scores.

TABLE 8

Table 8. Independent t-test of post-test results.

To test the hypothesis, the study used a 0.05 significance level in Table 9. This resulted in the value of 0.003 < 0.05. The evidence rejected the hypothesis because the value applied fell within the rejection domain. Pre- and post-test scores were significantly different for the experimental class. The findings indicate that students’ learning efficiency increased in the experimental class compared to before the experiment. After a successful intervention is promoted, students perform better academically. Before and after the experiment, the correlation test results show a correlation between experimental class scores on both tests with a Sig significance level (2-tailed) less than 0.05, as shown in Table 10. Table 11 shows a Pearson correlation coefficient of 0.659, which indicates a significant correlation.

TABLE 9

Table 9. Pair samples test of the experimental group.

TABLE 10

Table 10. Pair samples correlations of the experimental group.

TABLE 11

Table 11. Pair samples statistics of the experimental group.

With only one student in the experimental group, the post-test revealed that the control group had an unusually high percentage of students below average, accounting for 18.5% with five students, whereas the control group had only one student, accounting for 3.9%. With 13.8% of the students in the experimental class scoring a 10, the experimental class had more students scoring a 10. Because of the difference in performance between the experimental and control classes at milestones 7, 8, and 9, it can be concluded that many students in the experimental group performed exceptionally well. Meanwhile, most students scored between 5 and 6 points in the control class.

During the post-test, the control group saw a decrease in the percentage of students who received excellent scores and an increase in the number of students who received scores below the average, indicating that students were still having difficulty in solving real-world problems and applying their newly acquired knowledge. Compared to the pre-test, the experimental class tended to increase the number of students who received good grades; specifically, many students who received good grades of 8 or higher saw an increase of more than 10%. The experiment discovered that most students in the experimental class were more engaged and enthusiastic about real-world issues than their counterparts in the control group. The wide variety of mathematical applications found in diverse fields of study has led to the discovery that there is a correlation between the attraction of real-world problems and mathematical interest.

Results of a Survey of Student Opinion and Observation

It was observed that most students in the experimental group studied very actively and enthusiastically. More specifically, they expressed an interest in gaining practical experience as smart diners by enthusiastically contributing ideas and participating in group discussions to handle the given situation and choose the most cost-effective option. As a result, students better understand how mathematics can be applied in everyday life and progress after the experimental class.

The student survey results on Google Form conducted after the lesson demonstrated that students began to enjoy learning mathematics, with more than 75.9% of students completely agreeing and 20.7% of students agreeing in the question “I love to study maths more” following the experiment. Regarding question 6, “I want to learn similar experiential lessons,” in the experiment, 62.1% of students were completely in agreement, and 27.6% of students wanted to learn through hands-on experiences.

To better understand what students were experiencing after the lesson, the researchers also asked question 7 when evaluating students’ attitudes. Student responses to the lesson they had just completed were sought through this activity, which was designed to express their thoughts and feelings about the lesson they had just completed. Based on this, the researchers can see how much students enjoy creating situations and having the opportunity to connect knowledge and experience in order to overcome real-world math problems.

Some answers to the question “Do you have a different opinion about the class?” are as follows.

Student S01: “I really enjoyed today’s class because she made the lesson easy to understand and absorb. I hope you will do classes like this because it makes me feel interesting, fun, and receptive.”

Student S09: “This class is very fun because it gives me much knowledge and helps me love math more.”

Student S15: “The class was very fun, and the teacher spoke very interestingly.”

Student S26: “Tea teacher teaches very easy to understand.”

In regards to the individual assessment of students: based on the criteria established by the researchers and the results of the individual assessment of the students, it was concluded that the students were always enthusiastic and responsible and that they participated in the organization and management of the group with 34.5% of students; the majority of learners performed at a satisfactory level, and the evaluation points were at 3, 4, and 5 in the remaining criteria such as the spirit of cooperation, respect, and responsibility; the majority of students performed at a satisfactory level, and the evaluation points are. The test results after the experience period show that the students have made positive changes. As a result of this study, students’ learning outcomes in mathematics have been oriented toward assessment based on competence with the combination of different assessment methods, including learners’ self-assessments.

When it comes to group assessment, the groups worked quite actively, had lively discussions, and many students were able to manipulate technology quickly and effectively; they shared the screen on their own, prepared PowerPoint presentations, vivid and attractive videos, and shared the screen when giving a presentation with others on their own. It was decided to use the given criteria to evaluate the group evaluation results in content experiment 1. It was discovered that 41.4 and 27.3% of students participate in group activities, respectively, and that 6.9% of students participated in group activities only rarely because they had device problems when learning online, thereby reducing their participation.

In the arithmetic lesson, the students were aware that they were expected to observe, analyze, and consider making appropriate choices for the problem’s requirements. For instance, the students were presented with cases to select the most appropriate one for their needs and circumstances. From there, the students would better understand the value of money, learn how to manage money effectively, and learn how to organize their lives.

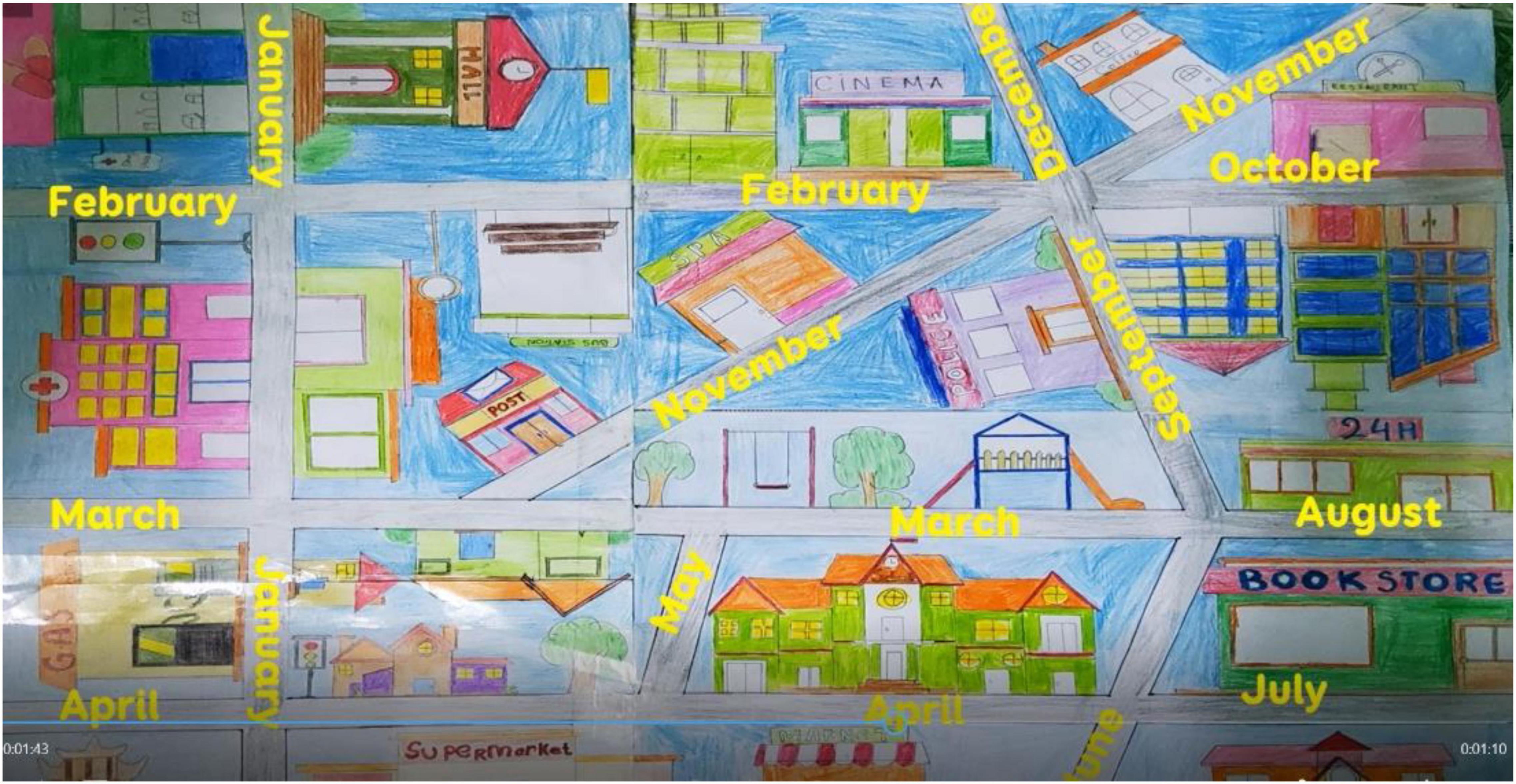
As a result of the design project “My Dream City” in geometric lessons in Figure 2, the researchers discovered a great deal of students imagination in designing and creating ideas, such as designing a city for residents who were bunnies or cities of fun and strength or designing a city for residents who would use utility apps during payment, among other things. As well as demonstrating knowledge through experiential activities and the spirit of cooperation, learners could connect their learning to the design of a great city filled with interesting and modern facilities.

FIGURE 2

Figure 2. Product of student work.

This finding demonstrates that incorporating exercises into group activities in the classroom had numerous benefits. For starters, it increased the practicality of learning while still in school. During their time at the school, students were exposed to a great deal of theoretical information about the subject matter they were studying. Indeed, an exercise associated with real-life situations that are related to mathematics assisted students in applying theory to practice more effectively. Furthermore, it encouraged students to take the initiative, be creative, and most importantly, be excited about their learning process. The lecture method imparted one-way theoretical knowledge, whereas active exercises assisted students in applying the knowledge they gained to analyze situations or devise solutions based on the theories they had learned. As a result, students became more involved and interested in the learning process, and nothing stood in the way of their ability to be creative when confronted with a challenge.

Additionally, this method aided the learners in developing teamwork and other skills. As soon as assignments were given out, students were divided into groups to work on them. They had to be given specific tasks to complete the work as a team. As a result, students’ teamwork abilities improved an important skill for them during the learning process and later in their educational careers. Aside from that, skills in analysis, presentation, and problem-solving were developed while defending the group’s points. Teaching students to work in groups provided teachers with diverse experiences and solutions that they could use to enrich their lessons and other students’ lessons.

The teacher’s evaluation: Due to the time constraints, the researchers only conducted group evaluations based on a few criteria. By the evaluation results, up to three groups were performing at a high level, scoring highly on the criteria of positivity, enthusiasm for group discussions, and coordination among group members. All five groups consulted teachers on a satisfactory level. However, only two of the participants made the necessary progress, and only two gave good presentations in the experiment. Groups in the experiments were split into seven, with four groups meeting all the requirements, while three did not sound all that great. As a result, mathematics teachers in schools should employ the same tools used to assess competence: mind maps, a criteria sheet for evaluation, and research products created by students during learning activities. In particular, the math test questions are designed to assess the ability to apply previously learned knowledge and skills to solve real-world problems. Generally speaking, this is considered to be one of the most significant characteristics of the learner’s competency assessment procedure.

The majority of the time, students actively and enthusiastically participated in activities, gaining skills such as mathematical communication, mathematical modeling, mathematical thinking, and reasoning in real-world situations. Aside from that, the design and organization of mathematical experiential activities aided students in developing necessary qualities through the delivery of content, messages, and integration that teachers had communicated. Specific to group activities, personalization was encouraged, whether in person or online learning, regardless of the setting. When students participated in hands-on activities that were related to arithmetic and geometry topics, their learning outcomes had shown to be better. Organizing activities in various situations provided the teacher with more hands-on experience. Aside from that, the teacher gained a better understanding of the difficulties and advantages faced by students and have launched appropriate activities as soon as possible, promoting students’ abilities and qualities while also fostering stronger relationships between students and teachers, among other things.

Discussion

Following the experiment, the researchers were able to obtain results that were consistent with the goals that had been established. In line with the authors’ research (Mayoral-Rodríguez et al., 2018; Wynn, 2018), additional results significantly impact student knowledge acquisition, comprehension of mathematical sequences, and application of that knowledge from experiential activities were planned and implemented. Researchers hypothesized that partly because of the short duration of the experiment, the students did not adjust well to the new learning method, which helped explain the average impact of the effect on the students’ average score on the test. Although the effect was not particularly large, this was a promising indication of the positive impact of experiential learning on student achievement in mathematics. Analyzing student work and tests revealed that their analytical and computational abilities had improved, as had their capacity for applying what they had learned in the classroom to the real world (Davidovitch et al., 2014; Mayoral-Rodríguez et al., 2018). Students’ interest and motivation to learn increased due to these activities observed in the classroom during experiential activities (Weinbern et al., 2011). Those findings can be explained by assuming that students’ learning activities were actively engaged due to participating in group work activities. These activities included instructing students on the skills of assigning tasks, debating, and reaching consensus while working in teams (Weinbern et al., 2011; Venkatraman et al., 2019). In addition, it was documented that the cooperative learning method improved students’ academic performance in mathematics (Algani and Alhaija, 2021).

Furthermore, the student survey results revealed that students had a positive attitude toward hands-on mathematics experiences related to arithmetic and geometric topics. This outcome is also in line with what was discovered by Pambudi’s (2022) investigation. This author has concluded that using outdoor learning methods to teach geometry to elementary students positively impacts their motivation and learning achievement. Based on students’ responses to survey questions, it appears that they were aware of the importance of experiential activities in the formation of knowledge and their ability to apply newly acquired knowledge to real-world problems. At the same time, students could see how far they had come in terms of mathematical reasoning and real-world problem-solving (Manfreda and Hodnik, 2021). Accordingly, students could provide valuable feedback through this outcome. After this feedback, students believed that this new learning method was effective enough to participate actively in future experiential activities to gain additional knowledge (Habib et al., 2021). This result also explains why many students expressed an interest in using this method in future lessons.

Conclusion

It has been discovered through observation and analysis of experimental teaching and assessment results that teaching through experiential activities is highly effective and feasible. After being exposed to experiential learning activities associated with two topics in arithmetic and geometry, it has been demonstrated that the experimental class achieves higher test scores than the control class. The students in the experimental class had a positive attitude toward learning and were eager to learn about lessons that included content-related math experiences that they could apply in their real-life situations. As a result of students’ active and enthusiastic participation, they developed skills in mathematical communication, modeling, thinking, and reasoning in real-life situations. Additionally, through the content, messages, and integration those teachers convey to students, the design and organization of experiential activities aid students in developing necessary qualities that they will need in the future. More specifically, personalization is encouraged in group activities regardless of the setting, face-to-face or online. Also, students’ learning outcomes improve due to their involvement in experiential activities. Students benefit from the knowledge and skills teachers have gained from organizing activities in a variety of settings.

Furthermore, teachers better understand the difficulties and advantages students face from this position. It appears that they can offer appropriate activities quickly, promote students’ abilities and qualities, and build stronger bonds between students and teachers. In addition, experiential math activities generate a great deal of information and data from students’ observations and observations. Teacher digital competencies are also required as a result of this in order to effectively analyze and manage data, which includes product analysis and evaluation, as well as student learning outcomes (Pozo-Sánchez et al., 2020b).

Experiential activities in math assisted students in developing personal qualities and competencies. From here, they gained the ability to adapt to various living, learning, and working environments, adapt to the changes that modern society brings; and organize their lives, work, and management. Moreover, they can develop an interest in a career related to mathematics and make decisions about choosing a future career; develop a training plan to meet the requirements of this career, and contribute to society as productive citizens. Consequently, the mathematics program must be open and flexible in order for educational institutions and teachers to choose the content actively, methods of instruction, location of operations, and hours of operation that are appropriate for their particular circumstances and conditions. the principle of ensuring educational goals and requirements for quality and competence at every level and in every classroom.

In addition to the findings, the research has some limitations. Time spent in experiments was short; activities had to be planned to fit into an already-short learning program, which was constrained in its duration. As a result of some students’ inability to adjust to the new way of doing things, some initial confusion has been on their part. Thus, some of these students’ educational outcomes are negatively impacted. Several other studies have also found that this is a problem (Cranton, 2011; Kolb and Kolb, 2017).

These findings and limitations suggest that future research on experiential learning in mathematics should consider long-term planning that includes both inside and outside classroom activities and an interdisciplinary approach. Mathematical topics in algebra, calculus, statistics, and probability can be studied at various levels of study. When combined, experiential, problem-based, and project-based learning should be used greatly in educational settings. Another trend to consider is incorporating technology elements into the classroom, becoming increasingly popular as science and technology advance (Tran et al., 2020).

The studies on improving teachers’ theoretical and practical knowledge of experiential learning are unnecessary to improve the effectiveness of this method for teaching mathematics and general education. According to this point of view, Jay and Miller (2016) present three models of teacher training programs that assist students in being fostered in the theory and practice of experiential learning, which is consistent with this viewpoint. The authors identify the most generalizable aspects of these programs, identify the factors that lead to the breakdown of theory and practice, and propose more sustainable models. Math projects, STEM, and competitions can all benefit from the integration of arithmetic and geometry, which is another area of study worth exploring further in the future.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by Institutional Ethics Committee of the School of Education at Can Tho University in Vietnam. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Thanks to all of the students who took part in this investigation, as well as the faculty and staff who assisted with it.

References

Algani, Y. M. A., and Alhaija, Y. F. A. (2021). The effect of the cooperative learning method on students’ academic achievement in mathematics. Multicult. Educ. 7, 329–339. doi: 10.5281/zenodo.4647901

CrossRef Full Text | Google Scholar

Amigó, M. F., and Lloyd, J. (2021). Changing roles and environments in experiential learning. High. Educ. Skills Work Based Learn. 11, 420–434. doi: 10.1108/heswbl-11-2019-0159

CrossRef Full Text | Google Scholar

Avelino, G., Ignacio, J., and Joseph, D. R. (2017). Exploring mathematics achievement goals using Kolb’s learning style model. Asia Pac. J. Multidiscip. Res. 5, 19–24.

Google Scholar

Behrendt, M., and Franklin, T. (2014). A review of research on school field trips and their value in education. Int. J. Environ. Sci. Educ. 9, 235–245.

Google Scholar

Breunig, M. (2017). Experientially learning and teaching in a student-directed classroom. J. Exp. Educ. 40, 213–230. doi: 10.1177/1053825917690870

CrossRef Full Text | Google Scholar

Burrell, A., McCready, J., Munshi, Z., and Penazzi, D. (2017). Developing an ‘outdoor-inspired’ indoor experiential mathematical activity. MSOR Connect. 16, 26–35. doi: 10.1186/s12913-016-1423-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Canino, M., Zanelli, A., Seri, M., Degli, E. A., and Torreggiani, A. (2021). Young raw matters ambassadors: high school students act as science communicators. Front. Educ. 6:690294. doi: 10.3389/feduc.2021.690294

CrossRef Full Text | Google Scholar

Chen, C. (2021). Effects of flipped classroom on learning outcomes and satisfaction: an experiential learning perspective. Sustainability 13:9298. doi: 10.3390/su13169298

CrossRef Full Text | Google Scholar

Chesimet, M. C., Githua, B. N., and Ng’eno, J. K. (2016). Effects of experiential learning approach on students’ mathematical creativity among secondary school students of Kericho east sub-county, Kenya. J. Educ. Pract. 7, 51–57.

Google Scholar

Chusni, M. M., Saputro, S., Suranto, S., and Rahardjo, S. B. (2022). Enhancing critical thinking skills of junior high school students through discovery-based multiple representations learning model. Int. J. Instr. 15, 927–944. doi: 10.29333/iji.2022.15153a

CrossRef Full Text | Google Scholar

Cline, K., Fasteen, J., Francis, A., Sullivan, E., and Wendt, T. (2020). A vision for projects across the mathematics curriculum. PRIMUS 30, 379–399. doi: 10.1080/10511970.2019.1600176

CrossRef Full Text | Google Scholar

Cohen, L., Manion, L., and Morrison, K. (2005). Research Methods in Education, 5th Edn. London: Taylor and Francis e-Library.

Google Scholar

Cotič, N., Plazar, J., Istenič Starčič, A., and Zuljan, D. (2020). The effect of outdoor lessons in natural sciences on students’ knowledge through tablets and experiential learning. J. Baltic Sci. Educ. 19, 747–763. doi: 10.33225/jbse/20.19.747

CrossRef Full Text | Google Scholar

Cranton, P. (2011). A transformative perspective on the scholarship of teaching and learning. High. Educ. Res. Dev. 30, 75–86. doi: 10.1080/07294360.2011.536974

CrossRef Full Text | Google Scholar

Darling-Hammond, L. (2016). Research on teaching and teacher education and its influences on policy and practice. Educ. Res. 45, 83–91. doi: 10.3102/0013189x16639597

CrossRef Full Text | Google Scholar

Davidovitch, N., Yavich, R., and Keller, N. (2014). Mathematics and experiential learning – are they compatible? J. Coll. Teach. Learn. 11, 135–148. doi: 10.19030/tlc.v11i3.8759

CrossRef Full Text | Google Scholar

Giroux, H. (2015). Dangerous Thinking in the Era of New Authoritarianism. New York, NY: Routledge.

Google Scholar

Habib, M. K., Nagata, F., and Watanabe, K. (2021). Mechatronics: experiential learning and the stimulation of thinking skills. Educ. Sci. 11:46. doi: 10.3390/educsci11020046

CrossRef Full Text | Google Scholar

Heinrich, W. F., and Green, P. M. (2020). Remixing approaches to experiential learning, design, and assessment. J. Exp. Educ. 43, 205–223. doi: 10.1177/1053825920915608

CrossRef Full Text | Google Scholar

Hossain, M. A., and Ariffin, M. R. K. (2018). Integration of structured cooperative learning in mathematics classrooms. Int. J. Psychol. Educ. Stud. 5, 23–29. doi: 10.17220/ijpes.2018.01.004

CrossRef Full Text | Google Scholar

Hsu, P. L. (2019). High school students’ and scientists’ experiential descriptions of cogenerative dialogs. Int. J. Sci. Math. Educ. 17, 657–677. doi: 10.1007/s10763-017-9877-4

CrossRef Full Text | Google Scholar

Jay, J., and Miller, H. (2016). Immersing teacher candidates in experiential learning: cohorts, learning communities, and mentoring. Glob. Educ. Rev. 3, 169–175.

Google Scholar

Kolb, A. Y., and Kolb, D. A. (2017). Experiential learning theory as a guide for experiential educators in higher education. ELTHE A J. Engaged Educ. 1, 7–44. doi: 10.5465/amle.2005.17268566

CrossRef Full Text | Google Scholar

Kolb, D. (2014). Experiential Learning: Experience as the Source of Learning and Development, 2nd Edn. Upper Saddle River, NJ: Pearson.

Google Scholar

Kolb, D. A. (1984). Experiential Learning: Experience as the Source of Learning and Development. Englewood Cliffs, NJ: Prentice-Hall.

Google Scholar

Kuczera, K. (2021). Experiential learning in simulated conditions. Procedia Comput. Sci. 192, 4186–4193. doi: 10.1016/j.procs.2021.09.194

CrossRef Full Text | Google Scholar

Lamya, A., Kawtar, Z., Mohamed, E., and Mohamed, K. (2020). Personalization of an educational scenario of a learning activity according to the learning styles model David Kolb. Glob. J. Eng. Technol. Adv. 5, 99–108. doi: 10.30574/gjeta.2020.5.3.0114

CrossRef Full Text | Google Scholar

Larmer, J. (2015). Project-Based Learning Vs. Problem-Based Learning Vs. X-BL. Available online at: http://www.edutopia.org/blog/pbl-vs-pbl-vs-xbl-john-larmer (accessed January 10, 2022).

Google Scholar

Lykke, M., Skov, M., and Jantzen, C. (2021). High pulse: exploring the exhibit features of a collaborative, Wholebody exhibition for experiential learning in science centers. Front. Educ. 6:675007. doi: 10.3389/feduc.2021.675007

CrossRef Full Text | Google Scholar

Manfreda, K. V., and Hodnik, T. (2021). Mathematical literacy from the perspective of solving contextual problems. Eur. J. Educ. Res. 10, 467–483. doi: 10.12973/eu-jer.10.1.467

CrossRef Full Text | Google Scholar

Mayoral-Rodríguez, S., Timoneda-Gallart, C., and Pérez-Álvarez, F. (2018). Effectiveness of experiential learning in improving cognitive planning and its impact on problem solving and mathematics performance / Eficacia del aprendizaje experiencial para mejorar la Planificación cognitiva y su repercusión en la resolución de problemas y el rendimiento matemático. Cult. Educ. 30, 308–337. doi: 10.1080/11356405.2018.1457609

CrossRef Full Text | Google Scholar

Mc Pherson-Geyser, G., de Villiers, R., and Kavai, P. (2020). The use of experiential learning as a teaching strategy in life sciences. Int. J. Instr. 13, 877–894. doi: 10.29333/iji.2020.13358a

CrossRef Full Text | Google Scholar

McCarty, J., Ford, V., and Ludes, J. (2018). Growing experiential learning for the future: REAL school gardens. Child. Educ. 94, 47–55. doi: 10.1080/00094056.2018.1451690

CrossRef Full Text | Google Scholar

Menon, P. R. (2021). Experiential learning: folklore as a learning experience. Int. J. Engl. Learn. Teach. Skills 3, 1963–1975. doi: 10.15864/ijelts.3202

CrossRef Full Text | Google Scholar

Ministry of Education and Training (2018). Mathematics General Education Curriculum. Hanoi: Ministry of Education and Training.

Google Scholar

Muro, P. D., and Terry, M. (2007). A matter of style: applying Kolb’s learning style model to college mathematics teaching practices. J. Coll. Read. Learn. 38, 53–60. doi: 10.1080/10790195.2007.10850204

CrossRef Full Text | Google Scholar

Mutmainah, Rukayah, and Indriayu, M. (2019). Effectiveness of experiential learning-based teaching material in mathematics. Int. J. Eval. Res. Educ. (IJERE) 8, 57–63. doi: 10.11591/ijere.v8.i1.pp57-63

CrossRef Full Text | Google Scholar

Mwei, P. K. (2017). Problem-solving: how do in-service secondary school teachers of mathematics make sense of a non-routine problem context? Int. J. Res. Educ. Sci. 3, 31–41. doi: 10.21890/ijres.267368

CrossRef Full Text | Google Scholar

Pambudi, D. S. (2022). The effect of outdoor learning method on elementary students’ motivation and achievement in geometry. Int. J. Instr. 15, 747–764. doi: 10.29333/iji.2022.15143a

CrossRef Full Text | Google Scholar

Payne, H., and Costas, B. (2021). Creative dance as experiential learning in state primary education: the potential benefits for children. J. Exp. Educ. 44, 277–292. doi: 10.1177/1053825920968587

CrossRef Full Text | Google Scholar

Pittaway, L., and Cope, J. (2007). Simulating entrepreneurial learning integrating experiential and collaborative approaches to learning. Manag. Learn. 38, 211–233. doi: 10.1177/1350507607075776

CrossRef Full Text | Google Scholar

Pozo-Sánchez, S., López-Belmonte, J., Fernández, M. F., and López, J. A. (2020a). Correlational analysis of the incident factors in the level of digital competence of teachers. Interuniversity Electron. J. Teach. Train. 23, 143–151. doi: 10.6018/reifop.396741

CrossRef Full Text | Google Scholar

Pozo-Sánchez, S., López-Belmonte, J., Rodríguez-García, A. M., and López-Núñez, J. A. (2020b). Digital competence of teachers in the use and analytical management of information in flipped learning. Cult. Educ. 32, 1–35. doi: 10.1080/11356405.2020.1741876

CrossRef Full Text | Google Scholar

Roberts, J. L., Breedlove, L., and Strode, D. B. (2016). Experiential learning at the Gatton academy of mathematics and science in Kentucky. Gifted Child Today 39, 228–235. doi: 10.1177/1076217516662097

CrossRef Full Text | Google Scholar

Scogin, S. C., Kruger, C. J., Jekkals, R. E., and Steinfeldt, C. (2017). Learning by experience in a standardized testing culture. J. Exp. Educ. 40, 39–57. doi: 10.1177/1053825916685737

CrossRef Full Text | Google Scholar

Sumirattana, S., Makanong, A., and Thipkong, S. (2017). Using realistic mathematics education and the DAPIC problem-solving process to enhance secondary school students’ mathematical literacy. J. Soc. Sci. 38, 307–315. doi: 10.1016/j.kjss.2016.06.001

CrossRef Full Text | Google Scholar

Tong, D. T., Loc, N. P., Uyen, B. P., and Cuong, P. H. (2020). Applying experiential learning to teaching the equation of a circle: a case study. Eur. J. Educ. Res. 9, 239–255. doi: 10.12973/eu-jer.9.1.239

CrossRef Full Text | Google Scholar

Tran, T., Nguyen, T. T., and Trinh, T. P. T. (2020). Mathematics teaching in vietnam in the context of technological advancement and the need of connecting to the real world. Int. J. Learn. Teach. Educ. Res. 19, 255–275. doi: 10.26803/ijlter.19.3.14

CrossRef Full Text | Google Scholar

Venkatraman, S., Overmars, A., and Wahr, F. (2019). Visualization and experiential learning of mathematics for data analytics. Computation 7:37. doi: 10.3390/computation7030037

CrossRef Full Text | Google Scholar

Voukelatou, G. (2019). The contribution of experiential learning to the development of cognitive and social skills in secondary education: a case study. Educ. Sci. 9:127. doi: 10.3390/educsci9020127

CrossRef Full Text | Google Scholar

Wang, L. (2006). Sociocultural learning theories and information literacy teaching activities in higher education. Ref. User Serv. Q. 47, 149–158. doi: 10.5860/rusq.47n2.149

PubMed Abstract | CrossRef Full Text | Google Scholar

Weinbern, A. E., Basile, C. G., and Albright, L. (2011). The effect of an experiential learning program on middle school students’ motivation toward mathematics and science. RMLE Online 35, 1–12. doi: 10.1080/19404476.2011.11462086

CrossRef Full Text | Google Scholar

Wynn, A. H. (2018). The Effect of Experiential Learning on Mathematics Achievement and Mathematics Anxiety of African-American Students. Doctoral Thesis. Lynchburg, VA: Liberty University.

Google Scholar

Yuberti, Latifah, S., Anugrah, A., and Saregar, A. Misbah, and Jermsittiparsert, K. (2019). Approaching problem-solving skills of momentum and impulse phenomena using context and problem-based learning. Eur. J. Educ. Res. 8, 1217–1227. doi: 10.12973/eu-jer.8.4.1217

CrossRef Full Text | Google Scholar