Inpainting with style: forcing style coherence to image inpainting with deep image prior

Morotti, Elena; Merizzi, Fabio; Evangelista, Davide; Cascarano, Pasquale

doi:10.3389/fcomp.2024.1478233

ORIGINAL RESEARCH article

Front. Comput. Sci., 22 November 2024

Sec. Human-Media Interaction

Volume 6 - 2024 | https://doi.org/10.3389/fcomp.2024.1478233

This article is part of the Research Topic Artificial Intelligence: The New Frontier in Digital Humanities View all 7 articles

Inpainting with style: forcing style coherence to image inpainting with deep image prior

$\r\nElena Morotti$ Elena Morotti¹

Fabio Merizzi²

Davide Evangelista²

Pasquale Cascarano³^*

¹Department of Political and Social Sciences, University of Bologna, Bologna, Italy
²Department of Computer Science and Engineering, University of Bologna, Bologna, Italy
³Department of the Arts, University of Bologna, Bologna, Italy

In this paper, we combine the deep image prior (DIP) framework with a style transfer (ST) technique to propose a novel approach (called DIP-ST) for image inpainting of artworks. We specifically tackle cases where the regions to fill in are large. Hence, part of the original painting is irremediably lost, and new content must be generated. In DIP-ST, a convolutional neural network processes the damaged image while a pretrained VGG network forces a style constraint to ensure that the inpainted regions maintain stylistic coherence with the original artwork. We evaluate our method performance to inpaint different artworks, and we compare DIP-ST to some state-of-the-art techniques. Our method provides more reliable solutions characterized by a higher fidelity to the original images, as confirmed by better values of quality assessment metrics. We also investigate the effectiveness of the style loss function in distinguishing between different artistic styles, and the results show that the style loss metric accurately measures artistic similarities and differences. Finally, despite the use of neural networks, DIP-ST does not require a dataset for training, making it particularly suited for art restoration where relevant datasets may be scarce.

1 Introduction

Art restoration aims at repairing damaged artworks, which often suffer from various forms of deterioration over time. These damages can result from environmental factors such as humidity or temperature fluctuations, as well as from physical impacts due to accidents, mishandling, or vandalism, as described in Scott (2017) and Spiridon et al. (2017). Image inpainting, a well-known technique in computational imaging, involves filling in missing or damaged areas of an image. This task has been effectively tackled for the restoration of artworks, helping reconstruct and preserve their original appearance. For insightful examples, refer to the works by Fornasier and March (2007), Baatz et al. (2008), Calatroni et al. (2018), and Merizzi et al. (2024). Restoring the original state of a degraded image becomes highly challenging, or even impossible, when large areas are missing, as traditional digital image processing techniques struggle to recover the lost content due to the significant loss of information. Moreover, from a mathematical standpoint, image inpainting is an ill-posed problem, meaning that the computational process does not yield a unique solution. For further details on this topic, refer Bertalmio et al. (2000) and Bertero et al. (2021).

Deep learning (DL) paradigms enable the analysis and processing of vast amounts of data, unveiling intricate patterns and details that cannot be immediately perceived by humans, leveraging powerful and highly expressive models like neural networks. This topic can be deepened by Hohman et al. (2018) and Najafabadi et al. (2015). In the field of digital humanities, DL has provided novel tools for art restoration and analysis, as described in Gaber et al. (2023) and Santos et al. (2021). Specifically, DL techniques have already significantly impacted image inpainting, enabling precise reconstruction of damaged artworks. By analyzing large image datasets, DL tools can predict and reconstruct missing elements with remarkable accuracy, particularly in medium- to small-sized damaged areas. Results in Gaber et al. (2023), Gupta et al. (2021), and Adhikary et al. (2021) demonstrate that DL can restore artworks as closely as possible to their original state, and thus, it ensures the preservation of cultural heritage for future generations. One of the challenges with approaches relying on datasets is the requirement for a large number of images, representing a wide range of artistic styles, periods, and techniques. In fact, creating and accessing such datasets can be difficult, costly, and often subject to copyright restrictions. In this context, deep image prior (DIP), first proposed by Ulyanov et al. (2020) in the literature, emerges as a promising DL-based alternative, as it does not require a training dataset. Instead, it exploits the regularizing properties of convolutional neural network (CNN) architectures. Very recently, DIP has been successfully applied to art restoration in Merizzi et al. (2024), where the authors developed a technique designed to produce visually coherent restorations which enhance the understanding and interpretation of damaged images in historical research.

However, even for DL techniques, the task of image inpainting in large damaged regions is still significantly challenging, as incoherent elements might be generated to fill the damaged regions. Interestingly, so far, none of the restoration techniques proposed in the state-of-the-art does particularly account for the specific style of the original artwork, when computing new content for wide regions to be inpainted. Nelson Goodman, one of the most influential twentieth-century philosophers of art, argued that style “consists of those features of the symbolic functioning of a work that are characteristic of an author, period, place, or school,” in Goodman (1978). We believe that style could play a crucial role for inpainting approaches of large regions, because preserving the stylistic elements of an artwork enforces its identity and coherence. Thus, our goal was to enhance inpainting techniques by incorporating style information about techniques and choices that define an artist's work, including aspects such as the selection of colors, brushstrokes, themes, and overall composition.

So far, computer scientists have investigated the concept of artistic style mostly by developing methods able to identify artists and classify paintings for their styles, provided a large set of examples. Examples can be found in Milani and Fraternali (2021), Shamir (2012), Folego et al. (2016), and Lecoutre et al. (2017). However, these methods are currently limited to identifying style patterns only if the artists are well-represented in the training dataset, in terms of the number of samples. Furthermore, they are not yet capable of generating content in the same style.

Few years ago, the innovative technique of style transfer (ST) has been introduced by Gatys et al. (2016) and Jing et al. (2019). ST allows for the transformation of one image's style into another while preserving the original content. This is accomplished using neural networks that have learned to extract from one reference artwork some stylistic features (which are independent of the content) and to impose those features onto a given image. Such complex interplay and recombination between the content and style of an image leads to the creation of a completely new image. In the realm of art restoration, style transfer can be used to hypothesize the restoration of artworks by incorporating the artist's style into the reconstruction of damaged areas. This approach can result in restorations that are more aesthetically coherent to the original artist's style.

This paper focuses on the task of image inpainting, particularly in the context of artwork restoration. One of the key contributions is the introduction of the deep image prior with style transfer (DIP-ST) method. This innovative approach enhances the traditional DIP technique by incorporating a style loss term, which helps to maintain stylistic coherence with the original artwork. The style term is derived from the Gram matrices of a pre-trained CNN, allowing the method to capture stylistic elements to effectively fill the missing regions.

Moreover, the paper represents the first exploration into how artificial intelligence perceives style, highlighting the challenges associated with automatic style recognition, especially when interpreting digital representations of artworks. This is achieved through a style loss metric, capable of distinguishing different painters' styles by computing similarities between style elements of various artworks. The results show the metric's effectiveness in identifying both similarities and differences in style, aligning with human expertise in recognizing artistic styles.

The paper is organized as follows. Section 2 reviews existing inpainting techniques, including both traditional mathematical approaches and recent deep learning methods, as well as the application of style transfer in digital humanities. Section 3 describes the proposed DIP-ST approach, detailing the integration of the style term into the DIP framework and the technical implementation aspects. Section 4 presents experimental results demonstrating the effectiveness of the DIP-ST method in restoring artworks with large occlusions. This section includes a quantitative and qualitative analysis of the inpainted images, comparing them with the standard DIP approach and some state-of-the-art algorithms based on different paradigms. Moreover, we discuss the implications of the findings, the challenges faced, and the potential future research directions, particularly the exploration of how neural networks perceive “style” differently from human observers. Section 5 draws the conclusions.

2 A brief survey on image inpainting techniques

Image inpainting aims at filling regions of a damaged image, generating new content that is coherent from a visual perspective to the original image. Let $\bar{x} \in ℝ^{m \times n}$ represent an image of size m×n pixels, defined on the domain Ω = (i, j):i = 1, …, m, j = 1, …, n. We assume that $\bar{x}$ contains occlusions in the pixels located in the region D⊂Ω. The goal of the image inpainting task is to assign new values to the pixels in D. We define the masking operator m∈{0, 1}^m×n identifying the unoccluded pixels in the observed image, as the characteristic function of the set Ω\D. More specifically, m is defined as:

\begin{array}{l} m_{i, j} = {\begin{matrix} 1 & if {\bar{x}}_{i, j} \in Ω \ D \\ 0 & if {\bar{x}}_{i, j} \in D . \end{matrix} & (1) \end{array}

In the following, before discussing the DIP approach for image inpainting in Section 2.3, we first outline the main state-of-the-art techniques for image inpainting. These methods range from traditional mathematical handcrafted approaches, which focus on transferring existing image content using diffusion or transport processes and copy–paste methods with suitable patches (Section 2.1), to more contemporary data-driven techniques that involve generating image content using neural networks trained on extensive image datasets (Section 2.2).

2.1 Handcrafted approaches for image inpainting

Since the early 2000s, several handcrafted techniques for digital image inpainting have been developed. In works by Schönlieb (2015) and Bugeau et al. (2010), the algorithms usually use local diffusion techniques, which spread information from intact parts of the image into neighboring damaged areas. In particular, the inpainted image $\hat{x}$ is obtained as the solution of the following optimization problem:

\begin{array}{l} \hat{x} \in arg min_{x} || m ⊙ (x - \bar{x}) {||}^{2} + λ R (x) . & (2) \end{array}

The first term and the second term are usually referred to as fidelity term and regularization term, respectively. The former ensures that the solution $\hat{x}$ closely matches the original data $\bar{x}$ in the undamaged region Ω\D. The latter favors the propagation of contents within D. The positive scalar λ balances the contribution of the two terms. Finally, we remark that the operator ⊙ stands for the Hadamard (element-wise) product.

In Chan and Shen (2001), the authors propose to define R(·) in Equation (2) as the total variation (TV) functional popularized by Rudin et al. (1992). The TV prior favors piece-wise constant reconstructions via non-linear diffusion because it is defined on an image x as:

\begin{array}{l} T V (x) = \sum_{c \in {R, G, B}} \sum_{i = 1}^{m - 1} \sum_{j = 1}^{n - 1} \sqrt{{(x_{i + 1, j}^{c} - x_{i, j}^{c})}^{2} + {(x_{i, j + 1}^{c} - x_{i, j}^{c})}^{2}}, & (3) \end{array}

where $x_{i, j}^{c}$ denotes (i,j)-pixel value of the RGB channel c. TV is widely used in image processing because it effectively restores edges and important structural details, leading to clearer and more accurate images, as demonstrated in works by Chambolle (2004), Chan et al. (2006), Loli Piccolomini and Morotti (2016), and Cascarano et al. (2022b).

Partial differential equation (PDE) paradigms for image inpainting naturally arise from the variational formulation given by the optimization problem in Equation (2). In order to find the minimizers of this function, one can derive the associated Euler—Lagrange equations. These equations provide the necessary conditions that the optimal solution $\hat{x}$ must satisfy, and they can often be interpreted as PDEs. See Schönlieb (2015) for more technical information on this topic. The solution process typically involves simulating an artificial evolution, where the image is iteratively updated to reduce the value of the functional until convergence. For instance, advanced approaches making use of Navier—Stokes models propagating color information by means of complex diffusive fluid dynamics laws have been considered in Caselles et al. (1998), Bertalmio et al. (2000, 2001), and Telea (2004). Finally, other paradigms involving the use of transport and curvature-driven diffusion approaches can be found in Ballester et al. (2001), Chan and Shen (2001), and Masnou and Morel (1998).

The approaches described above favor local regularization. As a consequence, they are particularly suited to reconstruct only small occluded regions such as scratches, text, or similar. In the context of heritage science, they have been employed for restoring ancient frescoes in works by Bertalmio et al. (2000), Fornasier and March (2007), and Baatz et al. (2008), and they show effective performance. However, such techniques fail in reconstructing large occluded regions and in the retrieval of more complex image content such as texture. To overcome such limitations, non-local inpainting approaches have been proposed in the current literature by Criminisi et al. (2004), Aujol et al. (2010), and Arias et al. (2011), to propagate image information using patches. The main idea involves comparing image patches using a similarity metric that accounts for rigid transformations and patch rescaling. The PatchMatch approach proposed by Barnes et al. (2009) exemplifies this method, enhancing it by computing patch correspondence probabilities to weigh contributions from different locations. Improved versions, such as those in Newson et al. (2014, 2017), perform non-local averaging for better results. Patch-based inpainting methods, known for their strong performance in reconstructing geometric and textured content, are often sensitive to initialization and hyperparameter choices like patch size. In art restoration, Calatroni et al. (2018) combined local and non-local methods for restoring damaged manuscripts.

Selecting the best hand-crafted model, especially the most suitable term R(·) that promotes effective inpainting within the damaged region D, often demands significant technical expertise. This complexity limits the practical application of these approaches because choosing the optimal regularization term usually requires a deep understanding of advanced topics in linear and non-linear diffusion and smooth and non-smooth optimization techniques, which are not commonly familiar to most practitioners.

2.2 Data-driven approaches for image inpainting

Neural networks trained on extensive image datasets have demonstrated outstanding performances in the task of image inpainting. Given the important role played by data, in the following we will refer to these methods as data-driven approaches.

Data-driven approaches provide a valuable alternative to handcrafted methods by utilizing a vast amount of training data and neural techniques to predict mappings from occluded images to completed ones. Differently from handcrafted approaches, these methods benefit from the advanced encoding capabilities of deep neural networks. These learning-based paradigms are capable of recognizing both local and non-local patterns, as well as the semantic content of images, without the necessity of defining specific mathematical models or complex priors. Upon prior knowledge of the inpainting region, i.e., of the mask operator in Equation (2), data-driven inpainting approaches based on convolutional networks have been designed in Köhler et al. (2014) and Pathak et al. (2016) and improved in some recent works by Liu et al. (2018) and Wang et al. (2018), with the intent to adapt the convolutional operations only to those points providing relevant information.

In recent years, generative models have emerged as a powerful data-driven approach for image inpainting, achieving remarkable success. An exhaustive review is presented by Ballester et al. (2022). Generative models are capable of generating realistic patterns by learning from a given dataset using unsupervised learning. When applied to image inpainting, they can condition their output on a masked input to predict and fill in the missing regions. Among the most successful generative models for this task are generative adversarial networks (GANs) (Goodfellow et al., 2014) and denoising diffusion probabilistic models (DDPMs) (Ho et al., 2020). The advent of GAN architectures significantly boosted the effectiveness of data-driven inpainting techniques. Unlike traditional methods that minimize pixel-wise differences, GANs focus on aligning the distribution of reconstructed images with that of ground truth images. This is achieved by using two different networks: one that distinguishes between real and generated images (discriminator) and another that generates samples (generator). Provided a large dataset, GANs showed great performances for inpainting tasks in works by Pathak et al. (2016), Iizuka et al. (2017), Liu et al. (2019a), Liu et al. (2021), Lahiri et al. (2020), and Hedjazi and Genc (2021). Recently, DDPM approaches have shown potentially superior performance in image inpainting than GANs. These models excel in generative tasks without encountering common GAN-related drawbacks, such as adversarial training instabilities and high computational demands. This has been studied in Goodfellow et al. (2015). The advances in using diffusion models for inpainting include the work by Lugmayr et al. (2022), which demonstrated excellent results by incorporating mask information into the reverse diffusion process. Other notable neural data-driven inpainting approaches leveraging diffusion models can be found in works by Chen et al. (2023), Wang et al. (2023), Li et al. (2022), and Suvorov et al. (2022).

Despite their strong performance, data-driven methods have been relatively overlooked in digital inpainting applications (see Wang et al., 2021, Lv et al. (2022), and Deng and Yu (2023) and references therein). These methods depend on large datasets of high-quality and relevant data, as well as information about the types of occlusions, to produce appropriate image content. This dependency poses a significant challenge, especially when dealing with the restoration of heavily damaged frescoes by minor artists, where little training data are available. Additionally, these approaches can be unstable and are prone to introducing biases from irrelevant data during the inpainting process, which poses another limitation.

2.3 Inpainting with deep image prior

In 2020, Ulyanov et al. (2020) proposed a groundbreaking method for deep learning-based image processing known as the deep image prior (DIP). The main innovation of DIP is the usage of the architecture of the neural network itself as a prior for generating images, enabling effective image restoration without the need for pretrained models or external datasets. This concept has been further investigated in a number of subsequent works, such as Liu et al. (2019b), Cascarano et al. (2021a), Cascarano et al. (2021b), Cascarano et al. (2022a), Cascarano et al. (2023), Mataev et al. (2019), and Gong et al. (2018).

Let f_Θ denote the neural network with parameters Θ parameters, taking as input an image z sampled randomly from a uniform distribution with a variable number of channels. Given the damaged image $\bar{x}$ and its corresponding mask m, the traditional DIP algorithm looks for the optimal vector of parameters $\hat{Θ}$ by solving the following minimization problem:

\begin{array}{l} \hat{Θ} \in arg min_{Θ} || m ⊙ (f_{Θ} (z) - \bar{x}) {||}^{2} . & (4) \end{array}

Once this optimization problem is solved, the resulting parameters $\hat{Θ}$ are used to generate the DIP output image $\hat{x} = f_{\hat{Θ}} (z)$ , matching at best $\bar{x}$ outside D and filling contents in Ω\D via the effect of the architecture of $f_{\hat{Θ}}$ .

This optimization is typically approached using iterative methods such as gradient descent with back-propagation. As Equation (4) represents a non-convex optimization problem, different initializations for Θ can lead to diverse outcomes. Unlike traditional handcrafted and data-driven methods, DIP incorporates implicit regularization through its network structure. However, to prevent overfitting, it is essential to apply early stopping during the iterative process. The training for each specific observation $\bar{x}$ is conducted independently, leading to computational costs more comparable to model-based techniques rather than data-driven approaches.

In this study, we employ a classical DIP network architecture, as represented in the first part of Figure 1, being a simple U-Net architecture, first proposed by Ronneberger et al. (2015). We use LeakyReLU activation functions, Lanczos kernel for downsampling and bilinear upsampling layers, as done in Merizzi et al. (2024). We keep the filter size at 3 × 3 for all the convolutional layers, and we consider reflective boundary conditions for local coherence in the corner areas. As in typical U-Net architectures, we employ skip connections, which are direct links between different parts of the convoluted network. They make information flow not only within the architectural structure but also outside of it, allowing an alternative gradient back-propagation path. This technique proved to be one of the most effective tools in improving the performance of convoluted networks, see, e.g., Drozdzal et al. (2016), Orhan and Pitkow (2017), Morotti et al. (2021), and Evangelista et al. (2023). However, skip connections are typically viewed as disadvantageous in DIP because they tend to allow structures to bypass the architecture of the network, and it may lead to inconsistencies and smoothing effects, as outlined in Ulyanov et al. (2020). In our specific scenario, on the other hand, such a smoothing effect contributes positively to the overall consistency of the inpainted image.

Figure 1

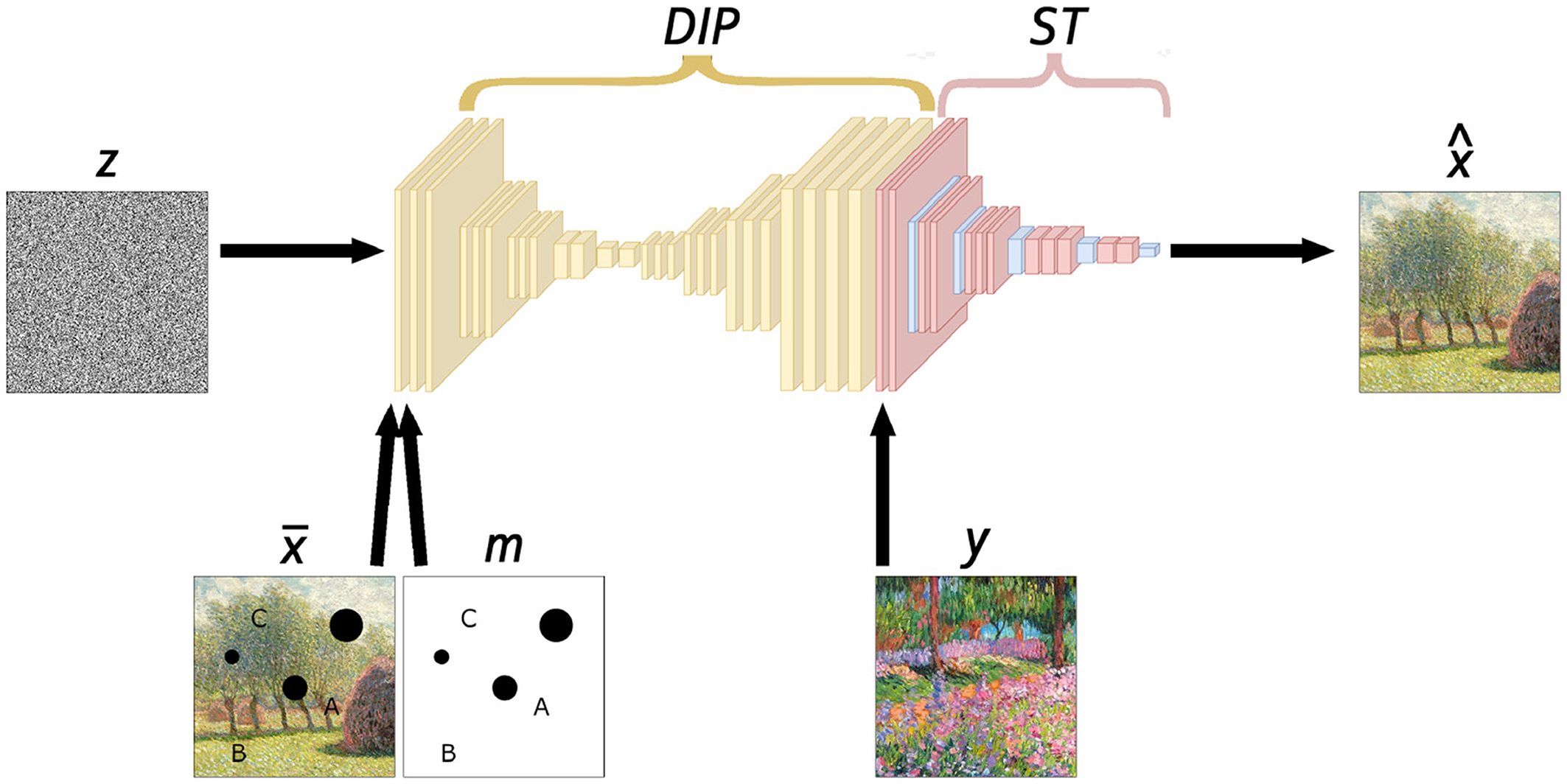
Figure 1. Deep image prior with style transfer. The DIP architecture is illustrated in yellow. The VGG-16 architecture, used to calculate the style loss, is shown in pink with the relevant filters highlighted in blue. The input to the implemented scheme includes z an image randomly sampled from a Gaussian distribution; $\bar{x}$ , the degraded image; m, the mask; y, the style image; and $\hat{x}$ , the resulting inpainted image.

In Section 4, we will use the TV-based DIP approach, obtained by adding a TV regularization term to Equation (4) with the intent of stabilizing the training procedure, as in Liu et al. (2019a), Cascarano et al. (2021b), and Liu et al. (2019b). Recalling the TV definition in Equation (3), the resulting DIP algorithm is thus determined by the following optimization problem:

\begin{array}{l} \hat{Θ} \in arg min_{Θ} || m ⊙ (f_{Θ} (z) - \bar{x}) {||}^{2} + λ \cdot T V (f_{Θ} (z)) . & (5) \end{array}

We remark that in comparison with Equation (4), using the model (5) for solving the inpainting task reduces the sensitivity to the stopping time, as the TV term prevents noise overfitting (if suitably balanced with the content term by λ in the overall loss). In the experiments, Equation 5 is solved by running the Adam optimizer for 3000 iterations with a learning rate of size 0.01.

3 Coding style for inpainting

In this section, we discuss the basics of style transfer and embed it in the DIP scheme for inpainting, providing the proposed DIP-ST scheme.

3.1 Style transfer technique

Style transfer is a neural technique introduced in computer vision by Gatys et al. (2015). It involves creating a new image by combining the content of one image x with the style of another image y, used as a reference. The separation of content and style is achieved via the application of a pre-trained convoluted network and with the use of Gram matrices, as described in Drineas and Mahoney (2005). In particular, a VGG-16 network [whose precise description can be found in Simonyan and Zisserman (2014)] is used to extract high-level information from the input image. It is then compared with the same information acquired from the reference image through filter activations which derive from the last convoluted layer at each level of resolution in the VGG-16 network (i.e., highlighted in blue in Figure 1). These activations, known as feature responses, represent the image at different deep levels, and they can then be used to quantify the style match, through Gram matrices.

A Gram matrix is a mathematical tool used to collect the correlation indices between multiple feature responses. It is obtained by making the dot product of the feature response of a given layer by its transpose. A loss element can then be defined as a match between the Gram matrices of our style source and our newly created image, for different network layers. More precisely, let $F_{x}^{k}$ and $F_{y}^{k}$ be the matrices representing the k-th feature response of the two images x and y. The Gram matrix, $G^{l} \in ℝ^{N_{l} \times N_{l}}$ , is defined as:

\begin{array}{l} G^{k} = vec (F^{k}) \cdot vec {(F^{k})}^{T}, & (6) \end{array}

where vec(·) is the operator that vectorizes a matrix by concatenating its rows. The style loss between an image x and a considered style image y can thus be defined as the average quadratic distance between corresponding couples of G^k Gram matrices, denoted respectively as $G_{x}^{k}$ and $G_{y}^{k}$ :

\begin{array}{l} L_{s t y l e} (x, y) : = \sum_{k} || G_{x}^{k} - G_{y}^{k} {||}^{2} . & (7) \end{array}

As $L_{s t y l e} (x, y)$ does not take into consideration local consistency, it is common to associate it with a form of regularization that promotes local smoothness. For instance, one could consider the total variation loss. This subject is particularly relevant in the context of style transfer applied to videos, and some improvements were reached in the past years (see Wang et al., 2020).

In the past years, additional research was conducted and brought significant improvements to style transfer. A useful review is given in Jing et al. (2019). The major contributions include the use of a generative transformation network for the creation of the image suggested by Johnson et al. (2016), the computation of Gram loss over horizontally and vertically translated features as proposed by Berger and Memisevic (2016), and the improvements in eliminating discrepancy in scale by subtracting the mean of feature representations before computing Gram loss, provided by Li et al. (2017a). Furthermore, Li et al. (2017b) made considerable contributions on the subject, proposing the demystification of style transfer, showing that minimizing Gram matrices between features is equivalent to minimizing maximum mean discrepancy with second-order polynomial kernels. More recently, painting style matching exploiting more advanced neural network architectures has been explored, such as patched CNN in Imran et al. (2023) and vision transformers in Iliadis et al. (2021).

3.2 Deep image prior inpainting with style transfer

Currently, we present our proposed approach for inpainting, combining the deep image prior scheme with style transfer elements. Our intent is to create an inpainting model with a methodology in-between the semantic approach of neural data-driven networks and the crafted prior algorithms. In addition, the feasibility of finding a relevant dataset for a specific fresco is poor while the chance of finding a well-preserved coherent image from the same author is usually quite high. Therefore, we approach the problem in such a way that we enable the leveraging of a single reference image for the inpainting process. Our solution consists of a combined model, having the first part synthesized the inpainted image and the latter serving as a loss term enforcing compatibility with a style-coherent image.

The general architecture of our model is reported in Figure 1. We apply a three-term loss, composed by the masked DIP (content) loss, the total variation regularization term, and style reference loss as defined in Equation (7). The complete loss is thus as follows:

\begin{array}{l} \hat{Θ} \in arg min_{Θ} || m ⊙ (f_{Θ} (z) - \bar{x}) {||}^{2} + λ \cdot T V (f_{Θ} (z)) + β \cdot \sum_{k} || G_{f_{Θ} (z)}^{k} - G_{y}^{k} {||}^{2}, & (8) \end{array}

where two positive parameters λ and β are used to balance the contribution of the three terms. We remark that by $\bar{x}$ and y we refer to the degraded image and the style image, respectively. As Equation (8) basically represents Equation (5) with an additional style reference loss as a regularization term, we name this approach deep image prior with style transfer (DIP-ST). We remark that, despite the complexity of the network structure, it is still a fully convolutional model, meaning it can be computed efficiently by working on GPUs.

The theoretical background of this novel architecture is to create a partially crafted prior, achieving the capability of semantic inpainting without the need for a large dataset of relevant images. In addition, the possibility of gathering information from a single relevant image is more correct for many applied tasks, such as restoration, where the restored piece should not be altered by information coming from undesired sources. With a data-driven method, this is particularly hard to enforce.

4 Experiements and discussion

We currently perform experiments on digital images to test the DIP-ST method for the inpainting of artworks.

In Figure 2, we report some of images we have considered in our tests: they all are square-cropped images from famous art masterpieces and reshaped to 512 × 512 pixels. We choose as the principal element of comparison the Starry Night (oil-on-canvas painting, 1889) by the Post-Impressionist painter Vincent Van Gogh. This masterpiece is widely considered an optimal reference for style transfer development (Huang et al., 2017; Li et al., 2017b) because of its vivid colors, dynamic brushwork, and emotional intensity. We also consider Van Gogh's Self-Portrait with Gray Felt Hat (1887) as a further Post-Impressionist style reference, characterized by short and rhythmic brushstrokes, striking color contrasts emphasizing emotional expression, and intricate texture. Claude Monet's Wheatstacks (End of Summer) (1890–91) and The artist's garden at Giverny (1900) paintings perfectly represent the sense of calm, harmony and beauty, reflecting the Impressionist aim to capture the essence of a moment. While Monet and Van Gogh have distinct styles, they share an emphasis on color, light, and expressive brushwork. In the following, these similarities will be highlighted by the style loss. Additionally, we consider a picture created by a generative neural network. Specifically, it has been obtained by feeding ChatGPT with a photo of one of the authors of this paper, and the prompt: “Given the attached image you should generate a second image with the same content but with the style of Van Gogh”. We refer to this image as Self-Portrait by ChatGPT in the following. Even if not reported in Figure 2, in this work we also take into account art movements significantly different from Impressionism and Post-Impressionism, such as Neo- and Abstract Expressionism. We select Jean-Michel Basquiat's Versus Medici (1982), which is an exemplary of Basquiat's neo-expressionist style, characterized by intense, expressive subjectivity, highly textured paint applications, and vividly contrasting colors. In addition, we select the Convergence oil-on-canvas painting (1952) by Jackson Pollock, whose chaotic energy and innovative use of the drip painting technique are hallmarks of Abstract Expressionism. The images of these last two paintings are not featured in this article due to copyright restrictions.

Figure 2

Figure 2. Images considered in the tests, characterized by evident style patterns. (A) Starry night by Van Gogh. (B) Starry night by Van Gogh, shifted crop. (C) Wheatstacks (End of Summer) by Monet. (D) The artist's garden at Giverny by Monet. (E) Self-portrait by Van Gogh. (F) Self-portrait by ChatGPT.

4.1 Measuring and comparing style on artworks

Before using style transfer for inpainting, we investigate the capability of the style loss in Equation (7) to identify painters' styles. In Table 1, we report the values of $L_{s t y l e}$ computed as in Equation (7) for each possible pair of images considered in the experiments. To enhance readability, the reported values have been scaled by a factor of 1000.

Table 1

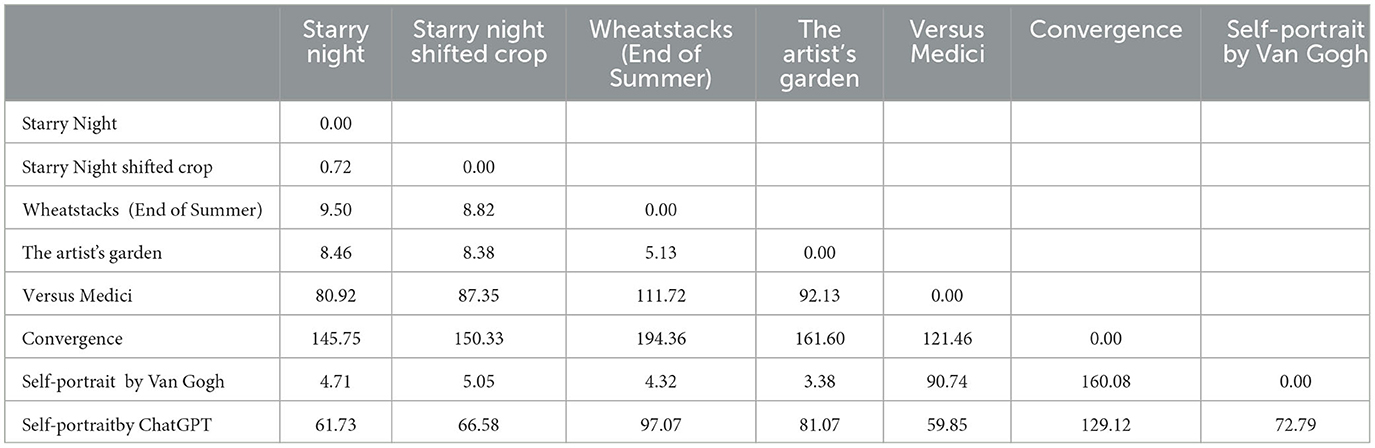
Table 1. Values of the style loss $L_{s t y l e}$ in Equation (7), computed for all possible pairs of the considered images.

Reasonably, the values are all equal to zero on the diagonal as the two involved images coincide and do not differ in style. All the other entries confirm the capability of the loss to measure similarities and dissimilarities between images in terms of small or high values, respectively. In fact, focusing on the Starry Night column, we observed that it is recognized to be almost equal ( $L_{s t y l e} = 0.72$ ) to the image extracted from the same painting with a shifted crop. Additionally, it is at only a 4.71 point distance from the Self-Portrait painting by the same author. When compared to Monet's works, the distance doubles up, but the metric increases remarkably when Starry Night is associated with the Expressionist paintings, touching the value of 145.75 with convergence. Coherent observations can be drawn for most of the painting pairs, suggesting the ability of the loss to grasp the presence and the absence of shared style patterns.

Interestingly, the ChatGPT-generated self-portrait exhibits a high loss with Van Gogh's works, with $L_{s t y l e}$ values ranging between 61.73 and 72.79 units. However, the lowest (though still high) value is hit with Versus Medici, suggesting that the best “style-association” for the ChatGPT-generated image is not with its intended Van Gogh's target but rather with Basquiat's style. This indicates that the style metric is effective at distinguishing between artistic styles and is not easily misled.

4.2 Inpainting with style

We have currently come to the inpainting results. We simulate painting damages with digital masks m we have overlaid on the original images. We have set λ = 1 and β = 0.01 in the loss function (Equation 8) for the DIP-ST executions, to achieve the best results heuristically. We compare the results by our method to the images inpainted by the TV-regularized DIP scheme, where λ = 1 in the loss in Equation (5).

In Figure 3, we aim at inpainting two rectangular big areas depicted in Figure 3A, and we compare the TV-DIP technique (Figure 3B) to the DIP-ST one. Specifically, we have exploited as style image y the Starry Night shifted crop and obtained the image in Figure 3C, whereas the Versus Medici image has been used as (incoherent) y and it has provided the inpainted result in Figure 3D.

Figure 3

Figure 3. Inpainting tests on the Starry Night cropped image depicted in Figure 2A. (A) Image with the inpainting mask. (B) Image by DIP. (C) Image by DIP-ST with Figure 2B as style image. (D) Image by DIP-ST with Versus Medici as style image.

If no style constraints are used, although generating elements with context appropriateness and colors similar to the original ones, the DIP algorithm can fill the wide regions with a limited consistency. It does not ensure that the inpainted areas seamlessly blend with the surrounding regions. Similarly, if y image suggests a style different than the one in $\bar{x}$ , semantic incorrectness arises, and out-of-place artifacts appear, disregarding the context appropriateness. Conversely, when a very coherent style prior is passed to the DIP-ST, the result presents good edge continuity and smooth transitions along the edges of the inpainted regions (as particularly evident in the top-left corner of Figure 3C).

With the tests on the Wheatstacks image detailed in Figure 4, we want to assess the reliability of the proposed DIP-ST inpainting on smaller regions, where inpainting is traditionally applied. To do that, we have superimposed onto the Wheatstacks image a mask composed of three capital letters written in a thin font and three circles of increasing size (see Figure 4A). Here, Figure 4B confirms that the DIP approach perfectly integrates the inpainted pixels with the original image contents on the letters. However, we can perceive on the DIP output many inconsistencies, even on the smallest circle. Exploiting the DIP-ST model using a crop without occlusions taken on the same painting, we still achieve solutions with very high visual coherence, inside all the thin and circular regions, as appreciable in Figure 4C. In Figure 4D, we use as style image y the artist's garden painting, i.e., a painting by the same author. The strong similarity between the detected styles (5.13 in Table 1) makes the inpainting appreciable. Only the pixels inside the biggest circle slightly break the harmony of the Impressionist artwork.

Figure 4

Figure 4. Inpainting tests on the Wheatstacks cropped image depicted in Figure 2C. (A) Image with the inpainting mask. (B) Image by DIP. (C) Image by DIP-ST with a non-overlapping crop from the same painting as style image. (D) Image by DIP-ST with Figure 2D as style image.

Finally, we examine how the final DIP-ST results depend on the β parameter, which weights the style loss in the deep image prior minimization (Equation 8). For the Basquiat image, we apply the DIP-ST algorithm to the simulated damaged image of Versus Medici. We then created the inpainted image obtained with β = 0.01. This value of β best restores the original graffiti, avoiding excessive blurring while producing very sharp lines and chromatically coherent results. We then set β = 0.001: in this case, the style component does not enforce sufficient style consistency, resulting in smooth regions that disrupt Basquiat's characteristic style. Conversely, when the parameter is set too high (β = 0.1 and β = 1), the algorithm introduces overly sharp objects that reflect the contents of the unoccluded areas of $\bar{x}$ .

To compare the results quantitatively, we compute the structural similarity index measure (SSIM), the peak signal-to-noise ratio (PSNR), and the learned perceptual image patch similarity (LPIPS) metrics between each solution image $\hat{x} = f_{\hat{Θ}} (z)$ and the corresponding ground-truth ones. The SSIM assesses the perceived similarity of digital images by comparing structural information, such as luminance, contrast, and texture. An SSIM value close to 1 indicates greater similarity between the inpainted image and the ground truth, suggesting that the algorithm successfully maintains visual coherence and image detail within the inpainted region. The PSNR metric quantifies the accuracy of image reconstruction looking at the pixel-level differences between the inpainted image and the ground truth. A higher PSNR implies fewer differences from the ground truth in terms of pixel values. The LPIPS is a perceptual metric that evaluates the difference between two images based on the internal activations of a neural network, giving a better representation of how humans perceive differences in image quality. A lower LPIPS score indicates higher perceptual similarity to the original image.

Specifically, we take into account only the pixels within the inpainted domain D [as stated in Equation (1)], not to skew the results with non-inpainted regions that would likely provide excellent metrics contributions. The resulting values are presented in Table 2. We also provide the metrics for the images generated using the DIP approach, which correspond to the table rows where y is not specified. Overall, the values in the table support the conclusions previously made through visual inspection. The improvements of DIP-ST over DIP are firmly confirmed, as the quality metrics are worse when no style images y are used. In the case of inpainting for the Starry Night artwork, the advantage of using a strictly coherent style is particularly evident, whereas for the Wheatstacks (with small regions to fill-in) also the DIP inpainting has a very high SSIM and the enhancement by DIP-ST is better caught by the LPIPS metric. In case of Versus Medici (last rows), the metrics endorse the variability of the results at different values of the hyperparameter β∈{0.001, 0.01, 0.1, 1}, above all in terms of PSNR and LPIPS.

Table 2

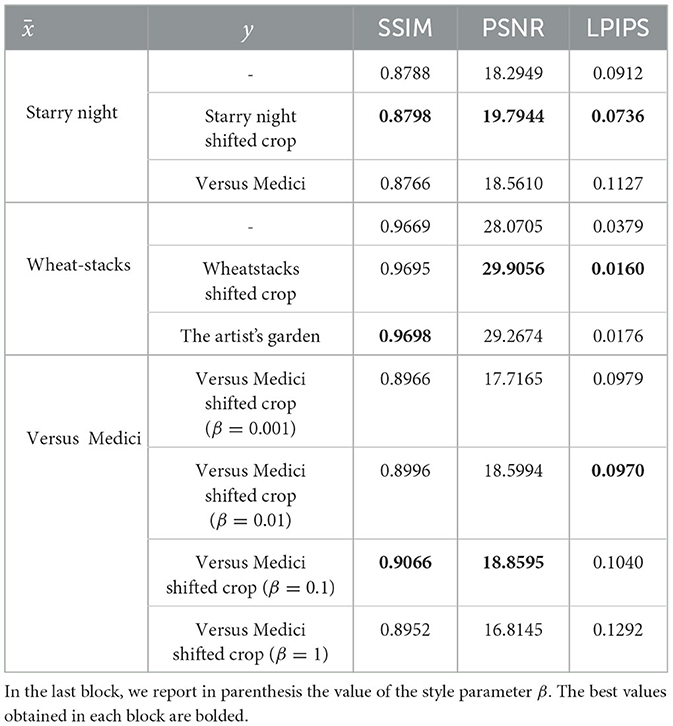
Table 2. SSIM, PSNR, and LPIPS between the ground-truth images and the inpainted reconstructions by the DIP (in cases where y is not present) and the DIP-ST frameworks.

4.3 Inpainting with state-of-the-art approaches

We conclude our experimental analysis by comparing the results achieved with the proposed DIP-ST approach to those computed by state-of-the-art methods for inpainting, for the three considered masked images (depicted in Figures 3A, 4A). The DIP-ST solutions we consider in this comparative phase are those reported in Figures 3C, 4C. Figure 5, instead, shows the inpainted images by two competitors. In particular, we consider as the first competitor a handcrafted variational approach. It solves an imaging problem stated as in Equation (2), with prior R(x) given by the total variation function defined in Equation (3). The minimization problem is solved by running 100 iterations of the popular iterative Chambolle—Pock algorithm, presented in Chambolle and Pock (2011). The results are shown in the first row of Figure 5. The second row of Figure 5 depicts the results by a black-box generative algorithm, freely available online at https://pincel.app.

Figure 5

Figure 5. Inpainting results on the test images depicted in Figures 3A, 4A. (A, B) Images by the Chambolle–Pock iterative algorithm used as an exemplar solver for the class of regularized handcrafted approaches. (C, D) Images by a trained generative neural network, implemented by an online tool.

As visible, the handcrafted regularized method is not effective in creating new content for large regions: the inpainted areas are very smooth, blurry, and not consistent at all with the styles of the artworks. Only the inpainted areas corresponding to the capital letters on Monet's painting are almost indistinguishable from the surrounding original pixels. Indeed, within the class of regularized approaches, the regularizers are generally designed to propagate or replicate information from the existing pixels, making them effective for inpainting only small areas.

Diversely, the results achieved by a generative network are closer to the real images: the painters' brushstrokes have been accurately reproduced and the inpainted regions are well integrated within the images. On this point, these images are quite similar to ours. However, some discontinuities corrupt the swirling movement of the clouds in the Starry Night sky and break the human shapes in Versus Medici somewhere. Interestingly, these distortions were attenuated in the images computed by DIP-ST (Figures 3A). In this regard, it is worth noting that the loss function of a generative network forces data consistency to a set of training images that are very different from each other, whereas our framework forces consistency to the sole $\bar{x}$ image, through the norm in Equation (2). This feature can help the DIP-based approach to inpaint large regions with higher congruence to the unmasked pixels. Additionally, including the TV prior in the DIP-ST loss [as we do in Equation (8)] specifically imposes local consistency among adjacent pixels, and it turns out to be particularly effective for inpainting across the mask edges.

Finally, we remark that the comparison cannot overlook the difference in computational cost, as the training of the generative network is particularly expensive and time-consuming, especially when working with a large dataset of images. Training a generative model on such a scale requires significant computational resources, often involving powerful GPUs and extensive processing time, making it a much more resource-intensive process compared to iterative approaches, such as the ones behind the TV-based handcrafted solver and the DIP-ST algorithm.

5 Conclusion

This paper tackles the image inpainting task, which is particularly challenging when the regions to fill in are sensibly large and the corresponding image contents are lost. In this case, traditional handcrafted techniques tend to fail because they often rely on surrounding pixel information and simple interpolation methods, which are insufficient for reconstructing extensive missing areas with complex textures or patterns. These methods typically result in blurred and visually inconsistent outcomes, unable to restore or even just mimic the original aesthetic or detailed structures. Conversely, data-driven approaches, which have recently become appealing to experts in art restoration for cases with small occlusions, may produce rich but incoherent content for larger regions. This is because neural networks typically learn image patterns from a vast corpus of very dissimilar images.

To address these limitations, in this paper, we enrich the deep image prior inpainting technique by incorporating a style component in its loss function, playing the role of a style constraint for the inpainting process. This requires passing to the algorithm one external image, from which our deep network can extract the style information and characterization. Afterward, assuming that the external and the damaged images share a similar style, the proposed DIP-ST approach generates high-quality inpainted images that preserve both the local textures and global style consistency of the original artwork.

We remark that, although based on a neural network, DIP does not require pre-training on a vast dataset and generates inpainting values by solving an optimization problem directly on the image to be inpainted. Only one style image (possibly characterized by high style consistency to the damaged one) is further required, and it can simply be a crop or a zoom-in on a well-preserved area of the original painting. This ensures high applicability to the proposed DIP-ST framework.

Through extensive experiments (reported in Section 4.2) of inpainting in large regions, we demonstrate the effectiveness of our method in producing visually pleasing and stylistically consistent results. This makes DIP-ST particularly useful for its application in digital humanities, where precise and contextually appropriate restorations are essential.

A limitation of the proposed DIP-ST method lies in its potential difficulty in handling artworks with highly complex or less consistent styles. The performance of the style loss component in capturing and applying the stylistic features depends on the clarity and uniformity of the reference style image. For highly intricate artworks, especially those with non-uniform styles, such as pieces where different sections exhibit contrasting techniques or textures, DIP-ST may struggle to maintain stylistic coherence across the inpainted regions. This limitation could lead to visible discrepancies in areas where the style transfer may not accurately capture the complex nuances of the original artwork.

Another challenge is the computational cost involved when applying the DIP-ST method, particularly for large images. The incorporation of a style loss term, which relies on computing Gram matrices over several layers of a pretrained CNN, increases the computational load compared to a standard DIP framework. Additionally, the iterative nature of DIP optimization combined with style regularization results in longer execution times and higher resource demands, when compared to classical iterative solvers. In practice, this could limit the scalability of the approach when applied to more extensive restoration projects. However, DIP-ST requires way lower computational resources than a generative deep learning approach, whose performance we have demonstrated to be comparable or even worse than ours.

Additionally, this paper includes an initial study (reported in Section 4.1) aimed at exploring how artificial intelligence conceives ‘style', which is intrinsically different from human perception. In art, ‘style', can be defined as the distinctive and recognizable manner or technique that characterizes the works of an individual artist, a specific period, or a particular movement. Furthermore, an artist's style is often identified through a combination of elements involving the artist's technique, materials, and visual and thematic contents, which viewers can observe and recognize when looking at the artwork in person. However, not all of these elements are easily accessible through digital representations; for instance, it can be difficult to perceive the dimensions of a painting or distinguish between canvas paintings and graffiti. This makes the automatic recognition of an artist's style challenging and understanding what is interpreted as 'digital style' by neural techniques even more intriguing for digital humanities. This fascinating dualism of 'style' will drive our future research endeavors.

Data availability statement

The data considered for this study can be found in the Github repository: https://github.com/devangelista2/DIP-Style-dataset.

Author contributions

EM: Conceptualization, Formal analysis, Funding acquisition, Investigation, Project administration, Resources, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. FM: Conceptualization, Methodology, Software, Validation, Writing – review & editing. DE: Data curation, Formal analysis, Software, Validation, Writing – review & editing. PC: Conceptualization, Formal analysis, Funding acquisition, Investigation, Project administration, Resources, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adhikary, A., Bhandari, N., Markou, E., and Sachan, S. (2021). “Artgan: artwork restoration using generative adversarial networks,” in 2021 13th International Conference on Advanced Computational Intelligence (ICACI) (Wanzhou: IEEE), 199–206.