DMPNet: dual-path and multi-scale pansharpening network

Introduction: Pansharpening is an important remote sensing task that aims to produce high-resolution multispectral (MS) images by combining low-resolution MS images with high-resolution panchromatic (PAN) images. Although deep learning-based pansharpening has shown impressive results, the majority of these models frequently struggle to balance spatial and spectral information, resulting in artifacts and a loss of detail in pansharpened images. Furthermore, these models may fail to properly integrate spatial and spectral information, leading to poor performance in complex scenarios. Additionally, these models face challenges such as gradient vanishing and overfitting.

Methods: This paper proposes a dual-path and multi-scale pansharpening network (DMPNet). It consists of three modules: the feature extraction module (FEM), the multi-scale adaptive attention fusion module (MSAAF), and the image reconstruction module (IRM). The FEM is designed with two paths, namely the primary and secondary paths. The primary path captures global spatial and spectral information using dilated convolutions, while the secondary path focuses on fine-grained details using shallow convolutions and attention-guided feature extraction. The MSAAF module adaptively combines spatial and spectral data across different scales, employing a self-calibrated attention (SCA) mechanism for dynamic weighting of local and global contexts and a spectral alignment network (SAN) to ensure spectral consistency. Finally, to achieve optimal spatial and spectral reconstruction, the IRM decomposes the fused features into low- and high-frequency components using discrete wavelet transform (DWT).

Results: The proposed DMPNet outperforms competitive models in terms of ERGAS, SCC (WR), SCC (NR), PSNR, Q, QNR, and JQM by approximately 1.24%, 1.18%, 1.37%, 1.42%, 1.26%, 1.31%, and 1.23%, respectively.

Discussion: Extensive experimental results and evaluations reveal that the DMPNet is more efficient and robust than competing pansharpening models.

1 Introduction

In pansharpening, the task involves fusing a low-resolution multispectral (MS) image with a high-resolution, texture-rich panchromatic (PAN) image. This process aims to produce a high-resolution multispectral image that combines the spectral fidelity of the original MS data with the spatial clarity of the PAN image (Zhang et al., 2023; Zhou et al., 2024; Shen et al., 2024). This technique is vital in applications such as land-use mapping, environmental monitoring, and urban planning (Chang et al., 2016; Hong et al., 2023). Despite its significance, achieving an optimal balance between spatial and spectral fidelity remains a challenging problem (Zhou et al., 2024; Li C. et al., 2024).

Traditional pansharpening techniques include methods like Brovey transform (Khan et al., 2019), principal component analysis (PCA) (Ghadjati et al., 2019), intensity-hue-saturation (IHS) fusion (Leung et al., 2013), and wavelet transform (Saxena and Balasubramanian, 2021). These methods rely on mathematical and statistical transformations to fuse PAN and MS images. Although these methods are computationally efficient and easy to implement, but these methods mostly struggle with a trade-off between spatial and spectral quality. These methods can introduce spectral distortions and artifacts, thus, compromise the fidelity of the original multispectral data. Additionally, these approaches lack adaptability to varying image contexts and typically require manual tuning of parameters. Therefore, these methods are less robust for diverse datasets (Yilmaz et al., 2022).

Compressive sensing approaches exploit the sparsity of the multispectral data to achieve better pansharpening results (Ghahremani and Ghassemian, 2015). While promising for sparse data, these methods mostly face challenges in handling the high dimensionality and computational complexity of real-world datasets (Amro et al., 2011). However, these methods are limited by their reliance on fixed models and assumptions. Thus, these methods are less adaptable to the complex relationships between PAN and MS images across diverse sensors and conditions.

Recently, machine learning and deep learning have significantly advanced pansharpening techniques by using data-driven models to learn complex spatial and spectral relationships from large datasets (Yang et al., 2022; Zhou et al., 2022b, 2023a; Jia et al., 2024). Convolutional neural networks (CNNs) (He et al., 2019), generative adversarial networks (GANs) (Gastineau et al., 2021), and transformer-based models (Su et al., 2022; Li et al., 2023) have been widely employed to achieve superior fusion quality. These methods excel in preserving both spatial and spectral fidelity. Thus, these models outperform traditional techniques in various benchmarks. However, their limitations include the need for extensive training datasets, high computational resources, gradient vanishing, and potential susceptibility to overfitting. Therefore, this paper proposes an efficient dual-path and multi-scale pansharpening network (DMPNet) for pansharpening to address these limitations.

The main contributions of the paper are summarized as follows:

(1) This paper introduces an efficient DMPNet for pansharpening. DMPNet is designed to address the challenges of balancing spatial and spectral fidelity while ensuring robust performance in complex scenarios. The proposed DMPNet comprises three major modules such as the feature extraction module (FEM), the multi-scale adaptive attention fusion module (MSAAF), and the image reconstruction module (IRM).

(2) The FEM in DMPNet adopts a dual-path architecture. The primary path captures global spatial and spectral features using dilated convolutions. While the secondary path focuses on extracting fine-grained details such as textures and edges through shallow convolutions and attention-guided feature refinement.

(3) The MSAAF is designed to integrate spatial and spectral features effectively across multiple scales. It employs a self-calibrated attention (SCA) mechanism for dynamic weighting of local and global contexts and a spectral alignment network (SAN) to maintain spectral consistency and fidelity.

(4) The IRM utilizes the discrete wavelet transform (DWT) to separate fused features into low- and high-frequency components. These components are refined individually, which enable optimal spatial and spectral reconstruction.

The remaining paper is organized as follows: Section 2 presents the related work. Section 3 introduces the workings of DMPNet. Section 4 provides the performance analysis. Finally, Section 5 concludes the paper.

2 Related work

In the field of pansharpening, recent studies have proposed efficient models to address the challenges and limitations in achieving high-quality pansharpened images. Yang et al. (2022) proposed a cross-scale collaboration network that used a pyramid framework and cross-scale attention modules for gradual pansharpening. The network included progressive subnetworks that handled specific pyramid levels and cross-scale attention modules to capture global and local spatial interactions. A fusion module further enhanced the spectral representations and enabled the network to fully utilize spatial and spectral information from cross-scale perspectives. Zhou et al. (2022b) introduced the spatial-frequency information integration network (SFIIN) that used both spatial and frequency domain features. SFIIN employed a dual-branch architecture, where one branch captured local spatial information using standard convolution, and the other extracted global contextual information via Fourier transformation. A dual-domain interaction module facilitated the flow of complementary information to achieve significant pansharpened images.

Liu et al. (2022) presented a multilevel and multiscale fusion network (MLMSFN) to achieve super-resolution pansharpening. It integrated spatial and spectral information from PAN and MS images while pushing beyond existing resolution limits. This architecture captured hierarchical and multiscale features that enabled the generation of pansharpened images. Zhou et al. (2022a) proposed a normalization-based feature selection and restitution mechanism to address the issue of inconsistent feature propagation between PAN and MS modalities. It used an adaptive instance normalization operation to modulate PAN features to match the MS style while restoring effective information from discarded features through contrastive learning. Hou et al. (2022) implemented a multi-level feature fusion network (MLFNet) using cross-layer guided attention mechanisms for hyperspectral pansharpening. Jin et al. (2022) proposed a Laplacian pyramid network (LPNet) for multispectral pansharpening, leveraging the hierarchical features extracted from the PAN and MS. Li et al. (2022) proposed HyperNet to enhance the spatial resolution of hyperspectral images by fusing them with multispectral and panchromatic images. Spectral information was preserved while spatial details were injected using specially designed blocks.

Zhang F. et al. (2022) developed the multiscale spatial-spectral interaction transformer (MSIT) to concurrently model local and global dependencies in PAN and MS images. The network employed convolution-transformer encoders for multiscale feature extraction and a spatial-spectral interaction attention module to efficiently merge spatial and spectral features. Shi et al. (2023) proposed a domain-specific knowledge-driven framework that used frequency-domain information and a detail-mapping GAN to enhance spatial and spectral performance. The method effectively combined domain-specific knowledge with data-driven learning to provide superior feature reconstruction and detail injection. Zhou et al. (2023b) introduced a modality-aware feature integration network to explore mutual dependencies between PAN and MS images. It employed cross-central difference convolution for PAN texture extraction and a hierarchical transformer for integrating spatial-temporal relationships. This method effectively captured cross-modality information across multiple datasets.

Zhou et al. (2023a) proposed a closed-loop regularization framework for pansharpening by utilizing an invertible neural network (INN) for bidirectional learning. This method simultaneously learned the forward operation for pansharpening and the backward degradation process to regularize the solution space. To enhance high-frequency textures critical for pansharpened images, a multiscale high-frequency enhancement module was incorporated. Liu et al. (2024) introduced a spatially-adaptive spectral modulation network (SSMNet) that emphasized band-private characteristics for accurate restoration of individual spectral bands. SSMNet featured three modules such as source-aware spectral modulator, cross-band information aggregation, and cross-stage feature integration to integrate features across stages. Additionally, a histogram loss was introduced to constrain the band-wise distribution of the final pansharpened image. Jia et al. (2024) developed a progressive attention-based pan-sharpening (PAPS) network. In PAPS, the detail enhancement module produced a high-quality base by enhancing low-resolution MS images. The progressive fusion module in PAPS extracted complementary information from the enhanced MS and PAN images.

Wang et al. (2024b) proposed a novel framework called intrinsic decomposition knowledge distillation that decomposed the MS image into reflectance and illumination components. The teacher network extracted these components from HR-MS images. The student network combined the reflectance component with the enhanced illumination from LR-MS images to obtain the pansharpened images. Li Z. et al. (2024) introduced the pyramid hierarchical network (PH-Net) for multispectral pansharpening. This U-Net-based architecture constructed an input pyramid to achieve multi-level receptive fields and extracted hierarchical features through the encoder and decoder. PH-Net required minimal training data and boasted high generalizability. Wang et al. (2024a) utilized a deep error removal network (DERN) to address errors caused by non-overlapping spectral responses. This model combined a prior-based approach to extract initial error maps and iteratively optimized the PAN and MS features to reduce errors and restore lost textures.

However, the aforementioned models often struggle to balance spatial and spectral fidelity, resulting in artifacts and a loss of detail in pansharpened images. Additionally, they may fail to effectively integrate spatial and spectral information, leading to suboptimal performance in complex scenarios. These models also face challenges such as gradient vanishing, susceptibility to overfitting, and limited generalizability across diverse datasets, further hindering their robustness and adaptability.

3 Dual-path and multi-scale pansharpening network

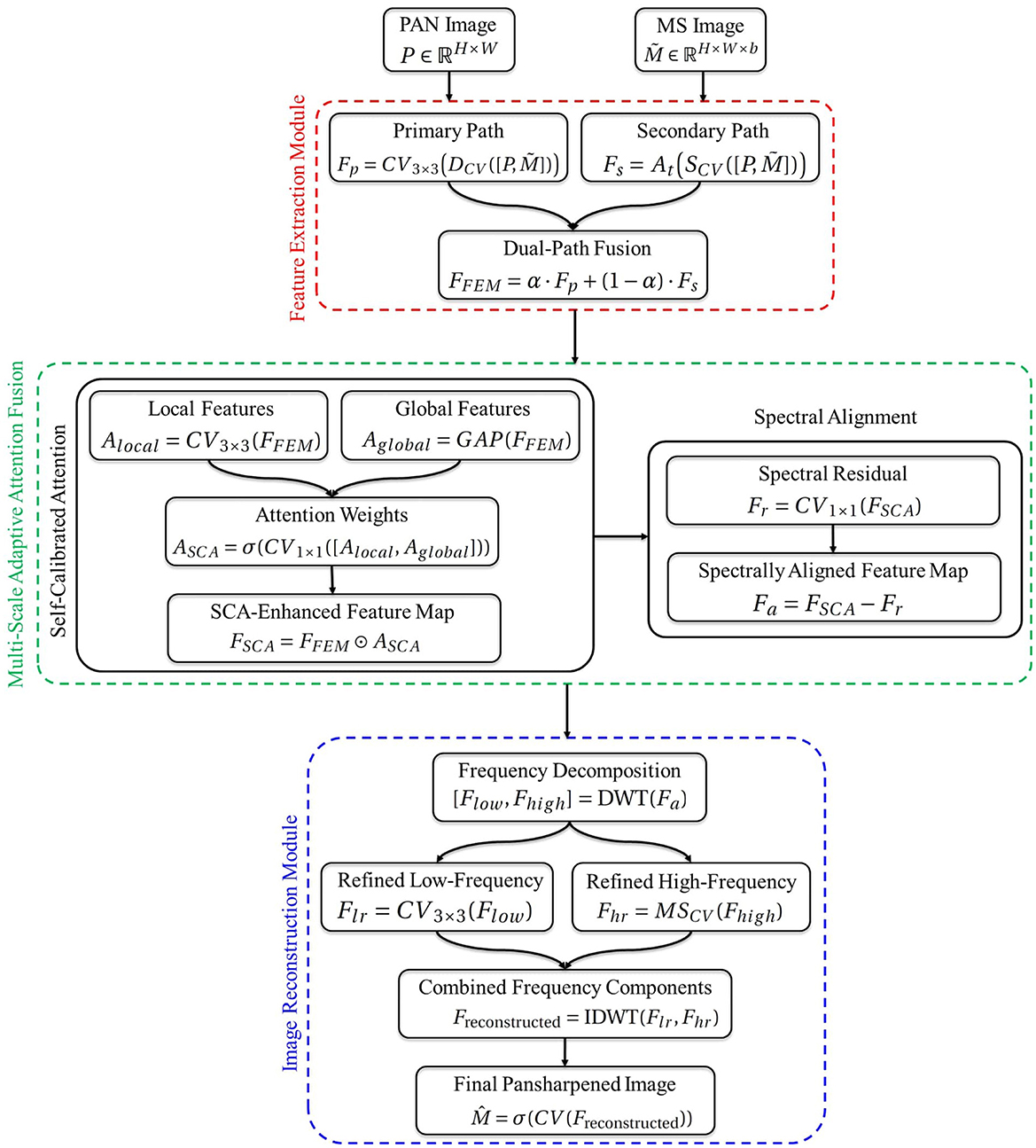
The DMPNet is designed to address the key challenges in pansharpening such as retaining spectral fidelity, enhancing spatial resolution, preserving texture and edges, and ensuring robustness to noise and sensor variability. Figure 1 shows the overall architecture of DMPNet. It comprises three main modules such as FEM, MSAAF, and IIRM. First, FEM extracts spatial and spectral features from input PAN and MS images through a dual-path design. Then, MSAAF merges spatial and spectral features adaptively across scales using self-calibrated attention and spectral alignment mechanisms. Finally, IRM refines and reconstructs the pansharpened image by handling low- and high-frequency components separately for optimal enhancement. These modules are further discussed in the subsequent sections.

Figure 1

Figure 1. Diagrammatic flow of DMPNet.

3.1 Feature extraction module (FEM)

FEM is designed to extract spatial and spectral features separately while ensuring both global context and fine-grained details are captured effectively. It employs a dual-path learning architecture, consisting of a primary path for global feature extraction and a secondary path for localized detail enhancement.

3.1.1 Primary path

It focuses on extracting global spatial and spectral features using deeper convolutional layers. It uses dilated convolutions (Wang et al., 2019) to expand the receptive field without increasing computational overhead.

Given the PAN image P∈ℝ^H×W and the upsampled MS image $\tilde{M}\in {ℝ}^{H\times W\times b}$, the feature extraction process in the primary path is defined as:

$\begin{array}{ll}{F}_p=C{V}_{3\times 3}(D_{CV}([P,\tilde{M}]))& (1)\end{array}$

where $\left[P,\tilde{M}\right]$ represents the concatenation of the PAN and MS images along the channel dimension. F_p represents the primary feature map. D_CV and CV_{3 × 3} represent dilated convolution and 2D convolution operations with a kernel size of 3 × 3, respectively.

3.1.2 Secondary path

It captures fine-grained spatial and spectral details using shallow convolutional layers (Lei et al., 2020) and attention-guided feature extraction (Zhang G. et al., 2022). This path ensures localized features, such as texture and edge information, are preserved. It is defined as:

$\begin{array}{ll}{F}_s=A_t(S_{CV}([P,\tilde{M}]))& (2)\end{array}$

where F_s represents the seconadry feature map. S_CV is the shallow convolutional network that processes $\left[P,\tilde{M}\right]$. A_t is the attention mechanism applied to the output of S_CV.

3.1.3 Dual-path fusion

The outputs of the two paths, i.e., F_p and F_s are dynamically fused using a learnable weighting mechanism as:

$\begin{array}{ll}{F}_{FEM}=\alpha ·F_p+(1-\alpha )·F_s& (3)\end{array}$

where α∈[0, 1] is a trainable parameter that balances the contribution of global and local features.

3.2 Multi-scale adaptive attention fusion (MSAAF)

This module combines spatial and spectral features adaptively across multiple scales using attention mechanisms. For this, it employs two techniques such as self-calibrated attention (SCA) and spectral alignment network (SAN). Inspired from Hu et al. (2018) and Liu et al. (2023), SCA is used to enhance feature fusion by dynamically weighting local and global contexts. Inspired from Xiao et al. (2023), and Nassar et al. (2018), SAN is used to ensure spectral consistency by explicitly aligning the spectral properties of the fused features.

3.2.1 Self-calibrated attention (SCA)

The SCA mechanism generates attention weights using both local and global context to ensure features are appropriately weighted (Hu et al., 2018; Liu et al., 2023). Local features (A_local) are extracted from F_FEM using 3 × 3 convolution operation as:

$\begin{array}{ll}{A}_{local}={CV}_{3\times 3}(F_{FEM})& (4)\end{array}$

Global features (A_global) are extracted from F_FEM using a global average pooling (GAP) as:

$\begin{array}{ll}{A}_{global}=GAP(F_{FEM})& (5)\end{array}$

Next, A_local and A_global features are concatenated and passed through a 1 × 1 convolution followed by a sigmoid activation (σ) as:

$\begin{array}{ll}{A}_{SCA}=\sigma ({CV}_{1\times 1}(\left[A_{local},A_{global}\right]))& (6)\end{array}$

where A_SCA represents attention weights that modulate the relative importance of A_local and A_global.

Finally, A_SCA are applied element-wise to F_FEM as:

$\begin{array}{ll}{F}_{SCA}=F_{FEM}\odot A_{SCA}& (7)\end{array}$

where F_SCA emphasizes significant details while suppressing irrelevant and redundant information.

3.2.2 Spectral alignment network (SAN)

It ensures spectral consistency by aligning the spectral characteristics of the fused features with the original MS image (Xiao et al., 2023; Nassar et al., 2018).

Initially, a 1 × 1 convolution is applied to F_SCA (Equation 7) to predict the spectral residual (F_r) as:

$\begin{array}{ll}{F}_r={CV}_{1\times 1}(F_{SCA})& (8)\end{array}$

where F_r represents the difference between the current spectral properties of F_SCA and the desired spectral alignment.

Thereafter, F_r is subtracted from F_SCA to align the spectral properties of fused features with the input MS image as:

$\begin{array}{ll}{F}_a=F_{SCA}-F_r& (9)\end{array}$

where F_a represents the spectrally aligned feature map.

3.3 Image reconstruction module (IRM)

IRM is the final module of DMPNet. It processes fused features by decomposing them into frequency components, refining each component individually, and then recombining them to obtain the final pansharpened image.

3.3.1 Frequency decomposition

F_a is decomposed into low- and high-frequency components using discrete wavelet transform (DWT) as Alessio and Alessio (2016):

$\begin{array}{ll}\left[F_{low},F_{high}\right]=\text{DWT}(F_a)& (10)\end{array}$

where F_low and F_high represent low- and high-frequency components, respectively.

3.3.2 Refinement networks

The low- and high-frequency components preserve spectral fidelity through smooth low-frequency processing and amplifying spatial details via targeted high-frequency refinement. Therefore, F_low and F_high are refined individually using shallow CNN and multi-scale convolutional networks.

F_low is refined using a shallow CNN (Gao et al., 2018) to smooth low-frequency components as:

$\begin{array}{ll}{F}_{lr}={CV}_{3\times 3}(F_{low})& (11)\end{array}$

F_high is refined using a multi-scale convolutional network (MS_CV) (Huang et al., 2022) to enhance textures and edges. It can be defined as:

$\begin{array}{ll}{F}_{hr}=M{S}_{CV}(F_{high})& (12)\end{array}$

3.3.3 Reconstruction

The refined components F_lr and F_hr are recombined using inverse DWT (IDWT). It is defined as:

$\begin{array}{ll}{F}_{\text{reconstructed}}=\text{IDWT}(F_{lr},F_{hr})& (13)\end{array}$

F_{reconstructed} is further refined using a convolutional layer with residual connections as:

$\begin{array}{ll}\widehat{M}=\sigma (CV(F_{\text{reconstructed}}))& (14)\end{array}$

where $\widehat{M}$ represents the final pansharpened image. σ is the sigmoid activation function.

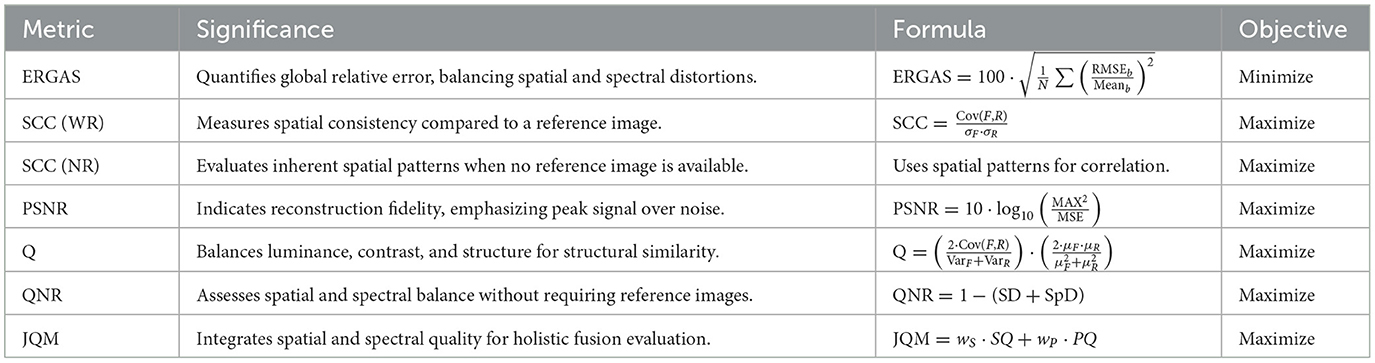
3.4 Performance metrics

Table 1 summarizes the performance metrics used for evaluating the proposed and competitive pansharpening models. These metrics include the spatial correlation coefficient (SCC) (Zhou et al., 1998), erreur relative globale adimensionnelle de synthèse (ERGAS) (Wald, 2002), Q-index (Wang and Bovik, 2002), and peak signal-to-noise ratio (PSNR). These metrics are employed during lower-scale validations to compare pansharpened outputs with reference images. For full-scale validations, SCC is again utilized, alongside the quality-with-no-reference (QNR) metric (Alparone et al., 2008) and the joint quality measure (JQM) (Palubinskas, 2015). These metrics provide insights into spatial correlation, spectral accuracy, and overall image quality. Note that SCC is referred to as SCC (WR) and SCC (NR), representing “With Reference” and “No Reference”, respectively.

Table 1

Table 1. Performance metrics used for evaluating proposed and competitive pansharpening models.

In the Table 1, N represents the number of bands, RMSE_b denotes the Root Mean Square Error of band b, and Mean_b refers to the band mean. F indicates the fused image, R corresponds to the reference image, and σ stands for the standard deviation. Similarly, MAX represents the maximum pixel intensity and MSE indicates the Mean Squared Error. For spatial and spectral distortions, SD and SpD measure spatial distortion and spectral distortion, respectively. The weights for spatial and spectral quality are denoted by w_S and w_P, with SQ and PQ representing spatial quality and perceived quality. Additionally, μ represents the mean, Var indicates the variance, and Cov is used for covariance.

3.5 Weighted loss function

In this paper, various loss functions are utilized to perform sensitivity analysis and determine the optimal combination for the final weighted loss function. These loss functions are as follows:

3.5.1 Loss functions

• Reconstruction loss (L_r): this loss measures the difference between original MS and pansharpened image. It ensures that the pansharpened image accurately retains the features of the original data (Jian et al., 2023). It can be computed as:

$L_r=\left|\right|M-\widehat{M}|{|}_1$

where M is the original MS image. $\widehat{M}$ is the obtained pansharpened image.

• Spectral consistency loss (L_s): this loss evaluates the consistency of the spectral properties between low-resolution MS image and the downsampled obtained pansharpened image (Doi and Iwasaki, 2019; Ciotola et al., 2023). It ensures spectral fidelity during reconstruction as:

$L_s=\left|\right|M_{\text{low-res}}-D_S(\widehat{M})|{|}_2$

where M_low-res is the low-resolution MS image. $D_S(\widehat{M})$ is the downsampled obtained pansharpened image.

• Gradient loss (L_g): this loss focuses on preserving spatial details by comparing the gradients of PAN image and the gradients of obtained pansharpened image Gao et al. (2024). It is defined as:

$L_g=\left|\right|{\nabla }_{H}M-{\nabla }_H\widehat{M}|{|}_2^2+||{\nabla }_{V}M-{\nabla }_V\widehat{M}|{|}_2^2$

where ∇_H and ∇_V represent horizontal and vertical gradients, respectively.

• Perceptual loss (L_p): this loss measures the similarity between obtained pansharpened image and reference image. This ensures perceptual consistency (see Zhou et al. (2020) for more details).

3.5.2 Sensitivity analysis

Sensitivity analysis was performed to evaluate the impact of each loss function and their combinations on the performance metrics. Figures 2, 3 provide detailed analysis of the behavior of DMPNet across different loss functions and their combinations during lower-scale and full-scale validations, respectively. For lower-scale sensitivity analysis, the focus is on metrics such as ERGAS, SCC (WR), PSNR, and Q (see Figure 2). Each loss function's contribution to spatial and spectral accuracy is analyzed to identify significant synergies among combinations. In full-scale sensitivity analysis, metrics such as SCC (NR), QNR, and JQM are used to understand the behavior of loss functions in preserving spatial details and overall image quality without reference images (see Figure 3).

Figure 2

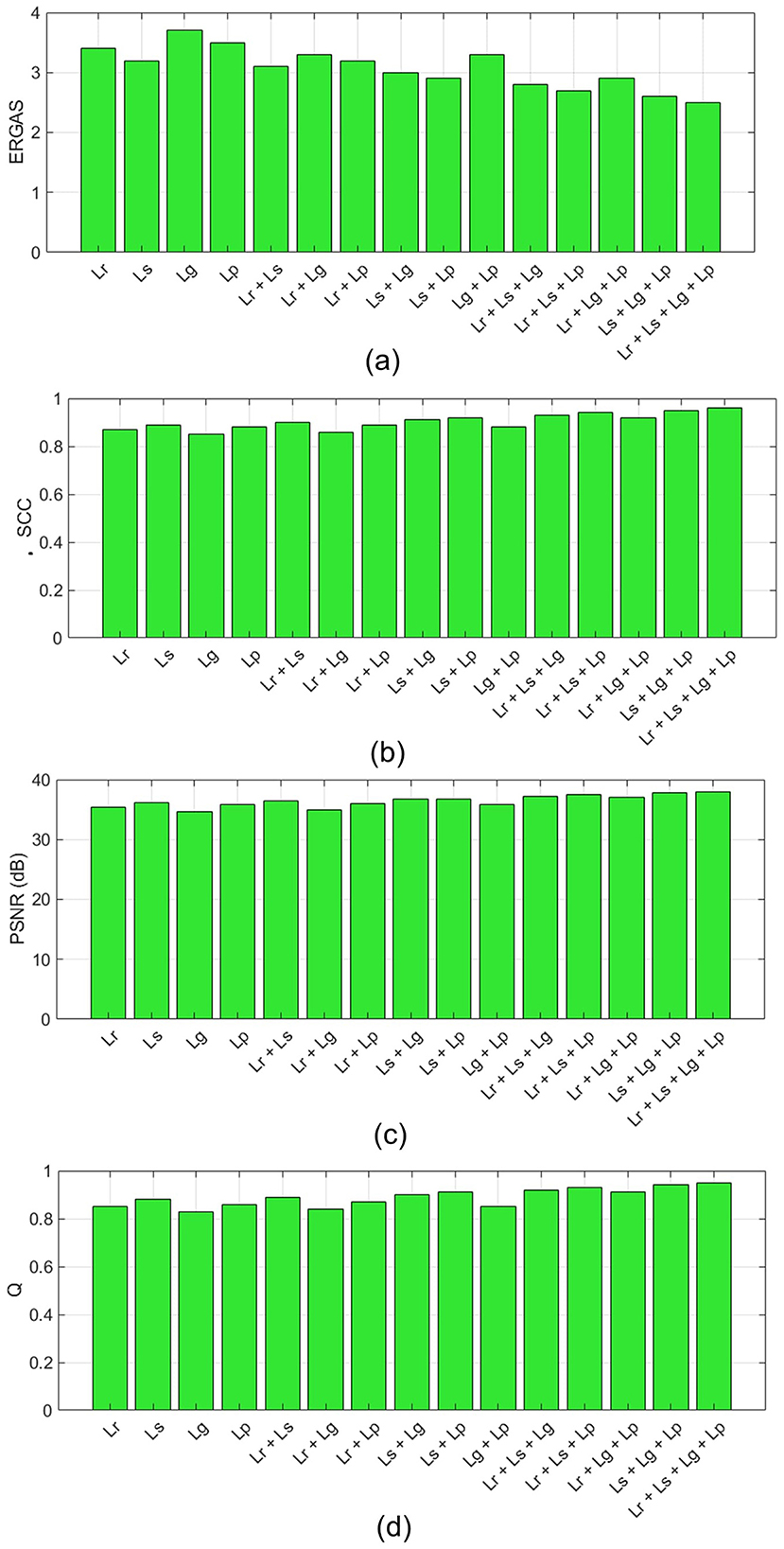
Figure 2. Sensitivity analysis for DMPNet during lower-scale validations: (A) ERGAS, (B) SCC (WR), (C) PSNR, and (D) Q.

Figure 3

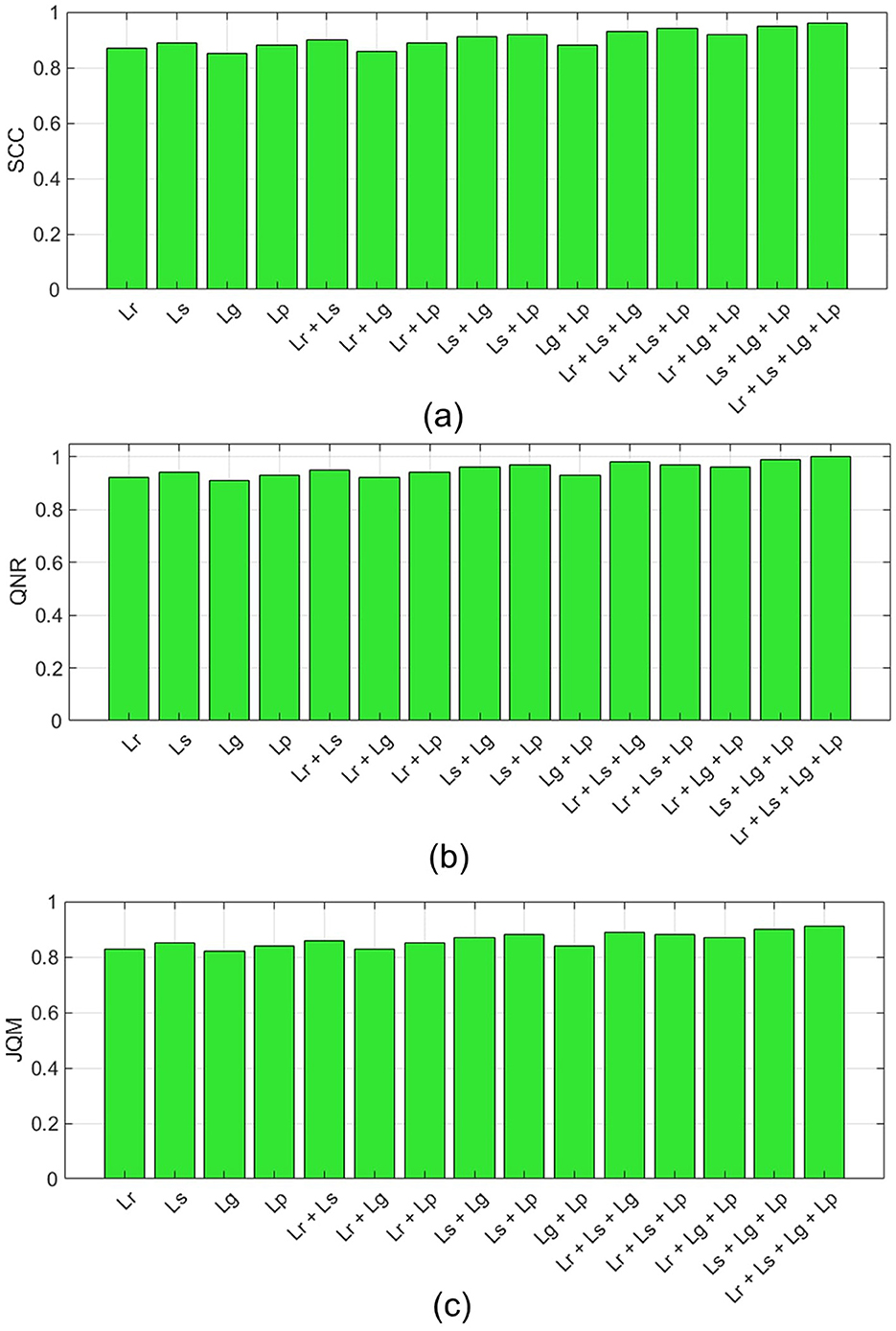
Figure 3. Sensitivity analysis for DMPNet during full-scale validations: (A) SCC (NR), (B) QNR, and (C) JQM.

Based on these sensitivity analysis, the final weighted loss function was selected to balance spatial and spectral fidelity while maintaining perceptual quality. The weighted loss function combines all loss functions as:

$L_{\text{final}}=\alpha L_r+\beta L_s+\gamma L_g+\delta L_p$

where α, β, γ, and δ are the weights assigned to each loss component. These weights are as 0.4, 0.2, 0.2, and 0.2, respectively.

4 Performance analysis

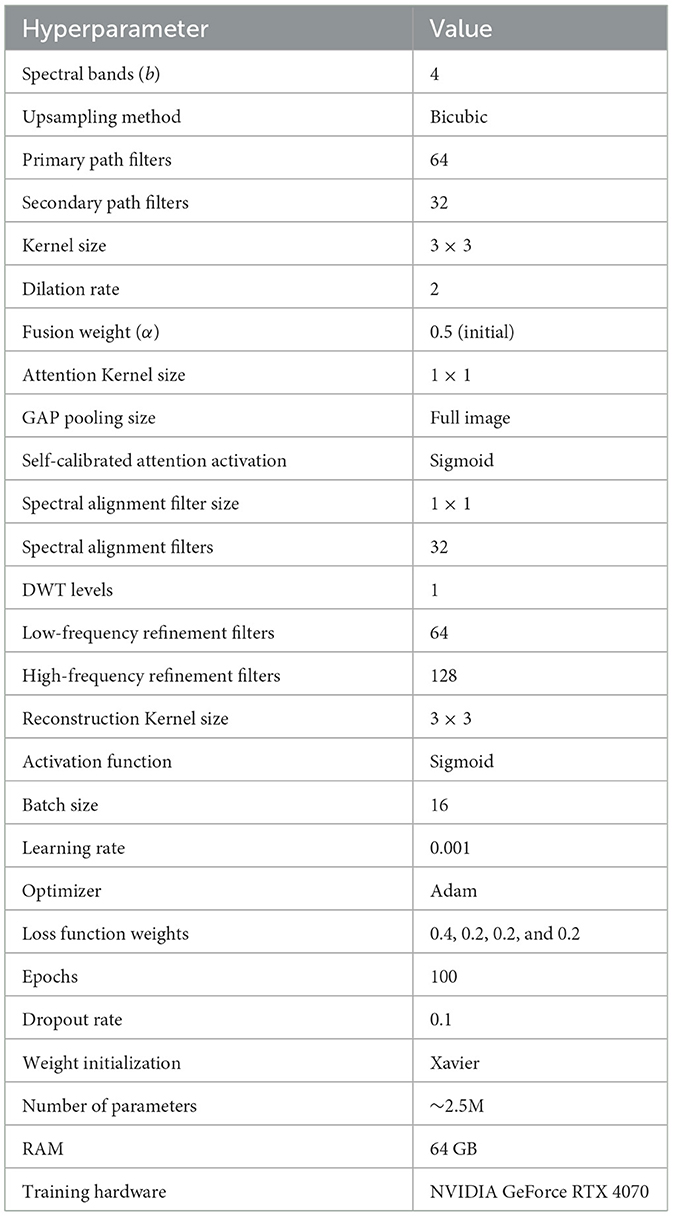
The proposed and competitive models are implemented using MATLAB 2024a software. Table 2 presents the hyperparameter settings for DMPNet. The pansharpening datasets utilized in this study comprise images captured by various satellite sensors, including WorldView-2, WorldView-3, QuickBird, and Gaofen-2. These datasets contain paired MS and PAN images along with high resolution reference images (see Deng et al., 2022 for dataset details). For comparative analysis, several competitive pansharpening models are considered, such as MSIT, INN, PAPS, MLFNet, LPNet, HybridNet, SSMNet, and PH-Net. Each model was trained using the parameter configurations detailed in their respective publications.

Table 2

Table 2. Hyperparameters of DMPNet with default values.

4.1 Visual analysis

Figures 4, 5 provide a comprehensive visual analysis of pansharpening performance on WorldView-3 and Quickbird datasets, respectively. Both figures show input PAN and MSI images (Figures 4A, B, 5A, B), alongside the corresponding ground truth images (Figures 4C, 5C). Pan-sharpened images generated by competitive models and the proposed DMPNet are presented in Figures 4D–K, 5D–K, respectively. The proposed DMPNet (see Figures 4L, 5L) achieved superior performance compared to other models. It achieved a balanced enhancement of spatial and spectral information while effectively preserving fine details. Thus, DMPNet producing the most visually appealing results across both datasets.

Figure 4

Figure 4. Visual analysis of WorldView-3 data: (A) PAN, (B) MS, (C) Ground truth, (D) MSIT, (E) INN, (F) PAPS, (G) MLFNet, (H) LPNet, (I) HybridNet, (J) SSMNet, (K) PH-Net, and (L) DMPNet.

Figure 5

Figure 5. Visual analysis of Quickbird data: (A) PAN, (B) MS, (C) Ground truth, (D) MSIT, (E) INN, (F) PAPS, (G) MLFNet, (H) LPNet, (I) HybridNet, (J) SSMNet, (K) PH-Net, and (L) DMPNet.

Since it is difficult to assess the outperforming performance through visual analysis of the competitive models and the proposed DMPNet (see Figures 4, 5), we have also evaluated the squared error between the ground truth and the obtained pansharpened images (see Figures 6, 7). This evaluation clearly shows that the proposed DMPNet achieves a lower squared error compared to competitive pansharpening models. This underscores the superiority of DMPNet in producing high-quality pansharpened outputs with enhanced fidelity and precision.

Figure 6

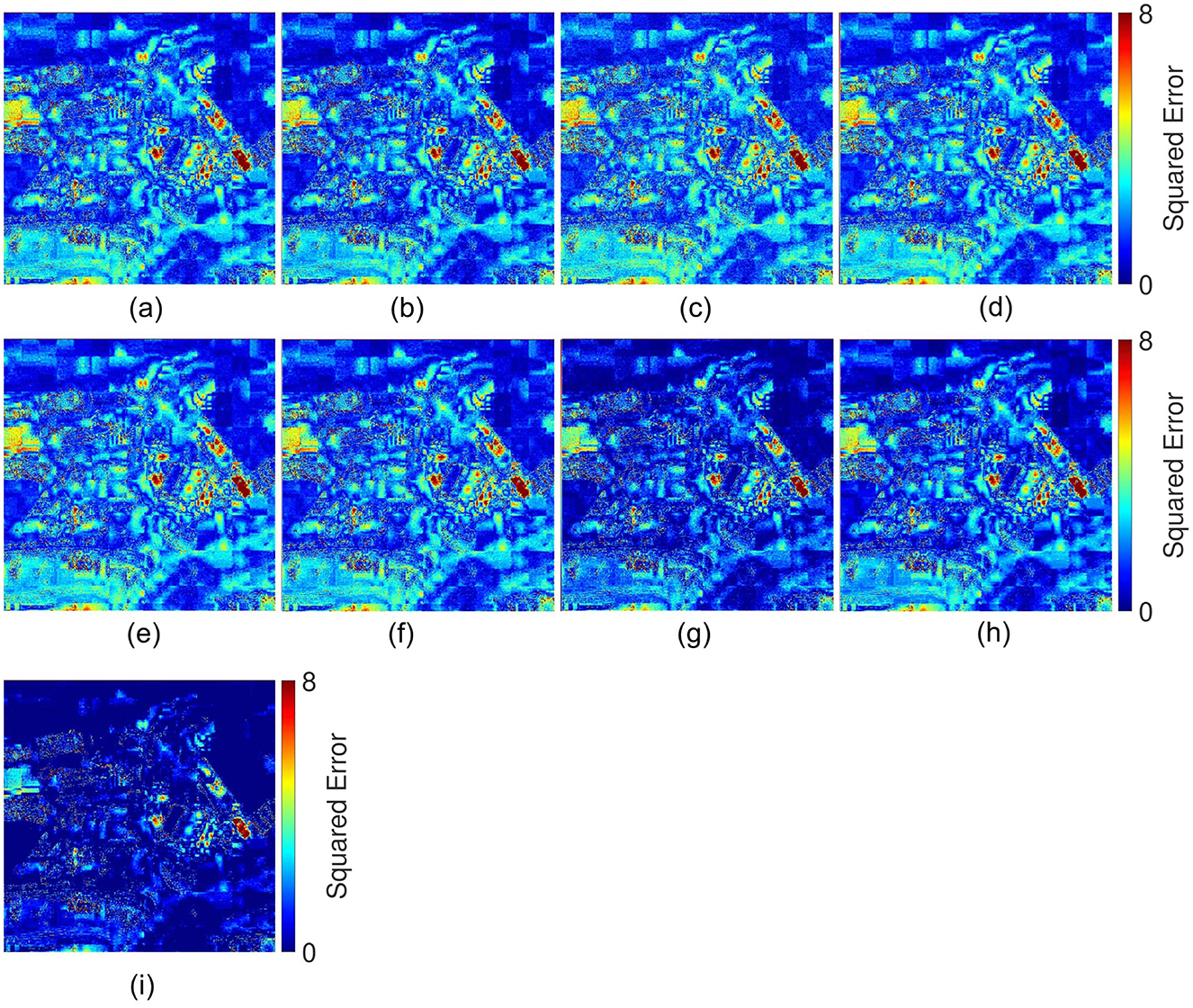
Figure 6. Error analysis of WorldView-3 data: (A) MSIT, (B) INN, (C) PAPS, (D) MLFNet, (E) LPNet, (F) HybridNet, (G) SSMNet, (H) PH-Net, and (I) DMPNet.

Figure 7

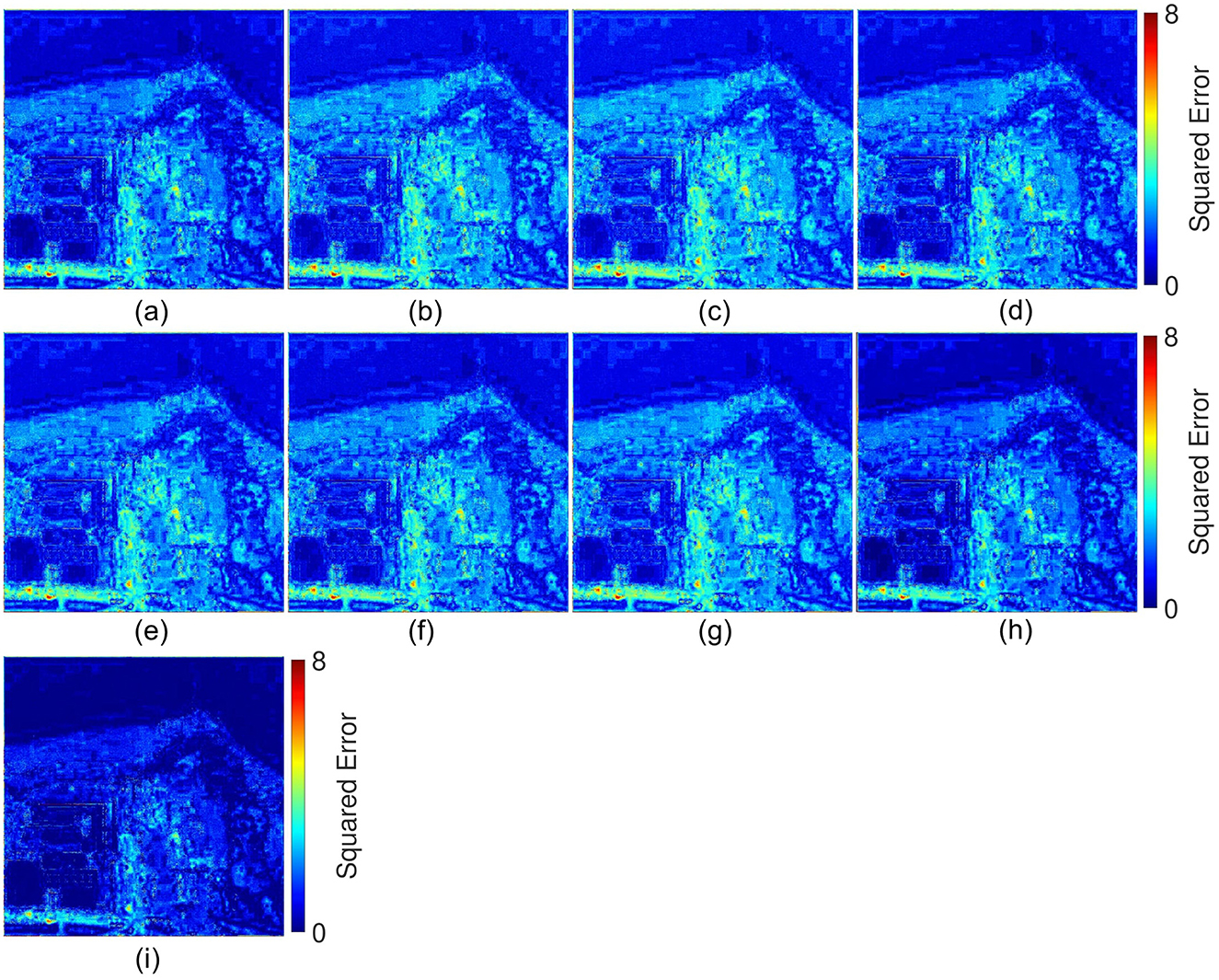
Figure 7. Error analysis of Quickbird data: (A) MSIT, (B) INN, (C) PAPS, (D) MLFNet, (E) LPNet, (F) HybridNet, (G) SSMNet, (H) PH-Net, and (I) DMPNet.

4.2 Quantitative analysis

Figure 8 illustrates the lower-scale performance analysis of competitive pansharpening methods and the proposed DMPNet. Figure 8A demonstrates the improvement in spectral fidelity through ERGAS, where DMPNet outperforms competitive models by approximately 1.24%. Figure 8B focuses on SCC (WR), showing an enhancement of 1.18%, indicating better spatial consistency. Figures 8C, D further evaluate the PSNR and Q metrics. DMPNet achieves an improvement of 1.42% in PSNR and 1.26% in Q. These results emphasize the DMPNet's ability to enhance structural similarity effectively.

Figure 8

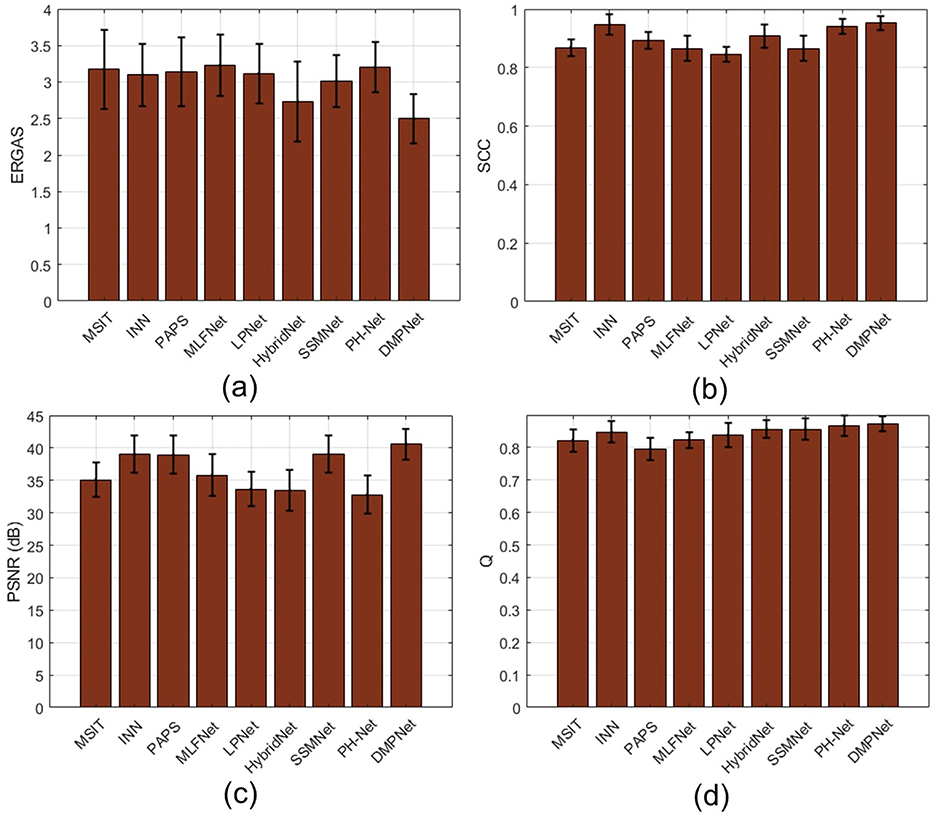
Figure 8. Lower-scale performance analysis of different pansharpening methods: (A) ERGAS, (B) SCC (WR), (C) PSNR, and (D) Q.

The full-scale performance analysis, depicted in Figure 9, reinforces the superiority of DMPNet. Figure 9A highlights a 1.37% improvement in SCC (NR), reflecting better spatial pattern preservation without reference data. Figure 9B shows a 1.31% enhancement in QNR, indicating balanced spatial and spectral fidelity. Finally, Figure 9C demonstrates a 1.23% improvement in JQM, emphasizing the overall joint quality of pansharpened images.

Figure 9

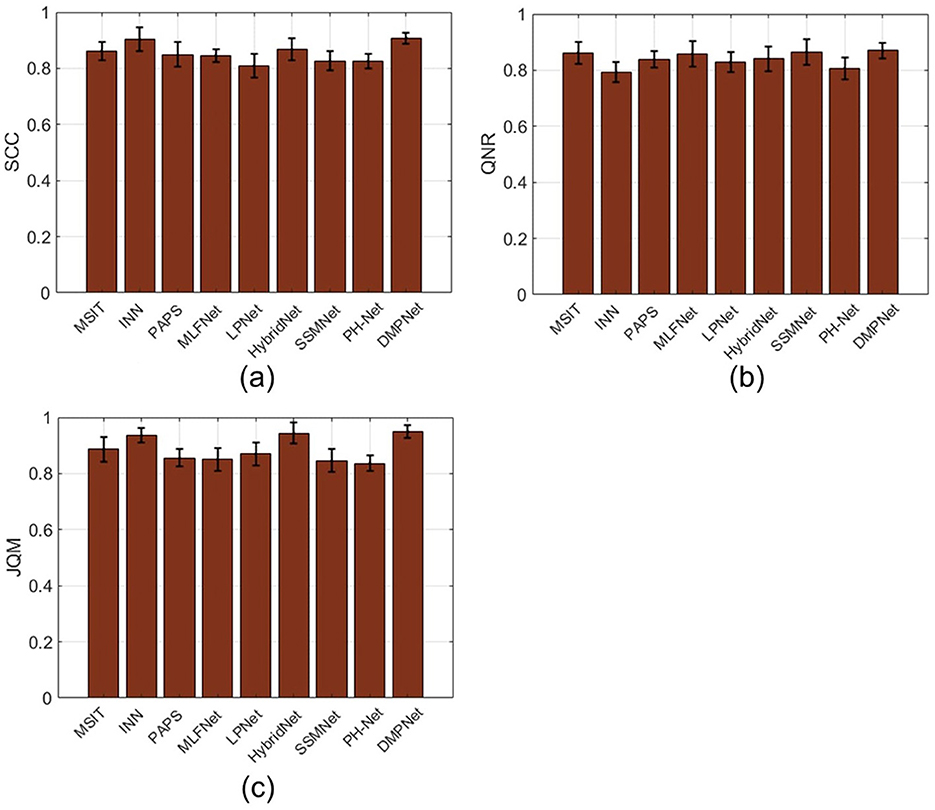
Figure 9. Full-scale performance analysis of different pan-sharpening methods: (A) SCC (NR), (B) QNR, and (C) JQM.

Figures 8, 9 collectively validate the robustness and efficiency of DMPNet, showcasing consistent improvements across both lower- and full-scale metrics compared to competitive models.

4.3 Limitations and future directions

4.3.1 Limitations of DMPNet

The limitations of the proposed DMPNet are as follows:

(1) Computational complexity: the inclusion of multiple advanced components, such as dilated convolutions, attention mechanisms, and DWT operations, has increased the computational complexity of DMPNet. Thus, the proposed DMPNet is difficult to deploy in resource-constrained environments.

(2) Reference data: like many competitive deep learning-based pansharpening models, DMPNet's performance heavily relies on the quality and quantity of the training data. Limited or biased training datasets could lead to suboptimal generalization in real-world scenarios.

(3) Scalability: in DMPNet, processing high-resolution satellite images across multiple scales can be resource-intensive. This might pose challenges for scalability to extremely large datasets or real-time applications.

(4) Sensitivity to hyperparameters: the performance of DMPNet is sensitive to the choice of hyperparameters. We selected the parameters using sensitivity analysis and guidance from the literature. Therefore, extensive tuning is required to achieve optimal results for different datasets or imaging conditions.

(5) Overfitting: despite the robust design, the model might still be susceptible to overfitting in cases where training data does not adequately represent the diversity of real-world conditions.

(6) Generalization: while DMPNet demonstrates robust performance in standard pansharpening tasks, its ability to handle extreme or unconventional imaging conditions remains uncertain. Scenarios such as heavily degraded input images still need to be thoroughly tested.

4.3.2 Future directions

Although the proposed DMPNet effectively address key pansharpening challenges, a number of areas for further research remain there. Since the proposed model is based on reference datasets, future work will concentrate on building self-supervised DMPNet to reduce reliance on large-scale labeled data. Furthermore, combining DMPNet with technologies like vision transformers (ViTs) and quantum computing has the potential to improve feature extraction and fusion methods. Furthermore, optimization methods such as reinforcement learning and metaheuristics could help to optimize the tuning of DMPNet settings across various contexts.

5 Conclusion

The proposed DMPNet addressed key pansharpening challenges by striking an efficient balance between spatial resolution and spectral fidelity. DMPNet contained three essential modules such as FEM, MSAAF, and IRM. These modules ensured the robust integration of spatial and spectral data. The dual-path architecture in FEM captures global context as well as fine-grained information. However, MSAAF uses SCA and SAN to dynamically fuse features while maintaining spectral consistency. Finally, the IRM refines and reconstructs features utilizing frequency decomposition and reconstruction to achieve optimal performance. The experimental results supported DMPNet's ability to produce high-quality pansharpened images when compared to previous models. It is observed that the proposed DMPNet outperforms competitive models in terms of ERGAS, SCC (WR), SCC (NR), PSNR, Q, QNR, and JQM by approximately 1.24%, 1.18%, 1.37%, 1.42%, 1.26%, 1.31%, and 1.23%, respectively.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/liangjiandeng/PanCollection.

Author contributions

GK: Conceptualization, Formal analysis, Investigation, Methodology, Validation, Visualization, Writing – original draft, Writing – review & editing. MM: Investigation, Project administration, Resources, Writing – review & editing. DS: Investigation, Project administration, Resources, Writing – review & editing. SS: Investigation, Project administration, Supervision, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alessio, S. M., and Alessio, S. M. (2016). “Discrete wavelet transform (DWT),” in Digital Signal Processing and Spectral Analysis for Scientists: Concepts and Applications, 645–714.

Google Scholar

Alparone, L., Aiazzi, B., Baronti, S., Garzelli, A., Nencini, F., and Selva, M. (2008). Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 74, 193–200. doi: 10.14358/PERS.74.2.193

Crossref Full Text | Google Scholar

Amro, I., Mateos, J., Vega, M., Molina, R., and Katsaggelos, A. K. (2011). A survey of classical methods and new trends in pansharpening of multispectral images. EURASIP J Adv Signal Proc. 2011, 1–22. doi: 10.1186/1687-6180-2011-79

Crossref Full Text | Google Scholar

Chang, N.-B., Bai, K., Imen, S., Chen, C.-F., and Gao, W. (2016). Multisensor satellite image fusion and networking for all-weather environmental monitoring. IEEE Syst. J. 12, 1341–1357. doi: 10.1109/JSYST.2016.2565900

Crossref Full Text | Google Scholar

Ciotola, M., Poggi, G., and Scarpa, G. (2023). Unsupervised deep learning-based pansharpening with jointly-enhanced spectral and spatial fidelity. IEEE Trans. Geosci. Remote Sens. doi: 10.1109/TGRS.2023.3299356

Crossref Full Text | Google Scholar

Deng, L. J., Vivone, G., Paoletti, M. E., Scarpa, G., He, J., Zhang, Y., et al. (2022). Machine learning in pansharpening: a benchmark, from shallow to deep networks. IEEE Geosci. Remote Sens. Magaz. 10, 279–315. doi: 10.1109/MGRS.2022.3187652

Crossref Full Text | Google Scholar

Doi, K., and Iwasaki, A. (2019). “SSCNET: spectral-spatial consistency optimization of CNN for pansharpening,” in IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium (Yokohama: IEEE), 3141–3144.

Google Scholar

Gao, F., Wu, T., Li, J., Zheng, B., Ruan, L., Shang, D., et al. (2018). SD-CNN: a shallow-deep cnn for improved breast cancer diagnosis. Comp. Med. Imag. Graph. 70, 53–62. doi: 10.1016/j.compmedimag.2018.09.004

PubMed Abstract | Crossref Full Text | Google Scholar

Gao, Y., Qin, M., Wu, S., Zhang, F., and Du, Z. (2024). GSA-SIAMNET: a siamese network with gradient-based spatial attention for pan-sharpening of multi-spectral images. Remote Sens. 16:616. doi: 10.3390/rs16040616

Crossref Full Text | Google Scholar

Gastineau, A., Aujol, J.-F., Berthoumieu, Y., and Germain, C. (2021). Generative adversarial network for pansharpening with spectral and spatial discriminators. IEEE Trans. Geosci. Remote Sens. 60, 1–11. doi: 10.1109/TGRS.2021.3060958

Crossref Full Text | Google Scholar

Ghadjati, M., Moussaoui, A., and Boukharouba, A. (2019). A novel iterative pca-based pansharpening method. Remote Sens. Lett. 10, 264–273. doi: 10.1080/2150704X.2018.1547443

Crossref Full Text | Google Scholar

Ghahremani, M., and Ghassemian, H. (2015). A compressed-sensing-based pan-sharpening method for spectral distortion reduction. IEEE Trans. Geosci. Remote Sens. 54, 2194–2206. doi: 10.1109/TGRS.2015.2497309

PubMed Abstract | Crossref Full Text | Google Scholar

He, L., Rao, Y., Li, J., Chanussot, J., Plaza, A., Zhu, J., et al. (2019). Pansharpening via detail injection based convolutional neural networks. IEEE J. Select. Topics Appl. Earth Observat. Remote Sens. 12, 1188–1204. doi: 10.1109/JSTARS.2019.2898574

PubMed Abstract | Crossref Full Text | Google Scholar

Hong, D., Zhang, B., Li, H., Li, Y., Yao, J., Li, C., et al. (2023). Cross-city matters: A multimodal remote sensing benchmark dataset for cross-city semantic segmentation using high-resolution domain adaptation networks. Remote Sens. Environm. 299:113856. doi: 10.1016/j.rse.2023.113856

Crossref Full Text | Google Scholar

Hou, S., Xiao, S., Dong, W., and Qu, J. (2022). Multi-level features fusion via cross-layer guided attention for hyperspectral pansharpening. Neurocomputing 506, 380–392. doi: 10.1016/j.neucom.2022.07.071

Crossref Full Text | Google Scholar

Hu, J., Shen, L., and Sun, G. (2018). “Squeeze-and-excitation networks,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Salt Lake City, UT: IEEE), 7132–7141.

Google Scholar

Huang, Y.-J., Liao, A.-H., Hu, D.-Y., Shi, W., and Zheng, S.-B. (2022). Multi-scale convolutional network with channel attention mechanism for rolling bearing fault diagnosis. Measurement 203:111935. doi: 10.1016/j.measurement.2022.111935

PubMed Abstract | Crossref Full Text | Google Scholar

Jia, Y., Hu, Q., Dian, R., Ma, J., and Guo, X. (2024). Paps: Progressive attention-based pan-sharpening. IEEE-CAA J. Automat. Sinica 11, 391–404. doi: 10.1109/JAS.2023.123987

Crossref Full Text | Google Scholar

Jian, L., Wu, S., Chen, L., Vivone, G., Rayhana, R., and Zhang, D. (2023). Multi-scale and multi-stream fusion network for pansharpening. Remote Sens. 15:1666. doi: 10.3390/rs15061666

Crossref Full Text | Google Scholar

Jin, C., Deng, L.-J., Huang, T.-Z., and Vivone, G. (2022). Laplacian pyramid networks: a new approach for multispectral pansharpening. Inform. Fusion 78, 158–170. doi: 10.1016/j.inffus.2021.09.002

Crossref Full Text | Google Scholar

Khan, S. S., Ran, Q., Khan, M., and Ji, Z. (2019). “Pan-sharpening framework based on laplacian sharpening with brovey,” in 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP) (Chongqing: IEEE), 1–5.

Google Scholar

Lei, F., Liu, X., Dai, Q., and Ling, B. W.-K. (2020). Shallow convolutional neural network for image classification. SN Appl. Sci. 2:97. doi: 10.1007/s42452-019-1903-4

Crossref Full Text | Google Scholar

Leung, Y., Liu, J., and Zhang, J. (2013). An improved adaptive intensity-hue-saturation method for the fusion of remote sensing images. IEEE Geosci. Remote Sens. Lett. 11, 985–989. doi: 10.1109/LGRS.2013.2284282

Crossref Full Text | Google Scholar

Li, C., Zhang, B., Hong, D., Zhou, J., Vivone, G., Li, S., et al. (2024). CasFormer: Cascaded transformers for fusion-aware computational hyperspectral imaging. Inform. Fusion 108:102408. doi: 10.1016/j.inffus.2024.102408

Crossref Full Text | Google Scholar

Li, K., Zhang, W., Yu, D., and Tian, X. (2022). Hypernet: a deep network for hyperspectral, multispectral, and panchromatic image fusion. ISPRS J. Photogrammet. Remote Sens. 188:30–44. doi: 10.1016/j.isprsjprs.2022.04.001

PubMed Abstract | Crossref Full Text | Google Scholar

Li, Z., Guo, X., Xiang, S., and Wu, X. (2024). Pyramid hierarchical network for multispectral pan-sharpening. Int. J. Comp. Sci. Eng. 27, 142–158. doi: 10.1504/IJCSE.2024.137282

PubMed Abstract | Crossref Full Text | Google Scholar

Li, Z., Li, J., Ren, L., and Chen, Z. (2023). Transformer-based dual-branch multiscale fusion network for pan-sharpening remote sensing images. IEEE J. Select. Topics in Appl. Earth Observat. Remote Sens. 17, 614–632. doi: 10.1109/JSTARS.2023.3332459

Crossref Full Text | Google Scholar

Liu, D., Sheng, N., Han, Y., Hou, Y., Liu, B., Zhang, J., et al. (2023). SCAU-Net: 3D self-calibrated attention U-Net for brain tumor segmentation. Neural Comp. Appl. 35, 23973–23985. doi: 10.1007/s00521-023-08872-8

Crossref Full Text | Google Scholar

Liu, X., Hou, J., Cong, X., Shen, H., Lou, Z., Deng, L.-J., et al. (2024). Rethinking pan-sharpening via spectral-band modulation. IEEE trans. Geosci. Remote sens. 62:3340193. doi: 10.1109/TGRS.2023.3340193

Crossref Full Text | Google Scholar

Liu, Y., Teng, Q., He, X., Ren, C., and Chen, H. (2022). Multimodal sensors image fusion for higher resolution remote sensing pan sharpening. IEEE Sensors J. 22, 18021–18034. doi: 10.1109/JSEN.2022.3195243

Crossref Full Text | Google Scholar

Nassar, H., Veldt, N., Mohammadi, S., Grama, A., and Gleich, D. F. (2018). “Low rank spectral network alignment,” in Proceedings of the 2018 World Wide Web Conference, 619–628.

Google Scholar

Palubinskas, G. (2015). Joint quality measure for evaluation of pansharpening accuracy. Remote Sens. 7, 9292–9310. doi: 10.3390/rs70709292

Crossref Full Text | Google Scholar

Saxena, N., and Balasubramanian, R. (2021). A pansharpening scheme using spectral graph wavelet transforms and convolutional neural networks. Int. J. Remote Sens. 42, 2898–2919. doi: 10.1080/01431161.2020.1864056

Crossref Full Text | Google Scholar

Shen, H., Zhang, B., Jiang, M., and Li, J. (2024). Unsupervised pan-sharpening network incorporating imaging spectral prior and spatial-spectral compensation. IEEE Trans. Geosci. Remote Sens. doi: 10.1109/TGRS.2024.3422896

Crossref Full Text | Google Scholar

Shi, N., Wang, P., and Li, F. (2023). Domain-specific knowledge-driven pan-sharpening algorithm. Neurocomputing 520, 129–140. doi: 10.1016/j.neucom.2022.11.068

Crossref Full Text | Google Scholar

Su, X., Li, J., and Hua, Z. (2022). Transformer-based regression network for pansharpening remote sensing images. IEEE Trans. Geosci. Remote Sens. 60, 1–23. doi: 10.1109/TGRS.2022.3152425

Crossref Full Text | Google Scholar

Wald, L. (2002). Data Fusion: Definitions and Architectures—Fusion of Images of Different Spatial Resolutions. Paris: Les Presses de l'École des Mines.

Google Scholar

Wang, J., Lu, T., Huang, X., Zhang, R., and Luo, D. (2024a). A deep error removal network for pan-sharpening. IEEE Geosci. Remote Sens. Lett. 21. doi: 10.1109/LGRS.2024.3454124

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, J., Zhou, Q., Huang, X., Zhang, R., Chen, X., and Lu, T. (2024b). Pan-sharpening via intrinsic decomposition knowledge distillation. Pattern Recognit. 149:110247. doi: 10.1016/j.patcog.2023.110247

Crossref Full Text | Google Scholar

Wang, Y., Wang, G., Chen, C., and Pan, Z. (2019). Multi-scale dilated convolution of convolutional neural network for image denoising. Multimedia Tools Appl. 78, 19945–19960. doi: 10.1007/s11042-019-7377-y

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, Z., and Bovik, A. C. (2002). A universal image quality index. IEEE Signal Process. Lett., 9, 81–84. doi: 10.1109/97.995823

Crossref Full Text | Google Scholar

Xiao, J., Ji, Y., and Wei, X. (2023). “Hyperspectral image denoising with spectrum alignment,” in Proceedings of the 31st ACM International Conference on Multimedia, 5495–5503.

Google Scholar

Yang, Z., Fu, X., Liu, A., and Zha, Z.-J. (2022). Progressive pan-sharpening via cross-scale collaboration networks. IEEE Geosci. Remote Sens. Lett. 19:3170376. doi: 10.1109/LGRS.2022.3170376

Crossref Full Text | Google Scholar

Yilmaz, C. S., Yilmaz, V., and Gungor, O. (2022). A theoretical and practical survey of image fusion methods for multispectral pansharpening. Inform. Fusion 79, 1–43. doi: 10.1016/j.inffus.2021.10.001

Crossref Full Text | Google Scholar

Zhang, F., Zhang, K., and Sun, J. (2022). Multiscale spatial-spectral interaction transformer for pan-sharpening. Remote Sens. 14:1736. doi: 10.3390/rs14071736

Crossref Full Text | Google Scholar

Zhang, G., Zhang, H., Yao, Y., and Shen, Q. (2022). Attention-guided feature extraction and multiscale feature fusion 3D resnet for automated pulmonary nodule detection. IEEE Access 10, 61530–61543. doi: 10.1109/ACCESS.2022.3182104

Crossref Full Text | Google Scholar

Zhang, K., Zhang, F., Wan, W., Yu, H., Sun, J., Del Ser, J., et al. (2023). Panchromatic and multispectral image fusion for remote sensing and earth observation: concepts, taxonomy, literature review, evaluation methodologies and challenges ahead. Inform. Fusion 93, 227–242. doi: 10.1016/j.inffus.2022.12.026

Crossref Full Text | Google Scholar

Zhou, C., Zhang, J., Liu, J., Zhang, C., Fei, R., and Xu, S. (2020). Perceppan: towards unsupervised pan-sharpening based on perceptual loss. Remote Sens. 12:2318. doi: 10.3390/rs12142318

Crossref Full Text | Google Scholar

Zhou, J., Civco, D. L., and Silander, J. A. (1998). A wavelet transform method to merge landsat tm and spot panchromatic data. Int. J. Remote Sens. 19, 743–757. doi: 10.1080/014311698215973

Crossref Full Text | Google Scholar

Zhou, M., Huang, J., Hong, D., Zhao, F., Li, C., and Chanussot, J. (2023a). Rethinking pan-sharpening in closed-loop regularization. IEEE Trans. Neural Netw. Learn. Syst. doi: 10.1109/TNNLS.2023.3279931

PubMed Abstract | Crossref Full Text | Google Scholar

Zhou, M., Huang, J., Yan, K., Yang, G., Liu, A., Li, C., et al. (2022a). “Normalization-based feature selection and restitution for pan-sharpening,” in 30th ACM International Conference on Multimedia (MM) (Lisboa: ACM).

Google Scholar

Zhou, M., Huang, J., Yan, K., Yu, H., Fu, X., Liu, A., et al. (2022b). “Spatial-frequency domain information integration for pan-sharpening,” in 17th European Conference on Computer Vision (ECCV), eds. S. Avidan, G. Brostow, M. Cisse, G. Farinella, and T. Hassner (Tel Aviv: ECCV).

PubMed Abstract | Google Scholar

Zhou, M., Huang, J., Zhao, F., and Hong, D. (2023b). Modality-aware feature integration for pan-sharpening. IEEE Trans. Geosci. Remote Sens. 61:3232384. doi: 10.1109/TGRS.2022.3232384

Crossref Full Text | Google Scholar

Zhou, M., Zheng, N., He, X., Hong, D., and Chanussot, J. (2024). Probing synergistic high-order interaction for multi-modal image fusion. IEEE Trans. Pattern Analy. Mach. Intellig. doi: 10.1109/TPAMI.2024.3475485

PubMed Abstract | Crossref Full Text | Google Scholar