Time-series forecasting of microbial fuel cell energy generation using deep learning

Soil microbial fuel cells (SMFCs) are an emerging technology which offer clean and renewable energy in environments where more traditional power sources, such as chemical batteries or solar, are not suitable. With further development, SMFCs show great promise for use in robust and affordable outdoor sensor networks, particularly for farmers. One of the greatest challenges in the development of this technology is understanding and predicting the fluctuations of SMFC energy generation, as the electro-generative process is not yet fully understood. Very little work currently exists attempting to model and predict the relationship between soil conditions and SMFC energy generation, and we are the first to use machine learning to do so. In this paper, we train Long Short Term Memory (LSTM) models to predict the future energy generation of SMFCs across timescales ranging from 3 min to 1 h, with results ranging from 2.33 to 5.71% Mean Average Percent Error (MAPE) for median voltage prediction. For each timescale, we use quantile regression to obtain point estimates and to establish bounds on the uncertainty of these estimates. When comparing the median predicted vs. actual values for the total energy generated during the testing period, the magnitude of prediction errors ranged from 2.29 to 16.05%. To demonstrate the real-world utility of this research, we also simulate how the models could be used in an automated environment where SMFC-powered devices shut down and activate intermittently to preserve charge, with promising initial results. Our deep learning-based prediction and simulation framework would allow a fully automated SMFC-powered device to achieve a median 100+% increase in successful operations, compared to a naive model that schedules operations based on the average voltage generated in the past.

1 Introduction

Climate change is already affecting every aspect of our society, widening existing socioeconomic disparities across the world. Some of the most dangerous changes are occurring in our global food systems, where extreme weather has made feeding our growing population a challenge. Data-driven agriculture techniques, such as moisture and nutrient monitoring, have enabled us to grow more food while using fewer resources (Zotarelli et al., 2009). Unfortunately, the adoption rates for the sensor networks that enable data-driven agriculture remain low (Rajak et al., 2023). Persistent monitoring systems consist of multiple components that must be integrated and weatherproofed. A typical outdoor sensor node connects a commercial sensor to a data logger, with additional costs and complexity added by wireless communication modules, power management modules and equipment like batteries and solar panels. Farms and other managed lands typically lack robust power and communication, making sensor systems are expensive and difficult to deploy and maintain. If present, sensing is likely limited in density or frequency—soil testing, for example, is usually done only once per year (if at all, Kashyap and Kumar, 2021), and of the 11% of US farms that sense soil moisture, the density of deployed sensors is typically far below the recommended amounts (Rossini et al., 2021; Zotarelli et al., 2016). The next wave of sensor systems must enable reliable, granular sensing at scale. One promising area of investigation to ease adoption barriers involves harvesting power for sensor networks from the soil itself (Josephson et al., 2022). Soil microbial fuel cells (SMFCs) are a compact, low-cost bioelectrochemical system that harvest power from exoelectrogenic microbes that occur naturally in the soil.

Though SMFCs only produce microwatts of power, electronics have progressed such that this is actually enough to power the latest generation of ultra-low power devices (Josephson et al., 2021; Yen et al., 2023; Feng et al., 2023). SMFCs are a renewable source of energy, and unlike more traditional power sources (chemical battery, solar, etc.), they are typically constructed using environmentally inert materials with a very low carbon footprint. Once fully developed, they could power outdoor sensor networks, giving farmers access to high-resolution, real-time data on their fields toward making educated decisions on farm management. They also have the potential to be biosensors in and of themselves (Olias et al., 2020). For example, the electricity generated by the microbial communities can be used as a signal to indicate heavy-metal contamination or dissolved oxygen in water (Abbas et al., 2022; Wang et al., 2023).

A key challenge with leveraging this unique source of biopower is that the electro-generative process is not yet fully understood, with rises and drops in energy production being common due to a variety of complex factors, including temperature, soil type, moisture and more. This makes SMFCs difficult to use as a source of consistent and reliable power. To address this barrier, we have created a deep learning model to predict SMFC energy generation over time, increasing their viability as an energy source for low-power applications. To our knowledge this is the first work to predict SMFC energy generation using deep learning.

In addition to making point estimates of future energy output, our work models the uncertainty of these estimates using quantile regression, as defined in Section 3.3.1. This helps us make conservative energy generation estimates when needed, reducing the risk of a device lacking the energy to perform predicted operations. It is often necessary for low-power applications, such as outdoor sensor networks, to shut down for periods of time to gather energy, activating only when necessary to perform operations (Marcano and Pannuto, 2021). This is known as intermittent computing (Lucia et al., 2017). Our approach is key for the types of intermittently active, low-power applications supported by SMFCs, where every microwatt makes a difference, and trying to activate a device before enough energy is stored would waste precious energy. Our models, which have been trained and evaluated on months of real SMFC data, predicts performance for future time horizons using recently observed data. These predictions make it possible to schedule device operations ahead of time, allowing for more effective resource allocation. For example, it would be possible to adjust the duty cycle of wireless data transmission—an operation with high power consumption—based on the predicted power budget. In times of low energy availability, for example, the number of attempted wireless data transmissions could be reduced to conserve energy for more essential operations (e.g. timekeeping, local data logging).

There are multiple advantage of predictive models over a naive approach that uses a fixed duty cycle. The first advantage is that overall system downtime can be reduced. When no prediction information is available, the only option to maximize longevity is reducing the frequency of operation to as low as acceptably possible. With a predictive model, the system can to take advantage of times of high energy availability to perform more frequent and/or sophisticated operations (e.g. over-the-air firmware updates). The second advantage is that we can avoid wasting energy. Intermittent computing applications should only activate only when there is enough energy available to perform the desired operations, e.g. transmitting a packet. If the operation is not successfully completed, then no useful progress is made, and the stored energy is wasted and unavailable to use in a future potentially-successful operation. Our work addresses this need by allowing for a lower-bound prediction of energy generation using quantile regression, as defined in Section 3.3.1. Likewise, we introduce three unique metrics in this paper to evaluate the usefulness of our models for intermittent computing applications. This is in addition to the more standard Mean Average Percent Error (MAPE), which is used to measure the overall accuracy of the model's predictions compared to the ground truth values. The domain-specific metrics in this paper include the Failed Prediction and Overestimation rates, designed to measure how often the model predicts greater energy generation than the true value, and the Missed Activation rate, designed to predict how many more times a device could have been activated by using a theoretical “perfect model” capable of predicting exact energy generation. These metrics are defined in further detail in Section 3.4.

2 Background

2.1 Microbial fuel cells

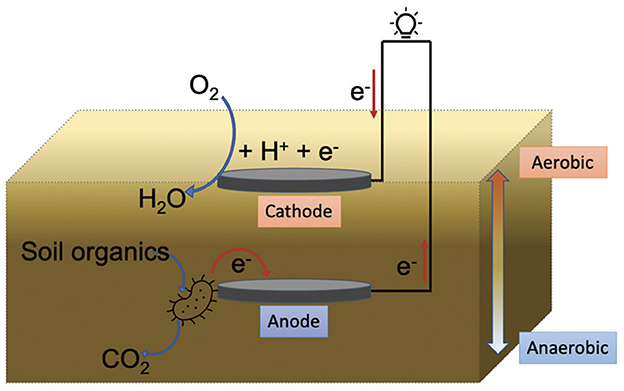
Most generally, microbial fuel cells (MFCs) are electrochemical cells that generate electricity from the transfer of electrons resulting from microbial interactions. Soil microbial fuel cells (SMFCs) use the microbial interactions within soil, but other types of MFCs can use wastewater or sediment as well (Josephson et al., 2022). Two key requirements for SMFCs to operate are anaerobic conditions and a sufficient presence of soil organic matter. Certain types of microbes, known as exoelectrogens, produce a spare electron as part of their natural respiration process. By placing an anode within the soil connected to a cathode outside the soil, the anode can receive these electrons from the soil microorganisms and allowing them to flow to the cathode, generating electricity. This process is described visually in Figure 1, adapted from Josephson et al. (2022).

Figure 1

Figure 1. Visual diagram of soil microbial fuel cell electrogenerative process.

2.2 Quantile regression in energy forecasting

Compared to other types of models, deep learning can be used to make extremely accurate predictions in various application areas. However, the non-statistical nature of deep learning makes model interpretation difficult. Quantile regression is one way to address this weakness by allowing deep learning models to obtain prediction intervals as well as point estimates. Previous works have used machine learning and deep learning with quantile regression to forecast renewable energy generation (Wang et al., 2019; Xu et al., 2023). However, our work is the first to use this technique to predict the energy output of SMFCs. Forecasting energy output for SMFCs is more difficult than for more traditional sources (e.g. wind, solar) for several reasons. SMFC energy generation is directly tied to microbial conditions, which are governed by complex biological processes that are not yet fully understood. For example, it can take microbial communities longer to respond to changes in environmental conditions than solar or wind systems, resulting in delayed and unpredictable changes to energy generation (Josephson et al., 2022).

2.3 SMFC modeling for incubation phase

Before being deployed in the field, SMFCs usually undergo an incubation phase within an indoor environment. Dziegielowski et al. (2023) created a physics-based mathematical model to predict the voltage of SMFCs during their incubation phase based on initial soil conditions. However, this work only predicts voltage (not current).

There are several key differences between this physics-based model and the one presented in our paper, which makes direct comparison of the models difficult. The physics-based model was validated on the same data used for training, while the data for our models are split into training, validation, and testing sets, used to fit the model, tune hyper-parameters, and evaluate performance, respectively. Furthermore, the physics-based model directly simulates the biophysical conditions of an SMFC over the course of several months in order to predict the output, starting from the initial conditions of the soil. In contrast, our models account for the rapidly-changing conditions of a non-laboratory deployment by periodically reading in sensor data to update the soil conditions, and uses this to predict SMFC at various time horizons into the future. Furthermore, this model considers only incubation data. The deployment (field, outdoors) and incubation (climate-controlled laboratory) environments are substantially different. We do provide a quantitative comparison of the physics-based model against a variant of our model trained only on incubation data in Section 4.4.2.

Overall, Dziegielowski et al. (2023) offers strong insight into soil conditions that promote high voltage output for SMFCs during incubation, but does not attempt to model these relationships in an out-of-lab deployment setting. At the time of this writing, our work is the first to (1) model and predict SMFC performance during field deployment outside of the lab, (2) predict current as well as voltage, and (3) predict for multiple time horizons with bounds on the uncertainty.

2.4 Intermittently active, SMFC-powered devices

Marcano and Pannuto (2021) successfully developed a low-power, e-ink display device powered exclusively by an SMFC, demonstrating the potential of this technology as a renewable energy source. This device was designed to be active intermittently: it is turned off while charging, and manually powered on once enough energy had been stored for activation. However, the evaluation was limited to laboratory settings where unrealistically high moisture levels were necessary to sustain the device.

Yen et al. (2023) created a proof-of-concept system that successfully powers an RF backscatter tag. They also developed a framework for calculating the number of operations various SMFC-powered devices can perform based on measured SMFC voltage traces, accounting for the complex harvesting process required to use SMFC-generated energy.

Our work focuses on modeling and predicting MFC energy output. This allows us to develop a framework for scheduling intermittent computing device operations in advance, so devices can activate only when they have enough energy to do so, thereby conserving energy. This would enhance the functionality of the prototypes discussed in Yen et al. (2023) and Marcano and Pannuto (2021), the latter of which required a human participant to monitor energy availability and manually activate the device.

2.5 Task scheduling frameworks for intermittently powered systems

This paper is the first work, to our knowledge, to present a deep learning based approach to predicting SMFC power output, and scheduling useful tasks and operations based on these predictions. However, other works have created task scheduling frameworks for intermittently powered systems not fueled by SMFCs. Zygarde is one such framework, which has been validated on four standard datasets—three consisting of labeled images for training machine learning models, and one containing audio files—and deployed in six real-world application settings, with RF and solar-powered systems (Islam and Nirjon, 2020). The applications used for validation are performed on audio and visual tasks, so we are unable to compare their performance to our regression-based model.

Furthermore, Zygarde does not directly predict energy generation, but rather uses a uses a probabilistic method to model energy randomness. In contrast, our work uses deep neural networks for regression to directly predict voltage, current and power output, as well as the upper and lower bounds for these values. A visual representation of this framework is given in Figure 2.

Figure 2

Figure 2. Overview and vision. This work aims to create a predictive model for scheduling the activation of SMFC powered devices, allowing them to activate intermittently and then shut down to conserve energy.

3 Materials and methods

3.1 Dataset description

The dataset used to train the models in this paper is taken from a cell that began operation at a Stanford laboratory in April 2021 and was retired in June 2022. We will refer to this as Dataset 1 for the remainder of the paper. Since Dataset 1 contains data from both the incubation and deployment phases, we use Dataset 1 (incubation) and Dataset 1 (deployment) to refer to the separate parts of the dataset. Most models in this paper are trained and validated on Dataset 1 (deployment), unless otherwise specified. A tabular representation of the various types of datasets and models used in this paper can be found in Table 1.

Table 1

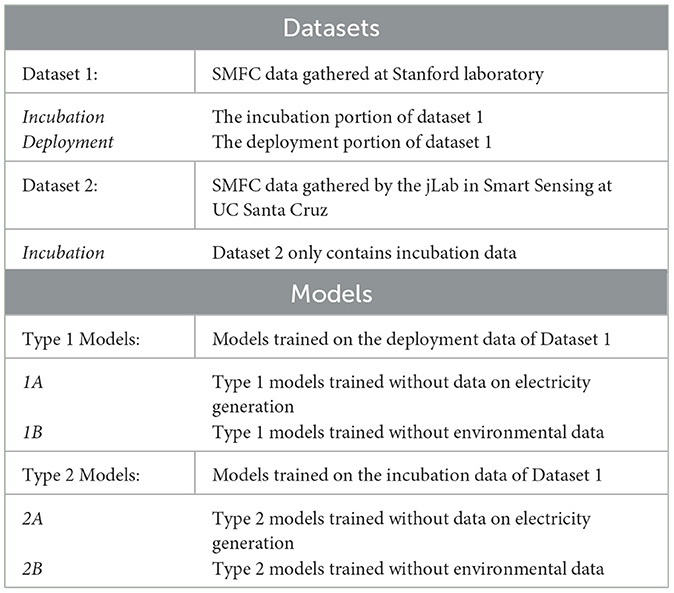
Table 1. A table representation of terminology related to datasets, which datasets are used to train which models, and models that omit certain types of training data.

For all models trained on Dataset 1 (deployment), we use the first 70% of as the training set, the subsequent 15% for our validation set, and the final 15% for our test set. Our input values consist of the average values of various features over a desired time interval, as described in Section 3.2. Therefore, the size of our sets vary in size from 2,559 to 51,400 values for the training set and 548 to 11,015 values for the validation and testing set, with larger values corresponding to shorter time intervals.

In addition to Dataset 1, a second dataset consisting solely of incubation data was created in 2024, using soil from Santa Cruz, CA. We will refer to this dataset at Dataset 2 for the remainder of the paper. The data from Dataset 2 is used as additional validation data for our models.

3.2 Data pre-processing and model features

Our models aim to forecast the power generation of an SMFC over five different timescales—3, 5, 15, 30, and 60 min in the future. These timescales were selected to explore how the accuracy of our models change over different prediction horizons, and correspond to the upper end of typical measurement frequencies for outdoor sensor systems. Soil moisture, for example, changes rather slowly (Josephson et al., 2020). Measuring even hourly is more than sufficient to determine whether a field needs water, while irrigation events might be monitored by taking more frequent samples every 3–5 min. To construct our models, we begin by sanitizing our data (removing occasional erroneous zero measurements due to data outages). The features we use to train the model are the power, current and voltage of the SMFC, and the electrical conductivity, temperature, and raw volumetric water content of the soil. The power, current and voltage values are gathered using the open-source RocketLogger system (Sigrist et al., 2017), and the electrical conductivity, temperature, and raw volumetric water content values are gathered using the commercial TEROS-12 sensor (Meter, 2018). These values are sampled every 12-15 seconds. For each model we also re-sample the input features to align with the prediction horizon (3, 5, 15, 30, or 60 min). For example, if we want to train a model that predicts the average SMFC power generation over the next hour, we resample our data to obtain the 1-h average for each of the model's features. Next we shift the data such that at each timestamp, the model is given access to the features of the previous three time intervals in order to predict the average power, voltage and current for the current time interval. Finally, we add the number of days since SMFC deployment, as well as the hour of the day, to our list of features. The input features are not normalized.

3.3 Model building

This work uses a Long Short-Term Memory (LSTM) model to predict future energy generation for LSTMs. LSTMs are one of the most-used deep learning models for time series data, data which is indexed and processed in temporal order. Many past studies have used LSTMs to predict solar and wind energy generation (Ying et al., 2023; Srivastava and Lessmann, 2018), and we apply this approach to SMFC energy forecasting for the first time.

We use a three-layer LSTM network with an input LSTM layer with 200 neurons and a ReLU activation functions, a hidden dense layer with 100 neurons and a ReLU activation functions, and a terminal dense layer with three neurons. Our models use the Adam optimizer at the default learning rate, and a sequence length of four for the input data. We change our batch size depending on the desired timescale of the prediction, with a batch size of 300 for 3 min, 150 for 5 min, 50 for 15 min, 20 for 30 min, and 8 for 60 min. More information on the structure of our models can be found in the open-source Github repository for this project at Hess-Dunlop et al. (2024).

3.3.1 Quantile regression

While deep learning models excel in making accurate predictions, it is difficult to calculate the uncertainty in the predictions of these models, limiting their usefulness in real-world settings (Gawlikowski et al., 2023). One method to establish bounds on uncertainty in deep learning models is quantile regression, which allows us to train multiple models, which each explicitly predict a different quantile of the data. For example, if we wish to predict the energy generation at a given time and establish bounds on uncertainty with a 90% confidence interval, we would train three separate models using quantile regression: one model to obtain point estimates by predicting the median quantile, one model to obtain the lower bound of the prediction interval by predicting the 5th quantile, and another model to obtain the upper bound of the prediction interval by predicting the 95th quantile (Wang et al., 2019). To train these models, we use the following loss function, also known as the “pinball loss” during training:

$\begin{array}{l}\text{if predicted }\le \text{ actual:}\\ \text{ loss}=\alpha *\text{(actual - predicted)}\\ \text{else:}\\ \text{ loss}=(1-\alpha )*\text{(predicted - actual)}\end{array}$

where α is the desired quantile, predicted is the predicted current, voltage, and power output for the SMFC, and actual is the actual current, voltage, and power output for the SMFC.

Since performing gradient descent requires a differentiable loss function, quantile regression cannot typically be used with deep learning. However, the pinball loss function allows us to overcome this limitation and use quantile regression to quantify the uncertainty of our models (Rodrigues and Pereira, 2018; Steinwart and Christmann, 2011). Several other works have also used quantile regression with pinball loss to quantify uncertainty for deep learning-based energy forecasting models (Wang et al., 2019; Xu et al., 2023).

It should be noted that the data does not follow a normal distribution, so the quantiles of our upper and lower bounds will not be equidistant from the median. Furthermore, as the model produces three outputs with different distributions (current, voltage, and power), the outputs are expected to diverge somewhat from the desired quantile, since the model training optimizes the average loss metric of the three.

3.4 Model evaluation

There are several techniques that we can use to interpret the prediction and the accuracy of our models. For most of this paper, we use our test set, as described in Section 3.1, to evaluate our model.

3.4.1 MAPE

Model accuracy for regression tasks can be calculated using Mean Average Percent Error (MAPE), defined as follows:

$\begin{array}{l}\frac{1}{n}\sum ^n\frac{|\text{actual}-\text{predicted}|}{\left|\text{actual}\right|}\times 100\end{array}$

Intuitively, this value is the average percent difference between the predicted values and the actual values in a model. There is no universally agreed upon acceptable value for MAPE, but a MAPE of 0% would indicate that the model predicts the data with zero error, whereas an MAPE of 50% indicates that on average, the predicted value is off by 50% of the actual value.

3.4.2 Total energy % error

This metric is the percent difference between the actual and predicted values of the total energy generated. Energy is the integral of power over time. The difference between predicted energy income and actual energy income is a more valuable metric than MAPE because the actual magnitude of over-predicting and under-predicting power does not actually matter if the over- and under-predictions compensate for each other. The results for the Total Energy % Error metric are recorded in Table 2, with negative values indicating underestimation and positive values indicating overestimation.

Table 2

Table 2. Model performances.

3.4.3 False positive rate

The false positive rate metric measures how often our models schedule a device activation when there is not enough energy available, resulting in the device failing to activate and the stored energy being wasted. The false positive rate will be calculated as follows:

$\begin{array}{l}\frac{\text{false\_positive}}{\text{active\_pred}}\end{array}$

false_positive refers to the amount of times the model predicted there would be enough energy to perform an operation when there was not enough energy, resulting in stored energy being wasted when the device failed to activate. active_pred is the total number of activations scheduled by our model.

3.4.4 Missed activation rate

Unlike overestimation and false positives, the missed activation rate metric measures how many more times the device could have successfully been activated, if we had access to a theoretical “oracle” model that could perfectly predict and make use of the available energy. It will be calculated as follows:

$\begin{array}{l}\frac{\text{missed\_active}}{\text{max\_active}}\end{array}$

missed_active is the number of additional times the device could been have activated if the model had perfectly predicted how much energy would be available. It is calculated as the theoretical maximum possible number of operations, minus the number of successful operations scheduled by our model. max_active is the theoretical maximum possible number of operations.

Readers will note the similarity of this metric to the false negative rate. However, we divide by the theoretical maximum amount of device activations (given by the oracle model) instead of the total amount of activations scheduled by our model. The reason we used the missed activation metric instead of false negative is because the total amount of device activations scheduled by our model is not necessarily indicative of the amount of activations that could be performed with the available energy, and we wanted to use a metric that highlights how well our model was able to make use of the actual available energy.

3.5 Comparison models

In addition to the rest of the metrics described in this section, we evaluate our scheduling framework by comparing it to two different models: the naive model and the oracle model.

The naive model, also referred to as the naive fixed-duty cycle, is used as a “baseline” model to compare our deep learning-based model to. It operates in the same way as the runtime simulation code described in Section 3.6, by using predictions of SMFC voltage to estimate how much usable energy the SMFC will have access to in the future, and then using these estimates to schedule activation of a device. However, while our runtime simulation predicts the voltage using deep learning models, the naive model simply takes the average voltage over the past x days before the start of the test set, with x being the size of the test set.

In contrast, the oracle model is designed to measure the maximum possible number of times we could activate a device using the energy generated during the duration of the test set. This allows us to compare our scheduling framework against a theoretical, perfect maximum. To obtain this maximum number of activations, we simply measure the energy generated in the test set, and divide by the energy required to activate our device.

3.6 Runtime simulation

Yen et al. (2023) have developed a framework for calculating the number of operations various SMFC-powered devices can perform based on measured SMFC voltage traces, accounting for the complex harvesting process required to use SMFC-generated energy. Our work adapts this simulation to use the voltage predictions from our LSTM models, using publicly available python code (Yen, 2023). To evaluate our model's performance, we investigate how many times an SMFC could be used to activate the Cinamin beacon, a low-power device designed exclusively to send BLE advertisement packets (Campbell et al., 2016). On average, this device requires 3.9 μJ to activate. We also make the following modifications to the code:

• The original simulation code uses an estimate of SMFC internal resistance calculated using the one-resistance method used in Fujinaga et al. (2022). We are unable to use this method for the cell which gathered the data used in this paper, since the deployment ended in 2022 and we no longer have access to the cell. However, the cell we used to gather our data is very similar to the v0 cell used in Yen et al. (2023), so we use the same internal resistance of 6,926Ω for our calculations.

• Furthermore, in the absence of a better estimator, a flat harvester efficiency of 60% is used for calculations, based on the lowest efficiency found in the ADP5091/ADP5092 energy harvester datasheet for V_in = 0.5V, V_SYS = 3V, and a lower range of input voltages of 0.01V (Analog Devices, 2016).

3.7 Time-series cross validation

In time-series analysis, models cannot be trained using data from a later time than the data in the validation or testing sets. Doing so would defeat the purpose of making future predictions, since the model would be trained on events taking place after the data used to test the model. Because of this, traditional k-folds cross validation, a method for testing the generalizability of a deep learning model, cannot be used. However, a modified version of k-folds called time-series cross validation can be used to test how well a time-series model generalizes to new data (Howell, 2023). Using this method, we train and test the performance of our deep learning model with 4 different distributions of training, validation, and test datasets. The first of these uses the first 20% of the data to train the model, the next 10% to generate the average voltage used in the naive model, as described in Section 3.5, and the next 10% as the test set to evaluate model performance. The second dataset distribution uses the first 40% of the data as a training set, the next 10% of the data for the naive model, and the next 10% as the test set. The third dataset distribution uses the first 60% of the data as a training set, the next 10% of the data for the naive model, and the next 10% as the test set, and the fourth dataset distribution uses the first 80% of the data as a training set, the next 10% of the data for the naive model, and the final 10% as the test set.

3.8 Generalizability

In order to test how our models generalize to out-of-domain data, we take the models trained on Dataset 1 (deployment), and without modification, test their performance on Dataset 2. As discussed in Section 3.1, these models are trained exclusively on Dataset 1 (deployment), which contains only data from the deployment phase, while Dataset 2 contains only data from an incubation phase. We were unable to acquire a second dataset of deployment data, therefore, it is currently unknown how well our models generalize when validated on never-before-seen deployment data. However, we were able to gain insight on how well a model trained solely on deployment data can predict behavior in a novel incubation. We also trained additional models on Dataset 1 (incubation) to evaluate how well models specifically trained on incubation data can generalize to novel incubation data. Further discussion of this can be found in our results (Section 4.4).

3.9 Removing parameters

The datasets used in this paper require several sensors to collect reliable data in real time. Some sensors are more energy intensive than others—for example, the sensors used to record the voltage and current of SMFC cells in real time are more energy intensive than those used to record soil temperature, electrical conductivity, and volumetric water content. Given the strict energy limitations of SMFC-powered devices, it may be useful for models to be able to make predictions without the use of certain data, in order to limit the energy consumption associated with various sensors. Therefore, we explore how well models trained and validated on Dataset 1 (both incubation and deployment) perform when certain parameters are omitted from the training data. Results can be found in Section 4.5.

4 Results

We present here the final performance of our models, trained across multiple timescales. In order to obtain upper and lower bounds for each prediction as well as a point estimate, we train three separate models for each timescale, using quantile regression: one to predict the upper bound, one to predict the lower bound, and one to predict the median. We evaluate these models using both standard metrics as well as the custom metrics (overestimation, false positive rate and missed activation rate) previously defined in Section 3.4. Unless otherwise specified, the results in this section refer to models trained and validated on Dataset 1 (deployment) described in Section 3.1. However, we also include results from models trained on both parts of Dataset 1 and validated on Dataset 2 in order to test the generalizability of our approach.

4.1 Predictions across different time horizons

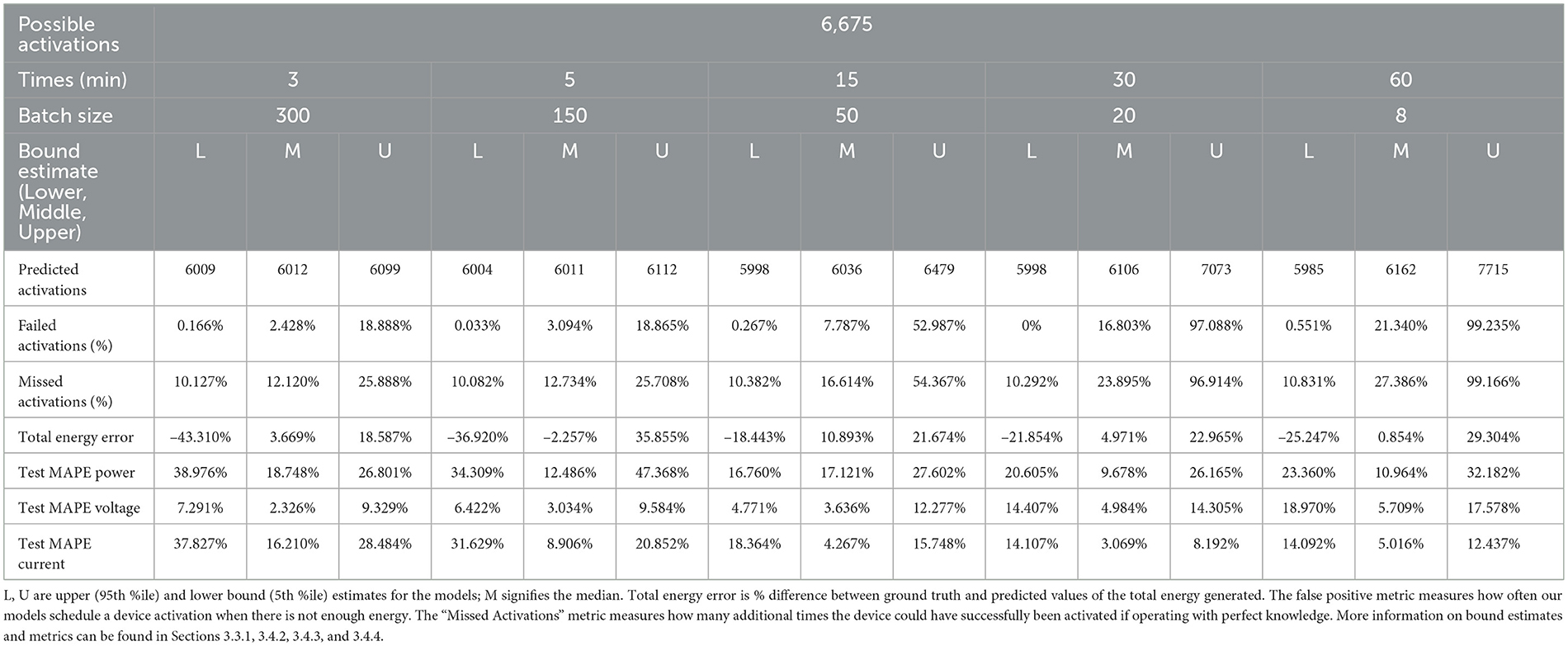
Our models predict average energy generation over 3, 5, 15, 30, and 60 min. In general, models trained at smaller timescales result in less wasted energy. Furthermore, the lower-bound models for each timescale allow for the most efficient use of energy compared to the other models of that timescale. For example, when scheduling device activation using our best performing models—the lower-bound 3 and 5 min models trained and validated on Dataset 1 as described in section 3.1—we only activate the device 0.27% fewer times than if we had made perfect use of available energy. The lower-bound 60 min model, in contrast, misses 0.90% of potential activations.

It is worth noting that in practice, using a model which makes predictions across smaller timescales would require frequent use of our prediction and scheduling framework, resulting in increased energy expenditure. Even checking the amount of energy currently present in the MFC cell, a neccesary function for this framework, requires energy expenditure. Therefore, a scheduling framework that operates every 3 min would have 20 times the operating costs as a model that operates every 60 min. Given the low energy generation of SMFCs, increasing energy efficiency from 99.10 to 99.73% may not be worth this increased energy cost. It may even be worthwhile to explore the performance of models which make predictions at timescales >60 min. Future work will attempt to quantify the costs and benefits across different prediction timescales in more detail, as well as exploring the performance of models which make predictions across longer timescales.

4.2 Evaluating Type 1 model performance

Initial results for our prediction and scheduling algorithm for intermittent SMFC-powered device use are promising. Predictions for a subset of our test set are graphed in Figure 3. We present and discuss our initial results in this section, and Table 2 contains a complete summary of the performance of each model.

Figure 3

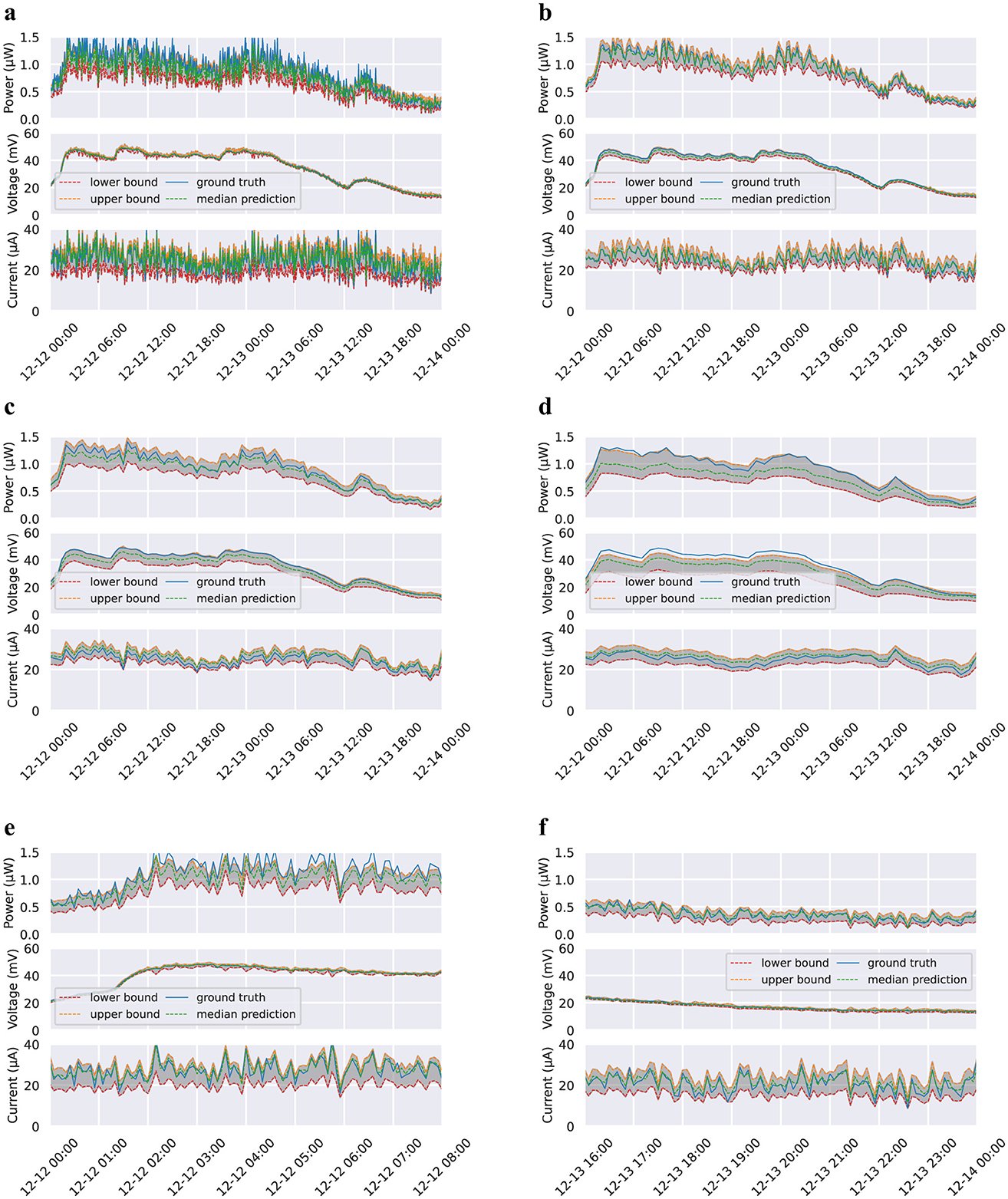
Figure 3. Estimates and prediction interval plots for various time horizons. Lower and upper bound lines refer to the 5th and 95th percentile predictions, respectively. Plots for 3 min time horizon omitted, but performance results are available in Table 2. These figures present a subset of the data in order to provide a more detailed view of model predictions. Since measurements vary so much for the 5 min time horizon, we also provide zoomed in graphs of the first and last 8 h of (A). Dataset and code used for plotting will be open-source and available on Github and Google Colab. (A) 5 min time horizon. (B) 15 min time horizon. (C) 30 min time horizon. (D) 60 min time horizon. (E) First 8 h of 5 min time horizon. (F) Last 8 h of 5 min time horizon.

It is important to note that there are a total of 15 models solely trained and validated on Dataset 1 (deployment), with three models (5th percentile, median/50th percentile, and 95th percentile) for each of the five time horizons (3, 5, 15, 30, and 60 min). We will call all of these models Type 1 models.

Using the lower bound of the model which predicts average energy generation an hour into the future, we schedule device activations for 549 h, or about 23 days. Compared to a naive model which schedules device activations based on the average voltage generated in the past, this framework allows the device to successfully activate a median of 2.08 more times—this is more than a 100% increase in successful operations. Furthermore, when compared to a theoretical model described in Section 3.5 that can perfectly predict and make use of available energy, this framework results in only 4.23% fewer device activations, if we use the worst-performing lower bound model trained with time-series cross validation. In comparison, when we exclude the models trained on only the first 20% of the data, the worst-performing lower bound model schedules only 1.13% less activations than the theoretical maximum.

The performance of the scheduling framework generally—but not always—becomes even stronger the lower the timescale of prediction. However, as discussed in Section 4.1, shorter prediction timescales require increased energy expenditure, and it may not be worth increasing energy cost for improvements in an already high operating efficiency. The tradeoffs between energy consumption and operating efficiency will be further explored in future work.

Another topic for future work will be scheduling different types of device operations, with different functions, energy costs, and consequences for failure. For example, a simple read/record operation could potentially be more aggressively scheduled than a wireless transmission operation, because if the less energy intensive read/record operation fails, the amount of wasted energy is less if the wireless transmission operation had failed.

4.3 Time-series cross validation

At the time of writing, we have no deployment data outside of Dataset 1, which we use to train our Type 1 models. Therefore, in order to test how well our Type 1 models generalize to different distributions of data, we perform time series cross validation to train and evaluate four different models for each timescale. The distribution of each training, validation, and test set is described in Section 3.7. On the whole, the models trained on these data distributions perform fairly strongly. Even the worst performing of the lower-bound estimate models was able to successfully schedule 84.701% of possible device activation when compared to the oracle model defined in Section 3.5. A full table of results for models trained with time series cross validation can be found in Table 3.

Table 3

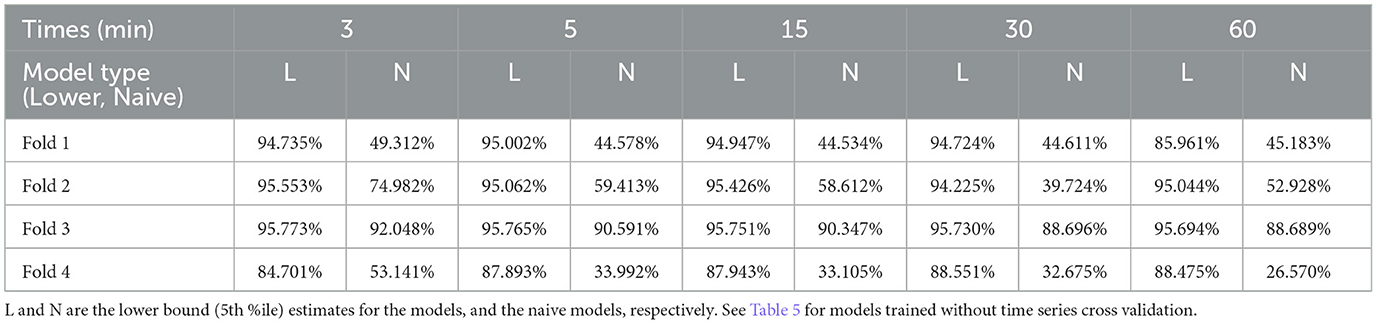
Table 3. Successful device activations for Type 1 models trained using time series cross validation, as described in Section 4.3.

4.4 Model generalizability

The results from Section 4.2 specifically discuss how Type 1 models (which are trained and validated solely on the deployment data from Dataset 1) perform. In this section, we will explore how Type 1 models generalize to out-of-domain data by quantifying how well these models can make predictions on Dataset 2, which contains new SMFCs with soil collected from a completely different location. We also train additional models, which we will call Type 2 models. These models will be trained on the Dataset 1 (incubation), rather than Dataset 1 (deployment). Type 2 models will be validated on the incubation data from Dataset 2.

4.4.1 Type 1 models validated on Dataset 2

At this point in our work, our Type 1 median models are not able to make accurate predictions on the incubation data from Dataset 2. This is not surprising, because cells in the incubation phase have significantly different behavior when compared to deployed cells. The voltage MAPE for Type 1 models validated on Dataset 2 ranges from 26.74 to 171.33%, and the magnitude of the total energy percent difference ranges from 32.77 to 423.75%. By comparison, the voltage MAPE for Type 1 models validated on Dataset 1 (deployment) ranged from 2.33 to 5.71%, and the magnitude of the total energy percent difference ranges from 2.55 to 10.89%.

Although it is clear that Type 1 models (trained on deployment data) poorly predict new incubation data, it remains to be seen how well the models would perform with novel deployment data. Results in Section 4.4.2, which evaluate models trained solely on incubation data and subsequently validate on novel incubation data, suggest that we would likely see significantly improved performance if we were able to validate Type 1 models on novel deployment data. We are actively trying to acquire novel deployment data to try and evaluate how well our Type 1 models generalize to novel deployment data.

4.4.2 Type 2 models validated on Dataset 2

While our Type 1 models were not able to generalize to the incubation data from Dataset 2, our Type 2 models, which were trained on Dataset 1 (incubation), generalize far better. The MAPE for the voltage predictions ranges from 2.65 to 6.43%, and the magnitude of the total energy percent difference ranges from 15.13 to 20.36%. By comparison, the MAPE for the voltage predictions of Type 1 models validated on Dataset 1 (deployment) ranged from 2.33 to 5.71%, and the magnitude of the total energy percent difference ranges from 2.55 to 10.89%.

The good performance of models trained and validated on incubation data from different SMFCs paints an optimistic picture for generalizability when we maintain “apples to apples” comparisons, and do not try to use deployment data to predict incubation behavior (or vice versa). We also attempt to compare these results to the physics-based model from Dziegielowski et al. (2023). Their model is only run on incubation data, similar to our Type 2 models, which were also trained and tested on incubation data. Dziegielowski et al. only provide Relative Error (RE) metrics for their model, so we calculate the same for the sake of comparison. RE is defined as the absolute error (real value minus predicted value), divided by the real value. As shown in Table 4, when averaging across all three soil types used in the Dziegielowski model, 82.7% of predictions had an RE of <10%, and 71.7% of predictions had a relative error of <5%. In contrast, 100% of our model's predictions achieve an RE of <10%. However, only 11% of model's predictions achieve an RE of <5%. This interesting result indicates that our model achieves good performance all the time, but rarely achieves excellent performance. In contrast, the Dziegielowski model exhibits sub-par performance (RE > 10%) for nearly a fifth of its predictions, but also achieves excellent performance (RE < 5%) much more often than our model does. This suggests that there may be opportunities to seek the best of both worlds by exploring techniques like physics-based machine learning (Karniadakis et al., 2021) in the future.

Table 4

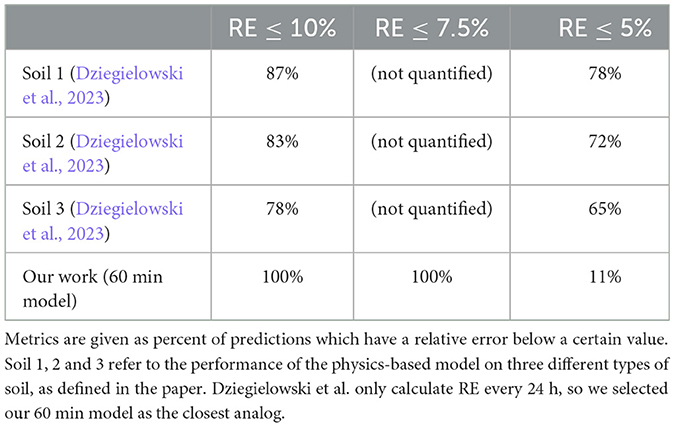
Table 4. Relative errors for our 60 min median Type 2 model (trained and tested on incubation data) and the physics based model from Dziegielowski et al. (2023).

4.5 Performance as a function of training parameters

There can be serious hardware and energy constraints when performing computing in outdoor environments. In real-world deployment situations, users might not have access to all the sensors and computational power used in this paper. This section explores how models perform with the removal of certain training parameters. For example, how will model performance change when temperature, electrical conductivity, or volumetric water content data are omitted? Or if we only use MFC power output at from two previous timesteps instead of 3? This serves as an initial exploration of how well our models would perform with the removal of some of these sensors or computational power.

We train the models in this section with three different combinations of input variables: Type 1A and 2A models, which omit eletricity generation data (voltage, current, and power), Type 1B and 2B models, which omit environmental data (soil temperature, volumetric water content, and electrical conductivity), and the default Type 1 and 2 models, which use all avaiable data. We also describe these different data combinations in Table 1 and in an itemized list below.

1. For Type 1 and 2 models training data includes voltage, current and power of previous three timesteps, soil temperature, electrical conductivity, volumetric water content, as well as the hour of the day and the time since deployment. Type 1 and 2 models also include variants (named Type 1A, Type 2B, etc.) that exclude certain parameters, such as the soil sensor data.

2. For Type 1A and 2A models, training data explicitly omits electricity generaton data, but includes sensor data on soil temperature, electrical conductivity, volumetric water content, as well as the hour of the day and the time since deployment.

3. For Type 1B and 2B models, training data omits soil sensor data, but includes voltage, current and power of previous three timesteps, as well as the hour of the day and the time since deployment.

4.5.1 Type 1 models validated on Dataset 1 (deployment)

All models in this section are trained and validated on data from the June 4th 2021 to January 6th 2022 Stanford deployment.

Type 1: For Type 1 models trained on all available data, the median model achieves between 2.55 and 10.89% for total energy percent difference, and between 2.33 and 5.71% for voltage MAPE.

Type 1A: For Type 1A models, which omit electricty generation data from the training set, our median models do not perform as well: total energy percent difference ranges from 1.0 to 25.1%, and voltage MAPE ranges from 6.9 to 21.7%. However, the lower bound models were still able to predict the lower bound of energy generation successfully, our scheduling framework was able to perform between 88.0 and 89.71% of possible device activations using these predictions. Table 5 compares the successful activation rate of all Type 1 models, as well as the naive model.

Table 5

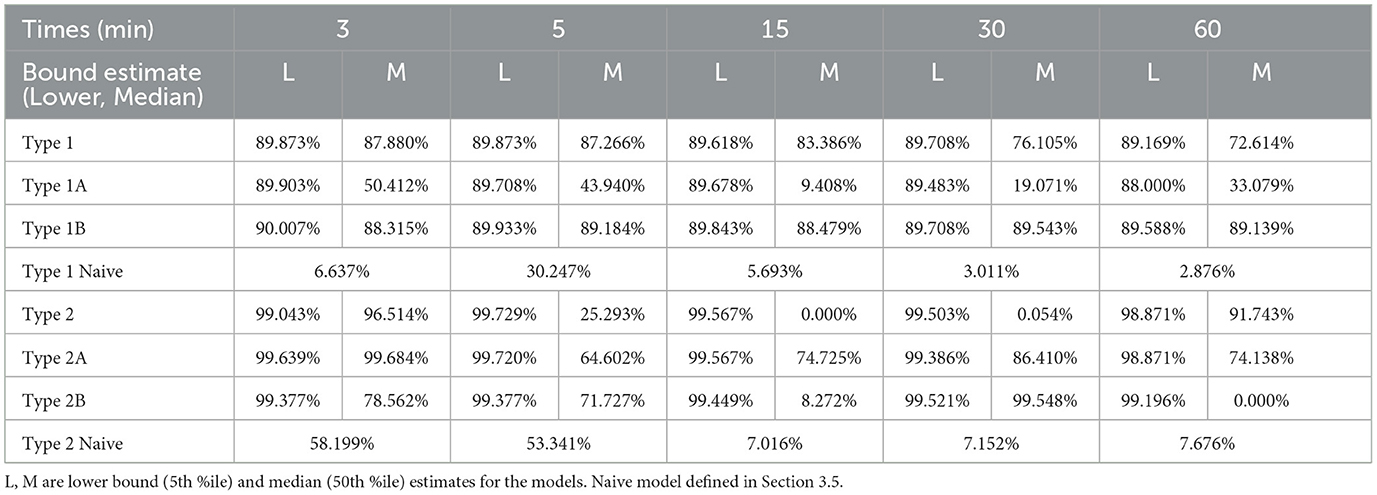
Table 5. Successful device activation rate for models trained without certain types of data, as described in Section 4.5.

Type 1B: However, we are able to achieve impressive accuracy when removing data from entire sensors from the training process. For Type 1B models, which omit environmental data from the training set, our median models still achieve 9.7 to 23.0% total energy percent difference, and 0.4 to 4.9% for voltage MAPE.

4.5.2 Type 2 models validated on Dataset 2

All models in this section are trained on data from the incubation period of Dataset 1 and validated on Dataset 2, which contains exclusively incubation data.

Type 2: For Type 2 models trained on all available data, the median model achieves between 15.13 to 20.36% for total energy percent difference, and between 2.65 and 6.43% for voltage MAPE. Again, we find that removing only one parameter from the data, or limiting the number of previous timesteps, has a negligible effect on the performance of the model.

Type 2A: For Type 2A models, which omit electricity generation data, we once again achieve similar results to the Type 1A models validated on Dataset 1 (deployment): total energy percent difference ranges from 3.0 to 27.0%, and voltage MAPE ranges from 6.7 to 18.7%. Graphs of the performances of these models can be found in Figure 4. Table 5 compares the successful activation rate of all Type 2 models, as well as the naive model.

Figure 4

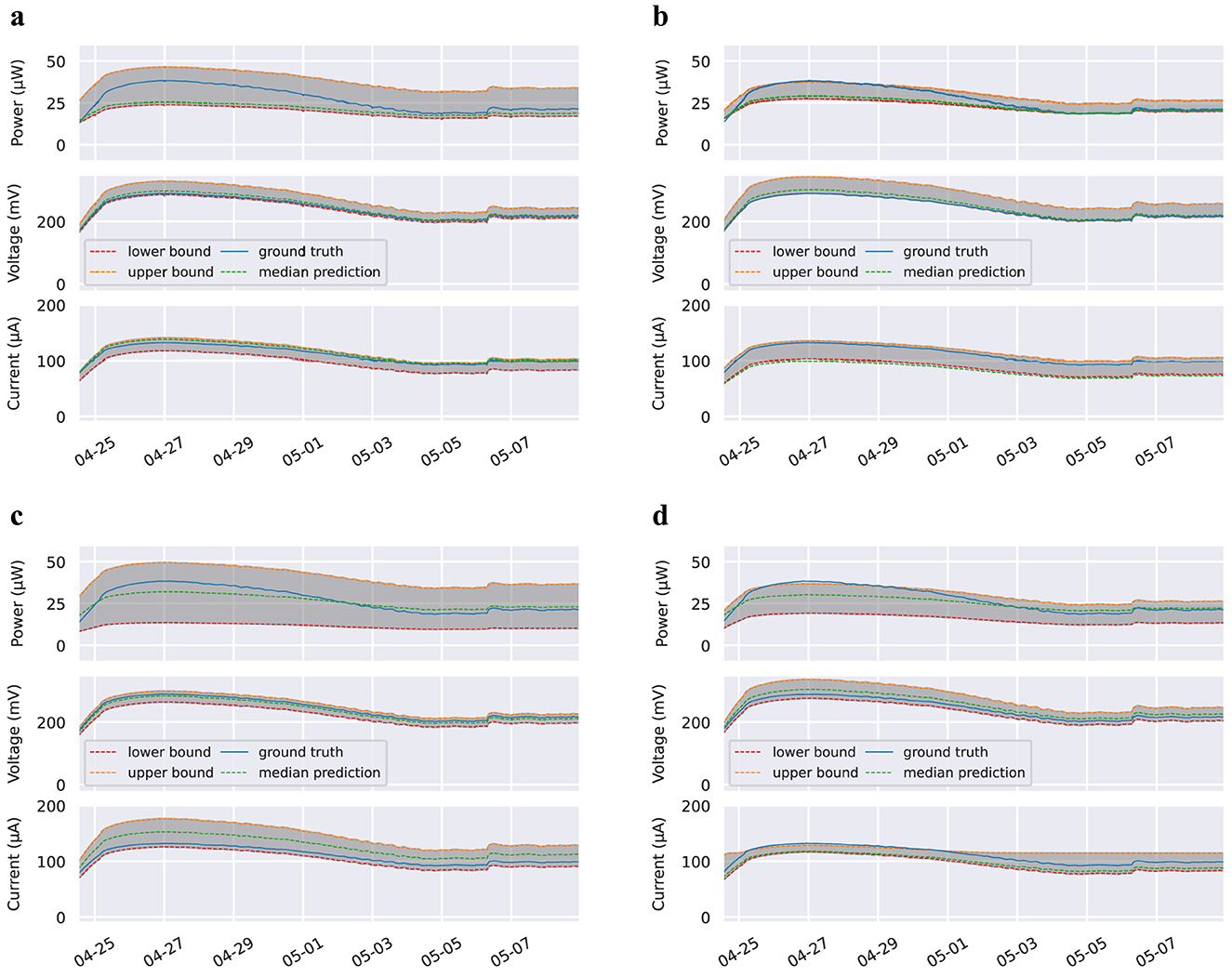
Figure 4. Estimates and prediction interval plots for Type 2 Electricity Generation Omitted models validated on Dataset 2 (incubation). Lower and upper bound lines refer to the 5th and 95th percentile predictions, respectively. Plots for 3 min time horizon omitted. These figures present a subset of the data in order to provide a more detailed view of model predictions. Dataset and code used for plotting will be open-source and available on Github and Google Colab. (A) 5 min time horizon. (B) 15 min time horizon. (C) 30 min time horizon. (D) 60 min time horizon.

Type 2B: For Type 2B models, which omit environmental data, we achieve similar results to the Type 1B models validated on Dataset 1 (deployment): total energy percent difference ranges from 14.2 to 26.8%, and voltage MAPE ranges from 0.5 to 4.9%. Graphs of the performances of these models can be found in Figure 5.

Figure 5

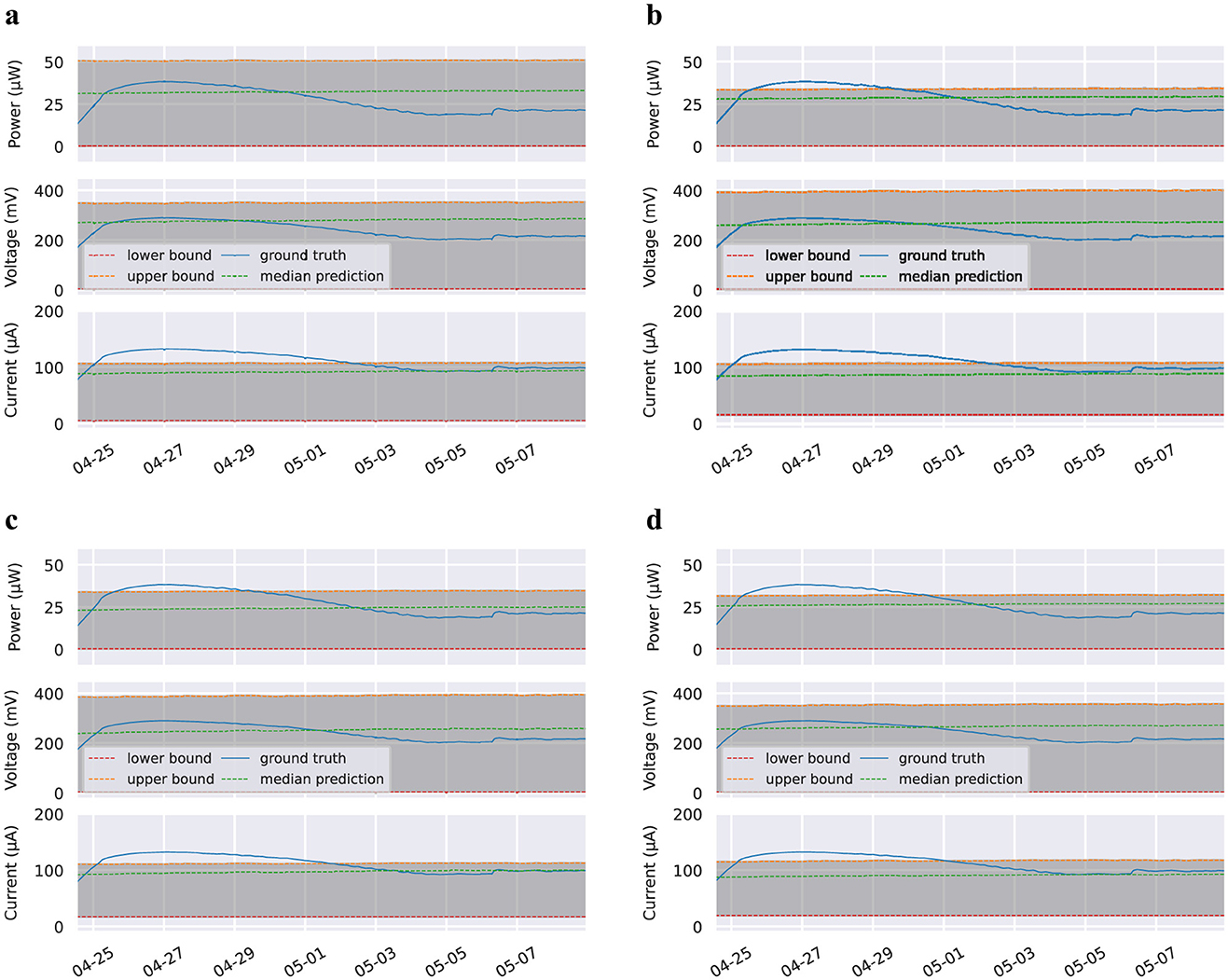
Figure 5. Estimates and prediction interval plots for Type 2 Environmental Data Omitted models validated on Dataset 2 (incubation). Lower and upper bound lines refer to the 5th and 95th percentile predictions, respectively. Plots for 3 min time horizon omitted. These figures present a subset of the data in order to provide a more detailed view of model predictions. Dataset and code used for plotting will be open-source and available on Github and Google Colab. (A) 5 min time horizon. (B) 15 min time horizon. (C) 30 min time horizon. (D) 60 min time horizon.

5 Discussion

5.1 Importance of SMFC energy prediction

The goal of a predictive model for SMFCs is to allow a system to plan future activities to maximize utilization of the harvested energy. This means wasting as little energy as possible while performing the maximum possible number of useful operations. SMFCs do not produce a great deal of energy, so it is vital that the energy they produce is used effectively. Therefore, it is extremely important for an SMFC powered device to activate only when there is sufficient energy available. If our models over-predict the energy available at a given time, attempting to activate a device when there is not sufficient energy available, this wastes our carefully stored energy.

To address this need, we go the single-point estimations most often used in deep learning, and instead generate a range of feasible predictions for energy production. By considering the confidence intervals on these predictions, we can minimize the possibility of wasting energy by activating a device only when there is a high probability of success.

5.2 Notes on performance

When using the predictions of the lower bound model, our scheduling framework rarely over-predicts how much energy will be available, resulting in a low rate of false positives for each timescale, as shown in Table 2. It is notable, however, that the lower bound Type 1 model at the 30 min timescale has 0 false positives, despite this metric generally trending upward as prediction timescales increase. The most likely cause of this is that our models predict three values simultaneously—voltage, current, and power—and so they optimize to predict the desired quantile, on average, across these three values. Because of this, for some models, certain predictions will be lower than the desired quantile. It is not completely unexpected for our framework to predict energy generation more conservatively for some models than others, resulting in device activations being scheduled only when there is enough available energy, resulting in no false positives.

It is also noteworthy that most of our models are able to predict voltage more accurately than current, particularly at lower timescales. This is likely due to the fact that current typically changes far more from moment to moment than voltage does in our dataset, though it tends to be more stable when averaged across larger timescales. This would also explain why current predictions are far less accurate at smaller timescales than larger ones. Furthermore, since power is the product of voltage and current, it makes sense that power is also predicted less accurately than voltage.

In the graph of the 1-h time horizon models in Figure 3, the ground truth voltage and power are greater than the upper bound estimate for the much of the graph. In order to make our graphs more legible, we chose a small subset of the test set to include in the graphs, which happens to include a disproportionate amount of data where the upper bound estimate is lower than the ground truth data for this particular model. However, the upper bound estimate performs much better for the rest of the dataset.

Readers may also note that there is not a monotonic relationship between the length of our prediction intervals and prediction uncertainty, with uncertainty of power predictions being especially variable. As discussed in Section 3.3.1, quantifying the uncertainty of deep learning models is an inherently difficult task. The method we use, quantile regression, attempts to directly predict the upper and lower bounds for each model by modifying the loss function, and there is a certain degree of randomness associated with this task. While we don't have a specific explanation for this variability in prediction uncertainty, it is not entirely unexpected given the nature of deep learning uncertainty quantification, particularly with data as variable as SMFC energy generation.

Finally, we acknowledge that the models in this paper were developed on hardware with more computation power than what is available in most edge computing operations. It may be necessary to modify the models in this paper to work with reduced energy and computation cost, which will likely change the performance. However, a full discussion of how the performance is likely to change is beyond the scope of this paper.

5.3 Limitations of current models

It is currently extremely difficult to collect reliable, timestamped data on both the power generation of a soil microbial fuel cell and the immediate soil conditions (temperature, volumetric water content, and electrical conductivity). It is import to gather data frequently, as our sensed parameters can fluctuate relatively quickly. Temperature typically changes diurnally with sun exposure between day and night, but soil moisture can change dramatically within minutes due to irrigation or weather events. Electrical conductivity varies similarly to moisture, and is also influenced by salinity Because of the difficulty in gathering data, none of the models in this paper have been validated on deployment data from an SMFC that is not also used to train that model. As such, it is currently unknown how well our Type 1 models, which are trained exclusively on the deployment data from Dataset 1, generalize to deployment data from novel SMFCs. Madden et al. (2023) have recently developed specialized logging hardware to gather real-time, accurate data for deployed SMFCs, and this work provides a promising path for making collection of this data easier and more affordable.

That being said, our Type 2 models, which are trained exclusively on the deployment data from Dataset 1, are able to make accurate predictions on Dataset 2, which contains only incubation data. Furthermore, as discussed in Section 4.3, our Type 1 models perform well with time series cross validation, a method designed to test the generalizabilty of a model in the absence of additional data. These results paint an optimistic picture regarding the ability of Type 1 models to generalize to novel deployment data.

5.4 Energy tradeoffs

Given the power limitations of embedded devices, we must consider the energy costs associated with using deep learning to schedule activations of intermittent powered devices. Recent advances in spiking neural networks have allowed certain machine learning tasks to be performed with 75–300 nW of power (Chundi et al., 2021), but this is on custom chip prototypes that are not commercially available. Recent developments have allowed deep learning inference to be performed at low power on commercially available micro-controllers (Sakr et al., 2020). Equation 1 describes the energy cost of running deep learning inference. Taking numbers from commonly-used hardware, we estimate that running a deep learning model should cost a maximum energy of 633.6 μJ per inference, assuming an absolute maximum inference time of 4 ms (Sakr et al., 2020), a typical current consumption of 4.4 μA and a maximum operating voltage of 3.6V (STMicroelectronics, 2020).

$\begin{array}{ll}\text{Energy}=\text{Power}·\text{Time}=\text{Voltage}·\text{Current}·\text{Time}& (1)\end{array}$

It is also possible to perform deep learning inference on the edge, instead of locally. This involves transmitting relevant data to a reliably-powered edge device, which runs the inference, schedules future device activations, and transmits this information back to the intermittently-powered sensor node. However, the energy savings gained by avoiding local inference must be balanced with increased communication costs–in small embedded systems, traditional active-radio wireless communications like WiFi or LoRa can consume orders of magnitude more energy than other system operations (Josephson et al., 2019). The cost of wireless communication can be significantly decreased when using passive RF backscatter based approaches. Backscatter communication has notoriously limited range, but techniques like mobile interrogation, in which a wireless excitation signal is emitted from autonomous UAVs or ground robots (Andrianakis et al., 2021), make it a feasible approach for outdoor sensor networks. This, however, severely constrains communication frequency, as realistically the mobile UAV/robot will be limited to just one or a few sensor node visitations per day. If we want to use a LoRa radio (which isn't bound by the communication constraints of backscatter), even if we assume the minimum possible power cost of 20 mW and the minimum possible uplink and downlink times of 30 and 17 ms respectively, it would still take a minimum of 940 μJ to transmit data and receive inference results (Eric, 2018). This relationship is described in Equation 2.

$\begin{array}{ll}\text{LoRa\_cost}=20\mu W·(20+17)mS=940\mu J& (2)\end{array}$

Even assuming minimum energy constraints, this exceeds the maximum estimated energy cost of running inference locally. A graph of the estimated energy consumption per hour for running inference both locally and on the edge, at different frequencies corresponding to model time horizons, can be found in Figure 6. We can see that running inference locally consumes less energy at every time horizon.

Figure 6

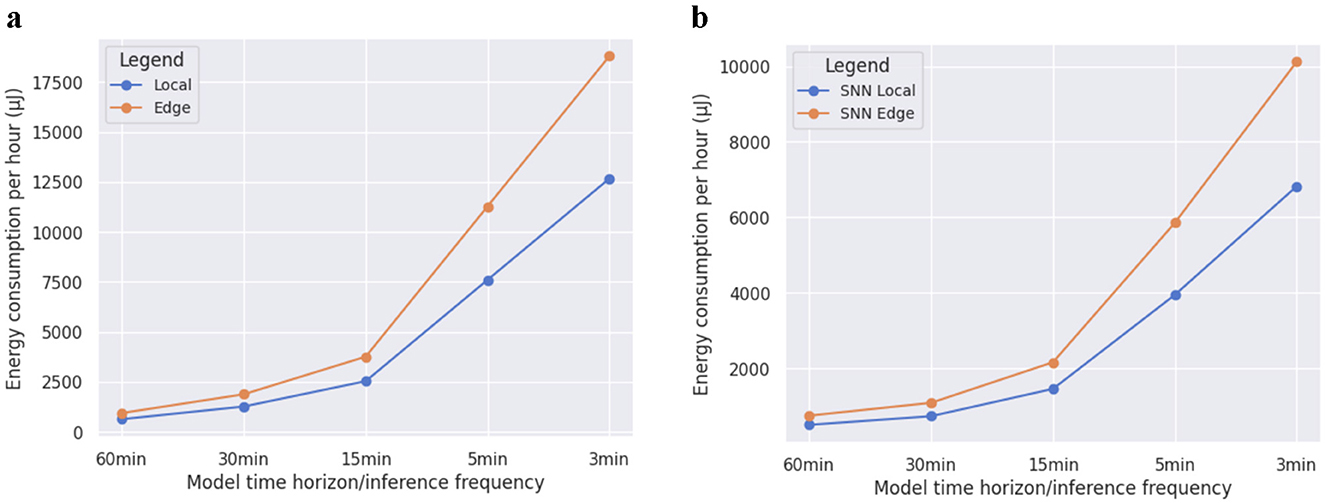
Figure 6. Energy consumption estimates for running models locally and on the edge for various time horizons/frequencies. (A) Estimated energy consumption for traditional ANNs. (B) Estimated energy consumption for SNNs.

Our scheduling framework also relies on knowing the actual energy stored in the capacitor at the beginning of each timestep. It takes ~22.5 μJ to measure the amount of energy in the capacitor and record it to nonvolatile memory, which is significantly less than the energy cost of local inference and LoRa radio usage. However, this energy consumption could still prove costly for an SMFC-powered device, especially for more frequent prediction horizons. For example, we would need to perform inference twenty times more often for a 3 min prediction horizon than for a 60 min prediction horizon. During deployment, the SMFC from Dataset 1 generated 422.6 μJ per hour, on average. This is enough power to check the capacitor once every 3.2 min. However, since the energy generation of SMFCs is wildly variable, we will not always have this amount of energy readily available. For example, during the last month of the deployment, the SMFC from Dataset 1 was generating an average of 48.5 μJ per hour, enough to check the capacitor once every 27.8 min.

To explore the tradeoffs between the various compute-communication architectures, we analyze four core use cases: (1) passive communications with edge inference, (2) active communication with local inference, (3) active communication with edge inference, and (4) passive communication with local inference. There are many more complex approaches to the compute-communication tradeoff, such as hybrid approaches that perform both local and edge inference, but in this paper we restrict our analysis to the four cases below.

5.4.1 Passive communication with local inference

This use case combines passive communication with local inference. Per Equation 1, we anticipate consuming an estimated 633.6 μJ per inference. The advantages to passive communication with local inference are that we can run the inference as frequently as our energy budget allows, and are not limited to the possibly constrained communication schedule of the passive device. However, the passive communication approach limits how frequently we can transmit our data to its intended destination (e.g. a database in the cloud). This and other factors makes this approach difficult to effectively implement. Zhao et al. (2022) created the only end-to-end implementation we are aware of, though a number of other works have explored approaches to intermittent ML without considering the impact of wireless communication (Montanari et al., 2020; Bakar et al., 2023; Islam and Nirjon, 2020; Gobieski et al., 2019; Lee et al., 2020). Our models make it easier to budget power for wireless communication in these embedded ML systems, and could lead to an increase in future intermittent systems able to implement passive communications with local inference.

5.4.2 Active communication with local inference

This use case combines active communication with local inference. We assume a LoRa radio, which per Equation 2, consumes an estimated minimum of 940 μJ to transmit data and receive inference results. Since inference is done locally, we would not have the same communication frequency constraints as with passive communication systems leveraging edge inference. Furthermore, the use of active communication would allow us to back up our data to an external storage more frequently, if needed, while still enjoying the reduced energy costs of local inference. A recent example of a system that uses an active communication/local inference approach is Desai et al. (2022), which performs local inference on image data and uses LoRa to communicate results.

5.4.3 Active communication with edge inference

While this approach still allows us to backup data to an external source more frequently than with passive communication, running inference on the edge means we need to transmit and receive data at regular intervals. Since local inference is less energy intensive than transmitting and receiving data—633.6 μJ per inference compared to 940 μJ to transmit data and receive inference results this option consumes more energy than active communication with local inference. Assuming the models run on the edge and those run on the embedded device are identical, this active communications/edge inference would not have any additional benefits over the active communication/local inference approach. However, models running on embedded devices often need to be significantly modified in order to operate successfully within resource constraints, and as a consequence may suffer from losses in accuracy. Therefore, an additional trade off of inference accuracy vs. energy cost is something that system designers must also consider. Works like Naderiparizi et al. (2017) and Chinchali et al. (2018) attempt to decrease the cost of communication by reducing the amount of data sent off-device, while hybrid approaches like Chinchali et al. (2021), Zeng et al. (2021), and Ben Ali et al. (2022) perform both local and edge inference depending on the necessary accuracy and available resources.

5.4.4 Passive communication with edge inference

This final use case combines passive communication with edge inference. Out of the four use cases proposed, this one is the least energy intensive with respect to the embedded device, as there is no active radio chain and no on-device computation resources are used for inference. Instead, the system transmits and receives data over short range using RF backscatter communication, which consumes several orders of magnitude less energy than LoRa (Andrianakis et al., 2021). A number of works have used this approach: Josephson et al. (2019), Wang and Xie (2020), and Saffari et al. (2021). An important drawback to pairing this approach with our energy income modeling is that due to the low communication frequency, the edge inference would have to predict energy income significantly further into the future—8, 12 or 24+ h. These time horizons are significantly larger than the <1 h horizons explored in Section 3.4, but initial tests suggest we would still be able to achieve 60%–85% of maximum possible operations.

5.5 Reducing inference costs

In this section, we explore the benefits of spiking neural networks (SNNs) compared to traditional artifical neural networks (ANNs), both in terms of energy efficiency and overall accuracy. First, we define a spiking neural network, and subsequently test its performance and compare it against non-spiking models.

ANNs and SNNs can model similar network topologies, but SNNs use spiking neurons instead of artificial neurons. Like artificial neurons (Rosenblatt, 1958), spiking neurons compute a weighted sum of inputs. Instead of applying a nonlinearity like sigmoid or ReLU, this sum contributes to the membrane potential U(t). When U(t) reaches a threshold θ, the neuron spikes, sending a signal to its connections. This introduces temporal dynamics that maintain the membrane potential over time.

One of the simplest and most common spiking neuron models is based on a low-pass filter constructed of resistive channels in thin-film membrane in spiking neurons, and capactive dynamics from the insulating thin-film of the bilipid membrane. This is represented by a simple RC circuit:

$\begin{array}{ll}\tau \frac{dU(t)}{dt}=-U(t)+I_{\text{in}}(t)R& (3)\end{array}$

where τ = RC is the time constant. The Forward-Euler method can be used to solve this equation, and along with several approximations that reduce the number of hyperparameters, the following solution is derived which describes a single leaky integrate-and-fire neuron in discrete-time form:

$\begin{array}{ll}U\left[t\right]=\beta U\left[t-1\right]+(1-\beta )I_{\text{in}}\left[t\right]& (4)\end{array}$

where β = e^−1/τ is the decay rate, and time is discretized. The coefficient of input current (1 − β) becomes a learnable weight W, simplifying to I_in[t] = WX[t]. For a single input to a neuron:

$\begin{array}{ll}U\left[t\right]=\beta U\left[t-1\right]+WX\left[t\right]-S_{\text{out}}\left[t-1\right]\theta & (5)\end{array}$

Here, S_out[t] ∈ 0, 1 is the output spike, which resets the membrane potential if activated. A spike is generated if:

$\begin{array}{ll}{S}_{\text{out}}\left[t\right]=\{\begin{array}{ll}1,& \text{if }U\left[t\right]>\theta \\ 0,& \text{otherwise.}\end{array}& (6)\end{array}$

Relating SNNs back to deep learning, this formulation in discrete-time recasts SNNs as a simple RNN with a diagonal recurrent matrix, i.e., each neuron is only recurrent with itself. Such models are considered efficient for computation because SNNs can be trained with an objective function that reduces firing activity, and as a result, there is less data traffic to access weights that are stored in main memory. This memory access is the dominant cost of deep learning.

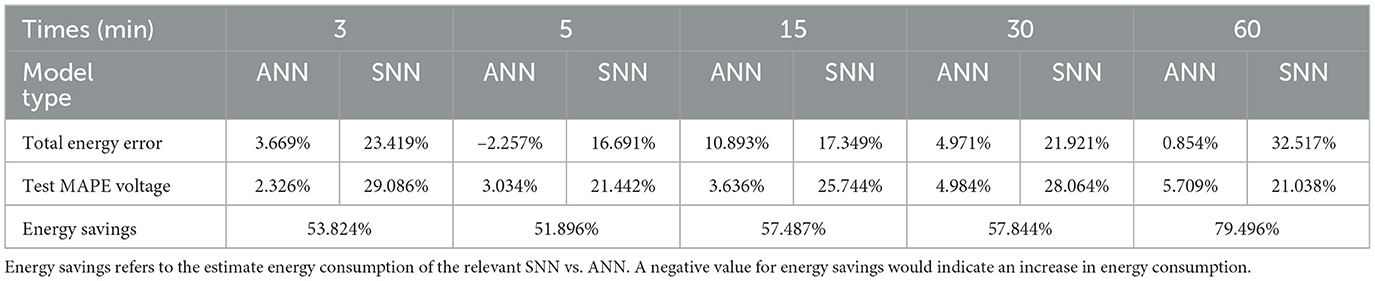
Estimating the energy consumption of a neural network is extremely difficult to do without directly running it on the desired hardware, but we can approximate the energy consumption of two neural networks relative to one another by measuring the number of floating point operations required to perform a single round of inference. Using this method, we find that Type 1 SNNs [which are trained on Dataset 1 (deployment)] are between 1.26 and 1.86 times more energy efficient than the traditional Type 1 ANNs presented in this paper. We also find the energy efficiency decreases at higher model timesteps, with the 3 min models being the most energy efficient and the 60 min models being the least energy efficient.

However, SNN models are not yet as accurate as their traditional ANN counterparts. For each Type 1 median model, we created our own SNN variants to quantify the differences in accuracy. These SNNs are all trained with the snnTorch framework developed by Eshraghian et al. (2023).¹ When validated on Dataset 1 (deployment), the Type 1 SNN median models achieve between 16.69 and 32.52% for total energy percent difference, and between 21.03 and 29.09% for voltage MAPE. By contrast, when validated on Dataset 1 (deployment), the traditional ANN median models achieve between 2.55 and 10.89% for total energy percent difference, and between 2.33 and 5.71% for voltage MAPE. A complete summary of the Type 1 SNN performances compared to the Type 1 ANNs can be found in Table 6.

Table 6

Table 6. Performance metrics for Type 1 ANN and SNN models presented in Section 5.5.

6 Conclusion and future work

Soil Microbial Fuel Cells show great potential as a renewable source of clean energy, but the unpredictability of their energy generation poses a significant challenge in their adoption. Our work attempts to address this challenge by modeling and predicting SMFC energy generation with deep learning, and is the first work to do so at the time of writing. We also simulate how our predictions could be used in a real-world deployment setting to perform useful tasks, and how effective these predictions would be in practice.

One of our highest priorities going forward is to gather novel deployment data which we can use to validate our Type 1 models, which are trained exclusively on deployment data. As discussed in Section 4.4.2, Type 2 models, which are trained exclusively on incubation data, are able to generalize well to novel incubation data. This paints an optimistic picture of how Type 1 models will generalize to novel deployment data, but we won't be sure of this until we acquire new deployment data to use for validation. We would also like to gather data on soil pH for future work, as it is well known that pH can impact fuel cell performance (Jadhav and Ghangrekar, 2009). To the best of our knowledge, there are no commercially-available continuous real time pH measurement systems for soil that do not require soil pre-treatment. Most of our data was collected from an active farm where this was not practical, which is why we did not consider pH in this work.

Another important area of future work involves considering the fact that the operation of the model itself consumes valuable harvested energy. There are opportunities to better quantify the tradeoffs of predicting energy availability and scheduling tasks across various timeframes, as well as accounting for the different types of device operations that would be performed by an SMFC-powered system. The framework scheduling presented by Islam and Nirjon (2020) successfully accounts for a range of tasks for intermittently powered (but not SMFC-powered) systems, outperforming state-of-the-art task schedulers, and we will need to determine to what extent this approach can be adapted to SMFC-powered devices. In Figure 6, we graph the expected energy needed to power models making predictions across various different timesteps. In Section 5.4, we provide an energy breakdown of various components that could be used to implement our scheduling framework, as well as the average energy generated in deployment by the SMFC from Dataset 1. However, these values are likely to change depending on the hardware and environmental conditions present in future deployments.

We believe the results presented in this paper represent a significant step toward realizing the potential of Soil Microbial Fuel Cells a renewable source of clean energy, and we look to continuing this promising line of research.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AH-D: Conceptualization, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. HK: Data curation, Investigation, Software, Writing – original draft, Writing – review & editing. ST: Data curation, Writing – review & editing. DL: Methodology, Software, Writing – review & editing. JE: Formal analysis, Methodology, Supervision, Writing – original draft. CJ: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Project administration, Resources, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by FFAR grant #22-000093. The content of this publication is solely the responsibility of the authors and does not necessarily represent the official views of the Foundation for Food and Agriculture Research (FFAR).

Acknowledgments

We thank Todd Farrell for his early feedback and guidance, as well as the Stanford Educational Farm for hosting the original soil microbial fuel cell field deployment.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2024.1447745/full#supplementary-material

Footnotes

1. ^More information can be found on the public Github repository created by Hess-Dunlop et al. (2024).

References

Abbas, S. Z., Wang, J.-Y., Wang, H., Wang, J.-X., Wang, Y.-T., Yong, Y.-C., et al. (2022). Recent advances in soil microbial fuel cells based self-powered biosensor. Chemosphere 303:135036. doi: 10.1016/j.chemosphere.2022.135036

PubMed Abstract | Crossref Full Text | Google Scholar

Analog Devices (2016). Ultralow Power Energy Harvester PMUs with MPPT and Charge Management. Available at: https://www.analog.com/media/en/technical-documentation/data-sheets/ADP5091-5092.pdf

Google Scholar

Andrianakis, E., Vougioukas, G., Giannelos, E., Giannakopoulos, O., Apostolakis, G., Skyvalakis, K., et al. (2021). “Drone interrogation (and its low-cost alternative) in backscatter environmental sensor networks,” in 2021 6th International Conference on Smart and Sustainable Technologies (Bol and Split: SpliTech), 1–6. doi: 10.23919/SpliTech52315.2021.9566340

Crossref Full Text | Google Scholar

Bakar, A., Goel, R., de Winkel, J., Huang, J., Ahmed, S., Islam, B., et al. (2023). “Protean: an energy-efficient and heterogeneous platform for adaptive and hardware-accelerated battery-free computing,” in Proceedings of the 20th ACM Conference on Embedded Networked Sensor Systems, SenSys '22 (New York, NY: Association for Computing Machinery), 207–221. doi: 10.1145/3560905.3568561

Crossref Full Text | Google Scholar

Ben Ali, A. J., Kouroshli, M., Semenova, S., Hashemifar, Z. S., Ko, S. Y., Dantu, K., et al. (2022). Edge-slam: edge-assisted visual simultaneous localization and mapping. ACM Trans. Embed. Comput. Syst. 22:18. doi: 10.1145/3561972

Crossref Full Text | Google Scholar

Campbell, B., Adkins, J., and Dutta, P. (2016). “Cinamin: a perpetual and nearly invisible ble beacon,” in Proceedings of the 2016 International Conference on Embedded Wireless Systems and Networks, EWSN '16 (Shippensburg, PA: Junction Publishing), 331–332.

Google Scholar

Chinchali, S., Sharma, A., Harrison, J., Elhafsi, A., Kang, D., Pergament, E., et al. (2021). Network offloading policies for cloud robotics: a learning-based approach. Auton. Robots 45, 997–1012. doi: 10.1007/s10514-021-09987-4

Crossref Full Text | Google Scholar

Chinchali, S. P., Cidon, E., Pergament, E., Chu, T., and Katti, S. (2018). “Neural networks meet physical networks: distributed inference between edge devices and the cloud,” in Proceedings of the 17th ACM Workshop on Hot Topics in Networks, HotNets '18 (New York, NY: Association for Computing Machinery), 50–56. doi: 10.1145/3286062.3286070

Crossref Full Text | Google Scholar

Chundi, P., Wang, D., Kim, S., Yang, M., Cerqueira, J., Kang, J., et al. (2021). Always-on sub-microwatt spiking neural network based on spike-driven clock- and power-gating for an ultra-low-power intelligent device. Front. Neurosci. 15:684113. doi: 10.3389/fnins.2021.684113

PubMed Abstract | Crossref Full Text | Google Scholar

Desai, H., Nardello, M., Brunelli, D., and Lucia, B. (2022). Camaroptera: a long-range image sensor with local inference for remote sensing applications. ACM Trans. Embed. Comput. Syst. 21:32. doi: 10.1145/3510850

Crossref Full Text | Google Scholar

Dziegielowski, J., Mascia, M., Metcalfe, B., and Di Lorenzo, M. (2023). Voltage evolution and electrochemical behaviour of soil microbial fuel cells operated in different quality soils. Sustain. Energy Technol. Assess. 56:103071. doi: 10.1016/j.seta.2023.103071

Crossref Full Text | Google Scholar

Eric, B. (2018). Available at: https://lora.readthedocs.io/en/latest/

Google Scholar

Eshraghian, J. K., Ward, M., Neftci, E., Wang, X., Lenz, G., Dwivedi, G., et al. (2023). Training spiking neural networks using lessons from deep learning. Proc. IEEE 111, 1016–1054. doi: 10.1109/JPROC.2023.3308088

Crossref Full Text | Google Scholar

Feng, Y., Xie, Y., Ganesan, D., and Xiong, J. (2023). “LTE-based low-cost and low-power soil moisture sensing,” in Proceedings of the 20th ACM Conference on Embedded Networked Sensor Systems, SenSys '22 (New York, NY: Association for Computing Machinery), 421–434. doi: 10.1145/3560905.3568525

Crossref Full Text | Google Scholar

Fujinaga, A., Umeda, S., Heya, M., Ogata, H., and Kishimoto, N. (2022). Evaluation of methods for measuring internal resistances of discharging microbial fuel cells. J. Water Environ. Technol. 20, 1–10. doi: 10.2965/jwet.21-087

Crossref Full Text | Google Scholar

Gawlikowski, J., Tassi, C. R. N., Ali, M., Lee, J., Humt, M., Feng, J., et al. (2023). A survey of uncertainty in deep neural networks. Artif. Intell. Rev. 56, 1513–1589. doi: 10.1007/s10462-023-10562-9

Crossref Full Text | Google Scholar

Gobieski, G., Lucia, B., and Beckmann, N. (2019). “Intelligence beyond the edge: inference on intermittent embedded systems,” in Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems, ASPLOS '19 (New York, NY: Association for Computing Machinery), 199–213. doi: 10.1145/3297858.3304011

Crossref Full Text | Google Scholar

Hess-Dunlop, A., Kakani, H., and Josephson, C. (2024). Available at: https://github.com/jlab-sensing/MFC_Modeling (accessed December 16, 2024).

Google Scholar

Howell, E. (2023). How to correctly perform cross-validation for time series.

Google Scholar

Islam, B., and Nirjon, S. (2020). Zygarde: time-sensitive on-device deep inference and adaptation on intermittently-powered systems. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 4:82. doi: 10.1145/3411808

Crossref Full Text | Google Scholar

Jadhav, G., and Ghangrekar, M. (2009). Performance of microbial fuel cell subjected to variation in pH, temperature, external load and substrate concentration. Bioresour. Technol. 100, 717–723. doi: 10.1016/j.biortech.2008.07.041

PubMed Abstract | Crossref Full Text | Google Scholar

Josephson, C., Jackson, N., and Pannuto, P. (2020). Farming electrons: Galvanic versus microbial energy in soil batteries. IEEE Sens. Lett. 4, 1–4. doi: 10.1109/LSENS.2020.3043666

Crossref Full Text | Google Scholar

Josephson, C., Kotaru, M., Winstein, K., Katti, S., and Chandra, R. (2021). “Low-cost in-ground soil moisture sensing with radar backscatter tags,” in Proceedings of the 4th ACM SIGCAS Conference on Computing and Sustainable Societies, COMPASS '21 (New York, NY: Association for Computing Machinery), 299–311. doi: 10.1145/3460112.3472326

Crossref Full Text | Google Scholar

Josephson, C., Shuai, W., Marcano, G., Pannuto, P., Hester, J., Wells, G., et al. (2022). The future of clean computing may be dirty. GetMobile: Mobile Comp. Comm. 26, 9–15. doi: 10.1145/3568113.3568117

Crossref Full Text | Google Scholar

Josephson, C., Yang, L., Zhang, P., and Katti, S. (2019). “Wireless computer vision using commodity radios,” in Proceedings of the 18th International Conference on Information Processing in Sensor Networks, IPSN '19 (New York, NY: Association for Computing Machinery), 229–240. doi: 10.1145/3302506.3310403

Crossref Full Text | Google Scholar

Karniadakis, G. E., Kevrekidis, I. G., Lu, L., Perdikaris, P., Wang, S., Yang, L., et al. (2021). Physics-informed machine learning. Nat. Rev. Phys. 3, 422–440. doi: 10.1038/s42254-021-00314-5

Crossref Full Text | Google Scholar

Kashyap, B., and Kumar, R. (2021). Sensing methodologies in agriculture for soil moisture and nutrient monitoring. IEEE Access 9, 14095–14121. doi: 10.1109/ACCESS.2021.3052478

Crossref Full Text | Google Scholar

Lee, S., Islam, B., Luo, Y., and Nirjon, S. (2020). Intermittent learning: on-device machine learning on intermittently powered system. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 3:141. doi: 10.1145/3369837

Crossref Full Text | Google Scholar

Lucia, B., Balaji, V., Colin, A., Maeng, K., and Ruppel, E. (2017). “Intermittent computing: challenges and opportunities,” in 2nd Summit on Advances in Programming Languages (SNAPL 2017) volume 71 of Leibniz International Proceedings in Informatics (LIPIcs) (Dagstuhl: Schloss Dagstuhl-Leibniz-Zentrum fur Informatik), 8:1–8:14.

Google Scholar

Madden, J., Marcano, G., Taylor, S., Pannuto, P., and Josephson, C. (2023). “Hardware to enable large-scale deployment and observation of soil microbial fuel cells,” in Proceedings of the 20th ACM Conference on Embedded Networked Sensor Systems, SenSys '22 (New York, NY: Association for Computing Machinery), 906–912. doi: 10.1145/3560905.3568110

Crossref Full Text | Google Scholar

Marcano, G., and Pannuto, P. (2021). “Powering an e-ink display from soil bacteria,” in Proceedings of the 19th ACM Conference on Embedded Networked Sensor Systems, SenSys '21 (New York, NY: Association for Computing Machinery), 590–591. doi: 10.1145/3485730.3493363

Crossref Full Text | Google Scholar

Meter (2018). Available at: https://metergroup.com/products/teros-12/

Google Scholar

Montanari, A., Sharma, M., Jenkus, D., Alloulah, M., Qendro, L., Kawsar, F., et al. (2020). “Eperceptive: energy reactive embedded intelligence for batteryless sensors,” in Proceedings of the 18th Conference on Embedded Networked Sensor Systems, SenSys '20 (New York, NY: Association for Computing Machinery), 382–394. doi: 10.1145/3384419.3430782

Crossref Full Text | Google Scholar

Naderiparizi, S., Zhang, P., Philipose, M., Priyantha, B., Liu, J., Ganesan, D., et al. (2017). “Glimpse: a programmable early-discard camera architecture for continuous mobile vision,” in Proceedings of the 15th Annual International Conference on Mobile Systems, Applications, and Services, MobiSys '17 (New York, NY: Association for Computing Machinery), 292–305. doi: 10.1145/3081333.3081347

Crossref Full Text | Google Scholar

Olias, L. G., Otero, A. R., Cameron, P. J., and Di Lorenzo, M. (2020). A soil microbial fuel cell-based biosensor for dissolved oxygen monitoring in water. Electrochim. Acta 362:137108. doi: 10.1016/j.electacta.2020.137108

Crossref Full Text | Google Scholar

Rajak, P., Ganguly, A., Adhikary, S., and Bhattacharya, S. (2023). Internet of things and smart sensors in agriculture: scopes and challenges. J. Agric. Food Res. 14:100776. doi: 10.1016/j.jafr.2023.100776

PubMed Abstract | Crossref Full Text | Google Scholar

Rodrigues, F., and Pereira, F. C. (2018). Beyond expectation: Deep joint mean and quantile regression for spatio-temporal problems. IEEE Trans. Neural Netw. Learn. Syst. 31, 5377–5389.

PubMed Abstract | Google Scholar

Rosenblatt, F. (1958). The perceptron: a probabilistic model for information storage and organization in the brain. Psychol. Rev. 65, 386–408. doi: 10.1037/h0042519

PubMed Abstract | Crossref Full Text | Google Scholar

Rossini, P. R., Ciampitti, I. A., Hefley, T., and Patrignani, A. (2021). A soil moisture-based framework for guiding the number and location of soil moisture sensors in agricultural fields. Vadose Zone J. 20:e20159. doi: 10.1002/vzj2.20159

Crossref Full Text | Google Scholar

Saffari, A., Tan, S. Y., Katanbaf, M., Saha, H., Smith, J. R., Sarkar, S., et al. (2021). “Battery-free camera occupancy detection system,” in Proceedings of the 5th International Workshop on Embedded and Mobile Deep Learning, EMDL'21 (New York, NY: Association for Computing Machinery), 13–18. doi: 10.1145/3469116.3470013

Crossref Full Text | Google Scholar

Sakr, F., Bellotti, F., Berta, R., and De Gloria, A. (2020). Machine learning on mainstream microcontrollers. Sensors 20:2638. doi: 10.3390/s20092638

PubMed Abstract | Crossref Full Text | Google Scholar

Sigrist, L., Gomez, A., Lim, R., Lippuner, S., Leubin, M., Thiele, L., et al. (2017). “Measurement and validation of energy harvesting IOT devices,” in Design, Automation &Test in Europe Conference &Exhibition (DATE) (Lausanne), 1159–1164. doi: 10.23919/DATE.2017.7927164

Crossref Full Text | Google Scholar

Srivastava, S., and Lessmann, S. (2018). A comparative study of LSTM neural networks in forecasting day-ahead global horizontal irradiance with satellite data. Solar Energy 162, 232–247. doi: 10.1016/j.solener.2018.01.005

Crossref Full Text | Google Scholar

Steinwart, I., and Christmann, A. (2011). Estimating conditional quantiles with the help of the pinball loss. Bernoulli 17, 211–225. doi: 10.3150/10-BEJ267

PubMed Abstract | Crossref Full Text | Google Scholar

STMicroelectronics (2020). Available at: https://www.st.com/resource/en/datasheet/DM00037051.pdf

Google Scholar

Wang, B., and Xie, Z. (2020). “Study on indoor human behavior detection based on wisp,” in Data Science: 6th International Conference, ICDS 2019, Ningbo, China, May 15-20, 2019, Revised Selected Papers 6 (Cham: Springer), 255–265. doi: 10.1007/978-981-15-2810-1_25

Crossref Full Text | Google Scholar

Wang, S.-H., Wang, J.-W., Zhao, L.-T., Abbas, S. Z., Yang, Z., Yong, Y.-C., et al. (2023). Soil microbial fuel cell based self-powered cathodic biosensor for sensitive detection of heavy metals. Biosensors 13:145. doi: 10.3390/bios13010145

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, Y., Gan, D., Sun, M., Zhang, N., Lu, Z., Kang, C., et al. (2019). Probabilistic individual load forecasting using pinball loss guided lstm. Appl. Energy 235, 10–20. doi: 10.1016/j.apenergy.2018.10.078

Crossref Full Text | Google Scholar

Xu, C., Sun, Y., Du, A., and Gao, D. (2023). Quantile regression based probabilistic forecasting of renewable energy generation and building electrical load: a state of the art review. J. Build. Eng. 79:107772. doi: 10.1016/j.jobe.2023.107772

Crossref Full Text | Google Scholar

Yen (2023). Ka moamoa practical SMFC design guide. Available at: https://github.com/ka-moamoa/Practical_SMFC_Design_Guide

Google Scholar

Yen, B., Jaliff, L., Gutierrez, L., Sahinidis, P., Bernstein, S., Madden, J., et al. (2023). Soil-powered computing: The engineer's guide to practical soil microbial fuel cell design. Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies, Vol. 7, 1–40. doi: 10.1145/3631410

Crossref Full Text | Google Scholar

Ying, C., Wang, W., Yu, J., Li, Q., Yu, D., Liu, J., et al. (2023). Deep learning for renewable energy forecasting: A taxonomy, and systematic literature review. J. Clean. Prod. 384:135414. doi: 10.1016/j.jclepro.2022.135414

Crossref Full Text | Google Scholar

Zeng, L., Chen, X., Zhou, Z., Yang, L., and Zhang, J. (2021). Coedge: cooperative dnn inference with adaptive workload partitioning over heterogeneous edge devices. IEEE/ACM Trans. Netw. 29, 595–608. doi: 10.1109/TNET.2020.3042320

Crossref Full Text | Google Scholar

Zhao, Y., Afzal, S. S., Akbar, W., Rodriguez, O., Mo, F., Boyle, D., et al. (2022). “Towards battery-free machine learning and inference in underwater environments,” in Proceedings of the 23rd Annual International Workshop on Mobile Computing Systems and Applications, HotMobile '22 (New York, NY: Association for Computing Machinery), 29–34. doi: 10.1145/3508396.3512877

Crossref Full Text | Google Scholar

Zotarelli, L., Dukes, M. D., and Paranhos, M. (2016). Minimum number of soil moisture sensors for monitoring and irrigation purposes. J. Irrig. Drain. Eng. doi: 10.32473/edis-hs1222-2013

Crossref Full Text | Google Scholar

Zotarelli, L., Scholberg, J. M., Dukes, M. D., Muoz-Carpena, R., and Icerman, J. (2009). Tomato yield, biomass accumulation, root distribution and irrigation water use efficiency on a sandy soil, as affected by nitrogen rate and irrigation scheduling. Agric. Water Manag. 96, 23–34. doi: 10.1016/j.agwat.2008.06.007

Crossref Full Text | Google Scholar