
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci., 01 November 2024
Sec. Space Physics
Volume 11 - 2024 | https://doi.org/10.3389/fspas.2024.1434367
A correction has been applied to this article in:
Corrigendum: Global Empirical Model of Sporadic-E Occurrence Rates
 Eli V. Parsch1*
Eli V. Parsch1* Anthony L. Franz2
Anthony L. Franz2 Eugene V. Dao3
Eugene V. Dao3 Dong L. Wu4
Dong L. Wu4 Nimalan Swarnalingam4,5
Nimalan Swarnalingam4,5 Cornelius C. J. H. Salinas4
Cornelius C. J. H. Salinas4 Daniel J. Emmons2*
Daniel J. Emmons2*Intense ionization enhancements in the Earth’s ionosphere, known as sporadic-E (
Elevated metallic ion concentrations in the E-region of the ionosphere, known as sporadic-E (
Sporadic-E is generally agreed to be caused by persistent metallic ions in the E-region of the ionosphere, and these ions are acted upon by forces caused by wind shears, tides, and gravity waves in mid-latitude regions, electromagnetic field (gradient) instabilities at equatorial regions, and high-energy particles driven by convection electric fields at high latitudes and poles (Whitehead, 1989; Mathews, 1998; Haldoupis et al., 2007). These forces result in the formation of
While many techniques have been used to monitor sporadic-E, including incoherent scatter radars (ISRs) (Mathews (1998); Hysell et al. (2009)), Super Dual Auroral Radar Network (SuperDARN) (Kunduri et al. (2023)), and long-wavelength arrays (LWAs) (Obenberger et al. (2021)), global
Taking into account these observational challenges, many studies have largely focused on examining ionosphere climatology using GNSS-RO and/or ionosonde data, with many focusing on describing the
In contrast, for OR models, the overall spatiotemporal data density is drastically reduced via the requirement to calculate ORs using a sufficiently large number of data points within a bin. For example, Hodos et al. (2022) developed OR climatology from ionosonde and GNSS-RO observations that required at least 25 measurements within a spatiotemporal bin to cap the standard error at 10%, which limited the final climatology to monthly 5°
However, considering the practical implications of blanketing
Hodos et al. (2022) created global maps of
These observations are displayed in Figure 1, and we can see that the GNSS-RO observations vary more significantly over geomagnetic latitude than longitude or local solar time. The large number of digisonde observations is also apparent and results in pronounced banding in the spatiotemporal data.
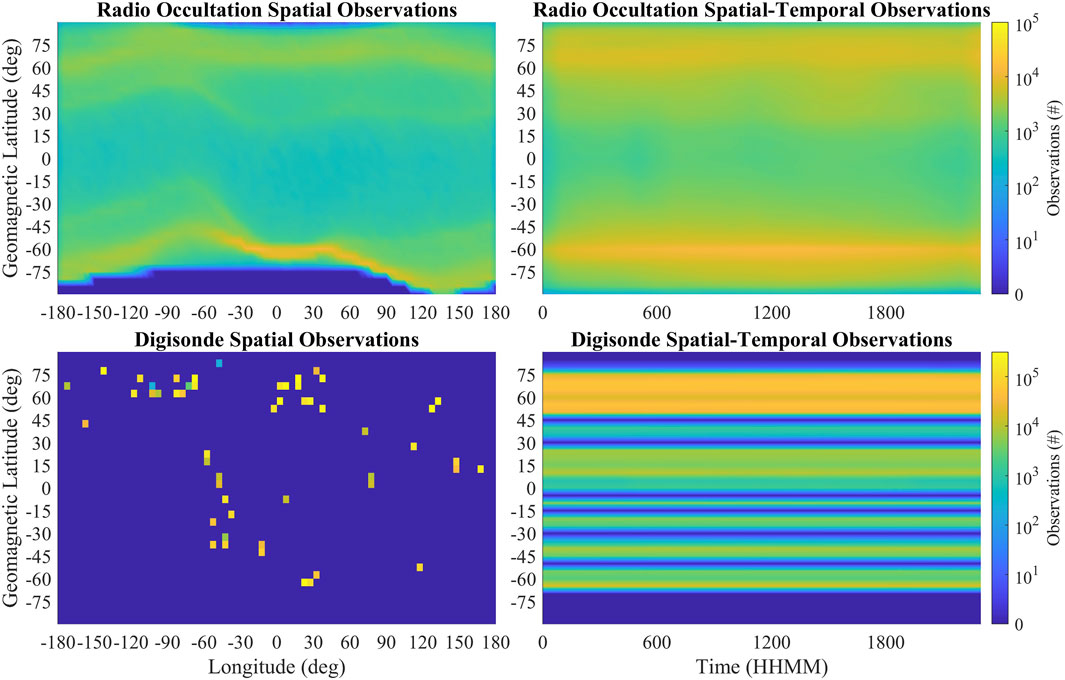
Figure 1. Top left: total observation count for GNSS-RO spatial measurements. Top right: total observation count for GNSS-RO spatiotemporal measurements. Bottom left: total observation count for digisonde spatial measurements. Bottom right: total observation count for digisonde spatiotemporal measurements. GPS-RO observations provide greater global coverage with lower data density than digisonde observations that provide higher data density at the cost of global coverage.
The presented model was developed using geomagnetic latitude and is defined as the dip angle or magnetic field inclination at an altitude of 100 km, as established by the World Magnetic Model (WMM). The average inclination from the 2010 WMM epoch was used for climatology and model development (Maus et al., 2010).
As described by Hodos et al. (2022), the sparsity of the COSMIC dataset and the requirement of at least 25 observations per bin result in a spatial resolution limited to 5° latitude
This study chose to integrate data over longitude in order to increase the temporal resolution, allowing the development of monthly fbEs OR maps with a spatial resolution of 5
To reduce the discontinuities resulting from the incorporation of irregularly spaced ionosonde sites combined with asymmetric spatial observation densities (Figure 1), both data sets were filtered using a 2D Gaussian smoothing kernel. This has the added benefit of adjusting bins that were previously set to 0 due to insufficient observations to a value dependent on its neighboring bins. Calculating the average difference between the original climatology and the Gaussian-filtered climatology on a monthly basis and averaging over a year yielded an OR mean absolute difference of 2
Karhunen–Loéve Expansion (KLE) has many different names, including principal component analysis (PCA), proper orthogonal decomposition (POD), and empirical orthogonal functions (EOFs) (Kirby, 2000; Björnsson and Venegas, 1997). The terminology of KLE is used throughout this report because it was used in the primary reference, Kirby (2000). KLE allows recasting each dataset as a combination of coefficients and modes:
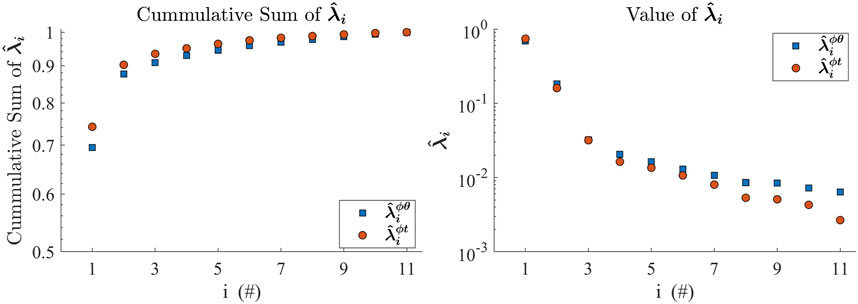
Figure 2. Left: cumulative sum of the normalized eigenvalues from largest to smallest for both the spatial and spatiotemporal data. Right: value of each normalized eigenvalue from largest to smallest for both the spatial and spatiotemporal data. Each dataset only requires two modes to explain
Typically, only the larger eigenvalues and modes more easily associated with a physically describable phenomenon are used for further analysis (Björnsson and Venegas, 1997). However, this study used all 11 nonzero modes for two reasons. First, only the largest eigenvalues are usually selected to reduce the impact of noise in the analysis, but this was addressed previously using the Gaussian filter. Second, limiting the number of modes will increase the uncertainty in the final outputs. Without the Gaussian filter, the primary modes associated with the largest eigenvalues retained much of the small-scale variation, which did not produce a smooth empirical model as desired. Therefore, the Gaussian filter was applied before KLE, and all 11 modes were retained to reduce uncertainties.
With the modes, columns of
where
The three largest coefficients and their corresponding modes are shown in Figure 3 for the spatial data and in Figure 4 for the spatiotemporal data. The modes were transformed into their two-dimensional representation prior to plotting. Figures 3, 4 show that mode and coefficient 1 for both the spatial and spatiotemporal analyses capture the well-documented seasonal variation that peaks in the boreal summer and winter months (Whitehead, 1989; Haldoupis et al., 2007). Mode and coefficient 2 highlight seasonal peaks in the spring and fall. Mode and coefficient 3 highlight particularly high-variance regions when analyzing the spatial domain and particularly high-variance latitude bands and times of day when analyzing the spatiotemporal domain.
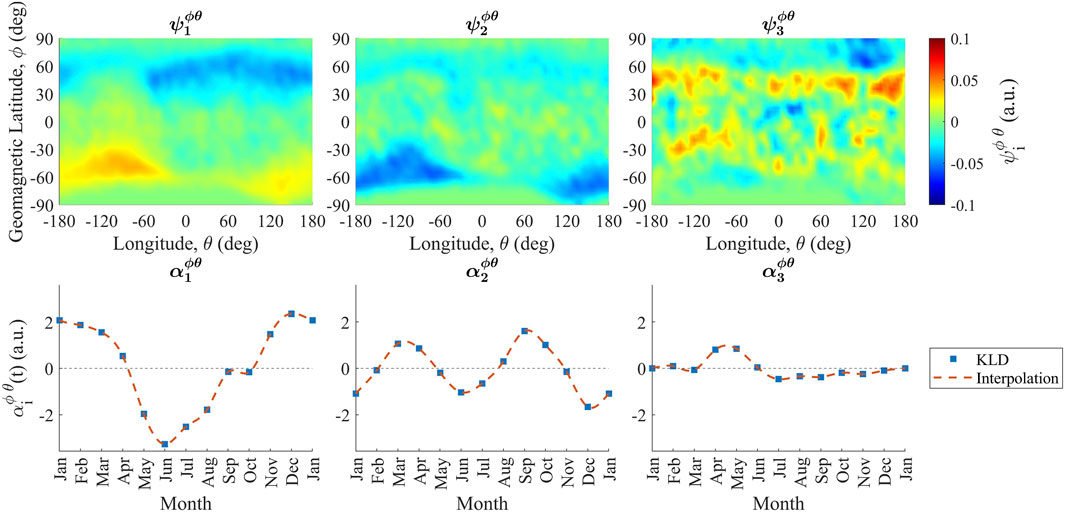
Figure 3. Top panel: eigenvectors as determined by the KLE when applied to the spatial data. Bottom panel: coefficients as determined by the KLE when applied to the spatial data. Regions of larger variance in the Northern and Southern Hemisphere are seen clearly in modes 1 and 2 with the corresponding seasonal changes seen in coefficients 1 and 2, respectively.
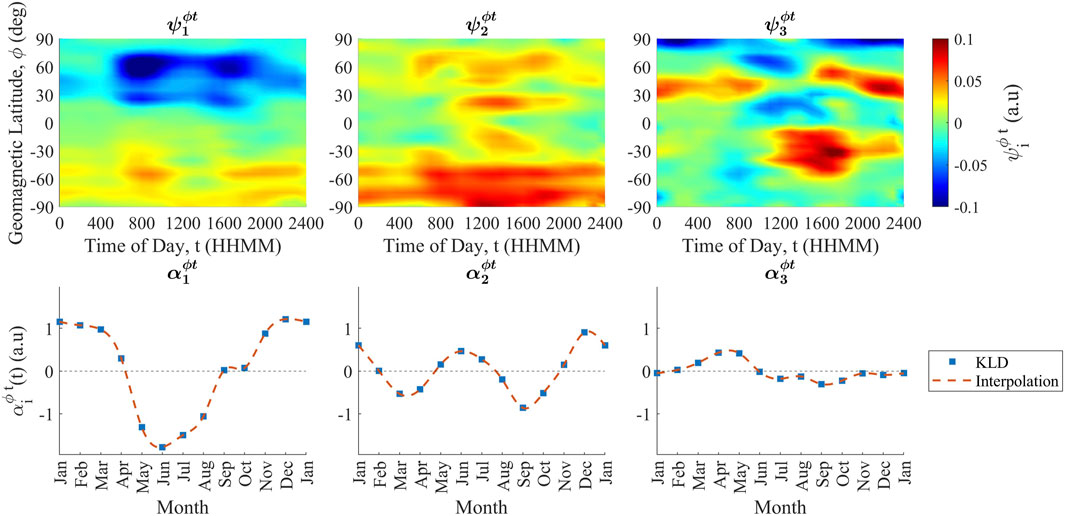
Figure 4. Top panel: eigenvectors as determined by the KLE when applied to the spatiotemporal data. Bottom panel: coefficients as determined by the KLE when applied to the spatiotemporal data. Latitudes and times of day with larger variance are seen with their corresponding changes throughout the year, as shown in the coefficients.
With the data represented in the KL basis, the coefficients,
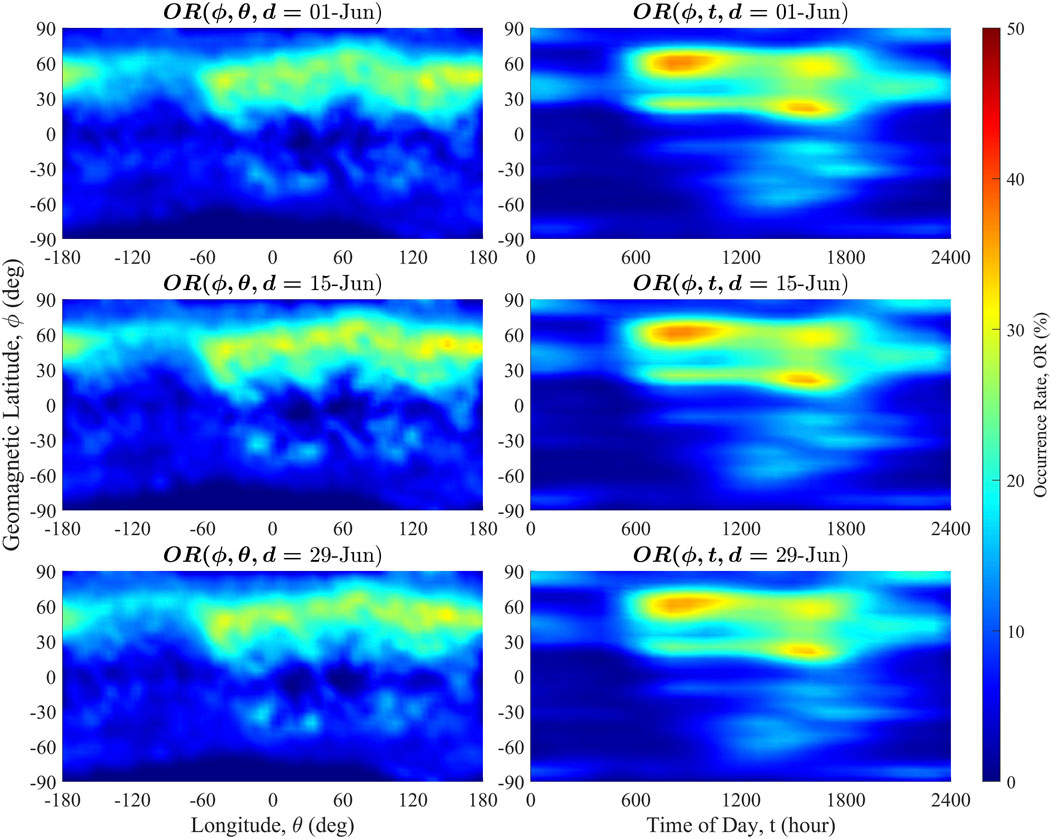
Figure 5. Top panel: results from interpolated coefficients corresponding to 1 June. Middle panel: results from interpolated coefficients corresponding to 15 June. Bottom panel: results from interpolated coefficients corresponding to 29 June. There are subtle but notable changes over time after applying the interpolated coefficients.
It is important to note that the daily spatial maps should be seen as averages for each bin over a day. After generating daily climatologies, the values were analyzed to determine whether any were nonsensical (
The interpolated global fbEs OR maps for every day of the year in both the spatial,
The following requirements were used for this calculation. First, for an fbEs OR,
where
For clarity, the array consisting of all hourly fbEs ORs for a given
and we use the same convention for an array of final output ORs for a given day,
Defining the mean of this array as
Equation 4 maintains the structure of the local solar time profile,
An example of this combination for throughout the year and at mid-latitudes is shown in Figure 6. It visually appears to satisfy all requirements and shows examples of where the scaling resulted in an increase in the hourly fbEs OR, a decrease in the hourly fbEs OR, and sometimes both. Figure 6 shows that, in the summer months, a distinct semidiurnal trend was apparent with peaks in the morning and afternoon, which is in agreement with the observations of Whitehead (1989) and Smith (1957). There was no significant increase in the model fbEs OR peak in the summer months due to the relatively small increase in the calculated spatial OR at this particular location during summer, as shown by the dotted red line. While the spatiotemporal data show larger peaks, they are integrated over longitude and may include other regions with substantially larger variation than the longitude of interest. The scaling method forced the hourly fbEs OR to average to this value over a day. Since the underlying data did not support a large average increase in the fbEs OR at this location, the model could not support it as well.
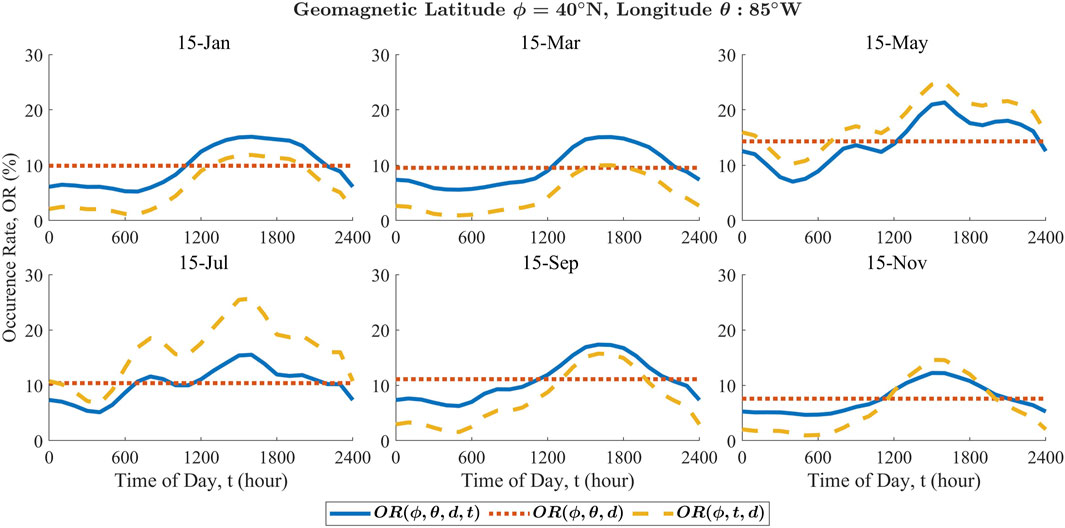
Figure 6. Results of scaling the interpolated climatologies at mid-latitudes. Blue indicates the final result, red indicates the interpolated spatial data, and yellow indicates the interpolated spatiotemporal data. The imposed requirements are seen to produce results that are sensible and consistent between datasets. Each subplot depicts a different calendar day (day of year) at the given location.
Videos showing the final GEMSOR predictions on a global map with a time resolution of 3 h are given in Supplementary Material, and the model can be downloaded from GEMSOR-OSF.
Considering that each calculated fbEs OR was treated as a distribution of binary events, each bin follows a Bernoulli distribution and has a standard deviation,
where
Before performing the Gaussian filter, with the exception of bins that had insufficient observations for calculation,
The propagated uncertainties were averaged over both month and hour for the entire year, and uncertainties for some months are shown in Figure 7, and the uncertainties for some selected hours are shown in Figure 8. Larger uncertainties were observed when examining the model on a monthly basis compared to an hourly basis. This was likely due to the fact that there is more variance in the fbEs OR over a month at a given location than during a given hour over a year. This is supported by the clear increase in uncertainty during seasonal peaks and local solar time peaks, as shown in Figures 7, 8. When analyzing the entire globe on a monthly basis, the uncertainty only occasionally approached 20% and was location-dependent. During the boreal spring and fall months, the uncertainty rarely exceeded 10%. Peak uncertainty is shown at (Figure 8) approximately 1600 L, with the minimum uncertainty in the late-evening and early-morning hours. However, at all times of the day, the average uncertainty remains below 10%.
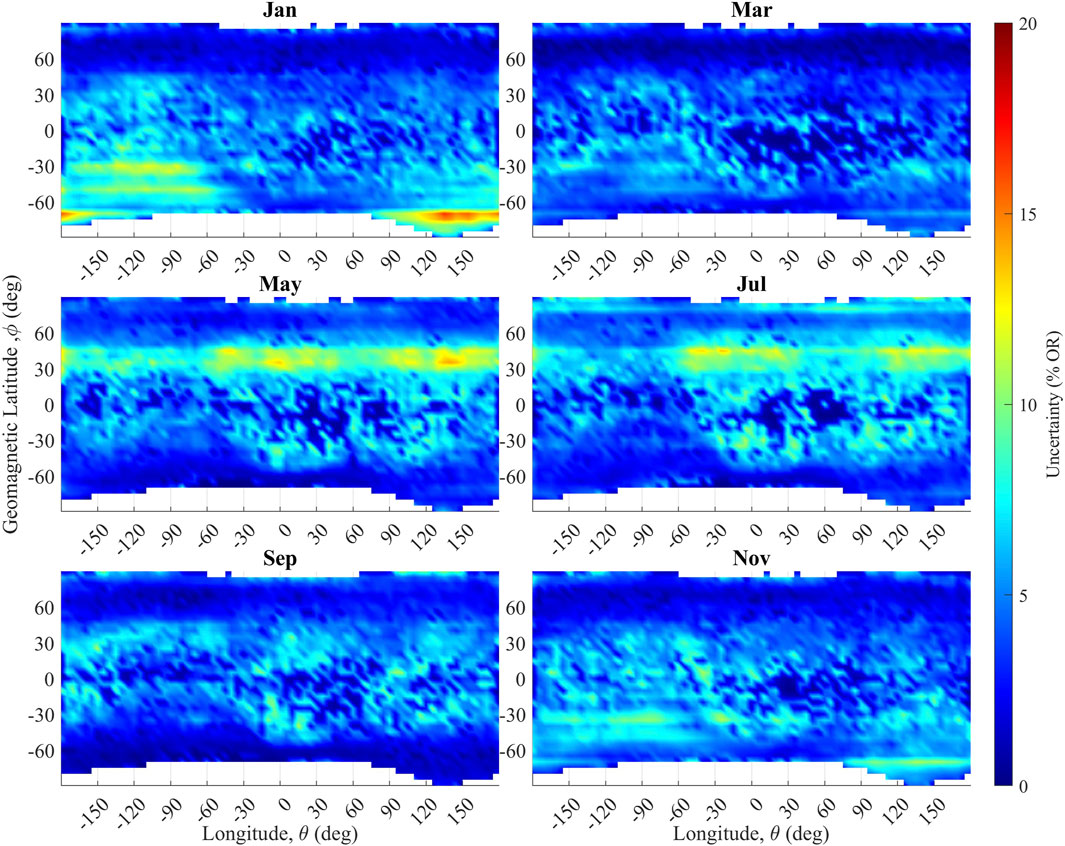
Figure 7. Average calculated uncertainty for selected months. Locations with insufficient observations are indicated by white. There is increased uncertainty at locations and times of year with higher ORs.
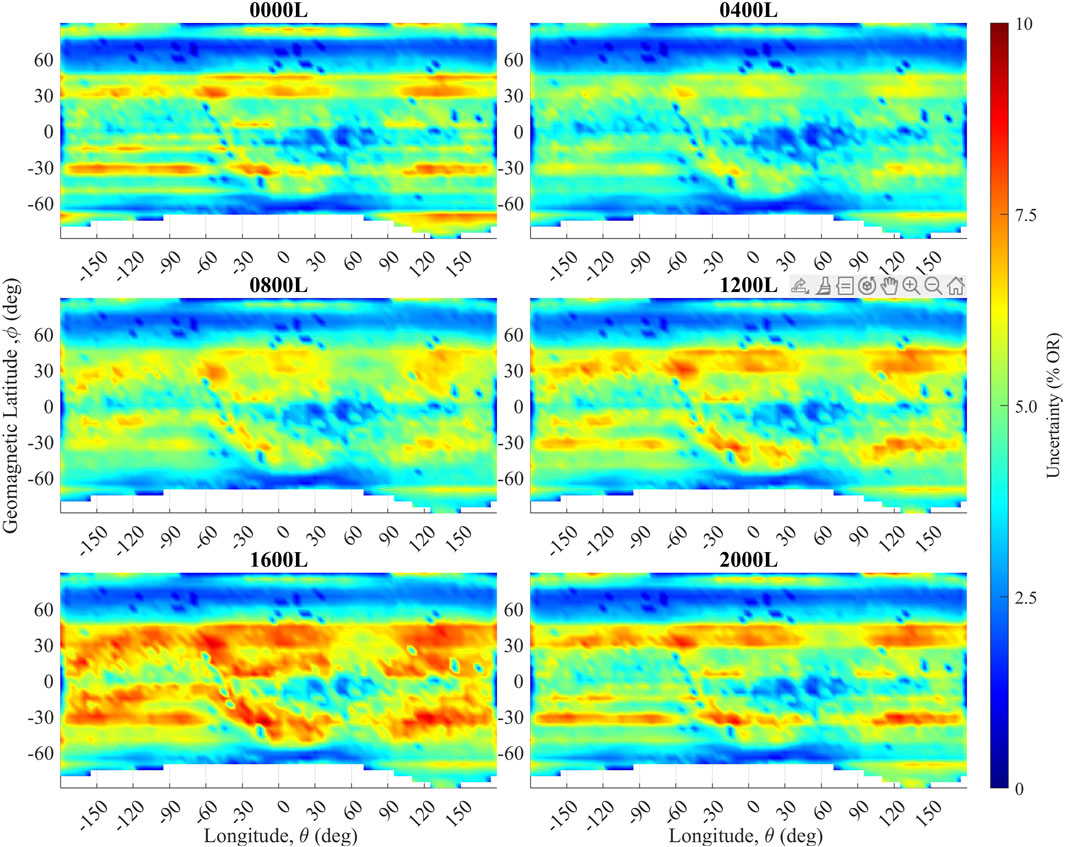
Figure 8. Average calculated uncertainty for selected hours. Note the change in scale from Figure 7. Locations with insufficient observations are indicated in white. There is increased uncertainty at times of day with higher ORs.
Since the total observation threshold was kept at 25, as outlined in Hodos et al. (2022), bins that did not have at least 25 observations had no calculated uncertainty, and their fbEs OR was set to 0% unless the Gaussian filter resulted in a weighted OR in that bin. As mentioned above, this largely affected high latitudes, in particular 75°S and below. Although this limits the use of the word global, these regions of the world are particularly impacted by auroral-E, which can be difficult to differentiate from sporadic-E (Roberts, 2024). Therefore, it may be more appropriate to develop a separate model that specifically accounts for auroral-E at these high latitudes.
Since the KLE resulted in 365 global maps of fbEs ORs and there were only measurement uncertainty values for each month, initial monthly uncertainties were used for all calculations for each month. Taking the average of all determined uncertainties results in a mean uncertainty,
While this error analysis considers the impacts of GNSS-RO sampling, smoothing, and combining ORs, it does not account for any uncertainty in ionosonde measurements. This analysis assumes that there are no errors associated with the ionosonde measurements, in particular, ionograms automatically scaled by ARTIST-5. Although ionosonde soundings were taken as “ground truth,” Stankov et al. (2023) showed automatically scaled foEs errors to range from
Validation was performed by comparing the model’s outputs to corresponding observations collected by the Global Ionosphere Radio Observatory at four different locations: El Arenosillo, Spain (37.1°N, 6.7°W); Fortaleza, Brazil (3.9°S, 38.4°W); Gakona, Alaska (62.38°N, 145.0°W); and Hermanus, South Africa (34.42°S, 19.22°E). Note that geographic coordinates are given above. These locations were selected to sample a variety of geomagnetic latitudes and at times will be referred to by their International Union of Radio Science (URSI) station codes: EA036, FZA0M, GA762, and HE13N, respectively. El Arenosillo was chosen to evaluate the performance in the Northern Hemisphere at geomagnetic mid-latitudes. Hermanus was chosen for Southern Hemisphere mid-latitudes, Gakona, for high latitudes, and Fortaleza, for low latitudes. Data from 2020–2022 were used, totaling 512,031 observations, and the average geomagnetic inclination from WMM 2020 at each location over the 3-year period was used as the geomagnetic latitude (Chulliat et al., 2020).
Two types of comparison are performed: an hour-to-hour comparison and a monthly averaged comparison. Hours that had total ionosonde observations of
Figure 9 shows that the model visually appears to perform well for El Arenosillo and Fortaleza and consistently overpredicts for Gakona and Hermanus. However, it is important to note the scale of these figures. On average, over a given month, the model tends to overpredict by approximately 10% OR for these two locations.
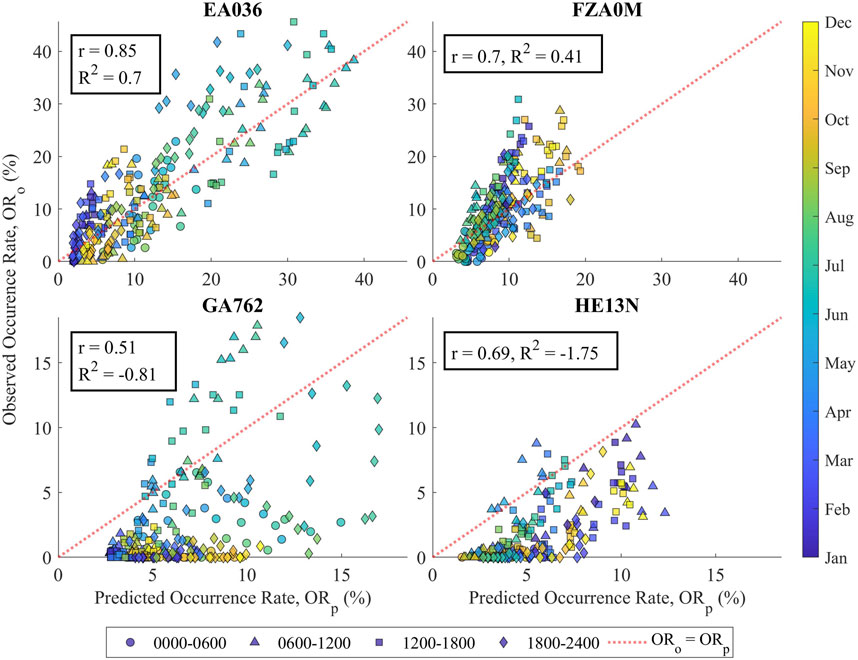
Figure 9. Monthly average of hourly (HHMM) fbEs ORs observed at each site plotted against the monthly average of hourly fbEs ORs predicted for each site. Pearson’s correlation coefficient,
The typical seasonal trends were observed for El Arenosillo and Hermanus. These mid-latitude locations also appear to have followed the expected semidiurnal trend of morning and afternoon peaks, as indicated by the triangles and squares in Figure 9. For Hermanus and Gakona, the model was overly cautious as it generally predicted higher probabilities of fbEs than actually occurred. The correlation coefficients,
Although Figure 9 provides a clear view of the monthly averaged model performance, it does not show the diurnal variations. Figure 10 shows the monthly averaged profiles as a function of local solar time compared to averaged ionosonde observations. Figure 10 also highlights the scales that must be considered when analyzing the accuracy of the model. There is considerably more variance in the fbEs OR for El Arenosillo and Fortaleza, and the model appears to generally match the observed trends. Specifically, for El Arenosillo, the model appears to underestimate peaks and overestimate the valleys but retains the trend and the overall increase that occurs in the summer. For Fortaleza, the model, on average, underestimates the OR, as shown in Figure 9. The consistent overestimation for Gakona and Hermanus was also apparent, but the errors were rarely greater than 10%, which makes them rather small on an absolute scale.
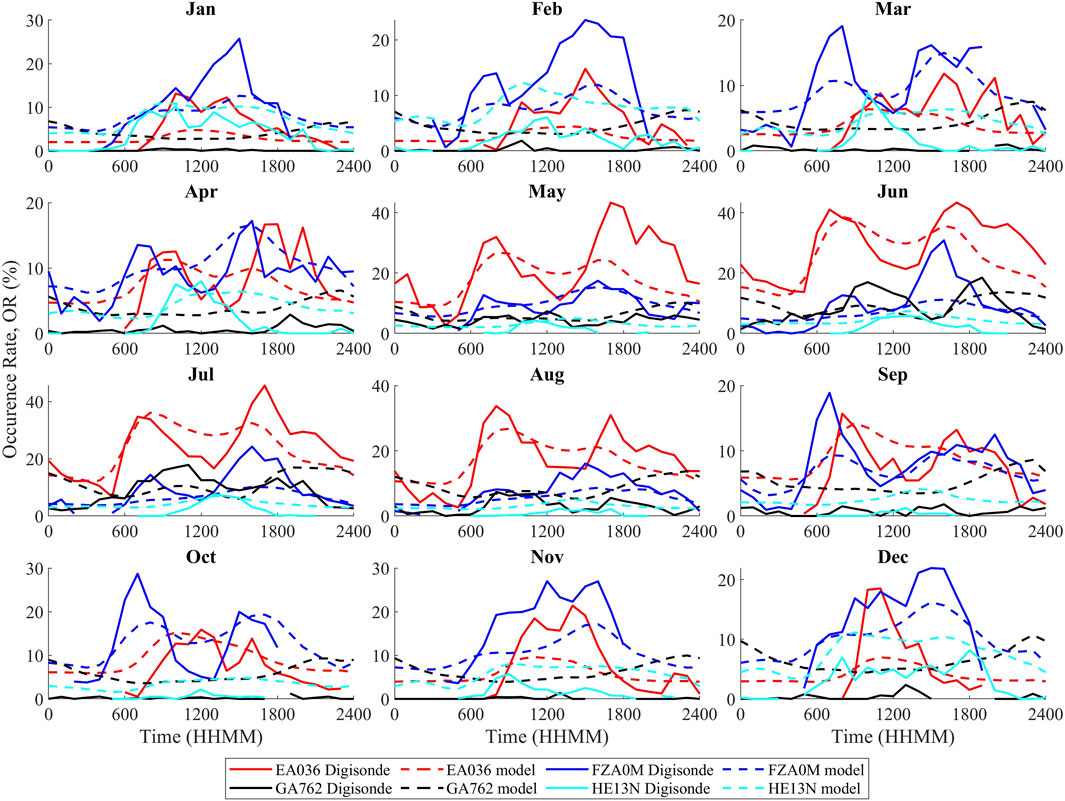
Figure 10. Monthly local solar time occurrence rates at each digisonde site, as observed by the digisonde and predicted by the model. Note the change in scale on the y-axis throughout, and hours that did not satisfy
The error was examined in several different ways. First, the mean absolute error (MAE) over different dimensions for each digisonde site was examined (Figure 11). When examining the monthly error, El Arenosillo and Fortaleza clearly show a higher average error, and this was especially true in the summer for El Arenosillo. Fortaleza appears to have a lower average error in the summer than in the winter. Gakona follows a pattern similar to that of El Arenosillo but has much lower average error values. Hermanus has the lowest average error values by month and by hour, with slightly higher errors during the daytime hours. This is shown in Figure 10 and is due to a consistent overestimation of the OR values. Gakona has a higher average error during the late-night hours, while the remaining two stations have a significantly higher error during the daytime hours, particularly in the late afternoon. Fortaleza stands out with the highest average error.
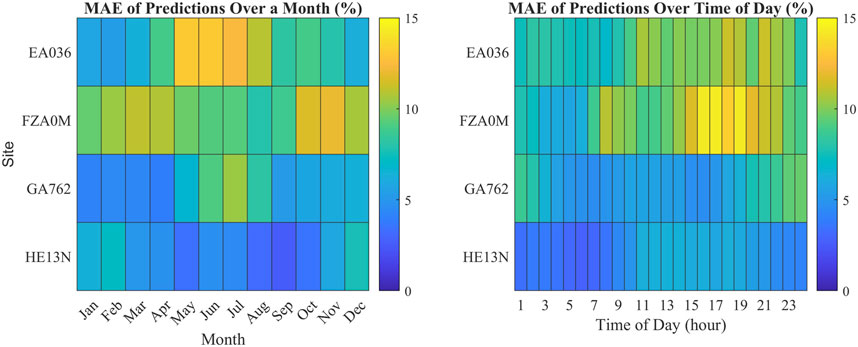
Figure 11. Mean absolute error of model outputs over different dimensions at each digisonde location. Left: MAE for each month. Right: MAE for each hour. Increases in MAE generally correspond to seasonal or daily OR peaks for each location.
The second way in which the error was examined was by comparing error distributions. Figure 12 displays a histogram of the error when comparing the hourly model predictions with the observations for all four sites. Note that only the hours meeting the observation threshold are displayed, and the percentage removed is shown in the legend. This discussion assumes that the unobserved hours follow the same distribution. The standard deviation of the hour-to-hour comparison is 11%. We can see that
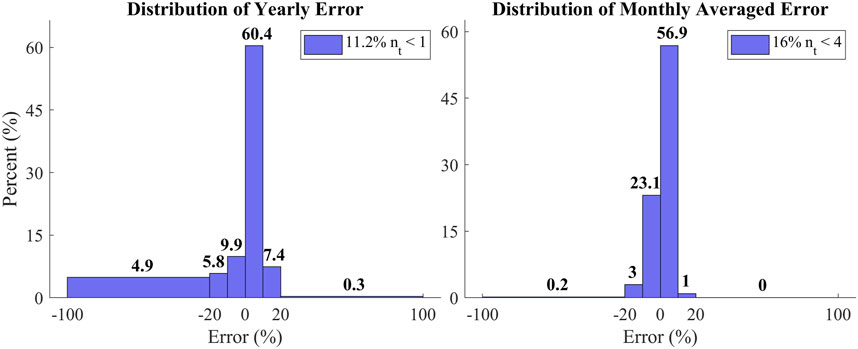
Figure 12. Histograms of the residual error. Left: hour-to-hour error (predicted vs. observed) over the entire year. Right: error when comparing the hourly occurrence rates when each hour is averaged over each month. Errors are generally overestimates, but large errors are large underestimates.
Looking at the errors from monthly averaged comparisons shows that they are much more tightly distributed than would be expected considering how the model was developed. However, this comparison also excludes much more data, as seen by the increase in the percentage of hours in which the observation threshold was not met (
Given the initial calculated average uncertainty of 12%, 95% of predictions are expected to have an error of less than 24%
The overarching goal of increasing the monthly climatological OR temporal resolution outlined by Hodos et al. (2022) was accomplished through an interpolation of the monthly KLE eigenvalues (Figures 3, 4). This process maintains the OR values for each month while providing estimates between the known periods. Gaussian smoothing of the original datasets helps reduce discontinuities typically found over ionosonde locations where the ionosonde-derived ORs did not match the surrounding GNSS-RO-derived ORs. Finally, the self-consistent combination of temporal and spatial results outlined in Equations 2–5 ensures that the local solar time structures are maintained, while the daily averages match the input spatial maps. In this respect, GEMSOR successfully provides fbEs
A minimum total observation threshold was used to limit the standard error to 10%, as outlined in Hodos et al. (2022), and this appears to have been effective. Propagation of the standard deviation of the individual bins through the combination algorithm and addition of the mean error of the Gaussian filter resulted in an estimated uncertainty of
Hermanus and Gakona not only had lower correlation coefficients compared to the other sites when analyzing the monthly averaged data but also a lower MAE when averaging over a month or over an hour. For Hermanus, this is likely due to the rather depressed fbEs in this region due to the proximity of the South Atlantic Anomaly (Arras et al., 2008). The model performed well at the mid-latitude location El Arenosillo, where it generally followed the observed semidiurnal behavior throughout the year. This location also had the highest correlation coefficient but also some of the higher MAEs, particularly in the summer. This error averaged to approximately 15% during its peak in the summer and not much more than 10% when examined hourly. Overall, the model showed strong performance in the mid-latitude region where
In the low-latitude or equatorial region, Fortaleza had the second highest correlation coefficient when averaged over a month. The model generally captured the semidiurnal trends but not as closely as for El Arenosillo. The monthly averaged correlation coefficient was lower, as was the MAE over the entire year. The highest hourly average errors were for Fortaleza, peaking at 15%. It must be noted that while the wind shear mechanism used to describe blanketing
Although the model showed modest success, there are some very important limitations that need to be understood prior to its application. Some locations, particularly geomagnetic latitudes south of 75°S, had an inadequate number of total observations to calculate an OR. The model only predicts 0
The less number of years in the validation (2019–2022) also limited the number of comparisons that could be made, particularly during local night. Sporadic-E forms primarily during the day with latitude-dependent peaks in either the late morning or early evening (Wu et al., 2005; Chu et al., 2014; Yu et al., 2022). Formation at night, especially during the early-morning hours, is minimal but nonzero with a general increase in mid- and high latitudes during local summer (Luo et al., 2021; Hodos et al., 2022). This behavior is also present in the ionosonde validation dataset displayed in Figure 10. However, many of the nighttime OR calculations for the digisonde sites contained relatively low numbers of observations, which increases the uncertainty in the validation rates at night.
In relation to other empirical
For future research, the primary challenge is to improve RO techniques for estimating the existence and strength of sporadic-E layers. Although this is a challenging task due to the integrated nature of the observations, recent studies (Emmons et al., 2023; Ellis et al., 2024) have shown a significant improvement over the baseline techniques compared by Carmona et al. (2022) and applied by Hodos et al. (2022). Implementing these improved RO techniques will improve the OR estimates that form the foundation of the empirical model. Additionally, expanding the validation to more digisonde locations over a greater period will provide further insight into the model’s strengths and weaknesses. Enhancing the spatial resolution would also be beneficial as the current bin size is rather large, especially in the equatorial regions
This study outlines the development of a GEMSOR through significant enhancements in time resolution from the dataset used by Hodos et al. (2022), which was derived from GNSS-RO and ionosonde observations with an fbEs threshold of 3 MHz. GEMSOR predicts the blanketing sporadic-E OR as a function of geomagnetic latitude, longitude, day of year, and local solar time at a resolution of 5°, 5°, day, and hour, respectively. The results of the model were compared to observations from four digisonde sites, and a general uncertainty of the model was developed. The purpose of this research was to provide a new tool that allows operators of HF equipment to better understand ionospheric conditions for a more effective application of the equipment.
Overall, this study sought to develop an empirical model of global fbEs
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
EP: conceptualization, formal analysis, investigation, writing–original draft, and writing–review and editing. AF: formal analysis, investigation, and writing–original draft. ED: conceptualization, formal analysis, investigation, and writing–original draft. DW: conceptualization, formal analysis, investigation, and writing–original draft. NS: formal analysis, investigation, and writing–original draft. CS: conceptualization, formal analysis, investigation, and writing–original draft. DE: conceptualization, formal analysis, investigation, writing–original draft, and writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Air Force Office of Scientific Research (AFOSR/RTB1), and NASA’s Living With Star and Sun-Climate research funds to the Goddard Space Flight Center (GSFC) under WBS 936723.02.01.12.48.
The authors acknowledge the Digital Ionogram Database (https://giro.uml.edu/didbase/) and the COSMIC Data Analysis and Archive Center (https://cdaac-www.cosmic.ucar.edu/) for the use of their data. The views, opinions, and/or findings expressed are those of the authors and should not be interpreted as representing the official views or policies of the Department of Defense or the US Government.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1434367/full#supplementary-material
Arras, C., Resende, L. C. A., Kepkar, A., Senevirathna, G., and Wickert, J. (2022a). Sporadic E layer characteristics at equatorial latitudes as observed by GNSS radio occultation measurements. Earth, Planets Space 74, 163. doi:10.1186/s40623-022-01718-y
Arras, C., Resende, L. C. A., Kepkar, A., Senevirathna, G., and Wickert, J. (2022b). Sporadic e layer characteristics at equatorial latitudes as observed by gnss radio occultation measurements. Earth, Planets Space 74, 163. doi:10.1186/s40623-022-01718-y
Arras, C., and Wickert, J. (2018). Estimation of ionospheric sporadic E intensities from GPS radio occultation measurements. J. Atmos. Solar-Terrestrial Phys. 171, 60–63. Vertical Coupling in the Atmosphere-Ionosphere System: Recent Progress. doi:10.1016/j.jastp.2017.08.006
Arras, C., Wickert, J., Beyerle, G., Heise, S., Schmidt, T., and Jacobi, C. (2008). A global climatology of ionospheric irregularities derived from gps radio occultation. Geophys. Res. Lett. 35. doi:10.1029/2008GL034158
Björnsson, H., and Venegas, S. (1997). A manual for EOF and SVD analyses of climatic data. CCGCR Rep. 97, 112–134.
Cameron, T., Fiori, R., Themens, D., Warrington, E., Thayaparan, T., and Galeschuk, D. (2022). Evaluation of the effect of sporadic-E on high frequency radio wave propagation in the arctic. J. Atmos. Solar-Terrestrial Phys. 228, 105826. doi:10.1016/j.jastp.2022.105826
Carmona, R. A., Nava, O. A., Dao, E. V., and Emmons, D. J. (2022). A comparison of sporadic-E occurrence rates using GPS radio occultation and ionosonde measurements. Remote Sens. 14, 581. doi:10.3390/rs14030581
Cathey, E. H. (1969). Some midlatitude sporadic-e results from the explorer 20 satellite. J. Geophys. Res. 74, 2240–2247. doi:10.1029/ja074i009p02240
Chartier, A. T., Hanley, T. R., and Emmons, D. J. (2022). Long-distance propagation of 162 mhz shipping information links associated with sporadic e. Atmos. Meas. Tech. 15, 6387–6393. doi:10.5194/amt-15-6387-2022
Chu, Y. H., Wang, C. Y., Wu, K. H., Chen, K. T., Tzeng, K. J., Su, C. L., et al. (2014). Morphology of sporadic E layer retrieved from COSMIC GPS radio occultation measurements: wind shear theory examination. J. Geophys. Res. Space Phys. 119, 2117–2136. doi:10.1002/2013JA019437
Chulliat, A., Brown, W., Alken, P., Beggan, C., Nair, M., Cox, G., et al. (2020). “The US/UK world magnetic model for 2020-2025: technical report,”. NOAA: National Centers for Environmental Information.
Ellis, J., Emmons, D., and Cohen, M. (2024). Detection and classification of sporadic e using convolutional neural networks. Space weather. 22, e2023SW003669. doi:10.1029/2023sw003669
Emmons, D. J., Wu, D. L., and Swarnalingam, N. (2022). A statistical analysis of sporadic-e characteristics associated with gnss radio occultation phase and amplitude scintillations. Atmosphere 13, 2098. doi:10.3390/atmos13122098
Emmons, D. J., Wu, D. L., Swarnalingam, N., Ali, A. F., Ellis, J. A., Fitch, K. E., et al. (2023). Improved models for estimating sporadic-e intensity from gnss radio occultation measurements. Front. Astronomy Space Sci. 10, 1327979. doi:10.3389/fspas.2023.1327979
Fontes, P., Muella, M., Resende, L., and Fagundes, P. (2024). Evidence of anti-correlation between sporadic (es) layers occurrence and solar activity observed at low latitudes over the brazilian sector. Adv. Space Res. 73, 3563–3577. doi:10.1016/j.asr.2023.09.040
Gooch, J. Y., Colman, J. J., Nava, O. A., and Emmons, D. J. (2020). Global ionosonde and GPS radio occultation sporadic-E intensity and height comparison. J. Atmos. Solar-Terrestrial Phys. 199, 105200. doi:10.1016/j.jastp.2020.105200
Haldoupis, C., Pancheva, D., Singer, W., Meek, C., and MacDougall, J. (2007). An explanation for the seasonal dependence of midlatitude sporadic E layers. J. Geophys. Res. Space Phys. 112. doi:10.1029/2007JA012322
Headrick, J. M., Anderson, S. J., and Skolnik, M. (2008). HF over-the-horizon radar. Radar Handb. 20.
Hodos, T. J., Nava, O. A., Dao, E. V., and Emmons, D. J. (2022). Global sporadic-E occurrence rate climatology using GPS radio occultation and ionosonde data. J. Geophys. Res. Space Phys. 127. doi:10.1029/2022ja030795
Hysell, D., Nossa, E., Larsen, M., Munro, J., Sulzer, M., and González, S. (2009). Sporadic e layer observations over arecibo using coherent and incoherent scatter radar: Assessing dynamic stability in the lower thermosphere. J. Geophys. Res. Space Phys. 114. doi:10.1029/2009ja014403
Kamide, Y., and Akasofu, S. I. (1983). Notes on the auroral electrojet indices. Rev. Geophys. 21, 1647–1656. doi:10.1029/RG021i007p01647
Kintner, P. M., Ledvina, B. M., and de Paula, E. R. (2007). GPS and ionospheric scintillations. Space weather. 5. doi:10.1029/2006SW000260
Kirby, M. (2000). Geometric data analysis: an empirical approach to dimensionality reduction and the study of patterns. John Wiley and Sons, Inc.
Ku, H. H., et al. (1966). Notes on the use of propagation of error formulas. J. Res. Natl. Bureau Stand. 70.
Kunduri, B. S. R., Erickson, P. J., Baker, J. B., Ruohoniemi, J. M., Galkin, I., and Sterne, K. (2023). Dynamics of mid-latitude sporadic-e and its impact on hf propagation in the north american sector. J. Geophys. Res. Space Phys. 128, e2023JA031455. doi:10.1029/2023ja031455
Luo, J., Liu, H., and Xu, X. (2021). Sporadic e morphology based on cosmic radio occultation data and its relationship with wind shear theory. Earth, Planets Space 73, 212–217. doi:10.1186/s40623-021-01550-w
MacDougall, J., Jayachandran, P., and Plane, J. (2000). Polar cap sporadic-E: part 1, observations. J. Atmos. Solar-Terrestrial Phys. 62, 1155–1167. doi:10.1016/s1364-6826(00)00093-6
Maeda, J., and Heki, K. (2015). Morphology and dynamics of daytime mid-latitude sporadic-e patches revealed by gps total electron content observations in Japan. Earth, Planets Space 67, 89–9. doi:10.1186/s40623-015-0257-4
Mathews, J. (1998). Sporadic E: current views and recent progress. J. Atmos. Solar-Terrestrial Phys. 60, 413–435. doi:10.1016/s1364-6826(97)00043-6
Maus, S., Macmillan, S., McLean, S., Hamilton, B., Thomson, A., Nair, M., et al. (2010). “The US/UK world magnetic model for 2010-2015,”. Keyworth, Nottinghamshire, England: British Geological Survey.
McNamara, L. F. (1991). The ionosphere: communications, surveillance, and direction finding. Malabar, Florida: Krieger publishing company.
Merriman, D. K., Nava, O. A., Dao, E. V., and Emmons, D. J. (2021). Comparison of seasonal foEs and fbEs occurrence rates derived from global Digisonde measurements. Atmosphere 12, 1558. doi:10.3390/atmos12121558
Nakagawa, S., and Schielzeth, H. (2013). A general and simple method for obtaining r2 from generalized linear mixed-effects models. Methods Ecol. Evol. 4, 133–142. doi:10.1111/j.2041-210x.2012.00261.x
Neubeck, K. (1996). Using the combined resources of amateur radio observations and ionosonde data in the study of temperate zone sporadic-E. J. Atmos. Terr. Phys. 58, 1355–1365. doi:10.1016/0021-9169(95)00170-0
Niu, J., Weng, L. B., Meng, X., and Fang, H. X. (2019). Morphology of ionospheric sporadic-E layer intensity based on COSMIC occultation data in the midlatitude and low-latitude regions. J. Geophys. Res. Space Phys. 124, 4796–4808. doi:10.1029/2019JA026828
Obenberger, K., Dowell, J., Fallen, C., Holmes, J., Taylor, G., and Varghese, S. (2021). Using broadband radio noise from power-lines to map and track dense Es structures. Radio Sci. 56, 1–17. doi:10.1029/2020rs007169
Reddy, C., and Mukunda Rao, M. (1968). On the physical significance of the es parameters fbes, fes, and foes. J. Geophys. Res. 73, 215–224. doi:10.1029/ja073i001p00215
Resende, L. C., Arras, C., Batista, I. S., Denardini, C. M., Bertollotto, T. O., and Moro, J. (2018). Study of sporadic e layers based on gps radio occultation measurements and digisonde data over the brazilian region. Ann. Geophys. 36, 587–593. doi:10.5194/angeo-36-587-2018
Resende, L. C. A., Batista, I. S., Denardini, C. M., Batista, P. P., Carrasco, A. J., de Fátima Andrioli, V., et al. (2017). Simulations of blanketing sporadic e-layer over the brazilian sector driven by tidal winds. J. Atmos. Solar-Terrestrial Phys. 154, 104–114. doi:10.1016/j.jastp.2016.12.012
Roberts, K. D. (2024). Investigation of high-latitude GNSS radio occultation sporadic-E and auroral-E measurements (Air Force Institute of Technology). Wright-Patterson AFB, Dayton OH: Master’s Thesis.
Schunk, R., and Nagy, A. (2009). Ionospheres: physics, plasma physics, and chemistry. Cambridge University Press.
Seif, A., and Panda, S. K. (2024). Characterizing global equatorial sporadic-e layers through cosmic gnss radio occultation measurements. Astrophysics Space Sci. 369, 60. doi:10.1007/s10509-024-04326-2
Smith, E. K. (1957). Worldwide occurrence of sporadic E, 582. Gaithersburg, Maryland: US Department of Commerce, National Bureau of Standards.
Stankov, S. M., Verhulst, T. G. W., and Sapundjiev, D. (2023). Automatic ionospheric weather monitoring with DPS-4D ionosonde and ARTIST-5 autoscaler: System performance at a mid-latitude observatory. Radio Sci. 58, 1–20. doi:10.1029/2022RS007628
Sun, W., Zhao, X., Hu, L., Yang, S., Xie, H., Chang, S., et al. (2021). Morphological characteristics of thousand-kilometer-scale es structures over China. J. Geophys. Res. Space Phys. 126, e2020JA028712. doi:10.1029/2020ja028712
Thayaparan, T., and MacDougall, J. (2005). Evaluation of ionospheric sporadic-E clutter in an arctic environment for the assessment of high-frequency surface-wave radar surveillance. IEEE Trans. geoscience remote Sens. 43, 1180–1188. doi:10.1109/tgrs.2005.844661
Tian, P., Yu, B., Ye, H., Xue, X., Wu, J., and Chen, T. (2023). Ionospheric irregularities reconstruction using multi-source data fusion via deep learning. EGUsphere 2023, 1–26. doi:10.5194/egusphere-2023-1304
Whitehead, J. (1970). Production and prediction of sporadic e. Rev. Geophys. 8, 65–144. doi:10.1029/rg008i001p00065
Whitehead, J. (1989). Recent work on mid-latitude and equatorial sporadic-E. J. Atmos. Terr. Phys. 51, 401–424. doi:10.1016/0021-9169(89)90122-0
Wu, D. L., Ao, C. O., Hajj, G. A., de la Torre Juarez, M., and Mannucci, A. J. (2005). sporadic-E morphology from GPS-champ radio occultation. J. Geophys. Res. Space Phys. 110. doi:10.1029/2004JA010701
Yu, B., Scott, C. J., Xue, X., Yue, X., Chi, Y., Dou, X., et al. (2021). A signature of 27 day solar rotation in the concentration of metallic ions within the terrestrial ionosphere. Astrophysical J. 916, 106. doi:10.3847/1538-4357/ac0886
Yu, B., Scott, C. J., Xue, X., Yue, X., and Dou, X. (2020). Derivation of global ionospheric Sporadic E critical frequency (f o Es) data from the amplitude variations in GPS/GNSS radio occultations. R. Soc. Open Sci. 7, 200320. doi:10.1098/rsos.200320
Yu, B., Xue, X., Scott, C. J., Yue, X., and Dou, X. (2022). An empirical model of the ionospheric sporadic E layer based on GNSS radio occultation data. Space weather. 20, e2022SW003113. doi:10.1029/2022sw003113
Yue, X., Schreiner, W. S., Pedatella, N. M., and Kuo, Y.-H. (2016). Characterizing GPS radio occultation loss of lock due to ionospheric weather. Space weather. 14, 285–299. doi:10.1002/2015SW001340
Keywords: ionosphere, sporadic-E, radio occultation, global climatology, Karhunen–Loéve Expansion
Citation: Parsch EV, Franz AL, Dao EV, Wu DL, Swarnalingam N, Salinas CCJH and Emmons DJ (2024) Global Empirical Model of Sporadic-E Occurrence Rates. Front. Astron. Space Sci. 11:1434367. doi: 10.3389/fspas.2024.1434367
Received: 17 May 2024; Accepted: 15 October 2024;
Published: 01 November 2024.
Edited by:
Philip J. Erickson, Massachusetts Institute of Technology, United StatesReviewed by:
Sampad Kumar Panda, KL University, IndiaCopyright © 2024 Parsch, Franz, Dao, Wu, Swarnalingam, Salinas and Emmons. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Eli V. Parsch, ZWxpLnBhcnNjaEBhZmFjYWRlbXkuYWYuZWR1; Daniel J. Emmons, ZGFuaWVsLmVtbW9uc0BhZml0LmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.