Numerical optimization of large-scale monotone equations using the free-derivative spectral conjugate gradient method

This study introduced an efficient method for solving non-linear equations. Our approach enhances the traditional spectral conjugate gradient parameter, resulting in significant improvements in the resolution of complex nonlinear problems. This innovative technique ensures global convergence and descent condition supported by carefully considered assumptions. The efficiency and effectiveness of the proposed method is highlighted by its outstanding numerical performance. To validate our claims, large-scale numerical simulations were conducted. These tests were designed to evaluate the capabilities of our proposed algorithm rigorously. In addition, we performed a comprehensive comparative numerical analysis, benchmarking our method against existing techniques. This analysis revealed that our approach consistently outperformed others in terms of theoretical robustness and numerical efficiency. The superiority of our method is evident in its ability to solve large-scale problems with accuracy in function evaluations, fewer iterations, and improved computational performance thereby, making it a valuable contribution to the field of numerical optimization.

1 Introduction

In recent years, large-scale systems of nonlinear equations have become increasingly important in many scientific and engineering fields. Solving these equations is essential for improving computational techniques across a variety of domains. This study introduces a novel approach that utilizes iterative optimization methods.

The main goal of this study is to find solutions for the nonlinear monotone system of equations presented below.

$\begin{array}{ll}\Psi (x)=0,x\in \Omega .& (1)\end{array}$

Lipschitz continuity and monotonicity are the characteristics that define the function Ψ:ℝⁿ → ℝⁿ, where Ω⊆ℝⁿ represents a non-empty closed and convex set. In this context, ℝⁿ denotes the n-dimensional real space equipped with the Euclidean norm ||·||. Additionally, Ψ_k refers to Ψ(x_k).

Definition 1.1. A mapping Ψ:ℝⁿ → ℝⁿ is defined as monotone for any x and y in ℝⁿ if the following condition holds:

$\begin{array}{ll}\langle \Psi (x)-\Psi (y),x-y\rangle \ge 0.& (2)\end{array}$

Therefore, Equation 1 is classified as a monotone system of nonlinear equations if function Ψ satisfies the condition outlined in Equation 2. The study of monotone mappings, which belong to a category of nonlinear equations, was initially explored in [26, 32, 42] within the framework of Hilbert spaces.

Many methods can be used to solve these problems, including Newton and quasi-Newton approaches, conjugate gradient techniques, fixed-point techniques, and their variations. For more details, refer to [4, 6, 45].

The system of nonlinear equations described in Equation 1 has various applications in multiple fields. For instance, they can be used in power flow calculations [38], motion control for planar robotic manipulators [36], economic equilibrium problems [18], and chemical equilibrium systems [31]. Furthermore, it has applications in generalized proximal algorithms that employ the Bregman distance in Iusem and Solodov [25]. Both fixed-point and normal maps are utilized to address problems related to monotone variational inequalities [20, 44]. Each of these contributes to the development of Equation 1. Recent developments highlight the effectiveness of signal and image recovery algorithms for solving nonlinear monotone equation systems [3, 5, 7, 39].

Initial approaches were developed to benefit from the rapid convergence. However, both techniques require the use of a Jacobian matrix or its approximation in each iteration to solve their respective problems. This reliance may affect their ability to handle complex nonlinear systems of equations (for more details see [6, 21, 40, 43]).

However, there are various techniques are available for solving large-scale unconstrained and constrained optimization problems, including spectral gradient methods, conjugate gradient methods, and spectral conjugate gradient methods. These approaches offer several advantages, such as ease of use and minimal storage requirements. These benefits motivated researchers to further explore the application of these techniques to solve nonlinear equations [33, 34].

For example, consider the projection method introduced by Solodov and Svaiter [35]. This method has inspired many researchers to expand the use of conjugate gradient (CG) methods to solve unconstrained optimization problems. These CG methods serve as effective tools for addressing systems of nonlinear equations by reformulating the problem to minimize an objective function. Gradient-based approaches, such as the gradient descent and conjugate gradient methods, iteratively adjust the variables in the direction of the steepest descent to find a solution.

The CG-DESCENT method determines the conjugate parameter for the conjugate gradient method, as discussed by Liu and Li [30]. To solve Equation 1, Dai et al. [17] introduced a modified version of Perry's conjugate gradient-based derivative-free approach. This approach is used to obtain the conjugate parameters.

Wang et al. [37] developed a projection-based method to solve systems of nonlinear monotone equations. At each iteration, a test point was generated by approximately solving a linear system of equations. They then created a predictor-corrector point using a line search technique that follows the search direction determined by both the test point and the current point. This approach effectively enhanced the iteration process. To demonstrate the effectiveness of the algorithm, the authors presented numerical tests and provided evidence for the global convergence of the method.

Cheng [15] addressed nonlinear monotone equations by introducing a new approach that combines the traditional Polak-Ribiere-Polyak (PRP) method with hyperplane projection techniques. This innovative combination sought to harness the strengths of both the methods. The PRP method is effective for iterative optimization, whereas hyperplane projection is useful for managing constraints and guiding solutions toward feasible regions.

Liu and Li [28] introduced a spectral DY-type method to solve nonlinear monotone equations, drawing inspiration from the well-known Dai-Yuan DY-conjugate gradient parameter [16]. This approach leverages the unique characteristics of the DY parameter, which is particularly effective in conjugate gradient methods, and applies them within a spectral framework to address nonlinear equations. Building on this, Liu and Li [29] introduced another DY-type algorithm to solve Equation 1 using a multivariate spectral approach. Their study integrated both the DY conjugate gradient parameter and multivariate spectral gradient methodology. They simulated these approaches and assessed their global convergence. Notably, before establishing global convergence, they impose a restriction on the Lipschitz constant, ensuring that L < 1−r with r∈(0, 1). In recent years, numerous techniques have been developed to solve Equation 1, several of which are referenced in [8–10, 12–14, 22, 24].

Abbass et al. [2] introduced a novel approach to solve monotone nonlinear equations with constraints. This innovative technique ensures both global and R-linear convergence rates while satisfying the essential descent conditions. To demonstrate the effectiveness of their method, the authors conducted two comprehensive sets of numerical tests [1]. In their study, they adapted the proposed search direction and extended it to address a system of nonlinear monotonic equations. Their modifications to the search direction ensured compliance with the descent condition, thereby eliminating the need for a line search.

The authors established the global convergence of their algorithm under valid assumptions, which provided a solid foundation for their study. The initial experiment highlighted the superior performance of their approach compared with existing methods, showcasing its potential for solving constrained monotone nonlinear equations. The second experiment further assessed the effectiveness of the algorithm in compressive sensing, underscoring its versatility and applicability across various problem domains. Overall, the search direction achieves sufficient descent without the necessity of a line search.

Motivated by the above-mentioned contributions, in this study, we introduce an effective spectral conjugate gradient method designed to tackle convex constraint approaches for systems of nonlinear monotone equations. Our approach builds on modifications made to the DY-conjugate gradient method proposed by Liu and Feng [27]. The proposed method utilizes a convex combination of the Dixon-type parameter and a modified conjugate gradient parameter to define the search direction. These enhancements are specifically tailored to address the unique challenges presented in this study.

The following are some of the contributions of this paper:

• The paper presents a new Dixon-type parameter and a modified conjugate gradient parameter.

• The search direction satisfies the sufficient descent without any line search.

• The proposed algorithm is applied to solve a large-scale system of monotone nonlinear equations and, ultimately, to address some signal processing problems.

2 Preliminaries and algorithm

We propose a spectral conjugate gradient method designed to effectively tackle nonlinear monotone equation systems with convex constraints. This method incorporates a modified CD parameter along with a convex Dixon-type parameter. Our approach can be viewed as a modification of the concept introduced by Yu et al. [41]. We demonstrated the global convergence of the proposed algorithm under reasonable assumptions. Furthermore, the algorithm was utilized to recover a noisy signal.

Definition 1.2. [3] Let Ω⊂ℝⁿ be a non-empty convex and closed set. Then for any x∈ℝⁿ its projection onto Ω is defined as

$\begin{array}{ll}{P}_{\Omega }(x)=argmin\left\{\left|\right|x-y\left|\right|:y\in \Omega \right\}& (3)\end{array}$

The following property is included in the projection map.:

$\begin{array}{ll}\left|\right|P_{\Omega }(x)-y\left|\right|\le \left|\right|x-y\left|\right|,\forall x,y\in {ℝ}^n& (4)\end{array}$

Spectral and conjugate gradient algorithms use the following formula to generate a sequence of iterations:

$\begin{array}{ll}{x}_{k+1}=x_k+{\alpha }_k{d}_k& (5)\end{array}$

where x_k is the previous iteration, while x_k+1 is the current iteration, α_K represents the step size, and d_k is the conjugate gradient search direction as follows:

$\begin{array}{ll}{d}_k=\{\begin{array}{ll}\text{-}{\Psi }_k,\hfill & if k\text{ = 0};\hfill \\ \text{-}{\Psi }_k\text{+}{\beta }_k{d}_{k\text{-1}},\hfill & ifk\ge \text{1},\hfill \end{array}& (6)\end{array}$

By using different values for parameters ν_k and β_k, various spectral and conjugate gradient directions can be developed. The method can satisfy sufficient descent conditions for direction d_k, which is necessary to ensure global convergence.

$\begin{array}{ll}{\Psi }_k^T{d}_k\le -c\left|\right|{\Psi }_k\left|\right|& (7)\end{array}$

where c>0. The DY conjugate gradient parameter, first proposed in Dai and Yuan [16], is a well-known parameter provided in this direction. This is defined as follows:

$\begin{array}{ll}{\beta }_k^{DY}=\frac{\left|\right|{\Psi }_k|{|}^2}{y_{k-1}^T{d}_{k-1}}& (8)\end{array}$

such that, in the direction of Equation 6,

$\begin{array}{ll}{d}_K=\{\begin{array}{ll}\text{-}{\Psi }_k,\hfill & if k\text{ = 0};\hfill \\ \text{-}{\Psi }_k\text{+}\frac{{\Vert {\Psi }_k\Vert }^{\text{2}}}{{\text{y}}_{k\text{-1}}^T{d}_{k\text{-1}}}\hfill & if k\ge \text{1},\hfill \end{array}& (9)\end{array}$

where y_k−1 = Ψ_k−Ψ_k−1. However, Equation 9 fails to satisfy Equation 7, which is crucial for global convergence. Liu and Feng [27], modified the approach proposed in Dai and Yuan [16]. They introduced a spectral conjugate gradient technique to solve Equation 1. The direction proposed by Liu and Feng adheres to the condition specified in Equation 7. Additionally, they presented adequate evidence demonstrating global convergence under mild assumptions.

Remark 2.2. To solve Equation 1, we propose a new spectral Dixon-type Global Algorithm convergence (GAC) approach. The method is described in more detail below, leveraging the convexity of the Dixon parameter along with a modified conjugate descent parameter to satisfy the sufficient requirement outlined in property (Equation 7).

$\begin{array}{ll}{d}_k=\{\begin{array}{ll}\text{-}{\Psi }_k\hfill & if k\text{ = 0};\hfill \\ \text{-}{\Psi }_k(1-{\Phi }_k)\text{+}{\beta }_k^{GAC}{d}_{k\text{-1}}\hfill & if k\ge \text{1},\hfill \end{array}& (10)\end{array}$

$\begin{array}{ll}{\Phi }_k=\frac{{\Psi }_k^T{d}_{k-1}}{{\left(d_{k-1}^T{y}_{k-1}\right)}^2}& (11)\end{array}$

$\begin{array}{ll}{\beta }_k^{GAC}{d}_{k-1}=-\frac{\left|\right|{\Psi }_k|{|}^2}{{(d_{k-1}^T{y}_{k-1})}^2}{d}_{k-1}and{y}_{k-1}={\Psi }_k-{\Psi }_{k-1}.& (12)\end{array}$

From the definitions of Equations 10, 12, it is easy to obtain

$\begin{array}{l}{\Psi }_k^T{d}_k=-\left|\right|{\Psi }_k|{|}^2(1-{\Phi }_k)-\frac{\left|\right|{\Psi }_k|{|}^2}{{(d_{k-1}^T{y}_{k-1})}^2}{\Psi }_k^T{d}_{k-1}\\ =-\left|\right|{\Psi }_k|{|}^2\left(1-\frac{{\Psi }_k^T{d}_{k-1}}{{\left(d_{k-1}^T{y}_{k-1}\right)}^2}\right)-\frac{\left|\right|{\Psi }_k|{|}^2}{{(d_{k-1}^T{y}_{k-1})}^2}{\Psi }_k^T{d}_{k-1}\\ =-\left|\right|{\Psi }_k|{|}^2+\frac{\left|\right|{\Psi }_k|{|}^2}{{\left(d_{k-1}^T{y}_{k-1}\right)}^2}{\Psi }_k^T{d}_{k-1}-\frac{\left|\right|{\Psi }_k|{|}^2}{{(d_{k-1}^T{y}_{k-1})}^2}{\Psi }_k^T{d}_{k-1}\\ \le -\left|\right|{\Psi }_k|{|}^2,& (13)\end{array}$

from Equation 13 for c = 1, a sufficient descent (Equation 7) is satisfied. Therefore, this assures that the sufficient-descent CG direction for the constrained monotone equation of the Dixon type is established.

3 Convergence analysis

The following section presents a detail investigation of the global convergence of the proposed method. Before that, we will provide some assumptions to help establish the theoretical framework of our study.

Assumption 3.1. (A1) The solution set of Equation 1 is nonempty and is symbolized by Ω.

(A2) The mapping Ψ is uniformly monotone, i.e., ∀x, y∈ℝⁿ, such that

$\begin{array}{ll}{(x-y)}^T(\Psi (x)-\Psi (y))\ge c\left|\right|x-y|{|}^2.& (17)\end{array}$

(A3) The mapping F is Lipschitz continuous, meaning that there exists a positive constant L such that

$\begin{array}{ll}\left|\right|\Psi (x)-\Psi (y)\left|\right|\le L\left|\right|x-y\left|\right|,\forall x,y\in \mathbb{N}.& (18)\end{array}$

Remark 3.2. From assumption (Equations 17, 18), we obtain

$\begin{array}{ll}{y}_{k-1}^T{d}_{k-1}\ge c{\stackrel{⌣}{\alpha }}_{k-1}\left|\right|d_{k-1}|{|}^2.& (19)\end{array}$

This implies

$\begin{array}{ll}\frac{1}{y_{k-1}^T{d}_{k-1}}\le \frac{1}{c{\stackrel{⌣}{\alpha }}_{k-1}\left|\right|d_{k-1}|{|}^2}<PWherePisapositivenumber.& (20)\end{array}$

Remark 3.3. It is true from the lemma 3.4 below that

$\left|\right|x_k-\bar{x}\left|\right|\le \left|\right|x_0-\bar{x}\left|\right|.$

Lemma 3.4. Let Assumptions A1–A3 hold, and that the sequences {x_k} and {z_k} are generated by GAC, it follows that both {x_k} and {z_k} are bounded. Furthermore, we have

$\begin{array}{ll}\left|\right|d_k\left|\right|\le \hat{P}where\hat{P}isapositiveconstant.& (21)\end{array}$

$\begin{array}{ll}{\displaystyle \underset{k\to \infty }{lim}}\left|\right|x_k-z_k\left|\right|=0& (22)\end{array}$

$\begin{array}{ll}{\displaystyle \underset{k\to \infty }{lim}}\left|\right|x_{k+1}-x_k\left|\right|=0.& (23)\end{array}$

Proof. Consider any solution $\bar{x}\in \Omega$ of Equation 1, and we show that the sequences {x_k} and {z_k} are bounded. By applying the monotonicity principle of Ψ, we arrive at the following conclusion.

$\begin{array}{l}{(x_k-\bar{x})}^T\Psi (z_k)={(x_k-z_k+z_k-\bar{x})}^T\Psi (z_k)\\ ={(x_k-z_k)}^T\Psi (z_k)+{(z_k-\bar{x})}^T\Psi (z_k)\\ \ge {(x_k-z_k)}^T\Psi (z_k)+{(z_k-\bar{x})}^T\Psi (\bar{x})\\ ={(x_k-z_k)}^T\Psi (z_k).& (24)\end{array}$

This can be ascertained by utilizing the characterization of z_k along with the line search criteria described in Equation 14.

$\begin{array}{ll}{(x_k-z_k)}^T\Psi (z_k)\ge \sigma {\alpha }_k^2\left|\right|d_k|{|}^2>0.& (25)\end{array}$

Nonetheless, by applying Definition 2.1 along with Equation 15, we can show

$\begin{array}{l}\left|\right|x_{k+1}-\bar{x}|{|}^2=||P_C\left[x_k-{\eta }_k\Psi (z_k)\right]-\bar{x}|{|}^2\\ \le \left|\right|x_k-{\eta }_k\Psi (z_k)-\bar{x}|{|}^2\\ =\left|\right|x_k-\bar{x}|{|}^2-2{\eta }_k{(x_k-\bar{x})}^T\Psi (z_k)+{\eta }_k^2|\left|\Psi (z_k)\right|{|}^2\\ \le \left|\right|x_k-\bar{x}|{|}^2-2{\eta }_k{(x_k-z_k)}^T\Psi (z_k)+{\eta }_k^2|\left|\Psi (z_k)\right|{|}^2\\ =\left|\right|x_k-\bar{x}|{|}^2-\frac{{({(x_k-z_k)}^T\Psi (z_k))}^2}{\left|\right|\Psi (z_k)|{|}^2}\\ \le \left|\right|x_k-\bar{x}|{|}^2,& (26)\end{array}$

from which we derive

$\begin{array}{ll}\left|\right|x_{k+1}-\bar{x}\left|\right|\le \left|\right|x_k-\bar{x}\left|\right|.& (27)\end{array}$

This indicates that for all k, the distance $\left|\right|x_k-\bar{x}\left|\right|$ is less than or equal to $\left|\right|x_0-\bar{x}\left|\right|$. Clearly, the sequence $\left\{\left|\right|x_k-\bar{x}\left|\right|\right\}$ exhibits a decreasing pattern. Consequently, set {x_k} is bounded. Additionally, by referring to Equation 27 and applying Assumptions A1–A3, we can gather more insights.

$\begin{array}{ll}\left|\right|{\Psi }_k\left|\right|=\left|\right|{\Psi }_k-\Psi (\bar{x})\left|\right|\le L\left|\right|x_k-\bar{x}\left|\right|\le L\left|\right|x_0-\bar{x}\left|\right|.& (28)\end{array}$

If we let $\hat{P}=L\left|\right|x_0-\bar{x}\left|\right|$, then we can conclude that Also, for k>0, using the Equations 10–12, we have

$\begin{array}{l}\left|\right|d_k\left|\right|=\left|\right|-{\Psi }_k(1-{\Phi }_k)-\frac{\left|\right|{\Psi }_k|{|}^2{d}_{k-1}}{{(d_{k-1}^T{y}_{k-1})}^2}\left|\right|\\ \le \left|\right|{\Psi }_k\left|\right|+\frac{\left|\right|{\Psi }_k\left|{|}^2\right|\left|d_{k-1}\right||}{|d_{k-1}^T{y}_{k-1}{|}^2}+\frac{\left|\right|{\Psi }_k\left|{|}^2\right|\left|d_{k-1}\right||}{|d_{k-1}^T{y}_{k-1}{|}^2}\\ \le \left|\right|{\Psi }_k\left|\right|+\frac{\left|\right|{\Psi }_k\left|{|}^2\right|\left|d_{k-1}\right||}{c^2{\stackrel{⌣}{\alpha }}_{k-1}^2\left|\right|d_{k-1}|{|}^4}+\frac{\left|\right|{\Psi }_k\left|{|}^2\right|\left|d_{k-1}\right||}{c^2{\stackrel{⌣}{\alpha }}_{k-1}^2\left|\right|d_{k-1}|{|}^4}\\ \le \left|\right|{\Psi }_k\left|\right|+2\frac{\left|\right|{\Psi }_k|{|}^2}{c^2{\stackrel{⌣}{\alpha }}_{k-1}^2\left|\right|d_{k-1}|{|}^3}\\ \le \hat{P}+\frac{2{\hat{P}}^2}{c^2{\stackrel{⌣}{\alpha }}_{k-1}^2\left|\right|d_{k-1}|{|}^3}\\ \le \hat{P}+2{\hat{P}}^{2}P\end{array}$

where $P=\frac{1}{c^2{\stackrel{⌣}{\alpha }}_{k-1}^2\left|\right|d_{k-1}|{|}^3}$. From inequality (Equation 20) in the Remark 3.2 therefore, $\underset{k}{lim}\to \infty {\alpha }_k\left|\right|d_k\left|\right|=0$, this implies that ${\alpha }_{k-1}^2\left|\right|d_{k-1}\left|\right|<\infty$. $\hat{P}$ bound of which defined in Equation 21.

From Equation 26, we have

$\begin{array}{ll}{({(x_k-z_k)}^T\Psi (z_k))}^2\le \left|\right|\Psi (z_k)|{|}^2(\left|\right|x_k-\bar{x}|{|}^2-||x_{k+1}-\bar{x}|{|}^2)& (29)\end{array}$

Based on the line search condition (Equation 14), we can infer

$\begin{array}{ll}{\sigma }^2{\alpha }_k^2\left|\right|d_k|{|}^4\le {\alpha }_k^2{(\Psi {(z_k)}^T{d}_k)}^2.& (30)\end{array}$

By merging Equation 29 with Equation 30, it can be concluded that

$\begin{array}{ll}{\sigma }^2{\alpha }_k^2\left|\right|d_k|{|}^4\le |\left|\Psi (z_k)\right|{|}^2(\left|\right|x_k-\bar{x}|{|}^2-||x_{k+1}-\bar{x}|{|}^2).& (31)\end{array}$

Because of boundedness of the sequence {Ψ(z_k)} and the convergence of $\left\{\left|\right|x_k-\bar{x}\left|\right|\right\}$, we can take the limit of both sides of Equation 31 to derive the following result.

$\begin{array}{l}{\sigma }^2{\displaystyle \underset{k\to \infty }{lim}}{\alpha }_k^2\left|\right|d_k|{|}^4\le 0,\end{array}$

thus

$\begin{array}{ll}{\displaystyle \underset{k\to \infty }{lim}}{\alpha }_k\left|\right|d_k\left|\right|=0.& (32)\end{array}$

By combining Equation 31 with the definition of z_k, we can deduce that Equation 22 is valid. Nonetheless, from the definition of η_k, we can derive

$\begin{array}{l}\left|\right|x_{k+1}-x_k\left|\right|=\left|\right|x_k-{\eta }_k\Psi (z_k)-x_k\left|\right|\\ =\left|\right|{\eta }_k\Psi (z_k)\left|\right|\\ \le \left|\right|x_k-z_k\left|\right|.& (33)\end{array}$

This refers to Equation 23.

Theorem 3.5. Assuming that Assumptions A1–A3 are satisfied, and considering the sequences {x_k} and {z_k} produced by the GAC method, we obtain the following result:

$\begin{array}{ll}{\displaystyle \underset{k\to \infty }{lim inf}}\left|\right|{\Psi }_k\left|\right|=0.& (34)\end{array}$

Proof. If we assume that Equation 34 is invalid, we can approach this with a proof by contradiction. This implies that there must be a positive value, denoted as ϵ₀, such that:

$\begin{array}{l}\left|\right|{\Psi }_k\left|\right|\ge {ϵ}_0\text{holds},\forall k>0.\end{array}$

If we assume that ||d_k||≠0 at all points except at the solution, then there exists a constant referred to as ϵ₁

$\begin{array}{l}\left|\right|d_k\left|\right|\ge {ϵ}_1.\end{array}$

If the step length α_k≠ξ , then α_k, ${\rho }^{-1}{\alpha }_k$ does not satisfy (Equation 14) i.e.,

$\begin{array}{ll}-\Psi {(x_k+{\rho }^{-1}{\alpha }_k{d}_k)}^T{d}_k<\sigma {\rho }^{-1}{\alpha }_k\left|\right|d_k|{|}^2.& (35)\end{array}$

Thus, combining Equations 13, 35 gives us

$\begin{array}{l}c\left|\right|{\Psi }_k|{|}^2\le -\Psi {(x_k)}^T{d}_k,\\ ={(\Psi (x_k+{\rho }^{-1}{\alpha }_k{d}_k)-\Psi (x_k))}^T{d}_k-\Psi {(x_k+{\rho }^{-1}{\alpha }_k{d}_k)}^T{d}_k,\\ \le \sigma {\rho }^{-1}{\alpha }_k\left|\right|d_k|{|}^2+L{\rho }^{-1}{\alpha }_k|\left|d_k\right|{|}^2.\\ ={\alpha }_k\left|\right|d_k\left|\right|(\sigma +L){\rho }^{-1}\left|\right|d_k\left|\right|.& (36)\end{array}$

Therefore, using Equation 36, we can conclude that

$\begin{array}{ll}{\alpha }_k\left|\right|d_k\left|\right|>\frac{c\left|\right|{\Psi }_k|{|}^2}{\left|\right|d_k\left|\right|}\frac{\rho }{(\sigma +L)}\ge \frac{c{ϵ}_0^2}{\hat{P}}\frac{\rho }{(\sigma +L)}.& (37)\end{array}$

The inequality in Equation 37 contradicts Equation 32. Therefore, Equation 34 holds, and the proof is complete.

4 Numerical simulation

This section assesses the numerical efficiency of the proposed Algorithm 1 GAC using two different methodologies: the ETTDFP technique introduced by Abdullahi et al. [5], and the MCHCG method outlined by Nermeh et al. [33]. To evaluate the performance of the algorithm, we considered key metrics such as the number of iterations (IT), number of function evaluations (FUNVAL), and computational time (CPUTIME) required to approximate a solution. The effectiveness of a solver is determined by its ability to achieve the lowest IT, FUNVAL, and CPUTIME values across a wide range of problem instances. Therefore, the most effective or exemplary solver is identified as one that demonstrates superior performance by minimizing these metrics across various problem sets. For the implementation of the GAC algorithm, we set the parameters as follows: γ = 1.9, ρ = 0.6, σ = 0.0001, μ = 0.23. Parameters for ETTDFP and MCHCG are adopted as specified in Abdullahi et al. [5], Nermeh et al. [33], respectively.

Algorithm 1

Algorithm 1. GAC

The experiments are carried out on a PC with an Intel Celeron (R) processor, 16GB of RAM, and a 2.9GHz CPU using Matlab 8.3.0 (R2014a). We set the number of iterations exceeds 1,000, or when $\left|\right|{\Psi }_k\left|\right|\le 10^{-6}$, the terminating condition is set.

The numerical simulation was conducted using the following five dimensions and six initial points. 1,000, 5,000, 10,000, 50,000, and 100,000 and $x_1={(1,\dots ,1)}^T$, $x_2={\left(\frac{1}{2},\dots ,\frac{1}{2^n}\right)}^T$, $x_3={(1-\frac{1}{n},1-\frac{2}{n},\dots ,0)}^T$, ${\tilde{x}}_4={\left(1,\frac{1}{2},\dots ,\frac{1}{n}\right)}^T$,$x_5={(2,\dots ,2)}^T$, and $x_6={(-10,\dots ,0)}^T$, respectively.

Eight different problems are used for the evaluation, where $\Psi ={({\Psi }_1,{\Psi }_2,...,{\Psi }_n)}^T.$

Problem 1 [11]

${\Psi }_1(x)=e^{x_1}-1,$

${\Psi }_i(x)=e^{x_i}+x_i-1,i=2,3,\dots ,n-1$,

where $\Omega ={ℝ}_{+}^n$.

Problem 2 [11]

${\Psi }_1(x)=e^{x_1}-1,$

Ψ_i(x) = x_i−sin|x_i−1|, i = 1, 2, …, n,

where $\Omega ={ℝ}_{+}^n$.

Problem 3 [11]

${\Psi }_1(x)=e^{x_1}-1,$

Ψ_i(x) = 2x_i−sin|x_i|, i = 1, 2, …, n,

where $\Omega ={ℝ}_{+}^n$.

Clearly, Problem 3 is non-smooth at y = 0.

Problem 4 [23]

${\Psi }_1(x)=e^{x_1}-1,$

${\Psi }_i(x)=e^{x_i}-1,i=1,2,\dots ,n$,

where $\Omega ={ℝ}_{+}^n$.

Problem 5 [2]

Ψ₁(x) = cos(x₁) − 9 + 3x₁ + 8 exp(x₂), i = 1, 2, …, n,

Ψ_i(x) = cos(x_i) − 9 + 3x_i + 8 exp(x_i−1), i = 1, 2, …, n,

whereas $\Omega ={ℝ}_{+}^n$.

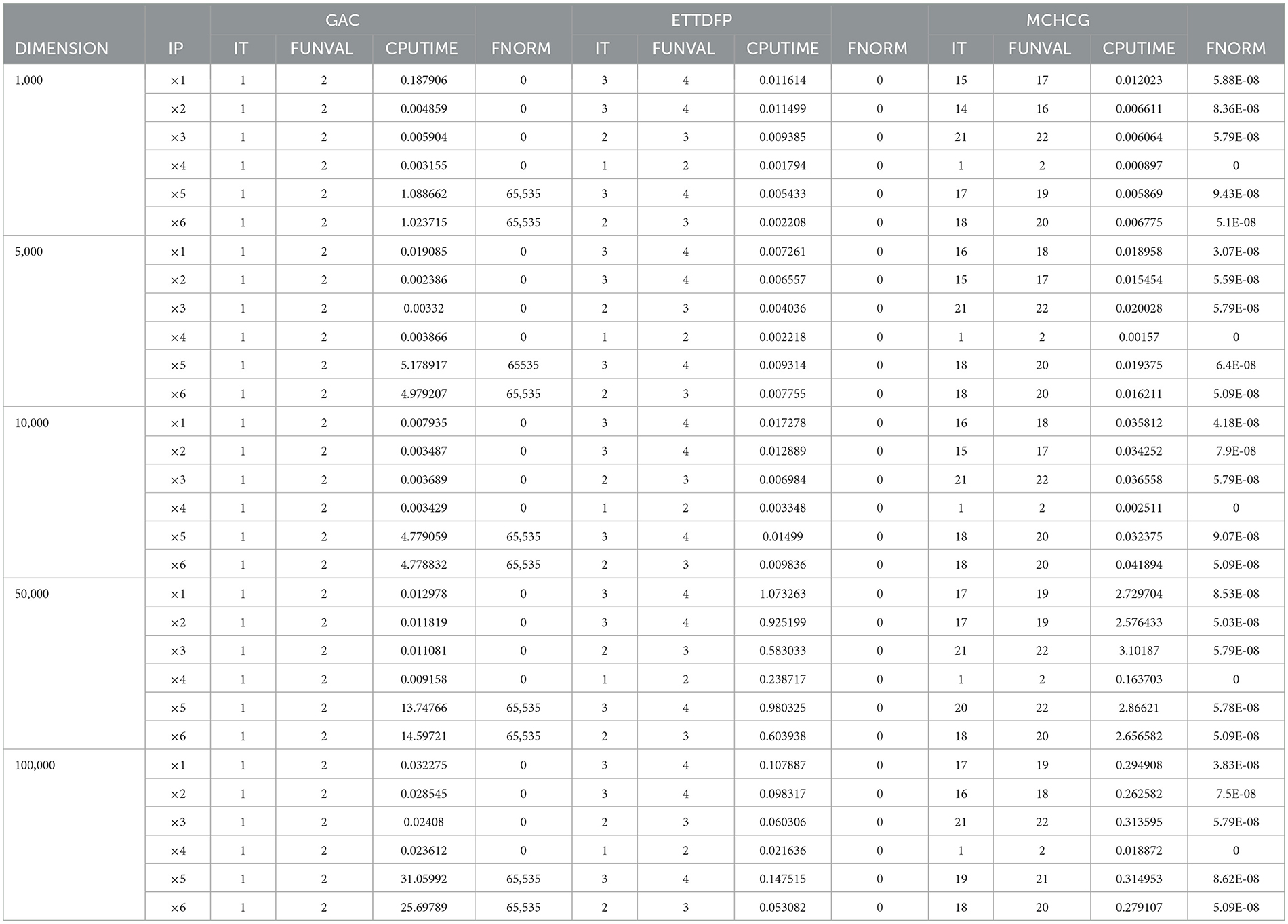
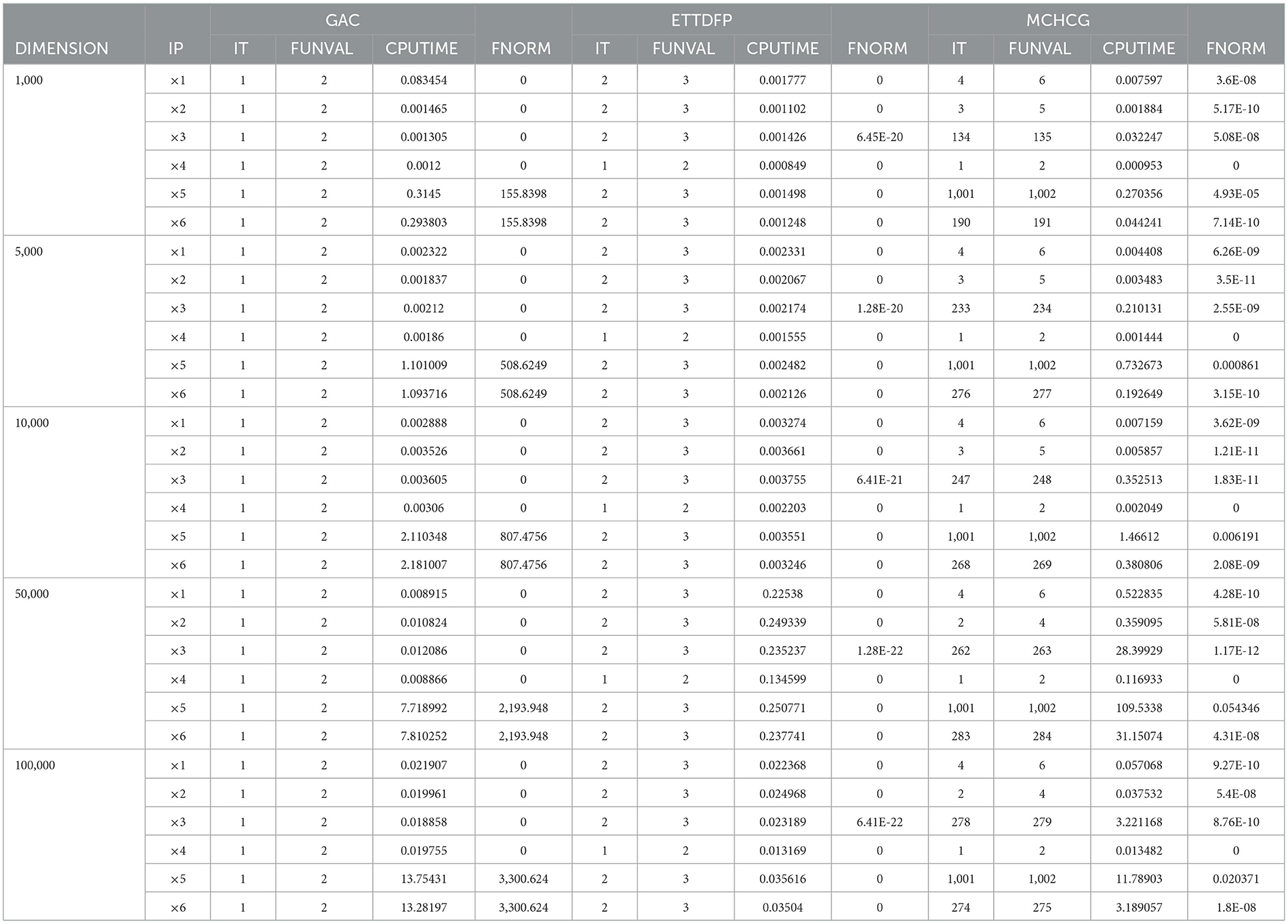
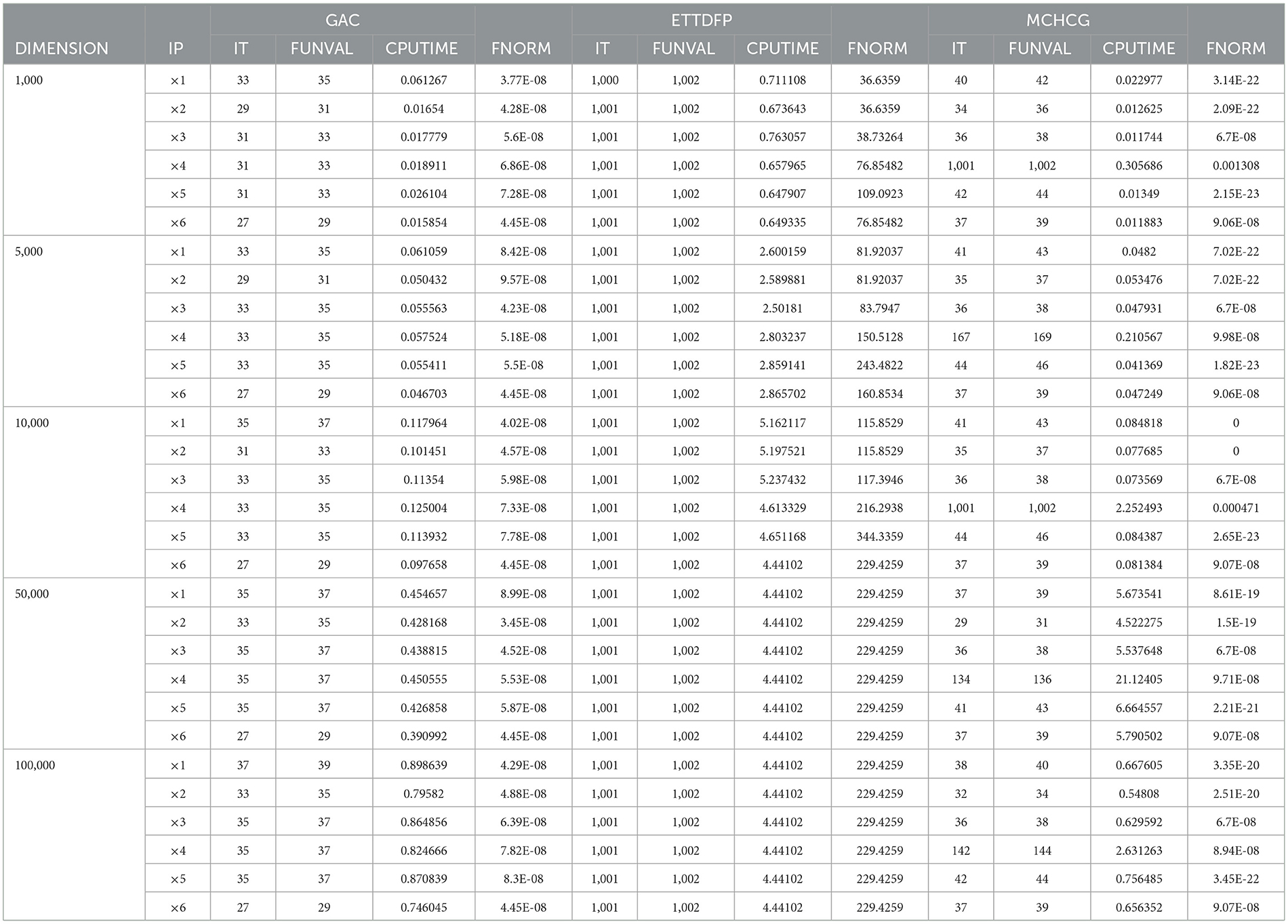
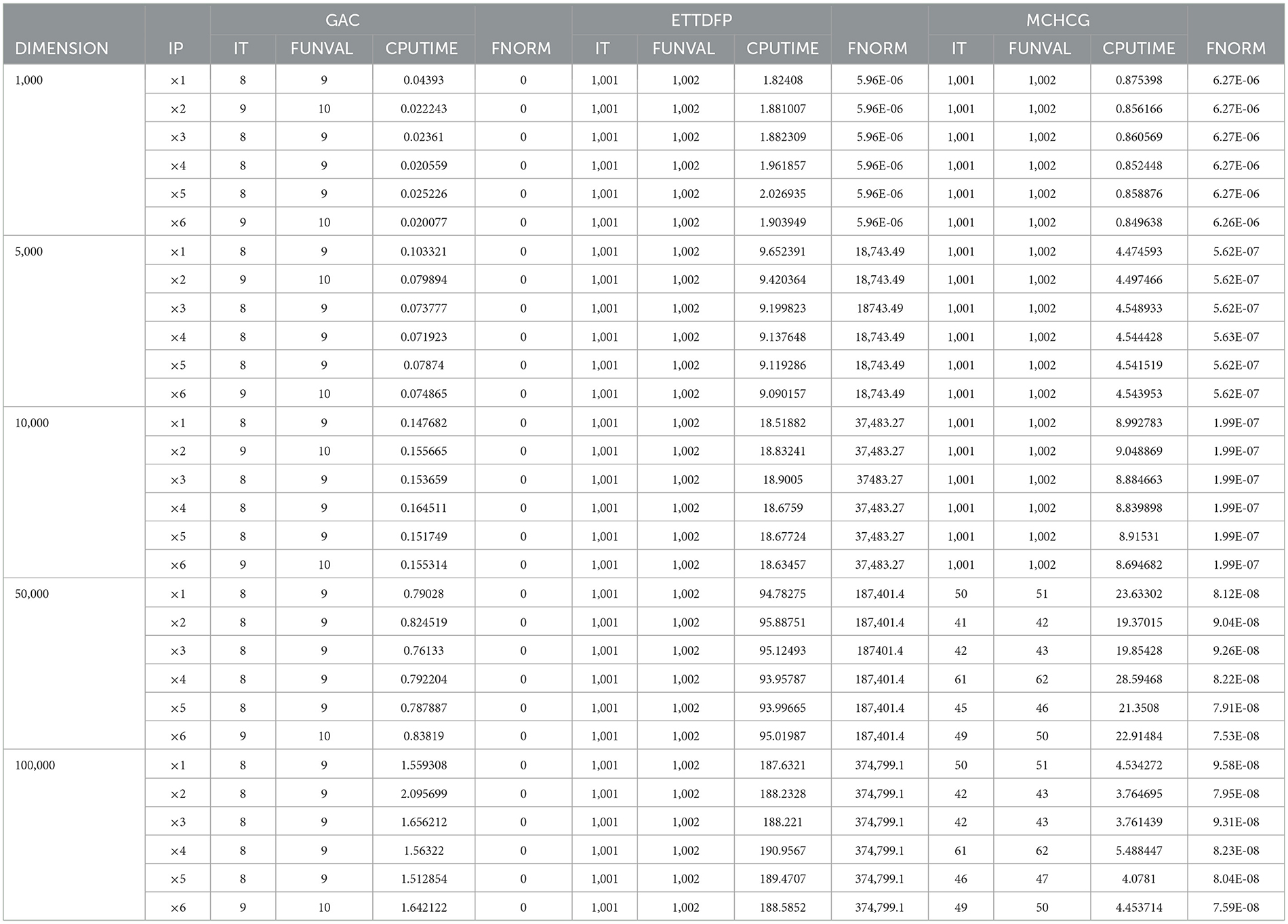
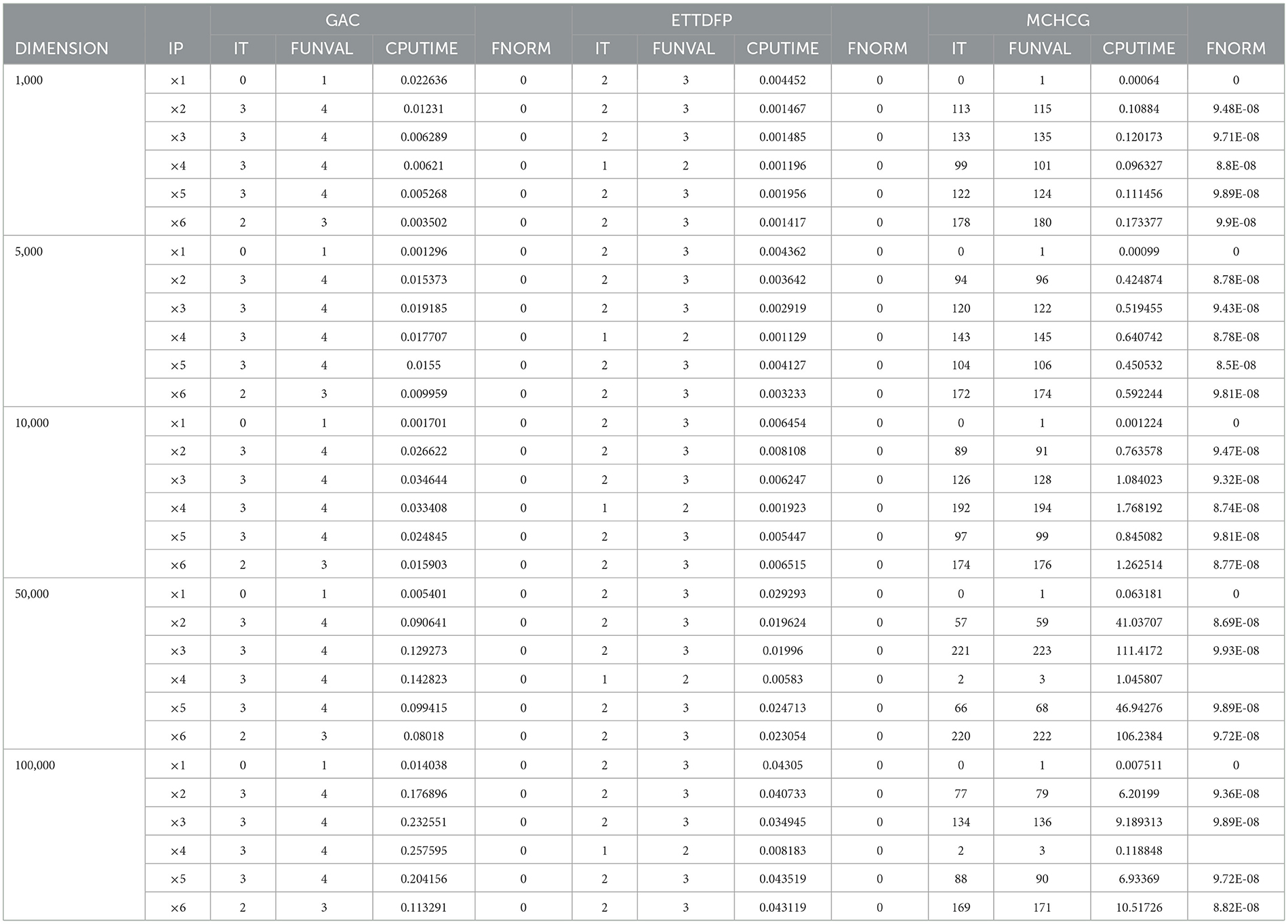
Tables 1–5 offer a thorough summary of the numerical experiments carried out, providing important information including the number of function evaluations (FVAL), iterations (ITER), CPU time (TIME), and the function value at the approximate solution. These tables are crucial for evaluating the efficiency and performance of the studied algorithms across various problem scenarios. By thoroughly analyzing the data presented in these tables, researchers can enhance their understanding of the convergence behavior, computational efficiency, and overall effectiveness of each method in addressing the optimization tasks.

Table 1

Table 1. Numerical results for GAC, ETTDFP, MCHCG on Problem 1.

Table 2

Table 2. Numerical results for GAC, ETTDFP, MCHCG on Problem 2.

Table 3

Table 3. Numerical results for GAC, ETTDFP, MCHCG on Problem 3.

Table 4

Table 4. Numerical results for GAC, ETTDFP, MCHCG on Problem 4.

Table 5

Table 5. Numerical results for GAC, ETTDFP, MCHCG on Problem 5.

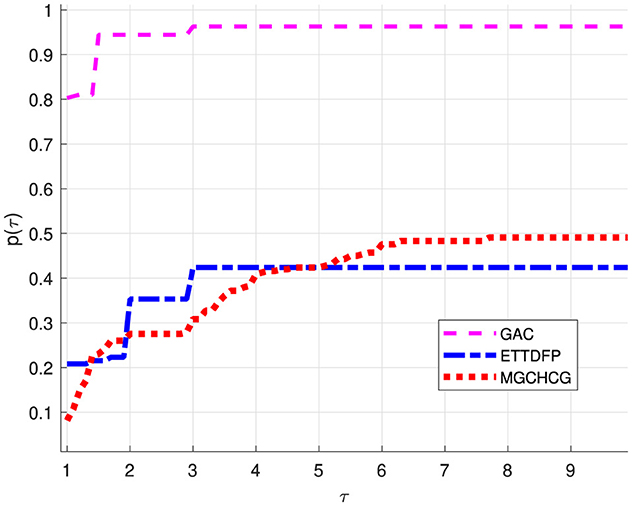
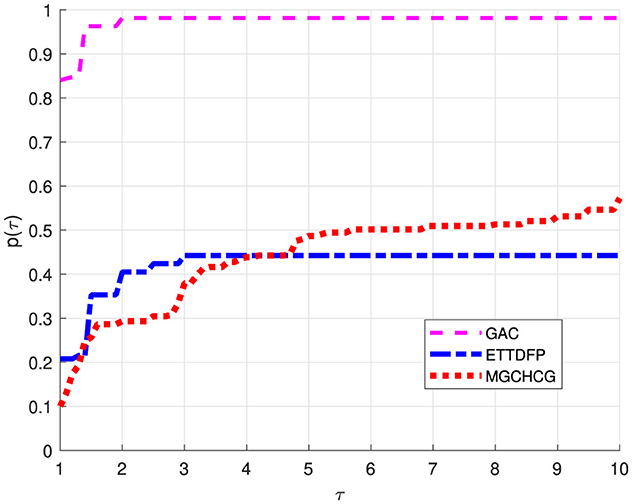
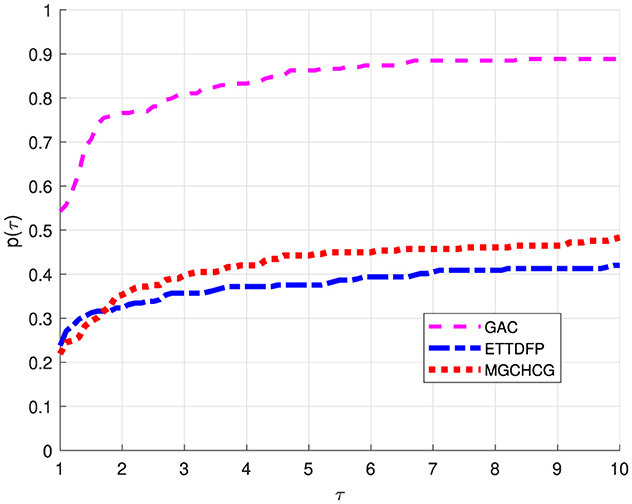
Figures 1–3 illustrate performance profiles using Dolan and Moré methodology [19]. These fig-depicts the comparative performance of the GAC algorithm in relation to HDP and DLP across key factors such as ITER, FVAL, and TIME. These profiles provide a comprehensive understanding of the relative efficiency and effectiveness of each algorithm in solving optimization problems.

Figure 1

Figure 1. Dolan and Moré performance profile with respect to ITER.

Based on the analysis in Figures 1–3, it is clear that the Global Algorithm Convergence (GAC) algorithm is the top performer. This demonstrates superior accuracy and potential across all evaluated parameters. One particularly notable aspect is the performance in terms of the number of iterations. As shown in Figure 1, GAC consistently outperformed HDP and DLP and, converged with fewer iterations in most cases. Importantly, the instance demonstrates exceptional performance, with GAC successfully converging in over 80% of the cases using fewer iterations compared to both HDP and DLP. This highlights the effectiveness and efficiency of the GAC algorithm in solving optimization problems, making it highly promising.

Furthermore, Figures 2, 3 shed light on the efficiency of GAC which proves to be more efficient by succeeding in almost 82% of the examples with a lower number of function evaluations. However, it is worth noting that GAC exhibits suboptimal performance in terms of CPU time compare to the other metrics.

Figure 2

Figure 2. Dolan and Moré performance profile with respect to FVAL.

Figure 3

Figure 3. Dolan and Moré performance profile with respect to TIME.

5 Conclusions

This study introduces a groundbreaking iterative optimization method that surpasses the traditional spectral conjugate gradient technique. By incorporating a novel line-search-independent projection approach tailored for solving complex monotone systems of nonlinear equations under convex constraints, we achieve global convergence with remarkable efficiency and effectiveness. Extensive numerical experiments on challenging problems with up to 100,000 dimensions validated the superior performance of our method. Comparative analyses against established techniques consistently highlight its robust theoretical foundations and exceptional numerical efficiency, establishing it as a significant advancement in iterative optimization.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

GA: Conceptualization, Methodology, Software, Writing – original draft. NK: Methodology, Writing – original draft. IM: Investigation, Writing – review & editing. HC: Data curation, Supervision, Writing – review & editing. FT: Funding acquisition, Resources, Visualization, Writing – review & editing. GT: Formal analysis, Validation, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Abbass G, Chen H, Abdullahi M, Muhammad AB. An efficient projection algorithm for large-scale system of monotone nonlinear equations with applications in signal recovery. J Ind Manag Optim. (2024) 20:3580–95. doi: 10.3934/jimo.2024066

Crossref Full Text | Google Scholar

2. Abbass G, Chen H, Abdullahi M, Muhammad AB, Musa S. A projection method for solving monotone nonlinear equations with application. Phys Scr. (2023) 98:115250. doi: 10.1088/1402-4896/acfc70

PubMed Abstract | Crossref Full Text | Google Scholar

3. Abdullahi M, Abubakar AB, Muangchoo K. Modified three-term derivative-free projection method for solving nonlinear monotone equations with application. Numer Algorithms. (2024) 95:1459–74. doi: 10.1007/s11075-023-01616-8

Crossref Full Text | Google Scholar

4. Abdullahi M, Abubakar AB, Feng Y, Liu J. Comment on: a derivative-free iterative method for nonlinear monotone equations with convex constraints. Numer Algorithms. (2023) 10:1551–60. doi: 10.1007/s11075-023-01546-5

Crossref Full Text | Google Scholar

5. Abdullahi M, Abubakar AB, Sulaiman A, Chotpitayasunon P. An efficient projection algorithm for solving convex constrained monotone operator equations and sparse signal reconstruction problems. J Anal. (2024) 32:2813–32. doi: 10.1007/s41478-024-00757-w

Crossref Full Text | Google Scholar

6. Abdullahi M, Halĩlu AS, Awwal AM, Pakkaranang N. On efficient matrix-free method via quasi-Newton approach for solving system of nonlinear equations Adv Theory Nonlinear Anal Appl. (2021) 5:568–79. doi: 10.31197/atnaa.890281

Crossref Full Text | Google Scholar

7. Abubakar AB, Ibrahim AH, Abdullahi M, Aphane M, Chen J. A sufficient descent LS-PRP-BFGS-like method for solving nonlinear monotone equations with application to image restoration. Numer Algorithms. (2024) 96:1423–64. doi: 10.1007/s11075-023-01673-z

Crossref Full Text | Google Scholar

8. Abubakar AB, Kumam P, Mohammad H, Awwal AM. A Barzilai-Borwein gradient projection method for sparse signal and blurred image restoration. J Frank Inst. (2020) 357:7266–85. doi: 10.1016/j.jfranklin.2020.04.022

Crossref Full Text | Google Scholar

9. Aji S, Kumam P, Awwal AM, Yahaya MM, Kumam W. Two hybrid spectral methods with inertial effect for solving system of nonlinear monotone equations with application in robotics. IEEE Access. (2021) 9:30918–28. doi: 10.1109/ACCESS.2021.3056567

Crossref Full Text | Google Scholar

10. Awwal AM, Wang L, Kumam P, Mohammad H, Watthayu W. A projection Hestenes–Stiefel method with spectral parameter for nonlinear monotone equations and signal processing. Math Comput Appl. (2021) 25:27. doi: 10.3390/mca25020027

Crossref Full Text | Google Scholar

11. Awwal AM, Kumam P, Abubakar AB. A modified conjugate gradient method for monotone nonlinear equations with convex constraints. Appl Numer Math. (2019) 145:507–20. doi: 10.1016/j.apnum.2019.05.012

Crossref Full Text | Google Scholar

12. Awwal AM, Kumam P, Mohammad H, Watthayu W, Abubakar AB. A Perry-type derivative-free algorithm for solving nonlinear system of equations and minimizing ℓ1 regularized problem. Optimization. (2021) 70:1231–59. doi: 10.1080/02331934.2020.1808647

Crossref Full Text | Google Scholar

13. Awwal AM, Kumam P, Wang L, Huang S, Kumam W. Inertial-based derivative-free method for system of monotone nonlinear equations and application. IEEE Access. (2020) 8:226921–30. doi: 10.1109/ACCESS.2020.3045493

Crossref Full Text | Google Scholar

14. Awwal AM, Wang L, Kumam P, Mohammad H. A two-step spectral gradient projection method for system of nonlinear monotone equations and image deblurring problems. Symmetry. (2020) 12:874. doi: 10.3390/sym12060874

Crossref Full Text | Google Scholar

15. Cheng W. A PRP type method for systems of monotone equations. Math Comput Model. (2009) 50:15–20. doi: 10.1016/j.mcm.2009.04.007

Crossref Full Text | Google Scholar

16. Dai YH, Yuan Y. A nonlinear conjugate gradient method with a strong global convergence property. SIAM J Optim. (1999) 10:177–82. doi: 10.1137/S1052623497318992

Crossref Full Text | Google Scholar

17. Dai Z, Chen X, Wen F. A modified Perry's conjugate gradient method-based derivative-free method for solving large-scale nonlinear monotone equations. Appl Math Comput. (2015) 270:378–86. doi: 10.1016/j.amc.2015.08.014

Crossref Full Text | Google Scholar

18. Dirkse SP, Ferris MC. MCPLIB: a collection of nonlinear mixed complementarity problems. Optim Methods Softw. (1995) 5:319–45. doi: 10.1080/10556789508805619

Crossref Full Text | Google Scholar

19. Dolan ED, Moré JJ. Benchmarking optimization software with performance profiles Math Program. (2002) 91:201–13. doi: 10.1007/s101070100263

Crossref Full Text | Google Scholar

20. Fukushima M. Equivalent differentiable optimization problems and descent methods for asymmetric variational inequality problems. Math Program. (1992) 53:99–110. doi: 10.1007/BF01585696

Crossref Full Text | Google Scholar

21. Gu Q, Chen Y, Zhou J, Huang J. A fast linearized virtual element method on graded meshes for nonlinear time-fractional diffusion equations. Numer Algorithms. (2024) 97:1141–77. doi: 10.21203/rs.3.rs-3147548/v1

Crossref Full Text | Google Scholar

22. Guo J, Wan Z. A modified spectral PRP conjugate gradient projection method for solving large-scale monotone equations and its application in compressed sensing. Math Probl Eng. (2019) 2019:5261830. doi: 10.1155/2019/5261830

Crossref Full Text | Google Scholar

23. Halilu AS, Majumder A, Waziri MY, Abdullahi H. Double direction and step length method for solving system of nonlinear equations. Eur J Mol Clin Med. (2020) 7:3899–913.

Google Scholar

24. Ibrahim AH, Kumam P, Abubakar AB, Yusuf UB, Yimer SE, Aremu KO. An efficient gradient-free projection algorithm for constrained nonlinear equations and image restoration. Aims Math. (2020) 6:235. doi: 10.3934/math.2021016

Crossref Full Text | Google Scholar

25. Iusem NA, Solodov VM. Newton-type methods with generalized distances for constrained optimization. Optimization. (1997) 41:257–78. doi: 10.1080/02331939708844339

Crossref Full Text | Google Scholar

26. Kachurovskii RI. Monotone operators and convex functionals. Uspekhi Matematicheskikh Nauk. (1960) 15:213–5.

Google Scholar

27. Liu J, Feng Y. A derivative-free iterative method for nonlinear monotone equations with convex constraints. Numer Algorithms. (2019) 82:245–62. doi: 10.1007/s11075-018-0603-2

Crossref Full Text | Google Scholar

28. Liu JK, Li S. Spectral DY-type projection method for nonlinear monotone system of equations. J Comput Math. (2015) 33:341–55. doi: 10.4208/jcm.1412-m4494

Crossref Full Text | Google Scholar

29. Liu JK Li S. Multivariate spectral DY-type projection method for convex constrained nonlinear monotone equations. J Ind Manag Optim. (2017). 13:283. doi: 10.3934/jimo.2016017

Crossref Full Text | Google Scholar

30. Liu JK, Li SJ. A projection method for convex constrained monotone nonlinear equations with applications. Comput Math Appl. (2015) 70:2442–53. doi: 10.1016/j.camwa.2015.09.014

PubMed Abstract | Crossref Full Text | Google Scholar

31. Meintjes K, Morgan AP. A methodology for solving chemical equilibrium systems. Appl Math Comput. (1987) 22:333–61. doi: 10.1016/0096-3003(87)90076-2

Crossref Full Text | Google Scholar

32. Minty GJ. Monotone (nonlinear) operators in Hilbert space. Durham: Duke University Press (1962). doi: 10.1215/S0012-7094-62-02933-2

Crossref Full Text | Google Scholar

33. Nermeh E, Abdullahi M, Halilu AS, Abdullahi H. Modification of a conjugate gradient approach for convex constrained nonlinear monotone equations with applications in signal recovery and image restoration. Commun Nonlinear Sci Numer Simul. (2024) 136:108079. doi: 10.1016/j.cnsns.2024.108079

Crossref Full Text | Google Scholar

34. Salihu SB, Halilu AS, Abdullahi M, Ahmed K, Mehta P, Murtala S. An improved spectral conjugate gradient projection method for monotone nonlinear equations with application. J Appl Math Comput. (2024) 70:3879– 915. doi: 10.1007/s12190-024-02121-4

Crossref Full Text | Google Scholar

35. Solodov MV, Svaiter BF. A globally convergent inexact Newton method for systems of monotone equations. In:Fukushima M, Qi L, , editors. Reformulation: Nonsmooth, Piecewise Smooth, Semismooth and Smoothing Methods. London: Kluwer Academic Publishers (1999). p. 355–69. doi: 10.1007/978-1-4757-6388-1_18

Crossref Full Text | Google Scholar

36. Sun M, Liu J, Wang Y. Two improved conjugate gradient methods with application in compressive sensing and motion control. Math Probl Eng. (2020) 2020:1–11. doi: 10.1155/2020/9175496

Crossref Full Text | Google Scholar

37. Wang C, Wang Y, Xu C. A projection method for a system of nonlinear monotone equations with convex constraints. Math Methods Oper Res. (2007) 66:33–46. doi: 10.1007/s00186-006-0140-y

Crossref Full Text | Google Scholar

38. Wood AJ, Wollenberg BF. Power Generation, Operation, and Control. Hoboken, NJ: John Wiley & Sons (2013).

Google Scholar

39. Xiao Y, Wang Q, Hu Q. Non-smooth equations based method for ℓ1-norm problems with applications to compressed sensing. Nonlinear Anal Theory Methods Appl. (2011) 74:3570–7. doi: 10.1016/j.na.2011.02.040

Crossref Full Text | Google Scholar

40. Xiong Y, Chen Y, Zhou J, Liang Q. Divergence-free virtual element method for the stokes equations with damping on polygonal meshes. Numer Math Theory Methods Appl. (2024) 17:210–42. doi: 10.4208/nmtma.OA-2023-0071

Crossref Full Text | Google Scholar

41. Yu Z, Lin J, Sun J, Xiao Y, Liu L, Li Z. Spectral gradient projection method for monotone nonlinear equations with convex constraints. Appl Numer Math. (2009) 59:2416–23. doi: 10.1016/j.apnum.2009.04.004

Crossref Full Text | Google Scholar

42. Zarantonello E. Solving functional equations by contractive averaging, Math. Research Center Report. Madison: Mathematics Research Center, United States Army, University of Wisconsin (1960). p. 160.

Google Scholar

43. Zhang D, Jiang T, Jiang C, Wang G, A. complex structure-preserving algorithm for computing the singular value decomposition of a quaternion matrix and its applications. Numer Algorithms. (2024) 95:267–83. doi: 10.1007/s11075-023-01571-4

Crossref Full Text | Google Scholar

44. Zhao YB Li D. Monotonicity of fixed point and normal mappings associated with variational inequality and its application. SIAM J Optim. (2001) 11:962–73. doi: 10.1137/S1052623499357957

Crossref Full Text | Google Scholar

45. Zheng L, Yang L, Liang Y, A. modified spectral gradient projection method for solving non-linear monotone equations with convex constraints and its application. IEEE Access. (2020) 8:92677–86. doi: 10.1109/ACCESS.2020.2990298

Crossref Full Text | Google Scholar