Agricultural commodity futures prices prediction based on a new hybrid forecasting model combining quadratic decomposition technology and LSTM model

The stability of agricultural futures market is of great significance to social economy and agri-cultural development. In view of the complexity of the fluctuation of agricultural futures prices, it is challenging to make up for the shortcomings of the existing data preprocessing technology so as to improve the prediction accuracy of the model. This paper puts forward a new VMD-SGMD-LSTM model based on improved quadratic decomposition technology and artificial intelligence model. First of all, in the data preprocessing part, VMD is used to decompose the original futures price data, and SGMD is used to further process the remaining components. Secondly, the LSTM model is used to predict a series of modal components, and the final result is obtained by synthesizing the predicted values of different components. Furthermore, based on the futures trading data of wheat, corn and sugar in China agricultural futures market, this paper makes an empirical study in the 1-step, 2-step and 4-step ahead forecasting scenarios, respectively. The results show that compared with other benchmark models, the VMD-SGMD-LSTM hybrid model proposed in this paper has better forecasting ability and robustness for different agricultural futures, which effectively makes up for the shortcomings of existing research.

1 Introduction

Price data in agricultural futures markets is an important basis for various market participants to make in-vestment decisions, providing opportunities for market participants to hedge and pursue risk–return (Paredes-Garcia et al., 2019). At the same time, the price fluctuation of agricultural futures also implies the potential price risk, and causes a certain degree of impact on agricultural production and management. Therefore, it is urgent to depict the in-ternal fluctuation rule of agricultural futures prices more scientifically and construct a more effective model to predict the trend of agricultural futures prices. It is of great significance for market participants to carry out investment activities and relevant government departments to monitor the risk of futures market (Jung and Cho, 2022). However, the price fluctuation of agricultural products is affected by many factors, including basic market supply and demand factors, social economic fluctuations and climate factors in the production process (Marfatia et al., 2021; Guo et al., 2022). The price series of agricultural futures shows the characteristics of seasonality, random fluctuation and non-linear (Kyriazi et al., 2019). Therefore, the prediction of agricultural futures price has become the focus of many scholars in recent years (Pinheiro and de Senna, 2017; Luo et al., 2023).

The existing price forecasting methods can be roughly divided into the following three categories: econometric forecasting method, artificial intelligence model method and hybrid model method. Among them, econometric forecasting research aims at revealing the causal relationship in economic phenomena, and usually establishes regression models according to the functional relationship between independent variables and dependent variables (Bollerslev, 1986; Lee and Tong, 2011). Zafeiriou and Sariannidis (2011) applied Mackey GARCH model to the short-term forecasting of cotton futures prices. Jadhav et al. (2017) used univariate ARIMA techniques to forecast grain prices, and tested the forecasting ability of univariate ARIMA technology with different evaluation indicators. Although econometric models have made some achievements in the field of forecasting, a large number of empirical studies also show that in the process of forecasting price series, linear assumptions make the traditional econometric models unable to fully reflect the true distribution of data, and it is difficult to obtain accurate forecasting results on more complex data sets of agricultural futures prices, which has great limitations (Mandal et al., 2006; Lin et al., 2011; Taylan, 2017).

The existing price forecasting methods can be roughly divided into the following three categories: econometric forecasting method, artificial intelligence model method and hybrid model method. Among them, econometric forecasting research aims at revealing the causal relationship in economic phenomena, and usually establishes regression models according to the functional relationship between independent variables and dependent variables (Bollerslev, 1986; Lee and Tong, 2011). Zafeiriou and Sariannidis (2011) applied Mackey GARCH model to the short-term forecasting of cotton futures prices. Jadhav et al. (2017) used univariate ARIMA techniques to forecast grain prices, and tested the forecasting ability of univariate ARIMA technology with different evaluation indicators. Although econometric models have made some achievements in the field of forecasting, a large number of empirical studies also show that in the process of forecasting price series, linear assumptions make the traditional econometric models unable to fully reflect the true distribution of data, and it is difficult to obtain accurate forecasting results on more complex data sets of agricultural futures prices, which has great limitations (Mandal et al., 2006; Taylan, 2017; Li et al., 2021).

The second kind of artificial intelligence model is dedicated to capturing nonlinear patterns in price series, and has stronger computational fitting ability (Sadgali et al., 2019; Kurumatani, 2020). Its main models include various artificial neural networks (Jha and Sinha, 2014; Zhang et al., 2018), extreme learning machine (ELM) (Xiong et al., 2018) and support vector machine (SVM) (Wang et al., 2018; Zhang et al., 2020) and so on. Compared with econometric methods, artificial neural network can capture the motion pattern of nonlinear dynamic data more sensitively in the process of processing complex data. However, the traditional artificial neural network faces the problems of over-fitting and local extremum. Therefore, recurrent neural network (RNN) has been developed, but it still faces the problem of gradient disappearance. On the basis of RNN, Long Short-Term Memory (LSTM) model can capture the long-term and short-term information in time series more accurately through the setting of internal department structure. Jaiswal et al. (2022) developed a model based on deep long-term memory to predict agricultural price series with nonlinear characteristics. Banerjee et al. (2022) used the LSTM model to make long-term predictions on the prices of vegetables such as cabbage, cauliflower and pepper traded in the Indian market. Gu et al. (2022) con-structed a dual-input attentional long short-term memory (DIA-LSTM) model with higher prediction accuracy to predict the monthly prices of cabbage and radish in the Korean market.

Compared with a single prediction model, the hybrid model combining the advantages of different models can capture the real motion pattern of data series more accurately (Zhang, 2003; Zeng et al., 2023). Among them, TEI@I complex system re-search methodology, which is based on the combination of data preprocessing technology and prediction model, has been widely used in the field of commodity price prediction in recent years because of its better processing ability for complex data (Zhang et al., 2008). Specifically, TEI@I complex system research methodology preprocesses the price series based on a series of decomposition methods such as Wavelet Analysis (WA), Empirical Mode Decomposition (EMD) and VMD, and further combines artificial intelligence prediction models to predict the processed components, and develops a series of hybrid models based on the “decomposition-integration” framework (Reboredo and Rivera-Castro, 2013; Li et al., 2021; Wu et al., 2022). Fang et al. (2020) applied ensemble empirical pattern decomposition (EEMD) technology to decompose the prices of different kinds of agricultural futures, and in the prediction model part, SVM, neural network and ARIMA are integrated to predict the obtained components. Liu et al. (2022) used CEEMDAN to process the original soybean price series in China market, and introduced fuzzy entropy to characterize the complexity of the series, and then used CNN-GRU model to predict the obtained components. Diop and Kamdem (2023) used wavelet analysis and a seasonal auto-regressive aggregation (SARIMA) model to analyze and forecast the monthly prices of agricultural futures prices. Sun et al. (2022) combined the improved complete ensemble empirical mode decomposition with adaptive noise (ICEEMDAN) method and the empirical mode decomposition (EMD) method to forecast the futures price of crude oil. He and Huang (2023) combined VMD and wavelet packet decomposition (WPD) to construct a new hybrid model to predict the price of non-ferrous metals. Yang et al. (2023) combined ICEEMDAN, complete ensemble empirical mode decomposition (CEEMD) and other optimization algorithms to construct a new hybrid model to deal with complex carbon price series.

To sum up, it is a research trend to predict the price of agricultural products by using hybrid model, and how to select appropriate data preprocessing technology to extract the main characteristics of agricultural product price time series is the key to accurately simulate the price of agricultural products. Although the existing hybrid model based on “decomposition-prediction” framework has improved the prediction performance to a certain extent, the existing research lacks the secondary decomposition algorithm for agricultural futures prices in terms of data preprocessing technology.

Specifically, an effective signal decomposition algorithm can reduce the complexity of the original data and improve the prediction accuracy of the mixed model as a whole. Based on different theoretical foundations, the single popular decomposition algorithms include empirical mode decomposition (EMD) (Wang et al., 2020; Zeng et al., 2023) complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) (Diop and Kamdem, 2023), singular spectrum analysis (SSA) (Huang et al., 1998), variational mode decomposition (VMD) (Lin et al., 2011; Li et al., 2021), and so on. However, only using a single decomposition technology to process the original data will cause problems such as excessive calculation and large residual noise.

Therefore, on the basis of the above analysis, this paper introduces VMD-SGMD secondary decomposition technology into the research of agricultural futures price prediction, and further combines with LSTM model to construct a VMD-SGMD-LSTM hybrid model to predict the agricultural futures price in China. Specifically, the contributions of this paper are as follows:

(a) The secondary decomposition technology was first applied to the forecasting of agricultural futures prices

As mentioned above, in the previous research on the prediction of agricultural futures prices, only a single decomposition algorithm was applied in the hybrid model, and the decomposed subsequences still had noise, which could not fully capture the characteristics of agricultural futures prices. Compared with other single decomposition algorithms, VMD can select and describe the characteristics of data more effectively and has higher decomposition accuracy (Wang et al., 2017; Liu et al., 2018; He et al., 2019). However, VMD’s ability to capture high-frequency fluctuation signals is limited in the process of signal reconstruction (Dragomiretskiy and Zosso, 2014).

In order to make up for this defect, this study constructs VMD-SGMD secondary decomposition technology to reduce the noise in agricultural futures price series. SGMD can effectively avoid and overcome the difficulties of pattern aliasing and sensitive parameter setting in the process of data decomposition (Pan et al., 2019). Specifically, VMD-SGMD uses VMD to extract the low-frequency components of the price series, and then uses SGMD to process the remaining components. The empirical results show that VMD-SGMD secondary decomposition has higher reconstruction accuracy and robustness than other single decomposition techniques (EMD, EEMD and CEEMDAN), and it can extract more effective information from the data and extract the fluctuation characteristics in the time series more effectively.

(b) Combining with the artificial intelligence model, a new hybrid model VMD-SGMD-LSTM is proposed

LSTM (Hochreiter and Schmidhuber, 1997) is essentially an improved RNN, which can improve the dilemma of gradient disappearance or explosion of standard RNN in the training process, and has better learning and forecasting ability for nonlinear time series (Vuong et al., 2022; Zhou et al., 2022). Therefore, this paper adopts LSTM as the prediction model in the hybrid model and constructs a new VMD-SGMD-LSTM model. VMD-SGMD-LSTM model, as a hybrid model combining quadratic decomposition and artificial intelligence model, is of great significance to fill the gap in the research of agricultural futures price prediction.

(c) Taking the futures market of agricultural products in China as the research object, the validity and robustness of the proposed model are verified by setting the forecasting scenario of unsynchronized numbers

As an important agricultural country, the price fluctuation of agricultural products in China affects the stable development of the national economy. With the increasing share of China’s agricultural futures in the international market, China’s agricultural futures market has an increasing influence on the world futures market. In this paper, the strong wheat, corn and sugar in China agricultural futures market are taken as the research objects, and the proposed VMD-SGMD-LSTM mixed model and a series of benchmark models (RNN, ANN, LSTM, EMD-LSTM, EEMD-LSTM, CEEMDAN-LSTM and VMD-LSTM) are adopted respectively, and $e_{MAE}$ , and $e_{MAPE}$ and $e_{RMSE}$ are used as the evaluation criteria. The empirical results based on different agricultural products verify the superiority and robustness of VMD-SGMD-LSTM hybrid model compared with other benchmark models.

The rest of the paper is arranged as follows: Section 2 describes the components of the VMD-SGMD-LSTM hybrid model and the specific construction steps. Section 3 analyzes and evaluates the predictive performance of the constructed hybrid model based on the empirical results of different agricultural products. Section 4 concludes this article.

2 Methodology

The VMD-SGMD-LSTM hybrid model consists of quadratic decomposition technique VMD-SGMD and LSTM. Firstly, the original futures price series is decomposed by VMD-SGMD, which reduces the complexity of the sequence and improves the interpretability, and further, the reconstructed sequence is predicted by combining the LSTM model, which significantly improves the performance of the prediction model.

2.1 VMD

As shown in Equation (1), by solving the constrained variational problem, the VMD algorithm decomposes the given vibration signal F into a series of sparse modal components, and constrains the sum of all modes to be equal to the original signal while seeking the minimum sum of the bandwidths of each mode, where each component has its own central frequency and limited bandwidth.

$\begin{array}{ll}\underset{\left\{u_k\right\},\left\{w_k\right\}}{\min }\left\{{\displaystyle \sum }_{k=1}^K\left[{\partial }_t\left(\delta \left(t\right)+\frac{j}{\pi t}\right)\ast u_k\left(t\right)\right]e^{-j{w}_k}{t}_2^2\right\},s.t={\displaystyle \sum }_{k=1}^K{u}_k=f\left(t\right)& (1)\end{array}$

Where $k$ is the number of components, $k=1,2\cdots K$ . In order to transform the constrained problem into an unconstrained problem, the quadratic penalty factor α and Lagrange multiplier $\lambda$ are introduced, and the desired augmented Lagrange equation is obtained. Among them, the value of α can ensure the reconstruction accuracy of the signal in the presence of Gaussian noise, and the Lagrange multiplier keeps the constraints strict.

$\begin{array}{ll}{\stackrel{\wedge }{u}}_k^{n+1}\left(w\right)=\frac{\stackrel{\wedge }{C}\left(w\right)-{{\displaystyle \sum }}_{i\ne k}{\stackrel{\wedge }{u}}_i\left(w\right)+\frac{\stackrel{\wedge }{\lambda }\left(w\right)}{2}}{1+2\alpha {\left(w-w_k\right)}^2}& (2)\end{array}$

$\begin{array}{ll}{\stackrel{\wedge }{w}}_k^{n+1}=\frac{{{\displaystyle \int }}_0^{\infty }w{\left|{\stackrel{\wedge }{u}}_k\left(w\right)\right|}^{2}dw}{{{\displaystyle \int }}_0^{\infty }{\left|{\stackrel{\wedge }{u}}_k\left(w\right)\right|}^{2}dw}& (3)\end{array}$

$\begin{array}{ll}{\stackrel{\wedge }{\lambda }}^{n+1}={\stackrel{\wedge }{\lambda }}^n\left(w\right)+\tau \left[\stackrel{\wedge }{C}\left(w\right)-{\displaystyle \sum }_{k=1}^K\left|{\stackrel{\wedge }{u}}_k^{n+1}\left(w\right)\right|\right]& (4)\end{array}$

According to the given solution accuracy ε, the iteration stops when Equation (5) is satisfied.

$\begin{array}{ll}{\displaystyle \sum }_{k=1}^K\frac{{\stackrel{\wedge }{u}}_k^{n+1}-{\stackrel{\wedge }{u}}_k^n{}_2^2}{{\stackrel{\wedge }{u}}_k^n{}_2^2}<\epsilon \left(\epsilon >0\right)& (5)\end{array}$

Update the relevant parameters sequentially according to Equations (2–4), and stop the iteration once the convergence accuracy is met or the maximum number of iterations is reached, and the final $K$ modal components and their center frequencies are obtained.

2.2 SGMD

According to Equations (6–10), by reconstructing the phase space of the one-dimensional vibration signal, the Hamilton matrix can be obtained, and then the eigenvalues and eigenvectors of the Hamilton matrix are solved by the symplectic transformation, and finally the symplectic geometric components are reconstructed by diagonal averaging. With a one-dimensional primordial vibration signal $x=\left(x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right)$ , the following form matrix is obtained by using the Takens embedding theorem.

$X=\left[\begin{array}{c}{x}_1\\ ⋮\\ x_m\end{array}\begin{array}{c}{x}_{1+\tau }\\ ⋮\\ x_{m+\tau }\end{array}\begin{array}{c}\cdots \\ \ddots \\ \cdots \end{array}\begin{array}{c}{x}_{1+\left(d-1\right)\tau }\\ ⋮\\ x_{m+\left(\mathrm{d}-1\right)\tau }\end{array}\right]\text{ (6)}$

Where $d$ is the embedding dimension, $\tau$ is the delay time, and $m=n-\left(d-1\right)\tau$ . In order to construct the trajectory matrix reasonably, $d$ is selected according to the power spectral density of the original vibration signal $x$ .

Let $A=X^{T}X$ , and construct the following Hamilton matrix $M$ .

$M=\left[\begin{array}{c}{A}^T\\ 0\end{array}\begin{array}{c}0\\ -A\end{array}\right]\text{ (7)}$

Let $N=M^2$ , where $M$ and $N$ are Hamilton matrices, and construct the following symplectic orthogonal matrix $Q$ .

$Q^{T}NQ=\left[\begin{array}{c}B\\ 0\end{array}\begin{array}{c}R\\ A^T\end{array}\right]\text{ (8)}$

Where $B$ is the upper triangular matrix. The eigenvalues of the matrix $B$ are ${\lambda }_1,{\lambda }_2,\cdots ,{\mathrm{\lambda }}_d$ . ${\sigma }_i=\sqrt{{\lambda }_i}\left(i=1\mathrm{,}2\mathrm{,}\cdots \mathrm{,}d\right)$ is the eigenvalue of matrix $A$ , $Q_i$ is the eigenvector corresponding to matrix $A$ . Furthermore, $S_i=Q_i^T{X}^T$ , $Z_i=Q_i{S}_i$ , where $S$ is the conversion coefficient matrix, $Z$ is the reconstructed trajectory matrix.

$\begin{array}{ll}Z=Z_1+Z_2+\cdots +Z_d& (9)\end{array}$

Where $Z_i=Q_i{S}_i$ , $S_i=Q_i^T{X}^T$ . Since the reconstructed one-component matrix is not a one-dimensional vibration signal, it is necessary to convert the single-component matrix $Z_i\left(1\le i\le d\right)$ into a vibration signal of length $n$ , so the sum of the vibration signals with length $n$ in group $d$ is the original time series signal $s$ . In which $Z_{m\times d}={\left(z_{ij}\right)}_{m\times d}$ , $1\le i\le m$ , $1\le j\le d$ . Let $d^{\ast }=\min \left(m\mathrm{,}d\right)$ , $m^{\ast }=\max \left(m\mathrm{,}d\right)$ , $n=m+\left(d-1\right)\tau$ . When $m<d$ , $y_{ij}^{\ast }=z_{ij}$ ; Otherwise, $y_{ij}^{\ast }=z_{ji}$ . The form of diagonal average transformation matrix is as follows.

$y_k=\{\begin{array}{c}\frac{1}{k}{\displaystyle \sum }_{p=1}^k{y}_{p,k-p+1}^{\ast },1\le k\le d^{\ast }\\ \frac{1}{d^{\ast }}{\displaystyle \sum }_{p=1}^{d^{\ast }}{y}_{p,k-p+1}^{\ast },d^{\ast }\le k\le m^{\ast }\\ \frac{1}{n-k+1}{\displaystyle \sum }_{p=k-m^{\ast }+1}^{n-m^{\ast }+1}{y}_{p,k-p+1}^{\ast },m^{\ast }\le k\le n\end{array}\text{ (10)}$

After obtaining the corresponding one-dimensional vibration signal $C_i=\left(c_1\mathrm{,}{c}_2\mathrm{,}\cdots c_n\right)$ by $Z_i\left(1\le i\le d\right)$ , each reconstruction matrix is averaged diagonally in turn to obtain d components.

2.3 LSTM

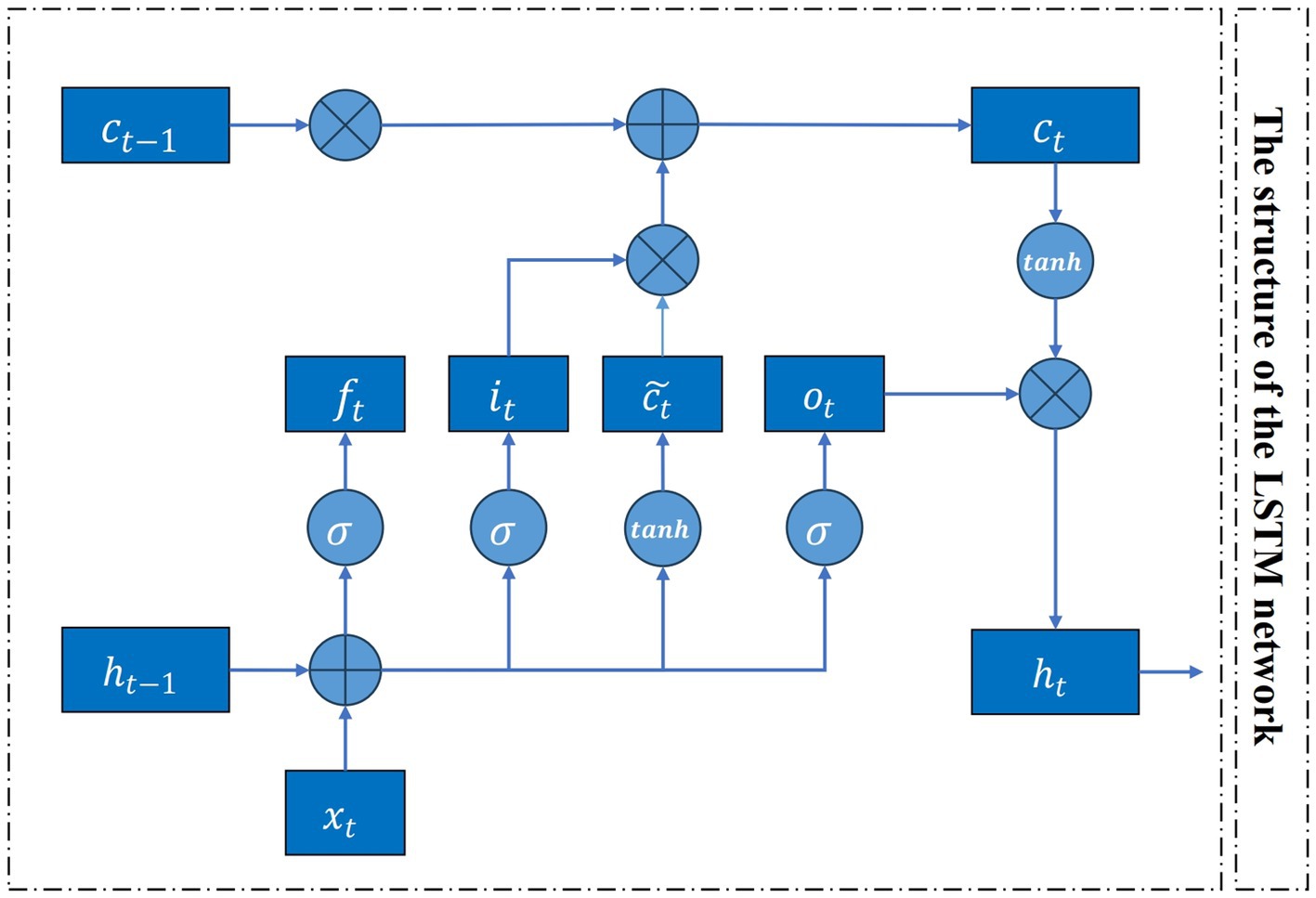
According to Equations (11–16), by LSTM is composed of input gate $\left(i_t\right)$ , forgetting gate $\left(f_t\right)$ , output gate $\left(o_t\right)$ and memory unit $c_t$ . By selectively inputing, exporting and forgetting information in the network through $i_t$ , $f_t$ and $o_t$ , the gradient disappearance problem of the general RNN can be effectively overcome. Figure 1 is the corresponding flow chart of the LSTM model. Its hidden unit calculation mathematical expressions are:

$\begin{array}{ll}{f}_t=\sigma \left(W_f.\left[h_{t-1}\mathrm{,}{x}_t\right]+b_f\right)& (11)\end{array}$

$\begin{array}{ll}{i}_t=\sigma \left(W_i.\left[h_{t-1}\mathrm{,}{x}_t\right]+b_i\right)& (12)\end{array}$

$\begin{array}{ll}{c}_t=\tanh \left(W_c.\left[h_{t-1}\mathrm{,}{x}_t\right]+b_c\right)& (13)\end{array}$

$\begin{array}{ll}{c}_t=f_t\ast C_{t-1}+i_t\ast c_t& (14)\end{array}$

$\begin{array}{ll}{o}_t=\sigma \left(W_0.\left[h_{t-1}\mathrm{,}{x}_t\right]+b_0\right)& (15)\end{array}$

$\begin{array}{ll}{h}_t=o_t\ast \tanh \left(c_t\right)& (16)\end{array}$

where $x_t$ is the input variable at moment $t$ , $c_t$ is the updated state of the memory cell, $h_t$ is the final output of the LSTM, and $b$ is the bias vector. The specific calculation process of LSTM is as follows:

Figure 1

Figure 1. Flowchart of the LSTM model.

Step 1: Using the external state $h_{t-1}$ at the last moment and the input $x_t$ at the current moment to calculate three gates and $c_t$ in the candidate state;

Step 2: Update the memory cell with the forgetting gate $\left(f_t\right)$ and input gate $\left(i_t\right)$ ;

Step 3: Utilize the output gate $o_t$ to pass the information of the internal state to the external state $h_t$ .

2.4 The construction of VMD-SGMD-LSTM hybrid model

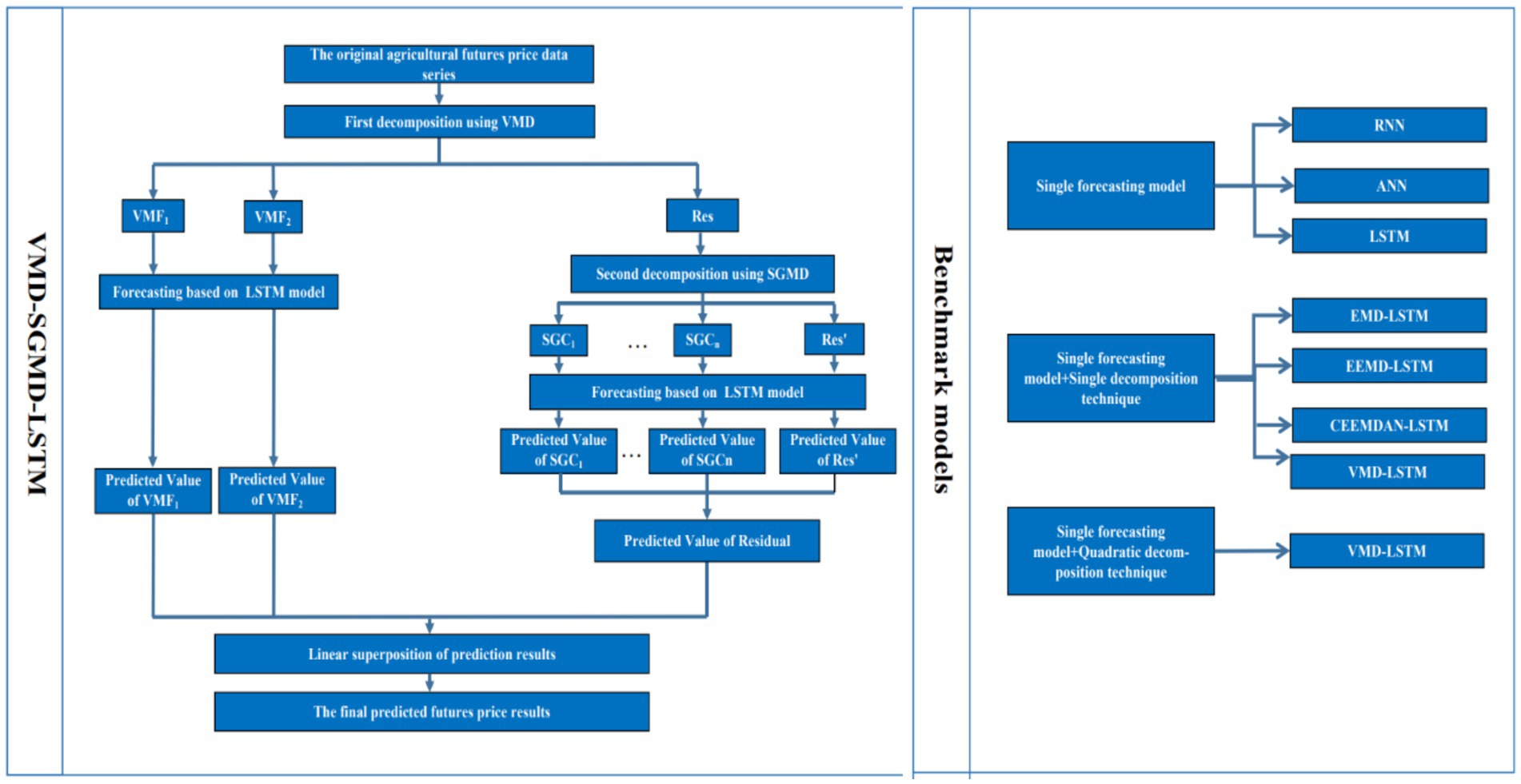
The VMD-SGMD-LSTM hybrid model combines the advantages of different decomposition technologies, and combines with artificial intelligence model to improve the overall prediction accuracy. Figure 2 shows the specific process of the model, and the corresponding steps are as follows:

Figure 2

Figure 2. The research framework of VMD-SGMD-LSTM hybrid model.

Step 1: Use VMD to decompose the price data. Set the number of stages of VMD to 3. Specifically, the main low-frequency parts IMF1 and IMF2 are extracted from the original data, and the remaining high-frequency parts are obtained by the difference between the original sequence and IMF1 and IMF2.

Step 2: Application of SGMD. The remaining components are processed by SGMD, and then a series of independent symmetric geometric components (SGC) and residual terms are obtained. VMD-SGMD, a data preprocessing technology, can make full use of the information in the price signal and obtain multiple independent and simple decomposition results.

Step 3: Prediction of different components. The data of each modal is divided into training set and test set, and the LSTM model is used to predict the mode with different frequencies. LSTM avoids model complexity while ensuring the accuracy of prediction results. Furthermore, the final prediction result can be obtained by integrating the predicted values of all modes linearly.

Step 4: Seven other different benchmark models are established to compare with the proposed hybrid model, including single prediction model, prediction model combined with single decomposition technology and prediction model combined with secondary decomposition technology.

3 Empirical study

3.1 Source of data

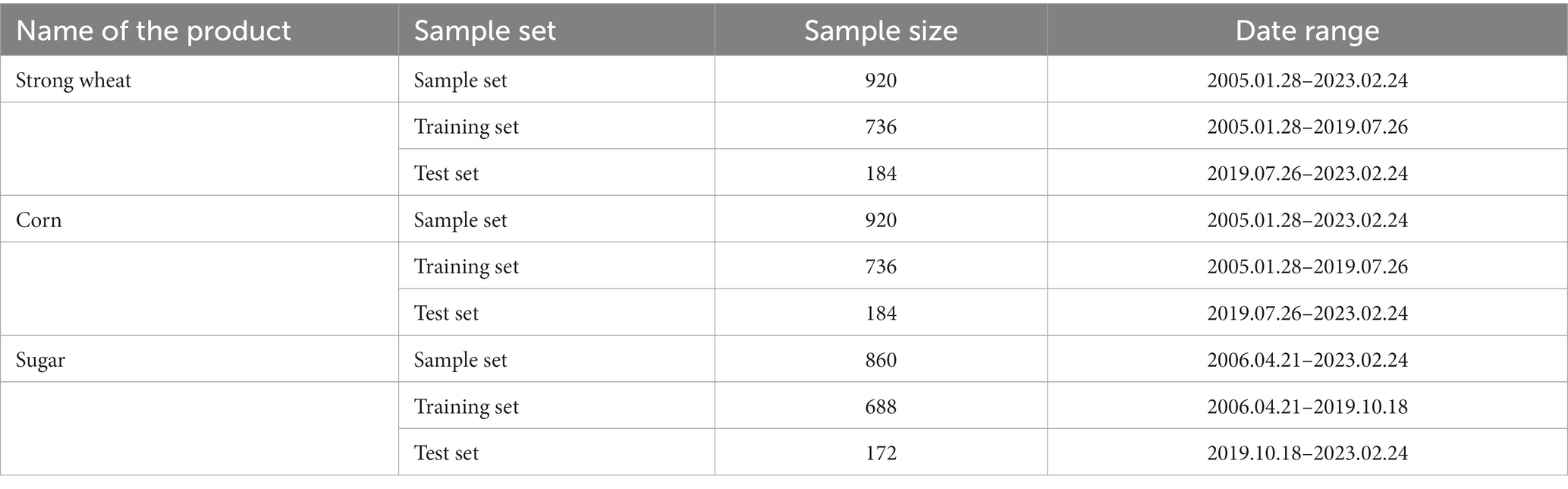
This paper examines weekly data on three different agricultural products, namely strong wheat, corn and sugar, in China’s agricultural futures market, from the Wind Database.¹ All sample data were divided into training and test sets, and the proportions of training and test sets were 0.8 and 0.2, respectively. Table 1 shows specific information on the sample data for different agricultural products. Figure 3 show the price charts of strong wheat, corn and sugar during the sample period, respectively. It can be seen from the figure that the fluctuation degree of price dispersion of different agricultural futures prices is large, and the price fluctuation has a certain periodicity, which contains random and nonlinear change characteristics.

Table 1

Table 1. The size and date range of the sample.

Figure 3

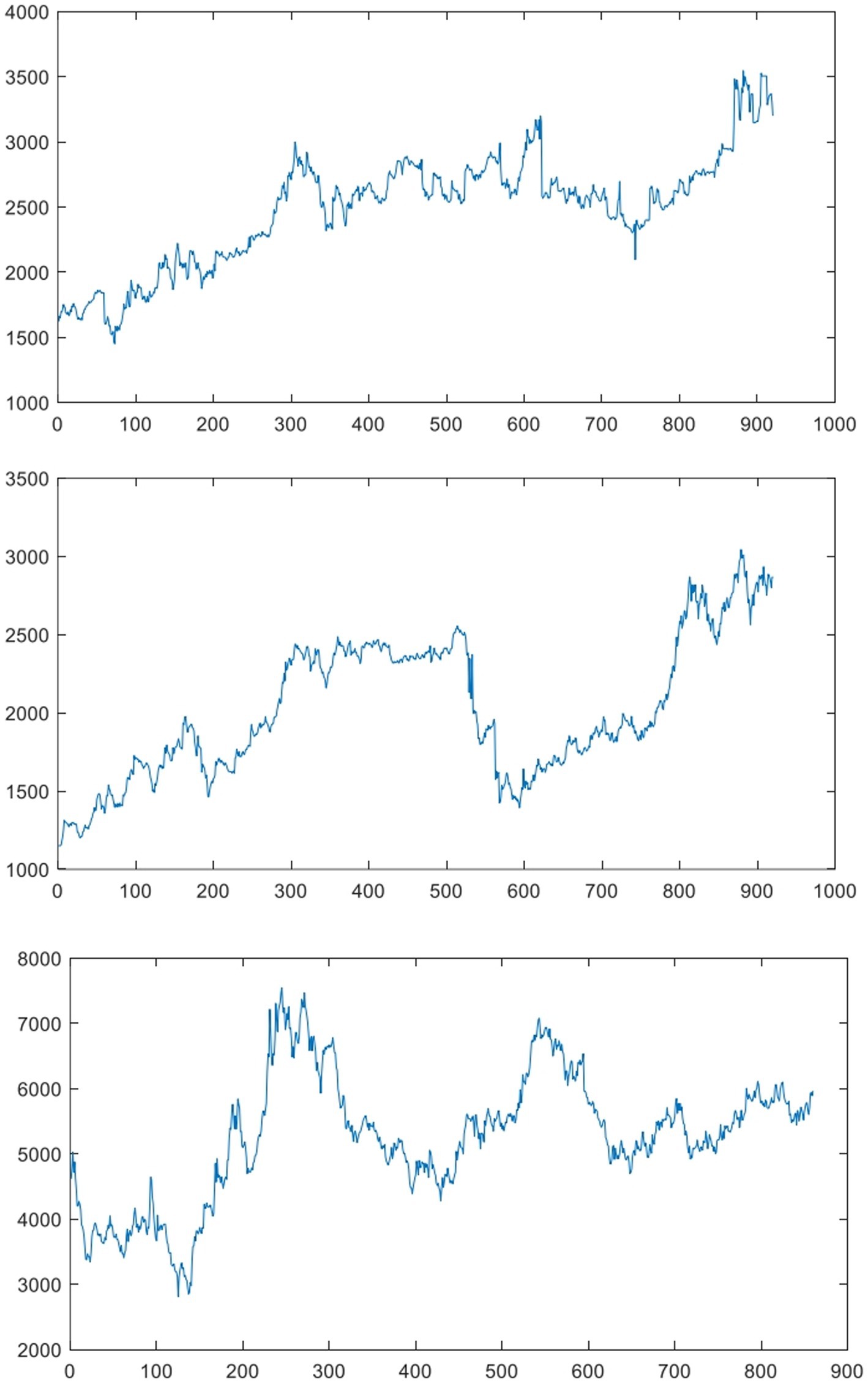
Figure 3. The trend chart of price during the sample period (From top to bottom are strong wheel, corn and sugar respectively).

3.2 The benchmark model

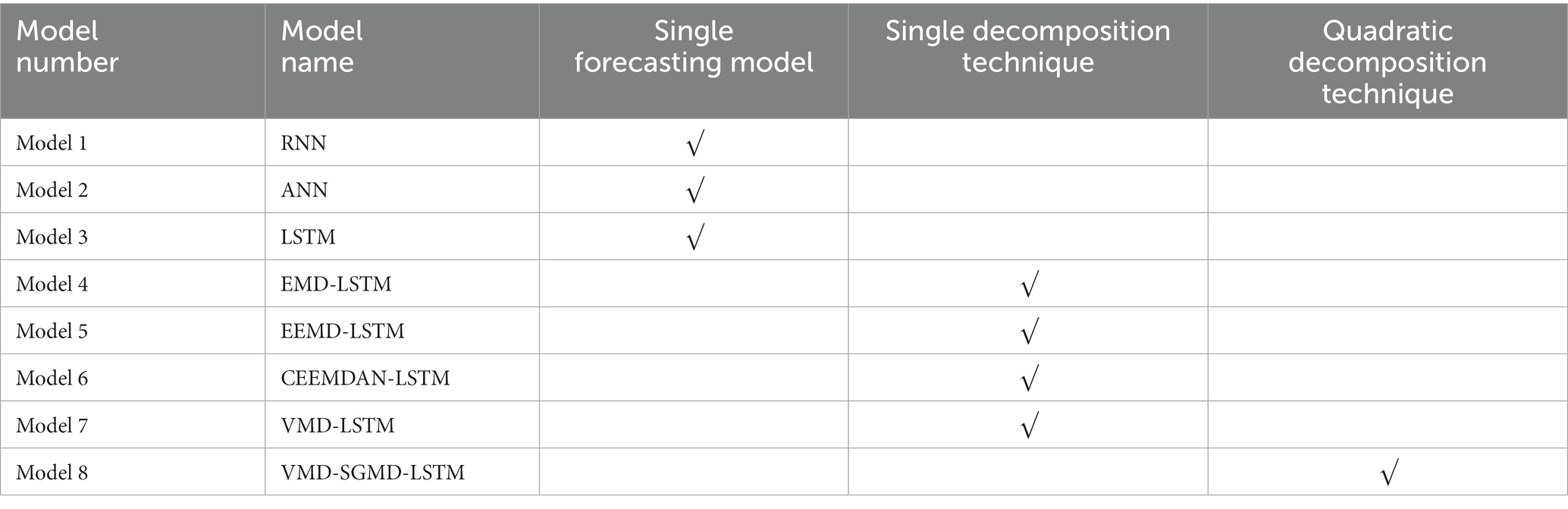
In order to verify the superiority of the prediction performance of the VMD-SGMD-LSTM hybrid model proposed in this paper, a series of corresponding benchmark models are constructed based on the “decomposition-prediction” framework, in which models 1 to 8 correspond to RNN, ANN, LSTM, EMD-LSTM, EEMD-LSTM, CEEMDAN-LSTM, VMD-LSTM and VMD-SGMD-LSTM, respectively. Table 2 shows the characteristics of different models. First of all, in order to test the difference between the “decomposition-prediction” framework and the single prediction model, and verify the superiority of the LSTM prediction model adopted in this paper, three single prediction models, RNN, ANN and LSTM, are constructed, respectively. Secondly, in order to verify the superiority of the quadratic decomposition technology proposed in this paper, a series of benchmark models combined with single decomposition technology (EMD-LSTM, EEMD-LSTM, CEEMDAN-LSTM, VMD-LSTM) are further constructed. All the models are applied to the 1-step, 2-step and 4-step ahead forecasting scenarios, respectively, through the software Matlab 2019b.

Table 2

Table 2. Characteristics of different models.

3.3 Evaluation indicators

In view of the complexity of sample data, it is difficult for a single evaluation indicator to comprehensively evaluate the prediction performance of different models. Therefore, this paper selects three different evaluation indicators, $e_{MAE}\left(\mathrm{mean\; absolute\; error}\right)$ , $e_{MAPE}\left(\mathrm{mean\; absolute\; percentage\; error}\right)$ and $e_{RMSE}$ (root mean square error) to evaluate the model performance. Where $e_{MAE}$ is the average of the difference between the actual value and the predicted value, which can reflect the actual situation of the predicted value error. $e_{MAPE}$ not only takes into account the deviation of the predicted value from the true value, but also measures the ratio between the deviation and the true value, which does not change due to the global scaling of the target variable. $e_{RMSE}$ can be used to detect deviations between the model’s predicted and true values.

$\begin{array}{l}{e}_{MA\mathrm{E}}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|y_i-{\hat{y}}_i\right|,e_{MAPE}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|y_i-{\hat{y}}_i\right|/\\ y_i\ast 100,e_{RMSE}=\sqrt{1/n{\displaystyle \sum }_{i=1}^n{\left(y_i-{\hat{y}}_i\right)}^2}\end{array}\text{ (17)}$

Where $n$ is the number of observation points, $y_i$ and ${\hat{y}}_i$ represent the real value and the predicted value. With the smaller values of each evaluation indicator, the higher the prediction accuracy of the model is.

3.4 The analysis of empirical results

In this part, the sample data of strong wheat, corn and sugar are set as different cases (Case I, Case II and Case III), and the forecast results of different models for futures prices of various agricultural products are recorded and analyzed.

With the deepening development of the financial market, the agricultural futures market in China has grown rapidly in the past 30 years. At present, China is entering the process of weakening the guiding position of the government in agricultural product market pricing and forming a price pricing mechanism relying on the market. Under the background of the transformation and upgrading of consumption structure, rising agricultural production costs and the impact of international market, the prices of agricultural products in China fluctuated frequently and violently under the combined action of demand, cost and market transmission. The data based on the real trading market shows that the VMD-SGMD-LSTM hybrid model proposed in this paper has achieved the best performance in all forecasting scenarios, which proves the effectiveness of the model in forecasting agricultural futures prices.

3.4.1 Analysis of the results of case I

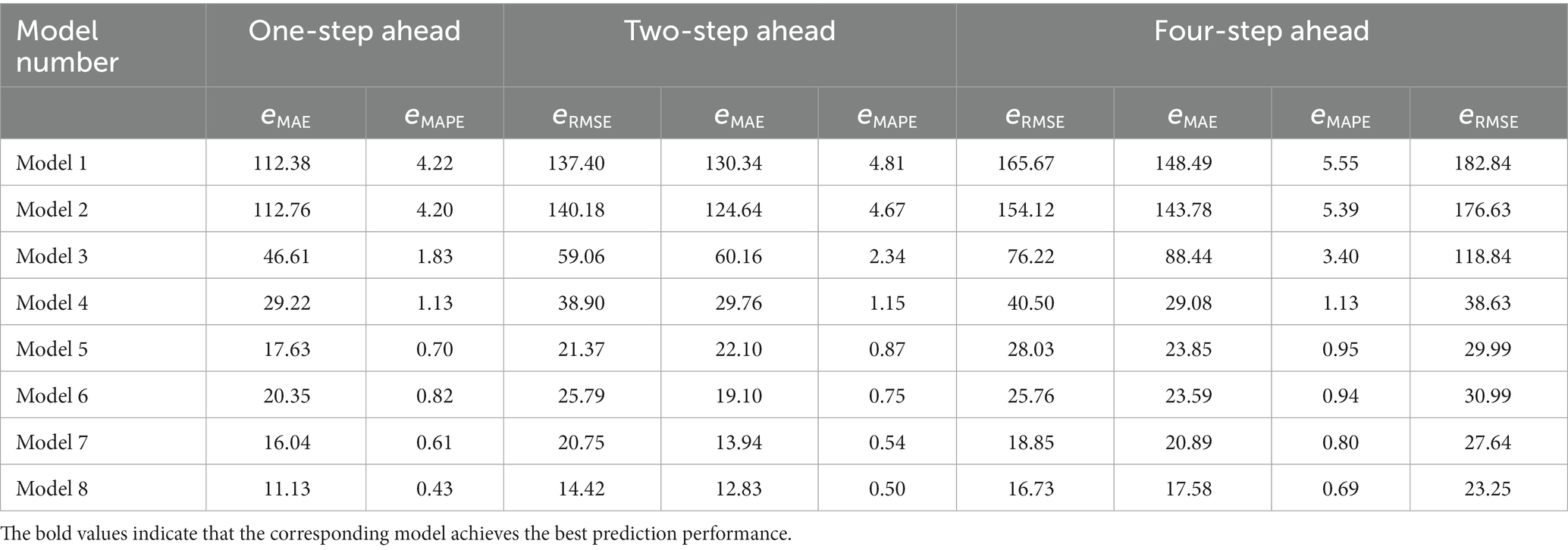
Table 3 records the specific numerical results of 1-step, 2-step and 4-step ahead forecasting of strong wheat futures prices by each model. Figure 4 shows the results of various error indicators of different models in forecasting scenarios. Figure 5 shows the fitting ability of different models to real values in various forecasting scenarios. The specific analysis are as follows.

(a) Compared with RNN and ANN, LSTM model has higher prediction accuracy

Table 3

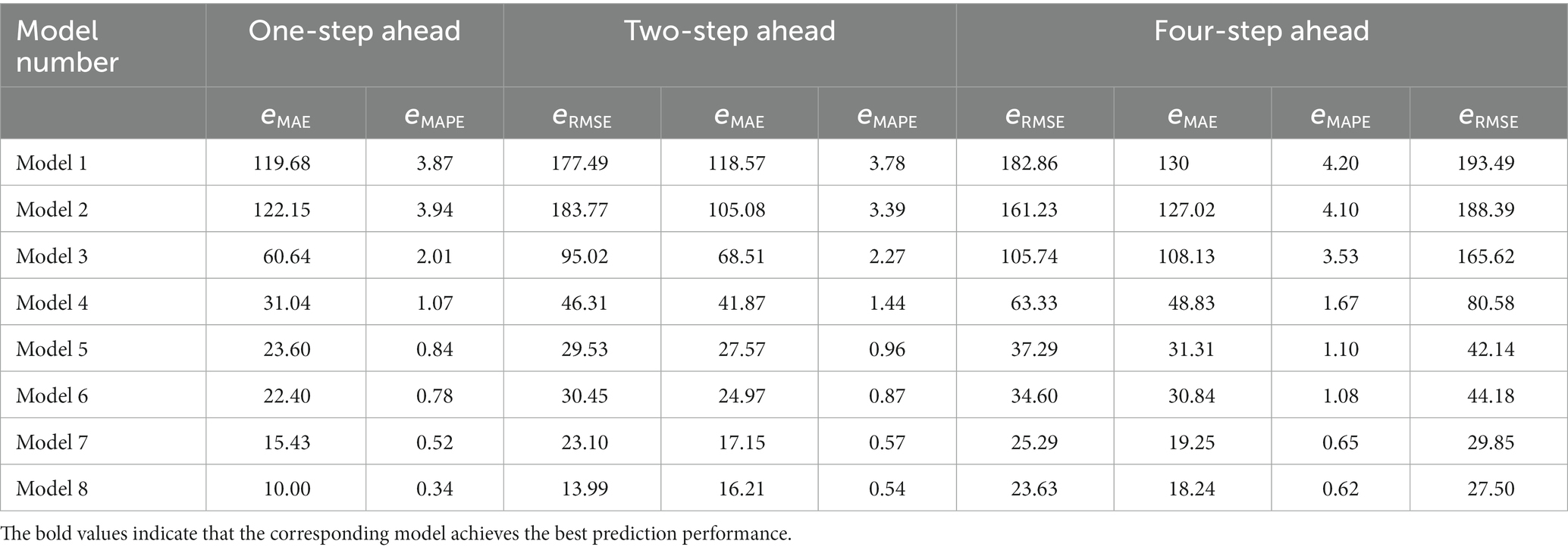
Table 3. The numerical results of different models for forecasting the futures price of strong wheat.

Figure 4

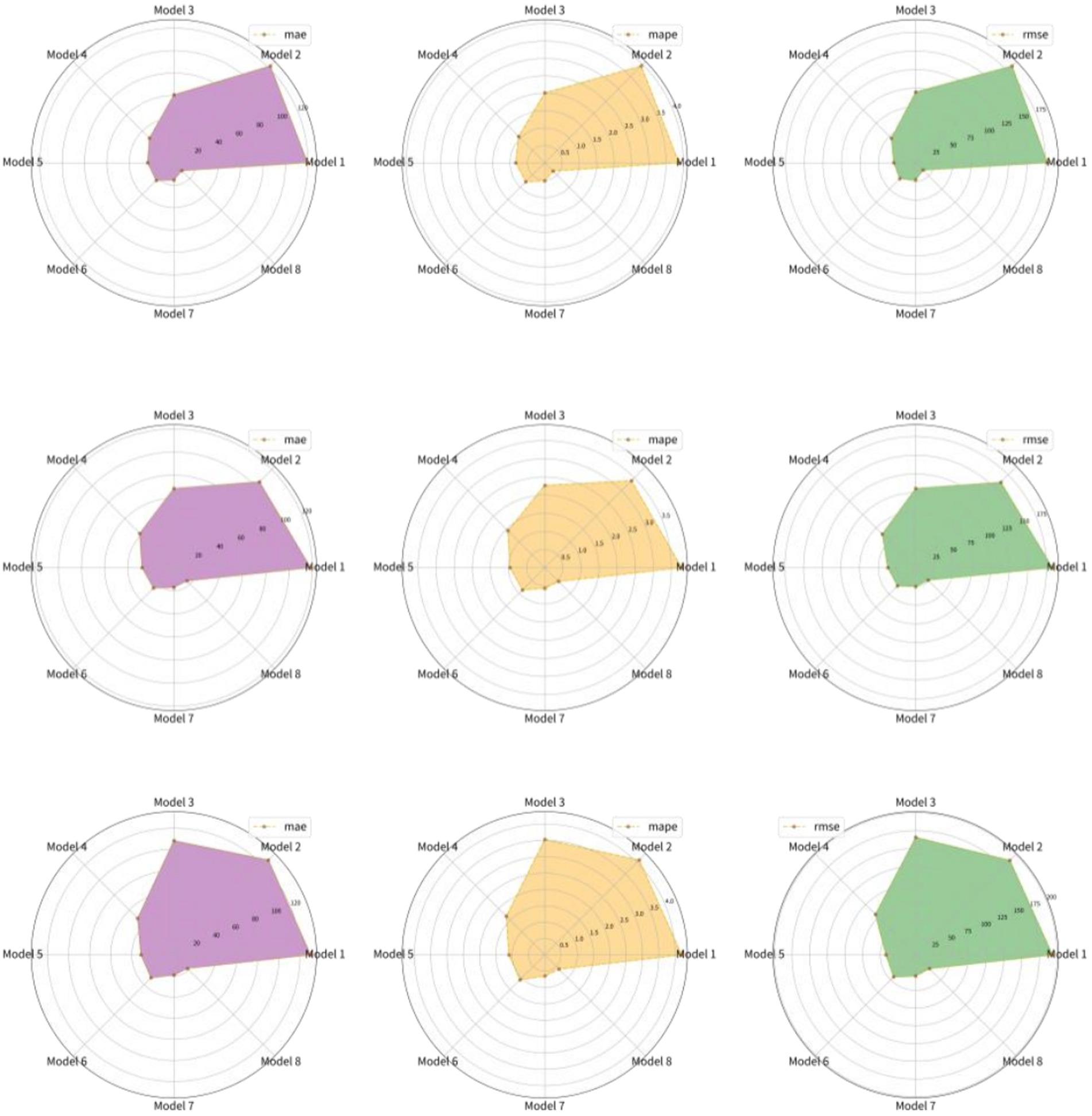
Figure 4. The multi-step ahead forecasting results for strong wheat futures prices (From top to bottom are the results of I-step ahead, 2-step ahead and 4-step ahead forecasting).

Figure 5

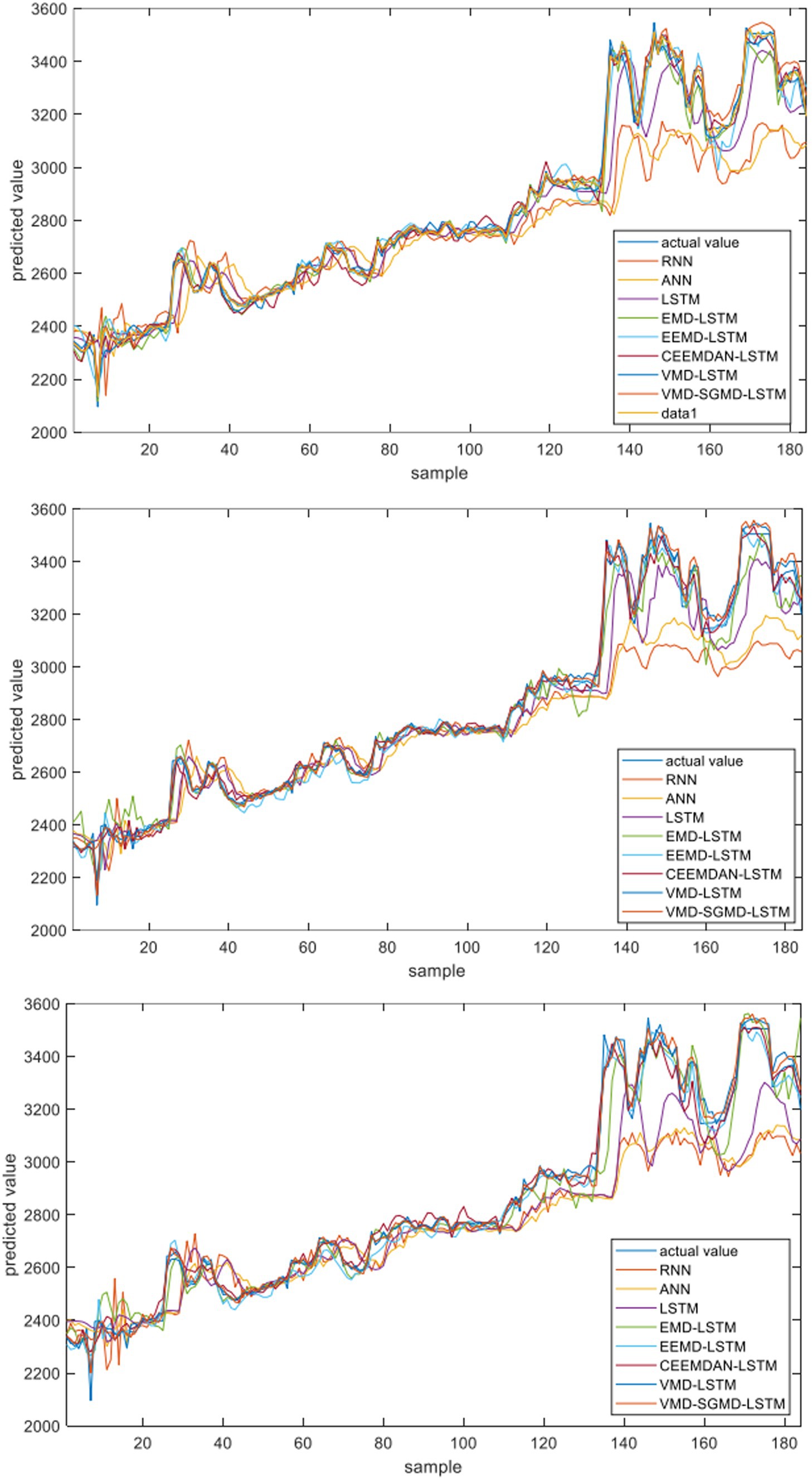
Figure 5. The fitting results of different models on the futures price of strong wheat (From top to bottom are the results of 1 -step ahead, 2-step ahead and 4-step ahead forecasting).

The results show that LSTM performs better in different forecasting scenarios in the research of forecasting the futures price of strong wheat by using different single artificial intelligence models. Taking the prediction results of the 1-step ahead forecasting as an example, compared with RNN, the $e_{MAE}$ 、 $e_{MAPE}$ and $e_{MAPE}$ of LSTM are improved by 49.33, 48.06 and 46.46% respectively, and compared with ANN, the $e_{MAE}$ 、 $e_{MAPE}$ and $e_{MAPE}$ of LSTM are improved by 50.35% and 48.98, respectively.

The reason for this result is that RNN and ANN have great limitations in processing complex time series, and problems such as dimensional disasters or invalid feature representations of parameters will occur, and it is difficult to achieve the ideal prediction effect. As a neural network with memory function, LSTM has better performance in time-series data processing. Therefore, LSTM is selected as the predictive model in the hybrid model.

(b) Compared with the single prediction model, the hybrid model combined with decomposition technology has improved the prediction accuracy

Compared with the LSTM model, the hybrid model has made a breakthrough in forecasting accuracy in both single decomposition technology and secondary decomposition technology, which shows the adaptability of decomposition technology to the price processing of strong wheat futures. Taking the prediction results of the 1-step ahead forecasting as an example, compared with LSTM, the $e_{MAE}$ 、 $e_{MAPE}$ and $e_{MAPE}$ of VMD-LSTM are improved by 74.55, 74.12 and 75.68% respectively, while those of VMD-SGMD-LSTM are improved by 74.55, 74.12 and 75.68%, respectively.

The reason for this phenomenon is that when applying neural network models to predict agricultural prices, it is necessary to use the necessary data preprocessing for the collected time series, while the application of a single forecasting model (RNN, ANN and LSTM) cannot effectively preprocess the time series, and there will be large errors in the final price prediction. The hybrid model combined with decomposition technology can extract the fluctuation frequency contained in the price time series, reduce the fluctuation amplitude of the time series, thereby improving the accuracy of the prediction results, and further verifying the importance of data preprocessing technology to the forecast model.

(c) In a series of applications of single decomposition technology, VMD technology has better performance

Compared with the single LSTM model, although EMD-LSTM, EEMD-LSTM and CEEMDAN-LSTM show better forecasting ability, the forecasting performance of VMD-LSTM is still better than other models combined with single decomposition technology in all forecasting scenarios. Taking the prediction results of the 1-step ahead forecasting as an example, compared with EMD-LSTM, the $e_{MAE}$ 、 $e_{MAPE}$ and $e_{MAPE}$ of VMD-LSTM are improved by 50.28, 51.4 and 50.11% respectively, compared with EEMD-LSTM, The $e_{MAE}$ 、 $e_{MAPE}$ and $e_{MAPE}$ of VMD-LSTM are improved by 34.61, 38.09 and 21.77%, respectively. Compared with CEEMDAN-LSTM, the $e_{MAE}$ 、 $e_{MAPE}$ and $e_{MAPE}$ of VMD-LSTM are improved by 31.11 and 33.33%, respectively. The reason for this phenomenon is that VMD can handle agricultural futures prices with high complexity, nonlinearity and non-stationarity better than EMD, EEMD and CEEMDAN.

(d) The VMD-SGMD-LSTM hybrid model has the best prediction performance

Compared with other benchmark models, VMD-SGMD-LSTM hybrid model has the highest prediction accuracy. Taking the prediction results of the 1-step ahead forecasting as an example, compared with VMD-LSTM, the $e_{MAE}$ 、 $e_{MAPE}$ and $e_{MAPE}$ of VMD-SGMD-LSTM are improved by 35.19, 34.61 and 39.43%, respectively. The reason for this result is that it is difficult to completely extract the complex characteristics of agricultural futures price series by single decomposition technology, while VMD-SGMD secondary decomposition technology combines the advantages of VMD and SGMD, which can describe the fluctuation characteristics of price series more effectively, and can decompose complex and changeable original data series into multiple subsequences with more stable components, so it has better forecasting performance.

(e) The VMD-SGMD-LSTM hybrid model is robust in different forecasting scenarios

The VMD-SGMD-LSTM hybrid model proposed in this paper has the highest prediction accuracy in different step-size ahead forecasting scenarios. In the prediction of strong wheat futures price, the prediction errors of all models accumulate with the increase of prediction step, and the VMD-SGMD-LSTM model constructed in this paper always has the lowest and more stable error. This shows that the VMD-SGMD-LSTM hybrid model is robust and can ensure high prediction accuracy.

3.4.2 Analysis of the results of case II and case III

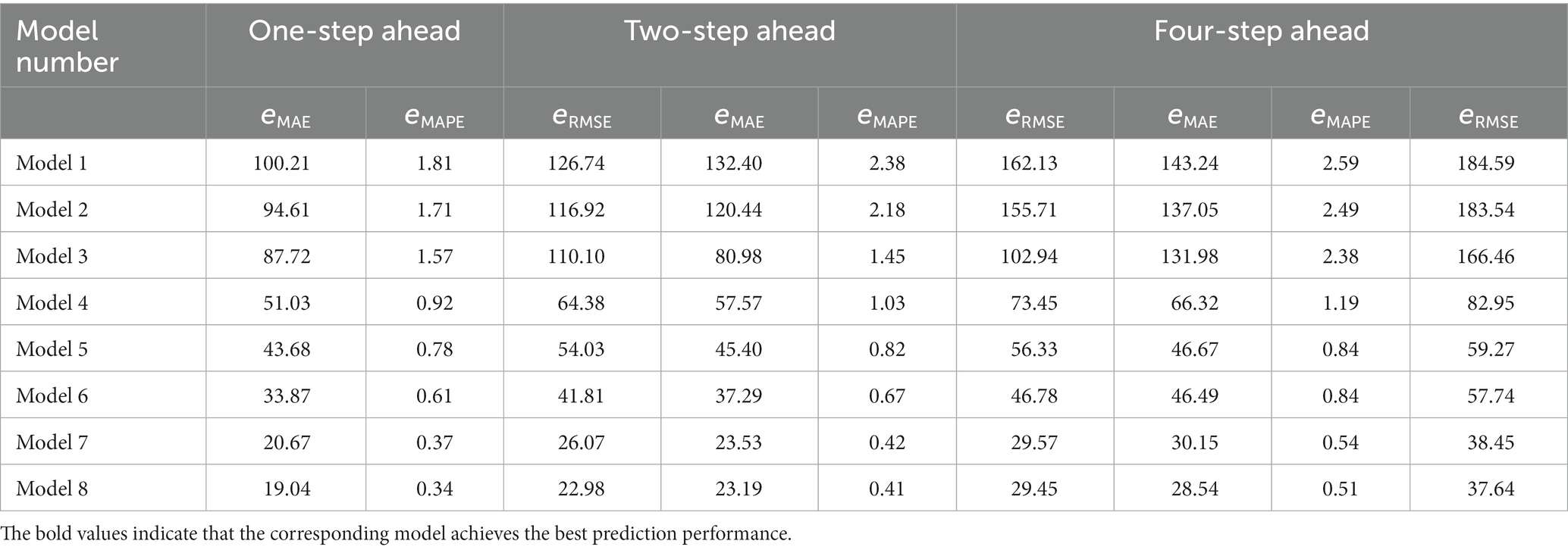
In order to test the adaptability of the proposed model to the agricultural futures market in China, this paper also selects the futures price data of corn and sugar as Case II and Case III for experiments. Tables 4, 5 show the results of corn and sugar futures prices, respectively. Figures 6, 7 show the forecast results of corn and sugar futures prices, respectively. Figures 8, 9 show the fitting ability of different models to real values in various forecasting scenarios. According to the relevant forecast results, the VMD-SGMD-LSTM hybrid model has achieved the same excellent forecast performance in the study of corn and sugar futures prices, and reached the same conclusion as that in the study of strong wheat futures prices, which shows the effectiveness of the VMD-SGMD-LSTM hybrid model in forecasting the agricultural futures market in China.

Table 4

Table 4. The numerical results of different models for forecasting the futures price of corn.

Table 5

Table 5. The numerical results of different models for forecasting the futures price of sugar.

Figure 6

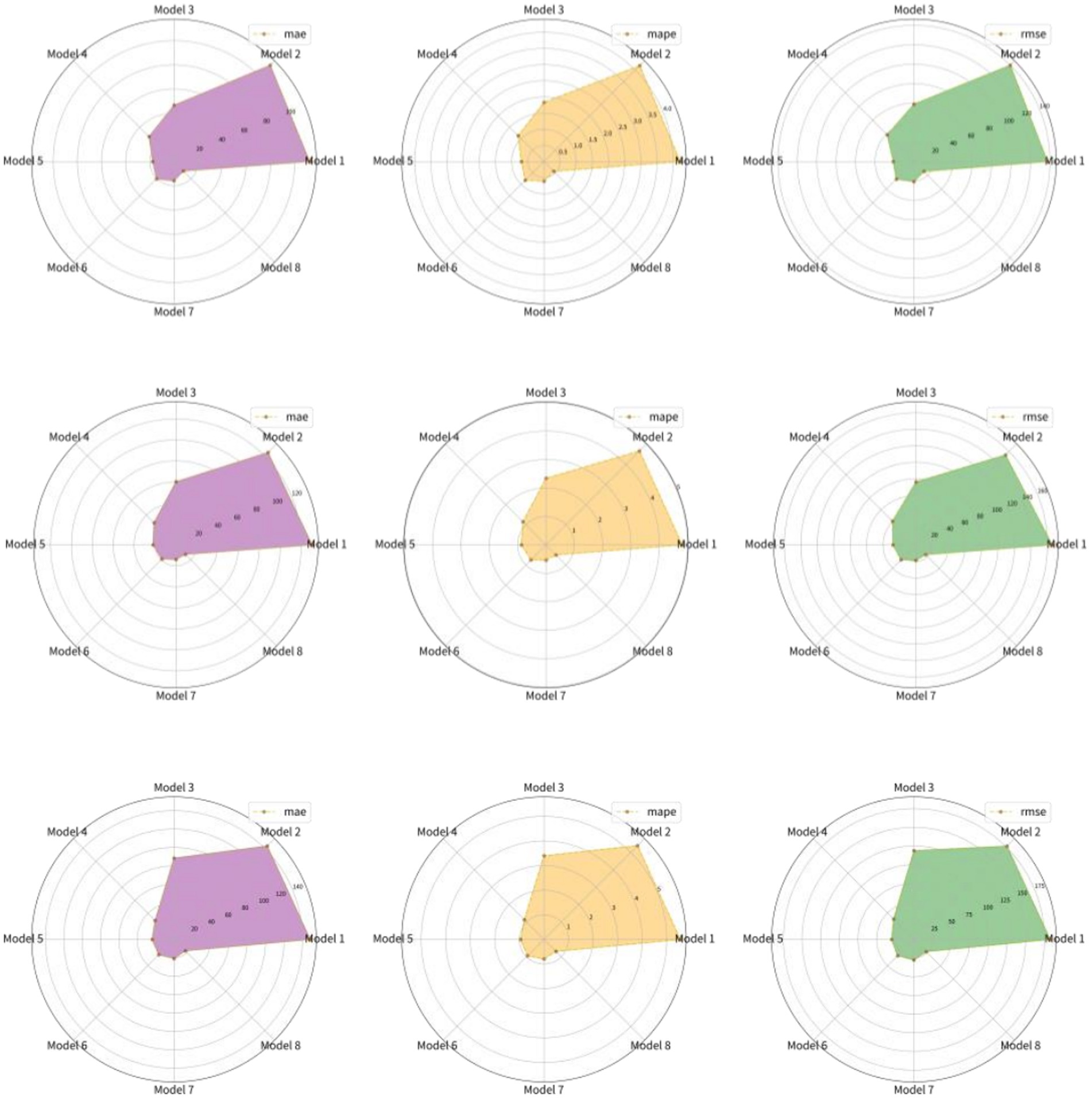
Figure 6. The multi-step ahead forecasting results for corn futures prices (From top to bottom are the results of I step ahead, 2-step ahead and 4-step ahead forecasting).

Figure 7

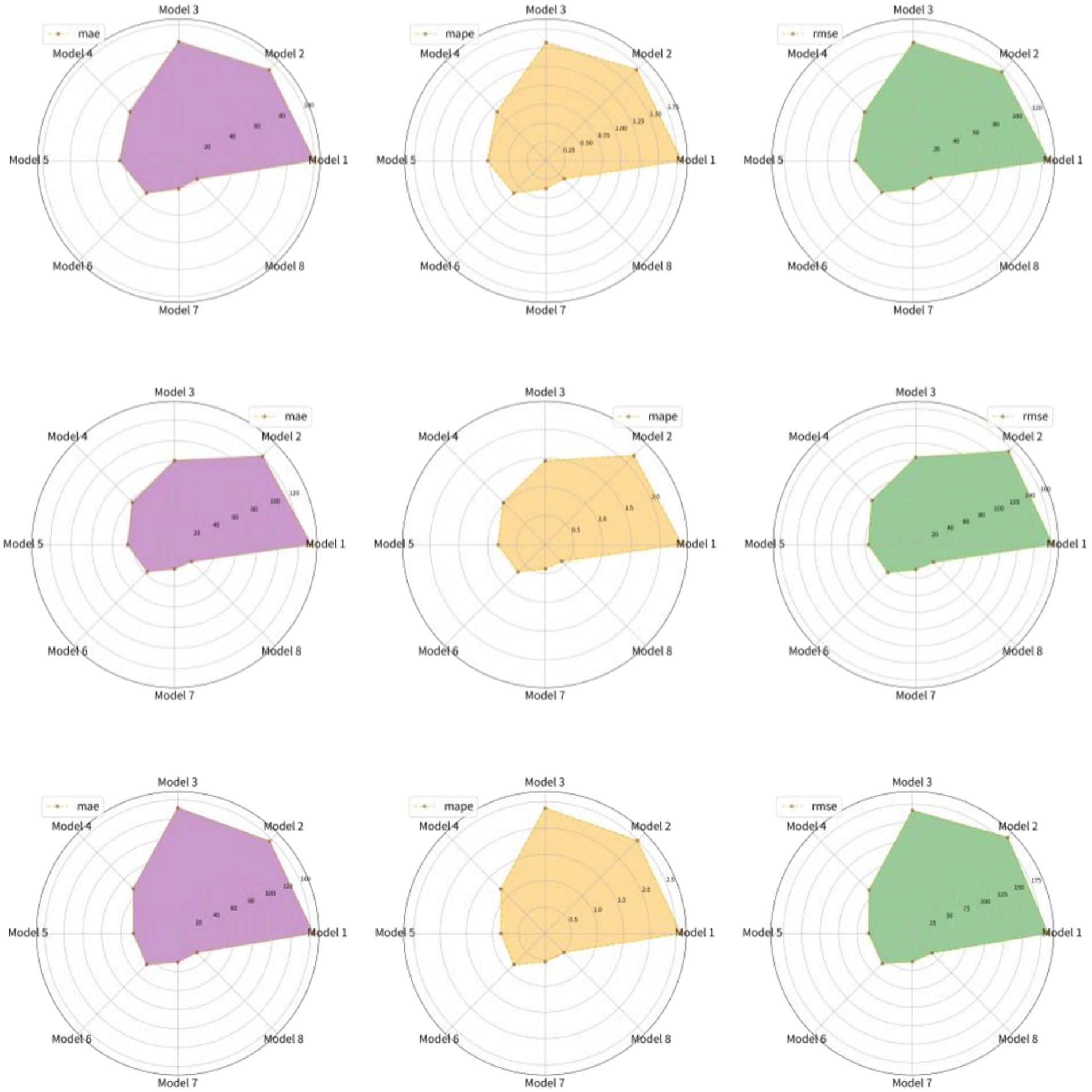
Figure 7. The multi-step ahead forecasting results for sugar futures prices (From top to bottom are the results of 1 step ahead, 2-step ahead and 4-step ahead forecasting).

Figure 8

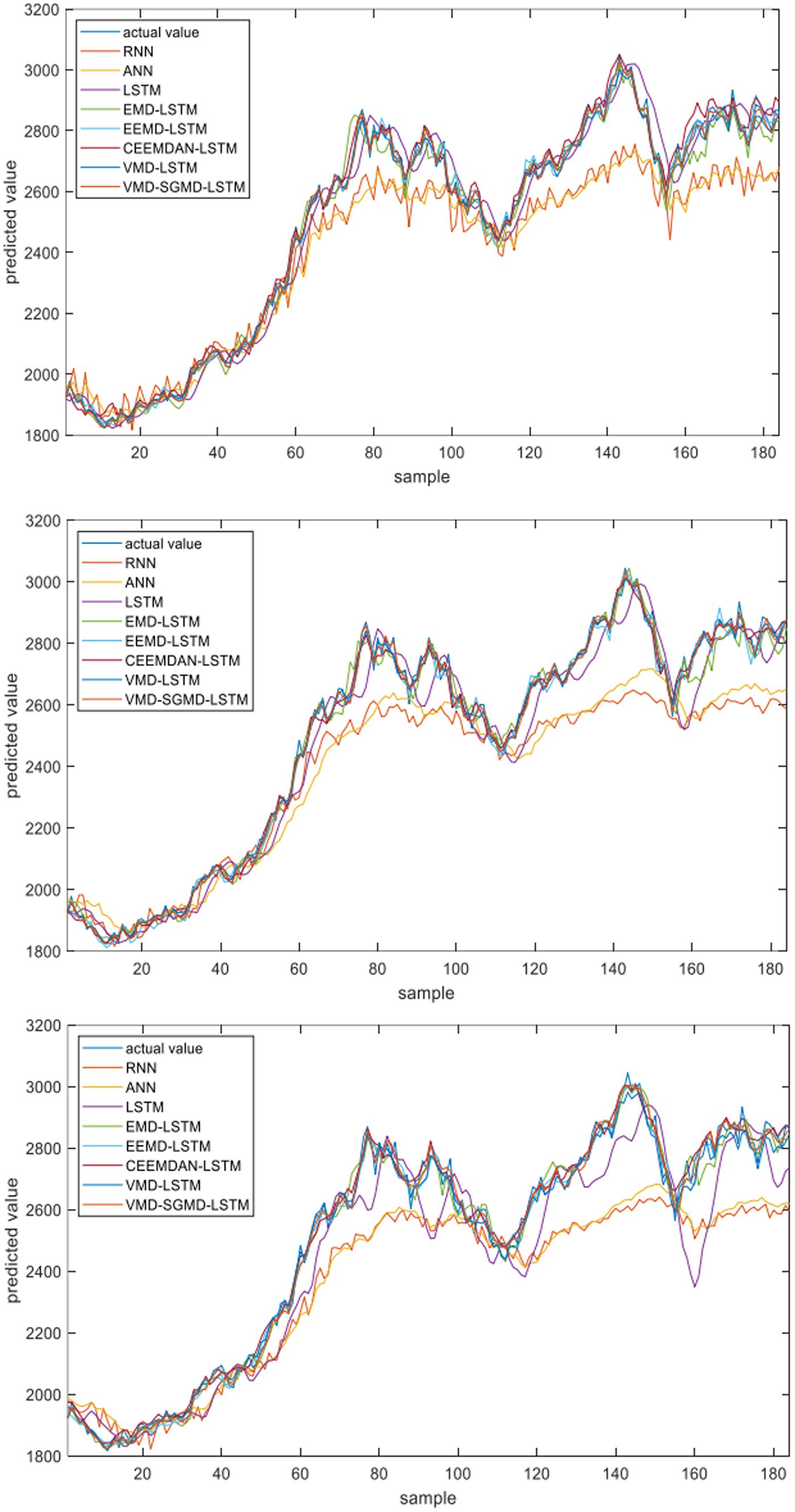
Figure 8. The fitting results of different models on the futures price of corn (From top to bottom are the results of I step ahead, 2-step ahead and 4-step ahead forecasting).

Figure 9

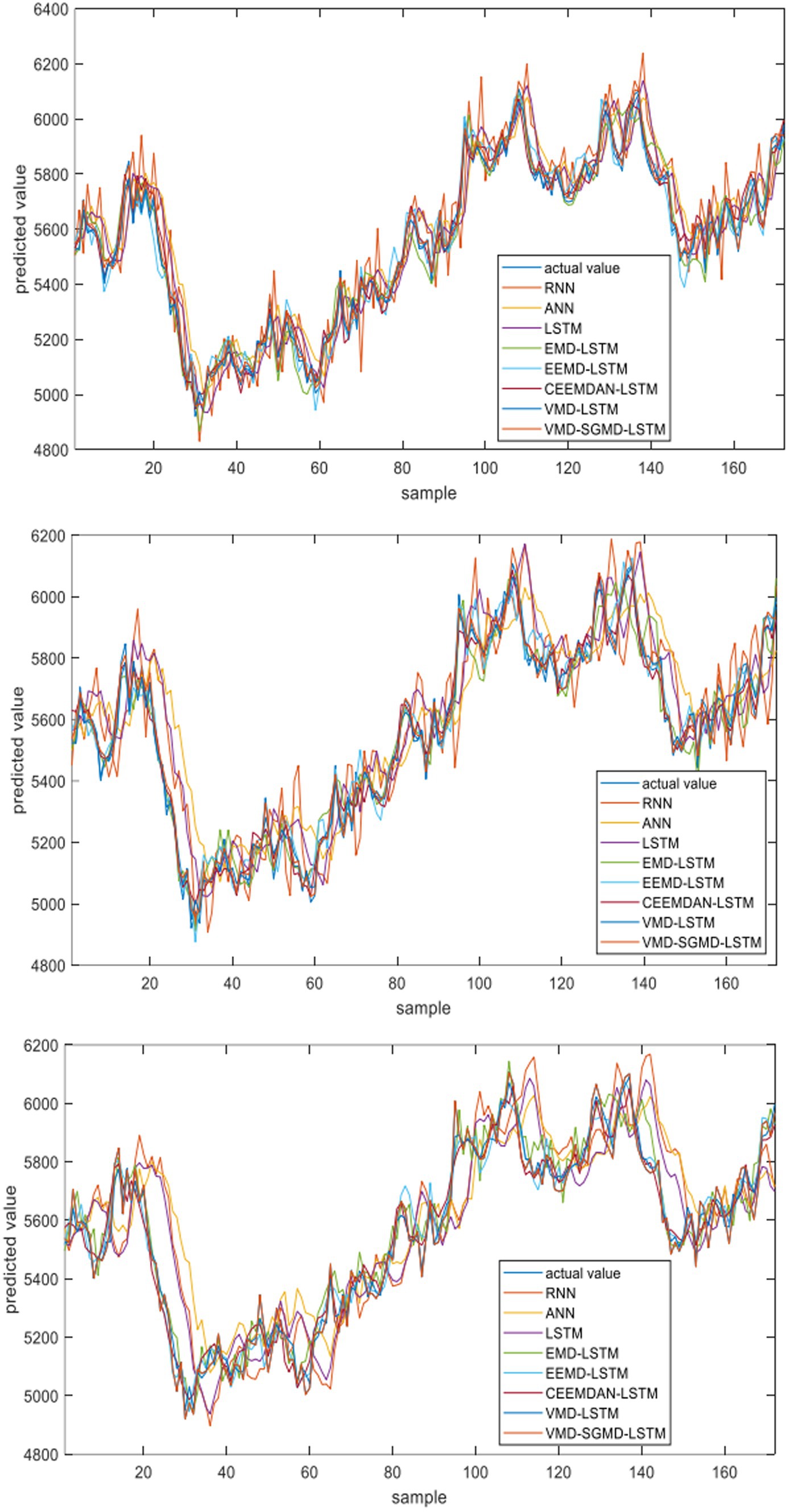
Figure 9. The fitting results of different models on the futures price of corn (From top to bottom are the results of 1-step ahead, 2-step ahead and 4-step ahead forecasting).

4 Conclusion

The price series of agricultural products contains complex fluctuations. In order to improve the forecasting accuracy of agricultural product prices, a new VMD-SGMD-LSTM hybrid model of agricultural product prices is proposed, which combines signal decomposition technology and deep learning model. In addition, the prices of strong wheat, corn and sugar traded in China agricultural futures market are predicted under the multi-step ahead forecasting scenario.

The empirical results based on different evaluation indicators show that: (1) All hybrid models combined with decomposition technology have better performance than single prediction model; (2) The quadratic decomposition algorithm has better performance than the single decomposition algorithm in extracting the hidden nonlinear relationship in the original data; (3) Compared with other models, the VMD-SGMD-LSTM hybrid model proposed in this study can effectively improve the accuracy of price forecasting; (4)The VMD-SGMD-LSTM hybrid model is robust in the multi-step ahead forecasting for different agricultural product data. The research in this paper provides a new idea and modeling method for agricultural product price prediction based on time series. It provides the necessary basis for effectively realizing the market risk management of agricultural products.

Based on the above analysis results, for investors, hedging strategies can be developed through more accurate prediction results of agricultural prices to help complete asset allocation decisions and reduce the risk of price fluctuations. In addition, for the government, in the future construction of agricultural futures market, it can increase the varieties of agricultural futures that foreign investors can trade, so as to enrich the participants and market information of China’s agricultural futures market, further improve the risk control and management mechanism of China’s agricultural futures market, and identify the risk of price bubbles in China’s agricultural futures market.

In the future research, the influence of factors such as international local wars and conflicts, storage and natural disasters on the price of agricultural products can be considered, the mechanism of action of key factors on agricultural products can be identified, and the quantified influencing factors can be included in the prediction model, so as to further improve the accuracy and interpretation of the prediction results of the model.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

TZ: Conceptualization, Methodology, Supervision, Visualization, Writing – original draft, Writing – review & editing. ZT: Data curation, Funding acquisition, Investigation, Project administration, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China under Grant No. 71973028 and Major projects of Fujian Social Science Fund under Grant No. FJ2023JDZ030.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^http://www.wind.com.cn/

References

Banerjee, T., Sinha, S., and Choudhury, P. (2022). Long term and short term forecasting of horticultural produce based on the LSTM network model. Appl Intell 52, 9117–9147. doi: 10.1007/s10489-021-02845-x

Crossref Full Text | Google Scholar

Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. J Econ 31, 307–327. doi: 10.1016/0304-4076(86)90063-1

Crossref Full Text | Google Scholar

Diop, M. D., and Kamdem, J. S. (2023). Multiscale agricultural commodities forecasting using wavelet-SARIMA process. J. Quant. Econ. 21, 1–40. doi: 10.1007/s40953-022-00329-4

Crossref Full Text | Google Scholar

Dragomiretskiy, K., and Zosso, D. (2014). Variational mode decomposition. IEEE Trans. Signal Process. 62, 531–544. doi: 10.1109/TSP.2013.2288675

Crossref Full Text | Google Scholar

Fang, Y. M., Guan, B., Wu, S. J., and Heravi, S. (2020). Optimal forecast combination based on ensemble empirical mode decomposition for agricultural commodity futures prices. J Forecast 39, 877–886. doi: 10.1002/for.2665

Crossref Full Text | Google Scholar

Gu, Y. H., Jin, D., Yin, H., Zheng, R., Piao, X., and Yoo, S. J. (2022). Forecasting agricultural commodity prices using dual input attention LSTM. Agriculture Basel 12:256. doi: 10.3390/agriculture12020256

Crossref Full Text | Google Scholar

Guo, Y., Tang, D. Z., Tang, W., Yang, S. Q., Tang, Q. C., Feng, Y., et al. (2022). Agricultural price prediction based on combined forecasting model under spatial-temporal influencing factors. Sustain. For. 14:10483. doi: 10.3390/su141710483

Crossref Full Text | Google Scholar

He, Z. C., and Huang, J. H. (2023). A novel non-ferrous metal price hybrid forecasting model based on data preprocessing and error correction. Resour Policy 86:104189. doi: 10.1016/j.resourpol.2023.104189

Crossref Full Text | Google Scholar

He, F., Zhou, J., Feng, Z., Liu, G., and Yang, Y. (2019). A hybrid short-term load forecasting model based on variational mode decomposition and long short-term memory networks considering relevant factors with Bayesian optimization algorithm. Appl. Energy 237, 103–116. doi: 10.1016/j.apenergy.2019.01.055

Crossref Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput 9, 1735–1780. doi: 10.1162/neco.1997.9.8.1735

Crossref Full Text | Google Scholar

Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Snin, H. H., Zheng, Q., et al. (1998). The empirical mode de-composition and the Hubert spectrum for nonlinear and non-stationary time series analysis. Proc R Soc A 454, 903–995. doi: 10.1098/rspa.1998.0193

Crossref Full Text | Google Scholar

Jadhav, V., Reddy, B. V. C., and Gaddi, G. M. (2017). Application of ARIMA model for forecasting agricultural prices. J Agric Sci Technol 19, 981–992.

Google Scholar

Jaiswal, R., Jha, G. K., Kumar, R. R., and Choudhary, K. (2022). Deep long short-term memory based model for agricultural price forecasting. Neural Comput Applic 34, 4661–4676. doi: 10.1007/s00521-021-06621-3

Crossref Full Text | Google Scholar

Jha, G. K., and Sinha, K. (2014). Time-delay neural networks for time series prediction: an application to the monthly wholesale price of oilseeds in India. Neural Comput Applic 24, 563–571. doi: 10.1007/s00521-012-1264-z

Crossref Full Text | Google Scholar

Jung, D. H., and Cho, Y. Y. (2022). A prediction model for Hallabong Tangor product prices using LSTM (Long short-term memory). Network 40, 571–577. doi: 10.7235/HORT.20220051

Crossref Full Text | Google Scholar

Kurumatani, K. (2020). Time series forecasting of agricultural product prices based on recurrent neural networks and its evaluation method. Appl. Sci. 2:1434. doi: 10.1007/s42452-020-03225-9

Crossref Full Text | Google Scholar

Kyriazi, F., Thomakos, D. D., and Guerard, J. B. (2019). Adaptive learning forecasting, with applications in forecasting agricultural prices. Int. J. Forecast. 35, 1356–1369. doi: 10.1016/j.ijforecast.2019.03.031

Crossref Full Text | Google Scholar

Lee, Y. S., and Tong, L. I. (2011). Forecasting time series using a methodology based on autoregressive integrated moving average and genetic programming. Knowl.-Based Syst. 24, 66–72. doi: 10.1016/j.knosys.2010.07.006

Crossref Full Text | Google Scholar

Li, K. Q., Shen, N., Kang, Y., Chen, H., Wang, Y. Q., and He, S. Q. (2021). Livestock product Price forecasting method based on heterogeneous GRU neural network and energy decomposition. IEEE Access 9, 158322–158330. doi: 10.1109/ACCESS.2021.3128960

Crossref Full Text | Google Scholar

Lin, K. P., Pai, P. F., and Yang, S. L. (2011). Forecasting concentrations of air pollutants by logarithm support vector regression with immune algorithms. Appl. Math. Comput. 217, 5318–5327. doi: 10.1016/j.amc.2010.11.055

Crossref Full Text | Google Scholar

Liu, H., Mi, X., and Li, Y. (2018). Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposi-tion, singular spectrum analysis, LSTM network and ELM. Energy Convers Manage 159, 54–64. doi: 10.1016/j.enconman.2018.01.010

Crossref Full Text | Google Scholar

Liu, D. G., Tang, Z. P., and Cai, Y. (2022). A hybrid model for China's soybean spot price prediction by integrating CEEMDAN with fuzzy entropy clustering and CNN-GRU-attention. Sustain. For. 14:15522. doi: 10.3390/su142315522

Crossref Full Text | Google Scholar

Luo, R., Liu, J., Wang, P., Tao, Z., and Chen, H. (2023). A multisource data-driven combined forecasting model based on internet search keyword screening method for interval soybean futures price. J Forecasting. doi: 10.1002/for.3035

Crossref Full Text | Google Scholar

Mandal, P., Senjyu, T., and Funabashi, T. (2006). Neural networks approach to forecast several hour ahead electricity prices and loads in deregulated market. Energy Convers Manag 47, 2128–2142. doi: 10.1016/j.enconman.2005.12.008

Crossref Full Text | Google Scholar

Marfatia, H. A., Ji, Q., and Luo, J. W. (2021). Forecasting the volatility of agricultural commodity futures: the role of co-volatility and oil volatility. J. Forecast. 41, 383–404. doi: 10.1002/for.2811

Crossref Full Text | Google Scholar

Pan, H., Yang, Y., Li, X., Zheng, J., and Cheng, J. (2019). Symplectic geometry mode decomposition and its application to rotating machinery compound fault diagnosis. Mech. Syst. Signal Process. 114, 189–211. doi: 10.1016/j.ymssp.2018.05.019

Crossref Full Text | Google Scholar

Paredes-Garcia, W. J., Ocampo-Velazquez, R. V., Torres-Pacheco, I., and Cedillo-Jimenez, C. A. (2019). Price forecasting and span commercialization opportunities for Mexican agricultural products 9, 826. doi: 10.3390/agronomy9120826,

Crossref Full Text | Google Scholar

Pinheiro, C. A. O., and de Senna, V. (2017). Multivariate analysis and neural networks application to price forecasting in the Brazilian agricultural market 47:e20160077. doi: 10.1590/0103-8478cr20160077,

Crossref Full Text | Google Scholar

Reboredo, J. C., and Rivera-Castro, M. A. (2013). A wavelet decomposition approach to crude oil price and exchange rate dependence. Econ. Model. 32, 42–57. doi: 10.1016/j.econmod.2012.12.028

Crossref Full Text | Google Scholar

Sadgali, I., Sael, N., and Benabbou, F. (2019). Performance of machine learning techniques in the detection of financial frauds. Proc Comput Sci 148, 45–54. doi: 10.1016/j.procs.2019.01.007

Crossref Full Text | Google Scholar

Sun, J. Y., Zhao, P. P., and Sun, S. L. (2022). A new secondary decomposition-reconstruction-ensemble approach for crude oil price forecasting. Resour Policy 77:102762. doi: 10.1016/j.resourpol.2022.102762

Crossref Full Text | Google Scholar

Taylan, O. (2017). Modelling and analysis of ozone concentration by artificial intelligent techniques for estimating air quality. Atmos. Environ. 150, 356–365. doi: 10.1016/j.atmosenv.2016.11.030

Crossref Full Text | Google Scholar

Vuong, P. H., Dat, T. T., Mai, T. K., Uyen, P. H., and Bao, P. T. (2022). Stock-price forecasting based on XGBoost and LSTM. Comput Syst Sci Eng 40, 237–246. doi: 10.32604/csse.2022.017685

Crossref Full Text | Google Scholar

Wang, L. Y., Feng, J. Y., Sui, X. J., Chu, X. Q., and Mu, W. S. (2020). Agricultural product price forecasting methods: research advances and trend. Br Food J 122, 2121–2138. doi: 10.1108/BFJ-09-2019-0683

Crossref Full Text | Google Scholar

Wang, B. J., Liu, P. Z., Chao, Z., Wang, J. M., Chen, W. J., Cao, N., et al. (2018). Research on hybrid model of garlic short-term price forecasting based on big data. Comput Mater Cont 57, 283–296. doi: 10.32604/cmc.2018.03791

Crossref Full Text | Google Scholar

Wang, D., Luo, H., Grunder, O., Lin, Y., and Guo, H. (2017). Multi-step ahead electricity price forecasting using a hybrid model based on two-layer decomposition technique and BP neural network optimized by firefly algorithm. Appl. Energy 190, 390–407. doi: 10.1016/j.apenergy.2016.12.134

Crossref Full Text | Google Scholar

Wu, J. H., Hu, Y., Wu, D. Q., and Yang, Z. Y. (2022). An aquatic product price forecast model using VMD-IBES-LSTM hybrid approach. Agric Basel 12:1185. doi: 10.3390/agriculture12081185

Crossref Full Text | Google Scholar

Xiong, T., Li, C., and Bao, Y. (2018). Seasonal forecasting of agricultural commodity price using a hybrid STL and ELM method: evi-dence from the vegetable market in China. Neurocomputing 275, 2831–2844. doi: 10.1016/j.neucom.2017.11.053

Crossref Full Text | Google Scholar

Yang, H., Yang, X. D., and Li, G. H. (2023). Forecasting carbon price in China using a novel hybrid model based on secondary decomposition, multi-complexity and error correction. J. Clean. Prod. 401:136701. doi: 10.1016/j.jclepro.2023.136701

Crossref Full Text | Google Scholar

Zafeiriou, E., and Sariannidis, N. (2011). Nonlinearities in the price behaviour of agricultural products: the case of cotton. J Food Agric Environ 9, 551–555.

Google Scholar

Zeng, L. L., Ling, L. W., Zhang, D. B., and Jiang, W. T. (2023). Optimal forecast combination based on PSO-CS approach for daily agricul-tural future prices forecasting. Appl. Soft Comput. 132:109833. doi: 10.1016/j.asoc.2022.109833

Crossref Full Text | Google Scholar

Zhang, G. P. (2003). Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 50, 159–175. doi: 10.1016/S0925-2312(01)00702-0

Crossref Full Text | Google Scholar

Zhang, D. B., Chen, S. Y., Ling, L. W., and Xia, Q. (2020). Forecasting agricultural commodity prices using model selection framework with time series features and forecast horizons. IEEE Access. 8, 28197–28209. doi: 10.1109/ACCESS.2020.2971591

Crossref Full Text | Google Scholar

Zhang, X., Lai, K. K., and Wang, S. Y. (2008). A new approach for crude oil price analysis based on empirical mode decomposition. Energy Econ. 30, 905–918. doi: 10.1016/j.eneco.2007.02.012

Crossref Full Text | Google Scholar

Zhang, D., Zang, G., Li, J., Ma, K., and Liu, H. (2018). Prediction of soybean price in China using QR-RBF neural network model. Comput. Electron. Agric. 154, 10–17. doi: 10.1016/j.compag.2018.08.016

Crossref Full Text | Google Scholar

Zhou, F. T., Huang, Z. H., and Zhang, C. H. (2022). Carbon price forecasting based on CEEMDAN and LSTM. Appl. Energy 311:118601. doi: 10.1016/j.apenergy.2022.118601

Crossref Full Text | Google Scholar