- 1Department of Agricultural Engineering and Soil Science, Faculty of Agriculture, Rajarata University of Sri Lanka, Anuradhapura, Sri Lanka
- 2Faculty of Agriculture, University of the Ryukyus, Nishihara-cho, Japan
- 3United Graduate School of Agricultural Sciences, Kagoshima University, Kagoshima-shi, Japan
In most countries where sugarcane is grown, new sugarcane varieties are frequently introduced to the market; however, the existing crop models are not frequently updated. Therefore, experiments are needed to parameterize and optimize crop and cultivar-specific parameters of crop models. In this study, we used GEM-SA -generated output files of a study conducted to perform emulator-based sensitivity analysis of the APSIM-Sugar model using GEM-SA software. We compared the accuracy of simulations performed with optimized parameters using four methods: (1) optimization of 26 parameters of the APSIM-sugar model, (2) optimization of the six most sensitive parameters of the APSIM-sugar model, (3) emulator-based optimization of 26 parameters of the APSIM-sugar model, and (4) emulator-based optimization of the six most sensitive parameters. We also evaluated the computational expensiveness of these optimization methods. The results showed that the emulator-based optimization methods provided fast results compared to optimization using APSIM simulations. Moreover, the emulator-based optimization of the six selected most sensitive parameters (which took only a few minutes) provided almost similar simulation results to those obtained with all optimized parameters using APSIM optimization, which took days. Considering the accuracy and computational complexity, we propose to perform the optimization of the most sensitive parameters using an emulator-based approach. Since the sensitivity analysis results were used in this study, this optimization process could be directly coupled with the emulator-based sensitivity analysis explained by Gunarathna et al. (2019c).
1. Introduction
Process-based crop models play an important role in simulating the underlying physiological processes of crops based on the given environmental, soil, abiotic stress, cultivar and management conditions (Lisson et al., 2005). APSIM-Sugar (Keating et al., 1999; Holzworth et al., 2014) and DSSAT-Canegro (Jones et al., 2003; Singels et al., 2008) are widely used models for sugarcane growth and yield simulation worldwide. These models are used as decision support for irrigation scheduling (Inman-Bamber and McGlinchey, 2003; Everingham et al., 2008), nitrogen fertilizer management (Thorburn et al., 2010; Skocaj et al., 2013), and climate impact management (Biggs et al., 2013; Singels et al., 2014). However, most of these process-based crop models do not include new improved varieties, which complicates the application of these crop models (Sexton et al., 2017; Gunarathna et al., 2019c).
Most countries growing sugarcane regularly introduce new sugarcane varieties suitable for modern management, pest and disease control, and abiotic stress to ensure higher production (Sexton et al., 2014, 2017). Since most of the crop models are limited to a few cultivars, the current process-based crop models such as APSIM, DSSAT, STICS, etc., have not included sugarcane many new cultivars introduced worldwide (Gunarathna et al., 2019c). This has also discouraged modelers from investigating the differences between sugarcane varieties through simulation (Sexton et al., 2017).
The parameters of process-based crop models need to be well parameterized and calibrated to achieve higher accuracy of simulations (Keating et al., 1999, 2000; Sexton et al., 2017). Therefore, some models include optimization tools along with the model release. An example is the DSSAT model (Jones et al., 2003; Singels et al., 2008), which includes the optimization tool GLUE (Birch et al., 1998; Soltani et al., 2006); however, this is still a computationally intensive process. Some authors have proposed some optimization tools for the APSIM model (Birch et al., 1998; Soltani et al., 2006); however, none of them is ready for use yet (Archontoulis et al., 2014). Since there are few reliable software options, researchers have to work on their model or use a trial-and-error method (Seidel et al., 2018). Sexton et al. (2017) evaluated the performances of Generalized Likelihood Uncertainty Estimation (GLUE) and Markov Chain Monte-Carlo (MCMC) and recommended the MCMC method to optimize the cultivar parameters of the APSIM sugar model. However, they did not mention the computational expensiveness of these methods. Since Monte Carlo simulation methods are easy to implement, they are very popular among scientists working on parameter optimization. However, MCMC depends on a large number of code runs generated at randomly selected input points. Therefore, it may not be practical for complex models such as process-based crop models (Kennedy and Petropoulos, 2017). This is because using a sufficient number of codes runs for accurate estimation may not be practical, especially when a high-dimensional input space is studied. Therefore, most calibration studies use a smaller number of parameters (Seidel et al., 2018). Therefore, a more efficient solution for parameter optimization of process-based crop models is needed.
The emulator-based approach can replace the computationally intensive process-based models as a computationally inexpensive surrogate (Yurko et al., 2015). An emulator is a probabilistic response, a very practical approach because the emulator's contribution to the overall uncertainty can be incorporated into the Bayesian calibration process. Therefore, an uncertain emulator would limit the posterior parameter accuracy compared to calibrating the parameters with the tedious optimization methods (Yurko et al., 2015). It is necessary to create accurate emulators that are as accurate as a computer model and limit the influence of errors and uncertainties on the results.
The selection of input parameters with an appropriate parameter prior distribution is a crucial aspect in the development of high-performance emulators. The selection of parameter prior distribution is controversial and depends heavily on expert opinions. Gunarathna et al. (2019c) used the parameter ranges of existing cultivars as the prior distribution range to determine the sensitivity of 26 cultivar/plant parameters to the selected outputs of APSIM-Sugar. Some authors used screening algorithms to identify statistically significant input parameters (Inman-Bamber and McGlinchey, 2003; Everingham et al., 2008). Regardless of the approach, the input parameters and their prior distribution must be specified, as proper prior distribution of input parameters can significantly increase efficiency (Kennedy and Petropoulos, 2017).
The emulators used in this work are based on the Gaussian process model (GP) and are considered Bayesian analysis of computer code output (BACCO) method, which assumes that the output is deterministic (Kennedy and Petropoulos, 2017). The tremendous efficiency of Bayesian methods with emulation (O'Hagan, 2006) inspires BACCO in this study.
In this study, the performance (accuracy and computational expensiveness) of emulator-based optimization was evaluated against simulator-based optimization using the APSIM-Sugar model.
2. Materials and methods
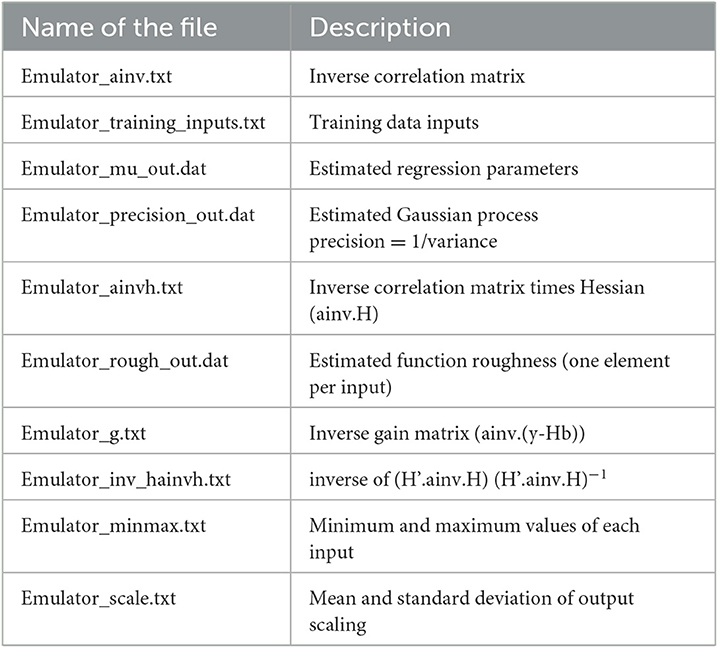
Gunarathna et al. (2019c) proposed an emulator-based sensitivity analysis method to determine the most sensitive parameters of the APSIM-Sugar model. In this study, they evaluated 26 parameters, including 14 cultivar parameters (some with different levels) and two plant parameters (with different levels) (Table 1). In this study, they developed 200 test points for each parameter using the apsimr package of R software. Then they developed emulators using the software GEM-SA and evaluated the accuracy of these emulators using the built-in error estimation methods. They found that these emulators behaved linearly and the accuracy was satisfactory. In addition to the results of the GEM-SA interface, GEM-SA generated a series of files (Table 2) related to the development of the emulators and the evaluation of their accuracy. In this study, we used the generated output files (Table 2) for the emulators developed in the above-mentioned study by Gunarathna et al. (2019c).
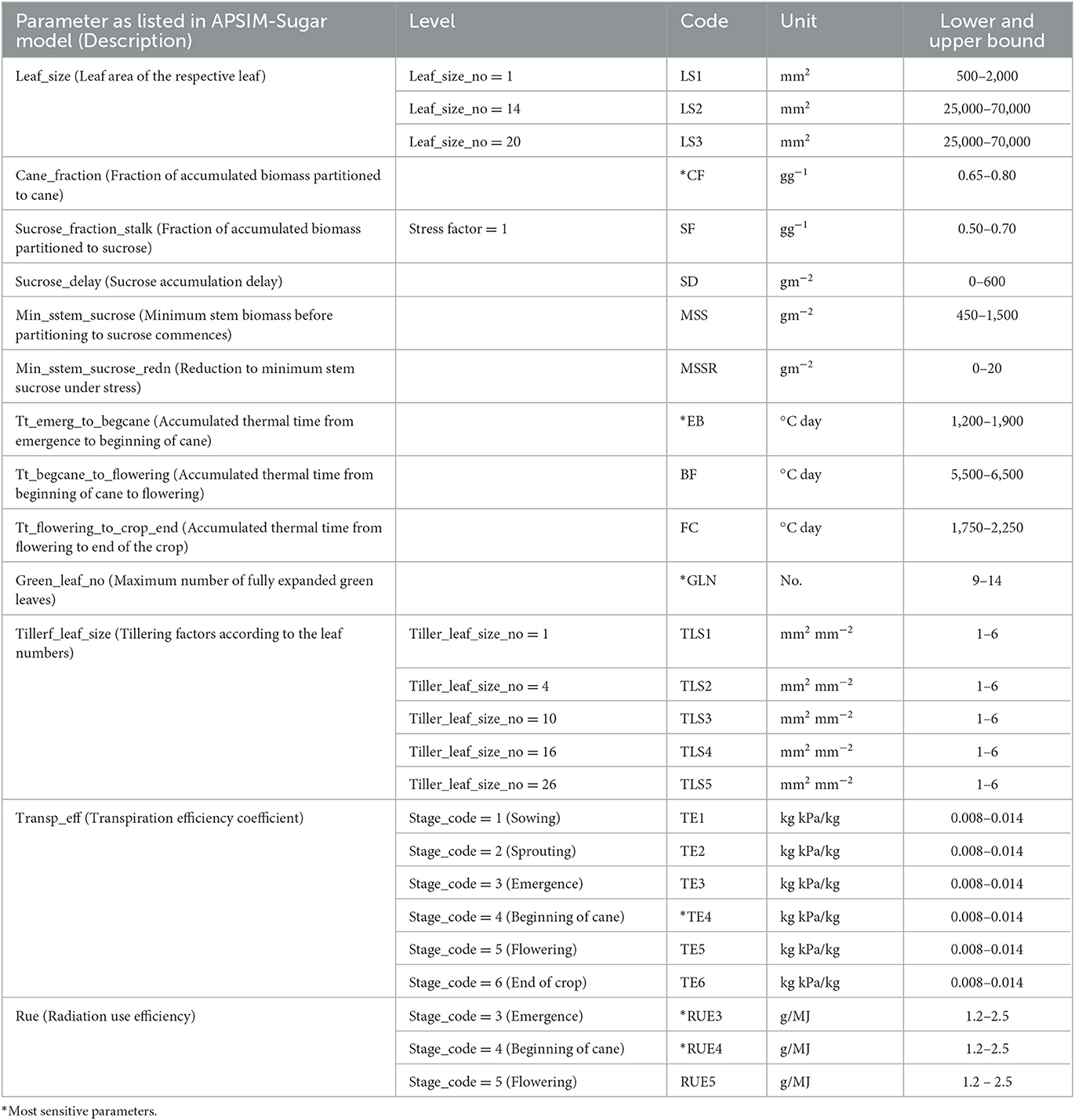
Table 1. Selected parameters used to assess the parameter sensitivity by Gunarathna et al. (2019c).
2.1. APSIM simulation
The APSIM crop model combines biophysical and management modules in a central engine to simulate crop growth and yield under different cropping systems (Keating et al., 2003; Holzworth et al., 2014). The APSIM sugar model simulates dry weight accumulation due to intercepted radiation in a daily time step. The accumulated dry weight is then partitioned among leaves, immature stem tips, structural stems, roots, and sucrose. Ultimately, APSIM-Sugar simulates key outputs such as fresh cane weight, sugar yield, and sucrose content (Keating et al., 1999; Sexton et al., 2017). This process is controlled by environmental factors, crop type, and cultivar-specific parameters (Keating et al., 1999, 2000; Dias et al., 2019).
Gunarathna et al. (2019c) conducted an APSIM simulation of sugarcane biomass from January 1, 2000 to December 31, 2010 under rainfed and irrigated conditions in two locations as Okinawa, Japan and Sevanagala, Sri Lanka. Although Gunarathna et al. (2019c) used four conditions (two locations and two water regimes), for this study we selected one condition (Sri Lankan sugarcane under irrigated conditions) to minimize other impacts to get the maximum effect of varietal and cultivar parameters. For this simulation, they used soil data derived using pedotransfer functions (Gunarathna et al., 2019a,b, 2020) and from a Soil Science Society of Sri Lanka (Dassanayake et al., 2010). They also used meteorological data extracted from the AgMERRA global gridded climate dataset (ElliottMüchller et al., 2015) using the NetCDF Extractor v. 2.0 tool from AgriMetSoft (https://www.agrimetsoft.com). Gunarathna et al. (2019c) explained more information about the climate and management conditions used for the APSIM simulation.
2.2. Gaussian emulation machine for sensitivity analysis
The Gaussian Emulation Machine for Sensitivity Analysis (GEM-SA) software can create emulators from a set of given inputs and outputs. It uses the BACCO approach to perform prediction, uncertainty analysis, and sensitivity analysis with a smaller number of code runs than Monte Carlo-based methods (Kennedy and Petropoulos, 2017). The underlying mathematical procedures used in GEM-SA are described in detail by Kennedy and O'Hagan (Kennedy and O'Hagan, 2001) and Kennedy and Petropoulos (Kennedy and Petropoulos, 2017). In addition to the results of the GEM-SA interface, all mathematical constants associated with the emulators and the data used to develop and evaluate the emulators are stored in files. Table 2 shows the list and description of the output files generated by the GEM-SA software (hereafter referred to as GEM-SA generated output files). These files can be used for applications other than the integrated analyzes of GEM-SA (Kennedy and Petropoulos, 2017). Kennedy et al. (2012) used such a set of emulator definition files to develop a probabilistic model for assessing bystander and resident exposure. In this study, we used the output files of the emulators from GEM-SA, which refer to the total aboveground biomass of irrigated sugarcane under Sri Lankan conditions. In developing the emulators, Gunarathna et al. (2019c) set the “prior mean” option for each input as linear and evaluated the emulators using the leave-one-out cross-validation procedure of GEM-SA. Based on the results, they confirmed the linearity of the developed emulators (Gunarathna et al., 2019c).
2.3. Parameter optimization with the DEoptim and apsimr packages
Since some model parameters are not directly or easily measurable, parameter optimization plays an important role in model development. In model optimization, selected parameters are allowed to vary within predefined bounds until the optimization objective is achieved (Song et al., 2012). Parameter optimization can be global, where the algorithm searches for the global optimum by using mechanisms to search larger parts of the search space, or local, where the algorithm searches for a local optimum of the objective function for a specific region of the input space. When there are many parameters in a model, the optimization process can become complex. Therefore, global optimization can achieve good results compared to local optimization. However, global optimization is time consuming and therefore characterized by high computational costs.
There is an increasing interest in meta-heuristics and improvements in their application to optimization problems (Song et al., 2012). For example, the College of Arizona's Shuffled Complex Evolution method (SCE-UA) (Duan et al., 1992) and dynamic programming (DP) for optimization use genetic algorithms, differential evolution, particle and swarm optimization (Song et al., 2012). Differential evolution (DE) is suitable for finding the global optimum of a real-valued function with real-valued parameters (Mullen et al., 2011). DE uses arithmetic operations instead of logical operations. It shows remarkable performance as a global optimization algorithm for continuous numerical minimization problems (Price et al., 2006). In DE, the population is represented by floating point elements. Therefore, it requires specified vectors containing lower and upper bounds with the same length as the parameter vector (Mullen et al., 2011).
In this study, we used the apsimr (Stanfill, 2015) and DEoptim (Ardia et al., 2020) packages of the R software (R Core Team, 2018) to perform the optimization of the parameters of APSIM-Sugar.
The apsimr package contains functions to create, edit, run APSIM simulations and visualize the results in the R software (Stanfill, 2015). It also includes functions for performing sensitivity and uncertainty analyzes of APSIM using third-party packages designed for sensitivity and uncertainty analyzes.
The DEoptim package (Mullen et al., 2011; Ardia et al., 2020) is the R implementation of the differential evolution strategy (DE) developed using the differential algorithm explained by Price et al. (2006). The DEoptim function is the core function of the DEoptim package. It searches for the minima of the objective function between the lower and upper bounds of each parameter to be optimized. For this purpose, it uses some arguments such as fn: the function to be optimized, lower, upper: two vectors indicating scalar real lower and upper bounds for each parameter to be optimized, control: a list of tuning parameters and itermax: the maximum number of iterations, which is 200 by default (Ardia et al., 2011). The DEoptim package has been used in several parameter optimization studies, including parameter optimization of process-based crop models (Lopez et al., 2017; Liu et al., 2018).
We tested four conditions: (1) optimization of 26 parameters of the APSIM sugar model, (2) optimization of the six most sensitive parameters (see Table 1) of the APSIM sugar model, (3) emulator-based optimization of 26 parameters of the APSIM sugar model, and (4) emulator-based optimization of the six most sensitive parameters of the APSIM sugar model. We developed two R codes, with an option to select all parameters (A) or selected parameters (S), to run the optimization of APSIM-Sugar and the emulators developed to represent the APSIM simulations, respectively. We used the root mean square error (RMSE) as the evaluation criterion. We ran the optimization for 200 iterations and estimated the error and computational expensiveness (CPU processing time) of four methods.
2.4. Statistical analysis
Since a single statistical index is not sufficient for evaluating the simulations, we used multiple indices (Mereu et al., 2019) to evaluate the accuracy of the simulations performed with the plant and cultivar parameters optimized by the four methods. We used the root mean square error (RMSE; equation 1), the coefficient of determination (R2; equation 2), the coefficient of residual mass (CRM; equation 3), and the index of agreement (d-index; equation 4). The RMSE indicates the standard deviation of the model prediction error (Zambrano-Bigiarini, 2017), while the R2 estimates the combined dispersion versus the single dispersion of the observed and estimated values (Krause et al., 2005). The CRM indicates how much the model is underestimated or overestimated overall (Aliyu and Bello, 2017). The d-index is a standardized measure of the degree of model prediction error and represents the ratio between the mean squared error and the potential error (Willmott, 1981; Krause et al., 2005).
Where, Ei and Mi are the simulated and measured biomass of the ith year, respectively, n is the number yield records, and and are the mean simulated and observed biomass, respectively.
3. Results and discussion
3.1. Optimized parameters
Table 3 shows the optimized values of plant- and cultivar specific parameters of the APSIM sugar model obtained by four optimization methods. We performed 200 iterations in the optimization process for all methods except the optimization of 26 parameters of the APSIM sugar model. For the optimization of 26 parameters of the APSIM sugar model, we performed only 100 iterations due to practical difficulties.
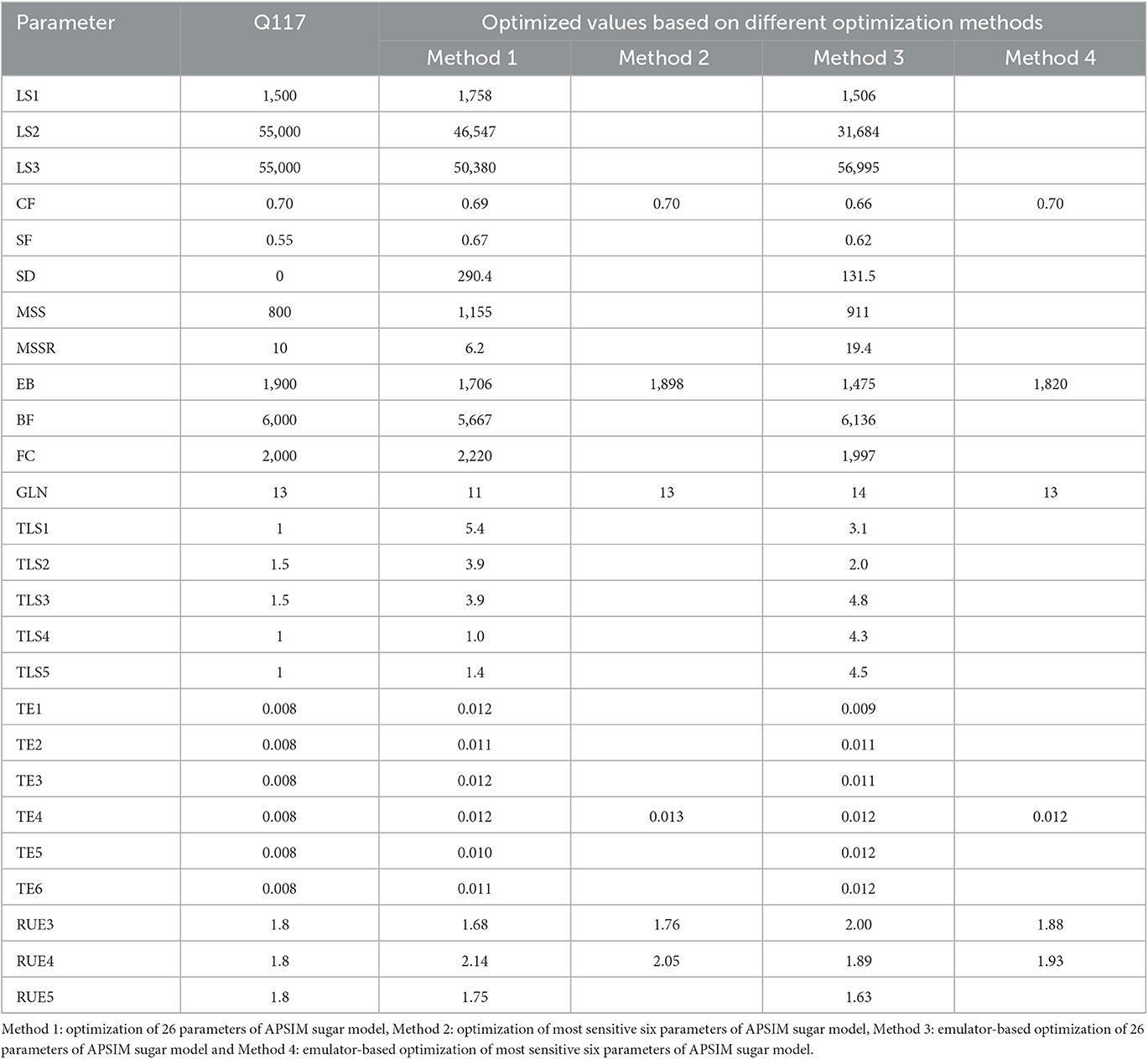
Table 3. Optimized parameters of plant and cultivar specific parameters of APSIM sugar model using different optimization methods.
3.2. Accuracy of biomass predictions
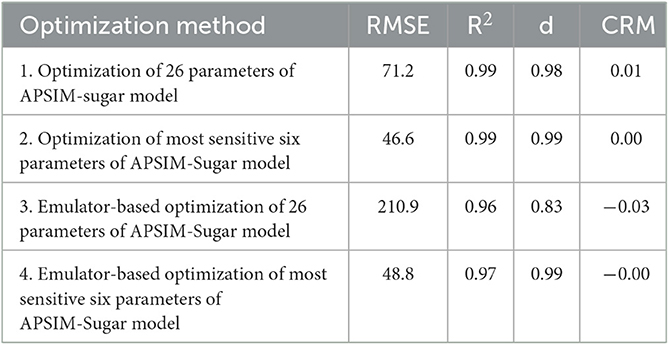
After optimizing the parameters with each optimization method, the respective crop and cultivar parameters were replaced with the optimized values and the biomass of sugarcane was simulated. The simulated biomass values were compared with the observed values and the accuracy of the simulations was evaluated using RMSE, CRM, R2, and d-index values (Table 4).
The results showed that all methods provided a good estimate of the plant- and cultivar-specific parameters of the APSIM sugar model, so that the simulations were close to the observations. However, optimization of selected parameters gave much better results than optimization of all parameters. This could be due to an insufficient number of iterations. Therefore, we performed 400 iterations for the emulator-based optimization of the most sensitive six parameters of the APSIM sugar model. Then we obtained the comparable results (RMSE = 53.0, R2 = 0.96, d = 0.99, and CRM = −0.00) to the parameters selected by the method.
3.3. The computational expensiveness of the optimization
The computer used for the optimization process is an Intel® Core™ i7-8550U @ 1.80 GHz processor and 8.00 GB RAM. The operating system of the computer is Windows™ 10 Home Edition. The time taken for the 200 iterations was measured and the time taken for one iteration is calculated and compared (Table 5). The results show that the emulator-based optimization takes significantly less time compared to the optimization of the APSIM model. Therefore, we can conclude that the emulator-based optimization method is not computationally expensive.
The complete process of emulator development, sensitivity analysis, and parameter optimization is shown in Figure 1. It shows that we can perform both sensitivity analysis and parameter optimization using the same input and output combinations and emulator results for sensitivity analysis. Therefore, we can complete both sensitivity analysis and parameter optimization within a short period of time compared to the conventional sensitivity analysis and parameter optimization methods. The accuracy of the simulations performed with the emulator-based parameter optimization is not different from the conventional optimization of APSIM. Therefore, we can propose the emulator-based parameter optimization using the output files of the software GEM-SA to drastically reduce the computational cost of the parameter optimization process. We can complete the whole process of emulator development, sensitivity analysis and parameter optimization in <3 h. Since all the software and packages used in this study are open source, this method would be feasible for many countries, including the resource-constrained areas of the world.
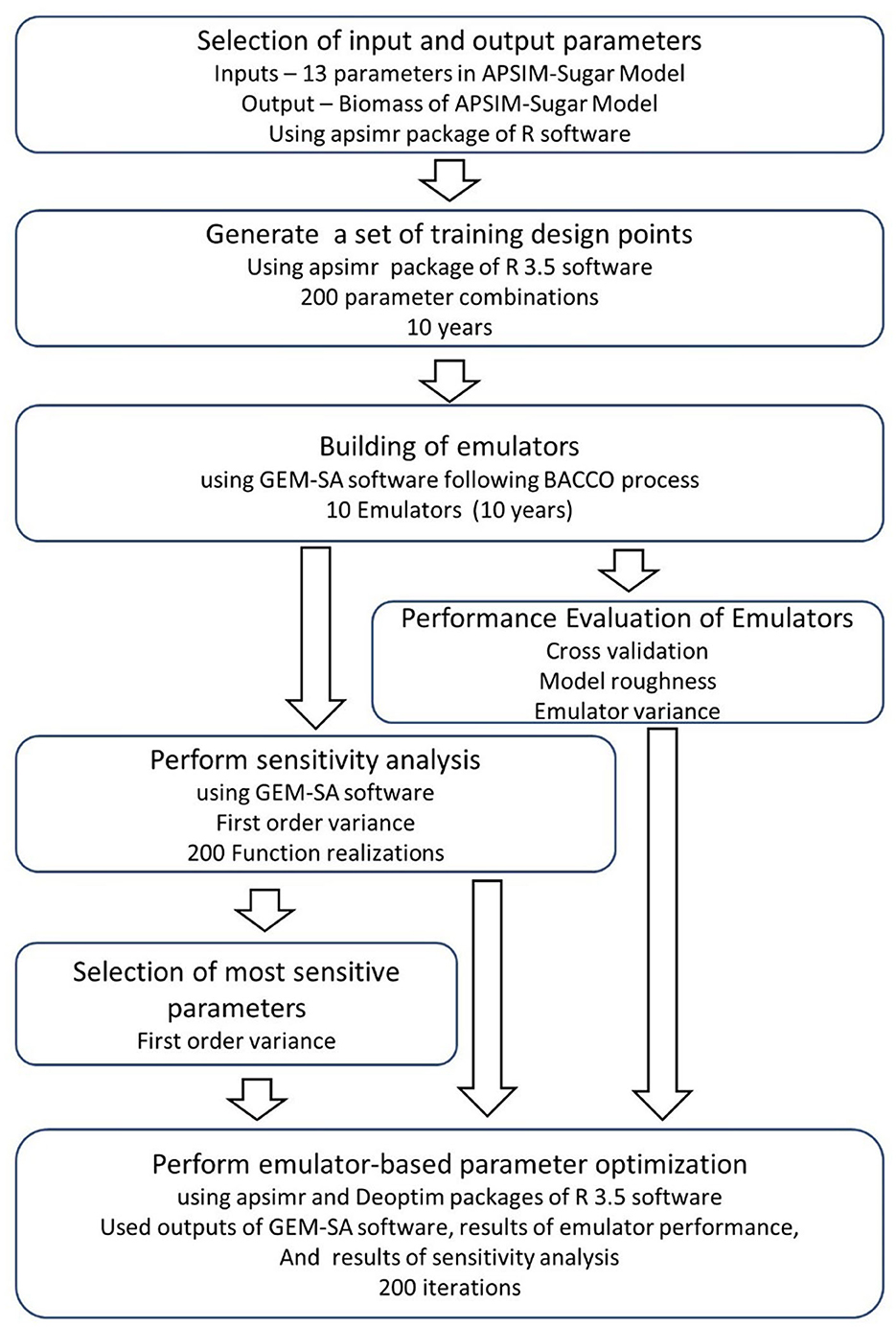
Figure 1. The complete process of emulator creation, sensitivity analysis, and parameter optimization using the apsimr and DEoptim packages of the R software and the GEM-SA software.
4. Conclusion
We performed parameter optimization of the APSIM sugar model using an emulator-based approach. For this purpose, we used the generated output files of a sensitivity analysis performed with GEM-SA. We compared the accuracy of the performance of the emulator-based optimization with the optimization of the APSIM sugar model. Both methods used the differential evolution method with the DEoptim package of the R software. Moreover, both methods were performed for two levels to optimize all parameters and select the most sensitive parameters reported by Gunarathna et al. (2019c). We simulated the total aboveground biomass of sugarcane of the APSIM-Sugar model using optimized parameters with four different methods. The results showed no differences between the biomass simulated using the four methods, although the optimization of APSIM required exceptionally more computational time than the emulator-based approach.
In addition, both optimization of selected parameters and optimization of the entire set of parameters of the APSIM sugar model were performed. The study concluded that the emulator-based optimization of the APSIM model is applicable using the output files generated by the sensitivity analysis of the software GEM-SA. In addition, we recommend that the sensitivity analysis followed by parameter optimization be performed using the GEM-SA, apsimr software and the DEoptim packages of the R software, as this procedure can drastically reduce the computational time without affecting the accuracy of the APSIM simulations.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
MHJPG and KS conceptualized, conceived, and performed. KS supervised the study. MHJPG, KS, and MKNK interpreted data and developed the manuscript. All authors read have and approved the final manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aliyu, S., and Bello, S. (2017). Performance assessment of hargreaves model in estimating global solar radiation in Sokoto, Nigeria. Int. J. Adv. Scientific Res. Eng. 3, 6–15. doi: 10.7324/ijasre.2017.32542
Archontoulis, S. V., Miguez, F. E., and Moore, K. J. (2014). Evaluating APSIM maize, soil water, soil nitrogen, manure, and soil temperature modules in the Midwestern United States. Agron J. 106, 1025–1040. doi: 10.2134/agronj2013.0421
Ardia, D., Boudt, K., Carl, P., Mullen, K. M., and Peterson, B. G. (2011). Differential evolution with deoptim. R J. 3, 27–34. doi: 10.32614/RJ-2011-005
Ardia, D., Mullen, K., Peterson, B., Ulrich, J., and Boudt, K. (2020). Package ‘ DEoptim '- Global Optimization by Differential Evolution (Version 2.2-5).
Biggs, J. S., Thorburn, P. J., Crimp, S., Masters, B., and Attard, S. J. (2013). Interactions between climate change and sugarcane management systems for improving water quality leaving farms in the Mackay Whitsunday Region, Australia. Agric. Ecosyst. Environ. 180, 79–89. doi: 10.1016/j.agee.2011.11.005
Birch, C. J., Hammer, G. L., and Rickert, K. G. (1998). Temperature and photoperiod sensitivity of development in five cultivars of maize (Zea Mays L.) from emergence to tassel initiation. Field Crops Res. 55, 93–107. doi: 10.1016/S0378-4290(97)00062-2
Dassanayake, A. R., Silva, G. G. R., De Mapa, R. B., and Kumaragamage, D. (2010). “Benchmark soils of the dry zone of Sri Lanka: factsheets,” in Soil Science Society of Sri Lanka, eds Mapa, R. B., Somasiri, S., Dassanayake, A. R.
Dias, H. B., Inman-Bamber, G., Bermejo, R., Sentelhas, P. C., and Christodoulou, D. (2019). New APSIM-sugar features and parameters required to account for high sugarcane yields in tropical environments. Field Crops Res. 235, 38–53. doi: 10.1016/j.fcr.2019.02.002
Duan, Q., Sorooshian, S., and Gupta, V. (1992). Effective and efficient global optimization. Water Resour. Res. 28, 1015–1031. doi: 10.1029/91WR02985
ElliottMüchller, C., Deryng, D., Chryssanthacopoulos, J., Boote, K.J., Büchner, M., Foster, I., et al. (2015). The global gridded crop model intercomparison: data and modeling protocols for phase 1 (v1.0). Geosci Model Dev. 8, 261–277. doi: 10.5194/gmd-8-261-2015
Everingham, Y., Baillie, C., Inman-Bamber, G., and Baillie, J. (2008). Forecasting water allocations for bundaberg sugarcane farmers. Clim Res. 36, 231–239. doi: 10.3354/cr00743
Gunarathna, M. H. J. P., Sakai, K., Kumari, M. K. N., and Ranagalage, M. (2020). A functional analysis of pedotransfer functions developed for sri lankan soils: applicability for process-based crop models. Agronomy. 10, 1–18. doi: 10.3390/agronomy10020285
Gunarathna, M. H. J. P., Sakai, K., Nakandakari, T., Momii, K., and Kumari, M. K. N. (2019a). Machine learning approaches to develop pedotransfer functions for tropical Sri Lankan Soils. Water (Switzerland). 11, 1940. doi: 10.3390/w11091940
Gunarathna, M. H. J. P., Sakai, K., Nakandakari, T., Momii, K., and Kumari, M. K. N. (2019c). Sensitivity analysis of plant- and cultivar-specific parameters of apsim-sugar model : variation between climates and management conditions. Agronomy. 9, 242. doi: 10.3390/agronomy9050242
Gunarathna, M. H. J. P., Sakai, K., Nakandakari, T., Momii, K., Kumari, M. K. N., and Amarasekara, M. G. T. S. (2019b). Pedotransfer functions to estimate hydraulic properties of tropical Sri Lankan soils. Soil Tillage Res. 190, 109–119. doi: 10.1016/j.still.2019.02.009
Holzworth, D. P., Huth, N. I., deVoil, P. G., Zurcher, E. J., Herrmann, N. I., McLean, G., et al. (2014). APSIM—evolution towards a new generation of agricultural systems simulation. Environ. Modell. Softw. 62, 327–350. doi: 10.1016/j.envsoft.2014.07.009
Inman-Bamber, N. G., and McGlinchey, M. G. (2003). Crop coefficients and water-use estimates for sugarcane based on long-term bowen ratio energy balance measurements. Field Crops Res. 83, 125–138. doi: 10.1016/S0378-4290(03)00069-8
Jones, J. W., Hoogenboom, G., Porter, C. H., Boote, K. J., Batchelor, W. D., Hunt, L. A., et al. (2003). The DSSAT Cropping System Model. Jama. 18, 1352392186. doi: 10.1016/S1161-0301(02)00107-7
Keating, B. A., Carberry, P. S., Hammer, G. L., Probert, M. E., Robertson, M. J., Holzworth, D., et al. (2003). An overview of APSIM: a model designed for farming systems simulation. Euro. J. Agron. 18, 267–288. doi: 10.1016/S1161-0301(02)00108-9
Keating, B. A., Robertson, M. J., Muchow, R. C., and Huth, N. I. (1999). Modelling sugarcane production systems I. development and performance of the sugarcane module. Field Crops Res. 61, 253–271. doi: 10.1016/S0378-4290(98)00167-1
Keating, B. A., Robertson, M. J., Muchow, R. C., and Huth, N. I. (2000). Modelling sugarcane production systems: ii: analysis of system performance and methodology issues modelling sugarcane production systems I. Develop. Field Crops Res. 68, 1–20. doi: 10.1016/S0378-4290(00)00108-8
Kennedy, M. C., Butler Ellis, M. C., and Miller, P. C. H. (2012). BREAM: A probabilistic bystander and resident exposure assessment model of spray drift from an agricultural boom sprayer. Comput. Electron. Agric. 88, 63–71. doi: 10.1016/j.compag.2012.07.004
Kennedy, M. C., and O'Hagan, A. (2001). Bayesian calibration of computer models. J. R. Stat. Soc. Series B. Stat. Methodol. 63, 425–464. doi: 10.1111/1467-9868.00294
Kennedy, M. C., and Petropoulos, G. P. (2017). GEM-SA: The Gaussian Emulation Machine for Sensitivity Analysis. London: Elsevier Inc.
Krause, P., Boyle, D. P., and Bäse, F. (2005). Advances in geosciences comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 5, 89–97. doi: 10.5194/adgeo-5-89-2005
Lisson, S. N., Inman-Bamber, N. G., Robertson, M. J., and Keating, B. A. (2005). The historical and future contribution of crop physiology and modelling research to sugarcane production systems. Field Crops Res. 92, 321–335. doi: 10.1016/j.fcr.2005.01.010
Liu, J. H., Yan, Y., Ali, A., Yu, M. F., Xu, Q. J., Shi, P. J., et al. (2018). Simulation of crop growth, time to maturity and yield by an improved sigmoidal model. Sci. Rep. 8, 6–11. doi: 10.1038/s41598-018-24705-4
Lopez, J. R., Winter, J. M., Elliott, J., Ruane, A. C., Porter, C., and Hoogenboom, G. (2017). Integrating growth stage deficit irrigation into a process based crop model. Agric. For. Meteorol. 243, 84–92. doi: 10.1016/j.agrformet.2017.05.001
Mereu, V., Gallo, A., and Spano, D. (2019). Optimizing genetic parameters of CSM-CERES Wheat and CSM-CERES Maize for durum wheat, common wheat, and maize in Italy. Agronomy. 9, 665. doi: 10.3390/agronomy9100665
Mullen, K. M., Ardia, D., Gil, D. L., Windover, D., and Cline, J. (2011). DEoptim: an r package for global optimization by differential evolution. J. Stat. Softw. 40, 1–26. doi: 10.18637/jss.v040.i06
O'Hagan, A. (2006). Bayesian analysis of computer code outputs: a tutorial. Reliab. Eng. Syst. Saf. 91, 1290–1300. doi: 10.1016/j.ress.2005.11.025
Price, K. V., Storn, R. M., and Lampinen, J. A. (2006). Differential Evolution - A Practical Approach to Global Optimization. Berlin Heidelberg: Springer-Verlag.
R Core Team (2018). R: A Language, and Environment for Statistical Computing R Foundation for Statistical Computing. Vienna, Austria. Available online at: https://www.R.ProjectOrg/ (accessed December 5, 2021).
Seidel, S. J., Palosuo, T., Thorburn, P., and Wallach, D. (2018). Towards improved calibration of crop models—where are we now and where should we go? European Journal of Agronomy. 94, 25–35. doi: 10.1016/j.eja.2018.01.006
Sexton, J., Everingham, Y. L., and Inman-Bamber, G. (2017). A global sensitivity analysis of cultivar trait parameters in a sugarcane growth model for contrasting production environments in Queensland, Australia. Euro. J. Agron. 88, 96–105. doi: 10.1016/j.eja.2015.11.009
Sexton, J., Inman-bamber, N. G., Everingham, Y., Basnayake, J., Lakshmanan, P., and Jackson, P. (2014). Detailed trait characterisation is needed for simulation of cultivar responses to water stress. Proc. Aust. Soc. Sugar Cane Technol. 36, 82–92.
Singels, A., Jones, M., Marin, F., Ruane, A., and Thorburn, P. (2014). Predicting climate change impacts on sugarcane production at sites in Australia, Brazil and South Africa using the canegro model. Sugar Tech. 16, 347–355. doi: 10.1007/s12355-013-0274-1
Singels, A., Jones, M., and van den Berg, M. (2008). DSSAT v4. 5 Canegro Sugarcane Plant Module: Scientific Documentation.
Skocaj, D. M., Hurney, A. P., Inman-Bamber, N. G., Schroeder, B. L., and Everingham, Y. L. (2013). Modelling sugarcane yield response to applied nitrogen fertiliser in a wet tropical environment. Proceed. Austr. Soc. Sugar Cane Technol. 35, 1–9.
Soltani, A., Hammer, G. L., Torabi, B., Robertson, M. J., and Zeinali, E. (2006). Modeling chickpea growth and development: phenological development. Field Crops Res. 99, 1–13. doi: 10.1016/j.fcr.2006.02.004
Song, X. M., Zhan, C. S., and Xia, J. (2012). Integration of a statistical emulator approach with the SCE-UA method for parameter optimization of a hydrological model. Chinese Sci. Bull. 57, 3397–3403. doi: 10.1007/s11434-012-5305-x
Thorburn, P. J., Biggs, J. S., Collins, K., and Probert, M. E. (2010). Using the APSIM model to estimate nitrous oxide emissions from diverse australian sugarcane production systems. Agric. Ecosyst. Environ. 136, 343–350. doi: 10.1016/j.agee.2009.12.014
Willmott, C. J. (1981). On the validation of models. Phys Geogr. 2, 184–194. doi: 10.1080/02723646.1981.10642213
Yurko, J. P., Buongiorno, J., and Youngblood, R. (2015). Demonstration of emulator-based bayesian calibration of safety analysis codes: theory and formulation. Sci. Technol. Nucl. Install. (2015) 15, 249. doi: 10.1155/2015/839249
Zambrano-Bigiarini, M. (2017). R Package “HydroGOF”. 76. Available online at: http://hzambran.github.io/hydroGOF/ (accessed May 15, 2021).
Keywords: crop model, computational complexity, sensitive parameters, sugarcane, cultivar-specific parameters
Citation: Gunarathna MHJP, Sakai K and Kumari MKN (2023) Emulator-based optimization of APSIM-Sugar using the results of sensitivity analysis performed with the software GEM-SA. Front. Sustain. Food Syst. 7:1157854. doi: 10.3389/fsufs.2023.1157854
Received: 03 February 2023; Accepted: 22 May 2023;
Published: 14 June 2023.
Edited by:
Asha Sajeewani Karunaratne, Sabaragamuwa University, Sri LankaReviewed by:
Françoise RUGET, INRAE EMMAH Avignon, FranceRasappa Viswanathan, Indian Council of Agricultural Research (ICAR), India
Copyright © 2023 Gunarathna, Sakai and Kumari. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. H. J. P. Gunarathna, amFuYWthNzhAYWdyaS5yanQuYWMubGs=
 M. H. J. P. Gunarathna
M. H. J. P. Gunarathna Kazuhito Sakai
Kazuhito Sakai M. K. N. Kumari
M. K. N. Kumari