Impacts of extension dissemination and technology adoption on farmers' efficiency and welfare in Ghana: Evidence from legume inoculant technology

Examining the welfare impact of agricultural development interventions that incorporate diffusion of improved production technologies to farmers within extension delivery programs can be very challenging, because of the difficulty in disentangling the individual impacts of the production technology and the extension delivery program. Using recent farm level survey data from extension dissemination program of legume inoculant technology of 600 farmers in Ghana, we employ a recent methodological approach to investigate, simultaneously, the impact of the inoculant technology adoption and the extension program participation on farmers' productivity, efficiency and welfare. We decompose each of these impact measures into subcomponents whose causal paths can be traced to both the adoption of the production technology and the extension delivery program. We find that, in terms of yields and net revenue, direct contribution of improved technology adoption alone is 34 and 64%, respectively, and 35 and 66% indirectly due to improved farmer efficiency, leading to 36 and 74% improvement in farmers' welfare, respectively. On the other hand, direct contribution of extension delivery program participation alone is 66 and 36%, respectively, with 66 and 34% indirectly due to improved farmer efficiency, resulting in 64 and 26% improvement in farmers' welfare, respectively. Based on the findings, we recommend that policymakers should invest in research and development to produce yield enhancing agricultural technologies suitable for poor and degraded soil conditions in developing countries which can contribute immensely to poverty and food insecurity reduction. The development of new agricultural technologies must be pursued with vigorous provision of extension services to farmers to be able to exploit the full potentials of the new technologies.

Introduction

The increasing global food demand calls for adoption of new agricultural technologies to increase food production. Similar concerns in the past led to the introduction of the green revolution, a policy that advocated for intensifying the use of high yielding varieties, mineral fertilizers and tractors among smallholder farmers in developing countries (Pingali, 2012). Although the policy led to an increase in agricultural productivity and food supply, it also contributed to worse environmental impacts such as degraded lands and impoverished soils (Pingali, 2012; Zhang et al., 2015). Increase in food production cannot be achieved without sufficient nitrogen supply, as nitrogen allows farmers to increase crop production per unit area of land (Zhang et al., 2015). To mitigate the effect of pollution from reactive nitrogen while ensuring sufficient food production, a new paradigm shift is required (Mutuma et al., 2014; Zhang et al., 2015).

The Integrated Soil Fertility Management (ISFM) is one of such new approaches employed to promote soil fertility enhancing technologies for resource-poor farmers in developing countries (Crowley and Carter, 2000). A technology promoted under the program among smallholder soybean farmers in northern Ghana is the legume inoculant technology. Soybean is targeted due to its potential to undergo sustainable intensification, its industrial value and nutritional quality (Foyer et al., 2018; van Heerwaarden et al., 2018). The inoculant technology is an organic input containing isolates of an elite strain of bacterial (Bradyrhizobium spp.) and organic carrier material (Lupwayi et al., 2000). The inoculant technology is seen as cost-effective alternative to rehabilitating poor soils by enhancing the build-up of biological nitrogen fixation (BNF) organisms in the soil (Giller, 2001). Evidence of the potential productivity gains from inoculant has been documented in the literature (e.g., Rurangwa et al., 2018; van Heerwaarden et al., 2018; Mohammed and Abdulai, 2022). Notably, grain yield of soybean from inoculated fields increased by 20–29% in Mozambique (Chibeba et al., 2018) and 12–19% in the northern region of Ghana (Ulzen et al., 2016), relative to uninoculated fields. Yield response to inoculant significantly varies across agro-ecological zones in Africa and depend on agronomic practices and varietal promiscuity to the strain of the Rhizobia in the inoculant (van Heerwaarden et al., 2018). To improve efficiency, organizations involved in the dissemination of the inoculant technology employ several innovative extension methods¹ to train farmers on good agronomic and crop management practices on the inoculant technology. However, the important issues that require investigations are: to what extent has the inoculant or the extension improved the efficiency of farmers, and differential impacts of the inoculant and extension provision on efficiency improvement, as well as the impact of the efficiency gain on farmers' welfare. Our goal in this study is to simultaneously assess the impact of the inoculant technology adoption and the extension participation on farmers' productivity and efficiency. Usually, agricultural development programs such as the inoculant dissemination program often have dual goals of inducing an upward shift in the production frontier and the promotion of better management practices, which incorporates two potentially endogenous treatments in a single program (Bravo-Ureta, 2014). That is, treatment of farmers to new superior technology and the building of human capital, each having the potential to influence both the technology frontier function and the inefficiency function independently (Huang and Liu, 1994; Kumbhakar and Tsionas, 2009).

However, empirical studies often overlook the double treatment endogeneity, most often addressing one of them, and subsuming the other into distributional assumptions of the model. For instance, in Dinar's et al. (2007) study on the impact of extension services in Greece, extension participation is analyzed as performing a dual role, an input in the production function and a factor narrowing the technology gap, exerting direct and indirect effects in the production process. Their approach implicitly assumed homogeneous technology and fail to account for selection bias in the extension participation. In the event that farmers self-select into an extension program or adopt a superior production technology, the direct and indirect effects due to heterogeneity in technology or enhanced farmer capacity will be unaccounted for and the full impact will be miss measured. Other studies following the seminal work of Dinar et al. (2007) employed a mixed multi-stage approach to address the issue of selectivity and technology heterogeneity (e.g., Bravo-Ureta et al., 2012, 2020; Villano et al., 2015; Abdulai and Abdulai, 2016; De los Santos-Montero and Bravo-Ureta, 2017; Abdul-Rahaman and Abdulai, 2018). Even though the mixed multi-stage approach accounts for selection bias, it fails to account for the direct and indirect impacts that heterogeneous production technologies may have on both the production frontier and the efficiency function. The mixed multi-stage approach also attempts to address technology heterogeneity among production units by estimating group-specific frontiers for different groups of production units and further use the group frontiers to obtain the meta-frontier for comparison. However, because the maximum likelihood estimates of the predicted group-specific frontier is neither known a prior nor estimated relative to the same frontier, some degree of biasness in this approach is unavoidable and difficult to ascertain (Huang et al., 2014). Moreover, as indicated by Triebs and Kumbhakar (2018), the approach subsumes observed variables like extension service with the potential to augment the farmer's managerial ability in the inefficiency parameter of the model. On the contrary, the managerial ability does not only influence the inefficiency function but also the technology frontier, resulting in non-neutrality of the production function (Huang and Liu, 1994; Triebs and Kumbhakar, 2018). Also, the endogeneity issues addressed in the mixed multi-stage approach center mainly on the feedback between the technology choice and the production model residuals, but not on accounting for endogeneity, which could separately and simultaneously affect the technology frontier and the production inefficiency function (Chen et al., 2020).

The present study attempts to fill the gap and contribute to the above literature on impact assessment and technical efficiency, using survey data of 600 farm households from northern Ghana. Specifically, we employ the stochastic frontier model with endogenous treatment and mediator effect (Chen et al., 2020), to estimate the impact of dual purpose development interventions, and to decompose the impact into direct and indirect effects. This recent approach brings together mediation analysis², treatment effect and that of the stochastic frontier models in a single framework.³ Using this approach, we are able to disentangle the dual purpose inherent in agricultural development interventions' impact into four components. That is, the direct effects on the technology frontier, the indirect effects on the technology frontier that go through the mediator, the direct effects on the technical inefficiency, and the indirect effects on the technical inefficiency that go through the mediator. Our approach departs from the conventional approaches in the literature (e.g., Bravo-Ureta et al., 2012, 2020; Villano et al., 2015; Abdulai and Abdulai, 2016; De los Santos-Montero and Bravo-Ureta, 2017), in which a conventional SPF (stochastic production frontier) model that corrects for sample selection bias is estimated. In particular, we estimate a treatment effect model using the stochastic frontier regression framework, while addressing endogeneity from selection bias, endogenous treatment and mediator variables. We also account for treatment heterogeneities among production units. An important requirement for successful implementation of this approach is the existence of good and valid instruments for identifying both the mediation and the treatment effects, something that may be considered a limitation, just like any instrumental variable approach.

The rest of the paper is organized as follows: In Sections Conceptual and empirical framework and The identification strategy, we present the conceptual and empirical framework and empirical identification of causal impact, respectively, Section Empirical specification and estimation discusses the empirical specification and the estimation procedure, while Section Study area, data and descriptive statistics describes the data and descriptive statistics. The Empirical results and the Conclusions and policy implications are presented in the last two sections.

Materials and methods

Conceptual and empirical framework

In agriculture, new production technologies such as high yielding varieties and complementary inputs like fertilizer (or as in our case, the legume inoculant technology) have the potential to shift the production frontier upwards (Huang and Liu, 1994; Kumbhakar and Tsionas, 2009; Triebs and Kumbhakar, 2018). Also, farmers who receive extension services or technical training on the new technology may experience further shift in the production frontier upwards by reducing production inefficiencies (Mohammed and Abdulai, 2022a). The two shifts involve two potentially endogenous treatments in a single agricultural development intervention that incorporates dissemination of new production technologies and training of farmers. First, adoption of a new superior technology that affects both the production frontier function and the inefficiency function (Kumbhakar and Tsionas, 2009), and second, extension training that builds human capital with the potential to influence both the production frontier function and the inefficiency function (Huang and Liu, 1994; Triebs and Kumbhakar, 2018).

To represent both frontiers, let Y denote individual farmer i observed output under a given production technology and X be a vector of observed covariates. We express the farmer's observed output in a conventional stochastic frontier form (Kumbhakar and Lovell, 2000) as;

$\begin{array}{ll}Y=Y^{*}-u,u\ge 0& (1)\end{array}$

where Y^*, is the unobserved stochastic frontier that may be influenced directly by the new technology and indirectly by extension training, and u ≥ 0, is the unobserved production inefficiency assumed to be randomly distributed, which may also be influenced directly by extension training and indirectly by the new technology. The expression in Equation 1 indicates that Y^* and u are two distinct unobserved random components, which can be separately identified. In line with Chen et al. (2020), we stochastically express each unobserved function in terms of observed covariates⁴ in a system of equations as follows;

$\begin{array}{l}Y=\{\begin{array}{c}{Y}^{\ast }=h\left(X,{\beta }^h\right)+v\\ u=g\left(X,{\beta }^g\right)+\tilde{u}\end{array}and\\ E\left[Y^{\ast }|X\right]=h\left(X,{\beta }^h\right)andE\left[u|X\right]=g\left(X,{\beta }^g\right),E\left[v|X\right]\\ =0,E\left[\tilde{u}|X\right]=0& (2)\end{array}$

where X is a vector of covariates, h(.) is the frontier function with parameter vector β^h and g(.) is a non-negative inefficiency function with parameter vector β^g, while v and ũ are error terms assumed to be independently and identically distributed. E[.] is the expectation operator which identifies the conditional mean expectations of the equations in the system. To relate the effect of the production frontier and the inefficiency to observed farmer-specific potential outcome, given his observed characteristics and inputs, we express Equation 1 in terms of its conditional mean representation in Equation 2 as follows;

$\begin{array}{ll}E\left[Y|X\right]=h(X,{\beta }^h)-g(X,{\beta }^g)& (3)\end{array}$

By letting Y₁ to be the potential outcome of a farmer who adopts the technology (i.e., the inoculant technology) and Y₀ be the potential outcome, if the same farmer did not adopt, then, the average treatment effect on the treated (ATT) for adopters can be specified as;

$\begin{array}{ll}ATT=E(Y_1-Y_0|D=1)=E(Y_1|D=1)-E(Y_0|D=1)& (4)\end{array}$

where D is a binary adoption indicator, with D = 1 if the farmer adopts and D = 0, otherwise.

The identification strategy

In observational data situation like ours, evaluating the impact of the inoculant dissemination program on farmers' welfare and the shifts in the production technology and inefficiency functions may suffer serious identification problems, resulting in biased estimates. However, with the availability of good and valid instruments, it is possible to categorize the whole population into well identified mutually disjoint sub-population of adopters who are compliers of the instruments (Imbens and Angrist, 1994; Angrist et al., 1996).

In our setting, we use rural electrification as the most likely exogenous instrument that can identify various sub-population of inoculant adopters. Given that the rhizobia in the inoculant survive within a temperature limit of about 25°C, it requires a controlled temperature storage facility. Hence, it is expected that farmers who live in communities connected to the national grid of electricity supply may have easy access to the technology, compared to their counterparts who live in communities without electricity supply. If we let Z₁ represent an instrumental variable (IV) that takes a value of 1, if the farmer's village is connected to national electricity grid, and 0 otherwise, the propensity of a farmer adopting the technology can be specified in a latent variable adoption decision model (i.e., D^*) as follows:

$\begin{array}{l}{D}^{\ast }={\gamma }_{z_1}{Z}_1+{\gamma }_{x}X+U_D,withD=\{\begin{array}{cc}1,& if{D}^{\ast }\ge 0\\ 0,& otherwise\end{array}\text{ and}\\ D=1({\gamma }_{z_1}{Z}_1+X{\gamma }_x+U_D\ge 0)& (5)\end{array}$

where D is a discrete adoption decision indicator, with D = 1 if the farmer adopts the inoculant technology and 0 otherwise, X is a vector of covariates, γ is the parameter of interest and U is the error term.

Naturally, it is expected that the effect of extension service participation, which improves the managerial skills of the farmer, is mainly observed after the farmer adopts the technology on which the extension training is based on. That is, when the farmer uses or adopts the inoculant technology. As such, extension functions as a post-adoption mediator and can be modeled as a function of adoption. With a potentially endogenous binary mediator, such as the extension service participation in this case, the mediation effect can be identified with a continuous exogenous variable with known distribution and whose level differs with adoption status (Frölich and Huber, 2017; Chen et al., 2020). In this circumstance, we rely on farmer's distance to the nearest extension office as a possible exogenous continuous instrument. We expect that farmer's propensity to participate in extension service programs would increase as the distance decreases and then decrease as the distance increases. If we let Z₂ be a continuous instrumental variable (IV) whose distribution⁵ and level decreases as mediation takes the value of 1, and increase as mediation goes to 0, then, the propensity of a farmer to participate in the extension program and also adopt the technology can be expressed in a latent variable mediation model (i.e., M^*) as follows:

$\begin{array}{l}{M}^{\ast }={\alpha }_{d}D+{\alpha }_{z_2}{Z}_2+X{\alpha }_x+U_M,with\\ M_i=\{\begin{array}{cc}1,& \\ & if{M}^{\ast }\ge 0\\ 0,& otherwise\end{array} \text{and }\\ M=1({\alpha }_{d}D+{\alpha }_{z_2}{Z}_2+X{\alpha }_x+U_M\ge 0)& (6)\end{array}$

where M is a binary mediation indicator, with M = 1 if the farmer participates in the extension program and 0 otherwise, D is the adoption status indicator, X is a vector of covariates, α is the parameter of interest and U is the error term. Considering Equations 5 and 6, (which identify both the potentially endogenous adoption and extension decisions), the post-mediation potential outcome Y is a function of D and M, assuming that the post-mediation potential outcome can be represented as Y(D, M(D)), where M(D) is the mediator function, whose effect depends on the adoption status of the farmer.

Given a binary adoption indicator [i.e., D(1), D(0)] and a binary IV (Z₁ ∈ {0, 1}), four potential outcomes representing four mutually disjoint sub-population of farmers can be identified as follows (Imbens and Angrist, 1994; Angrist et al., 1996);

$\begin{array}{ll}(D\left(1\right),D\left(0\right))=\{\begin{array}{c}\left(1,1\right),alwaystakers,\\ \left(1,0\right),compliers\left(C\right),\\ \left(0,1\right),defiers,\\ \left(0,0\right),nevertakers.\end{array}& (7)\end{array}$

where C is an indicator of instrument compliers, who are induced to adopt the technology based on the instrument. It is assumed that a randomly chosen farmer in the complier sub-population, no matter the circumstance, does not change adoption status other than the assigned status by the instrument (Angrist et al., 1996). Due to this known property of the compliers, their potential impact better approximates that of causal estimates from a full compliance experimentation. Therefore, by conditioning on the observed covariates X and the complier status C of the farmers, the average treatment effect on the treated as expressed in Equation 4 can be identified (Chen et al., 2020) as follows:

$\begin{array}{l}CLATE=E\left[Y\left(1,M\left(1\right)\right)|X=x,C\right]\\ -E[Y(0,M\left(0\right))|X=x,C]& (8)\end{array}$

where CLATE is the conditional local average treatment effect. Also, because the levels of the continuous instrumental variable for identifying the mediation effect varies with adoptions status, it is possible to decompose the unconditional local average treatment effect into direct and indirect effects as in Chen et al. (2020):

$\begin{array}{ll}CDLATE=E\left[Y(1,M(1))|X=x,\text{C}\right]-E\left[Y(0,M(1))|X=x,\text{C}\right]& (9)\end{array}$

$\begin{array}{ll}CILATE=E\left[Y(0,M(1))|X=x,\text{C}\right]-E\left[Y(0,M(0))|X=x,\text{C}\right]& (10)\end{array}$

where CDLATE is the conditional direct local average treatment effect and the CILATE is the conditional indirect local average treatment effect. Conversely, the unconditional average treatment effect can also be derived from the conditional local average treatment effects, by conditioning on only the sub-population of farmers who are compliers as follows;

$\begin{array}{l}LATE=E\left[CLATE(X)|C\right]=E\left[Y\left(1,M\left(1\right)\right)|C\right]\\ -E[Y(0,M\left(0\right))|C]& (11)\end{array}$

$\begin{array}{ll}DLATE=E\left[Y(1,M(1))|\text{C}\right]-E\left[Y(0,M(1))|\text{C}\right]& (12)\end{array}$

$\begin{array}{ll}ILATE=E\left[Y(0,M(1))|\text{C}\right]-E\left[Y(0,M(0))|\text{C}\right]& (13)\end{array}$

where LATE is the local average treatment effect which captures the total effect, while DLATE and ILATE are direct and indirect local average treatment effects respectively, that capture the impact due to the adoption of a superior technology and mediation role of extension participation.

Empirical specification and estimation

A farmer's propensity to participate in extension services (i.e., the potential mediation model) may correlate with his inoculant adoption decision (i.e., the potential treatment model) either due to observed or unobserved factors. We assume that the error terms are independently and identically distributed and follow a bivariate normal distribution. In line with Chen et al. (2020), we specify the joint extension participation and inoculant adoption decisions as a bivariate probit model, with a bivariate normal distribution and CDF F_{UM, D}(., ., ρ_md) as follows:

$\begin{array}{l}P\left(M,D|Z_1,Z_2,X,\eta \right),\text{and}\\ \left[\begin{array}{c}{U}_M\\ U_D\end{array}\right]|(Z_1,Z_2,X)~N\left(\left[\begin{array}{c}{U}_M\\ U_D\end{array}\right],\left[\begin{array}{cc}1& {\rho }_{md}\\ {\rho }_{md}& 1\end{array}\right]\right)& (14)\end{array}$

where η ≡ (α_d, α_z2, α_x, γ_z1, γ_x, ρ_md) is a maximum likelihood estimator of a vector of parameters. In a first-stage estimation, a bivariate probit model is estimated to control for selection bias from both observables and unobservables. To unify the impact assessment and mediation analysis within the stochastic frontier analysis framework, we represent the frontier function of Aigner et al. (1977) and Meeusen and van den Broeck (1977) in the form of Chen et al. (2020), for d, d′ ∈ {0, 1}⁶, as follows:

$\begin{array}{l}Y\left(d,M\left(d^{\text{'}}\right)\right)=\stackrel{⌣}{h}\left(d,M\left(d^{\text{'}}\right),X,{\beta }_{dj}^h\right)\\ -\stackrel{⌣}{g}\left(d,M\left(d^{\text{'}}\right),X,{\beta }_{dj}^g\right)+U_Y(v\left(d,M\left(d^{\text{'}}\right)\right)\\ +\tilde{u}\left(d,M\left(d^{\text{'}}\right)\right))& (15)\end{array}$

where $\stackrel{⌣}{h}(d,M(d\prime ),X)$ and ğ(d, M(d′), X) are potential frontier and non-negative potential inefficiency functions, respectively; X is a vector of covariates; β is a parameter of interest; while v(d, M(d′)) and ũ(d, M(d′)) are potential random error terms. The binary adoption indicator is D = d, d′ ∈ {0, 1} and j = M(d′) is the mediator function whose distribution varies with adoption status. The conditional mean expectation of Equation 15 combines the potential outcome and mediator models as;

$\begin{array}{l}E[Y(d,M\left(d^{\text{'}}\right))|X,C]=h_{d^{\text{'}}}\left(X,{\alpha }_m,{\beta }_{dj}^h\right)-g_{d^{\text{'}}}\left(X,{\alpha }_m,{\beta }_{dj}^g\right)\\ \text{and}\\ E[v(d,M\left(d^{\text{'}}\right))|X,C]=0,E\left[\tilde{u}(d,M\left(d^{\text{'}}\right))|X,C\right]\\ =0,andE[M\left(d^{\text{'}}\right)|X,C]=m_{d^{\text{'}}}(X,{\alpha }_m)& (16)\end{array}$

where $md\prime (.)$ is a non-negative function of the potential mediator model in {0, 1} with a parameter vector α_m. To reflect variations in the distribution of the non-negative potential mediator model, as the adoption indicator takes the value within {0, 1} in the estimated parameters of interest, we rewrite Equation 16 as follows:

$\begin{array}{l}E[Y(d,M\left(d^{\text{'}}\right))|X,C]=h_{d^{\text{'}}}\left(X,{\alpha }_m,{\beta }_{d1}^h,{\beta }_{d0}^h\right)\\ -g_{d^{\text{'}}}\left(X,{\alpha }_m,{\beta }_{d1}^g,{\beta }_{d0}^g\right)& (17)\end{array}$

We estimate the parameters in Equation 17 using a two-stage weighted non-linear least squares (WNLS) method⁷. Let the individual farmer's observed outcome (Y), extension service participation (M), inoculant adoption (D) and covariates (X) be a weighted random vector W≡(Y, M, D, X) with sample size N, and ${\beta }_d\equiv ({\beta }_{d1}^h,{\beta }_{d0}^h,{\beta }_{d1}^g,{\beta }_{d0}^g)$ be an arbitrary vector space of a weighted non-linear least squares estimator (WNLSE) observed as $b_d\equiv (b_{d1}^h,b_{d0}^h,b_{d1}^g,b_{d0}^g)$. The parameter space can be expressed as the minimizer of the weighted mean square error (MSE) of the observed outcomes of interest (Frölich and Huber, 2017; Chen et al., 2020), which we expressed as follows;

$\begin{array}{l}{\beta }_d\equiv \mathrm{arg }{\min }_{b_{d\in \beta }}{}_d{{\displaystyle \sum }}_{d^{\text{'}}}=0,1\\ E[w(d,d^{\text{'}},{\alpha }_w){(Y-h_{d^{\text{'}}}\left(X,{\alpha }_m,b_{d1}^h,b_{d0}^h\right)+g_{d^{\text{'}}}(X,{\alpha }_m,b_{d1}^g,b_{d0}^g))}^2]& (18)\end{array}$

where $w(d,d\prime ,{\alpha }_w)\equiv w$(1,1, α_w), w(1,0, α_w), w(0,1, α_w), and w(0,0, α_w) is a weighted function of (D, Z₁, Z₂, X), with a parameter vector α_w obtained from the first-stage estimation. The weighting function $w(d,d\prime ,{\alpha }_w)$ accounts for heterogeneities within the production units that may be due to observed and unobserved firm-specific factors influencing production (or outcomes, which in our case is yield and farm net returns). The WNLS is estimated using the generalized method of moment (GMM) approach. The generalized moment-based approach overcomes the restrictive imposition of distributional functional form assumptions on traditional parametric family of production functions (e.g., Cobb-Douglas, Translog, and others) (Giannakas et al., 2003; Vidoli and Ferrara, 2015; Ferrara and Vidoli, 2017; Ferrara, 2020).

Study area, data and descriptive statistics

The study area is Northern Ghana. Prior to this study, the Northern Ghana constituted three regions namely; Northern, Upper East and Upper West regions. However, following the creation of new regions by the Government of Ghana in 2019, the Northern Ghana currently constitutes five regions, which include Northern, North-East, Savanna, Upper East and Upper West regions. Specifically, the study area was in the former Northern region. The northern region comprises twenty-six (26) districts, of which the study sampled eight (8) districts, in order to conduct a survey for this study (see Figure 1 for Map of study area northern region and the sampled districts). The region covers an area of about 70,384 square kilometers and is considered the largest region in Ghana in terms of land mass. The Northern region shares boundaries with the Upper East and the Upper West regions to the north, the Brong-Ahafo and the Volta regions to the south, Togo to the east, and Cote d'Ivoire to the west. The Black and White Volta Rivers and their tributaries such as the Nasia and Daka rivers drain the region [Ghana Statistical Service (GSS), 2013].

FIGURE 1

Figure 1. The map of study area.

The climate of the region is relatively dry, with a single rainy season that begins in May and ends in October. The amount of rainfall recorded annually varies between 750 millimeters and 1,050 millimeters. The dry season starts in November and ends in March/April with maximum temperatures occurring toward the end of the dry season (March–April) and minimum temperatures in December and January. The harmattan winds, which occur from December to early February, have considerable effect on temperatures in the region, making them vary between 14°C at night and 40°C during the day. Humidity is very low, aggravating the effect of the daytime heat. The main vegetation is grassland, interspersed with guinea savannah woodland, characterized by drought-resistant trees [Ghana Statistical Service (GSS), 2013].

The main occupation of the people in the region is agriculture (70.6%), who live in predominantly rural areas. Degradable soil conditions present major challenge to food productivity and farm livelihoods in the area. To maintain the productive capacity of soils in the region, scientific research organizations such as the International Institute of Tropical Agriculture (IITA) and the Council for Scientific and Industrial Research-Savannah Agricultural Research Institute (CSIR-SARI) and their partner organizations introduced the Rhizobia inoculant technology to smallholder grain legume farmers. The inoculant technology is an organic input containing isolates of an elite strain of bacterial (Bradyrhizobium spp) and an organic carrier material (Lupwayi et al., 2000). The inoculant technology is seen as a cost-effective alternative to rehabilitating poor soils by enhancing the build-up of biological nitrogen fixation (BNF) organisms in the soil (Giller, 2001). The inoculant technology is also expected to sustainably increase smallholder farmers' productivity, while minimizing cost of production, compared to inorganic inputs such as mineral fertilizers, which is sometimes priced out of reach for most smallholder farmers.

The inoculant dissemination program was centered in the three regions (Northern, Upper East and Upper West) of northern Ghana, due to their soybean production potential in the country as well as the high incidence of extreme poverty situation in these parts of the country. The northern region is second poorest (30.7%) region in the country in terms of extreme poverty incidence followed by the Upper East region (27.7%), with the Upper West region (45.2%) ranking first in the country [Ghana Statistical Service (GSS), 2018, 2019]. With soybean being a cash crop, it is expected that increase in productivity will lead to increase in the household income, which can contribute to poverty reduction for the poor households who depend on agriculture for income as well as food and nutrition security.

The present study uses farm level data obtained from the survey conducted in the northern region of Ghana from June to August 2018. The sample was drawn using a multi-stage sampling technique. Based on the proportion of beneficiary communities (78%) in the inoculant dissemination program and intensity of soybean production in Ghana, northern region was purposively selected. Cluster sampling technique was used to zone the region into two clusters, consisting of eastern corridor zone (ECZ) and western corridor zone (WCZ). Based on dissemination program participation status of districts and intensity of soybean production at the district level within the clusters, eight (8) districts, comprising four (4) from each cluster were purposively sampled. From the ECZ: Yendi, Saboba, Chereponi and Karaga districts were selected, while in the WCZ: East Mamprusi, East Gonja, Savelugu and Kumbungu districts were selected. In consultation with the field officers and agriculture extension agents (AEAs) in the selected districts, 5–7 communities were proportionally sampled, based on the extension channel received, dissemination program participation, and farmer population. One farmer-based organization (FBO) was randomly selected from a list of FBOs that were exposed to the inoculant technology and another randomly selected from a list of unexposed FBOs for each community. Using a lottery approach, we randomly drew five farmers from each FBO. After a preliminary interview session with each of the selected farmers, using a computer assisted personal interview (CAPI), a list of the farmers' information network members (INMs) was compiled. The CAPI random number generator then used farmers' unique identification numbers to randomly sample three network members from each farmer's INMs for interview. A total of 600 farm households, consisting of 325 inoculant exposed farmers and 275 unexposed farmers, were interviewed in a face-to-face session. The data collected include inoculant adoption status, dissemination program participation status, household demographic characteristics, location characteristics, input used, crop yield and farm net returns, plot level precipitation and soil quality.

Definitions and summary statistics of the variables used in the empirical analysis are presented in Table 1. It shows that 54% of our sampled farmers participated in the inoculant extension program. Table 1 also shows that 51% of farmers adopted the inoculant with an average yield of 830 kg/ha soybeans and net returns of 840 GHC/ha.

TABLE 1

Table 1. Definition and summary statistics.

As shown in Table 1, average land cultivated to soybeans is 5 ha, using an average total labor supply of 8 persons hours per day/ha and 4 kg/ha of agrochemicals (e.g., weedicides) in the process. It further shows that 57% of the farmers are located in the western corridor zone. Table 1 again, shows that 51% of the farmers live in communities that are connected to the national grid of electricity supply, and located at an average distance of 19 km to the nearest extension office and 2 km to the nearest market. In terms of inoculant knowledge test score, Table 1 reveals that farmers obtained an average of 56% inoculant knowledge score from participating in the dissemination program. A comparison of mean differences show some significant differences in observed characteristics between inoculant adopters and non-adopters (see Table A1 in Supplementary material).

On the socioeconomic characteristics of farmers, majority (71%) of the farmers in our sample are males with an average age of 42 years and about 23% attaining at least 1 year of schooling, which seems to be quite low.

Results and discussions

Empirical results

First, we discuss the results of the first-stage bivariate probit model estimates, as the identification of the outcome model hinges on the first-stage estimates. However, we present the estimates from the first-stage in the Table A2 in Supplementary material due to space limitation.⁸ Next, we present and discuss estimates of the weighted non-linear least-squares, estimated via the generalized method of moments procedure.

First-stage bivariate probit estimates

Table A2 in Supplementary material presents estimates from the bivariate probit model. The model is used to account for selection bias and for identification of the instrumental variable (IV) regression. Table A2 in Supplementary material shows that, both the extension participation model (i.e., the mediation model) and the adoption model are highly correlated due to unobserved heterogeneities. The p-value for the null hypothesis shows that ρ_md is significantly different from zero (at 1% level), indicating that farmers' extension participation and inoculant adoption decisions may be correlated due to unobserved heterogeneities. However, the sign for ρ_md is negative, suggesting that farmers are likely to substitute adoption of new technologies (such as the inoculant) with knowledge acquisition from extension participation (Huth and Allee, 2002; Mohammed and Abdulai, 2022b). This observation is intuitive, because both extension services and adoption of improved technologies tend to enhance farmers' production efficiency (Abdulai and Huffman, 2000; Kumbhakar and Tsionas, 2009; Triebs and Kumbhakar, 2018). The statistical significance of ρ_md also suggests that farmers may have self-selected into the extension program or adoption of the inoculant technology.

Table A2 in Supplementary material also shows that, the two instrumental variables are both statistically different from zero (significant at 1% level). In particular, distance to the nearest extension office (Z₂), which is used to identify extension program participation, is negative and significant at 1% level, suggesting that a decrease in distance to the nearest extension office by 4.3 km, increases the probability of farmers' extension participation. More importantly, farmer's community connection to the national electricity grid (Z₁), which we used to identify the inoculant adoption model, is positive and highly significant at the 1% level. This implies that a one percent increase in rural electrification of communities, increases the likelihood of inoculant adoption by 319%. Intuitively, this makes sense, because the rhizobia used in formulating the inoculant survive in a particular temperature range (25°C), which stands to reason that, communities with access to constant electricity supply could well operate cold storage facilities. As a result, farmers in such communities may have easy access to the inoculant, hence, are more likely to adopt, compared to farmers living in communities without constant electricity supply (Dzanku et al., 2020). Our finding of positive effect of community electricity connectivity on farm households' production activities is consistent with the existing literature on rural electrification impact on households' economic activities (see Cabraal et al., 2005; Independent Evaluation Group-World Bank, 2008; Thomas et al., 2020).

The validity of the instrument for identification of local average treatment effect in our IV regression estimation strategy requires that the instrument be a monotonic increasing function of the level of the instrumental variable (Z₁), and the level of the treatment (D) (see Chen et al., 2020). As shown in Table A2 in Supplementary material, the coefficients of both the instrument (Z₁) in the treatment model and the treatment indicator D in the mediation model have positive signs and are highly significant (at 1% conventional level), suggesting that our instrument is valid and strong. This also implies that inoculant adoption increases with increasing extension participation and community electricity connectivity.

Determinants of technology and inefficiency frontiers

Tables 2, 3 present factors that affect the production technology and inefficiency frontiers with respect to yield (lnKg/ha), for the case scenario that farmers adopt the inoculant technology with mediation (i.e., Adopters^M) and the counterfactual scenario of non-adoption with non-mediation (i.e., Non-adopters^M), respectively (see Tables 4, 5, for that of farm net returns). The factors explain the observed yield and net returns variabilities in each scenario among farmers with different adoption and mediation conditions in our sample. For the sake of brevity, we focus the discussion on the yield, which can be extended to that of the net returns.

TABLE 2

Table 2. Adoption with mediation—(weighted nonlinear least-squares)—yield (lnKg/Ha).

TABLE 3

Table 3. Adoption without mediation—(weighted nonlinear least-squares)—yield (lnKg/Ha).

TABLE 4

Table 4. Adoption with mediation—(weighted nonlinear least-squares)—farm net returns (lnGHC/Ha).

TABLE 5

Table 5. Adoption without mediation—(weighted nonlinear least-squares)—farm net returns (lnGHC/Ha).

The model estimated is a weighted non-linear least-squares regression using generalized method of moment. In particular, it does not represent any specific conventional production function model, and as such does not depend on any functional form distribution assumptions. Though we estimate a non-linear regression model with some of the covariates being logged, the parameter estimates can be interpreted as in a linear regression estimation (Chen et al., 2020). Our approach of estimating the stochastic production frontier is akin to that of the generalized additive models (GAMs) approach, that fits a response variable on a sum of smooth functions of explanatory variables in a regression context with normal distribution (Ferrara and Vidoli, 2017; Ferrara, 2020). This specification is preferred to the conventional functional form specifications, due to its flexibility in relaxing the need to impose strict linearity and monotonicity condition on the underlying stochastic frontier function between the explanatory variables and the outcomes of interest (Ferrara, 2020).

Each table contains two columns corresponding to two different adoption scenarios. In Table 2, column one contains estimates for the case scenario that a farmer participated in the extension program and also adopted the inoculant technology (i.e., Adopters^M), henceforth, mediated-adopters (MA), while column two represents the counterfactual case scenario, if the same farmer had neither participated in the extension program nor adopted the inoculant technology, referred to as non-mediated-non-adopters (NM-NA). In Table 3, column one represents the case scenario that a farmer adopted the inoculant technology without participating in the extension program (i.e., Adopters^N), hereafter, non-mediated-adopters (NM-A), whereas column two represents the counterfactual case, if the same farmer had participated in the extension program but did not adopt the inoculant technology (i.e., Non-adopters^M), hereafter refer to as mediated-non-adopters (M-NA).

The coefficient of the constant terms in Table 2 that captures the effect of unobserved farmer-specific characteristics are positive and statistically significant, suggesting that unobserved characteristics (such as farmers' inert abilities) may have contributed positively in enhancing farmers' ability to push the production frontier upward, irrespective of the superiority of the production technology employed or extension participation status. Similar positive and statistically significant trend is observed in Tables 3–5.

The results also show that observed farmer-specific characteristics such as education, gender and age have significant impact in shifting the production frontier of farmers. In particular, coefficient of education is positive for all farmers, but statistically significant at 10% level for only MA farmers, suggesting that an increase in education pushes the production frontier of this category of farmers upwards. Also in Table 2, gender (i.e., being a male farmer) has positive coefficient across all farmers, but statistically significant at 1% level for only MA farmers, suggesting that being a male farmer within our study area generally improve ones' productivity. This observation may be due to the fact that male farmers in most parts of developing countries have better access to family labor, extension service, quality land and other resources than female farmers, a finding that is in line with, Gebre et al. (2019) in their study on gender differences in agricultural productivity among maize farmers in Ethiopia. However, in Table 3, the coefficient of gender is negative for all farmers, but significant at 1% level for only NM-A farmers, suggesting that for female farmers with less access to extension services and quality land, adoption of the inoculant will greatly improve their productivity. The reverse is observed for the net returns in Tables 4, 5, suggesting that in terms of net returns, both male and female farmers are able to push their net returns frontier upwards.

Table 2 also shows that among the conventional inputs (land, labor, agrochemicals and improved seed variety), land has the highest effect on the production frontier. The coefficient of land is positive and statistically significant at 1% level across all farmers, suggesting that farm size has positive effect in pushing the production frontier of both MA and NM-NA farmers upward. Similar positive effect is observed in Tables 3–5.

The coefficient of improved seed variety in Table 2 is positive and statistically significant for all farmers, suggesting that availability of improved crop varieties have positive effect on pushing the production frontier upwards for all category of farmers. However, low quantity of agrochemicals usage, in particular, during weed control may have significant (at 1% level) negative effect in shifting the production frontier of farmers downwards, which could subsequently occasioned significant revenue losses as seen in Tables 4, 5.

In addition to the conventional and farmer-specific characteristics, we also controlled for environmental and geographical factors using zonal dummies, plot level soil quality and precipitation. The results in Table 2 reveal that the zonal dummy which indicates whether the farmer is located in the western corridor zone (WCZ) or eastern corridor zone (base category) is positive and statistically significant at 1% for all farmers, indicating that inoculant adoption and extension participation have positive effects in shifting the production frontier of farmers located in the western corridor zone upward, compared to farmers in the eastern corridor zone. Tables 2, 3 also reveal that soil quality at the farm level has positive effect (statistically significant at 1 and 10% levels, respectively) in shifting the production frontiers upwards for MA and NM-A farmers. However, the positive effect may erode due to insufficient precipitation at the plot level, leading to significant (at 5% level) shift in the production frontier downwards for NM-A farmers and subsequent loss of revenue as shown in Tables 4, 5.

In the last two rows of Tables 2, 3, we present estimates of post-mediation factor(s) that influence farmers' level of (in)efficiency in the usage of the inoculant technology that could have great impact on yields obtained from adoption. We conducted an inoculant technical knowledge quiz and used the test scores to proxy the post-mediation factors in the inefficiency frontier function.

In Tables 2, 3, the coefficient of a constant only inefficiency frontier model [represented as ${\beta }_{(0)}^g$] is positive for all farmers, but statistically significant at 1% level for NM-NA and NM-A farmers only, suggesting that adopting the inoculant technology without sufficient technical knowledge on its usage makes farmers highly inefficient and less beneficial.

On the other hand, the coefficient of the inefficiency model, with inoculant knowledge test score [represented as ${\beta }_{(ts)}^g$] is negative and statistically significant at 1% level for all category of farmers, except for NM-NA farmers, indicating that adopting the technology with sufficient technical knowledge increases farmers' production efficiency (Dzanku et al., 2020). Similar results pattern is obtained for net returns in Tables 4, 5.

Impact of mediation and inoculant adoption on productivity, efficiency and welfare

In this section, we report estimates of the treatment effects derived in Equations 11–13. The results for yields and net returns are presented in Tables 6, 7, respectively. Focusing on Table 6, the first column contains total impact of program participation on the farm household's welfare, decomposed into welfare contribution coming directly from adoption of new technology and indirectly from participation in the extension program. The second column contains total impact of inoculant adoption on the production frontier of inoculant adopters' relative to non-adopters, decomposed into the portion due directly to technological change which shifts the observed production frontier closer to the ideal production frontier (i.e., the potential yield frontier), and indirectly due to improvement in adopters' technical knowledge in shifting the production frontier. The estimates in the third column represent the total impact on the production efficiency of inoculant adopters relative to non-adopters, decomposed into efficiency gained due to technological change and indirectly due to improvement on inoculant adopters' technical knowledge.

TABLE 6

Table 6. Productivity, efficiency and welfare estimates on soybean yield—(lnKg/ha).

TABLE 7

Table 7. Productivity, efficiency and welfare estimates on net returns—(lnGHC/ha).

The results in column one of Table 6 show that, the total treatment effect [measured as the local average treatment effect (LATE)] on yields is positive and statistically significant at the 1% level. Specifically, the impact on yield is 34 kg/ha (and 47 GHC/ha for net returns), suggesting that farmers who participate in the extension program and adopt the inoculant technology increased their yields (and net returns), compared to if they had neither participated in the extension program nor adopted the inoculant technology. A decomposition of the welfare benefits due to mediation indicate that 36% (i.e., DLATE = 12 kg/ha) of the welfare benefits, in terms of marginal gains in yield, can be attributed to the farm household's adoption of improved technology (i.e., the inoculant), while 64% (ILATE = 22 kg/ha) is due to the farm household's participation in inoculant extension dissemination program.

The total treatment effect on the production frontier in column two of Table 6 shows that, the technological change led to a reduction in the yield gap between the production frontier of adopters and that of the best production frontier by 135 kg/ha. In order words, farmers who participated in the extension program and adopted the inoculant technology increased their yields by 135 kg/ha, a finding that is similar to that of Ulzen et al. (2018) who found 200 kg/ha increased in soybean yields with inoculant application in northern Ghana. Further decomposition of the impact on the shift of the production frontier shows that 34% (i.e., DLATE_h = 46 kg/ha) is due to adoption of the improved technology, while 66% (ILATE_h = 89 kg/ha) of the shift is due to enhancement in farmers' technical knowledge on the improved technology usage. Intuitively, the total effect is an interaction of adoption of the improved technology and technical knowledge in the management of the new technology that leads to realization of the full potential of the technology (Takahashi et al., 2020).

In column three of Table 6, the total effect on the technical efficiency shows that improvement in technical efficiency of farmers led to an increase in yield of about 169 kg/ha. This indicates that farmers who participate in the extension program and adopt the inoculant technology are able to cut down their inefficiency up to 169 kg/ha (i.e., yield that would have been lost due to inefficiency) by adopting improved technology with technical knowledge. The marginal gain due to technical efficiency appears to slightly outweigh that of yield at the production frontier (i.e., 135 kg/ha). This finding is consistent with the argument by Huang and Liu (1994) that farmers who acquire technical knowledge on a new technology prior to adoption of the technology tend to benefit more. A decomposition of the total effect of technical efficiency shows that 34% (i.e., DLATE_g = 58 kg/ha) of the improvement comes from the farmer's adoption of improved technology, while 66% (ILATE_g = 110 kg/ha) comes from technical knowledge on the technology, implying that the synergic effect of better technology and technical knowledge is required for farmers to be fully technically efficient. However, greater proportion of the improvement in productivity is achieved through the extension participation sub-component (i.e., ILATE), compared to the improved technology adoption sub-component (DLATE), implying that providing farmers with superior technology without knowledge on its usage could result in underexploiting the full potential of the technology. We find similar patterns of impact on the production technology frontier and the technical efficiency frontier in the net returns model presented in Table 7.

Production and technology gap profiles

In Figures 2, 3, we present the conditional (i.e., condition on being a complier) mean yield estimates in deciles across various sub-populations of adopters at the production technology and technical inefficiency frontiers, respectively (see Figures A2, A3 in the Supplementary material for net returns). This is important in characterizing the production and technology gap between the various sub-populations of adopters and non-adopters, since adoption of an improved technology may induce inequalities in the production structures of farmers, due to heterogeneity in production technology and technical efficiency of farmers at the respective frontiers. Recent literature in the stochastic frontier analysis employs quantile regression to profile the production and technology gap among firms for structural analysis (e.g., Huang et al., 2017; Lai et al., 2020). However, the quantile regression approach is somehow restrictive as it allows for characterization of firms only at the quantile means and not at the individual firm level means, as in the case of standard regression (Fortin et al., 2011), the approach employed in this paper.

FIGURE 2

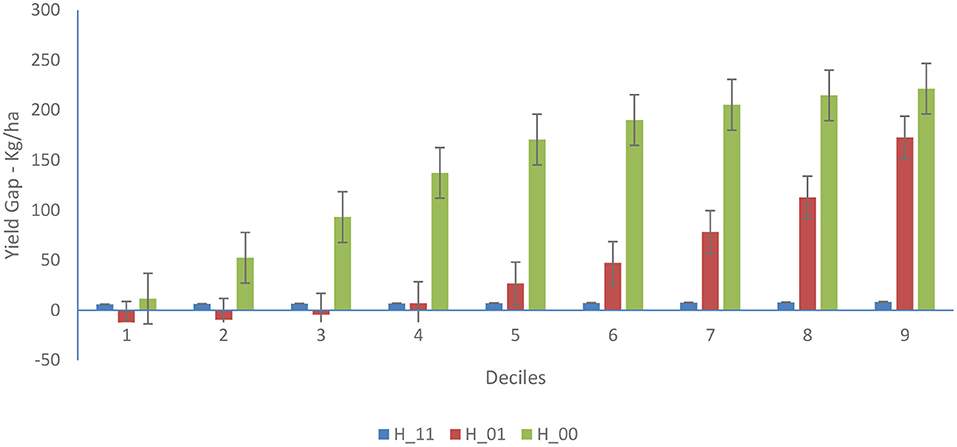
Figure 2. Yield gap profile at the production technology frontier (Kg/Ha). Where H-11, H-00 and H-01 indicates mediated-adopters, non-mediated-non-adopters and mediated-non-adopters, respectively at the production technology frontier function of yield. The figure illustrates the yield gap profile in deciles of farmers operating at different production technology frontiers, compared to farmers at the best production frontier operating at zero technological inefficiency.

FIGURE 3

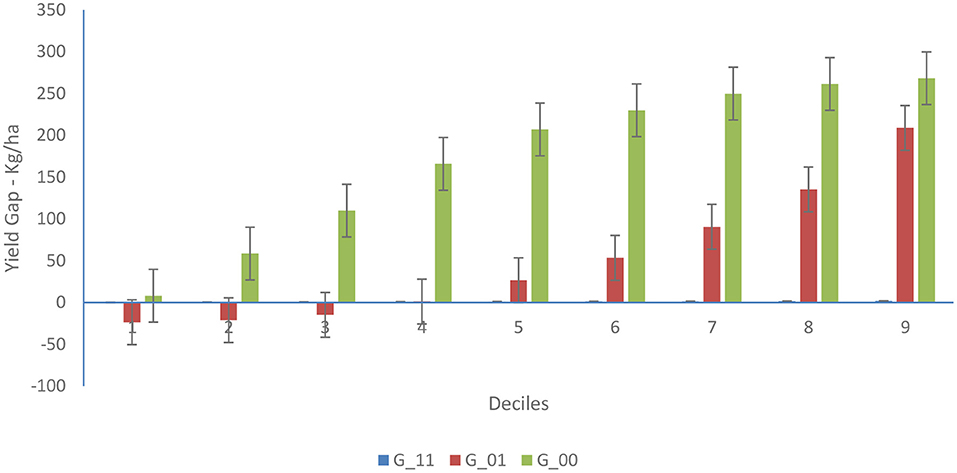
Figure 3. Yield gap profile at the inefficiency frontier (Kg/Ha). Where G-11, G-00 and G-01 indicates mediated-adopters, non-mediated-non-adopters and mediated-non-adopters, respectively at the technical inefficiency function of yield. The figure illustrates the yield gap profile in deciles of farmers operating at different levels of technical inefficiency, compared to farmers operating at zero technical inefficiency.

Figure 2 shows that, the yield distance of farmers who participate in the extension program and adopt the inoculant technology [i.e., the MA farmers (H-11)] at every decile is closer to zero, compared to farmers who neither participate in the extension program nor adopt the technology [i.e., the NM-NA farmers (H-00)]. Similarly, the MA farmers' yield gap is also narrower at the upper deciles (i.e., >4th decile), compared to farmers who participate in the extension program, but did not adopt the inoculant [i.e., the M-NA farmers (H-01)]. This implies that farmers who participated in the extension program before adopting the inoculant technology are closer to farmers producing at the best production frontier relative to other category of farmers. A similar pattern of distribution in the yield gap is observed in Figure 3, the conditional mean plot of the yield at the technical efficiency frontier. Figure 3 shows that, the average yield distance of MA farmers (G-11) at every decile is almost on the zero line, as compared to that of NM-NA (G-00) and M-NA (G-01) farmers respectively, indicating that farmers who participate in the extension dissemination program and adopt the inoculant are technically more efficient than those who neither adopt nor participate in the dissemination program.

However, a comparison of the yield distance at both the production frontier and the technical efficiency frontier between farmers who participated in the extension dissemination program but did not adopt the inoculant [i.e., the M-NA farmers—(H-01 and G-01)] is also lower, when compared to that of NM-NA farmers (i.e., H-00 and G-00), suggesting that extension participation even without adoption of a new technology may still be effective in improving farmers' productivity, compared to zero extension provision. We find similar production and technical efficiency profile patterns in the net returns estimates presented in Figures A2, A3 in Supplementary material.

Figures 4, 5 show the full conditional mean yield gap distributions for MA farmers (H-11) in Figure 4A, compared to NM-NA farmers (H-00) in Figure 4B and also that of M-NA (H-01) farmers in Figure 5A, compared to NM-NA (H-00) farmers in Figure 5B, respectively. The mean yield gap distribution at the production technology frontier of MA farmers is much lower (within 10 kg/ha), compared to that of the distributions of NM-NA and M-NA farmers. This observation implies that greater percentage of the yield variability among the farmers may be attributed to technology heterogeneity, which significantly minimizes the yield distance between the farmers' production frontier and that of farmers at the best production frontier. Similar pattern of distribution is observed for the net returns in Figures A4, A5 in the Supplementary material.

FIGURE 4

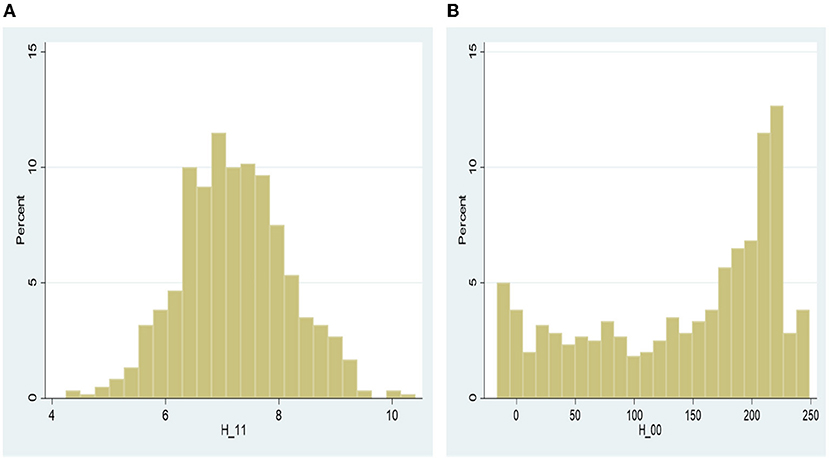
Figure 4. Comparison of yield (Kg/Ha) distributions at the technology frontier—direct effect. (A) Mediated-adopters, (B) non-mediated-non-adopters.

FIGURE 5

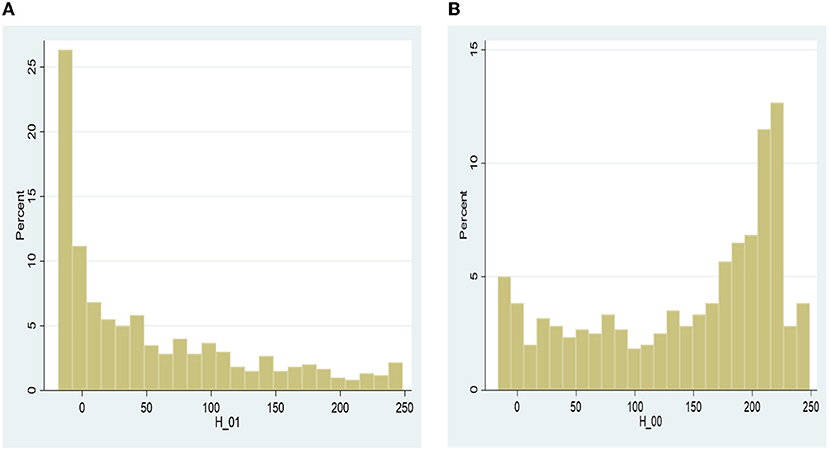
Figure 5. Comparison of yield (Kg/Ha) distributions at the technology frontier—indirect effect. (A) Mediated-non-adopters, (B) non-mediated-non-adopters.

Similarly, the mean yield gap distribution at the technical efficiency frontier in Figures 6, 7 show that the distribution for MA farmers (i.e., G-11) is densely skewed to the left (i.e., toward zero—within 2 kg/ha), compared to that of NM-NA (i.e., G-00) and M-NA (G-01) farmers, respectively. This results indicates that conditional on participating in the extension dissemination program and adopting the inoculant technology, all else being equal, greater percentage of yield variability at the frontiers may be due to random noise rather than technical inefficiency. We observed similar distribution patterns for the net returns in Figures A6, A7 in the Supplementary material.

FIGURE 6

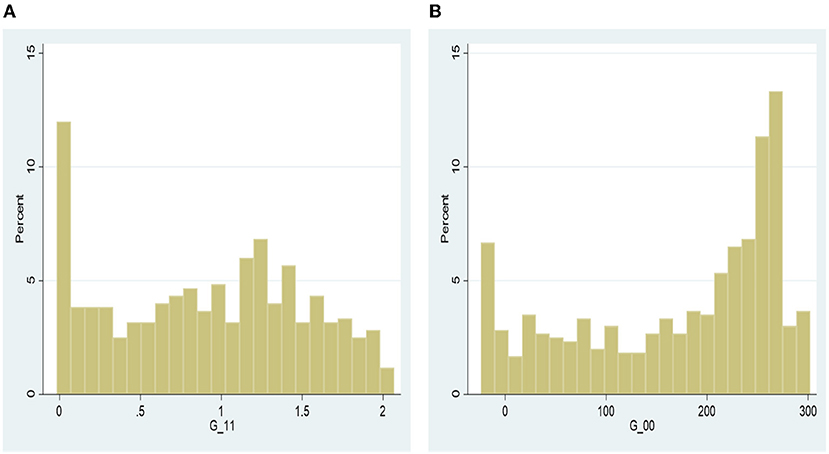
Figure 6. Comparison of yield (Kg/Ha) distributions at the inefficiency frontier—direct effect. (A) Mediated-adopters, (B) no-mediated-non-adopters.

FIGURE 7

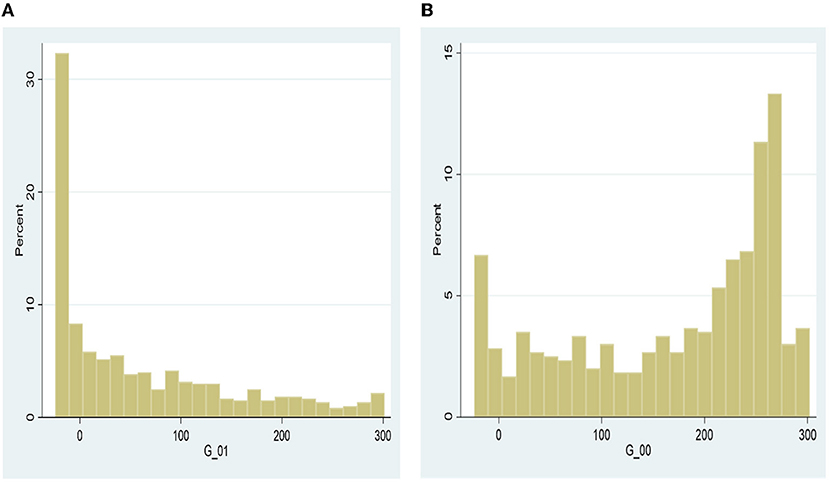
Figure 7. Comparison of yield (Kg/Ha) distributions at the inefficiency frontier—indirect effect. (A) mediated-non-adopters, (B) no-mediated-non-adopters.

Policy implications and conclusions

Our findings revealed that investing in either development of improved agricultural technologies such as the inoculant or intensifying extension delivery programs can to lead to increased productivity, as well as efficiency and welfare gains. Specifically, the study found that the contribution of adoption of improved agricultural technology alone (i.e., inoculant adoption) can lead to direct improvement in farm productivity, or indirectly through improved farmer efficiency led productivity gains, resulting in overall household welfare gains.

The study also made similar findings on extension delivery program participation alone, whose impact however, outweighs that of improved technology adoption alone. Our findings further indicate that making improved agricultural technologies available to farmers without complimentary extension knowledge supply could result in under exploiting the full potential of the technology. As the synergic effects of the two appears to be far greater than their individual effects.

The findings also show that investment in research and development to produce yield enhancing agricultural technologies suitable for poor and degraded soil conditions for farmers in developing countries, such as Ghana, can contribute immensely to poverty and food insecurity reduction. The development of new agricultural technologies must be pursued with vigorous provision of extension services to farmers, given that extension agents provide farmers with necessary knowledge needed to exploit the full potential of the technologies.

Our findings also reveal the significance of rural electrification in enhancing the diffusion and adoption of new agricultural technologies. Specifically, new agricultural technologies that need cold storage such as the rhizobia inoculant technology could go a long way to increase farm incomes and reduce rural poverty. This will also facilitate the deployment of new communication channels, such as the information and communication technologies (ICT) channels that rely on electricity for effective functioning, for extension delivery. As argued in this study, investment in rural electrification will also drive the development and expansion in rural enterprises such as sales of agro-inputs and perishable agro-based products, which must be stored under specific storage conditions.

Finally, our findings reveal that a policy intervention that subsidizes the inoculant technology to female farmers, who often have less access to extension services and quality land, will greatly improve their productivity.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation. The codes can be found under the Supplementary material at the publisher's web site https://doi.org/10.1080/07350015.2018.1497504.

Author contributions

The study's conception and design was done by SM and AA. Material preparation, data collection, analysis, and the first draft of the manuscript was written by SM. Edited and reviewed by AA. Both authors contributed to the article and approved the submitted version.

Funding

This research benefited from the funding support of the German Akademischer Austauschdienst (DAAD) as part of the Government of Ghana and German Government Doctoral Training Programme. Funding ID No. (57344816).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsufs.2022.1025225/full#supplementary-material

Footnotes

1. ^The extension channels employ are video documentaries, radio listening clubs, on-farm and off-farm trials, field days, brochures, use of community volunteers.

2. ^The mediation analysis is also known as the Baron and Kenny (1986) models in the applied statistics literature.

3. ^Caveat: please note that the approach employed in this paper is not a conventional production function, rather, a combination of mediation and treatment effect analysis, and therefore relaxes the stringent assumptions underpinning conventional production functions approach.

4. ^The frontier h(.) and the inefficiency g(.) functions allow for same or different covariates in both functions, however, for notational convenience, we use a general X.

5. ^See Figure A1 in the Supplementary material for the plot of the distribution of the continuous IV Z₂, showing both properties of increasing and decreasing propensities, as a necessary condition for identification.

6. ^The observed binary adoption decision indicator d varies as d′, taking the value of 1, if a farmer adopts the inoculant technology and 0, otherwise.

7. ^The two-stages are: in the first-stage, the adoption and the mediation [i.e., d and M(d′)] decisions are jointly estimated via a recursive binary probit model to obtain the propensities, conditional on the instrument compliance status, for a farmer to receive adoption and mediation. In the second-stage, the predicted propensities are used to construct the weights use to estimate the potential outcomes via a WNLSE.

8. ^Although the covariates in the bivariate probit model can be considered as determinants of inoculant adoption and extension participation, we focus on its identification properties, because the primary interest in this study is for proper model identification, and not to model determinants of participation and adoption decisions.

References

Abdulai, A., and Huffman, W. E. (2000). Structural adjustment and efficiency of rice farmers in Northern Ghana. Econ. Dev. Cult. Change 48, 503–21. doi: 10.1086/452608

CrossRef Full Text | Google Scholar

Abdulai, A.-N., and Abdulai, A. (2016). Examining the impact of conservation agriculture on environmental efficiency among maize farmers in Zambia. Environ. Dev. Econ. 22, 177–201. doi: 10.1017/S1355770X16000309

CrossRef Full Text | Google Scholar

Abdul-Rahaman, A., and Abdulai, A. (2018). Do farmer groups impact on farm yield and efficiency of smallholder farmers? Evidence from rice farmers in Northern Ghana. Food Policy 81, 95–105. doi: 10.1016/j.foodpol.2018.10.007

CrossRef Full Text | Google Scholar

Aigner, D., Lovell, C. A. K., and Schmidt, P. (1977). Formulation and estimation of stochastic frontier production function models. J. Econ. 6, 21–37. doi: 10.1016/0304-4076(77)90052-5

CrossRef Full Text | Google Scholar

Angrist, J. D., Imbens, G. W., and Rubin, D. B. (1996). Identification of causal effects using instrumental variables. J. Am. Stat. Assoc. 91, 444–455. doi: 10.1080/01621459.1996.10476902

PubMed Abstract | CrossRef Full Text | Google Scholar

Baron, R. M., and Kenny, D. A. (1986). The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. J. Pers. Soc. Psychol. 51, 1173–1182. doi: 10.1037/0022-3514.51.6.1173

PubMed Abstract | CrossRef Full Text | Google Scholar

Bravo-Ureta, B. E. (2014). Stochastic frontiers, productivity effects and development projects. Econ. Bus. Lett. 3, 51–58. doi: 10.17811/ebl.3.1.2014.51-58

CrossRef Full Text | Google Scholar

Bravo-Ureta, B. E., González-Flores, M., Greene, W., and Solís, D. (2020). Technology and technical efficiency change: evidence from a difference in differences selectivity corrected stochastic production frontier model. Am. J. Agric. Econ. 103, 362–385. doi: 10.1111/ajae.12112

CrossRef Full Text | Google Scholar

Bravo-Ureta, B. E., Greene, W., and Solís, D. (2012). Technical efficiency analysis correcting for biases from observed and unobserved variables: an application to a natural resource management project. Empir. Econ. 43, 55–72. doi: 10.1007/s00181-011-0491-y

CrossRef Full Text | Google Scholar

Cabraal, R. A., Barnes, D. F., and Agarwal, S. G. (2005). Productive uses of energy for rural development. Annu. Rev. Environ. Resour. 30, 117–144. doi: 10.1146/annurev.energy.30.050504.144228

CrossRef Full Text | Google Scholar

Chen, Y. T., Hsu, Y. C., and Wang, H. J. (2020). A stochastic frontier model with endogenous treatment and mediator. J. Bus. Econ. Stat. 38, 243–256. doi: 10.1080/07350015.2018.1497504

CrossRef Full Text | Google Scholar

Chibeba, M. A., Kyei-Boahen, S., Guimarães, F. M., Nogueira, A. M., and Hungria, M. (2018). Feasibility of transference of inoculation-related technologies: a case study of evaluation of soybean rhizobial strains under the agro-climatic conditions of Brazil and Mozambique. Agric. Ecosyst. Environ. 261, 230–240. doi: 10.1016/j.agee.2017.06.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Crowley, E., and Carter, S. (2000). Agrarian change and the changing relationships between toil and soil in Marigoli, Western Kenya 1900–1994. Hum. Ecol. 28, 383–414. doi: 10.1023/A:1007005514841

CrossRef Full Text | Google Scholar

De los Santos-Montero, L., and Bravo-Ureta, B. E. (2017). Productivity effects and natural resource management: econometric evidence from POSAF-II in Nicaragua. Nat. Resour. Forum 41, 220–233. doi: 10.1111/1477-8947.12133

CrossRef Full Text | Google Scholar

Dinar, A., Karagiannis, G., and Tzouvelekas, V. (2007). Evaluating the impact of agricultural extension on farms' performance in Crete: a non-neutral stochastic frontier approach. Agric. Econ. 36, 135–146. doi: 10.1111/j.1574-0862.2007.00193.x

CrossRef Full Text | Google Scholar

Dzanku, F. M., Osei, R. D., Nkegbe, P. K., and Osei-Akoto, I. (2020). Information delivery channels and agricultural technology uptake: Experimental evidence from Ghana. Eur. Rev. Agric. Econ. 2020, 1–39. doi: 10.1093/erae/jbaa032

CrossRef Full Text | Google Scholar

Ferrara, G. (2020). “Stochastic frontier models using R,” in Financial, Macro and Micro Econometrics Using R, Handbook of Statistics, Part III Chapter 9, pp. 299–326, vol. 42, eds. H. D. Vinod, C. R. Rao (Amsterdam: Elsevier), 1–333. doi: 10.1016/bs.host.2018.11.004

CrossRef Full Text | Google Scholar

Ferrara, G., and Vidoli, F. (2017). Semiparametric stochastic frontier models: a generalized additive model approach. Eur. J. Oper. Res. 258, 761–777. doi: 10.1016/j.ejor.2016.09.008

CrossRef Full Text | Google Scholar

Fortin, N., Lemieux, T., and Firpo, S. (2011). “Decomposition methods in economics,” in Handbook of Labor Economics, Chapter One. Amsterdam: Elsevier. doi: 10.1016/S0169-7218(11)00407-2

CrossRef Full Text | Google Scholar

Foyer, C. H., Siddique, K. H. M., Tai, A. P. K., Anders, S., Fodor, N., Wong, F.-L., et al. (2018). Modelling predicts that soybean is poised to dominate crop production across Africa. Plant Cell Environ. 42, 373–385. doi: 10.1111/pce.13466

PubMed Abstract | CrossRef Full Text | Google Scholar

Frölich, M., and Huber, M. (2017). Direct and indirect treatment effects - causal chains and mediation analysis with instrumental variables. J. R. Stat. Soc. B 79, 1645–1666. doi: 10.1111/rssb.12232

CrossRef Full Text | Google Scholar

Gebre, G. G., Isoda, H., Rahut, D. B., Amekawa, Y., and Nomura, H. (2019). Gender differences in agricultural productivity: evidence from maize farm households in southern Ethiopia. GeoJournal. 86, 843–64. doi: 10.1007/s10708-019-10098-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghana Statistical Service (GSS) (2013). 2010 Population and Housing Census. Regional Analytical Report, Northern Region. Accra: Ghana Statistical Service.

Google Scholar

Ghana Statistical Services (GSS) (2018). Ghana Living Standards Survey Round 7: Poverty Trends in Ghana 2005–2017. Accra: Ghana Statistical Services.

Google Scholar

Ghana Statistical Services (GSS) (2019). Ghana Living Standards Survey Round 7: Main Report. Accra: Ghana Statistical Services.

Google Scholar

Giannakas, K., Tran, K., and Tzouvelekas, V. (2003). On the choice of functional form in stochastic frontier modeling. Empir. Econ. 28, 75–100. doi: 10.1007/s001810100120

CrossRef Full Text | Google Scholar

Giller, K. E. (2001). Nitrogen Fixation in Tropical Cropping Systems. Second Edition. Wallingford: CAB International. doi: 10.1079/9780851994178.0000

CrossRef Full Text | Google Scholar

Huang, C. J., Fu, T.-T., Lai, H.-P., and Yang, Y.-L. (2017). Semiparametric smooth coefficient quantile estimation of the production profile. Empir. Econ. 52, 373–392. doi: 10.1007/s00181-016-1072-x

CrossRef Full Text | Google Scholar

Huang, C. J., Huang, T. H., and Liu, H. H. (2014). A new approach to estimating the metafrontier production based on a stochastic frontier framework. J. Prod. Anal. 42, 241–254. doi: 10.1007/s11123-014-0402-2

CrossRef Full Text | Google Scholar

Huang, C. J., and Liu, J. T. (1994). Estimation of a non-neutral stochastic frontier production function. J. Prod. Anal. 5, 171–180. doi: 10.1007/BF01073853

CrossRef Full Text | Google Scholar

Huth, P. K., and Allee, T. L. (2002). The Democratic Peace and Territorial Conflict in the Twentieth Century. New York: Cambridge University Press. doi: 10.1017/CBO9780511491405

CrossRef Full Text | Google Scholar

Imbens, G. W., and Angrist, J. D. (1994). Identification and estimation of local average treatment effects. Econometrica 62, 467–475. doi: 10.2307/2951620

CrossRef Full Text | Google Scholar

Independent Evaluation Group-World Bank (2008). The Welfare Impact of Rural Electrification: A Reassessment of the Costs and Benefits: An IEG Impact Evaluation. Washington, DC: World Bank.

Google Scholar

Kumbhakar, S. C., and Lovell, C. A. K. (2000). Stochastic Frontier Analysis. New York: Cambridge University Press. doi: 10.1017/CBO9781139174411

CrossRef Full Text | Google Scholar

Kumbhakar, S. C., and Tsionas, E. G. (2009). Joint estimation of technology choice and technical efficiency: an application to organic and conventional dairy farming. J. Prod. Anal. 31, 151–161. doi: 10.1007/s11123-008-0081-y

CrossRef Full Text | Google Scholar

Lai, H.-P., Huang, C. J., and Fu, T.-T. (2020). Estimation of the production profile and metafrontier technology gap: a quantile approach. Empir. Econ. 58, 2709–2731. doi: 10.1007/s00181-018-1589-2

CrossRef Full Text | Google Scholar

Lupwayi, N. Z., Olsen, P. E., Sande, E. S., Keyser, H. H., Collins, M. M., Singleton, P. W., et al. (2000). Inoculant quality and its evaluation. Field Crops Res. 65, 259–270. doi: 10.1016/S0378-4290(99)00091-X

CrossRef Full Text | Google Scholar

Meeusen, W., and van den Broeck, J. (1977). Efficiency estimation from Cobb-Douglas production functions with composed error. Int. Econ. Rev. 18, 435–444. doi: 10.2307/2525757

CrossRef Full Text | Google Scholar

Mohammed, S., and Abdulai, A. (2022). Heterogeneity in returns to agricultural technologies with incomplete diffusion: evidence from Ghana. Rev. Dev. Econ. 26, 323–353. doi: 10.1111/rode.12837

CrossRef Full Text | Google Scholar

Mohammed, S., and Abdulai, A. (2022a). Do Egocentric information networks influence technical efficiency of farmers? Empirical evidence from Ghana. J. Prod. Anal. doi: 10.1007/s11123-022-00643-2

CrossRef Full Text | Google Scholar

Mohammed, S., and Abdulai, A. (2022b). Do ICT based extension services improve technology adoption and welfare? Empirical evidence from Ghana. Appl. Econ. 54, 2707–2726. doi: 10.1080/00036846.2021.1998334

CrossRef Full Text | Google Scholar

Mutuma, S. P., Okello, J. J., Karanja, N. K., and Woomer, P. L. (2014). Smallholder farmers' use and profitability of legume inoculants in Western Kenya. Afr. Crop Sci. J. 22(3), 205–214.

Google Scholar

Pingali, P. L. (2012). Green revolution: Impacts, limits, and the path ahead. PNAS 109, 12302–12308. doi: 10.1073/pnas.0912953109

PubMed Abstract | CrossRef Full Text | Google Scholar

Rurangwa, E., Vanlauwe, B., and Giller, K. E. (2018). Benefits of inoculation, P fertilizer and manure on yields of common bean and soybean also increase yield of subsequent maize. Agric. Ecosyst. Environ. 261, 219–229. doi: 10.1016/j.agee.2017.08.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Takahashi, K., Muraoka, R., and Otsuka, K. (2020). Technology adoption, impact, and extension in developing countries: a review of recent literature. Agric. Econ. 51, 31–45. doi: 10.1111/agec.12539

CrossRef Full Text | Google Scholar

Thomas, D. R., Harish, S. P., Kennedy, R., and Urpelainen, J. (2020). The effects of rural electrification in India: An instrumental variable approach at the household level. J. Dev. Econ. 146, 1–10. doi: 10.1016/j.jdeveco.2020.102520

CrossRef Full Text | Google Scholar

Triebs, T., and Kumbhakar, S. C. (2018). Management in production: from unobserved to observed. J. Prod. Anal. 49, 111–121. doi: 10.1007/s11123-018-0526-x

CrossRef Full Text | Google Scholar

Ulzen, J., Abaidoo, R. C., Ewusi-Mensah, N., and Masso, C. (2018). On-farm evaluation and determination of sources of variability of soybean response to Bradyrhizobium inoculation and phosphorus fertilizer in northern Ghana. Agric. Ecosyst. Environ. 267, 23–32. doi: 10.1016/j.agee.2018.08.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Ulzen, J., Abaidoo, R. C., Mensah, N. E., Masso, C., and AbdelGadir, A. H. (2016). Bradyrhizobium inoculants enhance grain yields of soybean and cowpea in Northern Ghana. Front. Plant Sci. 7, 1770. doi: 10.3389/fpls.2016.01770

PubMed Abstract | CrossRef Full Text | Google Scholar

van Heerwaarden, J., Baijukya, F., Kyei-Boahen, S., Adjei-Nsiah, S., Ebanyat, P., Kamai, N., et al. (2018). Soyabean response to rhizobium inoculation across Sub-Saharan Africa: patterns of variation and role of promiscuity. Agric. Ecosyst. Environ. 261, 211–218. doi: 10.1016/j.agee.2017.08.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Vidoli, F., and Ferrara, G. (2015). Analyzing Italian citrus sector by semi-nonparametric frontier efficiency models. Empir. Econ. 49, 641–658. doi: 10.1007/s00181-014-0879-6

CrossRef Full Text | Google Scholar

Villano, R., Bravo-Ureta, B. E., Solís, D., and Fleming, E. (2015). Modern rice technologies and productivity in the Philippines: Disentangling technology from managerial gaps. J. Agric. Econ. 66, 129–154. doi: 10.1111/1477-9552.12081

CrossRef Full Text | Google Scholar

Zhang, X., Davidson, E. A., Mauzerall, D. L., Searchinger, T. D., Dumas, P., and Shen, Y. (2015). Managing nitrogen for sustainable development. Nat. Perspect. 528, 51–59. doi: 10.1038/nature15743

PubMed Abstract | CrossRef Full Text | Google Scholar