- 1Université Paris-Saclay, INRAE, AgroParisTech, Economie Publique, Thiverval-Grignon, France
- 2Université Paris-Saclay, INRAE, AgroParisTech, Applied Mathematics and Computer Science (UMR 518), Paris, France
- 3CIRAD, UMR CIRED, Nogent-sur-Marne, France
Agricultural price shocks strongly affect farmers' income and food security. It is therefore important to understand and anticipate their origins and occurrence, particularly for the world's main agricultural commodities. In this study, we assess the impacts of yearly variations in regional maize productions and yields on global maize prices using several statistical and machine-learning (ML) methods. Our results show that, of all regions considered, Northern America is by far the most influential. More specifically, our models reveal that a yearly yield gain of +8% in Northern America negatively impacts the global maize price by about –7%, while a decrease of –0.1% is expected to increase global maize price by more than +7%. Our classification models show that a small decrease in the maize yield in Northern America can inflate the probability of maize price increase on the global scale. The maize productions in the other regions have a much lower influence on the global price. Among the tested methods, random forest and gradient boosting perform better than linear models. Our results highlight the interest of ML in analyzing global prices of major commodities and reveal the strong sensitivity of maize prices to small variations of maize production in Northern America.
1. Introduction
Over the past decade, the four components of food security - availability, stability, utilization, and access - have become major sources of concern. At the turn of 2010, prices of main food crops in the international markets have shown high variability, sometimes doubling in a short time frame (Headey and Fan, 2010). For example, the price of maize increased by 75% from September 2007 to May 2008 (Headey, 2011). Poor harvests and rising prices of agricultural commodities had contributed to triggering the hunger riots of 2007–2008 and the Arab Spring of 2011 (Headey and Martin, 2016). High levels of volatility in the food prices are now recognized to affect food security for a growing number of households (Rosenzweig et al., 2001; Schmidhuber and Tubiello, 2007).
Several reasons have been put forward to explain the food crises at the turn of the decade: low levels of food stocks, rising prices of inputs - particularly fertilizers - and growing demand for biofuel (Headey and Fan, 2008). One of the reasons most frequently cited relates to idiosyncratic shocks on agricultural production at the regional level. It has been shown that extreme local environmental conditions in 2007 and 2010 (e.g., droughts in Russia and, extensive wildfires in Australia) and the resultant declines in regional production greatly contributed to the spike in global food prices (Tadasse et al., 2016). The heatwave in Russia in the summer of 2007 and 2010 led to a significant drop in local wheat production, which resulted in export restrictions and subsequent tensions on international markets (Wegren, 2011). Restrictions on rice exports in India and Vietnam in 2007/2008 also led to substantial price increases on international markets (Headey, 2011).
It is generally considered that increased interconnectivity in global food markets can be a source of resilience, as seen in the recent Covid-19 outbreak, but also of vulnerability, particularly when the agricultural production of a major exporter is affected. Least developed countries are particularly vulnerable as they may suffer greater import losses through their strong dependence on imports for staple foods (Puma et al., 2015). In this case, we speak of teleconnected supply shocks (d'Amour et al., 2016). d'Amour et al. (2016) find that the Middle East is most sensitive to teleconnected supply shocks in wheat, Central America to supply shocks in maize, and Western Africa to supply shocks in rice. In the future, climate change and the increasing frequency of extreme weather events could make the food system even more vulnerable to such teleconnected shocks. Several works study the transmission of prices and price volatility from international to domestic markets (Baquedano and Liefert, 2014; Kalkuhl, 2016). However, to our knowledge, no article has so far attempted to quantify the inverse link, namely the sensitivity of the world price to supply shocks at the regional level.
The international maize market is a highly relevant case study because maize is one of the most traded crops and plays an important role in food security in many countries. Accurate identification of the most influential maize producing regions would be potentially useful for decision-makers who need to optimize both their dates of commodity purchases and their stock usages (World-Bank, 2005). Although maize is the most widely traded crop in the world, only a few countries export their maize productions, suggesting that maize price might be impacted by the production of a small number of regions. As some countries rely heavily on maize imports to ensure food security (Wu and Guclu, 2013; Rouf Shah et al., 2016), it is important to be able to anticipate price shocks for this commodity. Models have been developed to provide relatively short-term maize price projections relevant to many stakeholders. For example, the WASDE forecasts are used for risk calculation and design of the federal US crop insurance program (US-HR, 2009). These models were criticized because of their complexity (Hoffman and Meyer, 2018) and, sometimes, because of their lack of accuracy (Warr, 1990; Hoffman, 2011; Hoffman et al., 2015; Lusk, 2016). Other forecasting models are run by private institutions, in particular by companies specialized in commodity trading. Auto-regressive methods are widely used to forecast food price in the academic literature (Shively, 1996; Li et al., 2010). Although all these tools are certainly useful for forecasting maize prices, they provide little insights into the effects of regional maize production variations on global maize prices.
Although it is difficult to predict precisely the extent to which global scale price variations could affect local prices, it has been previously shown that shifts in international prices can transmit into regional domestic prices (Headey and Fan, 2010). In a more recent research, Kalkuhl (2016) suggests that there is a strong relationship between international prices and domestic ones, even when the global market trades with futures.
The objective of our study is (i) to identify the maize-producing regions having the largest influence on the global price of maize through their production and (ii) to quantify the effects of regional production changes on global price changes. Under the assumption that maize prices are largely driven by regional production shifts (Hertel et al., 2016), we train several statistical and machine learning models using publicly available regional yearly production data and monthly price data. Monthly price data are pertinent because maize prices do not tend to change on a daily or weekly basis but rather monthly (Dorosh et al., 2004; Ochieng et al., 2019). Our input variables, i.e., regional maize productions or yields, directly inform on the level of commodity supply, which is usually an unstable component of the market. The trained models are used to analyze the relationships between regional maize production (or yield) and global prices, to identify the most and least influential producing regions in the maize global market, and finally to quantify the effect of regional production (or yield) changes on global price changes.
In our study, we chose to use a variety of statistical and machine learning methods. The use of different methods has several advantages. First, it allows us to study the robustness of the main conclusions to the data analysis method implemented. Second, it makes it possible to compare the precision of different methods and to determine the most efficient ones. Our comparison of models thus contributes to improve our understanding of the determinants of maize price and to develop operational and accessible predictive tools. In this way, our study is relevant for designing food security policies.
2. Materials and Methods
2.1. Data
Historical annual yield (hectograms per hectare) and production (tons) data were obtained from the FAO data website (FAOSTAT) for all years available (1961 to 2018) for 19 regional entities (defined by FAO) covering 242 countries. For further data definitions and the sources of the variables included in our models, see Supplementary Table 2 in Appendix A.
Data on maize global monthly price were extracted from the World Bank's commodity markets database as a US No. 2 yellow free on board (FOB) Gulf of Mexico, U.S. nominal price, per metric ton units. Although this price is the traditional representative price for the maize produced in the US, this quotation is also accepted as the leading benchmark price for the international maize trade (FAO, 2021)1.
The time series summarizes the monthly price of maize, as globally traded in FOB US Gulf ports, from January 1960 to December 2019. We converted these prices into real 2010 US Dollars, using the monthly agricultural index of the World-Bank2 (Figure 1).
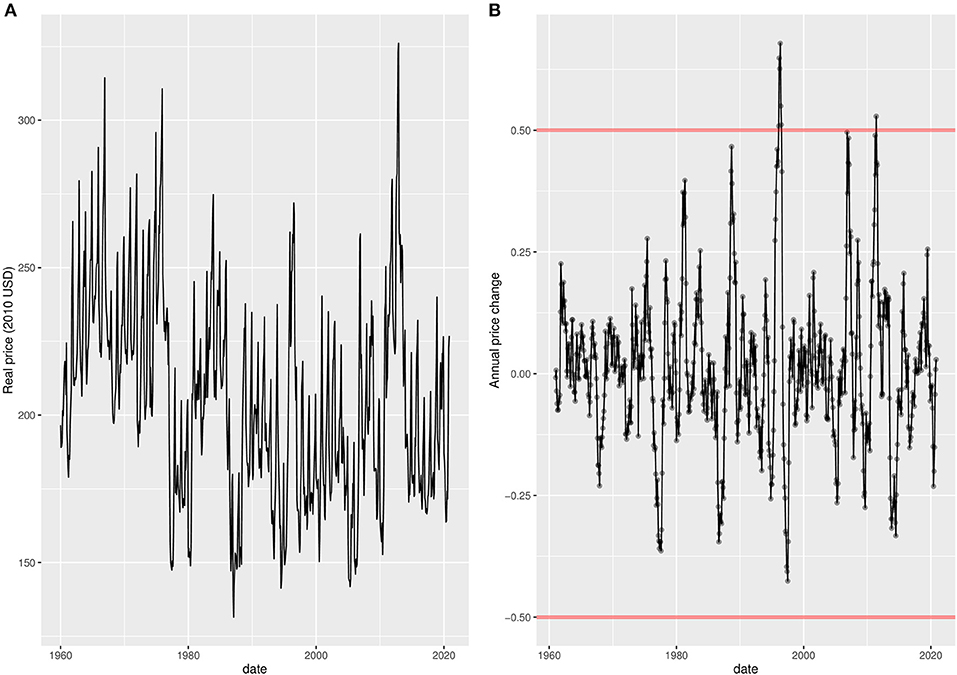
Figure 1. Time series of global maize price. (A) Real terms in 2010 US Dollars. (B) Real terms in relative change from the same month of the previous year (ratio).
The real prices are further denoted as qm, y, where m and y are the month and year indices, respectively. Exportable maize is usually harvested once a year, during the main harvest season, and levels of maize production can thus potentially have strong effects on yearly price changes. For this reason, the dependent variable in our analysis is defined as the relative price difference of maize expressed relatively to the same month of the previous year. It is defined as
and their values are shown in Figure 1B. From the series of pm, y, we define a binary variable equal to one in case of price increase (pm, y>0) and to zero otherwise.
Maize prices for month m in year y are estimated as a function of relative production (or yield) changes between the month m in year y and the same month in year y − 1. To accomplish this, we transformed regional yield (grain weight per unit of the cropping area, in hectograms per hectare) and production (total regional grain weight, in tons) data into relative changes compared to the previous year, as follows:
Where zk, y is the production (or yield) in a region k (k=1, …, 19) and year y, and xk, y is the relative production (or yield) change in the same region and the same year.
We predict prices during the last quarter of each year, that is in October, November, and December (m ∈ 10,11,12), i.e., when all regions have finished (or almost finished) their maize harvest and reported the yearly production and yield obtained. For a given year, it is indeed possible to obtain accurate estimates of maize yield and production from October onward and to use them to predict price shocks of the same year3.
In the next sections, we present and compare several methods to estimate pm, y and at m ∈ 10,11,12 as a function of xk, y, k ∈ 1,…,19. Each method is implemented twice; first using relative changes in regional productions as input variables and then using relative yield changes.
2.2. Linear and Generalized Linear Models
Although the relationships between price and production or yield changes may be non-linear, we use a linear regression model as a benchmark to estimate price fluctuation as a function of changes in regional productions or yields. Our linear model (LM) is defined as follows:
where α and βk are regression parameters and ϵm, y is the residuals. Additionally, we define a variant of this model including the price change of year y − 1 (i.e., pm, y − 1) as a supplementary input. This serves for investigating Granger causal relation between pm, y and xk, y (Granger, 1969). The significance of the effects of xk, y are tested with and without using pm, y − 1 as an additional input in the regression model. If some of the xk, y are still significant while taking pm, y − 1 into account, one can be considered that there is a Granger causal relation between pm, y and these xk, y.
For classification, we use a generalized linear model (GLM) with a binomial family and a logit link. This model computes the probability that =1 (i.e., price increase), given the values of the regional production (or yield) changes xk, y, k ∈ 1,…,19.
Both models are implemented with the glm function of R (R-Core-Team, 2020). As done with the other methods, we fit linear models for each month (October, November, and December) using successively production and yield changes as inputs. The most influential inputs were selected using a stepwise procedure implemented with the AIC criterion (step function of R).
2.3. CART
The three ML methods considered in this study are decision-tree based algorithms: classification and regression trees (CART), Random-forest (RF), and gradient boosting machine (GBM). None of these methods makes any strong assumption about the functional form of the relationship between the dependent variable and the explanatory variables, neither about the data distribution. They are thus able to capture nonlinear relationships between the inputs (regional production or yield changes) and the output (global price change). We shortly present our implementation of CART here, while RF, and GBM are presented in the next sections.
The purpose of CART is to build a binary decision tree. Let pm, y be a dependent variable and x1, y, xk, y, …, xK, y a series of explanatory variables. The tree is constructed by repeatedly distributing the observations into homogeneous groups relative to pm, y. The partitioning criteria is monotonous in the explanatory variable, xk, which defines a cross-section of xk, whereas higher valued observations belong to the right branch and lower-valued to the left branch. Additional partitions based on the same variable can be made, but at each stage, one cut-off point is determined. The subgroups that define the tree are called nodes. CART performs recursive partitioning, and searches for splits that minimize the test error rate in the chosen objective function. The choice of the objective function depends on whether the output is continuous (pm, y) or categorical (). In the former case, i.e., for predicting pm, y, CART is implemented using the residual sum of squares (RSS). To predict (classification), the objective function is a purity index based on the Gini index. Here, CART was implemented with the package rpart of the R software (Therneau et al., 2019) (rpart function).
2.4. Random Forest and Gradient Boosting
Although simple to visualize and interpret, CART results are usually unstable and tend to be sensitive to small data changes. Their price predictions are not always accurate (Kuhn and Johnson, 2013). For these reasons, ensemble learning algorithms based on bagging (for “bootstrap aggregating”) and boosting methods are frequently used instead of CART trees (Breiman, 2000). In this study we use Random-forest (RF) (Liaw and Wiener, 2002) as a bagging-based algorithm, and gradient boosting machine (GBM) as a boosting-based method.
The RF algorithm builds an ensemble of trees, each relying on a small subset of inputs (i.e., a subset of all regional productions or yields). Each tree is fitted to a randomly chosen training-set generated using a bootstrap procedure. This approach reduces the effects of correlations between variables while allowing different input variables to be selected. In RF, predictions are derived by computing the average of all trees. Here, we find that 500 trees lead to stable results. RF can rank the inputs according to their predictive powers and, here, the resulting ranking can be used to identify the regions whose maize productions (or yields) show the strongest influence on maize global price. In this study, RF is implemented with the randomForest function of the package randomForest (Breiman et al., 2018), both for quantitative predictions and for classification.
The method GBM is also based on an ensemble of trees (Efron and Hastie, 2016). At each iteration, GBM builds a simple tree (weak-learner), each of which is learning from the prediction errors of all the trees built so far. The final prediction is expressed as the sum of all the models calculated earlier. As RF, GBM is able to rank the inputs according to their predictive powers. In our case, we fit GBM using the gbm function of the gbm package (Friedman, 2001) both for regression and classification based predictions. Here, we find that the most accurate results are obtained with 100 trees for GBM.
Neither RF or GBM have analytical expressions, but standard methods can be used to rank their inputs according to their importance and visualize their effects on the output, here on price changes. Using these methods, we rank the model inputs xk, y from the most influential to the least by computing the mean decrease accuracy criterion (Calle and Urrea, 2010) for each input (i.e., each regional production or yield changes). This criterion measures the extent to which the accuracy of model predictions or classifications decreases when each of the input variables is set to a random value. Lastly, we use partial dependence plots (Greenwell, 2017) to visualize the response of the model outputs to the most influential inputs, averaging the overall values of the other inputs. These plots allow us to analyze the shapes of the responses and detect non-linearity. The same approaches were applied to LM and CART to compare the input rankings and the dependence plots of all methods on the same basis.
2.5. Models Evaluation
The accuracy of the quantitative price-estimation is assessed by root mean squared error (RMSE), which we estimate using leave-one-out cross-validation (LOOCV). In each step, one year of price (pm, y, m=10,11,12) and production/yield (xk, y) is extracted from the original data set. Then, the four models (CART, RF, GBM, and GLM) are trained using the remaining 55 years, to estimate the removed value of pm, y using the trained models. The procedure is performed 56 times—once for each year—to obtain a set of 56 estimations for each tested model and each month (m=10,11,12). Finally, a value RMSE is calculated for each model and each predicted month. The whole procedure is repeated twice, using regional maize production and regional maize yields as inputs, successively.
To evaluate the accuracy of the classification models, we apply the same LOOCV procedure, this time to calculate the area under the ROC curve (AUC). This criterion is commonly used to evaluate the performance of classification algorithms (Hernández-Orallo et al., 2012). An AUC higher than 0.5 indicates better performance than random classification. An AUC equal to 1 reveals a perfect classification.
3. Results
3.1. Quantitative Effects of Regional Productions on Price Changes
Table 1 shows that the best methods are either RF or GBM, depending on the considered month. For example, the most accurate predictions of global price changes in October (p10, y) are obtained by RF with an RMSE equal to 0.12. The least accurate results (i.e., the highest RMSE) are obtained either with the linear model (LM) or with CART, depending on the month considered.
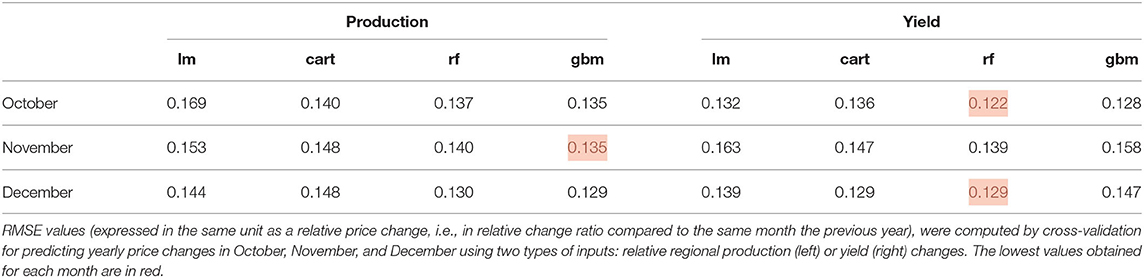
Table 1. Comparison of RMSE values for the four types of models (lm: linear model; cart: regression tree; rf: random forest; gbm: gradient boosting model).
The importance ranking of the regional maize yields is shown in Figure 2 for the three months considered and the four different statistical and machine learning methods. The ranking obtained when using regional production changes as inputs is shown in the Supplementary Figure A.a.4. The relative importance of each region is determined by its contribution to the prediction accuracy (RMSE) of the price in a given month. A region is considered influential if a random choice of its corresponding input value (i.e., a yield change or production change chosen at random) leads to a substantial increase of the RMSE of the price change predictions. On the other hand, a region is considered non-influential if a random choice of its corresponding input value does not affect the RMSE. Results clearly show that Northern America is by far the most influential region according to the four methods, with both types of inputs (production or yield changes), and for the three months considered. The only exception is the linear model (with yield change inputs) in November, but this model has low predictive power compared to others in November (Table 1). Considering the most accurate methods (GBM and RF), yield and production changes in Northern America have the strongest influence on global price changes. Moreover, according to the linear models, the effects of yield and production change in Northern America on global price change are statistically significant (p < 0.01) in October, November, and December, with and without the price change in year y-1 included as an additional explanatory input. This result indicates a Granger causality of yield and production changes in Northern America on global maize price. It reveals that yield and production changes are useful in forecasting price changes, even when previous price changes were taken into account.
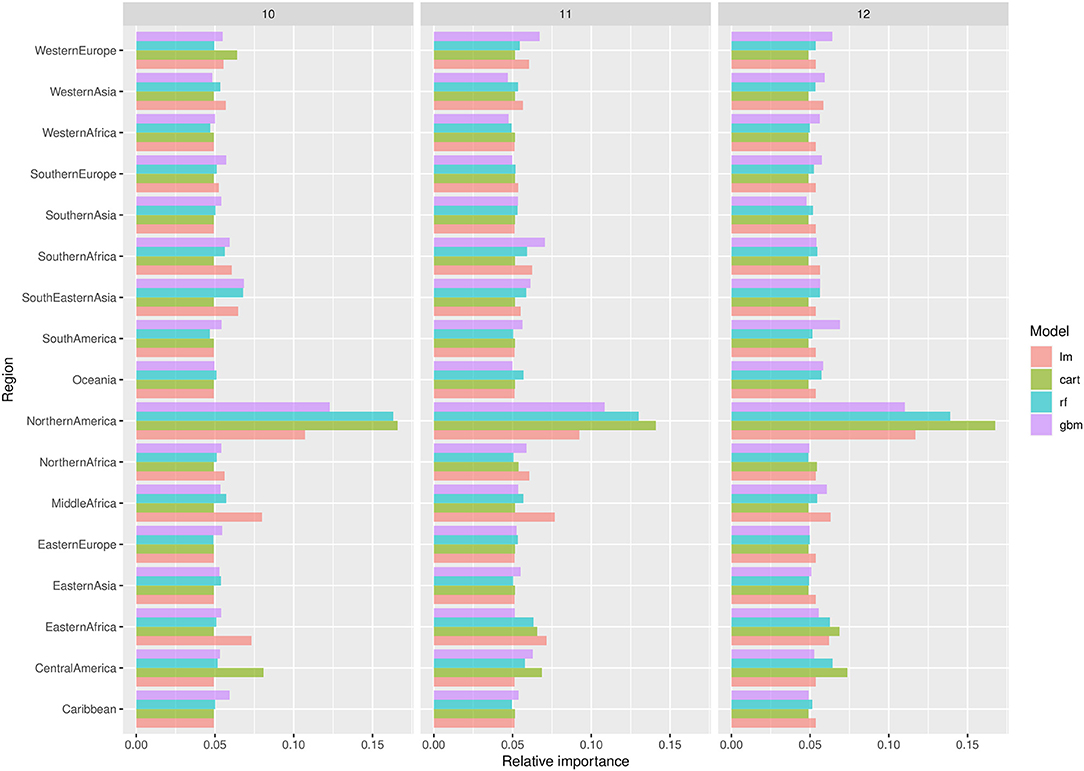
Figure 2. Importance levels of regional yield changes for predicting the global maize price in October (10), November (11), and December (12). Importance levels are computed using the RMSE criterion and measure the extent to which the model accuracy decreases with a random permutation of each input.
The partial dependence plot (PDP) shown in Figure 3 presents the average response of price changes in October (10), November (11), and December (12) to variations of maize yield compared to the previous year in the most influential region, i.e., Northern America (similar PDPs are shown in the Supplementary Figure 16 using production instead of yield). The PDPs obtained using the four models consistently show that an increase (decrease) of yield in Northern America leads to a decrease (increase) of global price. In October, for example, an 8% rise of relative maize yield in Northern-America leads to a reduction of maize price of 7% according to the gbm model, while a 0.1% decrease of relative maize yield in Northern America is expected to increase the global price by 7% according to the same model. This result confirms the strong influence of Northern American yield on global maize price. The PDPs obtained using the production and yield changes in other regions show much weaker trends and much flatter curves (see, for example, the PDPs obtained for the region Southern Africa, in Supplementary Figures 20, 21).
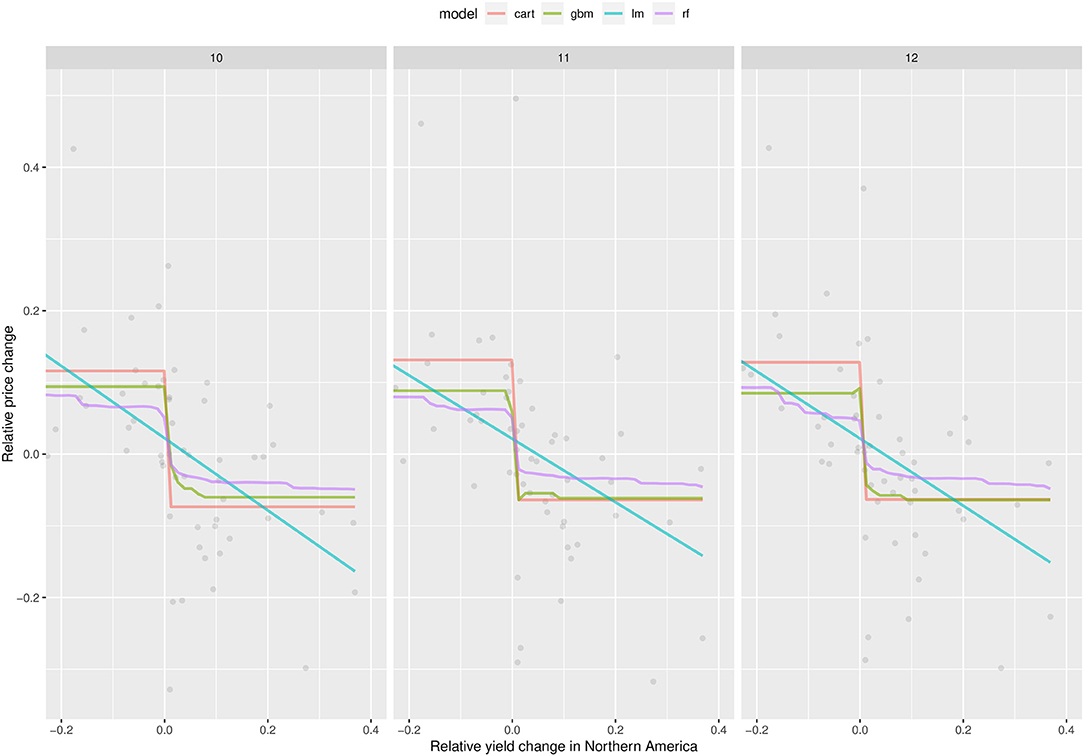
Figure 3. Partial dependence plots obtained with lm, cart, rf, and gbm showing the average response of relative price change in October (10), November (11), and December (12) to relative yield change in Northern America. The points indicate price variations as observed over the period of 1961–2019. The plot shows that, according to all models, any increase (decrease) of yield in Northern America compared to the previous year leads to a decrease (increase) of global price.
3.2. Classification of Price Increase vs. Decrease
Figure 4 shows the results that ROC analyses for the classification models for the three months considered. The results are in favor of GBM and RF with AUC falling in the range of 0.7–0.8 for these methods in most cases. The 95%CI are relatively large but those obtained with RF and GBM never include the benchmark value 0.5 characterizing a random classification. On the contrary, the 95%CI of CART and the linear model sometimes include 0.5, revealing that these methods do not systematically perform better than a random classification. For a given month and a given type of input, the lowest AUC is obtained by the linear model or CART. The two types of inputs did not lead to any systematic difference in AUC values.
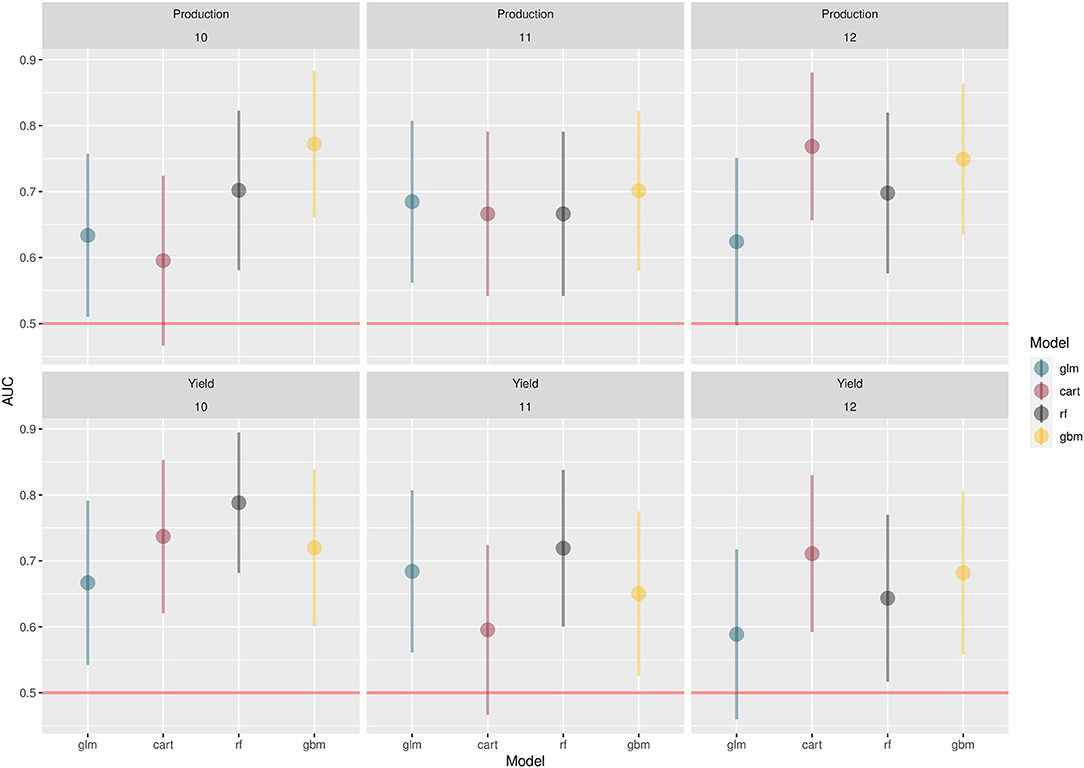
Figure 4. AUC values obtained for the classification models predicting price increase vs. price decrease in October (10), November (11), and December (12). The horizontal red line indicates AUC = 0.5, i.e random classification. Vertical bars indicate the 95% confidence intervals (CI). When these bars do not include 0.5, the AUC is significantly higher than 0.5 (p < 0.05).
As already noticed in the case of regression, the importance ranking of the regional production and yield inputs of the classification models reveals that Northern America is the most influential region, in particular for the model GBM which has a good classification power. For more details, see Figures A.a.5, A.a.5 in Supplementary Materials A.a.4.
Figure 5 shows the PDPs of the classification models. These PDPs represent the average responses of the probability of price increase to relative yield changes in Northern America (PDPs obtained with regional production inputs are shown in Supplementary F). The probability of a global price increase strongly decreases below 0.5 as soon as the yield change is positive in Northern America compared to the previous year, while it increases above 0.5 when the yield change is negative. The effect is particularly strong with the model GBM. As already noticed for quantitative price changes, the PDPs obtained with the classification models show much weaker trends and much flatter curves for regions other than Northern America (see, for example, the PDPs obtained for the region Southern Africa, in Supplementary Figures 22, 23).
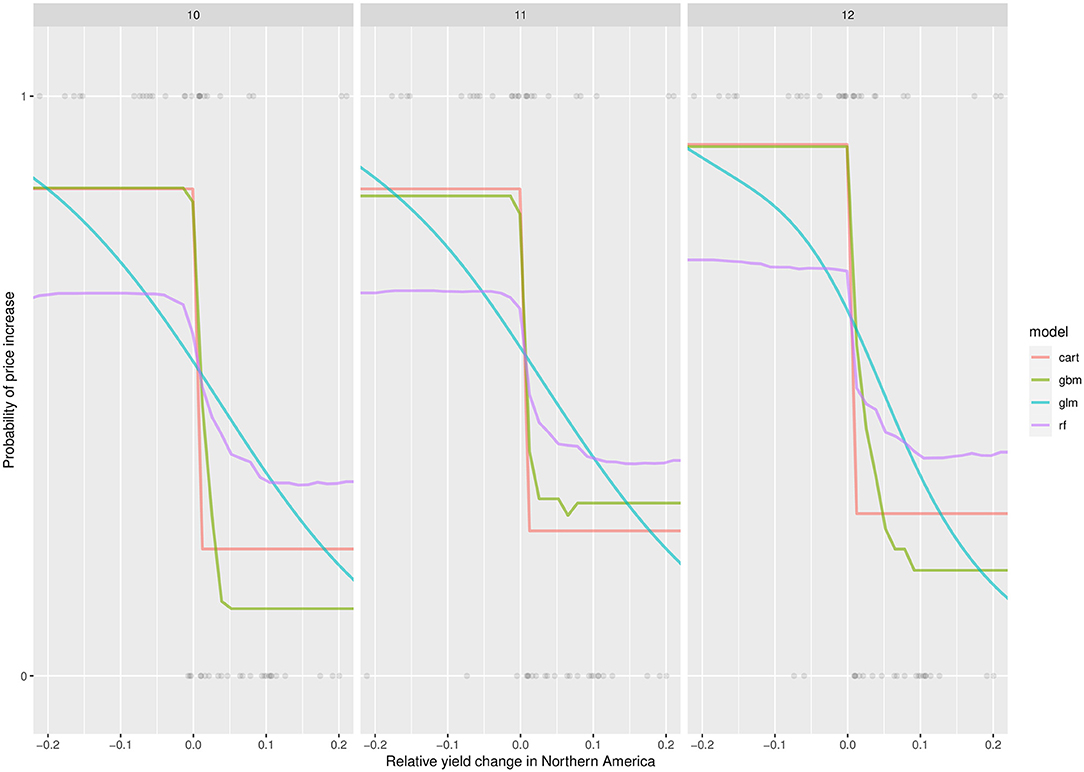
Figure 5. Partial dependence plots showing the probability of price increase in October, November, and December as a function of relative yield change in Northern America, for the four models considered. The points indicate price variations (on the y-axis, 1, price increase; 0, price decrease) as observed over the period of 1961–2019.
4. Discussion
Using regional maize production data and global maize prices, we were able to assess the effects of regional production and yield variations on late-season global maize prices. Because of the existing relationship between the global price and domestic prices, especially in the least developed countries (Caracciolo et al., 2014), the topic is important to dealing with food security issues in vulnerable regions.
Our study is the first to address this question using a large variety of statistical and machine learning methods. Overall, all models consistently show that the most influential region is Northern America, and both maize yields and maize productions seem to be equally influential. This result is somewhat expected as Northern America (and, more specifically, the USA) is the main maize producer and exporter at the global scale and as the USA is known to have a strong influence on the agricultural trade market Chatzopoulos et al. (2019). However, our models provide data-driven quantitative information on the effect of regional production variations on global maize prices. Our analysis provides real added value because it allows us to quantify the effect of an increase or decrease in the annual production of maize in this region on the global price of this commodity. All methods reveal that a small increase (decrease) of maize production or yield in Northern America is expected to decrease (increase) the global maize price by a few percent compared to the previous year. Considering the most accurate methods, an increase of maize yield relative to the previous year of +8% in Northern America negatively affect the global maize price by about –7%, while a decrease of yield in Northern America as low as –0.1% is expected to increase global maize price by more than 7%. The strong impact of maize production in Northern America is confirmed by the results obtained with the classification methods. Indeed, these methods indicate that the small increase (decrease) in maize yield or production in Northern America has a strong negative (positive) effect on the probability of maize price increase compared to the previous year. Even a very small decrease in maize production in Northern America can inflate the probability of a price increase.
Among all the considered modeling techniques, ensemble tree-based techniques (random forest and gradient boosting) show the lowest root mean squared error and highest AUC values, revealing that these methods were the best for both quantitative price prediction and classification. Indeed, in addition to being able to quantitatively predict price changes, the methods tested in this paper can be used to classify relative price increase vs. decrease situations. The principle is to compute the probability of price change increase (or decrease) as a function of regional production (or yield) changes. The tree-based models tend to outperform the simpler GLM model. Still, the rate of misclassification is approximately 25% with GBM and RF, which is relatively high but better than a random classification. As noticed for quantitative predictions, the production change in Northern America is, by far, the most influential input for classifying price increase vs. price decrease situations. All these results concur to show that maize production change in Northern America is a highly relevant indicator for assessing the risk of global maize price increase or decrease.
The performances of the methods considered are only marginally impacted by the nature of their inputs (i.e., production vs. yield changes). Thus, surprisingly, both GBM and RF do not perform better when regional production variations are used as inputs instead of yield. This is although production data combine two types of information, i.e., yields and cropping areas, whether yield variations alone do not account for possible variance in the regional maize cultivated areas.
Although the main purpose of our study is not to propose new forecasting tools, our models could potentially be used to predict global maize prices. Compared to other types of forecasting models, GBM and RF have several advantages but, also, a few disadvantages. Our models rely on public data and can be easily implemented using standard modeling open-source software. On the contrary, private forecasting techniques are usually unpublished, not freely available, and not transparent. Structural models constitute another category of models that can predict prices of agricultural commodities. These models rely on theories describing economic systems and are developed by international organizations such as FAO, OECD, and IFPRI. They simulate price fluctuations using a series of functions describing partial or general market equilibrium. Although these models are used to predict product prices in the long run, they are not usually implemented to make short-term predictions. They are also complex and cannot be easily run by non-specialists. The WASDE model is another example of an operational tool for maize price predictions. Similarly to our models, WASDE can forecast maize price at a monthly time step. According to Hoffman et al. (2015), WASDE relies on a combination of nine different structural and non-structural sub-models while GBM and RF can be easily implemented using free R packages and publicly accessible data. They could be thus easily run by any interested stakeholder and updated every year based on the most recent data.
In the future, our models could be adapted to predict price changes for other agricultural commodities from regional crop productions. From a practical point of view, a disadvantage of the ML tree-based models is that they rely on yearly regional production input data. In principle, these data are only available after harvest, but relatively accurate values can be estimated shortly before harvest from local expert knowledge and model predictions. Considering the maize growing season, it is not realistic to get reliable regional production data before the end of summer. This with regards to regions located in the Northern hemisphere, in particular in Northern-America, which is a key region for predicting global maize price. For this reason, all models were used here to predict global maize prices at the end of the year, more specifically in October, November, and December.
In this study, we analyzed the effect of regional productions on global maize prices during the last three months of the year. We made this choice to be consistent with the harvest date for maize in the main maize-producing region—North America—which takes place in the very late summer and fall. Although we did not carry out a detailed analysis for earlier months, we did perform a sensitivity analysis of the influence of North America depending on the month considered and found that this region retained a significant but lesser influence in the months preceding the harvest, probably due to the influence of the harvest forecasts anticipated by the maize market players. In the future, however, it would be very useful to deepen this analysis to identify more precisely the influence of the different producers on prices during the first months of the year.
Our approach could potentially be replicated for other crops whose production is less geographically concentrated. This would allow us to assess the world food price sensitivity to production shocks or an export ban in a given country.
5. Conclusions
This study demonstrates that it is possible to assess the impact of regional maize production variations on the global price of maize using machine-learning (ML) techniques on publicly available regional production and price data. As these methods can be easily implemented using only freely available packages and public information, our results contribute to making the forecasting of the global price of maize more accessible. As such, our price prediction technique can be included food security management programs and policies and possibly serve as a price forecaster. The methods considered can rank regional producers according to their influence on global maize prices and our results show that, out of all regions, Northern America is by far the most influential. More specifically, our results reveal that, for maize, small positive production changes relative to the previous year in Northern America have a strong and negative impact on maize global price. Our study highlights the potential interest of ML for predicting global prices of major commodities from regional production and assessing price sensitivity to regional crop producers.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: http://www.fao.org/faostat/en/#data; https://www.worldbank.org/en/research/commodity-markets.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This study was funded by the French ANR project CLAND (16-CONV-0003) and by the INRAE metaprogram GloFoods.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsufs.2021.655206/full#supplementary-material
Footnotes
1. ^The series of relative yearly maize price changes used in this paper is strongly correlated with the relative maize price changes obtained in other countries. For example, Argentina and Ukraine (correlation of about 0.75), according to the data made available in the GIEWS database of the FAO.
2. ^Although the most frequently use price index is the American CPI, we chose to use the World-Bank monthly agricultural price index. We base our decision on two factors: The first derives from Tadasse et al. (2016) indicating that the US CPI could be a biased deflator when dealing in a global market that includes both developed and developing countries. The second reason is a relatively smaller gap (RMSE) between the maize annual real prices as published by the World-Bank to the real maize global monthly price calculated for this study.
3. ^http://www.amis-outlook.org/amis-about/calendars/maizecal/en/, retrieved 23 March 2020.
References
Baquedano, F. G., and Liefert, W. M. (2014). Market integration and price transmission in consumer markets of developing countries. Food Policy 44, 103–114. doi: 10.1016/j.foodpol.2013.11.001
Breiman, L. (2000). Randomizing outputs to increase prediction accuracy. Mach. Learn. 40, 229–242. doi: 10.1023/A:1007682208299
Breiman, L., Cutler, A., Liaw, A., and Matthew, W. (2018). Breiman and Cutler's Random Forests for Classification and Regression. R package version 4.6-14.
Calle, M. L., and Urrea, V. (2010). Letter to the editor: stability of random forest importance measures. Brief. Bioinform. 12, 86–89. doi: 10.1093/bib/bbq011
Caracciolo, F., Cembalo, L., Lombardi, A., and Thompson, G. (2014). Distributional effects of maize price increases in malawi. J. Dev. Stud. 50, 258–275. doi: 10.1080/00220388.2013.833319
Chatzopoulos, T., Pérez Domínguez, I., Zampieri, M., and Toreti, A. (2019). Climate extremes and agricultural commodity markets: a global economic analysis of regionally simulated events. Weather Clim. Extremes 27:100193. doi: 10.1016/j.wace.2019.100193
d'Amour, C. B., Wenz, L., Kalkuhl, M., Steckel, J. C., and Creutzig, F. (2016). Teleconnected food supply shocks. Environ. Res. Lett. 11:035007. doi: 10.1088/1748-9326/11/3/035007
Dorosh, P. A., Subbarao, K., and Del Ninno, C. (2004). Food aid and food security in the short and long run: country experience from asia and sub-saharan africa (english). Working Paper 538, World Bank, Washington, DC.
Efron, B., and Hastie, T. (2016). Computer Age Statistical Inference Algorithms, Evidence, and Data Science. 1st edn, Cambridge University Press.
Friedman, J. H. (2001). Greedy function approximation: a gradient boosting machine. Annals Stat. 29, 1189–1232. doi: 10.1214/aos/1013203451
Granger, C. W. J. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37, 424–438. doi: 10.2307/1912791
Greenwell, B. M. (2017). pdp: an r package for constructing partial dependence plots. R J. 9, 421–436. doi: 10.32614/RJ-2017-016
Headey, D. (2011). Rethinking the global food crisis: the role of trade shocks. Food Policy 36, 136–146. doi: 10.1016/j.foodpol.2010.10.003
Headey, D., and Fan, S. (2008). Anatomy of a crisis: the causes and consequences of surging food prices. Agric. Econ. 39, 375–391. doi: 10.1111/j.1574-0862.2008.00345.x
Headey, D., and Fan, S. (2010). Reflections on the global food crisis: how did it happen? how has it hurt? and how can we prevent the next one? Intl. Food Policy Res. Inst. 165, 142. doi: 10.2499/9780896291782RM165
Headey, D. D., and Martin, W. J. (2016). The impact of food prices on poverty and food security. Ann. Rev. Resou. Econ. 8, 329–351. doi: 10.1146/annurev-resource-100815-095303
Hernández-Orallo, J., Flach, P., and Ferri, C. (2012). A unified view of performance metrics: Translating threshold choice into expected classification loss. J. Mach. Learn. Res. 13, 2813–2869.
Hertel, T. W., Baldos, U. L. C., and van der Mensbrugghe, D. (2016). Predicting long-term food demand, cropland use, and prices. Ann. Rev. Resou. Econ. 8, 417–441. doi: 10.1146/annurev-resource-100815-095333
Hoffman, L., and Meyer, L. (2018). Forecasting the US season-average farm price of upland cotton: derivation of a futures price forecasting model. Electr. Outlook Rep. Econ. Res. Serv.
Hoffman, L. A. (2011). Using Futures Prices to Forecast US Corn Prices: Model Performance With Increased Price Volatility, Chapter 7, New York, NY: Springer New York, 107–132.
Hoffman, L. A., Etienne, X. L., Irwin, S. H., Colino, E. V., and Toasa, J. I. (2015). Forecast performance of wasde price projections for us corn. Agric. Econ. 46, 157–171. doi: 10.1111/agec.12204
Kalkuhl, M. (2016). How Strong Do Global Commodity Prices Influence Domestic Food Prices in Developing Countries? A Global Price Transmission and Vulnerability Mapping Analysis. Cham: Springer International Publishing, 269–301.
Li, G.-Q., Xu, S.-W., and Li, Z.-M. (2010). Short-term price forecasting for agro-products using artificial neural networks. Agric. Agric. Sci. Procedia 1, 278–287. doi: 10.1016/j.aaspro.2010.09.035
Lusk, J. L. (2016). From farm income to food consumption: Valuing usda data products. Technical report.
Ochieng, D. O., Botha, R., and Baulch, B. (2019). Structure, conduct and performance of maize markets in malawi. Technical Report 29, Washington, DC: IFPRI.
Puma, M. J., Bose, S., Chon, S. Y., and Cook, B. I. (2015). Assessing the evolving fragility of the global food system. Environ. Res. Lett. 10:024007. doi: 10.1088/1748-9326/10/2/024007
R-Core-Team (2020). R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. version 3.6.3.
Rosenzweig, C., Iglesias, A., Yang, X., Epstein, P. R., and Chivian, E. (2001). Climate change and extreme weather events; implications for food production, plant diseases, and pests. Glob. Change Hum. Health 2, 90–104. doi: 10.1023/A:1015086831467
Rouf Shah, T., Prasad, K., and Kumar, P. (2016). Maize—a potential source of human nutrition and health: a review. Cogent Food Agric. 2:1166995. doi: 10.1080/23311932.2016.1166995
Schmidhuber, J., and Tubiello, F. N. (2007). Global food security under climate change. Proc. Natl. Acad. Sci. U.S.A. 104, 19703–19708. doi: 10.1073/pnas.0701976104
Shively, G. E. (1996). Food price variability and economic reform: an arch approach for ghana. Am. J. Agric. Econ. 78, 126–136. doi: 10.2307/1243784
Tadasse, G., Algieri, B., Kalkuhl, M., and Von Braun, J. (2016). “Drivers and triggers of international food price spikes and volatility,” in Food Price Volatility and Its Implications for Food Security and Policy. Springer, Cham, 59–82.
Therneau, T., Atkinson, B., Ripley, B., and Ripley, M. B. (2019). Package ‘rpart'. R package version 4.1-15.
US-HR (2009). Hearing to review the federal crop insurance program : hearing before the subcommittee on general farm commodities and risk management of the committee on agriculture.
Warr, P. G. (1990). Predictive performance of the world bank's commodity price projections. Agric. Econ. 4, 365–379. doi: 10.1016/0169-5150(90)90011-O
Wegren, S. K. (2011). Food security and russia's 2010 drought. Eurasian Geogr. Econ. 52, 140–156. doi: 10.2747/1539-7216.52.1.14
World-Bank (2005). Managing Food Price Risks and Instability in an Environment of Market Liberalization (english). Technical report, Washington, DC: World Bank.
Keywords: food-security, maize, agricultural commodity prices, regional productions, machine learning
Citation: Zelingher R, Makowski D and Brunelle T (2021) Assessing the Sensitivity of Global Maize Price to Regional Productions Using Statistical and Machine Learning Methods. Front. Sustain. Food Syst. 5:655206. doi: 10.3389/fsufs.2021.655206
Received: 18 January 2021; Accepted: 27 April 2021;
Published: 02 June 2021.
Edited by:
Ademola Braimoh, World Bank Group, United StatesReviewed by:
Hideyuki Doi, University of Hyogo, JapanJordan Chamberlin, The International Maize and Wheat Improvement Center (CIMMYT), Kenya
Copyright © 2021 Zelingher, Makowski and Brunelle. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rotem Zelingher, cm90ZW0uemVsaW5naGVyQGlucmFlLmZy
 Rotem Zelingher
Rotem Zelingher David Makowski
David Makowski Thierry Brunelle
Thierry Brunelle