Theoretical Clues for Agroecological Transitions: The Conuco Legacy and the Monoculture Trap

The multiple ecological crisis that we are facing forces us to ponder the transition toward sustainable agricultural systems. Two key uncertainties need to be unveiled in addressing this problem; first, we need to identify the general features of alternative models that make them sustainable, and second, we need to explore how to build them from the (flawed) existing systems. In this work we explore these two questions using an ethnoecological and theoretical approach. In the exploration of alternative models, we evaluate an ancestral farming system, the conuco, characterized by, (i) the use of the ecological succession to constantly renew its properties, (ii) the increase of its biodiversity over time (in the horizontal and vertical components), and (iii) the self-regulation of the associated populations. Next, we characterize the topology of ecological networks of agroecosystems along the transition from a monoculture to a conuco-like agroecological system. We use topologies obtained from field information of conventional and agroecological systems as starting and arrival points. To model the dynamics of the systems and numerically simulate the transitions, we use a model based on Generalized Lotka-Volterra equations, where all types of population interactions are represented, with outcomes based on a density-dependent conditionality. The results highlight the relevance of increasing the connectance and diminishing the degree centrality of the conventional systems networks to promote their sustainability. Finally, we propose that the transitions between the monoculture and the agroecological systems could be figuratively interpreted as a cusp catastrophe, where the two systems are understood as alternative stable states and the path from one to the other cannot be reverted by just reversing the values of the control parameter. That is, once a system is in either of these states there is a tendency to stay and a resistance to move away from it. This implies that in the process of transition from a monoculture to a multi-diverse system, it is prudent not to despair if there are no immediate improvements in the performance of the system because once a certain point is reached, the system may experience an abrupt improvement.

In Flanders, in 1547, Teofrastus explained everything to me. “They gave us the diversity of the world,” he told me, “but we only want gold. You found a treasure, an infinite jungle, and felt infinite disappointment, because you wanted that jungle of thousands of appearances to have only one appearance…”

William Ospina (The Country of Cinnamon)

Introduction

Theoretical and mathematically formal approaches help us appreciate patterns and processes outside the immediate context of our senses. For instance, measurements, statistics, and models, have allowed us to infer that the most important cause of greenhouse gas release on the planet is modern industrial agriculture system (conceived as a whole, from cropping fields to consumption and final disposal); that is, a system that relies on the production and use of agrochemical inputs, specialized machinery, a characteristic method of cultivation and a particular pattern of food distribution, consumption, and disposal (Goldsmith, 2004; Altieri, 2008). Also, mathematical models applied to the climate change issue put forward the possibility that in the future the growing seasons will be longer in many regions of the world, which may allow certain species of phytophagous insects and pathogenic microorganisms to complete a greater number of reproductive cycles and expand their geographic distribution, thus increasing the likelihood of severe pest and disease outbreaks (Altieri and Nicholls, 2008).

These threats reveal the urgent need to find alternative agricultural systems that are ecologically sound, thus, we need insights from different approaches and bodies of knowledge to explore other systems. Mathematics provide the tools for the theoretical representation of the systems and their dynamics, and in particular, for glimpsing relevant elements in the transition toward sustainable agricultural systems. Likewise, local indigenous knowledge on traditional farming and long standing practice are of great relevance because the agricultural systems they have developed contain critical ecological information that may provide keys to sustainability.

From a general point of view, the transition to sustainable agriculture is a complex process, in which assessments are needed on both current situations and future predictions, based on the exchange of information between the scientists and farmers communities (van Zonneveld et al., 2020). On very specific terms, to transition away from industrial agriculture we need to advance knowledge on two main topics: the general characteristics of alternative agricultural models and the fundaments on how to build them from the existing systems. In this work, we describe in some detail a biodiverse ancestral agriculture system and discuss how its ecological interactions structure (network topology) is associated to agroecologically desirable characteristics (e.g., self-regulation of populations). Then we explore, in theoretical terms, the process of possible transitions from topologically simpler systems (e.g., a monoculture) to those with characteristics similar to the more agroecological ones.

It is important to highlight that although the topic of transitions to sustainable agriculture is universal, the alternative studied here is specifically based on tropical ecosystems. Likewise, it should be clear that the results obtained in this study are essentially theoretical. In this work, we turn our attention to systems that are the result of more than 7,000 years of co-evolution between social human groups and particular ecosystems: the Amazonian agriculture (Levis et al., 2017). Specifically, we evaluate relevant ecological characteristics of an agricultural system called conuco. Not because we think the conuco as is practiced now is the solution for tropical agriculture, but because we consider that it encloses key ecological principles relevant for agriculture that are radically different from the ways of doing agriculture in the green revolution. Next, we establish and discuss, in theoretical terms, the main features of a possible path to this alternative starting from a conventional agricultural system.

In a nutshell, in this work we: (1) Describe ecologically relevant aspects of an ancestral sustainable farming system, and (2) Characterize, within a theoretical frame, some relevant topological and dynamical features that may occur in the transition from a conventional monoculture to this type of sustainable system (e.g., features that promote autonomous regulation of the system or that enhance the viability of the transition).

An Alternative, Grounded in Local Knowledge and Experience

From an ecological point of view, green revolution agriculture (particularly in the tropics) is characterized by: (1) promoting systems with minimal biodiversity, and (2) forcing the systems to remain in the initial stages of the ecological succession, i.e., in the early phases of the overtime process of change in its community structure after the disturbance produced by soil tillage (Griffon, 2008; Gliessman, 2015). It is important to recognize that these two characteristics are associated with the application of agrochemicals. The application of insecticides, fungicides, and herbicides are necessary to control population densities of phytophagous organisms, mainly because these systems lack the ecological complexity necessary to self-regulate. In addition, the fact that these systems are artificially kept in the early stages of succession prevents the accumulation of organic matter in the soil and therefore they need synthetic fertilizers. As a contrasting alternative, we examine here the conuco, an ancestral farming system in Venezuela (Sanoja, 1981; Griffon, 2020). There are many different forms of conuco, but in general ecological terms, it can be characterized as an agricultural system driven by disturbance and succession processes; this is a system that involves important human intervention in the beginning, and then a mix of natural succession and anthropic manipulation. A conuco starts with a partial disturbance of an ecosystem (typically a forest), where a proportionally very small area is deforested. Afterwards, a variety of harvests are obtained from the different arrangements of species (mainly planted crops and spontaneous wild plants, but also some game animals in the final stages) that occur along the ecological succession until it reaches a similar state to the original (pre-disturbance). The anthropic intervention of the system is very strong in the early stages, but it drastically decreases afterwards, becoming almost nil at the end. It should be mentioned here that there are conucos that do not correspond to this definition, some are simpler systems that do not include ecological succession. Here we focus on indigenous conucos, which typically involve the succession processes (combined natural and anthropic). From here on, we use the word conuco to refer to these.

The site where a conuco is grown is carefully chosen. When choosing a site, fine interpretation of signs and codes of nature are used (i.e., biosemiotic elements), mainly related to soil characteristics, topography, and flora (Villarreal et al., 2003; Bonilla-Bedoya et al., 2012; Saturno and Zent, 2016). In addition, once the site for the conuco has been chosen, there is a meticulous selection of the micro-planting sites for the different species, according to multidimensional agronomic clues, such as soil texture, natural drainage direction, brightness/shading (Ruíz, 2005). Thus, there is a central element of the conuco, in all its stages, which is one important focus of attention of this article: its biodiversity. In agricultural systems we talk about agrobiodiversity, and it is necessary to make the following distinction: within all agroecosystems, there is a set of organisms that live in close relationship with the crops, these are known as associated agrobiodiversity (Nicholls and Altieri, 2002). The identity of these organisms is determined by the interaction between the planned agrobiodiversity (i.e., the crops) and the biodiversity found in the surrounding wild areas (Vandermeer and Perfecto, 1995; Nicholls and Altieri, 2002).

In a conuco, typically 15–30 species of plants are used for the early succession stages (Freire, 2002; Villarreal et al., 2003), and there are numerous varieties of each species present. For example, 15–25 varieties of cassava can be cultivated at the same time (although typically five are dominant). In very traditional areas, 20–40 different species per conuco have been identified in the early stages and more than a 100 varieties (Freire, 2002). In conucos not all species are found in equal abundances, typically one or a few species show superior numbers of individuals than others.

One farmer may manage different conucos at the same time, showing great diversity when considered all together at the landscape level. Actually, farmers refer to and conceive their own conucos collectively (in early, middle, and late stages of succession), not individually, and in fact, crop diversity is a source of pride and status (Freire, 2002).

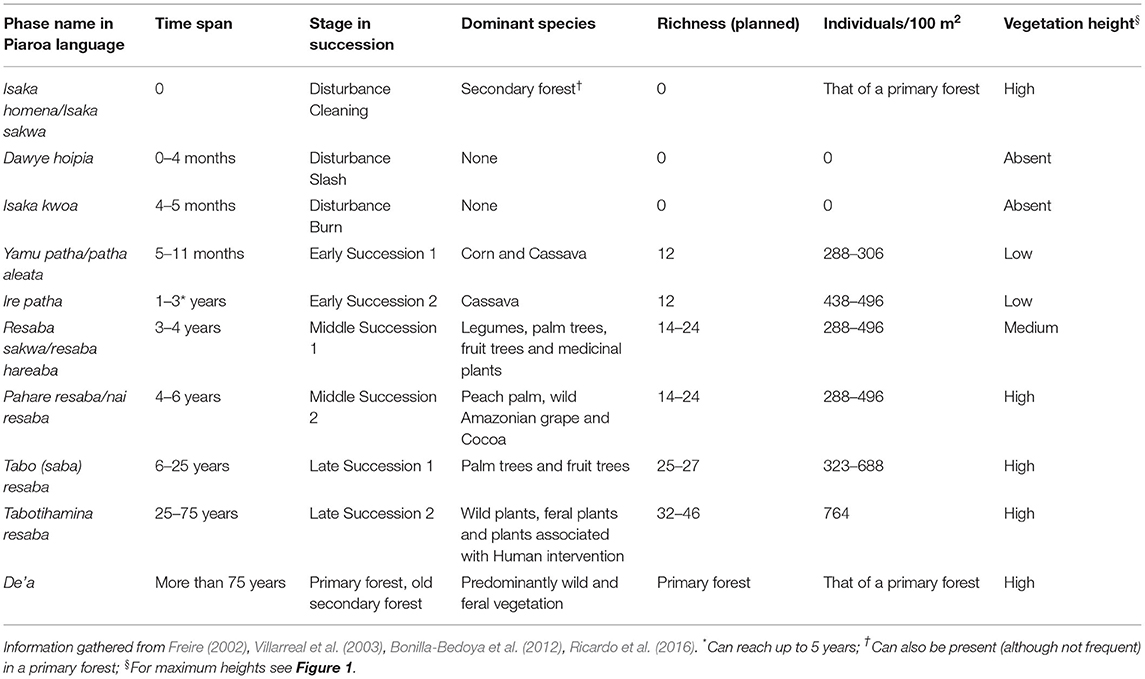
Another key element, crucial to understand the conuco in its proper complexity, is that it is a system composed of phases within a continuum (Freire, 2002; Villarreal et al., 2003; Ruíz, 2005; Saturno and Zent, 2016). In the conuco, a specific management is carried out in each phase, which involves different and very specialized ecological knowledge. The ecological complexity of these phases, can be depicted, for instance, with the Piaroa conuco. The Piaroa (also known as Huottüja or De'aruhua), is an indigenous group who live mainly on the banks of the Orinoco River and its tributary rivers in Venezuela, also in other areas of Venezuela and Colombia (Mansutti, 2003). The main distinction the Piaroa make in relation to the conuco phases is among the labor-intensive ones, known as patha, which correspond to what we have called early stages, and a series of phases described with the generic term resaba (Freire, 2002; Freire and Zent, 2007), which correspond to the medium and late stages, in which the emphasis is on the subtle manipulation of the ecological succession. It is interesting to note that the stages conceived by the Piaroa largely coincide with the external classifications that have been made on their system (see Table 1) (Freire, 2002; Ruíz, 2005; Bonilla-Bedoya et al., 2012; Ricardo et al., 2016). In other Venezuelan indigenous peoples we find classifications similar to the phases mentioned for the Piaroa (see for example Saturno and Zent, 2016).

TABLE 1

Table 1. Characteristics of the stages in a Piaroa Conuco.

A fundamental issue to understand the importance of succession in the conuco is to acknowledge the original limitations that typically present the soils in which they are developed: poor soils, of great acidity, and with severe chemical and biological limitations (Villarreal et al., 2003; Bonilla-Bedoya et al., 2012). In this context, this traditional way of farming has been possible thanks to the space-time dynamism of the areas used, which improves the agronomic characteristics of the soil (Bonilla-Bedoya et al., 2012). Arbuscular mycorrhizal fungi play a key role in this improvement during the middle and late stages of the succession (Cáceres, 1989; Kalinhoff et al., 2009; Cáceres et al., 2011).

From a spatial point of view, the conucos typically present a concentric development from the core of the indigenous community, thus, the conucos are spatially structured at different stages of the succession (Villarreal et al., 2003; Bonilla-Bedoya et al., 2012). The entire cycle, from the initial disturbance (known as cleaning, slash, and burn), to the late stages and the beginning of a new cycle (i.e., a new disturbance) generally lasts about 20–25 years (although in some cases can extend up to 75 years) (Freire, 2002; Bonilla-Bedoya et al., 2012; Ricardo et al., 2016).

It is relevant to highlight that the planned agrobiodiversity harvest is constant throughout the succession. However, in the medium and late stages, hunting and gathering of wild species become a very important part of the system (Freire, 2002; Freire and Zent, 2007). In general, the conucos increase their biodiversity as their age increases (Freire, 2002; Villarreal et al., 2003). Table 1 and Figure 1 show important variations and temporal patterns that occur along the succession stages in the conuco; there is a progressive increase in: species richness, the number of species per unit area, and the height of the vegetation, also there are changes in the identity of the dominant species in terms of abundances through time (Villarreal et al., 2003).

FIGURE 1

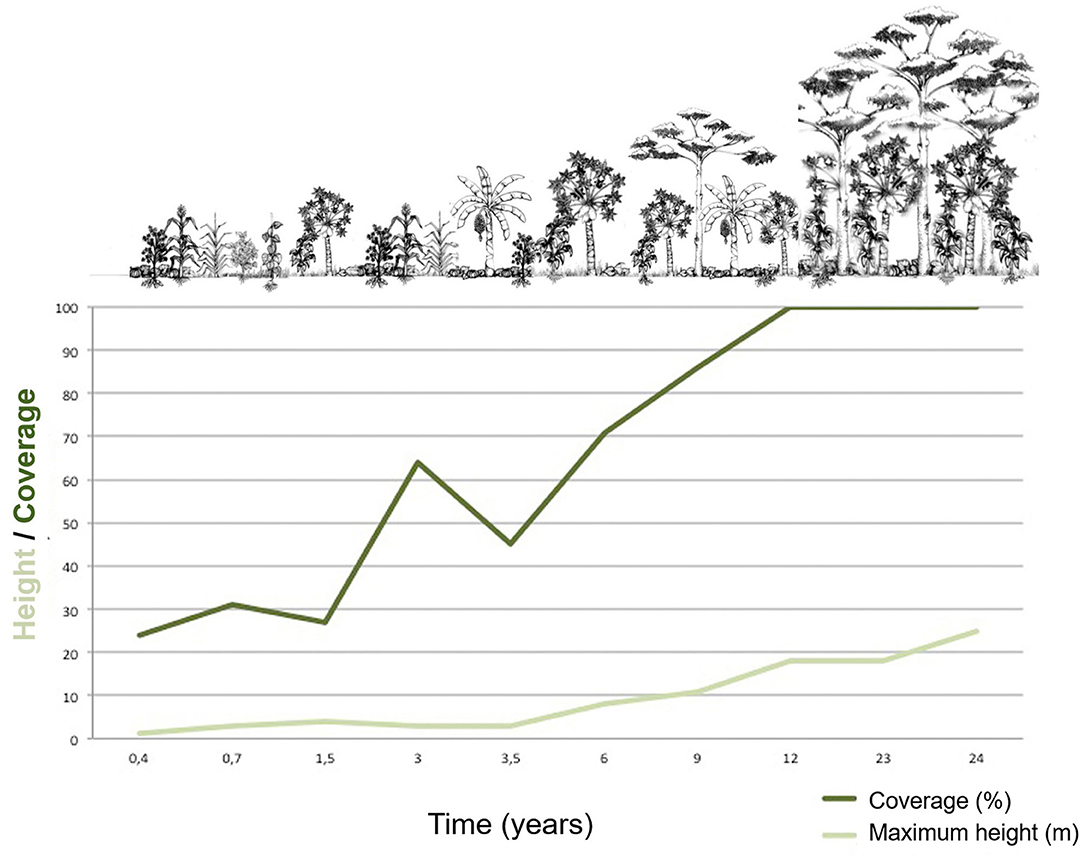
Figure 1. Piaroa Conuco temporal evolution: Ground cover and vegetation maximum height. Information gathered from Freire (2002), Villarreal et al., 2003, Bonilla-Bedoya et al. (2012), Ricardo et al. (2016).

In the conuco, apart from the diversity present in each moment (synchronously) there is also a diversification in time (diachronically). This works like a sophisticated rotation system, designed so that it emulates (i.e., biomimetically) the natural process of succession. Over time, the system becomes more complex both in its horizontal and its vertical composition, and new productive vertical strata are incorporated. Thus, the landscape perspective, where a set of areas in different stages of the succession coexist, portrays a vision of the real complexity of the system.

Ecological Networks: The Hiwi Conuco and a Corn Monoculture

The ecological interactions that occur among agrobiodiversity elements are fundamental in conucos at all stages. The contrast of this cultivation system with the corn monoculture in this regard is essential to understand the development of the work presented in this paper. Therefore, in this sub-section we present a brief, but somewhat detailed, account of the main features of the networks of ecological interactions associated with examples of these two cultivation systems in Venezuela. This information is taken from previous research published (in Spanish) by some of the authors of this work (Griffon and Hernandez, 2014; Griffon and Rodríguez, 2017).

It is important to mention that conuco and corn monoculture in Venezuela are related in historical, cultural, and geographical terms. The conuco was the most important cultivation system for white corn (from which the main staple food of Venezuela, the arepa, is made). Then, the cultivation of corn shifted from conucos to monocultures in most of the northern part of the country.

In this study, we will use a conuco model from the Hiwi cultivation system. The Hiwi people (also known as Jivi or Guahibo) inhabit a large savanna region between Venezuela and Colombia. The information concerning the conuco ecological network was gathered from traditional Hiwi farmers. The farmers specified the species involved in the conucos and the nature of the interactions between them; the corresponding scientific names of these species and interactions (e.g., herbivory, predation, competition, etc.) were assigned by agronomists and biologists, based on the organisms indicated by the farmers and the nature of their relationship. The ecological network associated with the corn monoculture was built from information gathered from agronomists, experts in the management of this crop in Venezuela. Each agronomist supplied the names of the species involved (according to their own experiences) and the nature of the interactions between them (e.g., herbivory, predation, competition, etc.) (Griffon and Hernandez, 2014; Griffon and Rodríguez, 2017). In both situations, the basic information was gathered using semi-structured interviews. When identification of a specific species was not possible, the name of the order, family or genus to which it belongs was placed in the graph (each node in both networks represents a single species). The resulting networks, in both conuco and monoculture, were the consensus topologies of the information obtained. In order to produce these consensuses, the authors established as a criterion that species, and particular interactions between them, appear in 50% of the data collected in the surveys, for each type of agroecosystem. Due to this conservative protocol, the networks finally assembled are a simplified version of the real ecologically complex systems. In a strict sense, these networks are representative of the worldview that Hiwi farmers (in the conuco case) and agronomists (in the corn monoculture) have about these systems. Therefore, they are idealized (and simplified) constructions that show us, apart from ecological information, important aspects of the subjectivities of the actors associated with them.

The fundamental characteristics of these consensus networks can be seen in Figure 2. The two networks have identical richness (i.e., equal number of species), but they are markedly different both in terms of the identity of the species present, and in the different types of interactions among them (more details on the interactions between the species can be found in Griffon and Rodríguez, 2017). In the monoculture, beyond maize, basically insects, and microorganisms capable of generating maize diseases are found. While in the conuco there is a greater diversity of plants and animal groups; and among these all types of ecological interactions are represented: competition, mutualism, commensalism, amensalism, and contramensalism (the latter refers to victim-exploiter or consumer-resource interactions such as herbivory, predation, or parasitism). In the monoculture network there is only competition, commensalism and contramensalism. In fact, it can be seen that there is one species (corn: Zea mays) to which all other species are directly linked. Interestingly, the links in this network represent, for the most part, ecological interactions of the contramensalism type where the corn always is the depleted species in the interaction. That is, corn serves as food for the other species. On the other hand, in the ecological network associated with the conuco no particular species captures most of the interactions. Furthermore, in the monoculture, of the 16 species present only one is harvested, while in the conuco 11 species are harvested. The characteristics of these networks reflect different types of management of the systems, and it is important to highlight here that the comparison we make is not based on the identity of the species per se, but rather on the topology of the networks (i.e., the architecture of their interactions).

FIGURE 2

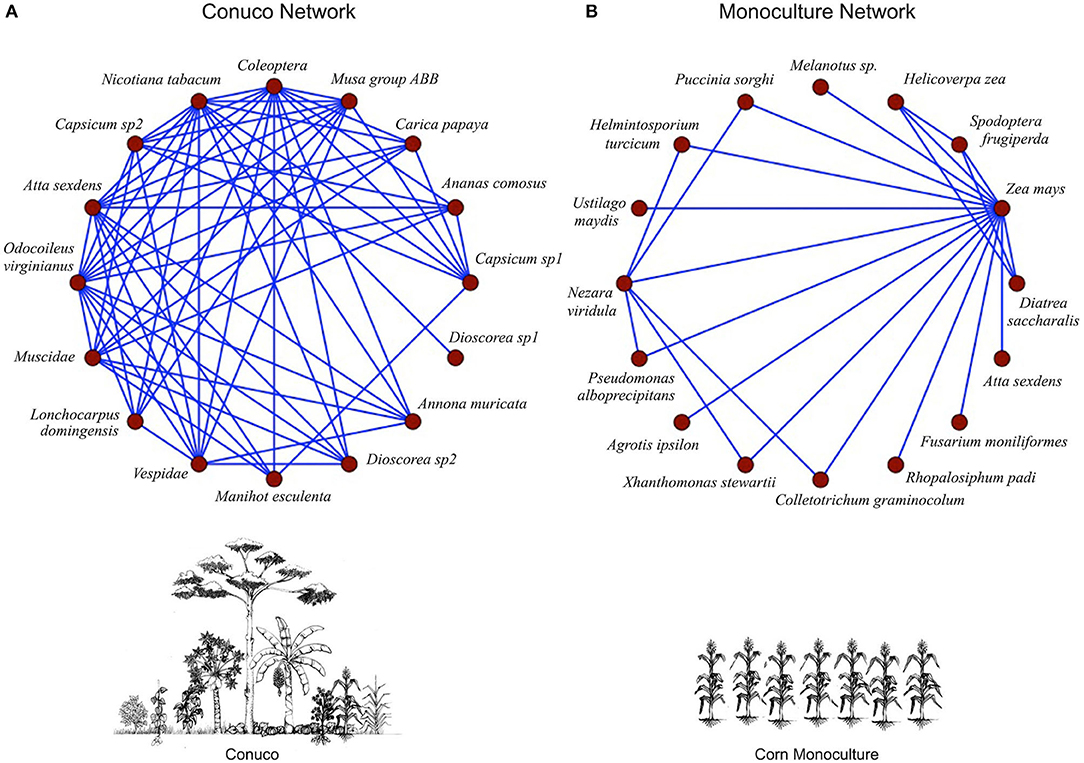
Figure 2. Ecological networks associated with a Hiwi conuco (A) and a corn monoculture (B). Nodes represent population species, links represent ecological interactions (modified from Griffon and Hernandez, 2014; Griffon and Rodríguez, 2017).

The Transition: To and Fro

Regarding the features of the transition between conventional and agroecological systems, Vandermeer and Perfecto (2017) state that the path from a pristine ecosystem to a monoculture could be different from the path from a monoculture to a pristine ecosystem. This is mainly because along the path that starts, for example, from a forest, a newly created agroecosystem benefits from a “positive legacy” that the forest has left (e.g., a complex ecosystem in the soil, which fosters its fertility); thus, although from an ecological point of view certain conditions deteriorate (e.g., may have less species richness), the ecosystem does not immediately experience a collapse in its properties. This legacy does not exist when the path starts from a monoculture because, for instance, the soil in the ecosystem is already deeply impoverished; hence, despite the fact that some components may have improved (e.g., some key microorganisms may have begun to colonize the soil because agrochemicals are no longer used), the system does not experience a general improvement immediately, a certain critical level should be attained first. Evidence of these types of transitions in tropical ecosystems is found in Staver et al. (2011a,b) and Hirota et al. (2011). On the other hand, El Mujtar et al. (2019) and Lupatini et al. (2014), based on field evidence, suggest that one of the key components in these transitions, are the biotic interactions among the elements of the system. The authors show that, although the components are essentially the same along the different stages of the transition, there are changes in the way these components interact (i.e., the ecological network architecture is different).

According to this contextual framework, it can be stated as a working hypothesis, that the differences in the paths, one direction or the other, may be significantly related to the structure of the interactions among the system components. Based on this, we explore in this article, from a theoretical point of view, the transition paths to and from networks with topological features similar to a corn monoculture and to a conuco, with specific emphasis on the role of the interactions between species (however, regardless of the actual biological identity of the species involved). That is, we study the consequences of modifying the interactions architecture on the dynamics of the agroecosystems, during these transitions. To do this, we translate the agroecosystems portrayed in Figure 2, into dynamical systems of equations that allow the study of their performance along the hypothetical transitions. Specifically, we build a theoretical model where the agroecosystems are represented by networks of interacting nodes, where the nodes represent different species (not biologically specified, but different), with explicit types of interactions between them that determine the dynamical behavior of the system at every step of the transition process.

It is important to note that using a theoretical approach implies that important adjustments and assumptions are made in the translation from the natural scenario to the theoretical representation (i.e., the model) in order to grasp (isolate the effect) the specific features we want the model to explore. For instance, although we are using topologies inspired by real agroecosystems and the works cited above provide empirical grounds for the focus of our study, in the model the nodes are abstract entities that do not represent actual biological species, but among which interactions occur and may change (unlike e.g., the works of El Mujtar et al., 2019, and Lupatini et al., 2014, where the interactions change, but the identity of the species are maintained). However, the dynamical model considers these nodes as different entities (populations) with specific types of interactions occurring between them, which allows to explore the particular matter intended. From here, then, follows a purely theoretical exploration on possible characteristics that the transition paths could have between two arbitrary networks with contrasting topologies.

Methods

The Model: Population Dynamics and Networks Dynamics

The dynamics associated with the ecological networks depicted in Figure 2, can be numerically studied using a model based on the classic Generalized Lotka-Volterra (GLV) system of equations in discrete time. We use here a variation of a model previously published by some of the authors of this article (Griffon and Hernandez, 2014, 2019; Griffon and Rodríguez, 2017). The model, as used here, is as follows. In the basic GLV model, the dynamics of population densities for each species in a community can be expressed as,

$\begin{array}{ll}{N}_{i,t+1}=N_{i,t}+r_i{N}_{i,t}+\frac{r_i{N}_{i,t}}{K_i}{\displaystyle \sum _{j=1}^{n-1}}{N}_{j,t}{\alpha }_{i,j}& (1)\end{array}$

where N_{i, t} is the population density of species i at time t, parameters r_i and K_i represent the discrete rate of growth and the environmental carrying capacity of species i, respectively, and n is the number of species in the system. The type of population interaction is determined by the sign of the interaction coefficients α_ij and α_ji, between each pair of species i and j. Thus, the actual values of all α_ij's in the system determine the architecture of the network, that is, the whole set covers how each species interact with every other (see e.g., Case, 1999).

Regarding the population interactions, we use the standard signs scheme to characterize them (Odum, 1953). When an interaction is favorable for a given species (i.e., when its growth rate is increased by the presence of the other species) the sign is positive (+); when an interaction is disadvantageous (i.e., its growth rate is decreased by the presence of the other species), the sign is negative (–); and in the case of a neutral (null) effect, zero (0) is used. In our model these effects are assigned unilaterally, i.e., each sign represents, on its own, how each species experiences the presence of the other. Thus, all combinations of signs can be obtained in the network, which represent the different possible interactions between any two species: –/– competition, +/+ mutualism, +/– contramensalism (predation, herbivory, parasitism), +/0 commensalism, and –/0 amensalism. Now, the model in Equation (1), as it is, implicitly assumes that the types of interactions remain constant over time; however, empirical evidence indicates that depending on various factors, the type of interaction between two species may vary in intensity and even in their nature (signs) over time (see e.g., Barkai and McQuaid, 1988; Cushman, 1991; Cushman and Addicott, 1991; Bronstein, 1994). These have been called interactions with conditional or variable outcome, and a wide conceptual framework has been developed regarding these, from both theoretical and empirical approaches (e.g., Hernandez, 1998, 2021; Addicott and Bao, 1999; Del-Claro and Oliveira, 2000; Holland et al., 2002; Holland and De Angelis, 2009; Yan and Zhang, 2014; Bageta et al., 2018; Revilla and Krivan, 2018; Krivan and Revilla, 2019; Zhang et al., 2021). For the sake of generality in our study, we are thus including the perspective of interactions with variable outcomes. This can be done by re-interpreting the interaction coefficients α_ij in the GLV model in Equation (1) as density-dependent interaction functions α_ij(N_j) that may vary in magnitude and sign with the population densities of the species involved. The shift in sign of the α_ij(N_j) function with the system dynamics allows for the change in the interaction outcome (more details on this theoretical approach in Hernandez, 1998, 2008, 2009, 2021; Hernandez and Barradas, 2003).

In terms of the study here, considering interactions with conditional outcomes means that the links in the networks can take different values, in both magnitude and sign, depending on the densities of the interacting species. The specific interaction function α_ij(N_j) used in this work to simulate the interactions in the networks is the non-linear quadratic α_ij(N_j) function with saturation; this was chosen because of its generality and biological soundness (see Hernandez, 1998, 2021). The model Equation (1) for the dynamics of species then becomes,

$\begin{array}{ll}{N}_{i,t+1}=N_{i,t}+r_i{N}_{i,t}+\frac{r_i{N}_{i,t}}{K_i}{\displaystyle \sum _{j=1}^{n-1}}{N}_{j,t}\left(\frac{b_i{N}_{j,t}-c_i{N}_{j,i}^2}{1+d_i{N}_{j,t}^2}\right)& (2)\end{array}$

where parameters b_i, c_i, d_i give the actual shape to the α_ij(N_j) function; they represent general biotic and abiotic environmental conditions that reflect on the interactions intrinsic features, e.g., saturation values, sensitivity of the interaction to changes in the partner's density, thresholds between positive and negative interactions, etc. The particular form of the interaction function α_ij(N_j) in Equation (2) describes a positive interaction for species i at low densities of N_j, becoming negative at higher densities, with a plateau (saturation). This is one of the most common forms of shift in outcome in nature, which may occur, for instance, from a mutualistic to an antagonistic interaction as partner's densities increase (see e.g., Bronstein, 1994; Hernandez, 2021).

Equation (2) is used to model the dynamics within the networks associated with the conuco and the monoculture communities depicted in Figure 2. Both involve n = 16 species, thus, the dynamics are determined by a system of 16 equations each; all parameter values and variable ranges used in the simulations are specified later in this section.

Some Preliminary Results as Starters

Using a modeling approach as described in Equations (1) and (2), Griffon and Hernandez (2014), and Griffon and Rodríguez (2017), studied the dynamical behavior of agroecosystem networks like a conuco and a monoculture. Their results were valuable as references for the starting points in this study on the transitions between these two agroecosystems. Their main results are illustrated by the graphs in Figure 3.

FIGURE 3

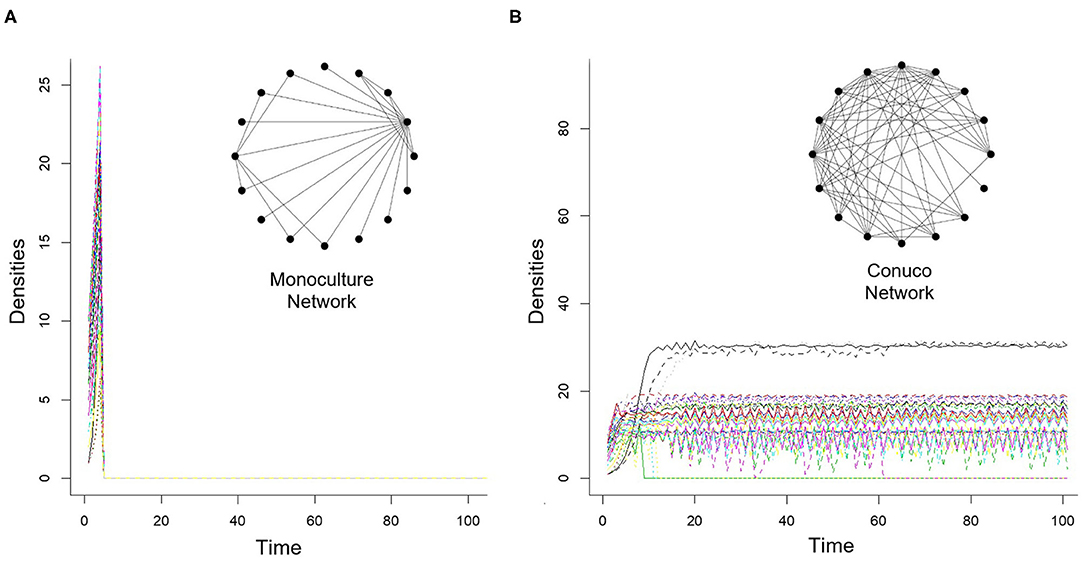
Figure 3. Characteristic population dynamics associated with the topologies of Monoculture (A) and Conuco (B). Each color line represents the density of a different species (modified from Griffon and Hernandez, 2014; Griffon and Rodríguez, 2017).

Figure 3A depicts the characteristic behavior that they obtained for populations in a monoculture community. It shows a rapid increase in population densities and a subsequent fall, until extinction, of all populations. This happened in all the simulations done. This may represent, for instance, a pest situation, where the densities of all the species that feed on the monoculture sharply increase and, after depleting the resource, become extinct. It is interesting to note then, that the ecological network that represents a monoculture generates non-persistent dynamics (under the modeling and simulation schemes used), that is, systems that do not extend over time, which is as much as saying that they are not sustainable. In this context, the non-persistence of the system means that its internal dynamics lead to its collapse. This is probably the reason why this kind of monoculture is so intervened with pesticides (to prevent the increase of phytophagous populations that would destroy the entire crop). That is, in the real system, the persistence is achieved only by incorporating external inputs. From a formal (mathematical) approach we say that the monoculture is a stable system, in the sense that it will always reach a stable (extinct) state, unless perturbed (e.g., addition of external elements).

On the other hand, the dynamics associated with the conuco behaves as shown in Figure 3B. Although some populations may become extinct, in the long run most of the populations remain (either at a plateau or within bounded positive values), which means that the system regulates itself and persists. This was observed in 100% of the cases explored. This shows that the mental image of traditional Hiwi farmers is sustainable in the sense expressed above. It should be noted that these behaviors obtained for both monoculture and conuco correspond to empirical evidence (Valdivia, 1994).

The Simulations: The Topology and the Transitions

These networks can be further explored and categorized based on two standard topological measures: connectance and degree centrality. The connectance of a network (sometimes referred to as density of a network) is the ratio between the number of links present in the network and the maximum possible for the same number of nodes (Costa et al., 2007). Centrality, in general terms, is a measure of the importance of specific nodes within a graph in terms of a given attribute. Different nodes could be considered important depending on the attribute assessed, thus, many centrality measures have been developed. The one of interest now is the degree centrality, in which the attribute evaluated is the degree of the nodes of the network. The degree of a node is equal to the number of links it holds. Thus, the degree centrality of a network tells us about how many links go through its central node. In familiar terms, we can describe degree centrality as measuring the opportunity of a node of receiving whatever is flowing through the network. Centrality measures in general, are normalized by dividing by the maximum theoretical score for a graph with the same number of links and nodes. In the degree centrality case, the score of a star-type graph (a graph in which all nodes connect to a hub) with the same number of nodes and links is used (Freeman, 1978). For simplicity, from now on we will refer to the degree centrality just as centrality.

The values of connectance and centrality can be calculated using standard formulas found in the literature (not shown here for neatness, see e.g., Costa et al., 2007). The values for these measures for the conuco and corn monoculture depicted in Figure 2 are presented in Table 2. This table clearly shows that a monoculture is characterized by a high centrality and a low connectance, while the conuco is the opposite.

TABLE 2

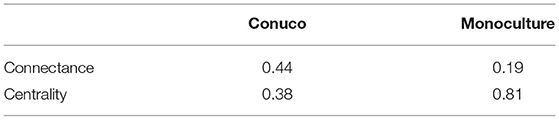
Table 2. Connectance and centrality values for Conuco and corn Monoculture networks in Figure 2.

Note then, that to emulate transitions to and from the monoculture and conuco type networks we can just manipulate these topological features, i.e., change the connectance and/or centrality values, progressively generating new networks from the original ones. Along the transition process, the effect on the dynamical properties of the systems (which is our ultimate interest, e.g., persistence) can be analyzed; that is, the complex equations in model (2) are studied through the simpler topological expressions.

Thus, to simulate the transition paths between the monoculture and conuco networks we modify their topological features. To do this we choose the protocol that involves fewer steps and decisions in terms of ad hoc hypotheses about the transition process. That is, (i) modify only one of the two topological measurements, this allows us to observe not only the effects on the dynamics of the systems, but also on the other topological measurement, (ii) choose to vary connectance over centrality, because as the number of nodes in both networks is the same, we only need to vary the number of links between nodes to generate the variants of the networks (varying centrality would involve having to make further assumptions, i.e., bias in the experiments), and (iii) as an extension of the same reason, we decide to make the changes in connectance randomly, this avoids involving other processes which could have a greater ecological bias. It is pertinent to comment here that the choice of this methodology is strictly theoretically oriented, aiming for consistency with the postulations of this study and thus, with the building of the model. That is, it is not based on empirical evidence about the way biological species actually interact, in which case other methods commonly used for the simulation of biological networks would apply, e.g., the preferential attachment algorithm (Barabási and Albert, 1999). Also note that adding and removing links is equivalent to say that we generate new ecological networks where we vary the number of population interactions (in this case unilaterally). We keep the number of nodes constant all throughout the simulations because we want to focus specifically on the effect of the variation on the number of population interactions; also note that because the number of nodes is constant there is always a linear relationship between the connectance and the number of links in the network. Simulations were performed in the R environment (R Core Team, 2019).

Transitions are simulated along two paths or routes:

1. Link up path (see Figure 4A). Starting from the monoculture topology (the “original network”, with 16 nodes and 45 links) we generate an “initial network”, with the same number of nodes and adding five links randomly. We analyze the dynamics of this network numerically using the model of Equation (2) for 120 iterations, and a “final network” is obtained. We call this “an experiment” and 40 repetitions of this are done. We repeat the whole procedure always adding random links, five at a time, until 105 links are reached (which is the number in the original conuco network).

2. Link down path (see Figure 4B): Starting from the topology of the conuco (the “original network”, with 16 nodes and 105 links) a procedure equivalent to the previous one is performed but eliminating links randomly, five at a time, starting from 105 down to 45 links (which is the number in the monoculture network).

FIGURE 4

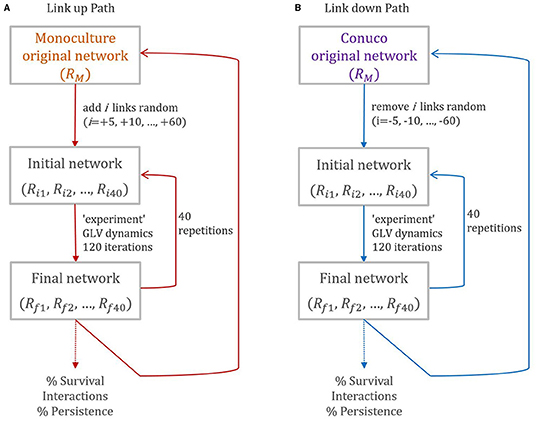
Figure 4. Schematic representation of the simulation process, for Link up (A) and Link down (B) paths. At each step data is registered, for each network, R_x= R_x(number nodes, number of links, connectance, centrality, transitivity, reciprocity), and for each experiment (percentage of population survival, types of interactions, percentage of persistence).

The dynamics of the systems are simulated numerically by 120 iterations, because in preliminary explorations we observed that for this number of iterations the systems have already achieved some type of characteristic behavior, such as extinction of all species or persistent bounded dynamics (in stationary or oscillating equilibrium densities, or a combination of both).

In the simulations, the values of parameters K, b, c of equation (2) (i.e., carrying capacity and two shape parameters of the conditional interactions), are assigned at random from a uniform distribution bounded between (1 and 100), (0.2 and 0.4), (0.1 and 0.4), respectively (following the methodology in Griffon and Hernandez, 2014, Griffon and Rodríguez, 2017). Other parameters are r = 0.5, and d = 2.0 (i.e., the discrete rate of growth and a shape parameter of the conditional interactions). Initial densities, N_{i, t}, for each species are randomly assigned taken from a uniform bounded distribution between 1 and 100. It is worth noting that this is an experimental approach to the theory, where more than generalizations, the interest is in finding the possibility of certain results or performance of the system (e.g., the persistence in time of a particular network).

From this procedure, we record the following data and results, for each path (link up and link down):

1. For each original or generated network in the process the number of nodes and links are registered, and from them the following is calculated, (i) Connectance, (ii) Degree centrality of the network, (both as defined above), (iii) Transitivity (also known as global clustering coefficient), which is the average, for all nodes of the network, of the observed number of three-node loops for each network node, with respect to the maximum number of three-node loops in which this particular node could participate (Costa et al., 2007), (iv) Reciprocity, which measures the relationship between all pairs of reciprocally connected nodes (i.e., reciprocal links) and all links in the graph, whether reciprocal or not (Costa et al., 2007). These metrics were calculated using the Igraph library of the R environment (Csárdiand and Nepusz, 2006).

2. From each experiment performed in the process the following is recorded, (i) Percentage of surviving populations in the community after the GLV dynamics process of Equation (2) is applied, for each number of different links, (ii) Percentage of persistence of the system after 40 repetitions of each experiment. The system persists if at least one population of the initial network survives, it is calculated for each number of different links, (iii) Types of interactions resulting in each experiment: (a) Percentage of positive interactions (unilateral) in the network at the end of the experiment, (b) Percentage of interactions with oscillating values (in intensity and/or sign) in the network at the end of the simulations.

It is important to bear in mind that although the initial network in each experiment is generated by random addition or removal of some links (of the original network), the final network is the result of a dynamical process lead by the types of interactions (beneficial, detrimental, or neutral) between pairs of nodes (species).

Results

Figures 5–9 show the results of the simulations. In all, the final network properties are depicted against the number of links in the initial network, which is to say, against the connectance. Bear in mind that the graphics are read from left to right for the link up path (number of links increasing) but from right to left for the link down path (number of links decreasing).

FIGURE 5

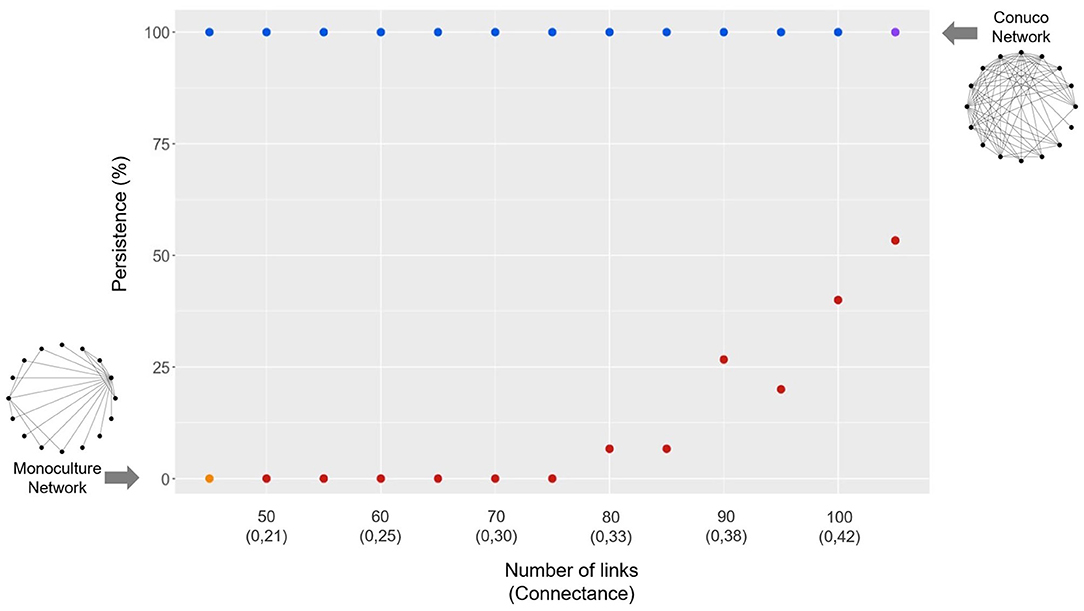
Figure 5. Relationship between percentage of persistence of final networks and number of links of initial networks (corresponding connectance value below), for the link up path (red dots) and link down path (blue dots). Original networks also shown, Monoculture (orange dot) and Conuco (purple dot). Arrows show the direction of the process for each path (see text and Figure 4).

Figure 5 shows the percentage of persistence (% of times in which the system persists after the GLV dynamics) obtained along each path. For the link down path (blue dots; starting from the conuco type network) 100% of the systems persist for all connectance values. On the other hand, along the link up path (red dots; starting from the monoculture type) the persistence is null for networks up to 75 links; at 80 links (connectance 0.33) and beyond, the persistence increases in an exponential pattern, reaching values close to 60% for 105 links. So, 80 links represent a critical point, where the dynamics of the system change; beyond that point a qualitatively different behavior emerges. In ecological terms, this means that the self-regulation of the system appears as a possibility, as could be, for example, the autonomous biological control of pests. It is worth noting that for low connectance values the networks can present such highly contrasting behaviors, i.e., 100% assured persistence or extinction.

Figure 6 shows the results for four measurements (variables); the left column along the link up path (red dots) and the right column along the link down path (blue dots). The size of the dots is proportional to the number of cases observed for each value of the variables. Figure 6A presents the survival percentage of populations (% of populations that survive in each experiment) for each value of number of links (connectance) of the initial networks. The results of 120 iterations (with 40 repetitions) are shown for each number of links. It can be seen that in the link up path (left) for values <80 links the survival percentage is always zero (as expected from results shown in Figure 5), and from 80 links and beyond, in addition to the null result, positive values also appear with very high percentage survivals (between 87.5 and 100%); although, according to the size of the dots most of the results still go to zero. However, note that the spectrum of these positive values increases progressively with the connectance, and that there is always a 100% value present. So, in simple terms, once 35 or more links have been incorporated at random into the monoculture network architecture, the dynamics achieved allow the possibility of survival of all populations (with bounded behaviors, i.e., without exponential growths). This represents a huge difference compared to the original dynamics of the monoculture. In contrast, in the link down path (right), survival is always >0 and for each number of links several options are obtained, limited between ~56 and 100% of survival, with an apparently uniform distribution on the plane.

FIGURE 6

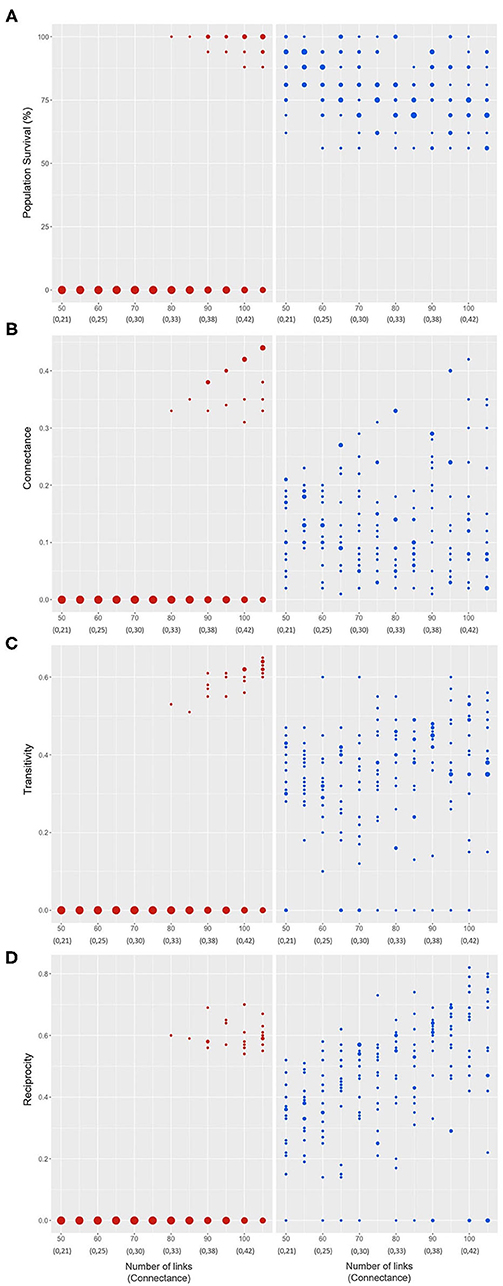
Figure 6. Final networks properties as a function of the number of links of the initial networks (corresponding connectance value below) after experiments. Percentage of survival of populations (A), Connectance (B), Transitivity (C), Reciprocity (D). Left column: link up path (red dots); right column: link down path (blue dots). The size of the dots represent the proportion of times that a result (of the 40 repetitions) yields a given value.

A general look at Figure 6 as a whole shows that there is a pattern of behavior, similar to that described for Figure 6A in relation to the link up and link down path results, for the other measures evaluated, that is, for connectivity, transitivity and reciprocity of the final networks. This is expected since it corresponds to measurements on the networks obtained in the experiments reported in Figure 5. Thus, in all cases, for the link up path the values are null until the threshold of 80 links, at which the positive options appear (although less frequent than the zero option), while in the link down path the positive options occur for all connectance values. However, observe that the positive values in the link up path appear in the form of bounded clouds of points, while in the link down path, the positive options occupy all or almost all the space, that is, they show a greater variance of values per experiment.

Apart from this general pattern, it is pertinent to highlight some trends in each of these figures. Figure 6B displays the connectance of the final vs. the initial network, and we observe that, (1) in all cases the final networks have equal or less connectance than the corresponding initial network, (2) the spectrum of positive values in the link up path increases with connectance, although they are bounded below by a value around 0.3, while in the link down path the values seem to simply occupy as much space as possible, and (3) in the link down path the final connectance is always >0, while in the link up path it can take values equal to zero; these may correspond to the non-persistent results shown in Figure 5, or to networks that survive with only one species.

Figures 6C,D present the values for transitivity and reciprocity, respectively, of the final networks, and we observe that, (1) the cloud of points of positive values (after the 80 links threshold, in the link up path) in transitivity presents an increasing tendency with the increase in connectance, reaching values above 50% and rising; reciprocity values occur in ranges around 55–70% with no apparent trend of change, (2) in the link down path, transitivity does not show an apparent trend of change, while reciprocity seems to show a tendency to decrease with the decrease in the number of links, and (3) in the link down path, both for transitivity and for reciprocity, values equal to zero are obtained, which means that persistent networks (they all are in this case) can have final transitivity and/or reciprocity equal to zero (the link up path graphs do not allow to distinguish between persistent or non-persistent networks, with respect to the null values of transitivity and reciprocity).

Figure 7 displays the final configuration of the types of population interactions, in terms of their signs (unilateral, as stated in the section Methods), after the Lotka-Volterra dynamics experiments. In the case of the link up path (left column), the figures show that for persistent networks (i.e., for values at 80 links or more) positive interactions occur, although in a low proportion, which is to say, most of the interactions are negative (Figure 7A), and there is always a percentage of interactions with oscillating values (i.e., conditional interactions taking different values in the iterations) (Figure 7B). Hence, in the link up path, once the addition of links has exceeded the critical point, there is a predominance of negative unilateral interactions in the networks. The results of the simulations in the link down path (right column), again show a greater variance.

FIGURE 7

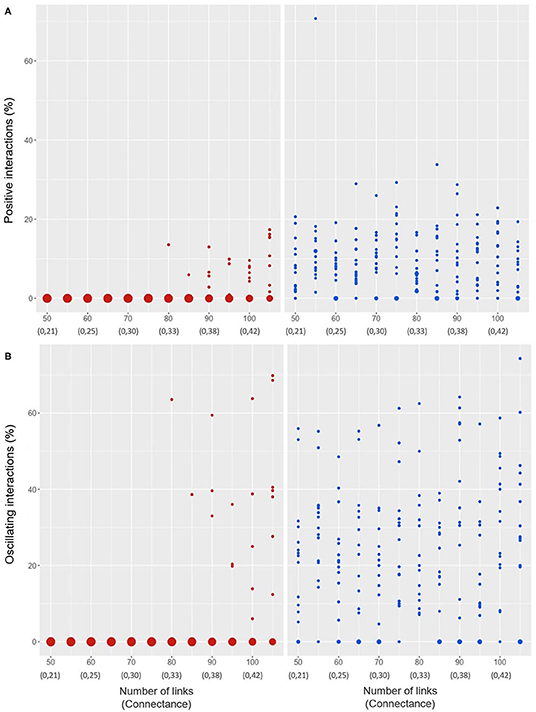
Figure 7. Positive (unilateral) interactions (A) and interactions with oscillating values (B) after experiments as a function of the number of links of the initial networks (corresponding connectance value below). Left column: link up path (red dots); right column: link down path (blue dots). The size of the dots represent the proportion of times that a result (of the 40 repetitions) yields a given value.

Finally, it is important to appreciate that the random addition or removal of links may affect other characteristics of the network topology. An especially relevant one in this study is the degree centrality of the network. Figure 8 depicts the effect of the whole process along the link up and the link down paths, and also, for the sake of including a universal comparison pattern, with the process performed on networks wired randomly (i.e., Erdös-Rényi networks), each constructed independently, for the same connectance values and number of nodes. The link up path (red line) shows that centrality decreases with the increase of connectance. The link down path (blue line, reading from right to left), shows that centrality also decreases during the process (decreasing connectance). The networks generated completely random (green line) present lower values of centrality than the above, and show independence from the connectance. A selection of typical networks obtained along the processes are also shown in the figure to appreciate visually the forms (topologies) for some connectance and centrality values. Corresponding to the link up path, for the 55 links network (top left), it is possible to identify a central node to which many links are directed (star type topology); however, it is not possible to identify a node that monopolizes the links in the equivalent 55 links network of the link down path, as neither is for any of the networks with 80 or 100 links.

FIGURE 8

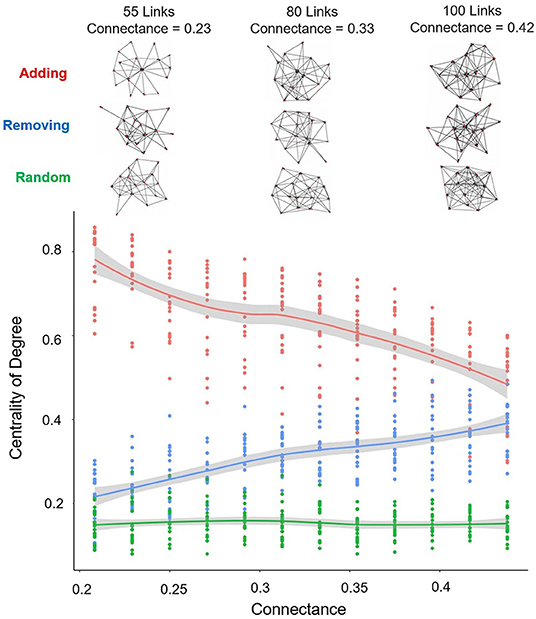
Figure 8. Relationship between the centrality of the final networks (mean and 95% confidence interval shown) and their connectance, along the link up path (red line), the link down path (blue line), and random networks (green line). Upper part: some examples of the networks topologies along the process shown in the graph below.

The relationship between centrality and connectance becomes relevant when we assess them jointly with the effect on the percentage of persistence of the communities. This is best appreciated in a three-dimensional representation, like Figure 9, which shows how the link up and the link down paths are clearly differentiated in terms of the percentage of persistence levels. This figure exhibits an integral reading of the general behavior of the two paths sequentially, in terms of the trajectory of the system along the persistence values (from 0 to positive values, up to 100%) with respect to the corresponding connectance and centrality values (centrality values obtained along the connectance modification process). It can be seen that the threshold of 80 links (connectance = 0.33), in the link up path, corresponds to a centrality of 0.65. What is important here, is that as the architecture of the network is no longer dominated by one node (as in monocultures), its probability of persistence increases, which represents an eloquent argument against this type of architecture.

FIGURE 9

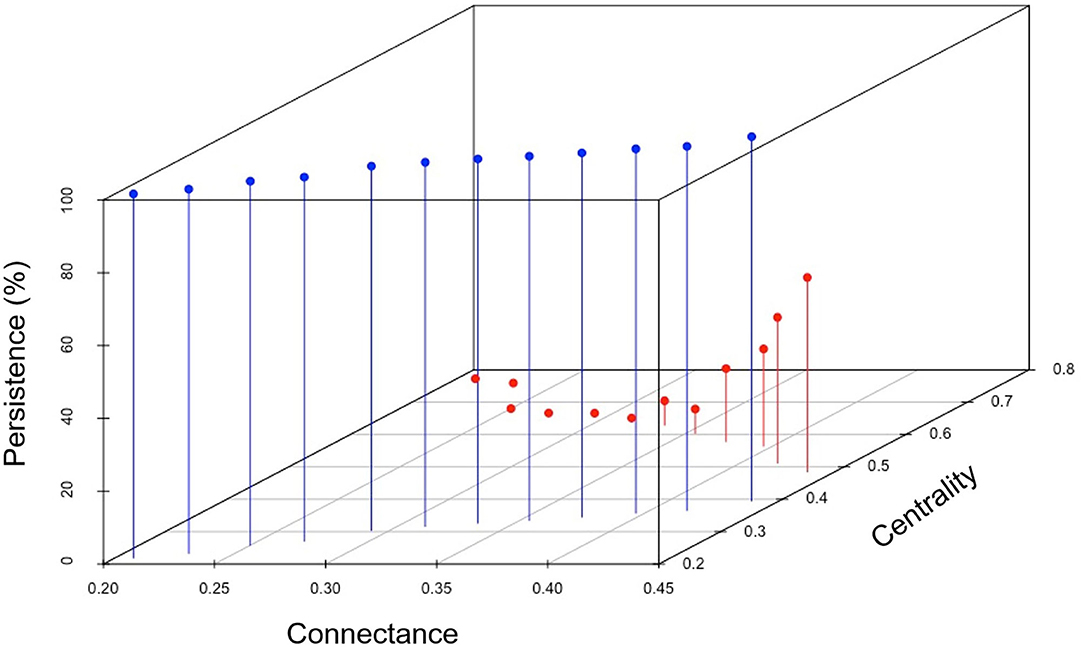
Figure 9. Relationship of the percentage of persistence of the final networks with the centrality and connectance of the initial networks, along the link up path (red dots) and the link down path (blue dots).

Succinctly, the results of the transition experiments indicate:

• A network with a monoculture type topology (high centrality, low connectance) subjected to a Lotka-Volterra dynamic process on its populations, reports a zero persistence. If from this topology we generate new networks in which the connectance (number of links between its components) is randomly increased, we observe that the centrality of the generated networks decreases, and when it reaches a threshold value or tipping point (of connectance and centrality) a percentage of these networks persists. See Figures 5, 6A, 8, 9 (link up path).

• A network with a conuco type topology (low centrality, high connectance) always persists after being subjected to the Lotka-Volterra dynamic process, that is, at least one of the species persists. If from this topology we generate new networks by randomly decreasing the connectance, we observe that the centrality of the generated networks also decreases. For all networks generated this way persistence is always maximum (100%). See Figures 5, 6A, 8, 9 (link down path).

Discussion

About the Transition

The results of the simulations show important qualitative differences in the fate of networks that originate from a monoculture or from a conuco topology type. In particular, these reveal the dynamic drawbacks associated with topologies with high centrality and low connectivity, which is a distinctive trait of all monocultures. On the other hand, the benefits of the conuco network (with low centrality and high connectivity) are maintained, even when the number of population interactions is reduced.

First we want to discuss the effect of the whole process on the network topologies. On topological terms, it is important to emphasize that in both the link up and link down paths (i.e., either adding or removing links), the centrality of the networks decreases. When we contrast the results of these paths with randomly generated networks (Figure 8) we observe that both the monoculture and the conuco networks have higher centralities than these, but the process brings the centrality values closer to the completely random networks, along both paths. That is, the randomness in the manipulation of the links move the networks (all of them) toward the random type. It is important to highlight then, that with the methodology used (add or remove links randomly) from the monoculture topology it is possible to achieve an architecture very close to that of the conuco, but not vice versa, that is, adjustments on the conuco do not lead to the centrality values of the monoculture. Note here, that other methodologies for adding/removing links might lead to topologies closer to the objectives. For example, a preferential elimination of links according to the degree of the node (i.e., an inverse, but equivalent, version of the Barabási and Albert, 1999, algorithm) could generate architectures closer to the monoculture starting from the conuco topology. This would probably lead to interesting results to contrast with the ones presented here, however, as stated above, for this study we chose to introduce the least ecologically biased choices possible.

Now we want to examine the topology outcome in the context of the persistence of the agroecosystems, which is ultimately the relevant issue here. It is illustrative to follow the progression of the persistence values along the whole process (Figure 9). Let us start at zero persistence, at the value of greater centrality and lower connectance: the monoculture topology (red dot at far end corner). From there, along the red path, some more zero values occur, but then the persistence rapidly increases becoming very high, reaching 100% at the value of greater connectance and medium centrality: the closest to the conuco topology. After that, a persistence of 100% occurs and is maintained along the entire blue path, in which both the centrality and the connectance keep decreasing, down to values close to the random network topology (all random networks in Figure 8 have a persistence of 100%, not shown in the figures).

Why then, from certain connectance and centrality values on, do persistent communities begin to emerge, and stay so? Although further theoretical exploration is needed (including more parameters and variables, and maybe additional network configurations) we could speculate so far that, from these threshold values of connectance and centrality onwards, some topological structures in the networks start to arise, which jointly promote the coexistence of populations. To assess and support this inference we examined former studies on these topics and compared their results with those obtained in this work. A first mechanism to take into account are ecological intransitive loops. These are interaction cycles (typically of competitive nature) analogous to the rock-paper-scissor game, where no species is absolutely superior to all the others (Gallien et al., 2017). For instance, there is evidence that suggests that intransitive loops facilitate the coexistence of species (Ulrich et al., 2014, 2018; Soliveres et al., 2015, 2018; Vandermeer, 2015; Maynard et al., 2017; Vandermeer and Perfecto, 2017; Gallien et al., 2018; Soliveres and Allan, 2018; Stouffer et al., 2018; Vandermeer and Jackson, 2018). Likewise, there is evidence that states that persistence is promoted by non-reciprocal (i.e., commensalism and commensalism) interactions (De Angelis, 1975; Odum and Biever, 1984; Lawton, 1989), unilateral negative interactions (these may promote the emergence of self-regulation mechanisms, such as negative feedback loops, which have been found in some cases to be related to the persistence of the systems) (May, 1973; Levins, 1974), and interactions with oscillating values (Yan and Zhang, 2014). With this in mind then, we draw attention to the following attributes and tendencies of the persistent networks obtained in this study, as connectance increases (after the 80 links threshold), as reported above in the results regarding Figures 6, 7:

• Transitivity increases (which is a proxy for intransitive three nodes loops), reaching significant values, above 50% and rising, as connectance is increased (also, in our simulations with random networks, transitivity increases linearly with the number of links; not shown here)

• More than 30% of non-reciprocal interactions occur

• Most unilateral interactions are negative

• There is always a percentage of interactions with oscillating values

In general terms, two arguments stand out from what was discussed above, (1) The conuco topology, with its greater connectance and lower centrality (compared to monoculture), serves as insurance against the extinction of its populations. (2) Networks generated from a monoculture, regardless of their connectance and centrality values, always present the possibility of extinction (even in the cases where there is also a surviving solution). These results strongly emphasize the importance of stimulating, as far as possible, the diversity of interactions between the components of agrobiodiversity.

A few comments on the scope and limitations of the exploration presented in this work are in order. It is important to emphasize that although the architecture of the original networks (conuco and monoculture) is based on field information, the simulation of the transition process done here is strictly theoretical. Therefore, our results show only possibilities, not in field (empirically confirmed) facts. It is also important to point out the limitations associated with the heuristic approach of this work; so, it may be possible that with other parameter values (not explored here), or including other variables and parameters in the models, we could obtain different results. Also, treating nodes as abstract entities and adding/removing links randomly can be justified in theoretical terms, but caution should be exercised in the ecological implications of this, which are not obvious and can lead to erroneous extrapolations. Finally, without a doubt, the real process of transition involves a much broader set of factors than those considered in our model, so the real phenomenon may be even more (or less) complex than our exploration here shows. Nevertheless, our study yields definite results for two specific network topologies and circumstances, which adequately represent typical agroecosystems found in the field; hence, this work provides a valuable frame of reference for both field workers and further research.

The Metaphor, the Legacy and the Trap: An Afterthought

The procedure that governs the dynamics of the simulations in this study, where links are sequentially added or removed, generates a relationship that can be antagonistic (of conflict) between centrality and connectance, in which variations in the connectance (increases or decreases) always translate into a decrease in centrality. Hence, the resulting paths, when applying the process in one direction or the reverse, are noticeably different. This means that in these experiments history matters (the traveled path); this in turn draws attention to the presence of a region with alternative states (i.e., different results for the same parameter values). All these characteristics evoke the type of systems studied by the Catastrophe Theory (Thom, 1977; Zeeman, 1979). In particular, the paths, as presented in Figure 9, bring to mind the graphic representation of a cusp catastrophe surface (i.e., a response variable in a two parameter space), on which divergent trajectories may lead to alternative stable states, with the possibility of shifting from one to the other either abruptly (catastrophe) or smoothly (along the surface). This provides a figurative approach to interpret the relationship presented in Figure 9, that is, the three-dimensional graph of the persistence of the systems (the variable of interest here) against the connectance (the control parameter) and its corresponding centrality values.

This figurative representation of the results as a surface containing alternative states provides a simplified system that allows visualizing and conceiving some interpretations, in the knowledge that it keeps the information from the complex dynamics operating underneath. That is, we can study the action of the Lotka-Volterra dynamics on the system (which is ultimately the responsible for any outcome, but can be really complex due to the myriad of parameters involved) by exploring the patterns that emerge with respect to the connectance and centrality parameters. In this context then, monoculture and conuco can be understood as alternative stable states.

When a system is in either one of these states, it means that the balance of influences acting on its domain is reinforcing its permanence in that state and moving away from it may require great effort. That is, in strict mathematical terms both states are stable equilibria, however, given the ecological features studied here that surround both attractors (e.g., persistence of the systems), we may indulge in the following allegorical conception of these border situations. We may say that the conuco has a “legacy” (or an “eco-history”) that allows it to continue generating persistent dynamics, even when the system gradually becomes impoverished or degraded (in terms of the decreased number of population interactions). However, at a certain level of impoverishment, the system will cease to be persistent and once there, getting it back to its previous state will require more effort. On the other hand, the monoculture behaves as a kind of “trap,” in which, even if the system conditions were improved, it would still generate non-persistent dynamics. This explanation helps to understand why the transition from a conventional to an agroecological system can be difficult, because improvements do not pay immediately; nevertheless, once at the other end the efforts may be more than rewarded.

This interpretation of the results supports the proposal that the transition from one agricultural syndrome of production (i.e., a collection of activities that characterizes a certain way of doing agriculture) to another (e.g., from a monoculture to a multi-diverse system), involves critical transitions (Vandermeer and Perfecto, 2012, 2017). It is important to take into account that it is not easy to identify in advance the moment at which these systems may experience abrupt qualitative shifts (Scheffer et al., 2009, 2012), but certainly it is important to know they may exist.

These results, although abstract and theoretical, contain lessons that can be empirically applied and that are of interest to farmers or field agroecologists. For instance, they point out that it is not a good idea to maintain an agroecosystem with most of the interactions concentrated in a single species, as occurs when the population density (or biomass) of a single crop disproportionately predominates in the system. Rather, it is favorable to increase the links among the elements of the system.

Unfortunately, it is not possible to establish fully in advance how the elements of agrobiodiversity will interact in the field. However, it is possible to design agroecosystems that increase the number of possible interactions in it. Although our study was performed keeping constant the number of species in the networks, it is clear that just by increasing the number of species in an agroecosystem the possible number of interactions will increase; this is something that can be easily done in the field. To support this notion, it is enough to realize how this phenomenon escalates: a system with a single species does not contain inter-species interactions, in a system with two species there is only one possible interaction, with three species there are three possible interactions, with four species there are 6, with 5 there are 10, and with 6 there are 15. The number of possible interactions grows according to n(n–1)/2, where n is the number of species. These are theoretically possible interactions, which under no circumstances means that they actually happen in agroecosystems. Nevertheless, it is true that increasing the biodiversity of the system increases the number of possible interactions and this, according to our results, increases the probability of persistence of the systems.

As a closing remark, the topologies discussed here, beyond any relevant ecological information they may contain, explicitly reveal particular subjectivities associated with the people who interact with these agricultural systems (in this case, traditional indigenous farmers and agronomists). For the agronomists, for example, the monoculture is conceived as a system in which all the species interact with the crop (specifically, feed on it); and the possible drawbacks this fact has on the crop are managed with the use of external inputs (i.e., pesticides). In that context, the architecture of the agroecosystem interactions is simply not taken into account; the management is just based on external control. Therefore, the idea that the system (or indeed, nature) can be easily controlled (no further consequences considered) is a notion that is firmly ingrained, not only in conventional agriculture, but also in our societies.

In this regard, it is important to recognize that “in every perception of nature there is actually present the whole of society” (Adorno, 1984) and it is unquestionable that “human beings observe the natural world as a reflection of the dominant social organization” (Levins and Lewontin, 1985). Hence, we find truthful the thesis of Bookchin (1982) that states that “nearly all of our present ecological problems originate in deep-seated social problems. It follows, from this view, that these ecological problems cannot be understood, let alone solved, without a careful understanding of our existing society and the irrationalities that dominate it”. Therefore, the changes necessary to achieve agroecosystems that help solve the many ecological crises we face go well-beyond the strict scope of agroecosystems.

Conclusions

The ancestral farming system known as conuco presents a set of attributes that makes it particularly valuable as a prototype in the construction of possible alternative agricultural models. The conuco is an eloquent example of the significance of the ecological context in which agriculture takes place. In particular, as far as tropical agriculture is concerned, this farming system underlines the agroecological importance of increasing biodiversity in its horizontal, vertical and temporal components, with the inherent consequence of an increase in the number and types of interactions among its populations.

The comparison between a conuco and a monoculture highlights the importance of the topology of ecological interactions in the persistence of agroecosystems. This paper delves into the relevance of the connectance and the degree centrality of these networks, and on the likelihood of self-regulation of population densities in agroecosystems, particularly in the transitions between monocultures and conucos. In this regard, the high centrality and low connectance characteristic of monocultures are pointed out as responsible for the inherent non-persistence of this type of agroecosystems, whereas the greater connectance and low centrality of the conuco network ensures its persistence.

The analyses of transitions between the two networks suggest that these dynamics could be figuratively interpreted as a cusp catastrophe surface, i.e., one on which divergent trajectories may lead the system to alternative stable states. Understanding the monoculture and the conuco systems as alternative stable states implies that the forces that operate around each of them act as a shield against transformation, hindering the transition. This conceptual framework allows us to understand some of the difficulties observed in the transition from monocultures to more diverse systems. Our results also indicate that diverse systems are capable of enduring (to some extent) the impoverishment or degradation of some of their attributes without impairing their overall performance. Thus, we must add that in the process of transition from a monoculture to a multi-diverse system, it is prudent not to despair if there are no immediate improvements in the performance of the system, because once a certain point is reached, the system may experience an abrupt improvement, which confers all the advantages of the multi-diverse systems already mentioned.

Data Availability Statement

The code supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

DG, M-JH, and DR contributed equally to the design and implementation of the research, to the analysis of the results, and to the writing of the manuscript. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Eglee Zent, Ivonne Rivas, and Fedora Briceño for pointing out relevant literature. Francisco Javier Velazco, Esteban Emilio Mosonyi, and Elsa Gabriela Rodríguez for their valuable comments, suggestions, and orientations in the anthropological approach. Fernando Núñez and Pedro Martínez for their help in the data collection. Diego Rodríguez, Renato De Nóbrega, and Jesús Alberto Léon for their comments and suggestions on the general model and the experiments design. All reviewers made valuable comments and suggestions that certainly improved this article.

References

Addicott, J. F., and Bao, T. (1999). Limiting the costs of mutualism: multiple modes of interaction between yuccas and yucca moths. Proc.R.Soc.Lond. B. 266, 197–202. doi: 10.1098/rspb.1999.0622

CrossRef Full Text | Google Scholar

Adorno, T. (1984). Aesthetic Theory. London; Boston, MA: Routledge and Kegan Paul.

Google Scholar

Altieri, M. A. (2008). Movilizándonos Para Rescatar Nuestro Sistema Alimentario. Ecoportal. Available online at: https://www.ecoportal.net/temas-especiales/desarrollo-sustentable/movilizandonos_para_rescatar_nuestro_sistema_alimentario/ (accesed January 10, 2020).

Google Scholar

Altieri, M. A., and Nicholls, C. (2008). Los impactos del cambio climático sobre las comunidades campesinas y de agricultores tradicionales y sus respuestas adaptativas. Agroecología 3, 7–24.

Google Scholar

Bageta, C., Alberto, M., Sartor, C., Cecconato, A., Bevaqua, A., Tirador, M., et al. (2018). Influencia de la vid (Vitis vinifera L.) sobre cultivos de cobertura: un modelo biomatemático de la transición de amensalismo a comensalismo. Rev. Fac. Cienc. Agrar. 50, 33–45.

Google Scholar

Barabási, A. L., and Albert, R. (1999). Emergence of scaling in random networks. Science. 286:509–512. doi: 10.1126/science.286.5439.509

PubMed Abstract | CrossRef Full Text | Google Scholar

Barkai, A., and McQuaid, C. (1988). Predator-prey role reversal in a marine benthic ecosystem. Science 242, 62–64. doi: 10.1126/science.242.4875.62

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonilla-Bedoya, S., Lugo-Salinas, L., and Mora-Garcés, A. (2012). Distribución de los cultivos piaroa y su relación con las propiedades y características edáficas, en los conucos de la Orinoquia Venezolana. Rev. Chapingo Ser. Cie. 18, 241–249. doi: 10.5154/r.rchscfa.2011.11.084

CrossRef Full Text | Google Scholar

Bookchin, M. (1982). The Ecology of Freedom. Palo Alto, CA: Cheshire Books.

Bronstein, J. L. (1994). Conditional outcomes in mutualistic interactions. Trends Ecol. Evol. 9, 214–217. doi: 10.1016/0169-5347(94)90246-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Cáceres, A. (1989). Las Micorrizas vesículo arbusculares en un bosque húmedo tropical y su evolución luego de la perturbación (conuco) y la sucesión por 60 años en San Carlos de Río Negro, TF. Amazonas (Master's thesis), Instituto Venezolano de Investigaciones Científicas, Caracas, Venezuela.

Google Scholar

Cáceres, A., Kalinhoff, C., Lugo, L., and Villarreal, A. (2011). “Efecto de la perturbación producida por el establecimiento de conucos tradicionales Piaroa sobre las micorrizas arbusculares (MA) en la Reserva Forestal Sipapo, Edo. Amazonas,” in Restauración Ecológica en Venezuela Fundamentos y Experiencias, eds F. Herrera, and I. Herrera (Caracas: Ediciones IVIC).

Case, T. J. (1999). An Illustrated Guide to Theoretical Ecology. New York, NY: Oxford University Press.

Costa, L., da, F., Rodrigues, F. A., Travieso, G., and Villas Boas, P. R. (2007). Characterization of complex networks: a survey of measurements. Adv. Phys. 56, 167–242. doi: 10.1080/00018730601170527

CrossRef Full Text | Google Scholar

Csárdiand, G., and Nepusz, T. (2006). The igraph software package for complex network research. Inter. J. Comp. Syst. 1695, 1–9.

Google Scholar

Cushman, J. H. (1991). Host-plant mediation of insect mutualisms: variable outcomes in herbivore-ant interactions. Oikos 61, 138–144. doi: 10.2307/3545416

CrossRef Full Text | Google Scholar

Cushman, J. H., and Addicott, J. F. (1991). “Conditional interactions in ant-plant-herbivore mutualisms,” in Ant-plant Interactions, eds C. R. Huxley, and D. F. Cutler (Oxford: Oxford University Press), 92–103.

Google Scholar

De Angelis, D. L. (1975). Stability and connectance in food web models. Ecology 56, 238–243. doi: 10.2307/1935318

CrossRef Full Text | Google Scholar

Del-Claro, K., and Oliveira, P. S. (2000). Conditional outcomes in a neotropical treehopper-ant association: temporal and species-specific variation in ant protection and homopteran fecundity. Oecologia 124, 156–165. doi: 10.1007/s004420050002

PubMed Abstract | CrossRef Full Text | Google Scholar

El Mujtar, V., Muñoz, N., McCormick, B. P., Pulleman, M., and Tittonell, P. (2019). Role and management of soil biodiversity for food security and nutrition; where do we stand? Glob. Food Sec. 20, 132–144. doi: 10.1016/j.gfs.2019.01.007

CrossRef Full Text | Google Scholar

Freeman, L. C. (1978). Centrality in social networks conceptual clarification. Social Netw. 1, 215–239. doi: 10.1016/0378-8733(78)90021-7

CrossRef Full Text | Google Scholar

Freire, G. (2002). Breakfast of biodiversity: the truth about rainforest destruction. (doctoral dissertation), Oxford: University of Oxford.

Google Scholar

Freire, G., and Zent, S. (2007). “Los Piaroa” in Salud Indígena en Venezuela, eds G. Freire, and A. Tillet, vol. 1 (Caracas: Ediciones de la Dirección de Salud Indígena), 133–208.

Gallien, L., Landi, P., Hui, C., and Richardson, D. M. (2018). Emergence of weak-intransitive competition through adaptive diversification and eco-evolutionary feedbacks. J. Ecol. 106, 877–889. doi: 10.1111/1365-2745.12961

CrossRef Full Text | Google Scholar

Gallien, L., Zimmermann, N. E., Levine, J. M., and Adler, P. B. (2017). The effects of intransitive competition on coexistence. Ecol. Lett. 20, 791–800. doi: 10.1111/ele.12775

PubMed Abstract | CrossRef Full Text | Google Scholar

Gliessman, S. (2015). Agroecology the Ecology of Sustainable Food Systems. Third Edition. Boca Raton, FL: CRC Press. doi: 10.1201/b17881

CrossRef Full Text

Goldsmith, E. (2004). Feeding the world under climate change. Sci. Soc. 24, 34–36.

Griffon, D. (2008). Estimación de la biodiversidad en agroecología. Agroecología 3, 25–31.

Google Scholar

Griffon, D. (2020). “Conuco: fruto del árbol Kalivirnae” in Dinámica multifuncional de la agricultura familiar. Alimentación, ecología y economía, eds J. Ramírez and I. Ocampo (Guadalajara: Colegio de Postgraduados - Universidad de Guadalajara).

Griffon, D., and Hernandez, M.-J. (2014). Los ecosistemas no bailan sobre la punta de un alfiler: consecuencias del espacio en el manejo ecológico de plagas. Agroecología 9, 67–78.

Google Scholar

Griffon, D., and Hernandez, M.-J. (2019). Some theoretical notes on agrobiodiversity: spatial heterogeneity and population interactions. Agroecol. Sust. Food. 44, 1–29. doi: 10.1080/21683565.2019.1649781

CrossRef Full Text | Google Scholar

Griffon, D., and Rodríguez, E. G. (2017). En lo micro y en lo macro. sobre la importancia de las interacciones en la agroecología. Acta Biol. Venez. 37, 89–119.

Google Scholar

Hernandez, M.-J. (1998). Dynamics of transitions between population interactions: a nonlinear interaction alpha-function defined. Proc. R. Soc. B. 265, 1433–1440. doi: 10.1098/rspb.1998.0454

CrossRef Full Text | Google Scholar

Hernandez, M.-J. (2008). Spatiotemporal dynamics in variable population interactions with density-dependent interaction coefficients. Ecol. Model. 214, 3–16. doi: 10.1016/j.ecolmodel.2008.01.007

CrossRef Full Text | Google Scholar

Hernandez, M.-J. (2009). Disentangling nature, strength and stability issues in the characterization of population interactions. J. Theor. Biol. 261, 107–119. doi: 10.1016/j.jtbi.2009.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Hernandez, M.-J. (2021). The big ifs in the outcomes of species interactions: review and insights from the Interaction Function (IF) model. Rev. Mod. Mat. Sist. Biol. 1, 73–90.

Hernandez, M.-J., and Barradas, I. (2003). Variation in the outcome of population interactions: bifurcations and catastrophes. J. Math. Biol. 46, 571–594. doi: 10.1007/s00285-002-0192-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirota, M., Holmgren, M., Van Nes, E. H., and Scheffer, M. (2011). Global resilience of tropical forest and savanna to critical transitions. Science 334, 232–235. doi: 10.1126/science.1210657

PubMed Abstract | CrossRef Full Text | Google Scholar

Holland, J. N., De Angelis, D., and Bronstein, J. L. (2002). Population dynamics and mutualism: functional responses of benefits and costs. Am. Nat. 159, 231–244. doi: 10.1086/338510

PubMed Abstract | CrossRef Full Text | Google Scholar

Holland, J. N., and De Angelis, D. L. (2009). Consumer-resource theory predicts dynamic transitions between outcomes of interspecific interactions. Ecol. Lett. 12, 1357–1366. doi: 10.1111/j.1461-0248.2009.01390.x

PubMed Abstract | CrossRef Full Text

Kalinhoff, C., Cáceres, A., and Lugo, L. (2009). Cambios en la biomasa de raíces y micorrizas arbusculares en cultivos itinerantes del amazonas venezolano. Interciencia 34, 571–576.

Google Scholar

Krivan, V., and Revilla, T. A. (2019). Plant coexistence mediated by adaptive foraging preferences of exploiters or mutualists. J. Theor. Biol. 480, 112–128. doi: 10.1016/j.jtbi.2019.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Lawton, J. H. (1989). “Food webs,” in Ecological Concepts, ed J. M. Cherett (Hoboken, NJ: Blackwell Scientific).

Google Scholar

Levins, R. (1974). Discussion paper: the qualitative analysis of partially specified systems. Ann. N. Y. Acad. Sci. 231, 123–138. doi: 10.1111/j.1749-6632.1974.tb20562.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Levins, R., and Lewontin, R. C. (1985). The Dialectical Biologist. Cambridge: Harvard University Press.

Google Scholar

Levis, C., Costa, F. R. C., Bongers, F., Peña-Claros, M., Clement, C. R., Junqueira, A. B., et al. (2017). Persistent effects of pre-Columbian plant domestication on Amazonian forest composition. Science 355, 925–931. doi: 10.1126/science.aal0157

PubMed Abstract | CrossRef Full Text | Google Scholar

Lupatini, M., Suleiman, A. K. A., Jacques, R. J. S., Antoniolli, Z. I., de Siqueira Ferreira, A., Kuramae, E. E., et al. (2014). Network topology reveals high connectance levels and few key microbial genera within soils. Front. Environ. Sci. 2:10. doi: 10.3389/fenvs.2014.00010

CrossRef Full Text | Google Scholar

Mansutti, A. (2003). Piaroa: Los guerreros del mundo invisible. Antropológica 97–116.

Google Scholar

May, R. M. (1973). Stability and Complexity in Model Ecosystems. Princeton: Princeton University Press.

Google Scholar

Maynard, D. S., Bradford, M. A., Lindner, D. L., van Diepen, L. T., Frey, S. D., Glaeser, J. A., et al. (2017). Diversity begets diversity in competition for space. Nat. Ecol. Evol. 1, 1–8. doi: 10.1038/s41559-017-0156

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicholls, C., and Altieri, M. (2002). Biodiversidad y diseño agroecológico: un estudio de caso de manejo de plagas en viñedos. Manejo Integrado de Plagas y Agroecología 65, 50–64.

Google Scholar

Odum, E. P. (1953). Fundamentals of Ecology. Philadelphia, PA: W. B. Saunders Company.

Google Scholar

Odum, E. P., and Biever, L. J. (1984). Resource quality, mutualism, and energy partitioning in food chains. Amer. Natur. 124, 360–376. doi: 10.1086/284279

CrossRef Full Text | Google Scholar

R Core Team (2019). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online at: https://www.R-project.org/

Google Scholar

Revilla, T. A., and Krivan, V. (2018). Competition, trait-mediated facilitation, and the structure of plant-pollinator communities. J. Theor. Biol. 440, 42–57. doi: 10.1016/j.jtbi.2017.12.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Ricardo, N. E., Álvarez, A. M., and Álvarez, L. (2016). Conucos y rastrojos de la etnia Piaroa en la cuenca media del río Cataniapo, estado Amazonas, Venezuela. Acta Bot. Cub. 3, 336–344

Google Scholar

Ruíz, R. (2005). Sistema agroecológico en la Reserva Forestal Sipapo. Un enfoque ecológico de paisaje. [Bachelor's thesis]. [Merida (Venezuela)]: Universidad de los Andes.

Google Scholar

Sanoja, M. (1981). Los Hombres de la Yuca y el Maíz: Un Ensayo sobre el Origen y Desarrollo de los Sistemas Agrarios en el Nuevo Mundo. Caracas: Monte Ávila Editores.

Saturno, S., and Zent, S. (2016). Aspectos etnoecológicos de la agricultura entre los Pumé. Boletim do Museu Paraense Emílio Goeldi. Ciências Humanas. 11, 653–676. doi: 10.1590/1981.81222016000300007

CrossRef Full Text | Google Scholar

Scheffer, M., Bascompte, J., Brock, W. A., Brovkin, V., Carpenter, S. R., Dakos, V., et al. (2009). Early-warning signals for critical transitions. Nature 461, 53–59. doi: 10.1038/nature08227

PubMed Abstract | CrossRef Full Text | Google Scholar

Scheffer, M., Carpenter, S. R., Lenton, T. M., Bascompte, J., Brock, W., Dakos, V., et al. (2012). Anticipating critical transitions. Science 338, 344–348. doi: 10.1126/science.1225244

PubMed Abstract | CrossRef Full Text | Google Scholar

Soliveres, S., and Allan, E. (2018). Everything you always wanted to know about intransitive competition but were afraid to ask. J. Ecol. 106, 807–814. doi: 10.1111/1365-2745.12972

CrossRef Full Text | Google Scholar

Soliveres, S., Lehmann, A., Boch, S., Altermatt, F., Carrara, F., Crowther, T. W., et al. (2018). Intransitive competition is common across five major taxonomic groups and is driven by productivity, competitive rank and functional traits. J. Ecol. 106, 852–864. doi: 10.1111/1365-2745.12959

CrossRef Full Text | Google Scholar

Soliveres, S., Maestre, F. T., Ulrich, W., Manning, P., Boch, S., Bowker, M. A., et al. (2015). Intransitive competition is widespread in plant communities and maintains their species richness. Ecol. Lett. 18, 790–798. doi: 10.1111/ele.12456

PubMed Abstract | CrossRef Full Text | Google Scholar

Staver, A. C., Archibald, S., and Levin, S. (2011b). Tree cover in sub-Saharan Africa: Rainfall and fire constrain forest and savanna as alternative stable states. Ecology 92, 1063–1072. doi: 10.1890/10-1684.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Staver, A. C., Archibald, S., and Levin, S. A. (2011a). The global extent and determinants of savanna and forest as alternative biome states. Science 334, 230–232. doi: 10.1126/science.1210465

PubMed Abstract | CrossRef Full Text | Google Scholar

Stouffer, D. B., Wainwright, C. E., Flanagan, T., and Mayfield, M. M. (2018). Cyclic population dynamics and density-dependent intransitivity as pathways to coexistence between co-occurring annual plants. J. Ecol. 106, 838–851. doi: 10.1111/1365-2745.12960

CrossRef Full Text | Google Scholar

Thom, R. (1977). Stabilité structurelle et morphogénèse. Paris: Interédition.

Google Scholar

Ulrich, W., Kubota, Y., Piernik, A., and Gotelli, N. J. (2018). Functional traits and environmental characteristics drive the degree of competitive intransitivity in European saltmarsh plant communities. J. Ecol. 106, 865–876. doi: 10.1111/1365-2745.12958

CrossRef Full Text | Google Scholar

Ulrich, W., Soliveres, S., Kryszewski, W., Maestre, F. T., and Gotelli, N. J. (2014). Matrix models for quantifying competitive intransitivity from species abundance data. Oikos 123, 1057–1070. doi: 10.1111/oik.01217

PubMed Abstract | CrossRef Full Text | Google Scholar

Valdivia, I. (1994). ¿Por qué el Conuco?. Tribuna del Investigador 1, 11–25.

van Zonneveld, M., Turmel, M. S., and Hellin, J. (2020). Decision-making to diversify farm systems for climate change adaptation. Front. Sustain. Food Syst. 4:32. doi: 10.3389/fsufs.2020.00032

CrossRef Full Text | Google Scholar

Vandermeer, J. (2015). Some complications of the elementary forms of competition in a source/sink and metacommunity context: the role of intranstive loops. arXiv [Preprint] arXiv:1502.05225.

Google Scholar

Vandermeer, J., and Jackson, D. (2018). Stabilizing intransitive loops: self-organized spatial structure and disjoint time frames in the coffee agroecosystem. Ecosphere 9:e02489. doi: 10.1002/ecs2.2489

CrossRef Full Text | Google Scholar

Vandermeer, J., and Perfecto, I. (1995). Breakfast of Biodiversity: The Truth About Rainforest Destruction. Oakland, CA: Food First Books.

Vandermeer, J., and Perfecto, I. (2012). Syndromes of production in agriculture: prospects for social-ecological regime change. Ecol. Soc. 17:39. doi: 10.5751/ES-04813-170439

CrossRef Full Text | Google Scholar

Vandermeer, J., and Perfecto, I. (2017). Ecological Complexity and Agroecology. New York, NY: Routledge. doi: 10.4324/9781315313696

CrossRef Full Text | Google Scholar

Villarreal, A., Arends, E., and Escalante, E. (2003). Caracterización estructural y florística de sistemas tradicionales conucos – barbechos de la etnia Piaroa, amazonas, Venezuela. Rev. Forestal Venezolana 47, 115–124.

Google Scholar

Yan, C., and Zhang, Z. (2014). Specific non-monotonous interactions increase persistence of ecological networks. Proc. R. Soc. B. 281:20132797. doi: 10.1098/rspb.2013.2797

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeeman, E. C. (1979). “Catastrophe Theory,” in Structural Stability in Physics, eds. W. Güttinger, and H. Eikemeier, Vol. 4 (Berlin: Springer). doi: 10.1007/978-3-642-67363-4_3

CrossRef Full Text | Google Scholar

Zhang, Z., Yan, C., and Zhang, H. (2021). Mutualism between antagonists: its ecological and evolutionary implications. Integr. Zool. 16, 84–96. doi: 10.1111/1749-4877.12487

PubMed Abstract | CrossRef Full Text | Google Scholar