Trends in Runoff From Dryland, Cropped Fields on the Texas High Plains, and Implications for Their Management

Capturing precipitation as soil moisture is essential for successful dryland crop production, especially in semi-arid regions. Runoff is a loss of precipitation that does not result in increased soil moisture. Therefore, understanding the factors affecting runoff from cropped fields is important to successful dryland farming. Runoff frequency and volume were assessed using data from 1990 to 2009 from a long-term wheat-sorghum-fallow rotation near Bushland, Texas (USA), an area with an annual precipitation of ~500 mm and pan evaporation rate of over 2,000 mm. The likelihood that a rainfall event generated runoff increased with increasing rainfall volume such that all storms in excess of 50 mm yielded runoff. Runoff volume also increased with storm intensity. Rainfall in the preceding week was positively related to runoff volume. Runoff tended to be greater in no-till plots as compared to stubble mulched plots. During El Nino phase of the El Nino-Southern Oscillation the number of precipitations during the months of December through February tended to be higher. During La Nina phase of the El Nino-Southern Oscillation the number of precipitations during the months of November through January, respectively, tended to be lower. There also was a tendency for rainfall events during the El Nino phase to be of greater volume. However, the data did not support the hypothesis that greater winter rainfall with the El Nino event was associated with greater runoff. Therefore, greater rainfall during the El Nino phases should have been available for crop production. These results are discussed with regarding crop management practices for the Texas High Plains.

Introduction

Crop production in semi-arid regions can be challenging because potential annual evapotranspiration (ET) exceeds annual precipitation, PRCP; however, world-wide semi-arid regions contribute significantly to the world food production [UNESCO (United Nations Educational, Scientific, and Cultural Organization), 1977]. For the Southern High Plains, precipitation tends to be 25–30% of potential ET (Baumhardt and Salinas-Garcia, 2006) with most of that falling from May to September. Use of rotations with a fallow period has evolved as a means of increasing the likelihood of success dryland crop production in semi-arid regions, because rain in the fallow period is stored as soil moisture for a future crop production. A 3-year rotation of wheat-sorghum-fallow has been found to be successful for the Southern High Plains region (Baumhardt and Salinas-Garcia, 2006). This rotation produces two crops in 3 years and has two fallow periods. The success of the wheat-sorghum-fallow rotations depends on an understanding of the regional rain events, and crop and soil management practices that can be used to increase storage of the rain that falls during these fallow periods. Crop and soil management practices that minimize runoff and evaporation from the soil will tend to maximize soil water storage during the fallow periods.

Jones et al. (1985) summarized 20 years (1960–1979) of PRCP and runoff data from plots in a wheat-sorghum-fallow rotation at Bushland, Texas (USA) on the Southern High Plains (35.19° N 102.07° W). There were 1,522 rainfall events, of which 790 had volumes of <2.5 mm. There were 13 storms in which rainfall volume exceeded 50 mm. Brauer et al. (2015) analyzed rainfall events from 1990 to 2009 using data from the same weighing rainfall gauge as Jones et al. (1985). The frequency of storms over 50 mm was similar for the 20-year period of 1990–2009 as for the period of 1960–1979 reported by Jones et al. (1985).

Jones et al. (1985) reported that rainfall events in excess of 50 mm caused runoff from cultivated plots. These 13 rainfall events comprised ~10% of the PRCP during the 20 years but resulted in ~40% of the runoff. Based on these results, Jones et al. (1985) concluded that a few rainfall events contributed to most of the region's runoff. As December 2019, the Jones et al. (1985) article has been cited over 50 times according to Google Scholar with these citations being related to the observation that a few rain events triggered nearly half of the runoff for the Southern High Plains. It appears that these results are rather unique for the Southern High Plains.

Runoff volume appeared to be an interaction between time of the year and the crop present in the wheat-sorghum-fallow rotation. In general, runoff from land in the wheat phase of the rotation was less than that from land in either sorghum or fallow phases (Jones et al., 1985). However, there were instances in which runoff from land in wheat was greater. For examples, runoff following two 50 mm rainfall in May 1974 was appreciably greater from wheat fields than land going into sorghum or fallow. Jones et al. (1985) did not analyze factors that might explain deviations from the mean results.

Data reported by Jones et al. (1985) were from fields in which stubble mulch (SM) tillage was practiced. Half of the plots were no-tilled (NT) farmed starting in 1983. Therefore, the impact of NT on runoff could be assessed from data collected since 1983. NT is thought to promote increased soil moisture (Unger and Baumhardt, 1999), because of a lack of disturbance of the soil surface and presence of crop residues decreased evaporation of soil moisture (Lascano and Baumhardt, 1996; Schwartz et al., 2010). Improved soil aggregates with NT has been associated with greater rain infiltration (Nielson et al., 2005; Baumhardt et al., 2012). Effective weed control was essential for successful NT crop production (Thomas et al., 2007). The presence of weeds was linked to decreased soil moisture due to increased ET.

Another difference since the 1980's is the recognition that weather in the United States is affected by the El Nino-Southern Oscillation (ENSO), a periodic change in the surface water temperatures in the central and eastern-central equatorial Pacific Ocean. When the ocean temperatures are warmer than average, the phenomenon is called an El Nino and when they are cooler, they are called La Nina. Mauget and Upchurch (1999) examined the occurrences of El Nino and La Nina during the 20th century and their effects on seasonal rainfall and mean seasonal daily temperatures for the central U.S., an area that contributes significantly to overall American agricultural output. The number of El Nino and La Nina phenomena was approximately the same, 20 and 22, respectively, with the ENSO neutral phase being three times more likely than either an El Nino or La Nina. For the Texas High Plains, the following climate trends were observed: (1) rainfall and mean daily temperature from July to September were unaffected by either E Nino or La Nina; (2) rainfall in December, January, and February was greater with El Nino but mean daily temperature was not significantly affected; and (3) rainfall in November, December, and January was less and mean daily temperature was greater with La Nina (Mauget and Upchurch, 1999). Results also indicated that significant portions of the central and northern Great Plains, and western Corn Belt (Indiana and west) had variations in climate that could be related to El Nino or La Nina phases of ENSO (Mauget and Upchurch, 1999). Various research teams have reported results to supporting the hypothesis that regional crop yields may also be affected by ENSO phase (Changnon and Winstanley, 2000; Kellner and Niyogi, 2015).

Increases in crop yields on the Texas High Plains with El Nino may be associated with greater rainfall (Mauget and Upchurch, 1999; Baumhardt et al., 2014, 2015, 2016, 2019; Marek et al., 2018). However, if the greater rainfall resulted in greater runoff, crop yields may not be affected. Runoff maybe more likely if the greater rainfall induced by the El Nino favored higher volume rainfall events. Currently, changes in rainfall volume per event as affected by El Nino or La Nina phenomenon have not been reported.

The objectives of this study were to: (1) determine if the trends in rainfall volumes and runoff in 1990–2009 period were comparable to those from 1960 to 1979; (2) compare runoff frequency and volume between NT and SM tilled fields; (3) determine if rainfall in the week prior to a storm event impacted runoff frequency and volume; (4) document spatial variations in rainfall and how these spatial variations in rainfall may affect runoff; (5) document the distribution of rainfall volume as affected by El Nino or La Nina phase; and (6) examine the possible effects of either El Nino or La Nina phase on runoff.

Methods

Description of Field Experiment and Plots

An experiment was conducted 1.5 km west of Bushland, Texas, USA (Figure 1). The mean elevation above sea level is 1,100 m. The long-term average (since 1938) annual rain fall is just <500 mm. The long-term effects of either SM or NT residue management and crop rotation phase on field hydrology were assessed using six large (>630 m long, 1.8–4.1 ha) contour-farmed graded terrace fields of moderately sloping (1.5%) Pullman soil (fine, mixed, superactive, thermic Torrertic Paleustolls) with a 0.5% channel slope. The location of the six plots are designated by the thick black box in Figure 1. Storm runoff was measured through 0.91 and 0.76 m type-H flumes (Hauser and Jones, 1991) equipped with FW-1 stage recorders according to methods of Brakensiek et al. (1979).

FIGURE 1

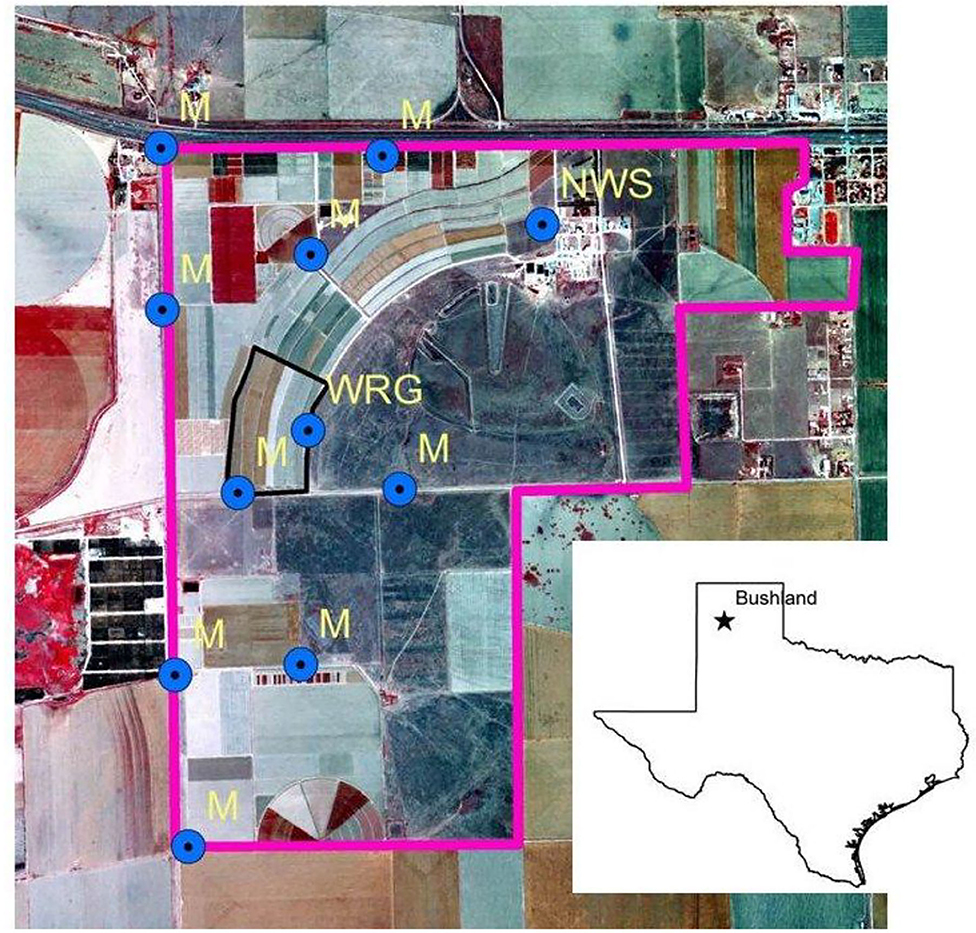
Figure 1. Locations of rain gauges, and runoff plots at the Conservation and Production Research Laboratory in Bushland, Texas, USA. The insert in the lower right corner shows the location of Bushland within the state of Texas in the United States. The area outlined with a pink line is the Conservation and Production Research Laboratory. The six runoff plots are outlined in a thinner black line. Rain gauges are depicted as blue circles with a black dot in the center. Those rain gauges designated with M as manual ones that are measured after each rain event. The rain gauge designed WRG is the continuous weighing rain gauge, the primary source for rain fall data. The rain gauge designated NWS is associated with National Weather Service weather station.

A typical wheat-sorghum-fallow rotation was established in 1949, such that all three phases of the crop rotation are present at any moment in time. In 1958, the three plots were instrumented with flumes and devices to measure runoff. Wheat (various cultivars) was sown during early September to late October, when soil water permitted crop establishment, with a high-clearance hoe opener grain drill at 45 kg ha⁻¹ to achieve 200 plants m⁻² in rows 0.3 m apart. Wheat was machine harvested in July and the fields remained idle for ~11 months at which time grain sorghum (various cultivars) was seeded in rows spaced 0.75 m apart at 8.0 seeds m⁻² using a six-row planter. Grain sorghum was harvested at maturity during November. The fields were fallowed for 10 months until wheat was planted. The rotation has been repeated ever since. At any point in time, all three phases of the wheat-sorghum-fallow rotation were present. Growing season weed control in wheat and sorghum was achieved using common contact and pre-emergence herbicides applied in accordance with recommended rates and timing for the region. During the fallow periods following wheat or sorghum harvest, either SM or NT residue management was maintained since 1983. On-demand SM weed control (three to four tillage operations) was performed at a 0.10-m depth with a 4.6-m-wide sweep-plow. Weed control for NT used various combinations of common contact and soil-active herbicides applied at recommended rates as governed by subsequent crop sensitivity to residual chemical.

Rainfall east of the plot was measured by a weighing rain gauge that provided continuous recordings of rainfall volumes (Brakensiek et al., 1979). Recordings were analyzed for total rainfall per event, the duration of the rainfall event and the maximum 30-min rainfall intensity. The location of the weighing rain gauge is denoted by the blue circle designated as WRG in Figure 1. Weather data were collected at National Weather Service station located at the blue circle designated NWS in Figure 1. Rainfall per event was also monitored at manual rainfall gauges at nine other locations designated as M next to the blue circles in Figure 1. All standard and recording rain gauges had a collector diameter of 20 cm.

Data Analyses

Data in this study were from 1990 to 2009. This time frame was chosen for the following reasons. Fist, a 20-year period was desired because this was the number of years that Jones et al. (1985) included in their analyses and a direct comparison of frequencies would be simpler if the number of years were held constant. Second reason, the years from 2011 to 2013 were the drought of record (since records were kept in 1938) in which the 3-year total for precipitation was ~840 mm, as compared to the long term mean of ~1,500 mm. No runoff occurred in 2011, 2012, and 2013. Finally, the year 2015 was the year of record for annual precipitation and a record monthly total for precipitation in May (~280 mm) damaged the terraces separating the runoff plots, thus invalidating some experimental results until 2017 when the terraces were fully repaired.

By 1990, tillage treatments had been imposed for at least two 3-year rotations prior to data analyses. Data from Baumhardt et al. (2017) indicated that at least 3 years were required for tillage effects to become apparent in another wheat-sorghum-fallow study at the location. Statistical analyses were performed using SAS (SAS Institute Inc, 2009). The spatial variation of rainfall over the plot area was examined using ArcMap [ESRI (Environmental Systems Research Institute), 2010]. Ten rainfall events with volumes in excess of 25 mm were randomly selected. The data from the 11 rain gauges were mapped to their geographic positions and the rainfall volume was determined by interpolation using Kriging function.

Daily rainfall data were obtained from the Co-Op National Weather Station located at the Conservation and Production Research Laboratory near Bushland, Texas, USA from 1939 to 1999 [NCDC (National Climate Data Center), 2019]. Daily rainfall volumes were segregated into either six volume categories (0–2.5, 2.6–6.3, 6.4–12.5, 12.6–25.4, 25.5–50.8, and >50.9 mm) or two volume categories (<6.3 mm or more than). The dividing point of 6.3 mm of daily rainfall volume was chosen because no runoff was observed when rainfall event was <6.3 mm in volume (data presented in RESULTS).

There were 9 El Nino and 14 La Nina phenomena as identified previously by Mauget and Upchurch (1999) during the study period of 1939–1999 (Table 1). Daily rainfall data from December, January, and February from El Nino years were extracted from the data set and the distribution of daily rainfall among either 2 or 6 volume categories were compared to all other years in the data set. Similarly, daily rainfall data from November, December, and January from the La Nina years were extracted from the dataset and the distribution of daily rainfall among either the 2 or 6 volume categories were compared to all other years in the dataset. These 3-month periods were chosen based on the report of Mauget and Upchurch (1999). PROC FREQ from SAS was used to determine if the distribution of the two datasets was similar (SAS Institute Inc, 2009). PROC Reg from SAS was used for regression analyses (SAS Institute Inc, 2009). Runoff dataset was expanded to include the years 1958–1999 to examine the frequency of runoff events as affected by La Nina and El Nino years. As above, the analyses focused on the months of December through February for El Nino events and November through January for La Nina.

TABLE 1

Table 1. Years with either El Nino or La Nina Phase.

Results

Brauer et al. (2015) previously compared rainfall events per rainfall volume categories from 1990 to 2009 to those reported by Jones et al. (1985) from 1960 to 1979. Analyses by Brauer et al. (2015) did not extend to the runoff data that are reported herein (Table 2). Brauer et al. (2015) concluded that the distribution of rainfall events exceeding 50.9 mm was not significantly different from the earlier period (Jones et al., 1985). No runoff was detected from any of the six plots when the rainfall volume in an event was <6.4 mm (Table 2). Only ~4.6% of the rainfall events in the 6.4–12.5 mm volume category resulted in runoff, indicating that these storms produced runoff infrequently. Rainfall events in the next highest volume category (12.6–25.4 mm) resulted in runoff less than half of the time. However, rainfall events in excess of 25.5 mm resulted in runoff almost all the time, with the two exceptions, those being two large volume snow events that do not result in runoff. So, the frequency of runoff tended to increase with increasing volume in a rainfall event.

TABLE 2

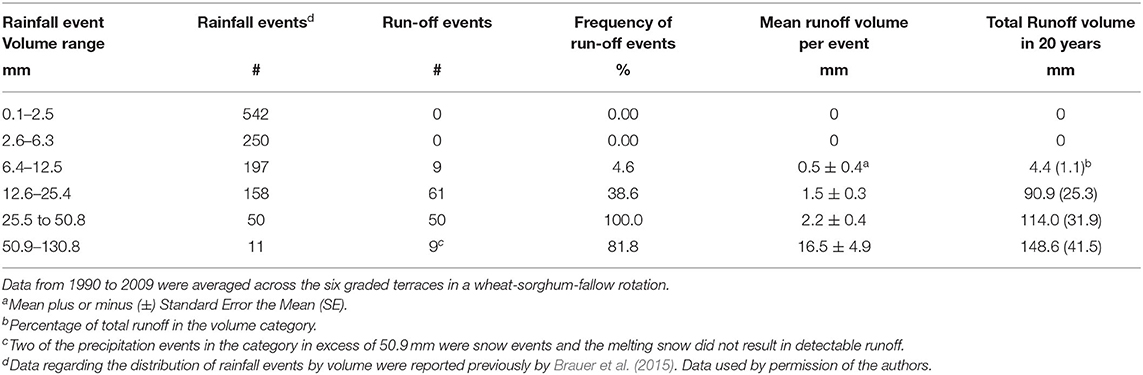
Table 2. Rainfall events by volume categories, and the frequency and volume of runoff from cropped graded terraces.

Similarly mean runoff volume increased with increasing volume in the rainfall event. Mean runoff volume from storms in the 6.4–12.5 mm category was 0.5 mm (Table 2). The volume of runoff increased progressively as the volume of the rainfall event increased. Mean runoff volume from the storms with volumes in excess of 50.9 mm was 16.5 mm. The percentage of the total runoff volume over the 20-year period (1990–2009) resulting from these high volumes storms was 41.5, a percentage that was very similar to that reported for the data from 1960 to 1979 (Jones et al., 1985). Therefore, these results supported the conclusion of Jones et al. (1985) that relatively infrequent, high volume storms produced most of the runoff from cultivated dryland plots.

Coefficient of variations in rainfall collected in 11 gauges located throughout the research farm were examined to determine if there was effect of rainfall volume on overall spatial variation in rainfall. In general, as rainfall volume per event increased, the variation in rainfall volume as reflected by the coefficient of variations decreased (Table 3). The coefficient of variations among the 11 gauges were largest among the two smallest rainfall volume categories, averaging ~28%. As the rainfall volume per event increased from the 6.4–12.5 mm category to the 50.9–130.8 mm category, there was a progressive decline in the coefficient of variations from 17.9 to 8.9%. Therefore, higher volume rainfall events tended to be more uniform throughout the research farm.

TABLE 3

Table 3. Variations in the coefficient of variation of rain volume captured per rainfall event.

To further explore the possibility that spatial variation in PRCP contributed to variations in runoff among the six plots, 10 rainfall events with volumes in excess of 25 mm were randomly selected and maps of recorded rainfall were produced using ArcMap [(ESRI (Environmental Systems Research Institute), 2010)]. A representative map from such a PRCP event that triggered runoff on September 7, 1996 is presented in Figure 2. The PRCP recorded by the 11 gauges ranged from 36 to 54 mm. However, the difference in interpolated rainfall volumes over the six runoff plots was substantially less, ranging from 36 to 38 mm. These results suggested that variations in PRCP over the plots was minor.

FIGURE 2

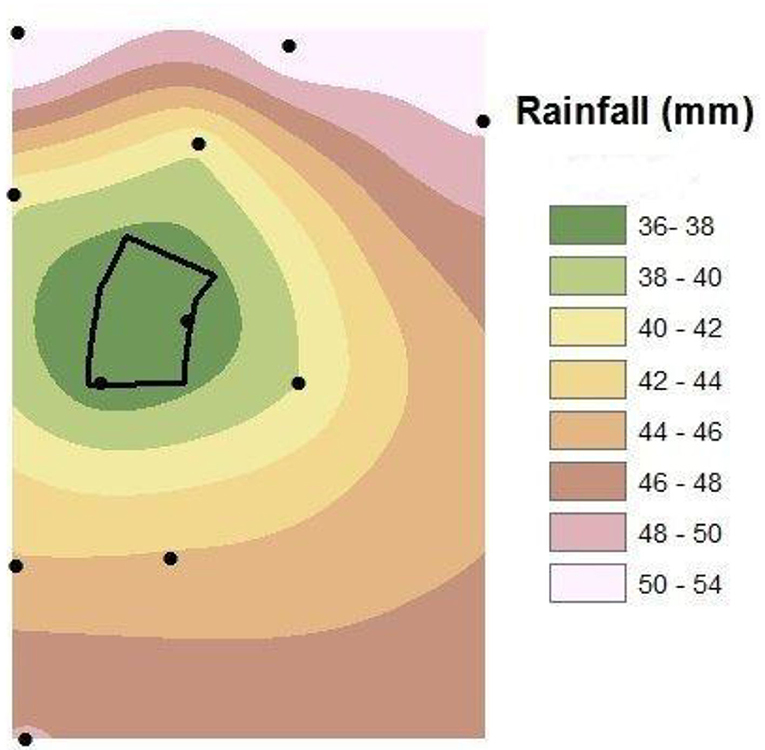
Figure 2. The distribution of rainfall from rainfall event on September 7, 1996 among the 11 rain gauges on the research farm. The rain gauges are defined by black circles. The six runoff plots are delineated by the thick black line. The rain fall volumes were plotted to the geographic position in ArcMap and the distribution was determined by interpolation using the Kriging routine.

Since Jones et al. (1985) reported their results, management of the plots has changed to allow the comparison of runoff from fields that were either NT or SM. The data in Table 4 compared the mean runoff volume from three plots in each of phases of the wheat-sorghum-fallow rotation that were subjected to either NT or SM. Overall, mean runoff from NT plots tended to be greater than SM, averaging 3.3 ± 0.6 (SE) mm vs. 2.2 ± 0.5 (SE) mm. Runoff volumes from NT plots tended to be greater than that from SM plots especially when comparing data from the highest two categories of storm volumes.

TABLE 4

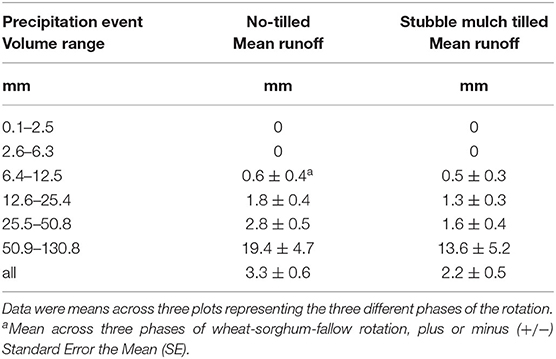
Table 4. The effect of precipitation event volume and tillage system on mean runoff volume for data collected from plots in wheat-sorghum-fallow rotation from 1990 to 2009.

The effects of tillage regime were also assessed using the Soil Conservation Service (SCS) curve number approach as initially described by Steenhuis et al. (1995) and employed recently (Steenhuis et al., 2013; Tilahun et al., 2015; Yang et al., 2015; Bayabil et al., 2016). The means of runoff across the three phases of the wheat-sorghum-fallow for NT and SM were regressed as a function of PRCP in the 24 h prior to runoff for each of the 129 events. The equation for NT plots was:

$\begin{array}{l}\text{Runoff }(\text{mm})=-5.3160+0.3080(\text{PRCP},\text{ mm}).\end{array}$

This regression equation was highly significant with F-value of 195.55 (P < 0.001) and R-square of 0.603. The SE for the intercept and slope were 0.7131 and 0.0220, respectively, and the t-values were significant at P < 0.001.

The regression equation predicting runoff from PRCP for SM plots was:

$\begin{array}{l}\text{Runoff }(\text{mm})=-4.4949+0.2389(\text{Precipitation},\text{ mm}).\end{array}$

The regression equation between precipitation and runoff for the SM plots was also highly significant with F-value of 126.67 (P < 0.001) and R-square of 0.495. The SE for the intercept and slope were 0.6873 and 0.0212, respectively, and the t-values were significant at P < 0.001.

The stored water prior to runoff can be estimated from the Y-intercept of the Soil Conservation Service (SCS) curve number approach (Steenhuis et al., 1995, 2013; Tilahun et al., 2015; Yang et al., 2015; Bayabil et al., 2016). By this approach, stored water prior to runoff was estimated to be 17.3 and 18.8 mm for NT and SM plots, respectively. These values were within the SE of each other's mean. The slopes of the regression equations were significantly different. The higher slope value for the NT plots indicated that once the stored soil water was exceeded, more of the PRCP resulted in runoff compared to the SM plots. Both the results in Table 4 and regression analysis of runoff volume as a function of PRCP indicated that runoff tended to be greater for NT plots.

Previous research has indicated that rainfall in the preceding days or week influenced the likelihood of runoff and volume (Steenhuis and van der Molen, 1986; Unger, 1992; Jones et al., 1994). The rationale being that soils with higher soil moisture content at the beginning of PRCP event had less ability to hold additional PRCP as soil moisture and therefore runoff was more likely. The runoff data from 1990 to 2009 were analyzed to determine the effect of PRCP volume in the preceding week on the likelihood of runoff and runoff volume. Runoff frequency was greater when the rainfall event inducing runoff was preceded by at least one rainfall event in the week prior (Table 5). OF the 129 runoff events, only 27 of those events, or 20.9%, occurred when there was no rain in the prior 7 days. The effects of at least one PRCP event in the prior week were greater at the lower PRCP volumes triggering runoff. A vast majority, 88.9% (8/9) of the runoff events triggered by a rainstorm of 6.4–12.5 mm, occurred when there was rainfall in the prior week. Seventy-six to 78% of the runoff events occurred when there was rainfall in the prior week for the other three rainfall volume categories. Likewise, runoff volume tended to be greater when the PRCP event triggering runoff was preceded by at least one rain event in the prior week. Mean runoff volume was six times greater in the rainfall volume category of 6.4–12.5 mm when it had rained in the prior week compared to no rain in the prior week (Table 5), four times greater for the 12.6–25.4 mm volume category, and only 30% greater for the highest two rainfall volume categories. These results suggested that rainfall in the prior week effected runoff triggered by a storm, but the volume of the triggering rainfall event had a large effect.

TABLE 5

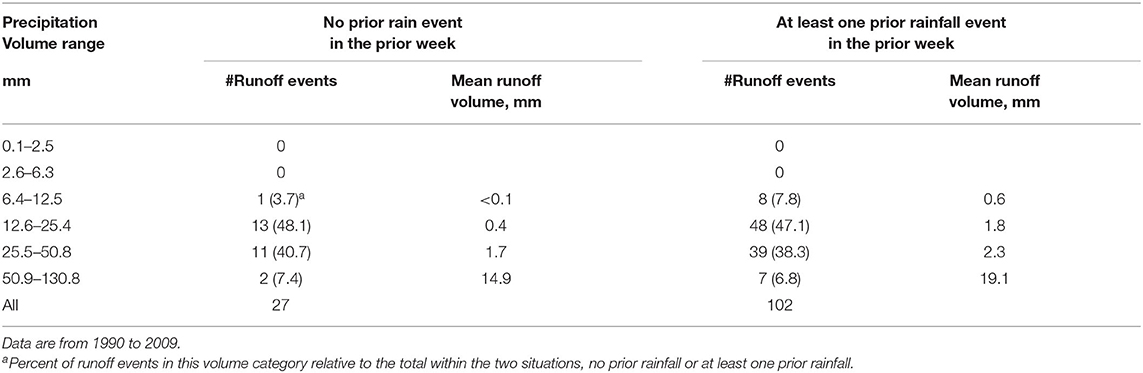
Table 5. Comparing runoff frequency and mean runoff volume for isolated storms and those storms that were followed by at least one rainfall event in the week prior.

The effect of prior week PRCP on runoff volume was explored further using linear regression in which the runoff volumes were regressed against the sum of PRCP volumes from 1 to 7 days prior and runoff volume of the storm triggering runoff. When averaged across the two tillage regimes, the regression equation predicting runoff volume as a function of PRCP volume in the triggering storm was:

$\begin{array}{l}\text{Runoff volume }(\text{mm})=-4.47+0.262(\text{PRCP volume},\text{ mm})\end{array}$

with R-square of 0.64 and F-value of 227.54. The equation using the sum of rain volumes from the prior 7 days had the greatest predictability. That equation was:

$\begin{array}{l}\text{Runoff volume }(\text{mm})=-6.40+0.221(\text{PRCP volume},\text{ mm})\\ +0.062(\text{PRCP volume in the previous }7-\text{day period},\text{ mm})\end{array}$

This equation was highly significant with R-square of 0.68 and F-value of 137.4. The addition of the rainfall volumes from the previous 7 days was significant; however, it did not improve power of model greatly. When rainfall volumes from previous day or two were added as separate variables, the resulting R-squares and F-values were not much different from using the sum of the previous 7 days rainfall totals. These results indicate that the rainfall in the preceding week had a small but significant effect on runoff volume. However, at least 30% of the variation in runoff volume was not accounted by PRCP parameters tested in these analyses.

The effects of either El Nino or La Nina phases on PRCP were initially investigated using weather data from 1939 to 1999. There were only 67 days with PRCP during the months of November, December, and January during La Nina years as compared to 507 during neutral and El Nino years in Bushland, Texas (Table 6). These 67 days during La Nina years corresponded to a mean of 4.8 events annually as compared to 10.8 events annually during Neutral and El Nino phases. In contrast, there were 118 days with PRCP during the months of December, January, and February during El Nino years, which corresponded to an average annual rate of 13.1 days with PRCP. In comparison, neutral and La Nina years had 482 days with PRCP in December through February, or an annual rate of 9.3. So overall, seasonal days with rain tended to be less during La Nina years and greater with El Nino years, which is consistent with the trends reported previously by Steenhuis et al. (1995).

TABLE 6

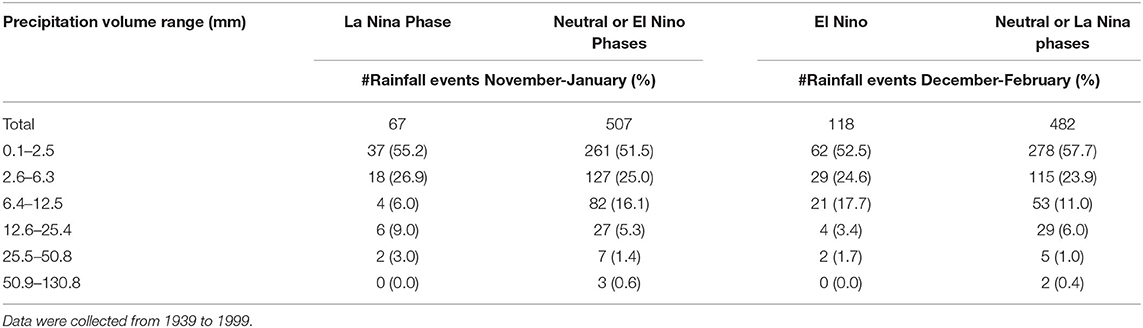
Table 6. Comparing rainfall volume distribution in November, December, and January during La Nina years to those during Neutral and El Nino phases and in December, January, and February during El Nino phases to those during Neutral and La Nina phases.

Daily PRCP values were segregated into six or two categories by volume. For the six categories, the authors herein used the same categories as in the original article of Jones et al. (1985). For the two categories, the authors used a PRCP volume of 6.3 mm as the dividing line, because the data in Tables 2, 4, 5 indicated that runoff did not occur with PRCP events of <6.3 mm.

The largest differences comparing the distribution of daily rainfall volume from La Nina years to those of neutral and El Nino phases, as found in Table 6, were: (1) La Nina years tended to have fewer daily rainfalls in the 6.4–12.5 mm category (6.0 vs. 16.1%) and the over 50.9 mm category (0 vs. 0.6%); and (2) La Nina years tended to have greater daily rainfalls in the 12.6–25.4 mm category (9.0 vs. 5.3%). However, these differences were not significant. The Chi-square value comparing the distribution of rainfall volumes among the six categories for La Nina years to Neutral and El Nino phases was 2.26 (P = 0.68). Similarly, when the distribution of daily rainfall between two categories (less than or more than 6.3 mm), the Chi-square comparing La Nina years to neutral and El Nino phases was 1.04 (P = 0.38). Therefore, it appeared that in La Nina years there was less days with rainfall but the distribution of the volume of these storms was unaffected.

The largest differences comparing the distribution of daily rainfall from El Nino years to those of Neutral and La Nina phases, as found in Table 6, were: (1) El Nino years tended to have more frequent daily rainfalls in the 6.4–12.5 mm (17.7 vs. 11.0%) and 25.8–50.8 mm (1.7–1.0%) categories; and (2) El Nino years tended to have fewer daily rainfall in the 12.6–25.4 mm category (3.4 vs. 6.0%). The greater number of daily rainfall events in 50.9 mm category with El Nino years and fewer with La Nina years was difficult to interpret because of the largest difference in total numbers in the two populations and the small frequency at which these daily rainfalls occur. It is interesting to note that the trends in the frequency of rainfall events in the 6.4–12.5 mm category for La Nina and El Nino phases paralleled differences in total number of events. The Chi-square test comparing the distribution of daily rainfall among the six volume categories indicated that the distributions were significantly different with a value of 576.05 (P < 0.001). The Chi-square test comparing the distribution of daily rainfall into two categories (less than and greater than 6.3 mm) also was significant with a value of 217.45 (P < 0.001). Thus, these results indicate that rainfall during December, January, and February of an El Nino year tended to occur more frequently and with greater daily volume than in Neutral and La Nina phases. The question that remains: did the increased frequency and PRCP volume result in greater runoff?

The distribution of runoff during the months of the year were examined prior to examining the effects of ENSO phase on runoff. The initial analyses were confined to the years of 1985–1999; however, there were few runoff events during the months of November, December, January, and February. To increase the possibilities of detecting a trend, the dataset was expended to include the years 1958–1999. For these analyses the runoff data from each of the three plots were averaged across rainfall event. The distribution of runoff events during each month during the year are presented in Figure 3. Runoff occurred most frequently in June and August, with runoff from June to August comprising ~2/3 of the total runoff events. The percentage of runoff events during these three summer months was slightly greater than the long-term proportion of PRCP volume. Runoff events from November through February were infrequent, comprising <5% of the total events.

FIGURE 3

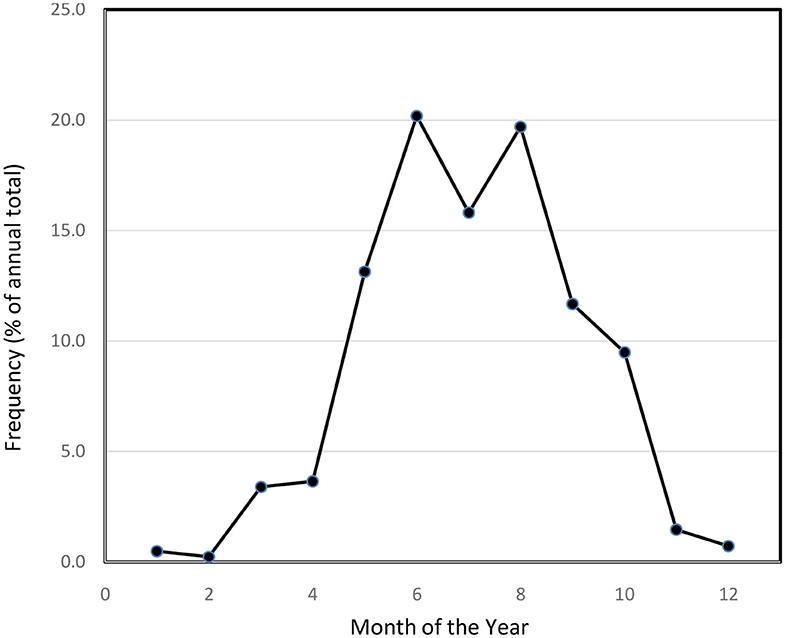
Figure 3. Frequency of runoff events occurring in each month of the year using data from 1958 to 1999.

The months of December through February are the months of interest when El Nino occurs (Mauget and Upchurch, 1999), and these 3 months comprised only <1.5% of the runoff events. The months of November through January, months of interest during La Nina (Mauget and Upchurch, 1999) had more runoff events; however, runoff events comprised <2.7% of the total events. Of the six runoff events that occurred from December through February, one of these occurred during an El Nino phase. Of the eight runoff events that occurred from November to January, four of these occurred during the La Nina phase. However, three of the four events occurred during the same week of November 1971. These analyses were inconclusive regarding the effects of ENSO phase on runoff during the months in which El Nino or La Nina have effects on PRCP on the Texas High Plains. These authors conclude that changes in PRCP during winter months with EL Nino and La Nina phases did not significantly alter runoff from cropped fields. Additional data may or may not support support this hypothesis.

Discussion and Conclusions

First, the data in this study confirmed the observations of Jones et al. (1985) that a few infrequent storms produced significant amount of the runoff from cultivated dryland, fields of the Texas High Plains (Table 2). As far as these authors know, the results of Jones et al. (1985) have not been verified previously. In both this study and that of Jones et al. (1985), storms in excess of 50 mm of PRCP volume produced ~40% of the runoff in a 20-year period. The previous study examined data collected from 1960 to 1979 as compared to 1990 to 2009 herein.

As reported earlier (Brauer et al., 2015), there were significant differences in the distribution of rainfall events among the six volume categories for the data collected in 1990 to 2009 as compared to data collected from 1960 to 1979. There were fewer rainfall events in the lower two volume categories (0.1–2.5, and 2.6–6.3 mm) for the time period from 1990 to 2009 as compared to the earlier time range. Rainfall events in these two lower categories accounted for 74% of the total events in 1960−1979 as compared to 65% in the later period. There was a tendency for the total rainfall volume in these two lower categories to be lower, 22% of total volume from 1960 to 1979 as compared to 18% from 1990 to 2009. It should be noted that rainfall events of <6.3 mm did not induce runoff as reported herein (Table 2). In addition, Marek et al. (2016) reported that all the soil moisture from rain events of <10 mm was lost as evaporation within 24 h. Therefore, it is unlikely that rain from events from these two lower volume categories contributed to crop growth under conditions of the Texas High Plains. A decrease in rain events in these two lowest volume categories suggested that the rainfall occurring in the time period from 1990 to 2009 as compared to 1960 to 1979 was more effective in supporting crop production.

Next, this study identified three parameters that affected runoff frequency and volume: rainfall volume of the triggering storm; rainfall in the prior week; and tillage. The volume of the rainfall triggering runoff had significant effects on both mean runoff volume and frequency (Table 2). Linear regression indicated that over 60% of the variation in runoff volume was due to the volume of the triggering storm. Rainfall in the preceding week also was a contributing factor affecting runoff volume (Table 5). Runoff volume was greater when rain occurred in the preceding week across all four of the rain volume categories (>6.5 mm) that triggered runoff. Rainfall in the prior week also increased the frequency that rainfall event in the 6.4–12.5 mm volume category from 3.7 to 7.8% (Table 5). Rainfall in the preceding week did not affect the frequency of runoff for the other three rainfall volume categories, that is, rainfall volume in excess of 12.5 mm. These two parameters (rainfall in the event triggering runoff and rainfall volume in the week prior) accounted for ~70% of the variation in runoff volume when data were averaged across the three phases of the wheat-sorghum-fallow.

Third parameter affecting runoff frequency and volume was tillage practice: NT tended to have higher frequency of runoff especially in response to greater volumes of PRCP (Table 4). We have not tried to assess the fraction of variation in runoff volume attributed to tillage system to date. NT having greater runoff seems counter to studies that have shown that NT promotes rainfall infiltration, precipitation storage, and water use efficiency (Lascano and Baumhardt, 1996; Unger and Baumhardt, 1999; Nielson et al., 2005; Schwartz et al., 2010; Baumhardt et al., 2012). Promoting rain infiltration may be the reason why NT plots had greater runoff. The increased rainfall infiltration in the NT plots could lead to greater soil moisture in the profile, especially toward the end of the fallow periods. With greater soil moisture, there is a tendency of slower and less infiltration and thus a greater possibility for runoff (Steenhuis and van der Molen, 1986; Unger, 1992; Jones et al., 1994). A similar hypothesis has been put forward previously by Baumhardt et al. (2017). Evidence to support such a hypothesis may come further analyses of this study's data. In addition, the effects of phase of the rotation and other management factors are being investigated as possible contributors to the variation in runoff. Data from Jones et al. (1994) suggested that there was an interaction between tillage system and phase of the crop rotation on the volume in runoff. The data analyses to date suggested that variations in PRCP across the plot is not a significant contributor to the variation in runoff (Figure 2).

The results from this study support the current recommendations for the use of NT to promote soil moisture and the concomitant dryland crop production on the Southern High Plains. Although NT plots tended to have greater runoff, the occurrence of higher runoff tend to be infrequent, <5% of rainfall events (Table 4), and probably occurred when the soil moisture was already high. Therefore, there is a greater potential to have increased crop production with NT under dryland practices in a semi-arid climate if weed control was similar (Baumhardt and Salinas-Garcia, 2006) and issues of soil compaction were avoided (Baumhardt et al., 2017). Increasing occurrence of glyphosate resistant weeds may make management of NT more difficult (Sivagamy et al., 2017). These results also indicated that infrequent SM tillage events were not going to substantially impact the runoff from cropped dryland fields.

The occurrence of El Nino and La Nina phases during the winter months in which winter wheat grows on the Texas High Plains was previously associated with increased and decreased PRCP, respectively (Mauget et al., 2009; Baumhardt et al., 2016; Marek et al., 2018). The results in this study indicated that these ENSO phases were associated with greater and lesser number of PRCP events during the winter months (Table 6); however, the distribution of rainfall among volume class was affected only by the El Nino phase. Rainfall was more likely to occur with volumes in excess of 6.3 mm during the El Nino phase (Table 6). Since a substantial amount of the soil moisture was lost from storms of <10 mm (Marek et al., 2016), these results suggested that rainfall during the El Nino phases would be more effective in promoting wheat growth. Analysis of runoff events during the December through February months indicated that few runoff events occurred during these months (Figure 3) and the El Nino phase did not significantly increase the possibility of runoff. These results support the hypothesis that El Nino phase increased PRCP during the winter wheat growing season on the Texas High Plains, that this increased PRCP did not increase runoff, and thus the resulting soil moisture was more likely available for crop growth.

Finally, these results have a bearing on the usefulness of predictions of either El Nino or La Nina on the management of dryland cropping practices on the Texas High Plains. Previous researcher results indicated that pre-planting predictions of El Nino or La Nina phase can be used to adjust farmers' management decisions that may result in greater profits or return on investments (Mauget et al., 2009; Baumhardt et al., 2016; Marek et al., 2018). These results support the recommendations of Mauget et al. (2009) that when El Nino conditions were predicted that farmers can manage their wheat for higher yields by investing in N fertilization and increased carrying capacity for grazing stocker cattle. Conversely, farmers should avoid investments in inputs when a La Nina phase was forecasted. Unfortunately, crop management cannot compensate when PRCP was less than a certain amount. All six of the winter wheat crop failures from 1954 to 2011 at the Bushland research farm occurred during La Nina years and no wheat crop failures occurred during El Nino years.

These results also support the utility of using the existence of forecast of El Nino or La Nina phases for dryland production of summer crop (cotton and sorghum) on the Texas High Plains. The success of these summer crops was affected by soil moisture at planting (Baumhardt et al., 2015, 2019). The occurrence of El Nino or La Nina should result in higher or lower, respectively, soil moisture at planting, thus affecting their yield potential. In summary, the results presented herein support the notion that changes in PRCP with ENSO phases maybe useful in making dryland crop production management decisions on the Texas High Plains. Although knowledge has been advanced regarding factors affecting runoff from dryland crop fields, additional knowledge is needed to determine factors that affect about 30% of the variation in runoff volume. As knowledge of these effects become known, further refinements to best management practices for dryland crop production on the Texas High Plain may be possible.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All authors were involved in designing, executing, and reporting the described research.

Funding

This research was funded by USDA-ARS under the research plan for CRIS project 3090-13000-15-00-D entitled Precipitation and Irrigation Management to Optimize Profits from Crop Production and contributes to research conducted under the ARS led Ogallala Aquifer Program.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Baumhardt, R. L., Johnson, G. L., and Schwartz, R.C. (2012). Residue and long-term tillage and crop rotation effects on simulated rain infiltration and sediment transport. Soil Sci. Soc. Amer. J. 76, 1370–1378. doi: 10.2136/sssaj2011.0331

CrossRef Full Text | Google Scholar

Baumhardt, R. L., Johnson, G. L., Schwartz, R. C., and Brauer, D. K. (2017). Grazing and tillage effects on soil properties, rain infiltration and sediment transport during fallow. Soil Sci. Soc. Amer. J. 81, 1548–1556. doi: 10.2136/sssaj2017.04.0133

CrossRef Full Text | Google Scholar

Baumhardt, R. L., Mauget, S. A., Gowda, P. H., and Brauer, D. K. (2014). Modeling cotton lint yield response to irrigation management as influenced by el niño-southern oscillation. Agron. J. 106, 1559–1568. doi: 10.2134/agronj13.0451

CrossRef Full Text | Google Scholar

Baumhardt, R. L., Mauget, S. A., Gowda, P. H., Brauer, D. K., and Marek, G. W. (2015). Optimizing cotton irrigation strategies as influenced by el niño southern oscillation. Agron. J. 107, 1895–1904. doi: 10.2134/agronj14.0471

CrossRef Full Text | Google Scholar

Baumhardt, R. L., Mauget, S. A., Schwartz, R. C., and Jones, O.R. (2016). El niño southern oscillation effects on dryland crop production in the texas high plains. Agron. J. 108, 736–744. doi: 10.2134/agronj2015.0403

CrossRef Full Text | Google Scholar

Baumhardt, R. L., and Salinas-Garcia, J. (2006). “Dryland agriculture in Mexico and the U.S. Southern Great Plains,” in Dryland Agriculture, 2 ed. Agron Monograph, 23. eds, G. A. Peterson, P. W. Unger, and W. A. Payne. (Madison: ASA, CSSA, and SSSA), 341–64. doi: 10.2134/agronmonogr23.2ed.c10

CrossRef Full Text | Google Scholar

Baumhardt, R. L., Schwartz, R. C., Marek, G. W., and Moorhead, J. E. (2019). Modeled El niño-southern oscillation effects on grain sorghum under varying irrigation strategies and cultural practices. Agron. J. 111, 1913–1922. doi: 10.2134/agronj2018.09.0616

CrossRef Full Text | Google Scholar

Bayabil, H. K., Tebebu, T. Y., Stoof, C. R., and Steenhuis, T. S. (2016). Effects of a deep-rooted crop and soil amended with charcoal on spatial and temporal runoff patterns in a degrading tropical highland watershed. Hydrol. Earth Syst. Sci. 20, 875–885. doi: 10.5194/hess-20-875-2016

CrossRef Full Text | Google Scholar

Brakensiek, D. L., Osborn, H. B., and Rawls, W. J. (1979). Field Manual for Research in Agricultural Hydrology. Washington, DC : USDA, Agric. Handbook 224. U.S. Gov. Print. Office.

Google Scholar

Brauer, D., Baumhardt, R. L., Gitz, D., Gowda, P., and Mahan, J. (2015). Characterization of trends in reservoir storage, streamflow, and precipitation in the Canadian River watershed in New Mexico and Texas. Lake Reservoir Mgt. 31, 64–79. doi: 10.1080/10402381.2015.1006348

CrossRef Full Text | Google Scholar

Changnon, S. A., and Winstanley, D. (2000). Long-term variations in seasonal weather conditions important to corn production in illinois. Clim. Change 47, 353–372. doi: 10.1023/A:1005639829544

CrossRef Full Text | Google Scholar

ESRI (Environmental Systems Research Institute) (2010). ArcMap version 10.0 (Build 2414) (San Jose, CA).

Google Scholar

Hauser, V. L., and Jones, O. R. (1991). Runoff curve numbers for the Southern High Plains. Trans. Amer. Soc. Agr. Biol. Eng. 34, 142–148. doi: 10.13031/2013.31636

CrossRef Full Text | Google Scholar

Jones, O. R., Eck, H. V., Smith, S. J., Coleman, G. A., and Hauser, V. L. (1985). Runoff, soil, and nutrient losses from rangeland and dry-farmed cropland in the Southern High-Plains. J. Soil Water Cons. 40, 161–164.

Google Scholar

Jones, O. R., Hauser, V. L., and Popham, T. W. (1994). No-tillage effects on infiltration, runoff, and water conservation on dryland. Trans. Amer. Soc. Agric. Eng. 37, 473–479. doi: 10.13031/2013.28099

CrossRef Full Text | Google Scholar

Kellner, O., and Niyogi, D. (2015). Climate Variability and the U.S. Corn Belt: ENSO and AO episode-dependent hydroclimatic feedbacks to corn production at regional and local scales. Earth Interac. 19, 1–32. doi: 10.1175/EI-D-14-0031.1

CrossRef Full Text | Google Scholar

Lascano, R. J., and Baumhardt, R. L. (1996). Effects of crop residue on soil and plant water evaporation in a dryland cotton system. Theor. Appl. Climatol. 54, 69–84. doi: 10.1007/BF00863560

CrossRef Full Text | Google Scholar

Marek, G. W., Baumhardt, R. L., Brauer, D. K., Gowda, P. H., Mauget, S. A., and Moorhead, J. E. (2018). Evaluation of the oceanic nino index as a decision support tool for winter wheat cropping systems in the Texas high plains using SWAT. Comput. Electron. Agric. 151, 331–337. doi: 10.1016/j.compag.2018.06.030

CrossRef Full Text | Google Scholar

Marek, G. W., Gowda, P., Marek, T., Auvermann, B., Evett, S., Colaizzi, P., et al. (2016). Estimating preseason irrigation losses by characterizing evaporation of effective precipitation under bare soil conditions using large weighing lysimeters. Agric. Water Mgt. 169, 115–128. doi: 10.1016/j.agwat.2016.02.024

CrossRef Full Text | Google Scholar

Mauget, S., Zhang, J., and Ko, J. (2009). The value of ENSO forecast information to dual-purpose winter wheat production in the U.S. southern high plains. J. Appl. Meteorol. Climatol. 48, 2100–2117. doi: 10.1175/2009JAMC2018.1

CrossRef Full Text | Google Scholar

Mauget, S. A., and Upchurch, D. R. (1999). El Nino and La nina related climate and agricultural impacts over the great plains. J. Prod. Agric. 12, 203–215. doi: 10.2134/jpa1999.0203

CrossRef Full Text | Google Scholar

NCDC (National Climate Data Center) (2019). Available on the internet at https://www.ncdc.noaa.gov/data-access. Verified December 27, 2019

Google Scholar

Nielson, D. C., Unger, P. W., and Miller, P. R. (2005). Efficient water use in dryland cropping systems in the Great Plains. Agron. J. 97, 364–372. doi: 10.2134/agronj.2005.0364

CrossRef Full Text | Google Scholar

SAS Institute Inc (2009). SAS OnlineDoc^® 9.1.3. Cary, NC: SAS Inst. Inc.

Google Scholar

Schwartz, R. C., Baumhardt, R. L., and Evett, S. R. (2010). Tillage effects on soil water redistribution and bare soil evaporation throughout a season. Soil Tillage Res. 110, 221–229. doi: 10.1016/j.still.2010.07.015

CrossRef Full Text | Google Scholar

Sivagamy, K., Chinnusamy, C., and Parsuraman, P. (2017). Weed management options in transgenic stacked and non transgenic maize (Zea mays) hybrids- a review. Agric. Rev. 38, 245–259. doi: 10.18805/ag.R-1671

CrossRef Full Text | Google Scholar

Steenhuis, T. S., Hrncir, M., Poteau, D. A., Luna, E. J. R., Tilahun, S. A., Caballero, L. A., et al. (2013). Saturated excess runoff pedotransfer function for vegetated watersheds. Vadose Zone J. 12, 1–10. doi: 10.2136/vzj2013.03.0060

CrossRef Full Text | Google Scholar

Steenhuis, T. S., and van der Molen, W. H. (1986). The Thornthwaithe-Mather procedure as a simple engineering method to predict recharge. J. Hydrol. 84, 221–229. doi: 10.1016/0022-1694(86)90124-1

CrossRef Full Text | Google Scholar

Steenhuis, T. S., Winchell, M., Rossing, J., Zollweg, J. A., and Walter, M. F. (1995). SCS Runoff equation revisited for variable-source runoff areas. J. Irrig. Drain. 121, 234–238. doi: 10.1061/(ASCE)0733-9437(1995)121:3(234)

CrossRef Full Text | Google Scholar

Thomas, G. A., Titmarch, G. W., Freebaim, D. M., and Radford, B. J. (2007). No-tillage and conservation farming practices in grain growing areas of Queensland- a review of 40 years of development. Austr. J. Exp. Agric. 47, 887–898. doi: 10.1071/EA06204

CrossRef Full Text | Google Scholar

Tilahun, S. A., Guzman, S. D., Zegeye, A. D., Dagnew, D. C., Collick, A. S., Yitaferu, B., et al. (2015). Distributed discharge and sediment concentration predictions in the sub-humid Ethiopian highlands: the debre mawi watershed. Hydrol. Proces. 29, 1817–1828. doi: 10.1002/hyp.10298

CrossRef Full Text | Google Scholar

UNESCO (United Nations Educational Scientific, and Cultural Organization). (1977). World Map of Desertification. United Nations Conference on Desertification. A/Conf.74/2. Rome: FAO, United Nations

Google Scholar

Unger, P. W. (1992). Infiltration of simulated rainfall: tillage system and crop residue effects. Soil Sci. Soc. Amer. J. 56, 283–289. doi: 10.2136/sssaj1992.03615995005600010045x

CrossRef Full Text | Google Scholar

Unger, P. W., and Baumhardt, R. L. (1999). Factors related to dryland sorghum yield increases: 1939 through 1997. Agon. J. 91, 870–875. doi: 10.2134/agronj1999.915870x

CrossRef Full Text | Google Scholar

Yang, X., Chen, Y., Pacenka, S., Gao, W., Zhang, M., Sui, P., et al. (2015). Effect of diversified crop rotations on groundwater levels and crop water productivity in the North China Plain. J. Hydrol. 522, 428–438. doi: 10.1016/j.jhydrol.2015.01.010

CrossRef Full Text | Google Scholar