Non-linear Interactions Driving Food Security of Smallholder Farm Households in the Western Highlands of Guatemala

Barba-Escoto, Luis; van Wijk, Mark T.; López-Ridaura, Santiago

doi:10.3389/fsufs.2020.00051

ORIGINAL RESEARCH article

Front. Sustain. Food Syst., 10 June 2020

Sec. Agroecology and Ecosystem Services

Volume 4 - 2020 | https://doi.org/10.3389/fsufs.2020.00051

This article is part of the Research Topic Mathematical Modelling and Complex Systems in Agroecology View all 8 articles

Non-linear Interactions Driving Food Security of Smallholder Farm Households in the Western Highlands of Guatemala

$\nLuis Barba-Escoto,$ Luis Barba-Escoto^1,2

Mark T. van Wijk³

Santiago López-Ridaura¹^*

¹Sustainable Intensification Program, International Maize and Wheat Improvement Center (CIMMYT), Texcoco, Mexico
²Posgrado en Ciencias de la Complejidad, Universidad Autónoma de la Ciudad de México, Benito Juárez, Mexico
³International Livestock Research Institute (ILRI), Quito, Ecuador

In the western highlands of Guatemala, the indigenous population is one of the most marginalized communities. The food security of subsistence and infrasubsistence smallholders within this population still relies on domestic agricultural production as the principal livelihood activity and the main source of food. Smallholder production systems in the region are complex, with multiple interacting subsystems functioning at different integration levels and with different temporal dynamics. Previous results, based on a data set of nearly 5,000 farm households using a robust food availability indicator (that quantifies agricultural production, consumption, transformation, and commercialization of produce), have shown large differences in food security between farmers in the western highlands of Guatemala. Another important finding was that more than half of the farm households do not have the means to produce enough energy for home consumption from their agricultural activities. Identifying the constraints, patterns, and underlying processes driving food security could give rise to a set of easy-to-measure variables that quickly and reliably assess household food security status; such a tool would be helpful for decision and policy makers trying to focus on actions more likely to succeed in improving food security in the region. In this study, we developed a predictive model of food security, through the application of machine learning techniques, to identify the most important factors, and their interactions, which account for variability in food security. The resulting “artificial neural network” model performed well, explaining nearly 85% of the variance in food security status. By applying different sensitivity analysis methods, we were able to detect highly non-linear interactions between the different factors driving food security. Land availability per person is detected as the main constraint for attaining food security. The median value of land availability per person in the region is 0.085 ha, explaining why 52% of the farm household population does not produce enough food energy from agriculture. Many other interactions were found between crop land allocation, diversity, yields, and food security, which can help to target interventions to improve the food security status in the region.

Introduction

Food Security in the Western Highlands of Guatemala

Guatemala is the country with the fourth highest level of children with undernutrition in the world [WFP (World Food Programme), 2018]. Poverty is widespread, and ~70% of the poor live in rural areas, where traditional agricultural production is the main source of food and income. Poverty and malnutrition are especially predominant among indigenous population, where only 19% of its inhabitants are food-secure (Gobierno de Guatemala, 2012).

Traditional campesino systems, in which landless and small-scale subsistence farmers are the least food-secure (Taylor et al., 2006), predominate in large areas of Guatemala. Food insecurity in the country is caused by a lack of food access that is, in turn, rooted in structural problems such as inequality (Guardiola et al., 2006; Gobierno de Guatemala, 2012). Inequality in Guatemala is characterized by a stratified society based on ethnicity, land ownership, health, education, gender, and age (Bruni et al., 2009).

The western highlands of Guatemala (WHGs) concentrate the most marginalized communities in Guatemala, where indigenous communities, implementing traditional agroecological practices (such as milpa), predominate. This region has also historically suffered exclusion, social inequality, and violence (Steinberg and Taylor, 2008). As in many rural areas of the world, food security in the WHGs is a complex phenomenon, as its inhabitants are simultaneously producers and consumers of food, and their livelihoods depend on agricultural as well as non-agricultural activities. This complexity is compounded in the WHGs by a high population density and limited land availability. The Ministry of Agriculture of Guatemala states that 62% of households in the region have <0.7 ha of arable land and 85% <1.4 ha [MAGA (Ministerio de Agricultura, Ganadería y Alimentación de la República de Guatemala), 2011]. With such limitations on land availability, the rural population of the WHGs has developed alternative sources of food and income (wages, migration, handcrafting, etc.). However, agriculture is still the most important livelihood for most of the population and the main contributor to local food security [IFAD (International Fund for Agricultural Development), 2011].

Food security is defined as “everyone having continued access to a sufficient quantity and quality of food” (FAO, 2003). Four dimensions of food security have been defined: availability, access, utilization, and stability (FAO, 2016). Recently, Lopez-Ridaura et al. (2019) conducted an analysis to assess one of these, food availability, among farm households (FHHs) in the WHGs, based on a data set of nearly 5,000 households and a simple indicator of food security, that is, potential food availability (PFA) measured in kcal/male adult equivalent per day. It was found that in the WHGs the most important agricultural production systems consist of maize and coffee as main crops and that there exist six types of contrasting FHHs in terms of the crops they produce and their food output level. These types also contrast in how many households attain food security. Three farm types [i.e., (a) diversified maize-based, (b) coffee-based, and (c) specialized coffee FHHs] had higher percentages of food-secure households, with values of 60, 83, and 74%, respectively. Farm households specialized in maize production and resource-constrained households were the types with the lowest percentage of food-secure households. According to Lopez-Ridaura et al. (2019), the contribution of agriculture to the Potential Food Availability (PFA) for the FHHs in the WHGs varies from almost zero to up to 10 times the kcal needs of the household members, and agricultural activities do not meet the needs of the habitants in more than half of the households (52%).

The Complexity of Food Security in the WHGs

Food security in the WHGs can be considered an intricate multiscale complex process in which a multitude of interacting subsystems within smallholder FHHs play a very important role. Smallholder systems are very diverse, in terms of both the configuration of their structural components and the dynamics of crop production, consumption, and commercialization (Camacho-Villa et al., 2019). How crop production affects food security in the region has been studied for many years since the 1990s. These studies, for example, showed that when farmers shift from traditional maize to only potato they are more likely to get less income, lower food security, and lower nutritional status. Other farmers growing wheat, vegetables, and potato in farms with large land sizes have increased household incomes. However, these increased incomes were not associated with significant improvements in their food security status (Immink and Alarcon, 1991). Commercial FHHs have also been shown to become more dependent on market access for adequate availability of food, with cash crops even further displacing food crops. In these commercial households, the consumption of own-produced staple foods is reduced, and this reduction has resulted in a nutritionally diminished diet (Immink and Alarcon, 1993).

The Need for Quick Reliable Methods to Detect Food Insecurity

Feed the Future (USAID) and the Western Highlands Integrated Program (WHIP) developed the Global Food Security Strategy (GFSS) Country Plan for Guatemala to address, among other issues, food security and nutrition in the country in 2018–2022. The plan is intended to identify the key drivers of food insecurity, malnutrition, and poverty. These drivers are recognized to stem from a complex set of underlying conditions at the individual, household, community, and system levels. Notably, the most vulnerable and poor, with limited resources, skills, and capabilities to participate in market operations, will need to be supported to improve their food production and participate in reliable value chains so that agriculture becomes a viable livelihood option. The need for the identification of the most vulnerable and poor is a call for quick alternative methods of food security assessment necessary for targeted policy interventions (Feed the Future, 2018, GFSS, Guatemala).

Modeling Approach Through Machine Learning Methods

Different modeling approaches have been used to assess and predict agricultural productivity, as well as food security of small-scale farming systems in different conditions (e.g., Frelat et al., 2016, Ritzema et al., 2017). Process-based models (usually a set of differential equations) are powerful tools for prediction for yield estimation of crops at the field scale, for example, as they simulate several interactions between the crops and the environment. These models, however, require intensive data collection and calibration of each of the processes that are incorporated in the model. On the other hand, statistical models estimate direct relationships between predictor variables, without considering the underlying processes (Jones et al., 2017) and can be applied easily if enough empirical observations are available.

“Machine learning” is a technique used for finding significant rules to explain or find patterns in data. We as humans have always been interested in finding rules that allow us to better understand a given system and accurately predict its future behavior. Historically, finding such rules has not been an easy task, but as data availability and computing power increase, it gets easier to try various rules and see which ones more accurately represent a process or phenomenon. Machine learning is a term used to describe a broad collection of pattern-finding algorithms designed for finding system rules empirically, the use of which has grown dramatically (Watt et al., 2020).

The models resulting from machine learning algorithms are sometimes referred to as black boxes: data go in, and outputs come out, but the relationships between input and output remain obscure (Zhang et al., 2018). An extensive literature attests to the superiority of machine learning in minimizing predictive error compared to traditional statistics model fitting as simple interpretable functions may not always make the most accurate predictions. Increasing accuracy of prediction in many cases requires methods that are able to deal with more complex interactions between the model inputs. This can be achieved by machine learning algorithms; however, what we may gain in predictive power we may lose in interpretability of the complex interactions (Goldstein et al., 2015).

The use of machine learning algorithms has a great potential to discover patterns and in consequence explore alternatives to fight poverty and also help in decision-making processes aiming to alleviate it (Blumenstock, 2016; Jean et al., 2016); particularly, it has been applied for predicting famine or food security aspects in sub-Saharan Africa. Artificial neural networks (ANNs) were used in Frelat et al. (2016) for an across-Africa study and in Egypt for predicting country-level future crop production needs (Khedr et al., 2015), whereas support vector machine algorithms were used in Uganda and Brazil for detecting famine-prone households (Okori and Obua, 2011; Barbosa and Nelson, 2016). A worldwide initiative to fight hunger with big data and artificial intelligence is also being developed (Worldbank, 2018).

The food security status indicator developed by Lopez-Ridaura et al. (2019) managed to capture the complex dynamics of the inputs and outputs of household nutritional energy through consumption, transformation, and commercialization of farm products. We hypothesize that a small set of simple variables can be found to capture the complexities of food production at the plot level and predict the food security status of the smallholders' FHHs of WHGs. In this study, (i) we develop, train, and test a model to predict the food security status of WHGs FHHs and (ii) explore the complex interactions between the input variables of this model, to better understand the relationships between agricultural production, land use, and food security.

Methods

Study Area and Data

The USAID's WHIP aims at fighting poverty and malnutrition and augmenting access to health services, access to markets, and improved agricultural production in the region. In 2013, as part of the impact evaluation of the program, a baseline survey targeting 6,301 households in the WHGs was conducted in 55 municipalities in five departments (Figure 1) (Ángeles et al., 2014).

FIGURE 1

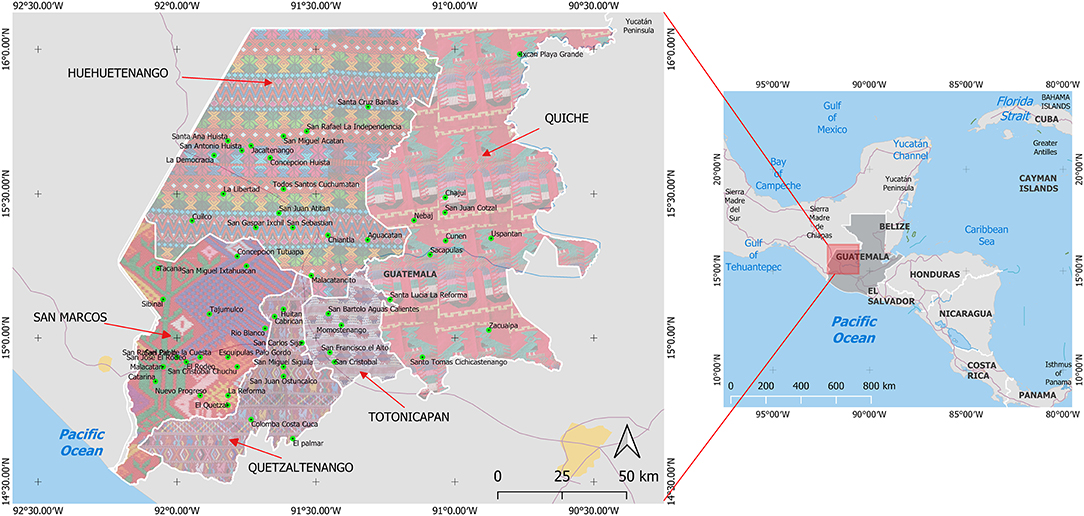
Figure 1. Municipalities in the WHGs surveyed in the “Encuesta de Monitoreo y Evaluación del Programa del Altiplano Occidental (EMEPAO)”.

The survey, Encuesta de Monitoreo y Evaluación del Programa del Altiplano Occidental, was developed to measure the program's impact and followed rigorous randomized sampling methods, considering the influence zone regarding two components: the rural value chains (RVCs) and the health program. The program directs its actions to different population sectors divided in three domains: those members to an association related to RVCs and health program beneficiaries, those with no direct participation in the RVCs, and those that are beneficiaries of the health program. Two other domains were profiled for comparison and evaluation. The survey includes detailed information on households members and characteristics, food security status, expenses, and consumption levels, empowerment, women reproductive dynamics, communities' basic infrastructure characteristics, and health services (see full details in Ángeles et al., 2014). We did not consider households reporting no agricultural activity or with inconsistent data (e.g., more land reported on a crop than the total area, or areas on crops with no production data). In total, we selected 4,790 households for analysis.

Potential Food Availability Indicator

The availability dimension of food security (FAO, 1996) quantified for WHGs smallholders by Lopez-Ridaura et al. (2019) consisted of calculating an indicator (Figure 2) that approximates the PFA at household level. This indicator is based on the transformation into kilocalories of all products derived from the farm (Frelat et al., 2016), regardless of whether those products are consumed directly inside the household or sold. The energy intake due to the consumption of each product (maize grain, beans, meat, etc.) can be calculated based on their caloric content and the number of kilograms consumed on a yearly basis. The potential energy intake generated from selling farm products is obtained by transforming all income from the sales into whatever quantity of staple food grain (maize) could potentially be bought with it and then converting this amount of “virtual grain” into energy as well. The total food energy potentially available to a farm family is thus obtained by adding the energy due to consuming some products, which is directly available, and the energy derived from selling others, which is indirect. The yearly energy requirement for the household is calculated based on the total number of household members (transformed to male adult equivalents), and an energy need of 2,500 kcal/day for each male adult equivalent. The indicator quantifies how much energy (expressed in kcals) is potentially available daily per male adult equivalent. When PFA is ≥2,500 kcal/day, the household has enough or more food than needed per day per family member and is, in consequence, food-secure. If PFA is <2,500 kcal/day, the household energy requirement is larger than what is available, and thus, the household is not food-secure.

FIGURE 2

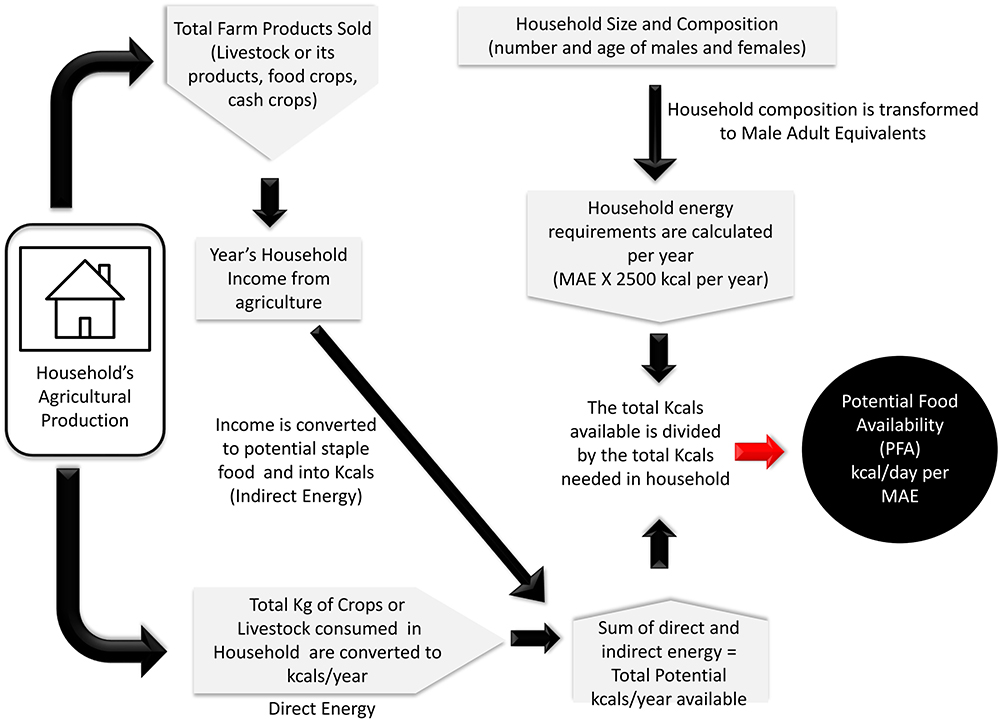
Figure 2. Representation of household food provisioning process expressed as potential food availability in kcal.

The data underpinning the PFA indicator can be complex as it is composed of inputs from a wide variety of sources. Different farm products might be directly consumed or might be sold for cash raw or converted, and the diversity of farm produce is described next. Livestock production involves several species, including horses, goats, sheep, chicken, turkey, pigs, cows, and even fish or bees. These animals can be commercialized either through live sales, or as their products, for example, honey, meat, eggs, milk, cheese, cream, fat, wool, or even sausages. The crop diversity of the Western Guatemalan systems includes maize, beans, coffee, fava, pea, potato, and, to a lesser extent, green beans, carrots, and Brussels sprouts. The average price of each product or crop included in the analysis is included in the Appendix 1, as well as the average amount of its production, consumption, and income generation. Household size, expressed in male adult equivalents, had a median value of 4.1 MAE and a mean value of 4.38 [standard deviation (SD) = 1.97], with a range (max. – min.) of 13.1 MAE.

Potential Food Availability Prediction Modeling Approach

Several methods for forecasting and prediction have been developed, and machine learning algorithms have proved particularly to be able to provide raw material for sensitivity analyses, which allow the disentanglement of coupled effects between predictors and pickup signals in massive amounts of data, something that becomes more time and resource consuming with traditional statistics methods (Kantardzic, 2020).

We fitted and compared several methods of supervised learning to find the best one for PFA prediction. Besides a multiple linear regression, we assessed machine learning classifiers random forest (Breiman, 2001) and ANN (Rosenblatt, 1958), ANN performed best in terms of prediction accuracy, and the results are presented in this study.

Data Selection for Food Security Prediction

Many factors are related to food production, quantity, quality, and diversity in the WHGs, and we selected variables to allow for a comprehensive representation of the FHHs, regarding land availability and its management. Another consideration for selecting variables was that they should be easy to capture or measure. We selected as predictor variables those related to land size, land allocation to crops, and crop diversity, as well as crop production levels. More specifically, we selected 14 variables for the 4,970 households analyzed: total land, land availability per person, total number of crops grown, land allocated to maize, land allocated to coffee, land allocated to potato, land allocated to other crops, livestock holdings [expressed in tropical livestock units (TLUs)], and the yield of each of the following crops: maize, coffee, bean, fava bean, pea, and potato.

Exploratory Data Analysis of Predictors vs. Target Variable

First, the data were screened to detect variables with zero or near-zero variance. These numerical variables may have a unique constant value or have very few unique values relative to the number of samples and thus are not useful for modeling approaches as they show no variation when other predictors change. Land under potato, fava bean, pea, and potato yield proved to possess zero or near-zero variance and therefore excluded at this point. Also, outliers were removed using a cutoff of the above 99% quantile and the below 1% quantile. This resulted in a data set of 4,499 FHHs for analyses.

To detect collinearity between the predictors, as well as their correlation with the target variable, we followed a pairwise Pearson product–moment correlation analysis and constructed scatterplots (see Appendix 2 for the results). We also quantified the descriptive statistics of the target variable (PFA) and predictors.

Algorithm for Model Fitting

Artificial neural network models could be considered as frameworks that represent non-linear mappings between multidimensional spaces, avoiding rigorous assumptions on data distribution. The use of these algorithms is gaining popularity in research areas not only where large amounts of data are available but also when the relationships between the variables are unknown or expected to present high-non-linear behavior (Jiang et al., 2017). The structure of an ANN is represented by layers, each composed of nodes. Normally, at least three layers (the input, hidden and output layers) are required for building an ANN model. The nodes are connected, layer by layer, by arrows that represent the strength of their interrelationship. The nodes of the input layer represent the input variables or predictors, whereas the nodes of the output layer represent the output variables. This structure is inspired on the neural processes in the brain, as information is shared across the network of neurons (nodes or processors). The network as a whole learns patterns by observing inputs (perceiving the environment) and outputs by adjusting the relationship between the variables and the internal nodes (by changing the weight of each connection connection) in the network. This so-called shallow neural network architecture is actually already quite old and has been around since 1960s (Rosenblatt, 1958; Schmidhuber, 2015). Other methods may overlook non-linear relationships, which ANNs can approximate through this flexible layer, node, and connection weighting setup (Landi et al., 2010; Dalatu et al., 2017).

The input and output layers correspond to input and output variables, respectively. In our case, the output layer is a single node, the PFA values, whereas the input layer consists of the set of predictor variables. As the model is trained, the weighted connections are adjusted using backpropagation, a gradient descent method (Schmidhuber, 2015). Each single node receives information from the nodes from the previous layer and calculates the weighted sum from these inputs as follows:

\begin{array}{l} t_{i} = \sum_{j = 1}^{n} w_{i j} x_{j} \end{array}

where t represents the weighted value to which a function is applied to calculate the node output, w represents the weight of the connection between nodes i and j, whereas x represents the input from node j, and n is the number of inputs. To generate the output node values, a transfer function is applied to t:

\begin{array}{l} o_{i} = f (t_{i}) \end{array}

We used the most common transfer functions: these are a logistic transfer function for the output layer nodes and a linear transfer function for the hidden layer nodes. The number of connections between inputs and outputs is determined by the number of nodes in the hidden layer. The appropriate number of hidden nodes may vary depending on the complexity of the relationships. If too many nodes are used, this can lead to overtraining during the calibration exercise, resulting in poor prediction (Garro and Vázquez, 2015). To control for this, a data set is normally split into two parts: one for the calibration and one for testing. When using a small number of hidden nodes, normally the model performance for both the calibration and testing data sets increases when adding extra hidden nodes. However, at a certain moment, the model performance for the testing set does not improve anymore by adding more hidden nodes and can actually start to decline. The latter indicates overtraining and means that the number of hidden nodes is getting too large (Chai and Draxler, 2014).

Data Transformation, Data Splitting, Model Training, and Performance Testing

Input data were preprocessed for the ANN. To control for different ranges of input variables, all values were standardized [0, 1] intervals using

z_{i} = \frac{x_{i} - min (x)}{max (x) - min (x)}

where x_i = (x₁…..x_n), x is the set of points of the variable to be transformed, and z_i is the transformed data point.

To properly assess and compare model performance, data were split into training and testing sets in a proportion of 0.75 (n = 3,375 FHHs) and 0.25 (n = 1,124 FHHs), respectively.

We used the package nnet combined with caret in R. The two packages combined allow for tuning the weight decay during the training and the number of nodes in the hidden layer. We tried several numbers of iterations to check the minimum length of training that would allow for a converged result. Then, several combinations of weight decay and number of nodes were tested to find the most accurate model. A 10-fold cross-validation was performed on each training procedure, using the root mean square error (RMSE with kcal/day per MAE unit) and R² of observed vs. predicted values as metrics. The testing data set was used to validate the ANN model performance. Also, for the testing data, RMSE and R² of observed vs. predicted values were computed from the predicted PFA vs. the food security indicator PFA to determine the precision and bias of the predictions, respectively. RMSE is computed as follows:

\begin{array}{l} RMSE = \sqrt{\frac{\sum_{i = 1}^{n} {(X_{obs, i} - X_{m o d e l, i})}^{2}}{n}} \end{array}

where n is the number of observations in the data set, and X_obs,i are the values of the target variable from the testing or training data set, and X_model,i are the values predicted by the model. Also, a scatterplot of predicted vs. observed values was constructed to assess visually the model's accuracy, linear model, and regression equation line, and 1:1 line was added for ease of interpretation.

Model Interpretation

We used three methods for interpretation of the ANN model. First, we determined variable importance to identify the most significant explanatory variables and their influence on the output variable (PFA). For this, we used Garson's (1991) (Goh, 1995) and Olden et al.'s (2004) algorithms. Garson's algorithm is based on partitioning neural network connection weights and uses them to define relationships between variables. Garson's algorithm reports relative importance of each input variable expressed as a percentage. The value of connection weight indicates the influence of the input variables on the output variable, and the higher the value of connection, the stronger importance of corresponding input variable. Olden's method, contrary to Garson's, uses raw connection weight values instead of absolute values, and therefore it accounts for negative and positive effects of the variables. Negative values account for a negative effect of the input variable over the output. Using both algorithms helps to confirm the absolute influence of input over output variables.

Partial dependence plots (PDPs) were developed by Friedman (2001) to help visualize the relationship between a subset of predictors and the response variable while considering the average effect of other predictors in the model. This could mask important interactions and heterogeneities that the model captures. Individual conditional expectation plots (ICEplots) extend on PDPs and disaggregate the average effect by displaying for each observation the estimated functional relationship that exists with the output when the predictor variable changes. The resulting curve for each observation helps to identify possible interactions of the predictor with other variables in the model, as well as to detect extrapolations in predictor space. We constructed ICEplots for each variable included in the model to detect such interactions. Partial dependency plots were used for visualizing the simultaneous interactions between 3 variables.

All analyses were done with R (R version 3.4.1; R Core Team, 2017) with the IDE Rstudio (version 1.1.423), caret (6.0–80, Kuhn et al., 2018) and nnet (7.3–12, Venables and Ripley, 2002) for ANN training and parameter tuning, ICEbox (Goldstein et al., 2015) for individual conditional expectation plots, NeuralNetTools (1.5.2, Beck, 2018) for Lek's profile and Olden's and Garson's variable importance analysis, and pdp (0.7.0, Greenwell, 2017) for visualization of PDPs.

Results and Discussion

Exploratory Data Analysis

The data showed high variation in PFA intermediate variation in land availability, yields and land allocation, and low variation in TLU and number of crops (Table 1). Land availability is very low, and plot sizes are small with a mean of 0.127 (SD = 0.131) and a median of 0.085 ha per person. Maize yield is on average low but highly variable: average yield was 2.25 ton/ha with an SD of 2 ton/ha. For coffee, the average yield is 0.374 ton/ha and a SD = 0.6, which is close to double of the average, so high variation in yield is found in the region. Most of the land is allocated to maize with an average value of 53%, although the variation between farms is large with an SD of 35%. Coffee is the second most important crop in terms of land allocation with an average value of 23%. But variation is also large for coffee, and the SD of 35% indicates that some farmers may allocate more than 50% of their land to coffee or have no land under coffee at all. Area under other crops is, on average, 8.6%, meaning that maize and coffee are indeed by far the two most important crops. On average, smallholders cultivate 2.5, but with an SD of 1.4, this value does mask quite a range of different crop diversity strategies. In general, the farms possess few livestock, with an average holding of 0.47 TLU and an SD of 0.66.

TABLE 1

Table 1. Descriptive statistics of the predictors and target variable.

This large diversity of farming systems in the WHGs region also manifests as large differences in their PFA. From the sample, 52% of FHHs in the region do not attain enough energy production from their farms (Lopez-Ridaura et al., 2019). It has been estimated that approximately 50% of children younger than 5 years in the western highlands are stunted because of chronic food insecurity. Also, indigenous people are concentrated in this region, and it is reported that the prevalence of chronically malnourished population may reach nearly 70% (USAID, 2018).

Algorithms Tuning and Performance

Despite the large data variability typical for household survey data (e.g., Fraval et al., 2019), we have been able to provide an accurate prediction of the food security status (i.e., food availability) of FHHs in the WHGs. A model that predicts PFA with a high level of precision was constructed using only a small set of input variables and the application of ANNs. We chose to keep the ANN because of its superior performance predicting PFA with the testing data set as compared to the other methods: the linear regression resulted in an RMSE = 4,766 kcal/day per MAE and an R² = 0.52, and the random forest algorithm gave an RMSE = 3,490 kcal/day per MAE and an R² = 0.78. For the ANN, after trying several maximum numbers of iterations by trial and error, 1,500 iterations allowed the model to converge in all the training rounds, while computing times were reasonable. Using this setting and evaluating different weight decay and number of hidden units using 10-fold cross-validation, the best-performing neural network was one with eight hidden nodes and a weight decay of 0.0009. This ANN setup resulted in an R² = 0.80 (RMSE = 3,410 kcal/day per MAE) in cross-validation. When validating with testing data set, the observed vs. predicted values yield an R² = 0.85 (RMSE of 2,891 kcal/day per MAE), meaning this simple response model can account for nearly 85% of variation of PFA, as seen in Figure 3.

FIGURE 3

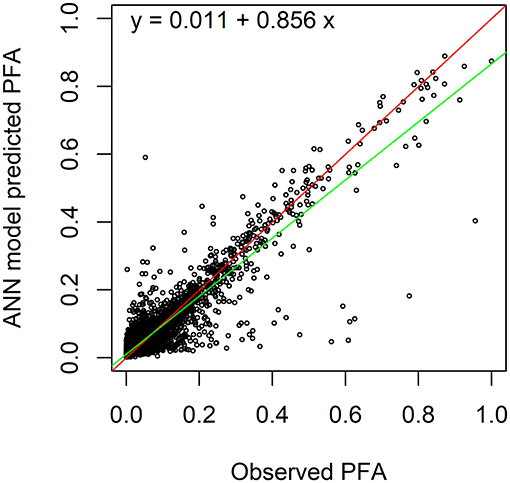
Figure 3. Artificial neutral network model performance with the testing data set. A red line represents the 1:1 relationship, whereas the green line represents the linear regression of observed vs. predicted PFA.

The resulting ANN model can then be used as an analytical tool to assess the effect of the single variables as well as their interactions, the thresholds and frontiers affecting the food security of smallholders generated through the decisions on agricultural activities, especially land allocation (i.e., to coffee or maize) and their yield levels.

Model Interpretation

The Variables Importance Based on Garson's and Olden's Algorithms

The most important variables for the prediction of households' PFA according to Garson's algorithm (Figure 4A) are, in diminishing importance, as follows: coffee yield > land under coffee > hectares per person > maize yield > land under maize > crops number > land under other crops > TLU.

FIGURE 4

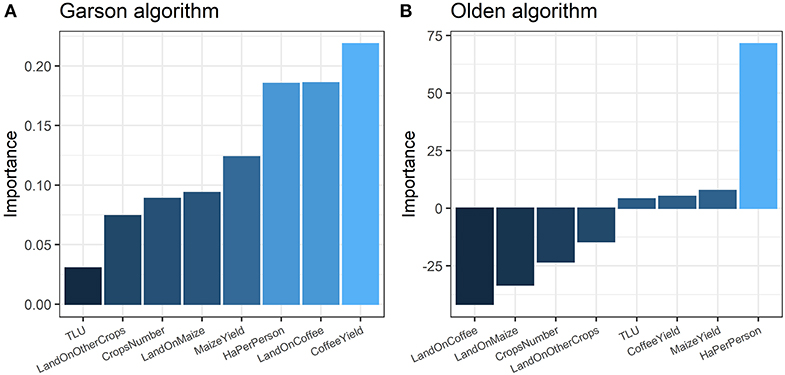
Figure 4. Variable importance for food security prediction in the ANN model according to two different algorithms: (A) the Garson algorithm, which orders variables by their explanatory power, and (B) the Olden algorithm, which orders the variables by their explanatory power and also shows the positive or negative effect on the predicted PFA.

According to Olden's algorithm (Figure 4B), the most important variables are hectares per person, with a positive effect on PFA (increasing land availability increases PFA); and land under coffee, with a negative impact on PFA. Other, less important, variables, such as land under maize, crops number, and land under other crops, have a negative effect on PFA. According to Olden's method, maize and coffee yields affect PFA positively, although not in a great manner, whereas Garson's algorithm identifies coffee and maize yields as highly important.

We can conclude that both algorithms find that the altogether least important variables, in terms of accounting for PFA variation, are livestock holdings, land on other crops, and crops number, and the most important are hectares per person and land under coffee. We found that land availability (hectares per person) and land under coffee (or inversely land under maize) are the variables with the highest predictive value (i.e., the ones sharing a larger proportion of the weights in the neural networks).

Non-linear Trends Detection in Single Variables for PFA Prediction

The ICEplots (individual conditional expectation plots) allowed us to identify how large is the effect of each predictor on PFA and if non-linear relationships between the predictors and PFA exist (Figure 5). The ICEplots show that, in general, the effect of single predictors on PFA is non-linear. For land availability, maize and coffee yield land under other crops, land under maize, and land under coffee, contrasting behaviors between households are evident; PFA either increases or decreases. The fact that there exists a contrasting behavior is indicative of the interaction with other variables; also, the PFA growth curves may present different growth rates (slopes) with either a positive or negative sign.

FIGURE 5

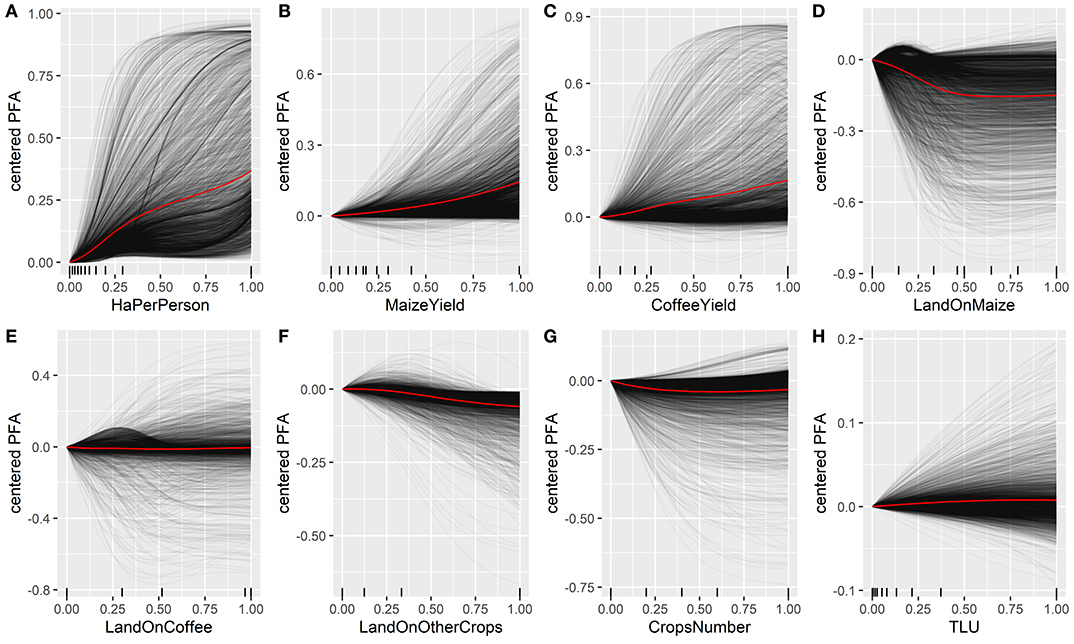
Figure 5. Individual conditional expectation plots (ICEplots) for variables (A) hectares per person, (B) maize yield, (C) coffee yield, (D) land on maize, (E) land on coffee, (F) land on other crops, (G) crops number, (H) tropical livestock units. The x axis is scaled to 0–1, and the y-axis is scaled and centered in 0. The red line represents the partial dependency plot (average). Each curve in gray shows the projection of each sample along the predictor's variation interval.

The land availability variable, hectares per person, has a positive relation with PFA, but this relation shows large variation; that is, the same value of hectares per person can yield a large range of PFA values- possibly driven by the non-linear relationships with other variables. Small increases in hectares per person, especially below the value of 0.25 ha per person, result in a substantial increase of PFA, but further increases in farm size enhance PFA only in modest amounts.

That PFA curves reach a saturation point as land availability increases agrees with other studies, such as that of Frelat et al. (2016), where they postulate that this saturation could be explained by a decline in productivity per unit land (kcal/ha), when land availability increases. This pattern of inverse land size productivity is also found in many studies of smallholder farmers (Larson et al., 2013; Ali and Deininger, 2014), showing that medium-sized farmers are more efficient per unit area (Muyanga and Jayne, 2014). The main concern here is that the minimum amount of ha per person needed to achieve 2,500 kcal/day per MAE is around 0.06 ha; land availability of the sample is on average 0.13 ha with a median of 0.08 ha, which means that only nearly half of the households' population may possess enough land to achieve 2,500 kcal/day per MAE, and possibly the other half might be not reaching even the 0.06 ha per person value. Even with excellent crops yields, PFA does not reach high values in situations in which land availability is very limited, so just trying to increase productivity might not be a useful intervention for households that lack a critical amount of land.

Given this information, increasing crops yield might be not the proper intervention for all FHHs because attaining high yield, with still very limited land availability, PFA would not reach high values. On the other hand, some farmers that possess enough land (e.g., 0.19 ha per person) but still present low food security may benefit from agroecological options for intensification and diversification.

This type of saturation effect is seen in other plots in Figure 5. Maize yield, coffee yield, and land on coffee individual curves present a growing trend but stabilize after certain point, although the average response curve for these variables is a relatively straight line. Land under maize shows a negative relation with PFA, again with a clear saturation signal, indicating that although maize is an important food security crop, there are other crops that generate more value on the same amount of land. The response curves of the other variables are all straight lines and close to zero value, indicating that they not have such a large effect on PFA as the variables already discussed.

Three-Way Interactions and Their Effects on PFA

While Figure 5 showed the single variable effects, we are also interested in the interactions between the drivers of PFA. We used contour partial dependency plots of three variables to analyze how they simultaneously affect PFA. Figure 6 presents the non-linear relationships between some of the variables with highest explanatory power for PFA prediction. Figure 6A shows the relationship between hectares per person, yield of coffee, and yield of maize (the latter divided in ranges pertaining each quartile in each panel). The most important limiting factor for attaining high values of PFA is, again, land availability (hectares per person). Even when coffee and maize yields are low, more land availability increases PFA substantially. Again, even when maize yields and coffee yields are high, it is difficult to reach PFA values that represent a food-secure household at low values of land availability. The area of PFA values representing food-secure households logically increases with higher yields of both crops. This allows us to identify under which levels of land availability and productivity household can be food-secure using the PFA indicator, and thereby given the current levels of land availability and productivity of the different household, we can identify land and productivity “gaps.”

FIGURE 6

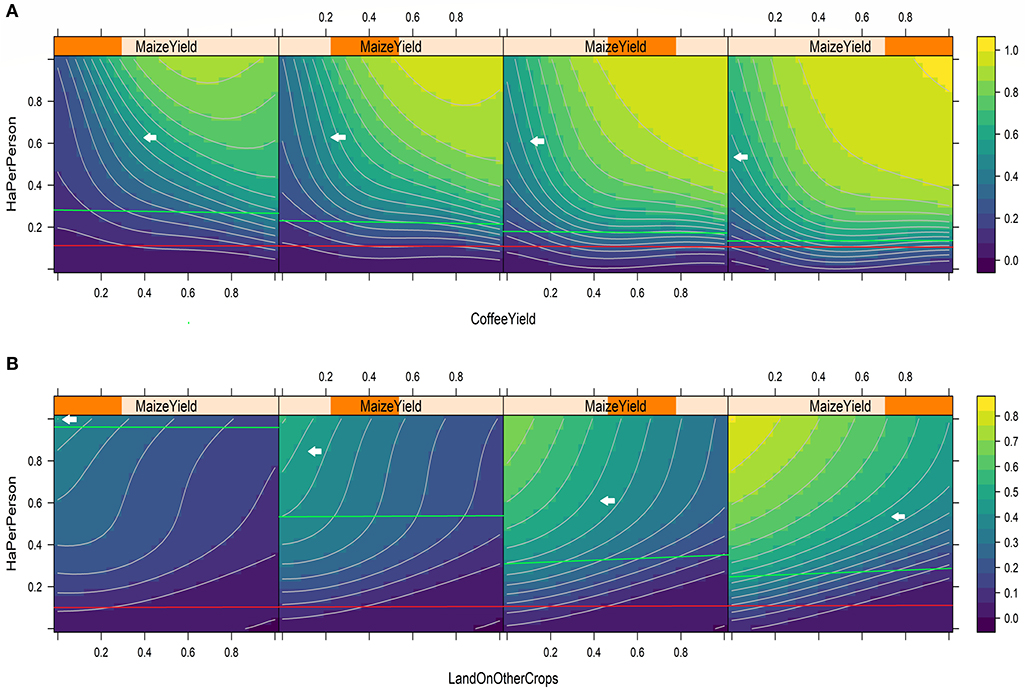
Figure 6. Partial dependency plots of three simultaneous variables. (A) Hectares per person - Coffee Yield - Maize Yield. (B) Hectares per person - Land Under Other Crops-Maize Yield. Contour curves show the regions of the values of scaled PFA. A second and third variable are represented on bottom and top edges respectively of each plot, the orange rectangle shows the quartile of the third variable that are plotted on each panel, from left to right. Arrows point to the contour line that is equivalent to a PFA interval between 2300 and 2740 kcal/day per MAE. Red line represents the average sample land availability (0.13 ha per person) and the green lines represent the land availability necessary to reach the 2300 and 2740 kcal/day per MAE interval.

A general trend found when three-variable interactions are analyzed is that PFA grows when land size increases in terms of land availability per person (Figure 6) and when maize and coffee crops yields are higher (Figure 6A). Although the results of Figures 5, 6 show a large variability, results indicate that there is a typical 0.25 ha per person threshold, under which land availability is the most constraining factor for achieving food security. Surprisingly, this threshold seems to be quite independent of the crop productivity values.

The average value for land availability in the households' sample in the WHGs is 0.13 ha per person (red line in Figure 6), for coffee yield 0.37 t/ha, and maize yield 2.25 t/ha. Following the interpretation of the relationship between these variables in Figure 6A, reaching a PFA on the limit of 2,500 kcal/day per MAE is possible only for land availabilities with values in the range of 0.19–0.3 ha per person that lie above the sample mean (green lines in Figure 6). Food security could only be attained for a land availability of 0.19 ha per person (fourth panel Figure 6A), with the highest yields predicted to be 8.7–11.6 t/ha for maize and 3.2 to 4.2 t/ha for coffee on the upper quartile, but these values are rare in the sample. With lower yields, land availability above the sample mean is mandatory. Something similar happens in Figure 6B; only the highest yield on maize in monocrop (i.e., zero land under other crops) could provide enough kcals, but the land availability necessary is even higher than when growing maize and coffee, as the lowest threshold (green line, fourth panel, Figure 6B) is 0.20 ha per person.

Our three simultaneous variables partial dependency plots approach allows seeing how important it is increasing yield when land is limited. Increasing the yield and yield stability of crops might become transcendent if we consider that land shows to be the most critical point defining food security of smallholders in the WHGs. It is important to see that those households that reach 2,500 kcal/MAE per day have, on average, some differences from those who do not, for example, more land availability, higher yields of coffee less land under maize, higher lands under coffee, and less land under other crops (Table 2).

TABLE 2

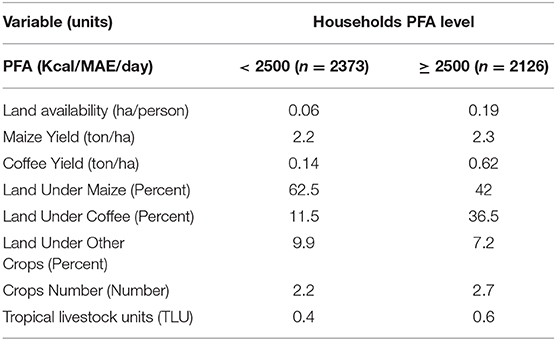
Table 2. Differences in the predictor variables between the sampled households grouped into two, those whose PFA values are below 2500 kcal/day per MAE and those with PFA equal or above 2500 kcal/day per MAE.

For most FHHs in the WHGs, maize contributes with a high percentage to the PFA and therefore is critical for food security. Maize yields in the region have been reported previously to be in a range from 1 to 2 t/ha (Hellin et al., 2017), and in our sample, the yields are, on average, 2.25 t/ha. Small-scale farmers in Guatemala are key actors in maize production–consumption. Farmers owning <7 ha of land represent 53% of the farmers growing maize. More than two-thirds of the maize they produce is for self-consumption, covering ~8 months of their needs (USAID/Guatemala, 2009). However, these subsistence farmers have experienced accelerated land fragmentation (Isakson, 2014). Currently, 55% of the national maize production is produced by farmers with <3.5 ha (Fuentes-López et al., 2005). This land fragmentation has been more dramatic in the WHGs. Hellin et al. (2017) found that, in 2016, farmers from this region owned an average of 4.3 ha in the 1980s, but currently they have only 0.4 ha. These findings coincide with Bellow et al. (2008) and Sigüenza Ramírez et al. (2010), who found that the average land size for a small-scale farmer was 0.34 ha. Hellin et al. (2017) also found a large variability in maize farmers' average landholdings, depending on their location within the five departments that comprise the western highlands.

For those still growing maize and coffee in different agroecologies, some alternatives could be explored for increasing crops yield and stability, for example, participatory breeding in which adapted maize seeds could be spread in regions with higher yield potential; also, as most of the farms are located in mountainous regions with steep slopes, soil could be retained or its qualities could be restored or improved through soil and water conservation strategies.

Another general trend shows that increasing land on other crops leads to decreasing PFA and that only with high maize yields and enough land available the window to diversity production opens up (Figure 6B). Analyzing the interactions between land availability, maize yield, and land under other crops, we again see the effect of increasing land availability on PFA, but more interestingly, we see a trade-off between more land under other crops and PFA. This means that the other crops add less value per unit hectare than maize and coffee (especially the latter, which is the major cash crop of the region). So, from a purely PFA perspective, diversifying production does not make much sense, but we need to take into account the limitations of the PFA indicator, which is only based on energy (kcal) production and consumption. Other crops are likely to have positive effects on other aspects of food security such as dietary diversity and/or risk management, among other functions of diversification. This analysis therefore shows the window of opportunity to bring in these other crops in these production systems: after satisfying the PFA indicator (basic energetic food security), it will be important to bring in other crops to improve dietary diversity. The model shows under which combinations of land availability and crop productivity such opportunities arise.

The dynamics and the effects of crops diversification in the WHGs in the past have shown that including commercial crops in the farming activity of smallholders in the region may affect their food security, posing risks to their availability dimension (Immink and Alarcon, 1991, 1993). This is reflected in our results as we can see that not necessarily having land allocated to fully commercial crops or to food crops alone has a positive effect on food security; our results support the need for diversification, but in an equivalent proportion regarding the land that is shared between the crops, especially coffee and maize.

When land availability per person is large, higher values of PFA are possible independently of the crop produced or the surface cultivated. Nevertheless, increasing crops diversity is to be considered carefully for these systems as we show that high crops diversity affects PFA. For some plots with high land availability, food security might be attained with a high-diversity mix of crops, but there is a threshold in the number of crops that can be cultivated in small plots to attain large PFA values. It is possible also that monocrop cultivation on large plots outputs high values of PFA.

The analyses' results show that, along the split into staple crop–cash crops (i.e., land under maize vs. land under coffee), roughly an equal share of both crops seems to give the highest probability of attaining food security. Again, this is possible only if enough land is available (>0.25 ha per person), and such an equal mix makes sure both basic calories and cash are available to the household.

For those FHHs possessing larger land extensions as diversifying crops seems to be beneficial, exploring alternatives to improve the systems efficiency could be beneficial, for example, crops rotations and systems integration of fruit trees which may add even more nutrients to diets or possibly provide even more products to commercialize while helping to avoid soil erosion as well.

For others, greatly limited by land availability, other strategies would need to be assessed. Previously, life history studies have revealed that besides growing coffee in small plots, which is a common practice, off-farm activities are of great importance for coping with food insecurity when land is limited (Beveridge et al., 2019) and also describe the way smallholders get involved in other activities such as selling their labor in nearby big farms or near big cities, raising chicken in home gardens as a way for making income, and timber wood production. Also, some positive factors are is highlighted that would help in improving food security such as women's own income production dependent on home garden activities and even handicrafts (Feed the Future, 2018).

An additional important analysis that could be performed would be to identify the effect of market access on increased PFA. As Frelat et al. (2016) found, access or means of commercialization are crucial to ensure or improve the livelihoods of smallholders and might impact more than crop productivity interventions. As the present study is only a snapshot of the food security in the region, crossing information about regional PFA and the access to markets, including how climatic and price variations would affect smallholders land allocation decisions and production, could aid in projecting PFA in the future and profiling the interventions that could take place.

Conclusions

Food security in the WHGs is the result of a socioecological complex dynamic system, with many layers interacting in many ways, and with bottom-up and top-down effects. However, it is interesting that through the application of machine learning algorithms we have been able to construct a tool that predicts the FHHs' PFA with an acceptable degree of precision. With a sample of nearly 5,000 smallholders, we were able to fit a model with an R² ~0.85.

The best-performing model for the prediction of the continuous PFA values (kcal/male adult equivalents per day) is an ANN based on a short set of simple variables (i.e., land availability, crops yields, land share of crops) than can be easily obtained with only a few questions to the farmers. Also, by using model interpretation and visualization techniques, certain patterns are found on the effects of land availability, the share of land of commercial and staple food crops, and their yields on food availability. This analytical framework represents an opportunity as these approaches could be easily implemented as quick and (to a certain extent) reliable tools for screening the food security status of FHHs. That could be helpful during baselining and evaluation for projects which objectives would be to improve food security in the WHGs or regions alike, with high population densities and high diversity of farming systems and activities. The power to quickly assess the food security status of a population would be that interventions would be easily targeted as the population could be sectorized.

The relationship of some of the predictor variables with PFA, extracted with the machine learning algorithm, reveals some non-linear patterns and allows us to extract some conclusions referring to the main constraints that prevent households from achieving food security. Large land availability and high yields of crops seem to ensure food security, but approximately half of the population does not possess enough land.

Data Availability Statement

The datasets generated for this study will not be made publicly available. Data is property of USAID.

Author Contributions

LB-E, MW, and SL-R contributed equally in conceptualizing, analysing, and writing this work.

Funding

We would like to acknowledge data shared and financial support provided by the United States Agency for International Development (USAID) through its Global Hunger and Food Security Initiative, Feed the Future under the BuenaMilpa project as well as the CGIAR research program (CRP) on Maize Agri-food Systems (MAIZE) which receives support from the governments of Australia, Belgium, Canada, China, France, India, Japan, Korea, Mexico, Netherlands, New Zealand, Norway, Sweden, Switzerland, U. K., and U. S., as well as the World Bank.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to acknowledge the Non-linear Dynamics and Complex Systems Group, faculty of the Master in Complexity Sciences from Universidad Autónoma de la Ciudad de México, for the critical reading of this manuscript that greatly improved this investigation.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsufs.2020.00051/full#supplementary-material

References

Ali, D. A., and Deininger, K. (2014). Is there a farm-size productivity relationship in African agriculture? Evidence from Rwanda. World Bank Policy Research Paper 6770 (Washington, DC: World Bank).