- 1Faculty of Electrical Engineering, Technion—Israel Institute of Technology, Haifa, Israel
- 2Faculty of Mechanical Engineering, Technion—Israel Institute of Technology, Haifa, Israel
Quantum computers promise a great computational advantage over classical computers, which might help solve various computational challenges such as the simulation of complicated quantum systems, finding optimum in large optimization problems, and solving large-scale linear algebra problems. Current available quantum devices have only a limited amount of qubits and a high level of noise, limiting the size of problems that can be solved accurately with those devices. Variational quantum algorithms (VQAs) have emerged as a leading strategy to address these limitations by optimizing cost function based on measurement results of shallow depth circuits. Recently, various pulse engineering methods were suggested in order to improve VQA results, including optimizing pulse parameters instead of gate angles as part of the VQA optimization process. In this paper, we suggest a novel pulse-based ansatz, which is parameterized mainly by pulses’ duration of pre-defined pulse structures. This ansatz structure provides relatively low amounts of optimization parameters while maintaining high expressibility, allowing fast convergence. In addition, the ansatz has structured adaptivity to the entanglement level required by the problem, allowing low noise and accurate results. We tested this ansatz against quantum chemistry problems. Specifically, finding the ground-state energy associated with the electron configuration problem, using the variational quantum eigensolver (VQE) algorithm for several different molecules. We manage to achieve chemical accuracy both in simulation for several molecules and on one of IBM’s NISQ devices for the H2 molecule in the STO-3G basis, without the need for extensive error mitigation. Our results are compared to a common gate-based ansatz and show better accuracy and significant latency reduction—up to 7× shorter ansatz schedules.
1 Introduction
Today’s quantum computers (QCs) are often described as noisy intermediate-scale quantum (NISQ) computers due to the relatively low numbers of qubits available (e.g., 10’s to 100’s) and the relatively high levels of noise associated with them (e.g., decoherence and gate fidelity errors) (Preskill, 2018; Córcoles et al., 2019; Bharti et al., 2022). These limitations result in circuits with short width and shallow depth.
To make use of these NISQ machines, a class of hybrid quantum-classical algorithms are being developed that seek to leverage the relative strengths of quantum and classical computers. The most common example of such algorithms are variational quantum algorithms (VQAs) (Cerezo et al., 2021). VQAs use a QC to prepare a short-depth parameterized quantum circuit (PQC) representing a trial solution or ansatz to the problem at hand. Measurements of a final quantum state are used to calculate a cost function, which is then minimized on a classical computer to estimate the problem solution. Prominent examples of VQAs include the variational quantum eigensolver (VQE) for quantum chemistry and materials applications (Peruzzo et al., 2014; Kandala et al., 2017), quantum approximate optimization algorithm (QAOA) for combinatorial optimization problems (Farhi et al., 2014), and variational quantum linear solver (VQLS) for linear algebra problems (Bravo-Prieto et al., 2019).
One of the main challenges associated with effective VQA implementations is related to the design of a suitable PQC/ansatz that balances expressibility and noise, while avoiding exponentially vanishing gradients of the cost function, referred to as the barren plateau (BP) problem. The two main categories of ansatz that have been considered include problem-inspired ansatz (PIA) and hardware-efficient ansatz (HEA) (Kandala et al., 2017). PIA structure is primarily determined by the details of the problem being solved. HEA structure is determined by the properties of the target hardware. HEAs are designed to reduce PQC depth while maintaining a general and expressive ansatz. There have been a number of attempts (Tilly et al., 2022) to improve the gate-based ansatz approach including ADAPT-VQE (Grimsley et al., 2019) and Noise-Adaptive Search (QuantumNAS) (Wang et al., 2022).
Recently, the idea of combining quantum optimal control (QOC), a method by which optimal pulses can be designed to improve qubit coherence and gate fidelity, with VQA has been proposed (Magann et al., 2021). A few recent studies have sought to implement this and related ideas, proposing to bypass the PQC at the gate level for a pulse-based state-preparation (Meitei et al., 2021; Asthana et al., 2022), ansatz generation (Choquette et al., 2021; Liang et al., 2022a), machine learning tasks (Liang et al., 2022c) and better gate compilation using QOC techniques tailored for VQAs (Earnest et al., 2021; Ibrahim et al., 2022; Leng et al., 2022; Niu and Todri-Sanial, 2022). These studies suggest either using gates in a way that resembles ideas from the QOC theory or optimizing the pulses’ amplitudes and the driving frequencies of the qubits during the VQA optimization, which are the parameters that are commonly used in gate calibrations also outside the context of VQAs. In this paper, we propose an ansatz at the pulse level with pulse duration as the main optimization parameter, along with the phase of the pulses which is manipulated with the phase of the classical control hardware. This new ansatz offers a way to reduce the incoherent noise of the circuit by dynamically matching the total schedule duration to the complexity of preparing the optimal state of the given problem. We show that our proposed ansatz can converge fast to an accurate result, thanks to its low amount of training parameters and high expressibility, achieved by parameterizing also the two-qubit interaction pulses.
2 Materials and methods
2.1 Gate-based ansatz
Most of today’s quantum computing logic is represented using quantum gates. The implementation of such quantum gates on quantum hardware is done using control pulses. In order to map between the desired logic of a quantum gate and a sequence of control pulses, a series of experiments that select the correct pulses has to be run on the hardware, which is usually referred to as the process of calibration. Today’s QCs are noisy and unstable, which leads to the requirement of repeating calibrations frequently to maintain high-fidelity of the gate operations.
The complexity of the calibration process and the need to do it very frequently limits the QC designers to only a small number of gates that will be mapped into control pulses. This set of gates should be universal (to allow universal computing) and is called the native gate set. Each quantum gate that is not included in the native gate set must be first decomposed into a sequence of native gates in a process termed transpilation. In most cases, such decompositions are not unique, and finding the optimal one is challenging. The process usually introduces redundancy and added latency in the qubits manipulation compared to the case where the original gate was part of the native gate set and had its own mapping to control pulses. An example of this type of redundancy is shown in Figure 1.
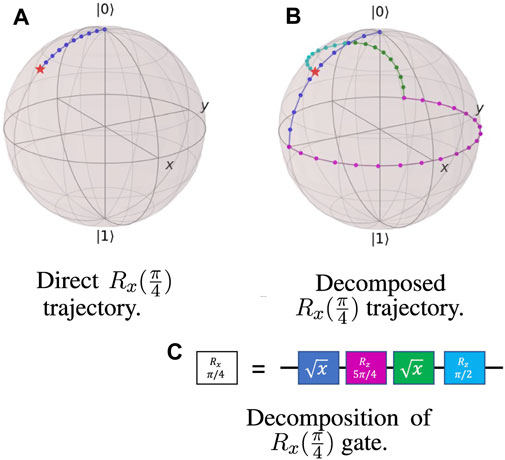
FIGURE 1. Demonstrating redundancy in the control pulses in non-native gate decomposition. (A) Qubit trajectory on the Bloch sphere which represents the logic of
The structure of the HEA tries to minimize the depth of the gates in their decomposed format in order to lower the noise of execution. Each HEA layer usually consists of an entangling layer, built from native two-qubit gates, followed by a parameterized single-qubit gate layer featuring rotation angles as parameters. In addition, there is another initial layer of parameterized single-qubit gates. Henceforth, we will refer to an ansatz built from gates a GANSATZ and use the Real Amplitudes Ansatz, which is commonly used in VQE problems, as a baseline for comparison to our new approach.
2.2 Our approach: pulse-based ansatz
The structure of our proposed pulse-based ansatz, which we will henceforth refer to as PANSATZ, is similar to the GANSATZ structure, where each gate is replaced with a parameterized pulse, including the two-qubit gates, which are also parameterized as part of the PANSATZ. This structure consists of consecutive layers, where each layer is built from two-qubit pulses followed by single-qubit pulses. The two-qubit pulses are ordered in an alternating layout of non-overlapping groups to maximize the number of qubit pairs manipulated at once and reduce the overall duration of each layer (as illustrated in Figure 2). As opposed to the GANSATZ, calibration is not performed and the pulses are not mapped into a logical unitary. Therefore, the logical unitary of the pulse sequences in the ideal case is unknown, and it is not trivial to trace the evolution of the qubits state after each pulse. Similar to other HEAs, the PANSATZ strives to prepare a quantum state while minimizing the incoherent noise associated with the preparation process [as VQAs have some resilience to coherent errors (McClean et al., 2016; O’Malley et al., 2016), our focus is only on incoherent errors]. By trading off knowledge about the unitary evolution in the noiseless case, the PANSATZ can have lower incoherent noise and better expressibility (with the same number of layers) compared to the GANSATZ, as each part of the unitary evolution can be parameterized, including the two-qubit gates. Each pulse has many degrees of freedom which can be parameterized. While keeping more degrees of freedom as parameters improves the expressibility of the PANSATZ, it might also create over-parameterization and introduce trainability issues. Therefore, fixing some of the degrees of freedom as hyper-parameters and limiting the optimization process of the algorithm to only a few parameters for each pulse is crucial for the trainability of the ansatz. As the structure and properties of the control pulses vary between different quantum hardware, the choice of the parameters to optimize should be hardware dependent. In this paper, we will focus on specific well-studied hardware technology, based on superconducting circuits. Recently, research on pulse level control on other technologies started to emerge, like the natural atoms technology (de Keijzer et al., 2023).
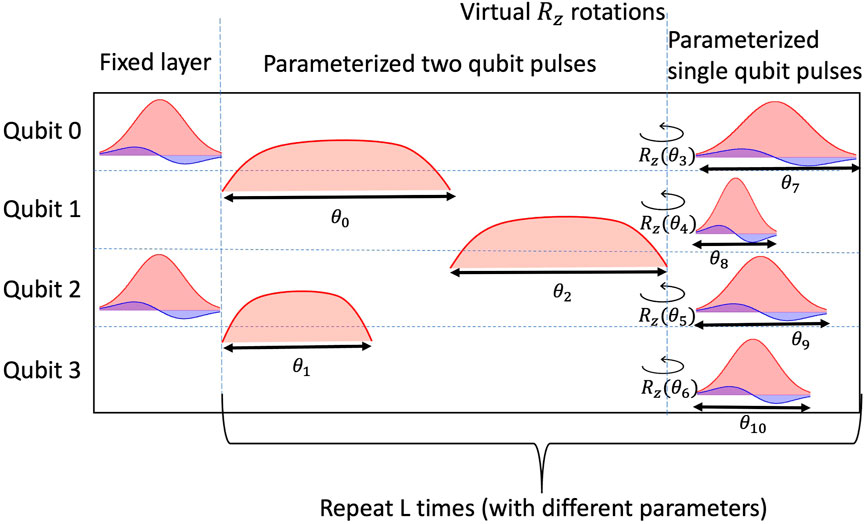
FIGURE 2. PANSATZ structure. The PANSATZ is built out from repeated L layers, each consisting of parameterized two qubit pulses ordered in two alternating layers according to the device connectivity, followed by virtual Rz gates and single qubit pulses on all qubits. The initial layer consists of fixed single qubit pulses which rotate the control qubits of the next layer to the XY plane. The two qubit pulses have flat-top Gaussian shape, and are coloured in light red, acting on the two qubits adjacent to the line it is drawn on. The single qubit pulses have DRAG shape, and are coloured in red (which represents the Gaussian part of the pulse) and blue (which represents the DRAG derivative part of the pulse).
2.3 Superconducting qubit implementation
This study is focused on fixed-frequency superconducting qubits, primarily because of their availability on devices accessible via IBM cloud access. The driving Hamiltonian of each qubit for this hardware can be expressed in the rotating frame using the rotating wave approximation (RWA) as Krantz et al. (2019):
where A(t), ωd(t), ϕ(t) are the time-dependent amplitude, frequency, and phase of the driving microwave, ωq is the frequency of the qubit and
Decoherence and dephasing are major sources of incoherent noise for this qubit architecture. Hence, the duration of a quantum schedule dramatically affects the amount of noise in the computation. Therefore, pulse duration was chosen as the main optimization parameter (as illustrated in Figure 2). This enables exploration of the Hilbert space with the shortest possible schedule duration. The pulse envelope shape, driving frequency ωd(t), amplitude and parameters associated with the chosen envelope shape, were chosen at the beginning of the algorithm as described below and kept fixed throughout the VQA computation. The phase ϕ(t) of the driving pulse is another optimization parameter, which is manipulated using virtual Rz gates, allowing the addition of only one parameter per qubit per ansatz layer, instead of an added parameter for each pulse envelope.
In our implementation, we choose derivative removal by adiabatic gate (DRAG) (Motzoi et al., 2009; Gambetta et al., 2011) as the shape of the single-qubit pulses to minimize leakage into higher energy levels of the device. The σ and δ parameters of the DRAG pulse were taken from the calibrated X gate of the device and kept fixed. We also use flat-top Gaussian functions as the shape of the cross-resonance (CR) (Chow et al., 2011) pulses to enable smooth waveforms with maximum amplitude for most of the pulse duration. The σ and the rise-fall ratio of the flat-top Gaussian are taken from the CR part of the CNOT gate of the device and kept fixed. The frequencies of the pulses were chosen as the resonance frequency of the qubit they are controlling and the amplitude was chosen in a quick calibration process to find the maximum amplitude for short pulses which creates negligible leakage. Negative duration was allowed in order to account for unconstrained optimizers, while negative time was translated into negative amplitude and the absolute value of the duration. Between the layer of the CR pulses and the single qubit DRAG pulses, a layer of Rz gates was added in order to enable changing the relative phase of each qubit, as the phase in the DRAG pulse is fixed. In superconducting qubits technology, such gates can be implemented as virtual gates with zero duration (McKay et al., 2017), therefore they are perfect gates that do not inject any noise to the system. We chose to keep the initial layer of single qubit pulses fixed with pulses that rotate some of the qubits to the XY plane of the Bloch sphere. The qubits that were chosen are those which will act as control qubits in the first entangling layer (which will be every other qubit if we assume linear nearest-neighbor connectivity). This was done in order to create as much entanglement as possible from this layer, as the creation of entanglement is usually the most computationally time consuming. Although the structure of the PANSATZ is fixed, by allowing some of the pulse duration parameters to be zero, some of the pulses and even entire layers can be kept out of the schedule (as opposed to the HEA, where the CNOT gates are not parameterized), adjusting the structure of the ansatz during the optimization process, benefiting from an adaptive approach similar to ADAPT-VQE (Grimsley et al., 2019).
2.4 Two qubit pulse implementation
The two qubit pulses are usually the most important, as they can create entanglement between the qubits, but also the most time-consuming and error-prone. Therefore, additional care should be taken in the optimization process of these pulses. The effective two-level system Hamiltonian describing the CR pulse can be approximated as the time-independent Hamiltonian (Alexander et al., 2020)
where the dominant terms are the entangling term ZX and the single-qubit terms ZI and IX (Sheldon et al., 2016; Ware et al., 2019; Magesan and Gambetta, 2020). The ZX term is crucial for creating entanglement and is usually the only desired term of the CR pulse when designing a CNOT gate, while the ZI and IX are usually referred as unwanted terms and have the largest coefficients. In the PANSATZ case, there is no target unitary for the CR pulse, only a search for the mapping between the parameters of the pulse and the cost function, therefore these terms are not considered coherent errors. However, in our numerical experiments, we observed that a relatively small change in a CR pulse duration caused a large change in the cost function, mainly as a result of these heavy weighted single-qubit terms. These frequent large changes in the cost function harm the flow of the classical optimizer and lead to problems with the convergence of the algorithm. Therefore, we changed the CR pulses into an echo format (Córcoles et al., 2013; Sheldon et al., 2016), which has a DRAG-shaped flip pulse (which needs to be calibrated a priori) on the control qubit between the two halves of a CR flat-top pulse. Such an echo cancels these single-qubit terms while keeping the entangling term. This makes each entangling pulse longer than it needs to be in the optimal case, but helps with the training process. This issue might be resolved by creating a tailor-made optimizer, but this is beyond the scope of this research.
2.5 Robustness of solution over time
There are some applications where using the pulse schedule of the optimal solution in future experiments is required. Gate-based ansatzes produce approximately the same quantum state for the same parameters vector when executed at some future time, as long as the native gates set is calibrated frequently. As opposed to that, pulse-based ansatzes might produce different results if there is a big gap between executions, even when using the same parameters vector. This inconsistency happens because of drifts in the quantum chip parameters, such as the qubits frequencies. Over a long period of time, such drifts may accumulate and create deviations in a repeated execution of an optimized pulse-based ansatz. The structure of PANSATZ produces pulse schedules with short pulse sequences, making the optimized result less sensitive to such drifts. We injected such drifts into some of the optimal pulse schedules we got from the simulations we have done (described in the next section). The drifts we simulated were in the form of random changes to the qubits frequencies and qubit driving strengths of the simulated device. The new parameters were sampled from a Gaussian distribution with a mean of the original parameter and a standard deviation of 10−4, resulting in deviations in the order of a few hundred KHz. We simulated the optimal schedule multiple times with the new parameters and examined the deviations from the optimal result. In most cases, the deviations were smaller than the standard deviation created by the shot noise of our simulations. For larger problems, the pulse schedule will probably be longer, and therefore the deviations will be larger. In order to address those cases, running a few additional iterations of the optimization process might be required in order to find the new optimal parameters vector that suits the new device characteristics.
3 Results
In order to test our method we implemented the standard VQE algorithm but with our PANSATZ as the ansatz to find the ground state energy of different molecules. We first implemented the algorithm as a simulation, using the Qiskit-dynamics package (Puzzuoli et al., 2022), which utilizes the JAX array library to enable accelerated GPU execution, to find the minimum energy of the H2, HeH+ and LiH molecules. Next, we implemented the algorithm on one of IBM’s devices, ibm_lagos, to find the minimum energy of H2. All of the molecular Hamiltonians used in this work were computed in the STO-3G basis using Qiskit-nature package. These Hamiltonians were converted into spin Hamiltonians using parity transformation, and encoded into qubits after utilizing symmetries in the Hamiltonian, to reduce the amount of qubits needed in order to encode the solution to the problem. The H2 and the HeH+ Hamiltonians were represented using 2 qubits, while the LiH Hamiltonian was represented using 4 qubits, which was achieved by reducing the active search space of the spin orbitals, as explained in Kandala et al. (2017). Such reduction introduces an error, especially in small atomic distances, but reduces the number of required qubits to encode the Hamiltonian significantly, which allows reaching better results. We compared our results to the full configuration interaction (FCI) result with respect to the minimal STO-3G basis calculated by diagonalizing the Hamiltonian. In both the simulation and on the actual IBM device hardware we used 10,000 shots for each circuit run to measure the expectation value with a small variance. In the run on ibm_lagos we used tensored readout error mitigation (Barron and Wood, 2020; Geller and Sun, 2021). For these tasks, we used PANSATZ with only 1 layer, consisting of fixed single-qubit pulses, followed by parametrized two-qubit pulses and parametrized single-qubit pulses (as described in the previous section). This structure generates 5 parameters for the H2 and HeH+ molecules (while GANSATZ has 4 parameters) and 11 parameters for the LiH molecule (while GANSATZ has 8 parameters). As initial pulse parameters, we chose duration for the single qubit pulses so the final state will be approximately the Hartree-Fock (HF) state. All the two-qubit pulses were initialized with zero duration (as there is no entanglement at the HF state). For example, the HF state for the H2 molecule is the |01⟩ state, so all the parameters were initialized with zero duration except the single qubit pulse of the first qubit. This pulse was initialized with the same duration as the pulse in the fixed layer (which is calibrated to create
3.1 Simulation
We simulated fixed-frequency transmon qubits by using the following device Hamiltonian
where ω is the qubit frequency, δ is the qubit anharmonicity, g is the neighboring qubit coupling strength and
where σ+ is the Pauli ladder operator (σx + iσy). We used Γ0, Γ1 which are proportional to T1 = T2 = 100[us]. At the end of each calculation of qubit evolution, we sampled the final qubit state with 10,000 shots in order to introduce shot noise caused by finite sampling to the simulation. For comparison we also ran a GANSATZ simulation with 1 layer using the IBM simulator. We used the same device parameters and connectivity and inserted relaxation and decoherence noises of T1 = T2 = 100[us], and simulated shot noise by sampling the results with 10,000 shots. In the gate model simulator leakage cannot be simulated, so we assumed that there was no leakage. The duration parameter can be seen either as a continuous parameter, or as a discrete parameter, with the smallest time unit of the classical control hardware of the quantum processing unit as the discrete unit (about 0.222[ns] for most of today’s IBM QCs). Therefore, we tested two different optimizers in the simulation—simultaneous perturbation stochastic approximation (SPSA), which is used for continuous parameters and approximates the gradient of the parameter vector using only 2 measurements regardless of size (Spall, 1992), and steepest-ascent hill climbing (Goldfeld et al., 1966; Selman and Gomes, 2006), which is used for discrete parameters. Both optimizers had similar accuracy, while the steepest-ascent hill climbing converged with much fewer iterations. As shown in Figure 3, using PANSATZ we reached chemical accuracy (0.0016 Hartree) compared to the FCI result, up to a standard deviation (calculated from the variance in the expectation value calculation), across all atomic distances studied for the H2 and HeH+ molecules. Because of the small number of parameters, this was achieved with only a few tens of iterations in the worst case. Throughout the optimization process of the parameters, the duration of the schedule slowly increased as entanglement was added to the prepared state by including also CR pulses (with non-zero duration) in the schedule. For cases where more entanglement was needed in order to reach chemical accuracy, the total duration of the schedule increased even further, until the optimizer converged to the correct result. For example, the entanglement of the ground state of the Hamiltonian of the H2 molecule after the parity transformation is higher for large atomic distances. Therefore, as entanglement is usually the most time consuming to create in superconducting qubits, the optimizer converged at a longer schedule duration when solving these problems, as can be seen in Figure 4. Even the longest duration schedule achieved by using PANSATZ is less than half the duration of the equivalent GANSATZ. For the LiH molecule, 1 layer is not expressive enough for large atomic distances (although it is more expressive than 1 layer of GANSATZ). Therefore, the optimizer converged with low entanglement state, which encountered minimal noise due to the short duration and had better results than having longer CR pulses. Because of the low noise, good results were achieved in small atomic distances, but the algorithm solutions deviate from the FCI as the atomic distance increases.
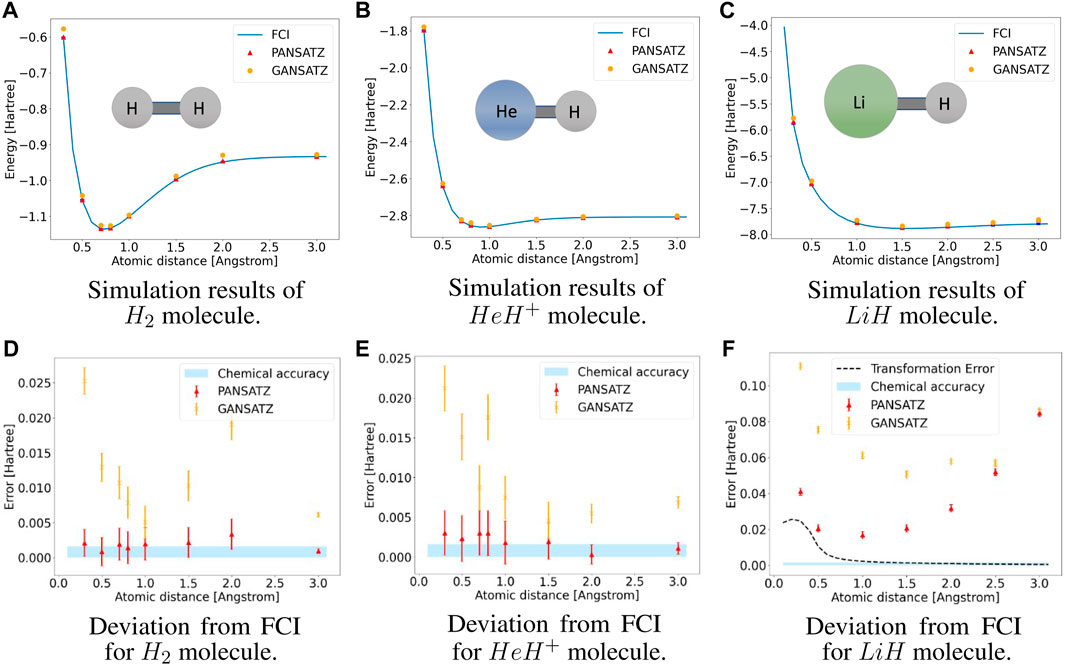
FIGURE 3. Simulations results. The top insets of each figure are representations of the molecular geometry, not drawn to scale. The error bars on the simulation data are smaller than the size of the markers. The reference on the FCI for each point is highlighted as blue tick marks. (A) Simulation results of the VQE on H2 molecule. (B) Simulation results of the VQE on HeH+ molecule. (C) Simulation results of the VQE on LiH molecule. (D) Deviation of the simulation result from the FCI result of the VQE on H2 molecule. (E) Deviation of the simulation result from the FCI result of the VQE on HeH+ molecule. (F) Deviation of the simulation result from the FCI result of the VQE on LiH molecule. The transformation error is the error introduced by reducing the number of qubits needed to encode the molecule’s Hamiltonian and effectively reducing the active search space.
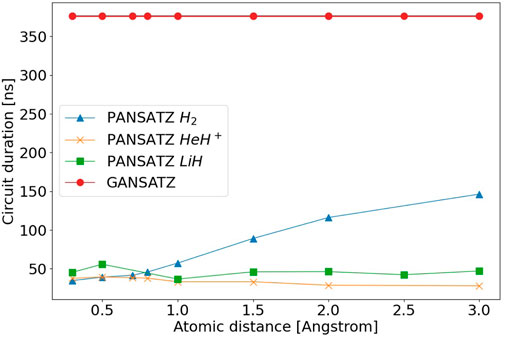
FIGURE 4. Duration of the PANSATZ schedules compared to Real Amplitudes HEA for H2, HeH+ and LiH molecules, based on numerical simulations. The duration of the GANSATZ is constant because the ansatz has the same number of gates for each atomic distance, and the duration of each gate is fixed.
Figure 3 shows excellent agreement between the PANSATZ predictions of the ground state energy in Hartree units versus interatomic distance in angstroms to the FCI result.
3.2 Real hardware
We used ibm_lagos, one of the IBM Quantum Falcon processors, to find the ground energy of the H2 molecule at various atomic distances. We used the open-pulse feature (Alexander et al., 2020) to create the algorithm ansatz at the pulse level, and the PANSATZ structure described above. We used the steepest-ascent hill climbing algorithm for the classical optimizer, as it converged with fewer iterations in our simulations. We also used uncorrelated readout error mitigation in our post processing of the hardware measurement results, which is a scaleable method that can be used also when solving larger VQA problems. The results are shown at Figure 5. The results were obtained in a single convergence process, while convergence was declared by either reaching chemical accuracy or reaching 30 iterations. The readout error mitigated results show excellent agreement with the FCI results, including multiple points which reached chemical accuracy. These results were achieved as a direct result of the short duration of the PANSATZ schedule, as shown in Figure 6, which was adaptive to the amount of entanglement needed for each atomic distance. The GANSATZ duration was taken as the duration of 1 layer of Real Amplitudes HEA compiled on the same device. By using a relatively small amount of parameters, a discrete optimization algorithm, and initial parameters which create a state close to the HF state, the PANSATZ reached the desired solution within only a few iterations (example shown in Figure 7), giving hope for convergence within a reasonable amount of iterations also in larger problems.
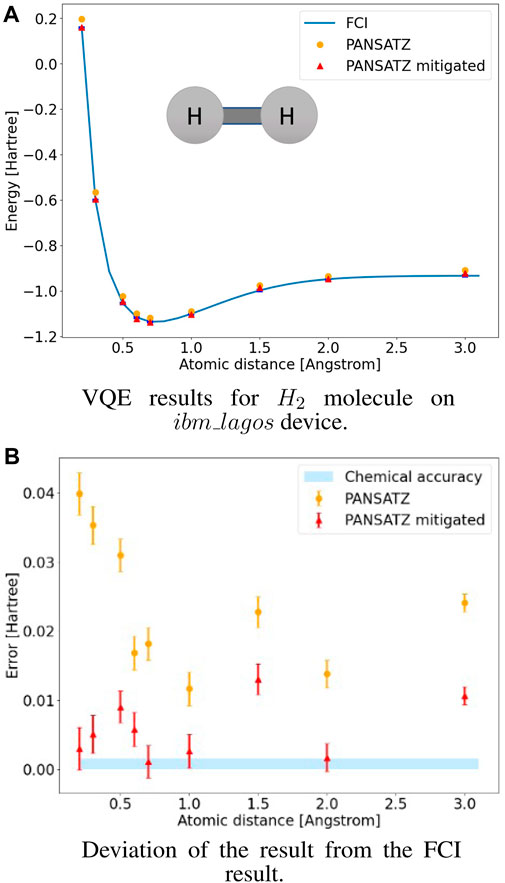
FIGURE 5. VQE results for H2 molecule on ibm_lagos device. (A) The final ground energy found by the algorithm with and without readout error mitigation. The error bars on the data are smaller than the size of the markers. The reference on the FCI for each point is highlighted as blue tick marks. (B) Deviation of the result from the FCI result with and without readout error mitigation.
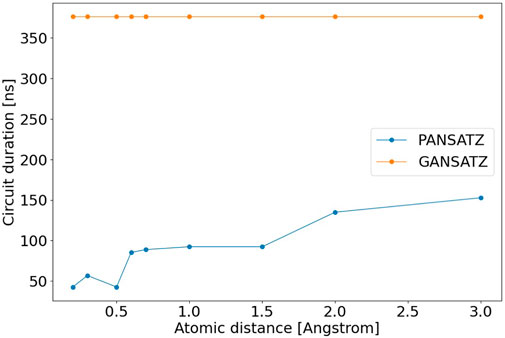
FIGURE 6. Duration of the PANSATZ schedules results from ibm_lagos compared to GANSATZ. The GANSATZ duration was taken as the duration of 1 layer of Real Amplitudes HEA transpiled on the same device.
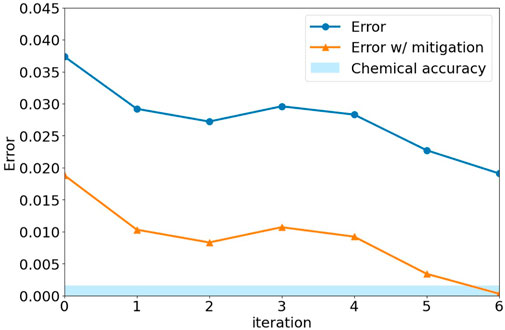
FIGURE 7. Convergence plot of the steepest-ascent hill climbing optimization algorithm for solving VQE for H2 molecule with 0.7 angstrom atomic distance, run on ibm_lagos.
4 Summary and discussion
We developed a parameterized pulse-based ansatz, which we call PANSATZ, to be used with VQAs. We chose pulse duration as the main parameter, along with qubit driving phase which is manipulated only once for each layer. We tested PANSATZ in the context of VQE to find ground state energies of small molecules on both simulation and actual IBM hardware. We achieved state of the art results, reaching chemical accuracy with the raw expectation value results (mitigating only readout errors), which, to the best of our knowledge, is an achievement that has not been shown yet on superconducting quantum hardware. Previous demonstrations of chemical accuracy on superconducting quantum hardware (McCaskey et al., 2019; Jones et al., 2022) used extensive post-processing error mitigation techniques such as zero noise extrapolation (ZNE) (Li and Benjamin, 2017; Temme et al., 2017), probabilistic error cancellation (PEC) (Temme et al., 2017) and purification (McCaskey et al., 2019), which might be used also with PANSATZ to make the results even more resilient to noise and help solve larger problems within the required accuracy. Adjustment of such mitigation techniques to make them suitable for pulses [for example, using pulse stretching instead of digital global folding in ZNE (Schultz et al., 2022)] is left for further research. Our experiments show significant latency reduction, resulting in improved accuracy of PANSATZ over typical gate-based ansatzes. The PANSATZ structure enables on-the-fly adaptation of the schedule latency depending on the entanglement level required to solve the given problem, potentially enabling simulations of larger molecules accurately. Our PANSATZ approach can be used with other VQAs as an improvement to the HEA. The use of PANSATZ in quantum algorithms where problem-inspired ansatze are used, such as QAOA, remains to be considered. Using a hybrid gate-based and pulse-based ansatz can be explored similarly to Liang et al. (2022b). Expanding PANSAZT into other hardware technologies is left for future research.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/dekelmeirom/PANSATZ.
Author contributions
DM: Writing–original draft. SF: Supervision, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The authors gratefully acknowledge the financial support of the Israel Science Foundation (ISF) on grant number 3457/21.
Acknowledgments
We would like to thank Dr. Adi Makmal for the fruitful technical discussions. We also gratefully acknowledge the use of IBM Quantum services for this work and to advanced services provided by the IBM Quantum Researchers Program.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Author disclaimer
The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team.
References
Alexander, T., Kanazawa, N., Egger, D. J., Capelluto, L., Wood, C. J., Javadi-Abhari, A., et al. (2020). Qiskit pulse: programming quantum computers through the cloud with pulses. Quantum Sci. Technol. 5, 044006. doi:10.1088/2058-9565/aba404
Asthana, A., Liu, C., Meitei, O. R., Economou, S. E., Barnes, E., and Mayhall, N. J. (2022). Minimizing state preparation times in pulse-level variational molecular simulations, 06818. arXiv preprint arXiv:2203. doi:10.48550/arXiv.2203.06818
Barron, G. S., and Wood, C. J. (2020). Measurement error mitigation for variational quantum algorithms. arXiv preprint arXiv:2010, 08520. doi:10.48550/arXiv.2010.08520
Bharti, K., Cervera-Lierta, A., Kyaw, T. H., Haug, T., Alperin-Lea, S., Anand, A., et al. (2022). Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys. 94, 015004. doi:10.1103/RevModPhys.94.015004
Bravo-Prieto, C., LaRose, R., Cerezo, M., Subasi, Y., Cincio, L., and Coles, P. J. (2019). Variational quantum linear solver. arXiv preprint arXiv:1909, 05820. doi:10.48550/arXiv.1909.05820
Cerezo, M., Arrasmith, A., Babbush, R., Benjamin, S. C., Endo, S., Fujii, K., et al. (2021). Variational quantum algorithms. Nat. Rev. Phys. 3, 625–644. doi:10.1038/s42254-021-00348-9
Choquette, A., Di Paolo, A., Barkoutsos, P. K., Sénéchal, D., Tavernelli, I., and Blais, A. (2021). Quantum-optimal-control-inspired ansatz for variational quantum algorithms. Phys. Rev. Res. 3, 023092. doi:10.1103/PhysRevResearch.3.023092
Chow, J. M., Córcoles, A. D., Gambetta, J. M., Rigetti, C., Johnson, B. R., Smolin, J. A., et al. (2011). Simple all-microwave entangling gate for fixed-frequency superconducting qubits. Phys. Rev. Lett. 107, 080502. doi:10.1103/PhysRevLett.107.080502
Córcoles, A. D., Gambetta, J. M., Chow, J. M., Smolin, J. A., Ware, M., Strand, J., et al. (2013). Process verification of two-qubit quantum gates by randomized benchmarking. Phys. Rev. A 87, 030301. doi:10.1103/PhysRevA.87.030301
Córcoles, A. D., Kandala, A., Javadi-Abhari, A., McClure, D. T., Cross, A. W., Temme, K., et al. (2019). Challenges and opportunities of near-term quantum computing systems, 02894. arXiv preprint arXiv:1910. doi:10.1109/JPROC.2019.2954005
de Keijzer, R., Tse, O., and Kokkelmans, S. (2023). Pulse based variational quantum optimal control for hybrid quantum computing. Quantum 7, 908. doi:10.22331/q-2023-01-26-908
Earnest, N., Tornow, C., and Egger, D. J. (2021). Pulse-efficient circuit transpilation for quantum applications on cross-resonance-based hardware. Phys. Rev. Res. 3, 043088. doi:10.1103/PhysRevResearch.3.043088
Farhi, E., Goldstone, J., and Gutmann, S. (2014). A quantum approximate optimization algorithm. arXiv preprint arXiv:1411.4028. doi:10.48550/arXiv.1411.4028
Gambetta, J. M., Motzoi, F., Merkel, S., and Wilhelm, F. K. (2011). Analytic control methods for high-fidelity unitary operations in a weakly nonlinear oscillator. Phys. Rev. A 83, 012308. doi:10.1103/PhysRevA.83.012308
Geller, M. R., and Sun, M. (2021). Toward efficient correction of multiqubit measurement errors: pair correlation method. Quantum Sci. Technol. 6, 025009. doi:10.1088/2058-9565/abd5c9
Goldfeld, S. M., Quandt, R. E., and Trotter, H. F. (1966). Maximization by quadratic hill-climbing. Econ. J. Econ. Soc. 34, 541–551. doi:10.2307/1909768
Grimsley, H. R., Economou, S. E., Barnes, E., and Mayhall, N. J. (2019). An adaptive variational algorithm for exact molecular simulations on a quantum computer. Nat. Commun. 10, 3007–3009. doi:10.1038/s41467-019-10988-2
Ibrahim, M. M., Mohammadbagherpoor, H., Rios, C., Bronn, N. T., and Byrd, G. T. (2022). Evaluation of parameterized quantum circuits with cross-resonance pulse-driven entanglers. IEEE Trans. Quantum Eng. 3, 1–13. doi:10.1109/TQE.2022.3231124
Jones, M. A., Vallury, H. J., Hill, C. D., and Hollenberg, L. C. (2022). Chemistry beyond the Hartree–Fock energy via quantum computed moments. Sci. Rep. 12, 8985. doi:10.1038/s41598-022-12324-z
Kandala, A., Mezzacapo, A., Temme, K., Takita, M., Brink, M., Chow, J. M., et al. (2017). Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246. doi:10.1038/nature23879
Krantz, P., Kjaergaard, M., Yan, F., Orlando, T. P., Gustavsson, S., and Oliver, W. D. (2019). A quantum engineer’s guide to superconducting qubits. Appl. Phys. Rev. 6, 021318. doi:10.1063/1.5089550
Leng, J., Peng, Y., Qiao, Y.-L., Lin, M., and Wu, X. (2022). Differentiable analog quantum computing for optimization and control, 15812. arXiv preprint arXiv:2210. doi:10.48550/arXiv.2210.15812
Li, Y., and Benjamin, S. C. (2017). Efficient variational quantum simulator incorporating active error minimization. Phys. Rev. X 7, 021050. doi:10.1103/PhysRevX.7.021050
Liang, Z., Cheng, J., Ren, H., Wang, H., Hua, F., Ding, Y., et al. (2022a). Pan: pulse ansatz on nisq machines, 01215. arXiv preprint arXiv:2208. doi:10.48550/arXiv.2208.01215
Liang, Z., Song, Z., Cheng, J., He, Z., Liu, J., Wang, H., et al. (2022b). Hybrid gate-pulse model for variational quantum algorithms, 00661. arXiv preprint arXiv:2212. doi:10.48550/arXiv.2212.00661
Liang, Z., Wang, H., Cheng, J., Ding, Y., Ren, H., Gao, Z., et al. (2022c). “Variational quantum pulse learning,” in 2022 IEEE International Conference on Quantum Computing and Engineering (QCE) (IEEE), 556–565. doi:10.1109/QCE53715.2022.00078
Magann, A. B., Arenz, C., Grace, M. D., Ho, T.-S., Kosut, R. L., McClean, J. R., et al. (2021). From pulses to circuits and back again: A quantum optimal control perspective on variational quantum algorithms. PRX Quantum 2, 010101. doi:10.1103/PRXQuantum.2.010101
Magesan, E., and Gambetta, J. M. (2020). Effective Hamiltonian models of the cross-resonance gate. Phys. Rev. A 101, 052308. doi:10.1103/PhysRevA.101.052308
McCaskey, A. J., Parks, Z. P., Jakowski, J., Moore, S. V., Morris, T. D., Humble, T. S., et al. (2019). Quantum chemistry as a benchmark for near-term quantum computers. npj Quantum Inf. 5, 99. doi:10.1038/s41534-019-0209-0
McClean, J. R., Romero, J., Babbush, R., and Aspuru-Guzik, A. (2016). The theory of variational hybrid quantum-classical algorithms. New J. Phys. 18, 023023. doi:10.1088/1367-2630/18/2/023023
McKay, D. C., Wood, C. J., Sheldon, S., Chow, J. M., and Gambetta, J. M. (2017). Efficient z gates for quantum computing. Phys. Rev. A 96, 022330. doi:10.1103/PhysRevA.96.022330
Meitei, O. R., Gard, B. T., Barron, G. S., Pappas, D. P., Economou, S. E., Barnes, E., et al. (2021). Gate-free state preparation for fast variational quantum eigensolver simulations. npj Quantum Inf. 7, 155–211. doi:10.1038/s41534-021-00493-0
Motzoi, F., Gambetta, J. M., Rebentrost, P., and Wilhelm, F. K. (2009). Simple pulses for elimination of leakage in weakly nonlinear qubits. Phys. Rev. Lett. 103, 110501. doi:10.1103/PhysRevLett.103.110501
Niu, S., and Todri-Sanial, A. (2022). Effects of dynamical decoupling and pulse-level optimizations on ibm quantum computers. IEEE Trans. Quantum Eng. 3, 1–10. doi:10.1109/TQE.2022.3203153
O’Malley, P. J., Babbush, R., Kivlichan, I. D., Romero, J., McClean, J. R., Barends, R., et al. (2016). Scalable quantum simulation of molecular energies. Phys. Rev. X 6, 031007. doi:10.1103/PhysRevX.6.031007
Peruzzo, A., McClean, J., Shadbolt, P., Yung, M.-H., Zhou, X.-Q., Love, P. J., et al. (2014). A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213–4217. doi:10.1038/ncomms5213
Preskill, J. (2018). Quantum computing in the nisq era and beyond. Quantum 2, 79. doi:10.22331/q-2018-08-06-79
Puzzuoli, D., Lin, S. F., Malekakhlagh, M., Pritchett, E., Rosand, B., and Wood, C. J. (2022). Algorithms for perturbative analysis and simulation of quantum dynamics, 11595. arXiv preprint arXiv:2210. doi:10.48550/arXiv.2210.11595
Schultz, K., LaRose, R., Mari, A., Quiroz, G., Shammah, N., Clader, B. D., et al. (2022). Impact of time-correlated noise on zero-noise extrapolation. Phys. Rev. A 106, 052406. doi:10.1103/PhysRevA.106.052406
Selman, B., and Gomes, C. P. (2006). Hill-climbing search. Encycl. cognitive Sci. 81, 82. doi:10.1002/0470018860.s00015
Sheldon, S., Magesan, E., Chow, J. M., and Gambetta, J. M. (2016). Procedure for systematically tuning up cross-talk in the cross-resonance gate. Phys. Rev. A 93, 060302. doi:10.1103/PhysRevA.93.060302
Spall, J. C. (1992). Multivariate stochastic approximation using a simultaneous perturbation gradient approximation. IEEE Trans. automatic control 37, 332–341. doi:10.1109/9.119632
Temme, K., Bravyi, S., and Gambetta, J. M. (2017). Error mitigation for short-depth quantum circuits. Phys. Rev. Lett. 119, 180509. doi:10.1103/PhysRevLett.119.180509
Tilly, J., Chen, H., Cao, S., Picozzi, D., Setia, K., Li, Y., et al. (2022). The variational quantum eigensolver: A review of methods and best practices. Phys. Rep. 986, 1–128. doi:10.1016/j.physrep.2022.08.003
Wang, H., Ding, Y., Gu, J., Lin, Y., Pan, D. Z., Chong, F. T., et al. (2022). “Quantumnas: noise-adaptive search for robust quantum circuits,” in 2022 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Seoul, Korea, Republic, 02-06 April 2022 (IEEE), 692–708. doi:10.1109/HPCA53966.2022.00057
Keywords: NISQ, VQA, VQE, pulse engineering, QOC, ansatz
Citation: Meirom D and Frankel SH (2023) PANSATZ: pulse-based ansatz for variational quantum algorithms. Front. Quantum Sci. Technol. 2:1273581. doi: 10.3389/frqst.2023.1273581
Received: 06 August 2023; Accepted: 26 September 2023;
Published: 09 October 2023.
Edited by:
Daniel Claudino, Oak Ridge National Laboratory (DOE), United StatesReviewed by:
Zixuan Hu, Purdue University, United StatesAbolfazl Bayat, University of Electronic Science and Technology of China, China
Copyright © 2023 Meirom and Frankel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dekel Meirom, dekelmeirom@gmail.com; Steven H. Frankel, frankel@technion.ac.il
 Dekel Meirom
Dekel Meirom