- 1Department of Physics, University of Strathclyde, Glasgow, United Kingdom
- 2Department of Physics, Durham University, Durham, United Kingdom
- 3Department of Financial Mathematics, Fraunhofer Institute for Industrial Mathematics, Kaiserslautern, Germany
In the last decade, public and industrial research funding has moved quantum computing from the early promises of Shor’s algorithm through experiments to the era of noisy intermediate scale quantum devices (NISQ) for solving real-world problems. It is likely that quantum methods can efficiently solve certain (NP-) hard optimization problems where classical approaches fail. In our perspective, we examine the field of quantum optimization, that is, solving optimization problems using quantum computers. We provide an entry point to quantum optimization for researchers from each topic, optimization or quantum computing, by demonstrating advances and obstacles with a suitable use case. We give an overview on problem formulation, available algorithms, and benchmarking. Although we show a proof-of-concept rather than a full benchmark between classical and quantum methods, this gives an idea of the current quality and capabilities of quantum computers for optimization problems. All observations are incorporated in a discussion on some recent quantum optimization breakthroughs, current status, and future directions.
1 Introduction
In November 1994, Peter Shor presented his pioneering algorithm at the IEEE Symposium on Foundations of Computer Science in Santa Fe, NM (Shor, 1994). Without a doubt, Shor’s algorithm threatened the underpinnings of public key cryptography, putting quantum computing on the proverbial map and forcing people outside the academic community to pay attention (Witt, 2022). Decades later, it remains the standard-bearer of quantum algorithms. Almost as important, Shor’s algorithm has currently led to investments of billions of (US) dollars worldwide into quantum computing technologies1. This drastic increase of funding has seen a spike in quantum computing research at public and private research institutes, R&D departments in the commercial sector, as well as the founding of new startups (Brooks, 2019; Gibney, 2019; MacQuarrie et al., 2020). As of 15 Dec 2022, 10,416 quantum physics articles have been published on the arXiv preprint server where nearly half these papers involve quantum computing. In tandem with the volume of publications, quantum computers have evolved from experiments to an era of noisy intermediate scale quantum (NISQ) devices (Preskill, 2018; Callison and Chancellor, 2022) where they play an increasingly popular role in real-world problems (Bova et al., 2021).
One exciting application area is optimization. In business, time is money. Everything can be reduced to an optimization problem. Every company decision is weighed against resources, financial cost, and opportunity cost. The longer it takes to make a decision, the greater the cost. Optimization problems exist across every industry (Yarkoni et al., 2022). They are difficult to solve due to incomplete or uncertain data, difficulties in stating the problem or examining the value of proposed solutions, or because they are NP-hard problems. Stemming from the P-versus-NP-problem (Fortnow, 2013), the time required to solve NP-hard problems is suspected to grow exponentially with the size of the problem. The problems are hard because of the large and exponentially growing solution space (combinatorial explosion). As a result, automotive companies such as BMW (BMW Group, 2018) and Volkswagen (Yarkoni et al., 2019; Yarkoni et al., 2021) are already (Zaman et al., 2021) exploring the possibility of quantum-based optimization for manufacturing. Additionally, quantum methods have been applied to portfolio optimization (Orús et al., 2019; Egger et al., 2020; Yalovetzky et al., 2021), logistics (Bentley et al., 2022), supply chain management (Weinberg et al., 2022), and energy economy (Mastroianni et al., 2022).
The aim of this perspective is to critically examine the status and future of quantum computing for optimization, which we define as quantum optimization, including some possible weaknesses. We intend to complement the Royal Society’s recent special edition on quantum annealing (Chakrabarti et al., 2023) and Applied Quantum Computing’s excellent review which provides accessible explanations for the technicalities of quantum computing and their practical uses (Cumming and Thomas, 2022). We also recommend Ref (Guenin et al., 2014) as an introduction to optimization. The outline of this paper is as follows. We identify suitable optimization problems that can benefit from quantum methods (Section 2). Then we address the challenges in formulating problems for quantum computers and algorithms (Section 3) before surveying the available algorithms (Section 4). In Section 5, we assess the current quantum computing hardware and determine possible weaknesses using a demonstration benchmark. Finally we present our perspective on quantum optimization, focusing on its present and future status.
2 Finding suitable use cases
Compared to classical computers, quantum computers cope well with large search spaces, complex problem structures and objective functions. For example, quantum annealing is used to solve optimization problems which can take many forms: unconstrained versus constrained; using differential equations as constraints; combinatorial and graph problems; supposedly simple linear problems. (For an overview of real-world applications, see (Hauke et al., 2020; Yarkoni et al., 2022).) Many publications in quantum optimization focus on science and engineering such as the use of quantum annealing in the drug discovery and development process (Paul et al., 2010; Langione et al., 2019a; Evers et al., 2021). Due to significant investment in R&D (Wouters et al., 2020; Evers et al., 2021; Brown et al., 2022), there are strong incentives to try new computational methods like Google DeepMind’s breakthrough AlphaFold platform (Senior et al., 2020; AlQuraishi, 2021) for the pharmaceutical industry. Quantum computing can overcome AlphaFold’s shortcomings (Mulligan et al., 2019; Wong et al., 2022) and dramatically change both landscape and revenue in the next few decades (Bobier et al., 2021).
While there have been substantial efforts in applying quantum methods to specific problems, less work has been done on finding systematic approaches to determine which problems are most promising (Chancellor et al., 2020). Use cases for quantum optimization are generally NP-hard or worse and difficult to approximate (with a constant factor). However, some NP-hard problems are solvable or heuristics/approximation algorithms provide acceptable results, e.g., the knapsack problem. A good example of an NP-hard problem is the Maximum Weighted Independent Set (MWIS) problem: Given a topology graph, we want to find a set of vertices with maximum weight such that no vertices of that set are connected by an edge (Lovász, 1994; Pardalos and Xue, 1994). The problem cannot be approximated to a constant factor unless P = NP (Arora and Barak, 2009) and approximation to a polynomial factor is NP-hard itself (Bazgan et al., 2005). MWIS has practical applications, for example in DNA sequencing (Joseph et al., 1992) and quantum computing (Ebadi et al., 2022). We use MWIS as our example problem for the rest of this paper.
3 Modeling
Solving real-world problems typically requires reformulating into a mathematical problem. Given a graph G = G (V, E) with m vertices, weight ai for each vertex V and set of edges E, the classical formulation of the MWIS problem is
For the quantum computing algorithms that we discuss in Section 4, the optimization problem must be in the form of a quadratic unconstrained binary optimization problem (QUBO),
with interaction strength Jij between two adjacent spins i, j and spin-external magnetic field interaction hi. Spins can be transformed to binary variables2 via xi = (si + 1)/2. The general method for transforming problems to QUBO involves:
1. Introducing slack variables (Boyd and Vandenberghe, 2004) to transform inequality constraints to equality constraints.
2. Transforming equality constraints to quadratic penalty terms.
3. For integer and continuous variables, defining a discrete set of possible values and applying a binary encoding of these values.
3.1 Modelling constraints
While the procedure above works to transform any linear or quadratic problem, it has its flaws. In MWIS for example, we must introduce a binary slack variable ye and add penalty term
A better formulation for the MWIS is
where we add no additional variables3 and have less connectivity. The challenging task of choosing the right scalar penalty factor p relies on domain knowledge and experience. We can also obtain decent estimates from the constraints (e.g. setting p: = maxiai ⋅ maxideg(i) + 1, where deg(i) is the number of edges vertex i is connected with). High penalty factors cause the original objective function to lose its significance, making it hard to distinguish between optimal and feasible solutions, particularly on NISQ devices. Feasible solutions are disregarded when penalties are too small. To our knowledge, no formal techniques exist although simple machine learning approaches could improve the formulation quality.
3.2 Modelling variables
Binary encoding (Lucas, 2014) is widely used for higher-than-binary model variables. The number of possible values a variable can attain is reduced to M which then can be encoded using ⌊ log(M)⌋ + 1 qubits. It is resource intensive, thus we highlight two alternative approaches.
Domain-wall is a (Palacios-Berraquero et al., 2019) recently proposed method for encoding discrete variables (Chancellor, 2019), dramatically improving both gate-model variational algorithms (Plewa et al., 2021) and annealers (Abel et al., 2021; Chen et al., 2021). In this method, arbitrary two-variable interactions between discrete variables of size m can be represented in an encoding which requires m − 1 qubits per variable, one less than the more traditional one-hot encoding method. Importantly, arbitrary pairwise interactions between discrete variables can be mapped to quadratic interactions between qubits. It is suitable for devices with limited connectivity (Chancellor, 2019) and uses the minimum number of qubits where such a guarantee is possible (Berwald et al., 2023). It has been explored for networking applications has (Chen et al., 2022).
A recent work (Bermejo and Orus, 2022) deviates from the standard QUBO approach by considering continuous variables without binary encoding. The qubit state can be given as a position on or in the Bloch sphere for pure and mixed states respectively, so they make use of the 3D coordinates given by two angles and the radius. They can encode two (three) continuous variables into each pure- (mixed-)state qubit.
4 Algorithms
Here we present two popular methods for solving optimization problems: Variational quantum algorithms and quantum annealing. Further methods exist like Grover adaptive search (Gilliam et al., 2021) and hybrid algorithms (Ajagekar et al., 2020; Callison and Chancellor, 2022) but these are beyond the scope of our work. For an exhaustive list of quantum algorithms, we recommend the Quantum Algorithm Zoo (Jordan, 2021).
4.1 Variational quantum algorithms
Variational quantum algorithms (VQAs) provide a general framework for solving many problems such as big data analysis and simulations for quantum chemistry and materials science (Kandala et al., 2017; Kokail et al., 2019). Their adaptive nature is due to the variational process: the optimization procedure varies the algorithm on-the-fly, similar to machine learning (Cerezo et al., 2021). The problem is encoded into a parametrized cost function that defines a hypersurface. The quantum circuit navigates this surface to estimate the global minima which correspond to solutions of the problem. The result is passed back to the classical computer to adjust the VQA parameters. Then this is returned to the quantum computer to repeat the process.
VQAs require an ansatz whose form dictates what the variational parameters are and how they can be trained to minimize the cost function. The ansatz structure depends on the problem at hand. One major bottleneck is the barren plateau phenomenon, where changes in the classical parameters have little effect on the optimality of the variational state. The presence of barren plateaus is tied to the expressivity of the variational ansatz (Holmes et al., 2022). Highly expressive ansatzes tend to cause the algorithms to become effectively lost in a vast space of highly sub-optimal solutions. This leads to a tradeoff: if the ansatz is not expressive enough, it may not be able to effectively solve the problem; if too expressive, then the algorithm cannot be efficiently trained (Cerezo et al., 2021; Callison and Chancellor, 2022).
There are two major VQAs:
1. The computationally universal quantum approximate optimization algorithm (QAOA) (Lloyd, 2018; Hadfield et al., 2019; Morales et al., 2020; Zhou et al., 2020), originally introduced to solve combinatorial optimization problems (Farhi et al., 2014a; Farhi et al., 2014b).
2. Variational quantum eigensolvers (VQEs) (Cerezo et al., 2021; Tilly et al., 2022) are the best-known application of VQAs and were originally used to find the ground state energy of molecules (Aspuru-Guzik et al., 2005; Wecker et al., 2015; McClean et al., 2016).
Further developments have, for example resulted in more sophisticated versions of QAOA (Egger et al., 2021) and more efficient use of quantum hardware for VQE (Amaro et al., 2022).4.2 Quantum annealing and D-Wave
Quantum annealing (Kadowaki and Nishimori, 1998; Hauke et al., 2020; Yarkoni et al., 2022) is a form of quantum computing based on continuous time evolution. Typically it operates outside the regime of adiabatic quantum computing which gives theoretical guarantees of performance (Farhi et al., 2000; Albash and Lidar, 2018). The Hamiltonian takes the general form.
Initially (t = 0), quantum annealing begins in a prepared state of Hamiltonian H0 with uniform probability (Figure 1). During the system evolution (0 < t < T), probabilities are gradually driven toward the global minimum (near-optimal solution) by final time T and the system is in the eigenstate of problem’s Hamiltonian Hp.
Quantum annealing can be done on D-Wave computers. Evolution is governed by the transverse field Ising Hamiltonian,
with Pauli-x and -z matrices σx,z, symmetric interaction strength Jnm = Jmn of qubits n and m, and on-site energy hn.
5 Hardware and benchmarking
There are numerous quantum computer manufacturing companies ranging from small startups to large well-established companies (MacQuarrie et al., 2020). We show examples of collaborations in Figure 2. A leading platform for solving optimization problems is D-Wave Systems which are based on a superconducting flux-qubit design (Bunyk et al., 2014). Other platforms such as IBM Q use superconducting electronics (transmons). For brevity, we focus on the most mature platforms with over 100 qubits: D-Wave and IBM. While D-Wave only applies quantum annealing (Section 4.2), IBM’s gate-based universal quantum computer allows various algorithms. D-Wave has been selling quantum computers since 2011 (Nimbe et al., 2021) and has become an important player in the quantum computer industry (Gerbert and Ruess, 2018). Both D-Wave and IBM’s methods involve time-evolving quantum systems (Crosson and Lidar, 2021), and the companies themselves have ambitious plans to shape the future of quantum computing4.
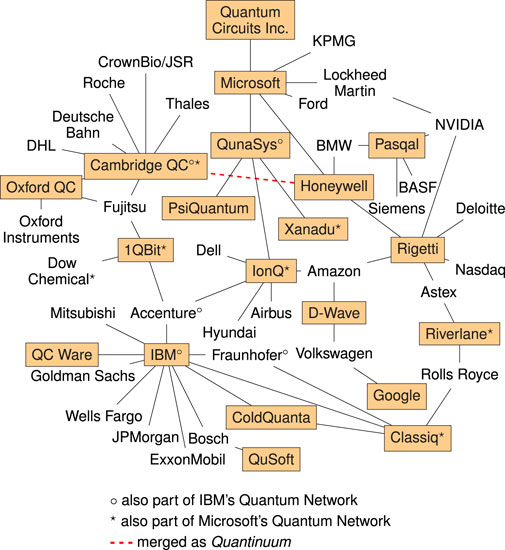
FIGURE 2. Quantum computing commercial landscape (selected companies only). Academic institutions and government organizations not shown. Details taken from press releases and publicly disclosed interactions with end users.
To compare quantum and classical methods, we perform a demonstration benchmark for the MWIS problem. We consider randomly generated graphs with different numbers of vertices (size k) and randomly selected vertex weights between 1 and 2k + 1. We briefly discuss the results here (see Supplementary Material for more details). We compare D-Wave Quantum Annealer’s results to Gurobi 10.0 (Gurobi Optimization and LLC, 2022) on classical hardware (Figure 3). Gurobi outperforms D-Wave, but the results up to size 25 are promising because D-Wave’s QPU embedding time is a similar order of magnitude to a state-of-the-art classical commercial solver. Increasing the number of vertices decreases solution quality and probability for D-Wave. Additionally, the embedding time dominates the total time required to solve the problem. (German Draft Budgetary Plan, 2020).
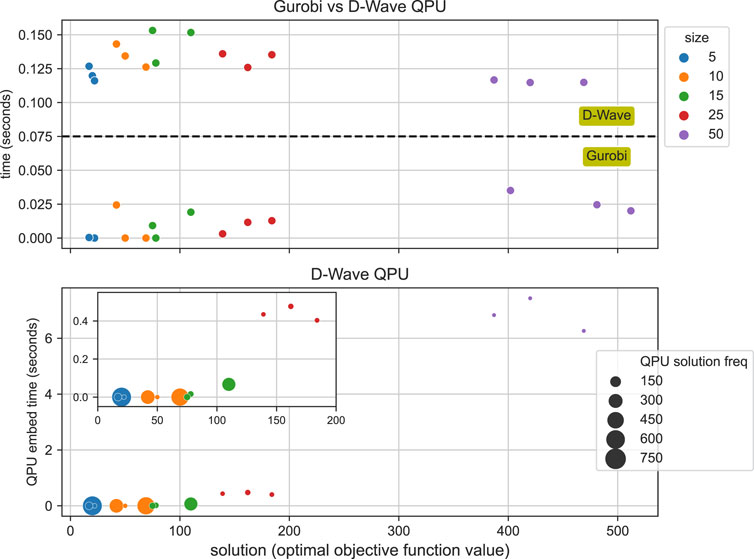
FIGURE 3. Benchmarking results for MWIS problem. For Gurobi, we show the optimal objective function value and total running time in seconds. For D-Wave, we show the embedding time and QPU access time required to solve the problem (both in seconds), plus the best solution found and its frequency in 1,000 shots. See data table in Supplementary Information.
Instances up to size 25 have also been tested on IBM via QAOA. Using QASM with Qiskit’s statevector simulator, IBM Qiskit can calculate optimal solutions up to size 10 but fails for size 25 and above. Using real quantum hardware (Falcon r6 QPU with 27 qubits), only a graph of size five occasionally gave the correct solution. We discuss the IBM results in the Supplementary Material. Note that Gurobi can certify the solution correctness by using (for example) duality. Gurobi confirmed optimality for all results. D-Wave and IBM do not certify their results.
To summarize, these results suggest that currently the classical approach is more efficient and that there is no practical quantum advantage for small numbers of graph vertices. Hence we may ask whether this is the best benchmarking strategy. Better and fairer strategies exist (Katzgraber et al., 2014), especially for D-Wave, and for analyzing how results will scale (Weinberg et al., 2020). However this is beyond the scope of this work where our benchmark is intended as a proof-of-concept. Only with more thorough benchmarking can we accurately assess the capabilities and speed-ups of quantum computers (Rønnow et al., 2014).
6 Discussion and outlook
In this work, we surveyed quantum methods for solving optimization problems. Our demonstration benchmarking compared quantum and classical methods for solving the MWIS problem. Now we discuss several key points and our perspectives on quantum optimization.
Finding a good problem formulation has a key impact on the solution quality. Historically, optimization practitioners have preferred constrained linear representations of problems. Quantum computing presents a different paradigm where the fundamental objects for optimization are quadratic expressions. Here we should minimize the number of qubits and connections. Mapping the Hamiltonian onto quantum hardware architecture is challenging but can be significantly improved via applying specialized graph optimization algorithms and machine learning methods. We stress that the transformation to QUBO is not inevitable. For example, Grover’s adaptive search (Bulger et al., 2003; Gilliam et al., 2021) can take any function at the cost of deeper circuits. While this is promising, practical advantage (compared to say, quantum annealers) is not definitive.
Practical application of quantum computing requires further progress in hardware. Measuring hardware quality and that of formulations and algorithms likewise is a research task on its own. Here, we need better evaluation and benchmarking methods, particularly for practical use cases where contested assertions like quantum supremacy5 do not play a role. For example, Tang proposed that we should “dequantize” quantum machine learning algorithms to check whether any quantum speedup exists (Tang, 2022).
Quantum computing R&D is a highly interdisciplinary process. Some parts of the research community believe that quantum hardware must be built first before we develop algorithms for applications. However to leverage the expertise of all participants, we should approach the entire quantum computing stack simultaneously, allowing cross-pollination of ideas across the stack (van Meter and Horsman, 2013; Fu et al., 2016). Engineers can build appropriate quantum devices when they know the problem statement and how best to solve it, whereas theorists can design algorithms or software once they understand the hardware capabilities and limitations.
Similarly, quantum optimization algorithms will benefit from classical approaches. Quantum algorithms often borrow ideas from classical methods (cf. quantum annealing and classical simulated annealing (Kirkpatrick et al., 1983; Bertsimas and Tsitsiklis, 1993)). However, few established optimization techniques other than, say branch-and-bound (Montanaro, 2020), have been adapted for quantum computation. We are confident that combining with classical methods can improve the performance of quantum optimization algorithms. For example, decomposition techniques implemented in mixed-integer solvers can split the problem in two and assign each part to classical and quantum hardware (Zhao et al., 2022).
Not every hard problem will benefit from quantum algorithms. For many hard problems, classical solvers are so efficient that quantum methods do not provide appreciable speed-ups, e.g., for the knapsack problem and our MWIS example. For example it is naive to assume that quantum optimization can speed up problems in P, e.g., linear continuous problems. An exception may be that particular subroutines could be improved with quantum algorithms. Hence despite the excitement over quantum speed-up, quantum computing itself is not a revolution but more like a new numerical toolbox that uses different processing units. It is likely that many future high performance computers (or computer centers) will contain a stack of CPUs, GPUs and QPUs similar to the JUNIQ program at the Jülich Supercomputing Centre (JUNIQ, 2019). Such a platform could involve one control unit that uses the CPUs, GPUs, and QPUs interchangeably for each part of the computation. We believe this is where quantum computing has the most potential for impact.
Quantum computing and optimization are forecast to be competitive in under a decade (Langione et al., 2019b). Now is the time to start planning for the future and hence maximize quantum computing’s commercial impact (Gerbert and Ruess, 2018). The best way to turn potential obstacles into opportunities is through collaboration between quantum theorists, computer scientists, engineers, end-users, and beyond. Then we can truly benefit from quantum optimization.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
RA acknowledges support from UK Quantum Technology Hub in Computing and Simulation (grant EP/T001062/1) and UKRI (grant EP/W00772X/2). NC was supported by UKRI grants EP/W00772X/1 and EP/T026715/1. PH is funded by the German Federal Ministry for Economic Affairs and Climate Action (grant no. 03EI1025A).
Conflict of interest
RA and PH declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. Although they did not directly fund this work NC was employed part time as a consultant by Quantum Computing Inc. At the time this manuscript was written.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frqst.2023.1128576/full#supplementary-material
References
Abel, S., Chancellor, N., and Spannowsky, M. (2021). Quantum computing for quantum tunneling. Phys. Rev. D. 103, 016008. doi:10.1103/PhysRevD.103.016008
Ajagekar, A., Humble, T., and You, F. (2020). Quantum computing based hybrid solution strategies for large-scale discrete-continuous optimization problems. Comput. Chem. Eng. 132, 106630. doi:10.1016/j.compchemeng.2019.106630
Albash, T., and Lidar, D. A. (2018). Adiabatic quantum computation. Rev. Mod. Phys. 90, 015002. doi:10.1103/RevModPhys.90.015002
AlQuraishi, M. (2021). Protein-structure prediction revolutionized. Nature 596, 487–488. doi:10.1038/d41586-021-02265-4
Amaro, D., Modica, C., Rosenkranz, M., Fiorentini, M., Benedetti, M., and Lubasch, M. (2022). Filtering variational quantum algorithms for combinatorial optimization. Quantum Sci. Technol. 7, 015021. doi:10.1088/2058-9565/ac3e54
Arora, S., and Barak, B. (2009). Computational complexity. Cambridge, United Kingdom: Cambridge University Press. doi:10.1017/cbo9780511804090
Aspuru-Guzik, A., Dutoi, A. D., Love, P. J., and Head-Gordon, M. (2005). Simulated quantum computation of molecular energies. Science 309, 1704–1707. doi:10.1126/science.1113479
Bazgan, C., Escoffier, B., and Paschos, V. T. (2005). Completeness in standard and differential approximation classes: Poly-(d)APX- and (d)PTAS-completeness. Theor. Comput. Sci. 339, 272–292. doi:10.1016/j.tcs.2005.03.007
Bentley, C. D. B., Marsh, S., Carvalho, A. R. R., Kilby, P., and Biercuk, M. J. (2022). Quantum computing for transport optimization. arXiv. doi:10.48550/arXiv.2206.07313
Bermejo, P., and Orus, R. (2022). Variational quantum continuous optimization: A cornerstone of quantum mathematical analysis. arXiv. doi:10.48550/arXiv.2210.03136
Bertsimas, D., and Tsitsiklis, J. (1993). Simulated annealing. Stat. Sci. 8, 10–15. doi:10.1214/ss/1177011077
Berwald, J., Chancellor, N., and Dridi, R. (2023). Understanding domain-wall encoding theoretically and experimentally. Philos. Trans. R. Soc. A 381, 20210410. doi:10.1098/rsta.2021.0410
BMW Group (2018). BMW Group corporate communications: BMW Group quantum computing challenge: The winners have been decided. Available at: https://www.press.bmwgroup.com/global/article/attachment/T0362463EN/515563.
Bobier, J. F., Langione, M., Tao, E., and Gourévitch, A. (2021). What happens when ‘if’ Turns to ‘when’ in quantum computing? Boston Consulting Group.
Bova, F., Goldfarb, A., and Melko, R. G. (2021). Commercial applications of quantum computing. EPJ Quantum Technol. 8, 2. doi:10.1140/epjqt/s40507-021-00091-1
Boyd, S., and Vandenberghe, L. (2004). Convex optimization. Cambridge, United Kingdom: Cambridge University Press. doi:10.1017/CBO9780511804441
Brooks, M. (2019). Beyond quantum supremacy: The hunt for useful quantum computers. Nature 574, 19–21. doi:10.1038/d41586-019-02936-3
Brown, D. G., Wobst, H. J., Kapoor, A., Kenna, L. A., and Southall, N. (2022). Clinical development times for innovative drugs. Nat. Rev. Drug Discov. 21, 793–794. doi:10.1038/d41573-021-00190-9
Bulger, D., Baritompa, W. P., and Wood, G. R. (2003). Implementing pure adaptive search with Grover’s quantum algorithm. J. Optim. Theory Appl. 116, 517–529. doi:10.1023/A:1023061218864
Bunyk, P. I., Hoskinson, E. M., Johnson, M. W., Tolkacheva, E., Altomare, F., Berkley, A. J., et al. (2014). Architectural considerations in the design of a superconducting quantum annealing processor. IEEE Trans. Appl. Supercond. 24, 1–10. doi:10.1109/TASC.2014.2318294
Callison, A., and Chancellor, N. (2022). Hybrid quantum-classical algorithms in the noisy intermediate-scale quantum era and beyond. Phys. Rev. A 106, 010101. doi:10.1103/PhysRevA.106.010101
Cerezo, M., Arrasmith, A., Babbush, R., Benjamin, S. C., Endo, S., Fujii, K., et al. (2021). Variational quantum algorithms. Nat. Rev. Phys. 3, 625–644. doi:10.1038/s42254-021-00348-9
Chakrabarti, B. K., Leschke, H., Ray, P., Shirai, T., and Tanaka, S. (2023). Quantum annealing and computation: Challenges and perspectives. Philos. Trans. R. Soc. A 381, 20210419. doi:10.1098/rsta.2021.0419
Chancellor, N., Cumming, R., and Thomas, T. (2020). Toward a standardized methodology for constructing quantum computing use cases. arXiv. doi:10.48550/arXiv.2006.05846
Chancellor, N. (2019). Domain wall encoding of discrete variables for quantum annealing and QAOA. Quantum Sci. Technol. 4, 045004. doi:10.1088/2058-9565/ab33c2
Chen, J., Date, P., Chancellor, N., Atiquzzaman, M., and Sreenan, C. (2022). Controller-based energy-aware wireless sensor network routing using quantum algorithms. IEEE Trans. Quantum Eng. 3, 1–12. doi:10.1109/TQE.2022.3217297
Chen, J., Stollenwerk, T., and Chancellor, N. (2021). Performance of domain-wall encoding for quantum annealing. IEEE Trans. Quantum Eng. 2, 1–14. doi:10.1109/TQE.2021.3094280
Crosson, E. J., and Lidar, D. A. (2021). Prospects for quantum enhancement with diabatic quantum annealing. Nat. Rev. Phys. 3, 466–489. doi:10.1038/s42254-021-00313-6
Cumming, R., and Thomas, T. (2022). Using a quantum computer to solve a real-world problem – what can be achieved today? arXiv. doi:10.48550/arXiv.2211.13080
Ebadi, S., Keesling, A., Cain, M., Wang, T. T., Levine, H., Bluvstein, D., et al. (2022). Quantum optimization of maximum independent set using Rydberg atom arrays. Science 376, 1209–1215. doi:10.1126/science.abo6587
Egger, D. J., Gambella, C., Marecek, J., McFaddin, S., Mevissen, M., Raymond, R., et al. (2020). Quantum computing for finance: State-of-the-art and future prospects. IEEE Trans. Quantum Eng. 1, 1–24. doi:10.1109/TQE.2020.3030314
Egger, D. J., Mareček, J., and Woerner, S. (2021). Warm-starting quantum optimization. Quantum 5, 479. doi:10.22331/q-2021-06-17-479
Evers, M., Heid, A., and Ostojic, I. (2021). Pharma’s digital Rx: Quantum computing in drug research and development. McKinsey.
Farhi, E., Goldstone, J., and Gutmann, S. (2014). A quantum approximate optimization algorithm. arXiv. doi:10.48550/arXiv.1411.4028
Farhi, E., Goldstone, J., and Gutmann, S. (2014). A quantum approximate optimization algorithm applied to a bounded occurrence constraint problem. arXiv. doi:10.48550/arXiv.1412.6062
Farhi, E., Goldstone, J., Gutmann, S., and Sipser, M. (2000). Quantum computation by adiabatic evolution. arXiv. doi:10.48550/arXiv.quant-ph/0001106
Fortnow, L. (2013). The golden ticket: P, NP, and the search for the impossible. Princeton, NJ: Princeton University Press.
Fu, X., Riesebos, L., Lao, L., Almudever, C. G., Sebastiano, F., Versluis, R., et al. (2016). “A heterogeneous quantum computer architecture,” in Proc. ACM ICCF (New York, NY: ACM), 323–330. doi:10.1145/2903150.2906827
Gerbert, P., and Ruess, F. (2018). The next Decade in quantum computing - and How to play. Boston Consulting Group.
German Draft Budgetary Plan (2020). German Draft budgetary plan 2021. Federal Ministry of Finance, Public Relations Division.
Gibney, E. (2019). Quantum gold rush: The private funding pouring into quantum start-ups. Nature 574, 22–24. doi:10.1038/d41586-019-02935-4
Gilliam, A., Woerner, S., and Gonciulea, C. (2021). Grover adaptive search for constrained polynomial binary optimization. Quantum 5, 428. doi:10.22331/q-2021-04-08-428
Glover, F., Kochenberger, G., and Du, Y. (2019). Quantum bridge analytics I: A tutorial on formulating and using QUBO models. 4OR 17, 335–371. doi:10.1007/s10288-019-00424-y
Glover, F., Kochenberger, G., Ma, M., and Du, Y. (2020). Quantum bridge analytics II: QUBO-plus, network optimization and combinatorial chaining for asset exchange. 4OR 18, 387–417. doi:10.1007/s10288-020-00464-9
Guenin, B., Könemann, J., and Tuncel, L. (2014). A gentle introduction to optimization. Cambridge, United Kingdom: Cambridge University Press.
Hadfield, S., Wang, Z., O’Gorman, B., Rieffel, E. G., Venturelli, D., and Biswas, R. (2019). From the quantum approximate optimization algorithm to a quantum alternating operator ansatz. Algorithms 12, 34. doi:10.3390/a12020034
Halffmann, P., Holzer, P., Plociennik, K., and Trebing, M. (2022). A quantum computing approach for the unit commitment problem. Proc. Int. Conf. Operations Res. 745, 012008. doi:10.1088/1757-899X/745/1/012008
Hauke, P., Katzgraber, H. G., Lechner, W., Nishimori, H., and Oliver, W. D. (2020). Perspectives of quantum annealing: Methods and implementations. Rep. Prog. Phys. 83, 054401. doi:10.1088/1361-6633/ab85b8
Holmes, Z., Sharma, K., Cerezo, M., and Coles, P. J. (2022). Connecting ansatz expressibility to gradient magnitudes and barren plateaus. PRX Quantum 3, 010313. doi:10.1103/PRXQuantum.3.010313
Jordan, S. (2021). Quantum algorithm Zoo. Available at: https://quantumalgorithmzoo.org.
Joseph, D., Meidanis, J., and Tiwari, P. (1992). “Determining DNA sequence similarity using maximum independent set algorithms for interval graphs,” in Algorithm theory — swat (Berlin Heidelberg: Springer), 326–337. doi:10.1007/3-540-55706-7_29
JUNIQ (2019). Launch of JUNIQ. Available at: https://www.fz-juelich.de/SharedDocs/Pressemitteilungen/UK/EN/2019/2019-10-25-juniq.html. Cached: https://web.archive.org/web/20220304012457/https://www.fz-juelich.de/SharedDocs/Pressemitteilungen/UK/EN/2019/2019-10-25-juniq.html.
Kadowaki, T., and Nishimori, H. (1998). Quantum annealing in the transverse Ising model. Phys. Rev. E 58, 5355–5363. doi:10.1103/PhysRevE.58.5355
Kandala, A., Mezzacapo, A., Temme, K., Takita, M., Brink, M., Chow, J. M., et al. (2017). Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246. doi:10.1038/nature23879
Karp, R. M. (1972). “Reducibility among combinatorial problems,” in Complexity of computer computations. Editors R. E. Miller, J. W. Thatcher, and J. D. Bohlinger (New York, NY: Plenum).
Katzgraber, H. G., Hamze, F., and Andrist, R. S. (2014). Glassy chimeras could be blind to quantum speedup: Designing better benchmarks for quantum annealing machines. Phys. Rev. X 4, 021008. doi:10.1103/PhysRevX.4.021008
Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Optimization by simulated annealing. Science 220, 671–680. doi:10.1126/science.220.4598.671
Kokail, C., Maier, C., van Bijnen, R., Brydges, T., Joshi, M. K., Jurcevic, P., et al. (2019). Self-verifying variational quantum simulation of lattice models. Nature 569, 355–360. doi:10.1038/s41586-019-1177-4
Langione, M., Bobier, J. F., Meier, C., Hasenfuss, S., and Schulze, U. (2019). Will quantum computing transform biopharma R&D? Boston Consulting Group.
Langione, M., Tillemann-Dick, C., Kumar, A., and Taneja, V. (2019). Where will quantum computers create value – and when. Boston Consulting Group.
Lloyd, S. (2018). Quantum approximate optimization is computationally universal. arXiv. doi:10.48550/arXiv.1812.11075
Lovász, L. (1994). Stable sets and polynomials. Discrete Math. 124, 137–153. doi:10.1016/0012-365X(92)00057-X
Lucas, A. (2014). Ising formulations of many NP problems. Front. Phys. 2. doi:10.3389/fphy.2014.00005
MacQuarrie, E. R., Simon, C., Simmons, S., and Maine, E. (2020). The emerging commercial landscape of quantum computing. Nat. Rev. Phys. 2, 596–598. doi:10.1038/s42254-020-00247-5
Mastroianni, C., Scarcello, L., and Settino, J. (2022). Quantum computing approach for energy optimization in a prosumer community. arXiv. doi:10.48550/arXiv.2209.04411
McClean, J. R., Romero, J., Babbush, R., and Aspuru-Guzik, A. (2016). The theory of variational hybrid quantum-classical algorithms. New J. Phys. 18, 023023. doi:10.1088/1367-2630/18/2/023023
Montanaro, A. (2020). Quantum speedup of branch-and-bound algorithms. Phys. Rev. Res. 2, 013056. doi:10.1103/physrevresearch.2.013056
Morales, M. E. S., Biamonte, J. D., and Zimborás, Z. (2020). On the universality of the quantum approximate optimization algorithm. Quantum Inf. process. 19, 291. doi:10.1007/s11128-020-02748-9
Mulligan, V. K., Melo, H., Merritt, H. I., Slocum, S., Weitzner, B. D., Watkins, A. M., et al. (2019). Designing peptides on a quantum computer. arXiv.
Nimbe, P., Weyori, B. A., and Adekoya, A. F. (2021). Models in quantum computing: A systematic review. Quantum Inf. process. 20, 80. doi:10.1007/s11128-021-03021-3
Orús, R., Mugel, S., and Lizaso, E. (2019). Quantum computing for finance: Overview and prospects. Rev. Phys. 4, 100028. doi:10.1016/j.revip.2019.100028
Palacios-Berraquero, C., Mueck, L., and Persaud, D. (2019). Instead of ‘supremacy’ use ‘quantum advantage. Nature 576, 213. doi:10.1038/d41586-019-03781-0
Pardalos, P. M., and Xue, J. (1994). The maximum clique problem. J. Glob. Optim. 4, 301–328. doi:10.1007/BF01098364
Paul, S. M., Mytelka, D. S., Dunwiddie, C. T., Persinger, C. C., Munos, B. H., Lindborg, S. R., et al. (2010). How to improve R&D productivity: The pharmaceutical industry’s grand challenge. Nat. Rev. Drug Discov. 9, 203–214. doi:10.1038/nrd3078
Plewa, J., Sieńko, J., and Rycerz, K. (2021). Variational algorithms for workflow scheduling problem in gate-based quantum devices. Comput. Inf. 40, 897–929. doi:10.31577/cai_2021_4_897
Preskill, J. (2018). Quantum computing in the NISQ era and beyond. Quantum 2, 79. doi:10.22331/q-2018-08-06-79
Rønnow, T. F., Wang, Z., Job, J., Boixo, S., Isakov, S. V., Wecker, D., et al. (2014). Defining and detecting quantum speedup. Science 345, 420–424. doi:10.1126/science.1252319
Senior, A. W., Evans, R., Jumper, J., Kirkpatrick, J., Sifre, L., Green, T., et al. (2020). Improved protein structure prediction using potentials from deep learning. Nature 577, 706–710. doi:10.1038/s41586-019-1923-7
Shor, P. W. (1994). “Algorithms for quantum computation: Discrete logarithms and factoring,” in Proc. 35th SFCS (IEEE), Santa Fe, NM, USA, 20-22 November 1994 (IEEE). doi:10.1109/SFCS.1994.365700
Tang, E. (2022). Dequantizing algorithms to understand quantum advantage in machine learning. Nat. Rev. Phys. 4, 692–693. doi:10.1038/s42254-022-00511-w
Tilly, J., Chen, H., Cao, S., Picozzi, D., Setia, K., Li, Y., et al. (2022). The variational quantum eigensolver: A review of methods and best practices. Phys. Rep. 986, 1–128. doi:10.1016/j.physrep.2022.08.003
van Meter, R., and Horsman, D. (2013). A blueprint for building a quantum computer. Commun. ACM 56, 84–93. doi:10.1145/2494568
Wecker, D., Hastings, M. B., and Troyer, M. (2015). Progress towards practical quantum variational algorithms. Phys. Rev. A 92, 042303. doi:10.1103/PhysRevA.92.042303
Weinberg, P., Tylutki, M., Rönkkö, J. M., Westerholm, J., Åström, J. A., Manninen, P., et al. (2020). Scaling and diabatic effects in quantum annealing with a D-Wave device. Phys. Rev. Lett. 124, 090502. doi:10.1103/PhysRevLett.124.090502
Weinberg, S. J., Sanches, F., Ide, T., Kamiya, K., and Correll, R. (2022). Supply chain logistics with quantum and classical annealing algorithms. arXiv. doi:10.48550/arXiv.2205.04435
Witt, S. (2022). The world-changing race to develop the quantum computer. Available at: https://www.newyorker.com/magazine/2022/12/19/the-world-changing-race-to-develop-the-quantum-computer.
Wong, F., Krishnan, A., Zheng, E. J., Stärk, H., Manson, A. L., Earl, A. M., et al. (2022). Benchmarking AlphaFold-enabled molecular docking predictions for antibiotic discovery. Mol. Syst. Biol. 18, e11081. doi:10.15252/msb.202211081
Wouters, O. J., McKee, M., and Luyten, J. (2020). Estimated research and development investment needed to bring a new medicine to market, 2009-2018. JAMA 323, 844–853. doi:10.1001/jama.2020.1166
Yalovetzky, R., Minssen, P., Herman, D., and Pistoia, M. (2021). NISQ-HHL: Portfolio optimization for near-term quantum hardware. arXiv. doi:10.48550/arXiv.2110.15958
Yarkoni, S., Alekseyenko, A., Streif, M., Dollen, D. V., Neukart, F., and Bäck, T. (2021). “Multi-car paint shop optimization with quantum annealing,” in 2021 IEEE Int. Conf. QCE (IEEE), October 17–22, 2021, Broomfield, CO (IEEE). doi:10.1109/QCE52317.2021.00019
Yarkoni, S., Leib, M., Skolik, A., Streif, M., Neukart, F., and von Dollen, D. (2019). Volkswagen and quantum computing: An industrial perspective. Digit. Welt 3, 34–37. doi:10.1007/s42354-019-0166-y
Yarkoni, S., Raponi, E., Bäck, T., and Schmitt, S. (2022). Quantum annealing for industry applications: Introduction and review. Rep. Prog. Phys. 85, 104001. doi:10.1088/1361-6633/ac8c54
Zaman, M., Tanahashi, K., and Tanaka, S. (2021). Pyqubo: Python library for mapping combinatorial optimization problems to QUBO form. arXiv. doi:10.48550/arXiv.2103.01708
Zhao, Z., Fan, L., and Han, Z. (2022). “Hybrid quantum benders’ decomposition for mixed-integer linear programming,” in 2022 IEEE wireless communications and networking conference, April 10–13, 2022, Austin, TX (WCNC), 2536–2540. doi:10.1109/WCNC51071.2022.9771632
Keywords: quantum computing, quantum optimization, perspecitves, optimization algorithms, problem modeling
Citation: Au-Yeung R, Chancellor N and Halffmann P (2023) NP-hard but no longer hard to solve? Using quantum computing to tackle optimization problems. Front. Quantum Sci. Technol. 2:1128576. doi: 10.3389/frqst.2023.1128576
Received: 20 December 2022; Accepted: 09 February 2023;
Published: 23 February 2023.
Edited by:
Oleksandr Kyriienko, University of Exeter, United KingdomReviewed by:
Prasanta Panigrahi, Indian Institute of Science Education and Research Kolkata, IndiaCopyright © 2023 Au-Yeung, Chancellor and Halffmann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rhonda Au-Yeung, cmhvbmRhLmF1LXlldW5nQHN0cmF0aC5hYy51aw==; Pascal Halffmann, cGFzY2FsLmhhbGZmbWFubkBpdHdtLmZyYXVuaG9mZXIuZGU=
†These authors have contributed equally to this work and share first authorship
 Rhonda Au-Yeung
Rhonda Au-Yeung Nicholas Chancellor
Nicholas Chancellor Pascal Halffmann
Pascal Halffmann