- Emergent Systems Laboratory, Ritsumeikan University, Kusatsu, Shiga, Japan
Assisting individuals in their daily activities through autonomous mobile robots is a significant concern, especially for users without specialized knowledge. Specifically, the capability of a robot to navigate to destinations based on human speech instructions is crucial. Although robots can take different paths toward the same objective, the shortest path is not always the most suitable. A preferred approach would be to accommodate waypoint specifications flexibly for planning an improved alternative path even with detours. Furthermore, robots require real-time inference capabilities. In this sense, spatial representations include semantic, topological, and metric-level representations, each capturing different aspects of the environment. This study aimed to realize a hierarchical spatial representation using a topometric semantic map and path planning with speech instructions by including waypoints. Thus, we present a hierarchical path planning method called spatial concept-based topometric semantic mapping for hierarchical path planning (SpCoTMHP), which integrates place connectivity. This approach provides a novel integrated probabilistic generative model and fast approximate inferences with interactions among the hierarchy levels. A formulation based on “control as probabilistic inference” theoretically supports the proposed path planning algorithm. We conducted experiments in a home environment using the Toyota human support robot on the SIGVerse simulator and in a lab–office environment with the real robot Albert. Here, the user issues speech commands that specify the waypoint and goal, such as “Go to the bedroom via the corridor.” Navigation experiments were performed using speech instructions with a waypoint to demonstrate the performance improvement of the SpCoTMHP over the baseline hierarchical path planning method with heuristic path costs (HPP-I) in terms of the weighted success rate at which the robot reaches the closest target (0.590) and passes the correct waypoints. The computation time was significantly improved by 7.14 s with the SpCoTMHP than the baseline HPP-I in advanced tasks. Thus, hierarchical spatial representations provide mutually understandable instruction forms for both humans and robots, thus enabling language-based navigation.
1 Introduction
Autonomous robots are often tasked with linguistic interactions such as navigation for seamless integration into human environments. Navigation using the concepts and vocabulary tailored to specific locations learned from human and environmental interactions is a complex challenge for these robots (Taniguchi et al., 2016b; Taniguchi et al., 2019). Such robots are required to construct adaptive spatial structures and place semantics from multimodal observations acquired during movements within the environment (Kostavelis and Gasteratos, 2015; Garg et al., 2020). This concept is closely linked to the anchoring problem, which is concerned with the relationships between symbols and sensor observations (Coradeschi and Saffiotti, 2003; Galindo et al., 2005). Understanding the specific place or concept to which a word or phrase refers, i.e., the denotation, is therefore crucial.
The motivation for research on this topic stems from the necessity for autonomous robots to operate effectively in human environments. This requires them to understand human language and navigate complex environments accordingly. The significance of this research lies in enabling autonomous robots to interact within human environments both effectively and intuitively, thereby assisting the users. The primary issue in hierarchical path planning is the increased computational cost owing to the complexity of the model, which poses a risk to real-time responsiveness and efficiency. Additionally, the challenge with everyday natural language commands provided by the users is the existence of specific place names that are not generally known and the occurrence of different places within an environment that share the same name. Therefore, robots need to possess environment-specific knowledge. Enhancements in the navigation success rates and computational efficiency, especially for tasks involving linguistic instructions, could significantly broaden the applications of autonomous robots; these applications would extend beyond home support to include disaster rescue, medical assistance, and more.
Topometric semantic maps are a combination of metric and topological maps with semantics that are helpful for path planning using generalized place units. Thus, they facilitate human–robot linguistic interactions and assist humans. One of the key challenges here is the robot’s capacity to efficiently construct and utilize these hierarchical spatial representations for interaction tasks. Hierarchical spatial representations provide mutually understandable instruction forms for both humans and robots to enable language-based navigation. They are generalized appropriately at each level and can accommodate combinations of paths that were not considered during training. As shown in Figure 1 (left), this study entails three levels of spatial representation: (i) semantic level that represents place categories associated with various words and abstracted by multimodal observations; (ii) topological level that represents the probabilistic adjacency of places in a graph structure; (iii) metric level that represents the occupancy grid map and is obtained through simultaneous localization and mapping (SLAM) (Grisetti et al., 2007). In this paper, the term spatial concepts refers to semantic–topological knowledge grounded in real-world environments.
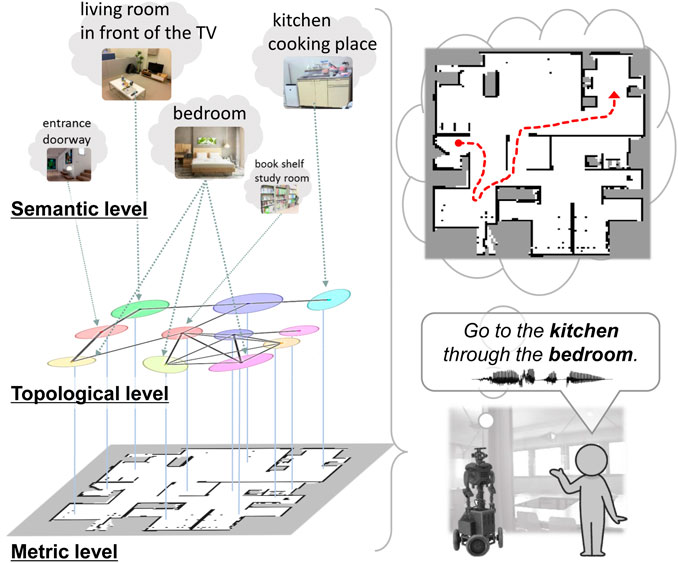
Figure 1. Overview of the proposed method. Left: hierarchy of spatial representation with topometric semantic mapping. Right: path planning from spoken instructions with waypoint and goal specifications.
The main goal of this study was to realize efficient spatial representations and high-speed path planning from human speech instructions by specifying waypoints using topological semantic maps incorporating place connectivity. This study was conducted in two phases, namely spatial concept learning and path planning. Spatial concept learning phase: In this phase, a user guides a robot in the environment by providing natural language cues1, i.e., providing utterances about various locations, such as “This is my father Bob’s study space, and it has many books.” Furthermore, the robot collects multimodal sensor observations from the environment, including images, depth data, odometry, and speech signals. Using these sensor observations, the robot acquires knowledge of the environmental map as well as connection relationships between the places, spatial concepts, and place names. Path planning phase: In this phase, the robot considers speech instructions such as “go to the kitchen” as basic tasks and “go to the kitchen through the bedroom” as advanced tasks (Figure 1 (right)). In particular, this study was focused on hierarchical path planning in advanced tasks. Although the shortest paths may not always be the most suitable, robots can select alternative paths to avoid certain areas or perform specific tasks based on the user instructions. For example, the robot may choose a different route to avoid the living room with guests or to check on the pets in the bedroom. Thus, users can guide the robot to an improved path by specifying waypoints. Furthermore, when multiple locations have the same name (e.g., three bedrooms), selecting the closest route among them is appropriate. By specifying the closest waypoint to the target, the robot can accurately select the target even when many places share the same name.
In this study, “optimal” refers to the scenario that maximizes the probability of a trajectory distribution under the given conditions. Specifically, the robot should plan an overall optimal path through the designated locations. This ensures that the robot’s path planning is practical and reduces the travel distance as well as time by considering real-world constraints and objectives. It also allows greater flexibility in guiding the robot through the waypoints, thereby enabling users to direct it along preferred routes while maintaining the overall effectiveness.
This paper proposes a spatial concept-based topometric semantic mapping for hierarchical path planning (SpCoTMHP) approach with a probabilistic generative model2. The topometric semantic map enables path planning by combining abstract place transitions and geometrical structures in the environment. SpCoTMHP is based on a probabilistic generative model that integrates the metric, topological, and semantic levels with speech and language models into a unified framework. Learning occurs in an unsupervised manner through the joint posterior distribution derived from multimodal observations. To enhance the capture of topological structures, a learning method inspired by the function of replay in the hippocampus is introduced (Foster and Wilson, 2006). Ambiguities related to the locations and words are addressed through a probabilistic approach informed by robot experience. In addition, we develop approximate inference methods for effective path planning, where each hierarchy level influences the others. The proposed path planning is theoretically supported by the idea of control as probabilistic inference (CaI) (Levine, 2018), which has been shown to bridge the theoretical gap between probabilistic inference and control problems, including reinforcement learning.
The proposed approach is based on symbol emergence in robotics (Taniguchi et al., 2016b, 2019) and has the advantage of enabling navigation using unique spatial divisions and local names learned without annotations, which are tailored to each individual family or community environment. Hence, the users can simply communicate with the robot throughout the process from learning to task execution, thus eliminating the need for robotics expertise. Moreover, the approach is based on the robot’s real-world experiences that enable daily behavioral patterns to be captured, such as where to travel more/less frequently.
We conducted experiments in the home environment using the Toyota human support robot (HSR) on the SIGVerse simulator (Inamura and Mizuchi, 2021) and in a lab–office environment with the real robot Albert (Stachniss, 2003). SpCoTMHP was compared with baseline hierarchical path planning methods in navigation experiments using speech instructions with a designated waypoint. The main contributions of this study are as follows:
1. We demonstrated that hierarchical path planning incorporating topological maps through probabilistic inference achieves higher success rates and shorter computation times for language instructions involving waypoints compared to methods utilizing heuristic costs.
2. We illustrated that semantic mapping based on spatial concepts and considering topological maps achieves higher learning performance than SpCoSLAM, which does not incorporate topological maps.
In particular, the significance of this work is characterized by the following four items:
1. Integrated learning–planning model: The learning–planning integrated model autonomously constructs hierarchical spatial representations, including topological place connectivity, from the multimodal observations of the robot, leading to improved performances for learning and planning.
2. Probabilistic inference for real-time planning: The approximate probabilistic inference based on CaI enables real-time planning of adaptive paths from the waypoint and goal candidates.
3. Many-to-many relationships for path optimization: The probabilistic many-to-many relationships between words and locations enable planning closer paths when there are multiple target locations.
4. Spatial concepts for environment-specific planning: The spatial concepts learned in real environments are effective for path planning with environment-specific words.
The remainder of this paper is organized as follows. Section 2 presents related works on topometric semantic mapping, hierarchical path planning, and the spatial concept-based approach. Section 3 describes the proposed method SpCoTHMP. Section 4 presents experiments performed using a simulator in multiple home environments. Section 5 discusses some experiments performed in real environments. Finally, Section 6 presents the conclusions of this paper.
2 Related works
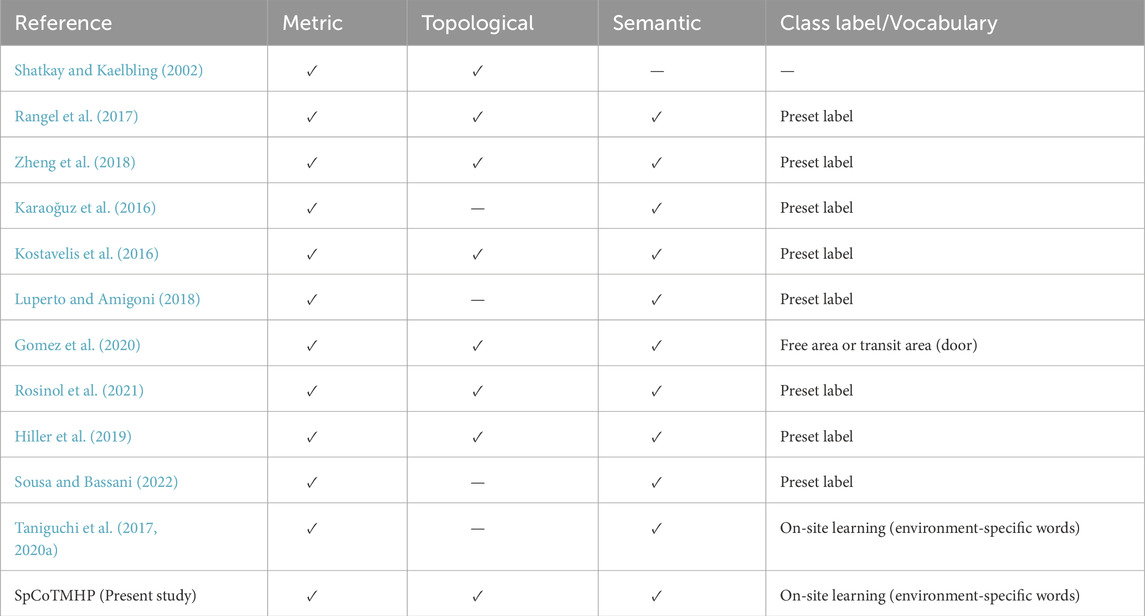
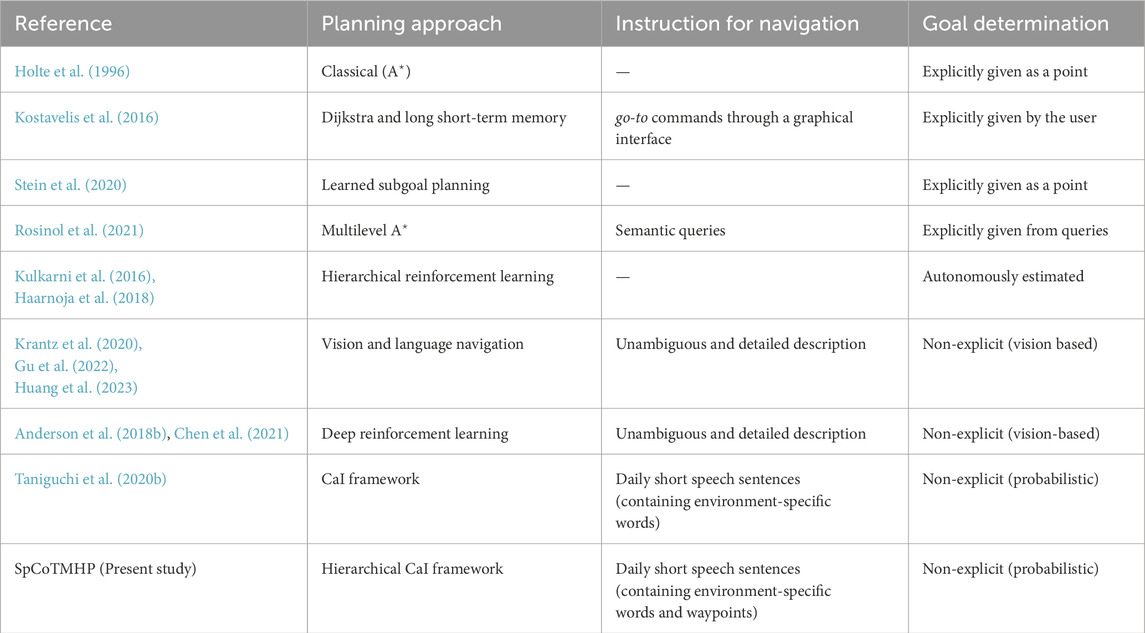
This section describes topometric semantic mapping in Section 2.1, hierarchical path planning in Section 2.2, robotic planning using large language models (LLMs) and foundation models in Section 2.3, and the spatial concept-based approach in Section 2.4. Table 1 displays the main characteristics of the map representation and differences between the related works. Table 2 presents the main characteristics of path planning and differences between the related works.
2.1 Topometric semantic mapping
For bridging the topological–geometrical gap, geometrically constrained hidden Markov models have been proposed as probabilistic models for robot navigation in the past (Shatkay and Kaelbling, 2002). The similarity between these models and that proposed in this study is that probabilistic inference is realized for path planning. However, the earlier models do not introduce semantics, such as location names.
Research on semantic mapping has been increasingly emphasized in recent years. In particular, semantic mapping assigns place meanings to the map of a robot (Kostavelis and Gasteratos, 2015; Garg et al., 2020). However, numerous studies have provided preset location labels for areas on a map. For example, LexToMap (Rangel et al., 2017) assigns convolutional neural network (CNN)-recognized lexical labels to a topological map, where the approach enables unsupervised learning based on multimodal perceptual information for categorizing unknown places
The use of topological structures enables more accurate semantic mapping (Zheng et al., 2018); this method is expected to improve performance by introducing topological levels. The nodes in a topological map can vary depending on the methods used, such as room units or small regions (Karaoğuz et al., 2016; Kostavelis et al., 2016; Luperto and Amigoni, 2018; Gomez et al., 2020). Kimera (Rosinol et al., 2021) used multiple levels of spatial hierarchical representation, such as metrics, rooms, places, semantic levels, objects, and agents; here, the robot automatically determined the spatial segmentation unit based on experience.
In several semantic mapping studies (Hiller et al., 2019; Sousa and Bassani, 2022), topological semantic maps were constructed from visual images or metric maps using CNNs. However, these studies have not considered path planning. In contrast, the method proposed herein is characterized by an integrated model that includes learning and planning.
2.2 Hierarchical path planning
Hierarchical path planning has been a significant topic of study for long, e.g., hierarchical
Given that the proposed method realizes a hierarchy based on the CaI framework (Levine, 2018), it is theoretically connected with hierarchical reinforcement learning, where the subgoals and policies are estimated autonomously (Kulkarni et al., 2016; Haarnoja et al., 2018). This study investigates tasks similar to hierarchical reinforcement learning to infer the probabilistic models, which are expected to be theoretically readable and integrable with other methods. Vision and language navigation (VLN) aims to help an agent navigate through an environment assisted by natural language instructions while using visual information from the environment (Krantz et al., 2020; Gu et al., 2022; Huang et al., 2023). The present study differs from those on VLNs in several respects. The first difference is in the complexity of the instructions. In VLN tasks, unambiguous and detailed natural language instructions are provided; in contrast, the proposed method involves tasks characterized by the terseness and ambiguity with which people speak daily. The second difference is the training scenario. The VLN dataset uses only common words annotated in advance by people. In contrast, the proposed approach can handle spatial words in communities living in specific environments. The third difference is that although VLNs use vision during path planning, vision was used in the present work to generalize spatial concepts only during training of the proposed method. This is due to the difference between sequential action decisions and global path planning. Finally, deep and reinforcement learning techniques have been used in recent studies on VLNs (Anderson et al., 2018b; Chen et al., 2021); however, the proposed probabilistic model autonomously navigates toward the target location using speech instructions as the modality.
2.3 Robotic planning using LLM and foundation models
Recently, there has been growing utilization of LLMs and foundational models for enhancing robot autonomy (Firoozi et al., 2023; Vemprala et al., 2023; Zeng et al., 2023). SayCan (Ahn et al., 2022) integrates pretrained LLMs and behavioral skills to empower the robots to execute context-aware and appropriate actions in real-world settings; in this approach, the LLM conducts higher-level planning based on language while facilitating lower-level action decisions grounded in physical constraints. However, a key challenge remains in accurately capturing the characteristics of the physical space, such as the walls, distances, and room shapes, using only LLMs. In contrast, our study tightly integrates language, spatial semantics, and physical space to estimate the trajectories comprehensively. Furthermore, our proposed method is designed to complement LLM-based planning and natural language processing, with the expectation of seamless integration.
Several studies have employed LLMs and foundational models to accomplish navigation tasks. LM-Nav (Shah et al., 2022) integrates contrastive language–image pretraining (CLIP) (Radford et al., 2021) and generative pretrained transformer-3 (GPT-3) (Brown et al., 2020); this system enables navigation directly through language instructions and robot-perspective images alone. However, this approach necessitates substantial amounts of driving data from the target environment. Conversely, an approach that combines vision–language models (VLMs) and semantic maps has also been proposed. CLIP-Fields (Shafiullah et al., 2023), natural language maps (NLMap) (Chen et al., 2023), and VLMaps (Huang et al., 2023) use LLMs and VLMs to create 2D or 3D spaces and language associations to enable navigation for natural language queries; these approaches mainly record the placements of objects on the map and cannot understand the meanings of the locations or planning for each location. Additionally, LLM/VLM-based approaches have a large common-sense vocabulary similar to an open vocabulary. However, using pretrained place recognizers alone makes it difficult to handle environment-specific names (e.g., Alice’s room). Although LLMs have the potential to handle environment-specific names through in-context learning, they have not been integrated with mapping and navigation in existing models at present. Our spatial concept-based approach addresses knowledge specific to the home environment through on-site learning.
2.4 Spatial concept-based approach
In Section 3, we present two major previous studies on which the proposed method is based. As presented in our previous research, SpCoSLAM (Taniguchi et al., 2017, 2020a) forms spatial concept-based semantic maps based on multimodal observations obtained from the environment; here, the multimodal observations for spatial concept formation refer to the images, depth sensor values, odometry, and speech signals. Moreover, the approach can acquire novel place categories and vocabularies from unknown environments. However, SpCoSLAM cannot estimate the topological level, i.e., whether one place is spatially connected with another. The details of the formulation of the probabilistic generative model are described in Supplementary Appendix SA1. The learning procedure for each step is described in Supplementary Appendix SA2. In the present study, we applied the hidden semi-Markov model (HSMM) (Johnson and Willsky, 2013) that estimates the transition probabilities between places and constructs a topological graph instead of the Gaussian mixture model (GMM) used in SpCoSLAM.
In addition, SpCoNavi (Taniguchi et al., 2020b) plans the path in the CaI framework (Levine, 2018) by focusing on the action decisions in the probabilistic generative model of SpCoSLAM. The details on the formulation of CaI are described in Supplementary Appendix SA3. Notably, SpCoNavi realizes navigation from simple speech instructions using a spatial concept acquired autonomously by the robot. However, SpCoNavi does not demonstrate hierarchical path planning, and scenarios specifying a waypoint are not considered. In addition, there are several problems that need to be solved: SpCoNavi based on the Viterbi algorithm (Viterbi, 1967) is computationally expensive given that all the grids of the occupied grid map are used as the state space; it is vulnerable to the real-time performance required for robot navigation; SpCoNavi based on the
3 Proposed method: SpCoTMHP
We propose the spatial concept-based topometric semantic mapping for hierarchical path planning (SpCoTMHP) approach herein. Spatial concepts refer to categorical knowledge of places from multimodal information obtained through unsupervised learning. The proposed method realizes efficient navigation from human speech instructions through inference based on a probabilistic generative model. The proposed approach also enhances human comprehensibility and explainability for communication by employing Gaussian distributions as the fundamental spatial units (i.e., representing a single place). The capabilities of the proposed generative model are as follows: (i) place categorization by extracting the connection relations between places through unsupervised learning; (ii) many-to-many correspondences between words and places; (iii) efficient hierarchical path planning by introducing two variables (
Three phases can be distinguished in probabilistic generative models: (a) model definition in the probability distribution of the generative process (Section 3.1), (b) inference of the posterior distribution for parameter learning (Section 3.2), and (c) probabilistic inference for task execution after learning (Sections 3.3 and 3.4).
3.1 Definition of the probabilistic generative model
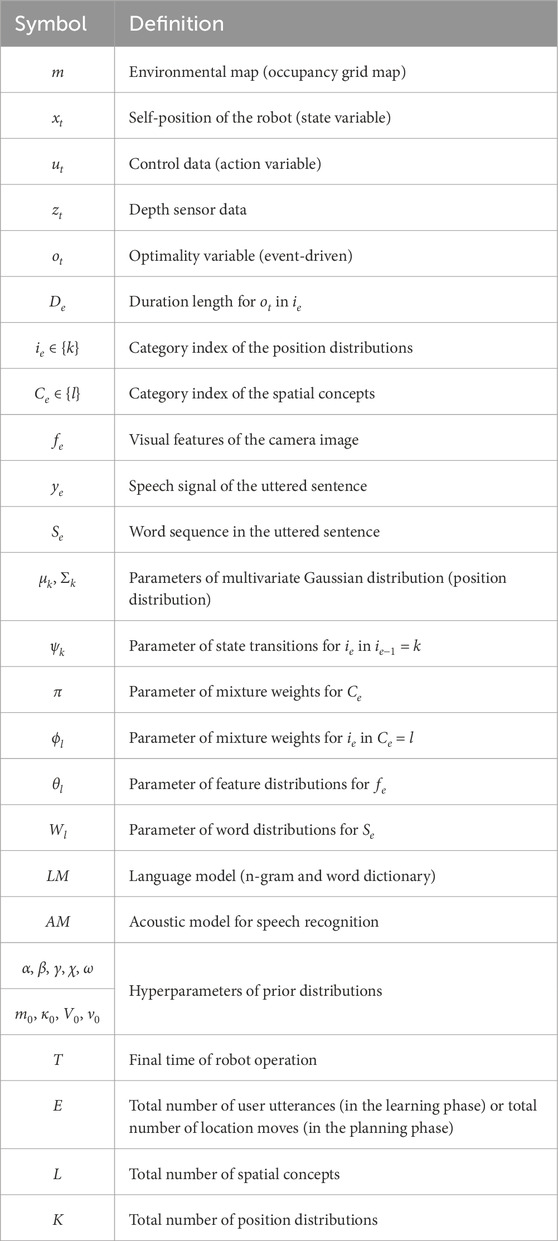
SpCoTMHP is designed as an integrated model for each module: SLAM, HSMM, multimodal Dirichlet process mixture (MDPM) for place categorization, and the speech-and-language model. Therefore, it is simple to distribute the development and further the module coupling in the framework of Neuro-SERKET (Taniguchi et al., 2020c). The integrated model has the advantage of the inference functioning as a whole to complement each uncertainty. Figure 2 presents the graphical model representation of SpCoTMHP, and Table 3 lists each variable of the graphical model. Unlike SpCoSLAM (Taniguchi et al., 2017), SpCoTMHP introduces two different time units (real-time robot-motion-based time step
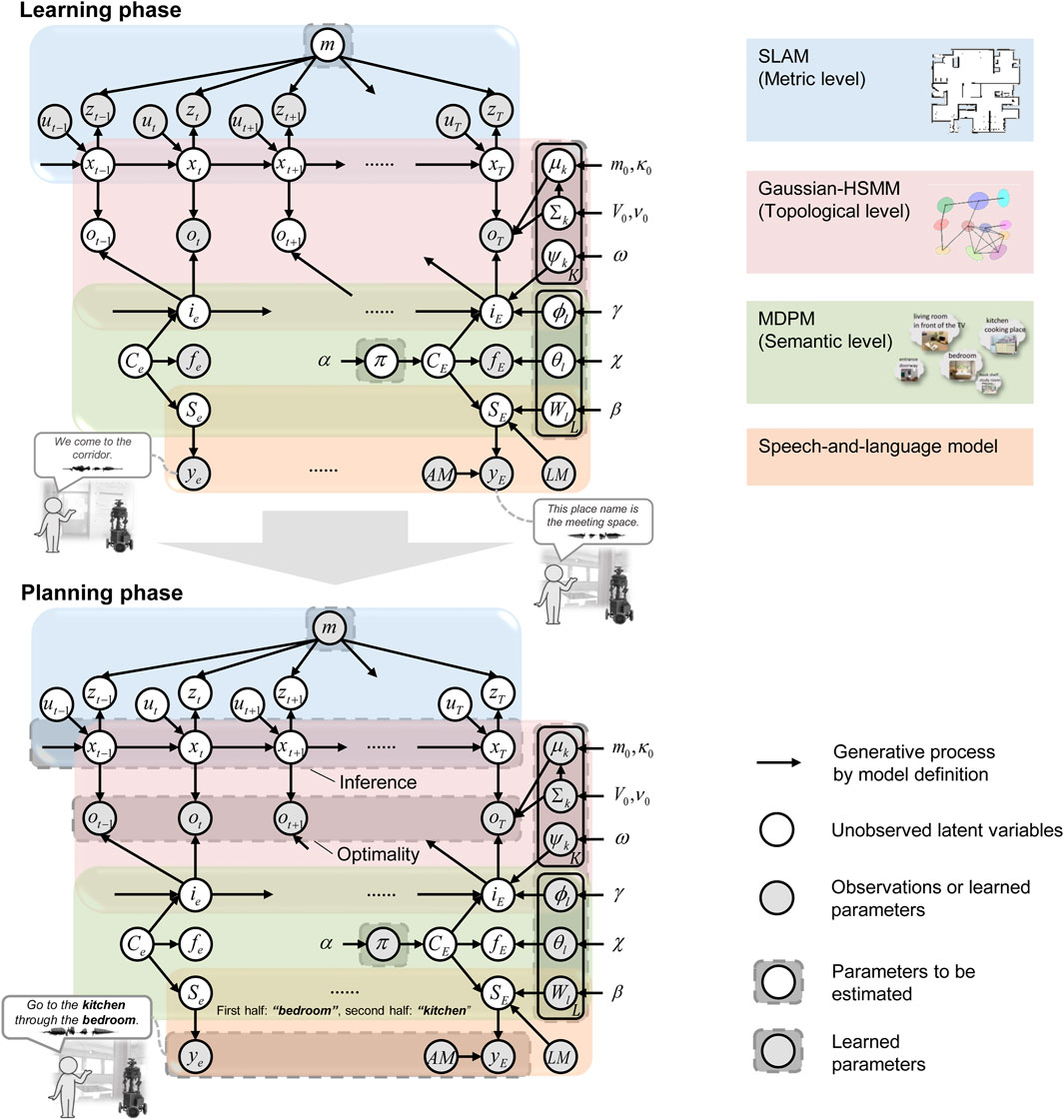
Figure 2. Graphical model representation of the SpCoTMHP (top) spatial concept learning and its path planning phases (bottom). The two phases imply different probabilistic inferences for the same generative model; this has the mathematical advantage that different probabilistic inferences can be applied under the same model assumptions. The integration of several parts into a single model allows the inferences to consider various probabilities throughout. The graphical model represents the conditional dependency between random variables. The gray nodes indicate observations or learned parameters as fixed conditional variables, and white nodes denote unobserved latent variables to be estimated. Arrows from the global variables to local variables other than
SLAM (metric level): The probabilistic generative model of SLAM represents the time-series transition of self-position, and the state space on the map corresponds to the metric level. These probability distributions have been standard in SLAM for probabilistic approaches (Thrun et al., 2005). Accordingly, Eq. (1) represents a measurement model that is a likelihood of a depth sensor
Here, self-localization assumes a transition at time
HSMM (from metric to topological levels): The HSMM can be used to cluster the location data of the robot in terms of position distributions and represent the probabilistic transitions between the position distributions. This refers to transitioning from the metric to topological levels. The HSMM connects two units, namely time
where
where the equation relating
where
HSMM + MDPM connection (from topological to semantic levels): The variable
where
MDPM (semantic level): The MDPM is a mixture distribution model for forming place categories from multimodal observations. Through the spatial concept
where
MDPM + language model connection (semantic level): The variable of a word sequence
where
Speech-and-language model: The generative process for the likelihood of speech given a word sequence is, as in Eq. 18:
This probability distribution does not usually appear explicitly but is internalized as an acoustic model in probability-based speech recognition systems.
3.2 Spatial concept learning as topometric semantic mapping
The joint posterior distribution is described as
where
In this paper, as an approximation to sampling from Eq. (19), the parameters are estimated as follows:
where
In the learning phase, the user provides a teaching utterance each time the robot transitions between locations. Given that the utterance is event-driven, it is assumed that the variables for the spatial concepts are observed only at event
Reverse replay: In the case of spatial movements, we can transition from
3.3 Hierarchical path planning by control as inference
The probabilistic distribution, which represents the trajectory
The planning horizon at the metric level
where
In the present study, we assumed that the robot could extract words indicating the goal and waypoint from a particular sentence utterance. In topological-level planning including the waypoint, the waypoint word is input in the first half while the target word is presented in the second half of the utterance.
3.4 Approximate inference for hierarchical path planning
The strict inference of Eq. (24) requires a double-forward backward calculation. In this case, reducing the calculation cost is necessary to accelerate path planning, which is one of the objectives of this study. Therefore, we propose an algorithm to solve Eq. (24). Algorithm 1 presents the hierarchical planning approach as produced by SpCoTMHP. Here, the path planning is divided into topological and metric levels, and the CaI is solved at each level. Metric-level planning assumes that the partial paths in each of the transitions between places are solved in
Algorithm 1.Hierarchical path planning algorithm.
1: //Precalculation:
2:
3: Create a graph between the waypoint candidates
4: for all nodes,
5:
6: Calculate likelihoods
7: end for
8: //When a speech instruction
9:
10: Estimate an index
11:
12: Connect the partial paths
13:
Path planning at the metric level (i.e., partial path
This indicates that a metric-level path inference can be expressed in terms of the CaI.
Calculating Eq. (24) for all possible positions was difficult. Therefore, we used the mean or sampled values from the Gaussian mixture of position distributions as the goal position candidates, i.e.,
Therefore, as a concrete solution to Eq. (26), the partial paths in the transitions of the candidate points from place
where
The selection of a series of partial metric path candidates corresponds to the selection of the entire path. Thus, we can replace the formulation of the maximization problem of Eq. (24) with that of Eq. (28). Each partial metric path has corresponding indices
By taking the maximum value instead of the summation
where
4 Experiment I: planning tasks in a simulator
We experimented with path planning using spatial concepts by including topological structures via human speech instructions. In this experiment, as a first step, we demonstrated that the proposed method improves the efficiency of path planning when the ideal spatial concept is used. The simulator environment was SIGVerse Version 3.0 (Inamura and Mizuchi, 2021), and the virtual robot model used was the Toyota HSR. We used five three-bedroom home environments3 with different layouts and room sizes.
4.1 Spatial concept-based topometric semantic map
There were 11 spatial concepts and position distributions for each environment (Figure 3 bottom; Supplementary Appendix SA4). Fifteen utterances were provided by the user for each place as the training data. The SLAM and speech recognition modules were inferred individually by splitting from the model, i.e., the self-location
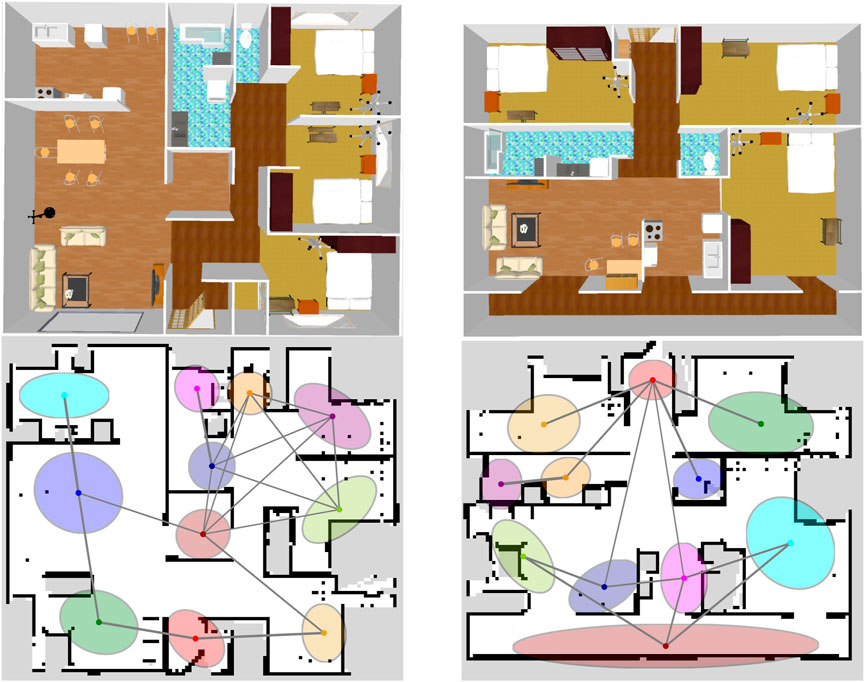
Figure 3. Overhead view of the simulator environments (top) and ideal spatial concepts expressed by SpCoTMHP on the environmental map (bottom) in Experiment I. The colors of the position distributions were randomly set. If
4.2 Path planning from speech instructions
Two types of path planning tasks were performed in the experiments, which included a variation where the waypoints and goals were recombined at different places. The waypoint and goal words in user instructions were extracted by a simple natural language process and entered into the model as
We compared the performances of the methods as follows:
(A)
(B) SpCoSLAM (Taniguchi et al., 2017) + SpCoNavi (Taniguchi et al., 2020b) with the Viterbi algorithm (Viterbi, 1967).
(C) SpCoSLAM (Taniguchi et al., 2017) + SpCoNavi (Taniguchi et al., 2020b) with
(D) Hierarchical path planning without CaI, similar to Niijima et al. (2020): the goal nodes were estimated by
(E) SpCoTMHP (topological level: Dijkstra, metric level:
The evaluation metrics for path planning include the success weighted by path length (SPL) (Anderson et al., 2018a) when the robot reaches the target location and calculated runtime in seconds (time). The N-SPL is the weighted success rate when the robot reaches the closest target from the initial position for several places having the same name. The W-SPL is the weighted success rate when the robot passes the correct waypoints. The WN-SPL is the weighted success rate when the robot reaches the closest target by passing the correct waypoints; the WN-SPL is the overall measure of path planning efficiency in advanced tasks.
Conditions: The planning horizons were
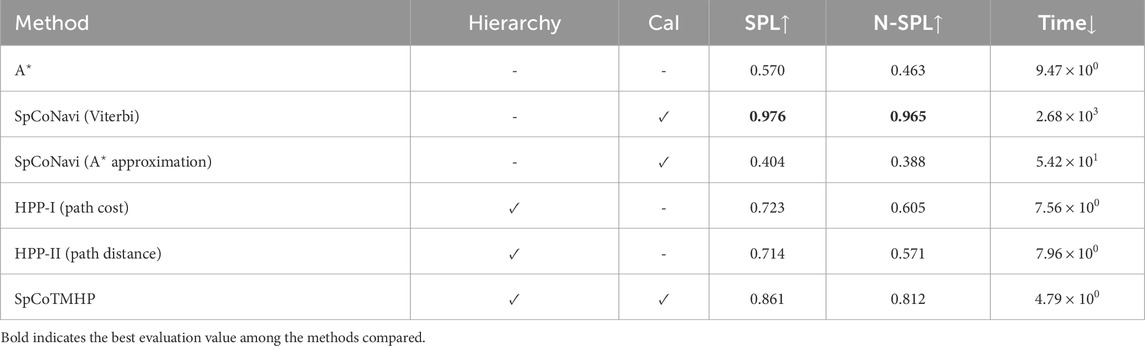
Results: Tables 4 and 5 present the evaluation results for the basic and advanced planning tasks. Figure 4 presents an example of the estimated path5. Overall, SpCoTMHP outperformed the comparison methods and had significantly reduced computation times. The basic task demonstrated that the proposed method could solve the problem of stopping along the path before reaching the objective, which occurs in SpCoSNavi (
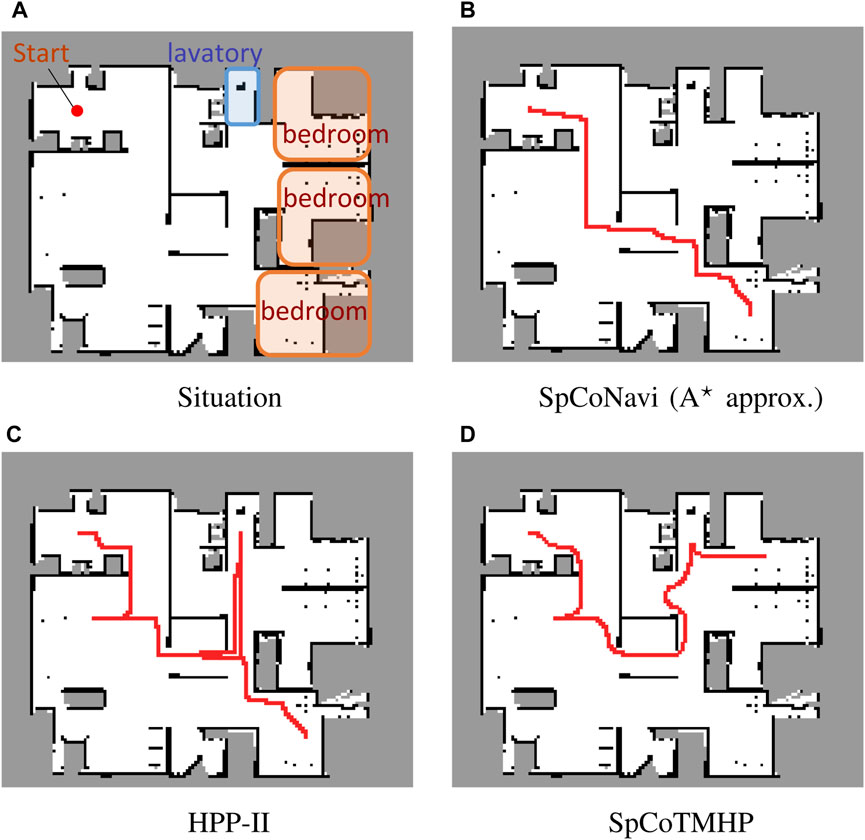
Figure 4. Example of path planning in the advanced task. The instruction: “Go to the bedroom via the lavatory” (Experiment I).
The advanced task confirmed that the proposed method could estimate the path via the waypoint (Figure 4D). Although SpCoTMHP had the disadvantage of estimating slightly redundant paths, the reduced computation time and improved planning performance render it a more practical approach than the conventional methods. Consequently, the proposed method achieved better path planning by considering the initial, waypoint, and goal positions.
SpCoTMHP exhibited faster path planning than SpCoNavi (Viterbi) despite its inferior performance in the basic path planning task. This improvement stems from the reduced number of inference states and computational complexity achieved through hierarchization and approximation. In both the basic and advanced tasks, SpCoTMHP notably enhanced the path planning performance over SpCoNavi (
5 Experiment II: real environment
We demonstrated that the formation of spatial concepts, including topological relations between places, could also be realized in a real-world environment. Real-world datasets are more complex and involve more uncertainties than simulators. Therefore, as detailed in Section 5.1, we first confirmed that the proposed method had improved learning performance over the conventional method SpCoSLAM. Thereafter, as detailed in Section 5.2, we determined the impacts of the spatial concept parameters learned in Section 5.1 on the inference of path planning. Additionally, we confirmed that the proposed method could plan a path based on the learned topometric semantic map.
5.1 Spatial concept-based topometric semantic mapping
Conditions: The experimental environment was identical to that in the open dataset albert-b-laser-vision6, which was obtained from the robotics dataset repository (Radish) (Stachniss, 2003). The details of the dataset are shown in Supplementary Appendix SA5. The utterances included 70 sentences in Japanese, such as “The name of this place is student workroom,” “You can find the robot storage space here,” and “This is a white shelf.” The hyperparameters for learning were set as follows:
Evaluation metrics: Normalized mutual information (NMI) (Kvalseth, 1987) and adjusted Rand index (ARI) (Hubert and Arabie, 1985), which are the most widely used metrics in clustering tasks for unsupervised learning, were used as the evaluation metrics for learning the spatial concepts. The NMI was obtained by normalizing the mutual information between the clustering results and correct labels in the range of 0.0–1.0. Moreover, the ARI is 1.0 when the clustering result matches the correct label and 0.0 when it is random. The time taken for learning was additionally recorded as a reference value.
Results: Figures 5A–D present an example of spatial concept learning. For example, the map in Figure 5C caused overlapping distributions in the upper right corner and skipped connections to neighboring distributions, which were mitigated by the map in Figure 5D. Table 6 presents the evaluation results from the average of ten trials of spatial concept learning. SpCoTMHP achieved a higher learning performance (i.e., NMI and ARI values) than SpCoSLAM, indicating that the categorization of spatial concepts and position distributions was more accurate when considering the connectivity of the places. In addition, the proposed method with reverse replay demonstrated the highest performance. Consequently, using both place transitions during learning and vice versa may be useful for learning spatial concepts. Moreover, Table 6 shows that there was no significant difference in the computation time of the learning algorithm.
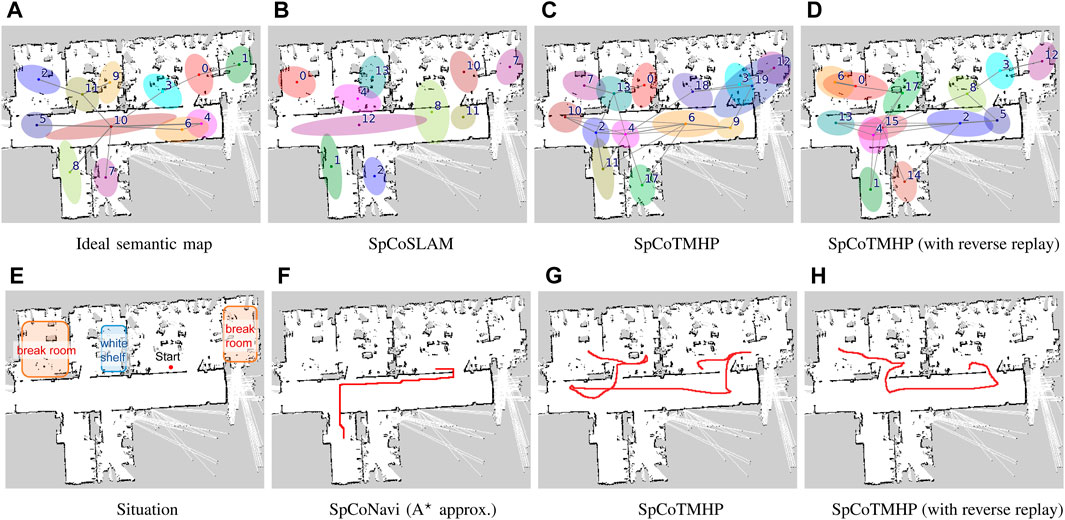
Figure 5. Top (A–D): Results of spatial concept learning. Bottom (E–H): Results of path planning. The speech instruction provided was “Go to the break room via the white shelf.” The break room was taught in two rooms: upper right and upper left corners. The white shelf is in the second room from the left on the upper half of the map (Experiment II).
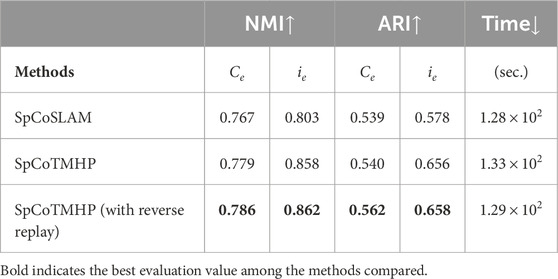
Table 6. Learning performances for spatial concepts and position distributions, as well as computation times of the learning algorithms (Experiment II).
5.2 Path planning from speech instructions
The speech instruction provided was “Go to the break room via the white shelf,” and all other settings were identical to those in Experiment I. Figures 5E–H present the results for path planning using the spatial concepts. Although SpCoSLAM could not reach the waypoint and goal in the map of Figure 5F, SpCoTMHP could estimate the path to reach the goal via the waypoint in the maps in Figures 5G, H. The learning with reverse replay in the map of Figure 5D shortened the additional route that would have resulted from the transition bias between places during learning in the map of Figure 5C. The failure observed in Figure 5F with SpCoNavi using waypoints is primarily attributed to the inputs with names of the given locations, regardless of these being waypoints or goals, in the bag-of-words format. The results revealed that the proposed method performs hierarchical path planning accurately, although the learning results are incomplete, as shown in Table 6. As a reference, the inference times for path planning were
6 Conclusion
We achieved topometric semantic mapping based on multimodal observations and hierarchical path planning through waypoint-guided instructions. The experimental results demonstrated improved performance for spatial concept learning and path planning in both simulated and real-world environments. Additionally, the approximate inference achieved high computational efficiency regardless of the model complexity.
Although these are encouraging results, our study has a few limitations as follows:
1. Scalability: The experiments assumed a single waypoint; however, the proposed method can theoretically handle multiple waypoints. Although the computational complexity increases with the topological planning horizon
2. Instruction variability: A typical instruction representation was used in the experiment. As a preprocessing step, LLMs can be used to handle instruction variability (Shah et al., 2022).
3. Redundant waypoints: Our approach may require passing through redundant waypoints, even if visiting the waypoint itself is unnecessary. For instance, in Figure 5, if it were possible to directly specify “the break room next to the white shelf,” there would be no need to pass by the white shelf as a waypoint. In such cases, extending the system to an open-vocabulary LLM-based semantic map could provide a viable solution.
4. Path restrictions: The paths generated by the proposed model are restricted by the transition probabilities between the locations encountered during training. In contrast, the model by Banino et al. (2018) can navigate through paths that are not traversed during training. Exploring the integration of such vector-based navigation techniques with our spatial concept-based approach could potentially enable shorter navigation while enhancing the model’s flexibility and robustness.
Future research on the proposed approach will therefore include utilizing common-sense reasoning (Hasegawa et al., 2023), such as foundation models and transfer of knowledge (Katsumata et al., 2020) with respect to the spatial adjacencies across multiple environments. In this study, we trained the model using the procedure described in Section 3.2. Simultaneous and online learning for the entire model can also be realized with particle filters (Taniguchi et al., 2017). The proposed method was found to be computationally efficient, thus rendering it potentially applicable to online path planning, such as model predictive control (Stahl and Hauth, 2011; Li et al., 2019). Additionally, the proposed model has the potential for visual navigation and generation of linguistic path explanations through cross-modal inference by the robot.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
AT: conceptualization, investigation, methodology, validation, visualization, writing–original draft, writing–review and editing, data curation, and funding acquisition. SI: writing–review and editing. TT: writing–review and editing and funding acquisition.
Funding
The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was partially supported by JST CREST (grant no. JPMJCR15E3); the AIP Challenge Program, JST Moonshot Research & Development Program (grant no. JPMJMS 2011); and JSPS KAKENHI (grant nos JP20K19900, JP21H04904, and JP23K16975).
Acknowledgments
The authors thank Cyrill Stachniss for providing the albert-b-laser-vision dataset. The authors also thank Kazuya Asada and Keishiro Taguchi for providing virtual home environments and training datasets for the spatial concepts in the SIGVerse simulator.
Conflict of interest
The authors declare that the research was conducted without any commercial or financial relationships that may be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frobt.2024.1291426/full#supplementary-material
Footnotes
1Alternatively, learning can be realized by active exploration based on generating questions or image captioning (Mokady et al., 2021) for the user (Ishikawa et al., 2023; Taniguchi et al., 2023). For example, the robot asks questions such as “What kind of place is this?” to the users.
2The source code is available at https://github.com/a-taniguchi/SpCoTMHP.git.
3Three-dimensional (3D) home environment models are available at https://github.com/a-taniguchi/SweetHome3D_rooms.
4This means a one-sample approximation to the candidate waypoints for the partial path. A related description can be found in Section 3.4. A one-sample approximation will be sufficient if the Gaussian distributions representing the locations and their transitions are obtained accurately.
5A video of the robot simulation moving along the estimated path is available at https://youtu.be/w8vfEPtnWEg.
6The dataset is available at https://dspace.mit.edu/handle/1721.1/62291.
References
Ahn, M., Brohan, A., Brown, N., Chebotar, Y., Cortes, O., David, B., et al. (2022). Do as I can, not as I say: grounding language in robotic affordances. arXiv Prepr. doi:10.48550/arxiv.2204.01691
Anderson, P., Chang, A., Chaplot, D. S., Dosovitskiy, A., Gupta, S., Koltun, V., et al. (2018a). On evaluation of embodied navigation agents. arXiv preprint.
Anderson, P., Wu, Q., Teney, D., Bruce, J., Johnson, M., Sünderhauf, N., et al. (2018b). “Vision-and-language navigation: interpreting visually-grounded navigation instructions in real environments,” in Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), 3674–3683.
Banino, A., Barry, C., Uria, B., Blundell, C., Lillicrap, T., Mirowski, P., et al. (2018). Vector-based navigation using grid-like representations in artificial agents. Nature 557, 429–433. doi:10.1038/s41586-018-0102-6
Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D., Dhariwal, P., et al. (2020). Language models are few-shot learners. Adv. neural Inf. Process. Syst. 33, 1877–1901. doi:10.48550/arxiv.2005.14165
Chen, B., Xia, F., Ichter, B., Rao, K., Gopalakrishnan, K., Ryoo, M. S., et al. (2023). Open-vocabulary queryable scene representations for real world planning. Proc. - IEEE Int. Conf. Robotics Automation 2023-May, 11509–11522. doi:10.1109/ICRA48891.2023.10161534
Chen, K., Chen, J. K., Chuang, J., Vázquez, M., and Savarese, S. (2021). “Topological planning with transformers for Vision-and-language navigation,” in Proceedings of the IEEE computer society conference on computer vision and pattern recognition (Nashville, TN, USA), 11271–11281. doi:10.1109/CVPR46437.2021.01112
Coradeschi, S., and Saffiotti, A. (2003). An introduction to the anchoring problem. Robotics Aut. Syst. 43, 85–96. doi:10.1016/S0921-8890(03)00021-6
[Dataset] Haarnoja, R., Hartikainen, K., Abbeel, P., and Levine, S. (2018). Latent space policies for hierarchical reinforcement learning.
Doucet, A., De Freitas, N., Murphy, K., and Russell, S. (2000). “Rao-Blackwellised particle filtering for dynamic Bayesian networks,” in Proceedings of the 16th conference on uncertainty in artificial intelligence (San Francisco, CA: Morgan Kaufmann Publishers Inc.), 176–183. doi:10.1007/978-1-4757-3437-9_24
Firoozi, R., Tucker, J., Tian, S., Majumdar, A., Sun, J., Liu, W., et al. (2023). Foundation models in robotics: applications, challenges, and the future. arXiv preprint arXiv:2312.07843.
Foster, D. J., and Wilson, M. A. (2006). Reverse replay of behavioural sequences in hippocampal place cells during the awake state. Nature 440, 680–683. doi:10.1038/nature04587
Galindo, C., Saffiotti, A., Coradeschi, S., Buschka, P., Fernández-Madrigal, J. A., and González, J. (2005). “Multi-hierarchical semantic maps for mobile robotics,” in 2005 IEEE/RSJ international conference on intelligent robots and systems, IROS, 2278–2283doi. doi:10.1109/IROS.2005.1545511
Garg, S., Sünderhauf, N., Dayoub, F., Morrison, D., Cosgun, A., Carneiro, G., et al. (2020). Semantics for robotic mapping, perception and interaction: a survey. Found. Trends® Robotics 8, 1–224. doi:10.1561/2300000059
Gildea, D., and Hofmann, T. (1999). “Topic-based language models using EM,” in Proceedings of the European conference on speech communication and technology (EUROSPEECH).
Gomez, C., Fehr, M., Millane, A., Hernandez, A. C., Nieto, J., Barber, R., et al. (2020). “Hybrid topological and 3D dense mapping through autonomous exploration for large indoor environments,” in Proceedings of the IEEE international conference on robotics and automation (ICRA), 9673–9679. doi:10.1109/ICRA40945.2020.9197226
Grisetti, G., Stachniss, C., and Burgard, W. (2007). Improved techniques for grid mapping with rao-blackwellized particle filters. IEEE Trans. Robotics 23, 34–46. doi:10.1109/tro.2006.889486
Gu, J., Stefani, E., Wu, Q., Thomason, J., and Wang, X. E. (2022). Vision-and-language navigation: a survey of tasks, methods, and future directions. Proc. Annu. Meet. Assoc. Comput. Linguistics 1, 7606–7623. doi:10.18653/V1/2022.ACL-LONG.524
Hasegawa, S., Taniguchi, A., Hagiwara, Y., El Hafi, L., and Taniguchi, T. (2023). “Inferring place-object relationships by integrating probabilistic logic and multimodal spatial concepts,” in 2023 IEEE/SICE international symposium on system integration (Atlanta, GA: SII 2023). doi:10.1109/SII55687.2023.10039318
Hiller, M., Qiu, C., Particke, F., Hofmann, C., and Thielecke, J. (2019). “Learning topometric semantic maps from occupancy grids,” in Proceedings of the IEEE/RSJ international conference on intelligent robots and systems (IROS). Venetian Macao, Macau (Piscataway, New Jersey: IEEE), 4190–4197. doi:10.1109/IROS40897.2019.8968111
Holte, R. C., Perez, M. B., Zimmer, R. M., and MacDonald, A. J. (1996). Hierarchical A*: searching abstraction hierarchies efficiently. Proc. Natl. Conf. Artif. Intell. 1, 530–535.
Huang, C., Mees, O., Zeng, A., and Burgard, W. (2023). “Visual Language maps for robot navigation,” in Proceedings of the IEEE international conference on robotics and automation (ICRA).
Hubert, L., and Arabie, P. (1985). Comparing partitions. J. Classif. 2, 193–218. doi:10.1007/bf01908075
Inamura, T., and Mizuchi, Y. (2021). SIGVerse: a cloud-based vr platform for research on multimodal human-robot interaction. Front. Robotics AI 8, 549360. doi:10.3389/frobt.2021.549360
Ishikawa, T., Taniguchi, A., Hagiwara, Y., and Taniguchi, T. (2023). “Active semantic mapping for household robots: rapid indoor adaptation and reduced user burden,” in 2023 IEEE international conference on systems, man, and cybernetics (SMC).
Johnson, M. J., and Willsky, A. S. (2013). Bayesian nonparametric hidden semi-markov models. J. Mach. Learn. Res. 14, 673–701.
Karaoğuz, H., Bozma, H. I. I., Karao, H., and Bozma, H. I. I. (2016). An integrated model of autonomous topological spatial cognition. Aut. Robots 40, 1379–1402. doi:10.1007/s10514-015-9514-4
Katsumata, Y., Taniguchi, A., El Hafi, L., Hagiwara, Y., and Taniguchi, T. (2020). “SpCoMapGAN: spatial concept formation-based semantic mapping with generative adversarial networks,” in Proceedings of the IEEE/RSJ international conference on intelligent robots and systems (IROS) (Las Vegas, USA: Institute of Electrical and Electronics Engineers Inc.), 7927–7934. doi:10.1109/IROS45743.2020.9341456
Kinose, A., and Taniguchi, T. (2020). Integration of imitation learning using GAIL and reinforcement learning using task-achievement rewards via probabilistic graphical model. Adv. Robot. 34, 1055–1067. doi:10.1080/01691864.2020.1778521
Kostavelis, I., Charalampous, K., Gasteratos, A., and Tsotsos, J. K. (2016). Robot navigation via spatial and temporal coherent semantic maps. Eng. Appl. Artif. Intell. 48, 173–187. doi:10.1016/j.engappai.2015.11.004
Kostavelis, I., and Gasteratos, A. (2015). Semantic mapping for mobile robotics tasks: a survey. Robotics Aut. Syst. 66, 86–103. doi:10.1016/j.robot.2014.12.006
Krantz, J., Wijmans, E., Majumdar, A., Batra, D., and Lee, S. (2020). Beyond the nav-graph: vision-and-language navigation in continuous environments. Tech. Rep., 104–120. doi:10.1007/978-3-030-58604-1_7
Kulkarni, T. D., Narasimhan, K. R., Saeedi, A., and Tenenbaum, J. B. (2016). “Hierarchical deep reinforcement learning: integrating temporal abstraction and intrinsic motivation,” in Proceedings of the advances in neural information processing systems (NeurIPS), 3682–3690.
Kvalseth, T. O. (1987). Entropy and correlation: some comments. IEEE Trans. Syst. Man, Cybern. 17, 517–519. doi:10.1109/tsmc.1987.4309069
Levine, S. (2018). Reinforcement learning and control as probabilistic inference: tutorial and review. Tech. Rep. doi:10.48550/arXiv.1805.00909
Li, N., Girard, A., and Kolmanovsky, I. (2019). Stochastic predictive control for partially observable Markov decision processes with TimeJoint chance constraints and application to autonomous vehicle control. J. Dyn. Syst. Meas. Control, Trans. ASME 141. doi:10.1115/1.4043115
Luperto, M., and Amigoni, F. (2018). Predicting the global structure of indoor environments: a constructive machine learning approach. Aut. Robots 43, 813–835. doi:10.1007/s10514-018-9732-7
Mokady, R., Hertz, A., and Bermano, A. H. (2021). ClipCap: CLIP prefix for image captioning. arXiv preprint arXiv:2111.09734. doi:10.48550/arxiv.2111.09734
Montemerlo, M., Thrun, S., Koller, D., and Wegbreit, B. (2003). “FastSLAM 2.0: an improved particle filtering algorithm for simultaneous localization and mapping that provably converges,” in Proceedings of the international joint conference on artificial intelligence (IJCAI) (Acapulco, Mexico), 1151–1156.
Neubig, G., Mimura, M., Mori, S., and Kawahara, T. (2012). Bayesian learning of a language model from continuous speech. IEICE Trans. Inf. Syst. 95, 614–625. doi:10.1587/transinf.e95.d.614
Niijima, S., Umeyama, R., Sasaki, Y., and Mizoguchi, H. (2020). “City-scale grid-topological hybrid maps for autonomous mobile robot navigation in urban area,” in IEEE international conference on intelligent robots and systems, 2065–2071. doi:10.1109/IROS45743.2020.9340990
Radford, A., Kim, J. W., Hallacy, C., Ramesh, A., Goh, G., Agarwal, S., et al. (2021). Learning transferable visual models from natural language supervision. Proc. Mach. Learn. Res. 139, 8748–8763.
Rangel, J. C., Martínez-Gómez, J., García-Varea, I., and Cazorla, M. (2017). LexToMap: lexical-based topological mapping. Adv. Robot. 31, 268–281. doi:10.1080/01691864.2016.1261045
Rosinol, A., Violette, A., Abate, M., Hughes, N., Chang, Y., Shi, J., et al. (2021). Kimera: from SLAM to spatial perception with 3D dynamic scene graphs. Int. J. Robotics Res. 40, 1510–1546. doi:10.1177/02783649211056674
Shafiullah, N. M. M., Paxton, C., Pinto, L., Chintala, S., Szlam, A., Mahi)Shafiullah, N., et al. (2023). CLIP-fields: weakly supervised semantic fields for robotic memory. Robotics Sci. Syst. doi:10.15607/rss.2023.xix.074
Shah, D., Osinski, B., Ichter, B., and Levine, S. (2022). “LM-nav: robotic navigation with large pre-trained models of language, vision, and action,” in Conference on robot learning (CoRL).
Shatkay, H., and Kaelbling, L. P. (2002). Learning geometrically-constrained Hidden Markov models for robot navigation: bridging the topological-geometrical gap. J. Artif. Intell. Res. 16, 167–207. doi:10.1613/jair.874
Sousa, Y, C. N., and Bassani, F. (2022). Topological semantic mapping by consolidation of deep visual features. IEEE Robotics Automation Lett. 7, 4110–4117. doi:10.1109/LRA.2022.3149572
Stahl, D., and Hauth, J. (2011). PF-MPC: particle filter-model predictive control. Syst. Control Lett. 60, 632–643. doi:10.1016/j.sysconle.2011.05.001
Stein, G. J., Bradley, C., Preston, V., and Roy, N. (2020). Enabling topological planning with monocular vision. Proceedings of the IEEE international conference on robotics and automation (ICRA) , 1667–1673. doi:10.1109/ICRA40945.2020.9197484
Taniguchi, T., Mochihashi, D., Nagai, T., Uchida, S., Inoue, N., Kobayashi, I., et al. (2019). Survey on frontiers of language and robotics. Adv. Robot. 33, 700–730. doi:10.1080/01691864.2019.1632223
Taniguchi, A., Hagiwara, Y., Taniguchi, T., and Inamura, T. (2017). “Online spatial concept and lexical acquisition with simultaneous localization and mapping,” in Proceedings of the IEEE/RSJ international conference on intelligent robots and systems (IROS), 811–818. doi:10.1109/IROS.2017.8202243
Taniguchi, A., Hagiwara, Y., Taniguchi, T., and Inamura, T. (2020a). Improved and scalable online learning of spatial concepts and language models with mapping. Aut. Robots 44, 927–946. doi:10.1007/s10514-020-09905-0
Taniguchi, A., Hagiwara, Y., Taniguchi, T., and Inamura, T. (2020b). Spatial concept-based navigation with human speech instructions via probabilistic inference on bayesian generative model. Adv. Robot. 34, 1213–1228. doi:10.1080/01691864.2020.1817777
Taniguchi, A., Tabuchi, Y., Ishikawa, T., Hafi, L. E., Hagiwara, Y., and Taniguchi, T. (2023). Active exploration based on information gain by particle filter for efficient spatial concept formation. Adv. Robot. 37, 840–870. doi:10.1080/01691864.2023.2225175
Taniguchi, A., Taniguchi, T., and Inamura, T. (2016a). Spatial concept acquisition for a mobile robot that integrates self-localization and unsupervised word discovery from spoken sentences. IEEE Trans. Cognitive Dev. Syst. 8, 285–297. doi:10.1109/TCDS.2016.2565542
Taniguchi, T., Nagai, T., Nakamura, T., Iwahashi, N., Ogata, T., and Asoh, H. (2016b). Symbol emergence in robotics: a survey. Adv. Robot. 30, 706–728. doi:10.1080/01691864.2016.1164622
Taniguchi, T., Nakamura, T., Suzuki, M., Kuniyasu, R., Hayashi, K., Taniguchi, A., et al. (2020c). Neuro-SERKET: development of integrative cognitive system through the composition of deep probabilistic generative models. New Gener. Comput. 38, 23–48. doi:10.1007/s00354-019-00084-w
Taniguchi, T., Piater, J., Worgotter, F., Ugur, E., Hoffmann, M., Jamone, L., et al. (2019). Symbol emergence in cognitive developmental systems: a survey. IEEE Trans. Cognitive Dev. Syst. 11, 494–516. doi:10.1109/TCDS.2018.2867772
Vemprala, S., Bonatti, R., Bucker, A., and Kapoor, A. (2023). ChatGPT for robotics: design principles and model abilities. Microsoft Auton. Syst. Robot. Res. 2, 20. doi:10.48550/arXiv.2306.17582
Viterbi, A. (1967). Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans. Inf. Theory 13, 260–269. doi:10.1109/tit.1967.1054010
Zeng, F., Gan, W., Wang, Y., Liu, N., and Yu, P. S. (2023). Large Language models for robotics: a survey. arXiv preprint arXiv:2311.07226.
Keywords: control as probabilistic inference, language navigation, hierarchical path planning, probabilistic generative model, semantic map, topological map
Citation: Taniguchi A, Ito S and Taniguchi T (2024) Hierarchical path planning from speech instructions with spatial concept-based topometric semantic mapping. Front. Robot. AI 11:1291426. doi: 10.3389/frobt.2024.1291426
Received: 09 September 2023; Accepted: 20 June 2024;
Published: 01 August 2024.
Edited by:
Malte Schilling, Bielefeld University, GermanyReviewed by:
Wataru Noguchi, Hokkaido University, JapanWagner Tanaka Botelho, Federal University of ABC, Brazil
Copyright © 2024 Taniguchi, Ito and Taniguchi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Akira Taniguchi, YS50YW5pZ3VjaGlAZW0uY2kucml0c3VtZWkuYWMuanA=
 Akira Taniguchi
Akira Taniguchi Shuya Ito
Shuya Ito Tadahiro Taniguchi
Tadahiro Taniguchi