Fine-grained similarity semantic preserving deep hashing for cross-modal retrieval

Cross-modal hashing methods have received wide attention in cross-modal retrieval owing to their advantages in computational efficiency and storage cost. However, most existing deep cross-modal hashing methods cannot employ both intra-modal and inter-modal similarities to guide the learning of hash codes and ignore the quantization loss of hash codes, simultaneously. To solve the above problems, we propose a fine-grained similarity semantic preserving deep hashing (FSSPDH) for cross-modal retrieval. Firstly, this proposed method learns different hash codes for different modalities to preserve the intrinsic property of each modality. Secondly, the fine-grained similarity matrix is constructed by using labels and data features, which not only maintains the similarity between and within modalities. In addition, quantization loss is used to learn hash codes and thus effectively reduce information loss caused during the quantization procedure. A large number of experiments on three public datasets demonstrate the advantage of the proposed FSSPDH method.

1 Introduction

As electronic technology and the Internet have advanced, the amount of multimedia data, such as images, texts, audio, and video, has experienced rapid growth. Therefore, how to effectively implement cross-modal retrieval has become a hot research field. However, due to the differences in data distribution and feature representation between different modalities, it is a huge challenge in cross-modal retrieval to narrow the semantic gap between multimodal data. Generally, the goal of cross-modal retrieval is to map the original data into a common potential space to maintain the similarity structure of the original features and find the most similar samples in the new feature space [1]. In addition, hashing technology can significantly reduce storage space and computational complexity because it only requires binary operation. Therefore, it becomes an effective way to solve cross-modal retrieval of massive data [2–4].

Cross-modal hashing is generally divided into two main categories, which are supervised hashing and unsupervised hashing. The unsupervised hashing [5,6] aims to project data features into a common feature space to reduce the difference between modalities. The supervised hashing methods [7,8] use label information to further enhance the semantic correlation between cross-modal data. The use of label information significantly narrows the gap between modalities and achieves excellent retrieval performance. Since deep learning has demonstrated its strong advantage in various fields, many deep cross-modal hashing methods have been proposed in recent years [9–11]. Tu et al. [12] proposed an end-to-end deep cross-modal hashing method, which obtains the unified hash codes of the training and the query samples through the joint learning of hash codes and hash functions. Self-supervised adversarial hashing (SSAH) [13] adopts two adversarial networks to jointly model semantic features of different modalities and then utilizes their semantic correlations to generate binary hash codes. At present, deep hashing methods have achieved excellent performances in cross-modal retrieve tasks, but there are still some issues to be solved urgently: 1) Most existing deep cross-modal hashing methods ignore the intra-modal and inter-modal similarities to guidance the hash code learning; 2) Existing hashing methods mainly focus on the hash code generation stage, and thus hash representations with less semantic information and spatial correlation cannot generate optimal hash codes; 3) Many methods often fail to consider the quantization loss of hash codes, resulting in the loss of semantic information during hash code learning.

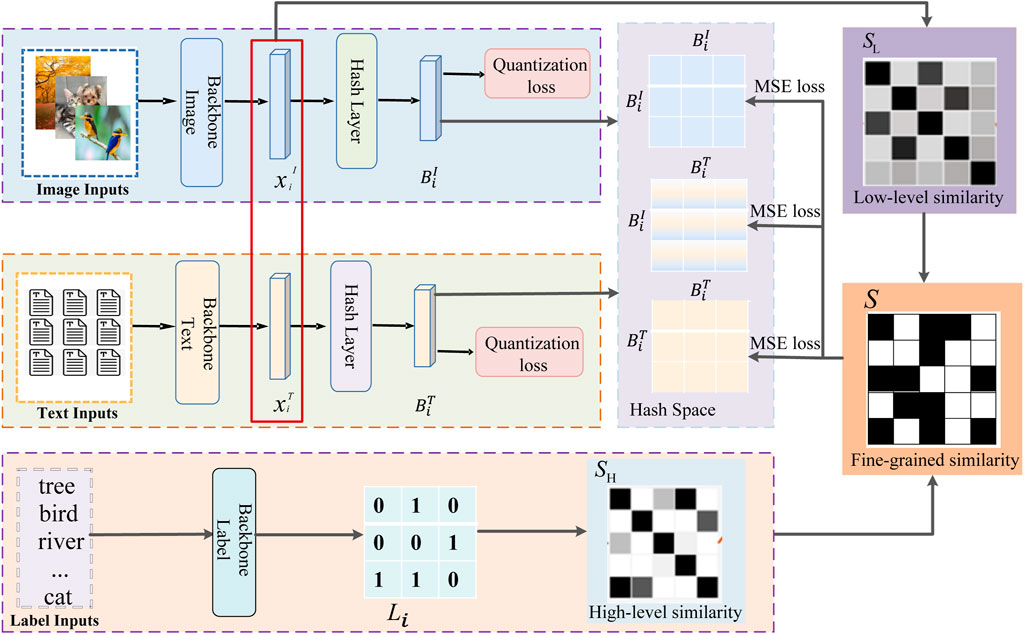
To solve the above problems, we propose a fine-grained similarity semantic preserving deep hashing (FSSPDH) method for cross-modal retrieval tasks. Figure 1 shows the framework of our proposed FSSPDH method. The main contributions of this work are given as follows.

1) The proposed FSSPDH approach unifies data feature extraction and hash code learning into an end-to-end deep learning framework. It can learn different hash codes from different modalities and thus maintains the intrinsic property of each modality. In addition, the proposed method combines the high-level semantic similarity constructed with labels and the low-level semantic similarity constructed with features to construct a fine-grained similarity matrix. Compared with traditional similarity constraints, the fine-grained similarity can effectively maintain inter-modal and intra-modal similarities to explore the semantic relationship between modalities and instances.

2) Our FSSPDH method considers the quantization loss in hash code learning, which further reduces the information loss caused by the hash code quantization. The quantization loss can make the learned hash codes with more feature information obtain more discriminative hash codes.

3) Experimental results conducted on three widely used multimodal datasets indicate that our proposed FSSPDH method achieves higher accuracy in cross-modal retrieval tasks compared with other hashing methods.

FIGURE 1

FIGURE 1. The framework of the proposed FSSPDH approach.

The remaining parts of this paper are organized as follows: Section 2 reviews the related works of cross-modal hashing retrieval. In Section 3, we introduce our FSSPDH approach in detail. Section 4 describes the experimental results and their results. Finally, our work is drawn in Section 5.

2 Related work

At present, cross-modal hashing can be roughly divided into the unsupervised method and supervised method according to whether it uses supervised information. This section will give a brief overview of these two types of methods.

2.1 Unsupervised cross-modal hashing

Since most multimodal data from real life are unlabeled, it is unrealistic to consume significant labor and time to label these data. Therefore, unsupervised hashing methods have received extensive attention in cross-modal retrieval. These methods attempt to learn the correlation and underlying structure of multimodality data. They can be further divided into graph-based methods and matrix factorization-based methods. The former seeks to maintain the correlation of hash codes by constructing a similarity graph. Linear cross-modal hashing (LCMH) [14] uses an anchor graph to keep the similarity within and between models in Hamming space. Hetero-manifold regularisation (HMR) [15] constructs multiple sub-manifolds defined by homogeneous data with the help of supervision information and alleviates the integration complexity and heterogeneity problems. Fusion similarity hashing (FSH) [16] constructs an asymmetric graph to model the fusion similarity and then embeds it into the hash codes. However, matrix factorization-based methods can explore the correlation in multimodal data through the potential semantic space, which can avoid the high training complexity of calculating similarity graphs. Collective matrix factorization hashing (CMFH) [2] is a typical method based on matrix factorization, which learns the common representation from different modality data, and then quantizes it to obtain their hash codes. Collective reconstructive embedding (CRE) [17] employs different schema-specific modalities to handle heterogeneous data, which can dispose of the complex structural and heterogeneity of multi-modality data.

With the continuous development of deep learning, many deep hashing approaches have also been for unsupervised cross-modal retrieval. Liong et al. [18] proposed a three-layer neural network structure, which seeks multi-level nonlinear transformations to learn binary codes. Lin et al. [19] put forword to learn discriminative hash codes by introducing three criterion terms in the last layer of the network. Do et al. [20] designed a novel deep hashing network to efficiently learn hash codes by relaxing binary constraints. Similarity adaptive deep hashing (SADH) [21] alternately trains three modules: similarity graph updating, deep hashing model training and hash code optimization to obtain high-quality hash codes. Multi-pathway generative adversarial hashing (MGAH) [22] makes full use of the representation learning advantages of generative adversarial networks on unsupervised data to explore the latent manifold structure of cross-modal data. Deep graph-neighbor coherence preserving network (DGCPN) [23] was derived from the graph model to exploit the consistency of the neighbor graph by integrating the structure information between the data and its neighbors.

2.2 Supervised cross-modal hashing

Different from the aforementioned unsupervised hashing methods, supervised hashing methods try to fully exploit more semantic correlation from supervised information to improve retrieval accuracy. Cross-modality metric learning using similarity-sensitive hashing (CMSSH) [24] employs a binary classification approach to generate hash codes and employs an enhanced strategy to optimize the model. Supervised matrix factorization hashing (SMFH) [25] preserves the similarity by constructing an adjacency matrix and then employs relaxed discrete constraint to learn binary representation. Fast discrete cross-modal hashing (FDCH) [26] regresses category information to learn hash codes and hash functions. Liu et al; [27] proposed a universal and flexible cross-modal hashing framework, which can handle various cross-modal retrieval scenarios, including paired or unpaired multi-modal data retrieval and retrieval scenarios with equal or variable hash length coding. Different from the linear projection from Hamming space to label space, subspace relation in semantic labels for cross-modal hashing (SRLCH) [28] learns the linear transformation from label space to Hamming space by reverse learning. Its essence is to regard label information as advanced features and embeds it into hash codes.

Deep neural networks have also been widely used in supervised cross-modal retrieval due to their powerful arbitrary nonlinear representation capabilities. Deep cross-modal hashing (DCMH) [29] generates hash codes that preserve cross-modal similarity by imposing a negative log-likelihood loss in an end-to-end deep learning framework. Adversarial cross-modal retrieval (ACMR) [30] utilizes an adversarial learning classification approach to distinguish different modalities and generate binary hash codes. Cross-modal deep variational hashing (CMDVH) [31] put forward to a two-step framework to separate hash code learning and hash function generation. In the first step, CMDVH learns the unified hash codes of the image-text pairs in the database. Then it uses the learned unified hash codes to generate hash functions in the second step. Therefore, the learned hash function in the second stage cannot guide the optimization of the unified hash codes. Wang et al. [32] proposed a deep semantic reconstruction hash method with pairwise similarity-preserving quantitative constraints. This method embeds advanced semantic affinity in each data pair to learn compact binary codes.

3 Our proposed method

3.1 Notations

This proposed method adopts the batch strategy to train the model, where the variables are represented in a batch-wise manner. Specifically, let $\mathit{O}=\left\{{\mathit{o}}_1,{\mathit{o}}_2,\dots .,{\mathit{o}}_k\right\}$ represent k instances in each batch, where $o_i=\left[{\mathit{I}}_i,{\mathit{T}}_i\right]$ is the i-th image-text pair. $X_I\in {\mathbb{R}}^{k\times d_1}$ and $X_T\in {\mathbb{R}}^{k\times d_2}$ denote the feature matrices of I_i and T_i, respectively. Generally, the image feature dimension d₁ and the text feature dimension d₂ should satisfy d₁ ≠ d₂. Besides, let ${\mathit{B}}_I\in {\left\{-1,+1\right\}}^{k\times l}$ and ${\mathit{B}}_T\in {\left\{-1,+1\right\}}^{k\times l}$ represent the hash codes generated for image and text modality, respectively, where l is the hash code length. In addition, the label matrix is defined as L ∈ R^k×c, where c represents the total category number.

3.2 Framework of our fine-grained similarity semantic preserving deep hashingmethod

3.2.1 Deep hashing networks for image and text modalities

The framework of the FSSPDH method is shown in Figure 1, which mainly consists of two parts: image hashing network and text hashing network. This network model can not only extract feature representations containing more semantic information for the two modalities of images and text, but also establish semantic relationships between the two modalities through a semantic similarity matrix.

1) Image hashing network (ImgNet). As traditional SIFT features are not sufficient to capture the intrinsic semantic relationships of images, the proposed model follows previous work in extracting deep features from CNNs (pre-trained on ImageNet) to replace SIFT features. Thus, 4096-dimensional features are extracted from the fc7 layer (after ReLU) of AlexNet [33] as the image features for each input image block. Therefore, we use AlexNet as the backbone of ImgNet and replace the classifier layer fc8 of AlexNet with a new fc with l hidden units to generate a continuous representation $H_I\in {\mathbb{R}}^{k\times l}$.

2) Text hashing network (TxtNet). For the text modality, LDA (Latent Dirichlet Allocation) topic vectors or token features are as X_T. In addition, we use multilayer perceptron (MLP) as the backbone of TxtNet. Due to the diversity and complexity of raw text descriptions, we directly use topic vectors or label occurrence features as the input of the MLP and then have 4096 units in the first fc layer. Besides, the second fc layer with l units generates a continuous representation $H_T\in {\mathbb{R}}^{k\times l}$ and ReLU is used as the activation function.

3.2.2 Constructing fine-grained similarity matrix

To improve the retrieval performance of cross-modal hashing methods using supervised information, most methods usually adopt the labels to construct a high-level semantic similarity matrix. Specifically, the high-level semantic similarity $S_H\in {\left\{-1,+1\right\}}^{k\times k}$ is computed by S_H = LL^T. If the i-th and j-th samples share at least one label, then ${\mathit{S}}_{H_{ij}}=1$, otherwise ${\mathit{S}}_{H_{ij}}=-1$. For multi-label datasets, samples with multiple labels should be more similar than these with only one label. However, the similarity only based on labels cannot effectively model this relationship, and a lot of useful information is discarded. To solve this issue, we construct a high-level similarity S_H and a low-level similarity S_L using labels and features, respectively. Therefore, samples with the same high-level similarity can be further ranked according to their low-level similarity. The construction of the fine-grained similarity can be expressed as:

$S=\mu S_H+\theta S_L,(1)$

where μ and θ are used to balance high-level similarity and low-level similarity. In addition, according to the fine-grained similarity fusion rules described in Ref. [34], the fine-grained similarity matrix can be represented as follows:

$S=\frac{\mu \mathit{L}{\mathit{L}}^T+{\theta }_{\mathit{1}}{\mathit{X}}_{\mathit{t}}{{\mathit{X}}_{\mathit{I}}}^T+{\theta }_{\mathit{2}}{\mathit{X}}_{\mathit{T}}{{\mathit{X}}_{\mathit{T}}}^T}{\mu +1},(2)$

where θ₁ and θ₂ are the weight parameters of image and text, respectively.

3.2.3 Hash codes learning

The goal of our FSSPDH method is to learn different hash codes for different modalities and establish relationships between modalities and instances by similarity matrix. FSSPDH seeks to map the features of instances to the Hamming space that preserves semantic similarity. In this space, the hash codes of samples from the same category should be similar. However, the hash codes of samples from different categories should also be different. Therefore, we attempt to preserve the semantic similarity between the hash codes learned from different modalities and the hash codes learned from the same instance of the same modality. Specifically, if S_ij = 1 indicates that the hash codes b_i and b_j are similar, the Hamming distance between b_i and b_j should be the minimum value of 0, which means that $b_i^T{b}_j=c$. Otherwise, the Hamming distance between b_i and b_j should be the minimum value of c, which means that $b_i^T{b}_j=0$. In the training stage, to calculate the gradient in backpropagation, we use the scaled tanh function to obtain approximate hash codes [35]. Therefore, B_I and B_T in the training phase can be calculated by the following formulas:

${\mathit{B}}_I=\tanh \left(\alpha {\mathit{H}}_I\right)\in {\left[-1,+1\right]}^{k\times l},(3)$

${\mathit{B}}_T=\tanh \left(\alpha {\mathit{H}}_T\right)\in {\left[-1,+1\right]}^{k\times l},(4)$

where α is a smooth parameter and needs to satisfy the following constraint: $\underset{\alpha \to 0}{\lim }\tanh (\alpha x)=\mathit{sgn}(x)$. sgn (⋅) is a symbolic function.

1) Fine-grained similarity semantic preserving learning. Our FDSSPH method considers both the inter-modality similarity and intra-modality similarity to guide the learning of hash codes. Therefore, we use Mean Square Error (MSE) to define the hash loss:

$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_s={‖\mathit{S}-\cos \left({\mathit{B}}_I,{\mathit{B}}_T\right)‖}_F^2+& {\beta }_1{‖\mathit{S}-\cos \left({\mathit{B}}_I,{\mathit{B}}_I\right)‖}_F^2+{\beta }_2{‖\mathit{S}-\cos \left({\mathit{B}}_T,{\mathit{B}}_T\right)‖}_F^2\hfill \\ \hfill s.t.{\mathit{B}}_I,{\mathit{B}}_T\in {\left[-1,+1\right]}^{k\times l},\hfill \end{array}(5)$

where β₁ and β₂ are the balance parameters of intra-modality similarity learning items.

2) Quantized loss learning. Hash loss defined by MSE can generate modal-specific hash representations B_I and B_T. However, there are differences between hash codes and hash representations. Therefore, we add a quantization loss to reduce the information loss from hash representations to hash codes. The quantization loss function can be defined as follows:

$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_q=& \lambda {\left(\left.‖\mathit{sgn}\left({\mathit{B}}_I\right)-{\mathit{B}}_I\right)\right.‖}_F^2+\left.{‖\mathit{sgn}\left({\mathit{B}}_T\right)-\left.{\mathit{B}}_T\right)‖}_F^2\right)\hfill \\ \hfill & s.t.{\mathit{B}}_I,{\mathit{B}}_T\in {\left[-1,+1\right]}^{k\times l},\hfill \end{array}(6)$

where λ is a non-negative parameter, and its role is to balance the weight of the quantization loss term.

3.2.4 Overall objective function

By integrating Eqs 5, 6 into a unified framework, the overall objective function of the proposed FSSPDH approach is given as follows:

$\begin{array}{c}\hfill \underset{B_I,B_T}{\min }\mathrm{\Gamma }={\mathrm{\Gamma }}_s+{\mathrm{\Gamma }}_q\\ \hfill & ={‖\mathit{S}-\cos \left({\mathit{B}}_I,{\mathit{B}}_T\right)‖}_F^2+{\beta }_1{‖\mathit{S}-\cos \left({\mathit{B}}_I,{\mathit{B}}_I\right)‖}_F^2+{\beta }_2{‖\mathit{S}-\cos \left({\mathit{B}}_T,{\mathit{B}}_T\right)‖}_F^2\hfill \\ \hfill & +\lambda {\left(\left.‖\mathit{sgn}\left({\mathit{B}}_I\right)-{\mathit{B}}_I\right)\right.‖}_F^2+\left.{‖\mathit{sgn}\left({\mathit{B}}_T\right)-\left.{\mathit{B}}_T\right)‖}_F^2\right)\hfill \\ \hfill & s.t.{\mathit{B}}_I,{\mathit{B}}_I\in {\left[-1,+1\right]}^{k\times l}.\hfill \end{array}(7)$

Algorithm 1 describes the overall training process of our proposed FSSPDH approach in detail.

Algorithm 1 FSSPDH.

Input: The feature matrices X_I and X_T, the label matrix L of the trainingset ${\left\{{\mathit{o}}_i=\left[{\mathit{I}}_i,{\mathit{T}}_i\right]\right\}}_{i=1}^n$, the hash code length l and the parameters ${\mathit{\psi }}_{{\theta }_1}$, ${\mathit{\psi }}_{{\theta }_2}$ of TxtNetnetwork and ImgNet network, the size k of training batch.

Output: Hash functions of image and text modalities.

Procedure:

1. Initialize t = 0.

Repeat

2 $t=t+1,\alpha =\sqrt{t}$

3 For all training samples enter the model do

4 Randomly select k samples from the training set.

5 Calculate the fine-grained similarity matrix S by Eq. 2.

6 Forward propagation $H_I={\mathit{\psi }}_{{\theta }_1}(X_I)$ and $H_T={\mathit{\psi }}_{{\theta }_2}(X_T)$.

7 Calculate hash representations B_I and B_T of image and text modalities by Eqs 3, 4.

8 Calculate overall objective function Γ by Eq. 7.

9 Update the whole parameters using back-propagating gradient by chain rule.

10 End for

Until convergence.

3.3 Out-of-sample problem

Since our proposed method can only obtain the hash codes of training data, it cannot effectively solve the out-of-samples problem. Therefore, it is still necessary to generate the hash codes of the query samples that are absent in the training set. To solve this problem, we can obtain the hash codes of query sample x_q by forward propagation

$b_q=\mathit{sgn}\left(\tanh \left({\mathit{\psi }}_{\theta }\left({\mathit{x}}_q\right)\right)\right).(8)$

4 Experiments

4.1 Datasets

The WIKI [36] dataset consists of 2,866 image-text pairs belonging to 10 different categories. For this experiment, the entire dataset was used as the retrieval dataset, with 2,173 pairs used for training and the remaining 693 pairs used for querying.

The MIRFLICKR-25K [37] dataset is a multi-label dataset obtained from the FLICKR website. In this experiment, 20015 samples were selected as experimental samples, each of which is tagged with at least one of the 24 categories. In this experiments, 2,243 samples were randomly selected as query samples, and the remaining 17772 samples were used as retrieval samples. From the retrieval samples, 5,000 samples were selected for training.

The NUSWIDE [38] dataset is a multimodal dataset consisting of 269648 image-text pairs, each of which corresponds to at least one or more of the 81 categories. Here, the most common 21 categories and their corresponding 195749 samples were selected to evaluate the effectiveness of the proposed FSSPDH approach. From these experimental data, 2000 samples were randomly selected as query samples, and the remaining samples were used as retrieval samples. Besides, 10000 samples were selected from the retrieval samples for traning model.

4.2 Baselines and implementation details

To demonstrate the superiority of the FDSSPH method, we compared it with several mainstream hashing methods, such as cross-view hashing (CVH) [39], joint and individual matrix factorization hashing (JIMFH) [40], discrete cross-modal hashing (DCH) [41], discrete latent factor model for cross-modal hashing (DLFH) [3], DCMH [29], SSAH [13], DCHUC [12], and deep joint-semantics reconstructing hashing (DJRSH) [42]. Besides, we evaluated these hashing methods on the WIKI, MIRFLICKR-25K and NUSWIDE datasets for both image-to-text (I2T) and text-to-image (T2I) retrieval tasks. The lengths of hash codes were set to 16, 32, 64, and 128 bits, respectively. The hyperparameters in the model were set to β₁ = 0.1, β₂ = 0.1 and λ = 0.01 according to our empirical knowledge.

4.3 Evaluation

In this paper, mean average precision (MAP) and TopN-precision curves are used to evaluate the performances of the proposed method and baseline methods. MAP is one of the most metrics in cross-modal retrieval tasks. Specially, the average precision of a given query sample and the returned results can be defined as follows:

$AP=\frac{1}{n}{\displaystyle \sum _{r=1}^R}P\left(r\right)\delta \left(r\right),(9)$

where n is the number of true samples returned. P(r) is the precision of the last r sample returned. If the returned sample is similar to the query sample, then δ(r) = 1, otherwise δ(r) = 0. In this experiment, R was empirically set to 1,000. In other words, the accuracy of the first 1,000 retrieved samples was reported. The MAP value is the average value of AP for all query samples, which is defined as follows:

$MAP=\frac{1}{Q}{\displaystyle \sum _{q=1}^Q}AP\left(x_q\right),(10)$

where Q is the number of query samples. In addition, TopN-precision is defined as similar for the first N instances retrieved from all queries within the Hamming distance. In order to return the results of a more accurate group, we set N to 1,000.

4.4 Experimental results and discussion

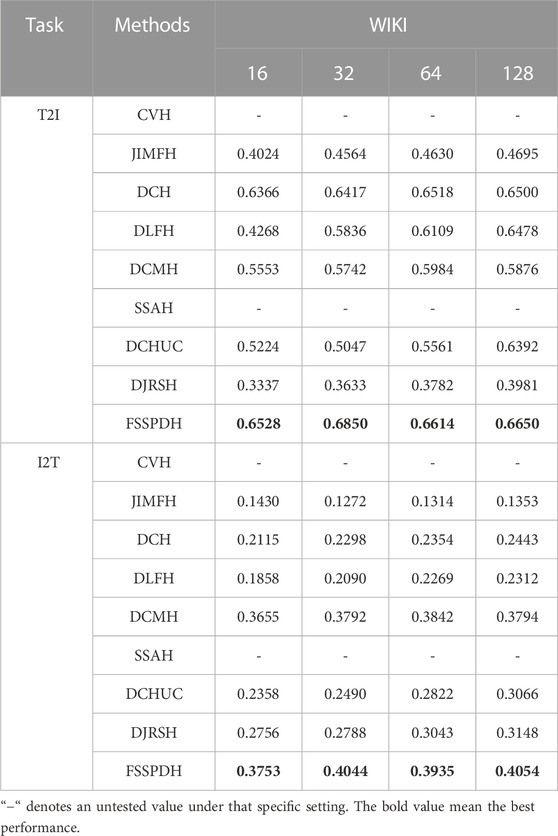
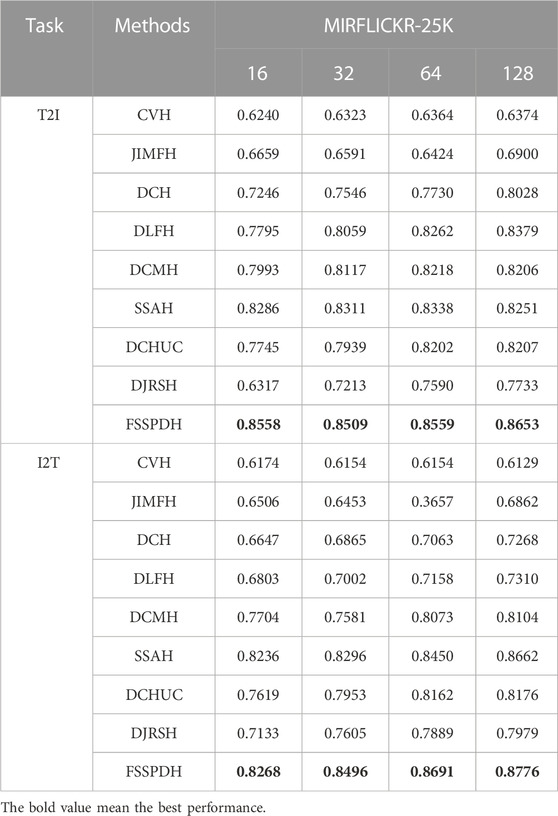
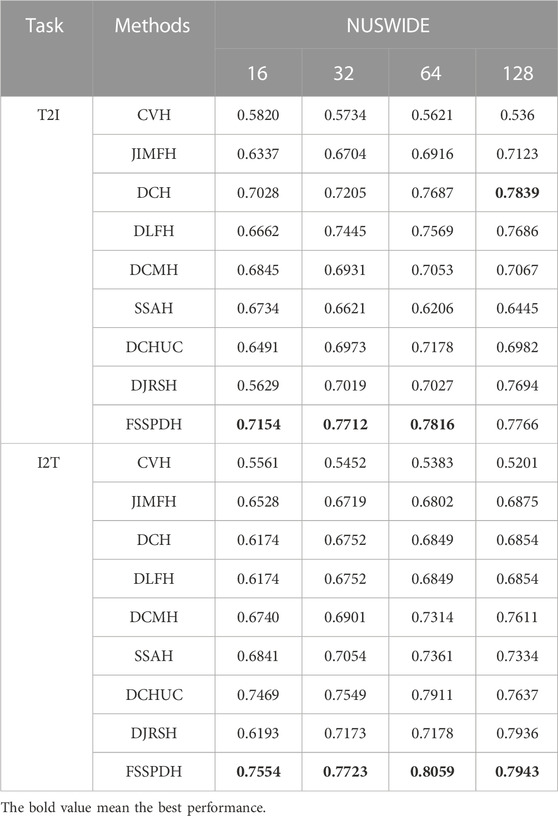
In this section, we conducted different retrieval experiments on the three datasets to evaluate the proposed FSSPDH method and its competitors. Table 1, Table 2, Table 3 shows the MAP values of the proposed method and baseline methods on different multimedia datasets.

TABLE 1

TABLE 1. The MAP values of cross-modal retrieval on WIKI dataset.

TABLE 2

TABLE 2. The MAP values of cross-modal retrieval on MIRFLICKR-25K dataset.

TABLE 3

TABLE 3. The MAP values of cross-modal retrieval on NUSWIDE dataset.

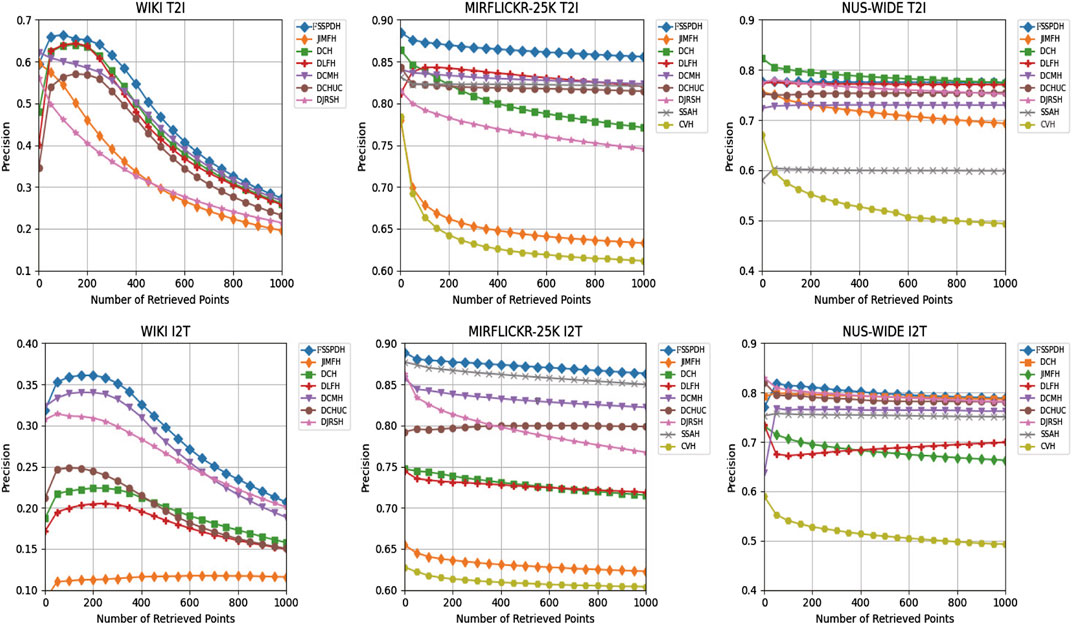
Table 1, Table 2, Table 3 show the mAP values of all methods on three datasets. Figure 2 shows the Top-N precision curves of the proposed approach and its competitors. Based on these retrieval results, we can draw some conclusions as follows.

1) It is clear from Table 1 that our proposed FSSPDH method outperforms other baseline methods on three multimedia datasets. Specifically, compared with the results with 128 bits, our FSSPDH method performs almost 2.2% better than the second best DLFH method in the T2I task on the WIKI dataset. On the MIRFLICKR dataset, our FSSPDH method performs nearly 2.0% better than the second best DLFH method. On the NUSWIDE dataset, the FSSPDH method has a performance improvement of almost 1.0% over the second-best method. Therefore, we can known from the retrieval results that the proposed FSSPDH method has greater advantages over other hashing methods in cross-modal retrieval tasks.

2) In addition, the experiments on the three different datasets also show that the FSSPDH approach improves the retrieval accuracy to some extent in the I2T task. Compared with the three data sets, we can find that the method on the MRIFLICKR-25K data set is higher than other two data sets. This is because the data distribution, division and size of the data set can affect the retrieval performance of the proposed method.

3) We can see that all methods cannot achieve excellent performances on the WIKI dataset. This is because this dataset contains fewer samples and lower data dimensionality for text modality features. Therefore, most deep hashing approaches cannot fully leverage the advantages of deep learning and thus lead to poor retrieval performance in general. However, our proposed FSSPDH method can still achieve the best performance among all cross-modal retrieval methods on this dataset.

4) It can be found from the experimental results that the performances of most methods can improve with the increase of hash code length. The main reason is that the longer hash codes usually contains more semantic information. However, the performance of some methods decreases when the hash code length ranges from 64 bits to 128 bits. The possible reason is that the learned hash codes contains more useless information, which leads to the decline of retrieval performance.

5) It is clear to see from Figure 2 that our FSSPDH method achieves the best performance among the compared methods from the perspective of TopN-precision. In addition, we can observe that the TopN-precision curve results are basically consistent with the MAP value results, as they are both calculated based on the Hamming distance. This indicates that our proposed FSSPDH method also achieves the best results in the Hamming ranking task.

6) We can find that the TopN-precision curves of all methods on three datasets show slightly different decreasing rates. Specifically, the WIKI dataset includes the least amount of data, and its curve decline rate is obviously higher than these of the other two datasets. Note that the NUSWIDE dataset contains the most data, so its TopN-precision curve is relatively flat. However, our proposed method considers the semantic similarity between and within modalities by constructing a fine-grained similarity matrix, thereby achieving the best results on three different scale datasets.

FIGURE 2

FIGURE 2. The TopN-precision curves of FSSPDH and its competitors on three datasets.

4.5 Ablation experiment and analysis

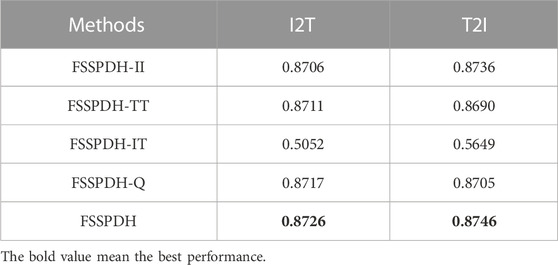
To verify the effectiveness of each component in the proposed FSSPDH approach, we constructed four variants of FSSPDH, i.e., FSSPDH-II, FSSPDH-TT, FSSPDH-IT, and FSSPDH-Q. FSSPDH-II was constructed by removing the intra-modal similarity learning for the image modality. FSSPDH-TT discarded the intra-modal similarity learning for the text modality. FSSPDH-IT removed the inter-modal similarity learning for both image and text modalities, while FSSPDH-Q discarded the hashing quantization loss term. These ablation experiments were conducted on the MIRFlickr dataset to validate the impact of each component on retrieval performance. Here, the hash code length was set to 128 bits in this experiments. Table 4 shows the retrieval performances of FSSPDH and its variants on two retrieval tasks.

TABLE 4

TABLE 4. Ablation results of our FSSPDH approach on the MIRFlickr dataset.

It can be seen from Table 4 that FSSPDH-IT cannot outperform other variants on different retrieval tasks, which indicates that inter-modal similarity learning is crucial for retrieval performance in our method. In addition, the performances of the FSSPDH-II, FSSPDH-TT, and FSSPDH-Q variants are also lower than that of FSSPDH in different retrieval tasks. It shows that both intra-modal similarity learning and hashing quantization loss can be beneficial in enhancing retrieval performance.

4.6 Parameter sensitivity analysis

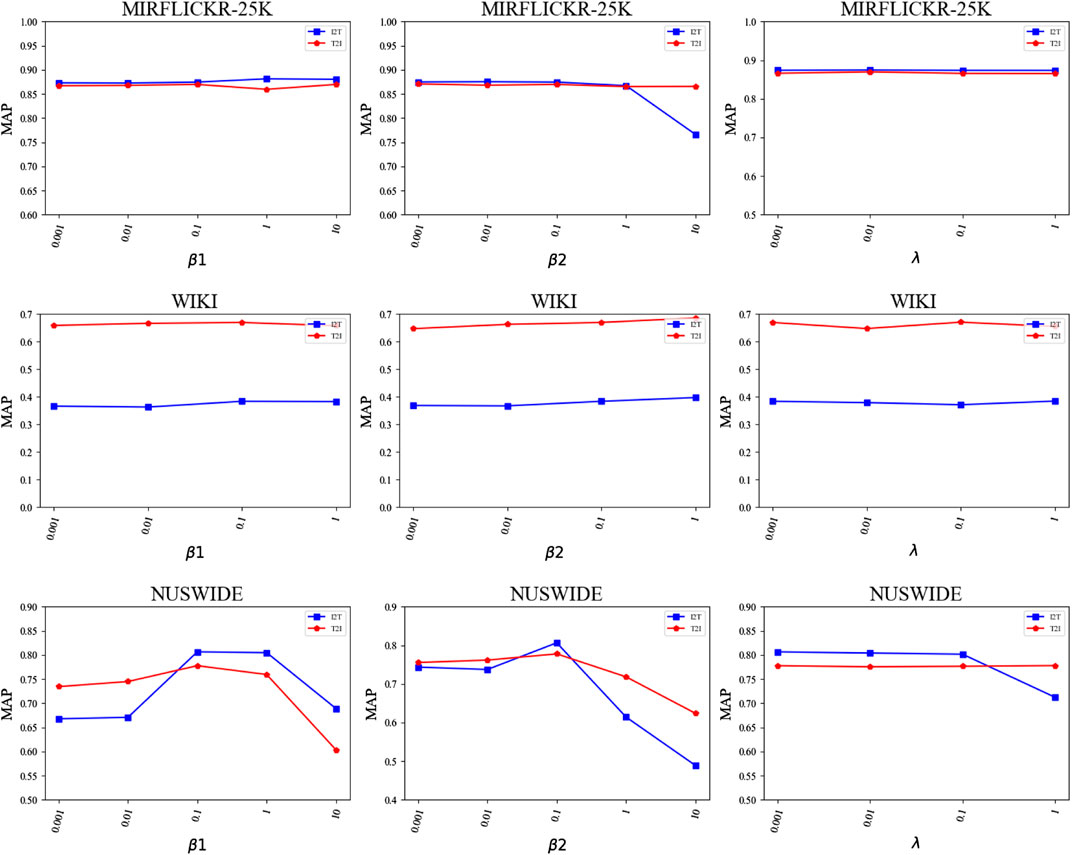
Our FSSPDH method mainly includes three hyperparameters: β₁, β₂ and λ. This subsection discusses the impact of different hyperparameter values in our proposed model. In this experiment, the length of the hash codes was designated as 128 bits. Specifically, we change the values of only one hyperparameter by fixing the values of the other two hyperparameters. Figure 3 plots the results of the proposed FSSPDH approach with different parameter settings on three datasets. We can see from Figure 3 that the performances of FSSPDH on the WIKI dataset and MIRFLICKR-25K dataset are relatively stable within a large range of hyperparameter values. Besides, our FSSPDH approach has fluctuated to a certain extent on the NUSWIDE dataset with different hyperparameter values. Fortunately, we can see that the FSSPDH approach can also obtain relatively stable performances within a certain range. Therefore, it can be found that our FSSPDH approach is insensitive to the hyperparameters from the parameter experiments.

FIGURE 3

FIGURE 3. The retrieval performances of the FSSPDH method with different parameter settings.

5 Conclusion

In this paper, we introduce a novel approach called fine-grained similarity semantic preserving deep hashing (FSSPDH) for cross-modal retrieval. Firstly, the FSSPDH approach attempts to learn a set of binary hash codes for each modality and thus effectively preserves the characteristics of each modality. In addition, our FSSPDH approach constructs a fine-grained semantic similarity matrix by using labels and features, which not only preserves the inter-modal similarity but also maintains the intra-modal similarity. Therefore, the fine-grained similarity preserving strategy is used to embed more semantic information into hash codes. Compared with other hashing methods, it can preserve the inter-modality similarity and maintain the semantic relationships between instances by the intra-modality similarity, simultaneously, thus narrowing the heterogeneous gap between different modalities. Additionally, to reduce the information loss from the continuous hash representation to discrete hash codes, our FSSPDH approach incorporates hash quantization loss to further improve the retrieval performance. A series of experimental results have demonstrated that the proposed FSSPDH method achieves superior performances in cross-modal retrieval tasks on different multimedia datasets.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, GL; methodology, QP; validation, GL, QP, DZ, and ZS; formal analysis, JY; writing—review and editing, ZS; investigation, ZS; resources, ZS All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China (61603159, 62162033) and Yunnan Foundation Research Projects (202201AT070154, 202101BE070001-056).

Conflict of interest

Author GL was employed by Yunnan Power Grid Corporation, China. Authors QP, DZ, and JY were employed by Electric Power Research Institute, Yunnan Power Grid Corporation, China.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kaur P, Pannu HS, Malhi AK. Comparative analysis on cross-modal information retrieval: A review. Comp Sci Rev (2021) 39:100336. doi:10.1016/j.cosrev.2020.100336

CrossRef Full Text | Google Scholar

2. Ding G, Guo Y, Zhou J. Collective matrix factorization hashing for multimodal data. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2014). p. 2075–82.

CrossRef Full Text | Google Scholar

3. Jiang Q-Y, Li W-J. Discrete latent factor model for cross-modal hashing. IEEE Trans Image Process (2019) 28:3490–501. doi:10.1109/tip.2019.2897944

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Shu Z, Yong K, Yu J, Gao S, Mao C, Yu Z. Discrete asymmetric zero-shot hashing with application to cross-modal retrieval. Neurocomputing (2022) 511:366–79. doi:10.1016/j.neucom.2022.09.037

CrossRef Full Text | Google Scholar

5. Song J, Yang Y, Yang Y, Huang Z, Shen HT. Inter-media hashing for large-scale retrieval from heterogeneous data sources. In: Proceedings of the 2013 ACM SIGMOD international conference on management of data (2013). p. 785–96.

CrossRef Full Text | Google Scholar

6. Zhou J, Ding G, Guo Y. Latent semantic sparse hashing for cross-modal similarity search. In: Proceedings of the 37th international ACM SIGIR conference on Research & development in information retrieval (2014). p. 415–24.

CrossRef Full Text | Google Scholar

7. Shu Z, Li L, Yu J, Zhang D, Yu Z, Wu X-J. Online supervised collective matrix factorization hashing for cross-modal retrieval. Appl intelligence (2022) 1–18. doi:10.1007/s10489-022-04189-6

CrossRef Full Text | Google Scholar

8. Shu Z, Yong K, Zhang D, Yu J, Yu Z, Wu X-J. Robust supervised matrix factorization hashing with application to cross-modal retrieval. Neural Comput Appl (2023) 35:6665–84. doi:10.1007/s00521-022-08006-6

CrossRef Full Text | Google Scholar

9. Deng C, Chen Z, Liu X, Gao X, Tao D. Triplet-based deep hashing network for cross-modal retrieval. IEEE Trans Image Process (2018) 27:3893–903. doi:10.1109/tip.2018.2821921

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Wang X, Zou X, Bakker EM, Wu S. Self-constraining and attention-based hashing network for bit-scalable cross-modal retrieval. Neurocomputing (2020) 400:255–71. doi:10.1016/j.neucom.2020.03.019

CrossRef Full Text | Google Scholar

11. Shu Z, Bai Y, Zhang D, Yu J, Yu Z, Wu X-J. Specific class center guided deep hashing for cross-modal retrieval. Inf Sci (2022) 609:304–18. doi:10.1016/j.ins.2022.07.095

CrossRef Full Text | Google Scholar

12. Tu R-C, Mao X-L, Ma B, Hu Y, Yan T, Wei W, et al. Deep cross-modal hashing with hashing functions and unified hash codes jointly learning. IEEE Trans Knowledge Data Eng (2020) 34:560–72. doi:10.1109/tkde.2020.2987312

CrossRef Full Text | Google Scholar

13. Li C, Deng C, Li N, Liu W, Gao X, Tao D. Self-supervised adversarial hashing networks for cross-modal retrieval. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2018). p. 4242–51.

CrossRef Full Text | Google Scholar

14. Zhu X, Huang Z, Shen HT, Zhao X. Linear cross-modal hashing for efficient multimedia search. In: Proceedings of the 21st ACM international conference on Multimedia (2013). p. 143–52.

CrossRef Full Text | Google Scholar

15. Zheng F, Tang Y, Shao L. Hetero-manifold regularisation for cross-modal hashing. IEEE Trans pattern Anal machine intelligence (2016) 40:1059–71. doi:10.1109/tpami.2016.2645565

CrossRef Full Text | Google Scholar

16. Liu H, Ji R, Wu Y, Huang F, Zhang B. Cross-modality binary code learning via fusion similarity hashing. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2017). p. 7380–8.

CrossRef Full Text | Google Scholar

17. Hu M, Yang Y, Shen F, Xie N, Hong R, Shen HT. Collective reconstructive embeddings for cross-modal hashing. IEEE Trans Image Process (2018) 28:2770–84. doi:10.1109/tip.2018.2890144

CrossRef Full Text | Google Scholar

18. Erin Liong V, Lu J, Wang G, Moulin P, Zhou J. Deep hashing for compact binary codes learning. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2015). p. 2475–83.

CrossRef Full Text | Google Scholar

19. Lin K, Lu J, Chen C-S, Zhou J. Learning compact binary descriptors with unsupervised deep neural networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2016). p. 1183–92.

CrossRef Full Text | Google Scholar

20. Do T-T, Doan A-D, Cheung N-M. Learning to hash with binary deep neural network. In: Computer Vision–ECCV 2016: 14th European Conference; October 11-14, 2016; Amsterdam, The Netherlands. Springer (2016). p. 219–34.

CrossRef Full Text | Google Scholar

21. Shen F, Xu Y, Liu L, Yang Y, Huang Z, Shen HT. Unsupervised deep hashing with similarity-adaptive and discrete optimization. IEEE Trans Pattern Anal Machine Intelligence (2018) 40:3034–44. doi:10.1109/tpami.2018.2789887

CrossRef Full Text | Google Scholar

22. Zhang J, Peng Y. Multi-pathway generative adversarial hashing for unsupervised cross-modal retrieval. IEEE Trans Multimedia (2019) 22:174–87. doi:10.1109/tmm.2019.2922128

CrossRef Full Text | Google Scholar

23. Yu J, Zhou H, Zhan Y, Tao D. Deep graph-neighbor coherence preserving network for unsupervised cross-modal hashing. Proc AAAI Conf Artif Intelligence (2021) 35:4626–34. doi:10.1609/aaai.v35i5.16592

CrossRef Full Text | Google Scholar

24. Bronstein MM, Bronstein AM, Michel F, Paragios N. Data fusion through cross-modality metric learning using similarity-sensitive hashing. In: 2010 IEEE computer society conference on computer vision and pattern recognition; 05 August 2010; San Francisco, CA, USA. IEEE (2010). p. 3594–601.

CrossRef Full Text | Google Scholar

25. Tang J, Wang K, Shao L. Supervised matrix factorization hashing for cross-modal retrieval. IEEE Trans Image Process (2016) 25:3157–66. doi:10.1109/tip.2016.2564638

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Liu X, Nie X, Zeng W, Cui C, Zhu L, Yin Y. Fast discrete cross-modal hashing with regressing from semantic labels. In: Proceedings of the 26th ACM international conference on Multimedia (2018). p. 1662–9.

CrossRef Full Text | Google Scholar

27. Liu X, Hu Z, Ling H, Cheung Y-m. Mtfh: A matrix tri-factorization hashing framework for efficient cross-modal retrieval. IEEE Trans Pattern Anal Machine Intelligence (2019) 43:964–81. doi:10.1109/tpami.2019.2940446

CrossRef Full Text | Google Scholar

28. Shen HT, Liu L, Yang Y, Xu X, Huang Z, Shen F, et al. Exploiting subspace relation in semantic labels for cross-modal hashing. IEEE Trans Knowledge Data Eng (2020) 33:3351–65. doi:10.1109/tkde.2020.2970050

CrossRef Full Text | Google Scholar

29. Jiang Q-Y, Li W-J. Deep cross-modal hashing. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2017). p. 3232–40.

CrossRef Full Text | Google Scholar

30. Wang B, Yang Y, Xu X, Hanjalic A, Shen HT. Adversarial cross-modal retrieval. In: Proceedings of the 25th ACM international conference on Multimedia (2017). p. 154–62.

CrossRef Full Text | Google Scholar

31. Erin Liong V, Lu J, Tan Y-P, Zhou J. Cross-modal deep variational hashing. In: Proceedings of the IEEE international conference on computer vision (2017). p. 4077–85.

CrossRef Full Text | Google Scholar

32. Wang Y, Ou X, Liang J, Sun Z. Deep semantic reconstruction hashing for similarity retrieval. IEEE Trans Circuits Syst Video Tech (2020) 31:387–400. doi:10.1109/tcsvt.2020.2974768

CrossRef Full Text | Google Scholar

33. Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Commun ACM (2017) 60:84–90. doi:10.1145/3065386

CrossRef Full Text | Google Scholar

34. Wang Y, Chen Z-D, Luo X, Xu X-S. A high-dimensional sparse hashing framework for cross-modal retrieval. IEEE Trans Circuits Syst Video Tech (2022) 32:8822–36. doi:10.1109/tcsvt.2022.3195874

CrossRef Full Text | Google Scholar

35. Li X, Hu D, Nie F. Deep binary reconstruction for cross-modal hashing. In: Proceedings of the 25th ACM international conference on Multimedia (2017). p. 1398–406.

CrossRef Full Text | Google Scholar

36. Pereira JC, Coviello E, Doyle G, Rasiwasia N, Lanckriet GR, Levy R, et al. On the role of correlation and abstraction in cross-modal multimedia retrieval. IEEE Trans pattern Anal machine intelligence (2013) 36:521–35.

Google Scholar

37. Huiskes MJ, Lew MS. The mir flickr retrieval evaluation. In: Proceedings of the 1st ACM international conference on Multimedia information retrieval (2008). p. 39–43.

CrossRef Full Text | Google Scholar

38. Chua T-S, Tang J, Hong R, Li H, Luo Z, Zheng Y. Nus-wide: A real-world web image database from national University of Singapore. In: Proceedings of the ACM international conference on image and video retrieval (2009). p. 1–9.

Google Scholar

39. Kumar S, Udupa R. Learning hash functions for cross-view similarity search. In: Twenty-second international joint conference on artificial intelligence (2011).

Google Scholar

40. Wang D, Wang Q, He L, Gao X, Tian Y. Joint and individual matrix factorization hashing for large-scale cross-modal retrieval. Pattern recognition (2020) 107:107479. doi:10.1016/j.patcog.2020.107479

CrossRef Full Text | Google Scholar

41. Xu X, Shen F, Yang Y, Shen HT, Li X. Learning discriminative binary codes for large-scale cross-modal retrieval. IEEE Trans Image Process (2017) 26:2494–507. doi:10.1109/tip.2017.2676345

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Su S, Zhong Z, Zhang C. Deep joint-semantics reconstructing hashing for large-scale unsupervised cross-modal retrieval. In: Proceedings of the IEEE/CVF international conference on computer vision (2019). p. 3027–35.

CrossRef Full Text | Google Scholar