ORIGINAL RESEARCH article

Front. Phys., 08 June 2022

Sec. Quantum Engineering and Technology

Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.896164

Unextendible Entangled Bases With a Fixed Schmidt Number Based on Generalized Weighing Matrices

  • 1. Department of Big Data, School of Science, Zhejiang University of Science and Technology, Hangzhou, China

  • 2. Department of Mathematics, College of Sciences, Yanbian University, Yanji, China

Article metrics

View details

1,2k

Views

394

Downloads

Abstract

We systematically study the constructions of unextendible entangled bases with a fixed Schmidt number k (UEBk) in a bipartite system . Motivated by the methods of [J. Phys. A 52 : 375,303, 2019], we construct (dd’ − v)-member UEBks in by using generalized weighing matrices and thus generalize the results of [arXiv: 1909.10043, 2020]. We also present the corresponding expressions of our constructions and graphically illustrate UEB3s in and .

1 Introduction

Entanglement is an essential resource of quantum information processing, and it presents the nature of quantum mechanics [1, 2]. It is also related to some fundamental problems in quantum mechanics such as reality and non-locality [3, 4]. Quantum entanglement has significant applications in many fields such as quantum teleportation [5], quantum dense coding [6], quantum tomography [7], and the mean kings problem [8].

In order to characterize quantum entanglement, the analysis of various bases in the state space has attracted extensive attention in recent years. The notion of unextendible product basis (UPB) in multipartite quantum systems has been deeply studied. The member of a UPB is not perfectly distinguishable by local positive-operator-valued measurements and classical communication, which shows the non-locality without entanglement [9]. As the generalization of UPB, the notion of unextendible maximally entangled basis (UMEB) has been proposed [10]. Since then, many results of UMEBs in arbitrary bipartite spaces are established: no UMEB in , 6-member UMEB in , 12-member UMEB in [10], 30-member UMEB in [11], d2-member UMEB in , and qd2-member UMEB in [12–14] and different members of UMEBs in [15–18].

In [19], Guo first proposed the unextendible entangled basis with a fixed Schmidt number k (UEBk) in ; thereafter, the concepts and constructions of entangled basis with Schmidt number k (EBk) and special entangled basis with Schmidt number k (SEBk) have been presented successively [20]. Later, Guo also generalized the construction of UEBk from bipartite systems to multipartite quantum systems [21].

Li et al [22] first constructed the SEBks in via some generalized weighing matrices, which is a breakthrough structure for dd’ is not the multiple of k. Furthermore, Wang [23] combines the decomposition of the whole matrix space and generalized weighing matrices to consrtuct the SUEBks, which provides a useful way to construct different members of UEBks in , but it still has some imperfections and unmentioned issues, such as the bounds of the space dimension, the order, and the concrete mathematical expression of the UEBks.

In this paper, we mainly focus on the construction of UEBks in bipartite systems. Motivatied by the method of [22, 23], using generalized weighing matrices, we provide flexible and diverse constructions of different members of UEBks. We first introduce some related notions and terminologies; then, we propose three different ways to construct (dd’ − v)-member UEBks in and present the corresponding mathematical expressions. We also give some examples of UEB3 in and .

2 Preliminaries

In order to better comprehend the notion of UEBk in , we first introduce the concept of EBk and SEBk in . In the sequel, we always assume that d ≤ d′.

The Schmidt number of a bipartite pure state , denoted by Sr (|ϕ⟩), is defined as the length of its Schmidt decomposition: if its Schmidt decomposition is , then its Schmidt number is k, that is, Sr (|ϕ⟩) = k. It is clear that Sr (|ϕ⟩) = rank (ρ1) = rank (ρ2), where ρi denotes the reduced state of the ith part of ρ = |ϕ⟩⟨ϕ|. If an orthonormal basis is constructed by such |ϕi⟩s, then it is called an entangled basis with Schmidt number k (EBk) [20]. Particularly, if it is an EBk and all the Schmidt coefficients of {|ϕi⟩}s equal to , then it is called a special entangled basis with Schmidt number k (SEBk). It is obvious that SEBk becomes a product basis (PB) when k = 1 and a maximally entangled basis (MEB) when k = d.

A set of states

is called an m-number unextendible entangled bases with Schmidt number

k

(UEB

k

) [

19

] if and only if

  • (i) Sr (|ϕi⟩) = k and |ϕi⟩, i = 1, 2, … , m are all entangled states;

  • (ii) ⟨ϕi|ϕj⟩ = δij;

  • (iii) if ⟨ϕi|ψ⟩ = 0 for all i = 1, 2, … , m, then Sr (|ϕi⟩) ≠ k.

Actually, there is a similar concept in matrix spaces [20]. Let {|k⟩} and {|ℓ′⟩} be the standard computational bases of and , respectively, and be an orthonormal basis of . Let Md×d′ be the Hilbert space of all d × d′ complex matrices equipped with the inner product defined by ⟨A|B⟩ = Tr (A†B) for any A, B ∈ Md×d′. If constitutes a Hilbert–Schmidt basis of Md×d′, where ⟨Ai|Aj⟩ = dδij, then there is a one-to-one correspondence between {|ϕi⟩} and {Ai} as follows [20]:

A set of

d

×

d

′ complex matrices {

Ai

:

i

= 1, 2,

…

,

n

,

n

≤

dd

′} is called an unextendible rank-

k

Hilbert–Schmidt basis of

Md×d′

[

24

] if and only if

  • (i) rank (Ai) = k for any i;

  • ;

  • (iii) if , i = 1, 2, … , n, then rank(B) ≠ k.

It turns out that {Ai: rank (Ai) = k} is an unextendible Hilbert–Schmidt basis of Md×d′ if and only if {ϕi} is a UEBk of . Therefore, the UEBk problem is equivalent to the unextendible rank-k Hilbert–Schmidt basis of the associated matrix space.

We next introduce the definition and properties of a generalized weighing matrix, which has been effectively used to construct SEBks in [22]. As a continuation, we will use it to construct UEBks in in this paper.

Definition 1:[22] A generalized weighing matrix is a square a × a matrix A all of whose non-zero entries are nth roots of unity such that AA† = kIa. It follows that is a unitary matrix so that AA† = kIa and every row and column of A has exactly k non-zero entries. k is called the weight, and n is called the order of A. Denoting the set of all such generalized weighing matrices by W(n, k, a).It is worth noting that the generalized weight matrix does not always exist; for the existence and detailed discussion of the generalized weight matrix, we can refer to Ref. [22].

Lemma 1:[22] Let a, b be two positive integers with a great common divisor being g. For any integers d, d′ ≥ max{a, b}, if g|dd’, then dd’ can be written as dd’ = sa + pb, where .

3 Three Kinds of (dd’ − v)-Member UEBks

Let Md×d′ be the Hilbert space of all d × d′ complex matrices, V be a subspace of Md×d′ such that each matrix in V is a d × d′ matrix ignoring v elements, depending on the position occupied by the ignored v elements: 1) all the ignored elements occupy N columns, 2) all the ignored elements occupy N rows, and 3) all the ignored elements occupy rows and columns; we construct three kinds of (dd’ − v)-member UEBks.

3.1 All the Ignored Elements Occupy N Columns

In this section, we first construct the (dd’ − v)-member UEBk in , in which all the v ignored elements occupied N columns in the matrix, and then present some examples of UEB3s in .

Theorem 1:

Let k be a positive integer, such that W(n, k, b) is non-empty, and gcd(k, b) = 1 (the greatest common divisor of k and b). Let V be a subspace of Md×d′ such that each matrix in V is a d × d′ matrix ignoring v elements which occupied N rows with N = 1, … , k − 1 and d − N ≥ b and dd’ − v = s ⋅ k + p ⋅ b with 1 ≤ v ≤ d′N. If min{d, d′}≥ max{k, b}, then there exists dd’ − v member UEBk in .

Proof. First, for different values of p and s, we construct different pure states as follows: when p ≥ 1 and s ≥ 1, set when s = 0, p ≥ 1, setwhen p = 0, s ≥ 1, setwhere ; means the t (0 ≤ t ≤ b − 1) row of the generalized weights matrix W (n, k, b), and sk − 1 + (l − s)b + u = c ⋅ (d − N + 1) + e = f ⋅ d′ + g; l ⋅ k + u = c ⋅ (d − N + 1) + e = f ⋅ d′ + g with 0 ≤ e < d, 0 ≤ g < d′. Also,withwhere C0 = 0, Cα = 1 denotes the ignored elements.

We next prove that all the above {|

ϕm.l

⟩} constitute a

dd

’ −

v

(1 ≤

v

≤

d

′

N

)-member UEB

k

in

:

  • (i) It is clear that Sr (|ϕl⟩) = k for any l, m, t.

  • (ii) Orthogonality.

According to the construction given by the above expression, the elements of each state lie in different rows and columns, so the proof of the orthogonality is as follows:

  • (iii) Unextendibility.

It is obvious that there are no UEBk in V⊥ since N < k.

In order to understand the above structure more intuitively, we give the following examples to illustrate it.

Example 1:Constructing 26-member UEB3 in .As d = 5, d′ = 6, k = 3, n = 2, b = v = 4, and 5 × 6–4 = 26 = 6 × 3 + 2 × 4, s = 6, p = 2, 0 ≤ l ≤ 7 andAccording to the proof of Theorem 1, we have the following pure states:;⋮;;;where m = 0, 1, 2, t = 0, 1, 2, 3.As C0 = 0, C1 = C (4, 4) = 1, C2 = C (4, 2) = 1, C3 = C (4, 4) = 1, C4 = C (4, 3) = 1,α = 0, |ri⟩ = |e ⊕ 5C (e, g)|g′⟩;α = 1, |ri⟩ = |e ⊕ 5C1 ⊕ 5C (e ⊕ 5C1, g)|g′⟩;α = 2, |ri⟩ = |e ⊕ 5(C1 + C2) ⊕ 5C (e ⊕ 5(C1 + C2), g)|g′⟩;α = 3, |ri⟩ = |e ⊕ 5(C1 + C2 + C3) ⊕ 5C (e ⊕ 5(C1 + C2 + C3), g)|g′⟩;α = 4, |ri⟩ = |e ⊕ 5(C1 + C2 + C3 + C4) ⊕ 5C (e ⊕ 5(C1 + C2 + C3 + C3), g)|g′⟩;Taking specific values into the above formula, the 26-member UEB3 in can be expressed as follows:where α = 1, ω, ω2 and .The following chart is indeed the space decomposition of the space of the coefficient matrices, whose first column and first row represent the bases of the previous space and latter space, respectively. The stars represent the ignored elements, and the same number or alphabet in Table 1 together constitutes a state in UEB3.

TABLE 1

|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩153a26
|1⟩a154b2
|2⟩3A164b
|3⟩b3A264
|4⟩5B****

6×3+2×4=30,−,4=26-member UEB3.

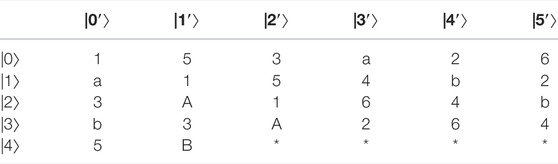
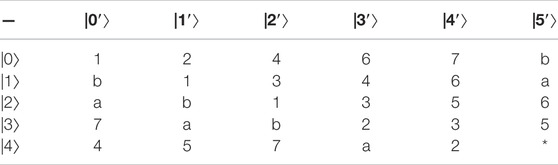
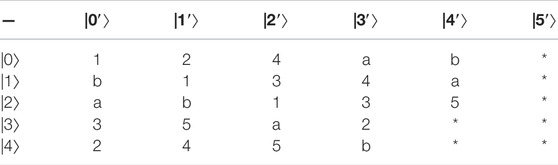
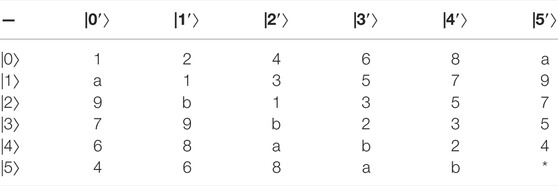
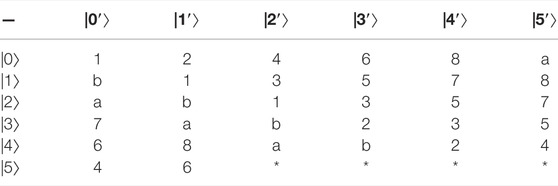
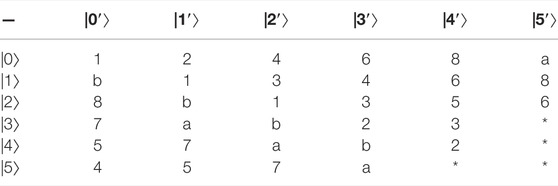
Example 2:Constructing 29,28,25,24-member UEB3s in .Similar to the analysis in Example 1, we only present the chart of corresponding matrix to represent the structure of UEB3s.Considering the following matrices,the specific UEB3s of V1, V2, V3, V4 are shown in Table 2‐5 respectively.

TABLE 2

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩1b7642
|1⟩31ba64
|2⟩531ba6
|3⟩7532ba
|4⟩a7542*

7×3+2×4=29-member.

TABLE 3

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩1a5427
|1⟩71a642
|2⟩381a64
|3⟩5382a6
|4⟩753a**

8×3+1×4=28-member.

TABLE 4

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩153a26
|1⟩7154a2
|2⟩37164a
|3⟩a37264
|4⟩5*****

7×3+1×4=25-member.

TABLE 5

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩153826
|1⟩715482
|2⟩371648
|3⟩537264
|4⟩******

8×3+0,×,4=24-member.

3.2 All the Ignored Elements Occupy N Rows

In this section, we first construct the (dd’ − v)-member UEBk in , in which all the v ignored elements occupied N rows in the matrix, and then present some examples of UEB3s also in .

Theorem 2:

Let k be a positive integer, such that W(n, k, b) is non-empty, and gcd(k, b) = 1. Let V be a subspace of Md×d′ such that each matrix in V is a d × d′ matrix ignoring v elements which occupied N rows with N = 1, … , k − 1, d′ − N ≥ b and dd’ − v = s ⋅ k + p ⋅ b with 1 ≤ v ≤ dN. If min{d, d′}≥ max{k, b}, then there exists dd’ − v (1 ≤ v ≤ dN)-member UEBk in .

Proof. First, for different values of p and s, we construct different pure states as follows: if p ≥ 1 and s ≥ 1, let if s = 0, p ≥ 1, letif p = 0, s ≥ 1, letwhere ; means the t (0 ≤ t ≤ b − 1) row in the generalized weights matrix W (n, k, b), and sk − 1 + (l − s)b + u = c ⋅ d + e; l ⋅ k + u = c ⋅ d + e with 0 ≤ e < d,withwhere C0 = 0, Cα = 1 denotes the ignored elements. It is worthy of note that β in formula (13) is a regulating term, β = 0 in the common cases, β = 1 if |e⟩|c ⊕(d′−N+1)e⟩ coincides with the previous answer of formula (13).

Similiar to Theorem 1, we can prove that {|ϕm.l⟩} constitute dd’ − v (1 ≤ v ≤ dN)-member UEBks in .

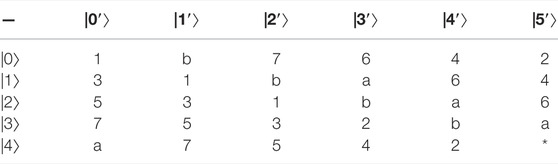
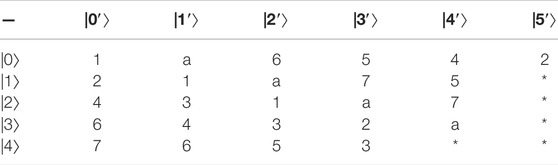
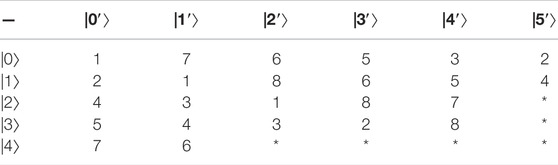
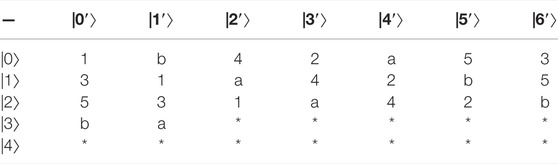
Example 3:Constructing 29,26,25,23-member UEB3 in .Considering the following matrices,the specific UEB3s of V1, V2, V3, V4 are shown in Table 6‐9 respectively.

TABLE 6

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩12467b
|1⟩b1346a
|2⟩ab1356
|3⟩7ab235
|4⟩457a2*

7×3+2×4=29-member.

TABLE 7

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩1246ab
|1⟩a1346*
|2⟩6b135*
|3⟩5ab23*
|4⟩45ab2*

6×3+2×4=26-member.

TABLE 8

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩12467*
|1⟩a1346*
|2⟩6a135*
|3⟩57a23*
|4⟩457a2*

7×3+1×4=25-member.

TABLE 9

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩124ab*
|1⟩b134a*
|2⟩ab135*
|3⟩35a2**
|4⟩245b**

5×3+2×4=23-member.

3.3 All the Ignored Elements Occupy Both x Rows and y Columns

In this section, we will construct (dd’ − v)-member UEBk in a bipartite system with all the v ignored elements occupying both x rows and y columns in the matrix, and we will also present some different examples of UEB3s in .

Theorem 3:

Let k be a positive integer, such that W(n, k, b) is non-empty, and gcd(k, b) = 1 (the greatest common divisor of k and b). Let V be a subspace of Md×d′ such that each matrix in V is a d × d′ matrix ignoring v elements which occupied x rows and y columns with x + y < k, d − x ≥ b and d′ − y ≥ b; dd’ − v = s ⋅ k + p ⋅ b with 1 ≤ v ≤ d′x + dy. If min{d, d′}≥ max{k, b}, then there exists (dd’ − v), (1 ≤ v ≤ d′x + dy)-member UEBk in .

Proof. First, for different values of p and s, we construct different pure states as follows: if p ≥ 1 and s ≥ 1, set if s = 0, p ≥ 1, setif p = 0, s ≥ 1, setwhere ; means the t (0 ≤ t ≤ b − 1) row in the generalized weights matrix W (n, k, b), and sk − 1 + (l − s)b + u = f ⋅ (d′ − N + 1) + g; l ⋅ k + u = c ⋅ (d − N + 1) + e = f ⋅ (d′ − N + 1) + g with 0 ≤ e < d, 0 ≤ g < d′. Denoting , , thenwithwhere C0 = 0, Cα = 1 denotes the ignored elements.

Similar to Theorem 1, we can prove that {|ϕm.l⟩} constitute dd’ − v (1 ≤ v ≤ d′x + dy)-member UEBks in .

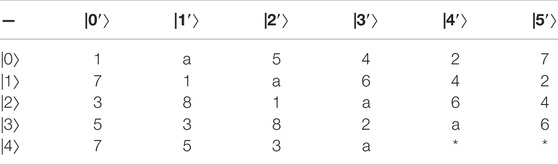
Example 4:Constructing 26,25,24,23-member UEB3 in .Considering the following matrices,the specific UEB3s of V1, V2, V3, V4 are shown in Table 10‐13, respectively.Comparing Tables 4, 8, 11, we can find that they are all 25-member UEB3s in , but they are different since the ignored elements occupy different positions. The above structure has given the location of the elements in each state, but the expressions are not always applicable when d = d′. For the case of d = d′, Ref. [23] provided a good method to construct the UEBk; now, we give some concrete examples to illustrate it.

TABLE 10

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩1edba2
|1⟩21edca
|2⟩ba1edc
|3⟩cba2e*
|4⟩dcb***

2×3+5×4=26-member.

TABLE 11

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩1a6542
|1⟩21a75*
|2⟩431a7*
|3⟩6432a*
|4⟩7653**

7×3+1×4=25-member.

TABLE 12

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩176532
|1⟩218654
|2⟩43187*
|3⟩54328*
|4⟩76****

8×3+0,×,4=24-member.

TABLE 13

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩1ba432
|1⟩21ba5*
|2⟩431ba*
|3⟩5432b*
|4⟩a5****

5×3+2×4=23-member.

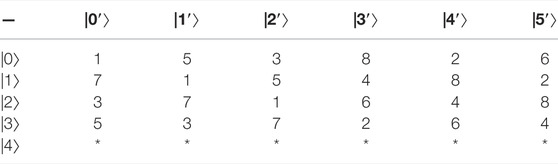
Example 5:Constructing 26,25,24,23-member UEB3 in .Considering the following matrices,the specific UEB3s of V1, V2, V3, V4 are shown in Table 14‐17, respectively.

TABLE 14

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩12468a
|1⟩a13579
|2⟩9b1357
|3⟩79b235
|4⟩68ab24
|5⟩468ab*

9,×,3+2×4=35-member.

TABLE 15

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩12468a
|1⟩b13578
|2⟩ab1357
|3⟩7ab235
|4⟩68ab24
|5⟩46****

8×3+2×4=32-member.

TABLE 16

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩12467a
|1⟩a13468
|2⟩86135*
|3⟩68b23*
|4⟩57ab2*
|5⟩457ab*

8×3+2×4=32-member.

TABLE 17

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩
|0⟩12468a
|1⟩b13468
|2⟩8b1356
|3⟩7ab23*
|4⟩57ab2*
|5⟩457a**

8×3+2×4=23-member.

Remark 1:We systematically show three methods (or orders) to construct the UEBks in different cases and present the corresponding mathematical expressions, which is better than that in [23] since it only provide one limited order. For example, we can construct 23-member SUEB3 in when a = 3, b = 4, which cannot be constructed by the order in [23], see Table 18, 19.

TABLE 18

|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩|6′⟩
|0⟩12345ab
|1⟩b12345a
|2⟩ab12345
|3⟩ab*****
|4⟩*******

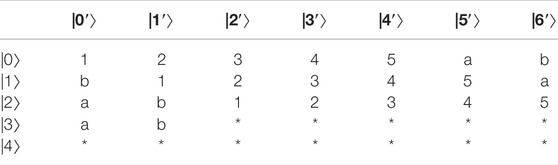
construction in [23].

TABLE 19

—|0′⟩|1′⟩|2′⟩|3′⟩|4′⟩|5′⟩|6′⟩
|0⟩1b42a53
|1⟩31a42b5
|2⟩531a42b
|3⟩ba*****
|4⟩*******

Our construction.

Remark 2:Our results cover wider spaces than that of Ref. [23]. The smallest space we can discuss is when a = 3, b = 4, while the smallest space [23] can discuss is when a = 3, b = 4, k = 3. Futhermore, even in , we also present different members of UEB3s.

4 Conclusion

We have proposed three ways to construct different members of UEBks in and have shown their concrete expressions. As an example of each method, we have presented different members of UEB3s in and . It is noteworthy that our result is based on the existence of generalized weighing matrices, so it is also of significance for us to find more generalized weighing matrices, such as skew Hadamard matrices.

By using our constructions, one can get at most (dd’ − v) members of UEBk in , which has not specifically mentioned in the previous literature studies.

Statements

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

Y-HT, X-LY, and S-HW write the paper together; others review and check the paper.

Funding

This work was supported by the Natural Science Foundation of China under Number 11761073.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

  • 1.

    NielsenMAChuangIL. Quantum Computation and Quantum Information. Cambridge, U.K.: Cambridge University Press (2004).

  • 2.

    EinsteinAPodolskyBRosenN. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?Phys Rev (1935) 47:777–80. 10.1103/physrev.47.777

  • 3.

    NikolopoulosGMAlberG. Security Bound of Two-Basis Quantum-Key-Distribution Protocols Usingqudits. Phys Rev A (2005) 72:032320. 10.1103/physreva.72.032320

  • 4.

    MafuMDudleyAGoyalSGiovanniniDMcLarenMJKonradTet alHigh-dimensional Orbital-Angular-Momentum-Based Quantum Key Distribution with Mutually Unbiased Bases. Phy Rev A (2013) 88:032305. 10.1103/physreva.88.032305

  • 5.

    Paw lowskiMZukowskiM. Optimal Bounds for Parity-Oblivious Random Access Codes. Phy Rev A (2010) 81:042326.

  • 6.

    WoottersWKFieldsBD. Optimal State-Determination by Mutually Unbiased Measurements. Ann Phys (1989) 191:363–81. 10.1016/0003-4916(89)90322-9

  • 7.

    Fernnadez-ParezAKlimovABSaavedraC. Quantum Proces Reconstruction Baed on Mutually Unbiased Basis. Phys Rev A (2011) 83:052332.

  • 8.

    EnglertBGAharonovY. The Mean king’s Problem: Prime Degrees of freedom. Phys Lett A (2011) 84:042306.

  • 9.

    BennettCHDivincenzoDPMorTShorPWSmolinJATerhalBMet alUnextendible Product Bases and Bound Entanglement. Phys Rev Lett (1999) 82:5385–8. 10.1103/physrevlett.82.5385

  • 10.

    BravyiSSmolinJA. Unextendible Maximally Entangled Bases. Phys Rev A (2011) 84:042306. 10.1103/physreva.84.042306

  • 11.

    WangY-LLiM-SFeiS-MZhengZ-J. Connecting Unextendible Maximally Entangled Base with Partial Hadamard Matrices. Quan Inf Process (2017) 16(3):84. 10.1007/s11128-017-1537-7

  • 12.

    ChenBFeiSM. Unextendible Maximally Entangled Bases and Mutually Unbiased Bases. Phys Rev A (2013) 88:034301. 10.1103/physreva.88.034301

  • 13.

    NanHTaoY-HLiL-SZhangJ. Unextendible Maximally Entangled Bases and Mutually Unbiased Bases in ℂd ⊗ ℂd′. Int J Theor Phys (2015) 54:927–32. 10.1007/s10773-014-2288-1

  • 14.

    LiMSWangYLFeiSMZhengZJ. Unextendible Maximally Entangled Bases in ℂd ⊗ ℂd′. Phys Rev A (2014) 89:062313.

  • 15.

    WangYLLiMSFeiSM. Unextendible Maximally Entangled Bases in ℂd ⊗ ℂd′. Phys Rev A (2014) 90:034301.

  • 16.

    GuoY. Constructing the Unextendible Maximally Entangled Bases from the Maximally Entangled Bases. Phys Rev A (2016) 94:052302. 10.1103/physreva.94.052302

  • 17.

    ZhangG-JTaoY-HHanY-FYongX-LFeiS-M. Unextendible Maximally Entangled Bases in ℂpd ⊗ ℂqd. Quan Inf Process (2018) 17:318. 10.1007/s11128-018-2094-4

  • 18.

    ShiFZhangXGuoY. Constructions of Unextendible Entangled Bases. Quan Inf Process (2019) 18:324. 10.1007/s11128-019-2435-y

  • 19.

    GuoYWuS. Unextendible Entangled Bases with Fixed Schmidt Number. Phys Rev A (2014) 90:054303. 10.1103/physreva.90.054303

  • 20.

    GuoYDuSLiXWuS. Entangled Bases with Fixed Schmidt Number. J Phys A: Math Theor (2015) 48:245301. 10.1088/1751-8113/48/24/245301

  • 21.

    GuoYJiaYLiXL. Multipartite Unextendible Entangled Basis. Quan Inf Process (2015) 14:3553–68. 10.1007/s11128-015-1058-1

  • 22.

    LiM-SWangY-L. Construction of Special Entangled Basis Based on Generalized Weighing Matrices. J Phys A: Math Theor (2019) 52:375303. 10.1088/1751-8121/ab331b

  • 23.

    WangYL. Special Unextendible Entangled Bases with Continuous Integer Cardinality. arXiv:1909.10043v1 (2019).

  • 24.

    ZhangGJTaoYHHanYFYongXLFeiSM. Constructions of Unextendible Maximally Entangled Bases in ℂd ⊗ ℂd′. Sci Rep (2018) 8(1):3193. 10.1038/s41598-018-21561-0

Summary

Keywords

unextendible entangled bases with a fixed schmidt number k, quantum entanglement, Schmidt number, generalized weighing matrix, entangled bases with a fixed Schmidt number

Citation

Tao Y-H, Yong X-L, Bai Y-R, Xu D-N and Wu S-H (2022) Unextendible Entangled Bases With a Fixed Schmidt Number Based on Generalized Weighing Matrices. Front. Phys. 10:896164. doi: 10.3389/fphy.2022.896164

Received

14 March 2022

Accepted

19 April 2022

Published

08 June 2022

Volume

10 - 2022

Edited by

Ming-Liang Hu, Xi’an University of Posts and Telecommunications, China

Reviewed by

Bin Chen, Tianjin Normal University, China

Yu Guo, Shanxi Datong University, China

Mao-Sheng Li, South China University of Technology, China

Updates

Copyright

© 2022 Tao, Yong, Bai, Xu and Wu.

This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Shu-Hui Wu,

This article was submitted to Quantum Engineering and Technology, a section of the journal Frontiers in Physics

Disclaimer

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Outline

Cite article

Copy to clipboard


Export citation file


Share article

Share on WeChat

Scan with WeChat to share this article

Article metrics