- 1Department of Physics and OPTIMAS Research Center, Technische Universität Kaiserslautern, Kaiserslautern, Germany
- 2Centre for Fusion, Space and Astrophysics, Department of Physics, University of Warwick, Coventry, United Kingdom
Intense ultrashort laser pulses can create highly excited matter with extraordinary properties. Experimental and theoretical investigations of these extreme conditions are very complex and usually intertwined. Here, we report on a theoretical approach for the electron scattering rates and the optical properties in gold at elevated temperatures. Our theory is based on the degree of occupancy of the conduction band as well as inputs from ab initio simulations and experimental data. After the electron system has reached a quasi-equilibrium, the occupancy is fully determined by the electron temperature. Thus, our approach covers the important relaxation stage after fast excitations when the two-temperature model can be applied. Being based on the electronic structure of solids, the model is valid for lattice temperatures up to melting but the electron temperature might exceed this limit by far. Our results agree well with recent experimental data for both the collision frequencies and the conductivity of highly excited gold. Scattering of sp-electrons by d-electrons is found to be the dominant damping mechanism at elevated electron temperatures and depends strongly on the number of conduction electrons, hence, revealing the microscopic origin of the conductivity change after heating. The supportive benchmarks with experiments are very valuable as the underlying scattering rates determine a number of other transport, optical and relaxation properties of laser-excited matter.
1 Introduction
The interaction of short laser pulses with matter has drawn broad attention over the last few decades due to its importance for fundamental science as well as for a plentitude of applications in diverse fields [1–9]. Advances in laser technology have opened new possibilities and new research areas [10–12] and allowed for remarkable qualitative improvements of temporal, spatial and energy resolution of experiments [13–18]. Accordingly, the capabilities to probe and control materials properties even at extreme conditions and ultrashort time scales have been enhanced considerably in the last decade. The combination of short-pulse optical lasers and free-electron lasers has proven to be a particularly suitable tool to create highly excited states of matter and probe its properties when utilizing the versatility of the free-electron laser with respect to photon energies and pulse duration.
The absorption of laser energy by solid materials drives the electrons in a nonthermal state with an energy distribution specific to the material and the excitation process [19–22]. Subsequently, the electrons relax to a Fermi distribution in each band on times scales of a few to a few hundred femtoseconds [23–25]. This stage is followed by the recombination of excited electrons into lower bands leading to the equilibration of the occupation numbers in the bands and finally an energy transfer from the electrons to the lattice that was initially unaffected by the laser [26, 27]. Transiently, there exists a stage in the relaxation that can be described with an elevated electron temperature and a relatively cold lattice. Understanding this stage is very useful when interpreting experiments with ultrafast excitations. Detecting this behavior sets a well-defined limit to the time the ultrafast equilibration processes need to establish a Fermi distribution and an equilibrium band occupation. Moreover, these states can deliver deep insights about the process of electron-phonon coupling and electron collisionality in general. Finally, this stage sets the initial conditions for melting or ablation processes at very high energy inputs.
The optical properties of materials are known to be modified during the excitation and relaxation process. Thus, they reflect the different relaxation stages and can be employed to probe the properties of matter at highly excited conditions. The optical response can be measured in pump-probe experiment through the reflection and/or the transmission [28–32]. These direct data can then be recast as internal optical properties like the dynamic conductivity either directly for bulk materials or with the help of the Helmholtz equations for heated films [33, 34]. Time-resolved ellipsometric measurements can also provide the complex refractive index of a material [35, 36]. Moreover, the DC electrical conductivity can be obtained with terahertz (THz) probe reflectivity [37] or probe transmission [38, 39]. THz probes provide more direct access to DC conductivity in contrast to measurements with optical frequencies that require to be extrapolated in the near zero-frequency limit [37].
Whereas reflection and transmission are the directly measured quantities in experiments, theoretical models usually start with the evaluation of the dielectric function or dynamic conductivity [40], which can be based on ab initio methods [41–44], quantum statistical approaches [45–47], classical simulations [48] or a Drude or Drude–Lorentz model [44, 49]. For extreme conditions and ultrashort time scales, the modelling of these properties remains challenging. The use of a constant value for the optical properties in many models is a crude approximation and may lead for instance to a wrong evaluation of the energy deposition and the damage threshold [50, 51]. The full nonequilibrium or, at least, temperature-dependent dielectric function should thus be rigorously evaluated. One crucial parameter is the damping rate of conducting electron states which is usually described as a scattering rate with other electrons, phonons and lattice imperfections. To date, this scattering rate and particularly its dependence on the electron temperature is still under discussion due to discrepancies found in both existing experiments [30, 39, 52] and also theoretical calculations [30, 53]. In a previous study by Fourment et al. [30], it has been shown that the scattering rate of the conduction electrons in gold is mostly determined by the number of holes in the d-band. These calculations have assumed that the sp and d-band states lie within certain energy boundaries instead of a projected density of states (PDOS) with orbitals hybridization. Moreover, a recent study by Chen et al. [39] has found a much smaller collision frequency of heated gold.
The resolution of the discrepancies and uncertainties of recent studies requires a thorough description of the material and optical properties, high-quality experimental data and well-suited relaxation codes to combine the two. With this combination, one can then harness the power of short-pulse excitations to reveal the relaxation pathways, collisionality and thermodynamics of strongly driven matter. Here, we report on the scattering rate and the electrical conductivity of gold under electron-phonon nonequilibrium with special emphasis to compare our theoretical approach to recent experimental results. Gold is an ideal candidate to study such properties of highly excited matter since it has been investigated extensively with short laser pulses [29, 30, 34, 39, 54, 55].
Our calculations are based on the temperature-dependent degree of filling of the sp and d-bands as in Ref. [30] but using a PDOS. We find that the electron-electron scattering is the major contributor to the total collision frequency at elevated electron temperature and is fully determined by the occupations of the bands. However, our results suggest a much lower electron-ion rate for cold gold in order to match the recent experimental data of Ref. [39]. These new settings translate into a good agreement with experiments for the DC and AC conductivities of heated gold. The latter reveals different qualitative behavior depending on the probe wavelength but remains constant and equals the DC conductivity at very low photon energies hence supporting THz radiations as an adequate probe for the static limit. The good agreement between the calculations and the experiment suggests that the Drude model is well suited to describe the DC and the real part of AC conductivity of highly excited matter at photon energies below the interband threshold once an appropriate description of the scattering rates is applied.
2 Theoretical Model
Laser-heating may induce strong modifications of the material’s optical properties due to the excited electron states created. Here, we consider optical excitation of gold, where two active bands contribute, namely, the 5d valence and the 6sp conduction electrons. The additional excitation of core electrons is possible with X-rays or XUV pulses [39, 56] but should not be addressed here, mainly, due to the ultrashort lifetimes of such core holes.
We consider times when the electron system is fully thermalized, hence a Fermi distribution is established. This relaxation stage is quickly reached as the kinetic stage with non-Fermi electron distributions lasts only a few femtoseconds [21, 24, 25]. Moreover, the sp and d-bands are assumed to be in equilibrium, i.e., they share a common temperature and chemical potential. This condition sets the lower temporal limit when our approach is valid since the occupation of these bands may stay out of equilibrium for several hundreds of femtoseconds [56, 57]. The assumption of equilibrated upper bands is fulfilled in many existing experiments [29–31, 33] since such a quasi-equilibrium state is reached at probe time [56]. For such cases, we can describe the material properties with quasi-equilibrium electron states that are uniquely defined by the electron temperature.
Still, the properties described here require ultrafast probing as part of the electron’s energy will be transferred to the lattice. This stage of nonequilibrium persists, at least, several picoseconds [54, 58]. Thus, our investigations can be seen as providing snap-shots of the optical properties during the electron-phonon temperature equilibration.
The density of states (DOS) of the two upper bands for solid gold is calculated from density functional theory employing Elk [59]. This code uses augmented-plane waves to treat all electrons. We use an 80 × 80 × 80 k-point grid, spin-orbit coupling and the local density approximation to evaluate the ground state which also sufficiently describes the elevated temperatures considered here [60]. Results for the DOS are shown in Figure 1, where the Fermi energy EF sets the zero of the energy scale. At room temperature, the DOS accounts for a fully occupied 5d-band and a half-filled 6sp conduction band. The equilibrium occupation of these states at elevated temperatures according to Fermi statistics,
with an electron temperature Te and a chemical potential μ is plotted in Figure 1 for different electron temperatures. As one can see, the sp-band is increasingly populated at higher electron temperatures while the corresponding chemical potential μ shifts towards higher energies. We obtain μ from the conservation of the total number of electrons, both in the sp- and d-bands, ntot [40], by solving the equation
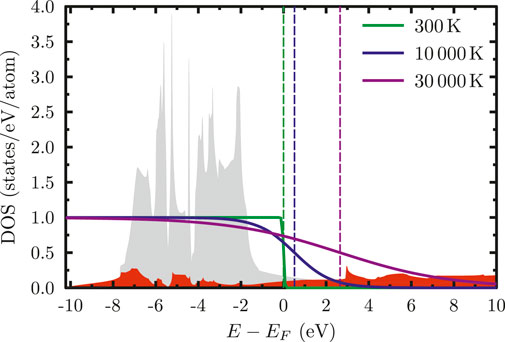
FIGURE 1. Partial density of states in gold for the 6sp electrons (red area) and the 5d-band (gray area), together with the equilibrium Fermi distributions at room temperature (green line), at 10 000 K (blue line) and at 30 000 K (purple line). The Fermi energy EF is located at energy zero. Dashed lines are the chemical potential demonstrating a shift at elevated electron temperatures.
The electron density of a given band is calculated as
where j denotes the band’s index, Dj the partial DOS of the band and f is the Fermi equilibrium distribution. The increase of the electron temperature leads to a rise of the conduction electron density and, correspondingly, a decrease in the occupation of the d-band, satisfying the conservation of the total electron density ntot = nsp + nd.
For matter initially at room temperature, the energy absorbed by the electrons while being heated to a new temperature Te can be written as
where Dtot = Dsp + Dd is the total density of states. The internal energy Eq. 3 also determines the heat capacity of the electrons, ce, via the temperature derivative at constant volume ce = ∂ u/∂ Te. Thus, all thermodynamic variables of the electron system are uniquely defined by the absorbed energy or, equivalently, the electron temperature.
Now we turn to the optical properties as expressed by the frequency-dependent conductivity. It is directly linked to the complex dielectric function via ɛ(ω) = ɛ∞ + iσ(ω)/ωɛ0, with the dielectric constant ɛ∞ and the vacuum permittivity ɛ0. The dielectric function is an intrinsic property and once known, all other optical properties like the absorption coefficient, the penetration depth or the reflectivity can easily be inferred [40]. For bulk materials, the reflectivity of the surface for normal incidence is given by
where n and k are the real and the imaginary parts of the complex refractive index
Within the Drude formalism, the complex frequency-dependent electrical conductivity is given by
where ω is the probe frequency. In the zero-frequency limit ω → 0, σ reduces to the DC conductivity σ0 with
Here, e is the electron charge and msp is the effective mass of the conduction electrons taken to be equivalent to the free electron mass for gold [62].
The total scattering rate νtot contains contributions from both electron-ion/phonon and electron-electron scattering:
where the constant B equals
3 Results and Discussion
We demonstrate how the optical properties of gold are modified by elevated electron temperatures up to 20 kK while we keep the lattice close to room temperature. Such quasi-equilibria with well-defined electron and phonon temperatures occur in many experiments [29–31, 33, 63] during the relaxation process after ultrafast excitation. Indeed, probing these states is essential to determine important parameters like the electron-phonon coupling.
The electron temperature reached in the experiment depends on the absorbed energy which is much easier to determine experimentally. Figures 2A,B show the electron temperature and the density in the conduction band of gold, respectively, in dependence of the absorbed energy. The temperature is determined by inverting Eq. 3 whereas the sp-density is evaluated by Eq. 2. To convert the absorbed energy per mass into the specific internal energy, we use a mass density of ρAu = 19.3 gcm−3. At ambient conditions, gold contains one sp electron per atom corresponding to a conduction band density of nsp ≃5.9 × 1022 cm−3.
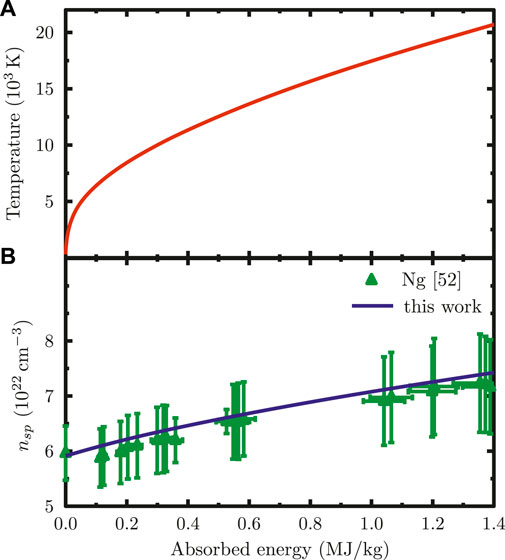
FIGURE 2. Predictions of (A) the electron temperature and (B) the electron density in the 6sp-conduction band of gold as a function of the absorbed energy. The conduction band density is compared with experimental data from Ref. [52].
The results shown in Figure 2 take the entire energy from an excitation process to be stored by the electron system directly after excitation. During and shortly after the excitation, energy may be transferred to the lattice even if the electron-phonon coupling in gold is small [58, 64], which can be included by simply adjusting the energy absorbed into the electrons. In Figure 2A, the electron temperature increases strongly nonlinearly with the absorbed energy. This effect can be attributed to the highly degenerate sp electrons at room temperature and the influence of d-band electrons which have a major contribution to the total heat capacity at higher electron temperatures.
With increasing energy density, hence temperature, the d-band electrons, located below the Fermi energy and serving as a reservoir of particles, are more and more excited into the empty states of the conduction band. This thermal excitation of d-electrons results in a rise of the sp-electron density as shown in Figure 2B, where we compare our calculations with experimental data (green triangles) inferred from measurements after short optical excitation [29, 52]. Our results show satisfactory agreement with the experiment although the large error bars do not confine the theory strongly.
The increase in sp-density strongly influences the electron-electron scattering rate shown in Figure 3A as a function of the electron temperature. It is obtained with the second term of Eq. 8 and, thus, is determined by the densities of electrons and holes in the d-band. At very low electron temperatures, the d-band of gold is fully occupied. Hence, Pauli blocking prevents scattering by the d-band electrons and νee remains nearly zero. For temperatures above ∼4 kK, thermal excitation of d-electrons becomes significant which increases the density in the conduction band as seen in Figure 2B and creates some empty states (holes) below the Fermi level. The increase of the density of holes in the d-band activates efficient electron-electron scattering leading to a strong rise of νee with the temperature. Moreover, the increase of νee shows a quadratic nature
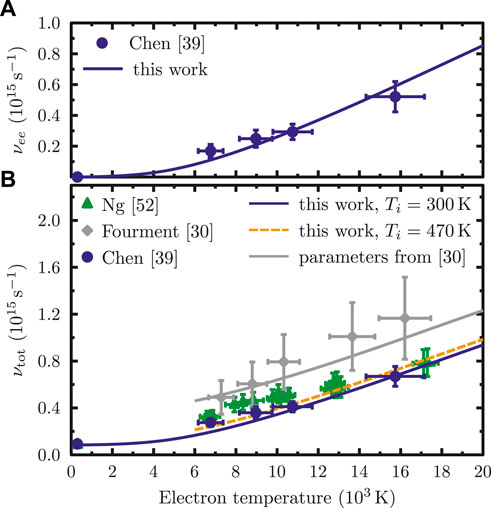
FIGURE 3. (A) Calculated temperature-dependent electron-electron scattering frequency in gold (blue line) compared with experimental data from Ref. [39] (blue circles). (B) Total scattering rate according to Eq. 8 for a cold lattice (blue solid line) and at a phonon temperature of 470 K (orange dashed line). Calculations are compared with different sets of experimental data obtained from Ref. [52] (green triangles), Ref. [39] (blue circle) and Ref. [30] (gray diamonds), respectively.
We compare our calculations with experimental data obtained from Ref. [39]. In the experiment, a thin gold foil was strongly heated with XUV pulses at different energy densities and probed with THz radiations. The temporal resolution was 700 ± 200 fs. νee was derived from the total scattering rate that was inferred from the THz conductivity measurements [39]. The comparison shows good agreement with the experimental data over a wide range of temperatures.
Figure 3B depicts the total scattering frequency νtot in gold in dependence of the electron temperature. This scattering rate is a crucial quantity for an accurate description of optical and transport properties in laser-excited materials as shown in Eqs 5–7. We obtain it via Eq. 8 as a sum of electron-electron and electron-ion contributions. For cold gold, the almost full occupation of the d-band at room temperature prevents electron-electron scattering. The scattering of sp-electrons with the phonons prevails and νtot ≈ νei. While increasing the electron temperature and keeping the lattice cold (blue solid line), we observe a strong rise of νtot with respect to Te. This can be directly attributed to an increase of the electron-electron scattering rate νee as seen in Figure 3A and resulting from an increase in the number of d-band holes. At such conditions, νee clearly dominates and has the largest contribution to the total collision frequency.
We compare our theoretical predictions with different sets of experimental data. There are some discrepancies between the THz data [39] (blue circles) and our results for a lattice at room temperature. However, to match the experimental conditions of the THz data including some electron-phonon energy transfer, we increase the lattice temperature up to Ti = 470 K. That corresponds to the value obtained with a two-temperature model at 700 fs, using a slow electron-phonon coupling [39, 64]. This small increase of Ti results in a rise of νei by a factor of 1.6 from its initial value, hence increasing νtot (orange dashed line) which now matches the THz data well. In contrast to Figure 3A, the data point at Te ≃6500 K also agrees much better with the theoretical line.
The experimental data shown with green triangles [52] and gray diamonds [30] were obtained from gold excited by optical pulses. The experiment of Ref. [52] uses an optical pump of 400 nm wavelength and probes at 800 nm with a temporal resolution of 540 fs whereas the experiment of Ref. [30] was pumped and probed with an 800 nm laser at a delay of 100 fs. Both of these data sets show similar qualitative behavior than the THz measurements [39] but are quantitatively higher. According to Ref. [39], this could be due to different experimental conditions especially the use of a thick target in Ref. [30].
The gray data points [30] in Figure 3B are only matched when input parameters from Ref. [30] are used, i.e., a much larger electron-ion collision frequency for cold gold and a lattice temperature at 880 K (gray solid line). In Ref. [30],
More directly measured optical properties provide a better test for existing models. Figure 4 shows results for the DC conductivity of gold as a function of the electron temperature. We obtain it according to Eq. 6 which includes the lattice contribution through
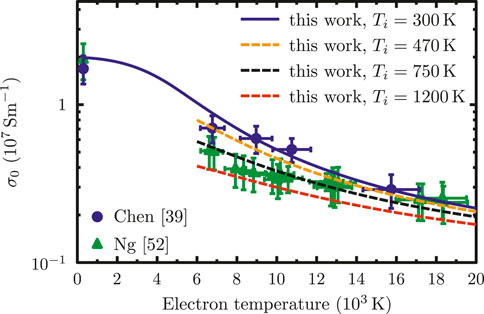
FIGURE 4. Temperature-dependent DC electrical conductivity of gold. The calculations according to Eq. 6 are shown for different phonon temperatures and compared with data from THz transmission measurements [39] (blue circles) and optical pump-probe experiments [52] (green triangles).
Figure 5 shows the real part of the AC conductivity in gold in dependence of the electron temperature and at different laser wavelengths. We observe quite different qualitative behaviors of the AC conductivity depending on the wavelength of the probe. Applying near-infrared probes, the AC conductivity monotonically rises with the electron temperature. That is the case observed for 2 µm wavelength, i.e. 0.62 eV photon energy, and similar to optical results at a wavelength of 800 nm in Refs. [29, 41]. In such regime of optical wavelengths, we have ω ≫ νtot and therefore σr ∝ νtot in Eq. 7 (note the logarithmic scale in Figure 5). At slightly longer wavelengths, see cases for 5–15 μm, our results show a still rising σr at low electron temperature, but it is reversed at elevated Te. The decrease of σr is due to a strong increase of νtot as seen in Figure 3B such that νtot ≫ ω and thus inverting the proportionality to σr ∝ 1/νtot, see Eq. 7.
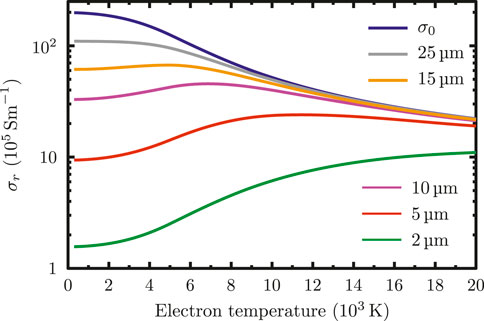
FIGURE 5. Real part of the AC conductivity as a function of the electron temperature for different laser wavelengths.
At 25 µm wavelength (49.6 meV) and above, the AC conductivity monotonically decreases with increasing electron temperature. The decrease of σr at elevated Te is due to the relation ω ≪ νtot, hence σr ∝ 1/νtot. For these wavelengths, σr displays a similar qualitative behavior than the DC conductivity. Moreover, for probe wavelengths above 15 μm, both σ0 and σr almost yield the same quantitative value at Te ≥ 10 kK.
Figure 6 displays the real part of the broadband AC conductivity for gold at different electron temperatures. Note the logarithmic scale of both axes. The rectangles represent the data obtained by measurements using THz transmission [39]. The horizontal dimension is the range of frequency components in the THz cycle and the vertical dimension indicates the uncertainty of the experimental data. The circles correspond to optical data at 1.55 eV photon energy and are inferred from reflection and transmission measurements [29].
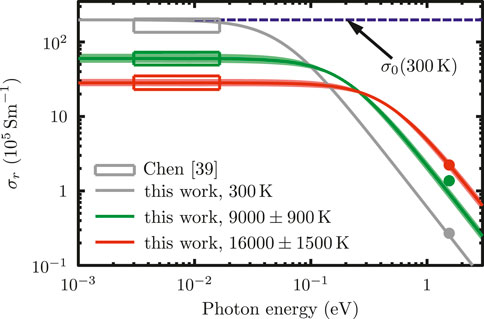
FIGURE 6. Real part of the broadband electrical conductivity σr for gold at room temperature (gray line) and at electron temperatures of Te = 9000 ± 900 K (green line) and 16,000 ± 1500 K (red line) according to Eq. 7. The calculations are compared with THz measurements (triangles) from Ref. [39] and with optical conductivity data from Ref. [29] (full circles). The DC electrical conductivity at room temperature is shown with a blue dashed line.
We plot the DC conductivity σ0 at room temperature with a blue dashed line. The calculated AC conductivity for cold gold (gray line) matches well the experimental data, both in the THz and optical regimes. Moreover, it shows that σr is constant and equals σ0 over the range from zero to 0.01 eV, hence, making THz radiations an adequate tool to probe DC conductivity of materials as in Refs. [37, 39]. We also show our results for electron temperatures of 9000 ± 900 K and 16,000 ± 1500 K, respectively, while keeping the lattice cold. The shaded areas are determined by the uncertainty of the electron temperature according to the experimental conditions of the THz data [39]. Our calculated σr agree well with both the THz measurements and the optical data. The green data point for optical photons is not fully matched. This is reasonable since, according to Ref. [39], the THz data average over a slightly different range of temperature conditions than the optical ones. Moreover, at probe time the lattice is slightly heated and, therefore, increases νtot (see Figure 3B), which should result in a rise of σr for optical photons. In the THz range, σr ∝ 1/νtot decreases with increasing Te, while the opposite behavior is observed at higher photon energies and in the optical regime (where σr ∝ νtot), as seen in Figures 4, 5, respectively. These comparisons demonstrate that the Drude model can describe the DC and the real part of the AC conductivity of strongly heated gold satisfactorily if interband contributions are small and the scattering rates and the band occupations are well determined.
4 Conclusion
We have studied the optical properties of highly excited gold in a nonequilibrium state with very different electron and phonon temperatures. We have shown that the scattering rates are the crucial quantities that determine most of the optical and transport properties in strongly heated metals. To that end, the occupation of the upper bands must be known as it fully determines the increase of the free carriers’ density and the electron-electron collision frequency which is the dominant rate at elevated electron temperatures. Although the lattice remains relatively cold at probe time, slight variations of the phonon temperature are observable in the optical properties. Our results match experimental data very well giving confidence in using the Drude model for probe wavelengths below the interband threshold.
The methods described here are also applicable to other metals with simple and complex band structures and, thus, can help to reveal the behavior of materials after short-pulse excitations. In particular, the phase of electron-phonon temperature equilibration can be studied as the electrons are in this phase in quasi-equilibrium that changes relatively slowly due to the energy transfer to the phonons/ions. In this case, the important electron-phonon energy transfer rate can be determined by combining optical probing and the modelling described here. Further work should be focused towards the optical properties for photon energies above the interband threshold, e.g., employing Drude Lorentz-like models. Given the propagation of uncertainties, comparison of optical properties is by far superior to comparisons of inferred quantities like the conduction band density when benchmarking theoretical models.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
PN implemented the models and performed the simulations. All authors contributed to the methods development and wrote the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Zhijiang Chen for providing the experimental data and Sebastian Weber for the partial DOS and for helpful discussions.
References
1. Chichkov BN, Momma C, Nolte S, Alvensleben F, Tünnermann A. Femtosecond, Picosecond and Nanosecond Laser Ablation of Solids. Appl Phys A (1996) 63:109–15. doi:10.1007/BF01567637
2. Vogel A, Noack J, Hüttman G, Paltauf G. Mechanisms of Femtosecond Laser Nanosurgery of Cells and Tissues. Appl Phys B (2005) 81:1015–47. doi:10.1007/s00340-005-2036-6
3. Barret PH, Palmer M. High-Power and Femtosecond Lasers: Properties, Materials and Applications. Hauppauge, NY: Nova Science Publishers (2009).
5. Balling P, Schou J. Femtosecond-laser Ablation Dynamics of Dielectrics: Basics and Applications for Thin Films. Rep Prog Phys (2013) 76:036502. doi:10.1088/0034-4885/76/3/036502
6. Hurricane OA, Callahan DA, Casey DT, Celliers PM, Cerjan C, Dewald EL, et al. Fuel Gain Exceeding unity in an Inertially Confined Fusion Implosion. Nature (2014) 506:343–8. doi:10.1038/nature13008
7. Kraus D, Vorberger J, Pak A, Hartley NJ, Fletcher LB, Frydrych S, et al. Formation of Diamonds in Laser-Compressed Hydrocarbons at Planetary interior Conditions. Nat Astron (2017) 1:606–11. doi:10.1038/s41550-017-0219-9
8. Hofherr M, Häuser S, Dewhurst JK, Tengdin P, Sakshath S, Nembach HT, et al. Ultrafast Optically Induced Spin Transfer in Ferromagnetic Alloys. Sci Adv (2020) 6:eaay8717. doi:10.1126/sciadv.aay8717
9. Terekhin PN, Oltmanns J, Blumenstein A, Ivanov DS, Kleinwort F, Garcia ME, et al. Key Role of Surface Plasmon Polaritons in Generation of Periodic Surface Structures Following Single-Pulse Laser Irradiation of a Gold Step Edge. Nanophotonics (2022) 11:359–67. doi:10.1515/nanoph-2021-0547
10. Strickland D, Mourou G. Compression of Amplified Chirped Optical Pulses. Opt Commun (1985) 55:447–9. doi:10.1016/0030-4018(85)90151-8
11. Hänsch TW. Nobel Lecture: Passion for Precision. Rev Mod Phys (2006) 78:1297–309. doi:10.1103/RevModPhys.78.1297
12. Rossbach J, Schneider JR, Wurth W. 10 Years of Pioneering X-ray Science at the Free-Electron Laser Flash at Desy. Phys Rep (2019) 808:1–74. doi:10.1016/j.physrep.2019.02.002
13. Chapman HN, Barty A, Bogan MJ, Boutet S, Frank M, Hau-Riege SP, et al. Femtosecond Diffractive Imaging with a Soft-X-ray Free-Electron Laser. Nat Phys (2006) 2:839–43. doi:10.1038/nphys461
14. Chapman DA, Gericke DO. Analysis of Thomson Scattering from Nonequilibrium Plasmas. Phys Rev Lett (2011) 107:165004. doi:10.1103/PhysRevLett.107.165004
15. Cocker TL, Jelic V, Gupta M, Molesky SJ, Burgess JAJ, Reyes GDL, et al. An Ultrafast Terahertz Scanning Tunnelling Microscope. Nat Photon (2013) 7:620–5. doi:10.1038/nphoton.2013.151
16. Fletcher LB, Lee HJ, Döppner T, Galtier E, Nagler B, Heimann P, et al. Ultrabright X-ray Laser Scattering for Dynamic Warm Dense Matter Physics. Nat Photon (2015) 9:274–9. doi:10.1038/nphoton.2015.41
17. Hayasaki Y, Fukuda S-i., Hasegawa S, Juodkazis S. Two-color Pump-Probe Interferometry of Ultra-fast Light-Matter Interaction. Sci Rep (2017) 7:10405. doi:10.1038/s41598-017-10709-z
18. Hartelt M, Terekhin PN, Eul T, Mahro A-K, Frisch B, Prinz E, et al. Energy and Momentum Distribution of Surface Plasmon-Induced Hot Carriers Isolated via Spatiotemporal Separation. ACS Nano (2021) 15:19559–69. doi:10.1021/acsnano.1c06586
19. Fann WS, Storz R, Tom HWK, Bokor J. Direct Measurement of Nonequilibrium Electron-Energy Distributions in Subpicosecond Laser-Heated Gold Films. Phys Rev Lett (1992) 68:2834–7. doi:10.1103/PhysRevLett.68.2834
20. Medvedev N, Zastrau U, Förster E, Gericke DO, Rethfeld B. Short-time Electron Dynamics in Aluminum Excited by Femtosecond Extreme Ultraviolet Radiation. Phys Rev Lett (2011) 107:165003. doi:10.1103/PhysRevLett.107.165003
21. Mueller BY, Rethfeld B. Relaxation Dynamics in Laser-Excited Metals under Nonequilibrium Conditions. Phys Rev B (2013) 87:035139. doi:10.1103/PhysRevB.87.035139
22. Rohde G, Stange A, Müller A, Behrendt M, Oloff L-P, Hanff K, et al. Ultrafast Formation of a Fermi-Dirac Distributed Electron Gas. Phys Rev Lett (2018) 121:256401. doi:10.1103/PhysRevLett.121.256401
24. Silaeva EP, Bevillon E, Stoian R, Colombier JP. Ultrafast Electron Dynamics and Orbital-dependent Thermalization in Photoexcited Metals. Phys Rev B (2018) 98:094306. doi:10.1103/PhysRevB.98.094306
25. Weber ST, Rethfeld B. Phonon-induced Long-Lasting Nonequilibrium in the Electron System of a Laser-Excited Solid. Phys Rev B (2019) 99:174314. doi:10.1103/PhysRevB.99.174314
26. Sundaram SK, Mazur E. Inducing and Probing Non-thermal Transitions in Semiconductors Using Femtosecond Laser Pulses. Nat Mater (2002) 1:217–24. doi:10.1038/nmat767
27. Rethfeld B, Ivanov DS, Garcia ME, Anisimov SI. Modelling Ultrafast Laser Ablation. J Phys D Appl Phys (2017) 50:193001. doi:10.1088/1361-6463/50/19/193001
28. Hohlfeld J, Wellershoff S-S, Güdde J, Conrad U, Jähnke V, Matthias E. Electron and Lattice Dynamics Following Optical Excitation of Metals. Chem Phys (2000) 251:237–58. doi:10.1016/S0301-0104(99)00330-4
29. Chen Z, Holst B, Kirkwood SE, Sametoglu V, Reid M, Tsui YY, et al. Evolution of Ac Conductivity in Nonequilibrium Warm Dense Gold. Phys Rev Lett (2013) 110:135001. doi:10.1103/PhysRevLett.110.135001
30. Fourment C, Deneuville F, Descamps D, Dorchies F, Petit S, Peyrusse O, et al. Experimental Determination of Temperature-dependent Electron-Electron Collision Frequency in Isochorically Heated Warm Dense Gold. Phys Rev B (2014) 89:161110. doi:10.1103/PhysRevB.89.161110
31. Ping Y, Hanson D, Koslow I, Ogitsu T, Prendergast D, Schwegler E, et al. Broadband Dielectric Function of Nonequilibrium Warm Dense Gold. Phys Rev Lett (2006) 96:255003. doi:10.1103/PhysRevLett.96.255003
32. Yurkevich AA, Ashitkov SI, Agranat MB. Permittivity of Gold with a Strongly Excited Electronic Subsystem. Phys Plasmas (2017) 24:113106. doi:10.1063/1.5000285
33. Widmann K, Ao T, Foord ME, Price DF, Ellis AD, Springer PT, et al. Single-state Measurement of Electrical Conductivity of Warm Dense Gold. Phys Rev Lett (2004) 92:125002. doi:10.1103/PhysRevLett.92.125002
34. Chen Z, Tsui YY, Mo MZ, Fedosejevs R, Ozaki T, Recoules V, et al. Electron Kinetics Induced by Ultrafast Photoexcitation of Warm Dense Matter in a 30-nm-Thick Foil. Phys Rev Lett (2021) 127:097403. doi:10.1103/PhysRevLett.127.097403
35. Rapp S, Kaiser M, Schmidt M, Huber HP. Ultrafast Pump-Probe Ellipsometry Setup for the Measurement of Transient Optical Properties during Laser Ablation. Opt Express (2016) 24:17572–92. doi:10.1364/OE.24.017572
36. Winter J, Rapp S, Schmidt M, Huber HP. Ultrafast Laser Processing of Copper: A Comparative Study of Experimental and Simulated Transient Optical Properties. Appl Surf Sci (2017) 417:2–15. doi:10.1016/j.apsusc.2017.02.070
37. Kim KY, Yellampalle B, Glownia JH, Taylor AJ, Rodriguez G. Measurements of Terahertz Electrical Conductivity of Intense Laser-Heated Dense Aluminum Plasmas. Phys Rev Lett (2008) 100:135002. doi:10.1103/PhysRevLett.100.135002
38. Ofori-Okai BK, Descamps A, Lu J, Seipp LE, Weinmann A, Glenzer SH, et al. Toward Quasi-Dc Conductivity of Warm Dense Matter Measured by Single-Shot Terahertz Spectroscopy. Rev Scientific Instr (2018) 89:10D109. doi:10.1063/1.5038944
39. Chen Z, Curry CB, Zhang R, Treffert F, Stojanovic N, Toleikis S, et al. Ultrafast Multi-Cycle Terahertz Measurements of the Electrical Conductivity in Strongly Excited Solids. Nat Commun (2021) 12:1638. doi:10.1038/s41467-021-21756-6
41. Holst B, Recoules V, Mazevet S, Torrent M, Ng A, Chen Z, et al. Ab Initio Model of Optical Properties of Two-Temperature Warm Dense Matter. Phys Rev B (2014) 90:035121. doi:10.1103/PhysRevB.90.035121
42. Blumenstein A, Zijlstra ES, Ivanov DS, Weber ST, Zier T, Kleinwort F, et al. Transient Optics of Gold during Laser Irradiation: From First Principles to Experiment. Phys Rev B (2020) 101:165140. doi:10.1103/PhysRevB.101.165140
43. Brouwer N, Recoules V, Holzwarth N, Torrent M. Calculation of Optical Properties with Spin-Orbit Coupling for Warm Dense Matter. Comput Phys Commun (2021) 266:108029. doi:10.1016/j.cpc.2021.108029
44. Silaeva E, Saddier L, Colombier J-P. Drude-lorentz Model for Optical Properties of Photoexcited Transition Metals under Electron-Phonon Nonequilibrium. Appl Sci (2021) 11:9902. doi:10.3390/app11219902
45. Hilse P, Schlanges M, Bornath T, Kremp D. Collisional Absorption of Dense Plasmas in strong Laser fields: Quantum Statistical Results and Simulation. Phys Rev E (2005) 71:056408. doi:10.1103/PhysRevE.71.056408
46. Grinenko A, Gericke DO. Nonlinear Collisional Absorption of Laser Light in Dense Strongly Coupled Plasmas. Phys Rev Lett (2009) 103:065005. doi:10.1103/PhysRevLett.103.065005
47. Veysman M, Röpke G, Winkel M, Reinholz H. Optical Conductivity of Warm Dense Matter within a Wide Frequency Range Using Quantum Statistical and Kinetic Approaches. Phys Rev E (2016) 94:013203. doi:10.1103/PhysRevE.94.013203
48. Morozov I, Reinholz H, Röpke G, Wierling A, Zwicknagel G. Molecular Dynamics Simulations of Optical Conductivity of Dense Plasmas. Phys Rev E (2005) 71:066408. doi:10.1103/PhysRevE.71.066408
49. Drude P. Zur Elektronentheorie der Metalle. Ann Phys (1900) 306:566–613. doi:10.1002/andp.19003060312
50. Ren Y, Chen JK, Zhang Y, Huang J. Ultrashort Laser Pulse Energy Deposition in Metal Films with Phase Changes. Appl Phys Lett (2011) 98:191105. doi:10.1063/1.3579539
51. Tsibidis GD. The Influence of Dynamical Change of Optical Properties on the Thermomechanical Response and Damage Threshold of noble Metals under Femtosecond Laser Irradiation. J Appl Phys (2018) 123:085903. doi:10.1063/1.5011738
52. Ng A, Sterne P, Hansen S, Recoules V, Chen Z, Tsui YY, et al. Dc Conductivity of Two-Temperature Warm Dense Gold. Phys Rev E (2016) 94:033213. doi:10.1103/PhysRevE.94.033213
53. Petrov YV, Inogamov NA, Migdal KP. Thermal Conductivity and the Electron-Ion Heat Transfer Coefficient in Condensed media with a Strongly Excited Electron Subsystem. JETP Lett (2013) 97:20–7. doi:10.1134/s0021364013010098
54. White TG, Mabey P, Gericke DO, Hartley NJ, Doyle HW, McGonegle D, et al. Electron-Phonon Equilibration in Laser-Heated Gold Films. Phys Rev B (2014) 90:014305. doi:10.1103/PhysRevB.90.014305
55. Hartley NJ, Ozaki N, Matsuoka T, Albertazzi B, Faenov A, Fujimoto Y, et al. Ultrafast Observation of Lattice Dynamics in Laser-Irradiated Gold Foils. Appl Phys Lett (2017) 110:071905. doi:10.1063/1.4976541
56. Ndione PD, Weber ST, Gericke DO, Rethfeld B. Nonequilibrium Band Occupation and Optical Response of Gold after Ultrafast Xuv Excitation. Research Square [Preprint] (2021). doi:10.21203/rs.3.rs-1181411/v1
57. Ndione PD, Weber ST, Rethfeld B, Gericke DO. Density Response to Short-Pulse Excitation in Gold. Contrib Plasma Phys (2019) 59:e201800186. doi:10.1002/ctpp.201800186
58. Medvedev N, Milov I. Electron-Phonon Coupling in Metals at High Electronic Temperatures. Phys Rev B (2020) 102:064302. doi:10.1103/PhysRevB.102.064302
59.ELK. The Elk Code. [Software] (2016). Available at: http://elk.sourceforge.net/ (Accessed 2016).
60. Bévillon E, Colombier JP, Recoules V, Stoian R. Free-electron Properties of Metals under Ultrafast Laser-Induced Electron-Phonon Nonequilibrium: A First-Principles Study. Phys Rev B (2014) 89:115117. doi:10.1103/PhysRevB.89.115117
62. Johnson PB, Christy RW. Optical Constants of the noble Metals. Phys Rev B (1972) 6:4370–9. doi:10.1103/physrevb.6.4370
63. White TG, Vorberger J, Brown CRD, Crowley BJB, Davis P, Glenzer SH, et al. Observation of Inhibited Electron-Ion Coupling in Strongly Heated Graphite. Sci Rep (2012) 2:889. doi:10.1038/srep00889
64. Mo MZ, Chen Z, Li RK, Dunning M, Witte BBL, Baldwin JK, et al. Heterogeneous to Homogeneous Melting Transition Visualized with Ultrafast Electron Diffraction. Science (2018) 360:1451–5. doi:10.1126/science.aar2058
Keywords: optical properties, electrical conductivity, scattering rate, highly excited matter, band occupation, ultrafast relaxation
Citation: Ndione PD, Gericke DO and Rethfeld B (2022) Optical Properties of Gold After Intense Short-Pulse Excitations. Front. Phys. 10:856817. doi: 10.3389/fphy.2022.856817
Received: 17 January 2022; Accepted: 21 February 2022;
Published: 15 March 2022.
Edited by:
Mianzhen Mo, Stanford University, United StatesReviewed by:
Andrew Baczewski, Sandia National Laboratories, United StatesChaobo Chen, University of Virginia, United States
Copyright © 2022 Ndione, Gericke and Rethfeld. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: P. D. Ndione, ndione@physik.uni-kl.de
 P. D. Ndione
P. D. Ndione