Weidong Ling 
Bo Chen
Qiyu Zeng 
Xiaoxiang Yu 
Shen Zhang 
Zengxiu Zhao 
Jiayu Dai- Department of Physics, National University of Defense Technology, Changsha, China
High pressure structural transformation of copper (Cu) is a rather complex physical process. One of the intriguing questions that are rarely discussed is the comparison between quasi-isentropic response and adiabatic response for copper lattice transition. The ambient face-centered-cubic structure of Cu is predicted to persist over 100 TPa from ab inito calculations and experimentally demonstrated to persist until 1.15 TPa in ramp compression and 150 GPa in static compression. However, a novel body-centered-cubic (BCC) order is observed merely at 180 GPa once shock compression is applied. The mechanism of body-centered-cubic phase transition occurred at low pressure under shock compression remains elusive so far and much attention is required on the dynamics in such a phase transition. In this work, we utilize the molecular dynamics method to simulate the shock compression on a copper lattice to uncover the structural transition in the atomic scale. We report the FCC–BCC phase transition occurred at 156 GPa, and lots of disordered structures are discovered in the BCC phase after impact, revealed by a series of structure analysis tools and free energy calculations. The plethora of transient disordered structures reduces the global Gibbs free energies, thus leading to the downgrade of the transition pressure in contrast to the ramp and static compression, which provides a new perspective for structural transformation under extreme conditions.
1 Introduction
The advances in high-pressure techniques [1–5] have largely progressed the investigation of condensed matter physics in an extreme condition, which significance has expanded in other associated subjects such as geophysics[6], planetary astrophysics[7,8], and inertial confinement fusion[9,10]. Two of the prevailing approaches are favored for achieving high pressure: diamond anvil cell (DAC) method and dynamic shock wave method, the former belongs to static compression and the latter is dynamic. Albeit a similar pressure environment can be generated by both strategies, the physical process by each method is largely different [11–16]. The static compression can be applied for significant long time in most material systems since a nearly isotropic strain is induced and the shear strain is negligible that is normally omitted. In contrast, the shock compression generates uniaxial strain with ultra-high rates that results in a rapid increment in temperature in candidate materials [17]. The experimental identification of phase transitions in such a drastic process is rather difficult. Although ultrafast probes such as in-situ time-resolved X-ray diffraction technique is readily available for identifying the transient dynamics in structural transformation, limited results are reported in comparing the structural transformation path between dynamic and static compressions, neither experimentally nor theoretically.
A standard single crystal in the field of high-pressure is copper (Cu), which is a typical close-packed face-centered-cubic (FCC) structure at ambient environment. The mechanical properties and equation of states for Cu have been extensively investigated in last few decades [18–24]. The stability of the FCC phase in Cu is believed to be so strong that can endure very high pressure before melting [25]. The previous studies of structural transformation in compression experiments by either the hydrostatic or shock impact approach have never reported the existence of the BCC phase [26]. Both strategies imply that only the FCC phase is identified: static compression reports that the FCC phase persists at 150 GPa by experiment [27] and even higher pressure to 100 TPa is predicted by first-principles calculations[28], while the ramp compression experiment finds that the FCC is preserved up to 1.15 TPa[29]. Recently, an anomalous FCC–BCC phase transition in Cu is revealed by in situ XRD experiment under shock compression[30], which motivates the retrospect for the remaining question of phase transitions in Cu.
In this work, we utilize molecular dynamics (MD) simulations to investigate the shock-induced phase transition of Cu. An explicit FCC–BCC phase transition is observed at 156 GPa, resembling the experimental value. Locally disordered structures induced by shock wave are resolved as opposed to a perfect crystal, which are favored in this drastic phase transition dynamics implied by free energy calculations. The structures are characterized as short-range disordered structures, which are identical with BCC structures in the long-time statistical average. This work sheds light on the understanding of microscopic picture in shock compression process in a traditional robust crystal.
2 Computational Methods
The embedded-atom-method (EAM) potential of copper presented by Mishin et al. [31] has been applied for MD simulations implemented under LAMMPS framework[32]. The popular non-equilibrium molecular dynamics (NEMD) approach is applied to generate a unidirectional planar shock wave. The shock wave is simulated by a piston applied to the sample. The method of Multi-Scale Shock Technique (MSST) [33] is a simulation technique based on the Navier-Stokes equations for compressible flow. All atoms in the system update positions and velocities following the modified Lagrangian, so as to restrain the systems to the Hugoniot-based thermodynamic conditions (see the Supplementary Material for details).
For NEMD simulations, the initial samples are first equilibrated by applying isothermal-isobaric at 300 K and 1 bar for 500 ps with a timestep of 1 fs Then, the propagation of shock waves is along the z-direction with a timestep of 0.1 fs. Period boundary conditions are performed in the x- and y-direction, a reflection boundary is performed in the z-direction. For MSST simulations, the initial configurations of the single FCC crystal have been equilibrated by applying the isothermal-isobaric, NPT ensemble integration scheme (for 500 ps with a timestep size of 1 fs) along with the Nose–Hoover thermostat algorithm at 300 K and 1 bar. Periodic boundary conditions are maintained in all three directions. After equilibrium, the applied shock speed ranged from 5.0 to 8.4 km/s with an interval of 0.2 km/s by MSST simulations for a duration of 500 ps. The masslike parameter Q was set to 3600, the artificial viscosity mu was set to 0.0903, and the converting factor tscale was set to 0.01. The data collection was performed after 100 ps when all physical quantities are stable. In all the MD simulations, the shock wave is applied to the single crystal FCC copper along (100) orientation.
Different analysis methods have been used to diagnose the structure. By using a simulated radiation of wavelength (0.5266 Å), X-ray diffraction intensities are calculated on a mesh of reciprocal lattice nodes (method described in Ref. [34]); the simulated XRD profiles of intensity versus scattering angle (2Θ) are fitted by a Gaussian function. The adaptive common neighbor analysis (a-CNA) method is to reveal the finite number of local arrangements with the FCC, BCC, or HCP crystal structure [35]; [36]. The a-CNA method (see the Supplementary Material for details), performed by the OVITO software [36], is a short-range diagnosis based on the coordination number of atoms. The effective coordination number (ECN) method [37] is utilized to distinguish the atoms unrecognized by a-CNA, and it is able to detect the symmetry structure in which a particular atom is surrounded by atoms at different distances (see the Supplementary Material for details). Ten snapshots were collected from MD simulation trajectories to obtain time-averaged information.
The nonequilibrium thermodynamic integration (neTI) method [38] is proposed for calculating the free energy. The commonly used thermodynamic integration technique [39] to evaluate free energy is performed by constructing a sequence of equilibrium states on a path between two thermodynamic states of interest. Compared with standard equilibrium free-energy calculations, the neTI method allows the calculations to be assessed along explicitly time-dependent processes. The shock-induced BCC structures are generated by MSST simulations in the shock velocity of 7.4 km/s, corresponding to a compression pressure of 156 GPa. The Gibbs free energy differences between FCC and shock-induced BCC are calculated at different temperature and pressure based on shock conditions (details in the Supplementary Material).
3 Results and Discussion
Different configurations have been used to check the convergence of NEMD simulations (Supplementary Table S1), and the initial configuration with 2160000 atoms is shown in Supplementary Figure S1 Based on the EAM potential of Cu developed by Mishin et al., the equation of states in this work matched well with previous results as shown in Supplementary Figure S2A. Variable sizes have been performed for MSST method testing (Supplementary Figure S2B). The peak longitudinal stress (P)–volume (V) states for high pressure Cu is shown in Figure 1A. The results determined from the present simulations coincide with the previously Hugoniot curve and recently shock wave experiment[30]. Based on the XRD measurement, the presence of the BCC structure has been found in lower pressure, as shown in Figure 1B. In the shock experiments, the measured XRD line profiles with (hkl) peaks indexed are used to identify the nature of the copper foils. At ambient condition, the MD simulation result is in good agreement with the experimental result. The line profiles of the shock experiment show that Cu remains in the FCC phase up to 156.8 GPa, only the first peak matches the MD result at 119 GPa. The peak indexed as the (110) BCC peak partially overlaps with the (111) FCC peak at 181.5 GPa indicates the mixed FCC–BCC phase. The observed overlapped peaks in MD simulation results are much similar to experiments, but the BCC peak is found at 155.9 GPa. With increased shock pressure, the FCC peaks completely vanish in both experiment and MD simulation at 211.5 and 196 GPa, respectively. The static compression and the ramp compression data [28, 29] (the FCC structure is preserved up to terapascal range) also have been plotted in Figure 1A. As shown in Figure 1, there is no observation of the BCC phase with static and ramp compression up to terapascal regime, while only shock loaded Cu generates the BCC structure in the range of gigapascal.
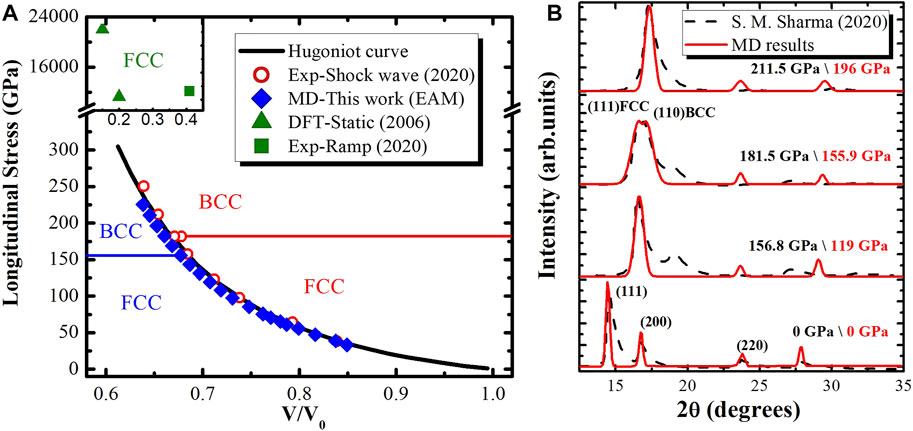
FIGURE 1. (A) Longitudinal stress vs. volume compressions for compressed copper. (B) The XRD profiles for shock compressed copper. The red solid curves denote MD simulations under different shock pressure. The black dash curves denote experimental results.
The structures of Cu at representative pressure by MSST simulations are exhibited in Supplementary Figure S3. Before the transition to the BCC phase, different types of stacking faults occur containing FCC and HCP. The fraction of atom types under different shock intensities by a-CNA is shown in Figure 2A. It can be observed that the FCC structure comprises the main part for low-intensity shock compression (below 38.8 GPa). The proportion of the HCP structure arises as shock intensities rise to 85.5 GPa. Prior to the occurrence of the BCC structure, both FCC and HCP structures contribute to the generation of stacking faults, which has not been reported by existed experiments. At 98 GPa, the fraction of FCC and HCP nearly dropped to zero, while the content of BCC atoms suddenly increased. It is shown that the onset pressure of phase transition is 98 GPa rather than 156 GPa through the XRD method. The difference between a-CNA and XRD methods results from short or long range diagnosis characteristics. The a-CNA is applied in a confined local crystal structure when analyzing an instantaneous neighbor environment. Hence, the termed “OTHER” in Figure 2A represents those particles not defined by a-CNA. The ECN of Cu on three typical shock compression is shown in Figure 2B. The probability distribution of ECN about four types of atoms classified by a-CNA. The coordination number (CN) of BCC atoms is different from FCC and HCP atoms. It is observed that “OTHER” type atoms are almost identical with BCC atoms based on the same peak position and wave broadening. The shape of probability distribution, both FCC and HCP types, is not smooth as the pressure is increased. Meanwhile, the shape of ECN distributions has a trend of broadening owing to increasing shock intensities accompanied with the temperature increase. These observations are also found under other shock pressures (Supplementary Figure S4). It can be concluded that “OTHER” type atoms are charactered as the BCC structure in the long-time statistical average. The radial distribution functions (RDFs) of the initio FCC structure, BCC structure (rebuilt perfect BCC crystal under 156 GPa static pressure), shock-induced BCC structure (156 GPa shock pressure), and liquid copper (156 GPa static pressure) have been compared (Supplementary Figure S5). The RDF suggests that short-ordered or medium-ordered structural features emerge after shock compression. Thus, “OTHER”-type atoms should be regrouped into either long-time statistical averaged BCC structures or short-range disordered structures. Compared with static compression, shock compression will cause instantaneous disordered structures due to strong uniaxial strain and temperature increase rapidly.
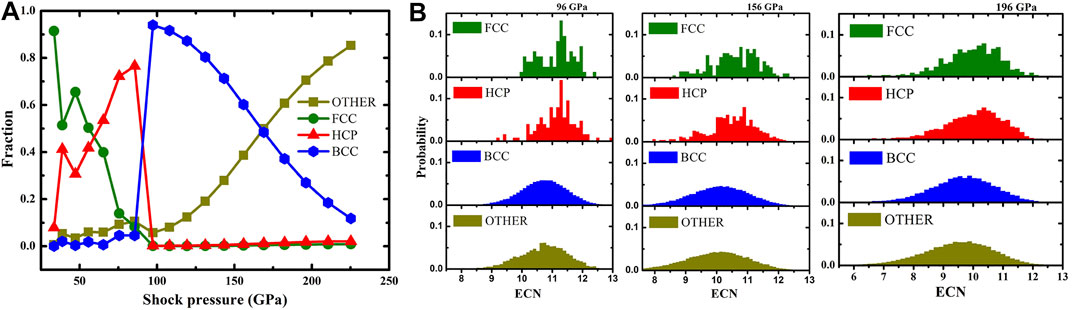
FIGURE 2. (A) The fraction of atoms with four structural types under different shock pressure are analyzed by a-CNA. (B) The ECN distribution of atoms with corresponding structures under three typical pressure.
In particular, the phase diagram of Cu has been known only to a pressure range below 500 GPa and mostly about solid–liquid transition[12,43]. The phase diagram of Cu is shown in Figure 3. The non-equilibrium processes based on the thermodynamic integration (ne-TI) method have been performed for the free energy calculations. The shock-induced BCC structures are generated by MSST simulations in the shock velocity of 7.4 km/s, corresponding to 156 GPa, 3400 K. The phase boundary of FCC–BCC along principal Hugoniot is located around 150 GPa (Supplementary Figure S6), which supported the results of XRD diagnosis. Based on the above discussion, the shock-induced BCC structure can be redefined as perfect BCC with disorders. This special structure found in simulation is characterized to be short-range disordered and meanwhile in long-time statistical averaged order. It is worthy to emphasize that the short-range disordered structures play a significant role in lowering the phase transition energy barrier in the FCC–BCC transition.
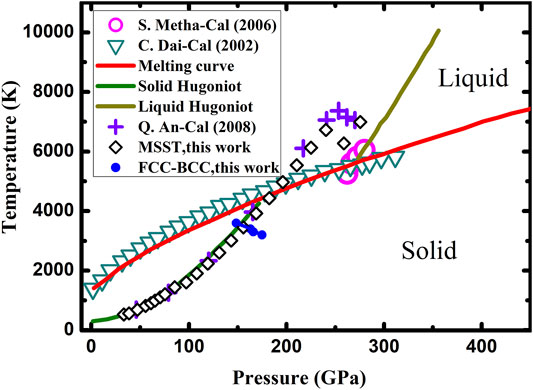
FIGURE 3. Phase diagram of compressed copper. The blue dots denote thermodynamic equilibrium states, which indicate that the Gibbs free energy difference equals to zero. The phase boundary of FCC–BCC (blue line) is obtained by square polynomial fitting on the blue dots (simulation data) [40]; [42]. Other results obtained from Ref [[12,43–45]].
4 Conclusion
In summary, the present investigation using molecular dynamics simulations to examine copper shock compressed to a wide range of P–T conditions provides detailed microscopic information about the structural transformation process that cannot be observed by experiments. The present finding regarding the FCC–BCC transition is in agreement with the recent in situ XRD results for shock-compressed Cu. In contrast to static and ramp compression, shock wave compression results in rapid pressure load and concomitant temperature increase. Shock compression of Cu generates the instantaneous disordered structure based on the a-CNA and ECN method; the particular structure is long-range ordered through XRD diagnosis. As discussed above, there is a clear link between the occurrence of the FCC–BCC phase transformation and the presence of shock-induced disordered structures. Therefore, the generation of disordered structures in shock-compressed Cu would reduce the Gibbs free energies of the BCC crystal. Such investigations would elucidate possible fundamental differences between shock compression and static compression in the microscopic nature.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.
Author Contributions
JD, ZZ, and BC designed the research; WL performed molecular dynamics simulations; QZ, XY, and SZ contributed to the analysis of the data; JD, WL, and BC wrote the manuscript.
Funding
This work was supported by the National Key R and D Program of China under Grant Nos. 2017YFA0403200, the Science Challenge Project under Grant Nos. TZ2016001, the National Natural Science Foundation of China under Grant Nos. 11774429, 11874424, and 12104507, the NSAF under Grant Nos. U1830206, and the Science and Technology Innovation Program of Hunan Province under Grant No. 2021RC4026.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We are grateful for the insightful discussions with Jiahao Chen. All calculations were carried out at the Research Center of Supercomputing Application at NUDT.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.838316/full#supplementary-material
References
1. Tateno S, Hirose K, Ohishi Y, Tatsumi Y. The Structure of Iron in Earth's Inner Core. Science (2010) 330:359–61. doi:10.1126/science.1194662
2. Dubrovinsky L, Dubrovinskaia N, Bykova E, Bykov M, Prakapenka V, Prescher C, et al. The Most Incompressible Metal Osmium at Static Pressures above 750 Gigapascals. Nature (2015) 525:226–9. doi:10.1038/nature14681
3. Boehly TR, Craxton RS, Hinterman TH, Kelly JH, Kessler TJ, Kumpan SA, et al. The Upgrade to the omega Laser System. Rev Scientific Instr (1995) 66:508–10. doi:10.1063/1.1146333
4. Hall CA, Knudson MD, Asay JR, Lemke R, Oliver B. High Velocity Flyer Plate Launch Capability on the sandia Z Accelerator. Int J impact Eng (2001) 26:275–87. doi:10.1016/s0734-743x(01)00088-4
5. Moses EI, Boyd RN, Remington BA, Keane CJ, Al-Ayat R. The National Ignition Facility: Ushering in a New Age for High Energy Density Science. Phys Plasmas (2009) 16:041006. doi:10.1063/1.3116505
6. Coppari F, Smith RF, Eggert JH, Wang J, Rygg JR, Lazicki A, et al. Experimental Evidence for a Phase Transition in Magnesium Oxide at Exoplanet Pressures. Nat Geosci (2013) 6:926–9. doi:10.1038/ngeo1948
7. Knudson MD, Desjarlais MP, Dolan DH. Shock-wave Exploration of the High-Pressure Phases of Carbon. Science (2008) 322:1822–5. doi:10.1126/science.1165278
8. Root S, Shulenburger L, Lemke RW, Dolan DH, Mattsson TR, Desjarlais MP. Shock Response and Phase Transitions of Mgo at Planetary Impact Conditions. Phys Rev Lett (2015) 115:198501. doi:10.1103/physrevlett.115.198501
9. Barrios MA, Boehly TR, Hicks DG, Fratanduono DE, Eggert JH, Collins GW, et al. Precision Equation-Of-State Measurements on National Ignition Facility Ablator Materials from 1 to 12 Mbar Using Laser-Driven Shock Waves. J Appl Phys (2012) 111:093515. doi:10.1063/1.4712050
10. Barrios MA, Hicks DG, Boehly TR, Fratanduono DE, Eggert JH, Celliers PM, et al. High-precision Measurements of the Equation of State of Hydrocarbons at 1-10 Mbar Using Laser-Driven Shock Waves. Phys Plasmas (2010) 17:056307. doi:10.1063/1.3358144
11. Kalantar DH, Belak JF, Collins GW, Colvin JD, Davies HM, Eggert JH, et al. Direct Observation of the Alpha-Epsilon Transition in Shock-Compressed Iron via Nanosecond X-ray Diffraction. Phys Rev Lett (2005) 95:075502. doi:10.1103/PhysRevLett.95.075502
12. An Q, Luo S-N, Han L-B, Zheng L, Tschauner O. Melting of Cu under Hydrostatic and Shock Wave Loading to High Pressures. J Phys Condens Matter (2008) 20:095220. doi:10.1088/0953-8984/20/9/095220
13. Murphy WJ, Higginbotham A, Kimminau G, Barbrel B, Bringa EM, Hawreliak J, et al. The Strength of Single crystal Copper under Uniaxial Shock Compression at 100 Gpa. J Phys Condens Matter (2010) 22:065404. doi:10.1088/0953-8984/22/6/065404
14. Turneaure SJ, Sinclair N, Gupta YM. Real-time Examination of Atomistic Mechanisms during Shock-Induced Structural Transformation in Silicon. Phys Rev Lett (2016) 117:045502. doi:10.1103/PhysRevLett.117.045502
15. McBride EE, Krygier A, Ehnes A, Galtier E, Harmand M, Konôpková Z, et al. Phase Transition Lowering in Dynamically Compressed Silicon. Nat Phys (2019) 15:89–94. doi:10.1038/s41567-018-0290-x
16. Sharma SM, Turneaure SJ, Winey JM, Gupta YM. What Determines the Fcc-Bcc Structural Transformation in Shock Compressed noble Metals? Phys Rev Lett (2020) 124:235701. doi:10.1103/physrevlett.124.235701
17. Liu Z-T, Chen B, Ling W-D, Bao N-Y, Kang D-D, Dai J-Y. Phase Transitions of Palladium under Dynamic Shock Compression. Acta Phys Sin (2022) 71:037102–1. doi:10.7498/aps.71.20211511
18. Mao HK, Bell PM, Shaner JW, Steinberg DJ. Specific Volume Measurements of Cu, Mo, Pd, and Ag and Calibration of the rubyR1fluorescence Pressure Gauge from 0.06 to 1 Mbar. J Appl Phys (1978) 49:3276–83. doi:10.1063/1.325277
19. Chijioke AD, Nellis WJ, Silvera IF. High-pressure Equations of State of Al, Cu, Ta, and W. J Appl Phys (2005) 98:073526. doi:10.1063/1.2071449
20. Wang Y, Ahuja R, Johansson B. Reduction of Shock-Wave Data with Mean-Field Potential Approach. J Appl Phys (2002) 92:6616–20. doi:10.1063/1.1518781
21. Mitchell AC, Nellis WJ. Shock Compression of Aluminum, Copper, and Tantalum. J Appl Phys (1981) 52:3363–74. doi:10.1063/1.329160
22. Mitchell AC, Nellis WJ, Moriarty JA, Heinle RA, Holmes NC, Tipton RE, et al. Equation of State of Al, Cu, Mo, and Pb at Shock Pressures up to 2.4 Tpa (24 Mbar). J Appl Phys (1991) 69:2981–6. doi:10.1063/1.348611
23. Yokoo M, Kawai N, Nakamura KG, Kondo K. Hugoniot Measurement by Hyper-Velocity Impact at Velocities up to 9 Km/s Using a Two-Stage Light-Gas Gun under Optimized Shot Conditions. Int J Impact Eng (2008) 35:1878–83. doi:10.1016/j.ijimpeng.2008.07.044
24. Kraus RG, Davis J-P, Seagle CT, Fratanduono DE, Swift DC, Brown JL, et al. Dynamic Compression of Copper to over 450 Gpa: A High-Pressure Standard. Phys Rev B (2016) 93:134105. doi:10.1103/physrevb.93.134105
25. Hayes D, Hixson R, McQueen R, 505. High Pressure Elastic Properties, Solid-Liquid Phase Boundary and Liquid Equation of State from Release Wave Measurements in Shock-Loaded Copper. AIP Conf Proc (2000). 483–8. doi:10.1063/1.1303521
26. Neogi A, Mitra N. A Metastable Phase of Shocked Bulk Single crystal Copper: An Atomistic Simulation Study. Sci Rep (2017) 7:7337–11. doi:10.1038/s41598-017-07809-1
27. Dewaele A, Loubeyre P, Mezouar M. Equations of State of Six Metals above 94 Gpa. Phys Rev B (2004) 70:094112. doi:10.1103/physrevb.70.094112
28. Greeff CW, Boettger JC, Graf MJ, Johnson JD. Theoretical Investigation of the Cu Eos Standard. J Phys Chem Sol (2006) 67:2033–40. doi:10.1016/j.jpcs.2006.05.055
29. Fratanduono DE, Smith RF, Ali SJ, Braun DG, Fernandez-Pañella A, Zhang S. Probing the Solid Phase of noble Metal Copper at Terapascal Conditions. Phys Rev Lett (2020) 124:015701. doi:10.1103/PhysRevLett.124.015701
30. Sharma SM, Turneaure SJ, Winey J, Gupta Y. Transformation of Shock-Compressed Copper to the Body-Centered-Cubic Structure at 180 Gpa. Phys Rev B (2020) 102:020103. doi:10.1103/physrevb.102.020103
31. Mishin Y, Mehl MJ, Papaconstantopoulos DA, Voter AF, Kress JD. Structural Stability and Lattice Defects in copper:Ab Initio, Tight-Binding, and Embedded-Atom Calculations. Phys Rev B (2001) 63:224106. doi:10.1103/physrevb.63.224106
32. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J Comput Phys (1995) 117:1–19. doi:10.1006/jcph.1995.1039
33. Reed EJ, Fried LE, Joannopoulos JD. A Method for Tractable Dynamical Studies of Single and Double Shock Compression. Phys Rev Lett (2003) 90:235503. doi:10.1103/physrevlett.90.235503
34. Coleman SP, Spearot DE, Capolungo L. Virtual Diffraction Analysis of Ni [0 1 0] Symmetric Tilt Grain Boundaries. Model Simul. Mater. Sci. Eng. (2013) 21:055020. doi:10.1088/0965-0393/21/5/055020
35. Tsuzuki H, Branicio PS, Rino JP. Structural Characterization of Deformed Crystals by Analysis of Common Atomic Neighborhood. Comp Phys Commun (2007) 177:518–23. doi:10.1016/j.cpc.2007.05.018
36. Stukowski A. Structure Identification Methods for Atomistic Simulations of Crystalline Materials. Model Simul. Mater. Sci. Eng. (2012) 20:045021. doi:10.1088/0965-0393/20/4/045021
37. Stukowski A. Visualization and Analysis of Atomistic Simulation Data with OVITO-The Open Visualization Tool. Model Simul. Mater. Sci. Eng. (2009) 18:015012. doi:10.1088/0965-0393/18/1/015012
38. Piotrowski MJ, Piquini P, Da Silva JLF. Density Functional Theory Investigation Of3d,4d, And5d13-Atom Metal Clusters. Phys Rev B (2010) 81:155446. doi:10.1103/physrevb.81.155446
39. Freitas R, Asta M, De Koning M. Nonequilibrium Free-Energy Calculation of Solids Using Lammps. Comput Mater Sci (2016) 112:333–41. doi:10.1016/j.commatsci.2015.10.050
40. Frenkel D, Smit B. Understanding Molecular Simulation: From Algorithms to Applications, 1. Elsevier (2001).
41. Straatsma TP, Berendsen HJC. Free Energy of Ionic Hydration: Analysis of a Thermodynamic Integration Technique to Evaluate Free Energy Differences by Molecular Dynamics Simulations. J Chem Phys (1988) 89:5876–86. doi:10.1063/1.455539
42. Taniuchi T, Tsuchiya T. The Melting Points of Mgo up to 4 Tpa Predicted Based on Ab Initio Thermodynamic Integration Molecular Dynamics. J Phys Condens Matter (2018) 30:114003. doi:10.1088/1361-648x/aaac96
43. McCoy CA, Knudson MD, Root S. Absolute Measurement of the Hugoniot and Sound Velocity of Liquid Copper at Multimegabar Pressures. Phys Rev B (2017) 96:174109. doi:10.1103/physrevb.96.174109
44. Mehta S. Theoretical Melt Curves of Al, Cu, Ta and Pb. In: AIP Conference Proceedings, 845. American Institute of Physics (2006). p. 258–61. doi:10.1063/1.2263312
Keywords: shock compression, structural transformation, molecular dynamics simulation, multi-scale shock technique, free energy calculation
Citation: Ling W, Chen B, Zeng Q, Yu X, Zhang S, Zhao Z and Dai J (2022) Atomic Insight Into Phase Transition Lowering in Shock Compressed Copper. Front. Phys. 10:838316. doi: 10.3389/fphy.2022.838316
Received: 17 December 2021; Accepted: 21 March 2022;
Published: 26 April 2022.
Edited by:
Venugopal Rao Soma, University of Hyderabad, IndiaReviewed by:
Ranjan Mittal, Bhabha Atomic Research Centre (BARC), IndiaPrem Kiran Paturi, University of Hyderabad, India
Copyright © 2022 Ling , Chen, Zeng , Yu , Zhang , Zhao and Dai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bo Chen, chenbochain@nudt.edu.cn; Jiayu Dai, jydai@nudt.edu.cn