Wind-wave forecasting in enclosed basins using statistically downscaled global wind forcing

Accurate wind-wave forecasting in enclosed and semi-enclosed basins is a challenging task, demanding primarily for high-resolution wind forcing at regional scale. This is generally obtained with dynamical downscaling from a low-to-mid resolution atmospheric model. In this context, a new wave forecasting system for the marginal Adriatic Sea is herein presented aimed at proposing an alternative strategy for accurate wind-wave forecasting in (semi-) enclosed basins that does not require an ad-hoc regional atmospheric model. The system is based on the state-of-the-art WAVEWATCH III^® spectral wave model forced by the global IFS-ECMWF forecast. At first, wind speed is quantile-corrected to account for the systematic underestimation over the Adriatic Sea. Then, the significant wave height in the target region and for regimes associated with marine storms is calibrated following standard procedure. Wind and wave observations from different sources are used for calibration and validation of the wave forecasts, which achieve satisfactory scores. We also compare results with those of other forecasting systems in the area, highlighting the importance of the wind forcing accuracy and the wave model calibration. Doing so, we discuss the challenges that characterise (semi-) enclosed environments in order to propose effective solutions for them and future developments.

Introduction

Nowadays the numerical prediction of sea-state characteristics (e.g., the significant wave height) has achieved such a level of development that it allows to forecast sea storms several days in advance with good accuracy (see for instance, Cavaleri et al., 2020; Haiden et al., 2021). However, frequently the wave forecasts show systematic errors in the significant wave height that need to be taken into account and eventually corrected. This happens at both global and regional scales, although it is particularly common in enclosed (or semi-enclosed) basins and along their coasts, where wind-wave forecasting is often far from being satisfactory.

It is well known that wind forcing quality is pivotal for accurate wave modelling as it represents the main source of error (Ardhuin et al., 2007; Cavaleri et al., 2018). In enclosed basins, wind waves are frequently underestimated because the wind fields used to force the wave models are not suitably reproduced. This happens when the horizontal resolution of the atmospheric model is not fine enough to properly represent the land/sea interface and the transition of the wind flow from land to sea, especially in the presence of orography (for a recent review on the topic, see Cavaleri et al., 2018). The most obvious solution to overcome this issue is the use of high-resolution wind fields, result of an atmospheric regional model that dynamically downscales the fields of a global circulation model. This operation is straightforward if a regional model is already operational in the target area and the wind fields are available, but it can become a serious obstacle for wave modellers if the atmospheric model is not available, for the effort and skills required to set-up and operate such a wind forecasting system with good scores. An alternative solution is the use of the available wind forcing, e.g., the global atmospheric model wind fields produced and distributed by large forecasting centres (e.g., the European Centre for Medium-Range Weather Forecast, ECMWF, or the United States National Weather Service), properly corrected to account for the errors induced by the basin peculiarities. This procedure, combined to a wave model calibration, can lead equally to satisfactory results in wind-wave forecasting as we will show here. Indeed, for instance, Durrant et al. (2013) have shown that a wind correction to reduce the wind bias improves wave forecasts but not universally, with residual significant wave height biases ascribable to wave model deficiencies.

In this paper we propose a methodology to improve significant wave height forecasts in a semi-enclosed basin that relies on the use global wind forcing fields and on a two-step calibration: the first step involves wind correction and the second step wave model calibration. Our first goal is therefore the reduction of the wind forcing systematic error. Here, we pursue it by means of a statistical correction. Other wave forecasting systems benefit of such a wind correction: for instance, the HENETUS system operational in the Adriatic Sea (Bertotti et al., 2011) adopts a wind speed enhancement methodology based on wind speed scaling using a single basin-specific coefficient (1.16 in the last version). That type of scaling (hereinafter, “linear regression scaling”) is determined by the inverse of the slope of the linear regression line between model and observed wind speeds. More generally, Durrant et al. (2014) have discussed and tested different types of linear regression scaling of global wind fields for wave forecasts, accounting also for the spatial and temporal variability of the wind field errors. Here we follow a similar although more complex strategy. We obtain a scaling of the model wind speed that can account for different factors: (i) the wind speed regime, (ii) the wind direction and (iii) the geographical position. The rationale is that the wind speeds belonging to different regimes and coming from different directions need different scaling factors to match observations. At the same time, given the often complex geographical layout of enclosed basins and the high spatially variable wind fields, wind speeds at different positions may also require a different scaling as well. A speed-dependent scaling of the model wind can be obtained by means of the Quantile-Quantile Matching approach (hereinafter QQM; Wood et al., 2004; Deque, 2007; Michelangeli et al., 2009; Colette et al., 2012). QQM is a statistical technique originally developed to obtain information on the regional climate, downscaling the Global Circulation Model values by means of local observations or model reanalysis (Michelangeli et al., 2009; Adachi and Tomita, 2020). The advantage of QQM is that it potentially corrects all biases in the climate model distribution since the transfer function is quantile-specific. This allows for different scaling of the low, moderate and strong wind speeds (Li et al., 2019). Climate wave models forced by bias-corrected winds have shown a significant improvement of the simulated climate at different scales (Hemer Mark et al., 2012; Benetazzo et al., 2022). Here we apply it for the first time to our best knowledge to wind-wave forecasts.

As a paradigm for the proposed methodology, we present “PELMO”, an operational system purposely developed to forecast wind waves in the semi-enclosed Adriatic Sea, with special focus on the northern part of the basin where forecasts are even more challenging. Doing so, we also aim at targeting the stormy sea states that represent a threaten to littorals and cities in the Gulf of Venice. It is the first and only wave forecasting system for the Adriatic Sea based on the state-of-the-art WAVEWATCHIII^® model (WW3DG, 2019) to date. “PELMO” features a two-step calibration aimed at minimizing the systematic errors in the global wind forcing used, i.e., the operational wind forecasts produced by the Integrated Forecasting System of ECMWF (hereinafter, IFS-ECMWF), and in the corresponding wave forecasts. In the Adriatic Sea, the IFS-ECMWF forecasts have been shown previously to systematically underestimate the wind speed (Cavaleri and Bertotti, 2006), with different levels of performance depending on the horizontal resolution. Despite the increase in resolution with respect to the IFS-ECMWF model cycles considered in the Cavaleri and Bertotti (2006) study, the underestimation is also found in the wind forcing used to drive the “PELMO” wave model, as it will be shown later in the "Results" section.

The paper is structured as follows. In "Materials and methods" section, we start presenting the case study area, the wave model set-up, the wind forcing fields and the wind and wave observations used to calibrate and validate the system. Then, we present the correction and calibration methodologies adopted. In "Results" section, after assessing the wind forcing fields and showing the need for a correction, we present the calibration and validation results of the “PELMO” system and its forecasting skills, also compared to the results of other forecasting systems. Finally, we close the paper with "Discussions and conclusions" section, highlighting the strengths and limits of the methodology and of the “PELMO” system and foreseeing the future developments.

Materials and methods

The study area

The Adriatic Sea, in the northern part of the Mediterranean Sea (Figure 1), is a clear example of how difficult good quality wind-wave forecasts in a semi-enclosed basin can be (Bertotti et al., 2011). For this reason, it is a good context to test our proposed methodology. Indeed, with its narrow, elongated shape (800 km long and 200 km wide, on average) open only on the southernmost end, and with mountain ridges on the northern, eastern and western sides, it makes the wind and wave forecasts a challenging task, especially in the northernmost part of the basin, called the Gulf of Venice. This shallow area (27-meter deep on average) can experience high stormy waves and extreme sea levels bringing erosion and coastal flooding that threaten the littorals and the coastal cultural World Heritage sites (http://whc.unesco.org/, last access: 24 May 2022), including Venice (Italy) and its lagoon. The climate of the Adriatic Sea region is characterized by synoptic weather variations, modulated by a strong seasonal variability (see Cushman-Roisin et al., 2001). The synoptic variations are associated with the passage of mid-latitude pressure lows, which brings a change in the wind field, typically turning from southerly to northerly winds. Hence, the sea storms in the Adriatic Sea mainly occur in the cold seasons (i.e., late autumn, winter, early spring) and are driven by: (i) the southeasterly wind called “Sirocco” (Figure 1B), a humid wind blowing over the major basin axis and reaching the highest speeds on the eastern coasts; (ii) the northeasterly wind called “Bora” (Figure 1B), a dry katabatic wind blowing from the Trieste gap and other gaps of the Dinaric Alps (e.g., Split and Senj). During summer, weak northwesterly winds with daily sea-breeze variations along the coasts prevail. In the northern Adriatic Sea, waves generated by Sirocco wind are typically mature and well-developed waves as they have travelled for hundreds of kilometers still receiving energy from the blowing wind. They can reach significant wave height of several meters even close to the coast (e.g., 6-meter high, during the 2018 “Vaia” storm; Cavaleri et al., 2019), where the growth is however limited by the finite depth, causing erosion on the northern littoral. Wind waves generated by Bora are instead young, steep and fetch-limited waves that can occasionally reach very high wave heights over the western coast, in front of the Bora jets.

FIGURE 1

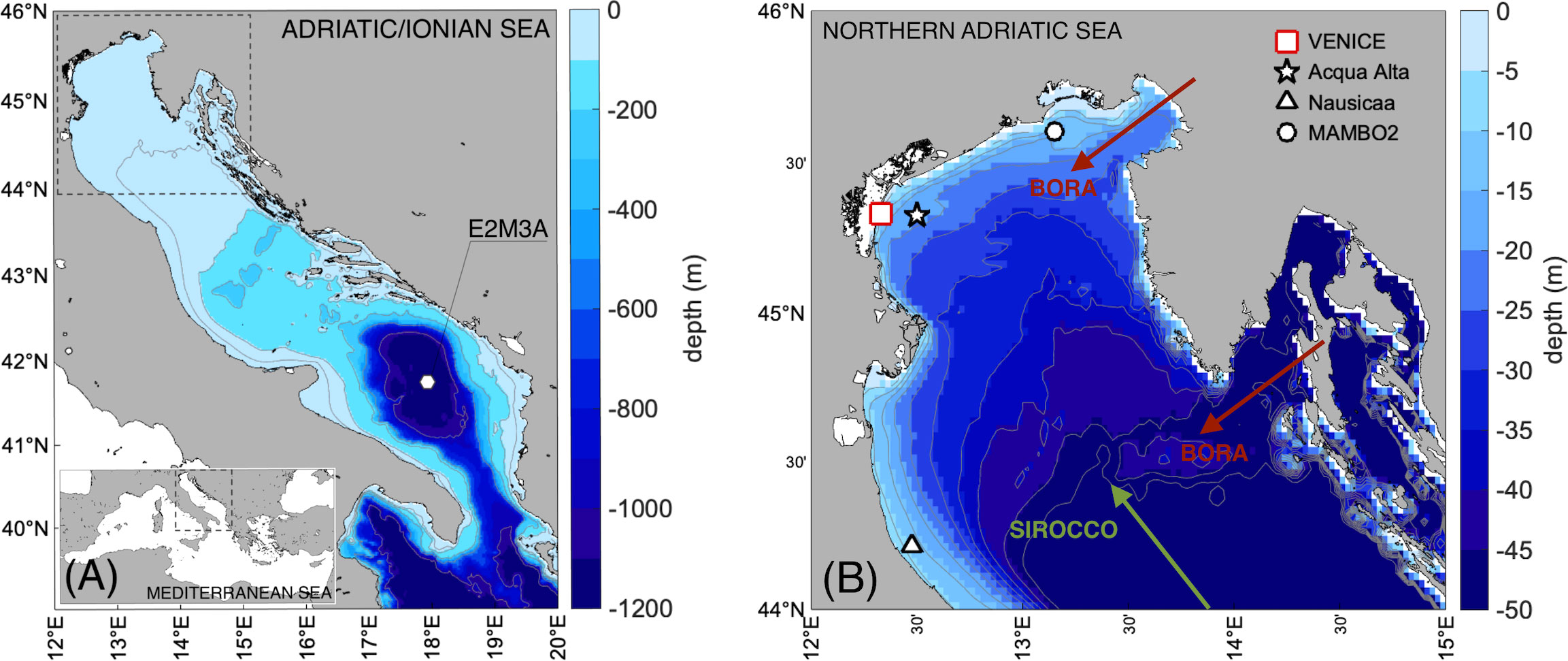
Figure 1 PELMO wave model computational grid (physical space). (A) Adriatic/Ionian Sea grid (colored region) and bathymetry. The Mediterranean Sea region is shown in the bottom-left corner. (B) northern Adriatic Sea zoom (target zone, dashed line square in (A). Venice lagoon and the four stations for in-situ measurements used in the study (“Acqua Alta”, “Nausicaa”, “E2M3A”, “MAMBO2”) are shown in (A, B) Principal winds in the northern Adriatic Sea (northeasterly Bora and southeasterly Sirocco) are shown as arrows in (B).

Forecasting wind waves in the Adriatic Sea, and in the “Gulf of Venice” in particular, is functional to the early warnings in case of sea storms, to support the protection of cities and littorals from coastal flooding and erosion, and to complement the storm surge forecasts for Venice during the so-called “Acqua Alta” events, i.e., the extreme sea levels caused by the combination of the astronomical tide and the meteorological surge (including wave set-up) forced by Sirocco wind (for a summary on the sea storm management strategy in the Adriatic Sea, see Ferrarin et al., 2020). Nowadays, there are several forecasting systems that include the Adriatic Sea as a part of larger computational domains, either at global (e.g., the Integrated Forecasting System of ECMWF) or at regional, i.e., Mediterranean, scale (e.g., ICON-EU7 of DWD). However, for the reasons we have introduced before, the geographical and meteorological complexity of the Adriatic Sea requires ad-hoc wind and wave model configurations to better forecast the sea states which are otherwise generally reproduced with larger systematic errors compared to other Mediterranean Sea sub-basins (Barbariol et al., 2021). There are only three forecasting systems developed for the Adriatic Sea presently operational: the “HENETUS” system (Bertotti et al., 2011), based on the WAM wave model, developed by CNR-ISMAR (Italy) and operated by the “Tide Forecast and Early Warning Center” (Venice, Italy); the “ADRIAC” system (Valentini et al., 2007), based on the SWAN model and operated by ARPAE (Agency for Envinronmental Protection and Energy of Emilia-Romagna, Italy); the “WWM” system (Dutour et al., 2018), based on the WWM model and operated at the Croatian Meteorological and Hydrological Service (Croatia).

Wave model setup

The PELMO wave forecasting system developed in this study relies on the state-of-the-art spectral wave model WAVEWATCHIII^® (hereinafter WW3; Tolman, 1991; WW3DG, 2019); https://polar.ncep.noaa.gov/waves), which numerically solves the spectral wave energy density balance equation expressed in terms of the wave action density $N=E\left(k,\theta ;x,y,t\right)/\sigma$ (Gelci et al., 1957):

$\begin{array}{ll}\frac{DN}{Dt}=\frac{S}{\sigma }& (1)\end{array}$

E is the directional wave spectrum, representing the distribution of the wave energy and its variation over a spectral space with dimensions θ and k (i.e., direction and wavenumber), over a physical space of dimensions x and y (i.e., longitude and latitude) and over time t, and σ is the intrinsic wave frequency. The left-hand side of the eq (1) represents the rate of change of the wave energy, advected over the physical and spectral spaces, including changes due to an ambient mean current (if any). Numerous parameterizations of the source terms S (right-hand side of eq (1)) allow the computation of, among the others, the growth of wave energy from wind input, the decay from dissipative processes (with breaking as the dominant one), the energy transfer by non-linear wave-wave interactions and the change due to nearshore processes (including shoaling, refraction and bottom friction).

The numerical solution of the spectral action density balance equation (1) by a spectral wave model as WW3 requires two computational grids: (i) one representing the physical space (x, y) and (ii) one the spectral space (k, θ). Both the grids have been implemented in this study with the goals of optimizing the representation of the sea states in the coastal areas of the northern Adriatic Sea and of keeping the computational cost compatible with the requirement of a forecasting system. With regard to the physical space grid, for the modelling system in subject a high-resolution regular structured grid of the Adriatic Sea and the northern Ionian Sea has been implemented (Figure 1A). The rectangular cells, that help capturing the fine structures, have sides of 0.025° both in longitude and latitude, corresponding in the northern Adriatic Sea area to linear lengths of 2 km and 2.8 km (Table 1). In the intermediate water regions, the bottom gradients are small and thus well reproduced by the width of the cells. The alternative choice of an unstructured mesh would have increased dramatically the computational cost if wishing to maintain the same degree of resolution. The northern Ionian Sea was included to keep the southernmost part of the semi-enclosed Adriatic Sea far from the model open boundary and to ensure a proper development of the south-easterly wave systems driven by the along-basin wind (namely, Sirocco), which are among the most intense in the northern Adriatic Sea given the long (800 km) fetch available. The model bathymetry was obtained by interpolating a high-resolution bathymetric dataset (1/16’, corresponding to about 80 m at this latitude; https://www.emodnet-bathymetry.eu), obtained by harmonizing a very high-resolution survey (CNR-ISMAR) and the GEBCO survey (General Bathymetric Chart of the Oceans; 15” resolution, i.e. about 330 m), on the computational grid.

TABLE 1

Table 1 Model setup: Computational domain characteristics (physical and spectral space) and timesteps ∆t.

The spectral computational grid consists of 36 directions and 32 wavenumbers (Table 1). The directions are uniformly distributed between 5° and 355°, with spacing of 10°. The wavenumbers obey the linear dispersion relationship, which relates them to the intrinsic wave frequencies f, herein set up in the $0.07\le f\le 1.34$ Hz range and geometrically distributed with a 1.1 factor increment from one frequency to the next. These cut-off frequencies, the minimum (0.07 Hz) corresponding to a period of 14.28 s and deep-water wavelengths of 318 m, the maximum (1.34 Hz) to 0.75 s and 0.85 m, have been chosen on the basis of the characteristics of the study area (its climatology in particular) and of the desired computational cost. Indeed, given the higher frequency of young and fetch-limited sea states in the Adriatic Sea with respect to mature waves (i.e., swell), a more detailed description of the shorter spectral wave components of the spectrum is preferred compared to the longer ones, which also directly influence the Courant-Friedrich-Levy condition (for stability purposes, the longer the longest spectral wave components, the finer the time discretization of eq. (1)). Appreciable energy levels below 0.07 Hz in northern Adriatic Sea model frequency spectra are only present at the peak of very intense storms. However, even in strong events with mature waves from the south (such as the 2018 “Vaia” storm) the variance associated with this long-wave range at the “Acqua Alta” tower is much smaller than the 1% of the total variance. The four time steps used, each corresponding to the numerical solution of a different part of the energy balance equation, are reported in Table 1.

The WW3 code is designed in a flexible way that enhances the efficiency at machine level: after a dedicated pre-processing the code actually passed to the compiler includes only the necessary model options and parametrizations declared via a “switch” flag list (WW3DG, 2019). PELMO’s WW3 code has been built choosing the following flags: F90 NOGRB NC4 DIST MPI PR3 UQ FLX0 LN1 ST4 NL1 BT1 DB1 MLIM TR0 BS0 IC0 IS0 REF0 XX0 WNT1 WNX1 CRT1 CRX1. The key options for the present implementation are the followings (for the other, non-defined, switches we point the reader to the WW3 manual; WW3DG, 2019):

● PR3-UQ: third-order accurate numerical scheme for the solution of the energy balance equation (Tolman, 2002), with treatment of the so-called Garden Sprinkler Effect. The default setting of WW3.

● FLX0: flux computation included in source terms.

● LN1: linear input from Cavaleri and Rizzoli (1981)

● ST4: parameterization of the wind input and dissipation source terms according to Ardhuin et al. (2010). The available tuneable parameters have been set to the values obtained during previous successful tests in the Mediterranean Sea (i.e., TEST471 by Ardhuin et al. (2010) with $z_{0,max}=0.002$; Barbariol et al., 2017; Benetazzo et al., 2021), while the ${\beta }_{max}$ parameter that controls the wind input (Janssen, 2004) has been chosen as the model calibration parameter (as suggested by previous studies, e.g., Stopa, 2018). The wind input source term calibration is described in details in the "Wave model calibration" section. Previous tests comparing the chosen ST4 parameterization with the more recent ST6 parameterization during stormy events in the northern Adriatic Sea shown rather similar statistical scores in the model-observation assessment of the significant wave height (Benetazzo et al., 2021).

● NL1: calculation of the nonlinear wave-wave interaction source term according to the Discrete Interaction Approximation (DIA; Hasselmann et al., 1985).

● BT1: bottom friction according to JONSWAP formulation (Hasselmann et al., 1973).

● DB1: depth-induced wave breaking according to Battjes and Janssen (1978) formulation.

● MLIM: Miche-style shallow water limiter for the maximum wave energy (Miche, 1944).

● REF0: no reflection used.

● TR0: no triad interactions used.

● BS0: no bottom scattering used.

● WNT1-WNX1: linear interpolation in space and time of the wind speed.

Wind forcing model data

In this study we use two wind model datasets: one is used to force the wave model and the other is used to calibrate the wind forcing. The first is presented in this section, while the second in the following one.

The wind data used to force the PELMO wave model are the zonal ($u_{10n})$ and meridional ($v_{10n})$ horizontal components of the 10-m neutral wind speed produced by the Integrated Forecasting System (IFS). IFS is the global coupled atmosphere-ocean-wave-land numerical weather prediction system of the European Centre for Medium Range Weather Forecast (ECMWF), at present the forecasting system with the highest scores among the ones of the major centres in the world (Haiden et al., 2021). The neutral wind is preferred to the real wind as it is more relevant to the wind input parameterisations used in the wave model and insensitive to the stability/instability conditions of the lower atmosphere. The deterministic forecast fields (HRES) are emitted four times a day at 00UTC, 06UTC, 12UTC and 18UTC analysis times. For PELMO, we use the 00UTC and 12UTC forecasts, which have hourly resolution for the first 90 fields and tri-hourly resolution for the last 34 fields, for a total 10-day forecast range. The dataset extends over 1.5 years, starting 01 January 2018 and ending 30 June 2019 (Table 2). The wind fields cover the entire Mediterranean Sea with a spatial resolution of 0.1° × 0.1° (approximately 11 km × 8 km in the northern Adriatic Sea). As pointed out by Signell et al. (2005), an accurate representation of the wind and wave fields in a semi-enclosed basin where orography plays an important role, as in the case of the Adriatic Sea, requires high resolution wind data (finer than about 10 km for the Adriatic Sea). They bring both a finer representation of small-scale atmospheric features and stronger and more accurate wind speeds, especially during storm events. For these reasons, IFS wind fields are here assessed against observations and then corrected to match (in a statistical sense) the observations. IFS-ECMWF model winds are complemented with collocated satellite-borne data, as described in next section.

TABLE 2

Table 2 Duration of calibration, validation and WW3 forcing periods, using scatterometer and IFS-ECMWF neutral wind speed.

Wind and wave observations

For the assessment and correction of the model wind fields we have used the scatterometer wind data provided by the Copernicus Marine Environment Monitoring Service (CMEMS; url: https://resources.marine.copernicus.eu/products; EU Copernicus Marine Service, 2020) as reference. We consider the METOP-A and METOP-B scatterometers ASCAT Level 3 (L3) stress-equivalent 10-m wind speed components ${\widehat{u}}_{10s}$ and ${\widehat{v}}_{10s}$ (hat denoting observations; OSI SAF/EARS Winds Team, 2019), gridded over a $0.125°\times 0.125°$ regular grid covering the Adriatic and northern Ionian seas. The REAL-TIME version of the observed wind speed data we use is accompanied by the co-located IFS-ECMWF wind speed product (received twice a day at 00UTC and 12UTC with hourly resolution and interpolated on the space and time scatterometer data coordinates), which are exactly the field we use to force the PELMO system, although they cannot be used to force the wave model. During the total 5.55 years considered (from March 2016 to November 2021, Table 3), although IFS-ECWMF has undergone model changes (from Cycle 41r2 through Cycle 47r2), the atmospheric model characteristics have not significantly changed (e.g., the horizontal resolution remained constant over time).

TABLE 3

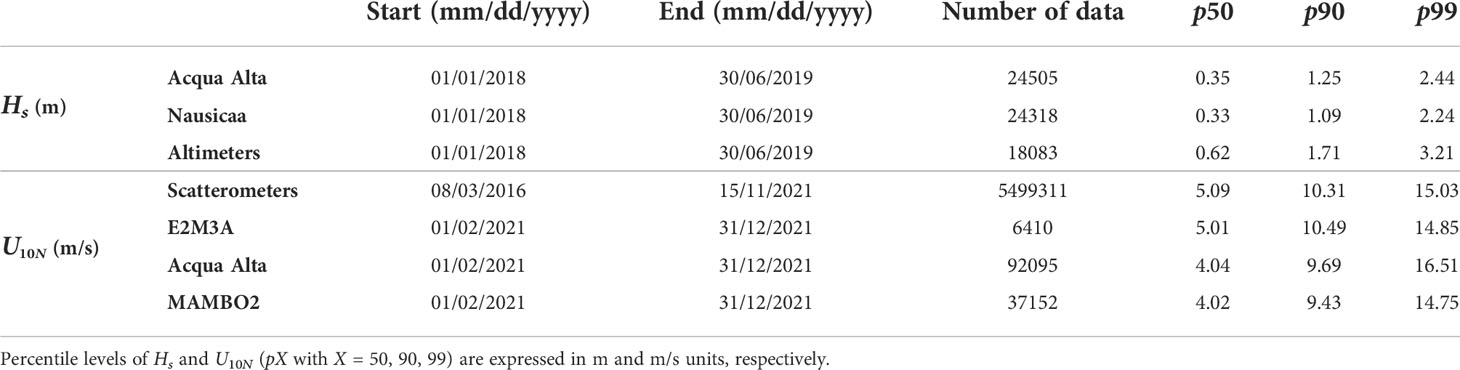
Table 3 Available in-situ and remote sensed observations of significant wave height H_s and 10-meter neutral wind speed $U_{10N}={\left(u_{10n}^2+v_{10n}^2\right)}^{0.5}$ used in the study for the calibration and validation of the PELMO wind forcing and wave model.

For the purpose of wind correction and validation, we have split the 5.55-year duration into (i) a 3.3-year calibration period (from March 2016 to June 2019), used to derive the wind speed correction, and (ii) a 2.25-year validation period (from July 2019 to September 2021), used to verify the correction over a different dataset. The 1.5-year forcing period (from January 2018 to June 2019) used to force the wave model for the purposes of this study is included in the wind calibration period. The characteristics of the three periods are summarized in Table 2. We have directly compared the observed and co-located model wind data provided by CMEMS to assess the quality of the model wind speed in the Adriatic Sea, derive a correction (calibration period, about 3-million co-located data), and verify the correction on a different dataset (validation period, about 2.5-million co-located data). Then, we have forced the WW3 wave model with the 1.5-year dataset described in "Wind forcing model data" section. As the wind products provided by CMEMS are stress-equivalent winds (10s subscript), while the forcing we use in the PELMO system are neutral winds (10n subscript), we have converted the CMEMS winds accordingly. The neutral wind speed components derive from the stress-equivalent components according to the following equation (Kloe et al., 2017):

$\begin{array}{ll}{x}_{10\text{n}}=\frac{{\rho }_{air,g}}{{\rho }_{air,l}}{x}_{10\text{s}}& (2)\end{array}$

where x can be the zonal or meridional component of the model or observed wind speed, ${\rho }_{air,g}=1.225$ kg m^-3 is the global average air density and ${\rho }_{air,l}$ is the IFS-ECMWF local air density provided by CMEMS over the same grid of the wind speed data.

Additional in-situ wind observations are considered for the validation purposes of the corrected wind forcing. To this end we use the wind speed measured by anemometers at three stations (shown in Figure 1A, B): two coastal stations in the northern Adriatic Sea, “Acqua Alta” (coordinates: 12.51°E, 45.31°N; url: http://www.ismar.cnr.it/infrastrutture/piattaforma-acqua-alta) and “MAMBO2” (coordinates: 13.15°E, 45.60°N; url: https://nodc.ogs.it/erddap/index.html), and an open-sea station in the southern Adriatic Sea, “E2M3A” (coordinates: 18.08°E, 41.53°N; url: https://nodc.ogs.it/erddap/index.html). Characteristics of the datasets are summarized in Table 3, including the 50^th, 90^th, and 99^th percentile levels, which points to the typical and extreme wind conditions. The real wind speed at these stations is transformed to a 10-m neutral wind speed to be compared to the model wind speed using the COARE3.0 algorithm (Fairall et al., 2003) fed with air and sea characteristics close to the surface (air and water temperatures, relative humidity, and mean sea level air pressure, provided by complementary instruments at the stations; short- and long-wave radiation and PBL height, by default). As the data at “MAMBO2” and “E2M3A” are only available for 2021, we have considered an 11-month period (February-December 2021) for the three stations.

For the calibration of the wind input source term and the verification/validation of the PELMO wave model outputs (i.e., the significant wave height H_s) we have used three different observational datasets over the 1.5-year period of wind fields availability (01/01/2018-30/06/2019): (i) the remote sensed H_s from satellite altimeters over the whole Adriatic Sea, (ii) the in-situ H_s at the “Acqua Alta” oceanographic tower in the northern Adriatic Sea, and (iii) the in-situ H_s at the “Nausicaa” wave buoy in the northern Adriatic Sea (see Table 3 for a summary of the characteristics of the datasets). The satellite altimeter data are taken from the “Integrated Marine Observing System” platform (IMOS; url: https://imos.org.au; Ribal and Young, 2019), which collects various quality controlled and calibrated (cross-validated between satellite platforms and calibrated against buoys) satellite datasets, including those herein considered, i.e., the measurements collected by SARAL, SENTINEL-3A and JASON-3 missions. Only satellite data flagged as “good data” are retained. The in-situ “Acqua Alta” data have been collected by a Nortek Acoustic Wave and Current meter (AWAC) lying on the 17-m deep bottom, 15 km off the Venice littoral (white star in Figure 1B). The AWAC permanently acquires wave data at 2 Hz in the 0.02-0.99 Hz frequency range (0.02-0.49 Hz in case the pressure sensor is activated). The in-situ “Nausicaa” data have been gathered by a Datawell Directional Waverider anchored 7 km off the Cesenatico littoral at 10 m depth (coordinates: 12.48°E, 44.22°N; url: https://www.arpae.it/it/temi-ambientali/mare/dati-e-indicatori/dati-boa-ondametrica; white circle in Figure 1B). The wave buoy collects wave data at 2.56 Hz in the 0.025-1.00 Hz range. Despite the frequency range covered by the two in-situ instruments is different from that covered by the wave model, they overlap in the range that contains most of the spectral energy in the target region (i.e., over 0.07 Hz and below 0.5 Hz). The empirical 50^th, 90^th and 99^th percentile levels of the three datasets are shown in Table 3 and provide a picture of the global and local (northern littorals) Adriatic Sea wave climate, although with the limitations coming from the short duration and the basic statistics. In this context, the 50^th percentile of H_s from the altimeters, “Acqua Alta” and “Nausicaa” datasets are 0.62 m, 0.35 m and 0.33 m, respectively, the 90^th percentiles are 1.71 m, 1.25 m and 1.09 m, and the 99^th percentiles are 3.21 m, 2.44 m and 2.24 m.

Calibration strategy

The PELMO system has been calibrated to minimize the systematic error (i.e., the bias) of the short-term forecast with respect to the available observations. Calibration has been performed in two sequential steps. First, we have corrected the wind speed fields by minimizing the U_10N model-observation bias, using the scatterometer data over the whole Adriatic Sea as a target. Second, in agreement with other authors (e.g., Mentaschi et al., 2015; Stopa, 2018) we have calibrated the WW3 wind input source term by minimizing the H_s model-observation bias in the northern Adriatic Sea. Others have chosen to act on the dissipation source term to calibrate the wave model (e.g., Alipour et al., 2021). The choice of taking into account the sole significant wave height is due to service purposes: the PELMO forecasting system serves as an H_s based warning system for the communities living on the shorelines. Other characteristics, as the wave period and direction, might be evaluated in the future to help a more detailed characterization of flood prediction in case of marine storms. In this section, we describe in detail both the calibration procedures.

Wind speed correction

In the most general case, we assume that the correction of the wind speed can be obtained by scaling its components $(u_{10\text{n}},v_{10\text{n}})$ with a scaling function f such that:

$\begin{array}{ll}\begin{array}{l}{u}_{10nc}=u_{10n}f\left(U_{10N},{\vartheta }_{10N},X\right)\\ v_{10nc}=v_{10n}f\left(U_{10N},{\vartheta }_{10N},X\right)\end{array}& (3)\end{array}$

where$(u_{10\text{nc}},v_{10\text{nc}})$ are the calibrated wind speed components, $U_{10N}={\left(u_{10n}^2+v_{10n}^2\right)}^{0.5}$ is the wind speed, ${\vartheta }_{10\text{N}}$ is the wind (coming from) direction, and X is the geographical position. Taking into account these factors altogether or partially, we have tested an incremental complexity of the correction that leads to different levels of agreement between modelled wind and observations. In practice, we have obtained a wind speed scaling (i) first as a function of the wind speed and direction (i.e., $f\left(U_{10\text{N}},{\vartheta }_{10\text{N}}\right)$) and (ii) then as a function of the wind speed, direction and of the geographical position (i.e., $f\left(U_{10\text{N}},{\vartheta }_{10\text{N}},X\right))$. A disadvantage of such an a-posteriori bias correction may be the introduction of different levels of physical inconsistency of the corrected variables (e.g., wind speed and air temperature), as well as the loss of spatio-temporal correlation of a given variable when a grid point is corrected independently (i.e., the integrity of the forcing is not guaranteed). While the former does not apply in our study (only one variable is constrained and considered, i.e., the wind speed), the latter will be evaluated by assessing the corrected winds against measured in-situ data.

In this study, we take the observed wind speed probability distribution over a long period of time as the basis for correction. We discretize the percentiles of the wind speed distribution with a variable resolution, enhancing the representation of the low-probability values (over the 90^th percentile): (i) 1-percentile step between 0^th and 90^th percentile, (ii) 0.25-percentile step between 90^th and 99^th percentile, (iii) 0.1-percentile step between 99^th and 99.9^th percentile. For each i-th percentile of the model $U_{10\text{N}}$ distribution, the scaling of the two model wind components in Eq. (3) is defined according to a coefficient $f_i\left(U_{10\text{N}}\right)$, which is determined by the ratio between the observed, ${\widehat{U}}_{10\text{N},\text{i}}$, and the modeled, $U_{10\text{N},\text{i}},$ percentiles of the wind-speed distributions:

$\begin{array}{ll}{f}_i\left(U_{10N}\right)=\frac{{\widehat{U}}_{10N,i}}{U_{10N,i}}& (4)\end{array}$

where ${\widehat{U}}_{10\text{N}}$ and $U_{10\text{N}}$ can be either a function of the direction only, i.e., $U_{10\text{N}}\left({\vartheta }_{10\text{N}}\right)$, or both direction and position, i.e., $U_{10\text{N}}\left({\vartheta }_{10\text{N}},X\right)$.

As far as the geographical position is concerned, we derive two sets of scaling coefficients: the first is built for the whole Adriatic/Ionic dataset and is called global QQM (from now on, GQQM); the second is built locally at every single position X and is called local QQM (from now on, LQQM). The directional dependence is simplified for GQQM and LQQM in a way that a single set of wind speed-dependent scaling coefficients is obtained for each quadrant of wind direction. A similar approach, although based on a model-model data comparison, has been applied by Benetazzo et al. (2022) in the Adriatic Sea to correct the bias of ERA5 reanalysis wind speed.

Wave model calibration

For the calibration of the wind input source term, we search for the dimensionless growth coefficient ${\beta }_{max}$ that minimizes the model error with respect to the observations. The set of observations taken as a target for calibration, namely, the calibration target, is chosen on the basis of the statistics in Table 3, together with the requirement of forecasting the wave heights in the northern Adriatic Sea and in front of the city of Venice in particular (red square in Figure 1B). The mild and severe sea state conditions of the northern Adriatic Sea datasets (“Acqua Alta” and “Nausicaa”), i.e., beyond the 90^th percentile (Table 3), can be represented by the $1.0\le H_{\text{s}}\le 3.0$ m range. On this basis, we define the calibration target as the significant wave height between 1 and 3 m at the “Acqua Alta” tower, which is the closest wave measurement station to the Venice littoral.

Practically, the calibration of the wind input source term consists in the reiteration of the wave forecast using different ${\beta }_{max}$ values and assessing the performance of the wave model with respect to the observations (assumed true by definition), in order to identify the ${\beta }_{max}$ value that minimises the model error. The calibration algorithm is the following:

1. cycle over the ${\beta }_{max}$ values. For each value:

a. wave model simulation over a limited period representative of the events in the calibration target.

b. co-location of the forecast values H_s at “Acqua Alta” with respect to observations ${\widehat{H}}_s$.

c. evaluation of an objective function Φ (representing the model error with respect to the observations, in our case, the bias $<H_s-{\widehat{H}}_s>$, where the angle brackets denote ensemble average).

2. search for the optimal value of Φ as a function of ${\beta }_{max}$.

The wave forecasts (00UTC and 12UTC synoptic hour runs, leadtime from +1 to +48 hours) are forced with the calibrated wind speeds (Table 2) and the period that was chosen for calibration is 01/01/2019-30/06/2019, 6 months entailing winter and spring seasons and comprising 738 sea states at “Acqua Alta” with $1.0\le H_{\text{s}}\le 3.0$ m. Each forecast is initialised with the leadtime +13 wave field of the previous forecast, which corresponds to leadtime +1 (i.e., the initial conditions) of the current forecast (the first neutral wind field is at leadtime +1 since no analysis is produced). The choice of using the first 48 hours of the forecast for the calibration (instead of the available 90 hours) meets the request to optimise the forecast on the first two days, i.e., those characterised by the most accurate forecast winds. As the nearest grid node to the “Acqua Alta” platform (12.50°E, 45.33°N) in the wave model has a water depth of 18.28 m (instead of the actual 17 m) we have verified that the results obtained at 18.28 m are comparable with those obtained in the same position but with a depth of 17 m.

Values of ${\beta }_{max}$ are tested in a range between 1.4 and 1.8. The default value for ST4 parameterization is 1.43, with common variations from to 1.33 to 2.0 (WW3DG, 2019). The choice of the bias as the objective function for calibration is also confirmed by Mentaschi et al. (2015) who, analysing the sensitivity of bias and root mean square error (rmse) to changes in the parameters of the WW3 input and dissipation source term, reported a little impact on rmse. Similarly to what we do here, those authors calibrated the ${\beta }_{max}$ of a WW3 implementation over the Mediterranean Sea by minimising the bias of H_s compared to observations from wave buoys.

Results

Model wind forcing assessment

The neutral wind speeds $U_{10N}$ derived from scatterometer observations and forecasted by the IFS model are assessed in Figure 2 for the two winds that mostly contribute to the sea state generation in the northern Adriatic Sea, namely the northeasterly Bora and the southeasterly Sirocco. Indeed, we have classified the winds in the Adriatic Sea according to their (coming from) direction ${\vartheta }_{10N}$: Bora (1^st quadrant, $0°N\le {\vartheta }_{10N}<90°N$), Sirocco (2^nd quadrant, $90°N\le {\vartheta }_{10N}<180°N$), Libeccio (3^rd quadrant, $180°N\le {\vartheta }_{10N}<270°N$), Maestrale (4^th quadrant, 27$0°N\le {\vartheta }_{10N}<360°N$). The statistics for the three periods considered are presented, but we discuss only those related to the calibration period (in black color), as differences are rather small (especially between calibration and forcing datasets), with the largest ones emerging for wind speed percentiles beyond the 99^th. The Quantile-Quantile (QQ) plots in Figures 2A, C confirm the systematic underestimation of the model wind speed, with emerging differences between the two wind directions. The best-fit line slope is always smaller than 1 (the largest one is 0.90 for Sirocco) and the bias ranges from -0.50 m/s (Sirocco) to -0.67 m/s (Bora). The random error (root mean square error, rmse) is the largest for Bora (1.91 m/s) and the smallest for Sirocco (1.61 m/s), the latter overall resulting in the best modelled wind among the four directions, with the smallest systematic and random errors (Libeccio and Maestrale not shown here). The vertical bars represent the 50^th, 90^th and 99^th percentiles of the wind speed datasets. The model-observation ratios of the three percentiles are, respectively 0.92, 0.91, 0.90 for Bora, and 0.89, 0.94, 0.91 for Sirocco, pointing out a small but not negligible variation of the model performance over the wind regimes, in particular for Sirocco.

FIGURE 2

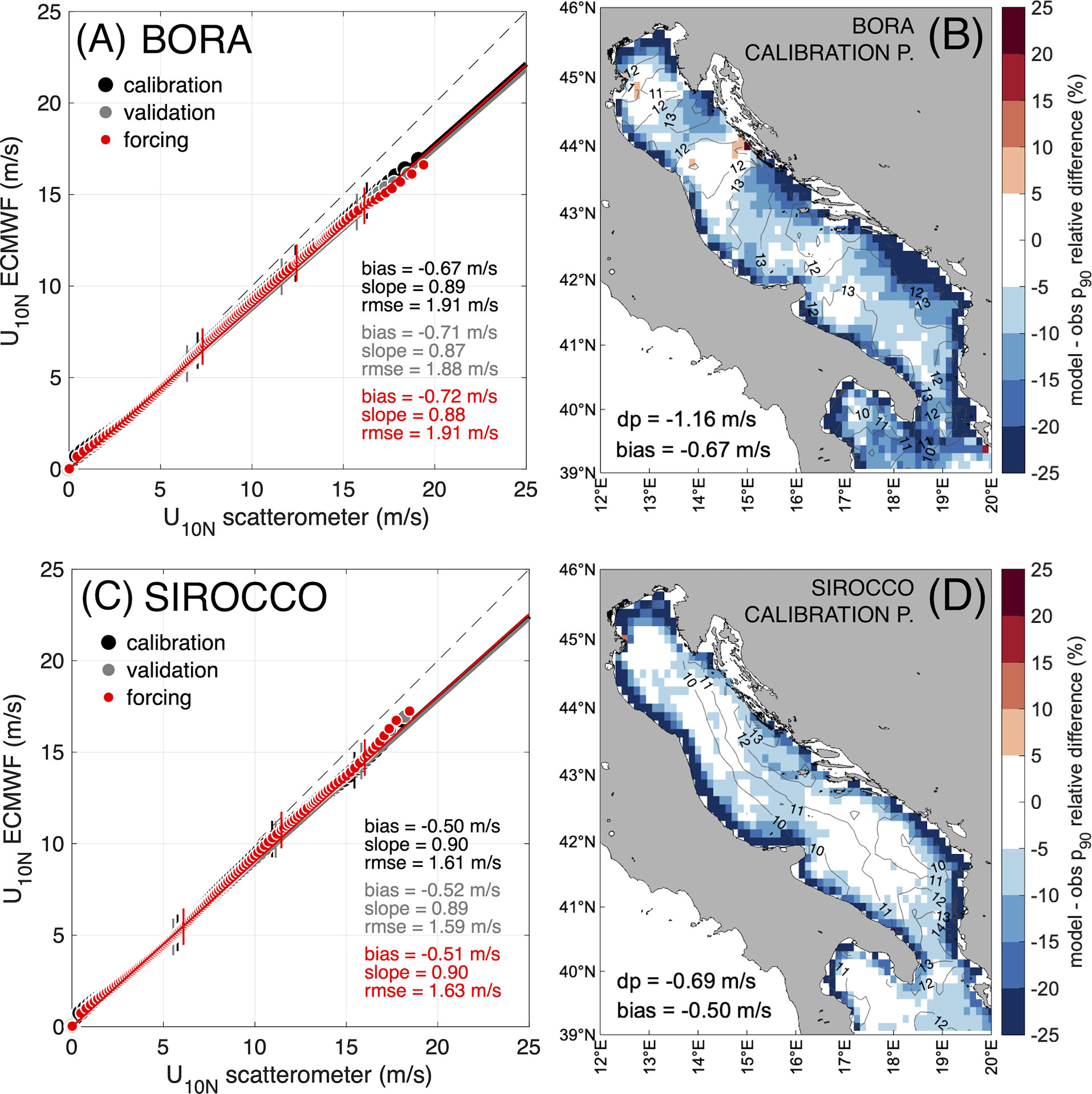
Figure 2 Comparison of wind speed U_10N from scatterometers and from IFS-ECMWF model (closest forecast) co-located on observations. Quantile-Quantile plots of Bora (A) and Sirocco winds (C) during wind calibration (black), wind validation (grey) and WW3 forcing periods (red; see Table 2). Statistical indicators of model performance: bias, root mean square error (rmse), and slope of the best-fit regression line (slope); see Appendix 1 for definition. Vertical bars represent (from left to right) the 50^th, 90^th and 99^th percentiles of the datasets. Model-observation 90^th percentile wind speed relative difference maps (%) during the calibration period for Bora (B) and Sirocco (D). dp is the relative difference of the ensemble 90^th percentile, bias is the bias of all the model with respect to the observed data. Contour lines are the observed wind speed 90^th percentile (m/s).

For Bora and Sirocco, the 90^th percentile wind speed is in the $10\le U_{10N}\le 12$ m/s range; those winds would theoretically generate fully developed sea states of $H_s=\left(0.21U^{{10}_{N}2}\right)/g$ (with g gravitational acceleration; (Ochi, 2005)) in the $2.14\le H_s\le 3.08$ m range. As this range almost completely falls within the $1.0\le H_s\le 3.0$ m target of the study, we now focus on the wind speed regime responsible for such wave heights. Accordingly, the maps in Figures 2B, D show the spatial distribution of the relative difference of the model-observation 90^th percentile wind speed, during the calibration period. The model underestimation is prevalent, especially close to the coasts, where the model wind speed can be down to -25% smaller than observations (see the "Discussions and conclusions" section for additional comments on this aspect). This is particularly evident in the northern Adriatic Sea, surrounded by coastlines on three sides. Offshore, the largest underestimation (down to -15%) is found in the regions where the strongest winds occur (see the contour lines in figures): (i) for Bora, in the wind jet regions in the east Adriatic (the northernmost one extending from the Gulf of Trieste towards the Gulf of Venice), (ii) for Sirocco, in the central Adriatic Sea. As a consequence, and particularly for Bora wind, the model-observation difference is characterised by a high spatial variability.

Summarizing, the IFS-ECMWF model wind speed systematically underestimates the observed wind speed over the Adriatic and Ionian Seas. The underestimation appears dependent on wind speed, wind direction and geographical position, so the correction should take these factors into account. Moreover, the three wind speed datasets have a similar statistic (although the validation and forcing datasets tend to be milder than the calibration dataset) and they will be used for the calibration/validation of the wind forcing in the next section.

Calibration

Wind speed correction

In Figure 3 the two correction strategies, GQQM and LQQM, are inter-compared during the wind calibration and validation periods, for Bora and Sirocco winds. The model-observation wind speed difference is shown as the relative difference of the local 90^th percentile, highlighting the difference of the ensemble 90^th percentile (dp) and the bias of all the data. Maps and comparative statistics for the calibration period (Figures 3A, C, E, G) aim at showing the effect of the quantile-specific bias correction on the calibration (including forcing) dataset, that is to abate the 90^th percentile difference and bias to zero for both Bora and Sirocco: globally, in case of the GQQM, and both globally and locally, in case of the LQQM. Indeed, LQQM fully corrects the systematic error (Figures 3C, G), while with the GQQM some local differences remain on the basin (Figures 3A, E): a negative difference belt persists along the coastlines (although narrower and with smaller differences compared to the uncalibrated dataset), while offshore regions present an alternance of negative and positive difference areas, with zero difference in-between. In general, model-observation differences for Bora are larger than for Sirocco (however, smaller than 25% in absolute value) and smaller where the wind speed is larger (see the contour lines in figures). For Bora, zero or negative difference occurs in the wind jet regions, with positive difference in-between the jets. For Sirocco, differences are mostly zero or slightly positive/negative, without a clear pattern. Thus, correction has been particularly effective in those offshore areas that presented the largest model underestimations (see Figures 2B, D).

FIGURE 3

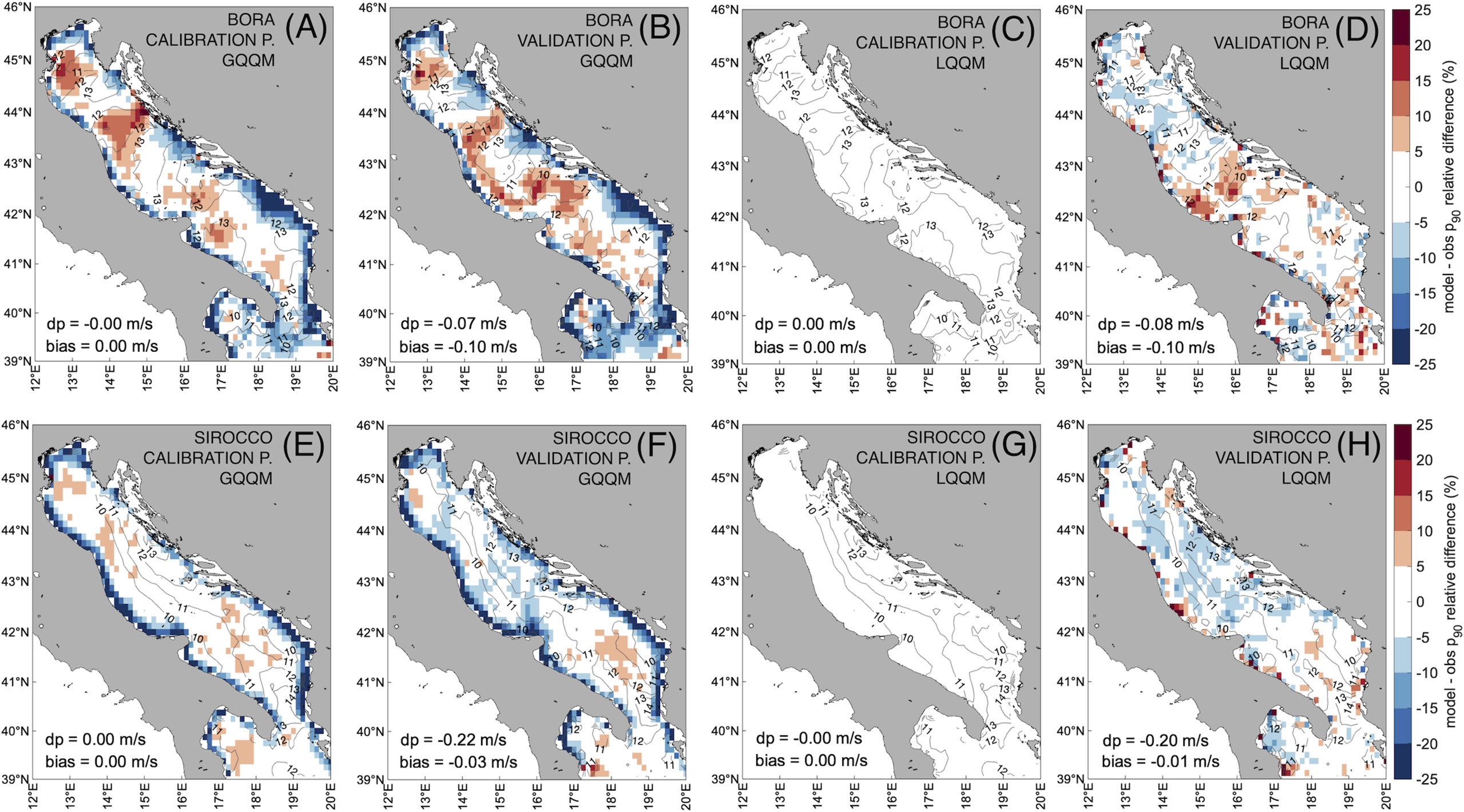
Figure 3 Comparison of wind forcing calibration strategies GQQM (A, B, E, F) and LQQM (C, D, G, H), during the calibration (A, C, E, G) and validation (B, D, F, H) periods, for Bora (A–D) and Sirocco (E–H). Model-observation 90^th percentile relative difference (%) over the Adriatic and Ionian Seas. dp is the difference of the ensemble 90^th percentile, bias is the mean model-observation difference of all the data. Contour lines are the observed wind speed 90^th percentiles (m/s).

Maps and comparative statistics for the validation period (Figures 3B, D, F, H) are used to assess the efficacy of the correction on a different, although statistically similar, dataset. Despite local differences, spatial patterns after GQQM resemble those observed in the calibration period. It is worth noting that the northernmost Bora wind jet that generates the young sea states in the Gulf of Venice is better modeled (though differences down to -15% persist close to the northern coast), whereas the Sirocco wind blowing from the southern Adriatic Sea and generating the mature sea states in the northern Adriatic Sea is well corrected with small model-observation differences (smaller than ±10%). Using LQQM (Figures 3C, D, G, H) small differences arise (mostly within ±10%), scattered over the Adriatic/Ionian seas without clear patterns. The model-observation differences after both GQQM and LQQM do not abate to zero as in the calibration period, although they reduce considerably with respect to the uncalibrated dataset, with ensemble bias of -0.10 m/s for Bora (it was -0.71 m/s, Figure 2) and smaller than -0.03 m/s for Sirocco (it was -0.52 m/s, Figure 2). The ensemble 90^th percentile difference is smaller than -0.08 m/s for Bora and -0.22 m/s for Sirocco.

To highlight the benefits of a quantile-specific correction, in Figure 4 we compare the two GQQM and LQQM scaling strategies over the wind speed percentile levels equal to or larger than 50 to a “directional linear scaling” (DLS) strategy, i.e., a linear regression scaling like the one adopted by the HENETUS system, applied to each wind direction quadrant. The two plots for Bora and Sirocco show the model performance in both the wind calibration and validation periods. The systematic underestimation of the uncorrected wind speed is evident, as it is evident its variability over all the percentile levels. The DLS does not correct the bias of the model data but simply scales them in a way that the difference over the percentiles (always positive in the percentile range shown) appears as a vertical shift towards 0 of the uncalibrated data difference. The slightly better agreement with observation of the uncalibrated data during the calibration period with respect to the validation period explains the better agreement of the DLS in the validation period (with respect to the calibration period), which is then a spurious effect. The figures show also that GQQM and LQQM fully correct the bias in the calibration period and achieve the best scores in the validation period. Indeed, despite a small underestimation, the QQM lines are generally closer to the 0-difference line (within 2%) than the DLS, especially for Bora at the largest percentiles (largest Sirocco percentiles are overestimated of a few percent).

FIGURE 4

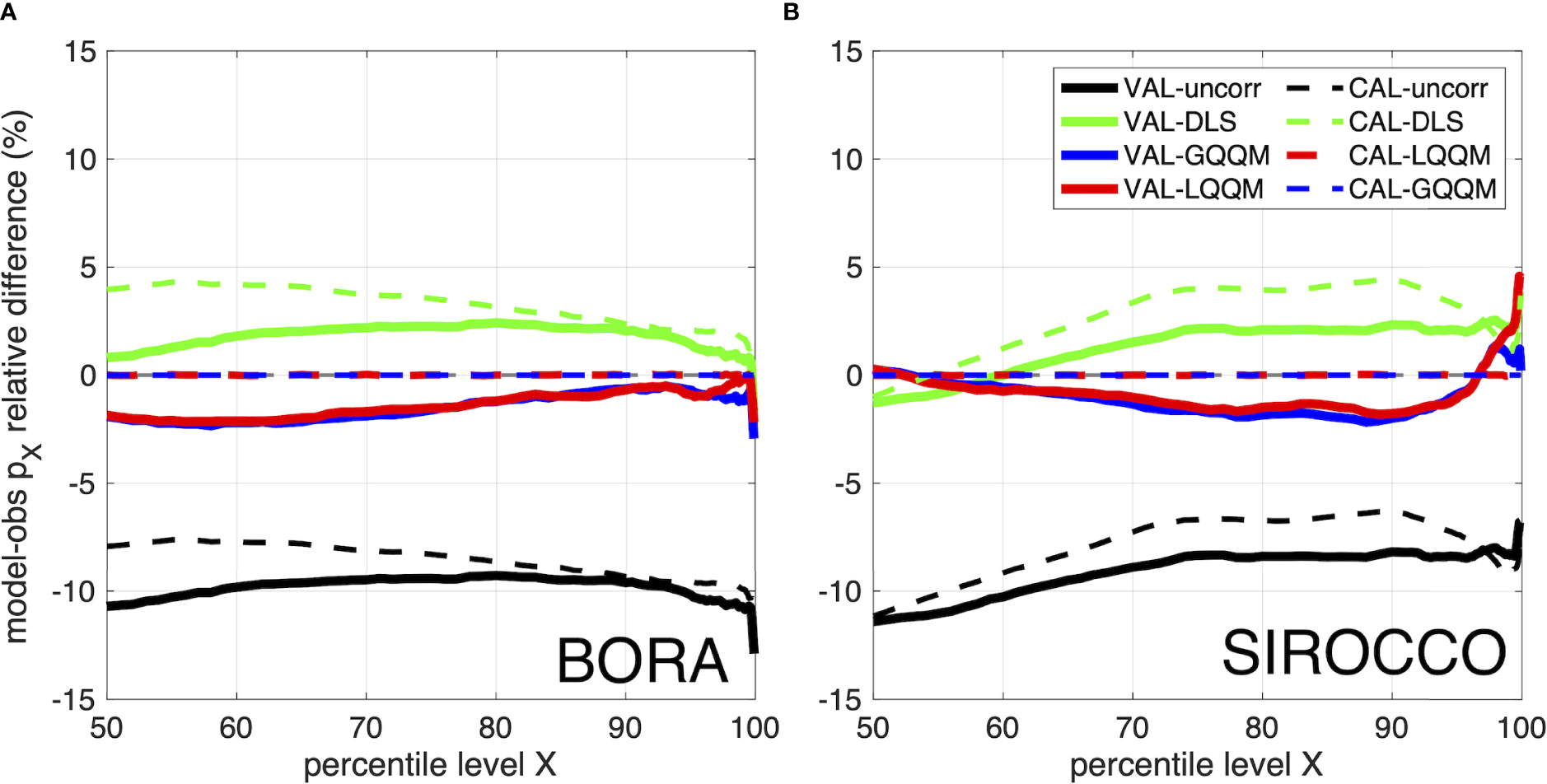
Figure 4 Comparison of different wind forcing calibration strategies for Bora (A) and Sirocco (B). Model-observation ensemble X^th percentile p_X relative difference (%) for percentiles from 50^th to 99.9^th: without correction (uncorr), after directional linear regression scaling (DLS), after global QQM scaling (GQQM) and after local QQM scaling (LQQM). Dashed lines represent values during the wind calibration period (CAL- labels in legend), solid lines during wind validation period (VAL- labels in legend).

In conclusion, the GQQM and LQQM strategies provide a similar correction of the wind speed and improve the correction obtained using DLS (Figure 3); the two QQM curves separate only at levels larger than 95, with GQQM doing better than LQQM for Sirocco. The ensemble 90^th percentile difference and the bias resulting after the two scaling strategies are comparable and the LQQM is not able to provide a full local bias correction (although the local differences are generally smaller than those after GQQM, Figure 4). Besides, LQQM has two drawbacks: the first is the need, for each geographical position, of a calibration dataset large enough (and ideally equal in the number of data) to provide a robust scaling, representative of the local climate; the second is the greater implementation complexity (especially in an operational context) compared to the simpler GQQM alternative. While this second issue can be overcome, the first is constrained by the observed data availability, which in the case of scatterometer data may not be guaranteed over all the geographical positions with the desired temporal and spatial frequencies. For all these reasons, despite the unquestionable preference for a local (position dependent) bias correction, in the following of the study and for the PELMO system we adopt the GQQM approach.

The GQQM strategy is further tested using independent wind speed datasets from three in-situ stations in the Adriatic Sea: the “E2M3A” open-sea station and the “Acqua Alta” and “MAMBO2” coastal stations (Figure 1A, B; Table 3). The quantile-quantile plots in Figure 5 compare the percentile levels of the uncorrected and GQQM-corrected model wind speed with the observed wind speed. Statistics of the systematic (bias) and random (rmse) errors are computed for the percentile levels larger than 50 (left vertical bar in the plots of Figure 5). At the open-sea station (Figure 5A) the GQQM scaling corrects the negative model bias (-0.80 m/s) bringing it close to 0 (0.03 m/s) and the slope of the regression line approaches the perfect-match 1:1 line, indicating an excellent performance in the southern Adriatic Sea offshore regions. The random error slightly increases after calibration (also at the coastal stations) but only of a few percent. At the coastal stations the calibration is not able to correct the bias, although it significantly reduces it, bringing it to -0.50 m/s (54% reduction) at “Acqua Alta” and to -0.57 m/s (57% reduction) at “MAMBO2”. The regression lines of the calibrated dataset and the quantile-quantile dots (close to the 1:1 reference line well over the 90^th percentile) show a significant improvement in the model-observation agreement after the GQQM scaling also in the coastal regions of the northern Adriatic Sea (target zone of the study), where the wind speed is now better represented despite a residual underestimation of the very intense wind speeds (at the 90^th percentile: -3% at “Acqua Alta” and “MAMBO2”; at the 99^th percentile: -14% at “Acqua Alta” and -15% at “MAMBO2”).

FIGURE 5

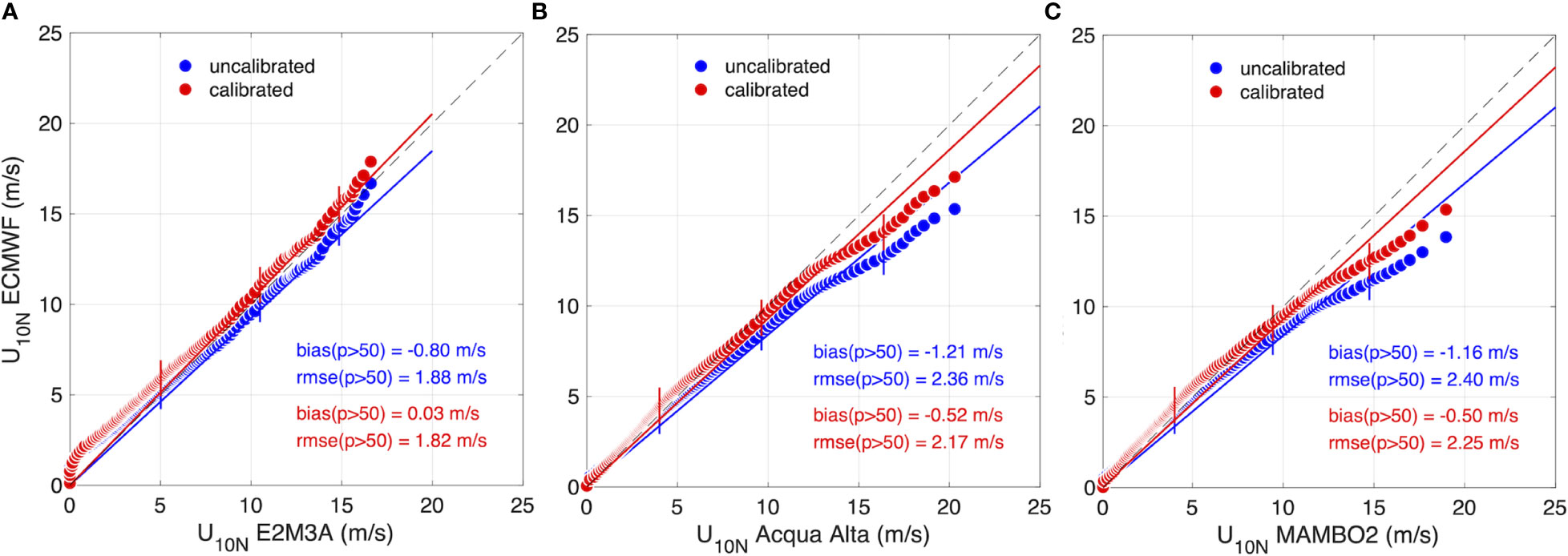
Figure 5 Verification of the wind forcing correction against in-situ wind speed data: comparison of uncorrected and corrected (GQQM) wind speed with observed wind speed at three stations in the Adriatic Sea ("E2M3A" (A), "Acqua Alta" (B), "MAMBO2" (C); Figure 1). Period: February-December 2021. bias and rmse are computed over the data exceeding the 50^th percentile observed values. Solid lines represent the regression lines and dashed line represent the reference 1:1 Line.

Implementation of GQQM in PELMO

Operationally, the GQQM scaling is used to correct the wind speed forcing in WW3 (Table 2). From the four wind speed-dependent scaling functions (one for each quadrant; Figure 6A), a two-dimensional array of wind scaling coefficients $f_i\left(U_{10\text{N}},\vartheta \right)$ (function of wind speed and direction) is obtained by interpolating the coefficients of each quadrant on a regular wind-speed axis (from 0 to 19.48 m/s, with step 0.02 m/s). Since the scaling functions are defined up to the 99.9^th percentile wind speed (smaller than 19.48 m/s for all the wind directions, see Figure 6A) we extrapolate beyond that value using the nearest neighbour approach, thus scaling the larger wind speeds (including those larger than 19.48 m/s) with the scaling value for the 99.9^th percentile. The interpolated/extrapolated coefficients are then imposed to all directions in the quadrant, except for the first and last 10 degrees of each quadrant (Figure 6B). Here, to smooth the transition between nearby directions belonging to different quadrants, we linearly interpolate the coefficients in each wind-speed bin over the 20° from one quadrant to the other. A FORTRAN program is used to efficiently correct 90 hourly fields over the whole Adriatic and northern Ionian seas taking about 3.5 minutes, which meets the operational requirements of the PELMO system. Correction coefficients in the wind regime effective for wind-wave generation (i.e., $U_{10\text{N}}>5$ m/s) are larger than one and vary between 1.06 and 1.14. The largest values occur at very low wind speeds (1.185 at 3 m/s), while smaller-than-one values occur at even smaller wind speeds. The smallest coefficients (i.e., least correction) are those associated with Sirocco, which is the best-modelled wind by IFS in the Adriatic Sea.

FIGURE 6

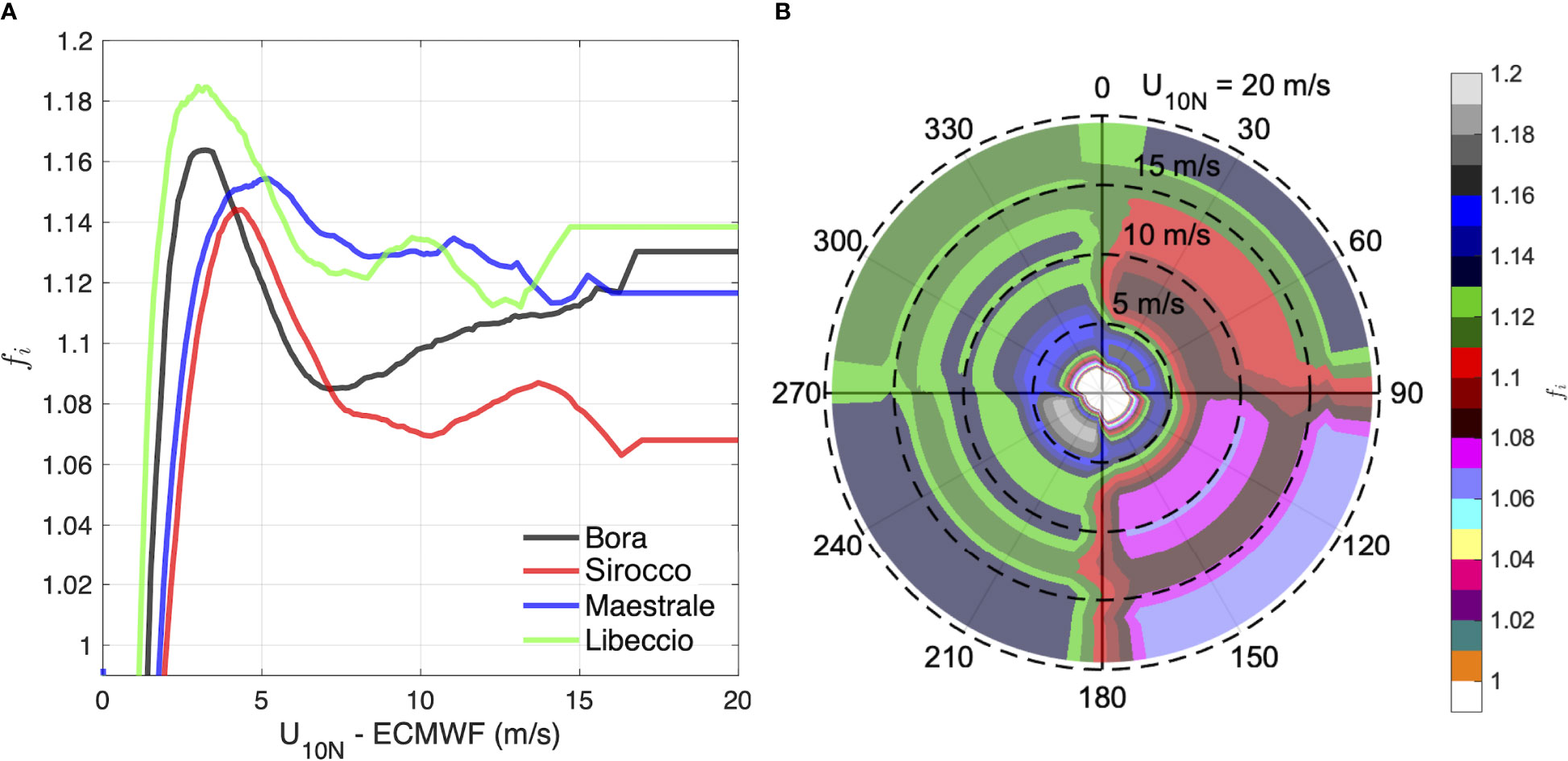
Figure 6 GQQM wind speed scaling coefficients f_i, as a function of wind speed U_10N for the four wind directions (A) and operational implementation over the wind speed and direction (B).

Wave model calibration

The results of the wind input source term calibration are summarised in Table 4, where the values of bias and of the other statistical indicators considered (slope, rmse and si; definitions in Appendix 1) are reported as a function of ${\beta }_{max}$. The strategy of the calibration followed the steps described in the “Materials and methods - Wave model calibration” section. The model performance is evaluated at the “Acqua Alta” tower and in the calibration range ($1.0\le H_s\le 3.0$ m). We observe that the parameters representing the systematic error (bias and slope) vary significantly with ${\beta }_{max}$, the lowest (highest) values being associated with a model underestimation (overestimation). On the contrary, the random error parameters (rmse and si) are less sensitive to ${\beta }_{max}$ variations, even if it is confirmed that the largest error is associated to the largest ${\beta }_{max}$. This is in agreement with findings of Mentaschi et al. (2015). The ${\beta }_{max}$ value that minimises the bias (equal to 0.01 m) and that is adopted in this study and for the PELMO system is ${\beta }_{max}=1.7$. With this value, slope, rmse and si are 0.99, 0.31 m and 0.21, respectively, denoting an excellent representation of the sea states with respect to both the systematic and random errors.

TABLE 4

Table 4 Calibration of the wind input source term. Performance of the wave model at the “Acqua Alta” tower station in the calibration range (1.0 ≤ H_s ≤ 3.0 m), for different values of the coefficient β_max.

Wave model validation

The wave model setup obtained from the calibration is now applied to the longest dataset of wind forcing available (01/01/2018-30/06/2019) for the validation of the PELMO system. The simulation strategy is the same used for the calibration of the wind input source term, the only difference being that the numerical simulations last 90 hours, instead of 48 hours (covering the whole hourly forecast range). The wave model performance is verified in the northern Adriatic Sea, at the “Acqua Alta” tower (over a longer period and range than calibration) and the “Nausicaa” buoy stations, and over the whole Adriatic Sea, using the satellite altimeter observations. Moreover, PELMO wave model forecasts at “Acqua Alta” tower are compared against those of two wave forecasting models operational in the Adriatic Sea, namely, the IFS-ECWAM and HENETUS wave models, which use the same forcing of PELMO (with a different, or without, calibration). Results of the three systems are presented also as a function of the forecasting range, to assess the performance of PELMO and the other systems in forecasting storm events with days in advance.

Validation of the PELMO wave model

The statistical indicators of the model performance in the calibration range ($1.0\le H_s\le 3.0$ m) are shown in Table 5. At the “Acqua Alta” tower, the systematic error indicators are as small as the ones observed for the calibration results (bias is even smaller, i.e., 0.00 m, while the slope is 0.97), while the rmse and si indicators slightly increase (0.38 m and 0.23, respectively), however still denoting a small random error. Compared to “Acqua Alta”, model performance at the “Nausicaa” station and from satellite altimeters over the entire Adriatic Sea is characterised by larger systematic error (at “Nausicaa”, bias is 0.05 m; from altimeters, bias is 0.12 m), with a slight tendency to overestimate observations. Random error is comparable over the Adriatic Sea (altimeters) and smaller at “Nausicaa”. Differences between performance in the northern (“Acqua Alta”) and in the rest of the Adriatic Sea may be partially due to the fact that the model has been calibrated to minimise the systematic error in the northern Adriatic Sea and partially (in particular for the random error) to the fact that we are comparing results of the same model to measurement by different instruments, with different characteristics and intrinsic measurement errors.

TABLE 5

Table 5 Validation of the wave model H_s, within the calibration range (1.0 ≤ H_s ≤ 3.0 m) at the “Acqua Alta” and “Nausicaa” stations, and over the whole Adriatic Sea using satellite altimeters.

The scatter plots comparing the observations and the forecasts of PELMO in all conditions ($H_s\ge 0.1$ m) are shown in Figure 7. The representation of the sea states by the model is satisfactory, as shown by the linear regression slope, very close to the 1:1 reference line, in particular at “Nausicaa”, and by the bias which is 0.04 m at “Acqua Alta”, 0.05 m at “Nausicaa” and 0.08 m over the whole Adriatic Sea. The rmse decrease with respect to the ones in the calibration range, while the si increase because of smaller average observed H_s in all conditions. An excellent representation of the percentiles well beyond the 99^th is observed for both “Acqua Alta” and “Nausicaa” stations. At “Acqua Alta”, the model shows a tendency to underestimate values with $H_s\ge 3.5$ m, which in the analysed period only occurred during the “Vaia” storm event (29 October 2018; the comparison of the AWAC measurements with those of another instrument on board the platform might indicate a potential overestimation of H_s during this event from AWAC). But there can be also other reasons for this underestimation of the largest H_s that might be investigated in the future: for instance, the proper model representation of the nonlinear interactions during the strong events producing intermediate and shallow water waves at the “Acqua Alta” and “Nausicaa” stations. Over the whole Adriatic Sea, the percentiles are well reproduced until the 99^th, while a small overestimation is observed for the larger values. The residual between forecast and observed H_s percentiles (dPXX, with XX = 50, 90, 99, in Figure 7) provides a quantification of the model-observation agreement under typical (50^th percentile) and intense-to-extreme (90^th and 99^th percentiles) conditions. PELMO is well performing in both cases, but a distinction should be made between the northern part and the whole Adriatic Sea. In the former (represented by “Acqua Alta” and, to a smaller extent, by “Nausicaa” stations) the most intense and extreme conditions are better forecasted than the typical ones, with a -0.01 m residual at the 99^th percentile, 0.02 and 0.09 m residuals at the 90^th percentiles (at “Acqua Alta” and “Nausicaa”, respectively), and 0.05 and 0.06 m at the 50^th percentile. Over the whole Adriatic Sea the opposite is true, with the 99^th percentile residual at 0.23 m, and the 90^th and 50^th percentiles at 0.12 m.

FIGURE 7

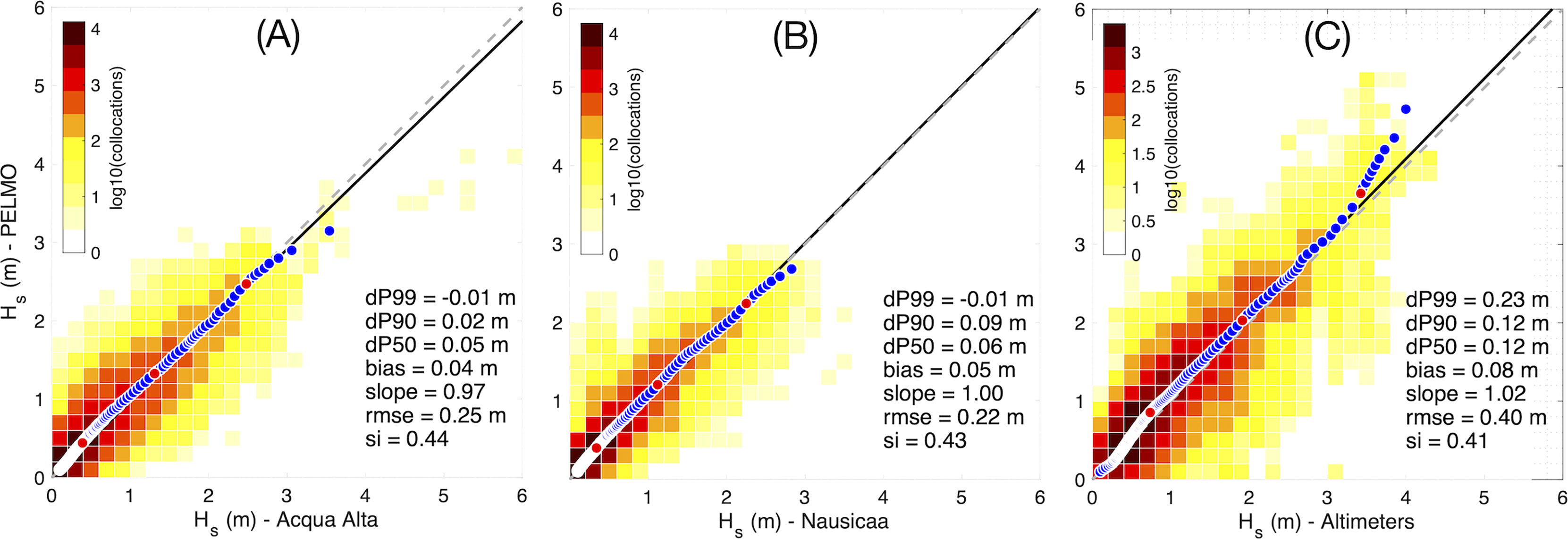
Figure 7 Validation of the wave model in all conditions ($H_s\ge 0.1$m) at the “Acqua Alta” (A) and “Nausicaa” (B) stations, and over the whole Adriatic Sea using satellite altimeters (C). The black line is the linear regression line of the data (reference 1:1 line is gray colored and dashed). Blue dots represent the percentiles of the quantile-quantile plot, from 1^st to 99.9^th; red dots represent the 50^th, 90^th and 99^th percentile (from left to right), respectively.

Comparison with other wave models

In this section we compare the forecast of the PELMO system at the “Acqua Alta” tower station (01/01/2018-30/06/2019) with the forecast of two other systems operational in the Adriatic Sea that use the same wind forcing as PELMO:

● IFS-ECWAM: the wave module of ECMWF coupled IFS system. It is based on the implementation of the WAM model at ECMWF (ECMWF, 2019). It has a horizontal spatial resolution of 14 km and is bi-directionally coupled to the IFS atmospheric model (horizontal resolution 0.1°), from which it receives the 10-metre neutral wind speed (assessed in Figure 2). The parameterization of the input and dissipation source terms is based on the work of Janssen (1991). We have considered the first 90 hours of forecast from the 00UTC and 12UTC synoptic hours.

● HENETUS: the wave prediction system used by the Tide Forecast and Early Warning Center of the City of Venice, developed and managed by ISMAR-CNR (Bertotti et al., 2011). It is based on the WAM model, has a horizontal spatial resolution of 1/12° (corresponding to about 9 km) and is forced with the IFS real wind speed at 0.1° resolution, interpolated on a regular grid at 0.25°x0.25° resolution over the whole Adriatic area and calibrated using a linear regression strategy with a 1.16 scaling factor (see Bertotti et al. (2011) for the presentation of the scaling approach). We have considered the first 90 hours of the forecast of the only available run, the one of the 12UTC synoptic hours.

The statistical indicators in the calibration range are shown in Table 6. Overall, the model that obtains the best score is PELMO. For what concerns the systematic error, HENETUS shows similar statistics, with a positive bias of a few centimetres (0.05 m in the calibration range) and slope very close to 1. IFS-ECWAM considerably underestimate H_s at “Acqua Alta” tower, with a much larger negative bias and a slope well below 1 (-0.21 m and 0.86, respectively). For what concerns the random error, PELMO has the lowest rmse (0.38 m in the calibration range), despite differences among the three systems are small, while IFS-ECWAM has the smallest si (0.21 in the calibration range) and HENETUS the largest one, with PELMO in-between the two.

TABLE 6

Table 6 Performance of PELMO in the calibration range (1.0 ≤ H_s ≤ 3.0 m) at “Acqua Alta” tower station compared to IFS-ECMWF and HENETUS.

The relative performance of the three systems in all conditions (at “Acqua Alta”) can be assessed by comparing the scatter plot for PELMO (Figure 7A) with the scatter plots for HENETUS and IFS-ECWAM in Figure 8. Overall HENETUS tends to overestimate (bias of 0.08 m) and IFS-ECWAM to underestimate (bias of -0.09 m) the observed H_s. The quantile-quantile plots and the H_s residuals at the 50^th, 90^th and 99^th percentile levels allow to see that the calibrated systems (PELMO and HENETUS) well forecast the sea states over all the regimes, from the typical conditions to the most extremes. Indeed, they maintain low H_s residuals, especially PELMO, which has the lowest ones, and quantile-quantile data points very close to the 1:1 reference line from the smallest to the largest percentile level (HENETUS up to the 99.9^th, PELMO up to the 99.8^th but with a straighter distribution of the data points). On the contrary, the non-calibrated IFS-ECWAM performance worsens with increasing percentile levels, from a small underestimation at the 50^th percentile (-0.05 m), to a considerable one at the 99^th percentile (-0.27 m).

FIGURE 8

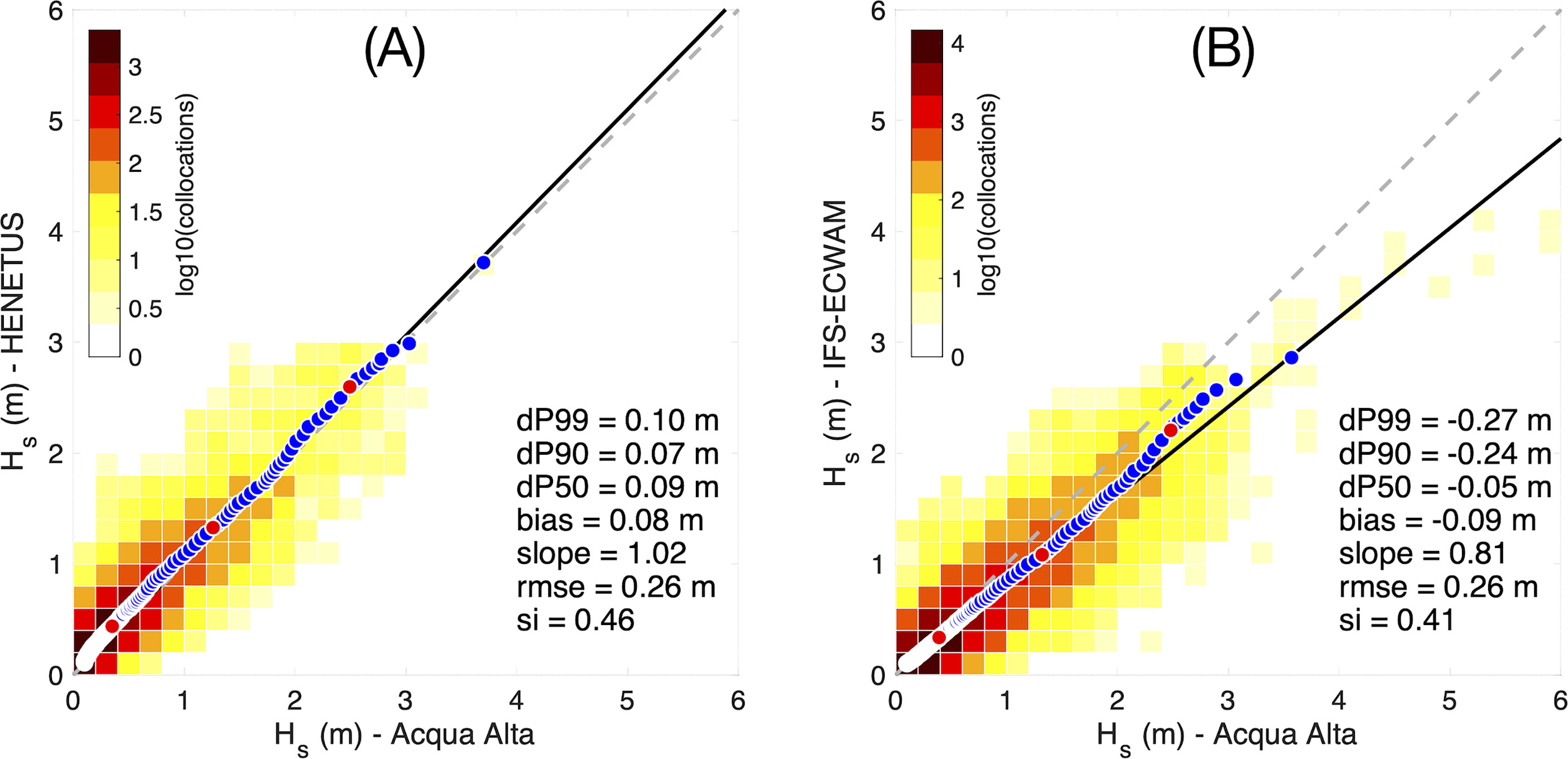
Figure 8 Performance of HENETUS (A) and IFS-ECMWF (B) in all conditions (H_s≥0.1m) at “Acqua Alta” tower station, for comparison with PELMO (Figure 7A). Black line is the linear regression line of the data (reference 1:1 line is gray colored and dashed). Blue dots represent the percentiles of the quantile-quantile plot, from 1^st to 99.9^th; red dots represent the 50^th, 90^th and 99^th percentile (from left to right), respectively.

The scores of the three systems at increasing forecasting range are shown in Figure 9 for different forecasting days (day 1, D1: 0-23 hours from initialisation; day 2, D2: 24-47 hours; day 3, D3: 48-71 hours; day 4, D4: 72-90 hours). Performance of PELMO is fair over the whole forecasting range, with only very small variations of the scores from D1 to D4, in particular of bias and slope. Both the curve representing the variation of bias and slope decrease with increasing range, meaning that at the largest ranges the model produces less and less energetic sea states (compared to observations). This is a common feature of the three systems, in particular of PELMO and HENETUS. As a consequence, the bias and slope curves can cross the no-error reference lines, thereby allowing the identification of an optimal forecasting range. For PELMO the optimal range occurs within the first 48 hours, which is also the interval chosen for the calibration. HENETUS has good scores too, despite a small positive systematic error that tends to reduce with increasing range, but most likely as a consequence of the aforementioned energy reduction. Instead, IFS-ECWAM systematically and considerably underestimates H_s at “Acqua Alta” tower over the whole forecast range. Regarding the random error, all the three systems have rmse and si increasing with the forecast range, as a result of the increase of the random error of the wind forcing (shown by Bertotti et al., 2013) common to all the three systems. The smallest values of rmse and si are obtained by PELMO and IFS-ECWAM, respectively, despite the differences among the three systems are small, especially for si.

FIGURE 9

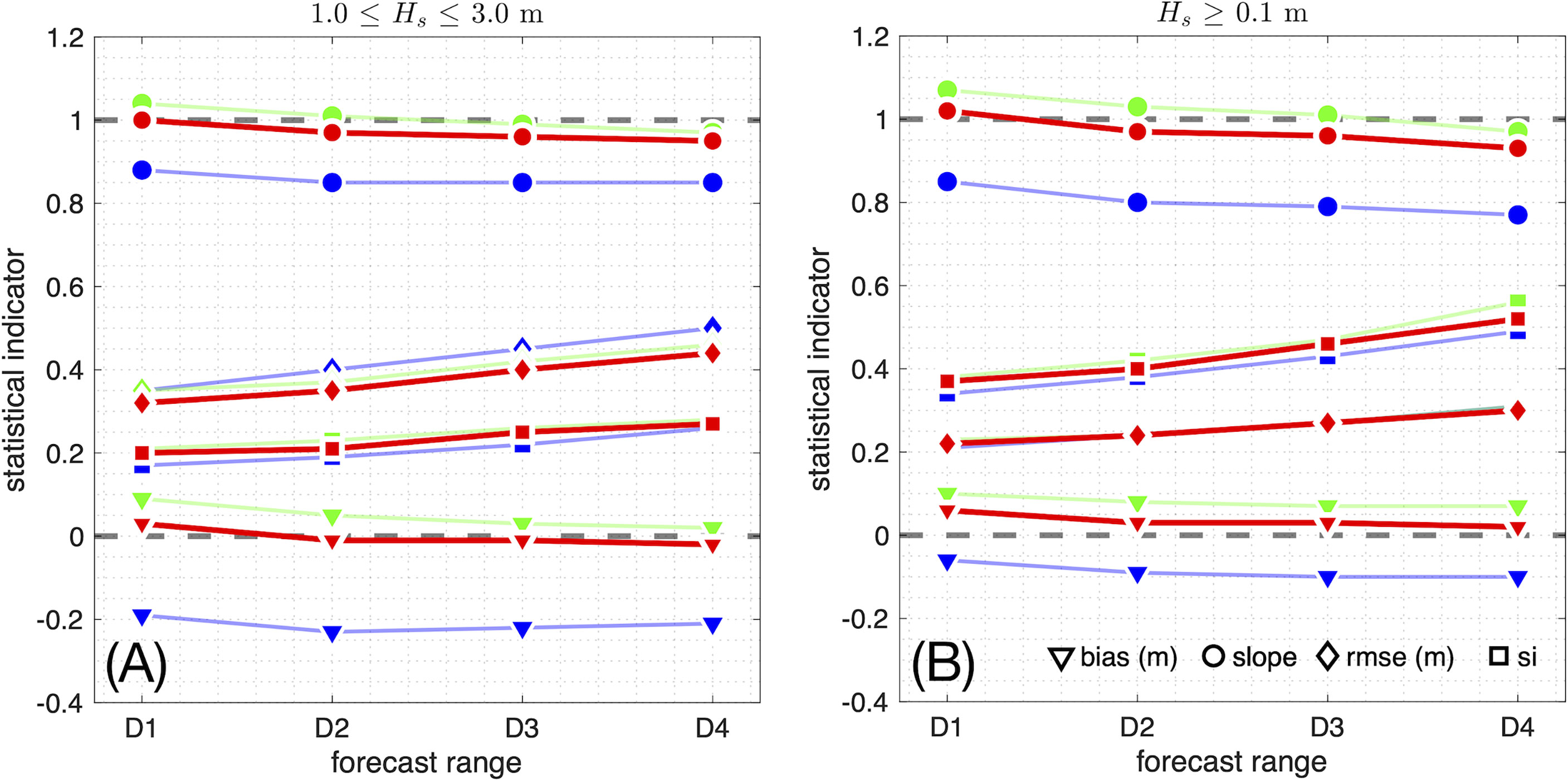
Figure 9 Performance of PELMO (red color) at “Acqua Alta” tower station in the calibration range [1.0≤H_s≤3.0 m, (A)] and in all conditions [H_s≥0.1m, (B)] for different forecasting ranges, compared to IFS-ECWAM (blue) and HENETUS (green): day 1 (D1, 0-23 hours from initialization), day 2 (D2, 24-47 hours), day 3 (D3, 48-71 hours), day 4 (D4, 72-90 hours). Markers point to different statistical indicators: bias (triangle), slope (circle), rmse (diamond) and si (square).

Discussions and conclusions

In this paper, we have proposed a methodology for wind-wave forecasting in enclosed and semi-enclosed basins using global wind forcing fields instead of setting up a dynamical downscaling to produce high-resolution wind forcing fields. To our end, we have presented PELMO, a novel WW3-based wave forecasting system for the northern Adriatic Sea, and the Venice (Italy) littoral. However, the methodology we have applied in the Adriatic Sea might be exported to any context having the same purpose and geophysical characteristics, i.e., for the wave forecast in the coastal regions of a (semi-) enclosed basin with surrounding orography (e.g., Red Sea, Black Sea, Great Lakes, just to mention a few), where calibration and validation usually target only the wave model component of the system (see e.g., Alves et al., 2014; Soran et al., 2022).

PELMO benefits of a two-step calibration procedure aimed at minimizing the systematic global wind model and wave model errors with respect to target observations in the area of interest. Although it produces, twice a day, the wave forecast in all sea-state conditions for a 10-day range over the whole Adriatic Sea, it has been calibrated in order to achieve the best results at short range (first 2 days) over the 1.0 ≤ H_s≤ 3.0 m range and in the northern part of the basin.

For our scopes, we have first corrected the wind forcing fields by means of a quantile-specific and direction-dependent scaling and on a multi-year satellite scatterometer wind speed reference dataset. The strategy adopted has been shown to be effective in reducing the model-observation wind speed difference both in open-sea and coastal stations, and over different wind regimes. We have carefully verified the correction close to the coasts as we are aware that a potential land contamination effect on the scatterometer data might produce a positive wind speed bias in the retrieved data (i.e., larger-than-real measured data; Lindsley et al., 2016) and contribute to the negative model-observation differences found in Figures 2B, D close to the coasts. However, land contamination bias mainly affects low-wind speed regimes and becomes smaller for the moderate and intense regimes (Lindsley et al., 2016), which are the target of PELMO. Therefore, in this study, we have used all the available data to derive and apply a quantile-specific correction (on wind speed) and we have verified a-posteriori the improvement of the wind correction along the coastline. Future developments of the wind forcing correction, though requiring a larger reference dataset than that used here, might be (i) the application of a geographical position-dependent scaling (i.e., a Local Quantile-Quantile Matching approach) that may correct the high-spatially variable model wind speed misestimate, (ii) accounting for the leadtime in deriving the scaling (at present, obtained only by considering the closest forecast to the observation).

The residual systematic error in the wave forecasts has been minimised by calibrating the wind input source term parameterisation. To this end, we have tuned the wave model β_max parameter in order to minimise the model-observation bias, using a portion of the “Acqua Alta” station dataset in the 1.0 ≤ H_s ≤ 3.0 m range as the target.

We have obtained a model setup that leads to good skills in the zone of interest (northern Adriatic Sea) both in the calibration range and in all conditions, during a validation period of 1.5 years including severe events. This allows us to state then that the choices made for the calibration produced the expected results, in particular the minimisation of the systematic model error in the calibration range, expressed by bias and slope (0.00 m and 0.97, respectively), and of the H_s residual at relevant percentile levels, representative of the typical, intense and extreme conditions. The model performance is satisfactory also over the rest of the Adriatic Sea, although not as good as over the northern Adriatic Sea area (bias of 0.08 m from satellite altimeters). This points out that finding a model setup that is optimal for the whole basin and in all conditions is challenging due to the limited capability of atmospheric models at those resolutions to reproduce the spatio-temporal variability of the wind fields in a narrow semi-enclosed basin surrounded by orography like the Adriatic Sea. Such an issue might require a position-dependent wind forcing correction and wave model calibration approaches. These are improvements that will be taken into account in the future development of the system. Besides this, on the wave model side, there are other aspects to look at and advancements to introduce, in order to further increase the performance of the forecasting system. For instance, the effect of currents and of variable water level on the wave forecasts, especially in the shallowest regions, may be considered by means of a coupled ocean-wave numerical model. Indeed, along the Venice shoreline, accounting for the underlying water column dynamics might increase H_s during the most intense Sirocco storms because of the reduced wave-bottom interaction caused by the storm surge. While it might reduce H_s during strong Bora storms because of the interaction of the following current and waves (Benetazzo et al., 2013). However, preliminary tests have shown that apart from the very intense events, the differences between accounting for current and level or not are very small.

In the meantime, the PELMO system has achieved the best scores in forecasting the significant wave height in the northern Adriatic Sea compared to two other two operational systems, i.e., IFS-ECWAM (using global wind product without correction) and HENETUS (using global wind product with a different correction). The three systems have shown comparable random error but very different systematic errors, which are actually very small for the high-resolution calibrated systems, i.e., PELMO and HENETUS, and very large for the lower resolution non-calibrated system (IFS-ECWAM). This points out the need in operational wave forecasting in enclosed and semi-enclosed basins for high-resolution modelling, for correction of wind forcing and calibration of the wave model, which are particularly effective in reducing the systematic error in the wave forecast, mostly, but not only, inherited by the global wind forecasts.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

FB and AB conceived and designed the study. FB, PP, AB, and SD performed the model development and the analyses. LB and LC contributed to the model development and the analyses. FB, AB, and LC provided the funding for the study. FB wrote the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The authors acknowledge the funding and support by Italian National Research Council (CNR, Italy) and the City of Venice (Italy) in the context of the joint research project PELMO.

Acknowledgments

The authors are grateful to Jean-Raymond Bidlot (ECMWF, UK) and Giuseppe Grieco (CNR-ISMAR, Italy) for useful discussions and to Mauro Bastianini (CNR-ISMAR) for providing "Acqua Alta" data.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adachi S. A., Tomita H. (2020). Methodology of the constraint condition in dynamical downscaling for regional climate evaluation: A review. J. Geophys Res: Atmos 125 (11), 1–30. doi: 10.1029/2019JD032166

CrossRef Full Text | Google Scholar

Alipour A., Siadatmousavi S. M., Jose F. (2021). Numerical simulation of waves in the Caspian Sea: Calibration and verification of the observation-based source terms. Ocean Dynamics 71, 699–714. doi: 10.1007/S10236-021-01465-W

CrossRef Full Text | Google Scholar

Alves J. H., Chawla A., Tolman H. L., Schwab D., Lang G., Mann G. (2014). The operational implementation of a great lakes wave forecasting system at NOAA/NCEP. Weather Forecast 29 (6), 1473–1497. doi: 10.1175/WAF-D-12-00049.1

CrossRef Full Text | Google Scholar

Ardhuin F., Bertotti L., Bidlot J.-R., Cavaleri L., Filipetto V., Lefevre J.-M., et al. (2007). Comparison of wind and wave measurements and models in the Western Mediterranean Sea. Ocean Eng. 34 (3–4), 526–541. doi: 10.1016/j.oceaneng.2006.02.008

CrossRef Full Text | Google Scholar

Ardhuin F., Rogers E., Babanin A. V., Filipot J, Magne R., Roland A., et al. (2010). Semiempirical dissipation source functions for ocean waves. part I: Definition, calibration, and validation. J. Phys. Oceanogr 40 (9), 1917–1941. doi: 10.1175/2010JPO4324.1

CrossRef Full Text | Google Scholar

Barbariol F., Alves J.-H. G. M., Benetazzo A., Bergamasco F., Bertotti L., Carniel S., et al. (2017). Numerical modeling of space-time wave extremes using WAVEWATCH III. Ocean Dynamics 67, 535–549. doi: 10.1007/s10236-016-1025-0

CrossRef Full Text | Google Scholar

Barbariol F., Davison S., Falcieri F. M., Ferretti R., Ricchi A., Sclavo M., et al. (2021). Wind waves in the Mediterranean Sea: An ERA5 reanalysis wind-based climatology. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.760614

PubMed Abstract | CrossRef Full Text | Google Scholar

Battjes J., Janssen J. P. F. M. (1978). “Energy loss and set-up due to breaking of random waves,” in Coastal Engineering Proceedings, Vol. 1 (16), 32. doi: 10.9753/icce.v16.32

CrossRef Full Text | Google Scholar

Benetazzo A., Barbariol F., Pezzutto P., Staneva J., Behrens A., Davison S., et al. (2021). Towards a unified framework for extreme Sea waves from spectral models: Rationale and applications. Ocean Eng. 219. doi: 10.1016/j.oceaneng.2020.108263

CrossRef Full Text | Google Scholar

Benetazzo A., Carniel S., Sclavo M., Bergamasco A. (2013). Wave–current interaction: Effect on the wave field in a semi-enclosed basin. Ocean Model. 70, 152–165. doi: 10.1016/j.ocemod.2012.12.009

CrossRef Full Text | Google Scholar

Benetazzo A., Davison S., Barbariol F., Mercogliano P., Favaretto C., Sclavo M. (2022). Correction of ERA5 wind for regional climate projections of Sea waves. Water 14, 1590. doi: 10.3390/W14101590

CrossRef Full Text | Google Scholar

Bertotti L., Canestrelli P., Cavaleri L., Pastore F., Zampato L. (2011). The henetus wave forecast system in the Adriatic Sea. Natural Hazards Earth Syst Sci. 11, 2965–2979. doi: 10.5194/nhess-11-2965-2011

CrossRef Full Text | Google Scholar

Bertotti L., Cavaleri L., Loffredo L., Torrisi L. (2013). Nettuno: Analysis of a wind and wave forecast system for the Mediterranean Sea. Monthly Weather Rev. 141 (9), 3130–3141. doi: 10.1175/MWR-D-12-00361.1

CrossRef Full Text | Google Scholar

Cavaleri L., Abdalla S., Benetazzo A., Bertotti L., Bidlot J. R., Breivik S., et al. (2018). Wave modelling in coastal and inner seas. Prog. Oceanogr. 167, 164–233. doi: 10.1016/j.pocean.2018.03.010

CrossRef Full Text | Google Scholar

Cavaleri L., Bajo M., Barbariol F., Bastianini M., Benetazzo A., Bertotti L., et al. (2019). The October 29, 2018 storm in northern Italy – an exceptional event and its modeling. Prog. Oceanogr 178. doi: 10.1016/j.pocean.2019.102178

CrossRef Full Text | Google Scholar

Cavaleri L., Barbariol F., Benetazzo A. (2020). Wind–wave modeling: Where we are, where to go. J. Mar. Sci. Eng. 8, 260. doi: 10.3390/JMSE8040260

CrossRef Full Text | Google Scholar

Cavaleri L., Bertotti L. (2006). The improvement of modelled wind and wave fields with increasing resolution. Ocean Eng. 33 (5–6), 553–565. doi: 10.1016/J.OCEANENG.2005.07.004

CrossRef Full Text | Google Scholar

Cavaleri L., Rizzoli P. M. (1981). Wind wave prediction in shallow water: Theory and applications. J. Geophys Res. 86 (C11), 10961–10973. doi: 10.1029/JC086iC11p10961

CrossRef Full Text | Google Scholar

Colette A., Vautard R., Vrac M. (2012). Regional climate downscaling with prior statistical correction of the global climate forcing. Geophys Res. Lett. 39 (13). doi: 10.1029/2012GL052258

PubMed Abstract | CrossRef Full Text | Google Scholar

Cushman-Roisin B., Gačić M., Poulain P.-M., Artegiani A. (2001). Physical oceanography of the Adriatic Sea. Eds. Cushman-Roisin B., Gačić M., Poulain P.-M., Artegiani A. (Dordrech: Springer Dordrecht). doi: 10.1007/978-94-015-9819-4

CrossRef Full Text | Google Scholar

Deque M. (2007). Frequency of precipitation and temperature extremes over France in an anthropogenic scenario: Model results and statistical correction according to observed values. Global Planet Change 57 (1–2), 16–26. doi: 10.1016/j.gloplacha.2006.11.030

CrossRef Full Text | Google Scholar

Durrant T. H., Greenslade D. J. M., Simmonds I. (2013). The effect of statistical wind corrections on global wave forecasts. Ocean Model. 70, 116–131. doi: 10.1016/J.OCEMOD.2012.10.006

CrossRef Full Text | Google Scholar

Durrant T. H., Greenslade D. J. M., Simmonds I., Woodcock F. (2014). Correcting marine surface winds simulated in atmospheric models using spatially and temporally varying linear regression. Weather Forecast 29 (2), 305–330. doi: 10.1175/WAF-D-12-00101.1

CrossRef Full Text | Google Scholar

Dutour S. M., Ivanković D., Roland A., Ivatek-Šahdan S., Tudor M. (2018). Operational wave modelling in the Adriatic Sea with the wind wave model. Pure Appl. Geophys 175 (11), 3801–3815. doi: 10.1007/S00024-018-1954-2/TABLES/7

CrossRef Full Text | Google Scholar

ECMWF (2019). “Part VII : ECMWF wave model”, in IFS documentation CY46R1 (Reading (UK): ECMWF).

Google Scholar

EU Copernicus Marine Service (2020). “PRODUCT USER MANUAL for wind- global ocean L3 wind WIND_GLO_WIND_L3_NRT_OBSERVATIONS_012_002 and WIND_GLO_WIND_L3_REP_OBSERVATIONS_012_005 (CMEMS-WIND-PUM-012-002-005)” (CMEMS).

Google Scholar

Fairall C. W., Bradley E. F., Hare J. E., Grachev A. A., Edson. J. B. (2003). Bulk parameterization of air-Sea fluxes: Updates and verification for the COARE algorithm. J. Climate 16 (4), 571–591. doi: 10.1175/1520-0442(2003)016<0571:BPOASF>2.0.CO;2

CrossRef Full Text | Google Scholar

Ferrarin C., Valentini A., Vodopivec M., Klaric D., Massaro G., Bajo M., et al. (2020). Integrated Sea storm management strategy: The 29 October 2018 event in the Adriatic Sea. Natural Hazards Earth Syst Sci. 20 (1), 73–93. doi: 10.5194/NHESS-20-73-2020

CrossRef Full Text | Google Scholar

Gelci R., Cazale H., Vassal J. (1957). “Prevision de la houle. la methode des densites spectroangulaires”, in Bulletin d’information Du comite d’Oceanographie et d’Etude des cotes, vol. 9. , 416–435.

Google Scholar

Haiden T., Janousek M., Vitart F., Bouallegue D.b., Ferranti L., Prates F., et al. (2021). “Evaluation of ECMWF forecasts, including the 2021 upgrade,” in ECWMF technical memorandum (Reading (UK): ECMWF), vol. 884. , 1–54. Available at: https://www.ecmwf.int/en/elibrary/20142-evaluation-ecmwf-forecasts-including-2021-upgrade.

Google Scholar

Hasselmann K., Barnett T. P., Bouws E., Carlson H., Cartwright D. E., Enke K., et al. (1973). “Measurements of wind-wave growth and swell decay during the joint north Sea wave project (JONSWAP).” (Deutches Hydrographisches Institut)

Google Scholar

Hasselmann S., Hasselmann K., Allender J. H., Barnett T. P. (1985). Computations and parameterizations of the nonlinear energy transfer in a gravity-wave specturm. Part II: Parameterizations of the nonlinear energy transfer for application in wave models. J. Phys. Oceanogr 15 (11), 1378–1391. doi: 10.1175/1520-0485(1985)015<1378:CAPOTN>2.0.CO;2

CrossRef Full Text | Google Scholar

Hemer Mark A., McInnes K. L., Ranasinghe R. (2012). Climate and variability bias adjustment of climate model-derived winds for a southeast Australian dynamical wave model. Ocean Dynamics 62 (1), 87–104. doi: 10.1007/s10236-011-0486-4

CrossRef Full Text | Google Scholar

Janssen P. A. E. M. (1991). Quasi-linear theory of wind-wave generation applied to wave forecasting. J. Phys. Oceanogr. 21 (11), 1631–1642. doi: 10.1175/1520-0485(1991)021<1631:QLTOWW>2.0.CO;2

CrossRef Full Text | Google Scholar

Janssen P. (2004). The interaction of ocean waves and wind. Cambridge: Cambridge University Press. doi: 10.1017/cbo9780511525018

CrossRef Full Text | Google Scholar

Kloe J. de, Stoffelen Ad, Verhoef A. (2017). Improved use of scatterometer measurements by using stress-equivalent reference winds. IEEE J. Selected Topics Appl. Earth Obs Remote Sens. 10, 234023–47. doi: 10.1109/JSTARS.2017.2685242

CrossRef Full Text | Google Scholar

Li D., Feng J., Xu Z., Yin B., Shi H., Qi J. (2019). Statistical bias correction for simulated wind speeds over CORDEX-East Asia. Earth Space Sci. 6 (2), 200–211. doi: 10.1029/2018EA000493

CrossRef Full Text | Google Scholar

Lindsley R. D., Blodgett J. R., Long D. G. (2016). Analysis and validation of high-resolution wind from ASCAT. IEEE Trans. Geosci. Remote Sens. 54 (10), 5699–5711. doi: 10.1109/TGRS.2016.2570245

CrossRef Full Text | Google Scholar

Mentaschi L., Besio G., Cassola F., Mazzino A. (2015). Performance evaluation of wavewatch III in the Mediterranean Sea. Ocean Model. 90, 82–94. doi: 10.1016/j.ocemod.2015.04.003

CrossRef Full Text | Google Scholar

Miche A. (1944). Mouvements ondulatoires de la mer en profondeur croissante ou d{é}croissante. Annales Des. Ponts Chaussées 114, 369–406.

Google Scholar

Michelangeli P.-A., Vrac M., Loukos H. (2009). Probabilistic downscaling approaches: Application to wind cumulative distribution functions. Geophys Res. Lett. 36 (11), L11708. doi: 10.1029/2009GL038401

CrossRef Full Text | Google Scholar

Ochi M. K. (2005). Ocean waves: The stochastic approach (Cambridge: Cambridge University Press).

Google Scholar

OSI SAF/EARS Winds Team (2019). ASCAT wind product user manual. (Royal Netherlands Meteorological Institute)

Google Scholar

Ribal A., Young I. R. (2019). 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Sci. Data 6. doi: 10.1038/s41597-019-0083-9

CrossRef Full Text | Google Scholar

Signell R. P., Carniel S., Cavaleri L., Chiggiato J., Doyle J. D., Pullen J., et al. (2005). Assessment of wind quality for oceanographic modelling in semi-enclosed basins. J. Mar. Syst. 53 (1), 217–233. doi: 10.1016/j.jmarsys.2004.03.006

CrossRef Full Text | Google Scholar

Soran M. B., Amarouche K., Akpınar A. (2022). Spatial calibration of WAVEWATCH III model against satellite observations using different input and dissipation parameterizations in the black Sea. Ocean Eng. 257, 111627. doi: 10.1016/J.OCEANENG.2022.111627

CrossRef Full Text | Google Scholar

Stopa J. E. (2018). Wind forcing calibration and wave hindcast comparison using multiple reanalysis and merged satellite wind datasets. Ocean Model. 127, 55–69. doi: 10.1016/J.OCEMOD.2018.04.008

CrossRef Full Text | Google Scholar

The WAVEWATCH III Development Group (WW3DG) (2019). “User manual and system documentation of WAVEWATCH III-version 6.07.” (MD, USA: College Park).

Google Scholar

Tolman H. L. (1991). A third-generation model for wind waves on slowly varying, unsteady, and inhomogeneous depths and currents. J. Phys. Oceanogr 21 (6), 782–797. doi: 10.1175/1520-0485(1991)021<0782:ATGMFW>2.0.CO;2

CrossRef Full Text | Google Scholar

Tolman H. L. (2002). Alleviating the garden sprinkler effect in wind wave models. Ocean Model 4 (3–4), 2692–89. doi: 10.1016/S1463-5003(02)00004-5

CrossRef Full Text | Google Scholar

Valentini A., Passeri L., Paccagnella T., Patruno P., Marsigli C., Cesari D., et al. (2007). The Sea state forecast system of ARPA-SIM. Bollettino Di Geofisica Teorica Ed Appl 48, 333–350.

Google Scholar

Wood A. W., Leung L. R., Sridhar V., Lettenmaier D. P. (2004). Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim Change 62 (1–3), 189–216. doi: 10.1023/B:CLIM.0000013685.99609.9e

CrossRef Full Text | Google Scholar

Appendix 1

The statistical indicators for the assessment of performance of the model U_10N and H_s compared to observations (denoted by the hat) are, for a generic variable X:

● $bias=\langle X-\widehat{X}\rangle$,

● slope: slope of the linear regression line,

● $rmse=\sqrt{\langle {\left(X-\widehat{X}\right)}^2}\rangle$,

● $si=\sqrt{\langle {\left(\left(\text{X}-\langle \text{X}\rangle \right)-\left(\widehat{X}-\langle \widehat{X}\rangle \right)\right)}^2\rangle }/\langle \widehat{X}\rangle$, (with angle brackets denoting ensemble average).