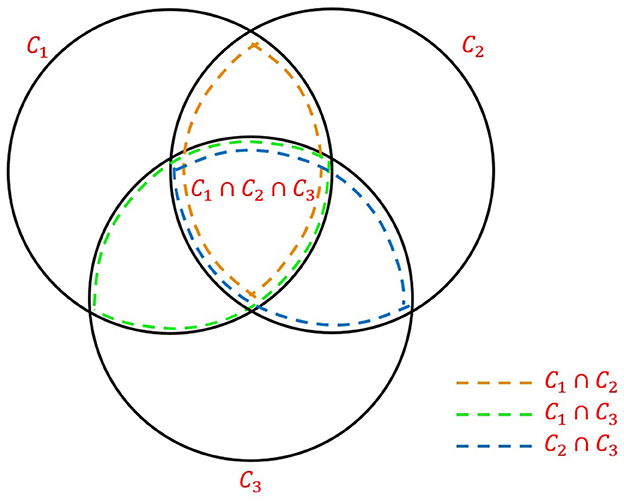Overhead fisheye cameras for indoor monitoring: challenges and recent progress

Monitoring the number of people in various spaces of a building is important for optimizing space usage, assisting with public safety, and saving energy. Diverse approaches have been developed for different end goals, from ID card readers for space management, to surveillance cameras for security, to CO₂ sensing for HVAC control. In the last few years, fisheye cameras mounted overhead have become the sensing modality of choice because they offer large-area coverage and significantly-reduced occlusions but research efforts are still nascent. In this paper, we provide an overview of recent research efforts in this area and propose one new direction. First, we identify benefits and challenges related to inference from top-view fisheye images, and summarize key public datasets. Then, we review efforts in algorithm development for detecting people from a single fisheye frame and from a group of sequential frames. Finally, we focus on counting people indoors. While this is straightforward for a single camera, when multiple cameras are used to monitor a space, person re-identification is needed to avoid overcounting. We describe a framework for people counting using two cameras and demonstrate its effectiveness in a large classroom for location-based person re-identification. To support people counting in even larger spaces, we propose two new person re-identification algorithms using N > 2 overhead fisheye cameras. We provide ample experimental results throughout the paper.

1 Introduction

Knowing how many people are in various spaces of a building is important for security/safety, space management, and saving energy. From the security standpoint, it is critical to know where people are in order to ensure everyone is accounted for in an emergency situation (e.g., fire). The recent experience with COVID-19 has shown the importance of understanding occupancy patterns to assure public safety (e.g., monitoring overcrowding). The pandemic has also dramatically impacted the office-building market, leading to new office-usage patterns. A trend of “flexible workspace” is emerging, where desks are not assigned to employees but can be reserved whenever employees return in-person for work, meetings, etc. Real-time, accurate knowledge of workspace occupancy is essential for an effective implementation of this concept. A similar knowledge of where people are is essential in other industries, such as retail, e.g., the number of people visiting a specific store isle or queuing for checkout. Finally, fine-grained occupancy information plays increasingly important role in HVAC control; by matching air flow to occupancy, significant energy savings can be realized compared to binary (on/off) control.

Many approaches have been proposed for occupancy sensing in commercial buildings, such as active methods that require carrying a cell-phone or swiping an ID card, and passive indirect approaches that use environmental data related to human presence (e.g., CO₂ level, humidity, temperature). However, passive direct methods that capture occupants' features such as appearance, movement, body heat, etc., are most robust and fine-grained. Unlike active methods, passive direct methods do not require carrying a beacon, and compared to passive indirect methods can provide fine granularity in people counts and their locations.

In this paper, we focus on fisheye cameras mounted overhead to capture appearance and movement of occupants. Figure 1 illustrates a potential deployment scenario of fisheye cameras in a large space. Firstly, we review benefits and challenges related to inference from top-view fisheye images. Then, we briefly summarize key image datasets captured indoors by overhead fisheye cameras. Subsequently, we review and evaluate five recent people-detection algorithms on these datasets. Although the best algorithms achieve excellent performance, we observe that under severe occlusions or significant pose changes they intermittently fail. To address this, we describe three extensions that leverage spatio-temporal continuity of human motion to improve the detection accuracy. As the space under monitoring increases in size, a single fisheye camera becomes insufficient for accurate detection of people. While a logical solution is to use multiple overhead fisheye cameras, it is unclear how to count and track people who simultaneously appear in the field-of-view (FOV) of multiple cameras. In order to resolve this, a person re-identification (ReID) algorithm is needed, but very few methods have been proposed for fisheye cameras. We describe a location-based ReID algorithm to match identities between two fisheye cameras and demonstrate its effectiveness in people-counting in a large classroom with highly-dynamic occupancy. To support even larger spaces, we propose two novel extensions to N>2 cameras and evaluate them as well. Throughout the paper, we provide numerous experimental results.

Figure 1

Figure 1. Typical monitoring scenario in a large space—multiple fisheye cameras are needed resulting in field-of-view overlap and ambiguities in people counting, tracking, etc. (photo by David Iliff. License: CC BY-SA 3.0).

2 Related work

2.1 Fisheye cameras

Unlike standard surveillance cameras, fisheye cameras are equipped with a wide-angle lens. This facilitates wide-area coverage, but leads to various challenges that we discuss in Section 3. Front-facing fisheye cameras have found applications in autonomous navigation, primarily for pedestrian and obstacle detection, and have been widely researched (Cordts et al., 2016; Yogamani et al., 2019; Ye et al., 2020; Liao et al., 2023). Down-facing fisheye cameras, mounted above the scene of interest, have recently emerged as an alternative to standard side-mounted surveillance cameras due to the wide-area coverage and reduced occlusions. While in outdoor scenarios this is very much limited by the ability to mount such cameras above the scene (e.g., lamp posts), in indoor scenarios the mounting is relatively straightforward (e.g., suspension from the ceiling).

2.2 People detection

People detection in images from standard surveillance cameras has rich literature spanning at least two decades, from classical methods applying SVM classification to Histogram of Oriented Gradients (HOG) features (Dalal and Triggs, 2005) or using AdaBoost classifier with Aggregate Channel Features (ACF) (Dollár et al., 2014) to more recent deep-learning methods such as YOLO (Redmon et al., 2016), SSD (Liu et al., 2016) and R-CNN (Girshick, 2015; Ren et al., 2015). However, such methods directly applied to top-view fisheye images perform poorly due to a dramatic range of viewpoints in the same image (people under the camera are seen from above, but those farther away are seen from a side perspective) and arbitrary body orientations (e.g., standing people appear radially in images and can be seen “upside-down”) as shown in Figure 2. Furthermore, although more subtle, lens distortions cause body-shape deformations, especially close to fisheye-image periphery, which also penalizes person-detection performance. We discuss these issues in more detail in Section 3.

Figure 2

Figure 2. Test spaces where most of the training/testing data were collected using Axis M3057-PLVE (3,072 × 2,048 pixels, 360° × 185° lens) fisheye cameras mounted 3.15 m above the floor, indicated by red arrows: (A) conference room with single camera (where HABBOF was recorded); (B) classroom with single camera (where CEPDOF was recorded); (C) large classroom with three cameras (where FRIDA was recorded). Corresponding typical occupancy scenarios are shown in the second row (D–F).

In the last decade, person-detection methods have been developed specifically for top-view fisheye images. Early attempts focused on model-based feature extraction and various adaptations to account for fisheye geometry. In perhaps the first work, background subtraction was combined with a probabilistic body-appearance model and followed by Kernel Ridge Regression (Saito et al., 2011). Chiang and Wang (2014) rotated each fisheye image in small angular steps and applied SVM to HOG features extracted from the top-center part of the image to detect people. Krams and Kiryati (2017) applied standard ACF classifier to dewarped features extracted from a fisheye image. Demirkus et al. (2017) also used ACF to learn different-size models dependent on the distance from image center.

The most recent methods are CNN-based end-to-end algorithms. Seidel et al. (2018) applied YOLO to dewarped versions of overlapping windows extracted from a fisheye image, but tested the algorithm on a private dataset only. Tamura et al. (2019) introduced a rotation-invariant version of YOLO, that was trained on rotated images from COCO 2017 (Lin et al., 2014), however the inference stage assumed that bounding boxes are aligned with the image radius thus not allowing for arbitrary body orientations. Li et al. (2019) rotated each fisheye image in 15° steps and applied YOLOv3 (Redmon and Farhadi, 2018) to the top-center part of the image where people usually appear upright, followed by post-processing to remove multiple detections of the same person. They also proposed an extension in which the algorithm is applied only to changed areas, as determined by background subtraction, rather than to the whole image. Minh et al. (2021) proposed an anchor-free CNN that allows bounding-box rotation and speeds up the inference. Chiang et al. (2021) proposed to unwrap patches from a fisheye image using simple fisheye-lens model in order to compose a perspective image for inference by YOLO, followed by post-processing to remove duplicate detections. Wei et al. (2022) applied a CNN with deformable convolution kernels to account for geometric distortions in top-view fisheye images, however tested the approach only on their own dataset. Finally, Tamura and Yoshinaga (2023) extended their earlier work by training on rectilinear datasets while leveraging ground-truth segmentations to fit bounding boxes more tightly around human bodies. Since deep-learning algorithms require extensive training data, a number of top-view fisheye-image datasets aimed at people detection have been published; we discuss the most commonly-used ones in Section 4.

2.3 Person re-identification

Person re-identification is a key component of people counting and by itself is a vast research area of critical importance for visual surveillance. While a detailed review of methods proposed for standard surveillance cameras is beyond the scope of this paper, below we briefly summarize key challenges and types of methods proposed.

Traditional person ReID is concerned with retrieving a person of interest across multiple cameras with non-overlapping FOVs. In closed-world person ReID, typically a single visual modality is used (e.g., RGB), person detections (bounding boxes) are assumed known and reliable, and the query person appears in the gallery set. There exist many methods developed in this context but they, in general, include three components: feature representation, metric learning and ranking optimization. Open-world person ReID attempts to address real-world challenges, such as multiple data modalities (e.g., RGB, depth, text), end-to-end ReID without pre-computed person detections (direct ReID from images/videos), semi-supervised or unsupervised learning with limited/unavailable annotations, dealing with noisy annotations, or open-set ReID when correct match is missing from the gallery. Two recent surveys by Ye et al. (2022) and by Zhang et al. (2024) discuss dozens of methods proposed and include experimental comparisons.

However, person ReID methods developed for rectilinear cameras perform poorly on top-view fisheye images, although re-training on fisheye data somewhat improves performance (Cokbas et al., 2022). In addition to arbitrary body orientations (e.g., “upside-down”), dramatic viewpoint differences (e.g., from above in one camera view, but from side-perspective in another camera view) and lens-distortions (more significant when a person appears at image periphery), another challenge for person ReID is body-scale difference between cameras. Traditional person ReID was developed for cameras with non-overlapping FOVs. Since each camera is oriented toward its own area of interest, people appearing in areas monitored by different cameras will often appear at a reasonably-similar size. This is not the case for fisheye ReID considered here. Since the overhead fisheye cameras have overlapping FOVs and since ReID is performed on images captured at the same time instant, a person might be under one camera but far away from another camera. In addition to different viewpoints, there will be a dramatic difference in person-image size and geometric distortion (person under a camera will be very large and seen from above, while person far away will be tiny and geometrically-distorted). For a detailed discussion and examples, please see Cokbas (2023) and Cokbas et al. (2023).

Very few methods have been proposed to date for person ReID using overhead fisheye cameras. The earliest work by Barman et al. (2018) considers only matching people who are located at a similar distance from each camera, thus assuring similar body size (and, potentially, similar viewpoint). Another work by Blott et al. (2019) uses tracking to extract three distinct viewpoints (back, side, front) that are subsequently jointly matched between cameras, which is similar in spirit to multiple-shot person ReID developed for standard cameras by Bazzani et al. (2010). However, this approach requires reliable tracking and visibility of each person from three very different angles—neither can be guaranteed. Both works report results only on private datasets. Another work somehwat related to person ReID is on tracking people in overhead fisheye views by Wang and Chiang (2023). The authors use their own person detection method (Chiang et al., 2021) and then apply a variant of DeepSORT for tracking.

3 Overhead fisheye cameras: benefits and challenges

3.1 Benefits

3.1.1 Wide field of view

The key advantage of fisheye cameras over their rectilinear counterparts is their wide FOV resulting from a particular lens design. The fisheye FOV covers 360° in plane parallel to the sensor and 165–200° orthogonally. In contrast, a typical surveillance camera equipped with rectilinear lens covers 60–100° in horizontal and vertical dimensions of the sensor. Suspended from the ceiling, a fisheye camera can effectively monitor large area (depending on the installation height). In comparison to rectilinear cameras, fewer fisheye cameras are usually needed to monitor a space thus reducing system complexity and cost. Figures 2A–C show a conference room and two classrooms with fisheye cameras suspended from the ceiling, in which our datasets were recorded (Section 4). Figures 2D–F show images from these cameras from typical testing. Clearly, people detection in such images faces several challenges.

3.1.2 Reduced occlusions

In addition to the wide FOV, the overhead camera mounting significantly reduces the severity of occlusions (by other people or furniture), which can be seen in Figures 2D–F. However, the overhead viewpoint results in certain challenges, discussed below.

3.2 Challenges

3.2.1 Circular field of view

In rectilinear-lens cameras, an RGB sensor records only the central rectangular portion of the FOV and the lens is carefully designed to project straight lines in the physical world onto straight lines on the sensor surface. However, in fisheye cameras only straight lines in the physical world that belong to a plane orthogonal to the sensor and pass through its center result in straight lines in the fisheye image; other lines are curved (e.g., horizontal edges of whiteboards in Figures 2D, E). This geometric distortion introduced by the fisheye lens also affects human-body shape, especially if a person is not in an upright position, thus posing a challenge for both person detection and ReID.

3.2.2 Non-linear foreshortening

In order to capture a wide FOV, the fisheye lens is designed in a particular way that introduces radial distortions (non-linearity) in the captured images. For example, the projection of a person standing directly under the camera (e.g., certain shoulder width), becomes smaller at 3 m away from the camera and even smaller at 6 m away. This size compression is linear in standard cameras thanks to rectilinear lens, but in fisheye cameras the doubling of the distance from the camera results in size compression by more than 2, especially pronounced close to FOV periphery. This non-linear mapping of physical distances (and of body sizes) poses challenges for person detection and ReID in fisheye images.

3.2.3 Overhead viewpoint

It may result in unusual human-body appearance; people directly under the camera are seen from above (Figures 2E, F) but those farther away are seen from a side-view perspective. This dramatic viewpoint variability is not encountered in images captured by a side-mounted rectilinear camera. Another important consequence of the overhead viewpoint is that standing people appear in radial directions in a fisheye image, including horizontal and “upside-down” orientations. In fact, people can appear at any orientation in overhead fisheye images. This is unlike in images captured by side-mounted rectilinear cameras, where standing people appear upright and for which the vast majority of people-detection algorithms have been developed (bounding boxes aligned with image axes).

4 Overhead fisheye datasets

In order to develop people-detection algorithms for overhead fisheye cameras, annotated image datasets are needed for performance evaluation and, potentially, algorithm training. While very large fisheye-image datasets have been collected in front-facing scenarios for autonomous navigation (Cordts et al., 2016; Yogamani et al., 2019; Ye et al., 2020; Liao et al., 2023), few and much smaller fisheye-image datasets are available in overhead scenario intended for indoor surveillance. A recent survey by Yu et al. (2023) describes 16 natural and synthetic datasets collected with top-view fisheye cameras, but most of them either focus on action recognition, or contain very few frames, or do not provide full-body bounding boxes. In Table 1, we summarize a subset of these datasets that are composed of natural, as opposed to synthetic, overhead images and annotated with full-body bounding boxes either aligned with image axes or rotated.

Table 1

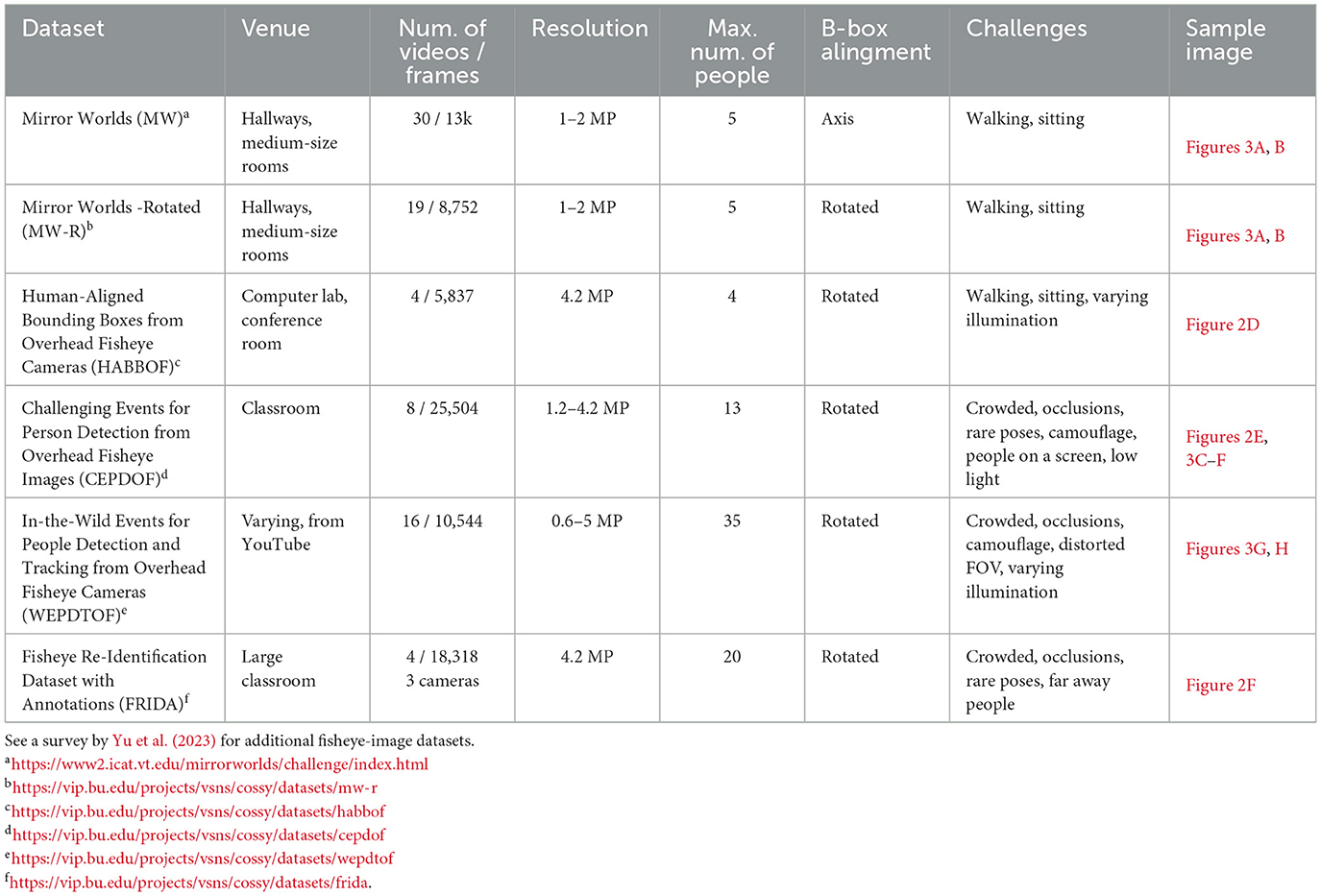
Table 1. Recent image datasets captured by overhead fisheye cameras in various venues and occupancy scenarios, annotated with full-body bounding boxes either aligned with image axes or rotated.

These datasets are essential for training modern data-driven person detection and ReID algorithms so that they can learn how to handle various challenges, such as dramatic viewpoint changes, arbitrary body orientations, geometric body-shape distortions and dramatic body size (scale) differences (ReID), as already discussed in Sections 2, 3.

5 Finding people in overhead fisheye images

All people-detection algorithms for overhead fisheye cameras discussed in Section 2 perform inference for each video frame separately. In the next section, we show that while the performance of such algorithms has steadily improved on “staged” datasets, when applied to real-life videos it significantly degrades. In the subsequent section, we show that by leveraging the spatio-temporal continuity of human motion, the detection performance can be significantly improved.

5.1 Detection using a single video frame

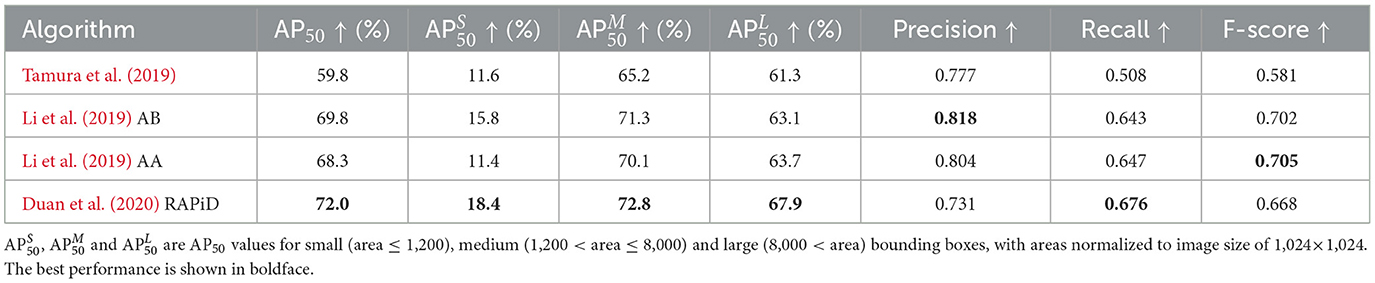
Many recent approaches use RAPiD (Rotation-Aware People Detection) (Duan et al., 2020) as a benchmark for performance evaluation. RAPiD is a CNN based on YOLOv3 (Redmon and Farhadi, 2018) adapted to accommodate bounding-box rotation and trained using the original YOLOv3 loss function augmented with a novel periodic loss for angle regression. RAPiD handles unusual body viewpoints by training on a variety of fisheye images and its source code is publicly available¹. Table 2 compares performance of four recent algorithms against RAPiD. All algorithms were pre-trained on COCO 2017 (Lin et al., 2014) and then fine-tuned and tested on MW-R, HABBOF and CEPDOF via cross-dataset validation. Specificallly, two datasets were used for training and the third one was used for testing, and then the roles were swapped. This resulted in three sets of performance measures that were averaged and are shown in Table 2. The two versions of RAPiD differ in training/testing image resolutions to allow comparison with other methods. Even at the lower resolution, RAPiD significantly outperforms other methods in all performance metrics. However, ARPD by Minh et al. (2021) offers much faster inference than RAPiD at the cost of accuracy.

Table 2

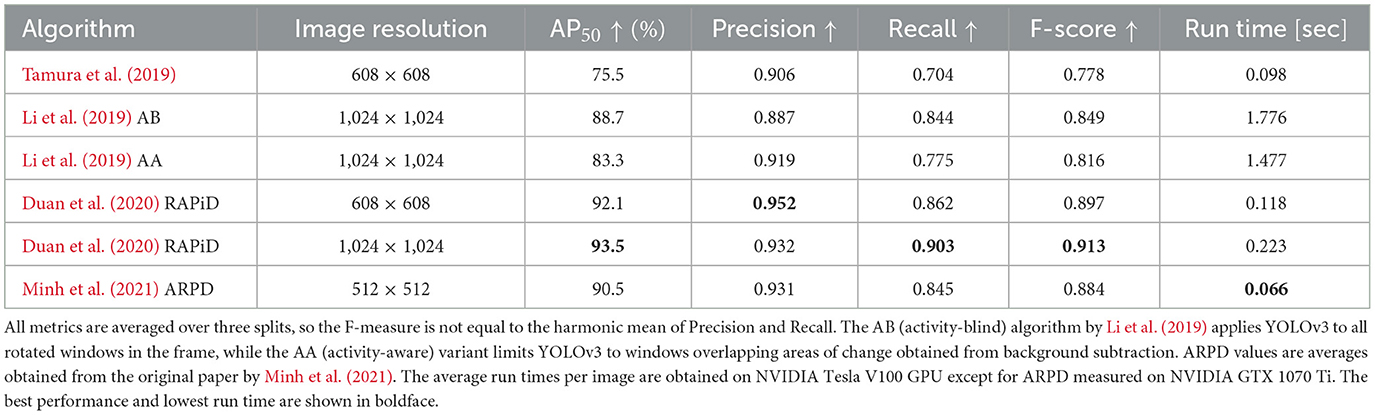
Table 2. Performance of recent single-frame people-detection algorithms on MW-R, HABBOF and CEPDOF via 3-fold cross-dataset validation.

We would like to point out that although the test datasets consist of top-view fisheye images, challenges vary (Table 1). While in MW-R and HABBOF people are either standing or walking, CEPDOF is more challenging with many unusual poses, severe occlusions and low-light conditions. Figures 3A–F show sample detections produced by RAPiD under various challenges. Except for extreme cases (people on the screen, low light), RAPiD performs exceedingly well. This is confirmed by AP₅₀ which exceeds 93%, and Precision, Recall and F-score that are over 0.9. However, all three datasets were recorded using high-quality cameras in “staged” scenarios (controlled environment, subjects instructed to behave in a certain way). Would these algorithms perform equally well “in the wild”, that is in uncontrolled real-life situations?

Figure 3

Figure 3. Examples of people detections by RAPiD on videos with a wide range of challenges: (A) different body poses (MW-R); (B) person directly under camera (MW-R); (C) various body angles (CEPDOF); (D) occlusions (CEPDOF); (E) people visible on the screen (CEPDOF); (F) low-light scenario (CEPDOF); (G) severe camouflage (WEPDTOF); and (H) tiny moving people (WEPDTOF). Green boxes are true positives, red boxes are false positives, and yellow boxes are false negatives.

Table 3 shows performance of four of these algorithms² on the WEPDTOF dataset collected from YouTube, that includes real-life challenges as detailed in Section 4. In addition to AP₅₀, similarly to the MS COCO challenge (Lin et al., 2014), we report this metric for small, medium and large bounding boxes denoted as ${\mathrm{\text{AP}}}_{50}^S$, ${\mathrm{\text{AP}}}_{50}^M$, and ${\mathrm{\text{AP}}}_{50}^L$, respectively. Clearly, RAPiD outperforms other algorithms in terms of AP₅₀ but is outperformed by AA and AB in terms of Precision and F-score. This is largely due to the fact that AA and AB compute bounding-box predictions from overlapped crops of a rotated image and combine these results in a post-processing step. Thus, they analyze a person's appearance multiple times, each at a slightly-different rotation angle, which boosts the confidence score of the bounding box for that person but hugely increases the complexity (Table 2).

Table 3

Table 3. Performance of recent single-frame people-detection algorithms on WEPDTOF.

Note that all metrics in Table 3 are significantly lower than those in Table 2 due to challenges captured in WEPDTOF. When visually evaluating these results by playing video with superimposed detections, we observed that some bounding boxes produced by RAPiD appear intermittently (they disappear for a frame or two but then reappear again) thus contributing to the reduced performance. Visual examples of misses (false negatives) in two challenging sequences from WEPDTOF are shown in Figures 3G, H.

5.2 Detection using a group of video frames

To address the intermittent behavior of detections and improve performance, some form of temporal coherence of detections should be incorporated into the people-detection algorithm since people are either static or move incrementally in space-time. In this context, we developed three extensions of RAPiD (Tezcan et al., 2022) each leveraging temporal information differently, that we briefly summarize below. The source code for these algorithms is publicly available³.

5.2.1 RAPiD + REPP

This method first applies RAPiD to individual frames and then revises the detections by applying post-processing based on Robust and Efficient Post-Processing (REPP) algorithm proposed by Sabater et al. (2020). Since REPP produces axis-aligned bounding boxes, it was modified to account for bounding-box rotations. In the training step, a similarity function is computed from annotated data using the following features from pairs of bounding boxes in consecutive frames: Euclidean distance between their centers, ratio of their widths, ratio of their heights, absolute difference between their angles, and Intersection over Union (IoU) between them. In the inference step, first bounding boxes are detected by RAPiD and linked between consecutive frames into “tubelets” using similarity scores computed by the trained similarity function. Then, the confidence score, location, size and angle of the bounding boxes in each “tubelet” are smoothed out. This results in more temporally-consistent bounding-box characteristics potentially leading to more consistent behavior in time.

5.2.2 RAPiD + (FG)FA

This is an end-to-end approach that extends RAPiD by integrating information from a group of neighboring video frames to stabilize intermittent detections. The integration mechanism was inspired by Flow-Guided Feature Aggregation (FGFA) proposed by Zhu et al. (2017). More specifically, since RAPiD is a YOLO-based algorithm, it first extracts feature maps from the input image at three resolutions. In order to integrate temporal information, at each resolution level feature maps from 10 past frames and 10 future frames are warped to the current feature map by means of motion compensation and all of them are linearly combined. Unlike in Zhu et al. (2017), RAPiD + FGFA uses the Farnebäck algorithm (Farnebäck, 2003) to compute optical flow since it outperforms FlowNet (Dosovitskiy et al., 2015) on overhead fisheye videos. The aggregated feature maps are then transformed into bounding-box-related feature maps, and based on them the detection head predicts bounding boxes. RAPiD + FA is a simplified version of RAPiD + FGFA and applies feature aggregation with adaptive weights but without motion compensation.

Table 4 shows performance of the three multi-frame detection algorithms described above against single-frame algorithms from Table 3 on the WEPDTOF dataset. The multi-frame algorithms significantly outperform single-frame algorithms in terms of all AP₅₀ metrics. Interestingly, the AB algorithm by Li et al. (2019) (YOLOv3 applied to all rotated windows) again achieves the highest Precision although at the cost of very high computational complexity. This is due to overlapping windows resulting in multiple detections of the same person that pruned by subsequent post-processing rarely results in a false positive. Among the multi-frame algorithms, RAPiD + REPP turns out to be very complex computationally. The other two algorithms are about 3 times more complex than the one by Tamura et al. (2019) but offer over 15% points boost in AP₅₀. Figure 4 shows people-detection examples produced by RAPiD and three multi-frame algorithms for three challenging video sequences from WEPDTOF. While RAPiD+REPP corrects one false positive and one false negative, and RAPiD + FA corrects four false negatives and one false positive, it also introduces one false positive. However, RAPiD + FGFA corrects four false negatives and one false positive without introducing any errors.

Table 4

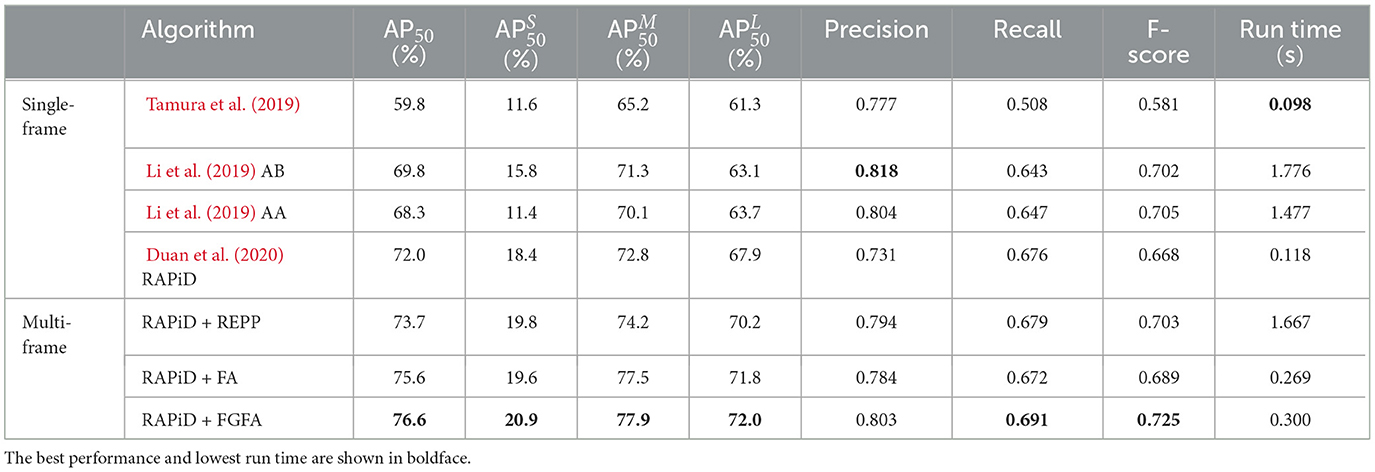
Table 4. Performance of three multi-frame people-detection algorithms (Tezcan et al., 2022) against recent single-frame algorithms on WEPDTOF. The average run times per image are obtained on NVIDIA Tesla V100 GPU.

Figure 4

Figure 4. Qualitative results of RAPiD and its multi-frame extensions on videos from WEPDTOF. Green boxes are true positives, red boxes are false positives, and yellow boxes are false negatives.

6 Counting people using overhead fisheye cameras

6.1 Counting metrics

If a people-detection algorithm, such as those discussed in Section 5, is perfectly accurate, then counting people is as simple as counting bounding boxes. However, certain errors in people detection may still result in a correct people count, for example when a false positive and false negative occur in the same image. These two errors cancel each other, so an accurate metric for people counting should ignore such scenarios. Furthermore, we are interested in how far off is an estimated count from a true count. In this section, we use the following metrics to evaluate performance of people-counting algorithms:

$\begin{array}{r}MAE=\frac{1}{M}{\displaystyle \sum _{i=1}^M}|{\hat{\eta }}_i-{\eta }_i|,\\ MA{E}_{pp}=\frac{\frac{1}{M}\sum _{i=1}^M|{\hat{\eta }}_i-{\eta }_i|}{\frac{1}{M}\sum _{i=1}^M{\eta }_i},\\ Ac{c}_X=\frac{1}{M}{\displaystyle \sum _{i=1}^M}1(|{\hat{\eta }}_i-{\eta }_i|\le X),\end{array}$

where η_i and ${\hat{\eta }}_i$ are the true and estimated people counts in frame number i, M is the total number of frames and 1(ε) is an indicator function, that is 1(ε) equals 1 if ε is true and 0 otherwise. While the Mean Absolute Error (MAE) is a commonly-used metric, it is not meaningful when comparing algorithms at different occupancy levels (e.g., 80 people vs. 8 people). This is addressed by the Mean Absolute Error per person (MAE_pp) which divides MAE by the average occupancy over M frames. The X-Accuracy (Acc_X) quantifies people-counting performance as “accuracy with slack of X”. For X = 0 this definition reverts to the traditional definition of accuracy, but for larger values of X it tolerates the departure of ${\hat{\eta }}_i$ from η_i by up to X. For example, Acc₅ gives the percentage of frames in which the estimated count is within 5 of the true count.

6.2 Dataset

To evaluate performance of various algorithms, we recorded data over 3 days in a large classroom (Figure 2C) equipped with three cameras. On day 1 there were 11 high-occupancy periods (lectures) with up to 87 occupants (Figure 2F), on day 2 there were four such periods with up to 65 occupants, while on day 3 the classroom was mostly empty with maximum occupancy of 9 for a short period of time. We annotated all frames in terms of the number of people in the classroom, but not in terms of bounding boxes.

6.3 Counting people using one camera

Table 5 shows the people-counting performance of RAPiD on this dataset for each of the three cameras. The much larger values of MAE on days 1 and 2 are due to high average occupancy on these two days. MAE_pp, on the other hand, is similar across all days confirming its relative independence of occupancy scenarios. Its value of about 0.4 suggests RAPiD commits an error of about 40% per person which is high. This mediocre performance is confirmed by the values of Acc_X. Cumulatively over 3 days, RAPiD produces exact counts in 46–55% of frames depending on the camera and only in 76–79% frames with count error of up to 10. Clearly, a single camera is incapable of accurate counting in this large a space.

Table 5

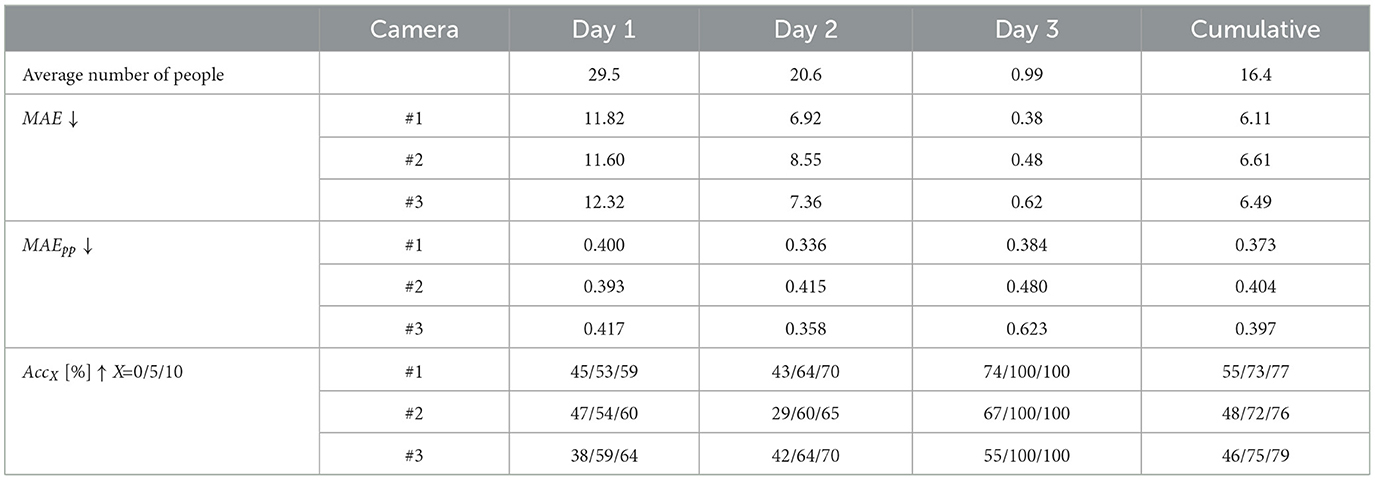
Table 5. Single-camera people-counting performance of RAPiD in a 3-day test in large classroom (Figure 2C) equipped with three cameras. The last column shows cumulative metrics computed over 3 days.

6.4 Counting people using two cameras

Increasing the number of cameras to 2 creates a problem of potential overcounting since the same person may be captured by both cameras due to their wide fields of view (Figure 1). In order to make sure that each person is counted only once, person re-identification is needed.

6.4.1 Person re-identification between two cameras

Traditional PRID considers scenarios where images of people have been recorded by cameras with non-overlapping fields of view at widely-varying times. For example, some cameras may be mounted at entrances to an airport terminal, another group of cameras may be placed at security checkpoints, and yet another group—at the boarding gates. Images of people captured at the entrances and security checkpoints are assumed known and form the gallery set. Similarly, images of people captured at the boarding gates are assumed known and form the query set. The traditional person ReID attempts to match identities between these two sets. For each identity in the query set, the goal is to find all matching identities in the gallery set.

However, the ReID scenario we consider here is different since multiple cameras with overlapping fields of view simultaneously monitor a space (Figure 1). Person ReID for the purpose of people counting can be performed in two steps: detect people in each camera view at the same time instant and then use their appearance (images) to match identities. Identities present in the view of one camera are considered to be the query set and those in the view of another camera are considered to be the gallery set. Therefore, a query identity can match at most one identity in the gallery set or none at all, in the case of occlusion or failed person detection, which is an example of the open-world scenario. Note, that in this work we consider frame-to-frame identity matching (single shot), however it would be interesting to extend this to multiple-shot fisheye ReID similarly to a method proposed for rectilinear cameras by Bazzani et al. (2010). However, this would require reliable tracking in overhead fisheye cameras, a topic still in its infancy.

Traditional person ReID methods rely on appearance of a person, such as color, hand-crafted features or deep-learning features, but they tend to be unreliable for overhead fisheye images since a person's appearance and size dramatically differ depending on this person's location in the room (see Figure 2) as demonstrated in Cokbas (2023) and Cokbas et al. (2023). However, in our scenario of simultaneous image capture by cameras with overlapping fields of view, a person can be also re-identified based on their location. Since the cameras are fixed, a person appearing in a camera's FOV appears at a specific location of another camera's FOV; this location depends on intrinsic camera parameters, installation height, distance between cameras, etc. A ReID method based on this idea was developed by Bone et al. (2021) and shown to be very effective. This method requires camera calibration, which we summarize next. Then, we describe key ReID steps shown in a high-level block diagram in Figure 5.

Figure 5

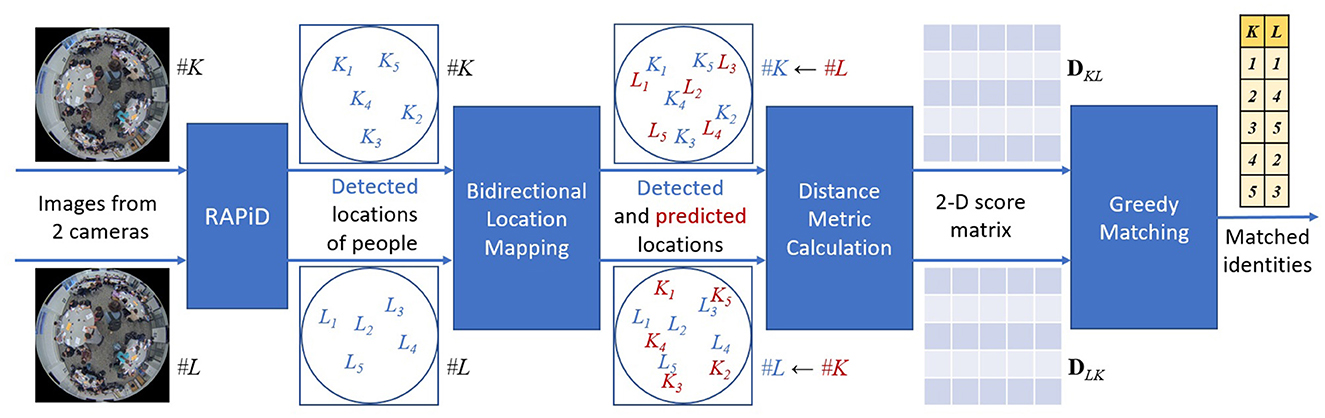
Figure 5. Block diagram of location-based person re-identification (Bone et al., 2021). Locations of people detected by RAPiD in image from camera #K (blue K_i's) and those predicted from camera #L (red L_i's) are used to compute 2-D score matrix D_KL using either the PPD or CBD distance metric. An analogous score matrix is computed for locations of people detected in camera #L image (D_LK). A greedy algorithm applied to matrix $S_{KL}=D_{KL}+D_{LK}^T$ matches identities (yellow table).

For a pair of identical and level ceiling-mounted fisheye cameras (#K and #L), this method uses five intrinsic parameters [2-D scaling factor, 2-D optical center offset, and a scalar parameter of the unified spherical model for fisheye cameras (Geyer and Danilidis, 2001; Courbon et al., 2012)] and two extrinsic parameters (distance between cameras and relative rotation angle between them). The distance between cameras was precisely measured using a laser measure, but the remaining five parameters were estimated using images of the test space with lights off when rolling a cart with a spherical red LED light mounted at a fixed height. This allowed us to record precise projection of the LED light on two fisheye images at the same time instant. Such pairs of projections are related through a bidirectional mapping (#K→#L or #L→#K) which is a function of the intrinsic and extrinsic parameters (Bone et al., 2021). In order to estimate the intrinsic parameters and rotation angle, the Euclidean distance between 1,000+ projection pairs was minimized using stochastic gradient descent by sequentially iterating through the two bidirectional mappings. This calibration has to be performed only once for a given camera model (intrinsic parameters). The extrinsic parameters (camera installation height, distance between cameras, rotation angle, etc.) need to be measured or calibrated with each camera-layout change or when adding new cameras. An interesting direction of research would be to develop an unsupervised approach in such cases, similarly to adaptive ReID proposed by Panda et al. (2017) for open-world dynamic networks of rectilinear cameras.

During ReID (Figure 5), first RAPiD is applied to same-time images from cameras #K and #L to detect people; the center of each detected bounding box marks a person's location (blue K_i's and L_i's). Then, using the intrinsic and extrinsic parameters, and the average height of a person (168 cm), the detected locations in each camera view (blue symbols) are mapped to predict these locations in the other camera view (red symbols). Ideally, the predicted locations should coincide with the detected ones, but in reality this is not the case due to imperfect camera model and calibration. In practice, the closer a predicted location (red) is to a detected location (blue) the more likely it is that these are locations of the same person. Bone et al. (2021) proposed four different distance metrics to quantify the proximity of a predicted location to detected locations in a given view. The fastest metric to compute is called Point-to-Point Distance (PPD). It calculates the Euclidean distance between each predicted location and each detected location to form a 2-D score matrix (Figure 5). The best-performing metric in their tests is called Count-Based Distance (CBD). Unlike PPD, which assumes average height of a person and is not accurate for very tall and short individuals, CBD considers a range of human heights (150–190 cm in 2 cm increments). For each detected location in one view, it produces 21 predicted locations in the other view (corresponding to different heights of a person). Then, for each detected location the number of predicted locations (out of 21) for which this detected location is closest establishes a count. This count is subtracted from the total number of considered person-heights (21) to establish a distance measure; the smaller the measure (the larger the count) the more likely it is that the detected and predicted locations have the same identity. This metric is computed for each detected and predicted identity to form a 2-D score matrix. Score matrix D_KL (Figure 5) is computed for the detections in camera #K and predictions from camera #L, while score matrix D_LK is computed for the detections in camera #L and predictions from camera #K. Finally, to perform bidirectional identity matching a combined score matrix $S_{KL}=D_{KL}+D_{LK}^T$ is used in a greedy fashion. First, the smallest entry in S_KL is found, the corresponding identities are considered a match, and their row and column are removed from the matrix reducing its size by 1 in each dimension. This process is repeated until no more matches are possible.

This location-based approach to person ReID was shown to outperform appearance-based methods by a large margin (over 11% points in mAP for the PPD metric and over 14% points for the CBD metric) on the FRIDA dataset (Cokbas et al., 2023), and is our method of choice for people counting discussed next.

6.4.2 Removal of double-counts

The ReID method discussed in the previous section is essential for accurate people counting using two cameras. Let ${\hat{\eta }}_i^K$ and ${\hat{\eta }}_i^L$ be the estimated people counts in frame number i from cameras #K and #L, respectively, for example obtained by counting bounding boxes detected by a person-detection algorithm, such as RAPiD. Let ${\hat{\eta }}_i^{KL}$ be the number of people detections successfully re-identified between these two frames. The people-count estimate for this pair of frames is then computed as follows:

$\begin{array}{ll}{\hat{\eta }}_i={\hat{\eta }}_i^K+{\hat{\eta }}_i^L-{\hat{\eta }}_i^{KL},& (1)\end{array}$

where the subtraction of ${\hat{\eta }}_i^{KL}$ removes double counts discovered by person re-identification.

6.4.3 Experimental results for two cameras

Table 6 shows a 2-camera people-counting performance of RAPiD (to compute ${\hat{\eta }}_i^K$ and ${\hat{\eta }}_i^L$ in each frame pair) followed by location-based person re-identification with either the PPD or CBD distance metric (to compute ${\hat{\eta }}_i^{KL}$). Compared to Table 5, both cumulative MAE and MAE_pp are reduced about 4 times for both distance metrics. The CBD metric performs slightly better than PPD achieving cumulative MAE of 1.59 and MAE_pp of 0.097. This is a huge performance improvement over the single-camera results. In particular, the MAE_pp value suggests that the two-camera approach commits an error of less than 10% per person compared to 40% for single camera. While the cumulative X-Accuracy for X = 0 is slightly reduced compared to Table 5, the one for X = 5 is improved to 92% and one for X = 10 is 98%. Clearly, using two cameras in a large space significantly improves the people-counting accuracy of RAPiD.

Table 6

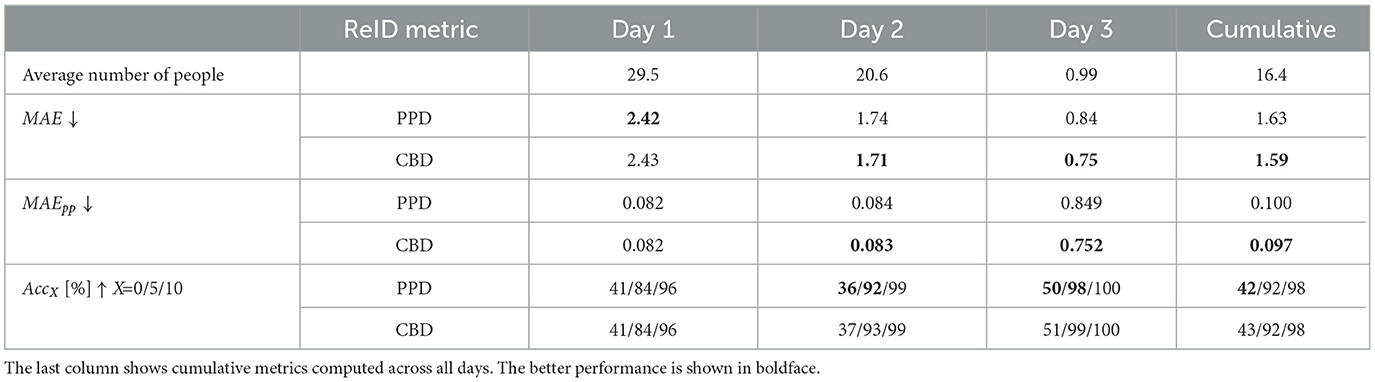
Table 6. Two-camera people-counting performance of RAPiD in a 3-day test in large classroom using cameras #2 and #3 (Figure 2C) and location-based person-re-identification using the PPD or CBD distance-error metric.

7 Counting people in large spaces using N > 2 overhead fisheye cameras

The results in Section 6 indicate that two overhead fisheye cameras are sufficient for quite accurate people counting in a 187 m² space (Figure 2C). However, in larger spaces more cameras would be needed to maintain a similar level of performance. This would require person ReID between more than two fisheye cameras, a task unexplored to-date. In this section, we propose two novel approaches to accomplish this and demonstrate their performance for people counting using three overhead fisheye cameras.

7.1 General person ReID based on N-dimensional score matrix

We propose a general approach to person ReID using N-D score matrices. Such matrices can quantify similarity between identities using people locations, as proposed by Bone et al. (2021), or their appearance, as explored by Cokbas et al. (2023). We first consider a 3-camera setup (N = 3) of our test classroom shown in Figure 2C, however we note that, in general, cameras need not be collinear. In Figure 6, we graphically illustrate (Venn diagram) the general relationship between sets of person detections from three cameras. In this diagram, C₁, C₂, C₃ denote the sets of people detections in images simultaneously captured by cameras #1, #2 and #3, respectively. The Venn diagram allows us to compute the actual people count η as follows:

$\begin{array}{c}\eta =\left|C_1\right|+\left|C_2\right|+\left|C_3\right|-|C_1\cap C_2|-|C_1\cap C_3|\\ -|C_2\cap C_3|+|C_1\cap C_2\cap C_3|,& (2)\end{array}$

where |C| denotes the cardinality of set C. Clearly, |C₁|, |C₂|, |C₃| are people counts in respective camera views provided by a people-detection algorithm (e.g., RAPiD). The numbers of identities matched between two cameras, namely |C₁∩C₂|, |C₁∩C₃|, |C₂∩C₃|, are provided by a two-camera ReID algorithm, such as the one described in Section 6.4.1. However, we still need to identify the number of identities matched across all three cameras: |C₁∩C₂∩C₃|. This necessitates a 3-camera ReID algorithm.

Figure 6

Figure 6. Venn diagram graphically illustrating people-counting scenario for N = 3 cameras.

As discussed in Section 6.4.1 and shown in Figure 5, person ReID between two cameras results in a 2-D score (distance) matrix D that is subject to a greedy search to match identities. With three cameras, this matrix would become 3-dimensional with each entry containing, for example, a measure of appearance similarity for a triplet of people detections (one detection from each camera view), or a distance metric computed from locations of this triplet. Rather than defining a new 3-camera distance metric, we adopt 2-camera metrics developed by Bone et al. (2021), apply them to 3 pairs of cameras and average the resulting scores as follows:

$\begin{array}{ll}{S}_{123}(i_1,i_2,i_3)=\frac{1}{3}\times (S_{12}(i_1,i_2)+S_{13}(i_1,i_3)+S_{23}(i_2,i_3)),& (3)\end{array}$

where S₁₂, S₁₃, S₂₃ are 2-D score matrices (like those in Figure 5), S₁₂₃ is a 3-D score matrix and i_K is the identity detected in view from camera #K. Clearly, S₁₂(i₁, i₂) quantifies the location mismatch for identities i₁ and i₂ from cameras #1 and #2, respectively, and S₁₂₃(i₁, i₂, i₃) represents the location mismatch for identities i₁, i₂, i₃, each from its respective camera.

An extension to N>3 is relatively straightforward but one must carefully consider various combinations of n out of N cameras, across which identities need to be matched. For example, for N = 4 cameras, re-identifications between 2, 3, or 4 camera views are needed in order to obtain the correct overall count. For N cameras, the total number of camera combinations to be considered is:

$\begin{array}{ll}{\displaystyle \sum _{n=2}^N\left(\begin{array}{c}N\\ n\end{array}\right)}=2^N-1-N,& (4)\end{array}$

where the summation starts at n = 2 since re-identification requires at least two camera views. For N = 3, this amounts to four camera combinations which is consistent with four intersections in the Venn diagram in Figure 6. For N = 4, there are 11 camera combinations (6 two-camera combinations, 4 three-camera combination, and 1 four-camera combination), and for N = 5 there are 26 camera combinations, rapidly increasing with a growing number of cameras.

Clearly, score matrices S of up to N dimensions are needed for N-camera re-identification. One possibility is to generalize Equation (2) to N dimensions through the use of the well-known inclusion-exclusion principle by van Lint and Wilson (1992) as follows:

$\begin{array}{ll}{S}_{12\dots N}(i_1,i_2,\dots ..,i_N)=\frac{1}{\left(\begin{array}{c}N\\ 2\end{array}\right)}{\displaystyle \sum _{k=1}^N{\displaystyle \sum _{l=k+1}^N{S}_{kl}}}(i_k,i_l).& (5)\end{array}$

We would like to emphasize that this approach to N-camera person ReID is general and can be applied to both appearance- and location-based features. However, in the remainder of this section we focus on location-based matching due to its superior performance for overhead fisheye cameras (Cokbas et al., 2023) and low computational complexity. The computational complexity is a serious concern for large N since the number of camera combinations that need to be considered grows exponentially with a growing N (4).

7.2 Person ReID based on clustering of real-world locations

The approach we proposed in the previous section is general and applies to both appearance- and location-based features. If applied to location-based features, it effectively performs identity matching based on locations in the 2-D image plane (pixel coordinates); identities are matched based on the proximity of detected and predicted locations in a given camera view. All the predicted locations are obtained by first inverse-mapping 2-D locations detected in one camera view to 3-D coordinates and then forward-mapping these 3-D coordinates to 2-D locations in the other camera view (bidirectional location mapping in Figure 5). This may result in location-error imbalance since the detected locations do not undergo any mapping, while the predicted locations are obtained via inverse-forward mapping that uses intrinsic and extrinsic parameter estimates⁴, unlikely to be perfectly accurate.

In order to avoid this location-error imbalance, we propose to perform identity matching in real-world coordinates, that is map person-detection locations in all camera views to 3-D coordinates. An explanation is required at this point. The inverse mapping from a 2-D location in a camera view to 3-D coordinates must be constrained due to scale ambiguity (the problem is underconstrained). In the scenario of indoor monitoring, considered here, with people positioned on a room's floor, this ambiguity can be removed by assuming average height of a person (168 cm). Then, the location of a person detection (center of the bounding box) in any camera view can be mapped to 3-D room coordinates such that the 3-D point is 84 cm above the floor (vertical center of human body of average height). The inverse mapping of all person-detection locations from N camera views to 3-D space results in a point “cloud”, or rather a 2-D point “spatter” on a plane parallel to and 84 cm above the floor. We propose to cluster the locations in this “spatter” to match identities.

We note that, ideally, the number of location clusters should correspond to the number of people in the room. Therefore, we cannot use a clustering algorithm such as K-means (Lloyd, 1982) since we do not know the value of K in advance. We adopt DBSCAN (Ester et al., 1996) since it requires no advance knowledge of the number of clusters. DBSCAN is a density-based clustering algorithm that has two parameters, ϵ and minPoints. In DBSCAN, first one picks a random point as the point of interest and finds all points that are within radius ϵ from it. All such points, including the point of interest, get assigned to the same cluster. This process is repeated; each point in the cluster is treated as the new point of interest, thus enlarging the cluster. One continues to spread out the cluster until there is no point within ϵ distance from any of the points in the cluster. Then, one picks another point from the dataset that has not been visited yet and repeats the process. For a group of points to be considered a cluster, there should be at least minPoints elements in the cluster. Also, if a certain data point has no other data points within ϵ radius, it is labeled as noise and gets discarded.

Similarly to DBSCAN, we propose clustering of the mapped real-world coordinates using two parameters: ϵ and maxPoints. While ϵ has the same role as in DBSCAN, maxPoints is used differently. In DBSCAN, the size of a cluster has a lower bound of minPoints with no upper bound. In our case, cluster size must be between 1 and maxPoints due to the nature of person re-identification and people counting that we are tackling. Each person should have their own cluster, where each point in the cluster corresponds to a detection of the same person in a different camera view. In re-identification across N cameras, some people can get detected in one camera view only due to occlusions or failed detections, potentially resulting in a single point in their cluster. On the other hand, a person can be detected in at most N camera views, so a cluster may have at most N points and so maxPoints = N.

In experiments reported in the next section, we use 3-D Euclidean distance as the distance measure between the mapped real-world locations. However, since all such locations occur on a plane, as discussed above, effectively this is a 2-D distance in real-world coordinates.

7.3 Experimental results for 3 cameras

We evaluate the people-counting performance of both N-camera person ReID algorithms on the 3-day dataset captured by three cameras, that we introduced in Section 6.2. While in Table 5 we reported people-counting results using only camera #1 and in Table 6 using cameras #2 and #3, here we report results using all three cameras installed in the classroom.

We use location-based re-identification with the PPD distance metric to evaluate both N-camera algorithms. Note, that in the N-D score-matrix approach elements of S (PPD values) are expressed in pixels (i.e., the lower the score/distance, the more similar the identities). While the greedy algorithm (Figure 5) performs identity matching until no more matches are possible, some late matches may be unlikely if the corresponding element in S is large. To avoid such unlikely matches, we introduce a distance threshold λ (in pixels), and stop the matching once all remaining elements in S exceed λ. The N-camera location-clustering approach (Section 7.2) also has a tuning parameter ϵ, expressed in centimeters, that quantifies a threshold on distance in real-world coordinates.

In Figure 7, we show the people-counting performance of both N-camera algorithms (N = 3) when their respective tuning parameters vary. The N-D score-matrix approach yields the lowest MAE value for λ = 400 pixels, while the real-world location-clustering approach achieves the best performance for ϵ = 250 cm. We note that these values are relatively large considering the fact that we are working with 2,048 × 2,048-pixel images in a 22 × 8.5 m room. Very likely some identity matches are incorrect (as are some RAPiD detections) and yet the people count is quite accurate. However, since our dataset is labeled for people-counting only (no bounding boxes or identity labels), we cannot report ReID accuracy to verify this hypothesis.

Figure 7

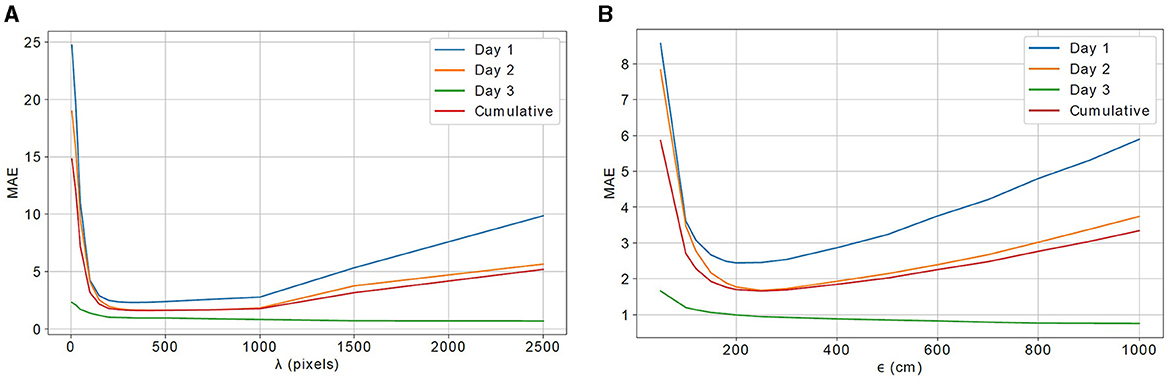
Figure 7. People-counting performance (cumulative MAE across 3 days of the test) for: (A) N-D score-matrix approach with varying λ; and (B) real-world location-clustering approach with varying ϵ, both for N = 3.

While a low MAE is maintained by the N-D score-matrix approach for a wide range of λ values (from about 100 pixels to 1,000 pixels), a high-performance range for the real-world location clustering approach happens only for ϵ between about 200 and 300 cm. Outside of these ranges, MAE increases and especially rapidly for small parameter values. For example, small values of threshold ϵ allow little room for image-to-3-D mapping errors; imprecisely mapped locations get absorbed into incorrect clusters. The more accurate the mapping algorithm, the smaller the value of ϵ that can be used. In the extreme case of ϵ = 0 cm, there is no room for mapping errors. Unless same-identity locations from all cameras are mapped to the same 3-D location, they cannot form one cluster. Since error-free mappings are very unlikely, for ϵ = 0 cm very few identities can be matched, thus resulting in small ${\hat{\eta }}_i^{KL}$ in Equation (1) and causing overcounting. As ϵ increases, the degree of overcounting gets reduced. At the other extreme, if ϵ is too large the mapped locations of different identities might fall into the same cluster thus potentially resulting in too many matches and leading to undercounting. Similar conclusions can be drawn for the impact of λ on performance of the N-D score-matrix algorithm.

In order to confirm our observations about overcounting and undercounting, Figure 8 shows the true occupancy during the 3-day test (red line) and occupancy estimated by the N-D score-matrix algorithm (blue line) for three values of λ: 100, 400 and 1,500 pixels. Notably, for λ = 100 pixels the algorithm significantly overcounts, while for λ = 1, 500 pixels it largely undercounts. However, for λ = 400 pixels, it closely follows the true people count. Figure 9 shows similar results for the real-world location-clustering algorithm and three values of ϵ: 50, 250, and 800 cm. Again, for ϵ = 50 cm the algorithm severely overcounts, for ϵ = 800 cm it largely undercounts, and for ϵ = 250 cm it is most accurate.

Figure 8

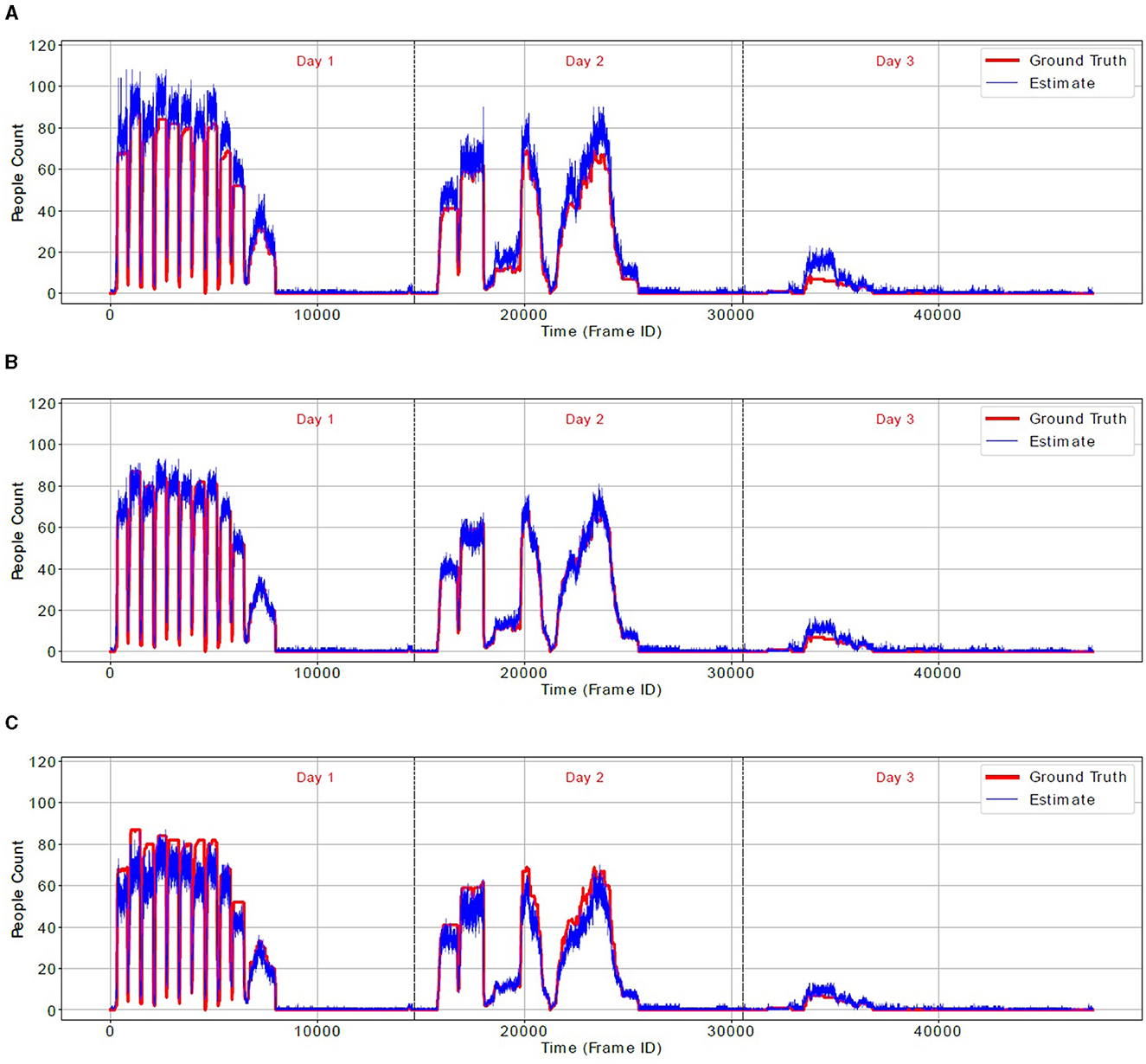
Figure 8. Ground-truth people count (red line) and an estimate by 3-camera score-matrix algorithm (blue line) for three values of threshold λ. (A) λ = 100 pixels. (B) λ = 400 pixels. (C) λ = 1,500 pixels.

Figure 9

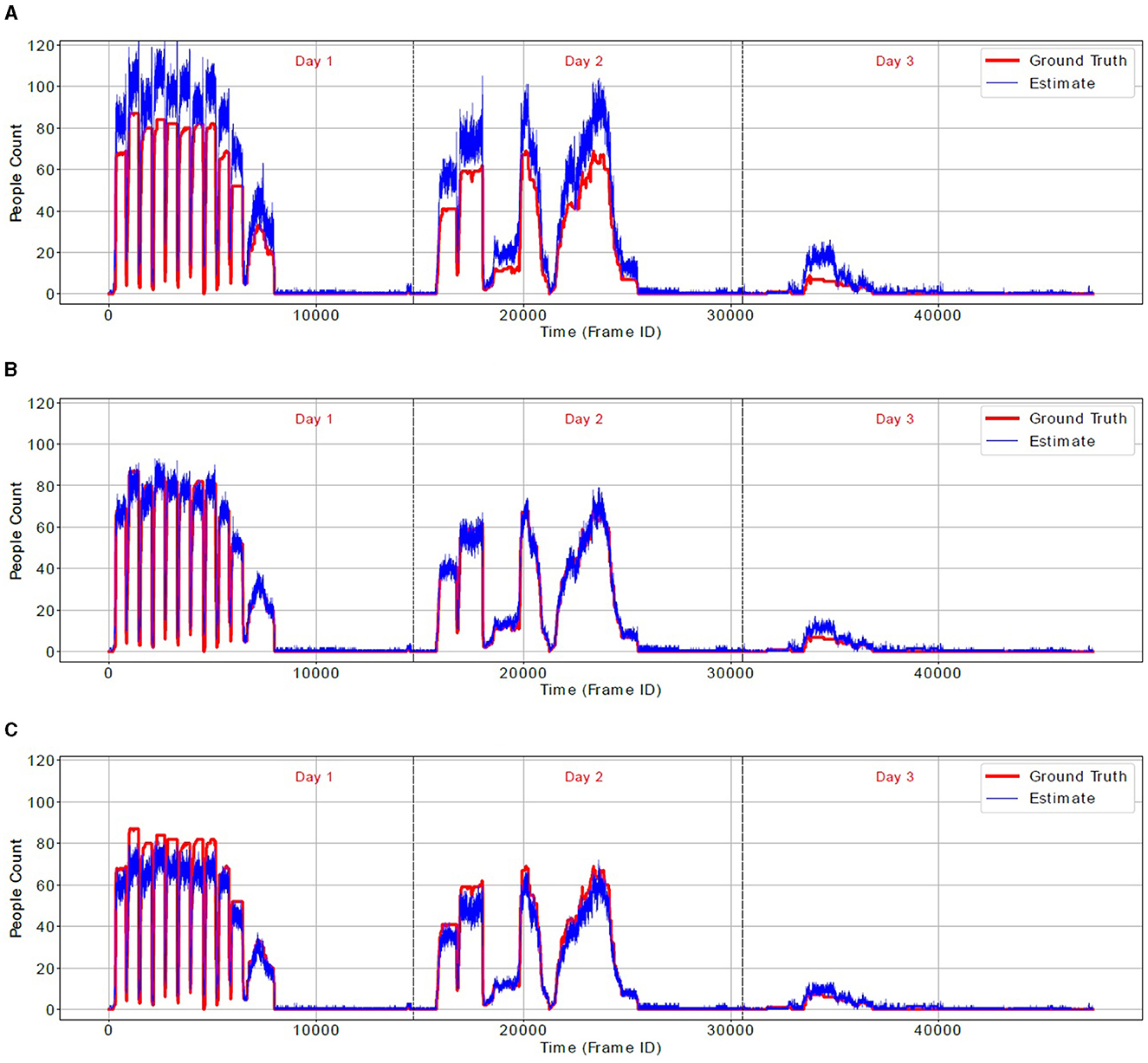
Figure 9. Ground-truth people count (red line) and an estimate by 3-camera real-world location-clustering algorithm (blue line) for three values of threshold ϵ. (A) ϵ = 50 cm. (B) ϵ = 250 cm. (C) ϵ = 800 cm.

Table 7 quantifies performance of both algorithms in terms of MAE, MAE_pp, Acc_X for the tuning parameters that yielded the smallest cumulative MAE value (Figure 7), namely λ = 400 pixels and ϵ = 250 cm. For ease of comparison, included are also results for the 2-camera people-counting algorithms from Table 6 that employ greedy search of a 2-D score matrix populated by either PPD or CBD values. We note, that in terms of cumulative metrics the 3-camera score-matrix algorithm using the PPD metric slightly outperforms the same algorithm using 2 cameras. However, it performs equally well-compared to the 2-camera score-matrix algorithm with the CBD metric in terms of MAE and MAE_pp, and results are mixed in terms of Acc_X (slightly better for X = 5 and 10, and slightly worse for X = 0). As for the 3-camera real-world location-clustering algorithm, it does not perform as well; its cumulative MAE and MAE_pp values are higher by 0.07 and 0.04, respectively, than corresponding values for the 3-camera score-matrix algorithm, and the Acc_X values are lower by up to 1% point.

Table 7

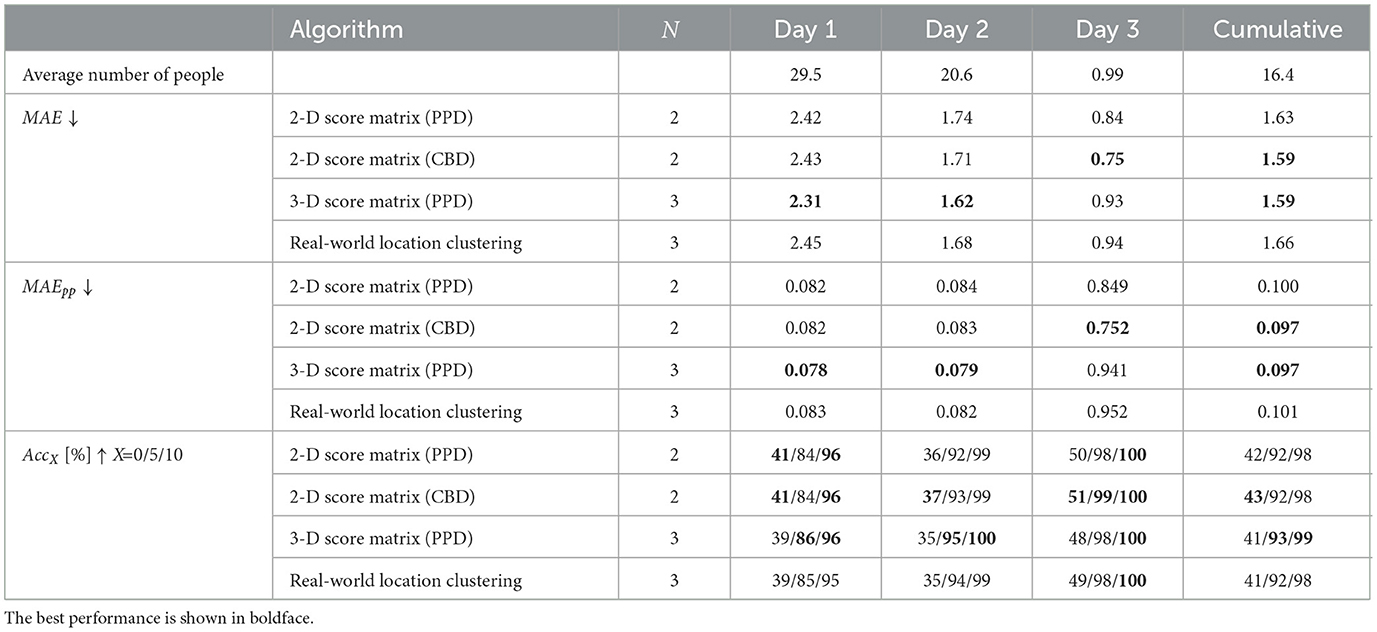
Table 7. People-counting performance of the RAPiD detection algorithm combined with 2-camera or 3-camera location-based re-identification algorithms in a 3-day test in the large classroom (Figure 2C).

With respect to different occupancy scenarios, the 3-camera score-matrix approach quite consistently outperforms other algorithms on days 1 and 2 (high average occupancy), but is outperformed by the 2-camera approaches on day 3 (mostly empty). Interestingly, on day 3 the single-camera results (Table 5) are even better than those for two cameras; for example, camera #1 mounted in the center of the classroom produces MAE and MAE_pp twice lower than those for the 2-camera algorithms. This is due to the fact that the few occupants on day 3 are located in classroom center which is effectively covered by camera #1. With no challenges (people are directly under the camera, no occlusions, no occupants at FOV periphery), people counting using one camera is erroneous only if people detection fails. However, when multiple cameras are needed for large-area coverage, additional errors may be introduced by person ReID. Clearly, under spatially-localized low occupancy, single-camera RAPiD may be sufficient. However, in large spaces with spatially-distributed high occupancy, a multi-camera people-counting system is essential.

The results in Table 7 may seem somewhat disappointing since the better 3-camera approach only slightly outperforms the best 2-camera approach and only in crowded scenarios. However, there is a reason for this. The 2-camera score-matrix (CBD) approach performs very well in this 187 m² test space producing cumulative MAE_pp of only 0.097 (9.7% error per person) vastly outperforming the 1-camera RAPiD performance (no re-identification) that produced a 0.373 cumulative MAE_pp (or 37.3% error per person) as shown in Table 5. As reported in Konrad et al. (2024), RAPiD applied to a single-camera video stream can deliver MAE_pp of 0.065 (6.5% error per person) up to about 75 m² (≈800 ft²) of a square-room area and 0.133 (or 13.3%) up to about 116 ft² (≈1,250 ft²). Considering that this is a 22 × 8.5 m space and that each of the cameras used by the 2-camera score-matrix approach (cameras #2 and #3 in Figure 2) roughly covers one half of the classroom (about 11 × 8.5 m space with 93.5 m² area), it is clear that little improvement can be expected from additional cameras in this case. However, the N-camera ReID algorithms proposed in this paper are expected to be highly beneficial in larger spaces in which two cameras would be insufficient. We believe that the proposed N-camera methodology would be very valuable in scaling up people-counting to much larger spaces such as convention halls, food courts, airport terminals, train/bus stations, etc.

Theoretically, a fisheye camera with FOV covering 360° in plane parallel to the sensor and at least 180° orthogonally should capture an area of any size. However, due to radial distortions of its lens and finite sensor resolution, details captured at FOV periphery are insufficient for reliable person detection (and re-identification). As discussed above, in our test scenario (Figure 2C) a single camera mounted 3.15 m above the floor can produce reliable detections up to about 8.7 × 8.7 m square area (≈75 m²). However, in a square area of 87 × 87 m, it is unlikely that 100 fisheye cameras used jointly by person ReID methods described in Sections 7.1 and 7.2 would produce reliable results using a location-based approach (PPD or CBD). As the physical distance between cameras increases, the bidirectional projection errors will grow due to errors in intrinsic and extrinsic parameters. Depending on the accuracy of these parameters, a very large area may need to be partitioned into sections, each monitored independently by a smaller group of cameras (e.g., 2 × 2 or 3 × 3). One could consider using the N-D score matrix approach with appearance features (instead of location), but a person captured by far apart cameras may appear dramatically smaller in one FOV than in the other posing very serious challenges for ReID. Again, small groups of nearby cameras would be more effective.

8 Conclusions and future directions

There exists a significant demand for occupancy analytics in commercial buildings with applications ranging from security and space management to reduction of energy use. Technologies deployed today serve each of these needs individually (e.g., surveillance cameras for security, ID card access for space management, CO₂ sensing for energy reduction) and are not easily adaptable to other uses. While surveillance cameras could, in principle, serve all three applications, their usefulness is limited by their narrow field of view (many cameras would be needed, significantly complicating processing). Contrary to that, top-view fisheye cameras have a wide field of view and largely avoid occlusions, but few algorithms have been developed to date for the analysis of human presence and behavior using such cameras. In this paper, we reviewed some of the recent developments in this field and demonstrated that in small-to-medium size spaces (up to about 75 m²) one can very accurately detect (and count) people using a single overhead fisheye camera mounted about 3 m above the floor. However, in larger spaces several cameras are needed requiring additional processing to resolve ambiguities; for example, in counting and tracking one needs to match identities between cameras. To address this, we proposed two N-camera person re-identification algorithms and demonstrated their efficacy in large-space people counting.

Beyond detecting and counting people using overhead fisheye cameras, another challenge is in tracking. While we have been successful in re-identifying people between calibrated cameras based on location, reliable methods are needed for tracking people across the field of view of one camera and between cameras that do not have overlapping fields of view. This cannot be performed based on location, so advanced appearance-based methods are needed. Another unique challenge is in action recognition. A particular difficulty is the unusual viewpoint if an action is performed directly under the camera, not observed in traditional action recognition. Also, if a person moves away from under the camera while performing an action, even just a few meters, a dramatic viewpoint change occurs, again uncommon in typical action recognition studied today. There is also an application-specific challenge. In this work, people are localized in image coordinates but for security applications it would be of interest to map these locations to 2-D room layout, along the lines of real-world location clustering presented in Section 7.2. Finally, there exists a substantial performance gap between visual analysis methods developed for side-mounted rectilinear cameras and top-view fisheye cameras that needs to be closed; only then will fisheye-based indoor monitoring enter the mainstream video surveillance market. One methodology that can help achieve this goal is domain adaptation, for example by leveraging the richness of algorithms and datasets developed for front-facing fisheye cameras used in autonomous navigation. All these challenges need to be addressed before overhead fisheye cameras become ubiquitous in autonomous indoor monitoring.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://vip.bu.edu/projects/vsns/cossy/datasets/.

Ethics statement

Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author contributions

JK: Conceptualization, Funding acquisition, Methodology, Project administration, Supervision, Writing – original draft, Writing – review & editing. MC: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Writing – original draft, Writing – review & editing. MT: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Writing – original draft, Writing – review & editing. PI: Conceptualization, Funding acquisition, Methodology, Supervision, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the Advanced Research Projects Agency-Energy (ARPA-E) through agreement DE-AR0000944 and by Boston University Undergraduate Research Opportunities Program (UROP).

Acknowledgments

The authors would like to acknowledge Boston University undergraduates Ragib Ahsan, Christopher Alonzo, John Bolognino, Annette Hong, Nancy Zheng, and Jakub Zółkoś for helping annotate fisheye-image datasets used in this research.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^vip.bu.edu/rapid

2. ^ARPD (Minh et al., 2021) was developed and evaluated prior to the introduction of the WEPDTOF dataset.

3. ^vip.bu.edu/rapid-t

4. ^We used the 2-camera calibration method described in Section 6.4.1 except that instead of iterating through 2 camera pairs (#K→#L and #L→#K), we iterate through six camera pairs (#K→#L, #L→#K, #K→#M, #M→#K, #L→#M, #M→#L) during stochastic gradient descent.

References

Barman, A., Wu, W., Loce, R. P., and Burry, A. M. (2018). “Person re-identification using overhead view fisheye lens cameras,” in IEEE International Symposium on Technologies for Homeland Security (HST) (Piscataway, NJ: IEEE).

Google Scholar

Bazzani, L., Cristani, M., Perina, A., Farenzena, M., and Murino, V. (2010). “Multiple-shot person re-identification by HPE signature,” in International Conference on Pattern Recognition (Piscataway, NJ: IEEE), 1413–1416.

Google Scholar

Blott, G., Yu, J., and Heipke, C. (2019). Multi-view person re-identification in a fisheye camera network with different viewing directions. PFG J. Photogr. Remote Sens. Geoinf. Sci. 87, 263–274. doi: 10.1007/s41064-019-00083-y

Crossref Full Text | Google Scholar

Bone, J., Cokbas, M., Tezcan, O., Konrad, J., and Ishwar, P. (2021). “Geometry-based person reidentification in fisheye stereo,” in IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS) (Piscataway, NJ: IEEE).

Google Scholar

Chiang, A.-T., and Wang, Y. (2014). “Human detection in fish-eye images using HOG-based detectors over rotated windows,” in IEEE International Conference on Multimedia and Expo Workshops (ICMEW) (Piscataway, NJ: IEEE).

Google Scholar

Chiang, S.-H., Wang, T., and Chen, Y.-F. (2021). Efficient pedestrian detection in top-view fisheye images using compositions of perspective view patches. Image Vis. Comput. 105:104069. doi: 10.1016/j.imavis.2020.104069

Crossref Full Text | Google Scholar

Cokbas, M. (2023). Person Re-identification Using Fisheye Cameras With Application to Occupancy Analysis (PhD thesis). Boston University, Boston, MA, United States.

Google Scholar

Cokbas, M., Bolognino, J., Konrad, J., and Ishwar, P. (2022). “FRIDA: fisheye re-identification dataset with annotations,” in IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS) (Piscataway, NJ: IEEE).

Google Scholar

Cokbas, M., Ishwar, P., and Konrad, J. (2023). Spatio-visual fusion-based person re-identification for overhead fisheye images. IEEE Access 11, 46095–46106. doi: 10.1109/ACCESS.2023.3274600

Crossref Full Text | Google Scholar

Cordts, M., Omran, M., Ramos, S., Rehfeld, T., Enzweiler, M., Benenson, R., et al. (2016). “The Cityscapes dataset for semantic urban scene understanding,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Piscataway, NJ: IEEE), 3213–3223.

PubMed Abstract | Google Scholar

Courbon, J., Mezouar, Y., and Martinet, P. (2012). Evaluation of the unified model of the sphere for fisheye cameras in robotic applications. Adv. Robot. 26, 947–967. doi: 10.1163/156855312X633057

Crossref Full Text | Google Scholar

Dalal, N., and Triggs, B. (2005). “Histograms of oriented gradients for human detection,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Piscataway, NJ: IEEE), 886–893.

Google Scholar

Demirkus, M., Wang, L., Eschey, M., Kaestle, H., and Galasso, F. (2017). “People detection in fish-eye top-views,” in International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), Vol. 5 (SciTePress), 141–148.

Google Scholar

Dollár, P., Appel, R., Belongie, S., and Perona, P. (2014). Fast feature pyramids for object detection. IEEE Trans. Pattern Anal. Mach. Intell. 36, 1532–1545. doi: 10.1109/TPAMI.2014.2300479

PubMed Abstract | Crossref Full Text | Google Scholar

Dosovitskiy, A., Fischer, P., Ilg, E., Häusser, P., Hazirbas, C., Golkov, V., et al. (2015). “FlowNet: learning optical flow with convolutional networks,” in IEEE International Conference on Computer Vision (Piscataway, NJ: IEEE), 2758–2766.

Google Scholar

Duan, Z., Ozan, T. M., Nakamura, H., Ishwar, P., and Konrad, J. (2020). “RAPiD: rotation-aware people detection in overhead fisheye images,” in IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW) (Piscataway, NJ: IEEE).

Google Scholar

Ester, M., Kriegel, H.-P., Sander, J., and Xu, X. (1996). “A density-based algorithm for discovering clusters in large spatial databases with noise,” in International Conference on Knowledge Discovery and Data Mining (AAAI Press), 226–231.

Google Scholar

Farnebäck, G. (2003). “Two-frame motion estimation based on polynomial expansion,” in Image Analysis, eds. J. Bigun, and T. Gustavsson (Berlin, Heidelberg: Springer Berlin Heidelberg), 363–370.

Google Scholar

Geyer, C., and Danilidis, K. (2001). Catadioptric projective geometry. Int. J. Comp. Vision 45, 223–243. doi: 10.1023/A:1013610201135

Crossref Full Text | Google Scholar

Girshick, R. (2015). “Fast R-CNN,” in IEEE International Conference on Computer Vision (Piscataway, NJ: IEEE), 1440–1448.

Google Scholar

Konrad, J., Cokbas, M., Ishwar, P., Little, T. D., and Gevelber, M. (2024). High-accuracy people counting in large spaces using overhead fisheye cameras. Energy Build. 307:113936. doi: 10.1016/j.enbuild.2024.113936

Crossref Full Text | Google Scholar

Krams, O., and Kiryati, N. (2017). “People detection in top-view fisheye imaging,” in IEEE International Conference on Advanced Video and Signal-Based Surveillance (AVSS) (Piscataway, NJ: IEEE).

PubMed Abstract | Google Scholar

Li, S., Tezcan, M. O., Ishwar, P., and Konrad, J. (2019). “Supervised people counting using an overhead fisheye camera,” in IEEE International Conference on Advanced Video and Signal-Based Surveillance (AVSS) (Piscataway, NJ: IEEE).

Google Scholar

Liao, Y., Xie, J., and Geiger, A. (2023). KITTI-360: a novel dataset and benchmarks for urban scene understanding in 2D and 3D. IEEE Trans. Pattern Anal. Mach. Intell. 45, 3292–3310. doi: 10.1109/TPAMI.2022.3179507

PubMed Abstract | Crossref Full Text | Google Scholar

Lin, T.-Y., Maire, M., Belongie, S., Hays, J., Perona, P., Ramanan, D., et al. (2014). “Microsoft COCO: common objects in context,” in Computer Vision-ECCV 2014, eds. D. Fleet, T. Pajdla, B. Schiele, and T. Tuytelaars (Cham: Springer International Publishing), 740–755.

Google Scholar

Liu, W., Anguelov, D., Erhan, D., Szegedy, C., Reed, S., Fu, C.-Y., et al. (2016). “SSD: single shot multibox detector,” in Computer Vision-ECCV 2016, eds. B. Leibe, J. Matas, N. Sebe, and M. Welling (Cham: Springer International Publishing), 21–37.

Google Scholar

Lloyd, S. (1982). Least squares quantization in PCM. IEEE Trans. Pattern Anal. Mach. Intell. 28, 129–137. doi: 10.1109/TIT.1982.1056489

Crossref Full Text | Google Scholar

Minh, Q. N., Van, B. L., Nguyen, C., Le, A., and Nguyen, V. D. (2021). “ARPD: anchor-free rotation-aware people detection using topview fisheye camera,” in IEEE International Conference on Advanced Video and Signal-Based Surveillance (AVSS) (Piscataway, NJ: IEEE).

Google Scholar

Panda, R., Bhuiyan, A., Murino, V., and Roy-Chowdhury, A. K. (2017). “Unsupervised adaptive re-identification in open world dynamic camera networks,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Piscataway, NJ: IEEE), 1377–1386.

Google Scholar

Redmon, J., Divvala, S., Girshick, R., and Farhadi, A. (2016). “You only look once: unified, real-time object detection,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Piscataway, NJ: IEEE), 779–788.

Google Scholar

Redmon, J., and Farhadi, A. (2018). Yolov3: An Incremental Improvement. CoRR, abs/1804.02767.

Google Scholar

Ren, S., He, K., Girshick, R., and Sun, J. (2015). “Faster R-CNN: towards real-time object detection with region proposal networks,” in Advances in Neural Information Processing Systems, Vol. 28, eds. C. Cortes, N. Lawrence, D. Lee, M. Sugiyama, and R. Garnett (Curran Associates, Inc.).

Google Scholar

Sabater, A., Montesano, L., and Murillo, A. C. (2020). Robust and efficient post-processing for video object detection. arXiv [preprint]. doi: 10.1109/IROS45743.2020.9341600

Crossref Full Text | Google Scholar

Saito, M., Kitaguchi, K., Kimura, G., and Hashimoto, M. (2011). “People detection and tracking from fish-eye image based on probabilistic appearance model,” in SICE Annual Conference (Piscataway, NJ: IEEE), 435–440.

Google Scholar

Seidel, R., Apitzsch, A., and Hirtz, G. (2018). Improved person detection on omnidirectional images with non-maxima suppression. arXiv [preprint]. doi: 10.5220/0007388400002108

Crossref Full Text | Google Scholar

Tamura, M., Horiguchi, S., and Murakami, T. (2019). “Omnidirectional pedestrian detection by rotation invariant training,” in IEEE Winter Conference on Applications of Computer Vision (WACV) (Piscataway, NJ: IEEE).

Google Scholar

Tamura, M., and Yoshinaga, T. (2023). Segmentation-based bounding box generation for omnidirectional pedestrian detection. Visual Comp. 40, 2505–2516. doi: 10.1007/s00371-023-02933-8

Crossref Full Text | Google Scholar

Tezcan, M. O., Duan, Z., Cokbas, M., Ishwar, P., and Konrad, J. (2022). “WEPDTOF: a dataset and benchmark algorithms for in-the-wild people detection and tracking from overhead fisheye cameras,” in IEEE/CVF Winter Conference on Applications of Computer Vision (WACV) (Piscataway, NJ: IEEE), 1381–1390.

Google Scholar

van Lint, J. H., and Wilson, R. M. (1992). Chapter 10: A Course in Combinatorics (Cambridge University Press).

Google Scholar

Wang, T., and Chiang, S.-H. (2023). “Online pedestrian tracking using a dense fisheye camera network with edge computing,” in IEEE International Conference on Image Processing (ICIP) (Piscataway, NJ: IEEE), 3518–3522.

Google Scholar

Wei, X., Wei, Y., and Lu, X. (2022). RMDC: rotation-mask deformable convolution for object detection in top-view fisheye cameras. Neurocomputing 504, 99–108. doi: 10.1016/j.neucom.2022.06.116

Crossref Full Text | Google Scholar

Ye, M., Shen, J., Lin, G., Xiang, T., Shao, L., and Hoi, S. H. (2022). Deep learning for person re-identification: a survey and outlook. IEEE Trans. Pattern Anal. Machine Intell. 44, 2872–2893. doi: 10.1109/TPAMI.2021.3054775

PubMed Abstract | Crossref Full Text | Google Scholar

Ye, Y., Yang, K., Xiang, K., Wang, J., and Wang, K. (2020). “Universal semantic segmentation for fisheye urban driving images,” in IEEE International Conference on Systems, Man, and Cybernetics (SMC) (Piscataway, NJ: IEEE), 648–655.

PubMed Abstract | Google Scholar

Yogamani, S., Hughes, C., Horgan, J., Sistu, G., Chennupati, S., Uricar, M., et al. (2019). “Woodscape: a multi-task, multi-camera fisheye dataset for autonomous driving,” in IEEE International Conference on Computer Vision (Piscataway, NJ: IEEE), 9307–9317.

Google Scholar

Yu, J., Grassi, A. C. P., and Hirtz, G. (2023). “Applications of deep learning for top-view omnidirectional imaging: a survey,” in IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW) (Piscataway, NJ: IEEE).

Google Scholar

Zhang, P., Yu, X., Wang, C., Zheng, J., Ning, X., and Bai, X. (2024). Towards effective person search with deep learning: a survey from systematic perspective. Pattern Recognit. 152:110434. doi: 10.1016/j.patcog.2024.110434

Crossref Full Text | Google Scholar

Zhu, X., Wang, Y., Dai, J., Yuan, L., and Wei, Y. (2017). “Flow-guided feature aggregation for video object detection,” in IEEE International Conference on Computer Vision (Piscataway, NJ: IEEE), 408–417.

PubMed Abstract | Google Scholar