
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 09 November 2023
Sec. Solar Energy
Volume 11 - 2023 | https://doi.org/10.3389/fenrg.2023.1286376
In this paper, a mathematical and physical model is established to study the convective heat transfer performance of supercritical carbon dioxide (SCO2) in three kinds of horizontal semicircular channels (uniform cross-sectional channel, diverging and converging channels). The accuracy of the numerical model is verified by comparing with the experimental data. The computational results demonstrate that the converging channel can strengthen heat transfer effectively compared with the uniform cross-sectional channel under the same heat transfer area. In the range of calculated working conditions, the use of a converging channel resulted in a maximum improvement of 42.26% in the heat transfer performance of SCO2. However, the diverging channel deteriorates the heat transfer. It is discovered that the improvement of the field coordination of SCO2 in the converging channel is one of the main reasons for its enhanced heat transfer. In addition, the different distribution of turbulent kinetic energy and thermal conductivity are also an important factor affecting the heat transfer performance of SCO2 in different channels. Finally, we propose a new heat transfer correlation of the SCO2 cooling process in the horizontal semicircular converging channel. Compared with the five selected correlations, the new correlation has the best prediction accuracy, and its mean absolute relative error (MARE) and root mean square error (RMSE) are 9.49% and 10.6%, respectively. Our work will provide new insights and theoretical guidance for the design and optimization of coolers in SCO2 Brayton cycle system.
As a natural working fluid, carbon dioxide (CO2) has many advantages such as environmental friendliness, good thermal stability, non-combustible, non-toxic, etc. Supercritical CO2 (SCO2) Brayton cycle was first proposed by Sulzer in 1950 (Sulzer, 1950), which has the following advantages: 1) CO2 has low critical parameters (304.13 K/7.377 MPa) and easy to reach supercritical state. 2) When the steam temperature is higher than 550°C, the thermal efficiency of SCO2 Brayton cycle is higher than that of water steam Rankine cycle (Dostal, 2004; Ahn, et al., 2015). 3) The SCO2 Brayton cycle system is compact and has great flexibility. Hence, in recent 10 years, many countries have invested a lot of manpower and material resources in the research and development of SCO2 cycle. The combination of concentrated solar power generation technology and SCO2 Brayton cycle is an important direction in the development of solar thermal power technology, which has been studied by a large number of researchers in recent years (Reyes-Belmonte et al., 2016; Zhu et al., 2017; Chen et al., 2021). In addition, the SCO2 Brayton cycle is also considered an ideal candidate for next-generation nuclear reactor power conversion systems (Yoon et al., 2012).
Heat absorber, low-temperature/high-temperature recuperators and cooler are one of the key equipment to realize heat transfer in SCO2 power generation system driven by solar energy. Therefore, in the context of the development of the SCO2 power cycle, the heat transfer of SCO2 has been extensively studied. A large number of experimental and numerical simulation studies were reviewed by Luisa F. Cabeza et al. (Cabeza et al., 2017) and M. Monjurul Ehsan et al. (Ehsan et al., 2018), and more recently by Xie et al., 2020 and Zhang S. et al., 2020. Most of these studies are carried out in circular tubes. Various researchers analyzed the effects of operating parameters, flow direction, tube dimeter, buoyancy and flow acceleration on SCO2 heat transfer (Peng et al., 2022; Zhang S. et al., 2022; Zhu X. et al., 2022; Xu and Yi, 2023). At present, there are two theories to explain the abnormal behavior of SCO2 heat transfer, one is single-phase fluid theory and the other is two-phase theory. The single-phase theory suggests that the abnormal behavior of SCO2 heat transfer is caused by the buoyancy and flow acceleration effects (Kim D. E., and Kim M. H., 2010; Jackson, 2013). However, these criteria and correlations-based buoyancy and thermal acceleration effects fail to predict supercritical heat transfer accurately. In recent years, the two-phase theory of supercritical fluids has developed rapidly. Banuti, 2015 confirmed the existence of pseudo-boiling in supercritical fluids by analytical method, and believed that pseudo-boiling occurs at a finite temperature interval. They also determined the starting point temperature and the ending point temperature at which the pseudo-boiling occurs by thermodynamic methods. Wang Q. et al., 2021 made an analogy between supercritical heat transfer and subcritical boiling heat transfer, proposed a three-regime model of supercritical heat transfer and established a theoretical framework for supercritical boiling heat transfer. In our previous research, we first tried the quantitative analogy between subcritical boiling heat transfer and supercritical heat transfer based on the pseudo-boiling theory, and proposed the supercritical boiling number SBO and K number, which govern the thickness of gas-like film. SBO and K number successfully deal with the supercritical heat transfer and have been widely cited (Zhu B. et al., 2019; Zhu B. et al., 2020).
Printed circuit heat exchanger (PCHE) is considered as the most promising heat exchanger in SCO2 power generation system because of its compact structure, high heat transfer efficiency, small volume ratio, high temperature and high-pressure resistance (Liu et al., 2020). The heat exchange core is the most important part of PCHE, which is made of multi-layer heat exchange plate connected by diffusion welding. The flow channel on the heat exchange plate is the main heat exchange surface of the fluid. Thus, the flow channel structure of PCHE is the most important factor affecting its heat transfer and resistance characteristics. Figure 1 shows a geometry structure of a PCHE heat transfer core with a semicircular cross section channel. At present, the semicircular channel is the most commonly used channel structure in PCHE. In order to better design PCHE, some researchers have studied the flow heat transfer of SCO2 in a semicircular channel. Zhang Y. et al., 2019 numerically studied the local heat transfer characteristics of SCO2 in a horizontal semicircle micro tube, the influences of pressure, mass flux, heat flux and tube geometry on SCO2 local heat transfer characteristics near Tpc were studied, and they found that the dramatic variations of thermos-physical properties in pseudocritical region have significant effects on heat transfer mechanisms. Wang H. et al., 2021 studied the heat transfer of SCO2 in a semicircular pipe by direct numerical simulation. They focused on revealing the influence of heat flux, secondary flow, thermal acceleration, corner effect and geometric direction on heat transfer by analyzing the local temperature field and flow field. At the same time, they also found that the direction of the semicircle tube has an important effect on the heat transfer of SCO2. Alan Kruizenga et al. (Kruizenga et al., 2012) studied the convective heat transfer characteristics of SCO2 in a semicircular channel under different operating parameters through experimental and numerical simulation methods. They used the classical D-B correlation and Jackson’s correlation to evaluate the experimental data, and found that the prediction accuracy of the above correlation was poor in the pseudo-critical region. Zhong et al., 2023 used numerical methods to compare the local heat transfer characteristics of SCO2 in circular and semicircular channels under cooling conditions. The results show that the heat transfer performance of horizontal semicircular channel is weaker than that of circular channel due to the effect of buoyancy.
At present, the straight channel is the simplest flow channel structure of PCHE. In order to improve the heat transfer performance of PCHE, the zigzag channel, wavy channel, S-shaped fins channel and airfoil fins channel are proposed (Liu et al., 2020). Although the zigzag channel and wavy channel enhance the heat transfer, the corresponding flow resistance is also greatly increased. S-shaped fins channel and airfoil fins channel are usually more difficult to process, which will lead to high-cost problems.
The literature review above show that, most of these studies focused on the heat transfer of SCO2 in uniform cross-section channels. Recently, Li C. et al., 2022 studied numerically the convective heat transfer performance of SCO2 in the horizontal tube with variable cross-sectional under heating conditions. The results show that diverging tube effectively enhances the thermal hydraulic compared with the uniform cross-sectional tube, and the heat transfer coefficient of diverging tube is increased by 14%. Inspired by this, this paper studies the heat transfer characteristics of SCO2 in a semicircular channel with variable cross-section, aiming to improve the heat transfer performance of PCHE, since most channels of PCHE have semicircular cross sections. The main differences between this paper and Li C. et al., 2022 work are as follows: the channel in this paper is semicircular channel, mainly for PCHE, while the channel in Li C. et al., 2022. is circular channel. In addition, the thermal boundary condition of this paper is constant heat flux cooling, while the thermal boundary condition of Li et al. is constant wall temperature heating. To authors’ knowledge, the heat transfer characteristics of SCO2 in semicircular variable cross-sectional channel have not been reported so far. Thus, the objective of this work is to numerically study the heat transfer performance of SCO2 in horizontal semicircular variable cross-sectional channel. The present work aims to provide new ideas and theoretical guidance for designing high efficiency PCHE. This paper is organized below. In Section 2, the physical model, numerical methods and data reduction are presented. In Section 3, the heat transfer performance of SCO2 in three different channels under different operating parameters is first compared, and then the reason why the converging channel can enhance heat transfer is explained from the field synergy theory, turbulent kinetic energy distribution and physical property distribution. Finally, based on the numerical simulation data, a new heat transfer correlation for the SCO2 in horizontal semicircular variable cross-section channel is proposed. A conclusion is finally given in Section 4.
In this paper, the variable cross-sectional semicircular channels refer to the diverging and converging semicircular channel. Physical models of horizontal uniform cross-sectional, diverging and converging semicircular channels is shown in Figure 2. The thermal boundary condition is cooling condition. In order to reduce the inlet effect and outlet backflow, the inlet and outlet adiabatic sections are set in front and behind the heating section, and the lengths of inlet adiabatic section and outlet adiabatic section are all 100 mm. The length of cooling section of uniform cross-sectional semicircular channel is 1,000 mm. To maintain the same heat transfer area as the heat transfer section of the semicircular channel with uniform cross-sectional, the length of the cooling section of the diverging and converging channels is 1,199.99 mm. The diameter of the horizontal uniform cross-sectional semicircular channel is 0.75 mm, which is also the channel diameter range of most PCHE (Ma et al., 2022). The diameter of inlet of the diverging semicircular channel is 0.5 mm and the diameter of the outlet is 1 mm, and the diameter of inlet of the converging semicircular channel is 1 mm and the diameter of the outlet is 0.5 mm.
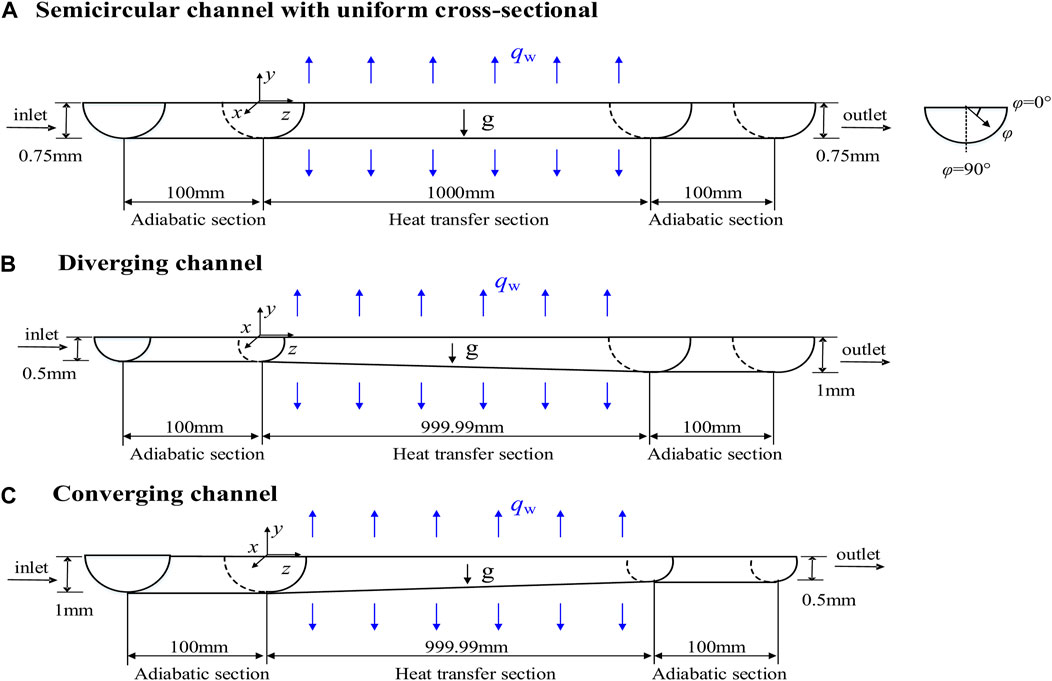
FIGURE 2. Physical models of three types of horizontal semicircular channels: (A) uniform cross-section semicircular channels; (B) Diverging channel; (C) Converging channel.
In present study, ANSYS Fluent software is used to simulate the convective heat transfer characteristics of SCO2 in uniform cross-section and non-uniform cross-section channels. It is assumed that the fluid flow is a steady turbulent flow without internal heat source, and the heat transfer between the fluid and the environment can be ignored. Gravity is considered. Then the Reynolds average governing equation of flow heat transfer can be expressed in the Cartesian coordinate system as follows (ANSYS Inc, 2018):
Continuity equation:
Momentum equation:
Energy equation:
where, ρ is density in kg/m3, u is the velocity vector in m/s, μ is viscosity coefficient in Pa·s, μt is the turbulent dynamic viscosity in N·s/m2, i is specific enthalpy in kJ/kg, the acceleration of gravity g is equal to 9.8 m/s2, Pr is Prandtl number,
The selection of turbulence model plays an important role in numerical simulation. Although a large number of numerical studies have been carried out, there is no general model for the prediction of heat transfer in supercritical fluids due to the strong nonlinearity of thermal properties near the pseudo-critical temperature. Recent review articles (Wang H. et al., 2018) show that SST k-ω turbulence model can obtain more accurate calculation results than other turbulence models in supercritical heat transfer. This is because the shear stress transport k-ω model combines the advantages of high accuracy of the k-ω model in the near-wall region with the independence and robustness of the k-ε model in the bulk fluid region (Menter, 1994; Han et al., 2023; Zhong et al., 2023). Therefore, the SST k-ω turbulence model is used for present numerical calculation. The SST k-ω turbulence model is described as follows (Menter, 1994):
Turbulent kinetic energy k equation:
Specific dissipation rate ω equation:
where, Gk is the generation term of turbulent kinetic energy, Gω is the generation term of specific dissipation rate, Yk and Yω represent the dissipation terms of turbulent kinetic energy k and specific dissipation rate ω, respectively, Dω is the cross-diffusion term, Sk and Sω represent the customized source terms of turbulent kinetic energy k and specific dissipation rate ω, respectively.
In this paper, ANSYS ICEM software is used for mesh division, and a structured hexahedral mesh was created. In order to obtain a high-quality grid, the cross section of the tube is divided by C-type grid, the meshing diagram is shown in Figure 3. Since the physical properties of SCO2 change dramatically near the pseudo critical point, the mesh should be locally dense near the wall of the fluid domain. In addition, in order to meet the requirements of SST turbulence model for dimensionless wall distance y+, the y+ of the first grid near the wall in the fluid domain was guaranteed to be less than 1.
ANSYS Fluent 15.0 was used to calculate the 3D steady flow and heat transfer of SCO2 in horizontal semicircular channels. The inlet was set as the mass flow rate inlet, the outlet as the pressure outlet. The inlet and outlet stability sections are set as adiabatic boundaries, uniform heat fluxes were applied on the wall of the heating section. No slip wall boundary condition is used. The governing equations were discretized by finite volume method, the second-order upwind method was used to improve the calculation accuracy, and the pressure-velocity coupling equations were solved by SIMPLEC algorithm. NIST real gas model was used to accurately reflect the influence of the physical properties of SCO2 on flow and heat transfer. When the maximum residuals of mass equation and momentum equation are less than 10−5, and the residuals of energy equation are less than 10−7, the calculation is considered convergent.
The local heat transfer coefficient is defined as follows:
where, qw is the heat flux in kW/m2, hz is the local heat transfer coefficient at different cross sections along the flow direction in kW/m2·K.
The bulk fluid temperature Tb at a cross-section is defined as:
where, dA is an elemental area of the tube across-section in m2.
The local Nusselt number along the flow direction is:
where, Dz is the hydraulic diameter of the channel in m and λ is the thermal conductivity of SCO2 in W/m·K.
For the semicircular channel with uniform cross-sectional area, Dz is determined by the following formula:
where, A is the cross-sectional area of the channel in m2 and d is the diameter of the semicircular channel in m.
For the diverging semicircular channel, Dz is expressed as the following formula:
For the converging semicircular channel, Dz is expressed as the following formula:
where, L is the length of the semicircular channel in m and z is the distance from the inlet in m.
The Reynolds number and Prandtl number are respectively:
where, Gz is the mass flux in kg/m2·s, μ is the viscosity in Pa·s, λ is the thermal conductivity of SCO2 in W/m·K, cp is the specific heat at constant pressure of SCO2 in kJ/kg·K, respectively.
In order to save calculation time and ensure the accuracy of calculation results, it is necessary to verify the mesh independence. The grid independence verification in this paper is carried out in a horizontal uniform cross-sectional semicircular channel. Three grid systems with different number of nodes were used to test the independence of grid. The calculation condition of grid sensitivity test is p = 8.5 MPa, m = 0.000264 kg/s, qw = 10 kW/m2s. Table 1 shows the results of the grid independence test.
It can be seen from the table that when the number of grids is greater than 961944, the heat transfer coefficient h is almost not affected by the number of grids, for example, the average deviation between case 3 and case 4 is only 0.2%. Therefore, selecting grid 3 for numerical simulation can ensure the accuracy and efficiency of the calculation.
To further verify the accuracy of numerical simulation under heating conditions, experimental conditions of Ref (Dang and Hihara, 2004; Lei et al., 2019). were used in this paper to verify the numerical model, and the size and boundary conditions of the calculated model were the same as those of the experimental conditions. Figure 4 shows the comparison of the experimental data with the predicted results of the present model, the black scatter is the experimental data, and the red curve is the predicted result. In Figure 4A, the total length of the test section is 0.5 m, the inner diameter of the inner tube is 6 mm, and the experimental operating condition is p = 8 MPa, G = 400 kg/m2s, and qw = 10 kW/m2. In Figure 4B, the inner diameter of the test section is 5 mm, and the length of the heat transfer section is 730 mm. The experimental operating condition is p = 10.5 MPa, G = 200 kg/m2s, and qw = 25 kW/m2. As can be seen from the picture, the numerical results are in good agreement with the experimental results. Hence, the numerical method used in the paper is accurate and feasible.
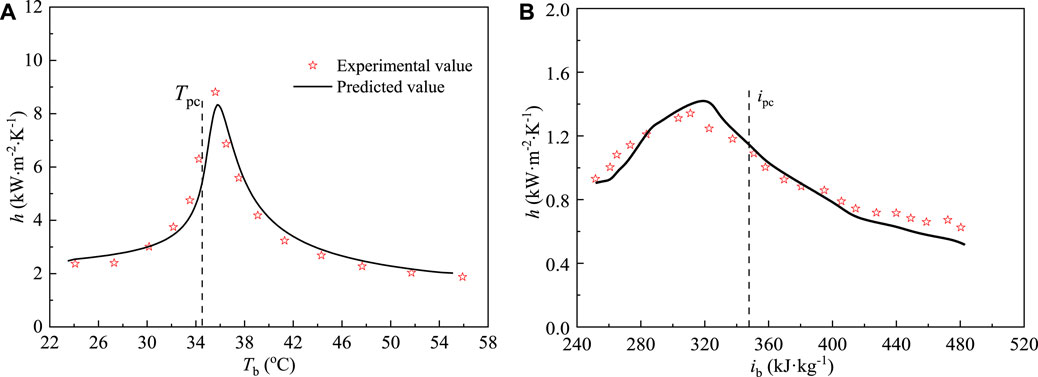
FIGURE 4. Numerical model validation: (A) The change of heat transfer coefficient with mainstream temperature; (B) The change of heat transfer coefficient with mainstream enthalpy.
Compared with constant physical properties fluids, the most important characteristic of supercritical pressure fluids is that their thermal physical properties change dramatically near the pseudo-critical temperature Tpc (the temperature corresponding to the maximum specific heat at a supercritical pressure), as shown in Figure 5. The region where the specific heat changes dramatically is often called a large specific heat region. This change of physical properties will cause the complex heat transfer behavior of SCO2. Thus, in this section, firstly, the heat transfer performance of the three types of channels is compared by keeping the heat transfer area and operating parameters the same. The effects of pressure P and mass flow rate m on heat transfer performance are discussed. Then, the mechanism of heat transfer is further discussed based on the analysis of local heat transfer characteristics. For the convenience of representation in figures and tables, UC, DC and CC represent uniform cross-sectional semicircular channel, diverging and converging semicircular channel, respectively.
Compared Figure 6 shows the influence of pressure P on the heat transfer characteristic of SCO2 flowing in three types of channels under the condition of the same mass flow rate m, heat flux qw and inlet temperature Tin. The two different operating pressures are 7.8 MPa and 8 MPa, respectively. Figure 6A shows the distribution of local heat transfer coefficients hz along the channel length direction under different operation pressures, and Figure 6B shows the comparison of heat transfer performance under different operation pressures. As can be seen from the Figure 6A, under different operation pressures, the general change trend of local heat transfer coefficient hz of SCO2 in three semicircular channels is the same, which increases first to reach a peak value and then decreases. The peak value of local heat transfer coefficient is mainly due to the fact that SCO2 passes through a large specific heat region (see Figure 5) during the cooling process, and the increase of specific heat strengthens the heat transfer. When the operating pressure increases from 7.8 MPa to 8 MPa, the location of the peak local heat transfer coefficient of SCO2 in the three semicircular channels decreases. For example, for UC channels, when the pressure is 7.8 MPa and 8 MPa, the peak heat transfer coefficient is 9.086 kW/m2 K and 7.828 kW/m2K, respectively. The above shows that the increase of pressure weakens the heat transfer. In addition, the location of the peak point of the local heat transfer coefficient tends to be closer to the inlet section with the increase of the pressure, which is mainly due to the difference of pseudo-critical temperature under different supercritical pressures.
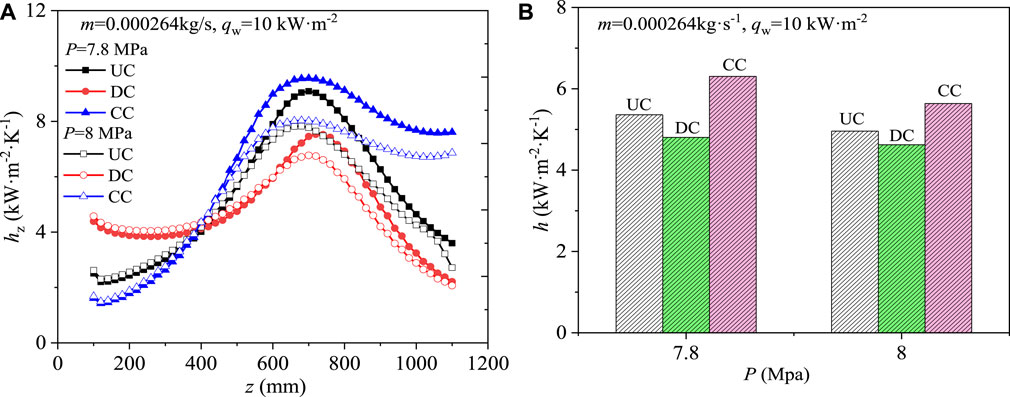
FIGURE 6. Effect of operating pressure on heat transfer of SCO2: (A) Distribution of local heat transfer coefficients along the channel length; (B) Comparison of heat transfer performance.
To evaluate the heat transfer performance of SCO2 in three semicircular channels, the total average heat transfer coefficient is defined as:
where, the value of n represents the total number of the local positions along the flow direction.
Figure 6B shows the heat transfer performance of SCO2 in the three channels under different operating pressures. As can be seen from the Figure 6B, under two different calculation conditions, the heat transfer coefficient h of SCO2 in the converging semicircular channel is always greater than the other two channels, the h of SCO2 in the diverging semicircular channel is the smallest, and the uniform cross-sectional semicircular channel is between the two. This means that, compared with the uniform cross-sectional channel, the converging channel enhances heat transfer, while the diverging channel weakens heat transfer. For example, under the operating condition p = 7.8 MPa, m = 0.000264 kg/s, qw = 10 kW/m2s, the heat transfer coefficient h of the converging channel increases by 17.6%, while that of the diverging channel decreases by 10.4%, compared with that of the constant section channel.
The influence of mass flow rate on the heat transfer performance of SCO2 in the different channel was studied with operation pressure P, heat flux qw and inlet temperature Tin of 7.8 MPa, 10 kW/m2s and 325.15 K. The results with the mass flow rate varying from 0.000264 kg/s to 0.000352 kg/s are shown in Figure 7. Figure 7A shows the change of local heat transfer coefficient hz along the cooling channel, and Figure 7B shows the comparison of total heat transfer coefficient h under different total mass flow rate. It can be seen from Figure 7A that the local heat transfer coefficient hz generally increases first and then decreases, except for the converging channel with a mass flow rate of 0.000352 kg/s. The increase of mass flow rate also causes the peak value of the local heat transfer coefficient to move to the outlet section. The results in Figure 7B also show that under the same operating conditions, the heat transfer performance of SCO2 in the converging channel is better than that of the other two channels, while the diverging channel deteriorates the heat transfer. At the same time, the increase of the mass flow rate greatly improves the heat transfer performance. For example, when the mass flow rate increases from 0.000264 kg/s to 0.000352 kg/s, the heat transfer coefficient of the converging channel increases from 6.3 kW/m2K to 9.84 kW/m2K. When the mass flow rate is 0.000352 kg/s, the h of the converging channel increases by 42.26% compared with that of the equal cross section channel.
FIGURE 7. Effect of mass flow rate on heat transfer of SCO2: (A) Distribution of local heat transfer coefficients along channel length; (B) Comparison of heat transfer performance.
In order to better analyze the potential physical mechanism of heat transfer enhancement or deterioration of SCO2 in converging and diverging channel, we selected the operating condition p = 8 MPa, m = 0.000264 kg/s, qw = 10 kW/m2s for analysis, see Figure 6A. As shown in Figure 6A, before cross-section z = ∼0.4 m, the hz of diverging channel is obviously greater than that of the other two channels, however, after z = ∼0.65 m, the curve of hz of converging channel is higher than that of other two channels. In general, the heat transfer enhancement process of converging channel is longer, the peak value of local heat transfer is the largest, and the local heat transfer coefficient curve at the outlet tends to be flat, which makes the overall heat transfer performance of the converging channel better than that of the other two channels. Thus, three characteristic cross sections (z = 0.2 m, z = 0.7 m and z = 1.0 m) were selected to analyze the cooling heat transfer process in the three channels.
Figure 8 shows the temperature field distribution of the three channels on the characteristic cross sections. It can be seen from the Figure 8 that the temperature of SCO2 in the three channels gradually decreases along the direction of channel length, and temperature stratification is observed at some cross sections. More importantly, at the same cross section, the distribution of SCO2 temperature in the three channels is different, which will lead to different distribution of velocity field. Figure 9 shows the corresponding velocity distribution at the characteristic cross section. It can be seen from the velocity distribution diagram that the velocity distribution of SCO2 in different channels is completely different on the same cross section, which indicates that compared with the uniform cross-sectional channels, the diverging and converging channels do change the distribution of temperature field and velocity field.
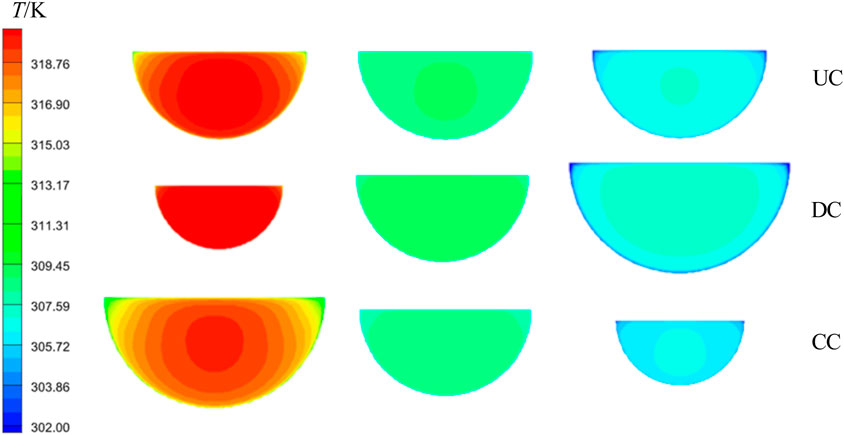
FIGURE 8. Temperature distribution of SCO2 in different channels at different characteristic cross sections.
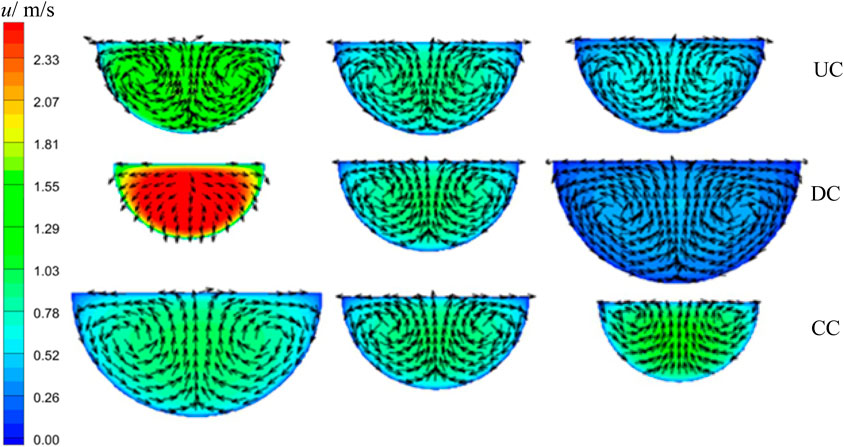
FIGURE 9. Velocity distribution of SCO2 in different channels at different characteristic cross sections.
Therefore, the difference in SCO2 heat transfer performance caused by the three channels can be explained by the field synergy theory. Guo et al., 1998. (Guo et al., 2005) proposed the field synergy principle. Starting from the boundary layer energy conservation equation, they obtained the dimensionless Nusselt number through a series of derivations, which can be written as follows:
where, Rex and Pr are Reynolds numbers and Prandtl numbers respectively.
where, θ is the angle between the velocity vector and the temperature gradient vector, and is defined as the field coordination Angle. The field synergy Angle represents the synergy between the velocity vector and the temperature gradient. When θ is less than 90°, heat transfer can be enhanced by decreasing the field coordination Angle. When θ is greater than 90°, increasing the field coordination Angle can improve the heat transfer efficiency under the same conditions.
Through calculation, the volume-average field coordination Angle θ of SCO2 in the semicircular uniform cross-sectional channel, the diverging channel and the converging channel is 88.47°, 88.77°, and 87.58°, respectively. According to the field synergy principle, the synergistic effect between velocity vector and temperature gradient is the worst in the semicircular diverging channel and the best in the semicircular converging channel. This is consistent with the conclusion that the semicircular converging channel can enhance the heat transfer, indicating that the semicircular converging channel can improve the synergistic effect of the velocity field and the temperature gradient field in the channel. From the above analysis, it can be seen that one of the main reasons why the semicircular converging channel can enhance heat transfer is that it changes the field cooperation.
Turbulent kinetic energy k is an important characteristic parameter of the turbulence intensity of the fluid in the channel. The greater the turbulent kinetic energy is, the better the mixing effect of the fluid in the channel is and the heat transfer is enhanced. In order to better compare k in the three semicircle channels, the contour distributions of turbulence kinetic energy k and radical change curves of k of the three channels at cross section z = 0.2 m, z = 0.7 m, and z = 1.0 m are shown in Figure 10. As can be seen from Figure 10A, at cross section z = 0.2 m, the k of SCO2 in diverging channel is significantly greater than that of the other two channels, while the k of SCO2 in converging channel is the smallest, and the larger k promotes the heat transfer from the core region to the channel wall, so the local heat transfer coefficient of SCO2 in the diverging channel at the entrance is the largest, see Figure 6A. At section z = 0.7 m, see Figure 10B, the contour distributions of turbulence kinetic energy k of SCO2 in the three channels is close, but from the radial distribution curve, the converging channel is slightly larger than the other two channels, and the k in the uniform cross section channel is the smallest. This is one of the main reasons that the local heat transfer coefficient hz of the convergent channel is slightly higher than that of the other two channels at the cross section z = 0.7 m (see Figure 6A). As can be seen from Figure 10C, at the cross section z = 1.0 m, k of SCO2 in converging channel is significantly larger than that of the other two channels, and k in diverging channel is the smallest. Therefore, the local heat transfer coefficient curve of the converging channel at the exit tends to be gentle, while the uniform cross-sectional and diverging channel decreases rapidly, see Figure 6A. It can be seen from the above that turbulent kinetic energy has an important effect on the heat transfer performance of SCO2, and the increase or decrease of local heat transfer coefficient of SCO2 in different channels can be well explained by turbulent kinetic energy.
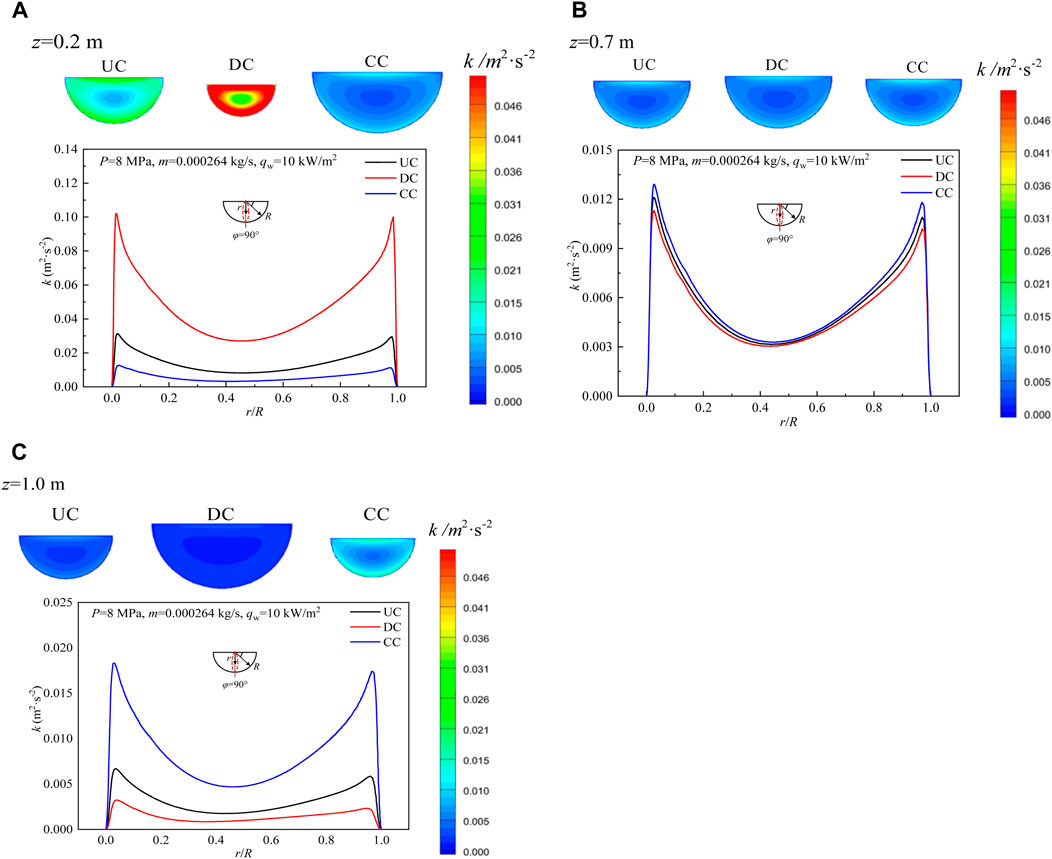
FIGURE 10. Distribution of turbulent kinetic energy of SCO2 at characteristic section in three channels: (A) Characteristic cross-section z = 0.2 m; (B) Characteristic cross-section z = 0.7 m; (C) Characteristic cross-section z = 1.0 m.
In addition, we found that the thermal conductivity also has a certain influence on the heat transfer of SCO2 during the cooling process, and the fluid with high thermal conductivity will promote the heat flow transport. Figure 11 shows the contour distributions of thermal conductivity λ at the characteristic cross sections of three semicircular channels. At the characteristic cross sections z = 0.2 m and z = 1.0 m, the λ of SCO2 in the three semicircular channels is basically the same, which has little influence on the heat transfer performance. At z = 0.7 m, the thermal conductivity of SCO2 in converging channel is obviously greater than that of the other two channels, and the fluid with high thermal conductivity occupies the entire section, and the heat transfer is enhanced, and the local heat transfer peak appears. Thermal conductivity is also one of the factors affecting the enhancement of heat transfer in converging channel.
Due to the characteristic that the thermal physical properties of supercritical pressure fluids change dramatically near the pseudo-critical temperature, the heat transfer correlations established on the basis of constant physical properties fluids are no longer applicable. In recent years, a large number of supercritical CO2 heat transfer correlations have been proposed, which are basically established on the basis of Dittus-Boelter formula by introducing physical property correction factors, buoyancy factors and flow acceleration factors et al. (Ehsan et al., 2018). These correlations are basically for circular channels of constant section and semicircular channels. As far as the author knows, the correlation of SCO2 heat transfer in variable section channels has not been reported.
For forced convection heat transfer in a tube, the Dittus-Boelter formula is the longest and most common correlation in history, expressed as (Liao and Zhao, 2002a):
Based on the Dittus-Boelter correlation, Li H. et al., 2011 introduced the specific heat ratio factor and the density ratio factor to establish the heat transfer correlation of SCO2 in the semicircular channel, which is expressed as:
where,
Hall et al., 1967 proposed a new correlation by modifying the Dittus-Boelter correlation and introducing the density ratio factor, which is expressed as:
where,
Liao and Zhao, 2002b experimentally studied the cooling heat transfer process of SCO2 in mini channels, and found that the influence of buoyancy on heat transfer could not be ignored. Therefore, they introduced the buoyancy factor into the correlation, and considered the influence of thermal properties, and proposed a new heat transfer correlation, which is expressed as:
where, Gr is the Graschev number,
Zhong et al., 2023 numerically studied the local heat transfer characteristics of SCO2 in horizontal circular and semicircular channels under cooling conditions. Based on the simulation data, they proposed the heat transfer correlation of SCO2 cooling heat transfer in semicircular channels, which is expressed as:
Figure 12 shows the comparison between the simulated heat transfer coefficient and the calculated heat transfer coefficient based on the above five correlation. As can be seen from the figure, the maximum error of D-B correlation, Hall et al., 1967. correlation and Liao and Zhao, 2002b. correlation is more than 50%, which is unacceptable in the engineering design stage, and the error of Li H. et al., 2011 correlation and Zhong et al. (Zhong et al., 2023) correlation is less than 50%.
From the above results, the existing correlations cannot better predict the heat transfer of SCO2 in a semicircular channel with variable cross-section. As we all know, in the process of flow heat transfer in a horizontal channel, due to the drastic change of SCO2 density near the pseudo-critical temperature, the fluid will generate buoyancy, which makes the lighter gas-like fluid flow upward and the heavier liquid-like fluid flow downward, thus triggering secondary flow on the tube cross section. From the velocity distribution in Figure 9, we can observe obvious secondary flow on the cross section, so the influence of buoyancy should be considered. The effect of buoyancy is usually characterized by dimensionless number
Rewriting Eq. 23 yields:
Eq. 24 can be written in matrix form
Based on the data obtained from the previous numerical calculation, multiple linear regression analysis was adopted, and the constant term C and the regression coefficients n1, n2, n3, and n4 are 0.2124, 0.5683, 0.2156, −0.0171, and 1.6071, respectively.
Therefore, the new heat transfer correlation can be expressed as:
In order to better evaluate the prediction accuracy of the new correlation, the mean absolute relative error (MARE) and root mean square error (RMSE) are introduced, which are expressed as:
where hcal,i is a single data point calculated by correlation, and hsim,i is a single data point obtained by simulation.
Figure 13 shows the comparison between the simulated heat transfer coefficient and the calculated heat transfer coefficient based on Eq. 26. The mean absolute relative error (MARE) and root mean square error (RMSE) are also given in the figure and are 9.49% and 10.6%, respectively, which is acceptable for applications. Figure 14 summarizes the mean absolute relative error (MARE) and root mean square error (RMSE) calculated by the new correlation and the other five correlations. As shown in the figure, the error of the new correlation is the smallest. Among other correlations, the error of Li et al. (Li H. et al., 2011) and Zhong et al., 2023 is relatively small, the MARE of Liao and Zhao, 2002b is the largest, and the RMSE of Hall et al., 1967 is the largest.
Figure 15 shows the variation of local heat transfer coefficients calculated by the new correlation formula and the other 5 correlation formulas with the bulk fluid temperature. It is shown that the heat transfer coefficients calculated by the new correlation formula are in good agreement with the simulated heat transfer coefficients. Other correlations seriously overestimate the local heat transfer coefficient in the pseudo-critical region, see Figure 15A.
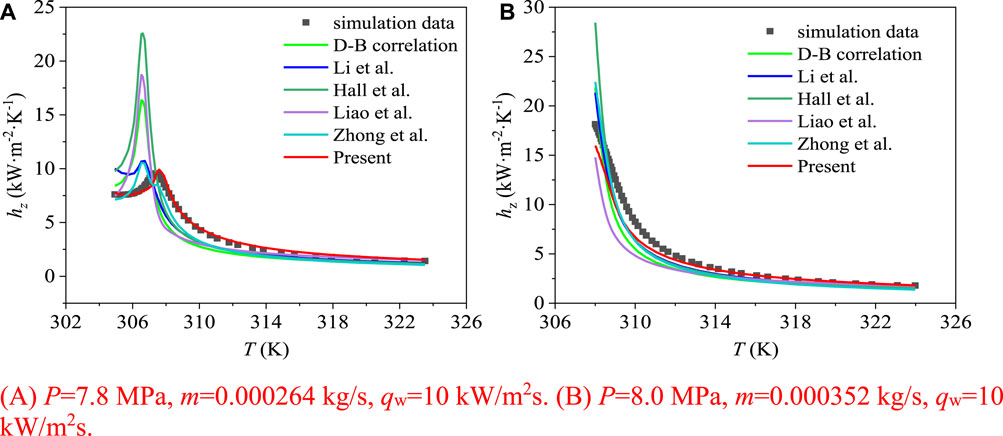
FIGURE 15. Comparison of local heat transfer coefficients hz predicted by new correlation and other correlations: (A) The local heat transfer coefficient changes with the mainstream temperature, and the operating condition is p = 7.8 MPa, m = 0.000264 kg/s, qw = 10 kW/m2; (B) The local heat transfer coefficient changes with the mainstream temperature, and the operating condition is p = 8.0 MPa, m = 0.000352 kg/s, qw = 10 kW/m2.
From the above analysis, it can be seen that the new heat transfer correlation can accurately predict the heat transfer characteristics of SCO2 in the horizontal semicircular converging channel within the scope of the operation pressure from 7.5 MPa to 8.5 MPa, mass flow rate from 0.000264 kg/s to 0.000352 kg/s and heat flux from 10 kW/m2 to 14 kW/m2.
This paper numerically investigated the convective heat transfer of SCO2 in horizontal uniform cross-sectional semicircular channel, diverging and converging semicircular channel under cooling conditions by using SST k-ω turbulent model. The main conclusions are summarized as follows.
(1) The effect of pressure and mass flow rate on heat transfer performance of SCO2 in various channels was analyzed in detail. The results show that variable cross-sectional channel affects the heat transfer performance of SCO2. Under the same working conditions, compared with the uniform cross-sectional semicircular channel, the converging channel can enhance heat transfer effectively, the heat transfer coefficient of SCO2 in the converging channel is increased by up to 42.26%. However, the diverging channel worsens the heat transfer.
(2) The reason why the converging channel can effectively enhance heat transfer is explained from the perspective of field coordination principle, the distribution of turbulent kinetic energy and thermos-physical property. The volume-averaged field synergy angle θ of uniform cross-sectional channel, diverging and converging channel are 88.47°, 88.77° and 87.58°, respectively, which indicates that the synergy between velocity vector and temperature gradient is the worst in the diverging channel and best in the converging channel. In addition, the turbulent kinetic energy distribution and thermal conductivity distribution also reasonably explains that the heat transfer performance of the converging channel is better than that of the other two channels.
(3) Based on the numerical simulation data, we propose a new heat transfer correlation for SCO2 in a semicircular converging channel. Compared with the five selected heat transfer correlations, the new heat transfer correlation has the best prediction accuracy, and its mean absolute relative error and root mean square error are 9.49% and 10.6%, respectively.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
MW: Formal Analysis, Investigation, Methodology, Software, Writing–original draft. BZ: Conceptualization, Funding acquisition, Methodology, Supervision, Writing–review and editing. JH: Investigation, Software, Validation, Writing–original draft. KG: Software, Validation, Investigation, Writing–original draft.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by Natural Science Foundation of Gansu Province, grant number 22JR5RA283. Project name: Hongliu Excellent Youth Fund of Lanzhou University of Technology (07-062310).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Ahn, Y., Bae, S. J., Kim, M., Cho, S. K., Baik, S., Lee, J. I., et al. (2015). Review of supercritical CO2 power cycle technology and current status of research and development. Nucl. Eng. Technol. 47, 647–661. doi:10.1016/j.net.2015.06.009
Banuti, D. T. (2015). Crossing the Widom-line – supercritical pseudo-boiling. J. Supercrit. Fluids 98, 12–16. doi:10.1016/j.supflu.2014.12.019
Cabeza, L. F., de Gracia, A., Fernández, A. I., and Farid, M. M. (2017). Supercritical CO2 as heat transfer fluid: a Review. Appl. Therm. Eng. 125, 799–810. doi:10.1016/j.applthermaleng.2017.07.049
Chen, R., Romero, M., González-Aguilar, J., Rovense, F., Rao, Z., and Liao, S. (2021). Design and off-design performance comparison of supercritical carbon dioxide Brayton cycles for particle-based high temperature concentrating solar power plants. Energy Convers. Manag. 232, 113870. doi:10.1016/j.enconman.2021.113870
Dang, C., and Hihara, E. (2004). In-tube cooling heat transfer of supercritical carbon dioxide. Part 1. Experimental measurement. Int. J. Refrig. 27, 736–747. doi:10.1016/j.ijrefrig.2004.04.018
Dostal, V. (2004). A supercritical carbon dioxide cycle for next-generation nuclear reactors. Dissertations & Theses. Cambridge, MA, USA: Department of Nuclear Engineering, Massachusetts Institute of Technology.
Ehsan, M. M., Guan, Z., and Klimenko, A. Y. (2018). A comprehensive review on heat transfer and pressure drop characteristics and correlations with supercritical co 2 under heating and cooling applications. Renew. Sustain. Energy Rev. 92, 658–675. doi:10.1016/j.rser.2018.04.106
Guo, Z. Y., Li, D. Y., and Wang, B. X. (1998). A novel concept for convective heat transfer enhancement. Int. J. Heat Mass Transf. 41, 2221–2225. doi:10.1016/s0017-9310(97)00272-x
Guo, Z. Y., Tao, W. Q., and Shah, R. K. (2005). The Field Synergy (coordination) principle and its applications in enhancing single phase convective heat transfer. Int. J. Heat Mass Transf. 48, 1797–1807. doi:10.1016/j.ijheatmasstransfer.2004.11.007
Hall, W. B., Jackson, J. D., and Watson, A. (1967). Paper 3: a review of forced convection heat transfer to fluids at supercritical pressures. Proc. Institution Mech. Eng. Conf. Proc. 182, 10–22. doi:10.1243/pime_conf_1967_182_262_02
Han, Z., Guo, J., and Huai, X. (2023). Theoretical Analysis of a novel PCHE with enhanced rib structures for high-power supercritical CO2 Brayton Cycle System based on Solar Energy. Energy 270, 126928. doi:10.1016/j.energy.2023.126928
Jackson, J. D. (2013). Fluid flow and convective heat transfer to fluids at supercritical pressure. Nucl. Eng. Des. 264, 24–40. doi:10.1016/j.nucengdes.2012.09.040
Kim, D. E., and Kim, M. H. (2010). Experimental study of the effects of flow acceleration and buoyancy on heat transfer in a supercritical fluid flow in a circular tube. Nucl. Eng. Des. 240, 3336–3349. doi:10.1016/j.nucengdes.2010.07.002
Kruizenga, A., Li, H., Anderson, M., and Corradini, M. (2012). Supercritical carbon dioxide heat transfer in horizontal semicircular channels. J. Heat Transf. 134. doi:10.1115/1.4006108
Lei, X., Zhang, J., Gou, L., Zhang, Q., and Li, H. (2019). Experimental study on convection heat transfer of supercritical CO2 in small upward channels. Energy 176, 119–130. doi:10.1016/j.energy.2019.03.109
Li, C., Hao, J., Wang, X., Ge, Z., and Du, X. (2022). Dual-effect evaluation of heat transfer deterioration of supercritical carbon dioxide in variable cross-section horizontal tubes under heating conditions. Int. J. Heat Mass Transf. 183, 122103. doi:10.1016/j.ijheatmasstransfer.2021.122103
Li, H., Kruizenga, A., Anderson, M., Corradini, M., Luo, Y., Wang, H., et al. (2011). Development of a new forced convection heat transfer correlation for CO2 in both heating and cooling modes at supercritical pressures. Int. J. Therm. Sci. 50, 2430–2442. doi:10.1016/j.ijthermalsci.2011.07.004
Liao, S. M., and Zhao, T. S. (2002a). An experimental investigation of convection heat transfer to supercritical carbon dioxide in miniature tubes. Int. J. Heat Mass Transf. 45, 5025–5034. doi:10.1016/s0017-9310(02)00206-5
Liao, S. M., and Zhao, T. S. (2002b). Measurements of heat transfer coefficients from supercritical carbon dioxide flowing in horizontal mini/micro channels. J. Heat Transf. 124, 413–420. doi:10.1115/1.1423906
Liu, G., Huang, Y., Wang, J., and Liu, R. (2020). A review on the thermal-hydraulic performance and optimization of printed circuit heat exchangers for supercritical CO2 in advanced nuclear power systems. Renew. Sustain. Energy Rev. 133, 110290. doi:10.1016/j.rser.2020.110290
Ma, Y., Xie, G., and Hooman, K. (2022). Review of printed circuit heat exchangers and its applications in solar thermal energy. Renew. Sustain. Energy Rev. 155, 111933. doi:10.1016/j.rser.2021.111933
Menter, F. R. (1994). Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 32, 1598–1605. doi:10.2514/3.12149
Peng, R., Lei, X., Guo, Z., Wang, Y., Li, H., and Zhou, X. (2022). Forced convective heat transfer of supercritical carbon dioxide in mini-channel under low mass fluxes. Int. J. Heat Mass Transf. 182, 121919. doi:10.1016/j.ijheatmasstransfer.2021.121919
Reyes-Belmonte, M. A., Sebastián, A., Romero, M., and González-Aguilar, J. (2016). Optimization of a recompression supercritical carbon dioxide cycle for an innovative central receiver Solar Power Plant. Energy 112, 17–27. doi:10.1016/j.energy.2016.06.013
Wang, H., Leung, L. K. H., Wang, W., and Bi, Q. (2018). A review on recent heat transfer studies to supercritical pressure water in channels. Appl. Therm. Eng. 142, 573–596. doi:10.1016/j.applthermaleng.2018.07.007
Wang, H., Wang, S., Zang, J., Wang, J., and Huang, Y. (2021b). Direct numerical simulation of the turbulent flow and heat transfer of supercritical CO2 in a semicircular pipe. Int. J. Heat Mass Transf. 168, 120882. doi:10.1016/j.ijheatmasstransfer.2020.120882
Wang, Q., Ma, X., Xu, J., Li, M., and Wang, Y. (2021a). The three-regime-model for pseudo-boiling in supercritical pressure. Int. J. Heat Mass Transf. 181, 121875. doi:10.1016/j.ijheatmasstransfer.2021.121875
Xie, J., Liu, D., Yan, H., Xie, G., and Boetcher, S. K. S. (2020). A review of heat transfer deterioration of supercritical carbon dioxide flowing in vertical tubes: heat transfer behaviors, identification methods, critical heat fluxes, and heat transfer correlations. Int. J. Heat Mass Transf. 149, 119233. doi:10.1016/j.ijheatmasstransfer.2019.119233
Xu, Y., and Yi, Z. (2023). Effect of flow direction on heat transfer characteristics of Supercritical CO2 in a heating Serpentine micro-tube. Energy 262, 125474. doi:10.1016/j.energy.2022.125474
Yoon, H. J., Ahn, Y., Lee, J. I., and Addad, Y. (2012). Potential advantages of coupling supercritical CO2 Brayton cycle to water cooled small and medium size reactor. Nucl. Eng. Des. 245, 223–232. doi:10.1016/j.nucengdes.2012.01.014
Zhang, G.-W., Hu, P., Chen, L.-X., and Liu, M.-H. (2018). Experimental and simulation investigation on heat transfer characteristics of in-tube supercritical CO2 Cooling Flow. Appl. Therm. Eng. 143, 1101–1113. doi:10.1016/j.applthermaleng.2018.07.108
Zhang, S., Xu, X., Liu, C., and Dang, C. (2020). A review on application and heat transfer enhancement of Supercritical CO2 in low-grade heat conversion. Appl. Energy 269, 114962. doi:10.1016/j.apenergy.2020.114962
Zhang, S., Xu, X., Liu, C., Li, X., Wu, C., and Dang, C. (2022). Experimental investigation and theoretical analysis on the heat transfer deterioration of Supercritical CO2 in mixed and forced convection in vertical-straight tube with downward flow. Int. J. Heat Mass Transf. 187, 122510. doi:10.1016/j.ijheatmasstransfer.2021.122510
Zhang, Y., Peng, M., Xia, G., and Cong, T. (2019). Numerical investigation on local heat transfer characteristics of S-CO2 in horizontal semicircular microtube. Appl. Therm. Eng. 154, 380–392. doi:10.1016/j.applthermaleng.2019.03.082
Zhong, S., Ren, Y., Wu, W., Yang, Y., and Yang, Q. (2023). Numerical Study on the local heat transfer characteristic of supercritical CO2 in semicircular/circular channel under cooling condition. Int. J. Heat Mass Transf. 209, 124098. doi:10.1016/j.ijheatmasstransfer.2023.124098
Zhu, B., Xu, J., Wu, X., Xie, J., and Li, M. (2019). Supercritical “boiling” number, a new parameter to distinguish two regimes of carbon dioxide heat transfer in tubes. Int. J. Therm. Sci. 136, 254–266. doi:10.1016/j.ijthermalsci.2018.10.032
Zhu, B., Xu, J., Yan, C., and Xie, J. (2020). The general supercritical heat transfer correlation for vertical up-flow tubes: K number correlation. Int. J. Heat Mass Transf. 148, 119080. doi:10.1016/j.ijheatmasstransfer.2019.119080
Zhu, H.-H., Wang, K., and He, Y.-L. (2017). Thermodynamic analysis and comparison for different direct-heated supercritical CO2 Brayton Cycles integrated into a solar thermal power tower system. Energy 140, 144–157. doi:10.1016/j.energy.2017.08.067
Zhu, X., Zhang, R., Du, X., Yu, X., and Qiu, Q. (2022). Experimental study on heat transfer deterioration of Supercritical CO2 in a round tube: a boundary assessment. Int. Commun. Heat Mass Transf. 134, 106055. doi:10.1016/j.icheatmasstransfer.2022.106055
Keywords: supercritical carbon dioxide, strengthened heat transfer, semicircular channel with variable cross-sectional, field synergy, heat transfer correlation
Citation: Wei M, Zhu B, He J and Gong K (2023) A new channel structure for strengthening heat transfer of SCO2 printed circuit heat exchanger (PCHE): variable sectional semicircular channel. Front. Energy Res. 11:1286376. doi: 10.3389/fenrg.2023.1286376
Received: 31 August 2023; Accepted: 30 October 2023;
Published: 09 November 2023.
Edited by:
Sudhakar Kumarasamy, Universiti Malaysia Pahang, MalaysiaReviewed by:
Yacine Addad, Khalifa University, United Arab EmiratesCopyright © 2023 Wei, Zhu, He and Gong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bingguo Zhu, zhubg@lut.edu.cn
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.