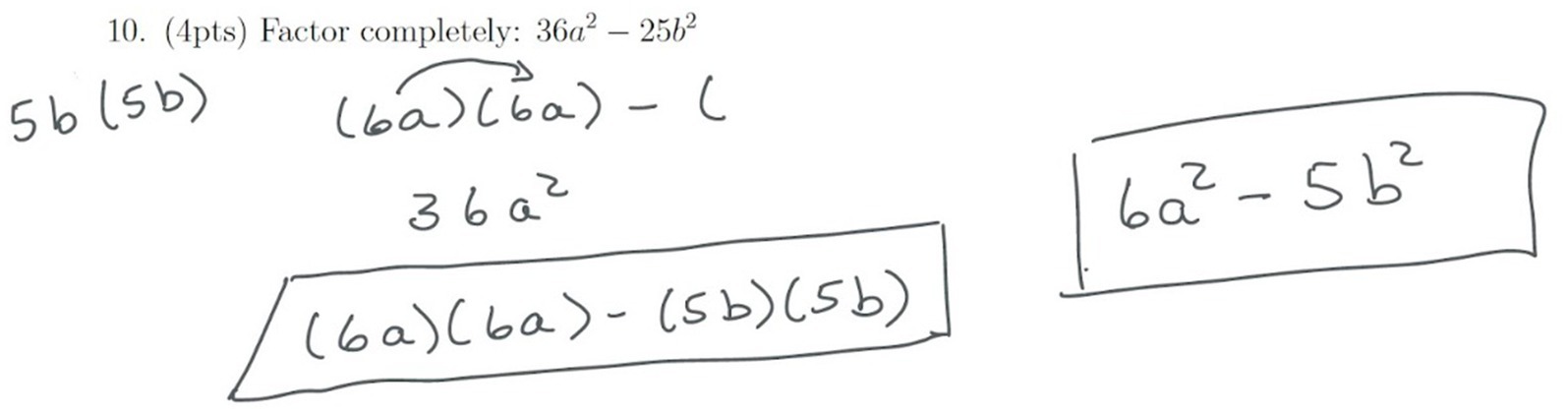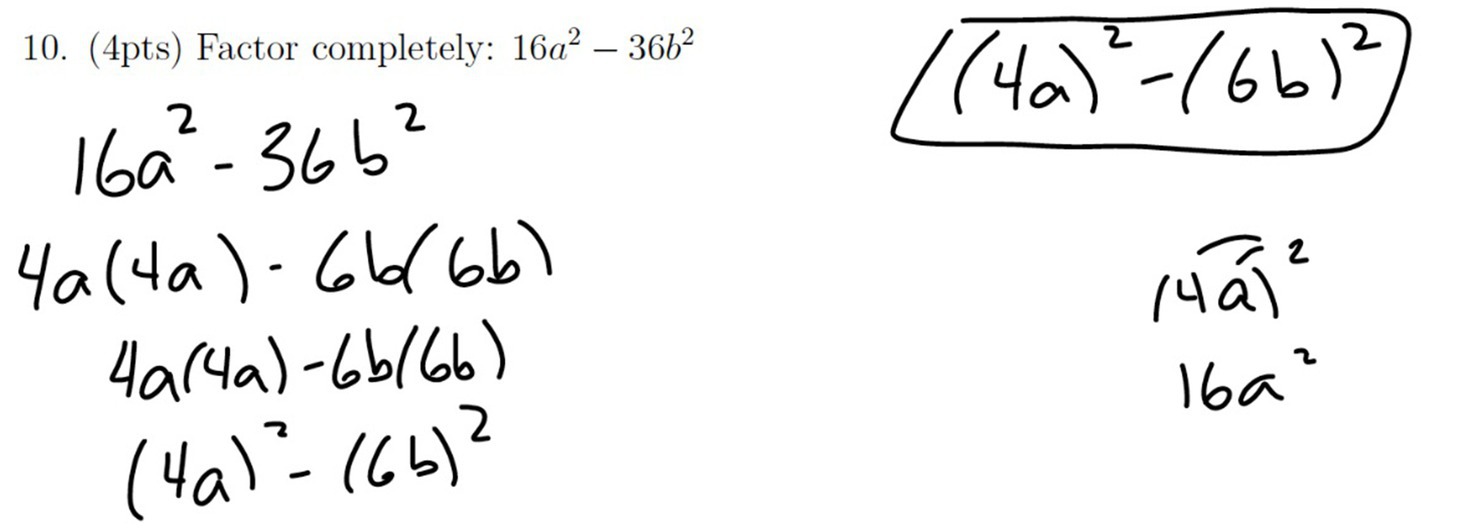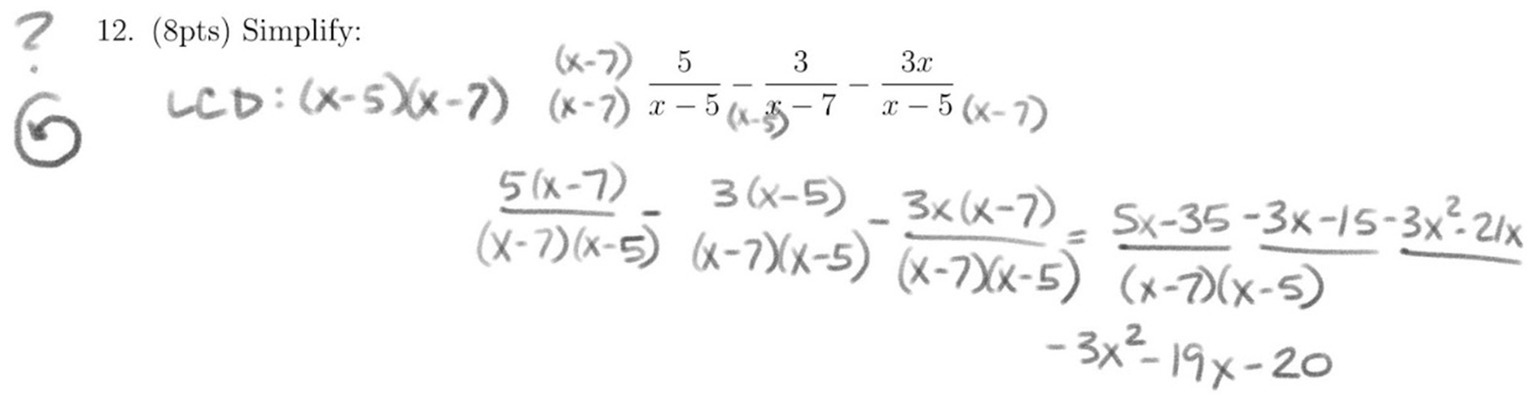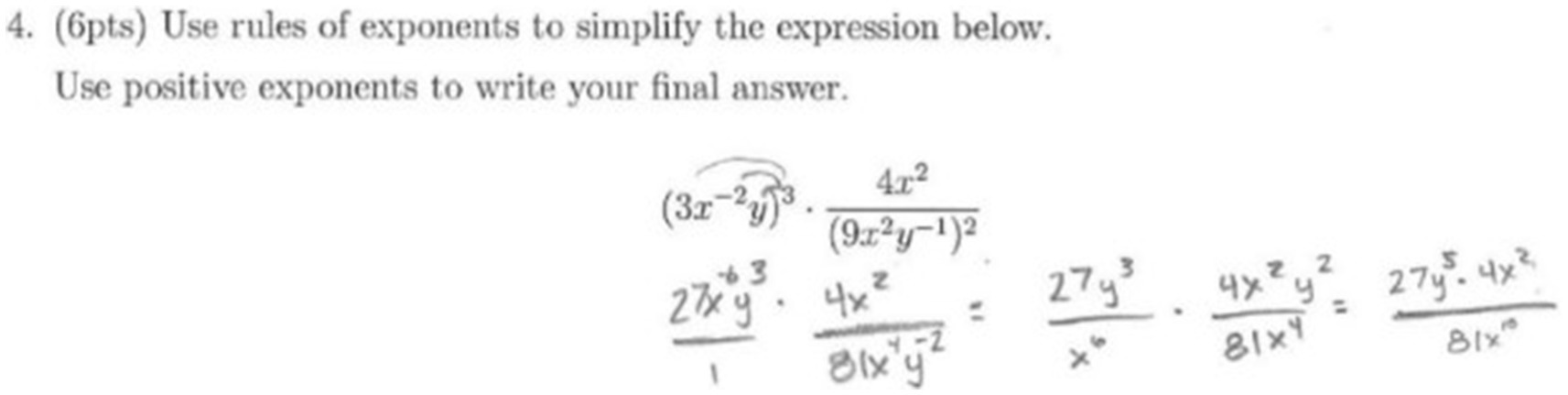College algebra students’ perceptions of exam errors and the problem-solving process

The first 2 years of college mathematics play a key role in retaining STEM majors. This becomes considerably difficult when students lack the background knowledge needed to begin in Calculus and instead take College Algebra or Precalculus as a first mathematics course. Given the poor success rates often attributed to these courses, researchers have been looking for ways in which to better support student learning, such as examining the impact of enhancing study habits and skills and metacognitive knowledge. One way that students can enhance their metacognitive knowledge in order to modify their study habits and practices is through reflection on mistakes. For this paper in particular, we focus on mistakes students make on exams. We interviewed students after they took an exam and completed an exam analysis worksheet. As part of a study on the impact of metacognitive instruction for College Algebra students we found that students often attributed their exam errors to “simple mistakes.” However, we identified many of these errors as “not simple.” To understand students’ perceptions of their mistakes within the context of problem-solving, we adapted an established problem-solving framework as an analytical tool. We found that students’ and researchers’ classifications of errors were not aligned across the problem-solving phases. In this paper we present findings from this work, sharing the adapted problem-solving framework, students’ perceptions of their exam mistakes, and the relationship between students’ categorizations of their errors and the problem-solving phase in which the errors occurred. Understanding students’ perceptions of their mistakes helps us better understand how we might support them as learners and better situate them for success in the future.

Introduction

Efforts to adequately support students from diverse backgrounds who pursue Science, Technology, Engineering, or Mathematics (STEM) majors often include a focus on improving students’ first college math experience (Seymour et al., 2019; Ellis et al., 2016; Seymour and Hewitt, 1997). In the United States, university students without the background needed to begin studying calculus will often have to take a prerequisite course, such as College Algebra, as their first math class. Given the high failure rates associated with these classes (Herriott and Dunbar, 2009), researchers look for ways to improve these courses (Sadler and Sonnert, 2018). Study skill instruction can often be an important component of first semester support courses. Study habits and skills have been shown to impact academic performance as much as prerequisite knowledge (Credé and Kuncel, 2008; Ohtani and Hisasaka, 2018; Schneider and Artelt, 2010). Further, metacognitive knowledge and skills can be taught in the classroom (Donker et al., 2014; Schneider and Artelt, 2010) and are most effective when taught in the context of a class throughout an entire term (Sitzmann and Ely, 2010).

We have been designing and implementing metacognitive activities for college algebra students. In that work we learned that students’ perceptions are different from ours as researchers and teachers, in particular when it comes to reflection on mistakes or errors. Understanding student perceptions, better positions instructors to support the students.

As part of our study on the impact of metacognitive instruction for college algebra students (Pilgrim et al., 2020), we found that it was common for students to attribute their errors to “simple mistakes” (Ryals et al., 2020, p. 494) and noticed that many mistakes which students identified as simple, we as practitioner-researchers identified as not simple. Seeing that students and researchers use the term simple mistakes to refer to different types of errors prompted us to explore students’ meanings about/of their mistakes and contrast them with our own definitions. In this paper we present the details of this comparison. Understanding how students think about their mistakes better positions us to know how to support their learning. The help and support we might normally offer may be misaligned with students’ needs. Knowing students’ perceptions of their mistakes helps us better understand how we might help them.

We conducted interviews with some of the students after students took an exam and completed a subsequent exam analysis worksheet. Their responses gave us a deeper understanding of students’ views of simple and not simple mistakes. In these interviews, students described their mistakes and explained why they believed the mistake was simple or not simple. As we analyzed this data to gain a deeper understanding of how explanations of errors relate to students’ view of simple and not simple mistakes (Ryals et al., 2022), we saw a network of connections forming between the codes assigned to student explanations of mistakes. We built on Carlson and Bloom's (2005) problem-solving framework and looked for relationships between the problem-solving phase in which the error occurred and whether students classified their errors as simple or not simple. In this paper, we consider the following research questions.

1. Is there a pattern between students’ classification of mistakes as simple or not simple and the problem-solving phase in which they describe the mistakes occurring?

2. How do students’ patterns of classification compare with those of the researchers?

A review of the literature

Error analysis is a metacognitive activity which has shown to be beneficial to learning mathematics (Rushton, 2018). While mistakes can be seen as opportunities to grow (Boaler, 2015; Kapur, 2014), it has been shown that corrective feedback is needed in order for students to learn from their errors (Metcalfe, 2017). An “error” in math has been defined as “the result of individual learning or problem-solving processes that do not match recognized norms or processes in accomplishing a mathematics task” (Kyaruzi et al., 2020). Error analysis, or understanding the cause of a student error, is beneficial to the student, teacher, and to the researcher (Koriakin et al., 2017). Exam wrappers, tasks which involve the student identifying the cause of the error, have been shown to be effective tools for improving student understanding specifically in university STEM courses (Hodges et al., 2020). Post-exam reflection is a strategy used in self-regulated learning as a way for students to examine their preparation for an exam and subsequent performance on the exam. This allows for students to identify strategies that were helpful in preparation for the exam, note strategies that were ineffective, recognize what went well on the exam, and determine an appropriate study plan for the future. Engaging in this level of reflection is an aspect of self-regulated learning and was the initial motivation for our study.

Self-regulated learning has been of interest to scholars for decades. Cognitive psychologists (e.g., Pintrich, 2000; Schunk and Zimmerman, 2012; Zimmerman, 2002) developed models of self-regulated learning which were then further built upon by mathematics education researchers (De Corte et al., 2011; De Corte et al., 2000), who showed that awareness of metacognition and use of learning strategies predict math performance. Further, Schneider and Artelt (2010) expanded upon this work showing that these learning strategies can be taught at primary and secondary levels. Until recently mathematics educators who focused on metacognition, such as Garofalo and Lester (1985), primarily focused on metacognition within the problem-solving process. Thus our literature review highlights three areas: self-regulation models, metacognition, and a cyclic problem-solving model.

Self-regulation models

Models of self-regulation from Pintrich (2000) and Zimmerman (2002) involve the learner doing work before a task, during a task, and reflecting after a task. Prior to a task, a learner analyzes what will be needed to complete the task, which involves assessing content knowledge, thinking about the context in which the task will be completed, and making judgments about the importance and also the difficulty of the task. Both Pintrich and Zimmerman refer to this as forethought. Essentially, a self-regulated learner establishes goals and makes self-judgments about their abilities needed for the task which subsequently impacts the learner’s motivation. As Zimmerman describes, “Forethought refers to influential processes that precede efforts to act and set the stage for [engaging with a task]” (p. 16).

Following forethought, a learner engages with the task. While Pintrich identifies two distinct components of the task engagement phase, namely monitoring and control (p. 545), Zimmerman combines these into the performance phase of self-regulation. While engaging with a task, the self-regulated learner has an awareness of the knowledge that they possess and the knowledge they lack that is necessary to complete the task. In addition, the learner considers the actions needed to complete the task by monitoring “their time management and effort levels” which allows them to “attempt to adjust their effort to fit the task” (Pintrich, 2000, p. 467). These aspects of self-control and self-observation are the primary components that affect a learner’s attention and action while engaged with a task (Zimmerman, 2002).

Once a task is completed, a self-regulated learner reflects on the forethought and performance phases. During this self-regulation phase the learner reflects on their preparation for the task as well as their engagement with the task. Both Zimmerman and Pintrich note the importance of this phase of self-regulation influencing the next cycle of pre-task planning to post-task reflection. For example, a learner who performed poorly on a task may, upon reflection, plan to seek help in advance of the next task. Additionally, a learner may identify ways in which their setting or time management could be adjusted for future task engagement. Such a framework provides a way to organize our understanding of how learners are engaged in our courses as well as a way to characterize learners’ behaviors around coursework, and a key component of self-regulation is metacognition (Pintrich, 2000).

Metacognition

Metacognition impacts how students will interact with content in the future. Flavell (1979) defined metacognition as “knowledge and cognition about cognitive phenomena” (p.906) and identified four such phenomena as: metacognitive knowledge, metacognitive experiences, tasks, and task-associated actions. Researchers (e.g., Credé and Kuncel, 2008; Ohtani and Hisasaka, 2018; Pintrich and De Groot, 1990; Schneider and Artelt, 2010; Schunk and Zimmerman, 2012) recognized that metacognitive activities contribute to productive learning, and researchers have generally focused on how metacognition can be taught in the classroom (Donker et al., 2014; Schneider and Artelt, 2010). Activities that have been used to develop metacognition include such tasks as learning strategy surveys to raise student awareness of their use of study strategies as well as post exam wrappers to help students identify ways they could prepare differently to avoid making similar mistakes on tests in the future (Soicher and Gurung, 2017; McGuire et al., 2015).

Cyclic problem-solving framework

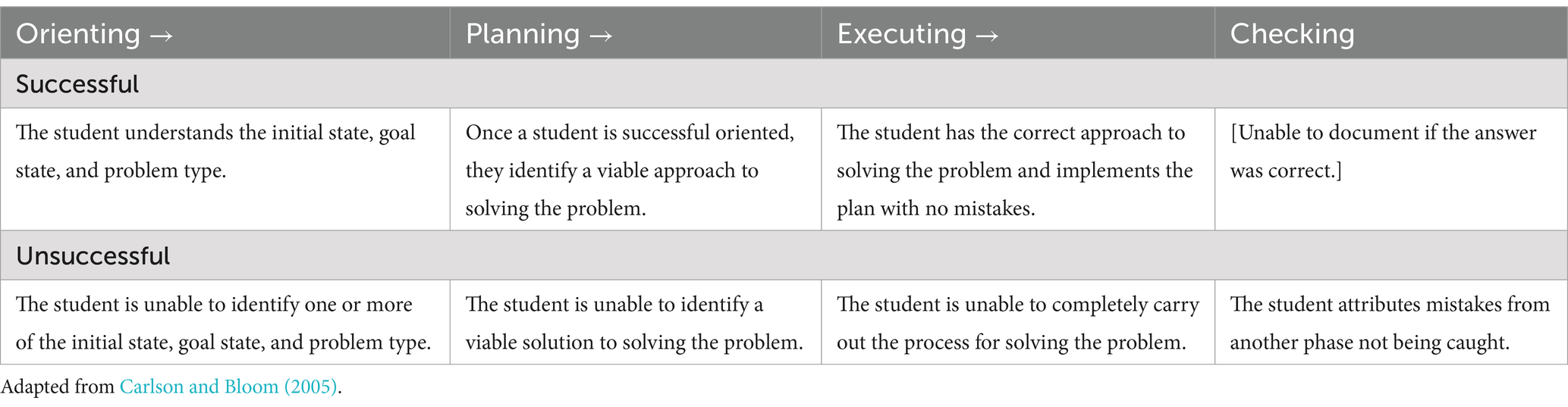
While self-regulated learning (SRL) models provide a way to understand how learners prepare for, engage with, and reflect upon learning a skill through repeated practice, Carlson and Bloom (2005) framework captures metacognitive aspects of a an expert mathematician’s process during a distinct problem-solving task and provides a tool we can use to analyze how learners engage with tasks. Carlson and Bloom present problem-solving as a four-stage process (orienting, planning, executing, checking); their framework connects the cognitive and metacognitive demands of problem-solving. They unpack the mathematicians’ use of resources, application of heuristics, and behaviors related monitoring during the four stages of the problem-solving process.

Broadly speaking, the expert identifies a problem’s initial state and goal state and establishes a plan to execute to move from the initial state to the goal state (Carlson and Bloom, 2005; Polya and Conway, 1957). When mathematicians are presented with a problem to solve, there is typically a period of time where they orient themselves to the problem. Behaviors that arise during the orienting phase of the problem-solving process include making sense of the problem, organizing given information, and constructing images related to the problem (Carlson and Bloom, 2005). Identifying what the problem is asking, similar to setting a goal in the SRL forethought phase, is part of the orienting process. Once they are oriented to a problem, the expert then moves onto planning, where they outline steps for solving the problem. This may involve identifying formulas, tools, or other resources needed to achieve the identified goal. Planning requires establishing a course of action to be carried out during the executing phase. Lastly, checking, involves assessing the accuracy of the work and returning to a previous phase as needed until the identified goal is reached. As Carlson and Bloom (p. 63) note: “When the checking phase resulted in a rejection of the solution, the solver returned to the planning phase and repeated the [planning-executing-checking] cycle.”

Other problem-solving frameworks do exist. For example, Polya and Conway (1957) presents a problem-solving framework that is not specific to expert problem-solvers with similar phases (Understand the problem, Devise a plan, Carry out the plan, Look back). Further, Mairing (2017) as well as Gallagher and Infante (2022) applied Polya’s model to novice problem-solvers. However, this model, like others (Garofalo and Lester, 1985; Schoenfeld, 1985), is static rather than cyclic like that of Carlson and Bloom’s framework. Although Garofalo and Lester (1985) applied metacognition and Polya and Conway (1957) problem-solving framework to algebra problems, their model is not cyclic. In addition, while College Algebra problems may not be perceived by many as “novel” (Carlson and Bloom, 2005, p. 69), we have found in our work that College Algebra students often engage with exam problems as if they were novel. For example, some students who had been regularly practicing factoring quadratic expressions of the form $a{x}^2+bx+c$ where a, b, and c are nonzero integers, perceived $x^2+8x$ to be different and thus required a different approach. Thus, problems that may be perceived as routine to experts, these problems are challenging to students.

Methods

In this section we first describe the larger study context and course activities that led to the current project. This paper builds upon previous work that began examining students’ classifications of mistakes as being simple or not simple (Ryals et al., 2020). We began with thematic analysis (Clarke and Braun, 2017) on students’ first exam problem responses. The themes that emerged were reflective of behaviors that aligned with those present in Carlson and Blooms’s problem-solving framework. We adapted Carlson and Bloom’s problem-solving framework to analyze students’ perceptions of mistakes as simple or not simple. Note that researchers tended to use the term “errors,” while students tended to use the term “mistakes.” We use the two terms interchangeably.

After taking an exam and identifying the reasons for their errors on that exam, students participated in interviews where they were asked to classify their mistakes as simple or not simple. The reason for asking this question of students was due to students on their exam reflections making comments such as, “I thought I did well but I made simple mistakes to get this grade,” “I made simple careless mistakes,” and “I believed I would do better but I had small mistakes” (all when reflecting upon the first exam). This led us to inquire not only about students’ reasons for errors but also if they identified those errors as being simple or not simple. We see our work as a bridge between self-regulation and problem-solving literature.

After describing the data collection for the current project, we detail our coding scheme using Carlson and Bloom’s (2005) cyclic problem-solving framework. We will also provide examples of our coding scheme which present as phases of the problem-solving framework.

Context and data sources

This study takes place in a College Algebra course at a large (over 30,000 enrolled students), Southwestern, public, Hispanic-Serving Institution. College Algebra can be a first mathematics course for STEM majors at this institution, unless they place into a higher course, such as Precalculus or Calculus I. Broadly, major course topics include linear equations and inequalities, quadratic equations, linear and quadratic functions, rational expressions, and applications of these topics. At the time of this study, the course met 3 days each week in sections of size 60–70 students. College Algebra has a support course, College Algebra Support (CAS), for a subset of College Algebra students who are identified through multiple measures (e.g., high school grades, college entrance exams) by the university as having weaker prerequisite backgrounds. This support course (at some institutions referred to as a co-requisite course) meets in smaller sections of size 30 and provides additional practice on College Algebra content. In addition, CAS instructors focus on helping students develop effective study strategies. During the fall 2019 semester, approximately 420 students were enrolled in one of seven sections of College Algebra. Thirty-one students were enrolled in one of two sections of CAS. Both CAS sections were taught by the same instructor, who also taught one of the seven lecture sections of College Algebra. This instructor was experienced in teaching both College Algebra and CAS. All students in CAS were invited to participate in this IRB-approved study. The data obtained in this study is from those students who consented to participate. Data sources from CAS students included work from their first College Algebra exam, responses on a post-exam analysis worksheet, and interviews. The student work printed here was rewritten to avoid identification by handwriting.

Metacognitive coursework

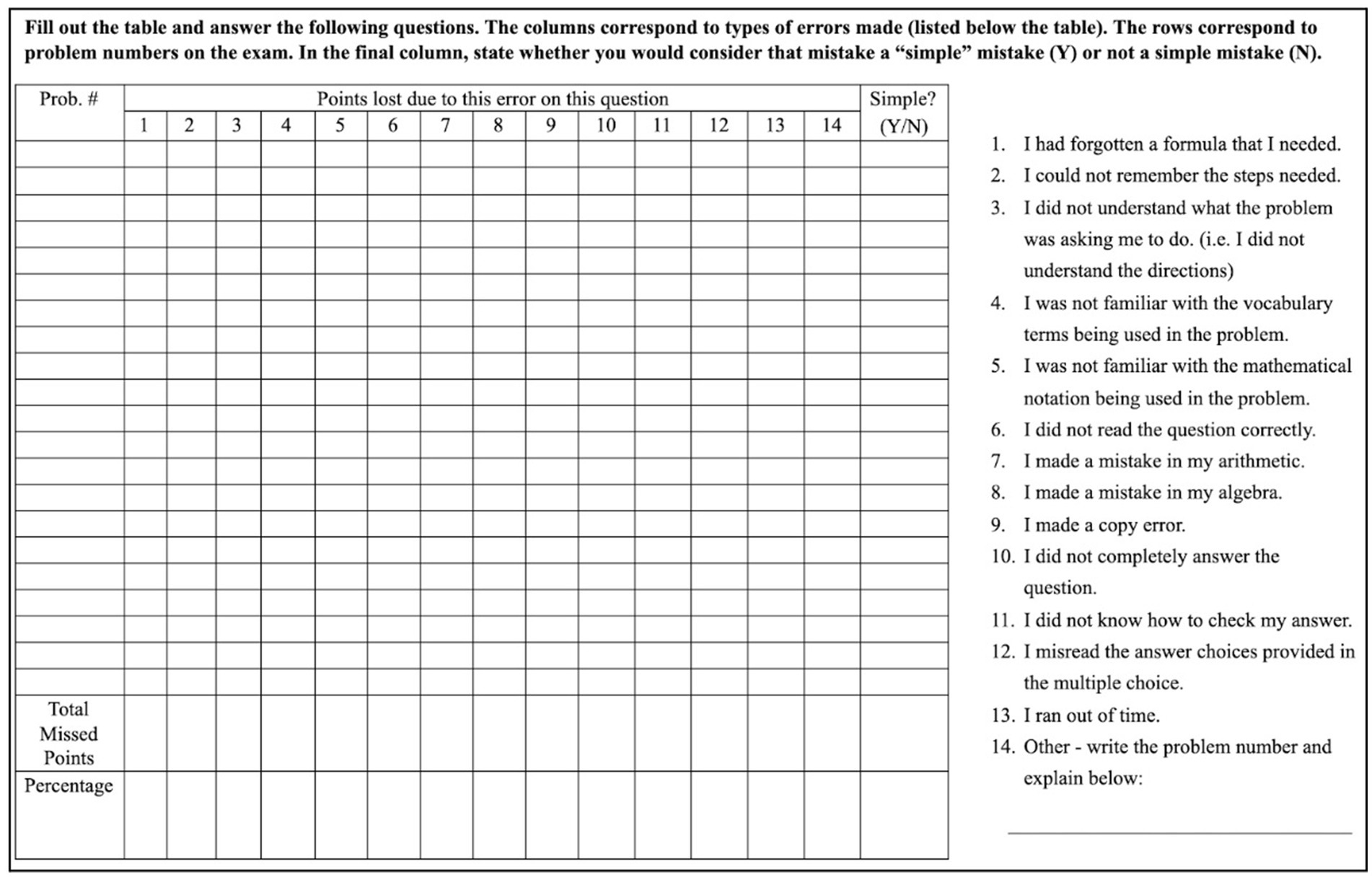
As previously stated, the CAS course served multiple purposes, including just-in-time content support, discussion of study strategies, and metacognitive development activities. A metacognitive activity motivated this study and led to student interviews. Specifically, following each exam, students filled out an exam analysis worksheet (Figure 1) where they classified the errors on their exams. Exams were scheduled for two-hour blocks and consisted of open response and multiple-choice questions. Exam 1 had 13 open response questions and 8 multiple choice questions. A student’s solution to an exam problem could have multiple errors; different errors, even if from the same problem, were listed individually.

Figure 1

Figure 1. Exam analysis worksheet.

Interviews

Following completion of the exam analysis worksheet, students were invited to participate in a voluntary interview. Students were incentivized to participate in the interviews with a one-on-one exam review session with the interviewer following the interview. Eight CAS students volunteered. Interviews, which lasted approximately 30 min, consisted of students being asked to discuss their exam errors, referencing their exam analysis worksheet during the interview as needed. In particular, students identified the type of mistake they made, classified it as simple or not simple for each error, and then explained why they made that classification. Then, at the end of the interview, students summarized their definitions of simple and not simple mistakes. Students were not provided with definitions of simple and not simple; this was something they decided on their own, as we were trying to understand their perceptions of mistakes being simple or not simple.

While exam review was intended to occur after each interview, the interviewer ended up reviewing problems with students as they discussed their errors and how to correct them. This process grew organically as students were trying to understand their mistakes, why they made them, and how they could be corrected. Students were then able to classify their mistakes as simple or not simple, once they had a better understanding of their mistakes.

Classifying errors

In our analysis, we first classified mistakes as simple or not simple for both students and researchers. Students’ classifications were made during interviews. Separately and prior to interviews, researchers looked at student work and classified each of the errors made by students as simple or not simple. While students used their own reasoning to classify their mistakes, the research team identified a simple mistake as one that “could be made accidentally, would likely not be repeated, or violated a mathematical convention rather than a rule (i.e., not reducing coefficients),” whereas a not simple mistake emerges from a “lack of conceptual understanding” (Ryals et al., 2020). Table 1 provides three examples of student work with researcher’s classifications as simple or not simple. Following the interviews, the research team then determined the problem-solving phase in which student errors occurred based on two pieces of data: student work and student interviews.

Table 1

Table 1. Example classifications of simple and not simple mistakes.

Problem-solving framework

Since some of the data was collected in the form of student interviews after an exam (i.e., post-task), much of the responses were reflective in nature and provided insight about students’ problem-solving process. Carlson and Bloom (2005) cyclic problem-solving framework focuses on the problem-solving behaviors of expert problem-solvers when they were presented with “problems” they did not know how to solve by familiar or routine procedures. As described by Wickelgren (2012), an algebra student’s first step of the solution is a complete understanding of the given information; this occurs in Carlson and Bloom (2005) orienting phase. A student then identifies an operation or plan to solve the problem. Once a strategy for solving is identified, a student would need to execute that plan. Lastly, though not a common practice for students in this particular study, students might have a strategy for checking their solution.

The problems given to the College Algebra students on their exam were not “novel” like those Carlson and Bloom (2005, p. 69) presented to their expert problem solvers. However, we can still characterize their approach to problems with consideration for a problem’s initial state and goal state (Wickelgren, 2012). Further, to achieve an outcome or solution, these students still do engage in problem solving phases that align with Carlson and Bloom’s model. The cyclical nature of the model also fits for a variety of learners and has been applied to novice problem solvers (Gallagher and Infante, 2022; Mairing, 2017; Garofalo and Lester, 1985). While we recognize that Polya and Conway (1957) problem-solving phases are not restricted to experts, we were seeking out a framework that was cyclic in nature, as that better aligns with the self-regulation models (Zimmerman, 2002; Pintrich, 2000; Schunk and Zimmerman, 2012) that guided our initial work.

Problem-solving phases

Carlson and Bloom (2005) characterizations of problem-solving phases allowed us to identify in which phases particular errors occurred. We determined that setting a goal for a specific problem turned out to be a key component of a student successfully completing the orienting phase. To clearly identify whether the student error took place during the orienting, planning, executing, or checking phases, the initial state and goal state of the particular problem type was first determined by the researchers.

Orienting mistakes were related to the initial state, goal state, and problem type. In order to not be an orienting mistake, students must have accurately determined all three: initial state, goal state, and problem type. If a student was unsure of what a problem was asking, we classified such a mistake as an orienting mistake. Mistakes classified as occurring in the planning phase were made when a student understood what a problem was asking but did not successfully identify a viable approach to solving the problem. When students demonstrated a correct overall approach to solving the problem, we then moved on to examine their execution of their plan. Executing errors occurred when a student recognized the correct formula or process required but implemented it incorrectly, such as recognizing difference of squares and knowing the formula to factor difference of squares but carrying out the formula incorrectly. Errors that did not fall in the orienting or planning phase were either executing or checking errors, and the distinction between these two phases was made by the student discussing (or not) answer validation or examining their execution steps. If a student explicitly referred to checking their work in some way without being prompted by the interviewer, then an error would be classified as occurring in the checking phase rather than the executing phase.

Final coding structure with examples

The final coding framework utilized for this study is provided in Table 2. As we have already stated, student explanations were examined in parallel with student work. Student work alone was not sufficient for identifying the problem-solving phase in which an error occurred, and we discuss several examples that illustrate this point.

Table 2

Table 2. Final version of coding framework.

Orienting versus planning

A factoring question on the exam provides us with examples (Figures 2, 3) contrasting orienting and planning. Students were asked to completely factor a difference of squares. In this exam problem, researchers identified the initial state as a difference of squares. The goal state was a correctly factored product of two binomials. While using a memorized formula for factoring a difference of squares was not required, the overall plan required was to apply an appropriate factoring method. Thus correct orientation required recognizing that the problem was a difference of squares factoring problem. For example, both C (Figure 2) and AY (Figure 3) made mistakes on problem 10 and their work did not appear to be much different from each other. However, upon examining their reasons for their respective mistakes provided in interviews, it could be determined that Student AY’s error occurred during orienting, while C’s error occurred during planning. Student C explained that they needed to spend more time on the problem to recognize which factoring method was appropriate for the problem, but at the time of the exam they said that they did not realize they could have gone further noting “I guess I did not completely answer the question… if I knew that I had-I had more ahead, then I probably would have done it.” Further Student C was confident that they could do such a problem in the future. In contrast, Student AY explained that they did not “know factoring at all” and “did not even know what [difference of squares] was.” These are examples of why looking only at the student work was not sufficient for identifying problem-solving phases in which errors occurred. Student explanations and discussion provided details that could not be captured with student work alone and allowed us to better understand nuances in student mistakes and in what stage of the problem-solving process these errors occurred.

Figure 2

Figure 2. Student C’s work on problem 10 (planning phase error).

Figure 3

Figure 3. Student AY’s work on problem 10 (orienting phase error).

Planning versus executing

Students were given a true/false statement with instructions to simplify the left side of the equation to justify their answer. Researchers identified the problem type as simplification using exponent rules, the initial state as a fraction involving the product of multiple variables raised to different powers, and the goal state as a simplified fraction with the overall plan being to expand the numerator, expand the denominator, and then cancel. Again we compare Student C (Figure 4) and Student AY (Figure 5). Both students made errors in using exponent rules, though their mistakes were coded differently. Student C had two errors. The first was a copy error (forgot to write an additional 3z term on their second line of their work) which student C and the authors classified as simple. C’s second mistake is forgetting that ${\left(4x\right)}^0$ is equal to 1 (Figure 4), stating “Umm I just said I made a copy error and then I made a mistake in my algebra because I did not remember that ${\left(4\right)}^0$ is 1.” We coded this second error as an executing error, as Student C had a plan that, if executed correctly, would get them to the desired result. Student AY, on the other hand, was unsure of how to use exponent rules. In fact, Student AY viewed the rules as something to be memorized and did not fully understand what was happening conceptually. They explained their own mistake, shown in Figure 5, quite differently.

Figure 4

Figure 4. Student C’s work on problem 3 (executing phase error).

Figure 5

Figure 5. Student AY’s work on problem 3 (planning phase error).

I know there’s some instances where you are supposed to add them but I just-I do not remember which instances that you actually like bringing the power like 3 to 9 instead of adding to 5. I feel like simple because it’s memorizing rules of exponents.

Student AY did not know the correct rule of exponents to apply nor how they worked mathematically. Because of this Student AY could not formulate a correct plan. They did not have a plan for how to distribute or how to reduce terms, thus their mistake was coded as a planning error. This distinction could only be made when examining student work with their reasoning.

Executing versus checking

Checking did not come up often, and was only applied if a student discussed that they had indeed checked their work. For example, when asked to completely factor 8x²y-2xy + 12xy-3y, both Student J and Student MF had a final answer of (2xy + 3y)(4x-1). Student MF did not recognize that they could keep factoring, while Student J stated that they checked their work and thought that this final answer would be acceptable. Thus, Student MF’s error was coded as executing, while Student J’s error was coded as occurring during the checking phase. The checking code applied only when the students brought up checking based on how they described their errors in the interviews. Students either expressed not checking their work or not catching the mistake while checking.

It should be noted that student work on a problem could contain multiple errors. If the initial errors began in the orienting or planning phase, then subsequent errors were not classified in additional phases, as there were fundamental knowledge issues that prevented a student from progressing successfully out of that phase. For example, if a student did not know that a problem required factoring (such as in Figure 4), and were thus not successfully oriented to the problem, we did not then classify additional mistakes as occurring in planning or executing phases. However, if a student successfully oriented to and planned for a problem, then it was not unusual for there to be more than one executing mistake in that problem.

Results

Simple and not simple mistakes across all phases and all students

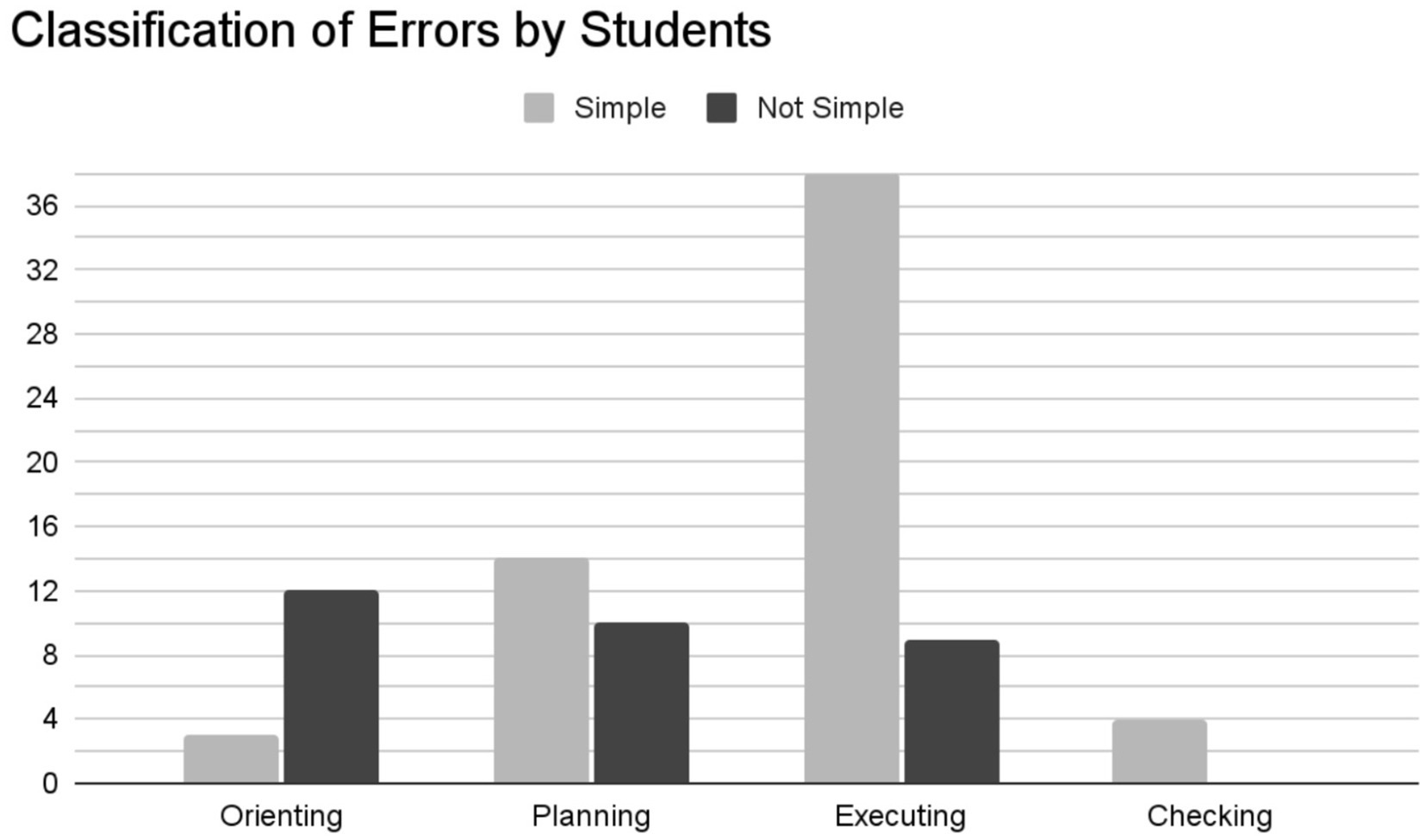
Some patterns emerged between students’ classification of simple/not simple and problem-solving phase (research question 1). Figure 6 shows the classification of mistakes by students and illustrates the phase in which those mistakes occurred. Students generally classified orienting mistakes as not simple, making comments such as “I kind of just like did not know what was going on” and “Um I really I did not know it.” In contrast, checking mistakes were classified as simple. Researchers’ classifications (Figure 7) of simple/not simple were in greatest alignment with students in these two phases of problem-solving (research question 2).

Figure 6

Figure 6. Classification of errors by students.

Figure 7

Figure 7. Classification of errors by researchers.

Students did not consistently classify planning errors as simple or not simple, and their classifications did not necessarily align with the researchers’ classifications of those mistakes. As with orienting, researchers generally saw errors made in the planning phases as being predominantly not simple, as errors made in either of these phases are typically tied to lack of conceptual understanding. However, students who classified their planning mistakes as being simple often attributed them to memorization issues or stated something to the effect of “Now that I’ve seen it, I know how to do it.” When students were unsure of what strategy to use, they classified their mistakes as not simple.

The mistakes that occurred during the executing phase, however, were more nuanced in that they involved both simple and not simple mistakes. A student could make a copy error (simple) during execution, or they could make a conceptual error (not simple) during the execution phase if that error concerned concepts outside the scope of orienting or planning for that problem. For example, Figure 4 shows that Student C had two executing errors: (1) the student evaluated ${\left(4x\right)}^0$ as 4x rather than 1; and (2) the student had a typo where they forgot to write a fourth 3z term in the denominator of the second step of their work (but they had it in the previous step). It should be noted that the data presented in Figures 6, 7 are total mistakes in a particular phase.

For executing mistakes that researchers perceived to be not simple, but students considered to be simple, a common refrain from students to justify this classification was “now that I have seen the problem worked, I can do it.” Some students attributed their simple execution mistakes to memorization issues. However, in both cases, researchers identified these mistakes as not simple as they often involved a depth of understanding that seemed to be missing for the student (e.g., Student C’s first executing error in Figure 4).

Table 3 includes each students’ course grade as well as frequencies of each student’s classification of mistakes on exam 1. For example, the row that corresponds to Student MF shows that Student MF had 9 mistakes that occurred in the executing phase. Student MF identified 7 of these mistakes as being simple and 2 being not simple. It can be seen from Table 3 that Students MM, C, and AY have the most mistakes and thus their data comprises most of the data shown in Figures 6, 7.

Table 3

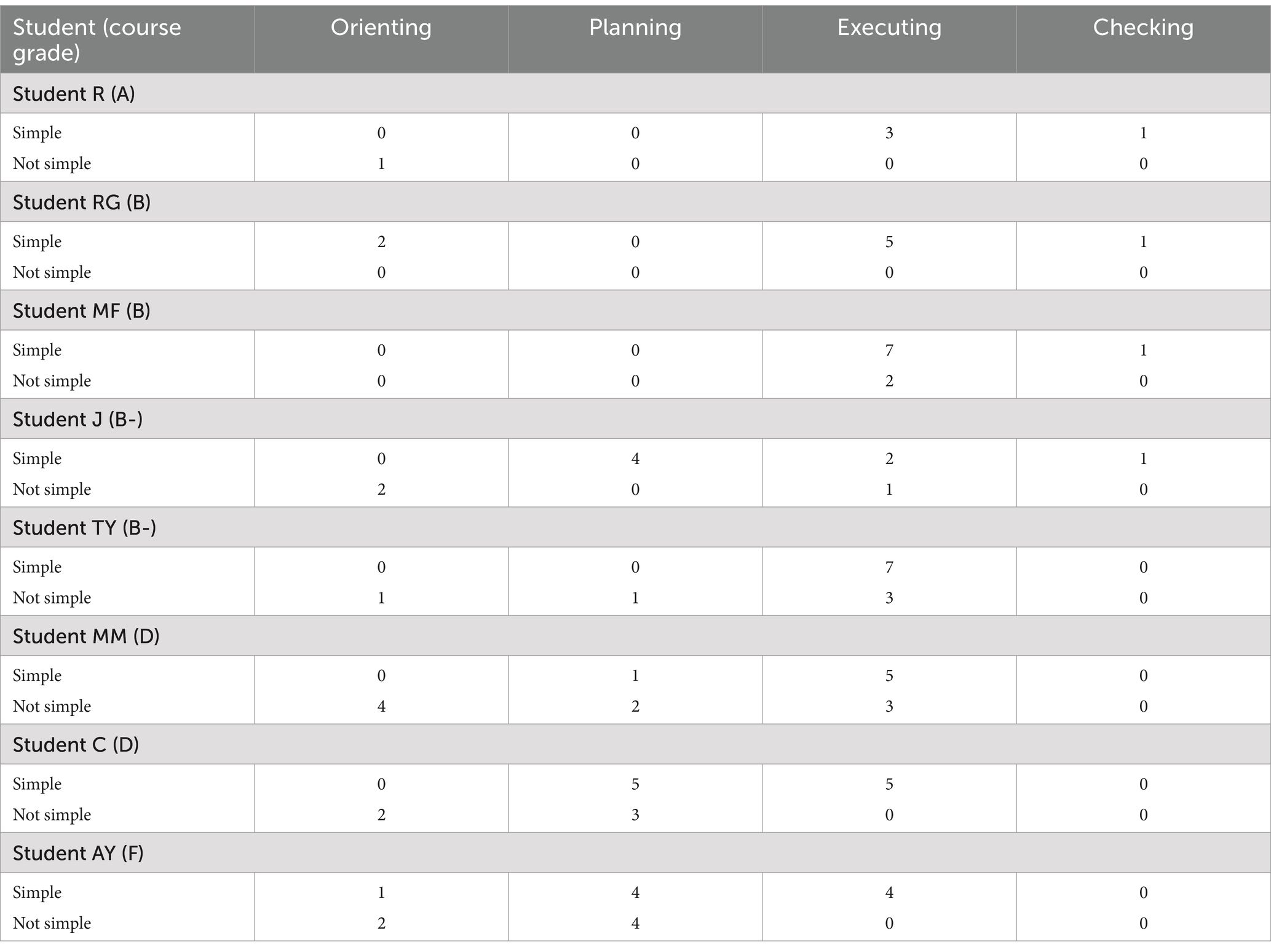
Table 3. Course grades and students’ classification of exam 1 mistakes for each problem-solving phase.

We next briefly describe three specific students: one with a high final grade (A), one with a low final grade (D), and finally one with a B. Each of these students’ perceptions regarding what made a simple mistake were very different. Among the eight students we interviewed, these three capture the different behaviors and characteristics we found through our analysis of the 8 students. Specifically, we discuss Student R, Student C, and Student RG.

The case of Student R

Student R’s classification of simple and not simple mistakes aligned well with the researchers. Student R earned a final grade of A in the course. Student R had only five mistakes on exam 1. Both student R and the researchers were in agreement, identifying four of these mistakes as simple and one as not simple. The simple mistakes occurred in the executing and checking phases, and the not simple mistake was in the orienting phase. This parallels Figure 7, where researchers identified simple mistakes as occurring more often in executing and checking phases and not simple mistakes occurring more often in orienting and planning stages. Student R seemed to be more metacognitive than other students and took ownership of their mistakes. They studied regularly and noted when they had to spend more time “to think about it [the problem]” and were persistent in working problems, “for like 30 min” until they were satisfied with their work. In addition, they described their problem-solving process as being cyclic:

I just have to like really like think about the problems a lot, and a lot of times I don’t know how to do the problem when I first see it, it’s not always like oh I know exactly how to do that! It’s like a ok, look at it, three or four times you know, then I like, I do it a few times, then I leave the problem, then I come back to it, like I hope that other problems like make me remember how to do it.

Student R recognizes that they will not always know how to solve a problem, but notes that they read and attempt problems multiple times in order to identify an appropriate strategy. In some cases, they may have to move on to other problems to try to identify a connection between the problems they are trying to solve.

The case of Student C

In contrast, Student C’s definition of simple and not simple did not align well with researchers. The authors identified mistakes that were conceptual in nature or indicated a lack of understanding as not simple. Student C had a final grade of D in the course. Out of 15 errors on exam 1, Student C identified 8 of these errors as simple; whereas, researchers identified only 1 as simple. In other words, researchers identified 14 of Student C’s 15 mistakes as being not simple. Student C and the researchers did agree that the 2 orienting errors were not simple. However, researchers classified Student C’s 8 planning errors as not simple, which differed from Student C’s view that 5 of these planning errors were simple. Student C thought all 5 of the errors in executing were simple, but researchers thought only 1 of those 5 errors were simple. Student C had no errors in checking. Student C attributed not simple mistakes to not engaging with a problem type enough, making statements such as “if I would practiced more” and “I guess I did not put in the effort to like practice it on my own” and “if I practiced, I’d probably would not forget, like, the basics.”

The case of Student RG

Student RG had a final grade of B, and they classified all of their mistakes as simple. While Student RG had mistakes in every phase, most of their errors were in executing. Researchers classified all of RG’s orienting errors and three out of five execution errors as not simple. Student RG was quite confident and believed that their mistakes were preventable with little time or effort as long as someone showed them in advance how to work relevant problems. A common refrain from Student RG was essentially “now that I see it I’ll be able to correct it” and “We went over it. You told me. Not really the kind of mistake that I would make twice.” However, Student RG had previously been shown exam-type problems during class. Further, they had repeated mistakes on their exam, which indicated a lack of understanding to the research team. To researchers, it seemed as if Student RG did not have an awareness of what they did know and did not know.

Simple versus not simple: (dis) agreement between researchers’ and students’ perspectives

Within each phase of the problem-solving process, students were asked to classify their errors as being simple or not simple. How students characterized their errors did not always align with how researchers would have classified students’ errors. The researchers recognized that some errors were deeper than just a copy error and could likely occur again. However, students did not often recognize this. In the next sections we answer the second research question by describing the agreement (or lack thereof) between us, the researchers, and students within each phase of the problem-solving process.

Orienting

Orienting is the first phase in the problem-solving process, and if a student gets stuck at this stage, they may not have much to write down or end up making a guess at how to approach the problem. Students recognized when they had orienting issues and often characterized these mistakes as being not simple. Thus, there was 73% agreement among students and researchers about errors that occurred in this phase. Orienting requires accurate interpretation of the problem in order to know what strategies are needed to solve it. If proper orienting fails, a student usually does not get very far in solving the problem or may leave the problem blank.

Statements such as “I kind of just like did not know what was going on” and “Um I really I did not know it” were made by students who identified orienting errors as not being simple. Student RG, as previously discussed, was an exception as they characterized all their mistakes, including those in the orienting phase, as simple. Most often, though, for errors in the orienting phase, students noted that they did not know what to write down or did not have much to write down.

Planning

Like with errors in the orienting phase, we identified all planning mistakes as being not simple. In contrast, the students were split between simple and not simple. There was only 42% agreement between students and researchers classification of simple and not simple in the planning phase. Students who identified planning mistakes as being simple, attributed this distinction to either a memorization issue or stated that now that they have seen how to do the problem, they could do it in the future on their own. Some students even said their mistakes were simple even though they did not know what specific strategy was required to solve a problem. For example, Student J stated that one of their planning mistakes was simple because “if I would have remembered the equation and then remembered the step, it would have been simple.” However, we identified these mistakes as not being simple as the students were missing fundamental ideas or strategies for approaching the problems.

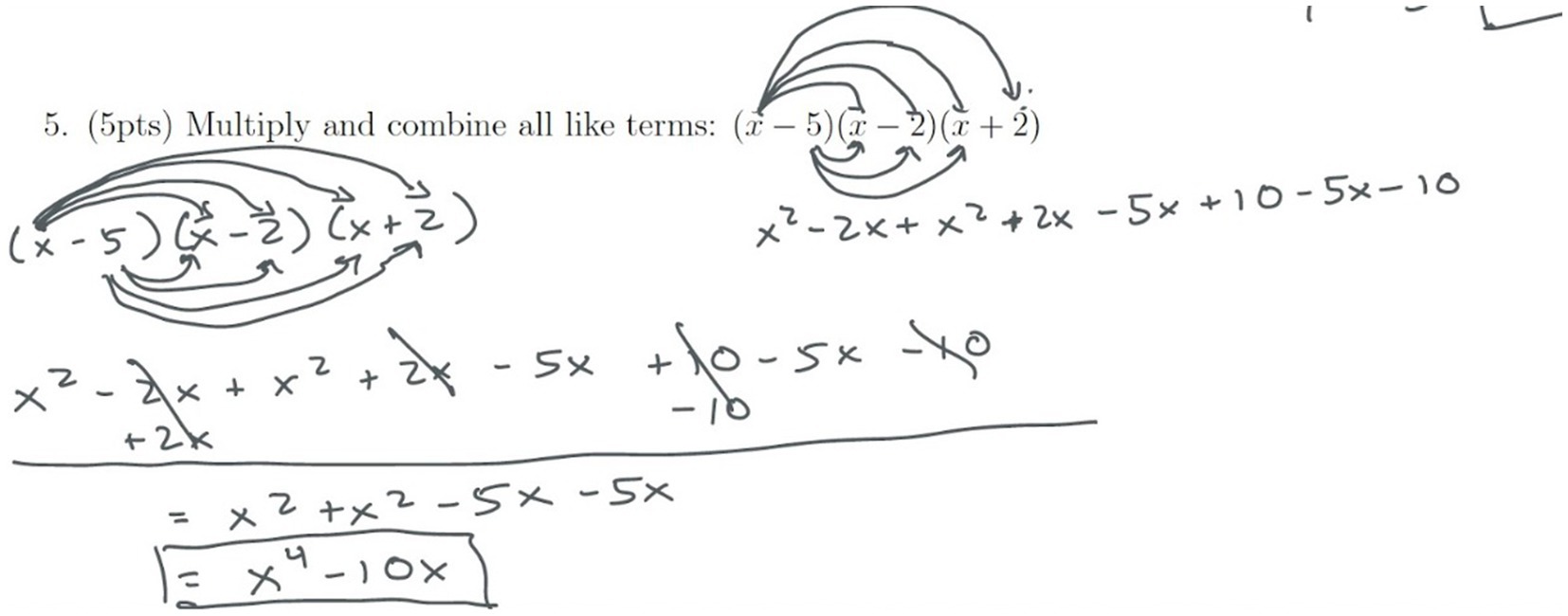
In Figure 8 Student C’s work on problem 5 can be seen. This error occurred in the planning phase. While the error looks initially like an execution error, we classified it as a planning error. The goal of this problem is to expand the product of three binomials. This requires a student recognizing that goal and, in order to achieve that goal, to multiply exactly two of the binomials and then multiply the third with the result. In this case, Student C began multiplying everything at once, which is a planning error. Student C identified this mistake as being simple because they could have done it but “overthought” what was needed for the problem, making it “more complicated” for themselves. In contrast, Student C identified the planning error on problem 4 (Figure 9) as being not simple because they did not know what strategy to use, explaining:

Figure 8

Figure 8. C’s work on problem 5 (planning phase).

Figure 9

Figure 9. C’s work on problem 4 (planning phase).

Yeah. I started that step and I was like, “Nahh, that can’t be the answer”, so I crossed it out or tried. So I honestly-I didn’t know what I was doing. Ummm, I guess I did not completely answer the question like I had two different methods and I didn’t know which one to follow through.

Executing

Errors that were identified as occurring during executing were often seen as simple mistakes by students, but not necessarily so by researchers. Students and researchers agreed on simple/not simple for 55% of the errors in the executing phase. For example, Student C made an executing error on exam problem 3 (Figure 4) and classified the mistake as simple. Student C actually had two errors in this problem: (1) a copy error from their first to second line of work, and (2) not evaluating ${\left(4x\right)}^0$ as 1. While there was agreement among researchers and Student C regarding the copy error (classifying it as simple), there was not agreement with regard to the second error. Student C identified this mistake as being simple. In contrast, we identified this error as being not simple because of the misunderstandings regarding exponent rules and power of 0, which were concepts covered by the College Algebra course content. Student C identified this error as simple because they attributed it to a memorization issue.

Like Student C, Student RG also made an executing error on a similar problem (Figure 10) and classified the error as simple. RG’s final answer was not simplified completely, according to mathematical convention, but exponent rules were correctly applied; therefore, the researchers also classified the error as simple since the student had demonstrated the ability to simplify in previous problems and was not likely to repeat the error.

Figure 10

Figure 10. Student RG’s work on problem 4 (executing phase).

Most (81%) of the executing errors were identified by students as being simple. Whereas we classified about 40% of the errors as simple and 60% as not simple. On problems where students and researchers disagreed (i.e., students classified a mistake as simple, and researchers said not simple), most students attributed their errors to one or more of the following reasons

• Should have studied the problem/topic more.

• Have seen, have done, or knew the problem/topic before the exam.

• Had the right idea/approach to the problem.

• Made the problem harder; there was a simpler way.

• Rushed through the problem.

• Memorization issue.

In contrast, researchers viewed students’ mistakes as being not simple and resulting from significant misunderstandings or lack of understanding of concepts being assessed on the problems. For example, a student saying that they can work a problem now that they have been shown how to be not viewed as a simple mistake. Instructors worked problems similar to those on the exam during class prior to the exam, so students were shown how to work such problems and could still not successfully complete them on the exam. Thus, students were unable to demonstrate understanding. However, it is important to note that students do not recognize this subtlety. Student RG, for example, when discussing how to simplify a rational expression (Figure 11) stated “I feel like if I was to do a problem again, now I learned. We went over it. You told me. Not really the kind of mistake that I would make twice.” However, instructors did work multiple examples of these types of problems in class the day before the exam. For example, it can be seen from Student RG’s work that there are fundamental issues with how to grapple with subtraction of rational expressions and how to handle denominators for final answers.

Figure 11

Figure 11. Student RG’s work on problem 12.

Checking

Across the four phases, checking was the only phase for which both students and researchers completely agreed. Errors that students identified as occurring during the checking phase were agreed to be simple mistakes. There were not many of these errors, as these students often did not bring up checking as an issue. There is the question of whether or not a student did check their work, and certainly researchers do agree that this is good practice. However, mistakes that occurred during checking were only considered if the student brought it up. Thus, issues around what is meant by checking and whether or not checking occurred is not within the scope of this paper.

Discussion

Agreement between students and researchers varied across the four problems solving phases. Researchers consistently coded orienting and planning mistakes as not simple. Students tended to agree with researchers on the classification orienting mistakes being not simple, but were more mixed with regard to planning mistakes. Students with letter grades of Ds and Fs, namely Students MM, C, and AY, tended to have more mistakes in orienting and planning phases of the problem-solving process. In addition, these lower performing students classified several of these mistakes as being simple. It is possible that these students have less awareness about their conceptual understanding of the content and may lack the metacognitive skills to recognize that conceptual mistakes are not simple. In contrast, the higher performing students (Students those with grades above a C) tended to have more of their mistakes in later problem-solving phases (executing and checking). This is not surprising and is reaffirmed by the problem-solving literature (Ovadiya, 2023; Granberg, 2016), as these students likely have stronger content knowledge and thus can make it further through the problem-solving process.

If students are struggling to know what a problem is asking or what method is required to solve a problem, then they may not be able to write down much and therefore are not well-positioned to receive many points on these exam questions. As a result, these students are likely unable to earn the needed points to pass the class and lack the conceptual understanding needed to successfully progress to the next course. In contrast, students R, RG, and MG, all of whom received an A or B in the class, had errors primarily in the executing and checking phases. Generally, these students seemed to know what was needed to solve a problem, and what problems were asking them to do, but they may have struggled with carrying out the plan. Students who lack the metacognitive skills to successfully orient themselves to a problem, struggle with the planning phase.

We wonder if students whose definitions of simple mistakes that are more aligned with the researchers’ perspectives might be more likely to get a higher grade. Classifications of simple and not simple by students R, MF and TY were closely aligned with researchers’ classifications; student R received an A, student MF earned a B, and student TY received a B-. It is possible these students have a higher performance because they have more awareness about their errors - where they occur and how to address them. In contrast, student C did not align well with the researchers and performed poorly. This observation again suggests that metacognitive awareness influences test performance (Toraman et al., 2020; Ajisuksmo and Saputri, 2017; Vadhan and Stander, 1994). Thus, as research suggests, homework support should include training in accurately identifying mistakes and planning how to prevent making those same mistakes in the future (Soicher and Gurung, 2017; McGuire et al., 2015). We see this as a future line of inquiry. It could be that there are belief differences in what types of understanding or knowledge is important for this course or type of assessment, and thus students may see certain errors as simple when researchers see them as not simple (Dawkins and Weber, 2017).

These results suggest that it might be beneficial for homework support to focus on helping students carry out the orienting and planning phases (Lerch, 2004). This could influence the design of support courses. It could also impact the approach instructors take during office hours and the questions tutors ask at math learning centers. Identifying the goal of the math problem in the orienting phase, and then choosing an appropriate strategy to solve the problem in the planning phase.

Limitations and future work

The study is limited to students who were underprepared for the College Algebra course, and from that population the sample is small: 8 students with a total of 90 mistakes on the first exam. The majority of mistakes were made by students who performed the most poorly, which may have skewed the results (i.e., causing us to focus on the data in a particular way). It seems that students who made the most mistakes differed most from the researchers while students who made fewer mistakes classified mistakes more closely to the researchers.

Since our ultimate goal is to find ways for students to improve their study methods, coding with the problem-solving framework from the student perspective allows for us to better understand the student perspective regarding their work. As we consider ways to help students study more effectively, we need to continue to research ways that students’ views of mistakes may impact their study habits and performance in class. We wonder how students’ understandings of mistakes will help them develop metacognitive knowledge to learn from mistakes and then make changes to improve learning habits. We also wonder if the students whose perspectives are more aligned with the researchers’ view of simple mistakes may have stronger self-regulating behaviors.

We wonder about the possible impacts of students developing metacognitive strategies. As students develop metacognitive awareness of their mistakes, it may be that they will develop a more “cyclic” approach to problem-solving (like with Student R). Students who had multiple strategies, yet chose the wrong one, identified their mistake as simple. Perhaps the development of metacognitive strategies might help students return to a previous problem-solving phase if they are stuck, and if they might then identify mistakes of choosing the wrong strategy as not simple. In addition, the development of such skills and practices may lead to students checking their work more consistently. While there were few checking errors, this study did not gather data on how often students used checking when they answered a problem correctly. For those students who had mistakes, we saw that checking was not part of students’ regular problem-solving processes even when a check for the algebra problems seems fairly straightforward. For example, to check a factoring problem, students could multiply their answer. Future research could address how students’ use of the checking phase may be related to self-regulating behaviors as well as how students may develop a cyclic approach to their problem-solving practices.

It is likely that there are other factors, beyond metacognition, that influence students’ distinctions between simple and not simple. For example, Student RG’s labeling of most of their mistakes as simple may be a result of overconfidence. Similarly, students who identified most of their mistakes as not simple may feel a lack of confidence in their math ability. In a related study, it is suggested that self-efficacy and perseverance are related to students’ distinction of mistakes as simple or not simple (Ryals et al., 2022).

While this study focused on how students’ classification of simple and not simple related to the problem solving phase in which the error occurred, a fundamental difference of interpretation between the researchers’ simple and students’ simple is seen in researcher’s simple mistake being an oversight and the student understands and the students’ simple being that “it is an easy thing to do, I just did not do it.” as J described in a planning mistake. This difference could be further explored in a future study.

Conclusion

In closing, it is important to remind the reader of why we should care about students’ perceptions of their errors. The most important implication for us was realizing that students’ perceptions of their errors were often not at all aligned with our perceptions of their errors. This realization is important to us because it allows us to better understand how students are identifying these mistakes and how their perceptions of their mistakes may differ from our perspectives. As a result, the help and support we offer to students may be misaligned with their needs. For example, we may make recommendations about test taking strategies that may not be suited for addressing their needs. Therefore, knowing students’ perceptions of their mistakes helps us better understand how we might support them as learners and better situate them for success in the future.

Data availability statement

The datasets presented in this article are not readily available because we do not currently have IRB approval for sharing the data set beyond what is included in this publication. Requests to access the datasets should be directed to Linda Burks, bGJ1cmtzQHNjdS5lZHU=.

Ethics statement

The studies involving humans were approved by San Diego State University’s Human Research Protection Program (https://research.sdsu.edu/research_affairs/human_subjects). The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author contributions

MP: Conceptualization, Formal analysis, Methodology, Writing – original draft, Writing – review & editing. LB: Conceptualization, Formal analysis, Methodology, Writing – original draft, Writing – review & editing. MR: Conceptualization, Formal analysis, Methodology, Writing – review & editing. SH-L: Conceptualization, Formal analysis, Methodology, Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ajisuksmo, C. R., and Saputri, G. R. (2017). The influence of attitudes towards mathematics, and metacognitive awareness on mathematics achievements. Creat. Educ. 8, 486–497. doi: 10.4236/ce.2017.83037

Crossref Full Text | Google Scholar

Boaler, J. (2015). Mathematical mindsets: unleashing students' potential through creative math, inspiring messages and innovative teaching. San Francisco, California: John Wiley & Sons.

Google Scholar

Carlson, M. P., and Bloom, I. (2005). The cyclic nature of problem solving: an emergent multidimensional problem-solving framework. Educ. Stud. Math. 58, 45–75. doi: 10.1007/s10649-005-0808-x

Crossref Full Text | Google Scholar

Clarke, V., and Braun, V. (2017). Thematic analysis. J. Posit. Psychol. 12, 297–298. doi: 10.1080/17439760.2016.1262613

Crossref Full Text | Google Scholar

Credé, M., and Kuncel, N. R. (2008). Study habits, skills, and attitudes: the third pillar supporting collegiate academic performance. Perspect. Psychol. Sci. 3, 425–453. doi: 10.1111/j.1745-6924.2008.00089.x

PubMed Abstract | Crossref Full Text | Google Scholar

Dawkins, P. C., and Weber, K. (2017). Values and norms of proof for mathematicians and students. Educ. Stud. Math. 95, 123–142.

Google Scholar

De Corte, E., Mason, L., Depaepe, F., and Verschaffel, L. (2011). “Self-regulation of mathematical knowledge and skills” In D. Schunk and J Greene (Eds) Handbook of self-regulation of learning and performance, Routledge. 155–172.

Google Scholar

De Corte, E., Verschaffel, L., and Eynde, P. (2000). Self-regulation: A characteristic and a goal of mathematics education. In M. Boekaerts, P. Pintrich, and M. Zeidner (Eds) Handbook of self-regulation (Academic Press), 687–726.

Google Scholar

Donker, A. S., De Boer, H., Kostons, D., Van Ewijk, C. D., and van der Werf, M. P. (2014). Effectiveness of learning strategy instruction on academic performance: a meta-analysis. Educ. Res. Rev. 11, 1–26. doi: 10.1016/j.edurev.2013.11.002

Crossref Full Text | Google Scholar

Ellis, J., Fosdick, B. K., and Rasmussen, C. (2016). Women 1.5 times more likely to leave STEM pipeline after calculus compared to men: Lack of mathematical confidence a potential culprit. PloS one, 11, e0157447.

Google Scholar

Flavell, J. H. (1979). Metacognition and cognitive monitoring: a new area of cognitive–developmental inquiry. Am. Psychol. 34, 906–911. doi: 10.1037/0003-066X.34.10.906

Crossref Full Text | Google Scholar

Gallagher, K., and Infante, N. E. (2022). A case study of undergraduates’ proving behaviors and uses of visual representations in identification of key ideas in topology. Int. J. Res. Undergrad. Math. Educ. 8, 176–210. doi: 10.1007/s40753-021-00149-6

Crossref Full Text | Google Scholar

Garofalo, J., and Lester, F. K. (1985). Metacognition, cognitive monitoring, and mathematical performance. J. Res. Math. Educ. 16, 163–176. doi: 10.2307/748391

Crossref Full Text | Google Scholar

Granberg, C. (2016). Discovering and addressing errors during mathematics problem-solving—a productive struggle? J. Math. Behav. 42, 33–48. doi: 10.1016/j.jmathb.2016.02.002

Crossref Full Text | Google Scholar

Herriott, S. R., and Dunbar, S. R. (2009). Who takes college algebra? Primus 19, 74–87. doi: 10.1080/10511970701573441

Crossref Full Text | Google Scholar

Hodges, L. C., Beall, L. C., Anderson, E. C., Carpenter, T. S., Cui, L., Feeser, E., et al. (2020). Effect of exam wrappers on student achievement in multiple, large STEM courses. J. Coll. Sci. Teach. 50, 69–79. doi: 10.1080/0047231X.2020.12290677

Crossref Full Text | Google Scholar

Kapur, M. (2014). Productive failure in learning math. Cogn. Sci. 38, 1008–1022. doi: 10.1111/cogs.12107

Crossref Full Text | Google Scholar

Koriakin, T., White, E., Breaux, K. C., DeBiase, E., O’Brien, R., Howell, M., et al. (2017). Patterns of cognitive strengths and weaknesses and relationships to math errors. J. Psychoeduc. Assess. 35, 155–167. doi: 10.1177/0734282916669909

Crossref Full Text | Google Scholar

Kyaruzi, F., Strijbos, J. W., and Ufer, S. (2020). Impact of a short-term professional development teacher training on students’ perceptions and use of errors in mathematics learning. Front. Educ. 5:559122. doi: 10.3389/feduc.2020.559122

Crossref Full Text | Google Scholar

Lerch, C. M. (2004). Control decisions and personal beliefs: their effect on solving mathematical problems. J. Math. Behav. 23, 21–36. doi: 10.1016/j.jmathb.2003.12.002

Crossref Full Text | Google Scholar

Mairing, J. P. (2017). Thinking process of naive problem solvers to solve mathematical problems. Int. Educ. Stud. 10, 1–11. doi: 10.5539/ies.v10n1p1

Crossref Full Text | Google Scholar

McGuire, S., McGuire, S. Y., and Angelo, T. (2015). Teach students how to learn: Strategies you can incorporate into any course to improve student metacognition, study skills, and motivation. New York: Routledge.

Google Scholar

Metcalfe, J. (2017). Learning from errors. Annu. Rev. Psychol. 68, 465–489. doi: 10.1146/annurev-psych-010416-044022

PubMed Abstract | Crossref Full Text | Google Scholar

Ohtani, K., and Hisasaka, T. (2018). Beyond intelligence: a meta-analytic review of the relationship among metacognition, intelligence, and academic performance. Metacogn. Learn. 13, 179–212. doi: 10.1007/s11409-018-9183-8

Crossref Full Text | Google Scholar

Ovadiya, T. (2023). Implementing theoretical intervention principles in teaching mathematics to struggling students to promote problem-solving skills. Int. J. Math. Educ. Sci. Technol. 54, 4–28. doi: 10.1080/0020739X.2021.1944682

Crossref Full Text | Google Scholar

Pilgrim, M., Burks, L., Hill-Lindsay, S., and Ryals, M. (2020). Links between Engagement in Self-Regulation and Performance. In S. S. Karunakaran, Z. Reed, and A. Higgins (Eds.), Proceedings of the twenty-third conference on research in undergraduate mathematics education: Boston, MA.

Google Scholar

Pintrich, P. R. (2000). “The role of goal orientation in self-regulated learning” in Handbook of self-regulation (Elsevier), 451–502.

Google Scholar

Pintrich, P. R., and De Groot, E. V. (1990). Motivational and self-regulated learning components of classroom academic performance. J. Educ. Psychol. 82, 33–40. doi: 10.1037/0022-0663.82.1.33

Crossref Full Text | Google Scholar

Polya, G., and Conway, J. H. (1957). How to solve it: a new aspect of mathematical method. Princeton, NJ: Princeton university press.

Google Scholar

Rushton, S. J. (2018). Teaching and learning mathematics through error analysis. Fields Math. Educ. J. 3, 1–12. doi: 10.1186/s40928-018-0009-y

Crossref Full Text | Google Scholar

Ryals, M., Hill-Lindsay, S., Burks, L., and Pilgrim, M. E.. (2020). Metacognition in college algebra: an analysis of “simple” mistakes. In S. S. Karunakaran, Z. Reed, and A. Higgins (Eds.), Proceedings of the twenty-third conference on research in undergraduate mathematics education: Boston, MA.

Google Scholar

Ryals, M, Hill-Lindsay, S., Burks, L., and Pilgrim, M. (2022). College Algebra Students\u0027 Definitions of Simple Mistakes through a Causal Attribution Lens. In S. S. Karunakaran and A. Higgins (Eds.), Proceedings of the twenty-fourth annual conference on research in undergraduate mathematics education: Boston, MA

Google Scholar

Sadler, P., and Sonnert, G. (2018). The path to college calculus: the impact of high school mathematics coursework. J. Res. Math. Educ. 49, 292–329. doi: 10.5951/jresematheduc.49.3.0292

Crossref Full Text | Google Scholar

Schneider, W., and Artelt, C. (2010). Metacognition and mathematics education. ZDM 42, 149–161. doi: 10.1007/s11858-010-0240-2

Crossref Full Text | Google Scholar

Schoenfeld, A. H. (1985). Mathematical problem solving. Cambridge Massachusetts: Academic Press.

Google Scholar

Schunk, D., and Zimmerman, B. J. (2012). “Self-regulation and learning” in Handbook of psychology. eds. W. Reynolds and G. Miller. 2nd ed (Hoboken, NJ: John Wiley & Sons, Inc.), 59–78.

Google Scholar

Seymour, E., and Hewitt, N. M. (1997). Talking about leaving. Boulder, CO: Westview Press.

Google Scholar

Seymour, E., Hunter, A. B., and Weston, T. J. (2019). Talking about leaving revisited: persistence, relocation, and loss in undergraduate STEM education. Cham: Springer International Publishing.

Google Scholar

Sitzmann, T., and Ely, K. (2010). Sometimes you need a reminder: the effects of prompting self-regulation on regulatory processes, learning, and attrition. J. Appl. Psychol. 95, 132–144. doi: 10.1037/a0018080

PubMed Abstract | Crossref Full Text | Google Scholar

Soicher, R. N., and Gurung, R. A. (2017). Do exam wrappers increase metacognition and performance? A single course intervention. Psychol. Learn. Teach. 16, 64–73. doi: 10.1177/1475725716661872

Crossref Full Text | Google Scholar

Toraman, C., Orakci, S., and Aktan, O. (2020). Analysis of the relationships between mathematics achievement, reflective thinking of problem solving and metacognitive awareness. Int. J. Progress. Educ. 16, 72–90. doi: 10.29329/ijpe.2020.241.6

Crossref Full Text | Google Scholar

Vadhan, V., and Stander, P. (1994). Metacognitive ability and test performance among college students. J. Psychol. 128, 307–309. doi: 10.1080/00223980.1994.9712733

Crossref Full Text | Google Scholar

Wickelgren, W. A. (2012). How to solve mathematical problems. New York: W. H. Freeman & Co Ltd.

Google Scholar

Zimmerman, B. J. (2002). Becoming a self-regulated learner: an overview. Theory Pract. 41, 64–70. doi: 10.1207/s15430421tip4102_2

Crossref Full Text | Google Scholar