The Association of Strategy Use and Concrete-Operational Thinking in Primary School

Concrete-operational thinking depicts an important aspect of cognitive development. A promising approach in promoting these skills is the instruction of strategies. The construction of such instructional programs requires insights into the mental operations involved in problem-solving. In the present paper, we address the question to which extent variations of the effect of isolated and combined mental operations (strategies) on correct solution of concrete-operational concepts can be observed. Therefore, a cross-sectional design was applied. The use of mental operations was measured by thinking-aloud reports from 80 first- and second-graders (N = 80) while solving tasks depicting concrete-operational thinking. Concrete-operational thinking was assessed using the subscales conservation of numbers, classification and sequences of the TEKO. The verbal reports were transcribed and coded with regard to the mental operations applied per task. Data analyses focused on tasks level, resulting in the analyses of N = 240 tasks per subscale. Differences regarding the contribution of isolated and combined mental operations (strategies) to correct solution were observed. Thereby, the results indicate the necessity of selection and integration of appropriate mental operations as strategies. The results offer insights in involved mental operations while solving concrete-operational tasks and depict a contribution to the construction of instructional programs.

Introduction

Concrete-Operational Thinking

The concrete-operational stage depicts an important step in the cognitive development of children (Piaget, 1947). According to Piaget, thinking in this stage is characterized by logical operations, such as conservation, reversibility or classification, allowing logical reasoning. These mental acts cannot be applied in hypothetical situations and are still limited to concrete situations. Therefore, concrete-operational thinking is examined using specific tasks depicting concrete-operational concepts. More recent research indicated that it might not be appropriate to assume a concrete-operational stage, but to examine concrete operations as specific and independent (Berzonsky, 1971; Winkelmann, 1975; Lourenco and Machado, 1996).

Nonetheless, concrete-operational thinking represents an important prerequisite of formal thinking (Inhelder and Piaget, 1958; Powell and Kalina, 2009). It is associated with a range of learning outcomes and academic achievement (Jordan and Brownlee, 1981; Hattie, 2009), such as maths fluency and maths achievement (conservation ability; Arlin, 1981; Cooper and Schleser, 2006; Ramos-Christian et al., 2008; Krajewski and Schneider, 2009; Wubbena, 2013; Lambert and Spinath, 2018), as well as reading comprehension and reading achievement (conservation and classification ability; Arlin, 1981; Cartwright, 2002; Colé et al., 2014; Cartwright et al., 2017). At the same time, differences in the ability of concrete-operational thinking become clear, as e.g., students with learning disabilities show lower levels of concrete-operational thinking than their peers (Wember, 1986; Riley, 1989; Fakouri, 1991).

The aforementioned differences led to questions concerning the trainability of concrete-operational thinking (Brainerd, 1983). Piaget himself, emphasized the constructivist nature of cognitive development and therefore pays less importance to the influence of third persons (Marchand, 2012). In contrast to this, more recent research highlights the importance of interaction between child and educators for developing cognitive competencies (Vygotskij and Cole, 1981; Fischer and Bidell, 2007). In this sense, when it comes to promoting the ability to solve concrete operational tasks, instructing the use of specific strategies has proven to be a successful means (Brainerd, 1983).

Strategy Use

Strategies are commonly specified as “goal-directed mental operations that are aimed at solving a problem” (Bjorklund, 2012, 265). Furthermore, they can be described as a sequence or a pattern of interdependent mental operations (Pressley and Hilden, 2006). The use of strategies is conscious, controllable and effortful (Pressley and Hilden, 2006; Shaffer and Kipp, 2010). Level and quality of strategy use is associated with a broad range of learning outcomes, e.g., achievement in reading (Hong-Nam et al., 2014; Cromley and Wills, 2016), science (Akyol et al., 2010; Deekens et al., 2017) and mathematics (Torbeyns et al., 2006; Askeland, 2012).

At the same time, similarly to differences in the ability of concrete-operational thinking, differences in the quality and quantity of strategy use arise. In addition to age-related differences (Siegler, 1996), students of the same age differ in their strategy use. In particular, children with learning disabilities show limited and inefficient strategy use in comparison to their peers (Pressley and Levin, 1987; Reid and Lienemann, 2006; Bosson et al., 2010). These interindividual differences are demonstrated in terms of strategy utilization and strategy production deficiencies (Miller and Seier, 1994; Shaffer and Kipp, 2010; Bjorklund, 2012). Utilization deficiency defines an absent benefit of appropriate strategies, whereas production deficiency is described as the failure to produce a strategy spontaneously (Miller and Seier, 1994; Schwenck et al., 2007; Bjorklund, 2012). Internal causes of such deficiencies include poor working memory, low metacognitive and declarative knowledge, and low intelligence (Clerc and Miller, 2013). The observed deficiencies can consequently be due to a range of factors, for example not having knowledge about the tasks and relevant strategies, not applying appropriate known strategies, not being able to adapt or integrate multiple known strategies, failing to inhibit earlier strategies, or not being motivated to use strategic approaches (Miller and Seier, 1994; Pressley and Hilden, 2006; Shaffer and Kipp, 2010).

Interventions aimed at promoting strategy use have proven to be successful (Belmont, 1989; Klauer, 2001; Pressley and Hilden, 2006; Reid and Lienemann, 2006; Bosson et al., 2010; Krawec et al., 2013). Strategy instruction proves to be beneficial to students' learning, as students show a higher level of performance, strategic activity and transfer (Fuchs et al., 2003; Bosson et al., 2010; Swanson et al., 2015). However, one important prerequisite for developing strategy instruction are insights into the mental operations involved while solving a specific task. Klauer (2001) argues that the analysis of the mental operations and strategies involved in successful problem solving is a key issue in developing instructional programs.

Strategy Use and Concrete-Operational Thinking

Fakouri (1991) describes difficulties of students with learning disabilities in solving concrete-operational concepts as a consequence of relying on the wrong strategies during problem-solving. Previous research has therefore addressed the question of the trainability of concrete-operational thinking by instructing cognitive strategies (Brainerd, 1983). However, insights in the involved problem-solving processes are a prerequisite for designing such strategy instruction. In addition to the described processes by Piaget (1947), more recent studies focused on describing the involved strategies in variations of concrete-operational thinking (e.g., conservation: Bellin, 1965; seriation: Fragaszy et al., 2002; classification: Freund et al., 1990; conservation: Kospentaris et al., 2011 class inclusion: Siegler and Svetina, 2006). These studies differ in various ways, such as the age of the participants, the specific tasks that were used and the grain of the identified strategies. Freund et al. (1990) could show, that 3- and 5-year-old children applied different strategies in problem-solving. At the same time, these strategies were unequally associated with the correct solution of classification tasks. Similarly, Fragaszy et al. (2002) describes a less frequent use of strategies during the wrong solution of seriation tasks of 1- and 2-year-old children. Chen et al. (2016) examined processing strategies on matrix completion strategies and could find a more frequent use of processing strategies of high-performing 5- and 6-year-old problem-solvers. These findings indicate that the correct solution of concrete-operational concepts might be explained by qualitative aspects as well as the frequency of the used strategic operations. These differences in strategy use can be expected, based on the described observations of utilization and production deficiencies (Miller and Seier, 1994; Bjorklund, 2012) and need to be considered when designing strategy instructions. So far, an overview about differences in the effectiveness of strategy use of primary-school children are still lacking. Insights in this age group might be of particular interest, as the transition from pre-operational to concrete-operational stage occurs in early primary school (Bjorklund, 2012). Börnert and Wilbert (2015) explored the strategy use of first and second graders when solving concrete-operational concepts. At the same time, this study did not emphasize differences in the effects of strategy use in the problem-solving processes.

Research Questions

Summarized, the use of specific strategies is of relevance for solving tasks representing concrete-operational thinking. Particularly children with learning disabilities might profit from the instruction of strategies, as they show limited and inefficient strategy use. One prerequisite for instructing strategies involves insight into the individual solving processes of a specific task. So far, information about successful strategies applied with regard to concrete-operational thinking is lacking. As strategies are defined as sets of mental operations, it seems necessary to gain insights into the entire strategy as well as into the components of strategies. The effectiveness of strategy use might be a consequence of knowing appropriate mental operations and combining them in an appropriate manner. Therefore, knowledge of the mental operations involved might contribute to the development of effective instruction. In the present study, we focus on shedding light on the influence of specific mental operations as well as of pattern of these operations (strategies) on the solution of tasks depicting concrete-operational thinking in primary school. We aim to identify successful strategies for approaching the relevant tasks, highlighting the differences in the effects of different strategies. Instead of focusing on differences between participants, we will emphasize differences between problem-solving processes. We assume that differences among the particular single or sets of mental operations applied during problem-solving (i.e., strategies) affecting the probability of successfully solving the tasks do exist (Figure 1). In summary, we pose the following three research question:

1. Is there a variation in the contribution of different mental operations to the successful solution of concrete-operational tasks?

FIGURE 1

Figure 1. Differing effects of isolated mental operations on correct solution.

It was hypothesized that there are different effects of the observed mental operations on the correct solution in the concrete-operational tasks.

As strategies are defined as a set of mental operations (Pressley and Hilden, 2006); this question can be extended to differing effects of patterns of mental operations on the solution of concrete-operational concepts.

2. Are certain strategies, hereby defined as a set of mental operations, observed more frequently than could be expected based on the individual frequency of the isolated mental operations?

We thereby hypothesized that certain patterns of strategic operations can be observed more frequently than would be expected. The expected frequency is calculated on the frequencies of the use of the individual, isolated mental operations, which depict the components of the respective patterns.

3. Are the identified commonly used sets of mental operations (strategies) associated with the correct solution of the tasks?

It was hypothesized that certain patterns of strategic operations are associated with the correct solution of the tasks.

Answering these research questions, might contribute to the identification of patterns of mental operations, being particularly helpful in solving the described tasks. Moreover, the results might offer insights into pitfalls of the use of mental operations, leading to an incorrect solution of the task. In addition to offering insights into these aspects, we want to provide a valid approach for targeting questions concerning the identification of cognitive processes, e.g., strategic activity, in children when developing instructional or diagnostic programs aimed at the promotion of strategic activity.

Methods

Participants

Eighty first- and second-grade students (76% second grade; 24% first grade) from seven primary schools in Brandenburg (federal state in Germany) participated in this study (N = 80). Just over half of all participants were female (54% female, 46% male). The average age of the participants was M = 7.1 (SD = 0.6) years. Six participants had a migration background (due to information supplied by the teacher). The classroom teachers reported no special educational needs for any participant.

Measures

Concrete-operational concepts were assessed using the subscales conservation, classification, and sequences of the TEKO (“Testbatterie zur Erfassung kognitiver Operationen”; Winkelmann, 1975), (see Figure 2 for task examples). The restest reliability of the implemented subscales ranges between 0.68 < rtt < 0.85. (Winkelmann, 1975). As described by Borst et al. (2012), number conservation tasks consist of two rows with an equal number of objects but which differ in the length of the rows. The tasks used in our study differ in the content of the rows as well as the numbers of objects. Classification tasks are similar to matrix completion tasks and take the form of boxes with 3 × 3 rows containing both a horizontal and a vertical property. One of the fields is empty and the participants are asked to determine the correct answer. These tasks require multiple classification processes. In sequences tasks, a series of three different balls pass through a winding tube and end up in a box. The participants need to identify the correct series of balls. Relational thinking is required to complete the tasks.

FIGURE 2

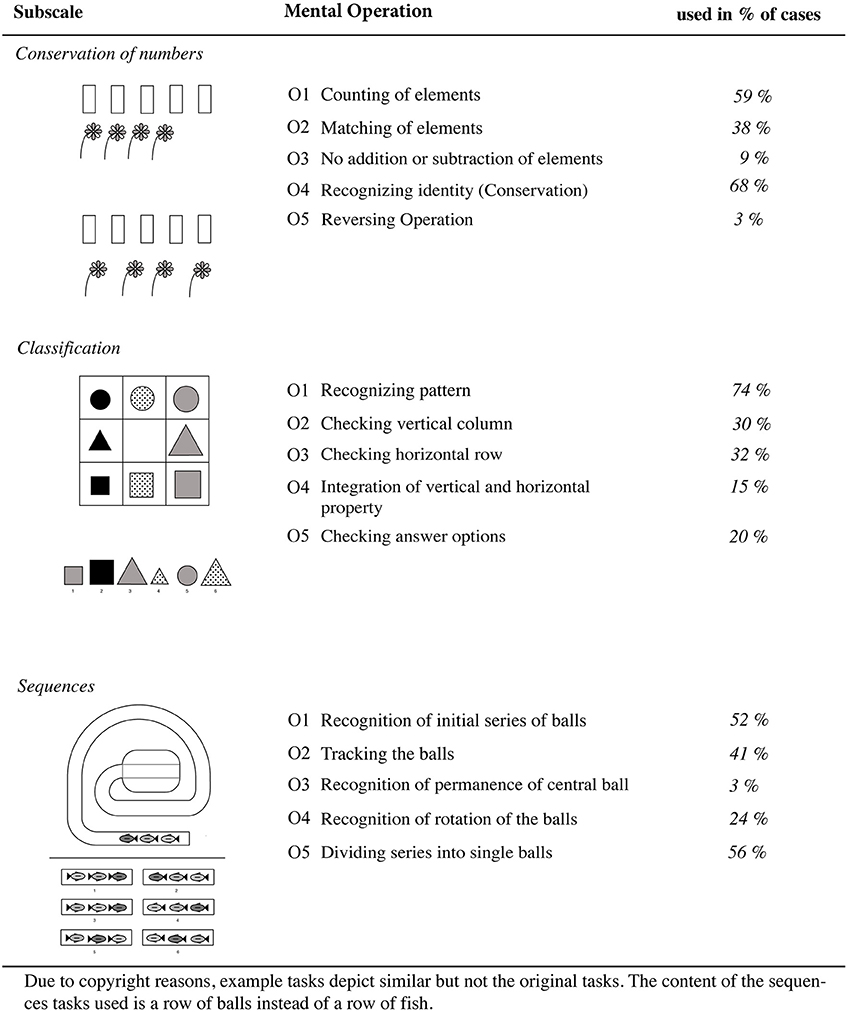
Figure 2. Overview of the subscales and use of related strategic operations in conservation, classification and sequences tasks.

Assessing strategic activity has proven to be a challenge, as it is referring to inner thought processes and can consequently not be observed directly. In research practice, different approaches are used to overcome this difficulty. Among others, collecting verbal data has proven to be promising in assessing inner thought processes (Ericsson and Simon, 1993). Especially on-line methods, summarized under the umbrella term of thinking aloud are discussed as possible methods allowing insights in thinking-processes (e.g., Bannert and Mengelkamp, 2008). Ericsson and Simon (1993) differentiate between different levels of thinking aloud (level 1: talk aloud; level 2: think aloud; level 3: reflect-when-prompted). At the same time, level 3 verbalizations seem to be more appropriate in the context of research with young children, as younger children might have difficulties verbalizing and may profit from prompts reminding them to verbalize. Level 3 verbalizations, however, has an impact on the involved cognitive processes as participants need to integrate the present information (Ericsson and Simon, 1993; Bannert and Mengelkamp, 2008). In contrast to the positive aspects of thinking-aloud methods, major critique arises concerning the completeness of verbal protocols. However, strategy use is mostly conscious, some aspects of problem-solving process might remain non-conscious and can therefore not be verbalized (Kihlstrom, 1987). This problem is supported by observations that some thinking activity is not expressed verbally, indicated by facial expression, non-verbal behavior or mumbling (Schellings et al., 2013). These aspects need to be considered in the transcription and coding process of the recorded verbal data (see Transcription and Coding). Nonetheless, thinking-aloud is a valid approach in assessing strategic activity.

In the light of the aforementioned information, strategy use was assessed using the reflect-when-prompted approach (Ericsson and Simon, 1993). Verbal reports are consequently transcribed and coded (see Figure 2 for an overview on the coded mental operations).

To control for the influence of intellectual abilities, cognitive abilities were measured using the CFT 20-R (Culture Fair Intelligence Test; Weiß, 2006). An adequate level of retest reliability (0.96) as well as of external validity (0.60–0.75) and construct validity are reported (Weiß, 2006). In addition, classroom teachers were asked to rate the students' current level of performance.

Procedure

Information on the study was sent out to 35 randomly selected schools, resulting in the participation of seven schools. Written informed consent of a parent or legal guardian was required for the children's participation in the study. The decision as to which and how many first- and second-grade classes should participate per school was made by the school representatives. The study was approved by the Federal Ministry of Education of Brandenburg (approval criteria: compliance with data protection regulations and educational relevance of research). Data collection was divided into two stages. In stage one, the intellectual abilities of all students were assessed using the CFT 20-R (Weiß, 2006). In stage two, students were interviewed individually and asked to solve concrete-operational tasks. In addition, students were instructed to verbalize their problem-solving process. The instruction was the following:

We are interested in how children solve these puzzles. Since we are not able to see what you are thinking and what is going on in your head, we need your help. Maybe you could say out loud every thought that comes to your mind while solving these tasks. I know that this is very difficult and even I find it hard to do that at times, but maybe you can do it. To support you, I will remind you to tell me what you are thinking. To get used to this, we are going to start with some example tasks.

As mentioned in the instruction, two tasks were solved in advance to familiarize the participants with the process of verbalizing. These tasks were taken from the Nobody is as smart as me program (“Keiner ist so schlau wie ich”; Marx et al., 2009), a German cognitive strategy training that addresses cognitive processes similar to the tasks of interest in this study.

Thereafter, the students solved three tasks from six subscales of the TEKO (Winkelmann, 1975), a German test battery assessing mastery of concrete-operational concepts. However, only the subscales conservation of numbers, classification and sequences were integrated in this study. These subscales are central concepts of the concrete-operational stage (Winkelmann, 1975) and are prerequisites to logical thinking (Woolfolk, 2014). Every task was instructed separately and the students were asked to verbalize their thoughts. If students struggled in the verbalization process, they were prompted to verbalize and were asked more specifically about their cognition.

All interviews were administered in a small room inside the schools during regular classes and recorded on video. Data were collected by the first author and pre-service teachers who were instructed in all procedures and instruments.

Transcription and Coding

In a first step, the recordings of the interviews were transcribed using the software MAXQDA 12 (VERBI Software, 2014). The average length of the videos was 18.01 min. Transcription was administered by three different student assistants after they were instructed in the transcription process and rules. In addition to verbal information, the students were asked to transcribe non-verbal activities of the participants (e.g., finger pointing, counting on fingers, and tilting or shaking the head).

In a second step, the transcripts were coded on the task level. Two external raters were invited for coder training. Following a three-step procedure proposed by Syed and Nelson (2015), a coding manual was introduced, randomly drawn sample data were provided for practice, and the coders' questions were clarified. The coding scheme contains mental operations used in the problem-solving process (see Figure 2). Following the definitions of strategies by Pressley and Hilden (2006) as well as Bjorklund (2012), operations are in this context defined as components of a strategy. Consequently, the used strategy is depicted by a pattern of coded operations. In this sense, a strategy, e.g., for solving classification tasks, might consist of multiple operations, such as e.g., firstly checking the columns, secondly checking the rows, thirdly combining both properties and eventually checking the answer options.

The coding scheme was developed inductively and validated by the authors in a pre-study (Börnert and Wilbert, 2015). In the pre-study, utterances of single students were assigned to a pre-existing or new category. During the development process, possible categories depicted either cognitive and task-specific or metacognitive operations (planning, self-control, self-reflection). In the study at hand, however, no metacognitive activity could be observed. The described operations are consequently specific for each subscale and were assigned only once for each task (operation used: yes/no). The category scheme consisted of the category, a description of the respective category and exemplary data.

To assess interrater agreement, 20% of the total recordings were coded by two raters until adequate interrater reliability was documented in the first coding step. Interrater agreement was fair to good for the reliability codings (two raters × transcripts of eight children ≈ 20% of total sample) (Cohen's kappa: K = 0.45–0.62; percentage agreement: P_A = 78–91). Afterwards, half of the remaining transcripts were assigned to each rater to complete the coding process.

Design

Data analyses focused on the task level instead of the subject level, that is, a data case consisted of one task rather than a person. Therefore, the total sample for data analyses is N = 240 (80 children × 3 tasks/subscale). The analyses were performed using the software R (R Core Team, 2016) and the packages lme4 (Bates et al., 2015) and confreq (Heine et al., 2015). In a first step, the data were analyzed on a descriptive level. In a second step, the research questions were addressed through different approaches.

Generalized Linear Mixed Model

To address the first research question regarding the individual contributions of single operations to the probability of finding the correct solution, we performed generalized linear mixed models (Cox, 1958) for all three subscales using a maximum-likelihood estimation method and logistically distributed error term.

The correctness of the problem solution was the outcome variable (dichotomous) and the strategic operations (each dichotomous: yes or no) were the predictor variables. In order to take care of the nested data structure (tasks in persons), multilevel models with random intercepts were applied. Therefore, differences among the participants in problem solving were taken into account. To estimate model validity, we compared the final models with candidate models with gender at the person level and a random intercept as predictors.

Configuration Frequency Analysis (CFA)

To answer the second and third research questions examining specific effects of combinations of mental operations, we chose a two-step approach. In a first step, we performed configuration frequency analysis (CFA) (Lienert, 1969). Types identify patterns or configurations of variables which occur more often than expected, whereas antitypes identify patterns that occur less often than expected (Stemmler, 2014). In a second step, we performed χ²-tests to examine whether the identified patterns were associated with correct solution of the task.

Results

Descriptive Statistics

An overview of the predefined mental operations can be found in Figure 2. For conservation tasks, the use of individual mental operations ranged between 3% (O5: reversing operation) and 68% (O4: recognizing identity). Only two mental operations were used in more than half of the verbalized problem-solving processes (O4: 68%; O1: 59%). In contrast, the mental operations O2 (matching of elements), O3 (no addition or subtraction of elements) and O5 were only used in less than a third of all problem-solving processes (O2: 37%; O3: 11%, O5: 3%). The results are similar for the subscale classification. Only mental operation O1 (recognizing pattern) was used in more than half of all relevant tasks (74%), while operations O2 to O5 were only applied in less than a third of all cases. A similar pattern can be found for sequences tasks. Mental operations O1 (recognition of initial series of balls: 52%) and O5 (dividing series into single balls: 56%) were used in more than half of the tasks, whereas operation O3 (recognition of permanence of central ball) was only applied in 3% of all tasks.

The average number of operations used per task in each subscale differs slightly between sequences, classification, and conservation tasks (1.75 < M < 1.79). Stronger differences become clear regarding the number of mental operations used per task within the same subscale (0.63 < SD < 0.90).

In addition, the rates of correct solution of the tasks vary across all subscales. The highest percentage of correct solutions can be found for the conservation tasks (84%), followed by classification (71%) and sequences tasks (61%). The sum of mental operations used per task is weakly associated with the correct solution (0.19 < r < 0.29).

The rates of correct solution of the three different tasks are only weakly associated (0.07 < r < 0.36). Similarly, the number of mental operations used per task is only weakly associated between the three tasks (0.11 < r < 0.23).

Research Question 1

Generalized mixed linear models were used to answer the first research question addressing the influence of mental operations on correctness of solution of the task (see Table 1). Intellectual abilities significantly predicted correctness of solution (Conservation: ß = 0.075, Std. Error: 0.023, p ≤ 0.01; Classification: ß = 0.089, Std. Error: 0.018, p ≤ 0.01; Sequences: ß = 0.098, Std. Error: 0.022, p ≤ 0.01). At the same time, intellectual abilities only significantly predicted the use of mental operations in classification and sequences tasks (Classification: ß = 0.015, Std. Error: 0.006, t = 2.34, p ≤ 0.05; Sequences: ß = 0.019, Std. Error: 0.008, t = 2.53 p ≤ 0.05).

TABLE 1

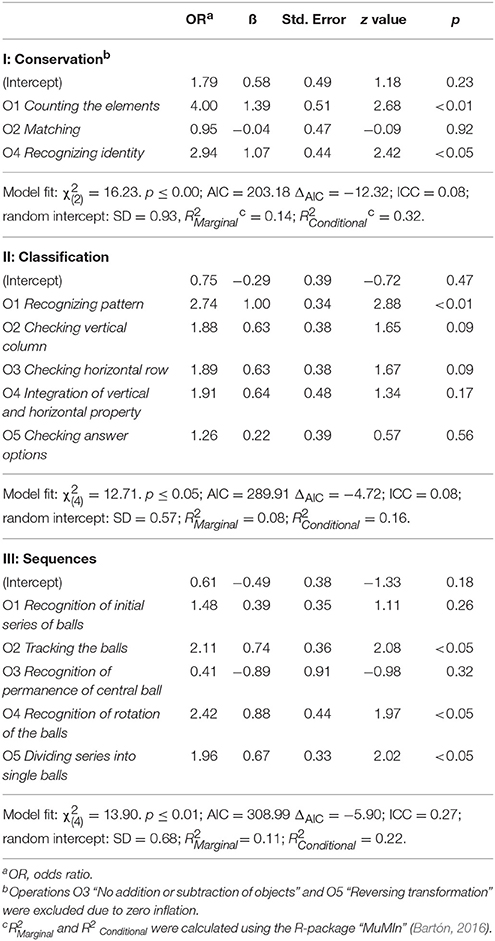
Table 1. Fixed effects of generalized linear mixed models describing the association of correct solution as a criterion and mental operations as predictors.

However, as this article focuses on the differences in strategic activity, these main effects do not preponderate. In addition, we controlled for the influence of gender, age, and school on the probability of correctness of solution. No significant main effects were identified. Therefore, the described models are reported without including school, gender, age or intellectual ability as covariates.

All the models described (see Table 1) show greater model fit in comparison to the candidate models considering only gender and subject, and are consequently more likely to minimize information loss [Model I Conservation: AIC = 203.18 Δ_AIC = −12.32, ${\chi }_{\left(2\right)}^2$ = 16.23. p ≤ 0.00; Model II Classification: AIC = 289.91 Δ_AIC = −4.72, ${\chi }_{\left(4\right)}^2$ = 12.71. p ≤ 0.05; Model III Sequences: AIC = 308.99 Δ_AIC = −5.90, ${\chi }_{\left(4\right)}^2$ = 13.90. p ≤ 0.01]. Differences regarding the isolated contribution of individual mental operations to finding the correct solution become clear.

In all described models, mental operations can be identified that have a positive effect on correct solution of the task. In conservation tasks (Model 1), it can be shown that the mental operation of counting the elements increases the probability of correct solution (O1; OR: 4.00; p ≤ 0.01). Likewise, the mental operation recognizing the identity (O4) has a positive effect on correct solution (OR: 2.94; p ≤ 0.05). In contrast, this effect cannot be found for matching the elements (O2; OR: 0.95; p = 0.92).

Similar results can be described for classification tasks (Model 2). The identified mental operations involved in solving classification tasks differ in their effect on the correct solution of the task as a dependent variable. Recognizing a pattern (O1) has a strong effect on correct solution (OR: 2.74; p ≤ 0.01). At the same time, Checking the vertical (M2; OR: 1.88; p = 0.09) and horizontal elements (O3; OR: 1.89; p = 0.09), as well as integrating both properties into a new element (O4; OR: 1.91; p = 0.17), increase the probability of correct solution; however, these effects are not significant.

In the sequences tasks (Model 3), similar observations can be made. Tracking the balls (O2; OR: 2.11, p ≤ 0.05), dividing the series of balls into single elements (O5; OR: 1.96, p ≤ 0.05), and recognizing the rotation of the balls (O4; OR: 2.42, p ≤ 0.05) each double the probability of a correct solution. In contrast, recognizing the initial series of balls has only few and non-significant effects on the probability of a correct solution (O1; OR: 1.48, p = 0.26). Using the mental operation of recognizing the permanence of the central ball (O3; OR: 0.41, p = 0.32) decreases the probability of correct solution.

Research Question 2

As the effects of the isolated operations depend on additional mental operations used, combinations or patterns of mental operations can be explored (see Table 2).

TABLE 2

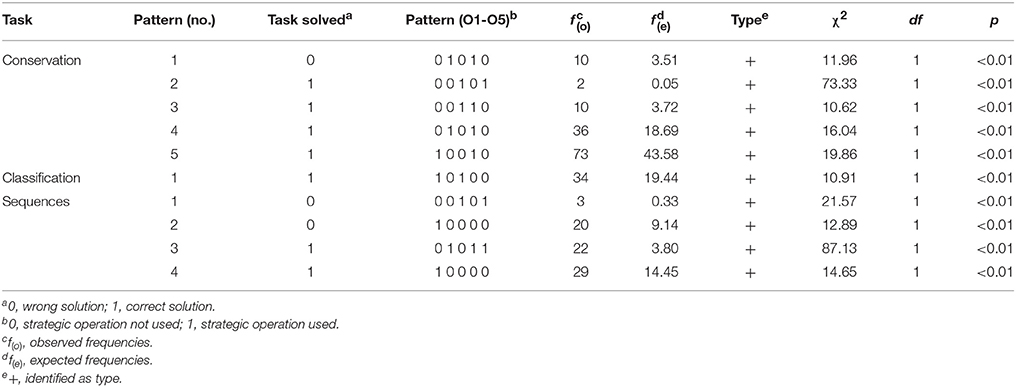
Table 2. Configural Frequency Analysis (CFA) and identified types in patterns of mental operations (strategies).

In conservation tasks, several patterns can be identified as types (i.e., occurring more frequently than expected based on the individual frequency of the isolated mental operations). The most frequent pattern co-occurring with the correct solution of conservation tasks is Pattern 5 [${\chi }_{\left(1\right)}^2$ = 19.86, p ≤ 0.01, f _(o) = 73]. This pattern comprises the operations counting the elements (O1) and recognizing the identity (O4). The frequency of Pattern 4 is also above chance [${\chi }_{\left(1\right)}^2$ = 16.04, p ≤ 0.01, f _(o) = 36]. It comprises matching the elements (O2) and, consequently, recognizing the identity (O4). However, Pattern 4 is also identified as a type co-occurring significantly often with the incorrect solution of conservation tasks [Pattern 1; ${\chi }_{\left(1\right)}^2$ = 11.96, p ≤ 0.01, f _(o) = 10]. In addition, three further models were identified as types; however, the observed frequencies are lower than 10% of the total analyzed patterns and are therefore not explained in detail at this point.

In classification tasks, only one pattern of mental operations could be identified as a type leading to correct solution of the tasks. This pattern comprises explicitly the checking of the horizontal row (O3) and the recognition of a pattern (O1) [Pattern 1; ${\chi }_{\left(1\right)}^2$ = 19.44, p ≤ 0.01, f _(o) = 34].

For the sequences tasks, two patterns of mental operations were identified as types co-occurring significantly often with a correct task solution. Pattern 3 [${\chi }_{\left(1\right)}^2$ = 87.13, p ≤ 0.01, f _(o) = 22] comprises dividing the series into single balls (O5), tracking the balls (O2), and thereby recognizing the rotation of the balls (O4). In contrast, solely the recognition of series of balls (O1) is identified as an ambivalent pattern, which significantly co-occurs with correct solutions [Pattern 4; ${\chi }_{\left(1\right)}^2$ = 14.65, p ≤ 0.01, f _(o) = 29] as well as incorrect solutions [Pattern 2; ${\chi }_{\left(1\right)}^2$ = 12.89, p ≤ 0.01, f _(o) = 20] to sequences tasks.

Research Question 3

To examine the third research question as to whether the patterns of strategic operations, identified as types, are significantly associated with the correct solution of the task, additional chi-square tests were performed for each pair of patterns (see Table 3). This step was necessary because in configural frequency analyses (CFA) only observed frequencies are compared with the expected frequencies of the same pattern and no assertion can be made with regard to differences between patterns. To gain additional insight into the benefit of a specific pattern, the distribution of the pattern associated with correct solution needs to be compared with the distribution of the same pattern associated with incorrect solution.

TABLE 3

Table 3. Association of identified patterns of mental operations (strategies) and correct solution.

In conservation tasks, only one pattern (Pattern 5) showed a significantly stronger association with the correct solution than the incorrect one [${\chi }_{\left(1\right)}^2$ = 8.22; p ≤ 0.01]. In classification tasks, no previously identified type showed a significantly stronger association with the correct solution than the incorrect one. In sequences tasks, only Pattern 3 was more strongly associated with the correct solution of the task than with the incorrect one [${\chi }_{\left(1\right)}^2$ = 8.64; p ≤ 0.01].

Discussion

The goal of the study at hand was to carve out differences regarding the influence of isolated and combined mental operations on the correct solution of concrete-operational tasks. Interestingly, only low associations between the different concrete-operational tasks could be described. This indicates, that it might be more appropriate to discuss concrete operations as specific competencies in comparison to associated facets of a concrete-operational stage.

As hypothesized, the use of strategic operations by the participants differs in terms of quantity, but most importantly in terms of the quality of the strategies used. Therefore, the assumption of existing differing effects of the used mental operations can be confirmed. Thereby, differences in the effect of isolated strategic operations become clear. Patterns of strategic operations co-occur frequently with correct solution of the specific concrete-operational tasks. At the same time, only few of these patterns were significantly stronger associated with the correct solution than the incorrect one. These observations can be made for conservation, classification, and sequences tasks.

Specifically, in conservation tasks, the operation O1 Counting the elements seems to be more effective than the operation O2 Matching. A possible explanation might be that matching is prone to an erroneous allocation of both elements. Use of counting as a strategic approach might result in a more robust performance. In sequences tasks, O2 tracking the balls is particular effective. This might be a consequence of the aspect, that the design of the task requires noticing the rotation of the balls. Tracking the balls most likely leads to the perception of the rotation. O5 Dividing the series into single balls might contribute to this effect, as this helps the participants to focus on the single elements and therefore decreases cognitive load. In classification tasks, the nature of the differing effects is not as clear, at the same time, differences in the effect are not as strong as in the other tasks. At least, it seems to be of particular importance to realize that a pattern is existing and that this pattern has to be assessed and integrated.

From a more general point of view, one possible explanation for the observed variation in the effect of mental operations may be based on utilization deficiencies in strategy use (Miller and Seier, 1994; Bjorklund, 2012). Children might produce an appropriate mental operation; however, this mental operation could lack efficiency and show no increase in task performance. Moreover, as the participants are not experienced in the use of certain strategies, it might demand more effort to produce an effective strategy than it would take for older peers (Miller and Seier, 1994). In addition, certain mental operations decrease the probability of finding a correct solution (e.g., O2 Matching in conservation tasks; O3 recognition of permanence of central ball in sequences tasks). In this context, neo-Piagetian approaches (Houdee and Guichart, 2001; Borst et al., 2012) emphasize processes of inhibiting incorrect mental operations as important aspects of cognitive development. Similarly, Stone et al. (2016) state that utilization deficiencies might be a consequence of individual differences in executive functions (such as inhibition and working memory). Clerc et al (2014) argue that executive functions and metacognition are influencing the transfer of strategy effectiveness.

Focusing on the frequency of the patterns identified, it becomes clear that these patterns include mental operations that are not effective when applied alone. Although not effective when used exclusively, these operations contribute to the successful solution of the task when integrated in a specific combination of mental operations. This goes in hand with the assumptions of Miller (2000) and Waters (2000), who argue that the change from partial to full strategy use is critical for strategy development. In this sense, the results support the assumptions of Miller and Seier (1994), who argue that the lack of integrating strategies might be an important cause of utilization deficiencies. Instructing children in strategy use, therefore, always needs to emphasize the possible integration of several mental operations instead of solely focusing on the promotion of isolated mental operations (e.g., in sequences tasks: O5 Dividing series into single balls, O2 Tracking the balls and O4 Recognition of rotation of the balls or in conservation tasks: O1 counting the elements and O4 recognizing identity).

At the same time, insights into the frequency of patterns of mental operations are limited, as some patterns co-occur simultaneously with incorrect solution of the task and cannot be identified as specifically associated with the correct solution. This might be due to some strategies being more effective if the tasks' characteristics do not require certain mental operations (e.g., in some sequences tasks, recognizing the rotation of the balls is necessary, while in some it is not). Therefore, patterns of mental operations not including recognition of the rotation might only be effective in the proportion of tasks described above.

Limitations

Although important insights into the mental processes involved in solving the relevant tasks can be described, the present paper shows some major limitations. Firstly, the use of verbalizations for identifying strategy use needs to be discussed with regard to the completeness of information. The ability to verbalize varies among individuals, and some children might not be able to express their thoughts and cognition. Although the authors tried to prevent this situation by carefully introducing the procedure with the help of example tasks, the risk of non-verbalized cognition cannot be ruled out.

Secondly, Pressley and Hilden (2006) argue that children might discover new strategies by performing the tasks. These strategies might lack effectiveness, as they are not practiced. Some identified strategies, therefore, might be more effective when practiced frequently. Consequently, their effect might be underestimated in this study.

Thirdly, the chronological sequence of the mental operations used might also be an important feature of appropriate strategy use. Although we analyzed patterns of mental operations, we did not take the temporal order into account. Future studies should therefore pay respect to this important aspect of strategy use. In addition, problems in strategy use for concrete-operational concepts cannot be generalized to other domains.

Conclusions

The results do offer some important insights into the strategic processes involved in solving concrete-operational tasks. These insights can be used for the construction of instructional programs aimed at the promotion of concrete-operational thinking. These programs should consider that effective strategy use is a consequence not only of one effective mental operation, but rather of a pattern of well-integrated mental operations. The results offer some hints about which patterns could be particularly helpful or misleading in solving concrete-operational concepts. The necessity of instructing strategy use becomes clear, as a range of participants did not show adequate and successful strategic activity.

At the same time, it can be stated that the chosen approach identifying valid and effective strategies is promising and might be transferred to various domains and concepts. It might serve as an example for an evidence-driven construction of instructional or diagnostic approaches aimed at the systematic promotion of strategic activity, such as dynamic testing (Sternberg and Grigorenko, 2002; Resing et al., 2012).

Ethics Statement

The study was approved by and carried out in accordance with the recommendations of the Federal Ministry of Education of Brandenburg (Germany) (approval criteria: compliance with data protection regulations and educational relevance of research). Written and informed consent was obtained from the parents/legal guardians of all research participants.

Author Contributions

MB-R designed the study, did the acquisition of the sample and the analyses of the data; he wrote the manuscript; JW provided general and scientific support for the conception, method as well as interpretation of this study; he gave important recommendations for data analysis; he assisted with the writing of the manuscript and revised it critically. All authors approved the final version to be published.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Lynn Scherreiks, Josephine Gutsche, Isabell Augustin and Pawel R. Kulawiak for assistance with data collection. We acknowledge the support of the Deutsche Forschungsgemeinschaft and Open Access Publishing Fund of University of Potsdam.

References

Akyol, G., Sungur, S., and Tekkaya, C. (2010). The contribution of cognitive and metacognitive strategy use to students' science achievement. Educ. Res. Eval. 16, 1–21. doi: 10.1080/13803611003672348

CrossRef Full Text | Google Scholar

Arlin, P. K. (1981). Piagetian tasks as predictors of reading and math readiness in grades K−2. J. Educ. Psychol. 73, 712–721. doi: 10.1037/0022-0663.73.5.712

CrossRef Full Text | Google Scholar

Askeland, M. (2012). Sound-based strategy training in multiplication. Eur. J. Spec. Needs Educ. 27, 201–217. doi: 10.1080/08856257.2012.669110

CrossRef Full Text | Google Scholar

Bannert, M., and Mengelkamp, C. (2008). Assessment of metacognitive skills by means of instruction to think aloud and reflect when prompted. Does the verbalisation method affect learning? Metacogn. Learn. 3, 39–58. doi: 10.1007/s11409-007-9009-6

CrossRef Full Text | Google Scholar

Bartón, K. (2016). MuMin: Multi-Model Inference. R Package Version 1.4. Available online at: https://CRAN.R-project.org/package=MuMIn

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting linear mixed-effects models using lme4. J. Stat. Softw. 67. doi: 10.18637/jss.v067.i01

CrossRef Full Text | Google Scholar

Bellin, H. (1965). Learning and operational convergence in logical thought development. J. Exp. Child Psychol. 2, 317–339. doi: 10.1016/0022-0965(65)90019-6

CrossRef Full Text | Google Scholar

Belmont, J. M. (1989). Cognitive strategies and strategic learning: the socio-instructional approach. Am. Psychol. 44, 142–148. doi: 10.1037/0003-066X.44.2.142

PubMed Abstract | CrossRef Full Text | Google Scholar

Berzonsky, M. D. (1971). Interdependence of Inhelder and Piaget's model of logical thinking. Dev. Psychol. 4, 469–476.

Google Scholar

Bjorklund, D. F. (2012). Children's Thinking: Cognitive Development and Individual Differences. Belmont, CA: Wadsworth/Cengage Learning.

Google Scholar

Börnert, M., and Wilbert, J. (2015). Thinking-aloud protocols of piagetian tasks: insights into problem-solving processes of primary school students. Insights Learn. Disabil. 12, 19–34.

Borst, G., Poirel, N., Pineau, A., Cassotti, M., and Houdé, O. (2012). Inhibitory control in number-conservation and class-inclusion tasks: a neo-Piagetian inter-task priming study. Cogn. Dev. 27, 283–298. doi: 10.1016/j.cogdev.2012.02.004

CrossRef Full Text | Google Scholar

Bosson, M. S., Hessels, M. G. P., Hessels-Schlatter, C., Berger, J.-L., Kipfer, N. M., and Büchel, F. P. (2010). Strategy acquisition by children with general learning difficulties through metacognitive training. Aust. J. Learn. Difficult. 15, 13–34. doi: 10.1080/19404150903524523

CrossRef Full Text | Google Scholar

Brainerd, C. J. (1983). “Varieties of strategy training in piagetian concept learning,” in Cognitive Strategy Research, eds M. Pressley and J. R. Levin (New York, NY: Springer), 3–27.

Google Scholar

Cartwright, K. B. (2002). Cognitive development and reading: the relation of reading-specific multiple classification skill to reading comprehension in elementary school children. J. Educ. Psychol. 94, 56–63. doi: 10.1037/0022-0663.94.1.56

CrossRef Full Text | Google Scholar

Cartwright, K. B., Coppage, E. A., Lane, A. B., Singleton, T., Marshall, T. R., and Bentivegna, C. (2017). Cognitive flexibility deficits in children with specific reading comprehension difficulties. Contemp. Educ. Psychol. 50, 33–44. doi: 10.1016/j.cedpsych.2016.01.003

CrossRef Full Text | Google Scholar

Chen, Z., Honomichl, R., Kennedy, D., and Tan, E. (2016). Aiming to complete the matrix: eye-movement analysis of processing strategies in children's relational thinking. Dev. Psychol. 52, 867–878. doi: 10.1037/dev0000113

PubMed Abstract | CrossRef Full Text | Google Scholar

Clerc, J., and Miller, P. H. (2013). Utilization deficiencies and transfer of strategies in preschoolers. Cogn. Dev. 28, 76–93. doi: 10.1016/j.cogdev.2012.09.003

CrossRef Full Text | Google Scholar

Clerc, J., Miller, P. H., and Cosnefroy, L. (2014). Young children's transfer of strategies: utilization deficiencies, executive function, and metacognition. Dev. Rev. 34, 378–393. doi: 10.1016/j.dr.2014.10.002

CrossRef Full Text | Google Scholar

Colé, P., Duncan, L. G., and Blaye, A. (2014). Cognitive flexibility predicts early reading skills. Front. Psychol. 5:565. doi: 10.3389/fpsyg.2014.00565

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooper, J. A., and Schleser, R. (2006). Closing the achievement gap: examining the role of cognitive developmental level in academic achievement. Early Child. Educ. J. 33, 301–306. doi: 10.1007/s10643-006-0075-1

CrossRef Full Text | Google Scholar

Cox, D. R. (1958). The regression analysis of binary sequences. J. R. Stat. Soc. Ser. B Methodol. 20, 215–242.

Google Scholar

Cromley, J. G., and Wills, T. W. (2016). Flexible strategy use by students who learn much versus little from text: transitions within think-aloud protocols. J. Res. Read. 39, 50–71. doi: 10.1111/1467-9817.12026

CrossRef Full Text | Google Scholar

Deekens, V. M., Greene, J. A., and Lobczowski, N. G. (2017). Monitoring and depth of strategy use in computer-based learning environments for science and history. Br. J. Educ. Psychol. 88, 63–79. doi: 10.1111/bjep.12174

PubMed Abstract | CrossRef Full Text | Google Scholar

Ericsson, K. A., and Simon, H. A. (1993). Verbal Reports as Data (Rev.Edn). Cambridge, MA: MIT Press.

Fakouri, M. E. (1991). Learning disabilities: a piagetian perspective. Psychol. Sch. 28, 70–76. doi: 10.1002/1520-6807(199101)28:13.0.CO;2-7

CrossRef Full Text | Google Scholar

Fischer, K. W., and Bidell, T. R. (2007). “Dynamic development of action and thought,” in Handbook of Child Psychology, eds W. Damon and R. M. Lerner (Hoboken, NJ: John Wiley & Sons, Inc.).

Google Scholar

Fragaszy, D. M., Galloway, A. T., Johnson-Pynn, J., and Brakke, K. (2002). The sources of skill in seriating cups in children, monkeys and apes. Dev. Sci. 5, 118–131. doi: 10.1111/1467-7687.00216

CrossRef Full Text | Google Scholar

Freund, L. S., Baker, L., and Sonnenschein, S. (1990). Developmental changes in strategic approaches to classification. J. Exp. Child Psychol. 49, 343–362. doi: 10.1016/0022-0965(90)90064-F

CrossRef Full Text | Google Scholar

Fuchs, L. S., Fuchs, D., Prentice, K., Burch, M., Hamlett, C. L., Owen, R., et al. (2003). Explicitly teaching for transfer: effects on third-grade students' mathematical problem solving. J. Educ. Psychol. 95, 293–305. doi: 10.1037/0022-0663.95.2.293

CrossRef Full Text | Google Scholar

Hattie, J. (2009). Visible Learning: A Synthesis of Over 800 Meta-Analyses Relating to Achievement. London; New York, NY: Routledge.

Heine, J. H., Alexandrowicz, R. W., and Stemmler, M. (2015). confreq: Configural Frequencies Analysis Using Log-Linear Modeling. R package version 1.4. Available online at: https://CRAN.R-project.org/package=confreq

Hong-Nam, K., Leavell, A. G., and Maher, S. (2014). The relationships among reported strategy use, metacognitive awareness, and reading achievement of high school students. Read. Psychol. 35, 762–790. doi: 10.1080/02702711.2013.807900

CrossRef Full Text | Google Scholar

Houdee, O., and Guichart, E. (2001). Negative priming effect after inhibition of number/length interference in a Piaget-like task. Dev. Sci. 4, 119–123. doi: 10.1111/1467-7687.00156

CrossRef Full Text | Google Scholar

Inhelder, B., and Piaget, J. (1958). The Growth of Logical Thinking: From Childhood to Adolescence. New York, NY: Basic Books.

Jordan, V. B., and Brownlee (1981). Meta-Analysis of the Relationship Between Piagetian and School Achievement Tests. Los Angeles, CA: American Educational Research Association.

Kihlstrom, J. (1987). The cognitive unconscious. Science 237, 1445–1452. doi: 10.1126/science.3629249

PubMed Abstract | CrossRef Full Text | Google Scholar

Klauer, K. J. (2001). Handbuch kognitives Training. 2., ed.überarb. und erw. Aufl. Göttingen: Hogrefe.

Kospentaris, G., Spyrou, P., and Lappas, D. (2011). Exploring students' strategies in area conservation geometrical tasks. Educ. Stud. Math. 77, 105–127. doi: 10.1007/s10649-011-9303-8

CrossRef Full Text | Google Scholar

Krajewski, K., and Schneider, W. (2009). Early development of quantity to number-word linkage as a precursor of mathematical school achievement and mathematical difficulties: findings from a four-year longitudinal study. Learn. Instr. 19, 513–526. doi: 10.1016/j.learninstruc.2008.10.002

CrossRef Full Text | Google Scholar

Krawec, J., Huang, J., Montague, M., Kressler, B., and Melia de Alba, A. (2013). The effects of cognitive strategy instruction on knowledge of math problem-solving processes of middle school students with learning disabilities. Learn. Disabil. Q. 36, 80–92. doi: 10.1177/0731948712463368

CrossRef Full Text | Google Scholar

Lambert, K., and Spinath, B. (2018). Conservation abilities, visuospatial skills, and numerosity processing speed: association with math achievement and math difficulties in elementary school children. J. Learn. Disabil. 51, 223–235. doi: 10.1177/0022219417690354

PubMed Abstract | CrossRef Full Text | Google Scholar

Lienert, G. A. (1969). “Die Konfigurationsfrequenzanalyse als Klassifikationsmethode in der klinischen Psychologie [Configural frequency analysis as a classification method in clinical psychology],” in Bericht über den 26. Kongress der Deutschen Gesellschaft für Psychologie in Tübingen 1968, ed M. Irle (Göttingen: Hogrefe), 244–253.

Lourenco, O., and Machado, A. (1996). In defense of piaget's theory: a reply to 10 common criticisms. Psychol. Rev. 103, 143–164. doi: 10.1037/0033-295X.103.1.143

CrossRef Full Text | Google Scholar

Marchand, H. (2012). Contributions of Piagetian and post-Piagetian theories to education. Educ. Res. Rev. 7, 165–176. doi: 10.1016/j.edurev.2012.04.002

CrossRef Full Text | Google Scholar

Marx, E., Bleyenberg, M., and Klauer, K. J. (2009). Keiner ist so schlau wie ich. Ein Förderprogramm für Kinder ab vier Jahren. Göttingen: Vandenhoeck and Ruprecht.

Miller, P. H. (2000). How best to utilize a deficiency. Child Dev. 71, 1013–1017. doi: 10.1111/1467-8624.00205

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller, P. H., and Seier, W. L. (1994). Strategy utilization deficiencies in children: when, where, and why. Adv. Child Dev. Behav. 25, 107–156. doi: 10.1016/S0065-2407(08)60051-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Piaget, J. (1947). The Psychology of Intelligence. Abingdon: Taylor and Francis.

Powell, K. C., and Kalina, C. J. (2009). Cognitive and social constructivism: developing tools for an effective classroom. Education 130, 241–250.

Google Scholar

Pressley, M., and Hilden, K. (2006). “Cognitive strategies,” in Handbook of Child Psychology, eds W. Damon and R. M. Lerner (Hoboken, NJ: John Wiley and Sons), 511–556.

Google Scholar

Pressley, M., and Levin, J. R. (1987). “Elaborative learning strategies for the inefficient learner,” in Handbook of Cognitive, Social, and Neuropsychological Aspects of Learning Disabilities, ed S. J. Ceci (Hillsdale, NJ: Lawrence Erlbaum Associates), 175–212.

Google Scholar

Ramos-Christian, V., Schleser, R., and Varn, M. E. (2008). Math fluency: accuracy versus speed in preoperational and concrete operational first and second grade children. Early Child. Educ. J. 35, 543–549. doi: 10.1007/s10643-008-0234-7

CrossRef Full Text | Google Scholar

R Core Team (2016). R: A Language and Environment for Statistical Computing. Vienna, Austria Available online at: https://www.R-project.org

Reid, R., and Lienemann, T. O. (2006). Strategy Instruction for Students With Learning Disabilities. New York, NY: Guilford Press.

Resing, W. C. M., Xenidou-Dervou, I., Steijn, W. M. P., and Elliott, J. G. (2012). A “picture” of children's potential for learning: looking into strategy changes and working memory by dynamic testing. Learn. Individ. Differ. 22, 144–150. doi: 10.1016/j.lindif.2011.11.002

CrossRef Full Text | Google Scholar

Riley, N. J. (1989). Piagetian cognitive functioning in students with learning disabilities. J. Learn. Disabil. 22, 444–451. doi: 10.1177/002221948902200710

PubMed Abstract | CrossRef Full Text | Google Scholar

Schellings, G. L., van Hout-Wolters, B. H., Veenman, M. V., and Meijer, J. (2013). Assessing metacognitive activities: the in-depth comparison of a task-specific questionnaire with think-aloud protocols. Eur. J. Psychol. Educ. 28, 963–990. doi: 10.1007/s10212-012-0149-y

CrossRef Full Text | Google Scholar

Schwenck, C., Bjorklund, D. F., and Schneider, W. (2007). Factors influencing the incidence of utilization deficiencies and other patterns of recall/strategy-use relations in a strategic memory task. Child Dev. 78, 1771–1787. doi: 10.1111/j.1467-8624.2007.01090.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Shaffer, D. R., and Kipp, K. (2010). Developmental Psychology: Childhood and Adolescence, 8th Edn. Belmont, CA: Wadsworth Cengage Learning.

Siegler, R. S. (1996). Emerging Minds: The Process of Change in Children's Thinking. New York, NY: Oxford University Press.

Siegler, R. S., and Svetina, M. (2006). What leads children to adopt new strategies? a microgenetic/cross-sectional study of class inclusion. Child Dev. 77, 997–1015. doi: 10.1111/j.1467-8624.2006.00915.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Stemmler, M. (2014). Person-Centered Methods: Configural Frequency Analysis (CFA) and Other Methods for the Analysis of Contingency Tables. Cham: Springer.

Sternberg, R. J., and Grigorenko, E. L. (2002). Dynamic Testing: The Nature and Measurement of Learning Potential. Cambridge: Cambridge University Press.

Stone, M. M., Blumberg, F. C., Blair, C., and Cancelli, A. A. (2016). The “EF” in deficiency: examining the linkages between executive function and the utilization deficiency observed in preschoolers. J. Exp. Child Psychol. 152, 367–375. doi: 10.1016/j.jecp.2016.07.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Swanson, H. L., Lussier, C. M., and Orosco, M. J. (2015). Cognitive strategies, Working memory, and growth in word problem solving in children with math difficulties. J. Learn. Disabil. 48, 339–358. doi: 10.1177/0022219413498771

PubMed Abstract | CrossRef Full Text | Google Scholar

Syed, M., and Nelson, S. C. (2015). Guidelines for establishing reliability when coding narrative data. Emerg. Adulthood 3, 375–387. doi: 10.1177/2167696815587648

CrossRef Full Text | Google Scholar

Torbeyns, J., Verschaffel, L., and Ghesquière, P. (2006). The development of children's adaptive expertise in the number domain 20 to 100. Cogn. Instr. 24, 439–465. doi: 10.1207/s1532690xci2404_2

CrossRef Full Text | Google Scholar

VERBI Software (2014). MAXQDA. Software für Qualitative Datenanalyse. Berlin: VERBI Software. Consult. Sozialforschung GmbH.

Vygotskij, L. S., and Cole, M. (1981). Mind in Society: The Development of Higher Psychological Processes. Nachdr. Cambridge, MA: Harvard University Press.

Google Scholar

Waters, H. S. (2000). Memory strategy development: do we need yet another deficiency? Child Dev. 71, 1004–1012. doi: 10.1111/1467-8624.00204

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiß, R. H. (2006). CFT 20-R Grundintelligenztest Skala 2. Göttingen: Hogrefe.

Wember, F. B. (1986). Piagets Bedeutung für die Lernbehindertenpädagogik - Untersuchungen zur Kognitiven Entwicklung und zum Schulischen Lernen bei Sonderschülern. Heidelberg: Edition Schindele.

Winkelmann, W. (1975). Testbatterie zur Erfassung kognitiver Operationen (TEKO). Braunschweig: Westermann.

Woolfolk, A. (2014). Pädagogische Psychologie [Educational Psychology]. Hallbergmoos: Pearson.

Wubbena, Z. C. (2013). Mathematical fluency as a function of conservation ability in young children. Learn. Individ. Differ. 26, 153–155. doi: 10.1016/j.lindif.2013.01.013

CrossRef Full Text | Google Scholar