Phase behavior analysis of methane confined in nanopores using molecular simulation

Interest in the phase behavior of hydrocarbons in shale reservoirs has grown in recent years. Petroleum fluid phase behavior has been observed to differ significantly between conventional reservoirs and shale reservoirs. Within shale reservoirs, notable surface-fluid interactions can lead to non-uniform molecule distribution and an alteration in fluid phase behavior, primarily caused by the existence of nano-scale porous materials. In this work, we study the phase behavior of methane in single cylindrical pore models. We apply the gauge Gibbs ensemble Monte Carlo (gauge-GEMC) simulation technique to investigate the phase behavior of methane in 4–10 nm single nanopores and calculate the saturation pressures at various temperatures using the grand canonical Monte Carlo (GCMC) simulation technique. A shift in the phase diagram has been found for methane in nanopores. As pore size decreases, the shift becomes more significant.

1 Introduction

The phase behavior study of reservoir fluids in shale reservoirs faces many challenges. A main challenge is to quantify the effects of surface-fluid interactions on the phase behavior of reservoir fluids. Shale formations encompass pores ranging in size from less than 10 nm to great than 100 nm (Clarkson et al., 2013; Zhu et al., 2021), in which a large portion of pore volume are occupied by pores smaller than 50 nm. In macropores, which have diameters exceeding 50 nm, reservoir fluids exist in a bulk state. In this regime, the influence of interactions between the pore surface and reservoir fluids (surface–fluid interactions) is minimal compared to the interactions between the reservoir fluids themselves (fluid–fluid interactions). Several equations of state, for example, Peng–Robinson equation of state (Peng and Robinson, 1976; Bi et al., 2020a; Bi et al., 2020b) and Soave–Redlich–Kwong equation of state (Soave, 1972), have been proposed in past decades. Traditional equations of state do not consider surface–fluid interactions, but they are suitable for accurately describing the phase behavior of reservoir fluids in bulk conditions. Nonetheless, within the mesopores (with diameters between 2 and 50 nm) and micropores (with diameters less than 2 nm) (Rouquerolt et al., 1994), where the pore dimensions closely match those of the reservoir fluid molecules, the interactions between the surface and fluid take on great importance and prominence. This phenomenon can result in uneven dispersion of molecules and a shift in the phase diagram (Jin et al., 2017; Jin and Nasrabadi, 2018; Luo et al., 2018; Yang et al., 2019; Jin and Firoozabadi, 2016a; Li et al., 2019). The influences on reservoir fluids within mesopores and micropores are commonly referred to as confinement effects. These effects become increasingly pronounced as the size of the pores decreases.

Monte Carlo simulation, a statistical approach that relies on the modeling of interactions between atoms or molecules, has become a commonly employed technique for studying phase behavior in shale reservoirs in recent years (Jin and Firoozabadi, 2016a; Li et al., 2014; Singh et al., 2009; Jin and Firoozabadi, 2016b). The breadth of the Monte Carlo simulation has substantially expanded thanks to increased computer capacity. The Monte Carlo simulations offer a range of statistical ensembles, such as the canonical ensemble ($NVT$ ensemble), isothermal-isobaric ensemble ($NPT$ ensemble), grand canonical ensemble ($\mu VT$ ensemble), and Gibbs ensemble (either $NVT$ or $NPT$) (Ungerer et al., 2005). The GCMC simulation, which defines a system with a specified chemical potential, volume, and temperature, is a valuable technique for investigating adsorption isotherms and hysteresis in both pure-component and multi-component systems within mesopores and micropores (Rowley et al., 1975; Coasne et al., 2005; Libby and Monson, 2004). By modeling scenarios across a broad range of chemical potentials, researchers can determine the chemical potentials at which phase transitions occur. These values are then used to calculate the condensation and vaporization pressures during the adsorption and desorption processes, respectively. Panagiotopoulos (Panagiotopoulos, 1987) introduced the Gibbs ensemble Monte Carlo (GEMC) simulation for investigating phase equilibria. It comprises two variants: the one with a fixed global volume (NVT-GEMC) and the one with fixed pressure (NPT-GEMC). The key distinction between the GEMC and the $NVT$ or $NPT$ ensembles discussed earlier lies in the fact that GEMC involves two simulation boxes, where phases can be separated within each box. This approach eliminates the need to explicitly model the interface between phases, resulting in greater efficiency when computing phase equilibrium (Ungerer et al., 2005). The NVT-GEMC system is defined with constant number of molecules, total volume, and temperature. This method can be employed to study both pure-component fluids and mixtures (Panagiotopoulos, 1987; Neubauer et al., 1999; Smit et al., 1989; Pathak et al., 2017). Typically, the coexistence pressure is determined using the gas phase pressure. A more efficient version, the NVT-GEMC (gauge-GEMC), was developed by Neimark and Vishnyakov and has been successfully applied to pure and binary substances in confined systems (Neimark and Vishnyakov, 2000; Vishnyakov and Neimark, 2001; Vishnyakov and Neimark, 2009). The gauge-GEMC simulation involves two simulation boxes, with one acting as a gauge meter and the other representing the fluid system. The gauge meter box has the ability to control density fluctuations in the fluid system, allowing the fluid to exist in potentially unstable states (Jin and Nasrabadi, 2016).

In this work, the gauge-GEMC simulations are applied to investigate the phase behavior of methane in single-pore models. Temperature-density diagrams for methane in 4–10 nm nanopores are constructed. Additionally, for the first time, we use GCMC simulation to calculate the saturation pressures of methane at various temperatures in the nanopores. Combining with the critical temperatures determined using the gauge-GEMC simulations, for the first time, completed temperature-pressure phase diagrams for methane in the 4–10 nm nanopores are constructed. Significant alterations of saturation pressures and critical properties of methane in the nanopores are observed.

2 Methodology

2.1 Monte Carlo moves

Monte Carlo simulation is a statistical thermodynamics technique that derives properties of a system by taking into account the individual position and conformation of every molecule. To attain the equilibrium state of a system, millions of Monte Carlo steps are executed in the simulation to reach the global minimum of the free energy. During each Monte Carlo step, one of several Monte Carlo moves is attempted.

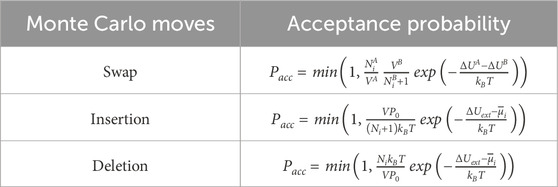
The most commonly used Monte Carlo moves are the translation move (center of mass), rotation move, and partial regrowth move. For the center of mass translation move, a molecule in the system is chosen randomly. The entire chosen molecule is then displaced a random distance in a random vector direction. The rotation move is to rotate a randomly chosen molecule by a random angle. In this move, the internal bond distances, bending angles, and torsion angles of the selected molecule are kept the same. In terms of the partial regrowth move, a random atom is chosen in a random molecule. Then, one end of the chosen atom is cut off and allowed to regrow at a randomly selected position. The new configuration (state) after a Monte Carlo move is accepted with a probability. The acceptance criterion for a move is:

$P_{acc}=\mathit{min}\left(1,\mathit{exp}\left(-\frac{1}{k_{B}T}\left(U_{new}-U_{old}\right)\right)\right),(1)$

where $P_{acc}$ is the acceptance probability, $k_B$ is the Boltzmann constant which equals $1.381\times {10}^{-23}$ J/K, $T$ is the temperature, and $U_{new}$ and $U_{old}$ are the potential energy of the new and the old configurations, respectively. The definition of the $P_{acc}$ indicates that if $U_{new}$ < $U_{old}$, in other words, $\mathit{exp}\left(-\frac{1}{k_{B}T}\left(U_{new}-U_{old}\right)\right)$ > 1, the Monte Carlo move and the new configuration are accepted. If $U_{new}$ > $U_{old}$ or $\mathit{exp}\left(-\frac{1}{k_{B}T}\left(U_{new}-U_{old}\right)\right)$ < 1, a random number q between 0 and 1 is generated. The Monte Carlo move and the new configuration are accepted only when $\mathit{exp}\left(-\frac{1}{k_{B}T}\left(U_{new}-U_{old}\right)\right)$ > q. If any of the above moves are rejected, the old configuration is recounted in the Markov chain of states.

Some Monte Carlo moves are applied to specific ensembles. For the ensembles that contain more than one simulation boxes (the GEMC and the gauge-GEMC), a swap move is implemented. The swap move is used to move a randomly chosen molecule in an arbitrary simulation box to the other simulation box. This move enables different phases within the system to attain an equal chemical potential for every molecule type (species of components). In terms of the GCMC ensemble, insertion and deletion moves are implemented. The insertion moves insert one type of molecule at a randomly selected position in the simulation box, while the deletion moves randomly delete one molecule of the selected type. It should be noted that, in a GCMC simulation, the attempts of insertion moves and the attempts of deletion moves should be equal. The acceptance probabilities of the specific moves are summarized in Table 1, where $P_{acc}$, $k_B$, $T$ are consistent with the definitions in Equation 1. $V$ is the volume, $∆U$ and $∆V$ represent the change of the potential energy and volume, respectively, and $N_i$ represents the number of type $i$ molecule. The acceptance probability of the swap move indicates that a type $i$ molecule is moved from simulation box A to box B. $U_{ext}$ in the acceptance probabilities of the insertion and deletion moves is the external potential energy (intermolecular energy from the interaction between molecules), and ${\overline{\mu }}_i={\mu }_i-{\mu }_{i0}$, where ${\mu }_{i0}$ is the chemical potential of a perfect gas of component $i$ under a reference pressure $P_0$ and $T$ (Ungerer et al., 2005).

Table 1

Table 1. Acceptance probabilities of the specific Monte Carlo moves.

2.2 Gauge-GEMC simulation

Gauge-GEMC is developed by Neimark and Vishnyakov (Neimark and Vishnyakov, 2000; Vishnyakov and Neimark, 2001; Vishnyakov and Neimark, 2009) based on the NVT-GEMC technique developed by Panagiotopoulos (Panagiotopoulos, 1987) previously. It is a prevalent technique for computing fluid properties at equilibrium (Jin et al., 2017; Vishnyakov and Neimark, 2001; Bi and Nasrabadi, 2019). The simulation involves two boxes: one represents the fluid system, while the other serves as a gauge meter (see Figure 1). The gauge-GEMC method preserves the benefits of the original NVT-GEMC technique, enabling the investigation of fluid phase equilibria without explicit surface modeling. Additionally, it effectively manages density fluctuations, enabling the fluid to exist in potentially unstable states (Ungerer et al., 2005; Jin and Nasrabadi, 2016).

Figure 1

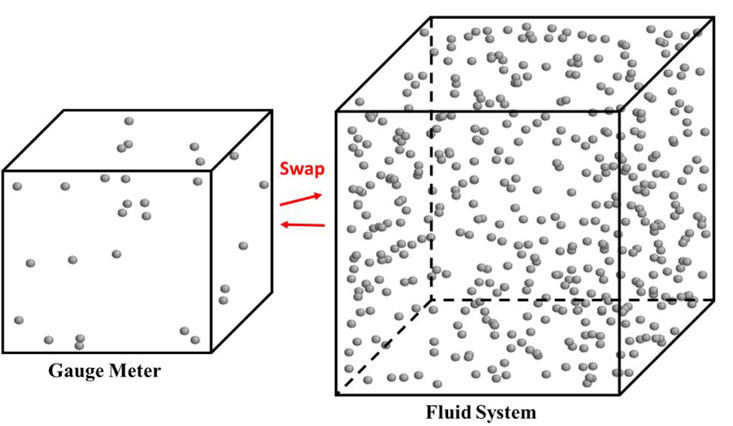
Figure 1. Schematic of the gauge-GEMC ensemble. Red arrows represent the swap move (particles are transferable between boxes). Grey balls are molecules which are methane in this example.

We use the gauge-GEMC simulation to study the phase behavior of methane in confined systems. The confined boundary, specifically nanopores, will be applied solely to the fluid system box, while the gauge meter box remains in the bulk condition. The gauge-GEMC simulation includes a series of cases that are with the same volume and temperature but cover a range of numbers of molecules (see Figure 4 in Section 4). In each case, simulations are conducted under constant number of molecules, total volume, and temperature conditions. The volume of each box is fixed so that the total volume remains constant. In this study, random center-of-mass translation and rotation moves are implemented along with the swap move. These moves are designed to happen with the same probability at each Monte Carlo step.

This method has the capability to produce a comprehensive phase diagram, such as the chemical potential-density (μ-ρ) diagram, represented as a van der Waals loop, encompassing both meta-stable and stable states. Phase equilibrium points can be calculated from the μ-ρ relationship through thermodynamic integration, using Maxwell’s equal area rule (Firoozabadi, 1999) (refer to Figure 4 in Section 4). A temperature–density ($T$–$\rho$) diagram can be generated by repeating the series of cases at various temperatures and collecting the vapor and liquid densities at equilibrium (see Figure 5 in Section 4). Once a significant number of equilibrium points are reached at temperatures below the critical temperature, it becomes possible to estimate the critical point, including both the critical temperature and density. This estimation can be accomplished by extrapolating simulation results from lower temperatures using the rectilinear diameter law (Reif-Acherman, 2010; Zoll Weg and Mulholland, 1972) and the density scaling law (Scott et al., 1991). The density represents the average density within the pore spaces. The chemical potentials derived from phase equilibrium measurements at different temperatures can be utilized in the GCMC simulation to determine the saturation pressures at those specific temperatures. The pressure computation using the GCMC simulation is discussed in the next section.

2.3 GCMC simulation

GCMC simulation is an efficient technique for studying adsorption isotherms and hysteresis in mesopores and micropores. Simulations are performed in a single simulation box at constant chemical potential, volume, and temperature conditions. During the GCMC simulation, the number of molecules is fluctuating to reach the imposed chemical potential at the specified volume and temperature. The increase and decrease of the number of molecules are achieved by insertion and deletion moves, respectively (Figure 2). Like the gauge-GEMC simulation, random center-of-mass translation and rotation moves are also implemented, and all the moves would happen with the same probability.

Figure 2

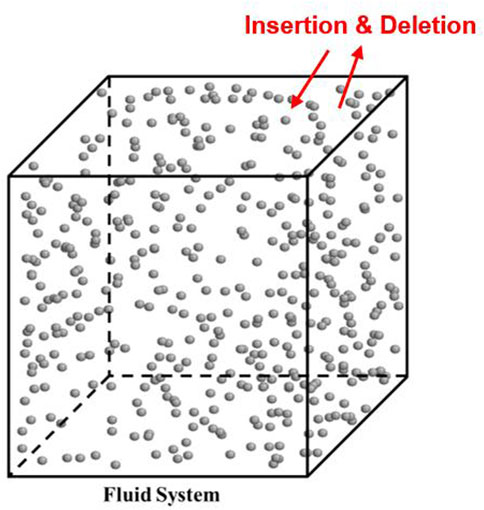
Figure 2. Schematic of the GCMC ensemble. Red arrows represent the insertion and deletion moves. Grey balls are molecules which are methane in this example.

In this work, the GCMC simulation has been used to determine the saturation pressure when confined systems exist. As mentioned above in Section 2.2, the vapor-liquid phase equilibrium study (the gauge-GEMC simulation) can calculate the chemical potential at the phase equilibrium of a confined system. Once the chemical potential at the phase equilibrium has been determined, a GCMC simulation in the bulk condition with the calculated chemical potential and specified temperature will be performed to compute the pressure. The pressure calculated in the bulk condition is referred to as the external pressure of the confined systems at the phase equilibrium (Yang et al., 2019; Jin and Firoozabadi, 2016b).

It’s important to be noticed that the pressure computed directly from the confined systems cannot be compared to the normal pressure physically measured in experiments. The pressure derived from molecular simulations is referred to as Virial pressure and is acquired through the use of the Virial equation (Ungerer et al., 2005):

$P=\frac{N{R}_{gas}T}{N_{a}V}+\frac{1}{3V}〈{\sum }_k\overrightarrow{r_k}\bullet \overrightarrow{F_k}〉,(2)$

where $R_{gas}$ is the gas constant, $N_a=6.022\times {10}^{23}$ mol^-1 is the Avogadro number, $\overrightarrow{r_k}$ and $\overrightarrow{F_k}$ represent the position of the center of mass of molecule $k$ and the intermolecular forces acting on the molecule $k$. The second term on the right side of Equation 2 is called Virial term which is an ensemble average in Monte Carlo simulations (arithmetic average over a number of configurations). When the density of the system is very low or the molecular distribution in the system is homogeneous (e.g., in the bulk condition), the Virial term tends to be zero and the pressure expression reduces to the ideal gas law ($PV=NRT/N_a$). Due to the confinement effect of the pore boundary, the distribution of molecules in nanopores is highly heterogeneous. Therefore, the ideal gas assumption is not valid in nanopores. The principal values of the intermolecular force acting on a molecule vary significantly (the Virial term strongly depends on the local density). Therefore, the pressure calculated in the confined region can be very high and has different implications from that in the bulk condition (Gubbins et al., 2014).

3 Models

3.1 Multi-layer graphite cylindrical pore model

Periodic boundary conditions are applied to the simulation boxes to avoid a boundary effect. Simulation boxes which are in the bulk condition (the gauge meter box in the gauge-GEMC simulation) are repeating identical replicas in all space directions, while simulation boxes which contain confined fluid systems (the fluid system box in the gauge-GEMC) are only replicating in the directions that have no pore boundaries. To compute molecular interactions with periodic boundary conditions using the minimum image convention method, it is essential to guarantee that the dimensions of the simulation boxes in all states are at least twice the value of $r_{cutoff}$ (Ungerer et al., 2005; Scott et al., 1991).

Since a majority of mesopores and micropores are formed in kerogen and one of the most significant elements in kerogen is carbon (Loucks et al., 2009; Loucks et al., 2012; Curtis et al., 2010), graphite has been widely used in molecular simulations for modeling nano-scale pore boundaries (Jin et al., 2017; Jin and Nasrabadi, 2016; Bi and Nasrabadi, 2019). Compared to directly using kerogen as the pore wall material, using graphite helps avoid the impact of pore wall roughness on the results, leading to faster computations. In this work, for investigating the phase behavior of methane in cylindrical pores, we model the pore boundaries explicitly using the multi-layer graphite.

In Figure 3, a schematic of the multi-layer graphite cylindrical pore model is presented. Graphite possesses a honeycomb structure with a bond length of 0.142 nm (Jin et al., 2017), as illustrated in Figure 3A. The multi-layer graphite model is derived from a multi-layer graphite cube with layer separation of 0.335 nm in the z-direction (Jin et al., 2017), as depicted in Figure 3B. To create the cylindrical features, we cut out redundant atoms and left a cylindrical pipe with a specific inner diameter and boundary thickness. The inner diameter of the pipe is the diameter of the cylindrical pore. In this work, we specify the thickness of the multi-layer graphite cylindrical pore is 4 Å (Figure 3C). This pore model has been applied in the fluid system box in the gauge-GEMC simulation with a 1D periodic boundary condition in the z-direction (the gauge meter box in the gauge-GEMC simulation is kept in the bulk situation with 3D periodic boundary condition).

Figure 3

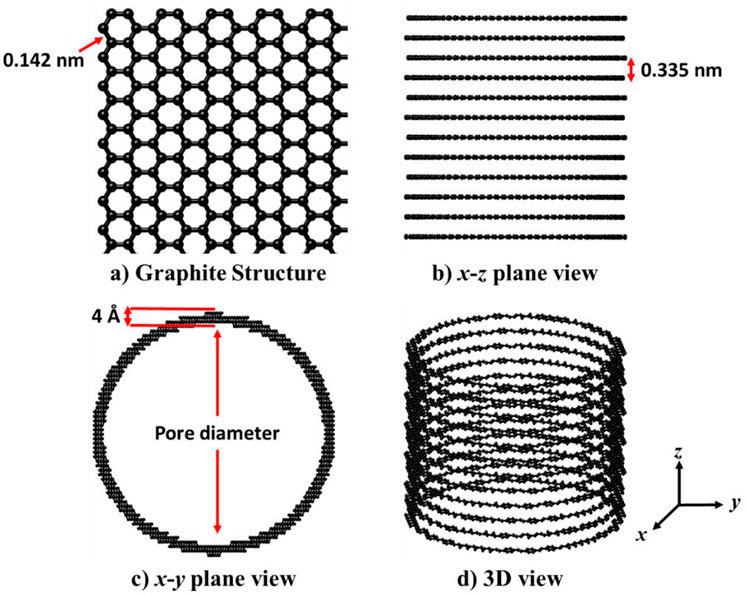
Figure 3. Schematic of the multi-layer graphite cylindrical pore model. (A). Graphite structure. (B). x-z plane view of the model. (C). x-y plane view of the model. (D) 3D view of the model.

3.2 Potential energy calculation model

The Lennard Jones (LJ) 12–6 potential is utilized for calculating the intermolecular energy, specifically non-bonded interactions, as follows:

$\mathrm{U}\left({\mathrm{r}}_{\text{ij}}\right)=4{ϵ}_{\text{ij}}\left[{\left(\frac{{\mathrm{\sigma }}_{\text{ij}}}{{\mathrm{r}}_{\text{ij}}}\right)}^{12}-{\left(\frac{{\mathrm{\sigma }}_{\text{ij}}}{{\mathrm{r}}_{\text{ij}}}\right)}^6\right],(3)$

where $\mathrm{U}\left({\mathrm{r}}_{\text{ij}}\right)$ represents the LJ intermolecular energy, ${\mathrm{r}}_{\text{ij}}$ signifies the distance between particles $\mathrm{i}$ and $\mathrm{j}$, ${\mathrm{\sigma }}_{\text{ij}}$ denotes the separation distance at which the LJ interaction equals zero for particles $\mathrm{i}$ and $\mathrm{j}$, and ${ϵ}_{\text{ij}}$ signifies the potential well depth at the minimum interaction energy. To calculate the cross potential between dissimilar particles, we employ the Lorentz-Berthelot combining rule, which can be described as follows:

${\mathrm{\sigma }}_{\text{ij}}=\frac{{\mathrm{\sigma }}_{\text{ii}}+{\mathrm{\sigma }}_{\text{jj}}}{2},(4)$

${ϵ}_{\text{ij}}=\sqrt{{ϵ}_{\mathrm{i}}{ϵ}_{\mathrm{j}}}.(5)$

In this study, we utilize the TraPPE-UA force field model (Martin and Siepmann, 1998) for all particles. The LJ parameters for these models can be found in Table 2.

Table 2

Table 2. Potential parameters in the LJ 12–6 potential.

The distance at which the LJ potential is no longer calculated is referred to as the truncated distance (${\mathrm{r}}_{\text{cutoff}}$). When the distance between two particles is not larger than the truncated distance (${\mathrm{r}}_{\text{ij}}$ ≤ ${\mathrm{r}}_{\text{cutoff}}$), the interaction energy between them is computed by Equations 3–5, while the interaction energy is negligible (${\mathrm{U}}_{\text{ij}}=0$) if ${\mathrm{r}}_{\text{ij}}$ > ${\mathrm{r}}_{\text{cutoff}}$. In this study, the LJ potential is truncated at a distance of ${\mathrm{r}}_{\text{cutoff}}=10\mathrm{\AA }$ to reduce unnecessary computations, and a long-range tail correction is incorporated. This configuration has been consistently applied in other studies, where molecular simulation outcomes closely align with experimental results (Ungerer et al., 2005; Potoff and Siepmann, 2001). All simulations in this work are conducted using a modified version of the Monte Carlo for Complex Chemical Systems (MCCCS) Towhee (Martin, 2013). Based on the needs of our simulations, we have restricted the range in Towhee within which molecules are allowed to be inserted and moved during the initial configuration and simulation processes. After the modification, fluid molecules are only allowed to undergo Monte Carlo moves within the pore. This modification is more aligned with the research objectives.

4 Phase behavior of methane in 4–10 nm cylindrical pores

The gauge-GEMC simulation is applied for investigating the phase behavior of methane in cylindrical pores of different sizes. The phase behavior of fluids in nanopores is influenced by the size of the nanopores. The smaller the pore diameter, the greater the impact of confinement effects on the fluid phase behavior, leading to greater deviation from the results observed in the bulk phase. Since a significant portion of the pore volume in shale consists of nanopores with diameters less than 10 nm (Clarkson et al., 2013), we selected pore diameters in the range of 4–10 nm, where the pores are as small as possible and represent a significant portion of the pore volume. For each pore size, simulations are performed at multiple temperatures from 130 K to 190 K. At each temperature, the gauge-GEMC simulation includes a series of cases that cover a range of numbers of molecules (Figure 4). It’s important to emphasize that, in each case, the system is characterized by a fixed number of molecules, total volume, and temperature. Further, two million Monte Carlo steps (Ungerer et al., 2005) are performed for the system to reach equilibrium.

Figure 4

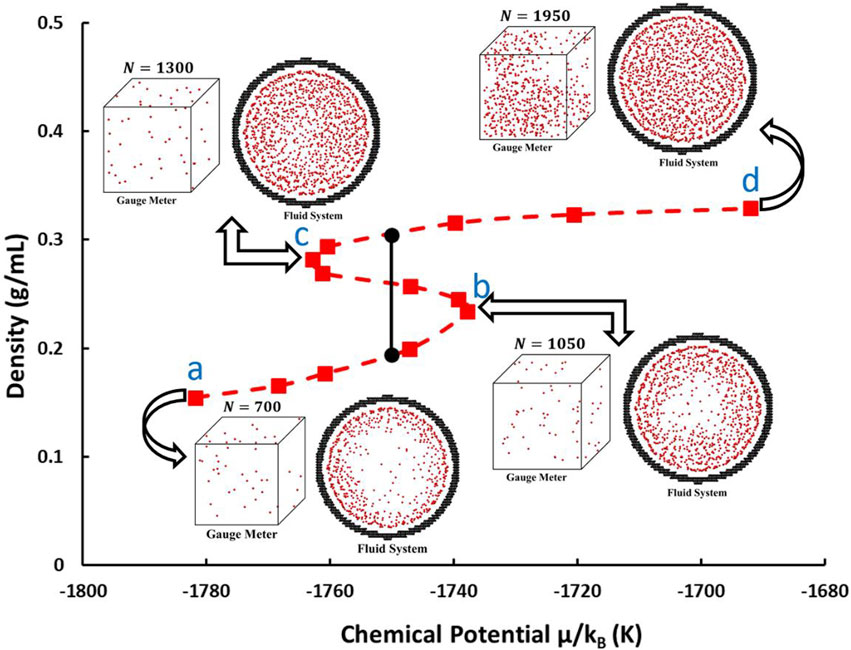
Figure 4. An example of the chemical potential–density relation for methane in a 6 nm cylindrical pore at $\mathit{T}=\mathbf{160}$ K from the gauge-GEMC simulations. Red squares represent the density of methane in the fluid system box at various chemical potentials. Black circles are the phase equilibrium points computed by the Maxwell equal area rule. Points a and d demonstrate the vapor and liquid stable state, respectively. Points b and c are in meta-stable states. Red and black balls in the simulation boxes are methane and pore boundary (graphite), respectively.

At each temperature, a chemical potential–density ($\mu$–$\mathrm{\rho }$) diagram (also known as the van der Waals loop) can be generated by running the designed series of cases (Figure 4). The van der Waals loop contains stable points and meta-stable points. Phase equilibrium points can be computed following the thermodynamic integration of the Maxwell equal area rule (Firoozabadi, 1999). Once the vapor and liquid densities at the equilibrium are obtained, they are used to construct the temperature–density ($T$–$\rho$) diagram (Figure 5). The critical points, encompassing the critical temperature and density, are estimated by extrapolating simulation results from lower temperatures using the rectilinear diameter law (Reif-Acherman, 2010; Zoll Weg and Mulholland, 1972) and the density scaling law (Scott et al., 1991).

Figure 5

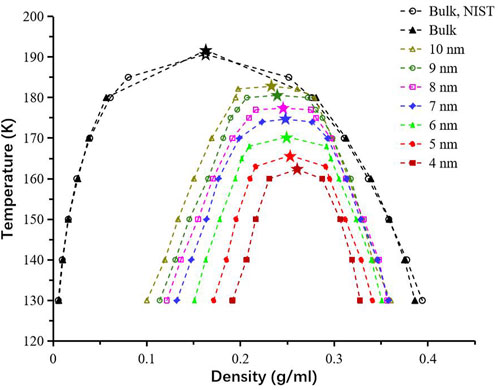
Figure 5. Temperature–density ($\mathit{T}$–$\mathit{\rho }$) diagrams for methane within cylindrical models of varying diameters.

First, the accuracy of the set-up in the gauge-GEMC method is tested in the bulk condition. In the bulk condition, there is no pore boundary involved in the fluid system box and further, the fluid system box is in the 3D periodic boundary condition. Our simulation can generate results as accurate as the laboratory results from the National Institute of Standards and Technology (NIST). Our results (represented as black triangles) from the simulation match the results (represented as black empty circles) from NIST in Figure 5. Additionally, we extend the work to confined systems that contain the multi-layer graphite cylindrical pore models (Figure 3) with varying diameters in the range of 4–10 nm in the fluid system box. By repeating the mentioned tests for each pore size, phase diagrams are computed, as shown in Figure 5. It is clear that the smaller the pores are, the more the temperature–density diagrams shrink. When compared to the bulk condition, the critical temperature decreases, and critical density rises within nanopores. The critical temperature in the 4 nm pore that deviates the most from the values in the bulk condition is reduced by around 15%. The increase in the critical density is the consequence of the dramatic increase in the vapor density and slight decrease in the liquid density at equilibrium. As the pore diameter expands, the phase diagram approaches values typical of the bulk material. The observed confinement effects align with trends seen in previous studies (Jin and Firoozabadi, 2016a; Li et al., 2014; Jin and Nasrabadi, 2016).

An example of the density profiles of methane at 130 K in the mentioned nanopores is shown in Figure 6. We measure the mass densities as a function of the distance from the pore surface ($r$). We divide the entire distance into series intervals (the width of each interval $∆r=0.05$ nm) and count how many molecules fall into each interval. As the figure shows, for both liquid and vapor phases, there are two obvious methane adsorbed layers near the pore boundary at around $r={\sigma }_{methane}$ and $2{\mathrm{\sigma }}_{methane}$, where $r$ is defined to be zero at the pore surface. The densities of the first adsorbed layers in both phases are the same, while the density of the second layer in the liquid phase is larger than that in the vapor phase. As the distance increases, the confinement effect by the wall decreases, and both the liquid and vapor densities gradually approach their bulk values (black lines in Figures 6A, B). There are some transition layers before the liquid and vapor densities reach their bulk values. It should be noted that in comparison with small pores (e.g., 4 nm pore), large pores (e.g., 10 nm pore) contain a larger free region in their center, but the same molecular distributions near the pore boundary.

Figure 6

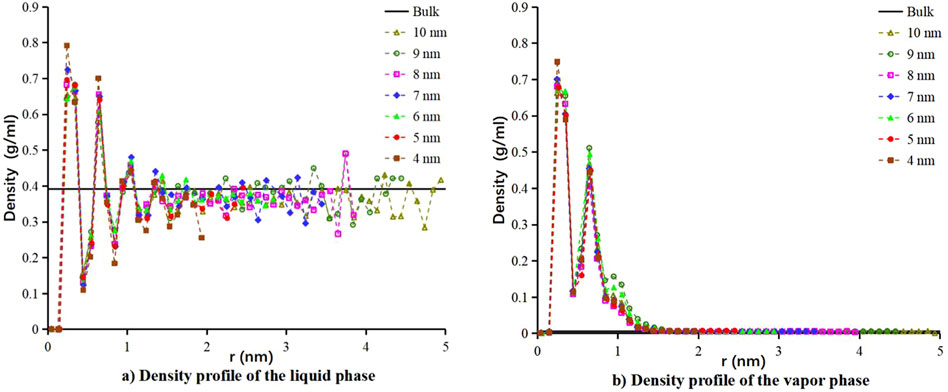
Figure 6. Density profile of methane in cylindrical models with different diameters at 130 K. The (A) liquid and (B) vapor phase densities as a function of the distance $\mathit{r}$.

Pressure–temperature diagrams (Figure 7) are generated from additional GCMC simulations (two million Monte Carlo steps) with the obtained chemical potentials at equilibrium states as imposed chemical potentials. As explained in Section 2.3, the additional GCMC simulations are performed in the bulk condition. In comparison with the bulk condition, the critical pressure is reduced in the nanopores. The smaller the pores are, the lower the pressure–temperature diagrams go. As a result, the saturation pressures at different temperatures are suppressed, compared with the value in the bulk condition. Overall, the saturation and critical pressure in the 4 nm pore, as the most confined condition, deviates the most from the values in the bulk condition. Compared with the bulk condition, saturation pressures in the 4 nm pore reduce 48%–60% at various temperatures and the critical pressure reduces by around 80%.

Figure 7

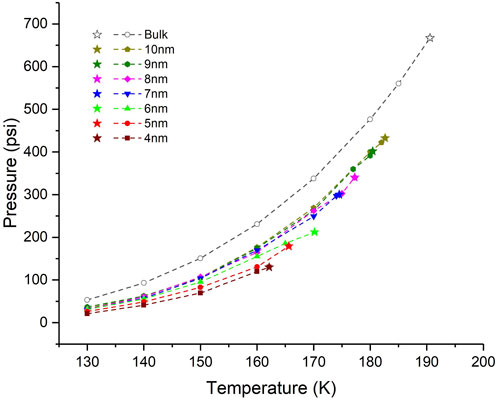
Figure 7. Pressure–temperature ($\mathit{P}$–$\mathit{T}$) diagrams of methane in cylindrical models with different diameters.

5 Conclusion

In the present work, the gauge-GEMC simulations are used to investigate the phase behavior of methane in single cylindrical pore models formed by multi-layer graphite. The phase behavior of methane is studied in nanopores with diameters of 4–10 nm. Results show that in comparison with the bulk condition, at vapor–liquid equilibrium in nanopores, the vapor phase has a dramatically increased density, but the density of the liquid phase is slightly decreased. The confinement effect would cause a shrunk temperature–density diagram with reduced critical temperature and increased critical density. Smaller pores exhibit a more pronounced confinement effect, leading to a greater reduction in the size of temperature–density diagrams. Conversely, as pore diameter increases, the phase diagram approaches values typical of the bulk material. The pressure–temperature diagrams have demonstrated that the saturation pressure and critical pressure of methane in nanopores are also suppressed from the bulk values.

Shifts in phase diagrams can impact phase state calculations, thereby directly affecting the physical properties of fluids, such as density, viscosity, and expansion coefficient. Inaccurate parameters can lead to deviations in fluid flow and reservoir behavior simulations, resulting in incorrect assessments of reserves and production forecasts. Inaccurate phase state measurements may cause either overestimation or underestimation of reservoir productivity, affecting the economic feasibility analysis of development plans and potentially leading to unreasonable development decisions. Errors in phase state measurements can also lead to incorrect predictions of the phase distribution (e.g., gas phase, liquid phase) of oil-gas mixtures under different temperature and pressure conditions, thereby affecting oil-gas phase separation, gas production predictions, and the efficiency of oil-gas mixture handling during production. Results from this work provide data support for modifying and validating equations of state.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

RB: Writing–original draft, Writing–review and editing. MH: Writing–review and editing. YW: Writing–review and editing. YP: Writing–review and editing. FC: Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bi, R., Firoozabadi, A., and Myint, P. (2020b). Efficient and robust phase-split computations in the internal energy, volume, and moles (UVN) space. Fluid Phase Equilib. 526, 112729. doi:10.1016/j.fluid.2020.112729

CrossRef Full Text | Google Scholar

Bi, R., and Nasrabadi, H. (2019). Molecular simulation of the constant composition expansion experiment in shale multi-scale systems. Fluid Phase Equilib. 495, 59–68. doi:10.1016/J.FLUID.2019.04.026

CrossRef Full Text | Google Scholar

Bi, R., Zidane, A., and Firoozabadi, A. (2020a). Efficient and robust stability analysis in the internal energy, volume, and moles (UVN) space. Fluid Phase Equilib. 512, 112468. doi:10.1016/j.fluid.2020.112468

CrossRef Full Text | Google Scholar

Clarkson, C. R., Solano, N., Bustin, R. M., Bustin, A. M. M., Chalmers, G. R. L., He, L., et al. (2013). Pore structure characterization of North American shale gas reservoirs using USANS/SANS, gas adsorption, and mercury intrusion. Fuel 103, 606–616. doi:10.1016/j.fuel.2012.06.119

CrossRef Full Text | Google Scholar

Coasne, B., Gubbins, K. E., and Pellenq, R. J. M. (2005). Temperature effect on adsorption/desorption isotherms for a simple fluid confined within various nanopores. Adsorption 11, 289–294. doi:10.1007/s10450-005-5939-y

CrossRef Full Text | Google Scholar

Curtis, M. E., Ambrose, R. J., Sondergeld, C. H., and Rai, C. S. (2010). Structural characterization of gas shales on the micro- and nano-scales. Soc. Pet. Eng. - can. Unconv. Resour. Int. Pet. doi:10.2118/137693-ms

CrossRef Full Text | Google Scholar

Firoozabadi, A. (1999). Thermodynamics of hydrocarbon reservoirs. McGraw-Hill.

Google Scholar

Gubbins, K. E., Long, Y., and Śliwinska-Bartkowiak, M. (2014). Thermodynamics of confined nano-phases. J. Chem. Thermodyn. 74, 169–183. doi:10.1016/j.jct.2014.01.024

CrossRef Full Text | Google Scholar

Jin, B., Bi, R., and Nasrabadi, H. (2017). Molecular simulation of the pore size distribution effect on phase behavior of methane confined in nanopores. Fluid Phase Equilib. 452, 94–102. doi:10.1016/j.fluid.2017.08.017

CrossRef Full Text | Google Scholar

Jin, B., and Nasrabadi, H. (2016). Phase behavior of multi-component hydrocarbon systems in nano-pores using gauge-GCMC molecular simulation. Fluid Phase Equilib. 425, 324–334. doi:10.1016/j.fluid.2016.06.018

CrossRef Full Text | Google Scholar

Jin, B., and Nasrabadi, H. (2018). Phase behavior in shale organic/inorganic nanopores from molecular simulation. SPE Reserv. Eval. Eng. 21, 626–637. doi:10.2118/187307-PA

CrossRef Full Text | Google Scholar

Jin, Z., and Firoozabadi, A. (2016a). Thermodynamic modeling of phase behavior in shale media. Soc. Pet. Eng. J. 21, 190–207. doi:10.2118/176015-PA

CrossRef Full Text | Google Scholar

Jin, Z., and Firoozabadi, A. (2016b). Phase behavior and flow in shale nanopores from molecular simulations. Fluid Phase Equilib. 430, 156–168. doi:10.1016/j.fluid.2016.09.011

CrossRef Full Text | Google Scholar

Li, J., Wu, K., Chen, Z., Wang, K., Luo, J., Xu, J., et al. (2019). On the negative excess isotherms for methane adsorption at high pressure: modeling and experiment. SPE J. 24, 2504–2525. doi:10.2118/197045-PA

CrossRef Full Text | Google Scholar

Li, Z., Jin, Z., and Firoozabadi, A. (2014). Phase behavior and adsorption of pure substances and mixtures and characterization in nanopore structures by density functional theory. SPE J. 19, 1096–1109. doi:10.2118/169819-PA

CrossRef Full Text | Google Scholar

Libby, B., and Monson, P. A. (2004). Adsorption/desorption hysteresis in inkbottle pores: a density functional theory and Monte Carlo simulation study. Langmuir 20, 4289–4294. doi:10.1021/la036100a

PubMed Abstract | CrossRef Full Text | Google Scholar

Loucks, R. G., Reed, R. M., Ruppel, S. C., and Hammes, U. (2012). Spectrum of pore types and networks in mudrocks and a descriptive classification for matrix-related mudrock pores. Am. Assoc. Pet. Geol. Bull. 96, 1071–1098. doi:10.1306/08171111061

CrossRef Full Text | Google Scholar

Loucks, R. G., Reed, R. M., Ruppel, S. C., and Jarvie, D. M. (2009). Morphology, genesis, and distribution of nanometer-scale pores in siliceous mudstones of the mississippian barnett shale. J. Sediment. Res. 79, 848–861. doi:10.2110/jsr.2009.092

CrossRef Full Text | Google Scholar

Luo, S., Lutkenhaus, J. L., and Nasrabadi, H. (2018). Multiscale fluid-phase-behavior simulation in shale reservoirs using a pore-size-dependent equation of state. SPE Reserv. Eval. Eng. 21, 0806–0820. doi:10.2118/187422-pa

CrossRef Full Text | Google Scholar

Martin, M. G. (2013). MCCCS Towhee: a tool for Monte Carlo molecular simulation. Mol. Simul. 39, 1212–1222. doi:10.1080/08927022.2013.828208

CrossRef Full Text | Google Scholar

Martin, M. G., and Siepmann, J. I. (1998). Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 102, 2569–2577. doi:10.1021/jp972543+

CrossRef Full Text | Google Scholar

Neimark, A., and Vishnyakov, a (2000). Gauge cell method for simulation studies of phase transitions in confined systems. Phys. Rev. E. Stat. Phys. Plasmas. Fluids. Relat. Interdiscip. Top. 62, 4611–4622. doi:10.1103/PhysRevE.62.4611

PubMed Abstract | CrossRef Full Text | Google Scholar

Neubauer, B., Boutin, A., Tavitian, B., and Fuchs, A. H. (1999). Gibbs ensemble simulations of vapour—liquid phase equilibria of cyclic alkanes. Mol. Phys. 97, 769–776. doi:10.1080/00268979909482877

CrossRef Full Text | Google Scholar

Panagiotopoulos, A. Z. (1987). Direct determination of phase coexistence properties of fluids by Monte Carlo simulation in a new ensemble. Mol. Phys. 61, 813–826. doi:10.1080/00268978700101491

CrossRef Full Text | Google Scholar

Pathak, M., Cho, H., and Deo, M. (2017). Experimental and molecular modeling study of bubble points of hydrocarbon mixtures in nanoporous media. Energy Fuels 31, 3427–3435. doi:10.1021/acs.energyfuels.6b02422

CrossRef Full Text | Google Scholar

Peng, D. Y., and Robinson, D. B. (1976). A new two-constant equation of state. Ind. Eng. Chem. Fundam. 15, 59–64. doi:10.1021/i160057a011

CrossRef Full Text | Google Scholar

Potoff, J. J., and Siepmann, J. I. (2001). Vapor–liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen. AIChE J. 47, 1676–1682. doi:10.1002/aic.690470719

CrossRef Full Text | Google Scholar

Reif-Acherman, S. (2010). The history of the rectilinear diameter law. Quim. Nova 33, 2003–2010. doi:10.1590/S0100-40422010000900033

CrossRef Full Text | Google Scholar

Rouquerolt, J., Avnir, D., Fairbridge, C. W., Everett, D. H., Haynes, J. H., Pernicone, N., et al. (1994). Recommendations for the characterization of porous solids. Pure Appl. Chem. 66, 1739–1758. doi:10.1351/pac199466081739

CrossRef Full Text | Google Scholar

Rowley, L. A., Nicholson, D., and Parsonage, N. G. (1975). Monte Carlo grand canonical ensemble calculation in a gas-liquid transition region for 12-6 Argon. J. Comput. Phys. 17, 401–414. doi:10.1016/0021-9991(75)90042-X

CrossRef Full Text | Google Scholar

Scott, R., Allen, M. P., and Tildesley, D. J. (1991). Computer simulation of liquids. Math. Comput. 57, 442. doi:10.2307/2938686

CrossRef Full Text | Google Scholar

Singh, S. K., Sinha, A., Deo, G., and Singh, J. K. (2009). Vapor− liquid phase coexistence, critical properties, and surface tension of confined alkanes. J. Phys. Chem. C 113, 7170–7180. doi:10.1021/jp8073915

CrossRef Full Text | Google Scholar

Smit, B., De Smedt, P., and Frenkel, D. (1989). Computer simulations in the gibbs ensemble. Mol. Phys. 68, 931–950. doi:10.1080/00268978900102641

CrossRef Full Text | Google Scholar

Soave, G. (1972). Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 27, 1197–1203. doi:10.1016/0009-2509(72)80096-4

CrossRef Full Text | Google Scholar

Ungerer, P., Tavitian, B., and Boutin, A., Applications of molecular simulation in the oil and gas: Monte Carlo methods, 2005.

Google Scholar

Vishnyakov, A., and Neimark, A. V. (2001). Studies of liquid-vapor equilibria, criticality, and spinodal transitions in nanopores by the gauge cell Monte Carlo simulation method. J. Phys. Chem. B 105, 7009–7020. doi:10.1021/jp003994o

CrossRef Full Text | Google Scholar

Vishnyakov, A., and Neimark, A. V. (2009). Multicomponent gauge cell method. J. Chem. Phys. 130, 224103. doi:10.1063/1.3124186

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Q., Jin, B., Banerjee, D., and Nasrabadi, H. (2019). Direct visualization and molecular simulation of dewpoint pressure of a confined fluid in sub-10 nm slit pores. Fuel 235, 1216–1223. doi:10.1016/j.fuel.2018.08.050

CrossRef Full Text | Google Scholar

Zhu, H., Huang, C., Ju, Y., Bu, H., Li, X., Yang, M., et al. (2021). Multi-scale multi-dimensional characterization of clay-hosted pore networks of shale using FIBSEM, TEM, and X-ray micro-tomography: implications for methane storage and migration. Appl. Clay Sci. 213, 106239. doi:10.1016/j.clay.2021.106239

CrossRef Full Text | Google Scholar

Zoll Weg, J. A., and Mulholland, G. W. (1972). On the law of the rectilinear diameter. J. Chem. Phys. 57, 1021–1025. doi:10.1063/1.1678352

CrossRef Full Text | Google Scholar

Nomenclature