The Influence of Fracture Growth and Coalescence on the Energy Budget Leading to Failure

Unraveling the details of fracture propagation leading to catastrophic rock failure is critical for understanding the precursors to earthquakes. Here we present numerical simulations of fracture growth using a work optimization criterion. These simulations apply work optimization to fracture propagation by finding the propagation orientation that minimizes the external work at each increment of fracture growth, repeating this process for each growing fracture tip in the model. We simulate published uniaxial compression experiments performed on a cylinder of marble with pre-cut fractures of varied lengths, orientations, and positions. This suite of experiments provides an ideal benchmark for the numerical simulations because of the relatively simple boundary conditions and the range of pre-cut fracture geometries that focus deformation. We compare the results of homogeneous, isotropic model material to results that incorporate hundreds of small randomly oriented and distributed microcracks representing internal weaknesses, such as grain boundaries. From these numerical models, we find that slip on and propagation of microcracks governs the non-linear stress-strain response observed before failure under axial compression. We use a suite of Monte Carlo realizations incorporating different initial seeding of microcracks to explore the range of fracture propagation paths that might result from inherent variation between rock samples. We find that while models that include microcracks begin to propagate fractures at smaller cumulative axial strains than an equivalent homogeneous isotropic model, ultimately, models including heterogeneity require more energy to reach failure than the homogeneous model. These results highlight the critical role of heterogeneity, such as microcracks, within the processes leading up to failure.

Introduction

The processes leading up to failure are of primary interest in the field of rock mechanics. Understanding the process of microcrack coalescence and how it relates to macroscopic failure can provide insights into earthquake precursory processes. Recent experimental studies have documented fine details of the failure process in rocks using methods like acoustic emission relocation, X-ray microtomography, and lab-scale seismic tomography (e.g. Aben et al., 2019; Renard et al., 2019; Cartwright-Taylor et al., 2020). Such studies document how distributed damage localizes into fracture networks, eventually leading to brittle failure of the samples (e.g., J. McBeck et al., 2021a). Experiments that document damage percolation in ice at varied strain rates provide another avenue for examining fracture growth processes similar to those observed in rock masses (e.g., Renshaw et al., 2019).

Since Griffith described failure via the propagation of cracks from pre-existing weaknesses 100 years ago (Griffith 1921), many experiments have confirmed the importance of pre-existing weaknesses and heterogeneity in controlling the behavior of failure processes. This control is reflected in the scale-dependence of strength tests, in which larger samples generally fail at lower stresses (Rocco et al., 1999; Kaklis and Vardoulakis 2004). Experiments performed on heterogeneous rock samples demonstrate that the presence of pre-existing flaws produces an inverse power law behavior prior to failure (e.g., Renard et al., 2018; Kandula et al., 2019) that enables better forecasting of macroscopic failure, compared to more homogeneous samples that fail abruptly and unpredictably (Cartwright-Taylor et al., 2020). While experimentalists can measure the forces on the outside of a sample and measure the growth and opening of fractures, it remains challenging to directly measure certain attributes of the system, such as the energy budget, stress state within the rock, and slip along microcracks. Given these constraints, numerical simulations of microcrack growth benchmarked against lab experiments provide an avenue for exploring the mechanical processes at work during fracture growth.

A variety of numerical approaches have been used to simulate fracture growth processes between several interacting and coalescing fractures (e.g. Bi, Zhou, and Qian 2016; Hazzard et al., 2000; Lunn et al., 2008; Madden et al., 2017; J. A.; McBeck et al., 2016; X. P.; Zhou X. P. et al., 2015; Zhou and Wang, 2016). Simulations of fracture growth have demonstrated that the mode of fracture growth is dependent on the length and orientation of pre-existing cracks, stress state, and interactions of fractures for a given experiment. Models of multiple crack interactions have explicitly included as many as 20 small cracks (e.g., Moir et al., 2010; Zhou X.-P. et al., 2015), or combinations of large and small pre-existing cracks (X. P. Zhou and Yang 2012). Large numbers of ‘flaws’ have been considered with DEM simulations of micro-crack coalescence that include fracture-like arrangements of bonds and particles, but these models do not explicitly consider fracture tips (e.g., Hazzard et al., 2000; J.; McBeck et al., 2021c; J.; McBeck et al., 2021b). 2D and 3D models of fracture growth driven by fluid pressure have also simulated complex interacting networks of faulting and crack reactivation (e.g., Thomas et al., 2020; Lei et al., 2021; Li and Zhang 2021).

The 2D Boundary Element Method code Fric2D coupled with the work optimization code GROW has been used both to simulate fracture growth and coalescence between two fractures, and to investigate the energy budget components of predicted fracture systems (Madden et al., 2017; J. A.; McBeck et al., 2016). However, this approach has not yet been used to investigate the critical role of preexisting flaws in fracture network development, and the corresponding evolution of the energy budget. In this study, we build on previous work by applying the work optimization approach to simulations with and without hundreds of distributed pre-existing weaknesses.

We use the work optimization code GROW to model fracture propagation based on experimental results published by Yang et al. (2009) (Figures 1A,B). GROW simulates fracture growth by selecting the propagation path that minimizes the external work of the fracture system. This work optimization method allows for mixed-mode failure, which arises often with microcrack coalescence, and avoids the ambiguity of two predicted planes of failure under Coulomb shear failure criteria (Madden et al., 2017). In order to efficiently investigate propagation potential from hundreds of crack tips, we add a screening step to the GROW algorithm that evaluates the relative likelihood of fracture growth from each crack tip in order to prioritize crack tips with the highest circumferential stress.

FIGURE 1

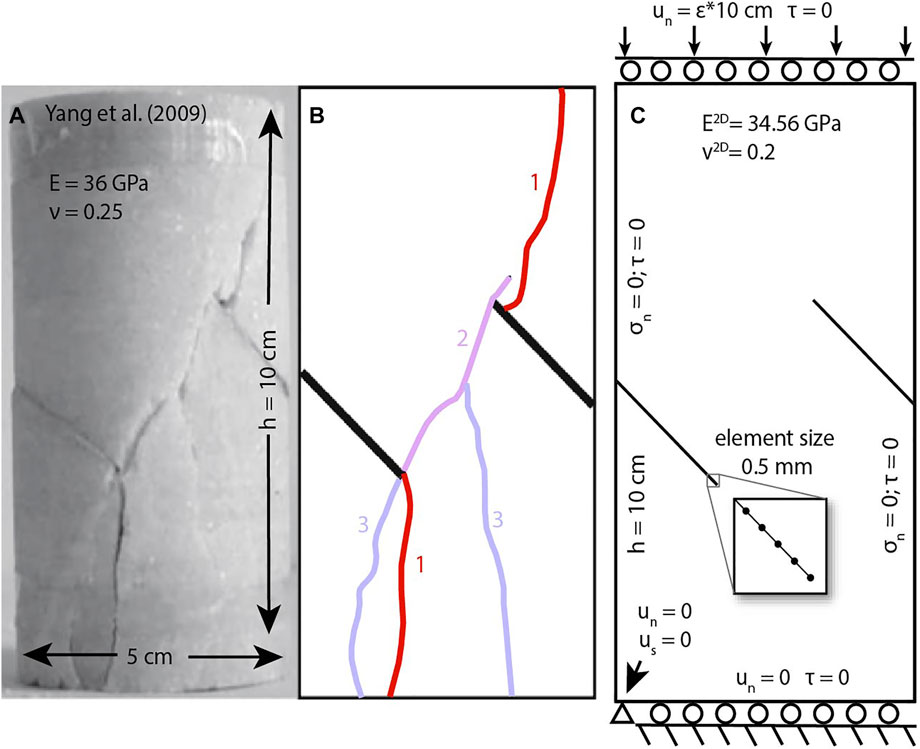
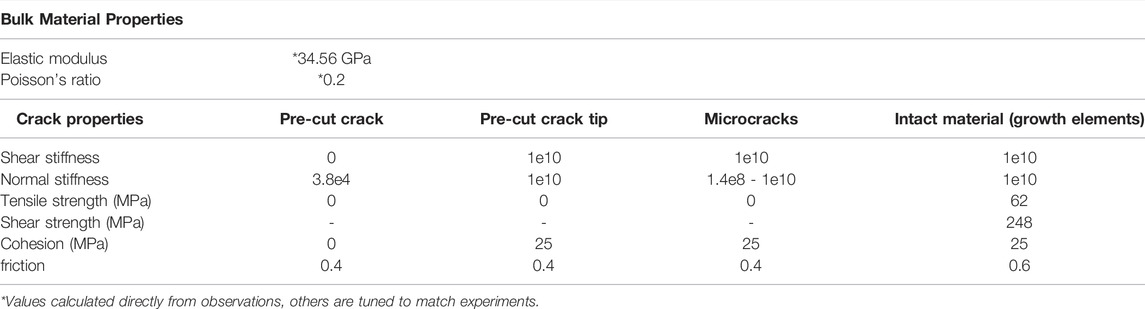
FIGURE 1. (A) Post-experiment image of Yang et al. (2009) uniaxial compression experiment C with two pre-cut fractures in a cylindrical sample of marble 10 cm tall and 5 cm in diameter. The marble sample has a height, h, of 10 cm, diameter of 5 cm, an elastic modulus, E, of 36 GPa and a Poisson’s ratio, ν, of 0.25. (B) Map of fractures produced during Yang et al. (2009) uniaxial compression experiment C, labeled according to order of propagation. (C) 2D model setup used in this study to simulate experiment C. Applied material properties are scaled to 2D. Boundary conditions are shown according to prescribed normal and shear tractions (σ_n, τ), and normal and shear displacements (u_n, u_s) in terms of the lab experiment axial strain (ε).

In this study, we apply the work optimization method to simulate the growth of fractures from two pre-cut fractures in a cylinder of marble subjected to unconfined uniaxial compression (Figure 1C, Yang et al., 2009). We compare simplified homogeneous simulations to simulations incorporating hundreds of pre-existing weaknesses on the scale of the marble’s grain size. We evaluate the impact of explicitly considering small pre-existing planes of weakness in models of fracture propagation, including the differences in the stress-strain curves and energy budgets produced by these contrasting models. We examine how slip, opening and closing on microcracks are distributed before and during fracture propagation, with the coalescence of microcracks into a fracture network. We also examine how natural variation in the orientations of weakness influence the range of predicted fracture paths.

Methods

We use the work optimization code GROW, which calls the 2D Boundary Element Method code Fric2D (McBeck et al., 2016) to assess the propagation of fractures and microcracks. Fric2D uses continuum mechanics to resolve the stress and strain response of a homogeneous linear-elastic material containing prescribed fractures under 2D plane-strain (Cooke and Pollard, 1997). McBeck et al. (2016) demonstrate using GROW that work optimization algorithms accurately simulate the propagation path and linkage of two nearby fracture tips separated by a releasing step within 2D models. Madden et al. (2017) extended this method to in-line growth of fractures, exploring how the energy budget of fracture growth differs between tensile and shear growth. Simulations presented here required adding new features to GROW to accommodate the large number of fractures included, which are detailed in this section along with our approach for simulating the 3D experiments with 2D models.

GROW Work Optimization Algorithm

GROW assesses potential orientations of crack growth from pre-existing fractures, assessed radially from a preexisting crack tip (i.e., parent). In this study, we assess growth at angles from 60° to 300° clockwise from the parent crack at 10° intervals (Figure 2B) to allow for a wide range of growth angles as growing cracks coalesce with pre-existing weaknesses. If none of the new growth elements fail, the model stops adding new elements. If any of the elements fail, either by tension or shear, GROW measures the change in external work that results from the addition of that element (Figure 2C). Following Cooke and Madden (2014), the external work of the system is calculated from the shear tractions and displacements, τ and u_s, and normal tractions and displacements, σ_n and u_n, integrated along the boundaries of the system. For displacement loading, such as applied here, the optimal orientation of new crack growth is that which minimizes external work. The growth orientation that minimizes the external work is added to the fault, and the process is iterated until either all growing cracks reach the model boundaries or no new elements slip at the applied loading (Figure 2C).

FIGURE 2

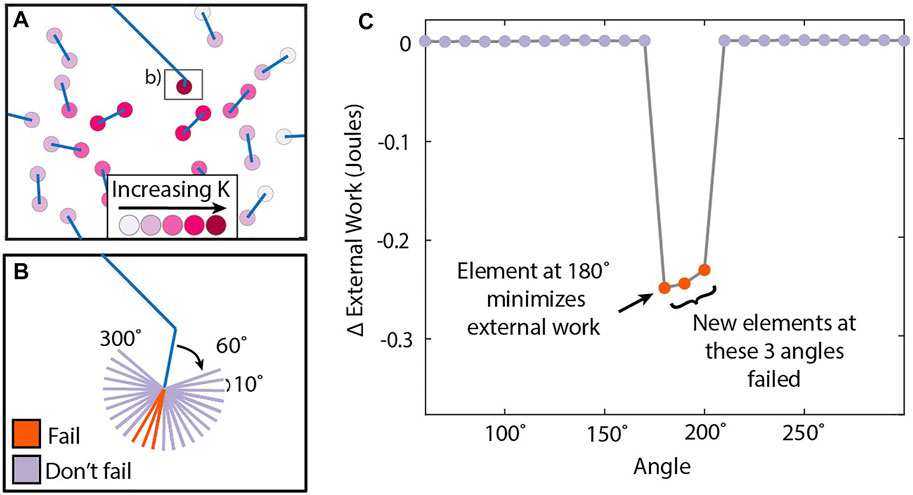
FIGURE 2. GROW uses work optimization to predict fracture propagation. (A) Model with a long fracture surrounded by smaller fractures. Mode I and II stress intensity factors (K) at the tips of fractures are used to calculate propagation potential. GROW selects the fracture tips with highest propagation potential (Eq. 1) to assess for growth in the next step. (B) GROW assesses new growth elements at a prescribed range of angles clockwise around the fracture tip(s). For this study, we assessed 10° increments from 60˚-300°. Elements can fail via slip or opening. (C) New growth elements that fail can reduce the external work on the displacement-loaded system. GROW assesses which orientation minimizes external work, that element is added, and the process is iterated. In this example, elements that propagate at 180°, 190°, and 200° fail, and the element at 180° is selected because it produces the lowest external work.

The code has many options for how to implement fracture growth when multiple fractures are included, which are detailed in McBeck et al. (2020). For this study, we used single mode, which allows for only one fracture to propagate at a time. This mode allows for more refined discernment of the order of fracture growth than multi-mode and better matches fault growth under displacement-controlled loading, such as within accretionary wedge sandbox experiments (McBeck et al., 2020).

Crack Tip Selection Criteria

In previous versions of GROW, propagation is assessed from every growing crack tip. For many of the models presented here, pre-existing weaknesses in the rock are simulated as hundreds of distributed small cracks which we will refer to as microcracks. The simulations can contain >500 cracks tips, making it computationally expensive to check for potential failure at each tip. Thus, GROW November 2021 version uses mode I and mode II stress-intensity factor values at each fracture tip to limit assessment to the fracture tips that have the greatest potential for propagation (Figure 2A). For this study, GROW uses the maximum circumferential stress, ${\sigma }_{\theta \theta }$, to assess the propagation potential of the fractures. Because tensile failure dominates the fracture growth in these unconfined experiments, ${\sigma }_{\theta \theta }$ captures the overall likelihood of fracture propagation. This criterion doesn’t limit the failure mode because GROW allows any combinations of shear and tensile failure at each assessed fracture tip. Rather, this step limits the assessment to only those fracture tips with the greatest ${\sigma }_{\theta \theta }$ and reduces the search from >500 tips to <10 tips. The σ_θθ can be calculated using mode I and II stress intensity, K_I and K_II, and the angle of maximum tensile stress, θ:

${\sigma }_{\theta \theta }=\frac{K_{\text{I}}}{\sqrt{2\pi r}}co{s}^3\frac{\theta }{2}-\frac{3K_{II}}{2\sqrt{2\pi r}}sin\theta cos\frac{\theta }{2}(1)$

Where θ at each crack tip is calculated from the stress intensity factors as:

$\theta =arcsin\left(\frac{K_{II}}{K_I} cos\varphi \right)-\varphi (2)$

$\varphi =\arctan \left(\frac{K_{II}}{K_I}\right)(3)$

All fracture tips that fall within 50% of the highest value of ${\sigma }_{\theta \theta }$ at any crack tip are assessed for growth.

Experimental Setup of Yang

We base the simulations of this study on a suite of uniaxial compression experiments performed by Yang et al. (2009) on cylinders of marble cut to be 10 cm high with a diameter of 5 cm. The marble sourced from eastern China is described as crystalline and homogeneous with a low porosity, composed of mainly calcite, dolomite, and magnesite, with a grain size of 1–2 mm and density of 2,700 kg/m³. They documented 12 experiments with servo-controlled displacement-controlled uniaxial compression at a rate of 0.002 mm/s, measuring the force on the top of the sample throughout the experiments. They performed one experiment with intact marble, and 11 experiments with two or more pre-cut cracks of varied length, orientations, and proximity to each other. The pre-cut cracks had a thickness of 0.3–0.5 mm and were filled with gypsum. Yang et al. (2009) documented the axial stress and strain throughout each experiment and from these data they derived values for elastic modulus and uniaxial compressive strength. The intact sample had a much higher peak strength and elastic modulus than pre-cut samples, as the pre-cut cracks increased the elastic compliance of the samples, and concentrated stresses within the sample to promote fracture growth at lower axial stresses. Fracture paths were documented at the end of each failure episode, but not continuously throughout the experiments.

Model Parameters

For the 2D plane strain numerical model to simulate the stress-strain response of a uniaxially loaded cylinder, we scale the model’s elastic material properties—Poisson’s ratio and Young’s modulus—such that the stress and displacements in the 2D model capture those of the 3D cylinder. For example, cylindrical samples expand radially under axial compression but plane strain limits strain to within the x-z plane (${\epsilon }_{yy}$ = 0). We can adjust the scaled Poisson’s ratio of the model, n, to account for this effect.

For a uniaxial loading of a cylindrical sample, the lateral stresses are zero (${\sigma }_{xx}={\sigma }_{yy}=0$; ${\sigma }_{zz}$ >0). For the 2D plane strain of our models, Hooke’s law states that lateral stresses are related to in-plane strains as:

${\sigma }_{xx}= \frac{E}{\left(1+\nu \right)\left(1-2\nu \right)}\left[\left(1-\nu \right){\epsilon }_{xx}+\nu {\epsilon }_{zz}\right](4)$

For our 2D simulation with no lateral loads Eq. 2 becomes:

$\left(1-\nu \right){\epsilon }_{xx}= -\nu {\epsilon }_{zz}(5)$

Re-arranging Eq. 3 allows us to calculate the scaled Poisson’s ratio, n, of our plane strain simulation in terms of the Poisson’s ratio measured in the cylinder $\left({\nu }^{\prime }\right)$:

$-\frac{{\epsilon }_{xx}}{{\epsilon }_{zz}}= \frac{\nu }{\left(1-\nu \right)}= {\nu }^{\prime }(6)$

So, for an unconfined cylindrical sample with a measured Poisson’s ratio of ${\nu }^{\text{'}}=$ 0.25, we use $\nu$ = 0.2 in the model. The lower Poisson’s ratio in the plane strain model compensates for the degree of lateral expansion that occurs within the cylindrical sample in the y-direction.

We can also calculate the scaled stiffness. The vertical stress, ${\sigma }_{zz},$ for plane strain are related to in-plane strains as

${\sigma }_{zz}= \frac{E}{\left(1+\nu \right)\left(1-2\nu \right)}\left[\left(1-\nu \right){\epsilon }_{zz}+\nu {\epsilon }_{xx}\right](7)$

Substitute Eq. 2 for ${\epsilon }_{xx}$ Into Eq. 5 Yields

${\sigma }_{zz}= \frac{E}{\left(1+\nu \right)\left(1-2\nu \right)}\left[\left(1-\nu \right){\epsilon }_{zz}- {\epsilon }_{zz}\frac{{\nu }^2}{\left(1-\nu \right)}\right](8)$

Which simplifies to:

${\sigma }_{zz}= \frac{E}{\left(1+\nu \right)\left(1-2\nu \right)}{\epsilon }_{zz}\left[\left(1-\nu \right)-\frac{{\nu }^2}{\left(1-\nu \right)}\right](9)$

Eq. 6 can be rearranged to calculate the measured Young’s Modulus, E′, from the scaled Young’s Modulus put into the plane strain model, E:

$E^{\prime }= \frac{{\sigma }_{zz}}{{\epsilon }_{zz}}= \frac{E}{\left(1+\nu \right)\left(1-2\nu \right)}\left[\left(1-\nu \right)-\frac{{\nu }^2}{\left(1-\nu \right)}\right](10)$

So, in the case of the rock sample from the experiments of Yang et al. (2009) with no pre-cut fracture, for ${\sigma }_{zz}$ = 36 MPa and ${\epsilon }_{zz}$ = 1e-3, a sample with E’ = 36 GPa, the scaled E put into the model should be 34.56 GPa. When we apply these scaled material properties to the homogeneous unfractured model, the model produces stresses and lateral strains consistent with the experimental observations (Figure 3, experiment A).

FIGURE 3

FIGURE 3. (A) Effective elastic modulus from Yang et al. (2009) experiments with varied arrangements of pre-cut fractures plotted against the effective elastic modulus produced in numerical simulations with the same pre-cut facture configurations. Gray shaded region shows ± 3 GPa range. (B) Pre-cut fracture configurations from Yang et al. (2009) experiments used for models.

To further tune the 2D model to the 3D experiments, we apply these scaled material properties to simulations of the other 11 experiments that have pre-cut cracks (Figure 3). Pre-cut cracks slip upon loading and consequently reduce the bulk elastic modulus of the sample. Furthermore, the initial aperture of the pre-cut cracks, an outcome of sawing cuts in the sample, also affects the bulk compliance of the sample as this aperture closes upon axial compression. Because initial crack aperture is not explicitly incorporated by the linear elements that represent the fractures in the model, we account for this additional compliance by adjusting the normal stiffness of the elements along the modeled fractures. We tune fracture normal stiffness so that the bulk model deformation matches experimental estimate of the overall Young’s modulus of pre-cut samples of configuration C. We focus our simulations on experiment C because Yang et al. (2009) provided more detailed data on the stress-strain evolution and order of fracturing for this experiment than for other configurations. This lower normal stiffness (Table 1) results in interpenetration of the fracture surface that is less than half the thickness of the pre-cut cracks of the experimental samples, indicating that this normal stiffness value serves as a reasonable proxy for the compliance of the pre-cut cracks. The aperture of the precut experimental fractures decreases at their tips. To simulate this variation in aperture within the model, we prescribe the two elements at the tip of the growing fracture higher normal stiffness than the rest of the fracture. Similarly, a low shear stiffness is prescribed to the larger aperture portions of the pre-cut fractures because that portion of the fracture does not have resistance to shear displacement, but a high shear stiffness is prescribed on the two elements at the fracture tip.

TABLE 1

TABLE 1. Model parameters.

When we use the experimental stress and strain data presented in Yang et al. (2009) to directly estimate the elastic moduli, we calculate different values than reported within the paper. While most differences were small (<2%), a few experiments had differences up to ∼10%. For the detailed stress-strain record for experiment C presented in Yang et al. (2009), we calculate a 10% difference in elastic modulus from the one reported in their results (they report 22.24 GPa, while we measure 24.4 GPa). Because we rely on the extracted data for model calibration, we subsequently use our own calculations of elastic modulus from the extracted experimental data. These differences are not large enough to change the interpretation of microcrack propagation model results.

To test our material properties, we apply the material and fault properties reported in Table 1, some of which are tuned to match the experiments A and C as already described, to the other experiments. Most of the model estimates of effective elastic modulus match the experimental measurements within ± 3 GPa (Figure 3). Our simulations significantly overestimate elastic modulus in two experiments—J and L. Experiment J is the only one with 4 pre-cut fractures, and experiment L has pre-cut fractures that are the most oblique to the axial displacement. These experiments were both outliers among the experiments--with especially low values for elastic modulus, and stress-strain paths with much different patterns than observed in other experiments--suggesting that pre-existing damage may have played a role in their reduced elastic modulus values. In this study, we only consider the deformation of experimental samples A, C, and H. Overall, the chosen material and fault properties provide a good match to the elastic stress-strain relationships observed in these experiments.

Microcrack Properties

To explicitly investigate the role of pre-existing weaknesses, such as grain boundaries, on fault propagation path and on the stress-strain relationship, we set up models that include hundreds of microcracks. The marble used for this experiment has low porosity and a grain size of 1–2 mm (Yang et al., 2009). Since the largest grain boundaries will have the greatest impact on deformation, we introduce many randomly oriented 2 mm long cracks throughout the model. Grain boundaries may both facilitate failure, as well as act as an endpoint for arresting growing intra-grain fractures. While experiments demonstrate that the earliest stages of microcrack growth are axially-oriented (e.g., Kandula et al., 2019), we include microcracks of random orientations to capture the full range of mechanical influences produced by heterogeneity, which includes opening on vertical microcracks as well as sliding on obliquely oriented microcracks.

Each crack has four elements of 0.5 mm length. Because unrealistic stress concentrations can arise when elements in the model are very close to each other without connecting at a node, we impose a minimum spacing of at least 1 mm between microcracks, pre-cut cracks, and model boundaries. We iteratively add randomly located microcracks while eliminating microcracks that have a center point <3 mm from another microcrack center point or fracture or boundary element center point. This ensures a distance of at least 1 mm (2 elements lengths) between microcrack tips. This method results in a uniform distribution of microcracks, whose exact position is determined randomly. We populated each model with the largest population of cracks that could be included with this imposed spacing—250 microcracks. GROW’s code was updated so that new crack growth elements that come within 1.5x an element length of another crack will be adjusted to connect at a node. This approach ensures that the growth and coalescence of cracks can be simulated without producing unrealistic stress concentrations between very close elements.

Microcracks have an initial cohesion that prevents them from slipping during the elastic portion of the experiment. The value for cohesion (25 MPa, Table 1) was tuned such that cracks start to slip at the observed strain where the experimental stress-strain curve deviates from linear-elastic and starts to show nonlinear behavior in experiment A (Figure 4, e = 2.05 e-3). Because the cracks are only slipping in the 2D plane of our model, we simulate the effect of out-of-plane slip by lowering the normal stiffness so that microcracks experiencing compressive normal stresses will interpenetrate to varying degrees. This value of normal stiffness was tuned so that the slip and interpenetration values are roughly equal. For this assessment we compare the 95th percentile of interpenetration and slip values from all the microcracks. The distribution of slip on microcracks contains smaller numbers of more extreme values, whereas values for closing are a more constant distribution proportionate with normal tractions. We use the 95th percentile of these values to provide a closer average match of these values despite their slightly different distributions. This lower normal stiffness, which simulates out-of-plane slip, was only applied to the models that are loaded past the threshold strain at which microcracks begin to slip. Models at lower applied strain do not have slip along microcracks and therefore do not require this adjustment. We set a high shear stiffness of closed cracks (1e10) so that elements that do not experience frictional failure will not have shear displacement. For this study, we do not prescribe any slip weakening on either the microcracks or fractures in the model.

FIGURE 4

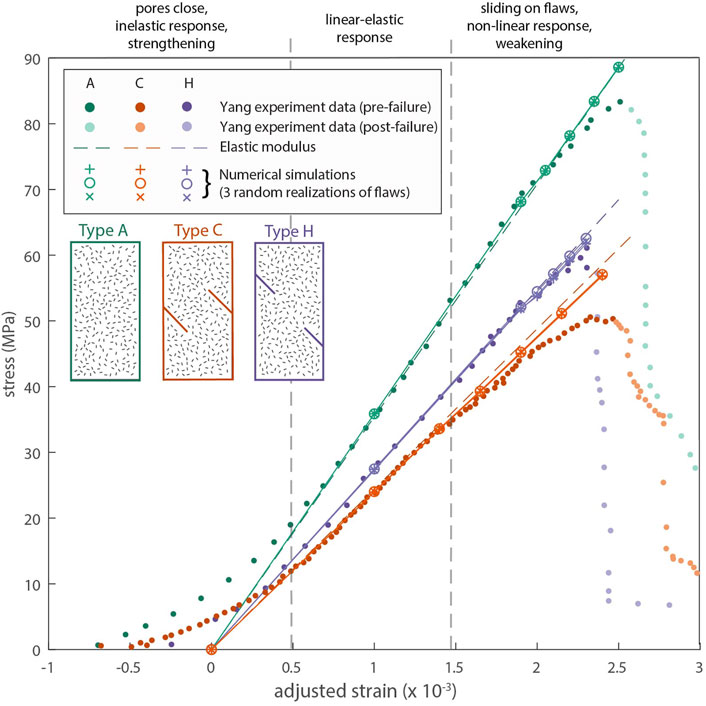
FIGURE 4. Pre-fracture growth models of stress-strain response for three experimental setups. Data from Yang et al. (2009) experiments is shown as solid dots (dark colors preceding failure, lighter colors after failure). Results are shown from three simulations of experiment setup (A,C, and H) that include different sets of randomly distributed microcracks that slide, open, and interpenetrate. These simulations do not include fracture growth, so as to isolate and highlight the impact of microcrack deformation alone. The strain values of the experiments were shifted to remove the nonlinear stress-strain response at the beginning of experiments when pore space closes, which is not captured in the model. Dashed lines show the effective elastic modulus for each setup derived from the experiment data. The deviation from the linear stress-strain response near macroscopic failure results from sliding and opening on microcracks at higher strain levels. This deviation is more prominent in simulations with pre-cut cracks.

Intact Rock Strength

Typical measurements of tensile strength of marble are between 4–10 MPa (Kaklis and Vardoulakis 2004), but can be higher depending on experimental setup (Chen and Hsu 2001). The inherent shear strength, estimated from uniaxial compressive tests, is about 83 MPa for the marble used in these experiments (Yang et al., 2009), and is similar to estimates from other experiments (Tal et al., 2016). Because these measurements of strength incorporate the effect of heterogeneities within the experimental samples, these values are lower than the local strength of intact rock (Olsson 1974; Rocco et al., 1999) and therefore not suitable for the material between the microcracks of our models.

We tuned the strength of the intact rock so that fracture propagation begins shortly after microcracks begin to slide in our experiment C setup—at a strain of 2.4e-3. The initial fracture propagation step from each pre-cut crack is a wing-crack produced by tensile normal stress at the fracture tip (Yang et al., 2009). The first fracture growth is thus controlled by the tensile strength of the material. Experimental comparisons of inherent shear and tensile strength for a variety of rock types demonstrate that inherent shear strength is typically 6–8 times greater than inherent tensile strength (Karaman et al., 2015). We used a conservative ratio of 1:4 ratio to approximately scale inherent shear strength to the tensile strength of the marble (Table 1). Tests of homogeneous simulations with higher prescribed inherent shear strength (1:8 ratio) yield identical results to those with the 1:4 ratio. These tuned tensile and shear strength values are greater than values typically produced in experiments of marble because we are tuning the local strength of the intact marble at the fracture tips, rather than the bulk strength of the sample.

Results

We compare results from several models that simulate fracture growth within the experiments of Yang et al. (2009), with a particular focus on their experiment C with two inclined and offset precut fractures (Figure 5A). Yang et al. (2009) provided greater detail on the stress-strain path and information about the order of cracking for this experiment. To build our intuition on the role of microcrack deformation and propagation, we investigate homogeneous models without microcracks as well as heterogeneous models with distributed microcracks.

FIGURE 5

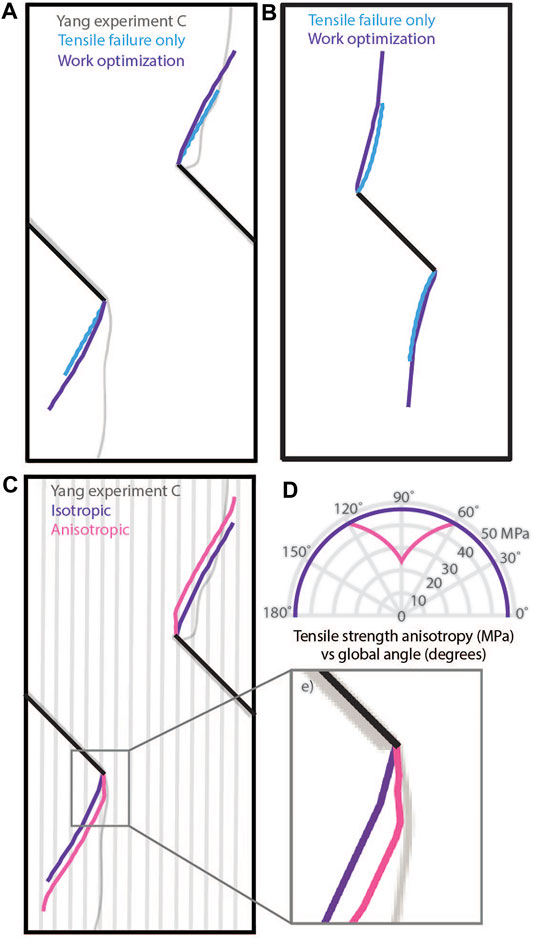
FIGURE 5. (A) Simulations of fracture growth using only tensile failure and using work optimization, including both tensile and shear failure in an isotropic, homogeneous model with pre-cut fractures matching geometry of Yang et al. (2009) experiment C. (B) Models of propagation paths from a center crack. (C) Work optimized propagation path from model with isotropic tensile strength compared to model with anisotropic tensile strength. (D) Tensile strength relative to a global reference frame. (E) Detail of work optimized crack growth from pre-cut fracture tip.

Homogeneous Models

We contrast fracture propagation paths from models of precut fractures where the fractures propagate via a tensile failure criterion against models where fractures propagate via a work optimization criterion, in an otherwise homogeneous and isotropic material (Figure 5A). Differences between the models demonstrate the role of shear failure and slip on the propagation path. We also explore the impact of tensile strength anisotropy on the work optimized propagation path.

Isotropic Models

Isotropic models do not incorporate the role of pre-existing microcracks on the growth of the pre-cut faults. For this study, we compare fracture growth from the Yang et al. (2009) experiment C using both GROW’s work optimization approach and Fric2d′s growth algorithm that only assesses tensile failure (Figure 5A). One advantage of GROW’s algorithm is that it does not rely on one specific failure criteria—failure can entail pure opening, pure shear, or any combination that optimizes the external work of the system.

The work optimization criterion and the tensile failure criterion produce similar but distinct propagation paths. Both criteria produce wing cracks in the zone of tension produced by right-lateral shear on the 45° dipping pre-cut fractures. The take-off angle for purely tensile failure is 270° measured clockwise from the parent crack, whereas work optimization prefers 235°. At this angle, the rock still fails in tension, but the growing fracture experiences more slip, making this orientation a more efficient geometry that minimizes the external work on the system compared to the orientation of maximum tensile stress. After the initial increment of fracture propagation, the propagation path becomes nearly colinear, with new propagation elements deviating less than 5° from the orientation of the parent fracture.

With both growth criteria, we observe that the crack propagates towards the traction-free sides of the model. We investigate the impact of the side boundaries on crack propagation by creating a center crack model with the same length and orientation that sits far from the boundaries (Figure 5B). In this simulation, the same style of wing crack forms as at the start of the edge crack models but with axially oriented propagation during the later stages of crack growth. Again, we see that while tensile failure and work optimization produce similar results, the onset of purely tensile failure occurs at a more oblique angle (270°) relative to the parent crack, and work optimization promotes the onset of tensile failure with a greater component of shear at a less oblique angle to the parent crack (240°). For both criteria, the fracture orientation approaches vertical as it propagates away from the initial center crack, which is the orientation predicted for tensile failure within axially-loaded specimens. This difference in propagation path between the center and edge crack models suggests that the geometry of the pre-cut fractures at the sides of the model and sample reduces axial compression in the stress shadow of the pre-cut fracture, altering the stress state so that the principal compressive stress direction is no longer vertical near the sides of the model. This variation prevents the fracture from propagating in an axial direction as it does for the center crack model.

The propagation paths in the isotropic models roughly overlap the path of the upper pre-cut fracture from experiment C, but do not match the lower fracture. This variation in propagation path could be caused by the preexisting flaws within the marble and the resulting strength anisotropy. We explore both of these potential impacts in this study.

Anisotropic Models

We investigate the potential impact of material tensile strength anisotropy on fracture propagation by using GROW’s options for varied material properties at specified orientations (McBeck et al., 2016). This method offers a proxy for considering anisotropy, such as along pre-existing fabric or from opening of axially-oriented microcracks such as observed in the earliest stages of experiments (e.g., Kandula et al., 2019). As samples are loaded in unconfined axial compression that allows for lateral expansion, microcracks that are oriented subparallel to the axial loading may open and provide preferential pathways for vertical fault growth. In the model, we prescribe potential growth elements that are oriented vertically to have lower tensile strength than obliquely oriented growth elements. Because tensile failure dominates fracture propagation of models simulating the Yang et al. (2009) experiments, variations to this property have the greatest impact on propagation paths. The vertical anisotropy is defined by a linear drop in tensile strength between global angles 60–120°, measured from the horizontal, with a minimum tensile strength at 90°, at 50% the initial tensile strength (Figure 5D).

Figure 5C shows propagation paths produced using GROW with both a uniform tensile strength at all orientations, and tensile strength with strong vertical anisotropy. The vertical anisotropy affects the initial propagation path (Figure 5E) such that stronger anisotropy promotes a more axial orientation of initial growth. After a few propagation steps, the fracture growth becomes sub-parallel to the isotropic fracture path as the cracks grow towards the side of the model under various anisotropy conditions. Stronger degrees of anisotropy with a minimum tensile strength value <50% the initial tensile strength produced an identical path to the 50% strength anisotropy condition. This result suggests that vertical anisotropy of material properties may not account for the natural variation of experimentally produced fracture paths as much as other factors, such as heterogeneities.

Heterogeneous Models

We explore the impact of heterogeneity on fracture path variation by incorporating many small, distributed and randomly oriented cracks, as detailed in the methods section. First, we explore the impact of these distributed small cracks, referred to here as microcracks, on the stress-strain response of models prior to the growth of new fractures (Figure 4). We then explore how fractures and microcracks deform, and the impact of microcracks on fracture propagation paths (Figures 6–8), stress-strain response (Figure 9), and energy budget evolution (Figure 10) compared to the simplified homogeneous isotropic simulation.

FIGURE 6

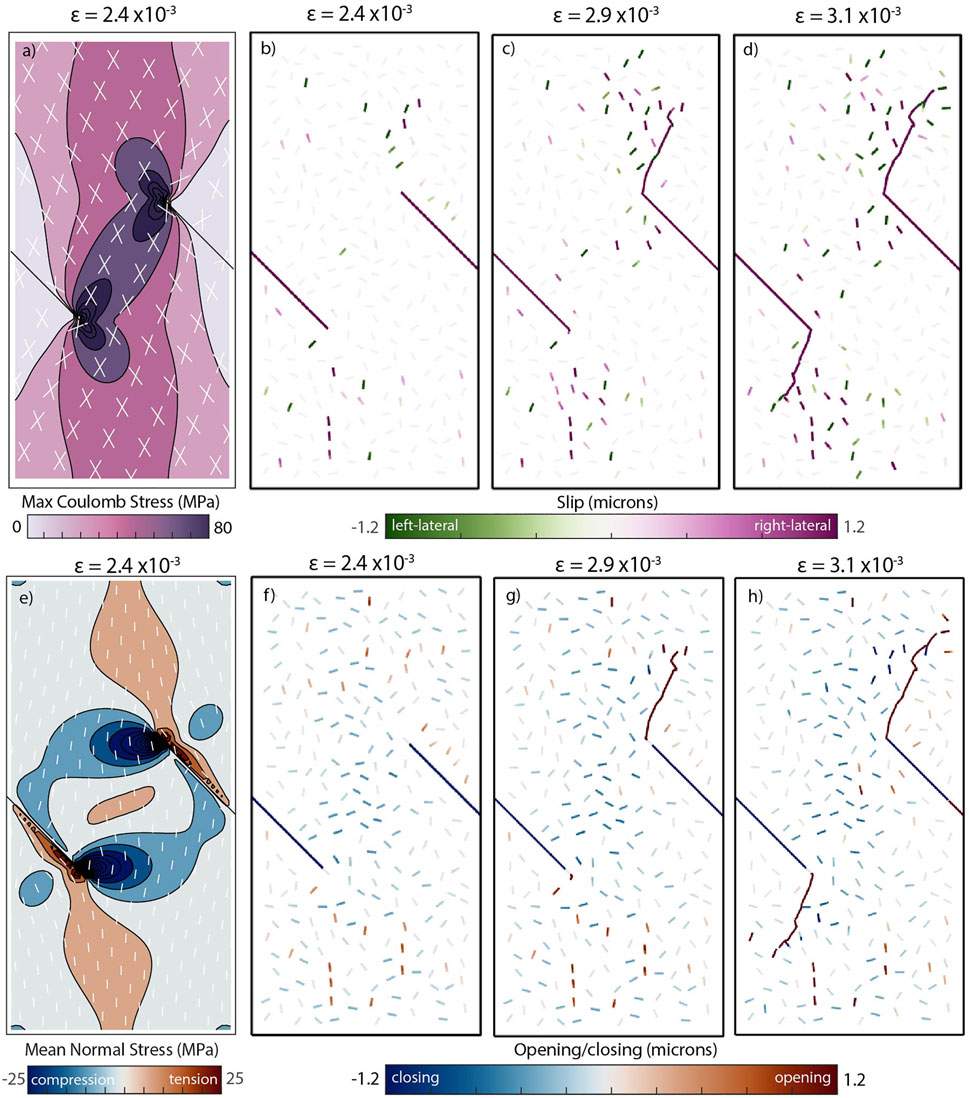
FIGURE 6. (A) Maximum Coulomb stress change produced by axial loading of model without microcracks illuminates the slip potential on flaws optimally-oriented for slip throughout the model, with Coulomb failure planes plotted as white lines. (B–D) Slip on pre-cut cracks and microcracks prior to fracture growth (b), after the early stage of fracture growth (c) and after full fracture growth (d). The color scale was chosen to highlight slip variation on microcracks, while slip on the pre-cut cracks ranges from tens to hundreds of microns (Figure 7). (E) Mean normal stress illuminating regions of tension and compression within the sample due to slip on pre-cut cracks and axial strain in a model without microcracks. Orientations of the maximum principal stress are plotted as white lines. (F–H) Map of opening and closing on pre-cut cracks and microcracks prior to fracture growth (f), after early stage of fracture growth (g) and after full fracture growth (h).

FIGURE 7

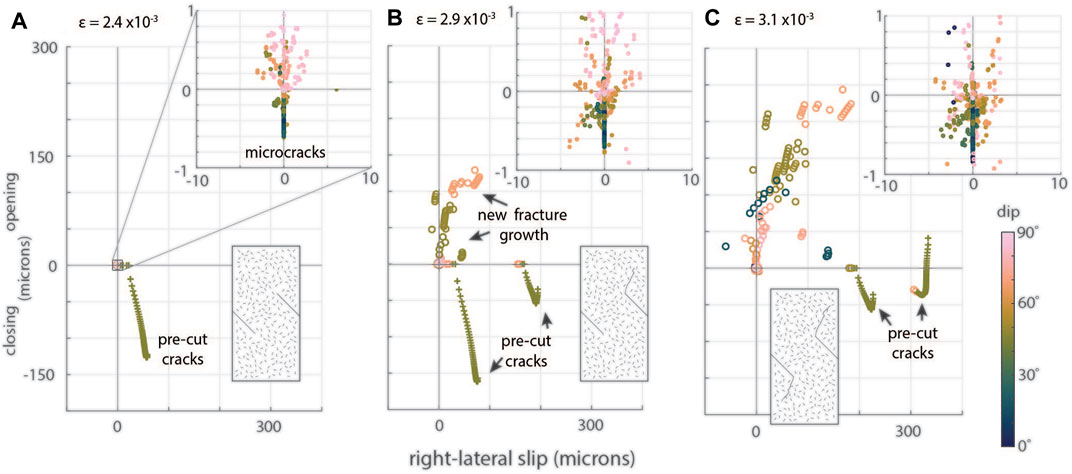
FIGURE 7. (A) Slip and closing/opening for each element in the model prior to new fracture growth from the tips of the preexisting cracks, at strain 2.4e-3. Inset shows values for microcracks clustered around the origin. Each point is color-coded by dip angle from 0° (horizontal) to 90° (vertical). (B) Slip and closing/opening on model elements after fracture growth at a strain of 2.9e-3. (C) Slip and closing/opening on model elements after fracture growth at a strain of 3.1e-3. As strain increases, fracture growth from one pre-cut crack promotes increased slip and decreased closing, while the pre-cut crack that does not grow exhibits more closing and only slightly more slip. New fracture growth is all opening mode and mixed-mode opening and shear, with mostly right-lateral slip. Increased strain increases slip, opening, and closing on microcracks (insets).

FIGURE 8

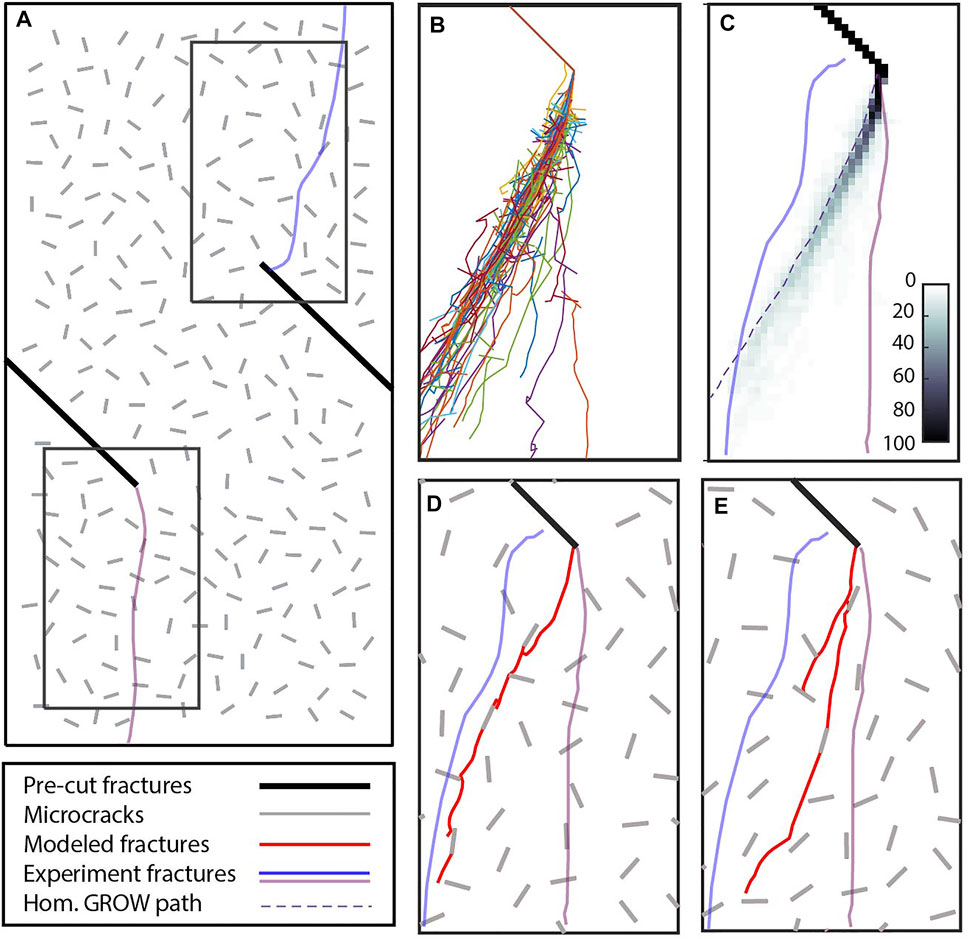
FIGURE 8. (A) Model incorporating 250 randomly oriented 2 mm microcracks representing grain boundaries. (B) Overlay of crack paths from 100 simulations with varied realizations of microcracks demonstrates the variation and complexity that arise from the incorporation of heterogeneity. (C) Gridded density of crack linkage from 100 simulations to highlight range of crack paths from the tip of the preexisting crack. Paths observed in Yang et al. (2009) experiments from both pre-cut fractures are shown in blue and purple. A dashed line shows the homogeneous model crack path. (D) Example crack path following central preferred path. (E) Example crack path that closely matches the axial propagation path from lower crack tip of the Yang et al. (2009) experiment.

FIGURE 9

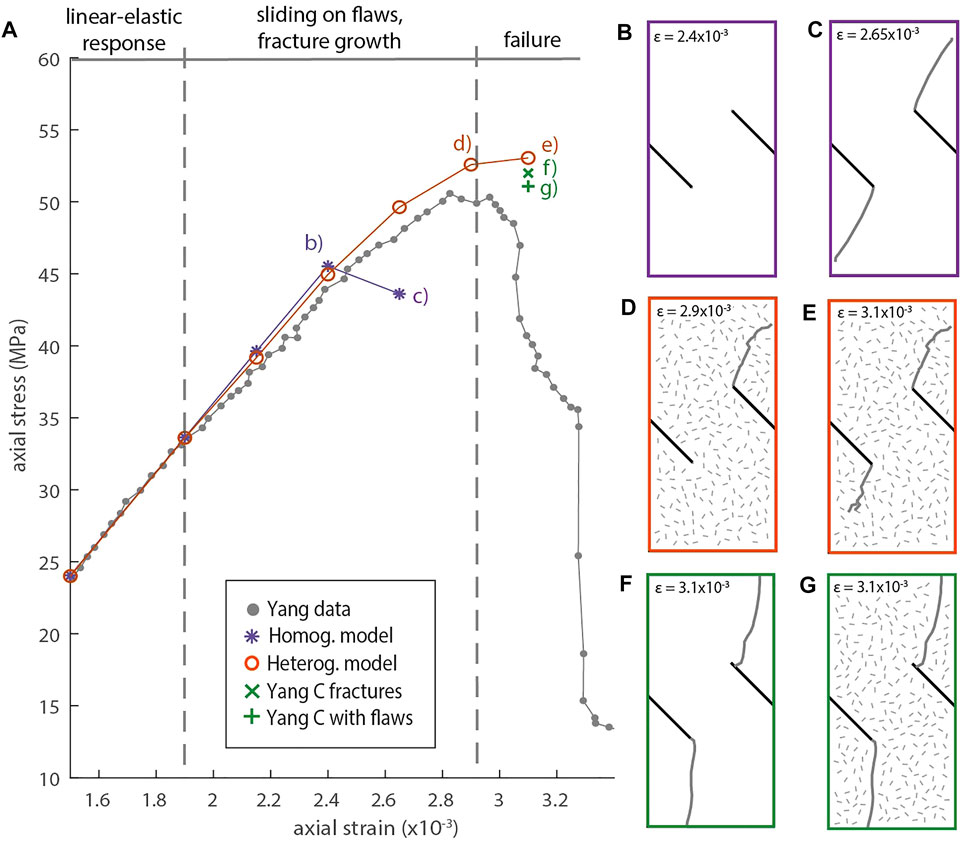
FIGURE 9. (A) Stress-strain data from Yang et al. (2009) experiment C is shown in grey circles. Stress-strain values from numerical simulations using two homogeneous models and a model incorporating distributed microcracks are shown in purple diamonds and asterisks, and orange circles, respectively. Green ‘+’ and ‘x’ symbols show post-failure stress values from models using the experimentally-observed fracture patterns, with and without inclusion of distributed microcracks respectively. (B) The first fracture growth from both pre-cut cracks occurs in the homogeneous model at strain 2.4 e-3, corresponding to the labeled location on the stress-strain plot. (C) Complete fracture growth in homogeneous model at strain 2.65 e-3. (D) Fracture growth in the heterogeneous model starts from the upper pre-cut crack first at strain 2.4 e-3, growing to the edge of the model once strain reaches 2.9 e-3. (E) Full fracture growth from both pre-cut cracks in the heterogeneous model at strain 3.1 e-3. (F) Model incorporating the observed fracture geometry of the experiment without microcracks corresponds to green cross on stress-strain plot, and (G) model incorporating observed fracture geometry and distributed microcracks, corresponds to green plus on stress-strain plot.

FIGURE 10

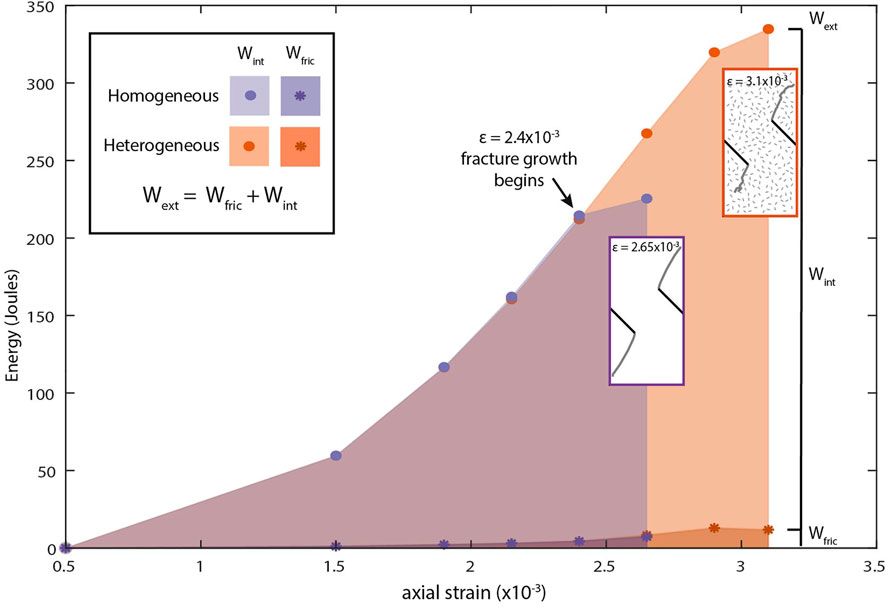
FIGURE 10. Evolution of energy budget with increasing axial strain. The internal work (W_int) and frictional work (W_fric) sum to the external work (W_ext) of the system at each strain. Stacked work values are shown for the homogeneous model in purple, and for the heterogeneous model containing distributed flaws in orange, such that the upper points are the total W_ext, the lower points are the W_fric, and W_int is the vertical difference between the two points. Values are derived from homogeneous and heterogeneous (i.e., with microcracks) that have the same prescribed intact rock strength. Failure occurs at a lower strain for the homogeneous model.

Pre-fracture Growth Stress-Strain Response

Here we focus on the response of the model setup to strain without fracture growth. These simulations isolate the impact that microcracks have prior to failure—that is, the compliance produced by slip and opening on pre-existing weaknesses in a sample before fracture propagation starts. Robust pre-fracture growth models provide an important baseline from which to meaningfully simulate failure processes. Because our microcrack parameters were tuned for appropriate behavior in the intact model simulating experiment A, we test the application of those parameters to two of the other experiments with pre-cut cracks (experiments C and H). We show these results plotted with an adjusted value of strain that shifts each stress-strain curve so that the line fit to the linear-elastic portion of the curve intersects with zero (Figure 4). This adjustment removes the beginning of each experiment when pores close, which is not explicitly included in the numerical simulations. These values for adjusted strain are the values input to the model, in the form of displacements applied to the model boundaries.

We find that microcracks begin to slip in all three model setups at the applied strains where the stress-strain curve begins to deviate from the linear-elastic response, affirming that the mechanical properties applied to the microcracks reproduce experimental behavior. Slip on distributed microcracks only slightly decreases the bulk elastic modulus of the sample compared to the homogeneous model without microcracks (Figure 4). This impact is more prominent for experiments with pre-cut fractures (C and H) compared to the intact experiment (A) due to increased slip and opening on microcracks near the stress concentrations produced by slip on larger pre-cut fractures (Figure 6). For each experiment geometry, we tested three models with different randomized configurations of microcracks. These variations produced negligible variation in the pre-fracture growth stress-strain curve (Figure 4).

Slip and Opening on Microcracks and Fractures

Maps of the maximum Coulomb stress and mean normal stress within a homogeneous isotropic model of the Yang et al. (2009) experiment C illuminate the impact of large pre-cut fractures on the stresses within the sample (Figures 6A,E). These stress distributions impact microcrack deformation (Figure 6B–D, F–H). Slip is suppressed in regions that experience strong compression perpendicular to the microcrack, such as within the lobes of compression to the side and front of the pre-cut fractures. Slip on microcracks is enhanced in regions with both high Coulomb stress and mean normal tension (Figure 6A–B, E–F). Because the Coulomb stress incorporates normal stress, the occurrence of cracks with greatest slip within zones of high Coulomb and lower compression suggests that unclamping of these cracks promotes slip. This is consistent with the pattern that vertical cracks have greater opening and slip than more obliquely oriented microcracks (Figure 7). While obliquely oriented microcracks may have greater shear stress than vertical microcracks, their greater clamping can inhibit slip. Interaction with other nearby slipping fractures and microcracks also affects slip and opening on individual microcracks. At the highest applied strain, for example, a microcrack in line with the growing fracture tip experiences slip and opening despite being nearly horizontal (Figure 6D, Figure7C).

The map of mean normal stress in the homogeneous model shows regions of tension along the central axis near the top and bottom of the sample, and along the outside edge of each pre-cut crack (Figure 6E). These regions within the sample promote the greatest amount of opening on the microcracks. Microcracks throughout the model experience compression and interpenetration, especially horizontally oriented microcracks that are perpendicular to the axial loading. Compression is concentrated in lobes at the interior edges and tip of the pre-cut fractures. Maps of opening and closing on microcracks reveal that microcracks along the central axis of the sample (Figures 6F–H) experience more closing than those along the lateral edges of the sample. This pattern is consistent with the compressive stress shadow at the sample sides that develops as the pre-cut fractures slip to accommodate significant axial compression (Figure 6).

As strain increases and pre-cut fractures grow, a greater number of microcracks slip and open (Figure 6C–D, G–H, Figure 7). The range of values plotted within Figure 6 highlights the variation in microcrack deformation. Because elements along pre-cut and growing fractures experience greater amounts of slip, opening, and closing than the plotted range, these features become saturated in Figure 6, so we plot their values on Figure 7 for the same three values of strain. Slip along the pre-cut fractures increases with increasing axial strain and fracture propagation. As slip increases and the fractures propagate, the pre-cut fractures also experience lesser closing, and a portion of a pre-cut fracture switches to opening at the highest modeled strain (Figure 7C). New fracture growth elements exhibit the most opening, and have less slip than the pre-cut fractures. Most of the slip along the large, connected fractures is right-lateral, but in a few places connections to microcracks produce small amounts of local left-lateral slip (Figures 7B,C).

Monte Carlo Realizations of Microcrack Linkage and Propagation

To assess the range of potential propagation paths possible with different populations of microcracks, we set up 100 simulations of crack growth in models with different random realizations of the 250 distributed microcracks (Figure 8A). For each simulation, we successively increase the applied strain on the models in increments of 0.2 × 10⁻³ to promote controlled fracture growth. The results of these simulations are overlain on each other in Figure 8B. A propagation path density plot (Figure 8C) shows that while heterogeneity does produce some variation to the fracture path, the locations with the most frequent fracture growth align closely with the fracture path produced in the homogeneous model.

Examples of individual fracture paths that align well with each of the two experimentally produced fracture paths of Yang et al. (2009) are shown in Figures 8D,E. In all simulations, fractures initiate at the precut fracture tip and propagate to link with microcracks. The rough topology of the fracture path compared with that of the homogeneous models owes to the linkage of microcracks. While the axially oriented fracture propagation path observed from the lower pre-cut fracture of Yang et al. (2009) experiment C is not the most common from our Monte Carlo analysis, this variation emerges from the realizations (Figure 8E). The axial alignment of the lower fracture in experiment C may arise from the particular arrangement of microcracks in part of that sample.

Fracture Propagation and Stress-Strain Curves

We expect that the stress-strain evolution from heterogeneous simulations that include microcrack deformation will differ from that of homogeneous simulations (Figure 9). In this comparison, the models have the same intact tensile and inherent shear strength (tuned such that failure begins at the start of inelasticity in experiment C; strain of 2.4e-3). We find that fracture growth in the homogeneous model starts with just one element of growth from each pre-cut crack (Figure 9B), and then under the next increment of increased strain (2.65e-3), the fractures grow 135 additional elements, to the edges of the model (9c). By contrast, the model with microcracks requires greater strain to propagate to the edge of the model and generally propagates with fewer new elements at each increment of strain. The heterogeneous model grows three new elements at the strain of 2.4e-3, 15 elements at the next increment of strain (e = 2.65e-3), 20 elements at the next increment of strain (e = 2.9e-3), and 42 elements of growth at strain of 3.1e-3.

Microcrack propagation contributes to the non-linearity of the stress-strain curve prior to failure. The heterogeneous model with microcracks reproduces the weakening and non-linear stress-strain response observed in the experiment (Figure 9). In contrast, the homogeneous model retains a purely linear stress-strain response prior to failure. The models do not reproduce the large stress drop that accompanies failure because our simulations do not fully disaggregate even as fractures near the model boundaries.

The Boundary Element Method code used here is well-suited to analyze continuum mechanics within a single body (e.g. Crouch and Starfield, 1990)but can become unreliable when fractures connect to the model edges to create multiple distinct bodies. Furthermore, the geometric complexity that arises from the coalescence of many microcracks can create numerical instabilities. Some elements intersect at sharp kinks, which produce high local stress singularities that sometimes resist convergence over many iterations of frictional slip. While both fractures in the model with microcracks have not grown to the edge of the model (Figure 9 c, e and g), we find that models with more elements of fracture growth than the final version shown here produce unreliable results due to accrued geometric complexities. Accordingly, we stop the simulation before macroscopic failure is reached and while the model results remain robust, as determined by the condition number.

We also simulate the final observed experimental fracture geometry with and without microcracks (Figures 9F,G) to see if the resulting axial stress differs from that of fracture paths that emerge by work optimization. For these models, we prescribe the experimental fracture pattern to the model and apply the highest axial strain. Models with the experimental fracture paths achieve a lower axial stress than the models with the work-optimal fracture paths. The experimental fracture path model that includes microcracks produces only a slightly lower stress than the model without microcracks. This result suggests that the smoother fracture geometry from the experiment is more efficient than the work-optimal path produced by GROW. The roughness of the simulated work-optimal path can locally impede slip producing a less efficient fracture network than within the experiments where abrasion and the production of gouge can smooth slip surfaces.

Energy Budget

We examine three components of the deformational energy budget from the simulated fracture propagation histories—external work, W_ext, internal work, W_int, and frictional work, W_fric. Work against gravity is not considered because it is negligible within these experiments. Consequently, the total external work on the model is the sum of the frictional work and the internal work. We follow Cooke and Madden (2014) for calculations of individual work budget components. Frictional work is calculated from shear traction and slip along all fractures and microcracks. External work is calculated from stress and displacement along the model boundaries. We consider the difference between W_ext and W_fric as the internal work because direct numerical calculations of W_int incur large uncertainties due to stress singularities around crack tips. The non-conservative seismic energy and energy consumed by fracture propagation can be implicitly considered from changes to the external work component with propagation and slip (e.g. Del Castello and Cooke 2007). For the analysis here, we investigate the frictional and internal work contributions that sum to the evolving W_ext and we do not explore how reductions in W_ext represent energy available for seismic shaking and fracture propagation.

At low strains, prior to slip on distributed microcracks, our homogeneous and heterogeneous work budgets are identical (Figure 10; Table 2). At higher applied strain levels, it takes greater external work to grow cracks and deform the model that includes microcracks. The increase of W_ext is non-linear with strain with decreasing slope after the onset of fracture propagation (2.4e-3). While the homogeneous model grows fractures to the edge of the model at a strain of 2.65e-3 and reaches peak external work of 225.4 J, the model with deforming microcracks experiences lesser fracture propagation and requires greater work of 267.5 J to deform the sample at the same applied strain value. While we stop the model with microcracks before it reaches the edges of the model, the external work on the system at its last stage is 334.8 J—demonstrating that, perhaps counterintuitively, including randomly-oriented microcracks requires greater loading to reach failure; the microcracks strengthen the sample. This strengthening is also consistent with the microcrack model requiring higher strain to propagate fractures. As previously noted, the absence of both gouge production and fracture smoothing in the model contributes to this effect as fractures terminate against existing microcracks and require greater applied loading to continue propagation.

TABLE 2

TABLE 2. Energy budget values for homogeneous and heterogeneous models. The homogeneous model reached failure at a strain of 2.65e-3 and therefore energy budget values are not reported for higher strains.

Frictional work in both simulations increases with strain and fracture growth, with the exception of the final strain for the heterogeneous model. The heterogeneous model at strain before the fractures propagate to the model edges (2.9e-3) has greater W_fric than the model when the fractures are finished propagating (Figure 10). All work values plotted in Figure 10 are calculated after all fracture growth at each applied strain. To further investigate the changes in frictional and external work with fracture propagation, we examine details of the heterogeneous model for each increment of fracture growth (Figure 11).

FIGURE 11

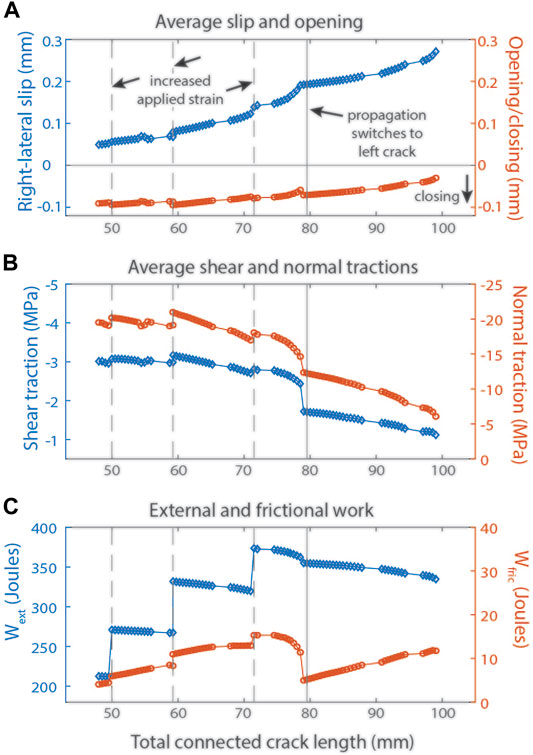
FIGURE 11. (A) Average slip and opening (negative values reflect closing) on the pre-cut cracks in the heterogeneous model (final fracture geometry shown in Figure 9E) at each increment of fracture growth, plotted against the total connected fracture length. Horizontal discontinuities reflect fracture growth steps that incorporated pre-existing microcracks, resulting in a bigger increase in the total connected fracture length than the addition of individual elements. Dashed grey lines mark where fracture growth stopped and the applied strain was increased. Solid grey lines indicate when fracture growth switched from the upper crack to the lower crack in the model. (B) Average shear and normal stress on the pre-cut cracks. (C) External work and frictional work, plotted for each increment of fracture growth, against the total connected fracture length.

As fractures propagate, the average slip and opening along the pre-cut fractures (Figure 11A), the shear and normal tractions on pre-cut fractures (Figure 11B), and the external and frictional work components of the energy budget (Figure 11C) all evolve in response to the changing fracture network. We focus on changes to the slip, closing, and tractions on the pre-cut fractures because they accommodate the most slip in the model (Figure 7C) and their behavior reflects the major changes to the system as a whole. Horizontal gaps between points in Figure 11 reflect the coalescence of microcracks with the growing fracture, adding significantly more length to the total fracture length than a typical growth step of one element. Throughout the simulation of fracture growth, average slip along the pre-cut fractures increases and the magnitude of closing decreases as fracture length grows (Figure 11A). The closing along the pre-cut fractures increases slightly at the onset of each axial strain increment (vertical dashed lines, Figure 11) but then decreases again with further fracture propagation. The magnitude of shear and normal tractions increase at the onset of each new applied strain increment, but decrease with new fracture growth (Figure 11B).

The rate of shear traction decrease is not steady. The shear traction along the pre-cut fractures decreases sharply around total fracture length ∼75 mm, where the upper growing fracture approaches the model boundary (Figure 6H). This decrease in shear traction from ∼75 to 80 mm of fracture length yields a drop in frictional work at the same stage in the simulation (Figure 11C) because frictional work is calculated as a product of slip and shear stress, and slip does not increase in proportion to the decrease in shear traction. When the fracture propagates towards the edge of the model, the axial compressive loading is channeled towards the center of the sample, evidenced as closing along microcracks (Figure 6H). This adjustment to the stress pattern reduces the magnitude of resolved shear and normal tractions on the pre-cut fracture but does not produce a comparable increase in slip. The limited increase in slip may owe to the geometry of the fractures. The sharpest decrease in shear traction and frictional work occurs during one increment of fracture growth, after which both begin to slowly increase again. This occurs a few fracture growth increments before the fracture growth switches to the left side pre-cut fracture, noted by a vertical line in Figure 11.

After fracture growth switches from the right-side pre-cut fracture to the left-side fracture, frictional work continues to slowly increase again with fracture propagation. External work increases with each increment of applied strain, and then decreases with fracture growth at each applied strain (Figure 11C). The decreases in frictional work also reduce external work between fracture lengths 70–80 mm. At other times in the simulation, W_ext decreases with increasing frictional work as fractures propagate. This requires that internal work decreases with fracture propagation, which is consistent with the energy for frictional slip deriving from the stored internal work.

Discussion

We find that the explicit inclusion of pre-existing microcracks affects the fracture path, stress-strain relationship, and abruptness of failure for simulations of fracture growth. The contrast between abrupt fracture propagation in our simulations of homogeneous volumes, versus propagation over several increments of loading in models with pre-existing weaknesses agrees with the observations of Cartwright-Taylor et al. (2020). Comparing experiments of brittle failure in intact granite versus granite with pre-existing weaknesses created using heat-stressing, Cartwright-Taylor et al. (2020) observed that more homogeneous samples without damage failed catastrophically and without useful precursory information in the transition to failure. In contrast, a heterogeneous sample damaged using heat-stressing produced a stable inverse power law acoustic emission event rate transition to failure. This aligns with the contrasting behavior of our simulations, in which the heterogeneous simulation requires several increments of increased strain to sustain fracture growth, whereas the homogeneous simulation propagates nearly its entire fracture length within one increment of axial strain. This finding is also in line with previous work demonstrating that failure forecasting power using acoustic emissions is improved by heterogeneous conditions (e.g., Vasseur et al., 2015).

Interestingly, within the experiments of Cartwright-Taylor et al. (2020), failure of the damaged sample occurs at a slightly lower axial strain (1.87% vs. 2.08%) and a slightly higher differential stress (185 MPa vs. 182 MPa) than for the intact sample. While this data does not match our simulation of failure at a higher strain for the heterogeneous sample, the higher peak stress for the damaged sample suggests that more energy is stored in the damaged sample prior to failure. This increase in energy required for failure is consistent with our model results (Figure 10). The values for failure strain and peak stress between the two experiments performed by Cartwright-Taylor et al. (2020) are not replicated with multiple experiments, limiting the interpretation of these differences. While their experiments differed in many ways from the numerical simulations presented here (triaxial, no pre-cut fractures) the first order difference between the stress at failure for homogeneous and heterogeneous samples is the same, suggesting that heterogeneity aids failure forecasting.

Our results contrast with experiments that demonstrate that increased heterogeneity in the form of porosity decreases the bulk strength of a sample (e.g. Palchik 1999). This difference suggests that void spaces impact bulk strength differently than weak grain boundaries in low-porosity material like marble. The approach used here, which simulates weak grain boundaries, would not be suitable to modeling a high-porosity material like sandstone. While one might not expect that adding weak grain boundaries to the model could strengthen the sample, the largest fractures in this experiment host much more deformation than microcracks at the grain boundary scale, and therefore exert the greatest control on the failure strength of the whole sample. These results do not necessarily conflict with general observations that larger rock masses are weaker due to containing more damage and larger flaws (e.g. Rocco et al., 1999; Kaklis and Vardoulakis, 2004), because the microcracks are not the largest fractures present in these simulations.

The role of weak grain boundaries on fracture propagation in the heterogeneous models aligns with research in materials science, showing that materials like fiberglass are strengthened by the heterogeneities that serve to arrest fracture propagation (Gordon 2006). At the onset of fracture propagation, the precut fractures in the homogenous model propagate to the model edges, whereas the heterogeneous model at that same strain arrests after linking to several existing microcracks. Greater applied axial strains are required for further growth because of the strengthening effect of pre-existing microcracks. Additionally, the rough fracture geometry that results from microcrack linkage in the numerical models enhances the strengthening effect.

Mapping slip and opening on microcracks in our simulations provides an opportunity to compare simulated strain distributions to those mapped in 3D tomography experiments that reveal the evolving fracture network during deformation, as well as time series of the local strain tensors (e.g. Renard et al., 2019). We observe that simulations at higher strains exhibit some clustering of similar-sense slip on microcracks, clustered adjacent to opposite-sense slip on other nearby microcracks and fractures (Figures 6C,D), especially near the tips of growing fractures and in clusters along the central axis of the model at the top and bottom. We also note that as some growing fractures accommodate opening, closing on nearby microcracks is enhanced. This is similar to the strain-mechanism clustering noted by Renard et al. (2019) in triaxial deformation experiments performed on monzonite. They describe a spatial correlation of microscale zones of large positive and negative volumetric strains, and opposite senses of shear strains, attributed to interactions of microcracks and heterogeneous stresses.

Relating our results to possible implications for crustal faulting and earthquakes, these findings suggest that regions with greater heterogeneity are more likely to produce precursory signals of large earthquakes, or produce more and smaller earthquakes. One study by Li and Xu (2013) compared discrete regions in eastern China with different scattering coefficients for seismic wave attenuation, one way of estimating crustal heterogeneity. They found that regions with greater crustal heterogeneity are more susceptible to tidal triggering of earthquakes than regions with less heterogeneity. This finding aligns with our results that heterogeneity contributes to the arrest of fractures, which may leave them near critical stress conditions that can be more easily tipped towards failure by the small stress variations produced by tidal forcing. Mancini et al. (2020) found that forecasting of aftershocks during the 2019 Ridgecrest earthquake sequence was improved by incorporating fault and stress field heterogeneity, affirming that the occurrence of multiple smaller quakes in a sequence may be strongly mediated by local heterogeneity.

These simulations of fracture propagation and microcrack linkage using work optimization demonstrate the utility of this approach in capturing some aspects of crack coalescence processes in a crystalline, low-porosity rock. These results suggest that simulations of fractures in crystalline rocks that do not explicitly consider heterogeneity may be underestimating the energy required to deform a sample or propagate fractures. This approach can be extended to simulations that include populations of fractures informed by experimental observations to explore the impact of various crack properties like length, orientation, and clustering on the propensity for propagation and coalescence.

Conclusion

1. Work optimization combined with 2D BEM mechanical models closely simulate fracture growth and the stress-strain response of uniaxial compression experiments on marble with pre-cut fractures.

2. The inclusion of microcracks in simulations of crack growth produce some variation in fracture propagation paths that resembles the natural variation documented in experiments. Fracture paths ultimately cluster around the path simulated with a homogeneous model.

3. Microcracks on the scale of grain boundaries play a critical role in the non-linear response of the model prior to failure.

4. Inclusion of microcracks that simulate weak grain boundaries strengthens the sample, requiring more energy to crack the sample than is required in a homogeneous simulation. This effect is produced in part by the arrest of fracture growth at microcracks and the absence of smoothing of slip surfaces that results from abrasion.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/l-fatt/Uniaxial_marble_models.

Author Contributions

LF developed models, processed results, and wrote the manuscript. MC supervised model development and results processing, and contributed text and significant revisions to the manuscript. JM developed and updated the numerical modeling code, guided the development of figures, and contributed ideas and significant revisions to the manuscript.

Funding

This work was funded by a National Science Foundation grant to MC (EAR-1650368). LF also received salary support from a UMass Geosciences Fellowship and UMass Dissertation Completion Fellowship. Numerical simulations were run in part on the Massachusetts Green High Performance Computing Center.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the editor Ernest Henry Rutter and reviewers Srisharan Shreedharan and Robin Thomas for their valuable feedback that improved the manuscript. We thank François Renard for feedback on the project from concept to execution. We thank Haiying Gao, Cong Li, and Evan Thaler for support in the use of the Massachusetts Green High Powered Computing Center. We thank Sanjay Arwade, Laurie Brown, Jack Loveless, Jenn Beyer, and Hanna Elston for valuable feedback on the project during its development. We thank William Clement for help troubleshooting code used to process results.

References

Aben, F. M., Brantut, N., Mitchell, T. M., and David, E. C. (2019). Rupture Energetics in Crustal Rock from Laboratory‐Scale Seismic Tomography. Geophys. Res. Lett. 46 (13), 7337–7344. doi:10.1029/2019GL083040

CrossRef Full Text | Google Scholar

Bi, J., Zhou, X. P., and Qian, Q. H. (2016). The 3D Numerical Simulation for the Propagation Process of Multiple Pre-existing Flaws in Rock-like Materials Subjected to Biaxial Compressive Loads. Rock Mech. Rock Eng. 49 (5), 1611–1627. doi:10.1007/s00603-015-0867-y

CrossRef Full Text | Google Scholar

Cartwright‐Taylor, A., Main, I. G., Butler, I. B., Fusseis, F., Flynn, M., and King, A. (2020). Catastrophic Failure: How and when? Insights from 4‐D In Situ X‐ray Microtomography. JGR Solid Earth 125 (8), 1–30. doi:10.1029/2020JB019642

CrossRef Full Text | Google Scholar

Chen, C. S., and Hsu, S. C. (2001). Measurement of Indirect Tensile Strength of Anisotropic Rocks by the Ring Test. Rock Mech. Rock Eng. 34 (4), 293–321. doi:10.1007/s006030170003

CrossRef Full Text | Google Scholar

Cooke, M. L., and Madden, E. H. (2014). Is the Earth Lazy? A Review of Work Minimization in Fault Evolution. J. Struct. Geology. 66, 334–346. doi:10.1016/j.jsg.2014.05.004

CrossRef Full Text | Google Scholar

Cooke, M. L., and Pollard, D. D. (1997). Bedding-Plane Slip in Initial Stages of Fault-Related Folding. J. Struct. Geology. 19, 567–581. doi:10.1016/S0191-8141(96)00097-1

CrossRef Full Text | Google Scholar

Crouch, S. L., and Starfield, A. M. (1990). Boundary Element Methods in Solid Mechanics. London: Unwin Hyman.

Google Scholar

Del Castello, M., and Cooke, M. L. (2007). Underthrusting-Accretion Cycle: Work Budget as Revealed by the Boundary Element Method. J. Geophys. Res. 112 (12), 1–14. doi:10.1029/2007JB004997

CrossRef Full Text | Google Scholar

Gordon, J. E. (2006). The New Science of Strong Materials; or, Why You Don’t Fall through the Floor. Harmondsworth: Penguin.

Google Scholar

Griffith, A. A. (1921). VI. The Phenomena of Rupture and Flow in Solids. Phil. Trans. R. Soc. Lond. A. 221, 163–198. doi:10.1098/rsta.1921.0006

CrossRef Full Text | Google Scholar

Hazzard, J. F., Young, R. P., and Maxwell, S. C. (2000). Micromechanical Modeling of Cracking and Failure in Brittle Rocks. J. Geophys. Res. 105 (B7), 16683–16697. doi:10.1029/2000jb900085

CrossRef Full Text | Google Scholar

Kaklis, K. N., and Vardoulakis, I. (2004). “An Experimental Investigation of the Size Effect in Indirect Tensile Test on Dionysos Marble,” in Proc. 7th Nat. Congress on Mechanics. Chania, Greece: Technical University of Crete Vol. 2, 151–157.

Google Scholar

Kandula, N., Cordonnier, B., Boller, E., Weiss, J., Dysthe, D. K., and Renard, F. (2019). Dynamics of Microscale Precursors during Brittle Compressive Failure in Carrara Marble. J. Geophys. Res. Solid Earth 124, 6121–6139. doi:10.1029/2019JB017381

CrossRef Full Text | Google Scholar

Karaman, K., Cihangir, F., Ercikdi, B., Kesimal, A., and Demirel, S. (2015). Utilization of the Brazilian Test for Estimating the Uniaxial Compressive Strength and Shear Strength Parameters. J. S. Afr. Inst. Min. Metall. 115 (3), 185–192. doi:10.17159/2411-9717/2015/v115n3a3

CrossRef Full Text | Google Scholar

Lei, Q., Gholizadeh Doonechaly, N., and Tsang, C.-F. (2021). Modelling Fluid Injection-Induced Fracture Activation, Damage Growth, Seismicity Occurrence and Connectivity Change in Naturally Fractured Rocks. Int. J. Rock Mech. Mining Sci. 138, 104598. doi:10.1016/j.ijrmms.2020.104598

CrossRef Full Text | Google Scholar

Li, Q., and Xu, G.-M. (2013). Precursory Pattern of Tidal Triggering of Earthquakes in Six Regions of China: the Possible Relation to the Crustal Heterogeneity. Nat. Hazards Earth Syst. Sci. 13 (10), 2605–2618. doi:10.5194/nhess-13-2605-2013

CrossRef Full Text | Google Scholar

Li, S., and Zhang, D. (2021). Development of 3‐D Curved Fracture Swarms in Shale Rock Driven by Rapid Fluid Pressure Buildup: Insights from Numerical Modeling. Geophys. Res. Lett. 48 (8), 1–12. doi:10.1029/2021GL092638

CrossRef Full Text | Google Scholar

Lunn, R. J., Willson, J. P., Shipton, Z. K., and Moir., H. (2008). Simulating Brittle Fault Growth from Linkage of Preexisting Structures. J. Geophys. Res. 113 (7), 1–10. doi:10.1029/2007JB005388

CrossRef Full Text | Google Scholar

Madden, E. H., Cooke, M. L., and McBeck, J. (2017). Energy Budget and Propagation of Faults via Shearing and Opening Using Work Optimization. J. Geophys. Res. Solid Earth 122 (8), 6757–6772. doi:10.1002/2017JB014237

CrossRef Full Text | Google Scholar

Mancini, S., Segou, M., Werner, M. J., and Parsons, T. (2020). The Predictive Skills of Elastic Coulomb Rate-And-State Aftershock Forecasts during the 2019 Ridgecrest, California, Earthquake Sequence. Bull. Seismological Soc. America 110 (4), 1736–1751. doi:10.1785/0120200028

CrossRef Full Text | Google Scholar

McBeck, J. A., Madden, E. H., and Cooke, M. L. (2016). Growth by Optimization of Work (GROW): A New Modeling Tool that Predicts Fault Growth through Work Minimization. Comput. Geosciences 88, 142–151. doi:10.1016/j.cageo.2015.12.019

CrossRef Full Text | Google Scholar

McBeck, J., Ben-Zion, Y., and Renard, F. (2021a). Fracture Network Localization Preceding Catastrophic Failure in Triaxial Compression Experiments on Rocks. Front. Earth Sci. 9 (11), 1–15. doi:10.3389/feart.2021.778811

CrossRef Full Text | Google Scholar

McBeck, J., Ben-Zion, Y., Zhou, X., and Renard, F. (2021b). The Influence of Preexisting Host Rock Damage on Fault Network Localization. J. Struct. Geology. 153 (11), 104471. doi:10.1016/j.jsg.2021.104471

CrossRef Full Text | Google Scholar

McBeck, J., Cooke, M., and Fattaruso, L. (2020). Predicting the Propagation and Interaction of Frontal Accretionary Thrust Faults with Work Optimization. Tectonophysics 786 (4), 228461. doi:10.1016/j.tecto.2020.228461

CrossRef Full Text | Google Scholar

McBeck, J., Mair, K., and Renard, F. (2021c). Decrypting Healed Fault Zones: How Gouge Production Reduces the Influence of Fault Roughness. Geophys. J. Int. 225 (2), 759–774. doi:10.1093/gji/ggab003

CrossRef Full Text | Google Scholar

Moir, H., Lunn, R. J., Shipton, Z. K., and Kirkpatrick, J. D. (2010). Simulating Brittle Fault Evolution from Networks of Pre-existing Joints within Crystalline Rock. J. Struct. Geology. 32 (11), 1742–1753. doi:10.1016/j.jsg.2009.08.016

CrossRef Full Text | Google Scholar

Olsson, W. A. (1974). Grain Size Dependence of Yield Stress in Marble. J. Geophys. Res. 79 (32), 4859–4862. doi:10.1029/jb079i032p04859

CrossRef Full Text | Google Scholar

Palchik, V. (1999). Influence of Porosity and Elastic Modulus on Uniaxial Compressive Strength in Soft Brittle Porous Sandstones. Rock Mech. Rock Eng. 32 (4), 303–309. doi:10.1007/s006030050050

CrossRef Full Text | Google Scholar

Renard, F., McBeck, J., Kandula, N., Cordonnier, B., Meakin, P., and Ben-Zion, Y. (2019). Volumetric and Shear Processes in Crystalline Rock Approaching Faulting. Proc. Natl. Acad. Sci. U.S.A. 116 (33), 16234–16239. doi:10.1073/pnas.1902994116

PubMed Abstract | CrossRef Full Text | Google Scholar

Renard, F., Weiss, J., Mathiesen, J., Ben-Zion, Y., Kandula, N., and Cordonnier, B. (2018). Critical Evolution of Damage toward System-Size Failure in Crystalline Rock. J. Geophys. Res. Solid Earth 123 (2), 1969–1986. doi:10.1002/2017JB014964

CrossRef Full Text | Google Scholar

Renshaw, C. E., Schulson, E. M., and Iliescu, D. (2019). Experimental Observation of the Onset of Percolation in Freshwater Granular Ice. J. Geophys. Res. Solid Earth 124 (3), 2445–2456. doi:10.1029/2018JB016414

CrossRef Full Text | Google Scholar

Rocco, C., Guinea, G. V., Planas, J., and Elices, M. (1999). Size Effect and Boundary Conditions in the Brazilian Test: Experimental Verification. Mat. Struct. 32 (3), 210–217. doi:10.1007/bf02481517

CrossRef Full Text | Google Scholar

Tal, Y., Evans, B., and Mok, U. (2016). Direct Observations of Damage during Unconfined Brittle Failure of Carrara Marble. J. Geophys. Res. Solid Earth 121 (3), 1584–1609. doi:10.1002/2015JB012749

CrossRef Full Text | Google Scholar

Thomas, R. N., Paluszny, A., and Zimmerman, R. W. (2020). Permeability of Three‐Dimensional Numerically Grown Geomechanical Discrete Fracture Networks with Evolving Geometry and Mechanical Apertures. J. Geophys. Res. Solid Earth 125 (4). doi:10.1029/2019JB018899

CrossRef Full Text | Google Scholar

Vasseur, J., Wadsworth, F. B., Lavallée, Y., Bell, A. F., Main, I. G., and Dingwell, D. B. (2015). Heterogeneity: The Key to Failure Forecasting. Sci. Rep. 5 (1), 1–7. doi:10.1038/srep13259

CrossRef Full Text | Google Scholar

Yang, S. Q., Dai, Y. H., Han, L. J., and Jin, Z. Q. (2009). Experimental Study on Mechanical Behavior of Brittle Marble Samples Containing Different Flaws under Uniaxial Compression. Eng. Fracture Mech. 76 (12), 1833–1845. doi:10.1016/j.engfracmech.2009.04.005

CrossRef Full Text | Google Scholar

Zhou, X.-P., Gu, X.-B., and Wang, Y.-T. (2015b). Numerical Simulations of Propagation, Bifurcation and Coalescence of Cracks in Rocks. Int. J. Rock Mech. Mining Sci. 80, 241–254. doi:10.1016/j.ijrmms.2015.09.006

CrossRef Full Text | Google Scholar

Zhou, X.-P., and Wang, Y.-T. (2016). Numerical Simulation of Crack Propagation and Coalescence in Pre-cracked Rock-like Brazilian Disks Using the Non-ordinary State-Based Peridynamics. Int. J. Rock Mech. Mining Sci. 89 (10), 235–249. doi:10.1016/j.ijrmms.2016.09.010

CrossRef Full Text | Google Scholar

Zhou, X. P., Bi, J., and Qian, Q. H. (2015a). Numerical Simulation of Crack Growth and Coalescence in Rock-like Materials Containing Multiple Pre-existing Flaws. Rock Mech. Rock Eng. 48 (3), 1097–1114. doi:10.1007/s00603-014-0627-4

CrossRef Full Text | Google Scholar

Zhou, X. P., and Yang, H. Q. (2012). Multiscale Numerical Modeling of Propagation and Coalescence of Multiple Cracks in Rock Masses. Int. J. Rock Mech. Mining Sci. 55, 15–27. doi:10.1016/j.ijrmms.2012.06.001

CrossRef Full Text | Google Scholar