
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci., 25 January 2023
Sec. Geohazards and Georisks
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.1076023
This article is part of the Research TopicGeological Disasters in Deep Engineering: Mechanism, Warning, and Risk Mitigation, volume IIView all 11 articles
The mesoscale heterogeneity of rock determines its macroscale mechanical performance to a large extent. In this paper, a sub-block element discontinuous deformation analysis (DDA) method coupled with a statistic heterogeneity model was used to simulate the fracturing failure of pre-notched rock specimens. The simulation recreated the macroscale whole-process nonlinear deformation and fracturing failure of pre-notched disc and rectangular specimens with some important features explored in experiments or other numerical simulations. Combing intact heterogeneous rock specimen simulations in previous work, the effect of the heterogeneity on the reproducibility of macroscale strength and failure patterns of the specimens were investigated. Results indicate that the influence degree of the heterogeneity on the macroscale equivalent strength and fracturing failure pattern reproducibility varies with the specimen particularities (disc or rectangular, pre-notched or intact, and inclination of the pre-existing flaw), and the reason behind was discussed from the point view of stress concentration. This work is meaningful for the understanding of the result discreteness of rock specimen experiments, and assures the importance to consider the rock heterogeneity in practical rock engineering.
Rock masses are composed of rock bulks and discontinuities such as joints and faults, while the rock bulk is a typical heterogeneous material consists of mineral grains, grain boundaries and defects like voids and microcracks, etc., at the mesoscale. The mesoscale mechanical heterogeneity of rock is charactered by the variation of the deformation and strength properties with the mesoscopic spatial locations, which consequently leads to the uncertain and statistic characters of the macroscale deformation and fracturing failure of rock (Tang et al., 1998; Li et al., 2022; Yang et al., 2022). An acknowledged phenomenon that could largely attributed to the heterogeneity of rock is that rock experiments of specimens generally show poor reproducibility of the macroscale strength and fracturing failure patterns (Alzaki et al., 2020; Shirole et al., 2020; Sun et al., 2022). For engineering practices, e.g., in the prediction of geological disasters and the design of rock engineering structures, the heterogeneity of rock is an important issue that should be carefully considered (Manouchehrian and Cai, 2016; He et al., 2019).
The mesoscale material components and distributions of rock could be well captured by high precision instruments and handled by the measure of image processing etc., which then could be correlated to the rock mechanical properties (Zheng et al., 2020; Wang and Sun, 2021). From the theoretical aspect, Bai et al. (2019) and Bai et al. (2021) developed thermo-hydro-mechanical models for geomaterials based on the tenet of particle rearrangement in porous granular materials. Regarding the study of the mesoscale mechanical behaviors of rock, therefore the macroscale equivalent mechanical performances could also be investigated, numerical simulation is an effective and favorable approach. For example, Gui et al. (2016) conducted a comprehensive investigation of grain effect (size and distribution) in discrete element modelling of intact rock through Brazilian disc and uniaxial compressive tests using Universal Distinct Element Code. Gao et al. (2016) developed a distinct element grain-based method to simulate the microstructure of rock-like materials, which allows the assignment of specific properties to both the grains and grain boundaries. Peng et al. (2021) investigated the effect of grain size on the strength of polymineralic crystalline rock using the grain-based modeling approach in discrete element method by interpreting micro-cracking process in response to loading. Rasmussen (2022) proposed a breakable grain scheme and a method to achieve bi-modular elastic material behavior in grain-based models of rocks using the hybrid lattice/discrete element method. Wu et al. (2017) and Zhou et al. (2022) developed Voronoi grain-based numerical manifold methods to investigate deformation and damage of intact rock at the mesoscale.
The above works simulated rock mechanical behaviors by explicitly representing the mesoscale structure of rock on the grain level, which may suffer high computational cost for large scale simulations. Alternatively, the mesoscale heterogeneity could be equivalently described by heterogeneity index of statistic models. For example, Liu et al. (2018) presented a heterogeneity index to describe mesoscale heterogeneity induced by grain size variation in intact rock. Li et al. (2022) used a random discrete element method to model rock heterogeneity. Yang et al. (2022) simulated the effect of heterogeneity on the characteristics of ubiquitiformal cracks in the Brazilian splitting test of rock by ABAQUS, in which the material heterogeneity is characterized by the Weibull distribution. In fact, the Weibull distribution has been widely applied to describe the mesoscale heterogeneity of materials, e.g., in the widely used rock mechanics software Rock/Realistic Failure Process Analysis (RFPA) (Tang et al., 1998; Tang et al., 2000; Tang et al., 2000). To understand the physical mechanism for the discrepancy of rock tension, Xu et al. (2020) carried out RFPA simulations of direct tension and semi-circular bending tests of intact heterogeneous rock. Tang and Zhang (2009) also presented a spatial correlation length factor into the traditional Weibull distribution to investigate the heterogeneity character of concrete failure. Combining linear elastic material constitutive relations and statistic heterogeneous models at the mesoscale, the macroscale nonlinear deformation and failure behaviors of rock could be well predicted (Tang et al., 1998).
Regarding the numerical methods to simulate the mesoscale deformation and fracturing failure of rock, discontinuous deformation analysis (DDA) (Shi and Goodman, 1985; Shi, 1992) could be a good choice among those widely used discontinuum-based methods like distinct element method (DEM) (Cundall and Hart, 1992). DDA has been widely used in various static and dynamic rock mechanics and engineering problems (Ning et al., 2017; Ning and Lv, 2022), in which rock fracturing could be successfully simulated by the sub-block element approach (Ning et al., 2011; Jiao et al., 2012; Ni et al., 2020). Ning et al. (2021) also have introduced a mesoscale statistic heterogeneity model for rock based on the Weibull distribution introduced into DDA. In that work, the fracturing failure of intact heterogeneous disc and rectangular specimens under compression were comprehensively simulated to investigate the influence of heterogeneity on the fracturing failure pattern and macroscale equivalent response of intact rock.
In the present work, the DDA method enhanced with the sub-block fracturing modeling algorithm and the Weibull distribution heterogeneity model is applied to simulate pre-notched rock specimens, and combing intact heterogeneous rock specimen simulations in previous work, the effect of the heterogeneity on the reproducibility of macroscale strength and failure patterns of the specimens are investigated. The arrangement of the rest sections of the paper is as follows. In Section 2, the applied sub-block element DDA method for fracturing simulation and the mesoscale statistic heterogeneity model for rock are briefly introduced. In Section 3, the radial compression of center-notched disc rock specimens and uniaxial compression of center-notched rectangular rock specimens are simulated with an emphasis to investigate the fracturing failure reproducibility, along with the comparison with intact heterogeneous disc and rectangular specimens. Finally, conclusion are dawn in Section 4.
DDA (Shi, 1992) is a block-based discontinuous numerical method that takes six variables as (u0 ν0 r0 εx εy γxy) with clear physical meanings for each block in two-dimension, where the first three are the translatory and rotary motions at the block center, and the last three are the normal and shear strains of the block, respectively. These variables represent a full first order approximation of the block deformation and lead to very simple form of energy formulas of elasticity, loading, constraint, inertia and contact penalty, etc. By the minimization of these energies, the corresponding sub-matrices are added to construct the global equilibrium equations of a block system through a time-marching schedule, and then the system equations are implicitly solved. Combing a strict open-close iteration to achieve the contact status convergence between blocks, DDA could be well used to solve the deformation and displacement problems of rock.
The sub-block approach is usually adopted to simulate material fracturing by DDA. As shown in Figure 1, sub-block elements are glued by artificial joints to represent continuum, and the fracturing is allowed to take place along artificial joint surfaces. In the present work, the sub-block element DDA fracturing simulation method which judges the tensile/shear fracturing along artificial joints based on the adjacent sub-block stress levels is adopted. The tensile and shear fracturing follows the maximum tensile strength criterion and the Mohr-Coulomb criterion, respectively. Compared with judging the fracturing based on the contact stresses on the artificial joint surface (Ning et al., 2011; Jiao et al., 2012), the adopted method greatly reduces the influence of sub-block divisions and especially the artificial joint orientations on the simulation results of fracturing path and failure strength, and it was also proved that triangular elements are effective for fracturing simulation with the sub-block element DDA (Ni et al., 2020).
An element-level mesoscale heterogeneity model is applied in DDA based on the Weibull distribution function. By introducing the mesoscale heterogeneity, the macroscale nonlinear behaviors of rock could be well represented based on the linear-elastic constitutive relation of DDA (Ning et al., 2021). From the Weibull distribution formula,
the cumulative distribution function can be obtained by integration as
Let Q (x) = y and simplify, it is derived that
where y is a random number between 0 and 1 m is the heterogeneous index that controls the heterodonty degree, x0 is the homogeneous material property, and x is the heterogeneous material property corresponding to the random number y. By replacing x0 with the homogeneous elastic modulus E, Poisson’s ratio μ, friction angle θ, cohesion c, and tensile strength σt, respectively, the corresponding heterogeneous rock properties related to the random number y and the heterogeneous index m can be obtained. For each DDA sub-block element, the random heterogeneous material properties are generated by a random number created by the computer, thus a heterogeneous DDA model for a problem to be simulated is constructed. Compared with the widely used finite element code RFPA for heterogeneous rock simulation, DDA gets the advantage to simulate the contacts and possible large displacements of rock.
It is worthy to be noted that most previous studies generally only considered the heterogeneity of the elasticity (modulus and Poisson’s ratio) and ignored the strength (tensile strength, cohesion, and friction angle) heterogeneity. However, it is a fact that the strength varies with locations like that of the elasticity in real rock at the mesoscale, which means that the heterogeneity of strength should be considered as well. It was proved that rock is more prone to be destructed accompanied by more dispersing cracks when considering the heterogeneity of elasticity and strength simultaneously (Ning et al., 2021). Therefore, in the present study the elasticity and strength heterogeneities are both considered.
Radial compression of disc specimens and uniaxial compression of rectangular specimens are widely applied experiments to test the deformation and fracturing failure behaviors of rock materials. Here, the fracturing failures of center-notched disc specimens and center-notched rectangular specimens are simulated to investigate the reproducibility of the radial compression test and the uniaxial compression test of rock, respectively, under the same heterogeneity degree. For the disc specimen, three different inclination angles of the pre-existing flaw are considered, and for each condition of the pre-existing flaw inclination, eight times of simulations are carried out under the same heterogeneity degree. Comparatively, to control the computational cost, for the rectangular specimen, two different inclination angles of the pre-existing flaw are considered, and for each condition of the pre-existing flaw inclination, five times of simulations are carried out under the same heterogeneity degree.
In the previous work (Ning et al., 2021), the influence of the heterogeneity degree on the fracturing failure of intact disc and rectangular specimens was investigated by considering five different values of the heterogeneity index m, namely, 1.5, 2.5, 5, 20, and 200. In the present work, a middle level heterogeneity, namely, m = 5, is considered for all the simulations. Moreover, the maximum displacement ratio, step time and the contact penalty spring stiffness in the DDA simulation are 5×10–4, 1×10–6 s, and 100 GPa, respectively, the same as those used in the previous work (Ning et al., 2021).
The geometrical model of the disc is shown in Figure 2. The radius of the disc is 50 mm, and there are two platforms with a central angle of 10° at the upper and lower ends. The radial compression is applied by two rigid loading plates at a velocity of 2 mm/s. A measuring plate is placed between the upper loading plate and the disc to capture the diametral macroscale equivalent mechanical response of the disc under the compression (note that each DDA block is in a constant stress state in each time step because of the first order assumption). The pre-existing flaw has dimensions of 29 × 0.25 mm (Al-Shayea, 2005) and an inclination angle β. The two ends of the flaw are arced like, that is, normally conducted in physical experiments.
Three different β values, namely, 30°, 45° and 60°, are considered and the corresponding sub-block element number of the model is 5511, 5469 and 5607, respectively. The mesh size is determined based on trial calculations considering the result convergency and the computational cost simultaneously. The homogeneous material properties of the disc are elastic modulus E = 20 GPa, Poisson’s ratio μ = 0.2, friction angle θ = 30°, cohesion c = 20 MPa and tensile strength σt = 5 MPa, respectively. The upper and lower platforms of the disc are set frictionless like that in the physical experiment to avoid the lateral constraint of the disc. For each disc model of the same inclination of the pre-existing flaw, eight times of simulations are carried out.
Figure 3 shows the fracturing failure pattern of the center-notched disc with three different inclination angles of the pre-existing flaw, respectively. Under each inclination of the pre-existing flaw, it can be found that the main crack paths are nearly the same in the eight simulations, which start from the two ends of the pre-existing flaw and grow to the two loading ends of the disc, similar to that in the typical experimental results in Figure 4. However, the secondary cracks differ obviously in the eight simulations under each inclination of the pre-existing flaw. When there are secondary cracks, they generally start from the disc edge and propagate to the end of the pre-existing flaw. This phenomenon also agrees with the experimental results. Therefore, for the center-notched discs, the discreteness of the fracturing failure pattern due to the heterogeneity is mainly reflected by the secondary cracks.
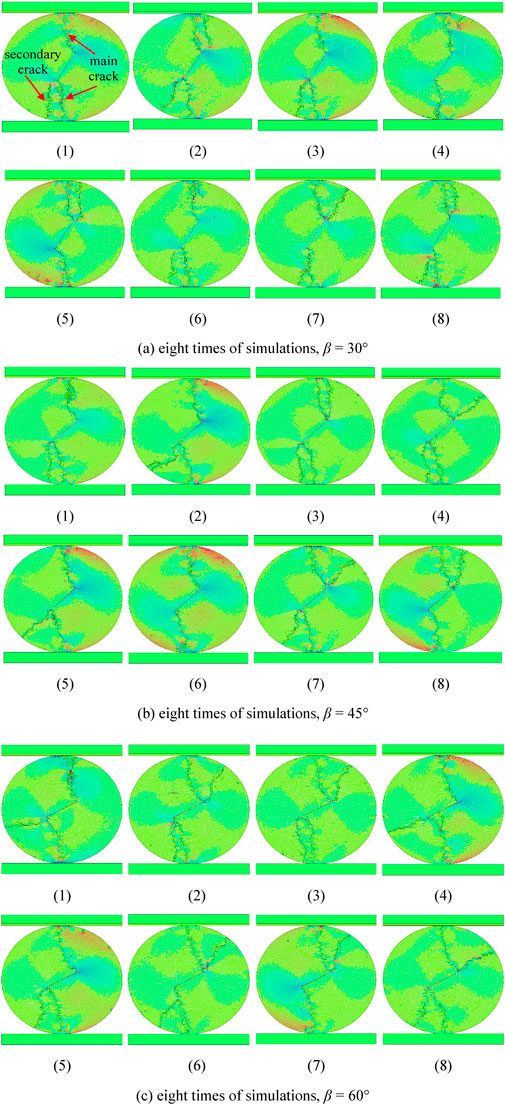
FIGURE 3. Fracturing failure patterns of the center-notched disc specimen with different β under the same heterogeneity degree (m = 5).

FIGURE 4. Typical experimental results of center-notched rock disc without (A) and (B), Huang et al., 2022) and with secondary cracks (C) and (D), Ou, 2020).
Figure 5 shows diametral equivalent stress-loading displacement curves of the disc simulations. These curves reflect the energy accumulation and dissipation characteristics of the specimens during the deformation and fracturing process under the diametral compression. It can be found that the curves are nearly linear at the initial stage and almost duplicate for the eight simulations under each inclination of the pre-existing flaw, which indicates that the heterogeneity does not influence the reproducibility of the macroscale equivalent modulus of rock evidently. The curves quickly drop after reaching the peak, and show occasional obvious rise thereafter during the falling stage. These phenomena are in good agreement with the reported experimental results (e.g., Zhang and Wang, 2009) of radial compression of center-notched rock discs. Each rising and falling of the curves represent the rest of the old cracks and the initiation and growth of new cracks.
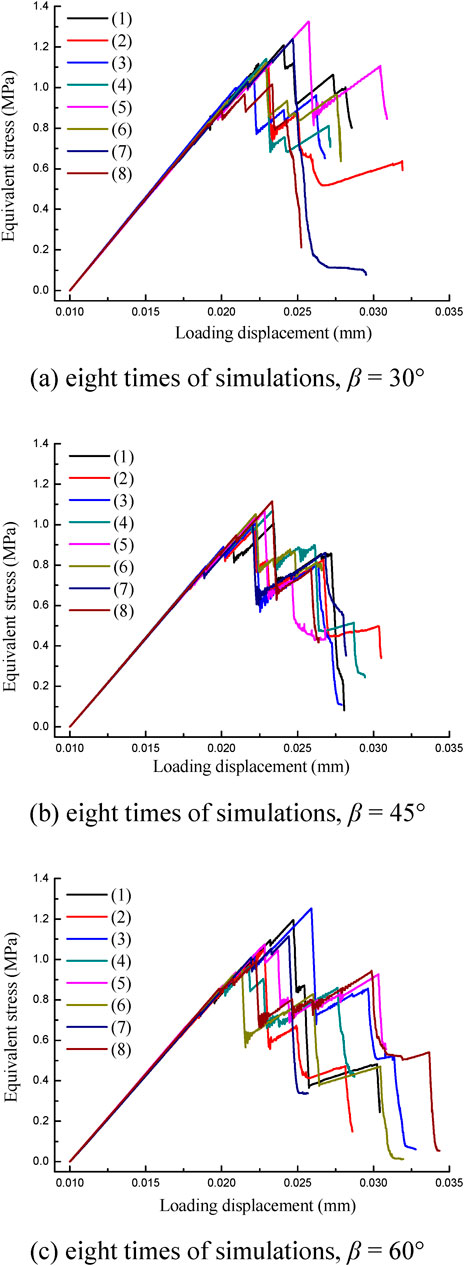
FIGURE 5. Diametral equivalent response curves of the center-notched disc specimen with different β under the same heterogeneity degree (m = 5).
Table 1 lists the maximum and minimum peak values of the curves. It can be found that, in general, the disc gets relatively lower peak strength when β = 45°, and the corresponding discreteness of the peak strength (20.7%) is the smallest among the three different conditions of the pre-existing flaw inclination. The three discreteness values for the center-notched specimens are all obvious larger than that of the intact rock disc (15.4%) with the same disc size, loading condition, material properties and heterogeneity degree (m = 5), indicating poorer strength reproducibility of the center-notched rock discs under heterogeneity, which could be attributed to the local stress concentration because of the pre-existing flaw. Figure 6 shows the fracturing failure results of the intact disc specimen for eight times of simulations. Compared with that in Figure 3, it can be found that the intact specimen gets relatively better reproducibility of the fracturing failure pattern. This could be attributed to that the intact disc gets ideal tensile stress concentration along the loading diameter.
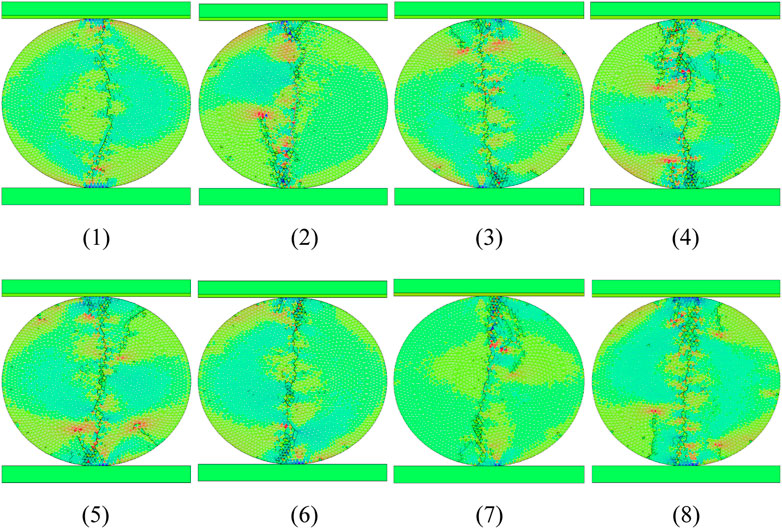
FIGURE 6. Fracturing failure patterns of the intact disc specimen with m = 5 (Ning et al., 2021).
The geometrical model of the rectangular specimen is shown in Figure 7A. The specimen has dimensions of 150 × 75 mm. The uniaxial compression is applied by two rigid loading plates at a velocity of 2 mm/s. A measuring plate is placed between the upper loading plate and the specimen to capture the axial macroscale equivalent mechanical response of the specimen under the compression. The pre-existing flaw has dimensions of 20 × 0.4 mm (Wong et al., 2002) and an inclination angle β. The two ends of the flaw are arced like, that is, normally conducted in physical experiments. Two different β values, namely, 30° and 45°, are considered and the corresponding sub-block element number of the model is 13515 and 14415, respectively. The homogeneous material properties of the specimen are elastic modulus E = 20 GPa, Poisson’s ratio μ = 0.2, friction angle θ = 30°, cohesion c = 5 MPa and tensile strength σt = 2.5 MPa, respectively. The upper and lower ends of the specimen are set frictionless like that in the physical experiment to avoid the lateral constraint of the specimen. For each rectangular specimen model of the same inclination of the pre-existing flaw, five times of simulations are carried out.
Figure 8 shows the fracturing failure pattern of the center-notched rectangular specimen with two different inclination angles of the pre-existing flaw, respectively. Under each inclination of the pre-existing flaw, it can be found that the main crack paths are nearly the same in the five simulations, which start from the two ends of the pre-existing flaw and grow to the two opposite corners of the specimen. However, similar to that in the above disc specimen simulations, the secondary cracks differ obviously. The secondary cracks, especially when β = 45°, generally start from the pre-existing flaw ends and propagate nearly parallel to the uniaxial loading direction. Figure 7B is the RFPA simulation result of a center-notched rectangular rock specimen that has close geometry with the specimen in Figure 8B. It can be found that the fracturing patterns obtained by DDA and RFPA agree well. Generally, for the center-notched rectangular specimens, the discreteness of the fracturing failure pattern due to the heterogeneity is also mainly reflected by the secondary cracks.
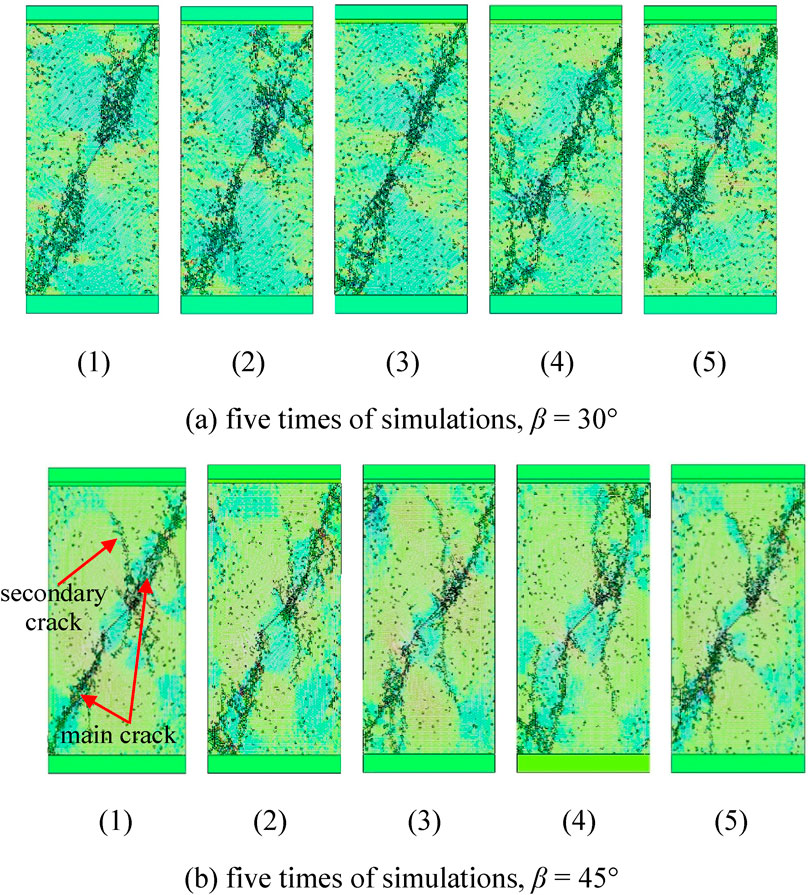
FIGURE 8. Fracturing failure patterns of the center-notched rectangular specimen with different β under the same heterogeneity degree (m = 5).
Figure 9 shows the axial equivalent stress-loading displacement curves of the rectangular specimen simulations. These curves reflect the energy accumulation and dissipation characteristics of the specimens during the deformation and fracturing process under the uniaxial compression. It can be found that the curves are nearly linear at the initial stage and almost duplicate for the five simulations under each inclination of the pre-existing flaw. Similar to that in the above disc simulations, it indicates that the heterogeneity does not influence the reproducibility of the macroscale equivalent modulus evidently. However, different from that of the disc specimens, the curves do not show the obvious occasional rise phenomenon during the falling stage after the peak for the rectangular specimens, which are also in good agreement with that of wide experiments.
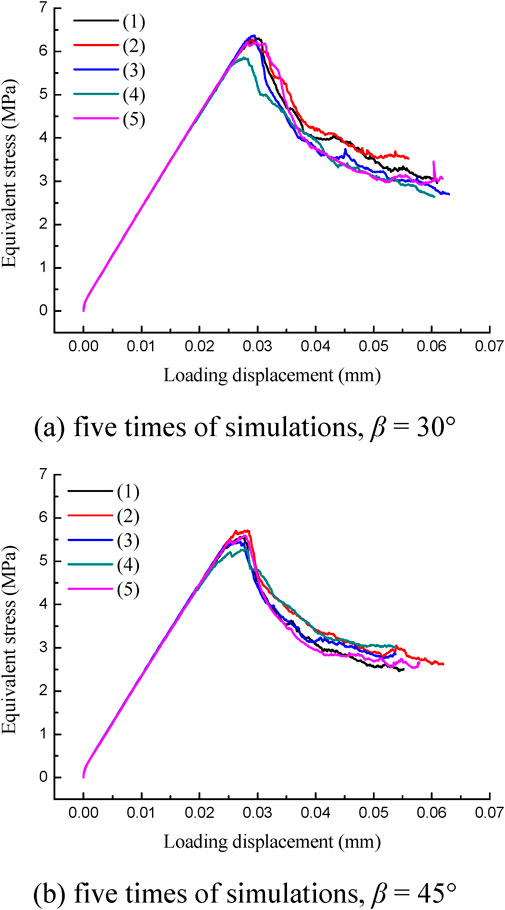
FIGURE 9. Axial equivalent response curves of the center-notched rectangular specimen with different β under the same heterogeneity degree (m = 5).
Table 2 lists the maximum and minimum peak values of the curves. It can be found that, in general, the specimen gets larger peak strength when β = 30°, and the corresponding discreteness of the peak strength (8.8%) is relatively smaller than that when β = 45° (9.2%). The two discreteness values for the center-notched specimens both are obvious larger than that of the intact rectangular specimen (5.0%) (Ning et al., 2021) with the same specimen size, loading condition, material properties and heterogeneity degree (m = 5), indicating poorer strength reproducibility of the center-notched specimens under heterogeneity again. Figure 10 shows the fracturing failure results of the intact rectangular specimen for five times of simulations. Compared with that in Figure 8, it can be found that the center-notched specimen gets much better reproducibility of the fracturing failure pattern. The poorer strength reproducibility and better fracturing pattern reproducibility of the pre-notched rectangular specimen relative to the intact rectangular specimen both could be attributed to the local stress concentration because of the pre-existing flaw. Moreover, compared with that in Table 1, it also can be concluded that the rectangular specimens, center-notched or intact, have better strength reproducibility than the disc specimens under the same heterogeneity degree.
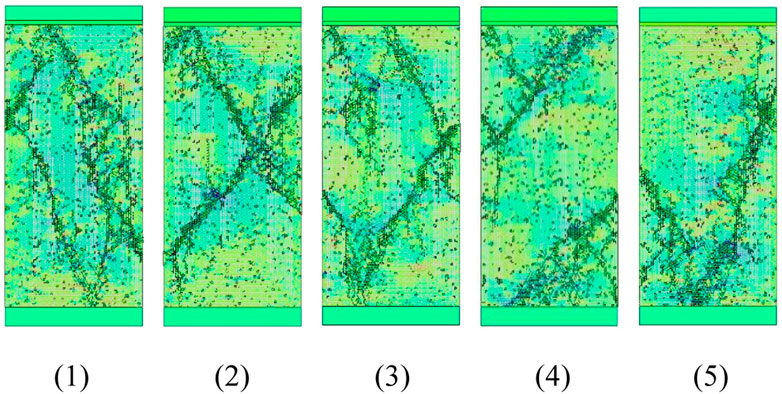
FIGURE 10. Fracturing failure patterns of the intact rectangular specimen with m = 5 (Ning et al., 2021).
In this work, by employing the sub-block element DDA method coupled with a statistic heterogeneity model based on the Weibull distribution, the fracturing failure of center-notched disc and rectangular rock specimens under the same heterogeneity degree is simulated. The simulations successfully recreate some important features of the macroscale whole-process nonlinear deformation and fracturing failure of pre-notched rock specimens that are explored in experiments or other numerical simulations. Regarding the reproducibility under the same heterogeneity degree, by combining previous work on intact heterogenous specimen simulations, it is mainly concluded that:
1) The influence of the heterogeneity on the fracturing failure pattern reproducibility is mainly reflected by the secondary cracks for the pre-notched specimens and the intact disc specimen. The pre-notched disc specimen has poorer fracturing failure pattern reproducibility than the intact disc specimen because of the ideal tensile stress concentration along the loading diameter in the intact disc. Comparatively, the pre-notched rectangular specimen has much better fracturing failure pattern reproducibility than the intact rectangular specimen because of the stress concentration induced by the pre-existing flaw.
2) The heterogeneity does not influence the reproducibility of the macroscale equivalent modulus of the specimens evidently, but its influence on the reproducibility of the macroscale equivalent strength is obvious. Generally, the pre-notched specimens have poorer macroscale strength reproducibility than the intact specimens, and the rectangular specimens have better macroscale strength reproducibility than the disc specimens. Moreover, for the pre-notched specimens, the macroscale strength reproducibility also varies with the inclination of the pre-existing flaw remarkably.
The exact microstructures of rock including the mineral grain shapes and microcracks etc., will be considered in the future work on DDA simulations of rock heterogeneities.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
DC: Methodology, Validation, Funding acquisition; ZY: Formal analysis, Writing—Original Draft; MW: Formal analysis; XJ: Formal analysis; YN: Conceptualization, Software, Writing—Review and Editing, Funding acquisition.
This research was financially supported by the open project of the State Key Laboratory of Coal Resources and Safe Mining, CUMT, China (Grant SKLCRSM16KF08), the National Key Research and Development Program of China (grant No. 2021YFC2902105), the National Natural Science Foundation of China (grant No. 51604261), and the Sichuan Province Science and Technology Support Program, China (grant No. 2020YJ0416).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Al-Shayea, N. A. (2005). Crack propagation trajectories for rocks under mixed mode I–II fracture. Eng. Geol. 81, 84–97. doi:10.1016/j.enggeo.2005.07.013
Alzaki, T., Al-Dughaimi, S., Muqtadir, A., Kandil, M. E., and Dvorkin, J. (2020). Effect of heterogeneity on failure of natural rock samples. Sci. Rep-UK. 10, 14723–14726. doi:10.1038/s41598-020-71780-7
Bai, B., Yang, G., Li, T., and Yang, G. (2019). A thermodynamic constitutive model with temperature effect based on particle rearrangement for geomaterials. Mech. Mat. 139, 103180. doi:10.1016/j.mechmat.2019.103180
Bai, B., Zhou, R., Cai, G., Hu, W., and Yang, G. (2021). Coupled thermo-hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics. Comput. Geotech. 137, 104272. doi:10.1016/j.compgeo.2021.104272
Cundall, P. A., and Hart, R. D. (1992). Numerical modelling of discontinua. Eng. Comput. 9, 101–113. doi:10.1108/eb023851
Gao, F., Stead, D., and Elmo, D. (2016). Numerical simulation of microstructure of brittle rock using a grain-breakable distinct element grain-based model. Comput. Geotech. 78, 203–217. doi:10.1016/j.compgeo.2016.05.019
Gui, Y., Zhao, Z., Ji, J., Wang, X., Zhou, K., and Ma, S. (2016). The grain effect of intact rock modelling using discrete element method with Voronoi grains. Géotech. Lett. 6, 136–143. doi:10.1680/jgele.16.00005
He, W., Hayatdavoudi, A., Shi, H., Sawant, K., and Huang, P. (2019). A preliminary fractal interpretation of effects of grain size and grain shape on rock strength. Rock Mech. Rock Eng. 52, 1745–1765. doi:10.1007/s00603-018-1645-4
Huang, J., Tang, H., Pan, X., Gan, Z., Hua, W., and Dong, S. (2022). Investigation of the compression–shear fracture propagation for rocks accounting for confining pressure and crack surface friction. Theor. Appl. Fract. Mec. 119, 103346. doi:10.1016/J.TAFMEC.2022.103346
Jiao, Y., Zhang, X., and Zhao, J. (2012). Two-dimensional DDA contact constitutive model for simulating rock fragmentation. J. Eng. Mech. 138, 199–209. doi:10.1061/(ASCE)EM.1943-7889.0000319
Li, L., Guan, J., and Liu, Z. (2022). A random discrete element method for modeling rock heterogeneity. Geomech. Geophys. Geo. 8, 12–13. doi:10.1007/S40948-021-00320-Y
Liu, G., Cai, M., and Huang, M. (2018). Mechanical properties of brittle rock governed by micro-geometric heterogeneity. Comput. Geotech. 104, 358–372. doi:10.1016/j.compgeo.2017.11.013
Manouchehrian, A., and Cai, M. (2016). Influence of material heterogeneity on failure intensity in unstable rock failure. Comput. Geotech. 71, 237–246. doi:10.1016/j.compgeo.2015.10.004
Ni, K., Yang, J., Ning, Y., and Kang, G. (2020). A modified sub-block DDA fracturing modelling method for rock. Eng. Anal. Bound. Elem. 111, 154–166. doi:10.1016/j.enganabound.2019.11.008
Ning, Y., and Lv, X. (2022). Research progress in DDA and NMM simulations of rock mechanics and engineering problems. Chin. J. Appl. Mech. 39, 657–672. doi:10.11776/j.issn.1000-4939.2022.04.007
Ning, Y., Yang, J., An, X., and Ma, G. (2011). Modelling rock fracturing and blast-induced rock mass failure via advanced discretisation within the discontinuous deformation analysis framework. Comput. Geotech. 38, 40–49. doi:10.1016/j.compgeo.2010.09.003
Ning, Y., Yang, Z., Wei, B., and Gu, B. (2017). Advances in two-dimensional discontinuous deformation analysis for rock-mass dynamics. Int. J. Geomech. 17, E6016001. doi:10.1061/(ASCE)GM.1943-5622.0000654
Ning, Y., Lv, X., and Yang, Z. (2021). DDA simulation study on mechanical failure of heterogenous rock. Geofluids 2021, 1416560. doi:10.1155/2021/1416560
Ou, C. (2020). Experimental and numerical study on dynamic splitting of Brazilian flattened disc with prefabricated cracks. Guangzhou Univ., 912. doi:10.27040/d.cnki.ggzdu.2020.000912
Peng, J., Wong, L. N. Y., and Teh, C. I. (2021). Influence of grain size on strength of polymineralic crystalline rock: New insights from DEM grain-based modeling. J. Rock Mech. Geotech. 13, 755–766. doi:10.1016/J.JRMGE.2021.01.011
Rasmussen, L. L. (2022). A breakable grain-based model for bi-modular rocks. Int. J. Rock Mech. Min. 151, 105028. doi:10.1016/J.IJRMMS.2021.105028
Shi, G. (1992). Discontinuous deformation analysis: A new numerical model for the statics and dynamics of deformable block structures. Eng. Comput. 9, 157–168. doi:10.1108/eb023855
Shi, G., and Goodman, R. E. (1985). Two dimensional discontinuous deformation analysis. Int. J. Numer. Anal. Mater. 9, 541–556. doi:10.1002/nag.1610090604
Shirole, D., Walton, G., and Hedayat, A. (2020). Experimental investigation of multi-scale strain-field heterogeneity in rocks. Int. J. Rock. Mech. Min. 127, 104212. doi:10.1016/j.ijrmms.2020.104212
Sun, S., Wang, J., Le, H., Fan, H., and Wang, W. (2022). Experimental and numerical investigation on compressive strength and crack behavior of rock-like specimens with open flaws under confining loads. Front. Earth. Sc-switz. 10, 972194. doi:10.3389/FEART.2022.972194
Tang, C., Yang, W., Fu, Y., and Xu, X. (1998). A new approach to numerical method of modelling geological processes and rock engineering problems—Continuum to discontinuum and linearity to nonlinearity. Eng. Geo. 49, 207–214. doi:10.1016/S0013-7952(97)00051-3
Tang, C., Tham, L. G., Lee, P. K. K., Tsui, Y., and Liu, H. (2000). Numerical studies of the influence of microstructure on rock failure in uniaxial compression—part II: Constraint, slenderness and size effect. Int. J. Rock Mech. Min. 37, 571–583. doi:10.1016/S1365-1609(99)00122-7
Tang, X., and Zhang, C. (2009). Meso-scale modeling of concrete: Effects of heterogeneity. J. Hydroelectr. Eng. 28, 56–62.
Wang, Y., and Sun, S. (2021). Image-based rock typing using grain geometry features. Comput. Geosci-UK. 149, 104703. doi:10.1016/J.CAGEO.2021.104703
Wong, R. H. C., Tang, C., Chau, K. T., and Lin, P. (2002). Splitting failure in brittle rocks containing pre-existing flaws under uniaxial compression. Eng. Fract. Mech. 69, 1853–1871. doi:10.1016/S0013-7944(02)00065-6
Wu, Z., Fan, L., Liu, Q., and Ma, G. (2017). Micro-mechanical modeling of the macro-mechanical response and fracture behavior of rock using the numerical manifold method. Eng. Geol. 225, 49–60. doi:10.1016/j.enggeo.2016.08.018
Xu, Y., Yao, W., and Xia, K. (2020). Numerical study on tensile failures of heterogeneous rocks. J. Rock Mech. Geotech. 12, 50–58. doi:10.1016/j.jrmge.2019.10.002
Yang, B., Cao, X., Han, T., Li, P., and Shi, J. (2022). Effect of heterogeneity on the extension of ubiquitiformal cracks in rock materials. Fractal. Fract. 6, 317. doi:10.3390/FRACTALFRACT6060317
Zhang, S., and Wang, Q. (2009). Determination of rock fracture toughness by split test using five types of disc specimens. Rock Soil Mech. 30, 12–18. doi:10.16285/j.rsm.2009.01.019
Zheng, K., Qiu, B., Wang, Z., Li, X., Li, J., and Gao, K. (2020). Image-based numerical study of three-dimensional meso-structure effects on damage and failure of heterogeneous coal-rock under dynamic impact loads. Particuology 51, 132–141. doi:10.1016/j.partic.2019.09.008
Keywords: rock fracturing failure, heterogeneity, reproducibility, pre-existing flaw, discontinuous deformation analysis (DDA)
Citation: Chen D, Yang Z, Wang M, Jiang X and Ning Y (2023) DDA simulation study on fracturing failure reproducibility of heterogenous rock. Front. Earth Sci. 10:1076023. doi: 10.3389/feart.2022.1076023
Received: 21 October 2022; Accepted: 09 December 2022;
Published: 25 January 2023.
Edited by:
Guang-Liang Feng, Institute of Rock and Soil Mechanics (CAS), ChinaReviewed by:
Bing Bai, Beijing Jiaotong University, ChinaCopyright © 2023 Chen, Yang, Wang, Jiang and Ning. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dayong Chen, Y2R5Y2hlbmRheW9uZ0AxNjMuY29t; Youjun Ning, Y25uaW5neWpAZm94bWFpbC5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.