Secure communication in the digital age: a new paradigm with graph-based encryption algorithms

In the contemporary technological landscape, ensuring confidentiality is a paramount concern addressed through various skillsets. Cryptography stands out as a scientific methodology for safeguarding communication against unauthorized access. Within the realm of cryptography, numerous encryption algorithms have been developed to enhance data security. Recognizing the imperative for nonstandard encryption algorithms to counter traditional attacks, this paper puts forth novel encryption techniques. These methods leverage special corona graphs, star graphs, and complete bipartite graphs, incorporating certain algebraic properties to bolster the secure transmission of messages. The introduction of these proposed encryption schemes aims to elevate the level of security in confidential communication, some of the applications of these schemes are given in the later section.

1 Introduction

Throughout history, military officers and diplomats have sought clandestine means of communication. In our contemporary era, characterized by widespread reliance on

the internet, mobile phones, and computer technology across various aspects of daily life, the imperative to safeguard crucial information has escalated steadily. Over time, as advancements in data security persist, novel methods of breaching private Correspondence are constantly emerging. Cryptography, aims to ensure secure transmission without the risk of unauthorized access. Initially employed for wartime strategies, classical cryptography boasts a history spanning over two millennia. The foundations of modern cryptography were laid by Shannon (1949). Cryptography has evolved into an indispensable element of contemporary society. Encryption is the process of transforming an original message into a coded format, and its reverse operation is referred to as decryption (Rosen, 2005). Encryption serves to prevent the interception of the original content, known as plaintext. The information is given in plaintext and then it is coded using encryption with specific keys to generate ciphertext. The ciphertext is then deciphered back into a readable message through the process of decryption. The key is a very important part of information employed to encode the original data and subsequently decrypt it to obtain the real text. With the provision of the correct key, the authorized recipient can effortlessly unveil the concealed message, while interception by an unauthorized entity becomes infeasible. Contemporary cryptographic methods mainly rely on three distinct schemes named as symmetric key cryptography employs a single key for both encryption and decryption operations then there is public key cryptography in which we utilize separate keys for encryption and decryption purposes, and lastly is hash functions where employ transformations to securely encrypt data in an irreversible manner (Stinson, 2018). These cryptographic techniques are fundamental in ensuring the security of digital communication and information.

1.1 Simplified explanation of key concepts

Our focus is on advancing encryption methods through the utilization of graph theory and algebraic concepts. To begin, let us revisit some essential concepts from graph theory (West, 2001).

Basic concepts of graph theory:

Graph: In graph theory, a graph, represented as $G=\left(V\mathrm{,}E\right),$ consists of two distinct sets: the vertex set $V\left(G\right)$ and the edge set $E\left(G\right)$ .

Bipartite graph: If the vertices in $V\left(G\right)$ can be separated into two non-overlapping subsets in such a way that every edge connects a vertex from one subset to a vertex in the other, the graph $G$ is classified as a bipartite graph.

Complete-bipartite graph: A bipartite graph becomes complete-bipartite when each vertex in one subset is linked to every vertex in the other subset.

Star graph: Among complete-bipartite graphs, a particular instance is the star graph, characterized by having only one vertex in one subset and all other vertices in the other subset.

Pendent vertex and pendent edge: Furthermore, a vertex with a degree of one is known as a pendent vertex, and the edge incident to it is referred to as a pendent edge.

Corona product of graphs: The corona product of two graphs $G\mathrm{\hspace{0.33em}}$and $H$ is denoted as $G\odot H$ , and defined as by taking one copy of graph $\mathrm{G}$ and $\mathrm{V}\left(\mathrm{G}\right)$ - copies of graph $H$ . In this construction, the vertex labeled $\prime i\prime$in G is connected to every vertex in the $\prime i-t{h}^{\prime }$ copy of H. This corona operation, introduced by Frucht and Harary (1970), proves to be a significant operation between graphs. An interesting example is the star graph Sn +1, consisting of $n+1$ vertices, which can be viewed as a corona graph $K_1\odot K_n$ . Additionally, the corona graph of the cycle $C_n$ with $C_n$ , i.e., $C_n\odot C_n$ , forms a graph with $n\left(n+1\right)$ vertices achieved by attaching $\mathrm{n}$ cycles to main cycle graph $C_n$ .

Graph-based encryption techniques: Using these graph structures, we can develop encryption methods that transform messages into secure, coded formats. Here’s a simplified overview of how these methods work:

Graph construction: We start by constructing specific graphs (like the star graph or corona graph) based on the message to be encrypted. Each part of the message corresponds to a vertex or an edge in the graph.

Encoding messages: The vertices and edges are labeled with parts of the message (letters, numbers, etc.). The structure of the graph (how vertices and edges are connected) helps encode the message in a way that is difficult to decipher without the correct key.

Key Generation: A key, which is an essential piece of information, is generated to help encode and decode the message. This key ensures that only authorized recipients can decrypt the message by understanding the graph structure used.

Encryption and decryption: During encryption, the plaintext message is transformed into a complex graph-based format (ciphertext) using the key. For decryption, the key is used to reconstruct the original graph and retrieve the plaintext message.

By understanding these fundamental graph theory concepts, readers can better appreciate the innovative encryption techniques presented in this paper.

Recent research has witnessed a surge in interest in leveraging graphs to propose innovative methodologies across various cryptographic domains (Selim, 2020). In (Ali et al., 2024a), Selvakumar and Gupta introduced a novel coding and decryption algorithm employing connected graphs. Authors in Kedia and Agrawal (2015), discussed an encryption approach incorporating numeric representation and letters, utilizing fundamental mathematical concepts such as Venn diagrams. Yamuna and Elakkiya (2015) proposed a graph-based encryption algorithm where fundamental circuits are chosen based on corresponding edge weights. Yamuna and Karthika (2015) presented a unique data transfer method using bipartite graphs and a numeric table for alphabet representation. Mahmoud and Etaiwi (2014) introduced a symmetric encryption algorithm (Arunkumar, 2015) explored extensive applications of bipartite graphs in computation. Sinha and Sethi (2016) introduced a data security scheme using line sigraph, a new graph concept with labeled edges belonging to $-1,+1$ . In (Hu et al., 2017), authors have proposed a bipartite graph-based encryption. Razaq et al. utilized coset diagrams in Ali et al. (2024b) to construct a substitution box (S-box) for cryptography, focusing on the action of $\mathrm{PSL}\left(2\mathbb{Z}\right)$ on the projective line over the finite field ${{\mathbb{F}}_2}^9$ . Strong $\mathrm{S}$ -box construction was further explored in Ali N. et al. (2023). In this paper we aim to introduce some new encryption schemes based on Explicit categories of graphs, defined by $C_n\odot C_n,K_1\odot \overline{K_n}$ (also known as a star graph), and complete bipartite graphs. The proposed algorithms facilitate the secure transmission of messages, regardless of word length, through the utilization of graph structures and specific Mathematical characteristics. Following the given algorithmic steps ensures comprehensive data protection, with the recipient ultimately recovering the original message from the labeled graph. Section 2 Presents cryptographic techniques using $C_n\odot C_n$ , accompanied by a formulated algorithm. An example illustrates the application of this algorithm. Section 3 introduces the use of complete bipartite graphs to construct a secure encryption scheme, accompanied by a detailed algorithm. The scheme’s applicability to important information is demonstrated through an example. Within the specified section 4, we introduce a robust encryption scheme based on a distinctive corona graph, denoted as $K_1\odot \overline{K_n}$ . The algorithm is detailed, accompanied by practical illustrations showcasing its application.

2 Encryption scheme using corona graph $C_n\odot C_n$

The encryption of the scheme is given as follows:

2.1 Plaintext Encoding

Begin with the plaintext message that needs to be securely transmitted. Each symbol in the message (including alphabetic characters, numbers, punctuation, and other special symbols) is encoded using a numeric representation. This can be based on an ASCII, Unicode, or any appropriate character encoding table. Let the encoded message consist of a sequence of numeric values $a_1,a_2,a_3,\mathrm{..},a_n$ , where $n$ is the length of the plaintext message.

2.2 Shift cipher

Apply a shift-type cipher to each numeric value of the encoded message. The shift is performed modulo m, where m is the size of the character encoding set (for example, $m=128$ for ASCII or $m=256$ for extended character sets). The shift cipher can be represented as:

$e_n\left(x\right)=\left(x+n\right)\mathrm{\hspace{0.33em}}\mathrm{mod}\mathrm{\hspace{0.33em}}m$

Here, $x$ is the numeric value of the character, and $n$ is a predefined shift value. This transformation ensures that each character in the message is shifted by n positions in the character set, providing an initial layer of encryption.

2.3 Selection of $b_i$ values

For each shifted numeric value a_i, randomly select a positive integer $b_i$ such that $\gcd \left(b_i\mathrm{,}{a}_i\right)=1and{b}_i>m$ (ensuring that $b_i$ is relatively prime to the numeric representation $a_i$ and greater than the size of the encoding set).

2.4 Corona graph $C_n\odot C_n$ construction

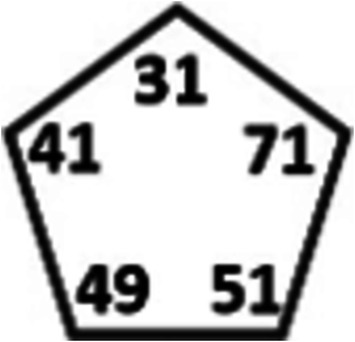
Consider the Corona graph $C_n\odot C_n$ which consists of $n\left(n+1\right)$ vertices. Assign the values $b_1,b_2,\mathrm{..},b_n$ to the main cycle vertices and distribute these values to the vertices adjacent to the new cycles in a random manner.

2.5 Modular inverses

For each $a_i$ , compute the inverse of $a_i\mathrm{\hspace{0.33em}}\mathrm{mod}\mathrm{\hspace{0.33em}}{b}_i.$ The inverse is denoted by $c_i$ , where:

$c_i=a_i^{-1}\mathrm{\hspace{0.33em}}\mathrm{mod}\mathrm{\hspace{0.33em}}{b}_i$

These inverse values $c_1,c_2,\mathrm{..},c_n$ are assigned to the cycles in the Corona graph, forming the encrypted message.

2.6 Transmission

The labeled Corona graph $C_n\odot C_n$ with the inverse values $c_i$ assigned to the cycles and the values $b_i$ assigned to the main cycle vertices, is transmitted to the receiver as the encrypted data.

3 Decryption algorithm

3.1 Receive the corona graph

The receiver obtains the transmitted Corona graph $C_n\odot C_n,$ which contains the labeled cycles with values $c_1,c_2,\mathrm{..},c_n$ and the main cycle vertices labeled with $b_1,b_2,\mathrm{..},b_n.$

3.2 Organize the values

Arrange the cycles in ascending order according to their associated $b_i$ values.

3.3 Modular inverse calculation

For each $c_i$ , compute the inverse modulo the corresponding $b_i$ , resulting in the values $a_i$ . This inverse operation is calculated as:

$a_i=c_i^{-1}\mathrm{\hspace{0.33em}}\mathrm{mod}\mathrm{\hspace{0.33em}}{b}_i$

These values $a_1,a_2,\mathrm{..},a_n$ correspond to the encoded message symbols.

3.4 Undo the shift cipher

Reverse the shift operation applied during encryption by computing:

$w_i=\left(a_i-n\right)\mathrm{\hspace{0.33em}}\mathrm{mod}\mathrm{\hspace{0.33em}}m$

for each $\mathrm{\hspace{0.33em}}i$ , where n is the original shift value used during encryption and m is the size of the character set.

3.5 Translate numeric values back to symbols

Convert the resulting numeric values $w_1,w_2,\mathrm{..},w_n$ back to their corresponding characters using the same character encoding table (e.g., ASCII or Unicode) that was used during encryption.

3.6 Reconstruct the plaintext

The translated symbols now represent the original plaintext message, completing the decryption process.

Example 1: Suppose the task at hand involves transferring information, denoted as “MATHS,” by encrypting it before sending it to the intended recipient. The first step involves transforming the alphabetic letters into their respective numerical positions, utilizing the encoding table ASCII.

$\begin{array}{lllll}M\hfill & A\hfill & T\hfill & H\hfill & S\hfill \\ 13\hfill & 1\hfill & 20\hfill & 8\hfill & 19\hfill \end{array}$

Here, with the word length $n=5$ , applying the shift cipher $e_n=x+n\left(\mathrm{mod}26\right)$ , we obtain:

$\begin{array}{r}\hfill 13+5=18=a_1,\\ \hfill 1+5=6=a_2,\\ \hfill 20+5=25=a_3,\\ \hfill 8+5=13=a_4\\ \hfill 19+5=24=a_5.\end{array}$

The given word is encrypted in the following form:

$R\mathrm{\hspace{0.33em}}\mathrm{\hspace{0.33em}}F\mathrm{\hspace{0.33em}}\mathrm{\hspace{0.33em}}Y\mathrm{\hspace{0.33em}}\mathrm{\hspace{0.33em}}M\mathrm{\hspace{0.33em}}\mathrm{\hspace{0.33em}}X.$

Choosing random increasing integers $b_i$ such that the value of $b_i$ is greater than 26:

$\begin{array}{l}\gcd \left(b_1\mathrm{,}{a}_1\right)=\gcd \left(18\mathrm{,}35\right)=1,\\ \gcd \left(b_2\mathrm{,}{a}_2\right)=\gcd \left(6\mathrm{,}41\right)=1,\\ \gcd \left(b_3\mathrm{,}{a}_3\right)=\gcd \left(25\mathrm{,}49\right)=1,\\ \gcd \left(b_4\mathrm{,}{a}_4\right)=\gcd \left(13\mathrm{,}51\right)=1,\\ \gcd \left(b_5\mathrm{,}{a}_5\right)=\gcd \left(24\mathrm{,}71\right)=1\end{array}$

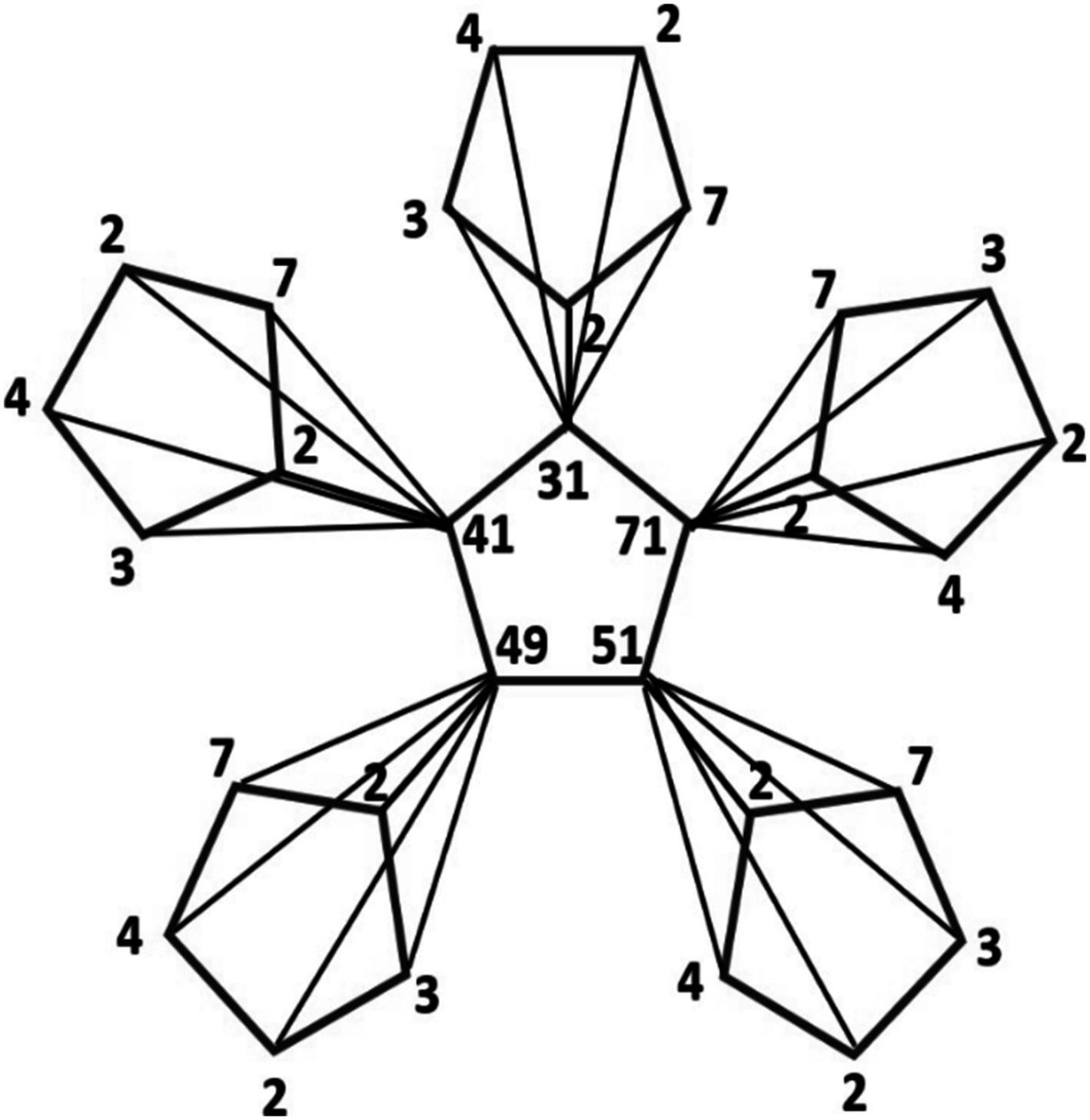
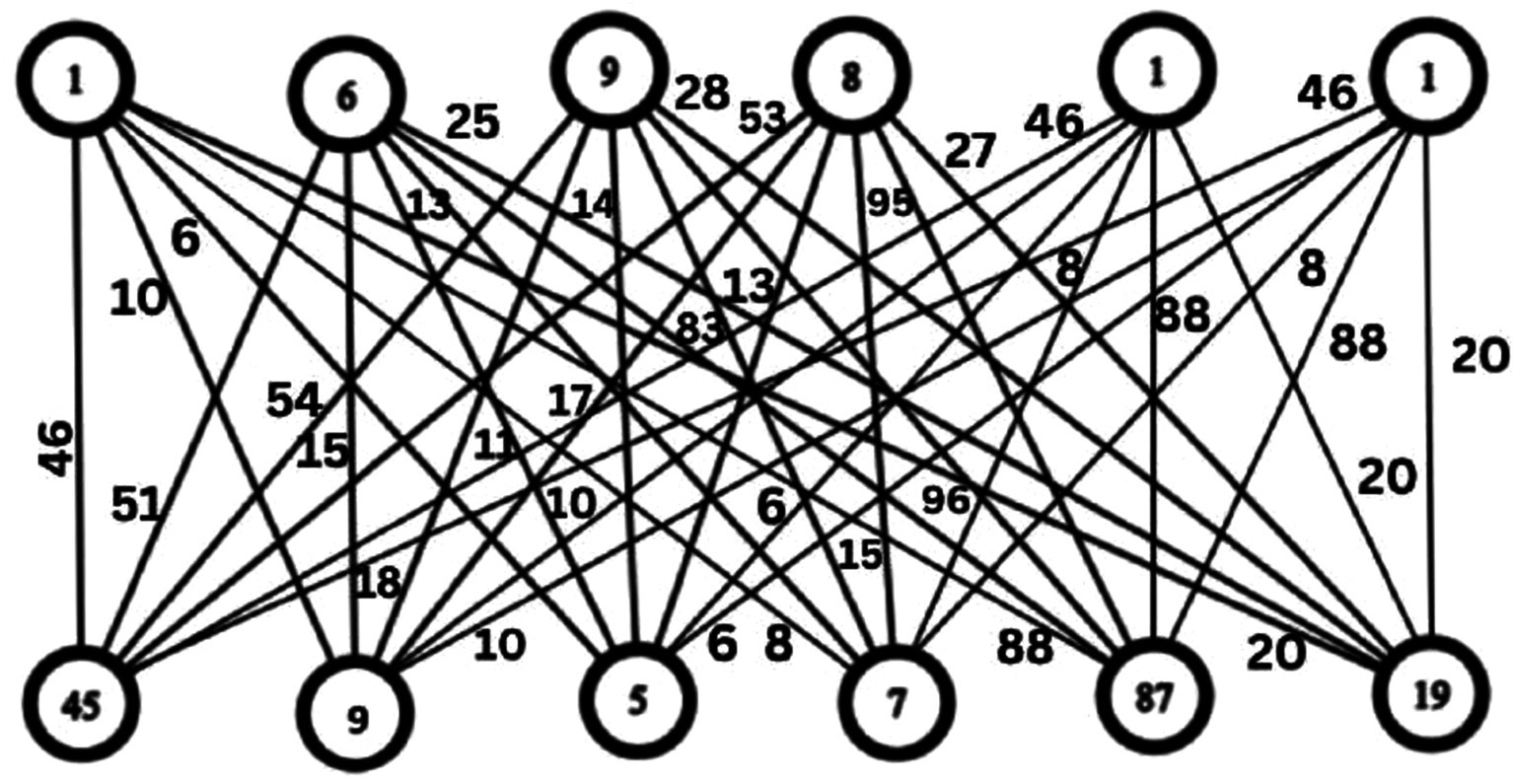
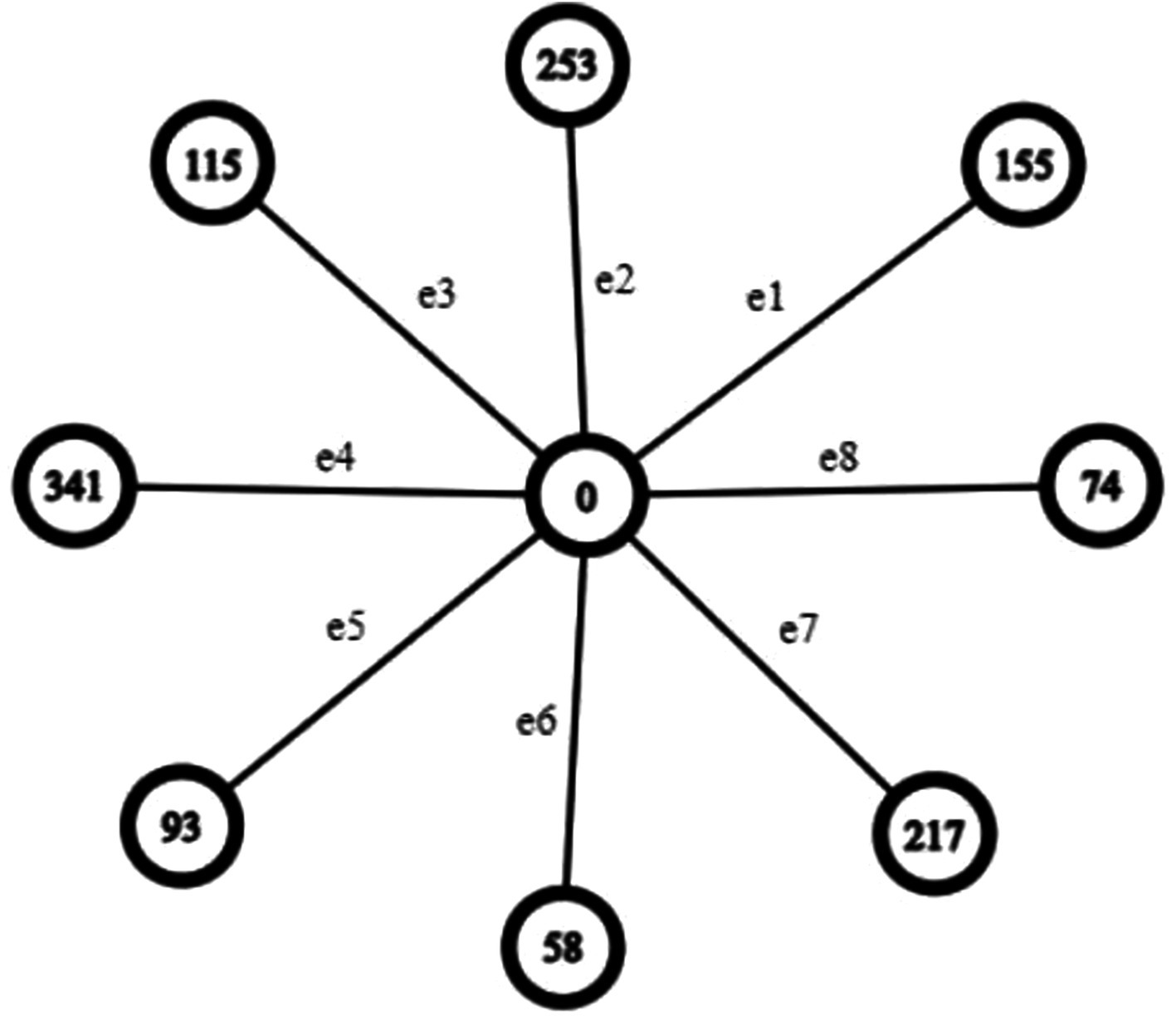
Constructing the Corona graph $C_n\odot C_n$ and randomly assigning the values of $b_i$ to the main vertices of the main cycle, as illustrated in Figures 1, 2.

Figure 1

Figure 1. Corona graph.

Figure 2

Figure 2. Encrypted message.

Now, proceeding with the following step:

$c_i={\left(a_i\right)}^{-1}\left(\mathrm{mod}{b}_i\right)$

we get.

$\begin{array}{l}{c}_1={\left(a_1\right)}^{-1}\left(\mathrm{mod}{b}_1\right)={\left(18\right)}^{-1}\left(\mathrm{mod}35\right)=2,\\ c_2={\left(a_2\right)}^{-1}\left(\mathrm{mod}{b}_2\right)={\left(6\right)}^{-1}\left(\mathrm{mod}41\right)=7,\\ c_3={\left(a_3\right)}^{-1}\left(\mathrm{mod}{b}_3\right)={\left(25\right)}^{-1}\left(\mathrm{mod}49\right)=2,\\ c_4={\left(a_4\right)}^{-1}\left(\mathrm{mod}{b}_4\right)={\left(13\right)}^{-1}\left(\mathrm{mod}51\right)=4,\\ c_5={\left(a_5\right)}^{-1}\left(\mathrm{mod}{b}_5\right)={\left(24\right)}^{-1}\left(\mathrm{mod}71\right)=3.\end{array}$

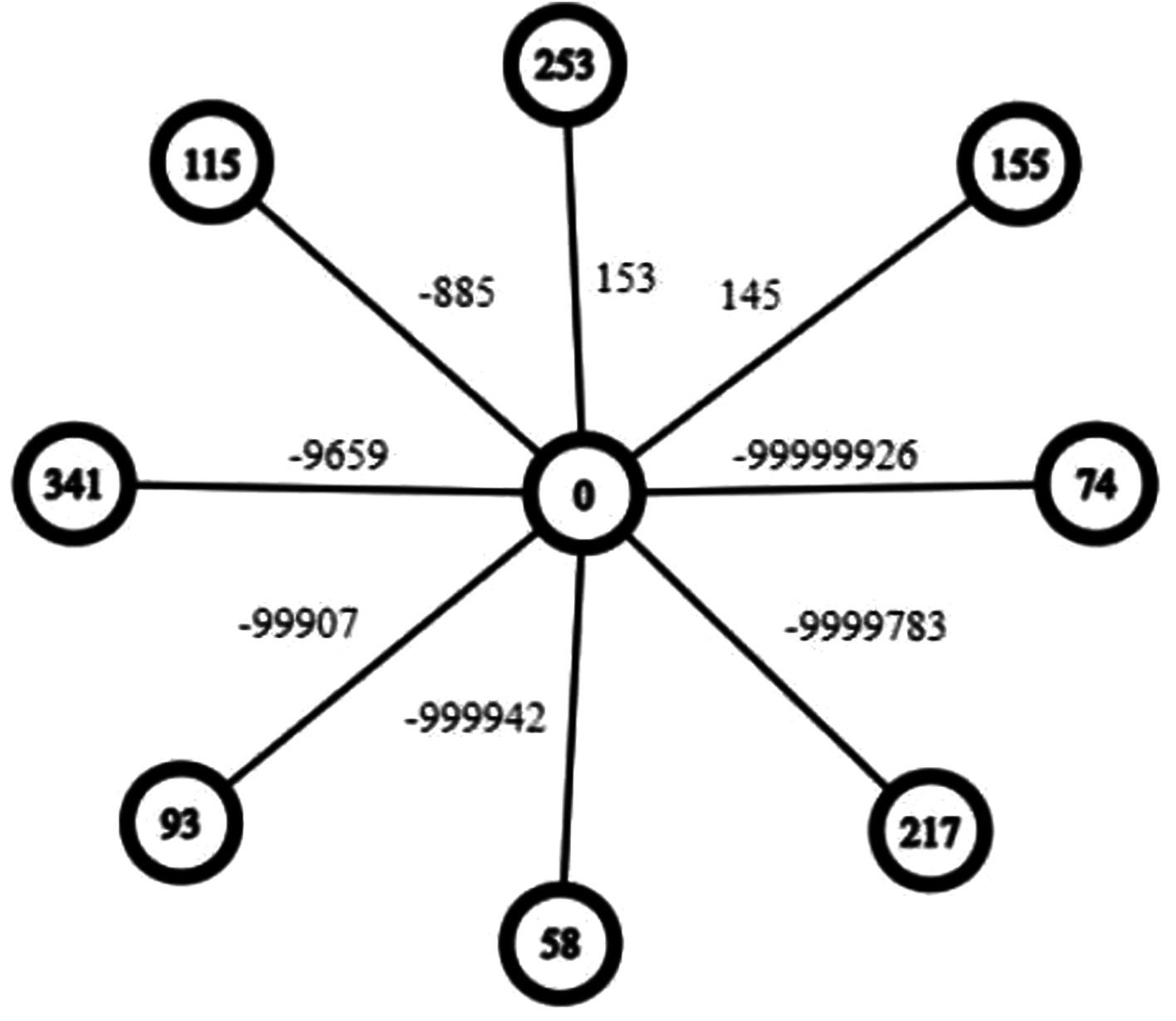
The reciprocal values obtained are assigned to the neighboring cycles of main cycle in Figure 2, as illustrated in Figure 3.

Figure 3

Figure 3. Tabular representation.

Proceed with the transmission of this labeled graph (Figure 3) to the recipient.

Decryption process:

Upon receiving the labeled graph, the recipient organizes the main vertices in ascending order, ensuring the security and integrity of the encrypted information.

$35<41<49<51<71$

and regards these numbers as the values of $b_i$ in the process.

$b_1<b_2<b_3<b_4<b_5$

Taking inverses of corresponding new cycles of adjacent main cycle in reference to the value of each $b_i$ , illustrated in Figure 3, we obtain.

$\begin{array}{l}{2}^{-1}\left(\mathrm{mod}35\right)=18=a_1\\ 7^{-1}\left(\mathrm{mod}41\right)=6=a_2\\ 2^{-1}\left(\mathrm{mod}49\right)=25=a_3\\ 4^{-1}\left(\mathrm{mod}51\right)=13=a_4\\ 3^{-1}\left(\mathrm{mod}71\right)=24=a_5.\end{array}$

Now, for $w_i$ ,

$w_i=a_i-\left(\frac{n\left(n+1\right)}{n+1}\right)\mathrm{mod}26$

Find values of $a_1,a_2,a_3,a_4$ , and $a_5$ :

$\begin{array}{l}{w}_1=a_1-\left[\frac{5+1\left(5\right)}{5+1}\right]\mathrm{mod}26=13=M,\\ w_2=a_2-\left[\frac{5+1\left(5\right)}{5+1}\right]\mathrm{mod}26=1=A,\\ w_3=a_3-\left[\frac{5+1\left(5\right)}{5+1}\right]\mathrm{mod}26=20=T,\\ w_4=a_4-\left[\frac{5+1\left(5\right)}{5+1}\right]\mathrm{mod}26=8=H,\\ w_5=a_5-\left[\frac{5+1\left(5\right)}{5+1}\right]\mathrm{mod}26=19=S.\end{array}$

In conclusion, we obtain the original text “MATHS.”

4 Encryption scheme using complete bipartite graphs

In this section, we introduce an encryption method tailored to ensure the confidentiality and security of communication between two parties involved in message interchange. The foundation of this encryption method lies in utilizing a bipartite graph in conjunction with the principles of a unique factorization domain (UFD).

The algorithm comprises the following steps:

Begin by choosing a UFD that encompasses infinite primes. As an illustrative example, consider the set of integers, denoted as $\mathbb{Z}$ .

Create a set, denoted as $P_n\mathrm{\hspace{0.33em}}$comprising the initial $"n"$ prime numbers, where $n=\left(26/k\right)+k$ and $2<k<13$ . The value of $k$ serves as the key, which remains fixed based on the desired word length.

Take a message of length S characters that you aim to encrypt

Construct a table with dimensions $\left(n-k\right)\times k$ , where the first value represents the number of rows, and the second value denotes the number of columns.

Partition the alphabets into the table, filling each cell with a distinct alphabet from the message. Begin the allocation by populating the table row-wise and continue until the entire message is accommodated.

Subsequently, the alphabets are grouped into two categories: those at the 1^st through k^th prime positions (arranged horizontally),

and those at the ${\left(k+1\right)}^{th}\mathrm{\hspace{0.33em}}$through nth prime positions (arranged vertically).

Now, associate each alphabet with the corresponding integers $r_i{c}_i$ , Where as $r_i$ stands for the row position and $c_i$ stands for the column position.

Classify the entry $ij$ with $r_i{c}_i$ , where $k+1\le i\le n,1\le j\le k$ constructing each number as a vertex within a path graph based on the sequence of letters.

We calculate the product of $i$ and $j$ , denoted as $i.j,$ and assign each vertex a label corresponding to that product, represented as $a_p$ where p ranges from $1$ to $k$ . It should be noted that digits in the tens place are not considered for the column position. In simpler terms, we ensure that the column position consists solely of two-digit prime numbers.

Create a path graph by associating consecutive pairs of numbers $i,j$ with each vertex.

Organize the graph labels based on their corresponding row and column numbers. $V_1$ is set of vertices are in descending order and $V_2$ is set of vertices are in ascending order with thier repetition.

$V_1=\{$Initially, arrange numbers starting from $i\}$

$V_2=\{$The numbers securing the second position from $j\}$

The edge set of $G$ is formed by the pairs $\left(r_1\mathrm{,}{c}_i\right),\left(r_2\mathrm{,}{c}_i\right),\dots ,\left(r_n\mathrm{,}{c}_i\right)$ .

Proceed to create a complete bipartite graph using the specified set of edges. Edges move from $\left(r_1\mathrm{,}{c}_i\right),\left(r_2\mathrm{,}{c}_i\right),\dots ,\left(r_n\mathrm{,}{c}_i\right)$ .

Apply weights to the adjacent edges by sum of two labeled vertices.

Send that labeled graph.

Decryption process:

The recipient obtains the fully labeled complete bipartite graph sent by the sender.

Arrange the weights of edges in the complete bipartite graph in descending order.

Organize the edges based on their weights, forming a set of ordered pairs. Each ordered pair should indicate the number of rows at the first position and the number of columns at the second position, respectively, $V_1$ is set of vertices and $V_2$ is set of vertices are consider as shown in graph with thier repetition.

Utilize the ordered pair information to construct a path graph. Connect vertices based on the specified rows and columns, creating a linear graph.

Perform prime factorization on each vertex label of the path graph. Decompose the labels into their prime factors.

Retrieve the required alphabets corresponding to the prime factorization by referencing the decoding table mentioned earlier in the algorithm.

Example 2: Let us take a word UNITED.

$\begin{array}{llllll}U\hfill & N\hfill & I\hfill & T\hfill & E\hfill & D\hfill \\ 21\hfill & 14\hfill & 9\hfill & 20\hfill & 5\hfill & 4\hfill \end{array}$

Step 1: Select a unique factorization domain (UFD) containing an infinite number of prime elements. i.e., $\mathbb{Z}$ .

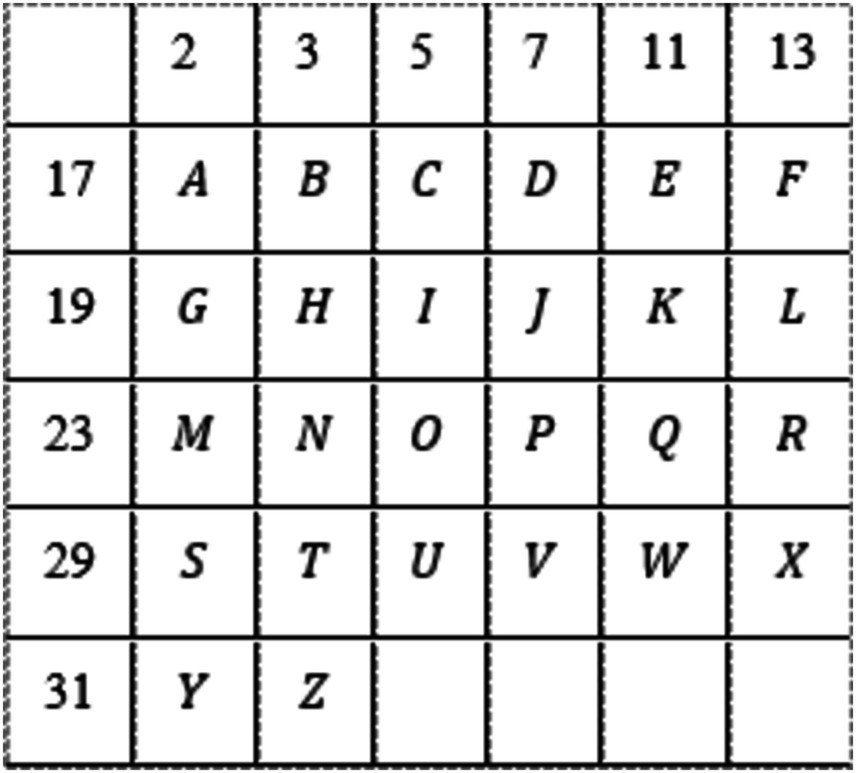
Step 2: In this example, $n=\left(26/6\right)+6;2<k<13$ . Hence, $n=11$ . We consider a set $P_{11}$ of first 11 primes denoted as $P_{11}=\left\{2\mathrm{,}3\mathrm{,}5\mathrm{,}7\mathrm{,}11,13,17,19,23,29,31\right\}$ .

Step 3: In Figure 4, a tabular representation is depicted. This illustration pertains to the creation of a table, showcasing, $\left(n-k\right)\times k=5\times 6$ . First value, i.e., 5 shows the no. of rows and 6 the no. of columns.

Figure 4

Figure 4. Path graph for values of $a_{i.}$

Step 4: message becomes $c_i$ to $r_i$

$U=529,N=323,I=519,T=329,E=1117,D=717;5\le i\le 11,1\le j\le 6.$

Step 5: Values that correlate with each other are determined.

$\begin{array}{r}\hfill a_1=5\times 29=145,\\ \hfill a_2=3\times 23=69,\\ \hfill a_3=5\times 19=95,\\ \hfill a_4=3\times 29=87,\\ \hfill a_5=11\times 17=187,\\ \hfill a_6=7\times 17=119,\end{array}$

Step 5: Now, we construct a path graph of these corresponding values $a_i$ . See Figure 5.

Figure 5

Figure 5. Complete bipartite graph.

Here,

$V_1=\left\{1\mathrm{,}6\mathrm{,}9\mathrm{,}8\mathrm{,}1\mathrm{,}1\right\}$

$V_2=\left\{45\mathrm{,}9\mathrm{,}5\mathrm{,}7\mathrm{,}87\mathrm{,}19\right\}$

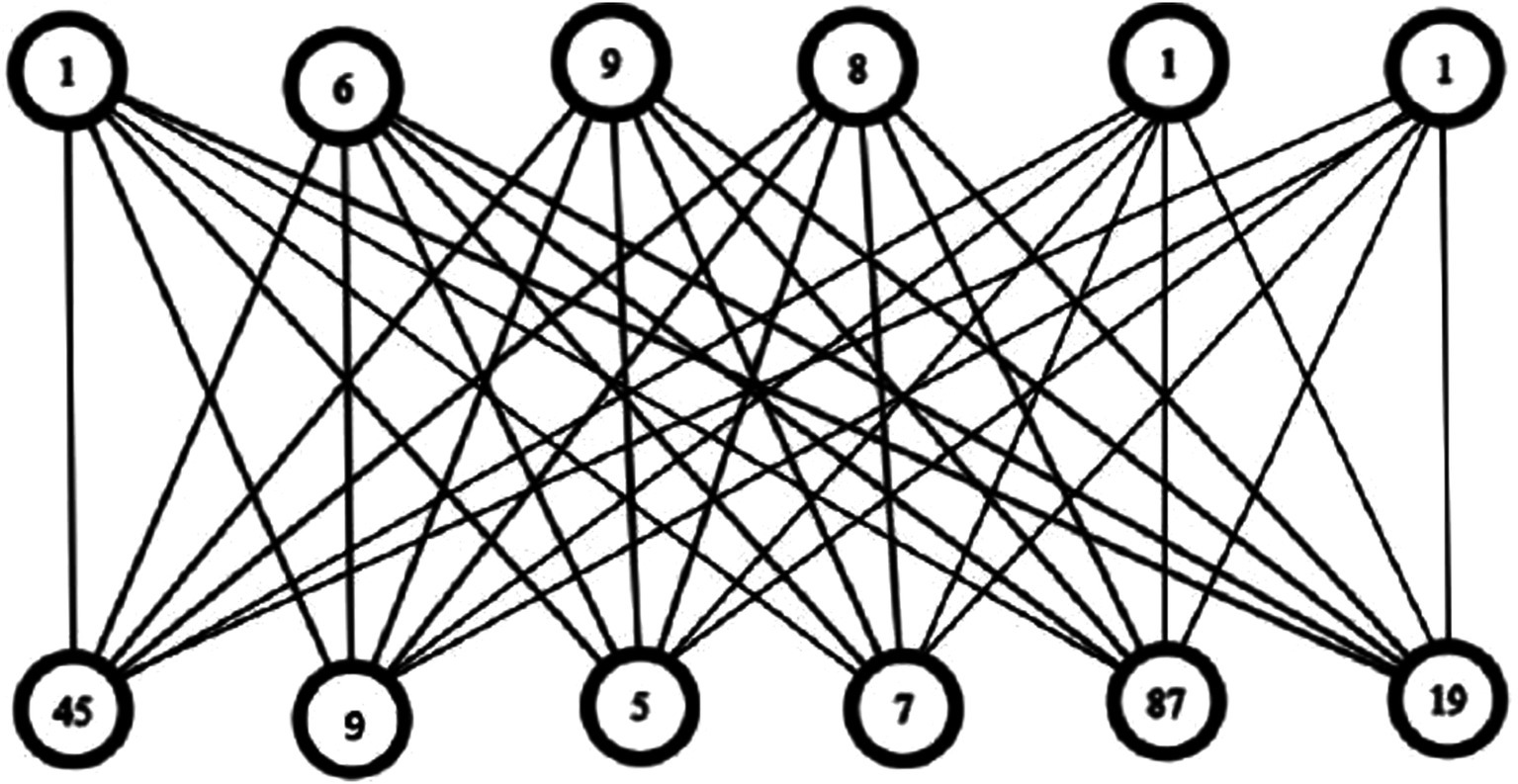
Now, the vertices set of complete bipartite graph becomes,

$\mathrm{G}\left(V_1\mathrm{,}{V}_2\right)=\left(\left(r_1\mathrm{,}{c}_i\right)\mathrm{,}\left(r_2\mathrm{,}{c}_i\right)\mathrm{,}\dots \mathrm{,}\left(r_n\mathrm{,}{c}_i\right)\right)$

$\mathrm{G}=\left(1\mathrm{,}{V}_2\right),\left(6\mathrm{,}{,}_2\right),\left(1\mathrm{,}{V}_2\right),\left(9\mathrm{,}{V}_2\right),\left(8\mathrm{,}{V}_2\right),\left(1\mathrm{,}{V}_2\right),\left(1\mathrm{,}{V}_2\right)$

Step 6: Assign weights to the edges connecting adjacent vertices in the complete bipartite graph, calculated as the sum of the incident weights on the respective 2-vertices (Figure 6).

Figure 6

Figure 6. Complete bipartite graph with weights.

Step 7: Send labeled graph.

Decryption process:

Step 1: Our initial action involves organizing the edge weights in a descending order:

$\begin{array}{l}W=\{96,94,93,88,88,88,54,53,51,46,46,\\ 46,28,27,25,20,20,20,18,17,16,15,15,14.\end{array}13,13,11,10,10,10,8,8,8,6,6,6\}$

Step 2: Now, arrange the edges based on their weights in descending order.

$\begin{array}{l}\{\left(9\mathrm{,}87\right),\left(8\mathrm{,}87\right),\left(6\mathrm{,}87\right),\left(1\mathrm{,}87\right),\left(1\mathrm{,}87\right),\\ \left(1\mathrm{,}87\right),\left(9\mathrm{,}45\right),\left(8\mathrm{,}45\right),\left(6\mathrm{,}45\right),\left(1\mathrm{,}45\right),\end{array}$ $\begin{array}{l}\left(1\mathrm{,}45\right),\left(1\mathrm{,}45\right),\left(9\mathrm{,}19\right),\left(8\mathrm{,}19\right),\left(6\mathrm{,}19\right),\left(1\mathrm{,}19\right),\\ \left(1\mathrm{,}19\right),\left(1\mathrm{,}19\right),\left(9\mathrm{,}9\right),\left(8\mathrm{,}9\right),\left(6\mathrm{,}9\right),\left(8\mathrm{,}7\right),\end{array}$ $\begin{array}{l}\left(9\mathrm{,}5\right),\left(8\mathrm{,}5\right),\left(6\mathrm{,}7\right),\left(6\mathrm{,}5\right),\left(1\mathrm{,}9\right),\left(1\mathrm{,}9\right),\\ \left(1\mathrm{,}9\right),\left(1\mathrm{,}7\right),\left(1\mathrm{,}7\right),\left(1\mathrm{,}7\right),\left(1\mathrm{,}5\right),\left(1\mathrm{,}5\right),\left(1\mathrm{,}5\right)\}\end{array}$

Step 3: Now, Construct the set of vertices $V_1$ arrange the elements as shown in graph upper labbelled vertices, and $V_2$ is consist of lower labbeled vertices.

$V_1=\left\{1\mathrm{,}6\mathrm{,}9\mathrm{,}8\mathrm{,}1\mathrm{,}1\right\}$

$V_2=\left\{45\mathrm{,}9\mathrm{,}5\mathrm{,}7\mathrm{,}87\mathrm{,}19\right\}$

Step 3: Construct the corresponding path graph (Figures 7, 8).

Figure 7

Figure 7. Corresponding path graph.

Figure 8

Figure 8. Corresponding tabular representation.

Step 4: Apply the prime factorization of each labeled vertices in the path graph.

$\begin{array}{r}\hfill a_1=145=5\times 29,\\ \hfill a_2=69=3\times 23,\\ \hfill a_3=95=5\times 19,\\ \hfill a_4=87=3\times 29,\\ \hfill a_5=187=11\times 17,\\ \hfill a_6=119=7\times 17,\end{array}$

So, Numerical values are 529, 323, 519, 329, 1,117, 717.

Step 5: We finally get the alphabets UNITED.

5 Secure data transfer using star graphs

Numerous strategies have been devised to safeguard data, and the highlighted approach centers around star graphs. This particular scheme ensures the complete confidentiality of the primary concept during the transmission of information. This encryption algorithm is built upon the utilization of a star graph and the principles of a unique factorization domain (UFD). The encryption and decryption processes involve a systematic set of steps.

The encryption process follows the algorithm outlined below:

Begin by choosing a UFD that encompasses infinite no. of primes. As an illustrative example, consider the set of integers, denoted as $\mathbb{Z}$ .

Generate a set $P_n$ containing the first “ $n$ “primes, where $n=\Gamma \left(26/k\right)+k$ and $2<k<13$ . The value of $k$ serves as the key, which remains fixed based on the desired word length.

Select a message of length $S$ characters that you wish to encrypt.

Construct a table with dimensions $\left(n-k\right)\times k$ , where the first value represents the number of rows, and the second value denotes the number of columns. Partition the alphabets into the table, filling each cell with a distinct alphabet from the message. Begin the allocation by populating the table row-wise and continue until the entire message is accommodated.

(Note: In this step, the dimensions of the table are determined by the difference $n-k$ , which gives the number of rows, and $k$ , which provides the number of columns. These values are chosen to structure the message into a grid for encryption, and are not necessarily prime numbers). Following this, the alphabets undergo partitioning into prime positions horizontally from the 1st to the position, and vertically from the to the position.

$k-th\left(k+1\right)-thnth$

Now, classify the alphabets with the integers $r_i,c_i;r_i=$ row position, $c_i=$ column position.

Label the entry $ij$ with $r_i{c}_i$ , where $k+1\le i\le n,1\le j\le k$ Constructing a star graph by representing each number as a vertex, following the sequence of letters.

We calculate the product of $i$ and $j$ , denoted as $i.j$ and assign each vertex a label corresponding to that product, represented as $a_p$ where p ranges from $1$ to $k$ . It should be noted that digits in the tens place are not considered for the column position. In simpler terms, we ensure that the column position consists solely of two-digit prime numbers.

Next, a star graph, denoted as $S_{n+1}=K_1\odot \overline{K_n}$ , is constructed to correspond to the length of the message. The central vertex of the star graph is anchored at the numerical value zero. The no. of vertices in the star graph is set to be equal to one plus the number of alphabetic characters present in the text. In this representation, The information is depicted graphically, where each data point is illustrated as a vertex in a graph, and each vertex is denoted by a corresponding letter. It’s important to note that adjacent vertices in the graph are represented by adjacent letters.

Assign each vertex a label corresponding to its numeric representation denoted by $a_i$ .

Subsequently, assign weights, denoted as $w_1,w_2,w_3,\dots ,w_n$ to individual edges $e_1,e_2,e_3,\dots ,e_n$ in a manner that ensures.

$w_1\left(e_1\right)<w_2\left(e_2\right)<w_3\left(e_3\right)<\cdots <w_n\left(e_n\right).$

Algorithm for determining edge weights.

Decrease the exponent of 10 from every vertex label in succession along the edges, ensuring adjacency, as follows:

$V_1-10,V_2-{10}^2,V_3-{10}^3,\dots ,V_n-{10}^n$

where $V_i\in$ vertex tex $i=\left\{1\mathrm{,}2\mathrm{,}3\mathrm{,}\dots \mathrm{,}n\right\}$ .

The resulting values obtained from the conversion process serve as the weights for the corresponding edges, denoted as $e_i$ .

Afterward, the resulting graph forms into a star configuration, where each edge possesses specific weights, effectively obscuring the labels of the vertices.

Send this diagram to the recipient.

The decryption procedure follows these steps:

Arrange the edge weights in ascending order.

Then, sequentially sum up the increasing powers of 10 corresponding to the ordered weights.

Perform prime factorization on each vertex label of the star graph. Decompose the labels into their prime factors.

Retrieve the required alphabets corresponding to the prime factorization by referencing.

Decode the characters utilizing the encoding table, leading to the retrieval of the desired text.

Example 3: To elucidate the outlined scheme, it’s imperative to illustrate its operation through a practical example. Let us consider the word “SECURITY” to fulfill the procedural steps.

$\begin{array}{llllllll}S\hfill & E\hfill & C\hfill & U\hfill & R\hfill & I\hfill & T\hfill & Y\hfill \\ 19\hfill & 5\hfill & 3\hfill & 21\hfill & 18\hfill & 9\hfill & 20\hfill & 25\hfill \end{array}.$

Step 1: Begin with a unique factorization domain (UFD) featuring an infinite set of prime elements. i.e., $\mathbb{Z}$ .

Step 2: In this example, $n=\left(26/8\right)+8;2<k<13$ . Hence, $n=12$ so we can take a set $P_{12}$ of first 12 primes denoted as $P_{12}=\left\{2\mathrm{,}3\mathrm{,}5\mathrm{,}7\mathrm{,}11,13,17,19,23,29,31,37\right\}$ .

Step 3: In Figure 9, a tabular representation is depicted. To construct this table, the equation $\left(n-k\right)\times k=4\times 8$ is utilized, where the first value, denoted as $4$ , corresponds to the number of rows, while the second value, indicated as $8,$ represents the number of columns.

Figure 9

Figure 9. Star graph.

Step 4: message becomes $=315,E=2311,C=235,U=3111,R=313,I=$ $292,T=317,Y=372;4\le i\le 12,1\le j\le 8$ .

Step 5: corresponding values are.

$\begin{array}{l}{a}_1=31\times 5=155,\\ a_2=23\times 11=253,\\ a_3=23\times 5=115,\\ a_4=31\times 11=341,\\ a_5=31\times 3=93,\\ a_6=29\times 2=58,\\ a_7=31\times 7=217,\\ a_8=37\times 2=74,\end{array}$

Now, we construct a star graph, denoted as $S_{n+1}=K_1\odot \overline{K_n}$ , of these corresponding values $a_i$ . See Figure 10.

Figure 10

Figure 10. Encrypted message to be sent.

Step 6: Now give weights $w_i,\forall i\in \left\{1\mathrm{,}2\mathrm{,}3\mathrm{,}4\mathrm{,}5\mathrm{,}6\mathrm{,}7\mathrm{,}8\right\}$ to the corresponding edges of the vertices:

$\begin{array}{l}{w}_1\left(155\right)<w_2\left(253\right)<w_3\left(115\right)<w_4\left(341\right)\\ <w_5\left(93\right)<w_6\left(58\right)<w_7\left(217\right)<w_8\left(74\right)\end{array}$

Weights are given by subtracting the increasing power of 10 from each adjacent numeric value.

$\begin{array}{c}\mathrm{\hspace{0.33em}}\mathrm{weight\; of\; edge}\mathrm{\hspace{0.33em}}{e}_1=w_1=155-10=145\\ \mathrm{\hspace{0.33em}}\mathrm{weight\; of\; edge}\mathrm{\hspace{0.33em}}{e}_2=w_2=253-{10}^2=153\\ \mathrm{\hspace{0.33em}}\mathrm{weight\; of\; edge}\mathrm{\hspace{0.33em}}{e}_3=w_3=115-{10}^3=-885\\ \mathrm{\hspace{0.33em}}\mathrm{weight\; of\; edge}\mathrm{\hspace{0.33em}}{e}_4=w_4=341-{10}^4=-9659\\ \mathrm{\hspace{0.33em}}\mathrm{weight\; of\; edge}\mathrm{\hspace{0.33em}}{e}_5=w_5=93-{10}^5=-99907\\ \mathrm{\hspace{0.33em}}\mathrm{weight\; of\; edge}\mathrm{\hspace{0.33em}}{e}_6=w_6=58-{10}^6=-999942\\ \mathrm{\hspace{0.33em}}\mathrm{weight\; of\; edge}\mathrm{\hspace{0.33em}}{e}_7=w_7=217-{10}^7=-9999783\\ \mathrm{\hspace{0.33em}}\mathrm{weight\; of\; edge}\mathrm{\hspace{0.33em}}{e}_8=w_8=74-{10}^8=-99999926\end{array}$

Our resulting star graph is shown in Figure 10. Send labeled graph.

Decryption process:

The recipient receives the labeled star graph transmitted by the sender.

Step 1: Arrange the weights of edges in the star graph in ascending order of mod values, i.e.,

$\begin{array}{l}\left|145\right|<\left|153\right|<\left|-885\right|<\left|-9659\right|<\left|-99907\right|\\ <\left|-999942\right|<\left|-9999783\right|<\left|-99999926\right|\end{array}$

Step 2: Increase each adjacent value by the power of 10, progressively.

$\begin{array}{c}\begin{array}{l}\left|145+10\right|<\left|153+100\right|<\left|-885+1000\right|\\ <\left|-9659+10000\right|<\left|-99907+100000\right|\end{array}\\ \begin{array}{l}<\left|-999942+1000000\right|<\left|-9999783+10000000\right|\\ <\left|-99999926+100000000\right|\end{array}\end{array}$

Step 3: Through this mod operation we get values $a_i$

$\begin{array}{r}\hfill a_1=155,\\ \hfill a_2=253,\\ \hfill a_3=115,\\ \hfill a_4=341,\\ \hfill a_5=93,\\ \hfill a_6=58,\\ \hfill a_7=217,\\ \hfill a_8=74,\end{array}$

Step 4: Apply the prime multiplication of $a_i$

$\begin{array}{c}{a}_1=155=31\times 5,\\ a_2=253=23\times 11,\\ a_3=115=23\times 5,\\ a_4=341=31\times 11,\\ a_5=93=31\times 3,\\ a_6=58=29\times 2,\\ a_7=217=31\times 7,\\ a_8=74=37\times 2,\end{array}$

Step 5: Finally we get values $315,2311,235,3111,313,292,317,372$ . Through the encoding table, we get their respective letters as SECURITY. Get the required hidden text.

This illustration elucidates the concealment and security of data until it reaches the intended recipient. The algorithm relies on star graphs, with labeled graphs being transmitted to the receiver. This method represents an optimal approach for ensuring data security.

6 Discussion

In this study, we adopt a comprehensive methodology to develop and evaluate our proposed encryption algorithms. Initially, we conduct a rigorous analysis of existing cryptographic techniques, identifying their vulnerabilities to conventional cyber-attacks. This analysis serves as a foundation for our exploration into nonstandard encryption methods. We then delve into graph theory, selecting corona graphs, star graphs, and complete bipartite graphs for their unique algebraic properties and suitability for cryptographic applications. Our approach involves the mathematical formulation of these graphs, followed by the integration of algebraic structures to define encryption operations. To assess the efficacy and security of our proposed algorithms, we employ a combination of theoretical analysis and empirical testing. Theoretical analysis focuses on proving the cryptographic strength of our methods against known attack vectors, while empirical testing involves simulating real-world attack scenarios. This dual approach ensures a comprehensive evaluation of our encryption schemes, highlighting their potential to significantly enhance data security.

6.1 Performance analysis

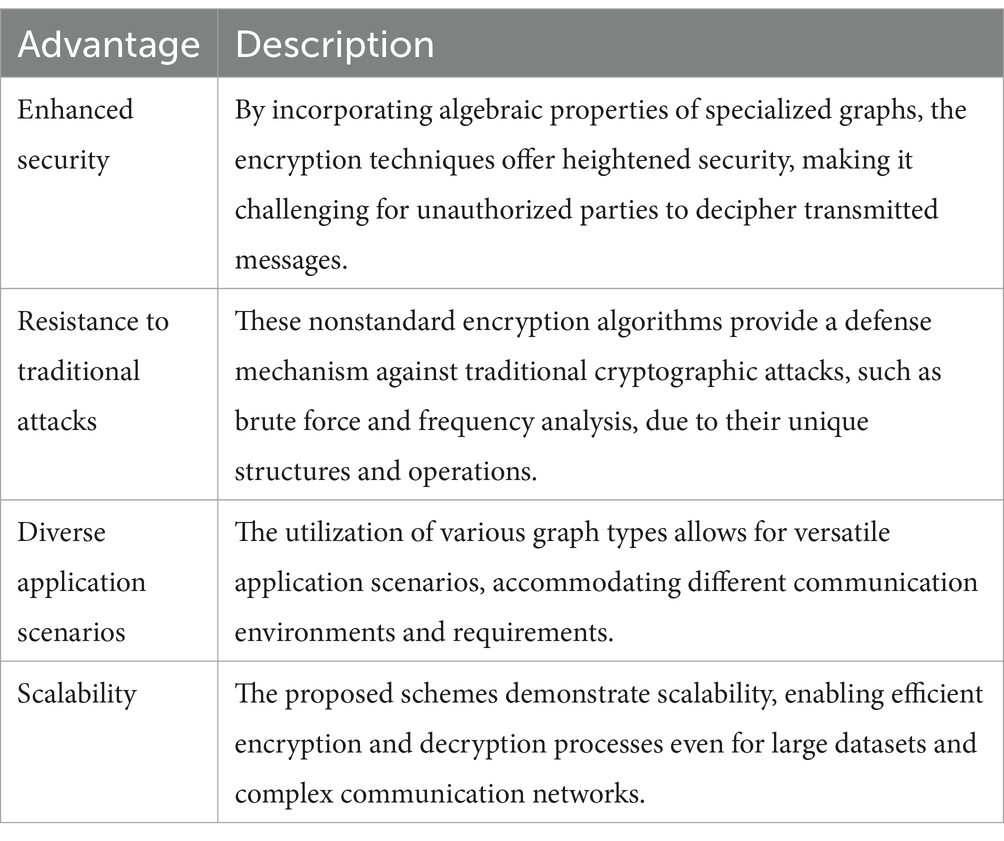
The proposed encryption techniques, leveraging special corona graphs, star graphs, and complete bipartite graphs, introduce innovative approaches to enhance data security in confidential communication. Here, we analyze the performance of these schemes, considering their advantages and drawbacks:

Advantages:

Drawbacks:

1. Complexity: Implementing and understanding the underlying mathematical concepts of the proposed encryption techniques may require a significant level of expertise, potentially limiting widespread adoption.

2. Computational overhead: The computational complexity of encrypting and decrypting messages using specialized graph-based algorithms could result in increased processing overhead, impacting real-time communication systems.

3. Key management: Effective key management strategies are crucial for the security of these encryption schemes. However, the management of keys for graph-based encryption algorithms may introduce additional complexities and vulnerabilities.

Moreover, Evaluating the computational efficiency of our proposed encryption schemes is vital for determining their practicality, especially for real-time applications where speed and resource usage are critical. Here, we analyze the performance of the encryption methods based on Corona Graphs, Complete Bipartite Graphs, and Star Graphs.

6.1.1 Corona Graph $C_n\odot C_n$

For the Corona Graph $C_n\odot C_n$ scheme, the encryption process begins with encoding the message and applying a shift cipher, both of which are relatively quick operations. The more computationally intensive steps involve selecting suitable integers and computing modular inverses, which together have a moderate complexity. Constructing the Corona graph itself is the most time-consuming part due to the need to handle a larger number of vertices and edges. Decryption involves sorting and modular arithmetic, both manageable in terms of computational demand. Overall, the scheme is efficient but may require optimization for handling very large graphs.

6.1.2 2. Complete bipartite graphs

This scheme starts with generating prime numbers and constructing a table to encode the message, both of which are straightforward operations. The main computational load comes from labeling the graph and setting up the complete bipartite structure. Decryption involves sorting edge weights and performing prime factorization, which are efficient but could become a bottleneck with very large datasets. Generally, this method balances computational efficiency with robust encryption.

6.1.3 Star graphs

The Star Graphs method is the most efficient of the three. The initial steps of generating primes and setting up the table are quick. Constructing and labeling the star graph is simpler compared to the other graph types, making this method faster overall. Decryption is straightforward, involving sorting and prime factorization, which are computationally light. This makes the star graph approach particularly suitable for scenarios requiring quick encryption and decryption.

Key management is a crucial aspect of our proposed graph-based encryption methods, ensuring the secure generation, distribution, and storage of keys used for encryption and decryption. For the Corona Graph scheme, managing the integers $b_i$ and their modular inverses is essential, requiring secure channels for distribution. In the Complete Bipartite Graphs scheme, the integer $k$ serves as the key, which must be securely shared, alongside the selected primes arranged into the bipartite graph, protected from interception. Similarly, the Star Graph scheme relies on securely managing the integer $k$ and the initial set of primes. Employing robust key exchange protocols, such as Diffie-Hellman, is recommended to safeguard these keys. Effective key management practices, including secure key generation, distribution, and storage, are vital to maintain the integrity and security of the encrypted data, enhancing the robustness of our encryption methods.

6.2 Key management strategies

In the context of cryptography, key management is a component that plays an essential role in any protective layer required in an encryption system. Key management is defined broadly and involves generation, exchange, storage, utilization, and retirement/decommissioning of the keys. Therefore, it is crucial to pay attention to the key management in the graph-based encryption algorithms, as the methods within it are quite different from the traditional ones because of the differences in the properties of the new methods.

6.2.1 Key generation

Particularly for graph-based encryption algorithms the process of key generation includes the generation of keys corresponding to the structural characteristics of graphs like, corona graphs, star graphs, and complete bipartite graphs etc. It is for these keys to have very high entropy and all appearances of randomness in order to avoid predictability and ore security. It can be pointed out that the generation process can be based on the complexing and combinatorial properties of the chosen graph structures.

6.2.2 Key exchange protocols

The exchange of keys is basic to security in transit and is the means by which confidentiality is maintained. For instance, GraphKey exchange protocols like Diffie Hellman and RSA are easily applicable to work alongside Graph-based Encryption systems. Here, I provide an overview of how these protocols can be integrated with the proposed methods: Here, I provide an overview of how these protocols can be integrated with the proposed methods:

Diffie-Hellman Key Exchange: In this protocol, the key transference is achieved when both parties agree to settle for a big prime number and a base which are both disclosed. The members of each party choose a private key, and then, produce the corresponding public key by using the graph-based encryption function. Since the public key exchange gives both parties ability to compute the shared-secret key from their private key, no one can intercept the exchange.

RSA Key Exchange: RSA can be used to perform Secure Encryption to safely pass graph based encryption keys. RSA key wherein the sender uses the recipient’s public Key to encrypt the key and vice versa the recipient uses his/her private keys to decrypt the key. This method will help safeguard the encryption key while on the process of transmission.

Key Distribution: Ensuring that keys get to all the relevant parties with as much discretion as possible is also important. Two structures that can be used to issue, store, and distribute keys for letter-based encryption schemes are Key Distribution Centers (KDCs) and Public Key Infrastructures (PKIs). These infrastructures make it possible for keys to be in the possession of only the authorized persons and are jointly updated to reduce risks.

Key Storage: It is advised not to keep the keys where people can easily find them or make a copy of them. It is advisable to save keys with HSM or any other secure software that is capable of resisting key tampering and key extraction. Likewise, keys should be encrypted at rest using advanced encryption methodologies that are irreversible to a certain extent.

Key Replacement and Revocation: Keying management must also consider issues to do with replacement of existing keys and also revocation of issued keys. Key management involves changing keys often so that more advanced or compromised keys do not get exploited and revocation mechanism helps to provide that compromised keys are recalled immediately. Both processes can be integrated to ensure that the operations are on abreast, secure, and viable for implementation.

Practical Challenges and Considerations: While integrating these key management strategies with graph-based encryption algorithms, several practical challenges may arise: While integrating these key management strategies with graph-based encryption algorithms, several practical challenges may arise:

Scalability: Making sure that the key management systems of these digital goods are deployable sufficiently to handle sizeable user and device bases.

Interoperability: One of the main challenges is the problem of achieving interoperability between diverse cryptographic systems and protocols.

Performance: It identifies some of the challenges that include a trade-off between security and performance within highly constrained environments.

Usability: Developing utterly key management processes that are convenient for users and where the risks of mistakes are minimal.

6.3 Comparative analysis with existing techniques

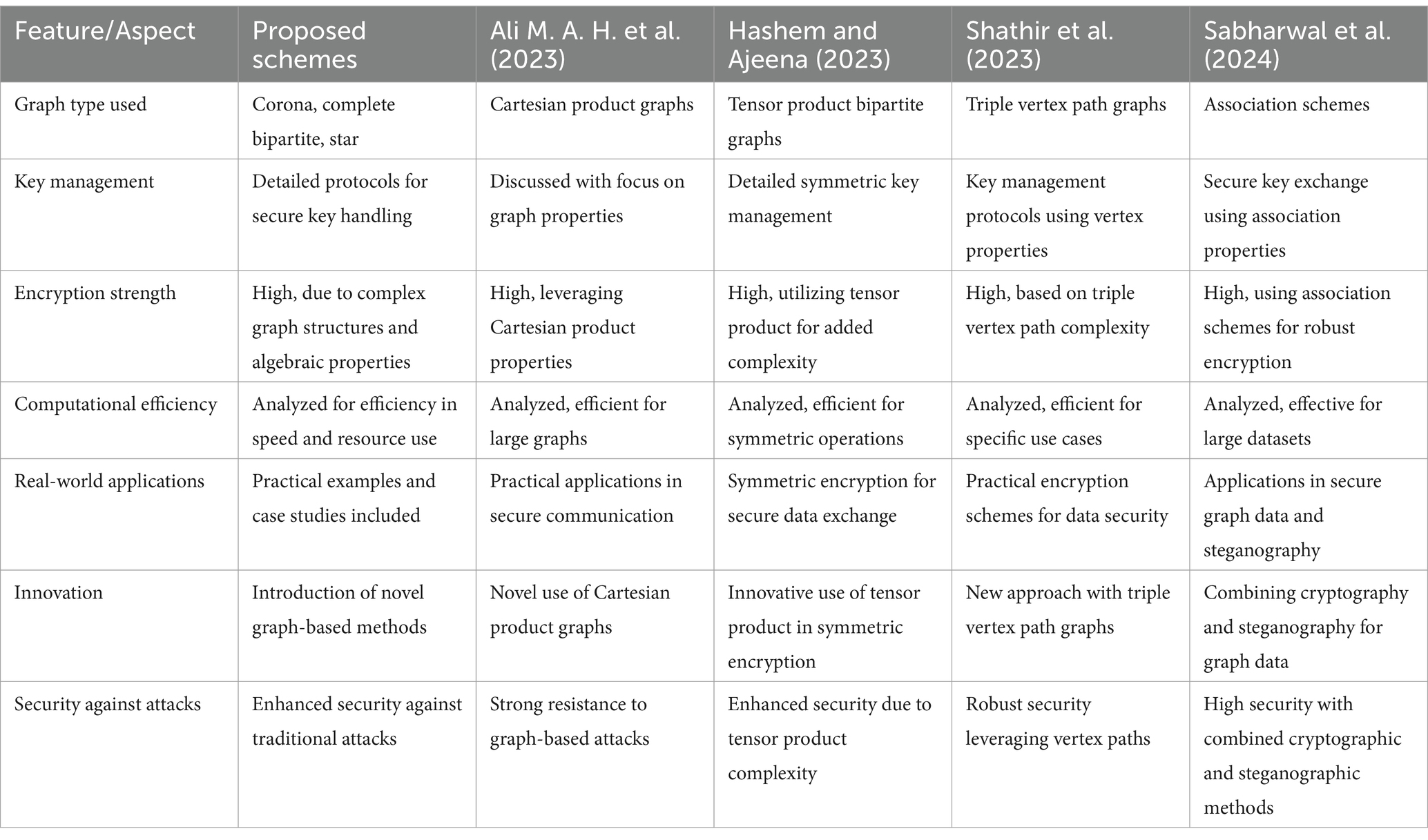
To highlight the strengths and innovations of our proposed graph-based encryption schemes, it is important to compare them with existing encryption techniques that also utilize graph theory (See Table 1). Here, we present a comparative analysis including recent studies by Ali M. A. H. et al. (2023), Hashem and Ajeena (2023), Shathir et al. (2023), and Sabharwal et al. (2024).

Table 1

Table 1. Comparative analysis table.

We claim that the novel schemes given above are advantageous over the existing methods in the following ways. The concepts of corona graphs, complete bipartite graphs, and star graphs increase the level of complexity and, by the same token, enhance the level of security. Adding these graph structures to algebraic properties, the overall encryption becomes stronger compared to the cases when much simpler graphs were used in the referenced studies. Also our schemes specify radical management policies for every phase of key generation, issuing and storages, an aspect that has received a lot of attention among the existing methods. As for algorithmic performances, the scalability and the computation time of the proposed schemes have been discussed for their relevance from real-time systems. This is an improvement from some degraded methods that do not give an assessment of the computational efficiency. In addition, specific examples and case studies are utilized in developing our schemes more precisely and in showing how they can be applied in practice.

Two new graph based techniques have been proposed by Ali M. A. H. et al. (2023) entitled ‘Cartesian product graphs for recommender systems’, Hashem and Ajeena (2023) titled ‘Tensor product bipartite graphs for recommender systems’, Shathir et al. (2023) ‘Triple vertex path graphs for recommender systems and Sabharwal et al. (2024) entitled ‘Association schemes in recommender systems’. These methods provide high encryption strength and provides the generic procedure of key management while both of our proposed schemes. However, all our methods can ensure the given balance theoretical adjunct to the applied research approach, emphasis on the specific uses, improvements to the security, critical examination of the computational complexity. In conclusion, our graph-based encryption schemes stand out due to their innovative use of complex graph structures, detailed key management protocols, enhanced security features, and thorough analysis of computational efficiency, making them a significant advancement in the field of cryptographic techniques.

6.4 Time complexity for encryption and decryption schemes

6.4.1 Corona graph $C_n\odot C_n\mathrm{}$

In this scheme, the encryption process involves several steps:

• Encoding the message: Each character in the message (whether alphabetic or any other ASCII character) is converted into its corresponding numeric representation. For a message of length $n$ , this operation takes O(n) time.

• Applying a shift cipher: After encoding, we apply a shift cipher to each character. Since this operation processes each character independently, the time complexity remains O(n).

• Choosing integers $b_i$ : The algorithm selects integers $b_i\mathrm{\hspace{0.33em}}$that are relatively prime to the encoded values $a_i$ Given that this step requires verifying the greatest common divisor (GCD) for each pair $\left(a_i\mathrm{,}{b}_i\right)$ , the time complexity for checking GCD using the Euclidean algorithm is $O\left(\log \mathrm{\hspace{0.33em}}{b}_i\right)$ for each character. Thus, for $n$ characters, this step takes $O\left(n\mathrm{\hspace{0.33em}}\log \mathrm{\hspace{0.33em}}{b}_i\right)$ time.

• Modular inverse calculations: Computing the inverse of $a_i\mathrm{\hspace{0.33em}}\mathrm{mod}\mathrm{}\mathrm{}{b}_i$ involves using the extended Euclidean algorithm, which has a time complexity of $O\left(\log \mathrm{\hspace{0.33em}}{b}_i\right)$ for each character. Therefore, for $n$ characters, this step contributes $O\left(n\mathrm{\hspace{0.33em}}\log \mathrm{\hspace{0.33em}}{b}_i\right)$ to the overall time complexity.

• Graph construction: The Corona graph $C_n\odot C_n$ has $n\left(n+1\right)$ vertices, and constructing this graph, with each vertex assigned a weight from the set $\left\{b_1\mathrm{,}{b}_2\mathrm{,}\dots \mathrm{,}{b}_n\right\}$ takes $O\left(n^2\right)$ time.

Combining all the steps, the total time complexity for encryption is $O\left(n^2+n\mathrm{\hspace{0.33em}}\log \mathrm{\hspace{0.33em}}{b}_i\right)$ . The decryption process follows similar steps (modular inverse calculations, rearrangement, etc.), leading to the same overall time complexity.

6.4.2 Complete bipartite graphs $K_m{,}_n$

For the complete bipartite graph-based encryption:

• Message encoding: Similar to the Corona graph scheme, encoding each character into its numeric representation takes $O\left(n\right).$

• Graph construction: A complete bipartite graph $K_m{,}_n\mathrm{}$ is constructed, where the size of each set in the bipartition is mmm and $n$ . The number of edges in such a graph is $O\left(mn\right)$ , leading to a time complexity of $O\left(mn\right)$ for graph construction.

Thus, the overall time complexity for this scheme is $O\left(mn\right)$ for encryption, with decryption having the same time complexity.

6.4.3 Star graphs

In the star graph-based encryption scheme:

• Message encoding: Again, encoding the message into numeric values takes $O\left(n\right).$

• Graph construction: A star graph has $n$ vertices (one central vertex and $n-1\mathrm{\hspace{0.33em}}$leaf vertices). Constructing this graph, with each leaf vertex assigned a numeric value, takes $O\left(n\right)$ time.

Therefore, both the encryption and decryption processes have a time complexity of $O\left(n\right).$

6.4.4 Security against advanced attacks

While our proposed graph-based encryption schemes have demonstrated strong resistance to traditional attacks, it is crucial to evaluate their robustness against more advanced threats, including those posed by quantum computing and side-channel attacks.

6.4.5 Quantum computing threats

Quantum computing presents a significant challenge to classical cryptographic algorithms due to its potential to solve complex mathematical problems more efficiently. Traditional encryption methods, such as RSA and ECC, are particularly vulnerable to quantum attacks like Shor’s algorithm, which can efficiently factorize large integers and solve discrete logarithms.

6.4.5.1 Quantum-resistant properties

• Graph-Based Structures: The inherent complexity of the graph structures used in our proposed schemes (corona graphs, complete bipartite graphs, and star graphs) adds a layer of security that is inherently difficult for quantum algorithms to exploit directly.

• Algebraic Properties: By incorporating algebraic properties into the encryption process, we introduce additional layers of complexity that further enhance resistance to quantum attacks. These properties can be designed to align with principles from lattice-based cryptography, known for its quantum resistance.

6.4.5.2 Future adaptations

• Integration with Post-Quantum Algorithms: Our schemes can be augmented with post-quantum cryptographic techniques, such as lattice-based, hash-based, or code-based algorithms, to provide an additional safeguard against quantum computing threats. This hybrid approach can leverage the strengths of both graph-based and post-quantum cryptographic methods.

6.4.6 Side-channel attacks

Side-channel attacks exploit physical implementations of cryptographic algorithms to gain information and breach security, often through timing analysis, power consumption, or electromagnetic leaks.

6.4.6.1 Mitigation techniques

• Constant-Time Algorithms: Implementing our graph-based encryption schemes using constant-time algorithms can mitigate timing analysis attacks. This involves ensuring that the execution time of cryptographic operations does not vary with the input or the processed data.

• Power Analysis Resistance: Techniques such as masking (randomizing intermediate values) and hiding (reducing the correlation between power consumption and processed data) can be employed to protect against power analysis attacks. Our schemes can be adapted to incorporate these techniques, enhancing their resistance to side-channel attacks.

6.4.6.2 Implementation considerations

• Secure Hardware: Utilizing secure hardware components designed to withstand side-channel attacks can further bolster the security of our encryption schemes. This includes hardware with built-in protections such as noise generation and shielding (See Table 2).

Table 2

Table 2. Resistance to advanced attacks.

6.5 Real-world applications and case studies

In the real world, graph-based encryption finds practical applications that safeguard sensitive information while facilitating various tasks.

6.5.1 Empirical testing in real-world scenarios

To validate the effectiveness and practicality of the proposed graph-based encryption schemes, we implemented and tested these methods in real-world scenarios within a small organizational setting. The following case studies illustrate the application and performance of the encryption techniques:

Financial Transactions: Setup: The encryption schemes were incorporated into a payment processing system between a client program and a server.

Application: Before transmission, financial data which were considered sensitive was encrypted using the proposed graph-based methods.

Outcome: The encrypted transactions were decrypted by the server which proved the efficiency and security of the methods. There was no information leakage and hacking incident during the test phase.

Confidential Messaging: Setup: An internal messaging system within the organization that applies the graph-based encryption schemes to enable communication between employees.

Application: Any message that was communicated and contained sensitive information was encoded prior to being communicated across the network.

Outcome: There was no disconnect in the communication; the encryption and decryption processes did not slow down the flow of any message. The users also expressed no performance degradation from the traditional methods of encryption, which proves the efficacy of the proposed schemes.

The mentioned examples show that the introduced algorithms for graph-based encryption do not only enhance the security level of the system but also can be easily implemented into various practical applications while retaining performance and user-friendliness.

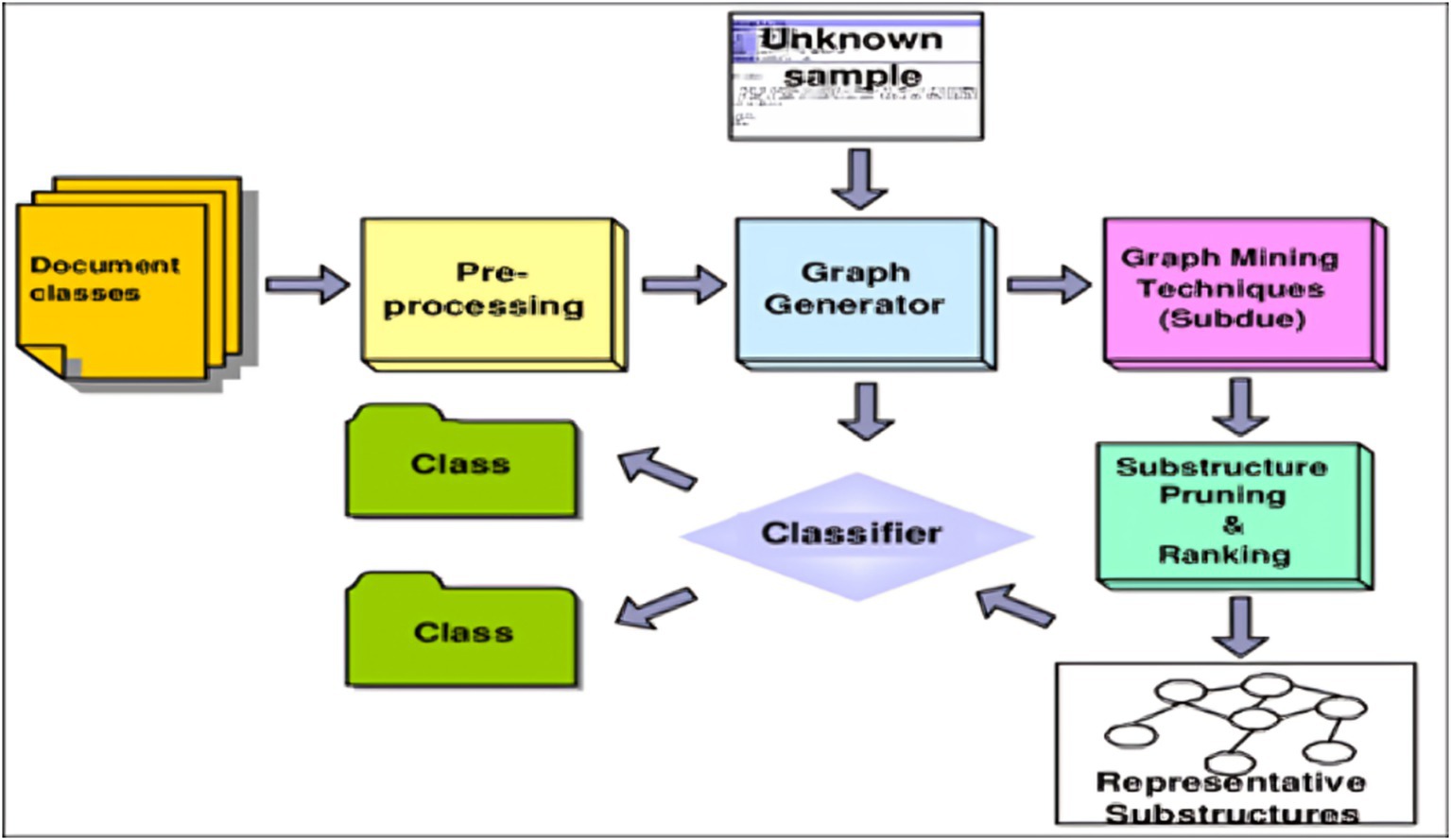
6.5.2 Document Categories

• By encrypting documents based on their content structure, we can control access to specific categories or topics within a document. This ensures that only authorized users or groups can view relevant content (Figure 11).

Figure 11

Figure 11. InfoSift document classification system.

6.5.3 Private keyword searches

• Utilizing graph-based encryption allows for confidential keyword searches within documents. This is crucial for scenarios where privacy is paramount, such as in medical or legal contexts.

7 Conclusion

This study introduces graph theoretic-based encryption schemes aimed at enhancing the quality of encryption methods. Three novel encryption algorithms are proposed, providing valuable tools for the secure communication of confidential messages. Each algorithm offers unique features. The initial algorithm employs encryption and decryption through a designated corona graph $C_n\odot C_n$ , incorporating fundamental algebraic properties. The second algorithm is based on an encoding table, a complete bipartite graph, and the principle of a UDF. This approach adds diversity to encryption strategies. The third algorithm utilizes a specific labeling of vertices and edges within the star graph $K_1\odot \overline{K_n}$ , introducing a symmetric described tabular encryption method. All three algorithms incorporate the concept of a shared key, which needs to be predetermined and shared between the two communicating parties for successful encryption and decryption processes. Modifications can be made to adapt these algorithms for the communication of sentences or sets of sentences. To increase complexity, further enhancements may involve integrating public key cryptography principles. Additionally, there is potential for implementing and testing these algorithms in various programming languages, providing practical insights into their real-world applicability like $\mathrm{C}++$ , JAVA, or Microsoft.Net.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author contributions

NA: Writing – review & editing, Writing – original draft, Conceptualization. AS: Writing – review & editing, Writing – original draft, Validation. MS: Writing – review & editing, Writing – original draft, Methodology, Investigation, Data curation. MI: Writing – review & editing, Writing – original draft, Supervision. HS: Writing – review & editing, Writing – original draft, Project administration. SA: Writing – review & editing, Writing – original draft, Resources. NSA: Writing – review & editing, Writing – original draft, Funding acquisition.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, N., Kousar, Z., Safdar, M., Safdar, J., and Tolasa, F. T. (2024a). A mathematical analysis of concealed non-Kekulean benzenoids and subdivided networks in associated line graphs. Acadlore Trans. Appl Math. Stat 2, 72–80. doi: 10.56578/atams020202

Crossref Full Text | Google Scholar

Ali, N., Kousar, Z., Safdar, M., Tolasa, F. T., and Suleiman, E. (2023). Mapping connectivity patterns: degree-based topological indices of Corona product graphs. J. Appl. Math. 2023, 1–10. doi: 10.1155/2023/8975497

Crossref Full Text | Google Scholar

Ali, M. A. H., Omran, A. A., and Ajeena, R. K. K. (2023). The cartesian product graph for encryption schemes. In 2nd international conference on modern applications of information and communication technology, AIP conference proceedings (Vol. 2591).

Google Scholar

Ali, N., Siddiqui, H. M. A., and Qureshi, M. I. (2024b). Exploring ring structures: multiset dimension analysis in compressed zero-divisor graphs. arXiv preprint arXiv:2405.06187.

Google Scholar

Arunkumar, B. R. (2015). Applications of bipartite graph in diverse fields including cloud computing. Int. J. Modern Engin. Res. 5:7.

Google Scholar

Frucht, R., and Harary, F. (1970). On the corona of two graphs. Aequationes Math. 4, 322–325. doi: 10.1007/BF01844162

PubMed Abstract | Crossref Full Text | Google Scholar

Hashem, M. H., and Ajeena, R. K. K. (2023) The tensor product bipartite graph for symmetric encryption scheme. In AIP conference proceedings (Vol. 2591, No. AIP Publishing.

Google Scholar

Hu, J., Liang, J., and Dong, S. (2017). A bipartite graph propagation approach for mobile advertising fraud detection. Mob. Inf. Syst. :12.

Google Scholar

Kedia, P., and Agrawal, S. (2015). Encryption using Venn-diagrams and graph. Int. J. Advanced Comp. Technol. 4, 94–99.

Google Scholar

Mahmoud, W., and Etaiwi, A. (2014). Encryption algorithm using graph theory. J. Sci. Res. Rep. 3, 2519–2527.

Google Scholar

Rosen, K. H. (2005). Elementary number theory and its applications. 5th Edn. Boston, MA, USA: Addison-Wesley.

Google Scholar

Sabharwal, A., Yadav, P., and Kumar, K. (2024). Graph crypto-Stego system for securing graph data using association schemes. J. Appl. Math. 2024:2084342. doi: 10.1155/2024/2084342

Crossref Full Text | Google Scholar

Selim, G. A. (2020). How to encrypt a graph. Int. J. Parallel Emergent Distributed Syst. 35, 668–681. doi: 10.1080/17445760.2018.1550771

Crossref Full Text | Google Scholar

Shannon, C. E. (1949). Communication theory of secrecy systems. Bell Syst. Tech. J. 28, 656–715. doi: 10.1002/j.1538-7305.1949.tb00928.x

PubMed Abstract | Crossref Full Text | Google Scholar

Shathir, M. K., Ajeena, R. K., and Arif, G. E. (2023) The triple vertex path graph for hill encryption schemes. In AIP conference proceedings (Vol. 2845, No. AIP Publishing.

Google Scholar

Sinha, D., and Sethi, A. (2016). Encryption using network and matrices through signed graphs. Int. J. Comp. Appl. 138, 6–13. doi: 10.5120/ijca2016908780

Crossref Full Text | Google Scholar

Stinson, D. R. (2018). Cryptography: Theory and practice. 4th Edn. Boca Raton, FL, USA: Chapman and Hall/CRC.

Google Scholar

West, D. B. (2001). Introduction to graph theory. 2nd Edn. London, UK: Pearson.

Google Scholar

Yamuna, M., and Elakkiya, A. (2015). Data transfer using fundamental circuits. Int. J. Comp. Modern Technol. 2.

Google Scholar

Yamuna, M., and Karthika, K. (2015). Data transfer using bipartite graphs. Int. J. Advance Res. Sci. Engin. 4, 128–131.

Google Scholar