Trustworthy and reliable computing using untrusted and unreliable quantum hardware

Security and reliability are primary concerns in any computing paradigm, including quantum computing. Currently, users can access quantum computers through a cloud-based platform where they can run their programs on a suite of quantum computers. As the quantum computing ecosystem grows in popularity and utility, it is reasonable to expect that more companies including untrusted/less-trusted/unreliable vendors will begin offering quantum computers as hardware-as-a-service at varied price/performance points. Since computing time on quantum hardware is expensive and the access queue could be long, the users will be motivated to use the cheaper and readily available but unreliable/less-trusted hardware. The less-trusted vendors can tamper with the results, providing a sub-optimal solution to the user. For applications such as, critical infrastructure optimization, the inferior solution may have significant socio-political implications. Since quantum computers cannot be simulated in classical computers, users have no way of verifying the computation outcome. In this paper, we address this challenge by modeling adversarial tampering and simulating it's impact on both pure quantum and hybrid quantum-classical workloads. To achieve trustworthy computing in a mixed environment of trusted and untrusted hardware, we propose an equitable distribution of total shots (i.e., repeated executions of quantum programs) across hardware options. On average, we note ≈ 30X and ≈ 1.5X improvement across the pure quantum workloads and a maximum improvement of ≈ 5X for hybrid-classical algorithm in the chosen quality metrics. We also propose an intelligent run adaptive shot distribution heuristic leveraging temporal variation in hardware quality to user's advantage, allowing them to identify tampered/untrustworthy hardware at runtime and allocate more number of shots to the reliable hardware, which results in a maximum improvement of ≈ 190X and ≈ 9X across the pure quantum workloads and an improvement of up to ≈ 2.5X for hybrid-classical algorithm.

1 Introduction

Quantum computing (QC) can solve many combinatorial problems exponentially faster than classical counterparts by leveraging superposition and entanglement properties. Examples include machine learning (Cong et al., 2019), security (Phalak et al., 2021), drug discovery (Cao et al., 2018), computational quantum chemistry (Kandala et al., 2017), and optimization (Farhi et al., 2014). However, quantum computing faces technical challenges like quantum bit (qubit) decoherence, measurement error, gate errors and temporal variation. As a result, a quantum computer may sample the wrong output for a specific quantum circuit. While quantum error correction codes (QEC) can provide reliable operations (Gottesman, 2010), they require thousands of physical qubits per logical qubit, making them impractical in the foreseeable future. In the presence of these errors, another method of getting the most out of qubit-constrained quantum computers is to use multiple executions of the same quantum circuit to obtain the output. Existing Noisy Intermediate-Scale Quantum (NISQ) computers have a few hundred qubits and operate in the presence of noise. The NISQ computing paradigm offers hope to solve important problems such as, discrete optimization and quantum chemical simulations. Since noisy computers are less powerful and qubit limited, various hybrid algorithms are being pursued, such as, the Quantum Approximate Optimization Algorithm (QAOA) and Variational Quantum Eigensolver (VQE), in which a classical computer iteratively drives the parameters of a quantum circuit. The purpose of the classical computer is to tune the parameters that will guide the quantum program to the best solution for a given problem. On high-quality hardware with stable qubits, the algorithm is likely to converge to the optimal solution faster, i.e., with fewer iterations.

Security and reliability are primary concerns in quantum computing. Researchers are currently exploring a suite of quantum computers offered by IBM, Rigetti, IonQ, and D-Wave (via a cloud-based platform) to solve optimization problems. The hardware vendors of quantum computers provide a compiler for their hardware, such as, IBM's Qiskit compiler (Aleksandrowicz et al., 2019), Rigetti's QuilC compiler (Smith et al., 2020), and so on. Users can create circuits for specific hardware and upload them to the cloud, where they are queued. The results of the experiment are returned to the user once the experiment is completed. As the quantum computing ecosystem evolves, third-party service providers are expected to emerge offering potentially higher performance at cheaper price points. This will entice users to utilize these services. For example, some third-party compilers like Orquestra (Computing, Z. 2021) and tKet (Computing, C. Q. 2021), are appearing that support hardware from multiple vendors. Baidu, the Chinese internet giant, recently announced an “all-platform quantum hardware-software integration solution that provides access to various quantum chips via mobile app, PC, and cloud.” referred to as “Liang Xi.¹” It provides flexible quantum services via private deployment, cloud services, and hardware access, and can connect to other third-party quantum computers. While trusted hardware remains the preferred choice for applications with significant economic or social impact, the scenario changes when dealing with hybrid quantum-classical algorithms. These algorithms, widely used in optimization problems and quantum machine learning, may incur substantial costs due to the high number of iterations required to reach a solution. Additionally, lengthy wait queues can further delay convergence. Even though dedicated resources may be an option for governments and larger entities, the steep costs associated with such solutions often prove prohibitive. Furthermore, geographical restrictions on computation location can introduce costly consequences and limit the application of quantum computing to a broader array of problems. These trends can result in a dependence on third-party compilers, hardware suites, and service providers that may not be as reliable or secure as trusted alternatives.

1.1 Proposed attack model

In this paper, we discuss a security risk associated with the use of third-party service providers and/or any untrusted vendor. In the proposed attack model, less-trusted quantum service providers can pose as trustworthy and tamper with the results, resulting in the worst-case scenario of users receiving a sub-optimal solution. To show the extent of damage done by the proposed tampering model, we run a simple program on tampered and non-tampered hardware and compare the probability distributions of basis states for both cases (Figure 1). The correct output is “111.” The tampering coefficient (t) models the various degrees of hardware tampering. As t increases, the probability of basis state “111” decreases while the probabilities of the other erroneous states increase. For the case of t = 0.5, state “111” is no longer the dominant output; instead, the incorrect state “100” becomes the dominant output. In practical scenario, as the correct solution to the optimization problem is unknown, the user must rely on the sub-optimal output of the tampered quantum computer.

Figure 1

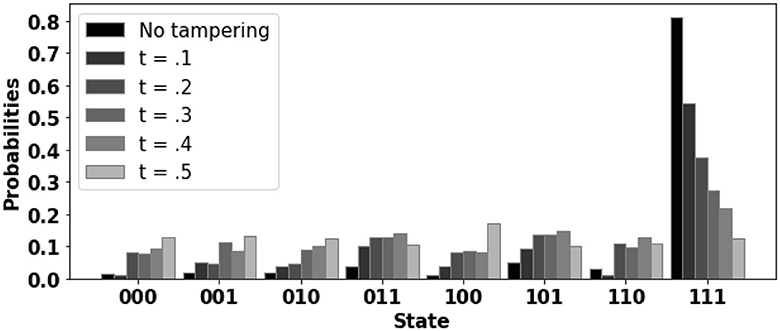
Figure 1. Sample benchmark (toffoli₋n3, correct output = “111”) simulated on the fake back-end (Fake₋montreal) for 10,000 shots. Changing the tampering coefficient (t) models the extent of adversarial tampering. For t = 0.5 erroneous state “100” becomes the most occurring output.

1.2 Novelty

Although the proposed attack model sound similar to classical domain, quantum computing bring new twists e.g., (a) users can not verify the results (which is possible in classical domain) after adversarial tampering since the correct output of a quantum program cannot be computed in classical computer, (b) the results of computation are probability distribution of basis states (instead of deterministic results in classical domain) which opens up new ways of tampering via manipulation of basis state probabilities, (c) the attack models could be low-overhead (e.g., by manipulation of gate error rates) which can be challenging to detect, while significantly affecting the probability of program's correct output.

1.3 Viability of the proposed attack model

The proposed attack model is feasible since, (a) Quantum computers are expensive. We examined cloud-based quantum computing pricing from AWS Braket, IBM, and Google Cloud for IonQ, OQC, Rigetti processors, and IBM's processors. Assuming 1ms runtime per shot, current prices range from $0.35 to $1.60 per second for qubit counts in the range of 8 to 40. With many new vendors entering the quantum service market, it is likely that some of these vendors will be untrusted who will offer access to quantum hardware via the cloud at a lower cost, enticing users to use their services. This is more likely if the third party is based offshore, where labor, fabrication, and packaging costs are cheaper. (b) Access to quantum computers incur long wait time. When a user submits a job to a quantum system, it enters the scheduler where it is queued. For IBM Quantum systems, Ravi et al. (2021) reports that only about 20% of total circuits have ideal queuing times of less than a minute. The average wait time is about 60 min. Furthermore, more than 30% of the jobs have queuing times of more than 2 h, and 10% of the jobs are queued for as long as a day or longer! Third party vendors may provide access to quantum hardware with little or no wait time. Quick access may be vital for quantum machine learning applications to lower the training and inference time.

1.4 Proposed solution

We propose two solutions, (a) Split and distribution of shots/trials: To mitigate the adversarial tampering we propose splitting shots on available hardware. The idea is to distribute the computation among the various hardware (a mix of trusted and untrusted ones or mixture of untrusted hardware for multiple vendors) available. The results from individual hardware and iterations are stitched or combined to obtain the probability distribution of the solution space. (b) Intelligent shot/trial split and distribution: Although splitting of shots is effective, users may end up using trusted and untrusted hardware equally which may not be optimal in terms of performance. We propose an intelligent run-adaptive shot distribution which leverages temporal variation in hardware quality to identify untrusted hardware and bias the number of shots to favor trusted/reliable hardware to maximize the overall computation quality.

1.5 Novelty

(a) Redundant computation for resilience is well-known in classical domain. However, the proposed approach in quantum domain avoids performing any redundant computation by keeping the total number of trails/shots fixed at original value while improving the resilience to tampering. Distribution of shots to multiple vendors/hardware may increase the overall expense only if a hardware with higher price than the baseline hardware is employed for shot distribution. (b) The proposed approach of identification of tampered hardware at run-time by monitoring the dynamic behavior of computation results by leveraging temporal variation is novel and specific to quantum domain. (c) Prior works have not investigated the proposed adaptive shot splitting approach, which not only allows user to identify tampering attempts but enables them to bias the number of shots to favor trusted/reliable hardware to maximize the overall computation quality.

1.6 Research challenges

Although the proposed tampering model and shot distribution based defense may appear trivial, there are many associated technical challenges. For example, (a) what should be the tampering approach? Should all qubits be tampered equally or randomly or selectively and by how much to evade detection? (Section 4.4) (b) how to decide the split boundary i.e., equal or asymmetric split? (Section 6.2) (c) since the trustworthiness of the hardware is not known in advance, how can the user distribute the shots to maximize the quality of solution? (Section 6.3) (d) what kind of metric should be used to evaluate the impact of tampering and effectiveness of the defense? (Section 5.4) (e) does the tampering affect all quantum algorithms equally? We address such research questions in this paper through extensive analysis (Section 6.4).

1.7 Contributions

(1) We propose and compare random vs. selective tampering model. (2) To counteract adversarial tampering, we propose equally distributing shots among available hardware and an intelligent run-adaptive shot splitting heuristic leveraging temporal variation. (3) We demonstrate the effectiveness of our proposed approach for pure quantum and hybrid quantum-classical workloads on a variety of fake back-ends. (4) We validate the attack model and the proposed defense on real hardware.

In the remaining paper, Section 2 provide quantum computing background and related work. The proposed attack model is described in Section 3. Section 4 proposes the tampering model, simulations and evaluation on real hardware. Section 5 presents and evaluates the defense using simulations and experiments on real hardware. Section 6 concludes the paper.

2 Background

In this section, we discuss the basics of a quantum computing and the terminologies used in this paper.

2.1 Qubits and quantum gates

Qubits are the building blocks of a quantum computer that store data as various internal states (i.e., |0〉 and |1〉). In contrast to a classical bit, which can only be either 0 or 1, a qubit can concurrently be in both |0〉 and |1〉 due to quantum superposition. A qubit state is represented as φ = a |0〉 + b |1〉 where a and b are complex probability amplitudes of states |0〉 and |1〉 respectively. The gate operations change the amplitudes of the qubits to produce the desired output. Mathematically, quantum gates are represented using unitary matrices (a matrix U is unitary if UU^† = I, where U^† is the adjoint of matrix U and I is the identity matrix). Only a few gates, known as the quantum hardware's native gates are currently practical in current systems. ID, RZ, SX, X (single qubit gates), and CNOT (2-qubit gate) are the basic gates for IBM systems. All complex gates in a quantum circuit are first decomposed to native gates.

2.2 Quantum error

Quantum gates are realized with pulses that can be erroneous. Quantum gates are also prone to error due to noise and decoherence (Suresh et al., 2021). The deeper quantum circuit needs more time to execute and gets affected by decoherence which is usually characterized by the relaxation time (T1) and the dephasing time (T2). The buildup of gate error (Reagor et al., 2018) is also accelerated by more gates in the circuit. Cross-talk is another form of quantum error where parallel gate operations on several qubits can negatively impact each others performance. Because of measurement circuitry imperfections, reading out a qubit containing a 1 may result in a 0 and vice versa. The qubit quality metrics e.g., gate error, measurement error, decoherence/dephasing and cross-talk vary significantly over time (Alam et al., 2019). A program running on quantum hardware may not always exhibit the repeatable behavior due to temporal variation. This also accounts for the hardware converging to a different outcome for the same program at different points in time. Hardware variability manifests itself in quantum computing as variation in hardware performance, or more precisely, different gate error rates, decoherence times and so on across quantum devices.

2.3 QAOA

QAOA is a hybrid quantum-classical variational algorithm designed to tackle combinatorial optimization problems. A p-level variational circuit with 2p variational parameters creates the quantum state in QAOA. Even at the smallest circuit depth (p = 1), QAOA delivers non-trivial verifiable performance guarantees, and the performance is anticipated to get better as the p-value increases (Zhou et al., 2020). Recent developments in finding effective parameters for QAOA have been developed (Wecker et al., 2016; Crooks, 2018; Guerreschi and Matsuura, 2019; Zhou et al., 2020). In QAOA, a qubit is used to represent each of the binary variables in the target C(z). In each of the p levels of the QAOA circuit, the classical objective function C(z) is transformed into a quantum problem Hamiltonian. With optimal values of the control parameters, the output of the QAOA instance is sampled many times and the classical cost function is evaluated with each of these samples. The sample measurement that gives the highest cost is taken as the solution (Brandao et al., 2018). In a quantum classical optimization procedure,the expectation value of H_C is determined in the variational quantum state E_p(γ, β) = φ_p(γ, β)|H_C|φ_p(γ, β). A classical optimizer iteratively updates these variables (γ, β) so as to maximize E_p(γ, β). A figure of merit (FOM) for benchmarking the performance of QAOA is the approximation ratio (AR) and is given as (Zhou et al., 2020):

$\begin{array}{ll}AR=E_p(\gamma ,\beta )/Cmax& (1)\end{array}$

where Cmax = MaxSat(C(z)).

2.4 Related work

Several recent works on the security of quantum computing (Tannu and Qureshi, 2019; Acharya and Saeed, 2020; Phalak et al., 2021; Saki et al., 2021; Suresh et al., 2021) exist in literature. The authors of Acharya and Saeed (2020) consider an attack model where a rogue element in the quantum cloud reports incorrect device calibration data, causing a user to run his/her program on an inferior set of qubits. The authors propose that test points be added to the circuit to detect any dynamic malicious changes to the calibration data. The objective of our attack model is to tamper with the result so that incorrect or sub-optimal outcome is reported to the user. As such, the impact of the proposed attack is much higher. The proposed attack is also low-overhead since it only involves manipulation of qubit outcomes post-measurement whereas (Acharya and Saeed, 2020) will require complex gate pulse manipulation to increase the error rate. The proposed equal shot distribution and adaptive shot splitting approach to improve resilience is also significantly different than test point insertion. In Tannu and Qureshi (2019), Ensemble of Diverse Mappings (EDM) is proposed to tolerate correlated errors and improve the NISQ machine's ability to infer the correct answer. Rather than using a single mapping for all the shots, EDM uses multiple mappings and divide their shots among these different mappings on a single piece of hardware, then merge the output to get the final solution space. However, this is yet another case of mapping agnostic optimization. If the hardware used for EDM is tampered, suboptimal solutions will be returned even with different mapping splits. In this paper, we propose heuristics to counter adversarial tampering as well as methods for detecting tampered hardware. The attack model in Phalak et al. (2021) assumes a malicious entity in the cloud that can schedule a user circuit to inferior hardware rather than the requested one. To authenticate the requested device, they propose quantum PUFs (QuPUFs). In our attack model, users have a choice of hardware but are unaware of their trustworthiness.

3 Proposed attack model

In this section, we describe the attack model and a few methods for the adversary to tamper with the results.

3.1 Basic idea

We consider that the quantum hardware available via cloud service may tamper with the computation outcome. The objective is to manipulate the results that could have financial and/or socio-political implications.

This is feasible under following scenarios, (a) untrusted third party may offer access to reliable and trusted quantum computers e.g., from IBM in the future but may tamper the computation results, (b) untrusted vendors may offer access to untrusted quantum hardware via cloud at cheaper price and/or quick access (without wait queue) motivating the users to avail their services. The less-trusted quantum service providers can pose as trustworthy hardware providers and inject targeted/random tampering, causing the sub-optimal solution to be sent back. For both scenarios, the user will be forced to trust the less-than-ideal output from the quantum computer since the correct solution to the optimization problem is unknown.

3.2 Adversary capabilities

We assume that adversary, (a) has access to the measured results of the program run by the user. This is likely if the quantum computing cloud provider is rogue, (b) does not manipulate the quantum circuit. This is possible since tampering the quantum circuit may drastically alter the computation outcome which can be suspected, (c) has the computational resources to analyze the program results to determine which qubit lines to tamper with, and (d) methods to mask the tampering from showing up as a significant change in errors (one such method is shown later in the paper using Example1).

3.3 Attack scenario

The adversary in the proposed attack model (Figure 2D) takes the form of a less reliable/untrusted quantum service provider while posing as a reliable/trusted hardware provider. The adversary then modifies the solution before reporting it to the users and seeks to minimally tamper with the output of the program, either by making the sub-optimal solution the optimal for the users or by lowering the probability of the most likely solution. For example, assuming a 3 qubit (q₂, q₁, q₀) quantum program that has optimal output of “100” while the next probable output being “101.” The adversary can target the q₀ and tamper the results such that “101” becomes the optimal output being sent to the user instead of “100.” This tampering can be accomplished in a variety of ways, one of which is to introduce a targeted bit flip error on the q₀ qubit line during measurement operation. Note that adversary has access to computation results (e.g., basis state probabilities of qubits) before sending to the user. Assuming that the quantum circuit itself is correct and optimal, the solution obtained by the adversary will be optimal which in turn can be tampered. In the following section, we will discuss some of the tampering models.

Figure 2

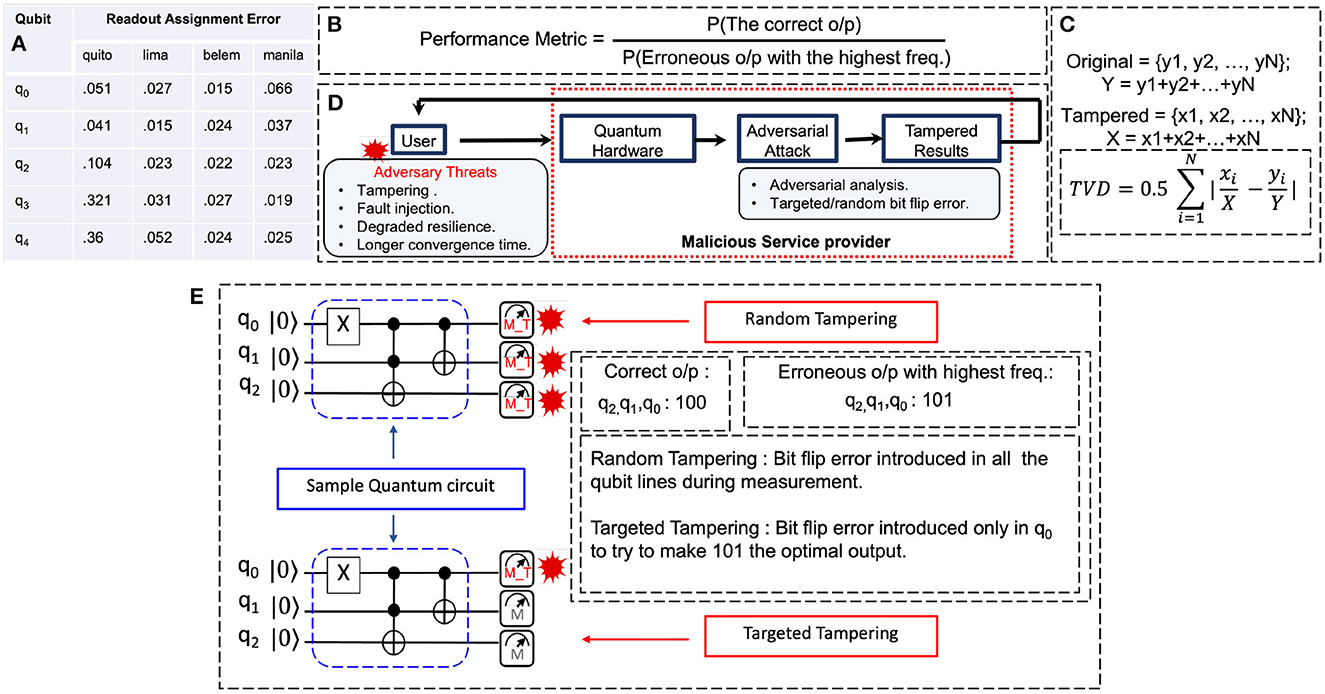
Figure 2. (A) Readout assignment errors for various IBM quantum hardware. (B) Performance Metric (PM). (C) Total Variational Distance (TVD) between two sets of probability densities. (D) Proposed attack model where the attacker introduces targeted or random tampering, resulting in the users receiving a less-than-optimal solution. (E) Adversarial random tampering and targeted tampering by introducing a bit flip error during measurement.

3.4 Adversarial tampering model

Various rogue providers may adopt their favorite method for tampering the results. Some examples are as follows.

3.4.1 Random tampering

While measuring the qubit lines, the adversary can introduce random bit flip error. In this type of tampering which has no overhead, the adversary tampers with the results by lowering the probability of the most likely solution. The adversary can introduce tampering in the form of qubit measurement error (Figure 2E), either on all of the qubit lines or on a subset of the qubit lines randomly.

3.4.2 Targeted tampering

In the case of targeted tampering, the attack will be more strategic in nature (Figure 2E) focusing on specific qubit lines to introduce measurement errors. The proposed algorithm for targeted tampering is described in Algorithm 1.

Algorithm 1

Algorithm 1. Adversarial targeted tampering.

4 Proposed tampering model

This section details the adversarial tampering model, starting with the simulation framework and benchmarks used. We then describe the evaluation metrics, followed by the impact of random and targeted tampering on hardware performance. Next, we discuss the effect of varying shot counts and the impact on QAOA performance. Additionally, the section includes modeling tampering on real hardware and concludes with a summary of the findings.

4.1 Tampering framework used for simulations

We model adversarial tampering by introducing extra measurement error on the qubit lines i.e., while performing final measurement on a qubit, we flip the state of the qubit with probability t, which we refer to in the paper as the tampering coefficient. The proposed sample attack model is depicted in Figure 2D. We use IBM's fake backends to mimic real hardware and add this bit flip error as an attempt by the adversary to tamper with it. This bit flip error can be added to either a targeted qubit (per the Algorithm 1), to all qubit lines, or randomly selected qubit lines. The extra measurement error can be easily hidden when reported alongside readout errors. Consider following example to understand how an adversary can conceal the tampering while reporting measurement errors of the hardware.

Example 1: We consider the real hardware measurement errors, quoted as Readout assignment error (RAE), for the IBM's 5 qubit devices (Figure 2A). Assuming tampering and RAE to be independent and uncorrelated sources of error, we can get the total error as:

$\begin{array}{ll}\Delta RA{E}_{net}=\sqrt{{(\Delta RA{E}_{qi})}^2+{(\Delta Tampering)}^2}& (2)\end{array}$

where (ΔRAE_qi) = RAE value for i^th qubit line and ΔTampering is defined as Equation 3:

$\begin{array}{ll}\Delta Tampering=t/n& (3)\end{array}$

where t= tampering coefficient, n= (total qubit lines−tampered qubit lines + 1).

Assuming that the adversary uses (t = 0.1 or t = 0.5), for ibmq₋lima q₁ RAE, we can calculate the final measurement error (which is 0.028 and 0.09, respectively) for that qubit line using Equation 2 for targeted tampering. These final error values are comparable to the values quoted for various devices (Figure 2A) and qubit lines. For example the new RAE (t = 0.1) for ibmq₋lima q₁ is comparable to RAE's of q₀, q₂ and even less than q₄. When the RAE value for t = 0.5 is compared with the tamper-free RAE values of other hardware such as ibmq₋quito q₃, it is still found to be less. However, our simulations show that an adversarial attack with a tampering coefficient (t = 0.1). As a result, the adversary can easily get away with the tampering.

4.2 Benchmarks

We use the open-source quantum software development kit from IBM (Qiskit) (Cross, 2018) for simulations. A Python-based wrapper is built around Qiskit to accommodate the proposed attack model.

4.2.1 Pure quantum workloads

The benchmark circuits/workloads include 2- and 3- qubit Grover search (grover₋n2 and grover₋n3), 3-qubit Fredkin gate (fredkin₋n3), 3-qubit Toffoli gate (toffoli₋n3), 4-qubit Hidden-Subgroup algorithm (hs4₋n4), 4 and 10-qubit Adder (adder₋n4 and adder₋n10), 4-qubit Inverse QFT (inverseqft₋n4), and 13-qubit Multiply (multiply₋n13). These are adopted from QASMBench (Li et al., 2020) which contains a low-level, benchmark suite based on the OpenQASM assembly representation. Selected benchmark suite covers a wide range of communication patterns, number of qubits, number of gates and depths that are needed to evaluate the proposed attack and defenses.

4.2.2 Hybrid quantum classical workload

We use the iterative algorithm QAOA (Zhou et al., 2020) to solve a combinatorial optimization problem MaxCut (Karp, 1972) to investigate the effects of adversarial tampering and its impact on the hybrid quantum-classical algorithms. The MaxCut problem involves identification of a subset S∈V such that the number of edges between S and it's complementary subset is maximized for a given graph G = (V, E) with nodes V and edges E. MaxCut is NP-hard problem (Karp, 1972), but there are effective polynomial time classical algorithms that can approximate the solution within a defined multiplicative factor of the optimum (Papadimitriou and Yannakakis, 1991). Using a p-level QAOA, an N-qubit quantum system is evolved with H₋C and H₋B p-times to find a MaxCut solution of an N-node graph. QAOA-MaxCut iteratively increases the probabilities of basis state measurements that represent larger cut-size for the problem graph.

4.3 Simulators and hardware

We use the fake provider module in Qiskit as noisy simulators to run our benchmarks. The fake backends are created using system snapshots to mimic the IBM Quantum systems. Important details about the quantum system, including coupling map, basis gates, and qubit parameters (T1, T2, error rate, etc.), are contained in the system snapshots. We use following backends (mimicking their actual hardware representations) for our experiments: Fake₋Montreal (27 qubit), Fake₋Mumbai (27 qubit), etc. We also run some of our benchmarks on ibmq₋manila (actual quantum hardware provided by IBM) and use the modeled tampering parameters for proof-of-concept demonstration of the proposed tampering and defenses.

4.4 Evaluation metric

4.4.1 Performance metric

We define Performance Metric (PM) (Figure 2B) (which is the ratio of the probability of correct and the most frequent incorrect basis states), Equation 4 as a way to measure how well a NISQ machine can infer the right response. PM greater that 1 indicates that the system will be able to correctly infer the output. As our objective is quantify the effect of tampering on sampled output, we use PM as the primary figure of merit in evaluations. This metric has also been used in previous works for performance quantification (Tannu and Qureshi, 2019). The equation for PM is given by:

$\begin{array}{ll}\text{PM}=\frac{P_{\text{correct}}}{P_{\text{incorrect}}}& (4)\end{array}$

where P_correct and P_incorrect are the probabilities of the correct output and erroneous output with the highest frequency, respectively. Example: Suppose a NISQ machine yields a probability of 0.6 for the correct basis state and 0.3 for the most frequent incorrect basis state. The PM would be 2.

4.4.2 Total variation distance

We also use total variation distance (TVD) (Figure 2C) as an additional metric to quantify the impact of tampering on the probability distribution of the output states for a given program. TVD compares the probabilities of the same binary states between two distributions. If the probabilities are identical, then TVD = 0. The TVD will also be higher for extremely diverse distributions. The Equation 5 for TVD is given by:

$\begin{array}{ll}\text{TVD}=\frac{1}{2}{\displaystyle \sum _{x\in X}}|P_1(x)-P_2(x)|& (5)\end{array}$

where P₁ and P₂ are the probability distributions of the binary states before and after tampering, respectively. Example: Assume two probability distributions P₁ and P₂ for a binary state x:

$P_1=\left\{0.4,0.6\right\},P_2=\left\{0.3,0.7\right\}$

The Equation 6 TVD would be:

$\begin{array}{ll}\text{TVD}=\frac{1}{2}(|0.4-0.3|+|0.6-0.7|)=\frac{1}{2}(0.1+0.1)=0.1& (6)\end{array}$

4.5 Simulation and results

This subsection presents simulation results, starting with a comparison of random vs. targeted tampering. We then discuss the impact of tempering on hardware performance, varying shot counts, and QAOA performance.

4.5.1 Random vs. targeted tampering

The performance of a randomly tampered version and a targeted tampered version of the Fake₋montreal backend is evaluated. The Figures 3A, B depicts the PM and TVD variation of the benchmark toffoli₋n3 after 10,000 shots on these tempered back-ends. We introduce bit flip error on all qubit lines during measurement to account for random tampering. However, for targeted tampering, we choose q₁ (as per the Algorithm 1) to introduce the bit flip error. We note a 75% reduction in PM for random tampering and an 80% reduction in PM for minimal tampering (t = 0.1). Therefore, the attack is able to degrade the resilience of computation significantly. At t = 0.5, the PM for all programs becomes less than 1, indicating that the correct result cannot be inferred. For t = 0.1, the probability distributions for random and targeted tampering differ by 24% and 29%, respectively, with a very high TVD of 70% and 72% for random and targeted tampering, respectively, when t = 0.5. We use targeted tampering in the simulations that follow throughout the paper since it is more effective in degrading performance.

Figure 3

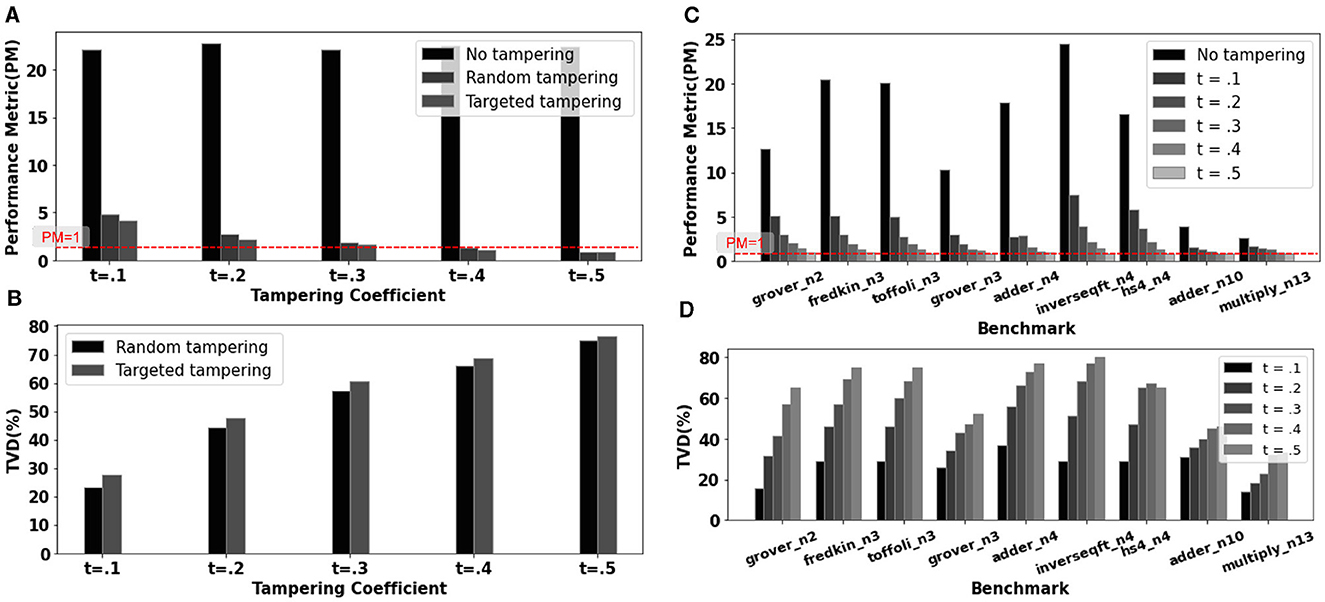
Figure 3. Comparison of (A) PM and (B) TVD for random vs targeted tampering. Benchmark (toffoli₋n3) is run for 10,000 shots on Fake₋montreal. Correct o/p: 111 (q2, q1, q0) and erroneous o/p with highest freq.: 101. As per Algorithm 1 we introduce targeted bit flip error on q1. Random tampering is simulated by introducing bit flip error to all the qubit lines. The (C) PM and (D) TVD variation with the tampering coefficient for various benchmarks. A PM < 1 indicates that the hardware has converged to an incorrect result.

4.5.2 Impact of adversarial tampering on hardware performance

Figures 3C, D depicts the performance metric (PM) and TVD variation with the tampering coefficient (which quantifies the amount of adversarial tampering) for the various programs in our benchmark suite. Each benchmark is run on the Fake₋montreal backend for 10,000 shots. A PM < 1 indicates that the hardware converges to the wrong result, i.e., the probability of the correct solution falls below the probability of the other incorrect states. PM should ideally be as high as possible (at least greater than 1.0). On the contrary, a lower value is preferred for TVD metric. As a result, the adversarial attack seeks to reduce the PM and increase the TVD for the programs, degrading the overall computation performance. The simulation result (Figures 3C, D) shows that as tampering coefficient is increased, the PM for all benchmarks drops significantly (≈ 65% on average at just t = 0.1) and a high TVD is observed. This pattern holds true across all benchmarks. Furthermore, at t = 0.5, the PM for all programs falls below 1, indicating that the correct result from cannot be inferred with reasonable confidence.

Following that, we run the benchmark (toffoli₋n3) for 10,000 shots across 10 fake backends to quantify the effect of the proposed tampering model on different hardware with varying number of available qubits, qubit connectivity, error rates, and so on. The PM and TVD variations with tampering with 10 different Fake backends is depicted in Figures 4C, D. The same trend of PM degradation (≈ 68% on average at just t = 0.1) and significant increase in TVD is observed. For t = 0.5, all of the tested fake backends fail to converge to the correct solution.

Figure 4

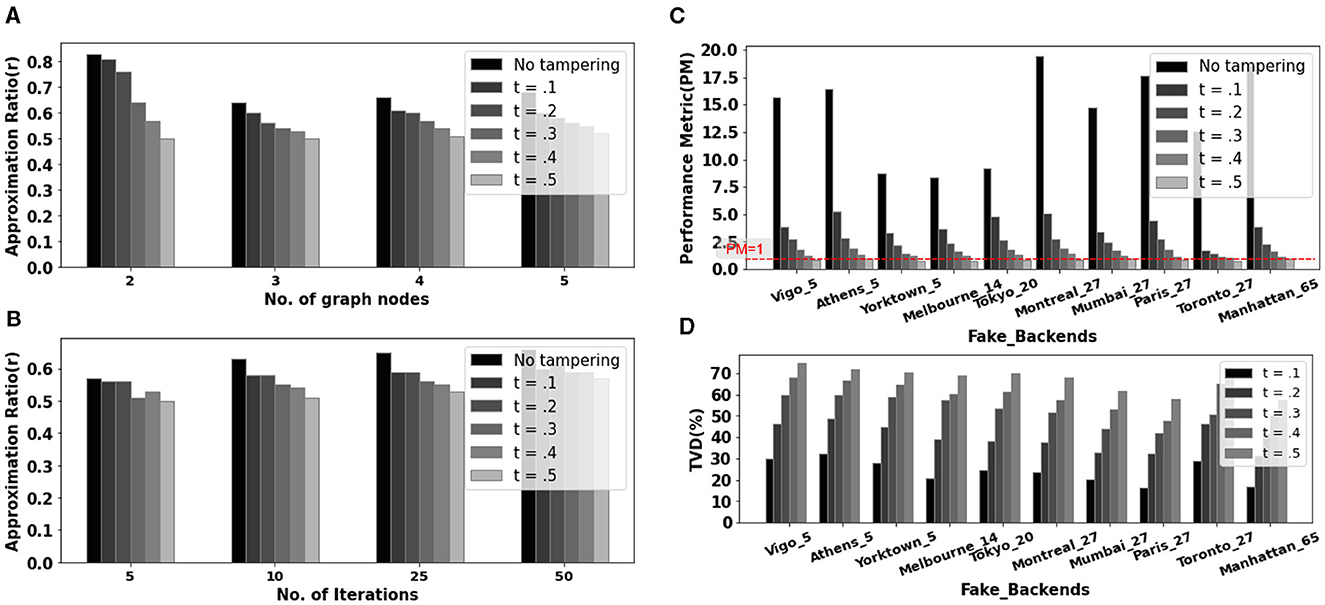
Figure 4. (A) Approximation ratio (r) variation for different graph sizes when run on tampered hardware fake₋montreal for 50 iterations. (B) Performance comparison of QAOA for four-node graph with varying iterations on fake₋montreal. (C) PM and (D) TVD variation with the tampering coefficient for benchmark toffoli₋n3 across various fake back-ends. All tested fake backends fail to converge to the correct solution at t = 0.5.

4.5.3 Effect of tampering with varying number of shots

We run various benchmarks with different number of qubits, depth, and gate sizes by varying the number of shots for t = 0.5. The results are summarized in the Table 1. Even 10,000 shots for a 2-qubit program (grover₋2) is insufficient to achieve correct convergence. When programs with a large number of qubits are run for a small number of shots, adversarial tampering has a greater impact.

Table 1

Table 1. PM vs. shots (tampering coefficient = 0.5) (_-t denotes tampered results).

4.5.4 Impact of tampering on QAOA performance

For the sake of simplicity, we will focus on MaxCut on unweighted d-regular graphs (UdR), where each vertex is connected to only adjacent vertices. We use the approximation ratio defined in Equation 1 as the performance metric for QAOA. We run QAOA for each node graph ten different times and report the average values for the approximation ratio (r). The greater the r value, the better the performance. Ideally, the performance of QAOA can improve as p increases, with r → 1 when p → ∞. For our simulations, we run QAOA for maxcut on U2R, U3R, U4R, and U5R graphs to investigate the effects of adversarial tampering on quantum-classical hybrid algorithms. Figure 4A shows the variation in AR for QAOA solving maxcut for various graph nodes. In each case, we run QAOA (p = 1) for 50 iterations (50 shots/iteration). We note 8% and 25% average reduction in AR for t = 0.1 and t = 0.5, respectively. Figure 4B depicts the variation in AR with the number of iterations for a 4-node graph run on tampered hardware with varying degrees of tampering. When we run QAOA for 10 iterations rather than 50, AR degrades by 10% for t = 0.1 and 25% for t = 0.5, indicating that the performance of the hybrid-classical algorithm QAOA is sensitive to the number of available iterations when run on tampered hardware. However, reducing the number of iterations from 50 to 10 for tamper-free hardware results in a marginal (2%) decrease in AR. Higher levels of tampering increase the variability in measurement outcomes, resulting in less reliable convergence or even failure to converge. As tampering increases, the algorithm may require more iterations or a higher number of shots to achieve similar levels of approximation ratios. Beyond a certain threshold of tampering, increasing the iterations or shots may still fail to achieve convergence. For instance, at a tampering level of t = 0.5, convergence significantly slows down, often resulting in no convergence or incorrect outcomes in most cases.

4.6 Modeling tampering on real hardware

We created fake backends to simulate real hardware and test adversarial tampering and proposed solutions in our experiments. Since adding bit flip errors during measurement on real hardware is not possible, we model a back-end to mimic the real hardware using Qiskit's fake provider module. Then, for a specific program, we mimic the effects of tampering on the backend we built and use those results to model tampering on real hardware for that particular benchmark. The Figure 5 compares the performance of the fake backend (fake₋manila) that we modeled from the real IBM hardware (ibmq₋manila) and the real hardware (ibmq₋manila). We simulate adversarial tampering by running benchmark toffoli₋n3 for 10,000 shots on the simulator and actual hardware. We find that the probability distributions are very similar. The effect of modeled tampering is similar to the trends seen with the fake backend. As the extent of adversarial tampering (t) increases, the probability of the correct output ‘111' decreases in both cases, and at t = 0.5, both the simulator and hardware fail to converge to the correct answer “111”.

Figure 5

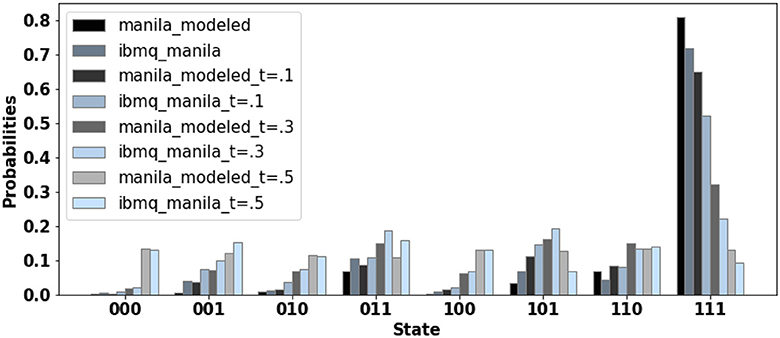
Figure 5. The proposed tampering model is used to compare the performance of a fake backend (manila₋modeled) modeled from the real hardware (ibmq₋ manila) and the actual hardware (ibmq₋manila). We observe that the tampering results are comparable, with only minor variations which can be attributed to temporal variations.

4.7 Summary of tampering analysis

(a) The adversary uses targeted tampering to degrade performance at the expense of computing the solution to the user's program from raw data. (b) Even minor tampering (t = 0.1) is enough to reduce the confidence in the correct output. (c) For benchmarks with a high qubit count, minimal tampering is sufficient to change the output. (d) Users are more sensitive to tampering when fewer shots are used for a given program. (e) Tampering (t = 0.1 to 0.5) can be easily masked by the adversary since the change in measurement error is negligible. (f) Performance of quantum-classical hybrid workloads is very sensitive to number of iterations when run on tampered hardware.

5 Proposed defenses

This section outlines defense mechanisms against adversarial tampering, beginning with the basic concepts and assumptions. We then describe the equal shot distribution and adaptive shot distribution methods. Following this, we present simulation results for pure quantum and hybrid quantum-classical workloads. The section also validates the defenses on actual hardware, discusses their scalability, and analyzes the computational and time overhead. It concludes with a summary of the defense analysis.

5.1 Basic idea and assumptions

We assume that, out of n hardware options available to the user, at least one is reliable, i.e., tamper-free (we show results for up to 2 tampered hardware out of 3). Furthermore, user may avail the services of multiple untrusted cloud vendors which may have different tampering model. However, the user is unaware of tamper-free and tampered hardware and the adversarial tampering model.

We propose splitting shots on available hardware to mitigate the effects of adversarial tampering. For example, one may assume hardware from well-established AWS or IBM to be trusted and from less-established vendor X to be untrusted. Since untrusted/reliable hardware will provide correct solution, the chances of masking the tampered results is higher with shot splitting. Even if the vendors are untrusted, their tampering model may differ. Therefore, splitting the shots may increase the likelihood of suppressing the incorrect outcomes and obtaining correct outcome. We explain the methodology reliability enhancements provided by the proposed shot distribution strategies below. The summary of the two shot splitting approaches is shown in Figure 6.

Figure 6

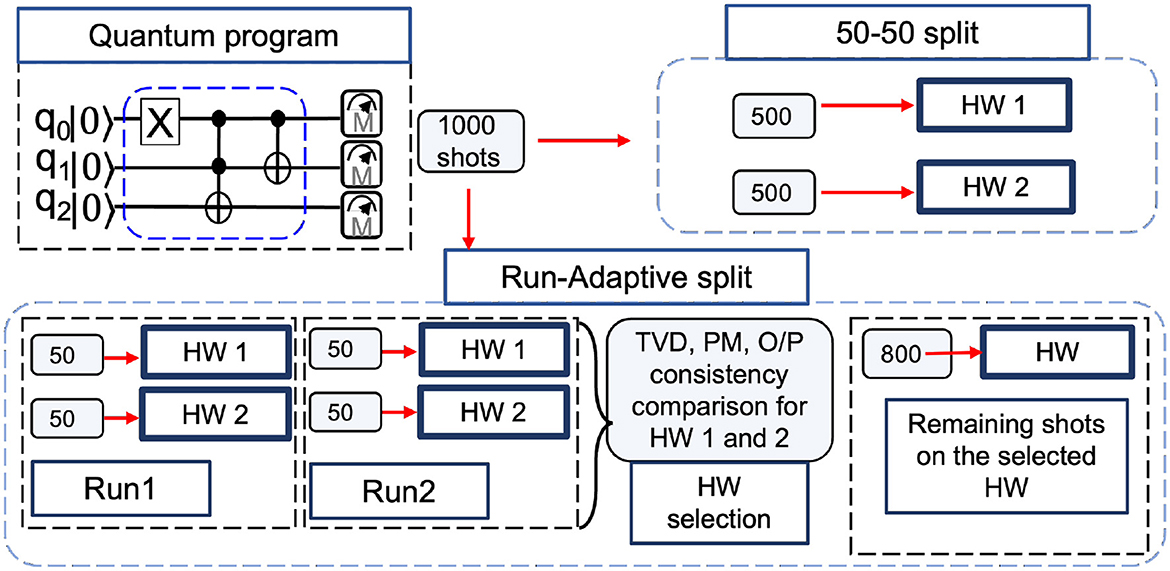
Figure 6. Two different shot splitting approaches to mitigate the effect of adversarial tampering. The user can either do a 50–50 split, where the shots are distributed equally on available hardware and the results are stitched together to get the converged result, or the user can start with two initial runs of small number of shots (say, 50) on both hardware, compare PM, TVD, and output confidence, and run the rest of the remaining shots on the hardware that appears to be better.

5.2 Equal shot distribution

The user can divide the shots evenly among the available hardware without incurring any computational overhead (assuming the hardware are homogeneous and queuing delays are identical). For example, assuming the user has access to hardware HW1 and HW2 provided by two different service providers. HW2 however is plagued with tampering. User has to run a program P1 with 1,000 shots. If he runs all those 1,000 shots on HW2, the results received will be tampered and unreliable. Therefore, we split the shots between these hardware equally to make the results more resilient, thereby mitigating the adversary's tampering (Figure 6). This can be generalized to a scenario with n number of available hardware.

5.3 Adaptive shot distribution

The user can also intelligently and adaptively distribute the shots. This can be done by running a few initial shots on all available hardware, comparing the results, doing majority voting, and then running the rest of the shots on the hardware that is more reliable (Algorithm 2). Reliable, tamper-free hardware is characterized by low noise levels. With a sufficient number of shots, programs on this hardware will converge to a specific solution. Additionally, it will exhibit minimal increases in Total Variation Distance (TVD) between batches and have higher Performance Metric (PM) values. The tampered hardware may return a different solution for each batch of shots run on it due to temporal variation in qubit quality and will exhibit higher TVD and lower PM among the batch of runs. For example, we assume the case of HW1 and HW2 again, with user having 1,000 shots to run. For Run 1, the user fires 50 shots on HW1 and HW2, records the results, and fires 50 shots again as Run 2. The TVD, PM, and repeatability of the final answer from the two iterations are then compared. The user will look for low TVD, high PM, and repeatable converged output and it's confidence (probability) to determine the best hardware (Figure 6). In this way, the user can choose a better hardware to allocate the remaining shots. If not, another iteration of 50 shots on each hardware can be fired and the process is repeated until the user is satisfied. When more than two hardware is available, the same procedure can be used, and majority voting can be done to select the tamper-free hardware from a batch of given hardware.

Algorithm 2

Algorithm 2. Adaptive shot distribution.

The number of shots per run in the adaptive shot distribution method should be determined based on the number of qubits, the depth of the program, and the complexity of the results. As these factors increase, more shots are needed to achieve reliable results. Based on the study in Kessler et al. (2023), which analyzes the required shots for Grover's search algorithm, we provide rough estimates for different scales of quantum circuits. The number of quantum states increases exponentially with the number of qubits, leading to an immense state space. For example, with 30 qubits, the number of possible states is 2³⁰ ≈ 10⁹. The required number of shots to estimate probabilities for each state with a certain confidence factor would be significantly high. However, our solution is typically represented by a single state or a smaller subset of the larger state space, so we focus on identifying these specific states with high probability rather than estimating the probabilities of all possible states. Therefore, increasing the number of shots by a few hundred will generally be sufficient to achieve reliable results. The proposed shot increases for small, medium, and large scale quantum circuits are rough estimates intended to provide a starting point. The exact optimal number of shots required will vary depending on the specific algorithm and the number of distinguishing output states needed. We recommend the following approach:

(a) Initial runs: Begin with a moderate number of shots (e.g., 50 to 100) for the initial runs. This allows for a preliminary assessment of hardware reliability without excessive computational overhead.

(b) Scaling shots:

• Small scale quantum circuits: For circuits using 2 to 10 qubits and depth less than 20, if reliable results are not obtained in initial runs, increase the shots by 1X–1.5X.

• Medium scale quantum circuits: For circuits using 11 to 27 qubits and depth greater than 20, increase the shots by 2X–3X if initial results are not reliable.

• Large scale quantum circuits: For circuits using 28 to 433 qubits or more, increase the shots by 3X-5X if initial results are not reliable.

(c) Iterative adjustment: Monitor the performance metrics (PM, TVD, and AR) after each batch of runs. If the metrics reveal significant noise or variability and reliable hardware has not been identified, incrementally increase the number of shots in subsequent runs until reliable hardware is determined and stable results are achieved.

5.4 Simulation results

5.4.1 Pure quantum workloads

The Figure 7 depicts the performance improvement from the 50–50 split countermeasure against adversarial tampering across multiple benchmarks. With t = 0.5, we simulate one tamper-free (Fake₋montreal) and one tampered hardware (Fake₋montreal₋ tampered). Figures 3C, D showed that t = 0.5 is so detrimental that the user no longer samples the correct output across all benchmarks. However, a 50–50 split shows a significant improvement (≈ 300% PM increase on average) for all simulated benchmarks compared to running all shots on the tempered hardware. Figures 8A, B shows the improvement in PM and TVD with t, validating the proposed defense for a single benchmark (toffoli₋n3) under the same assumption of one tampered and one tamper-free hardware. The proposed 50–50 split results in a significant TVD reduction (≈ 55% on average) and improvement in PM margin (≈ 125% on average and a maximum of ≈ 400% for t = 0.5). The Figures 8C, D depicts the improvements in PM and TVD as a function of the percentage of shots run on tamper-free hardware. The benchmark toffoli₋n3 is run for 10,000 shots on Fake₋montreal (tamper-free hardware) and Fake₋montreal₋tampered (tampered with t = 0.5). We note a ≈ 60% improvement in PM and a 50% reduction in TVD with the 50–50 split (than when all 10,000 shots are allocated to the tampered hardware). For the 90–10 split, we see a massive improvement in PM of approximately 1,900% and a significant TVD reduction 90% compared to the tampered hardware.

Figure 7

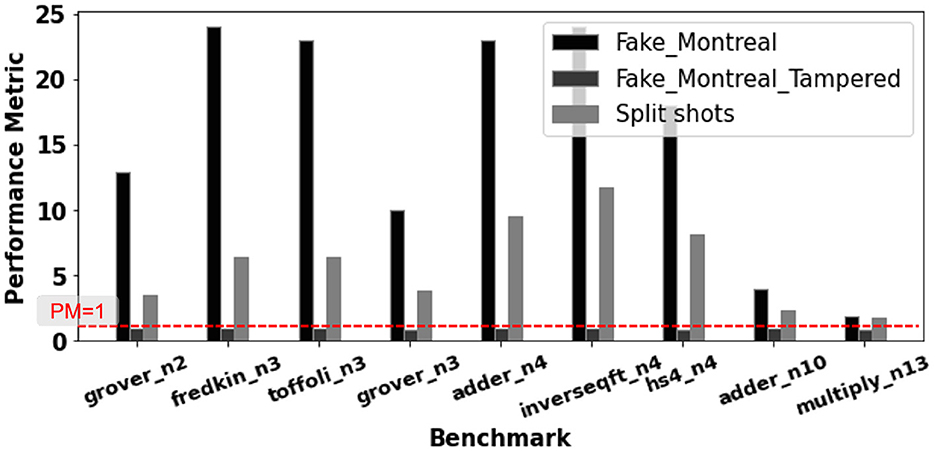
Figure 7. With t = 0.5 and 10,000 shots, we simulate one tamper-free (Fake₋montreal) and one tampered hardware (Fake₋montreal₋ tampered). A 50–50 split results in a significant improvement in PM (≈300% on average).

Figure 8

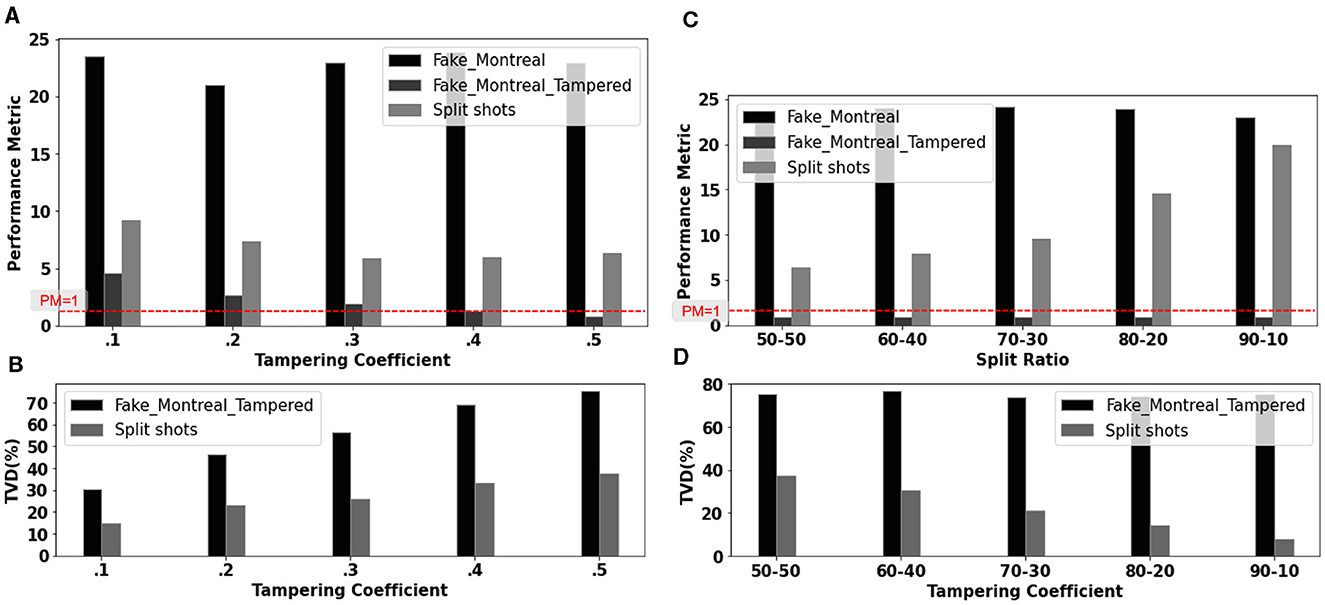
Figure 8. Improvement in (A) PM and (B) TVD for varying degrees of tampering. TVD reduction of ≈ 55% on average and improvement in PM margin (≈ 125% on average and a maximum of ≈ 400% for t = 0.5). (C) PM and (D) TVD improvements as a function of the percentage of shots run on tamper-free hardware. The benchmark toffoli₋n3 is run on Fake₋montreal (tamper-free hardware) and Fake₋montreal₋tampered (tampered with t = 0.5) for 10,000 shots. If the majority of shots are run on tamper-free hardware, the user can significantly improve resilience against tampering.

A sample simulation of how a user can determine the tamper-free hardware and allocate the majority of the shots to that preferred hardware is shown in the Table 2. We run two 50-shot runs for two benchmarks, toffoli₋n3 (3-qubit benchmark) and adder₋n10 (10-qubit benchmark), on two different hardware HW (Fake₋montreal) and HW₋t(Fake₋montreal₋tampered). The simulations account for the extent of tampering experienced by HW₋t (by varying t from 0.1 to 0.5). We compare the PM, TVD, frequent output, repeatability, and confidence factor (probability) across the two runs for each hardware. HW outperforms HW₋t for both distinct benchmarks in every way. Adversarial tampering (even minor tampering e.g., t = 0.1) along with the temporal variations in quantum hardware leads to the HW₋t converging to different outputs for the two different runs for benchmark addern10. In contrast, when other factors such as low TVD variation across two runs are considered as well, along with the tamper-free HW producing the same output for both runs, makes it more reliable. As a result, the user can choose to run the remaining shots in HW only. Hence the user can get a performance boost comparable to the 90-10 split (as much as 1,900% and 90% in two chosen performance metrics, Figures 8C, D).

Table 2

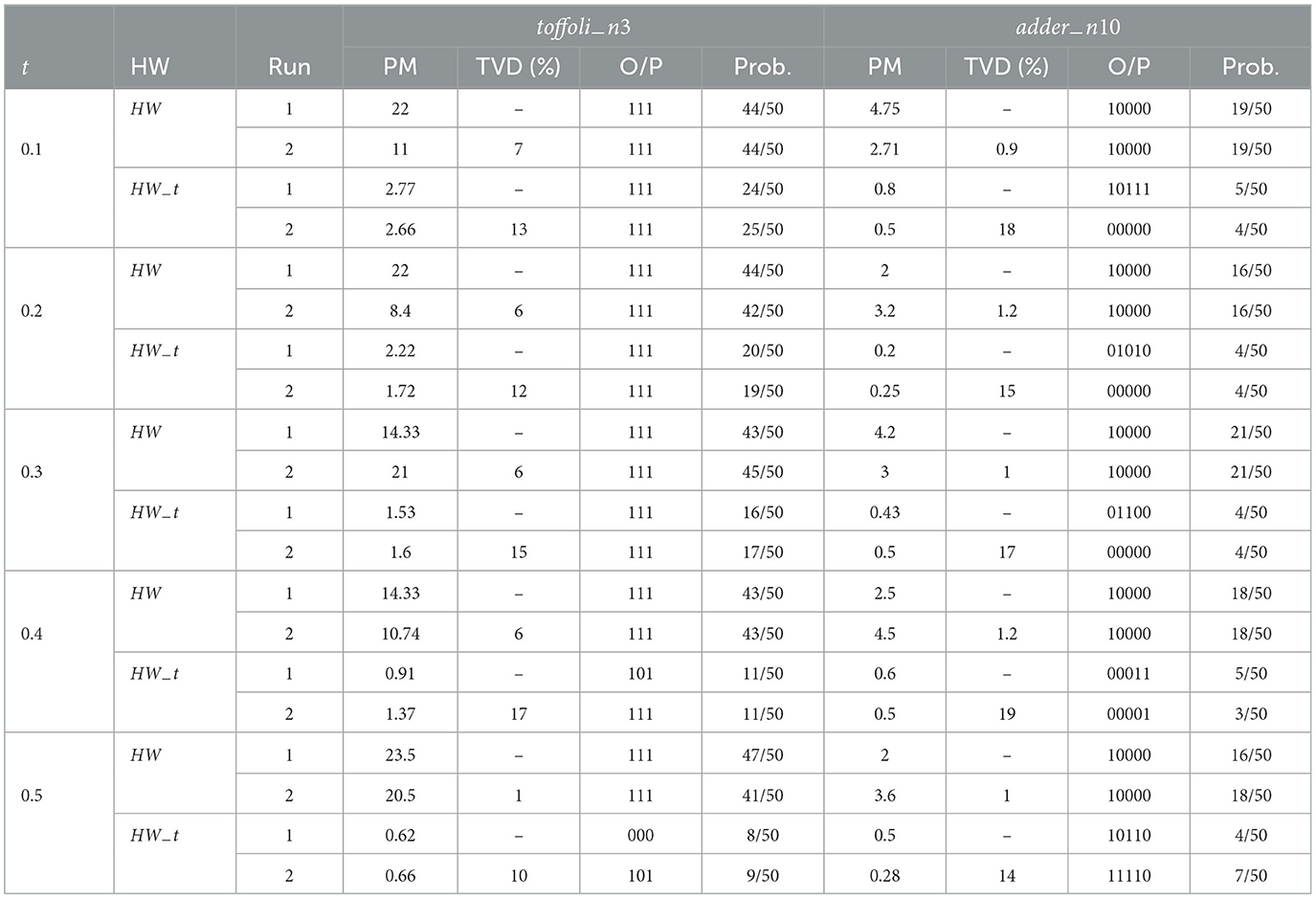
Table 2. Intelligent shot distribution: identifying tampered/bad hardware (shots/run = 50; _t denotes tampered results).

5.4.2 Hybrid quantum classical workload

The proposed 50–50 split is also applicable to hybrid-classical algorithms like QAOA. Figures 9A, B compares how the objective and the AR converges over 50 iterations using the 50–50 split. Table 3 shows the improvement in AR with t, assuming one tampered (HW₋t) and one tamper-free of hardware (HW). We run 25 iterations (50 shots/iteration) on HW (fake₋ montreal) out of a total of 50 iterations, extract the parameters (γ, β) after 25 iterations, and use them as a starting point for parameter optimization in HW₋t for another 25 iterations. We observe AR improvement for various levels of tampering. For t = 0.5, we report the maximum improvement in AR (15% on average) across various graph sizes.

Figure 9

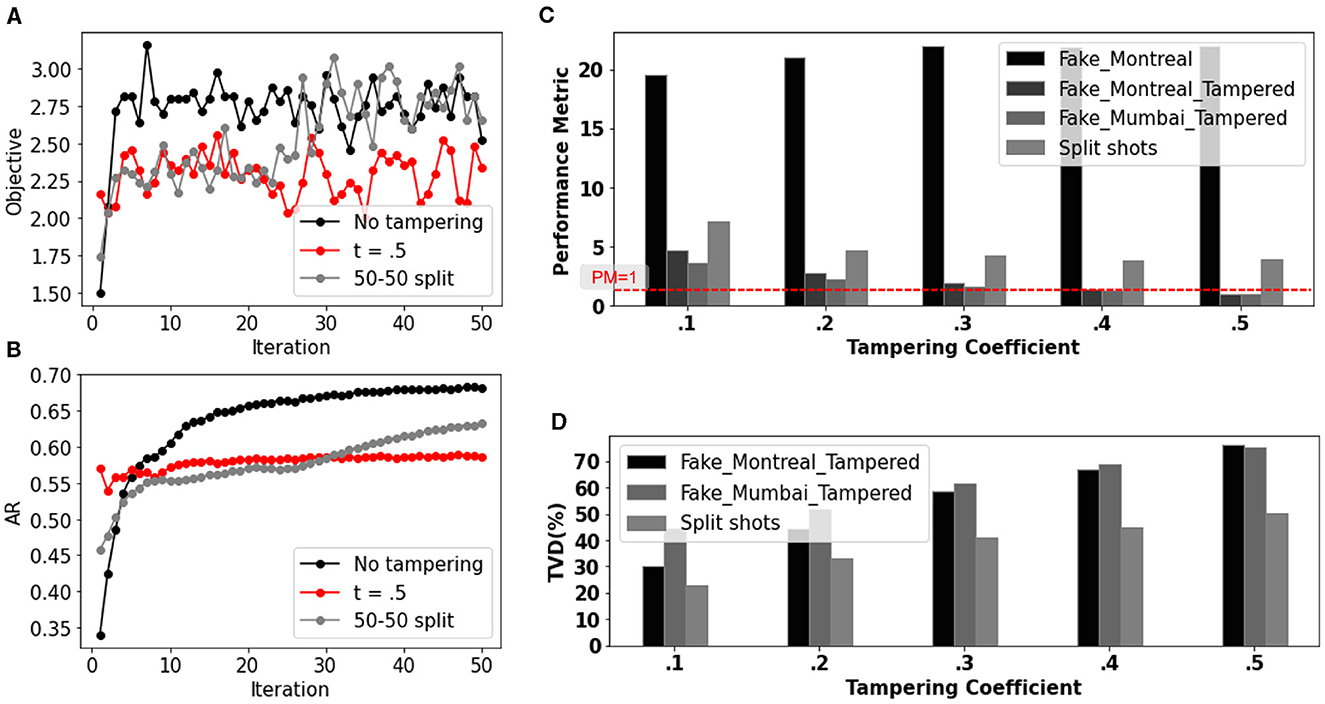
Figure 9. Effect of tampering (t = 0.5) on the (A) objective and (B) AR for a 4-node graph over 50 iterations and proposed 50–50 iteration split defense. (C) PM and (D) TVD variation with the 50–50 split heuristic, when 2 of 3 hardware are tampered (Fake₋montreal₋tampered, Fake₋mumbai₋tampered). Benchmark used: toffoli₋n3, no. of shots: 10,000.

Table 3

Table 3. AR vs. tampering (iterations = 50, Split = 50:50) (₋t denotes tampered results).

Table 4 shows a sample simulation of how a user can determine the tamper-free hardware and allocate the majority of iterations for a hybrid algorithm such as QAOA to that preferred hardware using the adaptive shot distribution method. We execute two 5-iteration (50 shot/iteration) runs on two different hardware HW (Fake₋montreal) and HW₋t (Fake₋montreal₋tampered) for a 4 node graph. The simulations account for the degree of tampering experienced by HW₋t (by varying t from 0.1 to 0.5). We compare the approximation ratio between the two runs for each hardware. Hardware with a higher AR is better and more reliable. The user can choose to run the remaining iterations in HW only. As a result, the user will benefit from better performance (upto 15%).

Table 4

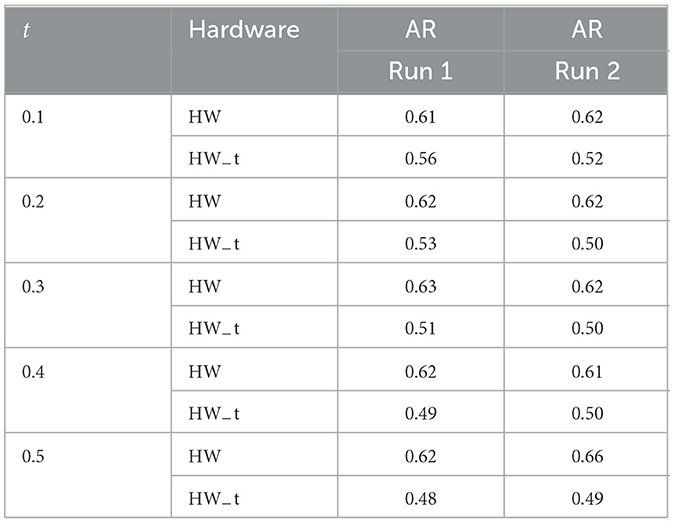
Table 4. Intelligent iteration distribution: identifying tampered/bad hardware by comparing the approximation ratio between the two runs for each hardware (iteration/run = 5; ₋t denotes tampered results).

5.5 Validation of defense on real hardware

We run a sample experiment on real hardware to validate the effectiveness of the proposed run-adaptive shot splitting heuristic against adversarial tampering. We extend the results of our tampering model from the fake backend simulations for the benchmark toffoli₋n3 to mimic tampering in the real IBM device ibmq₋manila. Table 5 summarizes the experiment's findings. The real ibmq₋manila device is represented as manila, and the tampered hardware is manila₋t (for which we run our benchmark on actual hardware and tamper by modeling the tampering results obtained from the fake manila that we created). The user performs two initial runs of 50 shots on each hardware, then compares the PM, TVD, frequent output, repeatability, and confidence factor (probability) across the two runs to determine the superior hardware. Adversarial tampering (even minor tampering with t = 0.2) combined with temporal variations in the real quantum hardware causes the tampered hardware to diverge to different outputs for the two different runs. For t = 0.2 and above, the tampered hardware manila₋t begins to diverge to different correct outputs across runs. The user can now allocate the rest of the shots intelligently on seemingly more reliable hardware manila.

Table 5

Table 5. Validation on IBM hardware (shots/run = 50).

5.6 Generalizing the proposed defense

The proposed heuristics (50–50 split and adaptive-run shots split) provide scalable improvement for a general case where the user must choose among n tampered and one tamper-free hardware (without knowing the idenity of tamper-free hardware). In Figures 9C, D we consider 2 tampered (montreal₋tampered, mumbai₋tampered) and 1 tamper-free hardware, with 10,000 shots for the program toffoli₋n3. We see PM improvement and TVD reduction when using the 50–50 split heuristic. Similarly, the user can perform two runs with 50 initial shots to determine the reliable hardware and divide the remaining shots accordingly to counter any adversarial tampering.

5.7 Computational and time overhead

We assumed that shot distribution among untrusted and trusted hardware will not incur performance overhead due to similar queue sizes, which may not always hold true. The queue depths of various vendors and their hardware can differ, potentially resulting in higher run times and performance overhead. In this work, we consider n shots that would have been run on a single hardware, and to defend against attacks, we split those n shots between multiple hardware options, keeping the total number of shots the same and incurring no overhead. However, cheaper and noisier hardware may require an increased number of shots, introducing further overhead. Therefore, careful consideration of hardware selection and queue management is essential to mitigate these impacts.

5.8 Summary of defense analysis

(a) The proposed 50–50 split effectively mitigates the worst-case tampering scenario where the user originally samples incorrect output. (b) The proposed intelligent run adaptive shot distribution enables the user to identify tamper-free hardware. (c) For purely quantum and hybrid workloads, the adaptive shot distribution heuristic almost entirely mitigates the proposed adversarial threat. (d) The proposed defense heuristics are applicable to real quantum hardware. (e) The proposed heuristics provide scalable improvement for a general case of n tampered and one tamper-free hardware.

6 Conclusion

In this paper, we propose an adversarial attack by a less reliable third-party provider. We report an average reduction of 0.12X in the PM and an increase in TVD of 7X across purely quantum workloads for minimally tampered hardware (t = 0.1) and an average reduction in AR of 0.8X (t = 0.1) and 0.25X (t = 0.5) for quantum classical workload. We propose distributing the total number of shots available to the user among various hardware options to ensure trustworthy computing using a mix of trusted and untrusted hardware. On average, we note a 30X improvement in PM, a 0.25X reduction in TVD for pure quantum workloads and AR improvement upto 1.5X. Our proposed heuristics mitigate the adversary's tampering (random/targeted) efforts, improving the quantum program's resilience.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author/s.

Author contributions

SU: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. SG: Conceptualization, Funding acquisition, Project administration, Resources, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported in parts by the NSF (CNS-1722557, CNS-2129675, CCF-2210963, CCF-1718474, OIA-2040667, DGE-1723687, DGE-1821766, and DGE-2113839), Intel's gift and seed grants from Penn State ICDS, and the Huck Institute of the Life Sciences.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^https://www.insidequantumtechnology.com/news-archive/chinas-baidu-rolls-beijing-based-quantum-computer-and-access-platform/

References

Acharya, N., and Saeed, S. M. (2020). “A lightweight approach to detect malicious/unexpected changes in the error rates of NISQ computers,” in Proceedings of the 39th International Conference on Computer-Aided Design, 1–9. doi: 10.1145/3400302.3415684

Crossref Full Text | Google Scholar

Alam, M., Ash-Saki, A., and Ghosh, S. (2019). “Addressing temporal variations in qubit quality metrics for parameterized quantum circuits,” in 2019 IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED) (IEEE), 1–6. doi: 10.1109/ISLPED.2019.8824907

Crossref Full Text | Google Scholar

Aleksandrowicz, G., Alexander, T., Barkoutsos, P., Bello, L., Ben-Haim, Y., Bucher, D., et al. (2019). Qiskit: an open-source framework for quantum computing. https://doi.org/10.5281/zenodo/2562111 (accessed March 16, 2023).

Google Scholar

Brandao, F. G., Broughton, M., Farhi, E., Gutmann, S., and Neven, H. (2018). For fixed control parameters the quantum approximate optimization algorithm's objective function value concentrates for typical instances. arXiv preprint arXiv:1812.04170.

Google Scholar

Cao, Y., Romero, J., and Aspuru-Guzik, A. (2018). Potential of quantum computing for drug discovery. IBM J. Res. Dev. 62, 6–1. doi: 10.1147/JRD.2018.2888987

PubMed Abstract | Crossref Full Text | Google Scholar

Computing, C. Q. (2021). “pytket,” Available at: https://cqcl.github.io/pytket/build/html/index.html

Google Scholar

Computing, Z. (2021). “Orquestra,” Available at: https://www.zapatacomputing.com/orquestra/

Google Scholar

Cong, I., Choi, S., and Lukin, M. D. (2019). Quantum convolutional neural networks. Nat. Phys. 15, 1273–1278. doi: 10.1038/s41567-019-0648-8

Crossref Full Text | Google Scholar

Crooks, G. E. (2018). Performance of the quantum approximate optimization algorithm on the maximum cut problem. arXiv preprint arXiv:1811.08419.

Google Scholar

Cross, A. (2018). “The IBM q experience and QISKIT open-source quantum computing software,” in APS Meeting Abstracts.

Google Scholar

Farhi, E., Goldstone, J., and Gutmann, S. (2014). A quantum approximate optimization algorithm. arXiv preprint arXiv:1411.4028.

Google Scholar

Gottesman, D. (2010). “An introduction to quantum error correction and fault-tolerant quantum computation,” in Quantum Information Science and Its Contributions to Mathematics, Proceedings of Symposia in Applied Mathematics, 13–58. doi: 10.1090/psapm/068/2762145

PubMed Abstract | Crossref Full Text | Google Scholar

Guerreschi, G. G., and Matsuura, A. Y. (2019). QAOA for Max-Cut requires hundreds of qubits for quantum speed-up. Sci. Rep. 9:6903. doi: 10.1038/s41598-019-43176-9

PubMed Abstract | Crossref Full Text | Google Scholar

Kandala, A., Mezzacapo, A., Temme, K., Takita, M., Brink, M., Chow, J. M., et al. (2017). Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246. doi: 10.1038/nature23879

PubMed Abstract | Crossref Full Text | Google Scholar

Karp, R. M. (1972). “Reducibility among combinatorial problems,” in Complexity of computer computations (Cham: Springer), 85–103. doi: 10.1007/978-1-4684-2001-2_9

PubMed Abstract | Crossref Full Text | Google Scholar

Kessler, M., Alonso, D., and Sánchez, P. (2023). Determination of the number of shots for Grover's search algorithm. EPJ Quant. Technol. 10:47. doi: 10.1140/epjqt/s40507-023-00204-y

Crossref Full Text | Google Scholar

Li, A., Stein, S., Krishnamoorthy, S., and Ang, J. (2020). QASMbench: a low-level QASM benchmark suite for NISQ evaluation and simulation. arXiv preprint arXiv:2005.13018.

Google Scholar

Papadimitriou, C. H., and Yannakakis, M. (1991). Optimization, approximation, and complexity classes. J. Comput. Syst. Sci. 43, 425–440. doi: 10.1016/0022-0000(91)90023-X

Crossref Full Text | Google Scholar

Phalak, K., Ash-Saki, A., Alam, M., Topaloglu, R. O., and Ghosh, S. (2021). Quantum PUF for security and trust in quantum computing. IEEE J. Emer. Select. Topics Circ. Syst. 11, 333–342. doi: 10.1109/JETCAS.2021.3077024

Crossref Full Text | Google Scholar

Ravi, G. S., Smith, K. N., Gokhale, P., and Chong, F. T. (2021). “Quantum computing in the cloud: analyzing job and machine characteristics,” in 2021 IEEE International Symposium on Workload Characterization (IISWC) (IEEE), 39–50. doi: 10.1109/IISWC53511.2021.00015

Crossref Full Text | Google Scholar

Reagor, M., Osborn, C. B., Tezak, N., Staley, A., Prawiroatmodjo, G., Scheer, M., et al. (2018). Demonstration of universal parametric entangling gates on a multi-qubit lattice. Sci. Adv. 4:eaao3603. doi: 10.1126/sciadv.aao3603

PubMed Abstract | Crossref Full Text | Google Scholar

Saki, A. A., Suresh, A., Topaloglu, R. O., and Ghosh, S. (2021). “Split compilation for security of quantum circuits,” in 2021 IEEE/ACM International Conference On Computer Aided Design (ICCAD) (IEEE), 1–7. doi: 10.1109/ICCAD51958.2021.9643478

Crossref Full Text | Google Scholar

Smith, R. S., Peterson, E. C., Skilbeck, M. G., and Davis, E. J. (2020). An open-source, industrial-strength optimizing compiler for quantum programs. Quant. Sci. Technol. 5:044001. doi: 10.1088/2058-9565/ab9acb

Crossref Full Text | Google Scholar

Suresh, A., Saki, A. A., Alam, M., Onur Topaloglu, R., and Ghosh, S. (2021). “Short paper: A quantum circuit obfuscation methodology for security and privacy,” in Proceedings of the 10th International Workshop on Hardware and Architectural Support for Security and Privacy, 1–5. doi: 10.1145/3505253.3505260

Crossref Full Text | Google Scholar

Tannu, S. S., and Qureshi, M. (2019). “Ensemble of diverse mappings: improving reliability of quantum computers by orchestrating dissimilar mistakes,” in Proceedings of the 52nd Annual IEEE/ACM International Symposium on Microarchitecture (pp. 253–265). doi: 10.1145/3352460.3358257

Crossref Full Text | Google Scholar

Wecker, D., Hastings, M. B., and Troyer, M. (2016). Training a quantum optimizer. Phys. Rev. A 94:022309. doi: 10.1103/PhysRevA.94.022309

Crossref Full Text | Google Scholar

Zhou, L., Wang, S. T., Choi, S., Pichler, H., and Lukin, M. D. (2020). Quantum approximate optimization algorithm: performance, mechanism, and implementation on near-term devices. Phys. Rev. X 10:021067. doi: 10.1103/PhysRevX.10.021067

Crossref Full Text | Google Scholar