- 1Department of Architecture and Building Science, School of Engineering, Tohoku University, Sendai, Japan
- 2Earthquake Engineering Laboratory, International Research Institute of Disaster Science, Tohoku University, Sendai, Japan
- 3Department of Environmental Engineering and Architecture, Graduate School of Environmental Studies, Nagoya University, Nagoya, Japan
- 4Dynamics Research Group, Department of Mechanical Engineering, University of Sheffield, Sheffield, United Kingdom
Recent massive earthquakes have raised concerns that megathrust earthquakes with magnitude 9 can occur in the near future. This article discusses the critical behavior of structures involving torsion caused by extreme ground motions. Unlike factors such as mass and stiffness eccentricity and accidental torsion in a structure that induce torsion, torsional buckling can occur in a moment-resisting frame (MRF) when all beam ends in the longitudinal and transverse directions yield in the lower stories, even if the frame is well designed and its eccentricity is negligibly small. In this study, the theoretically predicted buckling load was presented and validated via numerical analyses. This article shows that excluding the P-Delta effect resulted not only in underestimated deformation but also in overlooked torsional buckling. This study suggests that a high-rise MRF designed in accordance with modern seismic design codes can suffer torsional collapse when the beam ends of the lower stories yield owing to extreme ground motion. Based on these findings, we recommend considering the P-Delta effect when examining the critical behavior of high-rise buildings so as not to overlook the brittle failure mode.
1 Introduction
Recent massive earthquakes caused numerous buildings of various sizes, ages, and constructions to collapse, making us aware of seismic risks that exist worldwide. For example, several low-to-mid-rise buildings collapsed during the 2023 Turkey-Syria Earthquake. According to the reports on ground motion records provided at an early stage, this earthquake generated very intense ground motions with long-period directivity pulses and fling steps exceeding the peak ground acceleration of a return period of 476 years in 1.4% of Turkey’s land area (Baltzopoulos et al., 2023). In 2016 in Kumamoto, Japan, a mainshock of moment magnitude (Mw) 7.1 followed a foreshock of Mw 6.1 that had occurred the day before (Bhattacharya et al., 2018). This was the first event in which another destructive earthquake followed an earthquake greater than Mw 6 in the recorded history of Japan. The Great East Japan Earthquake in 2011 caused a tsunami that affected vast areas of the country. The long-period ground motion generated by the earthquake traveled all the way to Osaka, approximately 800 km away from the epicenter (Takewaki et al., 2011). Further, this motion was amplified by the soft surface subsoil in the Osaka Bay area, causing a high-rise steel building in Osaka to resonate with a 1.4 m maximum amplitude at the top. The resonance of structures with ground motion can lead to structural collapse, as observed in the Pino Suárez building group during the 1985 Mexico Earthquake (Osteraas and Krawinkler, 1989; Ger et al., 1993). There are growing concerns about the occurrence of massive earthquakes of magnitude 9, such as the potential Cascadia and Nankai Megathrust Earthquakes, in the near future (Marafi et al., 2020; Fukushima et al., 2023).
Many previous studies have focused on understanding the critical behavior of structures subjected to massive earthquakes to implement measures for protecting lives and properties from major disasters. Uetani and Tagawa (1998) reported that the yield of beam ends in a two-dimensional planer frame can lead to an undesirable collapse mode referred to as “deformation concentration in lower stories.” A similar phenomenon was also observed by Bernal (1992, 1998) in the study that estimated the response of a multi-DOF system using an equivalent single-DOF system, which was further developed by Adam et al. (2004). Efforts were made to track the progressive collapse (Kiakojouri et al., 2020; Kiakojouri et al., 2021) accurately and efficiently (Scott and Fenves, 2010; Lin et al., 2018), including experiments on full-scale four-story and reduced-scale eighteen-story specimens using E-Defense, which is the largest shake table in the world (Nakashima et al., 2018; Nishi et al., 2023).
Torsional collapse continues to be a challenge in understanding the critical behavior of building frames. Torsional irregularities and accidental torsion are commonly considered in structural design; however, torsional vibrations are often underestimated when the eccentricity is very small (Flores et al., 2018). Jenning and Husid, (1968), Wilson and Habibullah (1987), Osteraas and Krawinkler (1989), Ger et al. (1993), Uetani and Tagawa (1998), and Bernal (1992, 1998) revealed the influence of P-Delta effects on the behavior of structures subjected to severe earthquakes. Flores et al. (2018) reported that the P-Delta (P-Theta) effect accelerated torsion caused by other factors such as eccentricity and uncertainty when bidirectional ground motion was considered. Kohiyama and Yokoyama (2018) noted that the geometric nonlinearity of frame stiffness induced a parametric resonance in torsional vibration, which was designated as Q-Delta resonance. Later, their research works were further developed by Mizutori and Kohiyama (2021), Kohiyama et al. (2022), Kohiyama and Maki (2023), and Kohiyama and Kai (2023). Hong (2013) designated the second-order effect caused by instantaneous load eccentricities due to the motion of the center of mass as the A-Delta effect and noted that ignoring the A-Delta effect might underestimate seismic displacement. Furthermore, rotational components of ground motions can introduce significant influence including torsional response. Zhang et al. (2020) examined the seismic response of transmission towers considering the rocking and torsion components of the ground motion and noted that the rotational ground motion components should not be neglected. Zhang et al. (2021) realized that the nonuniformity and multidimensionality of ground motion can increase the seismic response of a large-span spatial structure; thus, the seismic response may be underestimated when only translational components of the ground motion are considered.
The inelastic torsional buckling examined in this study is different than any other known phenomena involving torsion (Uetani, 2018; Fukuda and Ikago, 2019; 2020; Fukuda et al., 2023). In this study, a numerical example demonstrated that a simple three-dimensional symmetric moment-resisting frame (MRF) model subjected to a horizontal load suffered from significant torsional deformation even though a horizontal load was applied to the centroid of the roof slab. Therefore, this study suggests that a well-designed high-rise building without eccentricity can suffer non-negligible torsional deformation in the lower stories when all beam ends of the lower stories in the longitudinal and transverse frames yield under severe bidirectional ground motion.
The remainder of this article is organized as follows. Section 2 discusses the similarity between the inelastic buckling theory of a simple three-dimensional frame and Shanley’s column theory (Shanley, 1947). In Section 3, a prediction of the column axial load that causes torsional buckling is derived from the condition that the uniqueness of the solution of governing equations is violated. In Section 4, numerical analyses are shown to validate the theoretically derived prediction of buckling load. Section 5 presents conclusions and recommendations.
2 Inelastic torsional buckling theory for a simple moment resisting frame
2.1 Inelastic three-dimensional moment resisting frame
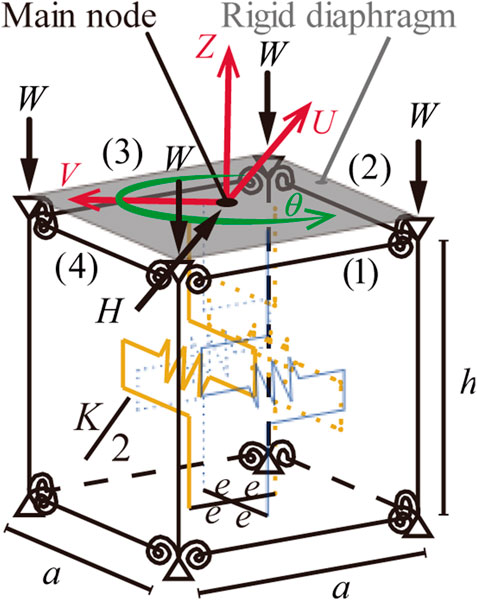
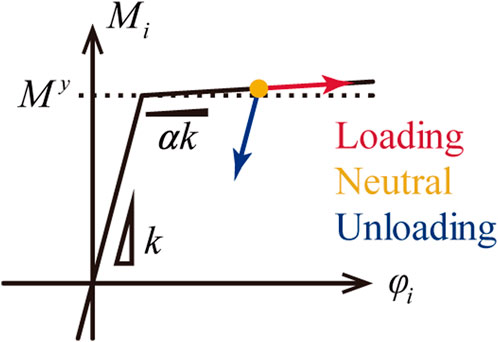
Figure 1 shows the three-dimensional MRF model employed in this study. The model comprises four columns whose tops and bottoms are connected via beams, thereby forming a rectangular parallelepiped. The bottoms of the columns are supported by pins, and the beams and columns are rigid bars. The vertical planes formed by the MRFs are labeled (1), (2), (3), and (4), as shown in Figure 1. The column tops and bottoms are connected to the beams via elastoplastic hinges with the moment–rotation angle relationship shown in Figure 2.
2.2 Review of inelastic buckling theory for a column subjected to axial load
Figure 3 shows a simple model of a column subjected to axial load
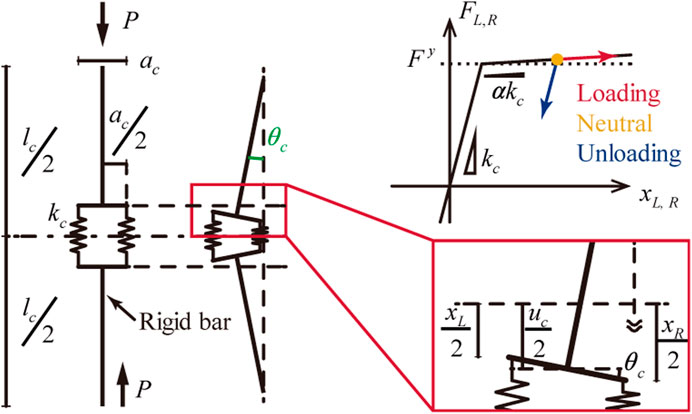
FIGURE 3. Shanley column (Shanley, 1947).
Figure 4 shows the bifurcation process in a Shanley column subjected to increasing axial loading. Both springs are in the loading state because the axial force increases immediately before buckling. When bifurcation occurs, the elongation and shrinkage caused by the rotation and the increasing axial force cancel each other, resulting in a neutral loading state of the left-hand side spring, while the spring on the right-hand side maintains the loading state. Strain reversal occurs on the left side of the spring after the column buckles. Thus, the Shanley column does not involve strain reversal under buckling, implying that replacing the elastic modulus with the tangent modulus in Euler’s formula yields a better prediction of the inelastic buckling load than by replacing it with the reduced modulus (von Kármán, 1910) when an increase in the axial load is considered during buckling.
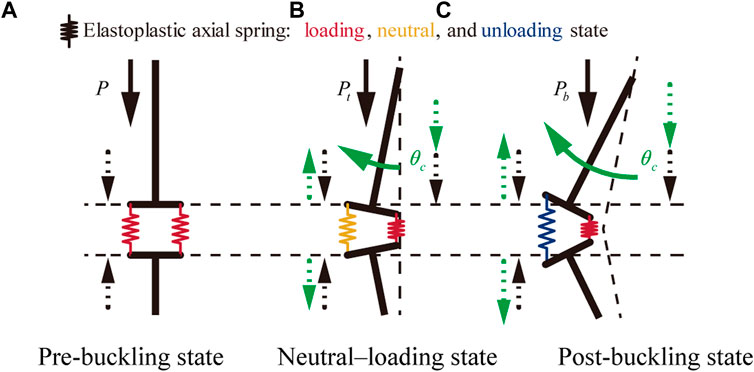
FIGURE 4. Bifurcation process in Shanley column. (A) Pre-buckling state (B) Neutral–loading state (C) Post-buckling state.
Figure 5 shows the top view of the bifurcation process of a simple MRF subjected to increasing horizontal loading in the diagonal direction. All beam ends are in the loading state immediately before torsional buckling. When torsion occurs, a counterclockwise rotation
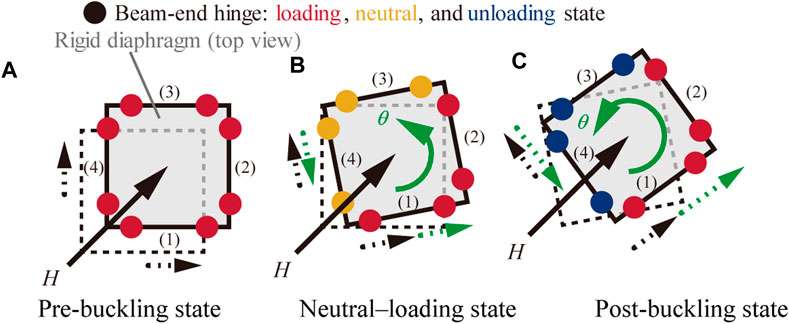
FIGURE 5. Bifurcation process in simple three-dimensional MRF. (A) Pre-buckling state (B) Neutral–loading state (C) Post-buckling state.
3 Prediction of the column axial force for torsional buckling
The relationships between the story drift angle of the
when we assume that the following approximations hold:
The shear force of the
The equilibrium equations with respect to the
where
The second terms on the righthand side of the above equations represent geometrical stiffnesses derived from the P-Delta effect.
The constitutive law of the beam-end hinges is given as
where
3.1 Uniqueness of the rate solution on the fundamental path
In this study, the path in which no buckling occurred is referred to as the fundamental path. Let the superscript
Compatibility condition
Equilibrium equations
Constitutive law
Let superscript
Compatibility condition
Equilibrium equations
Constitutive law
Let us define
Multiplying Eqs. (14), (15), and (16) by
Here, let us define vector
Then, Eq. (17) reduces to
The above equation holds if the rate solution of the equilibrium equation is not unique and a rate solution
Sufficient condition for the uniqueness of the rate solution
We introduce a virtual hinge element that is always in a loading state to simplify the evaluation of
Constitutive law for comparison hinge
This virtual hinge element (hereafter, comparison hinge) corresponds to the comparison solid (Sewell, 1973) proposed by Hill (Hill, 1956a, 1956b, 1957a, 1957b, 1958). Replacing the beam-end hinges with the comparison hinge enables simplifying the function
Because the above inequality holds,
The equality holds if and only if
Thus, the following condition is sufficient for uniqueness.
The above inequality is expanded as
If the following equations hold, the above condition is violated.
Eqs. (28) and (29) indicate that the post-yielding stiffnesses in the horizontal and rotational directions, respectively, become negative because of the geometric stiffness.
Here, we consider the case in which only Eq. (29) holds because torsional buckling is considered exclusively. Thus, we assume that
Solving Eqs. (29) and (30) with respect to
where
3.2 Post buckling behavior
When we assume that Eq. (31) is satisfied, torsional buckling can occur when all beam-end hinges yield. We assume that the displacement perpendicular to the horizontal loading
This section demonstrates that MRFs (3) and (4) turn to the unloading state after torsional buckling occurs with
The shear forces
where superscript
Substituting Eq. (33) into Eq. (4) yields
The equilibrium equation with respect to the
Eq. (37) contradicts the assumption that
In the following, we assume that
When
Substituting Eq. (39) into Eq. (4) yields
The equilibrium equation with respect to the
Upon substituting Eq. (41) into the upper part of Eq. (40), we obtain
where
If
Provided that
The above condition yields the upper bound of column axial force
By combining the conditions in Eqs. (31) and (46), the condition for torsional buckling can be modified as
4 Numerical analysis
4.1 Analytical model
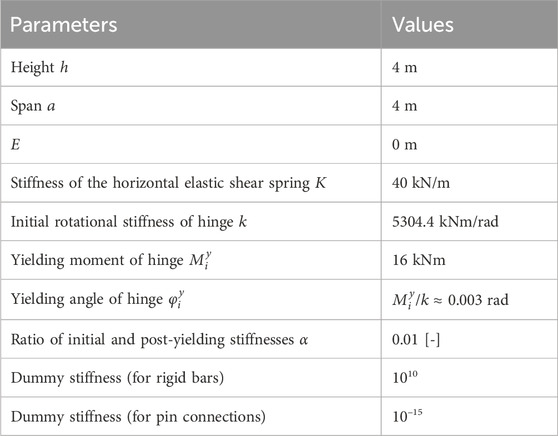
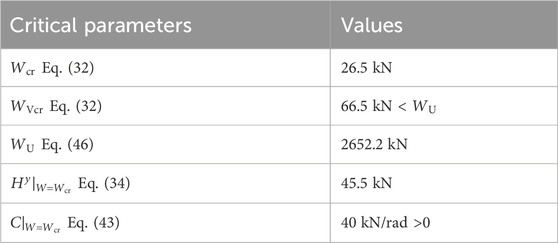
Tables 1 and 2 summarize the specifications of the analytical model and its critical vertical loads and constants. Further details regarding the modeling and analytical options are presented in the Supplementary Appendix.
Table 3 lists the values of the vertical and horizontal loads (
4.2 Analytical result
4.2.1 Verification of the theoretical buckling load and the relationship between the horizontal load and rotational angle
Figures 6A,B show the deformation of the MRF model at the end of the analysis for
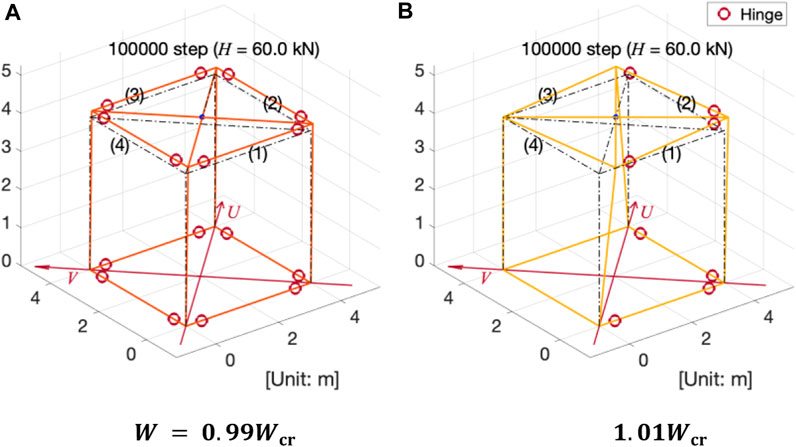
FIGURE 6. Comparison of overall deformation at the end of the analysis (Initial imperfection: 0.01%) (A)
Figures 7A,B show the
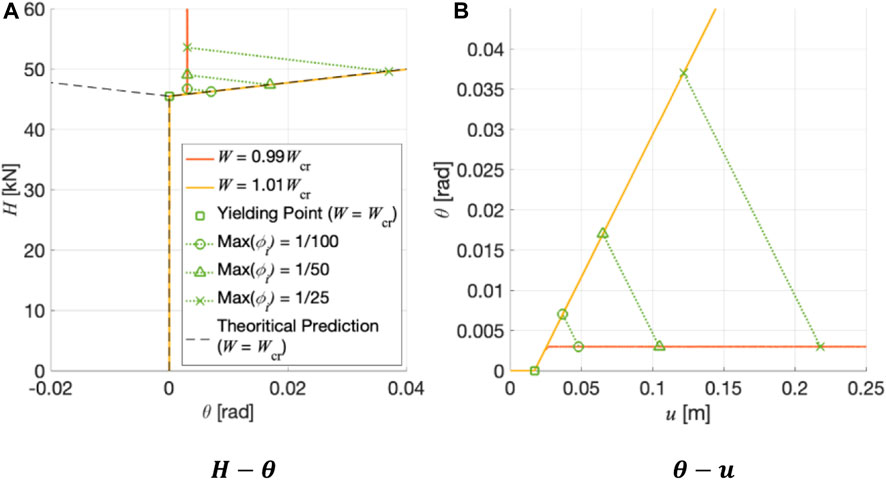
FIGURE 7.
An additional analysis was conducted for the case with a vertical load of
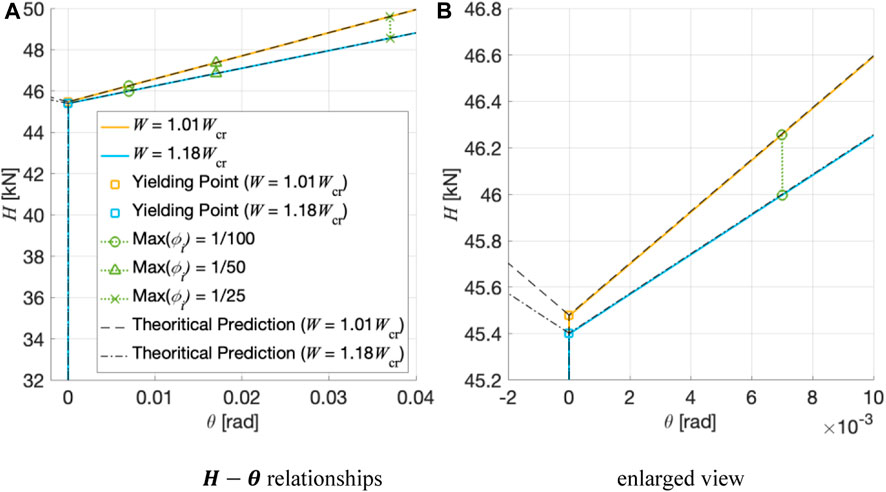
FIGURE 8.
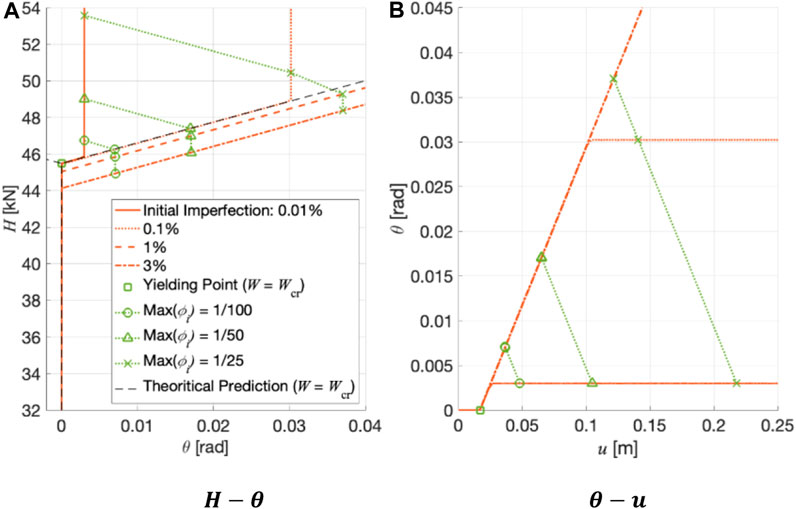
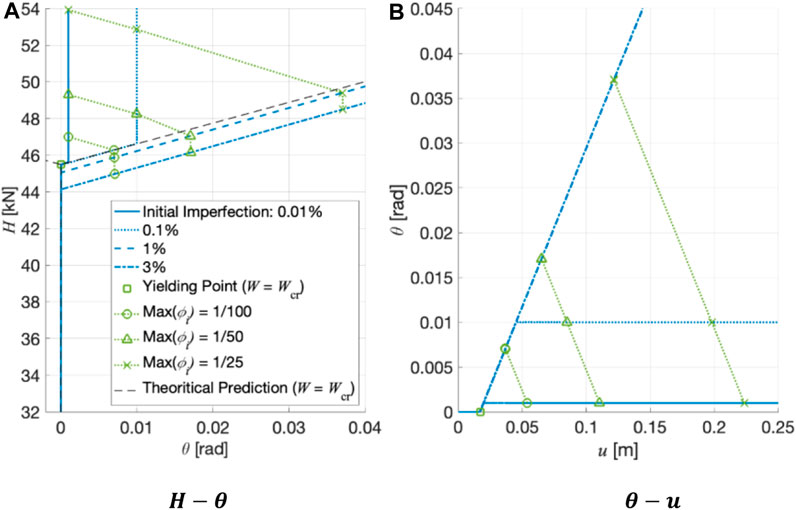
4.2.2 Sensitivity analysis with respect to the initial imperfection
The analytical results suggested that the buckling load
Figures 9 and 10 show
In cases where imperfections are very small (0.01% and 0.1%) and the vertical load is very close to the buckling load, the
4.2.3 Comparison of the analytical results with and without considering the P-Delta effect
The PDelta and Linear Transformation options for geometric transformation command in OpenSees are specified in the numerical model for cases with and without the P-Delta effect, respectively (Denavit and Hajjar, 2013). The static vertical load acting on each column and the initial imperfection were
Figure 11 compares the overall deformation of the MRF at the end of the analysis (
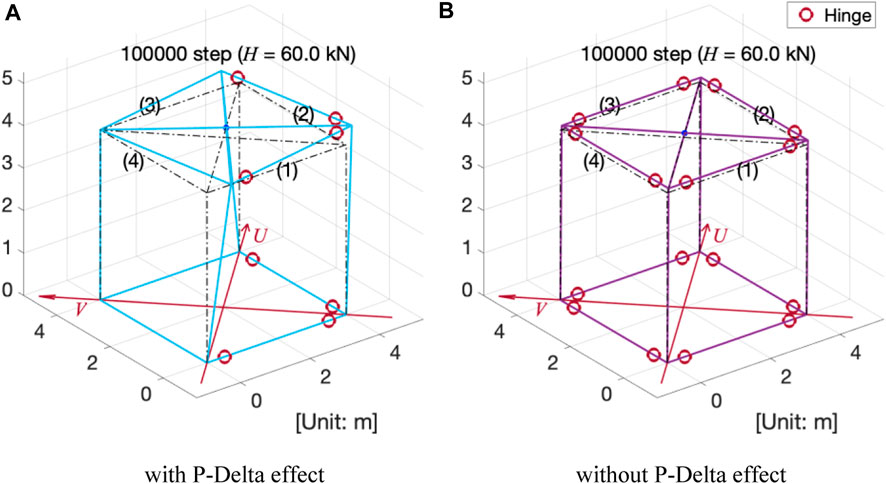
FIGURE 11. Comparison of the overall deformation (
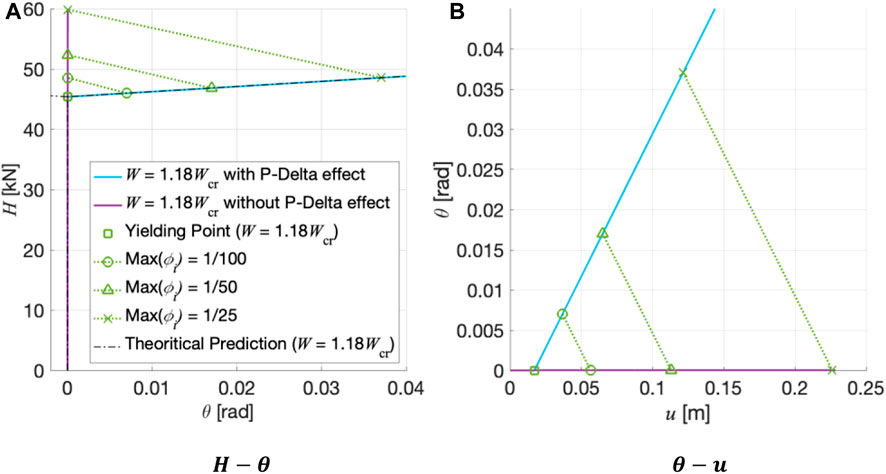
FIGURE 12.
5 Conclusion
This article presented the inelastic torsional buckling theory for a simple three-dimensional MRF model. The torsional buckling examined in this study was different from the torsional behavior caused by the eccentricity of the weight and/or stiffness in a structure or Q-Delta resonance.
The MRF examined in this study was designed such that the yielding of the beam ends preceded that of the columns following structural design practices. It was theoretically elucidated that a simple three-dimensional MRF, which was perfectly symmetric and had no eccentricity, suffered large torsional deformation when subjected to a horizontal force acting on the center of gravity of the structure in a diagonal direction. Similar to Shanley’s theory for the inelastic buckling of a column, bifurcation could occur without strain reversal in all beam-end hinges, and therefore, the critical vertical load that causes torsional buckling could be predicted assuming that all beam-end hinges were in the loading state, acting as comparison hinges.
An analytical example was used to validate the buckling load and post buckling force–deformation relationship predicted by the proposed theory. The analytical model yielded torsional deformation that did not occur when not considering the P-Delta effect and only occurred when it was considered. Further, the maximum interstory drifts of the frames were found to be larger than those when they were not considered.
Designing a steel MRF such that the yielding of the beam ends precedes that of the columns is a common practice to ensure ductility in the case of a severe seismic event. However, this study suggests that the lower part of a high-rise MRF can still suffer torsional buckling, thereby losing ductility despite the design intention when all beams end in the longitudinal and transverse frames yield owing to the bi-directional horizontal forces. The prediction of column axial force that can cause torsional buckling presented in this study is useful in deciding if the P-Delta effect should be considered.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
IF: Formal Analysis, Funding acquisition, Investigation, Methodology, Writing–original draft. KI: Supervision, Writing–review and editing. YA: Supervision, Writing–review and editing. DW: Supervision, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was financially supported by a Grant-in-Aid for JSPS Research Fellows (Grant Numbers: JP22J13566 and JP22KJ0266). The research environment of this study was supported by the International Joint Graduate Program in Resilience and Safety Studies (GP-RSS), Tohoku University, Japan.
Acknowledgments
The authors are grateful to Professor Emeritus of Kyoto University, Koji Uetani, for providing basic ideas regarding the torsional buckling of a simple three-dimensional MRF model, which inspired us to conduct this study. We thank Editage (http://www.editage.com) for editing this manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2024.1333949/full#supplementary-material
References
Adam, C., Ibarra, L. F., and Krawinkler, H. (2004). “Evaluation of P-delta effects in non-deteriorating MDOF structures from equivalent SDOF systems,” in Proceedings of 13th World Conference on Earthquake Engineering: 13 WCEE, Vancouver, BC, Canada, August, 2004.
Baltzopoulos, G., Baraschino, R., Chioccarelli, E., Cito, P., Vitale, A., and Iervolino, I. (2023). Near-source ground motion in the M7.8 Gaziantep (Turkey) earthquake. Earthq. Eng. Struct. Dyn. 52 (12), 3903–3912. doi:10.1002/eqe.3939
Bernal, D. (1992). Instability of buildings subjected to earthquakes. J. Struct. Eng. 118 (8), 2239–2260. doi:10.1061/(asce)0733-9445(1992)118:8(2239)
Bernal, D. (1998). Instability of buildings during seismic response. Eng. Struct. 20 (4–6), 496–502. doi:10.1016/s0141-0296(97)00037-0
Bhattacharya, S., Hyodo, M., Nikitas, G., Ismael, B., Suzuki, H., Lombardi, D., et al. (2018). Geotechnical and infrastructural damage due to the 2016 Kumamoto earthquake sequence. Soil Dyn. Earthq. Eng. 104, 390–394. doi:10.1016/j.soildyn.2017.11.009
Denavit, M. D., and Hajjar, J. F. (2013). Description of geometric nonlinearity for beam-column analysis in OpenSEES, department of civil and environmental engineering reports (No. NEU-CEE-2013-02). Boston, Massachusetts: Department of Civil and Environmental Engineering, Northeastern University. https://repository.library.northeastern.edu/files/neu:376268 (Accessed October 18, 2023).
Flores, F., Charney, F. A., and Lopez-Garcia, D. (2018). The influence of accidental torsion on the inelastic dynamic response of buildings during earthquakes. Earthq. Spectra 34 (1), 21–53. doi:10.1193/100516eqs169m
Fukuda, I., and Ikago, K. (2019). “Global buckling analysis of high-rise steel moment-resisting frames involving inelastic torsional deformation concentration,” in Proceedings of 12th Pacific Structural Steel Conference: PSSC’ 19, Tokyo, Japan, November, 2019.
Fukuda, I., and Ikago, K. (2020). “Inelastic torsional buckling analysis of a single-story cubic frame,” in 17th World Conference on Earthquake Engineering: 17WCEE, Sendai, Japan, September, 2020.
Fukuda, I., Ikago, K., Maeda, T., Nishimoto, A., and Araki, Y. (2023). “Inelastic torsional buckling of a symmetric three-dimensional moment-resisting frame subjected to horizontal force in the diagonal direction,” in Proceedings of 9th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering: COMPDYN 2023, Athens, Greece, June, 2023.
Fukushima, Y., Nishikawa, T., and Kano, Y. (2023). High probability of successive occurrence of Nankai megathrust earthquakes. Sci. Rep. 13 (1), 63. doi:10.1038/s41598-022-26455-w
Ger, J. F., Cheng, F. Y., and Lu, L. W. (1993). Collapse behavior of Pino suarez building during 1985 Mexico City earthquake. J. Struct. Eng. 119 (3), 852–870. doi:10.1061/(asce)0733-9445(1993)119:3(852)
Hill, R. (1956a). On the problem of uniqueness in the theory of a rigid-plastic solid—1. J. Mech. Phys. Solids 4 (4), 247–255. doi:10.1016/0022-5096(56)90033-3
Hill, R. (1956b). On the problem of uniqueness in the theory of a rigid-plastic solid—II. J. Mech. Phys. Solids 5 (1), 1–8. doi:10.1016/0022-5096(56)90002-3
Hill, R. (1957a). On the problem of uniqueness in the theory of a rigid-plastic solid—III. J. Mech. Phys. Solids 5 (3), 153–161. doi:10.1016/0022-5096(57)90001-7
Hill, R. (1957b). On the problem of uniqueness in the theory of a rigid-plastic solid—IV. J. Mech. Phys. Solids 5 (4), 302–307. doi:10.1016/0022-5096(57)90022-4
Hill, R. (1958). A general theory of uniqueness and stability in elastic-plastic solids. J. Mech. Phys. Solids 6 (3), 236–249. doi:10.1016/0022-5096(58)90029-2
Hong, H. P. (2013). Torsional responses under bidirectional seismic excitations: effect of instantaneous load eccentricities. J. Struct. Eng. 139 (1), 133–143. doi:10.1061/(asce)st.1943-541x.0000607
Jennings, P. C., and Husid, R. (1968). Collapse of yielding structures during earthquakes. J. Eng. Mech. 94 (5), 1045–1065. doi:10.1061/jmcea3.0001023
Kiakojouri, F., De Biagi, V., Chiaia, B., and Sheidaii, M. R. (2020). Progressive collapse of framed building structures: current knowledge and future prospects. Eng. Struct. 206, 110061. doi:10.1016/j.engstruct.2019.110061
Kiakojouri, F., Sheidaii, M. R., De Biagi, V., and Chiaia, B. (2021). Progressive collapse of structures: a discussion on annotated nomenclature. Structures 29, 1417–1423. doi:10.1016/j.istruc.2020.12.006
Kohiyama, M., and Kai, R. (2023). “Experiment and simulation of Q–Δ resonance using four-layer bending-shear type specimen,” in Proceedings of 9th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering: COMPDYN 2023, Athens, Greece, June, 2023.
Kohiyama, M., and Maki, S. (2023). “Three-dimensional frame analysis of Q–Δ resonance of center-core biaxially symmetrical high-rise building under long-period earthquake motion,” in Proceedings of 9th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering: COMPDYN 2023, Athens, Greece, June, 2023.
Kohiyama, M., and Yokoyama, H. (2018). Torsional response induced by lateral displacement and inertial force. Front. Built Environ. 4. Article 38. doi:10.3389/fbuil.2018.00038
Kohiyama, M., Yokoyama, H., and Maki, S. (2022). Torsional response of a bisymmetric structure induced by bending–torsion interaction in vertical members. Jpn. Archit. Rev. 5 (1), 3–19. doi:10.1002/2475-8876.12249
Lin, K., Lu, X., Li, Y., Zhuo, W., and Ye, L. (2018). Analytical model for multi-hazard resilient prefabricated concrete frame considering earthquake and column removal scenarios. Front. Built Environ. 4. Article 73. doi:10.3389/fbuil.2018.00073
Marafi, N. A., Makdisi, A. J., Eberhard, M. O., and Berman, J. W. (2020). Impacts of an M9 Cascadia subduction zone earthquake and Seattle basin on performance of RC core wall buildings. J. Struct. Eng. 146 (2), 4019201. doi:10.1061/(asce)st.1943-541x.0002490
McKenna, F., Fenves, G. L., and Scott, M. H. (2000). Open system for earthquake engineering simulation. Berkeley, CA, USA: University of California. http://opensees.berkeley.edu (Accessed October 18, 2023).
Mizutori, F., and Kohiyama, M. (2021). Experiment of torsional response induced by the Q–Delta resonance. Struct. Des. Tall Special Build. 30, e1829. doi:10.1002/tal.1829
Nakashima, M., Nagae, T., Enokida, R., and Kajiwara, K. (2018). Experiences, accomplishments, lessons, and challenges of E-defense—tests using world’s largest shaking table. Jpn. Archit. Rev. 1 (1), 4–17. doi:10.1002/2475-8876.10020
Nishi, R., Kawamata, Y., Enokida, R., Inoue, T., and Tabata, K. (2023). E-Defense shake table experiments implemented by NIED and collaborative research projects in 2005–2022. J. Disaster Res. 18 (5), 492–512. doi:10.20965/jdr.2023.p0492
Osteraas, J., and Krawinkler, H. (1989). The Mexico earthquake of september 19, 1985 – behavior of steel buildings. Earthq. Spectra 5 (1), 51–88. doi:10.1193/1.1585511
Scott, M. H., and Fenves, G. L. (2010). Krylov subspace accelerated Newton algorithm: application to dynamic progressive collapse simulation of frames. J. Struct. Eng. 136 (5), 473–480. doi:10.1061/(asce)st.1943-541x.0000143
Sewell, M. J. (1973). A yield-surface corner lowers the buckling stress of an elastic-plastic plate under compression. J. Mech. Phys. Solids 21 (1), 19–45. doi:10.1016/0022-5096(73)90028-8
Shanley, F. R. (1947). Inelastic column theory. J. Aeronautical Sci. 14 (5), 261–268. doi:10.2514/8.1346
Takewaki, I., Murakami, S., Fujita, K., Yoshitomi, S., and Tsuji, M. (2011). The 2011 off the Pacific Coast of Tohoku Earthquake and response of high-rise buildings under long-period ground motions. Soil Dyn. Earthq. Eng. 31 (11), 1511–1528. doi:10.1016/j.soildyn.2011.06.001
Uetani, K. (2018) Overall buckling phenomena and its suppression methods, Part 1: general views, Proceedings of the Annual Meeting of Architectural Institute of Japan, Structure I: 399–400. (in Japanese)
Uetani, K., and Tagawa, H. (1998). Criteria for suppression of deformation concentration of building frames under severe earthquakes. Eng. Struct. 20 (4–6), 372–383. doi:10.1016/s0141-0296(97)00021-7
von Kármán, T. (1910). Untersuchungen uber die Knickfestigkeit, Mitteilungen uber Forschungsarbeiten auf dem Gebiete des Ingenieurwensen. Berlin, Germany: Springer, 81.
Wilson, E. L., and Habibullah, A. (1987). Static and dynamic analysis of multi-story buildings, including P-delta effects. Earthq. Spectra 3 (2), 289–298. doi:10.1193/1.1585429
Zhang, J., Li, H., and Li, C. (2021). Seismic response of large-span spatial structures under multi-support and multidimensional excitations including rotational components. Earthq. Eng. Eng. Vib. 20 (1), 141–159. doi:10.1007/s11803-021-2011-1
Keywords: P-delta effect, Shanley column, inelastic buckling, bifurcation, stability, comparison solid
Citation: Fukuda I, Ikago K, Araki Y and Wagg DJ (2024) Inelastic torsional buckling of simple three-dimensional moment resisting frame. Front. Built Environ. 10:1333949. doi: 10.3389/fbuil.2024.1333949
Received: 06 November 2023; Accepted: 18 January 2024;
Published: 14 February 2024.
Edited by:
Songye Zhu, Hong Kong Polytechnic University, Hong Kong, SAR, ChinaCopyright © 2024 Fukuda, Ikago, Araki and Wagg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kohju Ikago, ikago@irides.tohoku.ac.jp
 Iori Fukuda
Iori Fukuda