Numerically disturbed shake table experimentation to examine nonlinear signal-based control

This study introduces a numerically disturbed experimentation to address the shake table control degradation commonly observed in shake table experiments. This degradation is caused by nonlinear characteristics, such as seismic damage, in the experiments; however, observing such nonlinear characteristics is a major purpose of these experiments. In the proposed numerically disturbed experimentation, a structure is numerically simulated, and its structural responses are fed back as the disturbance signal to the table in the physical domain via real-time interaction. This enables us to examine the control performance of a shake table with a structure, without having to place an actual structure on it. This experimentation is beneficial in cases wherein new control methods are applied for shake table control because the control performance can be examined safely and efficiently under various structural conditions by using numerical simulations. The proposed experimentation was applied to the shake table control examination of nonlinear signal-based control (NSBC), which has a nonlinear signal feedback action for nonlinear structural dynamics, as well as inversion-based control (IBC), which is a common feedforward method. In the numerically disturbed experiments, NSBC accurately realized a seismic acceleration record on the shake table with severe nonlinear characteristics, whereas IBC exhibited control degradation due to nonlinear characteristics. Similar results were obtained using actual shake table experiments with a steel structure. Therefore, the proposed numerically disturbed experimentation can be an alternative to shake table experiments using structures.

1 Introduction

A shake table is a key experimental facility for earthquake and structural engineering to examine the seismic performance of building structures or civil infrastructure (Severn 2011). The shake table excites a specimen placed on its top by an inertial force generated by the table movement. It is expected to accurately reproduce seismic acceleration data recorded during past earthquakes or synthesized for anticipated future earthquakes. In cases of inaccurate reproduction, the structure placed on the table is shaken by a different excitation from that of the expected, resulting in undesirable structural behavior. Accurate control of shake tables is critical for experimental purposes.

A proportional–integration–derivative (PID) controller or three-variable controller (TVC) (Tagawa and Kajiwara 2007) is commonly employed as a basic controller in shake table systems, and the controller is designed based on the bare condition. When a structure is placed on the table, the dynamics of the table change owing to its interaction with the structure (Blondet and Carlos 1988; Conte and Trombetti 2000). The dynamic change caused by an intact structure can be evaluated in advance via system identification of the main tests using seismic excitations and can be described using a transfer function. Its inversion is applied to the seismic record data to be realized by the table as feedforward compensation, which is referred to as inversion-based control (IBC). Its effectiveness is limited to structures with slight nonlinearity.

Shake table experiments are performed to observe structural failures, which are a type of nonlinear characteristics, and dynamics changes in the structure are inevitable (Nakashima et al., 2018). Control deterioration caused by nonlinear characteristics has been a fundamental and classical issue in these experiments (Tagawa and Kajiwara 2007; Yao et al., 2016; Ryu and Reinhorn 2017; Enokida and Kajiwara 2019). Many approaches and techniques have been developed as countermeasures against the nonlinear characteristics for shake table experiments.

Iterative control input modification (Plummer 2007) is a common offline compensation for nonlinear characteristics in shake table experiments. This is effective for structural systems that repeatedly display some fixed nonlinearity; however, it is ineffective for “one-time-only” nonlinearities, such as fractures or damage in structural components, because of the absence of feedback actions. H_∞ control, which incorporates the uncertainty of a controlled system to some degree into the controller design, was also applied to a shake table experiment (Maekawa, Yasuda, and Yamashita 1993). Minimal control synthesis (Stoten and Benchoubane 1990; Stoten, 1992), a type of model reference adaptive control (Landau 1979; Isidori, 1995), was applied to compensate for unknown dynamics within shake tables or dynamic changes caused by placing a structure on the tables (Stoten and Gómez 2001; Gizatullin and Edge 2007; Stoten and Shimizu 2007). The use of a class of adaptive control approaches has become prominent for shake table control in various applications (Gang et al., 2013; Shen et al., 2017; Yachun et al., 2018; Liu et al., 2019).

The addition of an error feedback controller to an IBC has recently gained much attention and has been employed in shake table experiments (Nakata 2010; Phillips, Wierschem, and Spencer 2014). This addition is motivated by the need to compensate for the drawback of the IBC (i.e., the absence of a feedback action), and its combined form is referred to as model-based control. This model-based control has been applied to a multiaxial shake table (Plummer 2016) and a single-axis shake table sustaining a structure that exhibits nonlinear characteristics associated with the fracture of a structural component (Najafi and Spencer 2020).

As another enhancement of the IBC, nonlinear signal-based control (NSBC) has been developed by employing a nonlinear signal feedback controller (Enokida, Takewaki, and Stoten 2014; Enokida 2019; Enokida 2022a). This controller acts on the nonlinear signal obtained from the outputs of a controlled system and its linear model subjected to the same input signal. The effectiveness of the feedback action on nonlinear structural dynamics has been demonstrated by dynamic substructuring experiments (Enokida and Kajiwara 2017a; Enokida and Kajiwara 2017b) and shake table experiments (Enokida 2022b). In its application to a single-axis shake table with a steel structure (Enokida and Kajiwara 2019), NSBC realized a seismic acceleration record with an accuracy of approximately 100.0%, despite the structure on the table exhibiting severe nonlinear characteristics owing to the yielding of its structural components.

Although the performance examination of shake table control with structural damage is an essential subject in the context of these experiments, there is a paucity of studies in this regard. This is because control degradation by structural damage has to be intentionally realized for examination purposes. However, the nonlinear characteristics, which are expected to appear, tend to degrade the shake table control as well as its stability margin, prompting the occurrence of instability. If instability occurs in a table with a heavy specimen, it can be critically harmful to the shake table system, other experimental equipment, and its facility. Consequently, it is difficult to employ an unsecured control approach to a shake table sustaining a structure. This aspect partially limits advancements in shake table experimentation, although advanced techniques have been actively investigated for shake table substructuring experiments (Horiuchi et al., 1999a; Lee et al., 2007; Zhang et al., 2017; Chen et al., 2020; Enokida 2020; Mukai et al., 2020; Tang et al., 2020; Tian et al., 2020).

To address this issue, this study introduces a numerically disturbed shake table experimentation to artificially realize control degradation caused by nonlinear structural characteristics without placing an actual structure on the table. In this experiment, structural responses are numerically simulated, and the responses are fed back to the shake table in the physical domain to disturb the table control via real-time interaction. This experiment can be executed with less concern than actual shake table experiments because of the absence of structures on the table. In addition, it is cost- and time-efficient because various structural conditions can be considered simply by tuning numerical models.

This experimentation is similar to real-time hybrid (RTH) simulations (Nakashima, Kato, and Takaoka 1992; Horiuchi et al., 1999b; Nakashima and Masaoka 1999), which also simultaneously use systems in the physical and numerical domains, with real-time interaction. In a typical RTH simulation, the system to be tested is divided into a set of substructures in the physical and numerical domains with real-time interaction, and the output signal of the numerical substructure becomes a reference signal to be realized in the physical substructure. The RTH simulation thus differs in the synthesis of signals from the proposed numerically disturbed shake table experimentation.

This study examines the reliability of numerically disturbed shake table experimentation via the application of NSBC and IBC to shake table experiments. The results are to be compared with those obtained from numerical simulations and actual shake table experiments performed using a steel structure.

2 Numerically disturbed shake table experimentation for NSBC

Numerically disturbed experimentation enables the investigation of shake table control with higher reality than that of numerical studies and with better safety than physical experiments that use actual structures. An advantage of numerically disturbed experimentation is that the structural conditions (e.g., properties or nonlinear characteristics) in the numerical simulation can be flexibly changed without physical burden or cost. It can be used as a preliminary examination of shake table control in advance of the actual experiments.

A numerically disturbed experiment is detailed in comparison with an actual shake table experiment in Section 2.1. NSBC, which is applied to the numerically disturbed experimentation in this study, is summarized in Section 2.2.

2.1 Shake table control

Shake table dynamics are significantly influenced by the structure placed on the table. Here, their influence on the shake table control is examined by comparing a bare shake table in Figure 1 and a table with a single-degree-of-freedom (SDOF) structure, as shown in Figure 2. Thereafter, the numerically disturbed shake table experiment shown in Figure 3 is introduced.

FIGURE 1

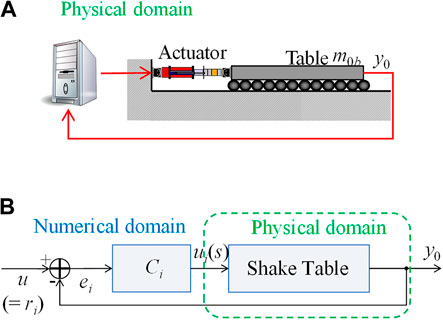
FIGURE 1. Shake table control with the bare condition: (A) conceptual drawing and (B) block diagram.

FIGURE 2

FIGURE 2. Shake table control with a structure: (A) conceptual drawing and (B) block diagram.

FIGURE 3

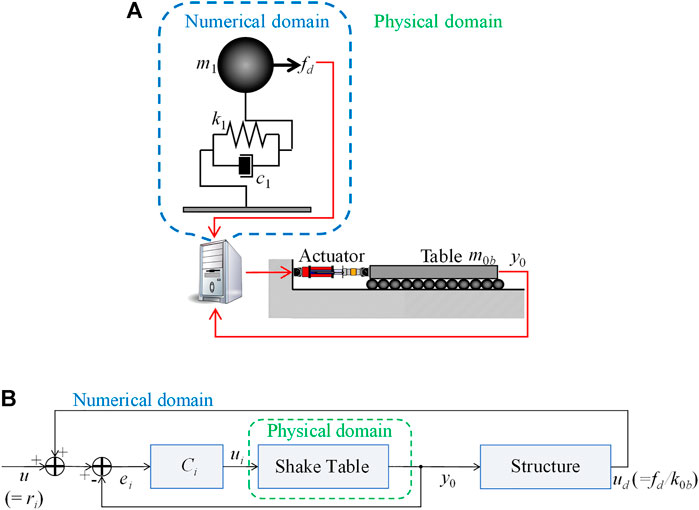
FIGURE 3. Numerically disturbed shake table experimentation: (A) conceptual drawing, and (B) block diagram.

2.1.1 Actual shake table experimentation

Regardless of the presence of a structure on its top, a shake table is driven by an actuation system that receives a command signal from a controller. For this controller, PID or TVC is commonly employed to minimize the error between the reference and feedback signals, as shown in Figure 1B, Figure 2B, respectively. When the table displacement (acceleration) is fed back to the controller, the table is operated by the displacement (acceleration) control. Displacement control is the basic approach employed for shake table control owing to its accessibility.

At displacement control, the controller is commonly designed such that the closed-loop in Figure 1B has the dynamics described by a second-order transfer function:

$G\left(s\right)\left(=\frac{y_0\left(s\right)}{r_i\left(s\right)}=\frac{y_0\left(s\right)}{u\left(s\right)}\right)=\frac{{\omega }_{0b}^2}{s^2+2{\zeta }_{0b}{\omega }_{0b}s+{\omega }_{0b}^2}(1)$

where s is the Laplace variable; r_i is the reference signal to the closed-loop; y₀ is the displacement of the shake table; ${\omega }_{0b}=\sqrt{\frac{k_{0b}}{m_{0b}}}$; ${\zeta }_{0b}=\frac{c_{0b}}{2\sqrt{k_{0b}{m}_{0b}}}$; and {m_0b, c_0b, k_0b } is the set of the table mass and equivalent coefficients of the damping and stiffness, respectively, when no specimen is placed on the table. Note that, when additional controllers are applied to the closed-loop from outside, r_i becomes the control input signal u to the loop. As this study is focused on this condition, hereafter, the notation of r_i is replaced by u.

According to Eq. 1, its equivalent form in the time domain is as follows:

$m_{0b}{\ddot{y}}_0\left(t\right)+c_{0b}{\dot{y}}_0\left(t\right)+k_{0b}{y}_0\left(t\right)=k_{0b}u\left(t\right)(2)$

where t is the time variable.

According to Eq. 2, when the table has a structure, the equations of motion are expressed as

$\{\begin{array}{l}{m}_1{\ddot{y}}_1\left(t\right)+f_d\left(t\right)=0\\ m_0{\ddot{y}}_0\left(t\right)+c_0{\dot{y}}_0\left(t\right)+k_0{y}_0\left(t\right)-f_d\left(t\right)=k_{0}u\left(t\right)\end{array}(3)$

where {m₁, y₁} is the set of the mass and displacement of the structure on the table; $f_d\left(t\right)=f_c\left(t\right)+f_k\left(t\right)$; {f_c, f_k} is the set of forces associated with structural damping and stiffness, respectively; and {m0, c0, k0} is the set of table mass, equivalent coefficients of damping, and stiffness of the shake table system, respectively, when a structure is placed on the table. Note that m₀ consists of m_0b and m_0α, which denotes the weight of the experimental rigs placed on the table. According to Eq. 3, the inertial force derived from the structural response $m_1{\ddot{y}}_1\left(t\right)$ acts as a disturbance to the shake table, and its influence on the control is proportional to the structural mass.

When the structure on the table is described as a linear system with constant damping and stiffness {c₁, k₁}, the forces become $f_c\left(t\right)=c_1\left({\dot{y}}_1\left(t\right)-{\dot{y}}_0\left(t\right)\right)$ and $f_k\left(t\right)=k_1\left(y_1\left(t\right)-y_0\left(t\right)\right)$. In this case, the influence of the structure on the shake table control can be simply determined from the transfer functions, and those of the table displacement and acceleration can be expressed as

$\{\begin{array}{l}{G}_{0d}\left(s\right)\left(=\frac{y_0\left(s\right)}{u\left(s\right)}\right)=\frac{k_0}{\left(m_0{s}^2+\left(c_0+c_1\right)s+k_0+k_1\right)-\left(c_{1}s+k_1\right)G_1\left(s\right)}\\ G_{0a}\left(s\right)\left(=\frac{s^2{y}_0\left(s\right)}{u\left(s\right)}\right)=s^2{G}_{0d}\left(s\right)\end{array}(4)$

where $G_1\left(s\right)\left(=\frac{y_1\left(s\right)}{y_0\left(s\right)}\right)=\frac{c_{1}s+k_1}{m_1{s}^2+c_{1}s+k_1}$^. An inversion of these expressions is used as a feedforward controller in the IBC, as shown in Figure 4. This feedforward control is effective for linear systems whose characteristics are well known; however, it is not effective for nonlinear systems.

FIGURE 4

FIGURE 4. Inversion-based control: K_r(s) = G(s)^-1.

2.1.2 Numerically disturbed shake table experimentation

According to Eq. 3, the shake table control in actual experiments is disturbed by the inertial force of a structure placed on its top, and its force is proportional to the mass of the structure. This indicates the necessity of a structure with sufficient mass to reproduce the disturbance in the actual experiments for shake table control examination. Shake table experiments driven by unsecured control pose a great danger to operators and facilities, and their risk must be minimized prior to execution. To this end, this study introduces a numerically disturbed experiment in which a structure disturbing shake table control is numerically considered, and its structural responses are returned as a disturbance to the actual shake table in the physical domain with real-time interaction.

The experimentation with a numerical SDOF structure is illustrated in the block diagram in Figure 3B. The equations of motion in the physical and numerical domains are expressed as

$\{\begin{array}{l}{m}_1{\ddot{y}}_1\left(t\right)+f_d\left(t\right)=0\\ m_{0b}{\ddot{y}}_0\left(t\right)+c_{0b}{\dot{y}}_0\left(t\right)+k_{0b}{y}_0\left(t\right)=k_{0b}\left(u\left(t\right)+u_d\left(t\right)\right)\end{array}(5)$

where u_d(t)( =f_d(t)/k_0b) is the disturbance signal calculated from the numerical structure. Here, the numerical structure is handled as a generator of the disturbance, and the bare shake table is operated solely in the physical domain. An advantage of this experiment is that the structural conditions (e.g., properties or nonlinear characteristics) in the numerical simulation can be flexibly changed, allowing for a variety of structural conditions without any effort or cost in the physical domain. However, numerical disturbance becomes a matter of control, although an actual shake table experiment with a structure can naturally realize it by the nature of dynamics.

In this experiment, all shake table output signals (i.e., displacement, velocity, and acceleration) must be transmitted to the numerical simulation via real-time interaction to calculate the responses of the numerical structure. However, in many shake table experiments, displacement and acceleration are commonly measured for table control and experimental purposes, whereas the velocity is rarely measured. Thus, in this study, the table velocity is estimated from the measured displacement and acceleration. Using a data fusion technique (Stoten 2001), the table velocity can be estimated by

${\dot{y}}_0\left(s\right)=F_d\left(s\right)y_0\left(s\right)+F_a\left(s\right){\ddot{y}}_0\left(s\right)(6)$

where F_a(s) = 1/(s+ω_c); F_d(s) = sω_c /(s+ω_c); and ω_c is the switching circular frequency, which determines the contribution of the signals to be fused. The estimation of velocity using Eq. 6 is primarily focused on low-frequency components of displacement response and high-frequency components of acceleration response. Thus, the switching frequency ω_c should be determined from a reliable range of both displacement transducers and accelerometers. For example, when the reliable range is 0.5–3 Hz, ω_c = 1.0⋅2π or 2.0⋅2π is a reasonable choice, which is the case in this study.

2.2 Application to shake table control performance examination

The numerically disturbed shake table experiment is applied to examine NSBC as shown in Figure 5, which relies on a nonlinear signal. The nonlinear signal can be expressed as follows:

$\sigma \left(s\right)\left(=y_0\left(s\right)-{\overline{y}}_0\left(s\right)\right)=\left(\left(1+\frac{\mathrm{\Delta }G\left(s\right)}{\overline{G}\left(s\right)}\right){\exp }^{-\mathrm{\Delta }\tau s}-1\right)\overline{G}\left(s\right){\exp }^{-\overline{\tau }s}u\left(s\right)(7)$

where ${\overline{y}}_0$ is the output of the linear model of the controlled system; $\tau$ is the pure time delay, $\overline{\tau }$ is the estimate of the delay; $\mathrm{\Delta }\tau =\tau -\overline{\tau }$; and $\mathrm{\Delta }G\left(=G-\overline{G}\right)$ is the unmodeled dynamics in the controlled system. The NSBC determines its control signal by

$u\left(s\right)=K_r\left(s\right)r\left(s\right)+K_e\left(s\right)e\left(s\right)+K_{\sigma }\left(s\right)\sigma \left(s\right)(8)$

where {K_r, K_e, K_σ} is the set of controllers acting on the signals {r, e, σ}, respectively. According to Figure 5, the error signal is expressed as

$e\left(s\right)\left(=r\left(s\right)-y_0\left(s\right)\right)=\frac{1-\overline{G}\left(s\right){\exp }^{-\overline{\tau }s}{K}_r\left(s\right)}{1+\overline{G}\left(s\right){\exp }^{-\overline{\tau }s}{K}_e\left(s\right)}r\left(s\right)-\frac{1+\overline{G}\left(s\right){\exp }^{-\overline{\tau }s}{K}_{\sigma }\left(s\right)}{1+\overline{G}\left(s\right){\exp }^{-\overline{\tau }s}{K}_e\left(s\right)}\sigma \left(s\right)(9)$

FIGURE 5

FIGURE 5. Nonlinear signal-based control for shake table.

NSBC controllers are designed to minimize the error, and the following transfer functions are suitable for minimization:

$\{\begin{array}{l}{K}_r\left(s\right)=\frac{F_r\left(s\right)}{\overline{G}\left(s\right)}\\ K_e\left(s\right)=\frac{F_e\left(s\right)}{\overline{G}\left(s\right)}\\ K_{\sigma }\left(s\right)=-\frac{F_{\sigma }\left(s\right)}{\overline{G}\left(s\right)}\end{array}(10)$

where {F_r, F_e, F_σ} is the set of filters associated with {K_r, K_e, K_σ}. When the linear model is exactly invertible and $\tau =\overline{\tau }=0$, the controllers $K_r\left(s\right)=-K_{\sigma }\left(s\right)=\overline{G}{\left(s\right)}^{-1}$ realize zero error in Eq. 9 even when K_e(s) = 0. The error feedback controller is typically used to further mitigate the error signal that remains even after the activation of K_r and K_σ. As NSBC with K_e(s) = K_σ(s) = 0 corresponds to IBC in Figure 4, it can be simply executed in the form of NSBC.

3 Numerical simulations

Prior to the experimental studies, NSBC and IBC were examined via numerical simulations that considered a shake table system and structure placed on the table. These examinations were simulated for the shake table system with the SDOF structure shown in Figure 2, with and without a nonlinear spring shown in Figure 6, which is commonly used in structural engineering.

FIGURE 6

FIGURE 6. Tri-linear hysteretic spring.

The restoring force of the spring is described by

$f_k\left(t\right)=r_{12}{k}_1{\delta }_1\left(t\right)+\left(1-r_{11}\right)k_1\cdot z_{11}\left(t\right)+\left(r_{11}-r_{12}\right)k_1\cdot z_{12}\left(t\right)(11)$

where ${\delta }_1\left(t\right)=y_1\left(t\right)-y_0\left(t\right)$; ${\dot{z}}_{1l}\left(t\right)={\dot{\delta }}_1\left(t\right)\left\{\chi \left({\dot{\delta }}_1\left(t\right)\right)\chi \left({\delta }_{1l}-z_{1l}\left(t\right)\right)+\chi \left(-{\dot{\delta }}_1\left(t\right)\right)\chi \left({\delta }_{1l}+z_{1l}\left(t\right)\right)\right\}$ (l = 1, 2); χ(a) = {1 (a ≥ 0), 0 (a < 0)}, and {δ_1l, r_1l} is the set of the lth elastic limit and stiffness reduction factor of the nonlinear spring in the structure, respectively.

For shake table experiments, this study employed the ground acceleration data in Figure 7, which was recorded by the Japan Meteorological Agency (JMA) during the Hyougo-ken Nanbu (or Kobe) earthquake, as the reference signal to be realized on the shake table. In this paper, this acceleration record is referred to as the JMA Kobe motion.

FIGURE 7

FIGURE 7. JMA Kobe motion.

To quantify the accuracy of shake table control, the following two indices were employed:

$\{\begin{array}{l}{S}_t\left(r,y_0\right)=\frac{1}{1+\frac{{\displaystyle \sum {\left(r\left(t\right)-y_0\left(t\right)\right)}^2}}{{\displaystyle \sum r{\left(t\right)}^2}}}\times 100\%\\ S_f\left(r,y_0\right)=\frac{1}{1+\frac{{\displaystyle \sum {\left(A_r\left(f\right)-A_{y0}\left(f\right)\right)}^2}}{{\displaystyle \sum A_r{\left(f\right)}^2}}}\times 100\%\end{array}(12)$

where {A_r, A_y0} is the set of Fourier amplitude spectra of signals r and y₀. The similarity between two signals in the time and frequency domains is calculated using Eq. 12, on the basis of mean square error (MSE) normalized by mean square (MS). It can describe the similarity within the 0–100% range, which is beneficial for the comparison of accuracies. S_t directly calculates the similarity of the two signals in the time domain, while S_f focuses on a limited frequency range. In general, S_t becomes more conservative, especially when the signal to be evaluated is raw data or data minimally postprocessed. In this study, S_f was focused on 0.01–20.0 Hz, which covers the prime frequency range of common earthquake excitations.

3.1 Numerical conditions and controller design

Dynamic properties of a shake table for displacement control were determined to be m_0b = 200 kg, c_0b = 19.8 kN s/m, and k_0b = 313.38 kN/m, resulting in ω_0b = 6.30∙2∙π rad/s and ζ_0b = 1.25, according to a system identification test on an actual shake table (described later herein). A pure time delay within the shake table control system and its estimate were set to $\tau =\overline{\tau }$= 4.0 m s. A structure to be placed on the table was designed to have the following parameters: m₁ = 200 kg, c₁ = 54.54 N m/s, and k₁ = 37.18 kN/m, resulting in the dynamic properties of ω = 2.17∙2∙π rad/s and ζ = 0.01. In the case of a nonlinear spring in the structure, its parameters were fixed as δ₁₁ = 0.03 m, δ₁₂ = 1.5∙δ₁₁, r₁₁ = 0.5, and r₁₂ = 0.05.

Regardless of the presence of a nonlinear spring, a linear model of the controlled system consisting of the shake table and structure was designed using $\left\{{\overline{m}}_0,{\overline{m}}_1\right\}=\left\{m_0,m_1\right\}$, $\left\{{\overline{c}}_0,{\overline{c}}_1\right\}=\left\{c_0,c_1\right\}$, and $\left\{{\overline{k}}_0,{\overline{k}}_1\right\}=\left\{k_0,k_1\right\}$. This condition is identical to that the initial parameters of the table and structure are exactly known.

Because the linear model can be transformed into a transfer function, its function for the input signal and table acceleration can be described by

${\overline{G}}_{0a}\left(s\right)\left(=\frac{s^2{\overline{y}}_0\left(s\right)}{u\left(s\right)}\right)=\frac{s^2{\overline{k}}_{0b}}{\left({\overline{m}}_{0b}{s}^2+\left({\overline{c}}_{0b}+{\overline{c}}_1\right)s+{\overline{k}}_{0b}+{\overline{k}}_1\right)-\left({\overline{c}}_{1}s+{\overline{k}}_1\right){\overline{G}}_1\left(s\right)}(13)$

where ${\overline{G}}_1\left(s\right)\left(=\frac{{\overline{y}}_1\left(s\right)}{{\overline{y}}_0\left(s\right)}\right)=\frac{{\overline{c}}_{1}s+{\overline{k}}_1}{{\overline{m}}_1{s}^2+{\overline{c}}_{1}s+{\overline{k}}_1}$ and ${\overline{y}}_1$ is the output signal of the linear model associated with the structure. By employing Eq. 13 as the linear model of NSBC for acceleration control: $\overline{G}\left(s\right)={\overline{G}}_{0a}\left(s\right)$, its control input signal is determined by

$u\left(s\right)=K_r\left(s\right)\ddot{r}\left(s\right)+K_{\sigma }\left(s\right)\ddot{\sigma }\left(s\right)(14)$

where

$\{\begin{array}{l}{K}_r\left(s\right)={\overline{G}}_{0a}{\left(s\right)}^{-1}\\ K_{\sigma }\left(s\right)={\overline{G}}_{0a}{\left(s\right)}^{-1}{F}_{\sigma }\left(s\right)\end{array}(15)$

$\ddot{\sigma }\left(s\right)={\ddot{y}}_0\left(s\right)-{\ddot{\overline{y}}}_0\left(s\right)$ and $F_{\sigma }\left(s\right)$ is the second-order Butterworth bandpass filters with the range of 0.2–20.0 Hz. This filtering design was found to be effective for maintaining stability when an estimate of a pure time delay was not accurate in actual shake table experiments using NSBC (Enokida and Kajiwara 2019). Based on Eq. 14 with K_σ(s) = 0, which corresponds to the IBC in Figure 4, NSBC was compared with IBC.

3.2 Numerical results

The performance of NSBC and IBC was examined by numerical simulations on the shake table with the structure in Figure 2, with and without the nonlinear spring in Figure 6. To examine the influence of the severity of nonlinear characteristics on control performance, the JMA Kobe motion was applied with three amplitudes: 50%, 80%, and 100%. In addition, the set of noise was added to the numerically simulated table acceleration and displacement to consider practical measurement conditions of shake table experiments. The numerical results are summarized in Table 1, and the results of 80% excitation for the nonlinear structure are illustrated in Figure 8.

TABLE 1

TABLE 1. Shake table control accuracies of IBC and NSBC in numerical simulations.

FIGURE 8

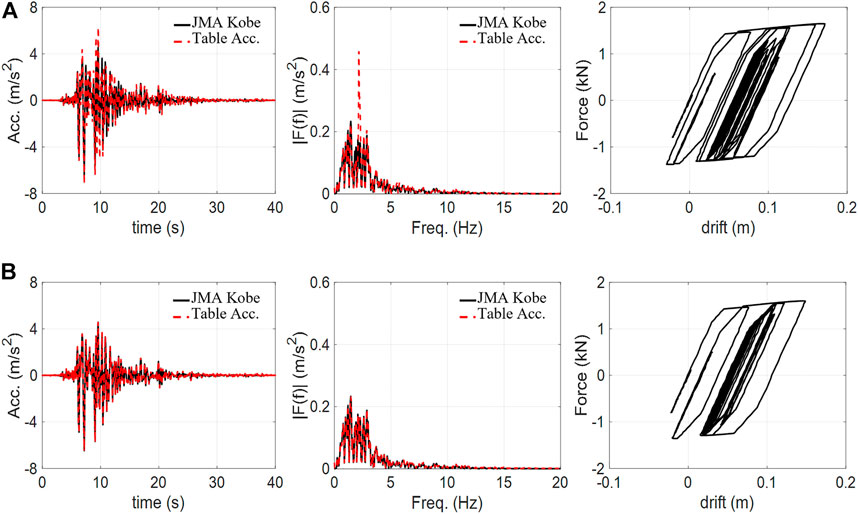
FIGURE 8. Numerical results of a shake table with a nonlinear structure and 80% JMA Kobe motion: (A) IBC and (B) NSBC. (Left: time-history table acceleration, middle: Fourier amplitude spectra of table acceleration, right: structural hysteresis.)

According to Table 1, the IBC is highly effective when the structure placed on the table is a linear system, and its parameters are accurately reflected in the controller. However, its performance was significantly degraded in the case of the nonlinear structure, and Figure 8A clearly shows its ineffectiveness in the nonlinear structure. Its degradation becomes more severe as the excitation amplitude increases owing to the nature of the nonlinear spring. In contrast, NSBC achieved excellent control to the shake table by sustaining the nonlinear structure, as shown in Figure 8B. According to Table 1, the accuracies of NSBC for all excitations are no smaller than 99.4%, and these accuracies are not affected by the excitation amplitudes.

4 Shake table experiments

A series of shake table experiments were performed using the single-axis electrodynamic table in Figure 9A with a size of 1.2 × 1.2 m and a weight of 200 kg. It was equipped with a magnetostrictive displacement transducer and two servo accelerometers for control. This table was operated using MicroLabBox (dSPACE) with MATLAB/Simulink 2020a by the sampling time interval of 1.0 m s. The sampling interval for the measurement was also set to be 1.0 ms. The inner PID controller shown in Figure 1B was designed to be C_i(s) = (0.25∙s² + 5.2∙s + 20)/(0.01∙s² + s). This controller was applied to the error signal obtained by the reference signal and table displacement, which was processed by a first-order low-pass filter: 50 × 2π/(s + 50∙2π).

FIGURE 9

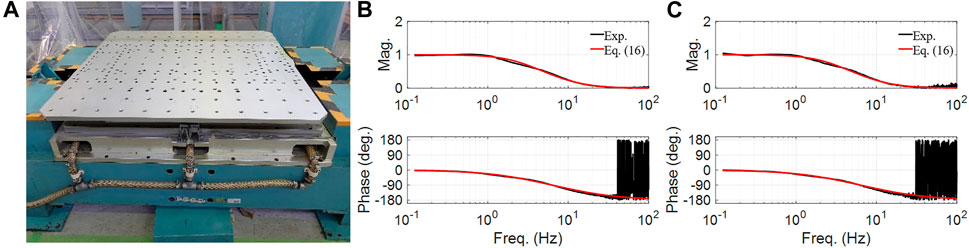
FIGURE 9. Shake table with bare condition: (A) photo and (B) table dynamics identified by the random excitation (15 mm) and (C) table dynamics identified by the random excitation (5 mm).

4.1 Numerically disturbed experiments

System identification tests were conducted to examine the dynamic characteristics of the bare shake table prior to experiments using seismic excitations. Based on the identified dynamics, numerically disturbed shake table experiments were executed.

4.1.1 Experimental conditions and controller design

In the system identification test for the bare table shown in Figure 9A band-limited white-noise random excitation containing frequency components of 0.1–50.0 Hz was used to obtain its dynamic characteristics. The maximum amplitude of the excitation was scaled to 15 mm, and the dynamics were identified, as shown in Figure 9B. The shake table system had a pure time delay of τ = 4.0 m s. Dynamic characteristics for table displacement and acceleration were found to be modeled by the following transfer functions, respectively:

$\{\begin{array}{l}{G}_{0d}\left(s\right)\left(=\frac{y_0\left(s\right)}{u\left(s\right)}\right)=\frac{1567}{s^2+98.96s+1567}\\ G_{0a}\left(s\right)\left(=\frac{s^2{y}_0\left(s\right)}{u\left(s\right)}\right)=s^2{G}_{0d}\left(s\right)\end{array}(16)$

According to Eq. 16, this table had the dynamic characteristics of ω_0b = 6.30∙2∙π rad/s and ζ_0b = 1.25. Based on the table weight m_0b = 200 kg, this shake table was found to have the following equivalent parameters: c_0b = 19.8 kN s/m and k_0b = 313.38 kN/m. Another identification test with the maximum amplitude scaled to 5.0 mm also produced a similar result as shown in Figure 9C.

The numerical structures in the numerically disturbed experiments were designed using the identical parameters used in the numerical simulations: m₁ = 200 kg, c₁ = 54.54 kN s/m, and k₁ = 37.18 kN/m. The nonlinear spring in the structure was set to the identical parameters used in the simulations: δ₁₁ = 0.03 m, δ₁₂ = 1.5∙δ₁₁, r₁₁ = 0.5 and r₁₂ = 0.05. In this study, the reliable range of the displacement transducers and accelerometers was 0.5–3.0 Hz; thus, the switching frequency in Eq. 6 was fixed to be ω_c = 1.0 × 2∙π rad/s.

In this case, a linear model of the controlled system $\overline{G}\left(s\right)$ in Figure 5 was designed using ${\overline{G}}_{0a}\left(s\right)$ in Eq. 13 with $\left\{{\overline{m}}_0,{\overline{m}}_1\right\}=\left\{m_0,m_1\right\}$, $\left\{{\overline{c}}_0,{\overline{c}}_1\right\}=\left\{c_0,c_1\right\}$, and $\left\{{\overline{k}}_0,{\overline{k}}_1\right\}=\left\{k_0,k_1\right\}$. The NSBC controllers in Eq. 15 were designed using this linear model for numerically disturbed shake table experiments. Based on the identification test, the delay was estimated to be $\overline{\tau }$= 4.0 m s.

4.1.2 Results of numerically disturbed experiments

Numerically disturbed experiments were executed for the JMA Kobe motion with the same amplitudes (i.e., 50%, 80%, and 100%) used in the numerical simulations. Actual experiments inherently have noise in measured data; therefore, these experiments were performed without the noise set additionally considered in the numerical simulations in Section 3. The experimental results are summarized in Table 2, and the results of the 80% excitation for the nonlinear structure are illustrated in Figure 10.

TABLE 2

TABLE 2. Shake table control accuracies of IBC and NSBC in numerically disturbed experiments.

FIGURE 10

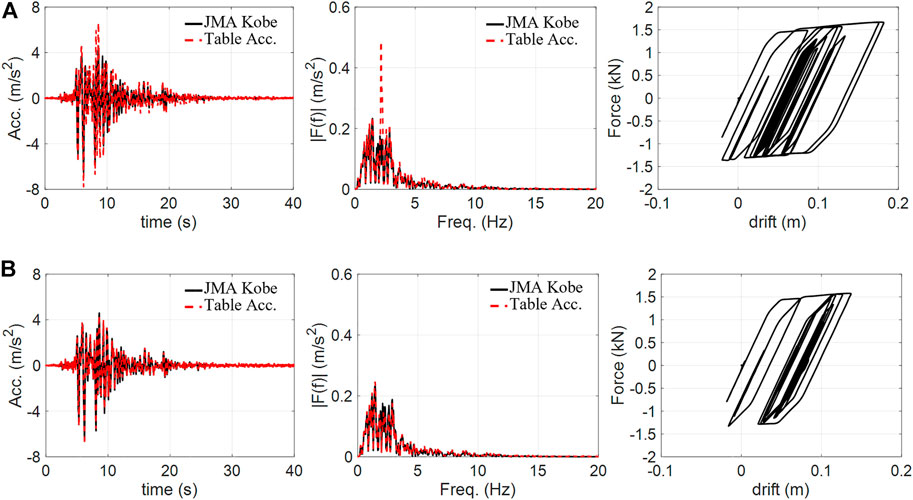
FIGURE 10. Numerically disturbed experiment with a nonlinear structure and 80% JMA Kobe motion: (A) IBC and (B) NSBC. (Left: time-history table acceleration, middle: Fourier amplitude spectra of table acceleration, right: structural hysteresis.)

In Table 2, the IBC is again effective only when the structure is a linear system, as observed in the simulation. In the case of a nonlinear structure, the IBC deteriorates as the excitation amplitude increases. In the case of 80% excitation, the table acceleration is clearly different from the reference signal in the time and frequency domains because of the nonlinear characteristics, as shown in Figure 10A. As these results were anticipated in the numerical simulations in Figure 8A, this experiment was found to properly disturb the shake table control.

In the numerically disturbed experiments, NSBC achieved excellent control in all cases, as shown in Table 2. In Figure 10B, the NSBC accurately realized 80% JMA Kobe motion, which is nearly identical to the reference signal, despite that the numerical structure displays severe nonlinear characteristics. These control accuracies are significantly higher than those of IBC, clearly demonstrating the superiority of NSBC.

Although NSBC showed excellent performance, its accuracies fell within the range of 94.5%–98.8%, which are lower than the accuracies expected in the numerical simulations (i.e., over 99.4%) in Table 1. This can be attributed to the nature of this experimentation: the numerical disturbance has to be handled as a part of the reference signal to be realized by the inner controller, which is ineffective for nonlinear system control.

4.2 Experiments with an actual structure

The NSBC and IBC were examined by shaking table experiments with a steel structure, as shown in Figure 11A The structural responses of the frame were measured using two wire displacement transducers placed between the table and steel mass, as well as two strain gauge accelerometers placed on the mass. System identification tests were conducted to examine the dynamic characteristics of the shake table with the steel structure prior to experiments using seismic excitations.

FIGURE 11

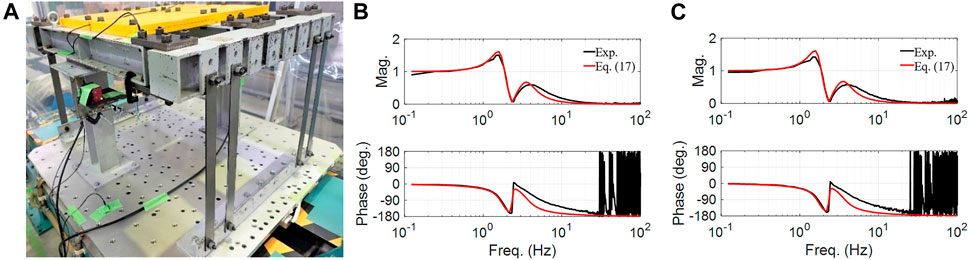
FIGURE 11. Shake table with steel structure: (A) photo, (B) table dynamics identified by the random excitation (15 mm) and (C) table dynamics identified by the random excitation (5 mm)

4.2.1 Experimental conditions and controller design

The same band-limited white-noise random excitation used in the identification of the bare table was again employed for the identification of the dynamics of the table sustaining the steel structure. The maximum amplitude of the excitation was first scaled to 15 mm, and then the dynamics were identified as shown in Figure 11B. The pure time delay with the shake table system was τ = 4.0 m s; dynamic characteristics for table displacement and acceleration were modeled by the following transfer functions:

$\{\begin{array}{l}{G}_{0d}\left(s\right)\left(=\frac{y_0\left(s\right)}{u\left(s\right)}\right)=\frac{276.3s^2+165.8s+5.941\cdot {10}^4}{s^4+17.67s^3+673.3s^2+3732s+5.941\cdot {10}^4}\\ G_{0a}\left(s\right)\left(=\frac{s^2{y}_0\left(s\right)}{u\left(s\right)}\right)=s^2{G}_{0d}\left(s\right)\end{array}(17)$

Based on m₀ (= m_0b + m_0α) = 250 kg, the equivalent table parameters were identified to be c₀ = 4.15 kN s/m and k₀ = 69.09 kN/m, and the parameters of the steel structure were m₁ = 200 kg, c₁ = 120.0 N s/m, and k₁ = 43.0 kN/m. The equivalent table parameters in this case became approximately 1/5 of c_0b and k_0b, indicating that they were affected by the structures placed.

Another system identification test was performed using the same excitation with the maximum amplitude scaled down to 5.0 mm and the table dynamics were obtained as shown in Figure 11C. In this figure, the gap between the experimental result and Eq. 17 became slightly larger than that in Figure 11B. This indicates that the shake table possesses nonlinear characteristics associated with amplitude dependency. This characteristic was not clearly observed at the system identification tests for the bare table in Section 4.1.1. The equivalent table parameters, which became smaller than those for the bare condition, may have caused the dynamics to be sensitive to the nonlinear characteristics.

Regardless of the presence of the nonlinear characteristics, this study employed Eq. 17 as the linear model of a shake table with a steel structure: $\overline{G}\left(s\right)=G_{0a}\left(s\right)$. Based on this linear model, the NSBC controllers for the actual shake table experiments were designed by Eq. 15 to determine the control input signal in Eq. 14. Similar to the numerically disturbed experiments, the delay was estimated to be $\overline{\tau }$= 4.0 m s from the system identification test.

4.2.2 Results of actual shake table experiments

Actual experiments with the shake table and steel structure in Figure 11A were performed using the JMA Kobe motion with amplitudes of 50% and 80%. Note that, 100% excitation was not possible owing to safety management, particularly regarding its structural deformation.

In the case of 50% excitation, IBC poorly realized the seismic excitation, as shown in Figure 12A, and resulted in low accuracies, as shown in Table 3. These accuracies are significantly lower than those of the nonlinear cases considered in the numerical simulations and numerically disturbed experiments. This indicates that the linear model obtained by system identification has a larger modeling gap than those in the numerical simulations and numerically disturbed experiments. Even with the linear model, NSBC accurately realized the seismic excitation with the results in Figure 12B, and high accuracies of over 97.4%, as shown in Table 3.

FIGURE 12

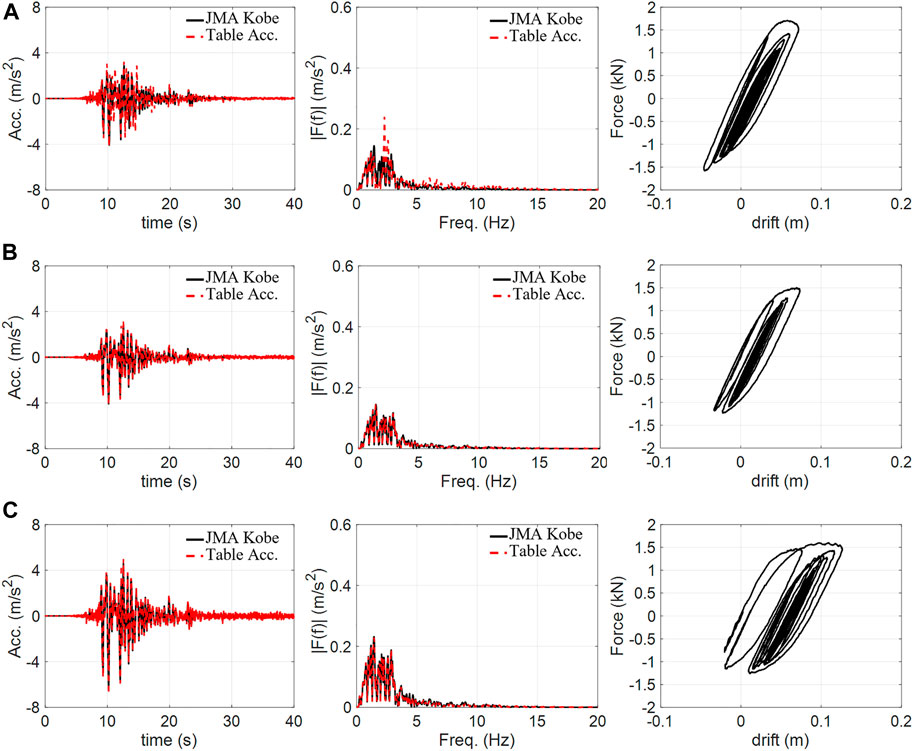
FIGURE 12. Shake table experiments with a steel structure: (A) IBC for 50% JMA Kobe motion, (B) NSBC for 50% JMA Kobe motion and (C) NSBC for 80% JMA Kobe motion. (left: time-history table acceleration, middle: Fourier amplitude spectra of table acceleration, right: structural hysteresis.

TABLE 3

TABLE 3. Shake table control accuracies of IBC and NSBC in actual experiments.

In the case of 80% excitation, the IBC was suspended because its poor result was simply anticipated from the result of 50% excitation. NSBC again achieved accurate control, as shown in Figure 12C, with high accuracies of over 96.9%, as shown in Table 3.

The NSBC results obtained by the actual shake table experiments were better than those obtained by the numerically disturbed experiments. This is because the disturbance to the shake table was realized by the nature of dynamics, and its influence was independent of the inner controller, although the numerically disturbed experiments relied on the inner controller. This indicates that numerically disturbed experimentation may be more susceptible to nonlinear characteristics within structures than actual shake table experimentation.

5 Conclusion

This study introduced a numerically disturbed experiment to examine the control performance of a shake table that involves the control degradation caused by nonlinear dynamics within a structure placed on the table. In this experiment, the structural responses are numerically simulated, and the calculated responses are fed back to the shake table in the physical domain to disturb the table control by real-time interaction. This enables us to examine shake table control with a wide variety of structures, which can be flexibly tuned in numerical simulations only by operating a bare shake table in the physical domain.

Numerically disturbed shake table experiments were performed to examine the NSBC and IBC. For comparisons, these two approaches were examined in numerical simulations and actual experiments; in numerical simulations (actual experiments), all systems: i.e., a shake table and structure, were fully considered (prepared) in the numerical (physical) domain. In all these examinations, NSBC achieved excellent shake table control even with severe nonlinear characteristics, whereas IBC failed in nonlinear cases.

In numerically disturbed experiments, the control degradation caused by nonlinear characteristics was observed, especially in the case of IBC, and the degradation was resolved by NSBC. This control degradation corresponded well with the numerical simulations, and similar results were obtained by actual shake table experiments using a steel structure. Thus, numerically disturbed experimentation, which does not require actual structures on the table, can be an alternative to actual shake table experimentation.

When compared to the actual shake table experiments, the proposed experimentation was found to gain its benefits at the expense of a little bit of accuracy. The numerical disturbance becomes a part of the reference signal to be realized by an inner controller, and its realization becomes a matter of control. Thus, this aspect may result in an overestimation of the control degradation when nonlinear characteristics are considered in the structures. This feature should be considered when numerically disturbed experimentation is used as a preliminary step in actual shake table experimentation.

This experimentation was used for the shake table control examination in this study. It can be extensively used for the pre-determination of the control input signal in actual experiments. Applications of this experimentation will be investigated further in future studies.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

RE, KI, and KK contributed to conception and design of the study. RE performed the numerical simulation. RE performed the experimental study under the supervision of KI and KK. RE wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This study was supported by the research Grant (No. 20H02228) from the Japan Society for the Promotion of Science.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Blondet, M., and Carlos, E. (1988). Analysis of shaking table-structure interaction effects during seismic simulation tests. Earthq. Eng. Struct. Dyn. 16 (4), 473–490. doi:10.1002/eqe.4290160402

CrossRef Full Text | Google Scholar

Chen, P., Dong, M. W. D., Chen, P.-C., and Nakata, N. (2020). Stability analysis and verification of real-time hybrid simulation using a shake table for building mass damper systems. Front. Built Environ. 6. doi:10.3389/fbuil.2020.00109

CrossRef Full Text | Google Scholar

Conte, J., and Trombetti, T. (2000). Linear dynamic modeling of a uni-axial servo-hydraulic shaking table system. Earthq. Eng. Struct. Dyn. 29 (9), 1375–1404. doi:10.1002/1096-9845(200009)29:9<1375:AID-EQE975>3.0.CO;2-3

CrossRef Full Text | Google Scholar

Enokida, R. (2020). Basic examination of two substructuring schemes for shake table tests. Struct. Control Health Monit. 27, 1–23. doi:10.1002/stc.2497

CrossRef Full Text | Google Scholar

Enokida, R. (2022a). Enhancement of nonlinear signal-based control to estimate earthquake excitations from absolute acceleration responses of nonlinear structures. Mech. Syst. Signal Process. 181, 109486. doi:10.1016/j.ymssp.2022.109486

CrossRef Full Text | Google Scholar

Enokida, R., and Kajiwara, K. (2019). Nonlinear signal-based control for single-axis shake tables supporting nonlinear structural systems. Struct. Control Health Monit. 26, e2376. doi:10.1002/stc.2376

CrossRef Full Text | Google Scholar

Enokida, R., and Kajiwara, K. (2017a). Nonlinear signal-based control with an error feedback action for nonlinear substructuring control. J. Sound. Vib. 386, 21–37. doi:10.1016/j.jsv.2016.09.023

CrossRef Full Text | Google Scholar

Enokida, R., and Kajiwara, K. (2017b). Nonlinear substructuring control for parameter changes in multi-degree-of-freedom systems. J. Sound. Vib. 407, 63–81. doi:10.1016/j.jsv.2017.06.029

CrossRef Full Text | Google Scholar

Enokida, R. (2022b). Nonlinear substructuring control for simultaneous control of acceleration and displacement in shake table substructuring experiments. Struct. Control Health Monit. 29. doi:10.1002/stc.2882

CrossRef Full Text | Google Scholar

Enokida, R. (2019). Stability of nonlinear signal‐based control for nonlinear structural systems with a pure time delay. Struct. Control Health Monit. 29, e2365. doi:10.1002/stc.2365

CrossRef Full Text | Google Scholar

Enokida, R., Takewaki, I., and Stoten, D. (2014). A nonlinear signal-based control method and its applications to input identification for nonlinear SIMO problems. J. Sound. Vib. 333, 6607–6622. doi:10.1016/j.jsv.2014.07.014

CrossRef Full Text | Google Scholar

Gang, S., Zhen-Cai, Z., Lei, Z., Yu, T., Chi-fu, Y., Jin-song, Z., et al. (2013). Adaptive feed-forward compensation for hybrid control with acceleration time waveform replication on electro-hydraulic shaking table. Control Eng. Pract. 21, 1128–1142. doi:10.1016/j.conengprac.2013.03.007

CrossRef Full Text | Google Scholar

Gizatullin, A. O., and Edge, K. A. (2007). Adaptive control for a multi-axis hydraulic test Rig. Proc. Institution Mech. Eng. Part I J. Syst. Control Eng. 221, 183–198. doi:10.1243/09596518JSCE314

CrossRef Full Text | Google Scholar

Horiuchi, T., Inoue, M., Konno, T., and Namita, Y. (1999a). Real-time hybrid experimental system with actuator delay compensation and its application to a piping system with energy absorber. Earthq. Engng Struct. Dyn. 28, 1121–1141. doi:10.1002/(SICI)1096-9845(199910)28:10<1121:AID-EQE858>3.0.CO;2-O

CrossRef Full Text | Google Scholar

Horiuchi, T., Inoue, M., Konno, T., and Yamagishi, W. (1999b). Development of a real-time hybrid experimental system using a shaking table. (Proposal of experiment concept and feasibility study with rigid secondary system). JSME Int. J. Ser. C 42, 255–264. doi:10.1299/jsmec.42.255

CrossRef Full Text | Google Scholar

Isidori, A. (1995). Nonlinear control systems. Third Edition. London: Springer-Verlag.

Google Scholar

Landau, Y. (1979). Adaptive control: The model reference approach. New York and Basel: Dekker.

Google Scholar

Lee, S. K., Park, E. C., Min, K. W., and Park, J. H. (2007). Real-time substructuring technique for the shaking table test of upper substructures. Eng. Struct. 29, 2219–2232. doi:10.1016/j.engstruct.2006.11.013

CrossRef Full Text | Google Scholar

Liu, J., Baijie, Q., Xingwu, Z., Ruqiang, Y., and Xuefeng, C. (2019). Adaptive vibration control on electrohydraulic shaking table system with an expanded frequency range: theory analysis and experimental study. Mech. Syst. Signal Process. 132, 122–137. doi:10.1016/j.ymssp.2019.06.024

CrossRef Full Text | Google Scholar

Maekawa, A., Yasuda, C., and Yamashita, T. (1993). Application of H_∞; control to a 3-D shaking table. T. SICE. 29, 1094–1103. doi:10.9746/sicetr1965.29.1094

CrossRef Full Text | Google Scholar

Mukai, Y., Yokoyama, A., Fushihara, K., Fujinaga, T., and Fujitani, H. (2020). Real-time hybrid test using two-individual actuators to evaluate seismic performance of RC frame model controlled by AMD. Front. Built Environ. 6, 1–15. doi:10.3389/fbuil.2020.00145

CrossRef Full Text | Google Scholar

Najafi, A., and Spencer, B. F. (2020). Modified model-based control of shake tables for online acceleration tracking. Earthq. Eng. Struct. Dyn. 49, 1721–1737. doi:10.1002/eqe.3326

CrossRef Full Text | Google Scholar

Nakashima, M., Kato, H., and Takaoka, E. (1992). Development of real-time pseudo dynamic testing. Earthq. Eng. Struct. Dyn. 21, 79–92. doi:10.1002/eqe.4290210106

CrossRef Full Text | Google Scholar

Nakashima, M., and Masaoka, N. (1999). Real-time on-line test for MDOF systems. Earthq. Engng Struct. Dyn. 28, 393–420. doi:10.1002/(SICI)1096-9845(199904)28:4<393:AID-EQE823>3.0.CO;2-C

CrossRef Full Text | Google Scholar

Nakashima, M., Nagae, T., Enokida, R., and Kajiwara, K. (2018). Experiences, accomplishments, lessons, and challenges of E-defense––tests using World’s largest shaking table. Jpn. Archit. Rev. 1, 4–17. doi:10.1002/2475-8876.10020

CrossRef Full Text | Google Scholar

Nakata, N. (2010). Acceleration trajectory tracking control for earthquake simulators. Eng. Struct. 32, 2229–2236. doi:10.1016/j.engstruct.2010.03.025

CrossRef Full Text | Google Scholar

Phillips, B. M., Wierschem, N. E., and Spencer, B. F. (2014). Model-based multi-metric control of uniaxial shake tables. Earthq. Eng. Struct. Dyn. 43, 681–699. doi:10.1002/eqe.2366

CrossRef Full Text | Google Scholar

Plummer, A. R. (2007). Control techniques for structural testing: A review. Proc. Institution Mech. Eng. Part I J. Syst. Control Eng. 221, 139–169. doi:10.1243/09596518JSCE295

CrossRef Full Text | Google Scholar

Plummer, A. R. (2016). Model-based motion control for multi-axis servohydraulic shaking tables. Control Eng. Pract. 53, 109–122. doi:10.1016/j.conengprac.2016.05.004

CrossRef Full Text | Google Scholar

Ryu, K. P., and Reinhorn, A. M. (2017). Real-time control of shake tables for nonlinear hysteretic systems. Struct. Control Health Monit. 24, e1871. doi:10.1002/stc.1871

CrossRef Full Text | Google Scholar

Severn, R. T. (2011). The development of shaking tables-A historical note. Earthq. Eng. Struct. Dyn. 40, 195–213. doi:10.1002/eqe.1015

CrossRef Full Text | Google Scholar

Shen, G., Li, X., Zhu, Z., Tang, Y., Zhu, W., and Liu, Shanzeng. (2017). Acceleration tracking control combining adaptive control and off-line compensators for six-degree-of-freedom electro-hydraulic shaking tables. ISA Trans. 70, 322–337. doi:10.1016/j.isatra.2017.07.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Stoten, D. P., and Benchoubane, H. (1990). Robustness of a minimal controller synthesis algorithm. Int. J. Control 51, 851–861. doi:10.1080/00207179008934101

CrossRef Full Text | Google Scholar

Stoten, D. P. (2001). Fusion of kinetic data using composite filters. Proc. Institution Mech. Eng. Part I J. Syst. Control Eng. 215, 483–497. I MECH E Part I Journal of Systems and Control in Engineer. Proceedings of the I Mechanica E Part I Journal of Systems & Control in Engineer. doi:10.1177/095965180121500505

CrossRef Full Text | Google Scholar

Stoten, D. P., and Gómez, E. G. (2001). Adaptive control of shaking tables using the minimal control synthesis algorithm. Philosophical Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 359, 1697–1723. doi:10.1098/rsta.2001.0862

CrossRef Full Text | Google Scholar

Stoten, D. P. (1992). Implementation of minimal control synthesis on a servo-hydraulic testing machine. Proc. Institution Mech. Eng. Part I J. Syst. Control Eng. 206, 189–194. doi:10.1243/PIME_PROC_1992_206_330_02

CrossRef Full Text | Google Scholar

Stoten, D. P., and Shimizu, N. (2007). The feedforward minimal control synthesis algorithm and its application to the control of shaking-tables. Proc. Institution Mech. Eng. Part I J. Syst. Control Eng. 221, 423–444. doi:10.1243/09596518JSCE246

CrossRef Full Text | Google Scholar

Tagawa, Y., and Kajiwara, K. (2007). Controller development for the E-defense shaking table. Proc. Institution Mech. Eng. Part I J. Syst. Control Eng. 221, 171–181. doi:10.1243/09596518JSCE331

CrossRef Full Text | Google Scholar

Tang, Z., Dietz, M., Hong, Y., and Li, Zhenbao. (2020). Performance extension of shaking table‐based real‐time dynamic hybrid testing through full state control via simulation. Struct. Control Health Monit. 27, 1–19. doi:10.1002/stc.2611

CrossRef Full Text | Google Scholar

Tian, Y., Shao, X., Zhou, Huimeng, and Wang, T. (2020). Advances in real-time hybrid testing technology for shaking table substructure testing. Front. Built Environ. 6. doi:10.3389/fbuil.2020.00123

CrossRef Full Text | Google Scholar

Yachun, T., Peng, P., Dongbin, Z., and Yi, Z. (2018). A two-loop control method for shaking table tests combining model reference adaptive control and three-variable control. Front. Built Environ. 4, 1–12. doi:10.3389/fbuil.2018.00054

PubMed Abstract | CrossRef Full Text | Google Scholar

Yao, J., Dietz, M., Xiao, R., Yu, H., Wang, T., and Yue, D. (2016). An overview of control schemes for hydraulic shaking tables. J. Vib. Control 22, 2807–2823. doi:10.1177/1077546314549589

CrossRef Full Text | Google Scholar

Zhang, R., Phillips, B. M., Taniguchi, S., Ikenaga, M., and Ikago, K. (2017). Shake table real-time hybrid simulation techniques for the performance evaluation of buildings with inter-story isolation. Struct. Control Health Monit. 24, 1–19. doi:10.1002/stc.1971

CrossRef Full Text | Google Scholar