Correlation between energy and displacement demands for infilled reinforced concrete frames

Introduction: It is well recognized that masonry infills, even though they are non-structural elements, might offer a significant earthquake resistance and can prevent the collapse of relatively weak reinforced concrete structures.

Methods: The goal of this study is to investigate the energy dissipation contribution of masonry infills in reinforced concrete frames subjected to earthquake ground motion. To this purpose, a sticktype model with and without infills is considered for the evaluation of the inelastic response of representative frame structures. The infills are modeled by means of equivalent strut elements, which can only carry compressive loads. To investigate the influence of their mechanical characteristics, different idealized type of masonry infills are considered, and the weakest one is selected for the dynamic analyses based on the whole strong motions database.

Results: Wide ranges of structural systems and natural periods are taken into account, in such a way to establish response spectra for several significant parameters, including those based on energy. The results of the present investigation demonstrate that the infills significantly contribute to the energy dissipation capacity, provided that they are present in all stories.

Discussion: It is found that the contribution of masonry infills is of great importance in reducing both dissipation and displacement energy demands in frame elements. The effectiveness of their contribution depends on the characteristics of the ground motion, especially for non-seismic frames.

1 Introduction

Reinforced concrete buildings infilled with masonry panels are a very common construction typology in Southern Europe, particularly in the Mediterranean countries. Infills are generally considered as non-structural elements (i.e., simple partitions), and their presence and position in plan and along the height of the building is not explicitly taken into account during the design stage.

However, as far as performance of reinforced concrete buildings during various recent earthquakes is concerned, the important role played by the infills on the overall structural seismic response has been recognized within several studies (Decanini et al., 2004b; Decanini et al., 2005; Celebi et al., 2010; Ricci et al., 2011; Decanini et al., 2012; Ricci et al., 2013; De Luca et al., 2014; Masi et al., 2019; Mollaioli et al., 2019; Furtado and De Risi, 2020; Furtado et al., 2021).

Infills not only limit the deformation of the frames and contribute to the energy dissipation during the earthquake, but also provide a global increment of stiffness and strength. In particular, in terms of stiffness variation, infills produce a change in the natural periods with a shift towards the shortest ones and a consequent variation of the vibration modes of the structures. The presence of infilled panels can be positive or not, depending on the regularity of their distribution in plan and along the height, among others. When some irregularities take place, failure mechanisms might develop into structural members that were not originally designed to undergo the corresponding effects.

Moreover, the seismic response of infilled frames is significantly influenced by several factors, namely: the characteristics of the earthquake that can modify the seismic behavior as a function of the frequency content, duration and amplitude of the corresponding ground motions; the mechanical properties of the infills; the frame-to-infill interface behavior, particularly at the corners; the presence of openings; the out-of-plane behavior of infilled frames also in terms of its interaction with in-plane response; etc.

Generally, the structural performance could be improved by increasing strength and dissipation capacity due to the masonry infills provided that they are regularly distributed, even if in presence of an increment of the seismic inertial forces. In this case, a lot of work has been made in checking the effective increment of strength corresponding to different typologies of infills (Bertero and Brokken, 1983; Bruno et al., 2000; Dolšek and Fajfar, 2008; Rodrigues et al., 2010; Haldar et al., 2013; Cavaleri and Di Trapani, 2014; De Risi et al., 2018; Morandi et al., 2018; Mollaioli et al., 2019; Di Trapani et al., 2020; Dias-Oliveira et al., 2020; Demir and Chengiz, 2021; De Risi et al., 2022; Di Domenico et al., 2022). Very limited research was accomplished regarding the dissipation demand capacity of infilled frames, even though the energy dissipation represents an important indicator of cumulative damage for structures under seismic loads, as highlighted in several studies (Decanini and Mollaioli, 1998; Decanini and Mollaioli, 2001; Benavent-Climent, 2007; Mollaioli et al., 2019; Gentile et al., 2019; Gentile and Galasso, 2020; Benavent-Climent et al., 2021; Cheng et al., 2021; Soleiman and Mollaioli, 2021). For instance, Benavent et al. (2014), after the Lorca earthquake in Spain, evaluated the level of damage in typical reinforced concrete frames by means of an energy-based index, and explained the role played by infills in the overall seismic response. Ozkaynak et al. (2014) asserted that the main part of the input energy imparted to the infilled structure is dissipated through hysteretic and damping energies. When studying the behavior of reinforced concrete frames infilled with masonry panels, Decanini et al. (2012) put in evidence the general agreement between observed damage with the energy demands of the 2009 L’Aquila earthquake in Italy. Kakaletsis and Karayannis (2007) deduced that masonry infills with eccentrically located openings can also be beneficial for the seismic capacity of reinforced concrete frames in terms of energy dissipation.

Therefore, the important contribution attributable to masonry infills in reducing the energy dissipation demand in the structural elements or preventing the development of serious damage in reinforced concrete elements deserves to be investigated. In this paper, the contribution of the infills in reinforced concrete structures is studied in case of masonry panels placed regularly throughout the structure so as do not cause shear failures of the columns. Moreover, frames not designed to resist to seismic forces are included in order to verify the importance of the infills for frames that do not comply with seismic design rules. In order to highlight the dissipation capacity of the infills, the correlation between input and hysteretic energy with a damage measure (herein represented by means of the maximum interstorey drift) is evaluated.

2 Modeling of reinforced concrete frames and seismic ground motions database

A stick model is used for modelling bare and infilled frames. Its lateral stiffness, inertial and strength characteristics are meant at approximating those of real frame structures (Mollaioli et al., 2011). The adopted multi-degrees-of-freedom (MDOF) system thus consists of a series of lumped masses connected by means of nonlinear springs, which are suitably calibrated for representing the behavior of reinforced concrete elements and masonry infills. This simplified numerical modeling allows for the analysis of a large number of records and structures, so as to obtain response spectra for the inter-story drift and the story energy dissipation demand. The methodology has been detailed by Mollaioli et al. (2011), and it allows to perform broad parametric analyses about the inelastic seismic response of different multi-story frame structures and to obtain a spectral representation of the most significant seismic demand parameters considered in this paper, such as the inter-story drift ratio (or index), IDI, and the amount of energy dissipated at each story. Obviously, such response parameters, though supplying important information about the damage level at the end portions of the columns of each story, are only able to provide an indirect and approximate assessment of the inelastic behavior of members connected to the columns.

The frames considered for the nonlinear dynamic analyses are selected in such a way that they are as representative as possible of the reinforced concrete buildings stock in Italy and within the Mediterranean region. The data employed for the present study refers to a recent Italian census about residential (De Sortis et al., 2007). It is observed that most of buildings (approximately 98% of the stock) have up to 8 stories. The cross-inspection of the data pertaining to number of stories, average stories area and number of bays led to the definition of five R/C two bay-frames having constant story height (h = 3.2 m) and beam spans (w = 5.0 m), with five different numbers of stories (N = 2, 4, 6, 8, 10). The ten-story configuration is chosen as upper bound. However, for the sake of spectral representation of energy and displacement parameters, other frames of 12, 14, 16, 20, and 24 stories are included, even though they do not represent realistic structures.

In spite of the long and documented history of destructive earthquakes that have hit Italy over time, the reinforced concrete frame buildings constructed before 1975 were designed with little or no consideration of provisions against the effect of lateral forces induced by earthquakes, with some exceptions in the regions where strong earthquakes occurred in the past. In 1976, the occurrence of two devastating earthquakes in Friuli, which caused more than a thousand victims and economic damages, triggered decisive changes in the state-of-practice. In fact, first national seismic regulations were published between 1975 and 1996, and were in force within those regions that were recognized as seismic zones. However, only after 1983 a large part of the Italian territory was considered exposed to the effects of future seismic events.

The frames are regular in terms of stiffness and mass distribution. They were designed in such a way to have a resistance capacity expressed through the seismic coefficient C_y (i.e., the ratio between the maximum base shear and the weight of the building) equal to 0.08, 0.15, 0.25, and 0.35. The first value can be considered representative of the weakest buildings, i.e., buildings designed for vertical loads only and built with materials having limited mechanical characteristics (Bruno et al., 2000). The other values of C_y refer to buildings built within different seismic zones in accordance with past (in force between 1975 and 2003) as well as current (starting from 2003) seismic regulations.

Three different configurations of infilled frames are considered: 1) bare frames (B); 2) infilled frames with masonry panels at each floor (T); 3) frames with infills placed everywhere except for the first floor (pilotis) (P) (Figure 1).

FIGURE 1

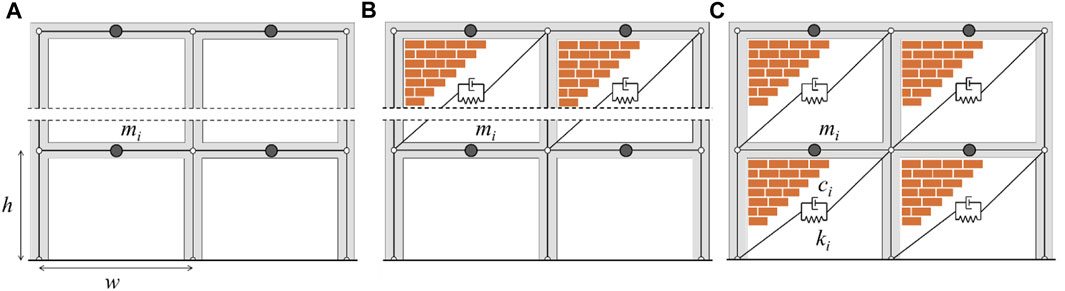
FIGURE 1. Shear-type models for n-story frame structures (interstorey height and beam span are equal to 3.2 m and 5.0 m, respectively): bare frame (A), pilotis frame (B) and infilled frame (C).

For the prediction of the inelastic response of the bare frames, equivalent discrete shear-type (ESTM) models are considered, whose effectiveness in evaluating the inelastic responses of the multi-story framed structures was validated in previous research works (Mollaioli et al., 2007). A stiffness-degrading hysteretic model was adopted to represent the cyclic behavior for each story. Stiffness degradation is defined as a function of ductility, the strength deterioration is function of both dissipated energy and ductility whereas pinching is modeled by two independent parameters. Even though such modeling neglects some information on local inelastic deformations and hysteretic dissipations, such as plastic curvature and dissipated energy in some portions of the members, it permits to analyze the seismic behavior of a large number of multi-story buildings. The bare frame is taken into account because it is the structural configuration that is commonly employed in the design stage.

Several macro-models have been proposed to simulate the infills behavior (Fardis and Panagiotakos, 1997; Crisafulli and Carr, 2007; Asteris et al., 2011; Di Trapani et al., 2017). Some of them also consider a large number of experimental results (Di Trapani et al., 2015; Sassun et al., 2016; Gaetani d’Aragona et al., 2021; Blasi et al., 2021). In this paper, the infills are represented by means of a system of two equivalent diagonal struts that carry load only in compression that are coupled with the shear-type model of the frame. The model used for the infills derives from the original work by Decanini and Fantin (1986), which was adapted to account for the openings by Decanini et al. (2014) and also modified recently so as to consider a large number of experimental tests by Liberatore et al. (2018).

The envelope of the force-horizontal displacement relationship (F_m-u) is shown in Figure 2 and is defined by a skeleton line composed by four branches. The first part represents the elastic phase and is characterized by high stiffness. Point F marks the beginning of the cracking phase, which is characterized by a reduction of the stiffness until the point FC when complete cracking occurs. Next, a degrading behavior follows, which concludes with another branch characterized by zero stiffness and constant strength equal to the residual strength.

FIGURE 2

FIGURE 2. Backbone curve of the force-displacement model adopted for the equivalent struts representing the walls.

The evaluation of the strength of the equivalent connecting rod takes into account four possible fundamental failure modes (Decanini and Fantin, 1986; Decanini et al., 2004): 1) failure due to diagonal tension; 2) sliding shear along horizontal joints; 3) compression failure in the corners of the infill; 4) failure due to diagonal compression of the infill. Each one of these failure modes is associated with a maximum resistant stress σ_br, which depends on the fundamental compressive strength of the infill σ_m0, the fundamental shear strength τ_m0 determined by means of the diagonal compression, the sliding resistance of the joints u, and the applied vertical stress σ_o. The rupture mechanism corresponds to the minimum value obtained for the fictitious rupture strength. The horizontal resistance of the equivalent connecting truss is therefore given by $F_{mfc}={\left({\sigma }_{br}\right)}_{\mathit{min}}tw\cos \theta$ (where t and w are the thickness of the masonry panel and width of the equivalent strut, respectively). The first cracking resistance F_mf (corresponding to the detachment between the frame and the panel) and the residual resistance F_mr are expressed as function of the complete cracking resistance F_fmc (Table 1).

TABLE 1

TABLE 1. Infilled masonry description and mechanical characteristics for weak (t1), intermediate (t2) and strong (t3) infill masonry types (Decanini et al., 2004).

Firstly, to investigate the effects the infills on the structural response as a function of different strong motion types, three different types of masonry infills are considered. The first type of infill, t1, represents a frequent typology in existing Italian structures: it consists of 24 cm × 12 cm × 12 cm clay bricks with horizontal holes and assembled by means of bastard mortar (sand, lime and cement). The second type, t2, is characterized by another usual type of infill in Italian buildings: it is made up of clay bricks measuring 30 cm × 20 cm × 15 cm with horizontal holes and assembled by means of cement mortar. The third type, t3, consists of semi-solid bricks (UNI type) with dimensions 6 cm × 12 cm × 24 cm and including small vertical holes with circular cross-section. Table 1 shows all the parameters that define the envelope and the hysteresis cycles of the constitutive model of the various infill walls.

The values of the elastic modulus of the infill walls (corresponding to the secant modulus between the origin and the point of complete cracking) is denoted as K_mfc. Since the stiffness of the infill walls has already been introduced via the elastic modulus corresponding to the secant stiffness with complete cracking, the ratios K_m0/K_mfc and K_mu/K_mfc (see Figure 2) are requested, since they allow to obtain the slope of the non-cracked elastic branch and of the post-cracking waning branch, respectively. A similar system is used to identify the characteristic points of the envelope by providing the values of the ratios F_mf/F_mfc and F_mr/F_mfc. The values shown in Table 1 are used.

It is noted that the slope of the softening branch for the t3 wall is two times that of t1. Hence, the masonry wall t3 is more brittle and, thus, more affected by cyclic degradation (first row of Figure 3).

FIGURE 3

FIGURE 3. Typical force-displacement envelopes and masonry hysteretic response under cyclic loads (first row). Hysteretic response of a one-story RC frame together with two equivalent struts describing the infilled frame under seismic record FN672 (second row).

The cyclic behavior of an infill is generally characterized by the degradation of stiffness in the unloading brunch, the degradation of strength under displacement cycles of constant amplitude and the pinching due to cracks developed in the previous cycles. For the sake of completeness, the second row of Figure 3 shows the hysteretic response of a representative infilled frame subjected to ground motion excitation.

2.1 Strong motion records

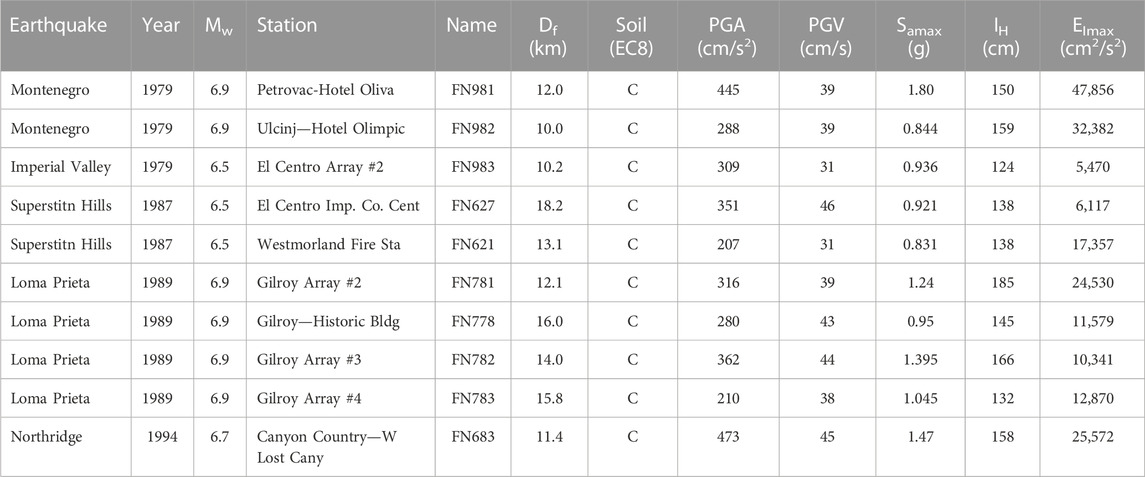
The dynamic response of the considered equivalent frames systems is calculated for a large number of strong ground motions recorded during 40 past and recent earthquakes (a total of 985 seismic records is taken into account). These ground motions were recorded either at the free field or the ground level of structures (no more than one story height). The selected records belong to a magnitude interval between M_w = 5.0 to M_w = 7.9 and source-to-site distance (herein, the closest distance from the surface projection of the fault rupture) D_f between 0 and 150 km. To take local site conditions at the recording stations into account, the ground motions belong to four different soil types, which are defined according to the stratigraphic profile and the average shear wave velocity in the upper 30 m V_S30, namely, A, B, C, and D according to Eurocode 8 (2004).

In Figure 4 is shown the distribution of the records according to magnitude M_w, and closest distance from the surface projection of the fault rupture D_f. It is possible to note that the records correspond to very different ground motions, so as to investigate more in depth the influence of their characteristics on the structural response.

FIGURE 4

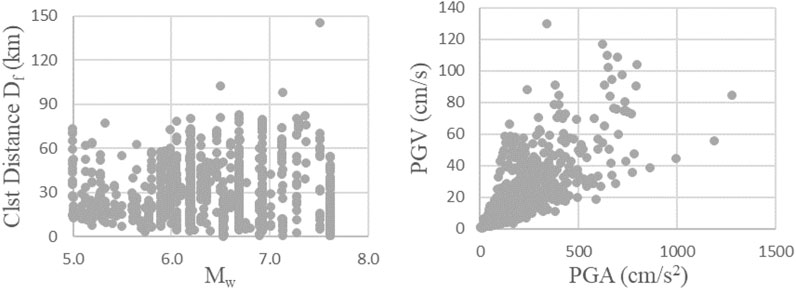
FIGURE 4. Magnitude M_w shortest projection to the surface of the distance to the causative fault D_f, peak ground velocity PGV and peak ground acceleration PGA.

3 Results of the analyses

3.1 Characterization of the correlation between energy and displacement demands

Including infill walls leads to a decrease of the natural period of the building with a consequent reduction of the displacement demand. As it was already pointed out (Decanini et al., 2004a), the period of the bare frame can be 2–3.5 greater than those of infilled frames, depending on the mechanical characteristics of the infills. The stiffness increment reflects into a variation of strength and energy demand. The increment or the reduction of such seismic demands is function of the most important general characteristic of ground motions, i.e., amplitude, duration and frequency content.

To illustrate the influence of the infills on the seismic demand, it is useful to consider a small set of seismic acceleration time histories having amplitude, frequency content, and duration within certain limits, so as to reduce the dispersion of the corresponding demand parameters. Ten records are selected considering narrow magnitude (6.5 ≤ M_w ≤ 7.0) and distance (10 km ≤ D_f < 20 km) ranges, for a soil type C according to Eurocode 8 (2004). Even though they belong to a narrow bin, they exhibit some scattering in frequency content, which is especially evident in the input energy spectra or in the pseudo-velocity spectra. In fact, even though the records exhibit comparable values of peak ground velocity (PGV) and Housner Intensity (I_H), with some differences only in peak ground acceleration (PGA) and maximum spectral acceleration (S_a,max), the dispersion in the energy parameters is larger.

As already pointed out in past research by comparing the response of the frames in terms of maximum story ductility demand μ_max, a large ductility demand is observed in the lowest frames as a function of the C_y coefficient (Bazzurro et al., 2005; 2006). In case of infilled frames, the ductility demand decreases as function of the mechanical characteristics of the infill walls, from t1 to t3, with a concentration towards the lowest stories. It is important to underline that the dissipated energy demand in the infilled frames does not seem to be substantially affected by the seismic coefficient C_y. Conversely, the energy demand in the bare frames tends to increase considerably as the coefficient C_y decreases. Anyway, the infilled frames suffer a highly non-uniform distribution of the story ductility demand since it tends to concentrate in a few stories.

In terms of maximum inter-story drift IDI, it was found that the influence of C_y is particularly large for the lowest frames, namely, between 2 and 6 stories for bare frames, as well as for the infilled frames t1, t2 and t3. The beneficial effects of the infill walls on reducing the IDI values are evident for the masonry infills characterized by high values of the maximum strength. Moreover, the maximum inter-story drift demand tends to shift to the bottom stories as strength and stiffness of infills increase. It is possible to note that the drift demand for frames with infill type t3 in several cases is greater than to the corresponding value for frames with infill type t2 due to local brittle behavior of the masonry, which implies the sudden loss of its contribution with subsequent local concentration of the drift demand. The consequence of the more brittle behavior of the masonry infill t3 is also reflected in the energy dissipation capacity during the cyclic degradation.

Although the selected ground motions belong to a narrow magnitude and distance range and to a specific soil class, it is found that the way by which the infills modify the structural behavior depends on the frequency content and amplitude of the ground motion, particularly in highly inelastic ranges.

To further highlight this evidence, a comparison between the IDI and the total energy dissipation E_H,tot, demand is shown in Figure 5, together with the energy dissipated by the infills alone E_H,inf as reference. It is possible to observe that, the presence of strong infills largely reduces the displacement demand in the RC frame, this is especially evident in the case of low seismic intensities (i.e., low values of E_H,tot). Moreover, even if energy dissipation and drift demand for infills type t3 are generally lower than those corresponding to infills type t1, there are some cases where the opposite occurs. That is to say, the brittle behavior of infills type t3 is amplified for some seismic records.

FIGURE 5

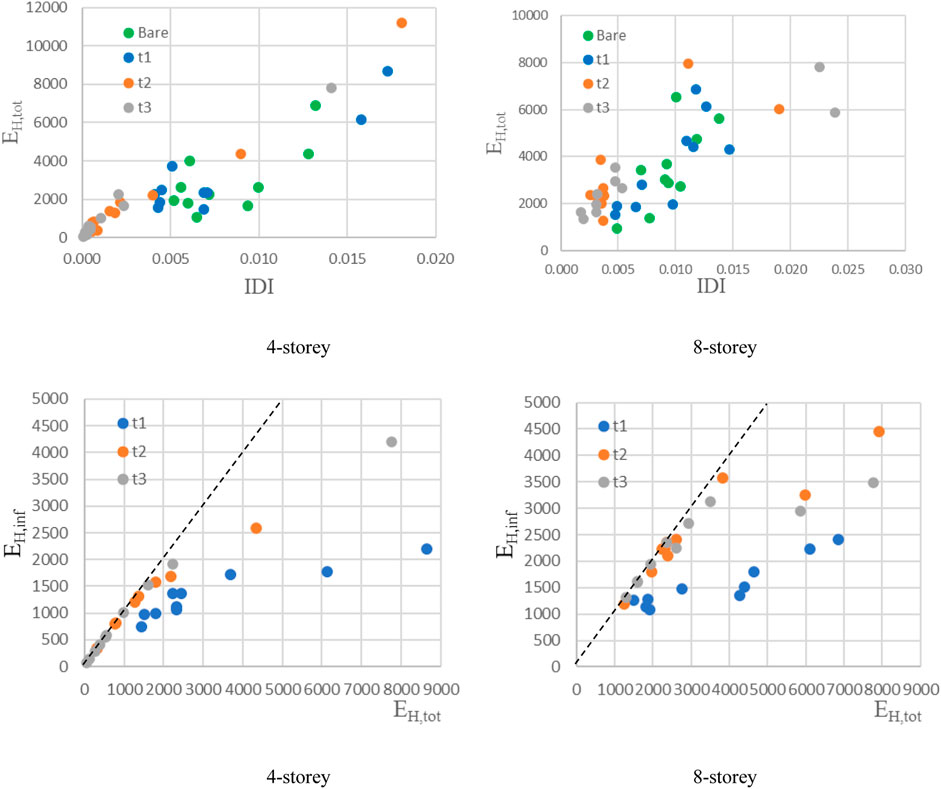
FIGURE 5. E_H,tot (cm²/s²) vs. IDI (first row). E_H,tot (cm²/s²) vs. E_H,inf (cm²/s²) (second row). Results are obtained for C_y = 0.15.

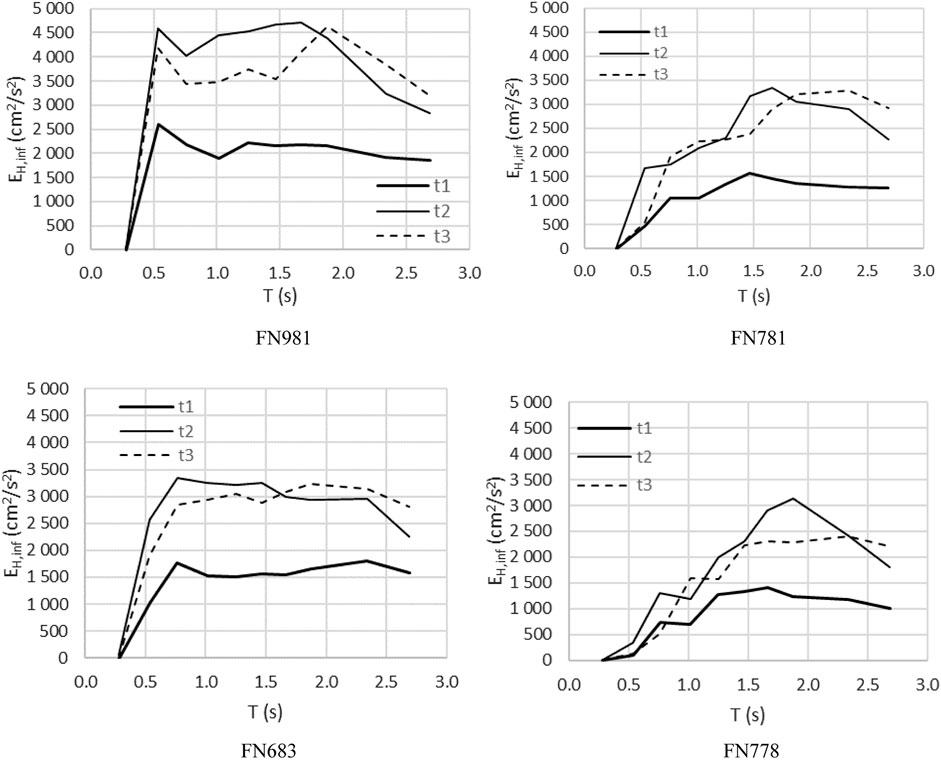
In the second series of plots into Figure 5, the contribution to the dissipation demand attributable to the infills is compared with the total dissipation demand. There are some overlaps between infills t2 and t3, while the energy dissipated by infill type t1 is usually less than that of the other two typologies. The reduced dissipation capacity of the infills type t1 can be better appreciated in Figure 6 where the energy spectra obtained from the whole dataset of frames and four records are shown.

FIGURE 6

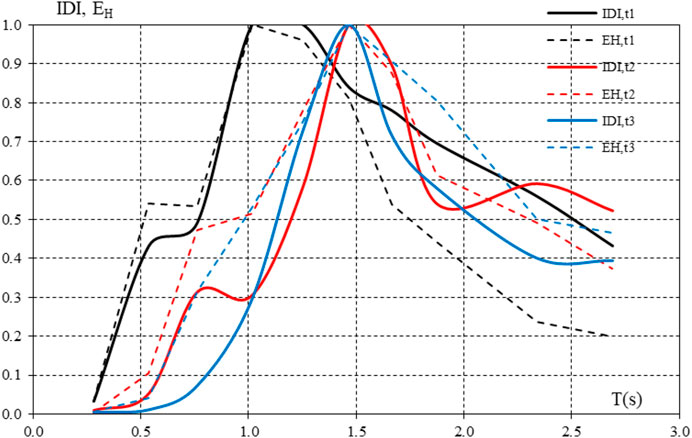
FIGURE 6. Normalized spectra of the total dissipated energy E_H and the maximum interstorey drift IDI (seismic record FN982, C_y = 0.15)

A satisfactory correlation between the maximum interstorey drift IDI and the total energy dissipated by the frames EH, tot can be recognized in Figure 5, even in presence of infills. Similar results have been found for all values of Cy, with an improvement as the seismic capacity of the frames increases. Mollaioli et al. (2011) highlighted that the shapes of the interstorey drift index IDI spectra are more influenced by the energy demand than acceleration and displacement spectra. Through a comparison of energy and drift spectra, it is evident that highest values are achieved at similar period values. On the contrary, such an agreement does not occur for acceleration and displacement spectra. This is why a strong local deformation demand can occur when a strong energy demand is imposed, while in general it does not necessarily produce large top displacement.

This trend is confirmed for the infilled frames as shown in Figure 6, where the spectra of the total dissipated energy and the peak interstorey drift are presented after proper normalization to their maximum absolute value. Even though these spectra are obtained for a single seismic event only (FN982 record in Table 2), energy and drift peaks and valleys are close each other in the other earthquakes. Another general result is the shift of the IDI values towards shortest periods for the infills type t1. This means that the maximum interstorey drift is obtained for the lowest frames with infill type t1.

TABLE 2

TABLE 2. Set of strong motion records for the preliminary analyses.

As far as infill walls t2 and t3 are concerned, the dissipated energy is fairly similar and several cases can be highlighted in which infill wall type t2 dissipates more energy than infill wall type t3. However, it can be clearly observed that the energy dissipated by infill panels t1 is always much lower than that found in the other two infill types. For the four cases reported in Figure 7, it is halved or even less. In general, this implies that, for the same energy input, there is a larger demand for energy dissipation in the reinforced concrete frames for the infill type t1. This circumstance can represent a critical issue for low values of Cy.

FIGURE 7

FIGURE 7. Energy dissipated by infills, E_H,inf (cm²/s²). C_y = 0.15.

Anyway, in infilled frames, the energy dissipation always grows up as the number of stories increases, whereas the energy dissipated in the bare frames tends to decrease as the number of stories increases until the elastic behavior is attained. Moreover, the response of the bare frames does not build in the inelastic range appreciably as shown in Figure 7.

Therefore, it seems that a correlation exists between IDI and dissipated energy, and that the frames with infill type t1 are weaker as compared to those with infill types t2 and t3. Hence, it is appropriate to evaluate the correlation between (total or input) energy and drift considering the entire record database. Once such correlation is thoroughly investigated, some relationships that allow the estimation of the drift as function of the energy can be obtained.

3.2 Correlation analysis

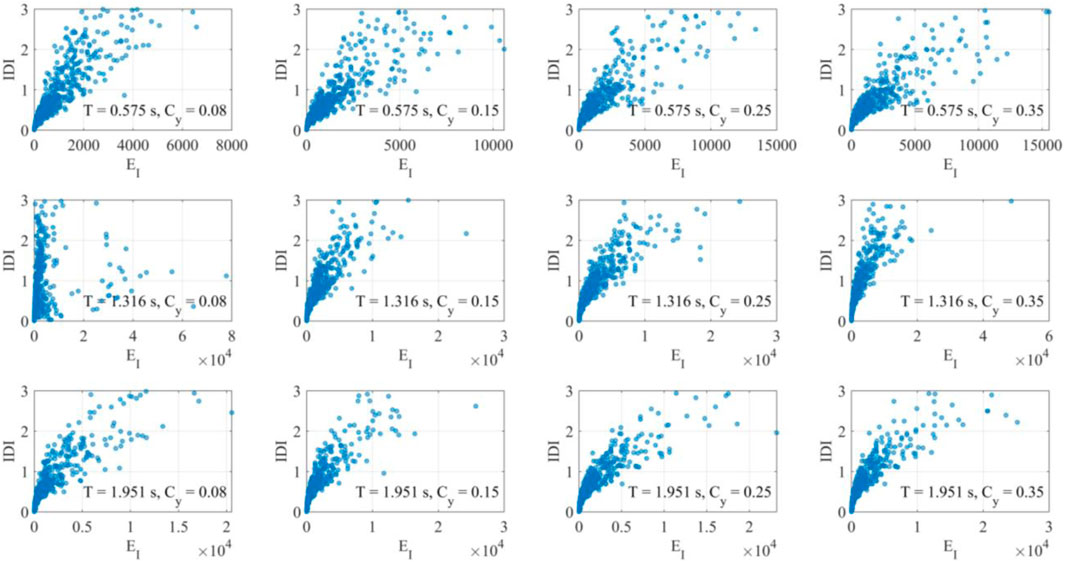
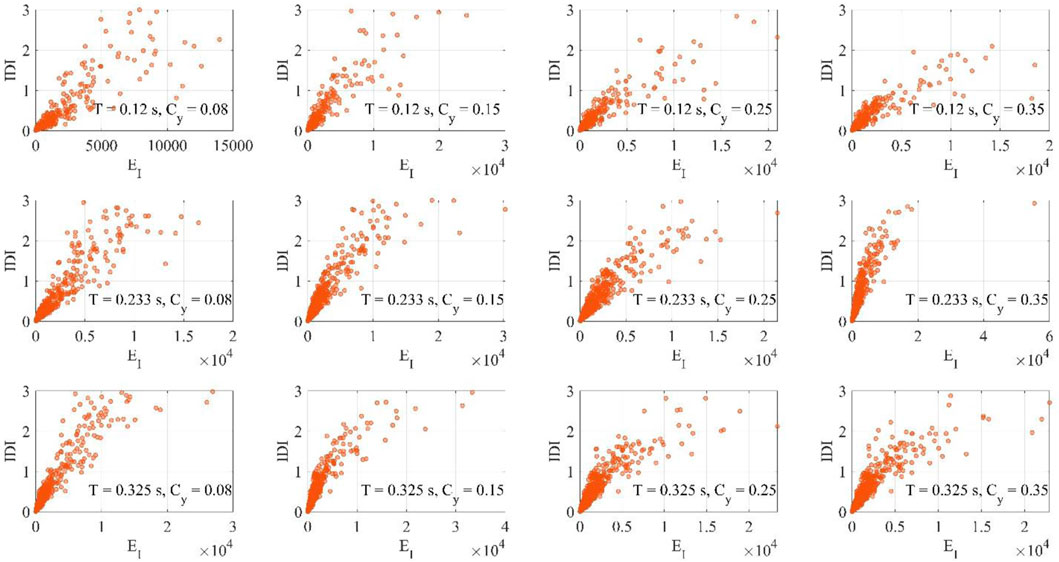
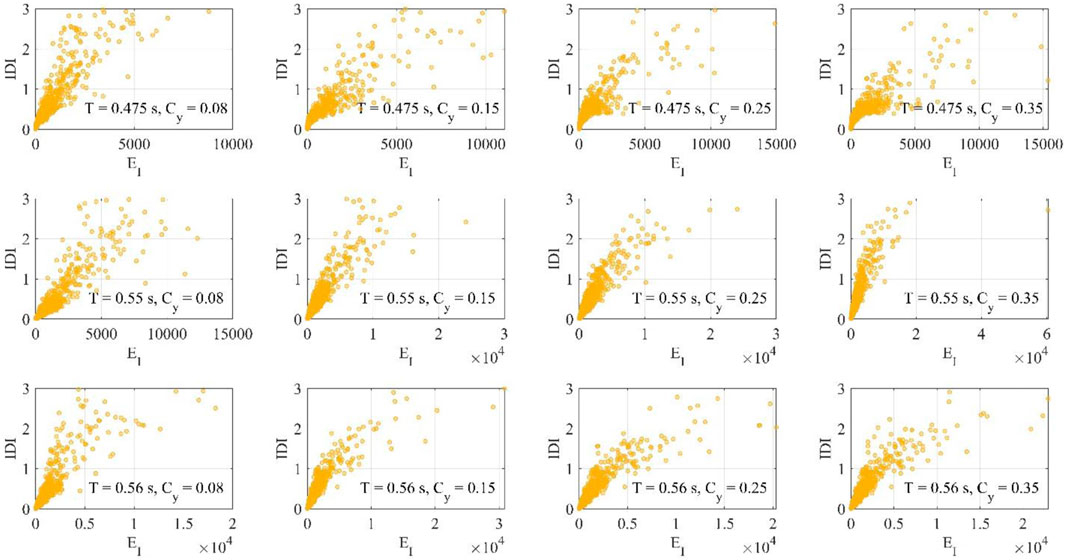
Figures 8–13 shows the IDI values as function of E_H for bare frames or E_H,tot for infilled/piloties frames and E_I, for different values of T and C_y. It is pointed out the data employed for the present analysis are restricted to IDI values equal to or less than 3%.

FIGURE 8

FIGURE 8. Hysteretic energy E_H and maximum inter-story drift ratio IDI for bare frames.

FIGURE 9

FIGURE 9. Input energy E_I and maximum inter-story drift ratio IDI for bare frames.

FIGURE 10

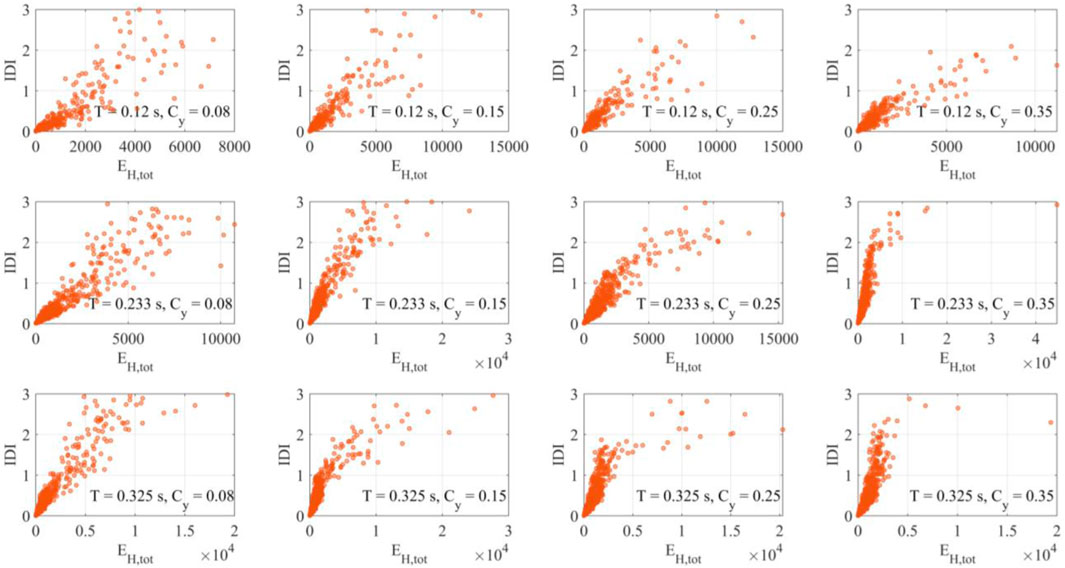
FIGURE 10. Total hysteretic energy E_H,tot and maximum inter-story drift ratio IDI for infilled frames.

FIGURE 11

FIGURE 11. Input energy E_I and maximum inter-story drift ratio IDI for infilled frames.

FIGURE 12

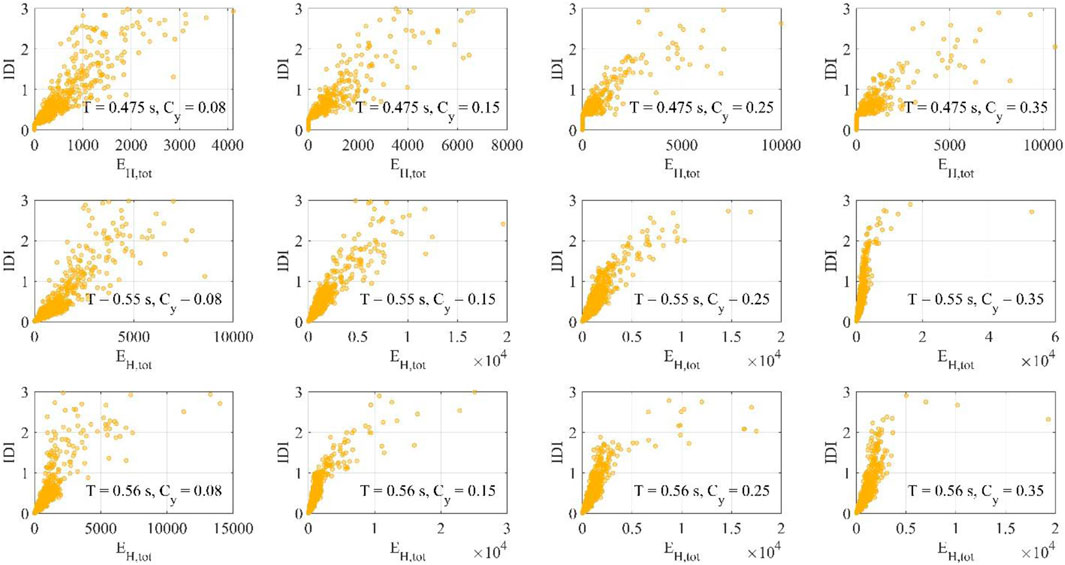
FIGURE 12. Total hysteretic energy E_H,tot and maximum inter-story drift ratio IDI for pilotis frames.

FIGURE 13

FIGURE 13. Input energy E_I and maximum inter-story drift ratio IDI for pilotis frames.

With the possible exceptions of a few cases corresponding to C_y = 0.08 and a large number of stories, the correlation between the energy-based intensity measures and the displacement-based seismic demand can be considered satisfactory for bare frames (Figures 8, 9), with small differences between E_H and E_I. It can also be noted for the tallest frames and the highest C_y values that, in some cases, the dissipated energy is zero even if the drift is different from zero. This is due to the fact that the response is almost elastic. This does not occur when the input energy is considered, since it is always different from zero.

The behavior tends to regularize when the infills are considered: no particular cases are highlighted thanks to the contribution of the infills in dissipating the energy (Figures 10, 11). In particular, for the tallest frames, in many cases the frame behaves elastically and a reduction of the drift demand occurs thanks to the dissipative capacity of the infills.

In the case of pilot frames (Figures 12, 13) there is an increment of the energy dispersion, especially for low frames, due to the concentration of the seismic demand at the first floor, but the trend is very similar to that observed in the previous cases.

The results obtained from the nonlinear time-history analyses have been organized in such way to derive compact symbolic formulations able to predict the value of IDI considering T, C_y, E_I, E_H (for infilled frame) and E_H,tot (for infilled frame) as candidate explanatory variables. To this end, a machine learning technique is employed, namely, genetic programming (Koza, 1994; Quaranta et al., 2020). This is an extension to computer programs of Darwin’s theory of evolution in use for genetic algorithms. Accordingly, starting from an initial random collection of candidate solutions, these computer programs are manipulated through an iterative procedure by means of a sequence of genetic operators until a stopping criterion is fulfilled. The approach proposed by Ekart and Nemeth (2001) has been implemented to cope with bloat phenomenon. This basically rests on a selection scheme based on tournament selection and Pareto’s nondomination concept. For the present study, the initial collection of candidate solutions is obtained according to the ramped half-and-half method (the population size is 1,500). The following genetic operators are applied throughout the iterative procedure: tournament selection (with a tournament size equal to 10), subtree crossover (with crossover rate equal to 0.90, where functions and leaves are selected as crossover point 90% and 10% of the times, respectively), point mutation (with mutation rate equal to 0.15), and reproduction (by duplicating 5 candidate solutions within the current population to the next without changes). The genetic programming is performed in order find the optimal predictive symbolic formulations by combining the candidate explanatory variables through standard arithmetic, logarithmic, exponential and power operators. The full set of data is partitioned into training and validation database: the training database includes 75% of the data (about 14,000 data for each type of frame) and it is employed to develop the final symbolic expressions, whereas the validation database includes the remaining 15% of the data (almost 3,000 data for each type of frame) and serves at testing the accuracy of the obtained symbolic expressions against new data.

Best trade-off between accuracy and complexity (the condition $0\%\le IDI\le 3\%$ applies to all formula):

$IDI=-15.20+3.20\log \left(113.65+1.23\sqrt[3]{C_y}+1.01{E_H}^{\frac{1}{11}}+1.27\sqrt[3]{E_H}+0.74\sqrt{E_I}\right.)\left(\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{b}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{s}\right)$

$IDI=-5.47+14.22\log \left(\log \left(\log \left(0.053\left(1462.23+0.27E_I\right)\right)\right)\right)\left(\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{f}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{s}\right)$

$IDI=-0.39+0.013\sqrt{\frac{0.18E_I}{C_y}+\frac{1.77\left(67.95+0.22E_I\right)}{T^3}}\left(\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{p}\mathrm{i}\mathrm{l}\mathrm{o}\mathrm{t}\mathrm{i}\mathrm{e}\mathrm{s}\mathrm{f}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{s}\right)$

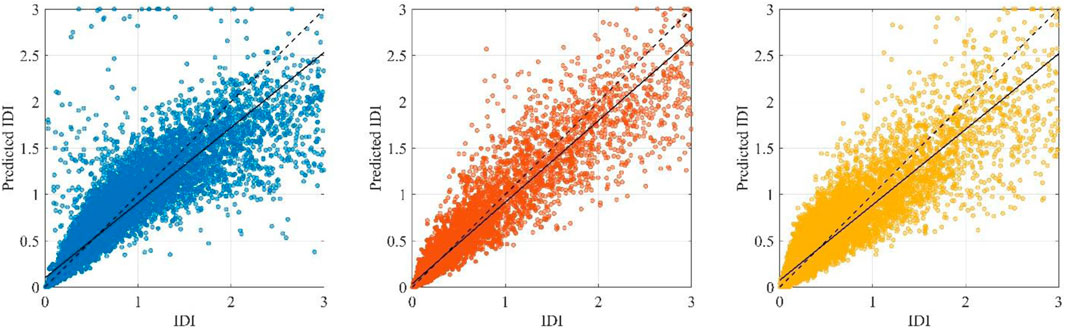
Table 3 show that the value of the coefficient R² corresponding to the obtained predictive formulations for IDI is close to 80% for bare and piloties frames whereas it is slightly larger for infilled frame, where R² is close to 85%. The robustness of the predictive formulations is confirmed by the fact that the values of R² for the training and the validation database are almost equal to each other. Overall, the accuracy of the obtained formulations is satisfactory, as further confirmed in Figure 14. The largest dispersion is observed in case of bare frame while the predictions for the infilled frames exhibit the minimum scattering. It can be noted that final IDI formulations mainly depend on E_I. In case of bare frame, IDI also depends on E_H and C_y whereas it also depends on T for piloties frame. Such relationships are consistent with general trends emerging from the data, as it can be inferred from the sensitivity analysis presented in Figure 15.

TABLE 3

TABLE 3. R² values for bare, infilled and piloties frames.

FIGURE 14

FIGURE 14. Comparison between actual and predicted maximum inter-story drift ratio IDI.

FIGURE 15

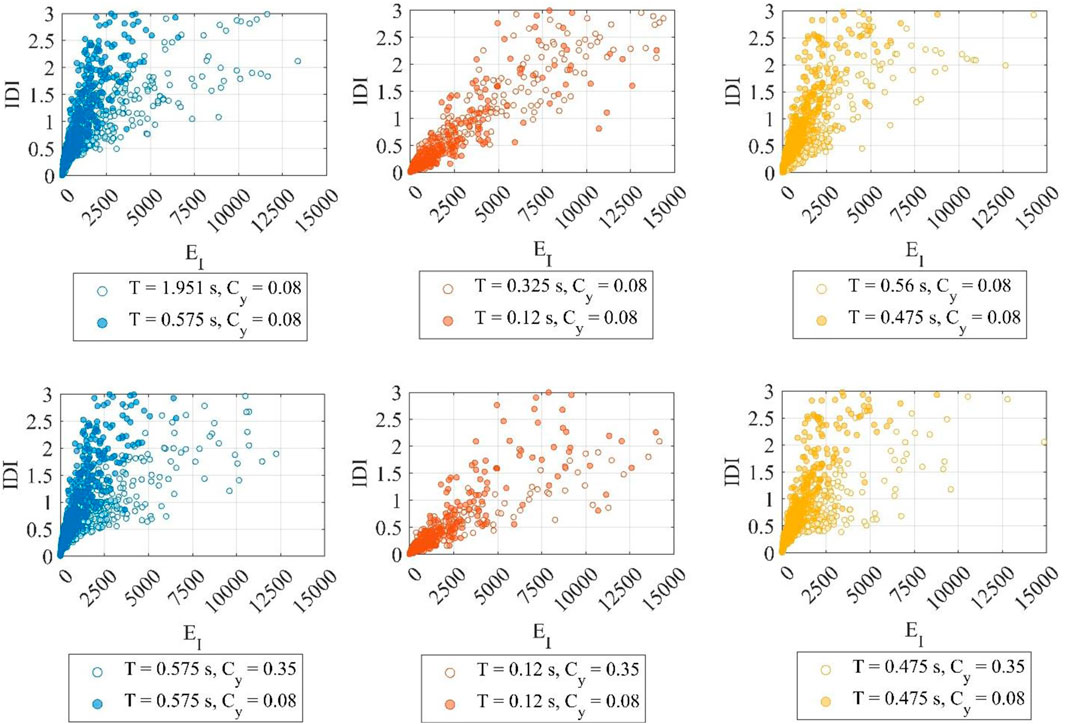
FIGURE 15. Sensitivity analysis of the maximum inter-story drift ratio IDI with respect to the input energy, E_I. The bare frame (left column) exhibits larger sensitivity to C_y than T. The infilled frame (center column) is almost insensitive with respect to both T and C_y. The piloties frame (right column) shows similar sensitivity with respect to both T and C_y.

4 Conclusion

Extended nonlinear analyses have been performed for the characterization of the relationship between energy and displacement demands in infilled reinforced concrete frames representative of a large portion of the Southern Europe building stock. The frames have been modelled by means of stick-like models, whose lateral stiffness, inertial and strength characteristics approximate those of actual frame structures. They are coupled with equivalent struts that carry load only in compression, so as to take into account the contribution of the masonry infills. Nonlinear analyses have been performed for multi-degree-of-freedom systems subjected to a large number of selected seismic ground motions in the attempt to investigate the correlation between seismic input features, dissipated energy and maximum interstorey drift.

Firstly, it was found a significant correlation between input energy and drift demand. This seems more evident when the dissipated energy is considered. Particularly, the presence of a regular distribution of infills along the height of the frames, besides reducing the drift demand, also improves the correlation. In case of pilotis frames, it was found a concentration of drift demand towards the first story, which depends on the capacity of the frame expressed through the C_y coefficient and reduces the goodness of the correlation.

Moreover, suitable symbolic formulations able to predict the seismic performance of the structures in terms of IDI have been obtained by means of a machine learning technique. The robustness of the predictive formulations is confirmed by the fact that the coefficient R² corresponding to the obtained predictive formulations for IDI is close to 80% for bare and piloties frames and to 85% for infilled frame. Finally, it is important to remark that the proposed symbolic formulations for the prediction of the maximum inter-story drift ratio are valid within the considered ranges of parameters adopted in the present study for the structural systems and the seismic ground motions.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

FM: conceptualization, methodology, review and editing visualization. GA: conceptualization, dynamic analyses, and writing. GQ: correlation analysis, review and editing. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Sapienza University of Rome Grant (No. RG11916B4C241B32).

Acknowledgments

The authors acknowledge the support of the Italian Ministry of University and Research (MUR).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Asteris, P. G., Antoniou, S. T., Sophianopoulos, D. S., and Chrysostomou, C. Z. (2011). Mathematical macromodeling of infilled frames: state of the art. J. Struct. Eng. 137 (12), 1508–1517. doi:10.1061/(ASCE)ST.1943-541X.0000384

CrossRef Full Text | Google Scholar

Bazzurro, P., De Sortis, A., and Mollaioli, F. (2005). “Seismic risk of Italian reinforced concrete frame buildings,” in Proceeedings of the ICOSSAR 2005, Rotterdam, January 2005 (Millpress).

Google Scholar

Bazzurro, P., Mollaioli, F., De Sortis, A., and Bruno, S. (2006). “Effects of masonry walls on the seismic risk of reinforced concrete frame buildings,” in Proceedings of the 8th U.S. National Conference on Earthquake Engineering, San Francisco, April 2006.

Google Scholar

Benavent-Climent, A. (2007). An energy-based damagemodel for seismic response of steel structures. Earthq. Eng. Struct. Dynam. 36 (8), 1049–1064. doi:10.1002/eqe.671

CrossRef Full Text | Google Scholar

Benavent-Climent, A., Donaire-Ávila, J., and Mollaioli, F. (2021). “Key points and pending issues in the energy-based seismic design approach,” in InInternational workshop on energy-based seismic engineering (Berlin, Germany: Springer), 151–168.

CrossRef Full Text | Google Scholar

Benavent-Climent, A., Escobedo, A., Donaire-Avila, J., ·Oliver-Saiz, E., and ·Ramírez-Márquez, A. L. (2014). Assessment of expected damage on buildings subjected to Lorca earthquake through an energy-based seismic index method and nonlinear dynamic response analyses. Bull. Earthq. Eng. 12, 2049–2073. doi:10.1007/s10518-013-9513-9

CrossRef Full Text | Google Scholar

Bertero, V. V., and Brokken, S. T. (1983). Infills in seismic resistant building. J. Struct. Eng. ASCE 109 (6), 1337–1361. doi:10.1061/(asce)0733-9445(1983)109:6(1337)

CrossRef Full Text | Google Scholar

Blasi, G., De Luca, F., Perrone, D., Greco, A., and Aiello, M. A. (2021). Mid 1.1: database for characterization of the lateral behavior of infilled frames. J. Struct. Eng. 147 (10), 04721007. doi:10.1061/(ASCE)ST.1943-541X.0003117

CrossRef Full Text | Google Scholar

Bruno, S., Decanini, L., and Mollaioli, F. (2000). “Seismic Performance of pre-code reinforced concrete buildings,” in PROCEEDINGS OF THE TWELFTH WORLD CONFERENCE ON EARTHQUAKE ENGINEERING, Auckland, New Zealand, January 2000.

Google Scholar

Cavaleri, L., and Di Trapani, F. (2014). Cyclic response of masonry infilled RC frames: experimental results and simplified modeling. Soil Dyn. Earthq. Eng. 65, 224–242. doi:10.1016/j.soildyn.2014.06.016

CrossRef Full Text | Google Scholar

Çelebi, M., Bazzurro, P., Chiaraluce, L., Clemente, P., Decanini, L., DeSortis, A., et al. (2010). Recorded motions of the 6 april 2009 Mw 6.3 L’aquila, Italy, earthquake and implications for building structural damage: overview. Earthq. Spectra 26 (3), 651–684. doi:10.1193/1.3450317

CrossRef Full Text | Google Scholar

Cheng, Y., Mollaioli, F., and Donaire-Ávila, J. (2021). Characterization of dissipated energy demand. Soil Dyn. Earthq. Eng. 147, 106725. doi:10.1016/j.soildyn.2021.106725

CrossRef Full Text | Google Scholar

Crisafulli, F. J., and Carr, A. J. (2007). Proposed macro-model for the analysis of infilled frame structures. Bull. N. Z. Soc. Earthq. Eng. 40 (2), 69–77. doi:10.5459/bnzsee.40.2.69-77

CrossRef Full Text | Google Scholar

De Luca, F., Verderame, G. M., Gómez-Martínez, F., and Pérez-García, A. (2014). The structural role played by masonry infills on RC building performances after the 2011 Lorca, Spain, earthquake. Bull. Earthq. Eng. 12, 1999–2026. doi:10.1007/s10518-013-9500-1

CrossRef Full Text | Google Scholar

De Risi, M. T., Del Gaudio, C., Ricci, P., and Verderame, G. M. (2018). In-plane behaviour and damage assessment of masonry infills with hollow clay bricks in RC frames. Eng. Struct. 168, 257–275. doi:10.1016/j.engstruct.2018.04.065

CrossRef Full Text | Google Scholar

De Risi, M. T., Di Domenico, M., Manfredi, V., Terrenzi, M., Camata, G., Mollaioli, F., et al. (2022). Modelling and seismic response analysis of Italian pre-code and low-code reinforced concrete buildings. Part I: bare frames. J. Earthq. Eng. 27, 1482–1513. doi:10.1080/13632469.2022.2074919

CrossRef Full Text | Google Scholar

De Sortis, A., Bazzurro, P., and MollaioliBruno, F. S. (2007). “Influenza delle tamponature sul rischio sismico degli edifici in calcestruzzo armato,” in Proceedings of the 12th Conference ANIDIS Seismic Engineering in Italy, Pisa, Italy, Pisa, June 2007, 10–14.

Google Scholar

Decanini, L. D., and Fantin, G. E. (1986). “Modelos simplificados de la mamposteria incluida en porticos,” in Caracteristicas de rigidez y resistencia lateral en estado limite (Buenos Aires, Argentina: Jornadas Argentinas de Ingenieria Estructural), 817–836.

Google Scholar

Decanini, L., De Sortis, A., Goretti, A., Liberatore, L., Mollaioli, F., and Bazzurro, P. (2004b). Performance of reinforced concrete buildings during the 2002 Molise, Italy, Earthquake. Earthq. Spectra 20 (S1), S221–S255. doi:10.1193/1.1765107

CrossRef Full Text | Google Scholar

Decanini, L., De Sortis, A., Liberatore, L., and Mollaioli, F. (2005). Estimation of near-source ground motions and seismic behaviour of RC framed structures damaged by the 1999 Athens earthquake. J. Earthq. Eng. 9 (5), 609–635. doi:10.1080/13632460509350559

CrossRef Full Text | Google Scholar

Decanini, L., Liberatore, L., and Mollaioli, F. (2012). Damage potential of the 2009 L’aquila, Italy, earthquake. Earthq. Tsunami 6 (3), 1250032–32. doi:10.1142/S1793431112500327

CrossRef Full Text | Google Scholar

Decanini, L., Liberatore, L., and Mollaioli, F. (2014). Strength and stiffness reduction factors for infilled frames with openings. Earthq. Eng. Eng. Vib. 13 (3), 437–454. doi:10.1007/s11803-014-0254-9

CrossRef Full Text | Google Scholar

Decanini, L., and Mollaioli, F. (2001). An energy-based methodology for the assessment of seismic demand. Soil Dyn. Earthq. Eng. 21 (2), 113–137. doi:10.1016/S0267-7261(00)00102-0

CrossRef Full Text | Google Scholar

Decanini, L., and Mollaioli, F. (1998). Formulation of elastic earthquake input energy spectra. Earthq. Eng. Struct. Dyn. 27, 1503–1522. doi:10.1002/(SICI)1096-9845(199812)27:12<1503::AID-EQE797>3.0.CO;2-A

CrossRef Full Text | Google Scholar

Decanini, L., Mollaioli, F., Mura, A., and Saragoni, R. (2004a). “Seismic performance of masonry infilled R/C frames,” in Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, B.C., Canada, August 2004.

Google Scholar

Demir, A., and Mete Cengiz, M. (2021). Effect of infill wall properties on seismic response of RC structures. Comput. Concr. 27 (6), 513–521. doi:10.12989/cac.2021.27.6.513

CrossRef Full Text | Google Scholar

Di Domenico, M., De Risi, M. T., Manfredi, V., Terrenzi, M., Camata, G., Mollaioli, F., et al. (2022). Modelling and seismic response analysis of Italian pre-code and low-code reinforced concrete buildings. Part II: infilled frames. J. Earthq. Eng. 27, 1534–1564. doi:10.1080/13632469.2022.2086189

CrossRef Full Text | Google Scholar

Di Trapani, F., Bolis, V., Basonec, F., and Preti, M. (2020). Seismic reliability and loss assessment of RC frame structures with traditional and innovative masonry infills. Eng. Struct. 208, 110306. doi:10.1016/j.engstruct.2020.110306

CrossRef Full Text | Google Scholar

Di Trapani, F., Macaluso, G., Cavaleri, L., and Papia, M. (2015). Masonry infills and RC frames interaction: literature overview and state of the art of macromodeling approach. Eur. J. Environ. Civ. Eng. 19 (9), 1059–1095. doi:10.1080/19648189.2014.996671

CrossRef Full Text | Google Scholar

Di Trapani, F., Shing, P. B., and Cavaleri, L. (2017). Macroelement model for in-plane and out-of-plane responses of masonry infills in frame structures. J. Struct. Eng. 144 (2), 1–13. 04017198. doi:10.1061/(ASCE)ST.1943-541X.0001926

CrossRef Full Text | Google Scholar

Dias-Oliveira, J., Rodrigues, H., Asteris, P. G., and Varum, H. (2022). On the seismic behavior of masonry infilled frame structures. Buildings 12, 1146. doi:10.3390/buildings12081146

CrossRef Full Text | Google Scholar

Dolšek, M., and Fajfar, P. (2008). The effect of masonry infills on the seismic response of a four-storey reinforced concrete frame — A deterministic assessment. Eng. Struct. 30 (7), 1991–2001. doi:10.1016/j.engstruct.2008.01.001

CrossRef Full Text | Google Scholar

Ekart, A., and Nemeth, S. Z. (2001). Selection based on the pareto nondomination criterion for controlling code growth in genetic programming. Genet. Program. Evolvable Mach. 2 (1), 61–73. doi:10.1023/a:1010070616149

CrossRef Full Text | Google Scholar

Fardis, M. N., and Panagiotakos, T. B. (1997). Seismic design and response of bare and infilled reinforced concrete buildings. Part II: infilled structures. J. Earthq. Eng. 1 (3), 475–503. doi:10.1080/13632469708962375

CrossRef Full Text | Google Scholar

Furtado, A., and De Risi, M. T. (2020). Recent findings and open issues concerning the seismic behaviour of masonry infill walls in RC buildings. Adv. Civ. Eng. 2020–20. 9261716. doi:10.1155/2020/9261716

CrossRef Full Text | Google Scholar

Furtado, A., Rodrigues, H., Arêde, A., and Varum, H. (2021). A review of the performance of infilled RC structures in recent earthquakes. Appl. Sci. 11, 5889. doi:10.3390/app11135889

CrossRef Full Text | Google Scholar

Gaetani d’Aragona, M., Polese, M., and Prota, A. (2021). Effect of masonry infill constitutive law on the global response of infilled RC buildings. Buildings 11, 57. doi:10.3390/buildings11020057

CrossRef Full Text | Google Scholar

Gentile, R., and Galasso, C. (2020). Hysteretic energy-based state-dependent fragility for ground-motion sequences. Earthq. Eng. Struct. Dyn. 50 (4), 1187–1203. doi:10.1002/eqe.3387

CrossRef Full Text | Google Scholar

Gentile, R., Pampanin, S., Raffaele, D., and Uva, G. (2019). Non-linear analysis of RC masonry-infilled frames using the SLaMA method: part 1—mechanical interpretation of the infill/frame interaction and formulation of the procedure. Bull. Earthq. Eng. 17, 3283–3304. doi:10.1007/s10518-019-00580-w

CrossRef Full Text | Google Scholar

Haldar, P., Singh, Y., and Paul, D. K. (2013). Identification of seismic failure modes of URM infilled RC frame buildings. Eng. Fail. Anal. 33, 97–118. doi:10.1016/j.engfailanal.2013.04.017

CrossRef Full Text | Google Scholar

Kakaletsis, D. J., and Karayannis, C. G. (2007). Experimental investigation of infilled R/C frames with eccentric openings. Struct. Eng. Mech. 26 (3), 231–250. doi:10.12989/sem.2007.26.3.231

CrossRef Full Text | Google Scholar

Koza, J. R. (1994). Genetic programming as a means for programming computers by natural selection. Statistics Comput. 4 (2), 87–112. doi:10.1007/bf00175355

CrossRef Full Text | Google Scholar

Liberatore, L., Noto, F., Mollaioli, F., and Franchin, P. (2018). In-plane response of masonry infill walls: comprehensive experimentally-based equivalent strut model for deterministic and probabilistic analysis. Eng. Struct. 167, 533–548. doi:10.1016/j.engstruct.2018.04.057

CrossRef Full Text | Google Scholar

Masi, A., Chiauzzi, L., Santarsiero, G., Manfredi, V., Biondi, S., Spacone, E., et al. (2019). Seismic response of RC buildings during the Mw 6.0 August 24, 2016 Central Italy earthquake: the Amatrice case study. Bull. Earthq. Eng. 17, 5631–5654. doi:10.1007/s10518-017-0277-5

CrossRef Full Text | Google Scholar

Mollaioli, F., Mura, A., and Decanini, L. (2007). Assessment of the deformation demand in multi-storey frames. J. Seismol. Earthq. Eng. 8 (4), 203–219.

Google Scholar

Mollaioli, F., AlShawa, O., Liberatore, L., Liberatore, D., and Sorrentino, L. (2019). Seismic demand of the 2016-2017 Central Italy earthquakes. Bull. Earthq. Eng. 17, 5399–5427. doi:10.1007/s10518-018-0449-y

CrossRef Full Text | Google Scholar

Mollaioli, F., Bruno, S., Decanini, L., and Saragoni, R. (2011). Correlations between energy and displacement demands for performance-based seismic engineering. Pure Appl. Geophys. 168 (1-2), 237–259. doi:10.1007/s00024-010-0118-9

CrossRef Full Text | Google Scholar

Mollaioli, F., Donaire-Avila, J., Lucchini, A., and Benavent-Climent, A. (2019). “On the importance of energy-based parameters,” in Procceidgs of the COMPDYN 2019 7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete, Greece, June 2019.

CrossRef Full Text | Google Scholar

Morandi, P., Hak, S., and Magenes, G. (2018). Performance-based interpretation of in-plane cyclic tests on RC frames with strong masonry infills. Eng. Struct. 156, 503–521. doi:10.1016/j.engstruct.2017.11.058

CrossRef Full Text | Google Scholar

Ozkaynak, H., Yuksel, E., Yalcin, C., Dindar, A. A., and Buyukozturk, O. (2014). Masonry infill walls in reinforced concrete frames as a source of structural damping: mASONRY infill walls in RC frames as A source of structural damping. Engng Struct. Dyn. 43, 949–968. doi:10.1002/eqe.2380

CrossRef Full Text | Google Scholar

Quaranta, G., Lacarbonara, W., and Masri, S. F. (2020). A review on computational intelligence for identification of nonlinear dynamical systems. Nonlinear Dyn. 99 (2), 1709–1761. doi:10.1007/s11071-019-05430-7

CrossRef Full Text | Google Scholar

Ricci, P., De Luca, F., and Verderame, G. M. (2011). 6th april 2009 L’aquila earthquake, Italy: reinforced concrete building performance. Bull. Earthq. Eng. 9 (1), 285–305. doi:10.1007/s10518-010-9204-8

CrossRef Full Text | Google Scholar

Ricci, P., De Risi, M. T., Verderame, G. M., and Manfredi, G. (2013). Influence of infill distribution and design typology on seismic performance of low- and mid-rise RC buildings. Bull. Earthq. Eng. 11, 1585–1616. doi:10.1007/s10518-013-9453-4

CrossRef Full Text | Google Scholar

Rodrigues, H., Varum, H., and Costa, A. (2010). Simplified macro-model for infill masonry panels. J. Earthq. Eng. 14 (3), 390–416. doi:10.1080/13632460903086044

CrossRef Full Text | Google Scholar

Sassun, K., Sullivan, T. J., Morandi, P., and Cardone, D. (2016). Characterising the in-plane seismic performance of infill masonry. Bull. N. Z. Soc. Earthq. Eng. 49 (1), 98–115. doi:10.5459/bnzsee.49.1.98-115

CrossRef Full Text | Google Scholar

Soleiman, F., and Mollaioli, F. (2021). Simulation of seismic collapse of simple structures with energy-based procedures. Soil Dyn. Earthq. Eng. 145, 106733. doi:10.1016/j.soildyn.2021.106733

CrossRef Full Text | Google Scholar